Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanisms of photoisomerization of the prenylated flavin mononucleotide cofactor: a theoretical study†
Pannipa Panajapo ,
Phorntep Promma and
Kritsana Sagarik
,
Phorntep Promma and
Kritsana Sagarik *
*
School of Chemistry, Institute of Science, Suranaree University of Technology, Nakhon Ratchasima, 30000, Thailand. E-mail: kritsana@sut.ac.th; Fax: +66-44-224635; Tel: +66-44-224635
First published on 24th June 2024
Abstract
The enzymatic decarboxylation of α,β-unsaturated acids using the ferulic acid decarboxylase (Fdc1) enzyme and prenylated flavin mononucleotide (prFMN) cofactor is a potential, environmentally friendly reaction for the biosynthesis of styrene and its derivatives. However, experiments showed that the enzyme activity of Fdc1 depends on the ring structure of prFMN, namely, the iminium and ketimine forms, and the loss of enzyme activity results from prFMNim → prFMNket photoisomerization. To obtain insight into this photochemical process and to improve the enzyme efficiency of Fdc1, two proposed photoisomerization mechanisms with different proton sources for the acid–base reaction were studied herein using theoretical methods. The potential energy surfaces calculated using the density functional theory method with the Becke, 3-parameter, and Lee–Yang–Parr hybrid functionals and DZP basis set (DFT/B3LYP/DZP) and TD-DFT/B3LYP/DZP methods confirmed that the light-dependent reaction occurs in the rate-determining proton transfer process and that the mechanism involving intermolecular proton transfer between prFMNim and Glu282 (external base) is energetically more favorable than that involving intramolecular proton transfer in prFMNim (internal base). The thermodynamic results obtained from the transition state theory method suggested that the exothermic relaxation energy in the photo-to-thermal process can promote the spontaneous formation of a high-energy-barrier transition state, and an effective enzymatic decarboxylation could be achieved by slowing down the formation of the undesirable thermodynamically favorable product (prFMNket). Because the rate constant for formation of the high-energy-barrier transition state varies exponentially over the temperature range of 273–298 K, and experimental results have shown that incubating Fdc1 on ice results in a complete loss of enzyme activity, it is recommended to perform the decarboxylation reaction at 285 K to strike a balance between minimizing enzyme stability loss at 273 K and mitigating the effects of UV irradiation. The computational strategy and fundamental insights obtained in this study could serve as guidelines for future theoretical and experimental investigations on the same and similar photochemical systems.
Introduction
The enzymatic decarboxylation of α,β-unsaturated acids using the ferulic acid decarboxylase (Fdc1) enzyme is envisioned as a potential environmentally friendly process for synthesizing styrene and its derivatives from natural resources.1–3 This enzymatic reaction can be effectively accomplished through 1,3-dipolar cycloaddition between substrates and enzyme cofactors,4 among which the prenylated flavin mononucleotide (prFMN) has been proven to be effective for the biosynthesis of styrene.1,3–5,7 Payne et al.4 proposed a mechanism for the enzymatic decarboxylation of α,β-unsaturated acids using the prFMN cofactor. The mechanism comprising four consecutive elementary reactions has been widely accepted and further studied using various theoretical and experimental methods. They are 1,3-dipolar cycloaddition, Grob-type decarboxylation, protonation, and retro 1,3-dipolarcycloaddition,4 among which the enzyme-catalyzed 1,3-dipolar cycloaddition of prFMN was suggested by a mechanism-based inhibitor experiment to play the most important role.2Ferguson et al.1 studied the enzyme efficiency of Fdc1 in styrene production from cinnamic acid by monitoring substrate consumption using spectroscopic and kinetic isotope effect methods, from which the cycloelimination was suggested to represent the rate-determining step. In ref. 1, two forms of prFMN with different ring structures were considered, namely, the iminium and ketimine forms, abbreviated prFMNim and prFMNket, respectively. The experimental results indicated that with prFMNim, the decarboxylation reaction proceeded via 1,3-dipolar cycloaddition, whereas the reaction with prFMNket occurred via Michael addition, and the enzyme activity was confirmed to be higher using prFMNim.
To study the effect of the prFMNim and prFMNket cofactors on the enzyme activity, the enzymatic decarboxylation using Fdc1 to generate styrene from cinnamic acid was further studied.5 High-resolution crystal structures and mass spectrometric and kinetic experiments revealed that the prFMNim → prFMNket isomerization could occur through an irreversible photochemical reaction, which is independent of the Glu277–Arg173–Glu282 residue network. This photoisomerization reaction was suggested to be the key factor for the loss of Fdc1 enzyme activity.
Two photoisomerization mechanisms with different proton sources for the acid–base reaction are proposed in Fig. 1.5 Type (1) mechanism involves four consecutive elementary reactions and begins with the intramolecular proton transfer in prFMNim, whereas for Type (2) mechanism, the intermolecular proton transfer between prFMNim and Glu282 represents the initial process with only three consecutive elementary reactions. Although the elementary reactions in Type (1) and (2) mechanisms were not known in detail, the light-dependent reaction was anticipated to be in the cyclization process, in which the exposure to UV light at λabs = 365 nm for 5 min led to a complete loss of enzyme activity and change in the absorption spectrum.5 This light-dependent reaction is similar to maleimide [5 + 2] photocycloaddition reported in ref. 6.
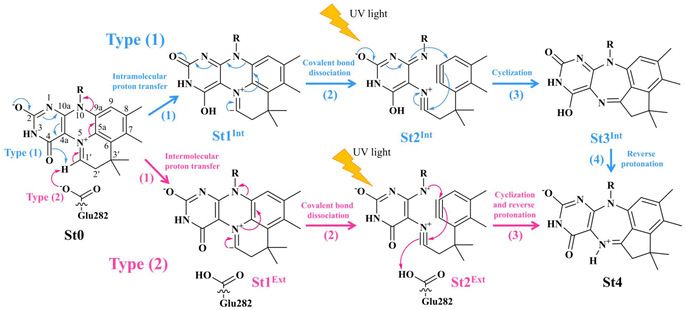 | ||
Fig. 1 The proposed prFMNim → prFMNket photoisomerization mechanisms obtained based on high-resolution crystal structures, mass spectrometric and kinetic experiments.5 All the symbols are explained in the text. Type (1) = mechanism involving intramolecular proton transfer in the 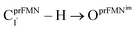 H-bond in prFMNim with four consecutive elementary reactions; Type (2) = mechanism involving intermolecular proton transfer in the H-bond in prFMNim with four consecutive elementary reactions; Type (2) = mechanism involving intermolecular proton transfer in the 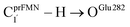 H-bond between prFMNim and Glu282 with three consecutive elementary reactions. Int = internal base; Ext = external base. H-bond between prFMNim and Glu282 with three consecutive elementary reactions. Int = internal base; Ext = external base. | ||
In our previous study,7 the elementary reactions proposed in ref. 4 were examined in low and high local dielectric environments (ε = 1 and 78) using the density functional theory (DFT) method with the Becke, 3-parameter, and Lee–Yang–Parr hybrid functionals and DZP basis set (DFT/B3LYP/DZP) and the transition state theory (TST) method. The active site models included the α-methylcinnamate (Cin) substrate, prFMNim cofactor, and all relevant Fdc1 residues. The results confirmed that the Fdc1 backbone does not play an important role in the decarboxylation reaction and that indirect cycloelimination in a low local dielectric environment is the rate-determining step.
Literature review showed that in the past decade (2014–2024), there were 44 published research articles reporting the design and/or improvement of enzymatic decarboxylation in organic syntheses, among which 30 studies focused on the decarboxylation of α,β-unsaturated acids, and 14 studies used the Fdc1 enzyme in the biosynthesis of styrene and its derivatives. Literature review also revealed that only 5 studies investigated the photoisomerization of the enzyme cofactors under UV exposure, among which only one experimental study5 examined in detail the loss of the enzyme activity through the prFMNim → prFMNket photoisomerization.
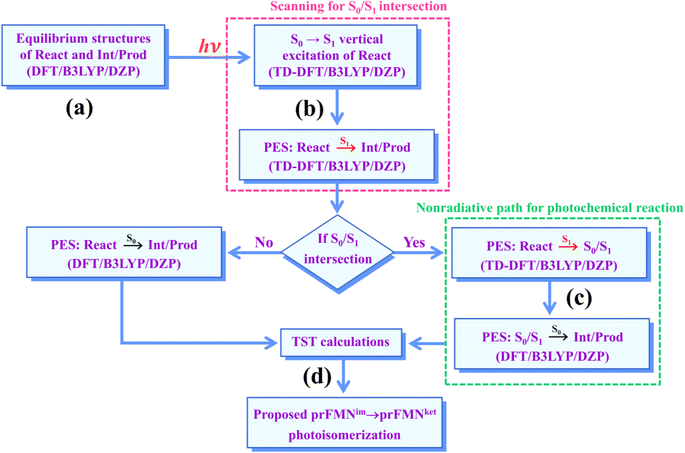
Because there is no theoretical study on this photoisomerization reaction, to bridge the gap between the experimental and theoretical knowledge, Type (1) and Type (2) mechanisms were studied in detail using the DFT/B3LYP/DZP, TD-DFT/B3LYP/DZP, and TST methods. To obtain insight into the prFMNim → prFMNket photoisomerization, this mechanistic study focused on the molecular processes (scenarios) in the lowest singlet excited (S1) state and on the kinetics and thermodynamics of nonradiative reaction pathways. The theoretical investigation began with calculations of the equilibrium structures and spectroscopic properties of the selected active site models, from which the potential energy surfaces (PESs) for prFMNim → prFMNket were optimized in the S1 and S0 states. The kinetic and thermodynamic properties of the PESs were computed using the TST method. To suppress/delay the prFMNim → prFMNket photoisomerization process, appropriate thermodynamic conditions were suggested in order to improve the enzymatic decarboxylation of α,β-unsaturated acids using Fdc1.
Computational methods
Active site models
Because the analysis of the equilibrium structures and PESs in our previous study7 showed that the Fdc1 backbone (Fig. 2a) does not play an important role in the decarboxylation reaction, the active site was modeled in this work by substituting the carbon atoms of the Fdc1 backbone that connect the residues with CH3 groups (Fig. 2b). For example, CGln190R is the carbon atom of the CH3 group that substitutes the carbon atom of the Fdc1 backbone that connects the Gln190 residue. Although the experiment suggested that prFMNim → prFMNket photoisomerization is independent of the Glu277–Arg173–Glu282 residue network,5 to obtain a realistic picture, the active site models used in this study consisted of Glu277, Arg173, Glu282, and Gln190 and prFMNim (Fig. 2b), regarded as the “active site cluster.”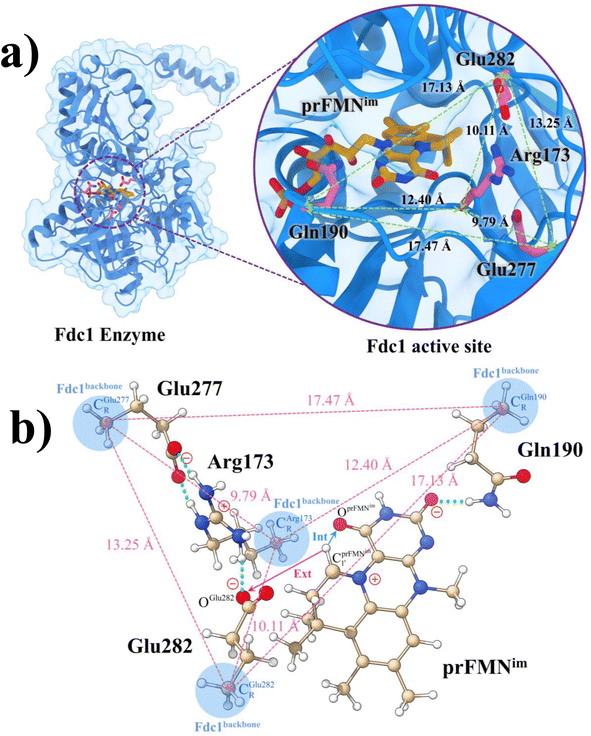 | ||
Fig. 2 (a) The structures of the active site, precursor, cofactor and residues involved in the enzymatic decarboxylation of α,β-unsaturated acid using Fdc1 enzyme and prFMNim cofactor obtained from DFT/B3LYP/DZP geometry optimizations.7 (b) An example of the model active site cluster (St0) used in the study of the prFMNim → prFMNket photoisomerization. Dash lines show the residue network distances. Int = intramolecular proton transfer in the 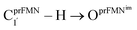 H-bond of prFMNim; Ext = intermolecular proton transfer in the H-bond of prFMNim; Ext = intermolecular proton transfer in the 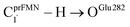 H-bond between prFMNim and Glu282; CArg173R, CGln190R, CGlu277R and CGlu282R = carbon atoms of the CH3 groups that substitute the carbon atoms of the Fdc1 backbone. H-bond between prFMNim and Glu282; CArg173R, CGln190R, CGlu277R and CGlu282R = carbon atoms of the CH3 groups that substitute the carbon atoms of the Fdc1 backbone. | ||
Equilibrium structures
The computational strategy and methods used in this study are shown in Fig. 3. The equilibrium structures of prFMNim, prFMNket, Glu277, Arg173, Glu282, and Gln190 (Table S1†) were optimized primarily in the S0 state (step (a) in Fig. 3) using the DFT/B3LYP/DZP method and the S0 → S1 energies (ΔEEx) were calculated using the TD-DFT/B3LYP/DZP method. These computational methods were chosen based on our good experience and benchmark calculations in several mechanistic studies. For example, for the photodissociation and formation of glycine,8,9 our benchmark calculations against the complete active space multiconfigurational second-order perturbation theory (CASPT2) method showed that the characteristic structures and energies on the S0 and S1 PESs (e.g., the transition structures and structures at the S0/S1 intersection) obtained from the DFT/B3LYP and TD-DFT/B3LYP methods were comparable with those obtained from the CASPT2 method, and the DFT/B3LYP/DZP and DFT/B3LYP/TZP methods yielded approximately the same equilibrium structures, relative interaction energies and energy barriers on the PESs for bifunctional proton transfers in the hydrogen-bonds (H-bonds) in poly(benzimidazole) (PBI) systems.10In this work, although our model active site clusters contain aromatic compounds, the dispersion correction was not included in the DFT and TD-DFT calculations, because the predominant intermolecular interactions are the H-bond and electrostatic interactions, and there is no π–π interaction directly involved on the hypothesized reaction pathways. Because the model active site clusters used in this work are large in view of quantum chemical methods, based on which the energy gradients on the S0 and S1 PESs had to be repeatedly calculated in the reaction pathway optimizations, to compromise between the numerical accuracy and computational resources, we decided to use the DFT/B3LYP/DZP and TD-DFT/B3LYP/DZP methods without the dispersion correction.
Remarks should be made on the application of the TD-DFT method with the B3LYP hybrid functional. The TD-DFT method has been a predominant method for excited state calculations on large molecules. The TD-DFT method circumvents explicit state calculations by focusing only on excitation energy and transition dipole moment.11 However, benchmark TD-DFT calculations revealed that pure density functionals tend to underestimate transition energies, whereas hybrid functionals such as B3LYP yield better results especially for low-lying singlet transition states.12
Practically, the presence of nearly degenerate HOMO and LUMO energies, particularly at the intersections of the S0 and S1 states, introduces spin instability, which is associated with holes positioned below the Fermi level. The theoretical results reported in ref. 13 demonstrated that for the photochemical ring opening in oxirane, this problem can be avoided by employing the Tamm–Dancoff approximation (TDA) in conjunction with the TD-DFT method. Because the TD-DFT/TDA method is a simplification of the full TD-DFT method, in which the full TD-DFT equations are truncated to mitigate the algorithmic failure due to spin instability, the computational efficiency can be significantly increased.14 Therefore, the TD-DFT/B3LYP method with TDA was applied in the present and all of our previous studies on large molecular systems.15,16
Analysis of the elementary reactions in Type (1) and (2) mechanisms5 resulted in seven active site clusters. In the initial active site cluster St0 (Fig. 1), prFMNim is connected to Gln190 via the NGln190–H⋯OprFMNim,− H-bond (Fig. 2b). The Glu277–Arg173–Glu282 network is associated via a carboxylate–guanidinium–carboxylate (COO−⋯Gdm+⋯COO−) salt-bridge-type interaction (Fig. 2b), which partly stabilizes the molecules in the active site clusters. The equilibrium structures and ΔEEx of the active site clusters were calculated using the DFT/B3LYP/DZP and TD-DFT/B3LYP/DZP methods, respectively (Table S2†). All quantum chemical calculations were performed using the TURBOMOLE 7.50 software package.17 The absorption spectra of the active site clusters were computed from 500 Wigner sampled structures using the NEWTON-X software package18 interfaced with TURBOMOLE 7.50.
prFMNim → prFMNket photoisomerization pathways
To simplify the discussion, the symbols shown in Fig. 1 are used and the proposed photoisomerization pathways5 are explained in detail. Type (1) mechanism comprises four elementary reactions: (1)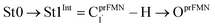 intramolecular proton transfer; (2) St1Int → St2Int = covalent bond dissociation; (3) St2Int → St3Int = cyclization; and (4) St3Int → St4 = reverse protonation. For the Type (2) mechanism, only three elementary reactions were proposed: (1)
intramolecular proton transfer; (2) St1Int → St2Int = covalent bond dissociation; (3) St2Int → St3Int = cyclization; and (4) St3Int → St4 = reverse protonation. For the Type (2) mechanism, only three elementary reactions were proposed: (1) 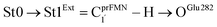 intermolecular proton transfer; (2) St1Ext → St2Ext = covalent bond dissociation; and (3) St2Ext → St3Ext → St4 = concerted cyclization and reverse protonation.
intermolecular proton transfer; (2) St1Ext → St2Ext = covalent bond dissociation; and (3) St2Ext → St3Ext → St4 = concerted cyclization and reverse protonation.
To characterize the structures and energetics of the active site clusters on the PESs, additional symbols are used; […]Int and […]Int,* denote structures on the S0 and S1 PESs of the Type (1) mechanism, respectively; […]Ext,‡ and […]Ext,§ denote transition structure (‡) and structure at the S0/S1 intersection (§) on the PESs of the Type (2) mechanism, respectively; ΔEEx = S0 → S1 energy; ΔE§ = energy at the S0/S1 intersection (§); and ΔE‡ = energy barrier. The equilibrium structures of the active site clusters obtained from the DFT/B3LYP/DZP geometry optimization (Table S2†) were used in the elementary reaction pathway optimization in the S1 state (step (b) in Fig. 3). The elementary reaction pathway optimization was aimed at finding the possibility of the S1 → S0 nonradiative relaxation of the S0 → S1 excited active site clusters.
Because the light-induced reaction was not clearly identified in ref. 5, the S0 → S1 excited precursors for photoisomerization were hypothesized based on the radiation wavelength used in the experiment (λabs = 365 nm/ΔEEx = 3.40 eV), ΔEEx obtained from TD-DFT/B3LYP/DZP calculations, and ΔE‡ for the formation of the precursors in the S0 state. Herein, 7–15 structures connecting the precursor, transition state, and intermediate/product were optimized using a constrained optimization algorithm19 included in TURBOMOLE 7.50. If the S0/S1 intersection was found, the pathway being optimized was refined using the S0/S1 structure as the intermediate/product (step (c) in Fig. 3).
Kinetics and thermodynamics of photoisomerization
Characteristic structures of the model active site clusters on the S0 and S1 PESs were used for the calculation of the rate constants using the TST method (step (d) in Fig. 3).20,21 Herein, the quantized-vibrational rate constants (kQ-vib) were computed over the temperature range of 273–353 K using eqn (1):22
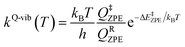 | (1) |
In eqn (1), the energy barrier (ΔE‡ZPE) was obtained with the zero-point vibrational energy correction. QRZPE and Q‡ZPE are the partition functions of the precursor and transition structures, respectively. kB and h are the Boltzmann and Planck constants, respectively.
The thermodynamic properties of interest were the activation free energies (ΔG‡) and enthalpies (ΔH‡). They were derived from kQ-vib (T) using eqn (2) and (3), respectively:
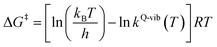 | (2) |
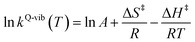 | (3) |
ΔS‡ in eqn (3) is the activation entropy and R is the gas constant. The value of ΔH‡ is obtained from the slope of the linear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQ-vib (T) and 1000/T. To calculate the thermodynamic properties of the nonradiative photoisomerization pathway, the S0 → S1 excited active site clusters were assumed to barrierlessly relax to the S0/S1 intersection and to the structures in the S0 state.
kQ-vib (T) and 1000/T. To calculate the thermodynamic properties of the nonradiative photoisomerization pathway, the S0 → S1 excited active site clusters were assumed to barrierlessly relax to the S0/S1 intersection and to the structures in the S0 state.
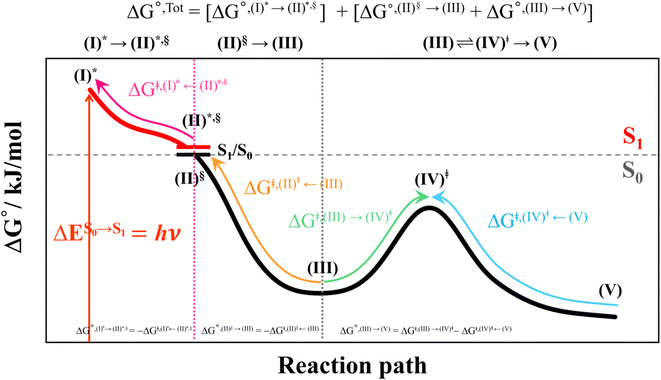
This led to the consecutive “photo-to-thermal pathway” in Fig. 4, the (I)* → (II)*,§ relaxation in the S1 state followed by (II)§ → (III) ⇌ (IV)‡ → (V) in the S0 state, in which (III) ⇌ (IV)‡ → (V) was assumed to be in quasi-equilibrium. Based on this hypothesized consecutive reaction pathway, the total Gibbs free energy (ΔG°,Tot) was computed using ΔG‡ obtained from the TST method. For (I)* → (II)*, ΔG°,(I)*→(II)*,§ = −ΔGr‡,(I)*←(II)*,§, whereas ΔG°,(I)*→(III) = −(ΔGr‡,(I)*←(II)*,§ + ΔGr‡,(II)§←(III)) for (I)* → (II)*,§/(II)§ → (III). For (III) ⇌ (IV)‡ → (V), ΔG°,(III)→(V) = ΔGf‡,(III)→(IV)‡ − ΔGr‡,(IV)‡←(V). Therefore, ΔG°,Tot = ΔG°,(I)*→(III) + ΔG°,(III)→(V). Likewise, the Gibbs free energy for the formation of the transition structure (IV)‡ in the S0 state ΔG°,(I)*→(IV)‡ = ΔG°,(I)*→(III) + ΔGf‡,(III)→(IV)‡. The same method was used to calculate the entropy changes (ΔS°,Rx) of the isomerization reaction (system). All the kinetic and thermodynamic properties were calculated using the DL-FIND program23 included in the ChemShell software package.24
Results and discussion
Equilibrium structures of the active site clusters
The DFT/B3LYP/DZP results show that starting from the seven hypothesized active site clusters shown in Fig. 1, the optimized structures are slightly changed (Table S2a†), except for St2Int and St2Ext. For St2Int, DFT/B3LYP/DZP geometry optimization yielded the precursor St0 (prFMNim in the active site cluster), whereas starting from St2Ext resulted in the product St4 (prFMNket in the active site cluster). These results suggest that only five active site clusters are stationary points (intermediates/products) on the S0 PESs, and St2Int and St2Ext could only be the transition structures on the reaction pathways.Analysis of the equilibrium structures of the five active site clusters revealed that in the S0 state, the residue-to-residue (R-to-R) distances in Fig. 2b are not significantly different, characterized by standard deviations less than ±0.15 Å (Table S2b†); the average R-to-R distances were calculated using the distances between the carbon atoms of the CH3 groups that substituted the carbon atom of the Fdc1 backbone. For example, 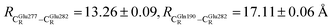 , and
, and 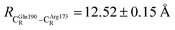 . Because our previous study7 also revealed that the residue-to-residue distances (active site volume) do not change significantly during the enzymatic reaction, the lock-and-key model could explain the substrate specificity of the Fdc1 enzyme, and the catalytic efficiency of this enzymatic decarboxylation reaction is partly connected to the efficiency of the proton exchange between the substrate and Glu282, which is a part of the conserved Glu277–Arg173–Glu282 residue network. These results further suggested that the model active site clusters without the Fdc1 backbone are reasonable and can be used for further studies.
. Because our previous study7 also revealed that the residue-to-residue distances (active site volume) do not change significantly during the enzymatic reaction, the lock-and-key model could explain the substrate specificity of the Fdc1 enzyme, and the catalytic efficiency of this enzymatic decarboxylation reaction is partly connected to the efficiency of the proton exchange between the substrate and Glu282, which is a part of the conserved Glu277–Arg173–Glu282 residue network. These results further suggested that the model active site clusters without the Fdc1 backbone are reasonable and can be used for further studies.
DFT/B3LYP/DZP geometry optimization further suggested that St4 possesses the lowest total energy in the S0 state, and St0 is 24 kJ mol−1 less stable. The TD-DFT/B3LYP/DZP method showed that the S0 → S1 energies of prFMNim and prFMNket are ΔEEx = 3.15 and 2.25 eV (λS0→S1 = 394 and 551 nm), respectively. Comparison of ΔEEx in Tables S1 and S2a† indicated that ΔEEx of St0 is red-shifted from that of prFMNim; ΔEEx of St0 is 0.55 eV (∼83 nm red-shifted) lower than that of prFMNim, whereas ΔEEx of St4 and that of prFMNket are almost the same. The red-shift is hypothesized to result from strong H-bond interaction between prFMNim and residues in the S1 state; based on TD-DFT calculations on the camphorsulfonic acid doped polyaniline,25 the electronic spectral red- and blue-shifts could be induced by the excited state H-bond dynamics, for which strong H-bond interaction in the excited states leads to an increase in the oscillator strength and red-shift.
Analysis of the HOMOs and LUMOs in Fig. 5a suggested that while the electron density distributions for prFMNket in the S0 and S1 states are not substantially different, those for prFMNim are significantly different, especially for the HOMOs, which are characterized by a lower π-character in the phenyl ring. The H-bond formation between the cofactor and residues results in nearly the same electron density distributions in the S0 and S1 states for St0 and St4 (Fig. 5b); in the S0 state, electron density distributions for St0 and St4 are extensive in the Glu277–Arg173–Glu282 network, whereas in the S1 state, the electron densities at the cofactor are the highest, resulting in an increase in the π-character at the cofactors. This could explain why ΔEEx for St0 and St4 are not significantly different (Table S2a†), ΔEEx = 2.60 and 2.69 eV, respectively.
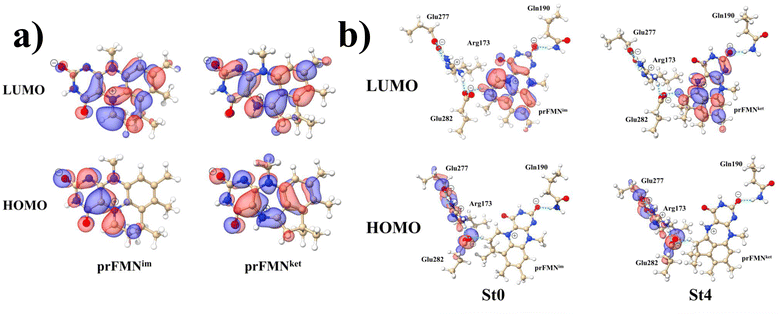 | ||
| Fig. 5 The HOMOs and LUMOs of the prFMNim and prFMNket cofactors (a), and model active site clusters (b), obtained from DFT/B3LYP/DZP geometry optimizations. | ||
Remarks should be made on the HOMOs of the Glu277–Arg173–Glu282 network in Fig. 5b. The extensive charge (electron density) distributions in the S0 state within the Glu277–Arg173–Glu282 network reflect the predominant electrostatic interactions in the COO−⋯Gdm+⋯COO− salt-bridge; Gdm+ stabilizes the two carboxylate anions. Because similar COO−⋯Gdm+⋯COO− salt-bridges were found in many protein structures, and theoretical studies have shown that the Gdm+⋯COO− attractive interaction affects the ligand recognition and binding, as well as enzyme folding and activity, the COO−⋯Gdm+⋯COO− salt-bridge with specific electrostatic interaction could be synthesized and applied, for example, in drug design; Gdm+ derivatives have already been used to treat various deceases related to muscle weakness, cancer and diabetes.26
Potential energy surfaces for prFMNim → prFMNket photoisomerization
The structures and energies of the active site clusters on the S0 and S1 PESs obtained from the DFT/B3LYP/DZP and TD-DFT/B3LYP/DZP reaction path optimization (Fig. S1–S6†) are analyzed in detail. To study the possibility of St2Int and St2Ext being the S0 → S1 photoexcited precursors in the [5 + 2] photocycloaddition, as proposed in ref. 6, the PESs for St0 → St1Int → St2Int and St0 → St1Ext → St2Ext in the S0 state were primarily calculated; the intra- and intermolecular proton transfers and covalent bond dissociation occurring in the S0 state serve as prerequisites for the light-dependent cycloaddition in Type (1) and Type (2) mechanisms,5 respectively.The results showed that both St0 → St1Int → St2Int and St0 → St1Ext → St2Ext involve extraordinarily high energy barriers in the S0 state, especially for the covalent bond dissociation, ΔE‡ = 456.4 and 435.9 kJ mol−1 (Fig. S1b and S2b,† respectively). Based on these findings and the observations that St2Int and St2Ext are not stationary points with S0 → S1 energies significantly different from the experimental radiation wavelength (λabs = 365 nm/ΔEEx = 3.40 eV),5 these two active site clusters were ruled out from further study; TD-DFT/B3LYP/DZP single point calculations suggested that for St2Int and St2Ext, ΔEEx = 2.96 and 1.88 eV, respectively (Table S2a†).
Similarly, because the intra- and intermolecular proton transfers (St0 → St1Int and St0 → St1Ext) possess high energy barriers in the S0 state, ΔE‡ = 262.6 (Fig. S1a†) and 125.7 kJ mol−1 (Fig. S2a†), respectively, it is unlikely that St1Int and St1Ext serve as the photoexcited precursors for S0 → S1. To study the possibility of St0 being the S0 → S1 photoexcited precursor, UV-visible absorption spectra were calculated at 277 and 300 K using 500 Wigner sampled initial conditions. The results in Fig. 6 show two outstanding peaks, e.g., at 300 K, λabs = 384 and 474 nm. Because the structured peak at λabs = 384 nm is close to the radiation wavelength used in an experiment,5 St0 was chosen as the S0 → S1 photoexcited precursor for Type (1) and Type (2) mechanisms.
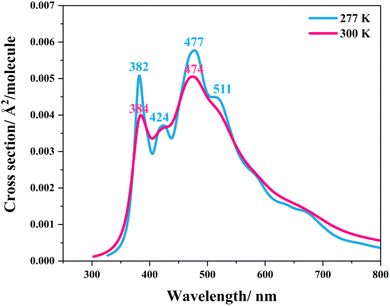 | ||
| Fig. 6 The UV-visible spectra of the model active site cluster St0 (prFMNim in the residue network) obtained based on 500 Wigner sample structures at 277 and 300 K. | ||
The PESs obtained from reaction path optimization show that the S0 → S1 vertically excited structure barrierlessly relaxes to the structure at the S0/S1 intersection (St0* → St0*,§ in Fig. S3a†). The S0 PES (Fig. S4†) illustrates that after the S1 → S0 nonradiative relaxation, the intramolecular proton transfer (St0§ → St0-[1]Int → St1Int) in the Type (1) mechanism possesses a rather high energy barrier, ΔE‡ = 209.5 kJ mol−1, whereas ΔE‡ = 86.9 kJ mol−1 is for the intermolecular proton transfer (St0§ → St0-[1]Ext → St1Ext) in the Type (2) mechanism (Fig. S5a†). Hence, one can conclude that the external base pathway is energetically more favorable than the internal one, and only the Type (2) mechanism is further discussed in detail.
To test the hypothesis that the red-shift in ΔEEx for St0 compared to that of prFMNim results from strong H-bond interaction between the prFMNim cofactor and residues in the S1 state, the variation of the NGln190–H⋯OprFMN,− H-bond distance in the S1 state was analyzed as an example. The results revealed that on the S1 PES (Fig. S3a†), while the RNGln190–H⋯OprFMN,− H-bond distance decreases, the RNGln190–H distance increases (Fig. S3b†), reflecting an increase in the NGln190–H⋯OprFMN,− H-bond strength (red-shift) in the S1 state towards the S0/S1 intersection.
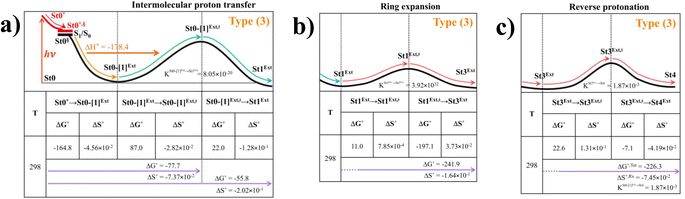
Because St2Ext had already been excluded from the photoisomerization pathway, an attempt was made to bypass this active site cluster. The results showed that after the S1 → S0 nonradiative relaxation at the S0/S1 intersection (Fig. S3a†) and 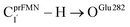 intermolecular proton transfer from prFMNim to Glu282 (Fig. S5a†), the S0 PES shows a low energy barrier for St1Ext → St3Ext, ΔE‡ = 11.2 kJ mol−1 (Fig. S5b†), represented by concerted NprFMN5–CprFMN5a and
intermolecular proton transfer from prFMNim to Glu282 (Fig. S5a†), the S0 PES shows a low energy barrier for St1Ext → St3Ext, ΔE‡ = 11.2 kJ mol−1 (Fig. S5b†), represented by concerted NprFMN5–CprFMN5a and 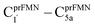 covalent bond dissociation and formation in Fig. 7a, respectively. This concerted process can be collectively regarded as “ring expansion.” To complete the formation of the St4 product (prFMNket in the active site cluster), the S0 PES for the reverse protonation from Glu282 to prFMNim (St3Ext → St4) has ΔE‡ = 63.9 kJ mol−1 (Fig. S5c†). The potential energy profile, which bypasses St2Ext, is regarded as the Type (3) mechanism shown in Fig. 7b.
covalent bond dissociation and formation in Fig. 7a, respectively. This concerted process can be collectively regarded as “ring expansion.” To complete the formation of the St4 product (prFMNket in the active site cluster), the S0 PES for the reverse protonation from Glu282 to prFMNim (St3Ext → St4) has ΔE‡ = 63.9 kJ mol−1 (Fig. S5c†). The potential energy profile, which bypasses St2Ext, is regarded as the Type (3) mechanism shown in Fig. 7b.
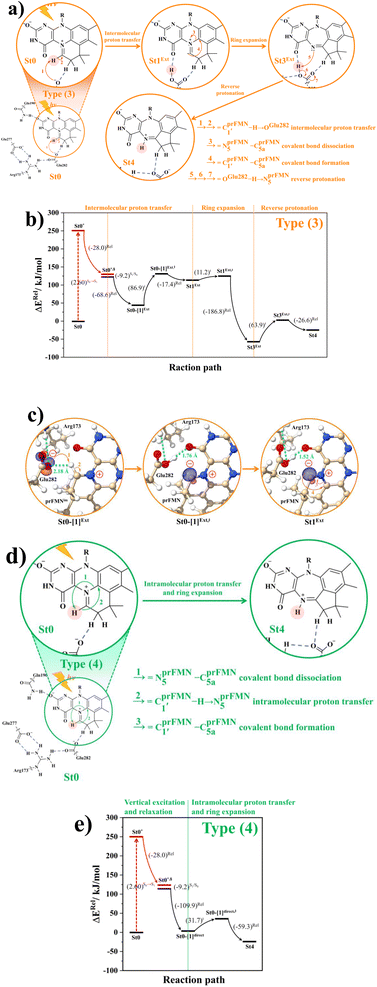 | ||
Fig. 7 (a) and (b) Type (3) mechanism and potential energy profiles involving the S0 → S1 excitation of St0, intermolecular proton transfer in 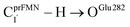 H-bond between prFMNim and Glu282, ring expansion and reverse protonation, respectively. (c) The H-bond distances ( H-bond between prFMNim and Glu282, ring expansion and reverse protonation, respectively. (c) The H-bond distances (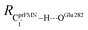 and ROGlu282–H⋯OprFMN) and local valence charge densities on the high-energy barrier intermolecular proton transfer process (St0-[1]Ext → St0-[1]Ext,‡ → St1Ext). (d) and (e) Type (4) mechanism and potential energy profiles involving the S0 → S1 excitation of St0 and concerted and ROGlu282–H⋯OprFMN) and local valence charge densities on the high-energy barrier intermolecular proton transfer process (St0-[1]Ext → St0-[1]Ext,‡ → St1Ext). (d) and (e) Type (4) mechanism and potential energy profiles involving the S0 → S1 excitation of St0 and concerted 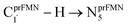 intramolecular proton transfer in prFMNim and ring expansion. The characteristic structures are shown in detail in Table S2.† (…)S0 → S1 = S0 → S1 vertical excitation energy; (…)Rel and (…)‡ = relative and transition energies on the PES; (…)S1/S0 = difference between the total energies in the S0 and S1 states at the S0/S1 intersection. intramolecular proton transfer in prFMNim and ring expansion. The characteristic structures are shown in detail in Table S2.† (…)S0 → S1 = S0 → S1 vertical excitation energy; (…)Rel and (…)‡ = relative and transition energies on the PES; (…)S1/S0 = difference between the total energies in the S0 and S1 states at the S0/S1 intersection. | ||
The analysis of the H-bond distances, local valence charge densities and energetics in the high-energy barrier intermolecular proton transfer process (St0-[1]Ext → St0-[1]Ext,‡ → St1Ext) in Fig. 7c reveals that although the 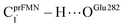 H-bond in St0-[1]Ext
H-bond in St0-[1]Ext 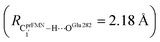 is longer than the OGlu282–H⋯OprFMN H-bond in St1Ext (ROGlu282–H⋯OprFMN = 1.52 Å), due to the strong electrostatic interaction between Glu282 and prFMNim, St0-[1]Ext is more stable than St1Ext. It also appears that proton transfer to one of the COO− groups in the COO−⋯Gdm+⋯COO− salt bridge leads to a strong decrease in the electrostatic interaction between Glu282 and prFMNim, recognized from a reduction of the local valence charge density at the COOH group of St1Ext, and the high-energy barrier in St0-[1]Ext → St0-[1]Ext,‡ → St1Ext could be attributed the
is longer than the OGlu282–H⋯OprFMN H-bond in St1Ext (ROGlu282–H⋯OprFMN = 1.52 Å), due to the strong electrostatic interaction between Glu282 and prFMNim, St0-[1]Ext is more stable than St1Ext. It also appears that proton transfer to one of the COO− groups in the COO−⋯Gdm+⋯COO− salt bridge leads to a strong decrease in the electrostatic interaction between Glu282 and prFMNim, recognized from a reduction of the local valence charge density at the COOH group of St1Ext, and the high-energy barrier in St0-[1]Ext → St0-[1]Ext,‡ → St1Ext could be attributed the 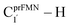 covalent bond breaking.
covalent bond breaking.
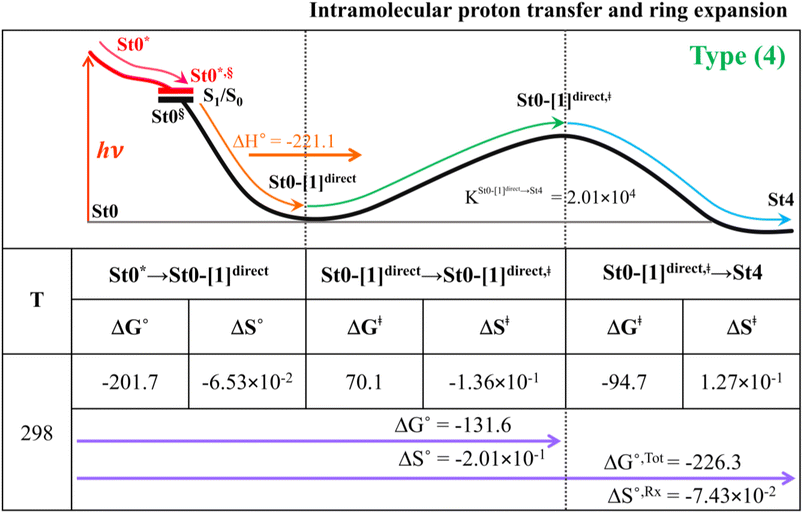
Because the Type (1) mechanism5 has been established in this work to be energetically not favorable, to search for an alternative internal base pathway, the S0 PES directly connecting structure St0§ at the S0/S1 intersection and St4 (St0§ → St4) was optimized. It appeared that St0§ → St0-[1]direct → St0-[1]direct,‡ → St4 (Fig. S6†) can occur without proton exchange between the prFMNim cofactor and the Glu282 residue. This internal base pathway (Type (4) mechanism shown in Fig. 7d) involves concerted 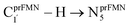 intramolecular proton transfer, NprFMN5–C5aprFMN and
intramolecular proton transfer, NprFMN5–C5aprFMN and 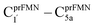 covalent bond dissociation and formation, respectively, with ΔE‡ = 31.7 kJ mol−1 (Fig. 7e).
covalent bond dissociation and formation, respectively, with ΔE‡ = 31.7 kJ mol−1 (Fig. 7e).
Thermodynamics of the elementary reactions
To study the kinetic and thermodynamic properties of the two energetically favorable pathways, the characteristic active site clusters in Type (3) and Type (4) mechanisms shown in Fig. 7 were used in TST calculations, and the results are summarized in Tables S3–S5.† The results discussed are included in Tables 1 and 2. Analysis based on the photo-to-thermal pathway in Fig. 4, (I)* → (II)*,§/(II)§ → (III), revealed that for the Type (3) mechanism at T = 298 K, although the entropy for the formation of St0-[1]Ext,‡ is negative (ΔS°,(I)*→(IV)‡ = −7.4 × 10−2 kJ mol−1), the high exothermic relaxation energy for St0* → St0§ → St0-[1]Ext (ΔH°,(I)*→(III) = −178.4 kJ mol−1 in Table 1a) allows the spontaneous formation of this high energy-barrier transition state with ΔG°,(I)*→(IV)‡ = −77.7 kJ mol−1.Based on the same approach, the total Gibbs free energy and reaction entropy for the prFMNim → prFMNket photoisomerization via the Type (3) mechanism were computed to be ΔG°,Tot = −226.3 kJ mol−1 and ΔS°,Rx = −7.5 × 10−2 kJ mol−1 K−1 at 298 K (Table 1c). For the Type (4) mechanism, ΔH°,(I)*→(III) = −221.1, ΔG°,Tot = −226.3 kJ mol−1, and ΔS°,Rx = −7.4 × 10−2 kJ mol−1 K−1, with the spontaneous formation of St0-[1]direct,‡, ΔG°,(I)*→(IV)‡ = −131.6 kJ mol−1 (Table 2). Therefore, based on the values of ΔG°,(I)*→(IV)‡ of the rate-determining step, the Type (4) mechanism is thermodynamically more favorable than the Type (3) mechanism. Because ΔG°,Tot and ΔS°,Rx of Type (3) and Type (4) mechanisms are the same (Tables 1 and 2, respectively), the hypothesized photo-to-thermal pathway in Fig. 4 is validated and the applicability of the TST method is confirmed.
Kinetics of elementary reactions
To correlate the theoretical results with the experimental data5 and to explore the possibility of improving the enzyme efficiency of Fdc1, the rate constants (kQ-vib) for Type (3) and Type (4) mechanisms (Tables S3 and S4,† respectively) were analyzed and discussed in detail. The experimental rate constants revealed that the enzyme activity of Fdc1 purified in the dark was slightly higher than that under visible light, kcat = 9.3 ± 0.1 and 7.6 ± 0.2 s−1, respectively, and when Fdc1 was prepared in the dark, the enzyme activity remained constant for many hours. However, direct exposure of the Fdc1 enzyme incubated in the dark with UV radiation at λ = 365 nm for ∼5 min led to a complete loss of enzyme activity and a change in the UV-visible spectra.The experimental results also showed that after purification, Fdc1 incubated on ice resulted in a loss of enzyme stability with a half-life τ1/2loss,T ≈ 30 min. Based on the assumption that the loss of enzyme activity at 273 K follows the first-order kinetics, kloss,T = 0.693/τ1/2loss,T = 3.85 × 10−4 s−1. In addition, assuming that the photochemical experiment5 was conducted at room temperature, the complete loss of enzyme activity due to UV radiation is approximated to be τloss,UV = 300 s, with the rate constant kloss,UV = 1/τloss,UV = 3.33 × 10−3 s−1 at 298 K. The value of kloss,UV is compatible with the rate-determining step in the Type (3) mechanism; for the 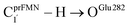 intermolecular proton transfer from prFMNim to Glu282, kfQ-vib = 3.53 × 10−3 s−1 at 298 K (Table S3†).
intermolecular proton transfer from prFMNim to Glu282, kfQ-vib = 3.53 × 10−3 s−1 at 298 K (Table S3†).
Although the internal base pathway in Type (4) mechanism is energetically and thermodynamically more favorable than Type (3) mechanism, the concerted rate-determining process is too fast compared with the experimental rate constant, kfQ-vib = 3.26 × 100 s−1 compared with kloss,UV = 3.33 × 10−3 s−1 at 298 K. Therefore, Type (3) mechanism, which requires an external base, is likely to represent the prFMNim → prFMNket photoisomerization mechanism.
Balance between the loss of enzyme stability and the efficiency by UV radiation
Based on the above discussion on the theoretical and experimental data,5 to reduce the prFMNim → prFMNket photoisomerization rate without substantial loss of the Fdc1 stability, an appropriate enzymatic decarboxylation temperature should be chosen; an effective enzymatic decarboxylation using Fdc1 could be achieved by slowing down the photo-to-thermal process (formation of the high-energy barrier transition state) in Type (3) mechanism, compared with the enzymatic decarboxylation rate.To recommend the appropriate temperature, at which the styrene production is kinetically controlled in the presence of UV radiation, the plot of the half-life for the formation of the high-energy barrier transition state (τ1/2Q-vib) versus T and the Arrhenius plot for this photo-to-thermal pathway were constructed over the studied temperature range and are shown in Fig. 8. Fig. 8a shows that τ1/2Q-vib varies exponentially over the temperature range of 273–298 K. Thus, to balance between the loss of the enzyme stability at 273 K and that under UV irradiation, the appropriate temperature should be in this temperature range, τ1/2loss,T = 1800 (T = 273 K) and τ1/2loss,UV = 208 s (T = 298 K).
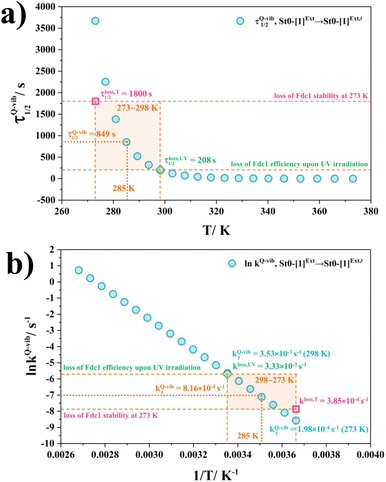 | ||
| Fig. 8 (a) and (b) Correlations between τ1/2Q-vib and T, and ln kfQ-vib and 1/T for the rate determining step (St0-[1]Ext → St0-[1]Ext,‡ in Fig. 7(b) in Type (3) mechanism obtained from the TST method, compared with experiment.5 τ1/2loss,T and kloss,T = half-life and first-order rate constant for the loss of enzyme stability at 273 K;5 τ1/2loss,UV and kloss,UV = half-life and first-order rate constant for the loss of enzyme activity due to UV radiation at 365 nm;5 τ1/2Q-vib and kfQ-vib = half-life and first-order rate constant for the rate-determining intermolecular proton transfer (St0-[1]Ext → St0-[1]Ext,‡) in Fig. 7(b). | ||
As a rule of thumb, the rate of chemical reaction doubles if the temperature increases by 10 K. Therefore, the experimental rate constants to produce styrene in this temperature range are kcat = 3.00 and 7.60 s−1, and the rate constants for the 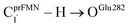 intermolecular proton transfer (rate determining step for prFMNim → prFMNket) are kfQ-vib = 1.98 × 10−4 s−1 (273 K) and 3.53 × 10−3 s−1 (298 K).
intermolecular proton transfer (rate determining step for prFMNim → prFMNket) are kfQ-vib = 1.98 × 10−4 s−1 (273 K) and 3.53 × 10−3 s−1 (298 K).
The Arrhenius plot in Fig. 8b reveals that in this temperature range, kloss,T = 3.85 × 10−4 s−1 (T = 273 K) and kloss,UV = 3.33 × 10−3 s−1 (T = 298 K), and the optimal temperature should be at T = 285 K with kfQ-vib = 8.16 × 10−4 s−1 for the photo-to-thermal pathway. Therefore, the enzyme activity of Fdc1 purified under visible light at 285 K is approximated to be kcat ≈ 3.8 s−1. This experimental rate constant is ∼4600 times larger than the rate-determining step for prFMNim → prFMNket at the same temperature, and styrene production becomes kinetically controlled in the presence of UV radiation at this temperature.
Conclusions
The enzymatic decarboxylation of α,β-unsaturated acids using the Fdc1 enzyme and prFMN cofactor is a potential, environmentally friendly reaction for the biosynthesis of styrene and its derivatives. However, an experiment indicated that the enzyme activity of Fdc1 depends on the ring structure of prFMN, namely, the iminium and ketimine forms, and the loss of the enzyme activity results from the prFMNim → prFMNket photoisomerization with the light-dependent reaction suggested to occur in the cyclization process.Herein, to obtain insight into the prFMNim → prFMNket photoisomerization process and to improve the enzyme efficiency of Fdc1, two proposed photoisomerization mechanisms with different proton sources for the acid–base reaction were studied using theoretical methods. This mechanistic study focused on the photoisomerization pathways in the S1 and S0 states and on the kinetics and thermodynamics of the photo-to-thermal process in the active site of Fdc1. Analysis of the equilibrium structures of the model active site clusters revealed that because the active site volumes (residue-to-residue distances) obtained from the DFT/B3LYP/DZP geometry optimization were not significantly different, the model active site clusters without the Fdc1 backbone were proved to be reasonable and can be used in the study of the enzymatic decarboxylation process.
The PESs calculated from the DFT/B3LYP/DZP and TD-DFT/B3LYP/DZP methods suggested that the light-dependent reaction occurs in the rate-determining proton transfer process (acid–base reaction), and the mechanism involving intermolecular proton transfer between prFMNim and Glu282 (external base) is energetically more favorable than that involving intramolecular proton transfer in prFMNim (internal base). The light-dependent reaction was confirmed by the calculated UV-visible spectra to be a high-energy-barrier proton transfer process, for which the S0 → S1 photoexcited precursor is St0 (prFMNim in the active site cluster). The thermodynamic results obtained from the TST method suggested that the exothermic relaxation energy in the photo-to-thermal process in the Type (3) mechanism can promote the spontaneous formation of the high-energy-barrier transition state.
Based on the analysis of the theoretical and experimental data, effective enzymatic decarboxylation of the α,β-unsaturated acids using Fdc1 could be achieved by slowing down the formation of the undesirable thermodynamically favorable product (prFMNket). Because the kinetic results suggested that the rate constant of formation of the high-energy-barrier transition state varies exponentially over the temperature range of 273–298 K, and because the experiment showed that incubating Fdc1 on ice could result in complete loss of enzyme stability, it is recommended to perform the decarboxylation reaction at T = 285 K. This temperature allows for kinetically controlled styrene production in the presence of UV radiation, thus addressing the balance between enzyme stability loss at 273 K and under UV radiation. The computational strategy and fundamental insights obtained in this study could serve as guidelines for future theoretical and experimental investigations on the same and similar photochemical systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the high-performance computer facilities provided by the National e-Science project of the National Electronics and Computer Technology Centre (NECTEC), and the National Science and Technology Development Agency (NSTDA). This work was supported by (I) Suranaree University of Technology (SUT), (II) Thailand Science Research and Innovation (TSRI), and (III) National Science, Research, and Innovation Fund (NSRF). The authors also acknowledge NSTDA Supercomputer Center (ThaiSC) for providing computing resources for this work. This research has received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research, and Innovation (PMU-B) [grant number B13F660060].References
- K. L. Ferguson, N. Arunrattanamook and E. N. G. Marsh, Biochemistry, 2016, 55, 2857–2863 CrossRef CAS PubMed.
- K. L. Ferguson, J. D. Eschweiler, B. T. Ruotolo and E. N. G. Marsh, J. Am. Chem. Soc., 2017, 139, 10972–10975 CrossRef CAS PubMed.
- C.-L. Lan and S.-L. Chen, J. Org. Chem., 2016, 81, 9289–9295 CrossRef CAS PubMed.
- K. A. Payne, M. D. White, K. Fisher, B. Khara, S. S. Bailey, D. Parker, N. J. Rattray, D. K. Trivedi, R. Goodacre and R. Beveridge, Nature, 2015, 522, 497–501 CrossRef CAS PubMed.
- S. S. Bailey, K. A. P. Payne, K. Fisher, S. A. Marshall, M. J. Cliff, R. Spiess, D. A. Parker, S. E. J. Rigby and D. Leys, J. Biol. Chem., 2018, 293, 2272–2287 CrossRef CAS PubMed.
- D. M. E. Davies, C. Murray, M. Berry, A. J. Orr-Ewing and K. I. Booker-Milburn, J. Org. Chem., 2007, 72, 1449–1457 CrossRef CAS PubMed.
- P. Promma, C. Lao-ngam, R.-Y. Lai and K. Sagarik, RSC Adv., 2022, 12, 14223–14234 RSC.
- J. Nirasok, P. Panajapo, P. Promma, P. Suwannakham and K. Sagarik, J. Photochem. Photobiol., A, 2023, 436, 114354 CrossRef CAS.
- P. Panajapo, P. Suwannakham, P. Promma and K. Sagarik, R. Soc. Open Sci., 2024, 11, 231957 CrossRef.
- J. Thisuwan, P. Promma and K. Sagarik, R. Soc. Open Sci., 2021, 8, 211168 CrossRef CAS PubMed.
- L. Gonzalez, D. Escudero and L. Serrano-Andres, ChemPhysChem, 2012, 13, 28–51 CrossRef CAS PubMed.
- D. Jacquemin, B. Mennucci and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 16987–16998 RSC.
- E. Tapavicza, I. Tavernelli, U. Rothlisberger, C. Filippi and M. E. Casida, J. Chem. Phys., 2008, 129, 124108 CrossRef PubMed.
- Y.-L. Wang and G.-S. Wu, Int. J. Quantum Chem., 2008, 108, 430–439 CrossRef CAS.
- T. Khrootkaew, S. Wangngae, K. Chansaenpak, K. Rueantong, W. Wattanathana, P. Pinyou, P. Panajapo, V. Promarak, K. Sagarik and A. Kamkaew, Chem.–Asian J., 2023, e202300808 Search PubMed.
- S. Siriwibool, N. Kaekratoke, K. Chansaenpak, K. Siwawannapong, P. Panajapo, K. Sagarik, P. Noisa, R. Y. Lai and A. Kamkaew, Sci. Rep., 2020, 10, 1283 CrossRef CAS PubMed.
- TURBOMOLE V 7.5 2020, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, BIOVIA.TURBOMOLE@3ds.com, V7.5 edn, 2019 Search PubMed.
- M. Barbatti, M. Bondanza, R. Crespo-Otero, B. Demoulin, P. O. Dral, G. Granucci, F. Kossoski, H. Lischka, B. Mennucci, S. Mukherjee, M. Pederzoli, M. Persico, M. P. Jr, J. Pittner, F. Plasser, E. S. Gil and L. Stojanovic, J. Chem. Theory Comput., 2022, 18, 6851–6865 CrossRef CAS PubMed.
- P. Plessow, J. Chem. Theory Comput., 2013, 9, 1305–1310 CrossRef CAS PubMed.
- E. Pollak and P. Talkner, Chaos, 2005, 15, 026116 CrossRef PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- J. E. House, Principles of Chemical Kinetics, Kindle Edition, Academic Press, USA, 2nd edn, 2007 Search PubMed.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- ChemShell, A Computational Chemistry Shell, https://www.chemshell.org/ Search PubMed.
- Y. Zhang, Y. Duan and T. Wang, Phys. Chem. Chem. Phys., 2014, 16, 26261 RSC.
- A. N. Muttathukattil, S. Srinivasan, A. Halder and G. Reddy, J. Phys. Chem. B, 2019, 123, 9302–9311 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02035a |
| This journal is © The Royal Society of Chemistry 2024 |