Open Access Article
Open Access ArticleFirst-principles study of molecular hydrogen binding to heme in competition with O2, NO and CO†
Yun-Kyong Ria,
Song-Ae Kimb,
Yun-Hyok Kyea,
Yu-Chol Jongc,
Myong-Su Kangb and
Chol-Jun Yu *a
*a
aChair of Computational Materials Design, Faculty of Materials Science, Kim Il Sung University, PO Box 76, Pyongyang, Democratic People's Republic of Korea. E-mail: cj.yu@ryongnamsan.edu.kp
bInstitute of Molecular Biology, Faculty of Life Science, Kim Il Sung University, PO Box 76, Pyongyang, Democratic People's Republic of Korea
cChair of Chemical Process, Faculty of Chemistry, Kim Il Sung University, PO Box 76, Pyongyang, Democratic People's Republic of Korea
First published on 22nd May 2024
Abstract
Molecular hydrogen shows antioxidant activity and distinct efficacy towards vascular diseases, but the understanding of this is not yet satisfactory at the atomic level. In this work, we study the binding properties of H2 to the heme group in relation with other diatomic molecules (DMs), including O2, NO and CO, and their displacement reactions, using first-principles calculations. We carry out molecular modeling of the heme group, using iron-porphyrin with the imidazole ligand, i.e., FePIm, and smaller models of Fe(CnHn+2N2)2NH3 with n = 3 and 1, and of molecular complexes of heme–DM and –H. Through analysis of optimized geometries and energetics, it is found that the order of binding strength of DMs or H to the Fe of heme is NO > O2 > CO > H > H2 for FePIm-based systems, while it is H > O2 > NO > CO > H2 for model-based systems. We calculate the activation energies for displacement reactions of H2 and H by other DMs, revealing that the H2 displacements occur spontaneously while the H displacements require a large amount of energy. Finally, our calculations corroborate that the rate constants increase with increasing temperature according to the Arrhenius relation.
1 Introduction
Recently, molecular hydrogen (or hydrogen gas, H2) has shown great potential for treating various fatal diseases including cancer and angiopathy.1–3 H2 is the smallest and lightest molecule, coupled with its non-polar nature, thereby readily accessing any organ through facile penetration across cell membranes and fast diffusion into cellular organelles.4,5 Moreover, hydrogen gas is odorless, colorless and non-toxic, and hydrogen is abundant on Earth as part of water molecules. At the early stage of therapeutic applications, hyperbaric H2 was applied to treat skin squamous carcinoma in mice,6 and later a clinically viable dose of H2 was found to significantly reduce cytotoxic reactive oxygen/nitrogen species (RONS),7 indicating that hydrogen may be an effective antioxidant in the clinic. The clinical effects of molecular hydrogen have been steadily reported in humans and animals over the past two decades.8–10In particular, various vascular diseases, such as diabetic vasculopathy, atherosclerosis and hypertension, which are mostly caused by cellular redox dysregulation, can be effectively treated by inhaling hydrogen gas or drinking H2-rich water.11–13 When inhaling hydrogen, the H2 concentration in venous and arterial blood was found to increase in proportion to the applied dose.14 According to Henry’s law, a 2% H2 concentration leads to a 15.6 μM H2 concentration in the blood. Considering that cellular redox dysregulation occurs as a result of homeostasis depression between RONS and self-defense antioxidants, H2 may react with RONS, typically the hydroxyl radical (˙OH) and peroxynitrite (ONOO−), in the presence of catalytic metal cations such as Fe2+ and Cu+.15,16 Although some enzymes, such as catalase and superoxide dismutase, may also alleviate RONS-induced cellular injury,17 their clinical efficacy is little demonstrated because of their inability to permeate cell-membrane barriers. In addition, hydrogen has also been applied to treat cerebral ischemia by buffering the destructive effects of oxidative stress in the brain, proving its ability to cross the blood–brain barrier.18,19
To explain the efficacy of H2 towards vascular diseases, it was suggested that the effects of H2 could be mediated by heme groups, such as those in catalase,20,21 peroxidases22 and matrix metalloproteins.23 Taking account of the fact that heme is the active site of hemoglobin (Hb), the main component of blood cells, we recently carried out the systematic study of hydrogen–protoheme (Fe-protoporphyrin with an imidazole ligand: FePIm) complexes using density functional theory (DFT) calculations.15 We suggested two types of bonding between H2 and the Fe(II) of heme (dihydrogen and Kubas bonding), and revealed that H2 can be dissociated with a relatively low activation barrier to form an FePIm–H complex, clarifying the key role of heme as an effective catalyst for antioxidant activity towards RONS by hydrogen gas. Some previous works also reported dihydrogen–metalloprotein complexes.24–28 Meanwhile, other diatomic molecules (DMs), such as O2, NO and CO, can be strongly bonded with heme, playing important biological roles in living organisms. The oxygen molecule O2 reacts reversibly with Hb, allowing the transport and storage of dioxygen in the respiratory chain. Having a high affinity for the iron of heme, both NO and CO exhibit medicinal effects, acting as intercellular signaling molecules on one hand, while being poisons on the other hand. There is considerable previous theoretical work in the literature on the binding of DMs to heme groups29–32 and on the geometrical and electronic properties of heme groups themselves.33–37 Putting all accounts together, a natural question is raised: if hydrogen is bound to heme by inhaling molecular hydrogen, can DMs such as O2, NO and CO displace the H2 molecule or H atom bound to heme? If so, how high are the activation barriers for such displacement reactions?
The aim of this work is to answer these questions. We perform DFT calculations and ab initio molecular dynamics (AIMD) simulations of FePIm complexes with DMs to estimate the binding energies and activation energies for substitution. We organized the paper as follows. After describing the computational methods, we briefly explain the binding features of the complexes together with their molecular vibrations and electronic structures. Then we present the results regarding the energetics of substitution of O2, NO and CO for a H2 molecule or H atom bound to heme.
2 Computational methods
DFT calculations were carried out with the NWChem (version 6.6) package,38 using the hybrid B3LYP exchange–correlation (XC) functional39,40 and the basis set combination described below. For the systems with odd numbers of electrons, a spin-unrestricted open-shell formalism was utilized throughout. In all the DFT calculations, the 6-311G basis was used for the non-metallic elements C, O, N, and H, while the standard effective core potential (ECP) was used for Fe(II) with the standard LANL2DZ_ECP basis.41 After the geometry optimizations, we performed frequency calculations on all the molecular systems. We considered the thermal correction (TC) and the zero-point correction (ZPC) to the total DFT energy. The basis set superposition error (BSSE) was corrected for binding energy calculations using the counterpoise method.42 For the geometry optimizations, the DRIVER module was used based in the quasi-Newton algorithm with the convergence criteria of “tight”, being the highest accuracy for geometry optimization among the possible selections in the NWChem package. The nudged elastic band (NEB) method was applied to estimate the activation energy for substitution reactions using 10 NEB beads, followed by a zero-temperature string calculation with 10 beads.43 For the AIMD simulations, the cutoff radius was set to 2.8 nm, the constant-temperature ensemble using Berendsen’s thermostat at T = 300 K was used, with a temperature relaxation time of 0.05 ps, and the time step and duration were set to 1 fs and 1 ps, respectively.Our calculations were performed on three molecular systems to mimic the heme group, as shown in Fig. 1. The first system is Fe(II)-porphyrin-imidazole ligand (FePIm), being the largest and most realistic system in the present work (Fig. 1a), and which has been widely used to study the reactions of small molecules with heme groups in DFT calculations.15,34,35,44 Since FePIm is too large to be used for calculation of the rate constant with direct dynamics for variational transition state theory (DIRDYVTST), the smaller models 1 and 2 were also considered. The chemical formulae of models 1 and 2 can be expressed as [Fe(CnHn+2N2)2NH3], where n = 3 and 1, respectively. Small models similar to 1 and 2 but with different ligands have been proved previously to reproduce some features of the FePIm model.29,35 In these models, the two ligands of vinylogous amidine C3H5N2− or amidine CH3N2− are located symmetrically around the Fe centre, having the same bonding geometry and charge as the full porphyrin ring. They are distinct from the FePIm system in their conjugation properties because there is no cyclic ring. The larger model1 is more similar to the FePIm system than model2, due to it having the same number of C atoms between the N atoms and thus a more similar bond angle to the porphyrin of FePIm. The ammonia molecule in the two models, having a small size, high symmetry and single lone-pair donated to Fe, was selected to mimic the imidazole group.
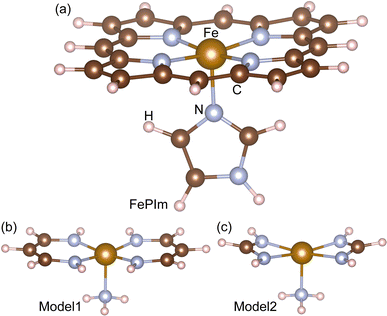 | ||
| Fig. 1 Molecular structures of (a) Fe-porphyrin with the imidazole ligand (FePIm), (b) model1, Fe(C3H5N2)2NH3, and (c) model2, Fe(CH3N2)2NH3. | ||
The chemical reaction rates were calculated for only model2 because of the quite heavy computational load for the FePIm system and model1. The calculations were carried out by connecting the NWChem and Polyrate packages.45–47 Using the optimized geometries of reactants, products and saddle points determined by the NEB calculations, we applied the DIRDYVTST module included in the NWChem package at B3LYP/6-31G and LANL2DZ level to carry out the electronic structure calculations. We selected the Page–McIver corrected local quadratic approximation (CLQA) for the integration method to follow the reaction path. The resultant energies, gradients, and Hessians were merged into file30, which is the input file for Polyrate. In using the Polyrate package, we selected reaction-path variational transition-state theory (RP-VTST),46 in which the canonical variational theory (CVT) forward rate constant was obtained by minimizing the generalized transition (GT) state theory rate constant with respect to the reaction coordinate s as follows:
 | (1) |
3 Results and discussion
3.1 Geometrical and binding features
The aim of this work is to study displacement reactions of H2 or H bound to heme with DMs such as O2, NO and CO. Therefore, the molecular systems to be considered were heme–DM and –H, where heme was modeled using FePIm, model1 and model2, and the DMs were H2, O2, NO and CO, resulting in 15 molecular systems in total. To begin with, the geometries of these 15 molecular systems were optimized at the B3LYP/6-311G and LANL2DZ_ECP level. Fig. 2 shows their optimized geometries, together with the frontier molecular orbitals including the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). As already clarified both in experiment48 and theory,31 the DMs O2, NO and CO were bound to ferrous iron, forming a new chemical bond. As such, molecular hydrogen and the hydrogen atom were also bound to the iron of heme, which has been confirmed in our previous work.15 Table 1 lists the typical bond lengths and bond angles, mostly around the Fe atom, for all the molecular systems.| FePIm | Model1 | Model2 | |||
|---|---|---|---|---|---|
| This | Prev. | ||||
| a PBE/DZP DFT supercell calculation.15b Experiment.48c B3LYP/lacv3p**+ DFT cluster calculation.31d Experiment.49e B3LYP/CCSD(T) DFT cluster calculations.29f B3LYP/CCSD(T) DFT cluster calculations.35 | |||||
| H2 | dFe–H | 1.952 | 1.71a | 1.839 | 1.827 |
| dH–H | 0.755 | 0.73a | 0.754 | 0.767 | |
| dFe–Np | 2.023 | 2.03a | 1.978 | 2.064 | |
| αFe–H–H | 78.8 | 77.7a | 79.1 | 77.9 | |
| Eb | 4.8 | 5.8 | 8.2 | ||
| H | dFe–H | 1.694 | 1.54a | 1.500 | 1.524 |
| dFe–Np | 2.014 | 2.02a | 1.938 | 1.999 | |
| Eb | −10.6 | −44.9 | −44.1 | ||
| O2 | dFe–O | 1.794 | 1.81b, 1.89c | 1.784 | 1.782 |
| dO–O | 1.317 | 1.24b, 1.35c | 1.328 | 1.334 | |
| dFe–Np | 2.019 | 2.02b, 2.09c | 1.970 | 2.015 | |
| αFe–O–O | 122.3 | 122b, 118.1c | 123.0 | 121.8 | |
| Eb | −27.3 | −32.6 | −38.4 | ||
| NO | dFe–NO | 1.821 | 1.82c | 1.818 | 1.815 |
| dNO–O | 1.203 | 1.20c | 1.217 | 1.225 | |
| dFe–Np | 2.026 | 2.06c | 1.965 | 2.033 | |
| αFe–NO–O | 141.1 | 142c | 136.4 | 139.8 | |
| Eb | −28.2 | −25d, −20e | −24.9 | −35.6 | |
| CO | dFe–C | 1.810 | 1.80c | 1.786 | 1.792 |
| dC–O | 1.163 | 1.17c | 1.169 | 1.168 | |
| dFe–Np | 2.027 | 2.05c | 1.986 | 2.056 | |
| αFe–C–O | 180.0 | 179.9c | 180.0 | 180.0 | |
| Eb | −16.7 | −23.3f | −20.2 | −31.3 | |
The binding geometries of O2, NO and CO molecules to heme were confirmed to reproduce those clarified previously with DFT calculations.29,31,44 That is, these DMs were bound to heme in the asymmetric mode by forming a chemical bond between one atom of the DM and the Fe of heme, such as Fe–O, Fe–N and Fe–C, and the other atom of the DM was not bonded, resulting in the formation of a bond angle between Fe and DM. The typical bond lengths and bond angles around Fe, calculated in the present work, were in overall agreement with the available experimental and theoretical data, as shown in Table 1. In contrast, the H2 molecule preferred the symmetric mode to the asymmetric mode when binding to the heme, forming two Fe–H bonds, as found in our previous work with a different DFT method.15 In the heme–H compounds, which could be formed by dissociation of an H2 molecule adsorbed on heme with a relatively low activation barrier, to act as an antioxidation catalyst, the hydrogen atom was bonded to Fe in a vertical line to the porphyrin ring.15 When comparing the different heme groups, the newly formed bond lengths of Fe–H, Fe–O, Fe–N and Fe–C were slightly decreased, while the intramolecular bond lengths of H–H, O–O, N–O and C–O were increased going from FePIm to the models. These indicate that the interaction between Fe and the DM can be enhanced while the interaction between the atoms within the DM can be reduced by using smaller models for the heme group. Compared with those in FePIm, the Fe–Np bond lengths (Np; nitrogen atom of porphyrin or heme) were decreased in model1 and increased in model2. The Fe–DM bond angles were more or less similar among the three heme models.
To evaluate the binding strength, the binding energy Eb was calculated as Eb = Eheme–DM(H) − (Eheme + EDM(H)), where Eb is the DFT total energy of the s species. For the heme–DM(H) compounds, the BSSE correction was considered. For all the species, ZPC and TC at T = 298.15 K were considered for the BSSE-corrected DFT total energy by performing calculations of vibrational frequencies (see Table S1†). For the three heme–H2 models, Eb was found to be positive, indicating an endothermic reaction of heme and H2 binding. However, the heme–H systems showed negative values of Eb, namely −10.6, −44.9 and −44.1 kcal mol−1 for FePIm, model1 and model2, respectively. This means that once the H2 molecule is dissociated on heme, the product of the heme–H compound exists in a stable state. For other DMs of O2, NO and CO, the values of Eb were negative for the three heme models. For the case of FePIm–NO, the calculated value of −28.2 kcal mol−1 agreed well with the experimental value of −25 kcal mol−149 and the previous theoretical value of −20 kcal mol−1.29 For the case of FePIm–CO, our value of Eb was 6.7 kcal mol−1 higher than the previous calculation using the B3LYP/CCSD(T) method.35 It should be noted that the binding structures and energies in these molecular systems depend strongly on the choice of XC functional and basis sets, thus giving a very wide spread of values, and the hybrid XC functionals like B3LYP predict much more accurate binding energies than the pure XC functionals for O2 and CO.35 Harvey and co-workers29,35 found that the B3LYP functional underestimated the bond strength of NO to heme and thus extensive large basis set CCSD(T) calculations should be performed. Alternatively, a multi-configurational method like the complete active space SCF (CASSCF) method can be applied to get more accurate electronic structures with much heavier computational load, as performed by Radón et al.44 In general, the models 1 and 2 showed Eb values that were larger in magnitude than those of FePIm, except for the heme–NO systems, but the differences were not so great.
The order of binding strength was NO > O2 > CO > H > H2 for the FePIm-based systems, while it was H > O2 > NO > CO > H2 for the model-based systems. Such binding characteristics can be explained by performing the analysis of the frontier molecular orbitals (FMOs) and the atomic charges. Fig. 2 shows the FMOs, such as the HOMO and LUMO, proving the quite strong covalent interaction between the Fe d orbitals and DM π* orbitals, especially for the O2 and NO cases. In fact, the π* orbital of O2 is closer in energy to the Fe dz2 orbital than the Fe π* orbitals, thereby obtaining more energy by bending and increasing the overlap.31 In previous work,29 it was found via B3LYP calculations that FePIm has a triplet ground state with a +2 oxidation state of iron. When binding of O2 to Fe(II)-heme occurs, the resultant [FeIIO2] system is isoelectronic with a total of 8 electrons in the d orbitals of iron and π* orbital of O2, leading to a singlet ground state. When binding of NO to Fe(II)-heme occurs, the interaction between three Fe d orbitals (dxz, dyz, and dz2) and two NO  orbitals with a total of 7 electrons induces two bonding orbitals
orbitals with a total of 7 electrons induces two bonding orbitals  , two antibonding orbitals
, two antibonding orbitals 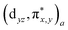 and one nonbonding orbital
and one nonbonding orbital  ,44 leading to a doublet ground state and larger bending angle (141°) than that of O2 (122°). The energy difference between the Fe dz2 orbital and the CO π* orbital is larger than those for O2 and NO, and stabilization is not gained by bending, leading to the almost straight geometry in the three models.31 The FMOs of the heme–H2 and –H compounds looked similar to those of heme–CO compounds, implying similar binding features. From the Mulliken charge analysis (see Table S2†), it was revealed that the ligands, i.e., the side ligand (porphyrin, vinylogous amidine, and amidine) plus the Im or NH3 ligand, accept electrons, and iron donates electrons, when forming the heme–DM or –H molecular systems. Among the adducts, H2, H and CO act as electron donors, whereas O2 and NO act as electron acceptors. Although the absolute amount of transferred electrons upon binding tends to decrease going from FePIm to model1 and to model2, the variation tendencies of the Mulliken charges according to the adducts look quite similar.
,44 leading to a doublet ground state and larger bending angle (141°) than that of O2 (122°). The energy difference between the Fe dz2 orbital and the CO π* orbital is larger than those for O2 and NO, and stabilization is not gained by bending, leading to the almost straight geometry in the three models.31 The FMOs of the heme–H2 and –H compounds looked similar to those of heme–CO compounds, implying similar binding features. From the Mulliken charge analysis (see Table S2†), it was revealed that the ligands, i.e., the side ligand (porphyrin, vinylogous amidine, and amidine) plus the Im or NH3 ligand, accept electrons, and iron donates electrons, when forming the heme–DM or –H molecular systems. Among the adducts, H2, H and CO act as electron donors, whereas O2 and NO act as electron acceptors. Although the absolute amount of transferred electrons upon binding tends to decrease going from FePIm to model1 and to model2, the variation tendencies of the Mulliken charges according to the adducts look quite similar.
Using the HOMO levels (EHOMO) and LUMO levels (ELUMO), we further estimated the chemical stability and reactivity of the molecules, such as the ionization potential (I = −EHOMO), electron affinity (A = −ELUMO), electronegativity  , global hardness (η = I − A), and electrophilicity index
, global hardness (η = I − A), and electrophilicity index  . Note that the electronegativity is the negative of the chemical potential (χ = −μ) and the electrophilicity index (ω) is a measure of the energy stabilization of the molecule caused by maximal electron flow from the environment.50 As listed in Table 2, the heme–O2 complexes have the lowest hardness (1.760, 1.699, and 2.332 eV for FePIm, model1 and model2, respectively) and the highest electrophilicity (5.092, 4.530, and 3.504 eV), indicating that they are the most soft and reactive. The second-lowest hardness and highest electrophilicity were found in NO-based compounds. Meanwhile, the heme–H complexes showed high values of hardness, especially in model1 and model2. Such analysis of global stability parameters is in accord with the findings from the analysis of binding features. It should be noted that the general tendencies of these parameters according to adducts in models 1 and 2 resemble the FePIm systems.
. Note that the electronegativity is the negative of the chemical potential (χ = −μ) and the electrophilicity index (ω) is a measure of the energy stabilization of the molecule caused by maximal electron flow from the environment.50 As listed in Table 2, the heme–O2 complexes have the lowest hardness (1.760, 1.699, and 2.332 eV for FePIm, model1 and model2, respectively) and the highest electrophilicity (5.092, 4.530, and 3.504 eV), indicating that they are the most soft and reactive. The second-lowest hardness and highest electrophilicity were found in NO-based compounds. Meanwhile, the heme–H complexes showed high values of hardness, especially in model1 and model2. Such analysis of global stability parameters is in accord with the findings from the analysis of binding features. It should be noted that the general tendencies of these parameters according to adducts in models 1 and 2 resemble the FePIm systems.
 , global hardness (η = I − A), and electrophilicity index
, global hardness (η = I − A), and electrophilicity index  in the heme–DM and –H compounds (units: eV)
in the heme–DM and –H compounds (units: eV)
| Compound | EHOMO | ELUMO | χ | η | ω |
|---|---|---|---|---|---|
| FePIm | −5.039 | −1.965 | 3.502 | 3.074 | 1.995 |
| FePIm–H2 | −4.941 | −1.957 | 3.449 | 2.983 | 1.994 |
| FePIm–H | −4.747 | −2.075 | 3.411 | 2.672 | 2.178 |
| FePIm–O2 | −5.114 | −3.354 | 4.234 | 1.760 | 5.092 |
| FePIm–NO | −5.013 | −2.172 | 3.592 | 2.842 | 2.271 |
| FePIm–CO | −4.998 | −2.085 | 3.542 | 2.913 | 2.153 |
| Model1 | −3.897 | −0.212 | 2.054 | 3.684 | 0.573 |
| Model1–H2 | −3.959 | −0.206 | 2.082 | 3.752 | 0.578 |
| Model1–H | −4.680 | −0.365 | 2.522 | 4.315 | 0.737 |
| Model1–O2 | −4.773 | −3.074 | 3.924 | 1.699 | 4.530 |
| Model1–NO | −4.507 | −2.397 | 3.452 | 2.110 | 2.823 |
| Model1–CO | −4.432 | −0.471 | 2.451 | 3.961 | 0.759 |
| Model2 | −4.126 | −0.095 | 2.110 | 4.031 | 0.552 |
| Model2–H2 | −4.193 | 0.183 | 2.005 | 4.376 | 0.459 |
| Model2–H | −5.156 | −0.145 | 2.650 | 5.011 | 0.701 |
| Model2–O2 | −5.208 | −2.876 | 4.042 | 2.332 | 3.504 |
| Model2–NO | −4.879 | −1.912 | 3.396 | 2.968 | 1.943 |
| Model2–CO | −4.748 | 0.012 | 2.368 | 4.760 | 0.589 |
3.2 Energetics for displacement reactions
Then, the work proceeded to the next stage of studying displacement reactions between H2 or H and other DMs, namely O2, NO and CO, binding to the heme groups. Firstly, the proper initial configurations were prepared by putting one DM on the FePIm–H2 and –H complexes, and were optimized to produce the initial states (IS) of FePIm–H2⋯DM and FePIm–H⋯DM complexes, where the distance between the DM and H2 or H was controlled to not form a chemical bond. For these optimized structures, we performed AIMD simulations at T = 300 K, confirming that the temperature, starting from 0 K, arrived at ∼300 K within about 0.3 ps and then fluctuated around 300 K after that (see Fig. S1†). For the FePIm–H2⋯DM (DM = O2, NO) complexes, it was observed that H2 was detached while O2 or NO was attached to the FePIm group after about 0.5 ps. In contrast, the CO molecule was observed to be hardly attached to the FePIm group, in accordance with the tendency of the binding energies as discussed above. These results indicate that O2 and NO molecules can easily displace a H2 molecule bound on the heme, but CO cannot do so at room temperature. Meanwhile, it was found from the AIMD simulations of the FePIm–H⋯DM complexes that none of the molecules of O2, NO and CO could displace the H atom attached to FePIm at room temperature. Therefore, there should be activation barriers for the displacement reactions of H by DMs.We determined the activation barriers for these reactions by applying the NEB method, which yielded the transition state (TS) structures lying on the MEP. To do NEB runs, the proper final states (FS) were also prepared by putting a H2 molecule or H atom on the heme–DM complexes and were optimized, resulting in heme–DM⋯H2 or ⋯H complexes. Since the NEB method constructs an approximate MEP between the initial (reactant) and final (product) structures, the TS structures were further refined by performing a saddle-point search using the Driver module, so that the TS had only one imaginary frequency. The displacement reactions of heme–H2 by O2, NO and CO were first considered.
Fig. 3(a)–(c) show the calculated energy profiles and the optimized geometries corresponding to the IS, TS and FS for displacement reactions of H2 by O2, NO and CO on FePIm, model1 and model2. The final states, being the complexes composed of the heme group with an attached DM and detached H2 molecule, were found to be energetically lower than the initial states of the heme–DM⋯H2 complexes for all the cases. When replacing H2 with O2, the final states were 26–32 kcal mol−1 lower in energy than the initial states, and the reaction barriers were calculated to be 3, 7, and 8 kcal mol−1 for FePIm, model1, and model2, respectively (Fig. 3a). For those reactions with NO, the energy reductions of the final states were found to be 5–8 kcal mol−1, being much smaller than those for the O2 and CO cases, and the activation barriers were 2, 3, and 6 kcal mol−1 for FePIm, model1, and model2, respectively (Fig. 3b). The final states of heme–CO⋯H2 were also found to have lowered in energy by 25–28 kcal mol−1 compared with the initial states of heme–H2⋯CO. For these displacement reactions, the activation barriers were calculated to be 3, 1, and 11 kcal mol−1 for FePIm, model1, and model2, respectively (Fig. 3c).
From the optimized structures of the molecular complexes corresponding to the IS and FS for the FePIm cases (Fig. 3a–c), it was found that the adsorbed structures of H2 and DMs onto FePIm were almost preserved, even in the presence of another molecule, for the initial and final states. The shortest distances between the adsorbed H2 and DM in the initial states were found to be 2.27, 3.34, and 3.22 Å for O2, NO, and CO, respectively. In the final states, the distances between the adsorbed DM and H2 were 2.83, 3.99, and 3.52 Å for O2, NO, and CO. Meanwhile, the transition states were observed at a distance over FePIm, and the distances between the H2 and DM were 2.03, 2.79, and 2.42 Å for O2, NO, and CO. Similar findings were obtained for models 1 and 2 (see Fig. S2†).
As found in this work, the activation barriers for displacement reactions of H2 by O2, NO, and CO on heme were quite small, ranging from 1 to 11 kcal mol−1, indicating that these reactions can occur spontaneously at finite temperature, as verified through AIMD simulations. Therefore, one can suppose that molecular hydrogen absorbed onto Hb in a blood cell can be readily displaced by other DMs, especially O2, thereby with no expected harmful influence on the storage and transport of oxygen in the respiratory chain. The same reasoning was also applied to other DMs, such as NO and CO, which exhibit a medicinal effect of propagating intercellular signals. When compared between the three DMs, the energy lowering of the final state was found to be the smallest for the case of NO, while those of O2 and CO were more or less comparable to each other and much larger than that of NO, but the activation barriers were found to be in a similar order. This indicates that O2 and CO can be more favourable for replacing H2 than NO. Interestingly, although they are very simplified structures, models 1 and 2 resembled the displacement reaction paths on FePIm for the three DM cases, in accordance with the binding tendencies.
Then, the displacement reactions of a H atom adsorbed onto heme by other DMs were considered. Fig. 3(d–f) present the energy profiles and optimized geometries of the molecular complexes obtained via NEB runs. In contrast to the H2 cases, the final states of heme–DM⋯H were found to be energetically higher than the initial states of heme–H⋯DM, except in the cases of FePIm–NO and –CO. Furthermore, the activation barriers were calculated to be much higher compared to the cases of H2, indicating that the displacement reaction of a H atom adsorbed on heme could require energy from external sources. This might be related to the stronger binding of H to the Fe of heme compared with that of H2. For the cases of O2, the final states were 35, 27, and 23 kcal mol−1 higher in energy than the initial states, and the activation barriers were calculated to be 55, 35, and 40 kcal mol−1 for FePIm, model1 and model2, respectively. When displacing H with NO, the energy differences between the final and initial states were −6, 16, and 15 kcal mol−1, and the activation barriers were 5, 46, and 38 kcal mol−1 for FePIm, model1 and model2. For the CO cases, the energy differences of the final states from the initial states were −15, 61, and 58 kcal mol−1, and the activation energies were calculated to be 11, 35, and 45 kcal mol−1 for FePIm, model1 and model2. It is distinctive for models 1 and 2 that the relative energies of the transition states are lower than those of the final states and relatively flat plateaus are observed in the energy profiles.
The optimized geometries corresponding to IS and FS were also shown to be well-reproduced compared with the adsorbed structures of H and DM without another molecule or atom. The distances between O2 and H were found to be the smallest (2.20, 1.82 and 2.79 Å in the IS, TS and FS; Fig. 3d) among the three DMs, indicating a strong interaction between O2 and H. Meanwhile, the distances between CO and H were observed to be the largest (3.37, 3.31 and 4.29 Å in the IS, TS and FS; Fig. 3f), proving the weak interaction between CO and H. Similar findings were observed for models 1 and 2 (see Fig. S3†). Such strong and weak interactions between the adsorbates may cause higher and lower activation barriers for the displacement reactions.
In most of the cases, the activation barriers were higher, over 30 kcal mol−1, compared with the H2 displacement reactions, indicating that the H displacement could not occur readily but H and a DM could coexist on heme for a long time. Such coexistence of H and O2 or CO was verified through AIMD simulations carried out at room temperature. Therefore, one can surmise that a H atom adsorbed on heme may disturb the regular respiration of cells with hemoglobin or myoglobin. However, the activation energy for H2 dissociation on protoheme was found to be as high as about 64 kcal mol−1 in our previous work.15 Exceptionally, the activation energy for the reaction with NO on FePIm was found to be very low (5 kcal mol−1), indicating the spontaneous displacement of H by NO, as confirmed by AIMD simulation. This might be associated with the unique interaction between NO and heme, which have unpaired electrons and thus make lone-pair electrons forming a dative chemical bond.
3.3 Kinetics for reactions based on model2
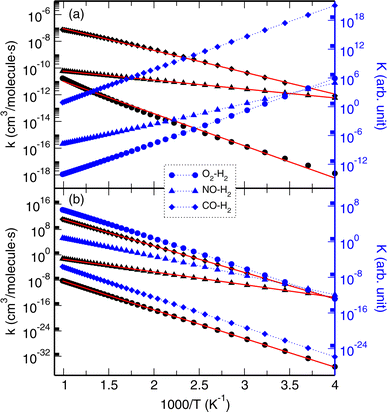
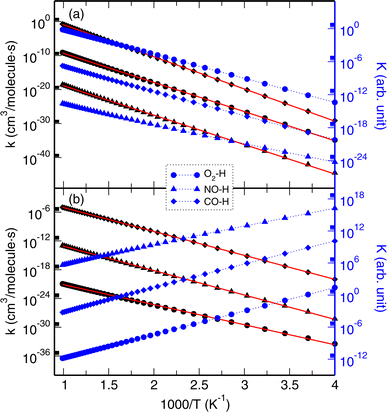
Finally, we calculated the rate constants (k) of H2 or H displacement reactions with DMs on model2 by applying the CVT and RP-VTST formalisms, as implemented in Polyrate using the output of a DIRDYVTST run of NWChem. The equilibrium constants (K) were derived from the calculated rate constants. The backward as well as forward reactions were also considered. The temperature T was changed, ranging from 250 to 1010 K with a step of 30 K.Fig. 4 illustrates the calculated k(T) and K(T) for the H2 displacement reactions. It was confirmed that the calculated rate constants, both for the forward and backward reactions, satisfied the general trend of an exponential increase with increasing temperature according to the Arrhenius equation k(T) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/RT), where R = 8.31 J mol−1 K is the gas constant and Ea is the activation energy. Table 3 lists the determined fitting parameters. For the forward reactions of model2–H2 + DM → model2–DM + H2, the activation energies were determined to be 11, 3, and 8 kcal mol−1 for O2, NO, and CO respectively, which are in reasonable agreement with those (8, 6, and 11 kcal mol−1) from the NEB calculations. The rate constants for the O2 reaction show the highest values in magnitude while those for CO exhibit the lowest values among the three DMs, indicating that the O2 displacement reaction has the slowest rate and the NO reaction has the fastest rate (Fig. 4a). The equilibrium constants exhibit a decreasing tendency with increasing temperature. In accordance with the tendency of the rate constants, the equilibrium constants of the O2 reaction have the lowest values while those of the CO reaction show the highest values in the whole range of temperatures. The rate and equilibrium constants of the NO reaction have moderate values, but the lowest value of the activation energy. For the backward reactions, the activation energies were calculated to be higher than those for the forward reactions, 41, 18, and 38 kcal mol−1 for the O2, NO, and CO cases, respectively, in agreement with the NEB calculations. In contrast to the forward reactions, the equilibrium constants for the backward reactions show an increasing trend with increasing temperature.
exp(−Ea/RT), where R = 8.31 J mol−1 K is the gas constant and Ea is the activation energy. Table 3 lists the determined fitting parameters. For the forward reactions of model2–H2 + DM → model2–DM + H2, the activation energies were determined to be 11, 3, and 8 kcal mol−1 for O2, NO, and CO respectively, which are in reasonable agreement with those (8, 6, and 11 kcal mol−1) from the NEB calculations. The rate constants for the O2 reaction show the highest values in magnitude while those for CO exhibit the lowest values among the three DMs, indicating that the O2 displacement reaction has the slowest rate and the NO reaction has the fastest rate (Fig. 4a). The equilibrium constants exhibit a decreasing tendency with increasing temperature. In accordance with the tendency of the rate constants, the equilibrium constants of the O2 reaction have the lowest values while those of the CO reaction show the highest values in the whole range of temperatures. The rate and equilibrium constants of the NO reaction have moderate values, but the lowest value of the activation energy. For the backward reactions, the activation energies were calculated to be higher than those for the forward reactions, 41, 18, and 38 kcal mol−1 for the O2, NO, and CO cases, respectively, in agreement with the NEB calculations. In contrast to the forward reactions, the equilibrium constants for the backward reactions show an increasing trend with increasing temperature.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp (−B/T) and the determined activation energy Ea = RB (units: kcal mol−1) for displacement reactions on model2
exp (−B/T) and the determined activation energy Ea = RB (units: kcal mol−1) for displacement reactions on model2
| Displacement reaction | Forward | Backward | ||||
|---|---|---|---|---|---|---|
| A | B | Ea | A | B | Ea | |
| O2–H2 | 2.5 × 10−9 | 5545 | 11 | 5.0 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
41 |
| NO–H2 | 2.7 × 10−10 | 1537 | 3 | 4.5 × 102 | 9254 | 18 |
| CO–H2 | 3.8 × 10−6 | 3761 | 8 | 3.3 × 1019 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
38 |
| O2–H | 0.2 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753 753 |
39 | 1.2 × 10−17 | 9618 | 19 |
| NO–H | 6.0 × 10−11 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 918 918 |
40 | 1.0 × 10−8 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720 |
23 |
| CO–H | 3 × 108 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 763 763 |
43 | 0.9 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 488 |
23 |
The calculated rate and equilibrium constants for the H displacement reactions of model2–H + DM → model2–DM + H are presented in Fig. 5. As listed in Table 3, the activation energies for the forward reactions were determined to be 39, 40, and 43 kcal mol−1 for the O2, NO, and CO cases, respectively, in agreement with the NEB calculations (40, 38, and 45 kcal mol−1). For the backward reactions, the activation energies were found to be lower at 19, 23, and 23 kcal mol−1 for the O2, NO, and CO cases, respectively. The H displacement reaction with CO might occur most rapidly among the DMs, whereas the reaction with NO might occur most slowly, due to them having the highest and lowest values of rate constants. For the backward reactions, the CO reaction also occurs most rapidly, while the O2 reaction progresses most slowly among the DMs. The equilibrium constants for the forward reactions show an increasing trend as temperature increases, but those for the backward reactions show a decreasing tendency.
4 Conclusions
In this work, we have studied the binding properties of molecular hydrogen to heme in competition with DMs, and their displacement reactions, using DFT and VTST calculations. The heme group was modeled using FePIm, model1 and model2, while various molecular complexes were constructed by combining DMs, namely H2, O2, NO and CO, or a H atom with the modeled heme groups. From the analysis of the structures and energetics of the molecular complexes, heme–DM and –H, which were optimized using the B3LYP/6-311G and LANL2DZ_ECP method, it was found that the Fe–DM bond angles were similar among the three heme models and the O2 complexes have the lowest hardness and the highest electrophilicity for the three models. Moreover, the general tendencies of the structural properties and reactivity in models 1 and 2 resemble those of FePIm, indicating that the simplified models can be used for further calculations. The difference was in the order of the binding strength of DMs or H to the Fe of heme, being NO > O2 > CO > H > H2 for the FePIm-based complexes but H > O2 > NO > CO > H2 for the model-based complexes. Through AIMD simulations of FePIm–H2⋯DM and FePIm–H2⋯DM complexes, it was observed that on FePIm, H2 could be readily replaced by O2 and NO but not by CO, whereas H could be displaced by NO but not by O2 and CO at room temperature. The activation energies for H2 or H displacement reactions with other DMs were determined by applying the NEB method, revealing that the H2 displacement by O2, NO and CO could occur almost spontaneously due to the very low activation energies of below 11 kcal mol−1, but H-atom displacement should require a large amount of energy, due to the high activation energies of over 30 kcal mol−1 for the three heme models. Finally, we calculated the rate and equilibrium constants as functions of temperature for the displacement reactions based on model2, confirming that the rate constants satisfy the general tendency of increasing with increasing temperature and the activation energies determined by fitting into the Arrhenius equation agreed well with those from the NEB calculations. With these findings, we believe that the present work can contribute to the understanding of the efficacy of molecular hydrogen towards vascular diseases and the development of enhanced medicine.Author contributions
Chol-Jun Yu developed the original project. Yun-Kyong Ri, Song-Ae Kim and Chol-Jun Yu performed the calculations and drafted the first manuscript. Yun-Hyok Kye, Yu-Chol Jong and Myong-Su Kang assisted with the post-processing of calculation results, and contributed to useful discussions. Chol-Jun Yu supervised the work. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported as part of the basic research project “Design of New Energy Materials” (No. 2021-12) funded by the State Commission of Science and Technology, DPR Korea. Computations have been performed on the HP Blade System C7000 managed by the Faculty of Materials Science, Kim Il Sung University.References
- T. W. LeBaron, B. Kura, B. Kalocayova, N. Tribulová and J. Slezák, Molecules, 2019, 24, 2076 CrossRef CAS PubMed
.
- D. Wang, L. Wang, Y. Zhang, Y. Zhao and G. Chen, Biomed. Pharmacother., 2018, 104, 788–797 CrossRef CAS PubMed
.
- T. Hasegawa, M. Ito, S. Hasegawa, M. Teranishi, K. Takeda, S. Negishi, H. Nishiwaki, J. Takeda, T. W. LeBaron and K. Ohno, Int. J. Mol. Sci., 2022, 23, 2888 CrossRef CAS PubMed
.
- R. Yamamoto, K. Homma, S. Suzuki, M. Sano and J. Sasaki, Sci. Rep., 2019, 9, 1255 CrossRef PubMed
.
- S. Ohta, Biochim. Biophys. Acta, Gen. Subj., 2012, 1820, 586–594 CrossRef CAS PubMed
.
- M. Dole, F. R. Wilson and W. P. Fife, Science, 1975, 190, 152–154 CrossRef CAS PubMed
.
- I. Ohsawa, M. Ishikawa, K. Takahashi, M. Watanabe, K. Nishimaki, K. Yamagata, K. ichiro Katsura, Y. Katayama, S. Asoh and S. Ohta, Nat. Med., 2007, 13, 688–694 CrossRef CAS PubMed
.
- Q. Hu, Y. Zhou, S. Wu, W. Wu, Y. Deng and A. Shao, Biomed. Pharmacother., 2020, 130, 110589 CrossRef CAS PubMed
.
- B. Kura, A. K. Bagchi, P. K. Singal, M. Barancik, T. W. LeBaron, K. Valachova, L. Šoltés and J. Slezák, Can. J. Physiol. Pharmacol., 2019, 97, 287–292 CrossRef CAS PubMed
.
- Y. Ming, Q. Ma, X. Han and H. Li, Exp. Ther. Med., 2020, 20, 359–366 CrossRef CAS PubMed
.
- M. Barancik, B. Kura, T. W. LeBaron, R. Bolli, J. Buday and J. Slezak, Antioxidants, 2020, 9, 1281 CrossRef CAS PubMed
.
- Y. Zhang, S. Tan, J. Xu and T. Wang, Cell. Physiol. Biochem., 2018, 47, 1–10 CrossRef PubMed
.
- T. Kiyoi, S. Liu, E. Takemasa, H. Nakaoka, N. Hato and M. Mogi, PLoS One, 2020, 15, e0227582 CrossRef CAS PubMed
.
- A. Tamasawa, K. Mochizuki, N. Hariya, M. Saito, H. Ishida, S. Doguchi, S. Yanagiya and T. Osonoi, Eur. J. Pharmacol., 2015, 762, 96–101 CrossRef CAS PubMed
.
- S.-A. Kim, Y.-C. Jong, M.-S. Kang and C.-J. Yu, J. Mol. Model., 2022, 28, 287 CrossRef CAS PubMed
.
- D. Moris, M. Spartalis, E. Spartalis, G.-S. Karachaliou, G. I. Karaolanis, G. Tsourouflis, D. I. Tsilimigras, E. Tzatzaki and S. Theocharis, Ann. Transl. Med., 2017, 5, 326 CrossRef PubMed
.
- E. Hood, E. Simone, T. Wattamwar, P. Dziubla and V. Muzykantov, Nanomedicine, 2011, 6, 1257–1272 CrossRef CAS PubMed
.
- H. Li, Y. Luo, P. Yang and J. Liu, J. Neurol. Sci., 2019, 396, 240–246 CrossRef CAS PubMed
.
- S. Takeuchi, K. Nagatani, N. Otani, H. Nawashiro, T. Sugawara, K. Wada and K. Mori, BMC Neurosci., 2015, 16, 22 CrossRef PubMed
.
- C. S. Huang, T. Kawamura, Y. Toyoda and A. Nakao, Free Radical Res., 2010, 44, 971–982 CrossRef CAS PubMed
.
- Y.-S. Ge, Q.-Z. Zhang, H. Li, G. Bai, Z.-H. Jiao and H.-B. Wang, Hepatobiliary Pancreatic Dis. Int., 2019, 18, 48–61 CrossRef CAS PubMed
.
- J. Yu, Q. Yu, Y. Liu, R. Zhang and L. Xue, PLoS One, 2017, 12, e0173645 CrossRef PubMed
.
- C. H. Chen, A. Manaenko, Y. Zhan, W. W. Liu, R. P. Ostrowki, J. Tang and J. H. Zhang, Neuroscience, 2010, 169, 402–414 CrossRef CAS PubMed
.
- G. J. Kubas, R. R. Ryan, B. I. Swanson, P. J. Vergamini and H. J. Wasserman, J. Am. Chem. Soc., 1984, 106, 451–452 CrossRef CAS
.
- Y. Jean, O. Eisenstein, F. Volatron, B. Maouche and F. Sefta, J. Am. Chem. Soc., 1986, 108, 6587–6592 CrossRef CAS
.
- P. J. Hay, J. Am. Chem. Soc., 1987, 109, 705–710 CrossRef CAS
.
- P. J. Hay, Chem. Phys. Lett., 1984, 103, 466 CrossRef CAS
.
- G. J. Kubas, Acc. Chem. Res., 1988, 21, 120–128 CrossRef
.
- J. Oláh and J. N. Harvey, J. Phys. Chem. A, 2009, 113, 7338–7345 CrossRef PubMed
.
- I. Degtyarenko, R. M. Nieminen and C. Rovira, Biophys. J., 2006, 91, 2024–2034 CrossRef CAS PubMed
.
- L. M. Blomberg, M. R. A. Blomberg and P. E. M. Siegbahn, J. Inorg. Biochem., 2005, 99, 949–958 CrossRef CAS PubMed
.
- M. Tsuda, E. S. Dy and H. Kasai, Eur. Phys. J. D, 2006, 38, 139–141 CrossRef CAS
.
- J. P. Arcon, P. Rosi, A. A. Petruk, M. A. Marti and D. A. Estrin, J. Phys. Chem. B, 2015, 119, 1802–1813 CrossRef CAS PubMed
.
- H. Chen, W. Lai and S. Shaik, J. Phys. Chem. B, 2011, 115, 1727–1742 CrossRef CAS PubMed
.
- N. Strickland and J. N. Harvey, J. Phys. Chem. B, 2007, 111, 841–852 CrossRef CAS PubMed
.
- I. Degtyarenko, X. Biarnés, R. M. Nieminen and C. Rovira, Coord. Chem. Rev., 2008, 252, 1497–1513 CrossRef CAS
.
- M. Tsuda, W. A. Dino, H. Nakanishi and H. Kasai, Chem. Phys. Lett., 2005, 402, 71–74 CrossRef CAS
.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS
.
- F. B. van Duijneveldt, J. G. C. M. Van Duijneveldt-Van De Rijdt and J. H. Van Lenthe, Chem. Rev., 1994, 94, 1873–1885 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- M. Radón, E. Broclawik and K. Pierloot, J. Phys. Chem. B, 2010, 114, 1518–1528 CrossRef PubMed
.
- B. Long, Y. Wang, Y. Xia, X. He, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2021, 143, 8402–8413 CrossRef CAS PubMed
.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC
.
- R. Steckler, W.-P. Hu, Y.-P. Liu, G. C. Lynch, B. C. Garrett, A. D. Isaacson, V. S. Melissas, D. h. Lu, T. N. Truong, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1995, 88, 341–343 CrossRef CAS
.
- J. Vojtechovsky, K. Chu, J. Berendzen, R. M. Sweet and I. Schlichting, Biophys. J., 1999, 77, 2153–2174 CrossRef CAS PubMed
.
- O. N. Chen, S. Groh, A. Liechty and D. P. Ridge, J. Am. Chem. Soc., 1999, 121, 11910–11911 CrossRef CAS
.
- R. G. Parr, L. V. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Tables for binding energetics and Mulliken charges, and figures for fluctuations in temperature and energy during AIMD simulations and optimized geometries corresponding to the IS, TS and FS during NEB runs for models. See DOI: https://doi.org/10.1039/d4ra02091j |
| This journal is © The Royal Society of Chemistry 2024 |