Probing the mechanism of guest–framework bonding interactions through a first-principles study on the structural and electronic properties of type-II clathrate A_xSi₁₃₆ (A = Na, K, Rb; 0 ≤ x ≤ 24) under pressure

Abstract

The role of noncovalent bonding, including multiatomic interactions (van der Waals-like forces) and ionic characteristics, in the intermetallic clathrate A_xSi₁₃₆ (A = Na, K, Rb; 0 < x ≤ 24) is qualitatively discussed. Using the local density approximation (LDA) to density functional theory (DFT), we investigated the effect of different guest filling and pressure parameters on the structural and electronic properties of these materials. In the context of the rigid-band model, we first noted that the competition between van der Waals-like multiatomic interactions and ionicity due to the extent of charge transfer responsible for guest–framework complexes accounts for the nonmonotonic structural response upon guest filling in A_xSi₁₃₆ (0 ≤ x ≤ 8), which is in good agreement with previous experimental findings as well as theoretical predictions. In comparison with computational work initiated under zero temperature and pressure conditions, the DFT calculations at high pressure (P = 3 GPa) show no apparent variation with respect to the electronic structure. Regarding the A₁₆Si₁₃₆ compound, the encapsulated sodium atoms residing in the 20-atom cage cavity act as centers of somewhat localized electrons compared with the alkaline metal sites inside Si₂₈ cage voids. Moreover, the substitution of heavier guest atoms (e.g., Rb) for all the Na atoms in Na₈Si₁₃₆ yields less significant charge transfer between the guest and framework constituents. The net effect of quickly increasing multiatomic interactions and slowly decreasing ionic bonding between the encapsulated atom and Si₂₈ cage may prevent the entire lattice configuration from contracting in a more rapid way when guest species are tuned from Na to Rb in A_xSi₁₃₆ (A = Na, Rb; 0 < x ≤ 8) with increased composition x. In other words, the coulombic attraction due to ionic bonding slightly outweighs the repulsive interaction between the Rb atom and Si₂₈ cage. In addition, the determined formation energy per conventional unit cell in K₈Si₁₃₆, Rb₈Si₁₃₆ and Na₁₂Si₁₃₆ attains a minimum value, demonstrating the stabilizing effect of guests incorporated into “oversized” cage cavities.

---

I. Introduction

Metastable materials with clathrate phases have recently emerged and become formidable in the field of thermoelectric (TE) applications.^1–5 Because it is capable of efficiently converting waste heat into recycled power, TE clathrate serves as a competitive candidate for harvesting energy.^6–10 In the group-14 clathrate, inorganic open-framework atoms (C, Si, Ge or Sn), indexed as the minimal “building blocks”, are in a fourfold coordinated sp³ bonding configuration. Group-14 clathrate structures are generally identified as type I or II according to their different stoichiometric compositions and polyhedral cage characteristics. Among these two expanded-volume phases, relatively few results have been obtained for the type II structure, which crystallizes in the cubic structure labeled Fd3̄m (space group no. 227) under ambient conditions.^11–13 Type II binary clathrate compounds are normally described by the general formula AL_xM₁₃₆ (AL = alkaline metal or alkaline-earth metal; M = Si, Ge, Sn; 0 < x ≤ 24). Here, the “guest” impurity denoted by AL can be filled into two different sized cages: 20-atom (M₂₀, dodecahedron) and 28-atom (M₂₈, hexakaidecahedron) cages. These two categories of cages are arranged periodically in a 2 : 1 ratio in the 136-atom unit cell. Moreover, 34 tetrahedrally bonded atoms are situated within the primitive unit cell of the “guest-free” clathrate, forming a face-centered cubic (FCC) structure. The larger cubic unit cell (M₁₃₆) can also be visualized as the supercell (SC) form of such a 34-atom unit cell. On the other hand, the conventional unit cell containing 136 atoms is “computationally equivalent” to its primitive counterpart. In other words, both of these unit cells are exactly and completely equivalent descriptions of the infinite lattice. In addition, the computation time length, which approximately scales with N² ln N (N: total number of atoms in the unit cell) within the framework of the periodic DFT method, is significantly prolonged when considering Si₁₃₆ rather than Si₃₄. Therefore, we chose to perform density functional theory (DFT) calculations on the basis of the A_xSi₃₄ (A = Na, K, Rb; 0 ≤ x ≤ 6) format instead of the chemical stoichiometry A_xSi₁₃₆ (A = Na, K, Rb; 0 ≤ x ≤ 24) throughout this entire paper.

A_xSi₁₃₆, a novel representative of guest–host complexes, has attracted increasing attention from researchers.^14–19 However, the detailed mechanism that governs the guest–framework bonding interactions in A_xSi₁₃₆ remains unresolved. The stabilizing effect of alkaline metal (Na, K, Rb) filling Si₂₈ cages (0 < x ≤ 8) as a preferential choice leads to a nonmonotonic structural response, which is qualitatively described by lattice contraction instead of expansion in our earlier study.²⁰ Accordingly, experimental results have shown a nonmonotonic structural response to guest filling in Na_xSi₁₃₆ (x = 0, 4, 8). Specifically, lattice contraction occurs as sodium is initially and solely introduced into Si₂₈ (28-atom cage) voids while leaving all 20-atom cage cavities intact. These novel findings motivated us to examine dissimilar guest–framework bonding interactions for Na@Si₂₈ (sodium “impurity” inside the silicon hexakaidecahedron) and Na@Si₂₀ (sodium “impurity” inside the silicon dodecahedron) in the current work. Furthermore, such guest–host complexes are held together in unique structural relationships through noncovalent bonding between guest atoms and framework constituents. Commonly mentioned types of noncovalent interactions include ionic bonding, hydrogen bonding and van der Waals forces (multiatomic interactions).²¹ Probing the impact of guest–framework bonding interactions on the structural and electronic properties of materials, which is of great interest, has become an important field because it can be fairly useful in material design. Moreover, the discovery of superconductivity in type I metal-doped Na_xBa_ySi₄₆ has led to a similar curiosity about type II “cage-structured” clathrate compounds with identical minimal “building blocks” originating from Si.²² For instance, H. Kawaji et al. observed a critical temperature (T_C) of approximately 4 K for (Na,Ba)_xSi₄₆.²³ In addition, the presence of metallic guests inside (Ba_1−xSr_x)₈Si₄₆ (0 ≤ x ≤ 1) can modify the electronic structure of bare Si₄₆, resulting in the formation of a high density of states (DOS) peak around the Fermi energy (E_F) level. It is then expected that the localized sharp peak of the DOS at E_F contributes to the increasing T_C of the superconducting phase. In addition, research concerning the structural and electronic behaviors of A_xSi₁₃₆ under pressure has rarely been conducted to the best of our knowledge. According to recent studies, G. K Ramachandran et al. examined the phase transformation of Si₁₃₆ in the pressure range of 0 to 12 GPa.²⁴ It is therefore of much interest to examine the impact of pressure on charge transfer from the guest to the silicon framework upon guest doping in this paper.

The interest in structural stability issues, electronic features, and guest–framework bonding interaction mechanisms of type II clathrate compounds is rooted not only in the field of experimenters but also within the scope of theoretical explorers. As early as 1965, scientists managed to synthesize the first-generation silicon clathrates Na₈Si₄₆ and Na_xSi₁₃₆ (x < 11), which paved the way for subsequent investigations within this field.²⁵ Combined with unprecedented progress in high-performance computing facilities, an increasing amount of theoretical work focusing on clathrate compounds has become widely recognized in recent decades. An early example of this is the calculational study on the electronic structure of Na_xSi₁₃₆ (x = 0, 4, 8, 16, 24) by Smelyansky et al. in 1997.²⁶ In this paper, the authors verified the prominent metallic character of Na_xSi₁₃₆ when the composition x of the Na metal exceeded 8. In addition, the lattice geometry changes very little as the Na composition x is tuned directly from 3 to 24 according to previous work. In addition to A_xM₁₃₆ and A_xM₄₆, ternary and quaternary type II clathrate compounds as well as their type VIII counterparts have drawn significant attention from many research groups.²⁷ For instance, first-principle work relating to the determination of the electronic and vibrational features of Rb_7.3Na₁₆Ga₂₀Si₁₁₆, Cs₈Na₁₆Ga₂₁Si₁₁₅, Cs₈Ga₈Si₁₂₈, and Rb₈Ga₈Si₁₂₈ has been presented by means of density functional theory (DFT).^28,29 Furthermore, structural and thermoelectric analyses with respect to Rb₈Na₁₆Si₁₃₆ and Cs₈Na₁₆Si₁₃₆ were also experimentally performed.³⁰ However, the detailed mechanism accounting for why framework contraction occurs upon impurity guest doping (x changes from 0 to 4 and to 8) in A_xSi₁₃₆ (A = Na, K, Rb; 0 < x ≤ 24) still awaits intensive exploration. In other words, it is necessary and intriguing to investigate how chemical bonding, which is closely related to guest–host interactions in A_xSi₁₃₆, affects the structural and electronic characteristics of the material of interest. Additionally, motivated by some of the above experimental studies on alkali metal-containing clathrate, we performed a theoretical investigation confirming the structural stability of the clathrate A₈Si₁₃₆, in which all the hexakaidecahedron cages preferentially encapsulate the guest (A), while the other dodecahedron cages appear to be empty even under high pressure conditions.^18,30–33

Recently, the search for state-of-the-art thermoelectric clathrates has prevailed. Despite the novelty associated with the cage structure, the quantitative parameter that marks a promising clathrate candidate for power generation is a high dimensionless figure of merit ZT (>1). Thermoelectric material normally possesses the dimensionless figure of merit defined as: ZT = TS²σ/κ where, Z is the figure of merit, T is the temperature, S is the Seebeck coefficient of the material, σ is the electrical conductivity and κ is the total thermal conductivity of the material. Many synthesized clathrate compounds (e.g., Eu₈Ga₁₆Ge₃₀ and Sr₈Ga₁₆Ge₃₀) that meet the “phonon glass electron crystal” (PGEC) criteria are known to exhibit semiconducting or intermetallic behavior while possessing excellent ZT values.³⁴ The encapsulated “guest” atoms inside the “cage-structured” voids can vibrate resonantly with framework atoms, thus contributing to scattering heat-carrying acoustic phonons and enhancing ZT. Apart from such resonant vibrations from the phonon spectrum standpoint, the guest–framework bonding interaction is still not precisely understood due to the lack of systematically detailed exploration of the relevant electronic band structure, total and projected electronic density of states, etc. In this paper, we perform ab initio calculations to inspect these unique properties of stabilized A_xSi₁₃₆ compounds from an electronic point of view. The effects of pressure and guest filling on relevant electronic structures are also discussed.

II. Methodology

Our calculational work implemented by the Vienna Ab initio Simulation Package (VASP) is within the framework of density functional theory.^35–37 As initially proposed by Hohenberg, Kohn, and Sham, the DFT method has experienced many refinements to reduce the discrepancy between the predicted ground state properties and their experimental counterpart results. Consequently, the local density approximation (LDA) or generalized gradient approximation (GGA) was appropriately incorporated into the exchange–correlation functional, while no d or f electrons need to be considered at the current stage. These approximations help increase the accuracy as the computational time increases. In this paper, only the LDA to density functional theory is employed to approximate the exchange–correlation effect, and the projected augmented wave (PAW) method is used to determine the electronic properties, including the band structure, total and projected density of states, bulk modulus, elastic constant, and other ground state properties in the chosen range of external pressures. In this paper, we also presented calculations of the total free energy and formation enthalpy concerning the phase stability of A_xSi₁₃₆. Normally, obtaining more accurate results requires us to choose PAW potentials rather than ultrasoft pseudopotentials. This is because of two obvious factors: first, the radial cutoffs of the core remain smaller than the radii used for the ultrasoft pseudopotentials; second, the PAW potentials reconstruct the exact valence wave functions with all nodes in the core region. In other words, using PAW potentials can guarantee the achievement of accuracy while reducing the computational effort. According to the outermost electron configuration of Si (3s²3p²), these electrons are selected as the valence electrons. It is widely recognized that alkaline metal atoms in A-doped silicon clathrates preferentially occupy the 8b Wyckoff position.

The first calculation step involved obtaining a geometrically optimized configuration, under which the electronic structure was then calculated. The ionic positions are optimized by minimizing the total binding energy, provided that a fixed unit cell volume has already been built. This self-consistent process is carried out repeatedly for a range of cell volumes. Group theory is simultaneously applied by the simulation package to reduce the computational cost of acquiring energy and force. Finally, the LDA energy versus volume is fit into the 3^rd Birch–Murnaghan equation of state (EOS), resulting in the structural and geometrical parameters at the equilibrium state. Moreover, the optimized lattice constant can be determined according to the global minimum energy generated from the Birch–Murnaghan EOS.

Due to the large number of atoms in the unit cell of the A_xSi₁₃₆ compounds, the Monkhorst–Pack scheme was used before setting up the k-points in the Brillouin zone in the 4 × 4 × 4 mode. Moreover, the Methfessel–Paxton scheme was also used. The energy cutoff parameters of the PAW potentials are carefully selected to ensure the accuracy of the calculations for each clathrate compound of interest. In other words, 250 eV was determined to be reliably effective for the entire calculational work. The energy convergence is set to 5 × 10⁻⁶ eV per atom, and the interatomic interaction force convergence standard is set to 0.1 eV nm⁻¹. Moreover, the inner crystal stress convergence standard is set to 0.02 GPa, while the maximum atomic displacement convergence standard is given by 5 × 10⁻⁵ nm. A conjugate-gradient (CG) algorithm is constructed to relax the ions into their instantaneous ground state before the electronic feature details are revealed.

III. Results and discussion

A. Structural properties

The A_xSi₁₃₆ binary clathrate system possesses a conventional unit cell, which faces the center cubic of Fd3̄m symmetry. In total, 136 silicon atoms are tetrahedrally coordinated and are pertinent to two types of polyhedral cages: eight hexakaidecahedra [5¹²6⁴] and sixteen dodecahedra [5¹²]. The interaction between neighboring silicon atoms in the bare Si₁₃₆ configuration is covalent. Although it is possible to have both [5¹²6⁴] and [5¹²] occupied after guest atoms are chemically “inserted”, the order of which type of polyhedron should be filled upon the doping process is not random. In other words, many early studies, including those involving power X-ray diffraction data, verified that hexakaidecahedron cages are preferentially occupied by sodium until they are full.¹⁸ Moreover, as the composition x (x > 8) exceeds 8, the dodecahedron cages can begin to encapsulate the remaining x − 8 guest atoms. Some early work reported that the order of guest filling concerning two different polyhedral cages is unique. This is believed to correlate with the degree of occupation of Si₁₃₆ antibonding states.³⁸ A detailed analysis of this topic is presented below. Furthermore, the preferential cage occupancy is accompanied by an unusual structural response, leading to lattice framework contraction rather than expansion occurring once x changes from 0 to 4 and to 8. To our knowledge, this work is the first to indicate that the dominant attractive interaction due to ionic bonding between positively charged guest and cage network atoms that carry negative charges outweighs the multiatomic bonding (van der Waals like) between the entire guest atom and cage cavity Si₂₈ in the case of Na_xSi₁₃₆ (x = 4, 8). This ionic character here is distinguished from the conventionally defined ionic bond between the monovalent cation and the monovalent anion in the NaCl structure. Instead, the charge transferred from sodium to the framework atoms is assumed to be uniformly distributed among the silicon network atoms, leading to the resultant ionic bonding between the Na atom and its surrounding cage cavity. In other words, the net interaction due to multiatomic bonding and ionic bonds is believed to be attractive, causing unusual lattice contraction. The replacement of heavy guest (e.g., Rb) by Na in A_xSi₁₃₆ (0 < x ≤ 8) with a fixed composition can lead to a smaller size difference between the guest and Si₂₈ framework, indicating the existence of stronger multiatomic bond repulsions while slightly weakening the extent of charge transfer between Rb and host atoms in the same cage cavity. Eventually, competition between repulsive multiatomic bonding and attractive ionic bonding causes the whole lattice of Rb_xSi₁₃₆ (x = 4, 8) to contract in a less rapid way (see Fig. 2(a) and (c)), indicating that net guest–host interactions are still attractive. For each A₁₆Si₁₃₆ (A = Na, K, Rb), the ionic bonding strength remains higher in Si₂₈ cages than in their Si₂₀ counterparts. This is because of the relatively low amount of charge transfer between the guest (A) and the constituent atoms of the Si₂₀ cages compared with the charge transfer behavior inside the Si₂₈ cage cavities. In short, the competition between multiatomic interactions and ionic bonding influences the net effect of various noncovalent bonding interactions. In addition to intensive discussions on the above issues, this paper initially examines the impact of pressure on the structural and electronic properties of the A_xSi₁₃₆ system.

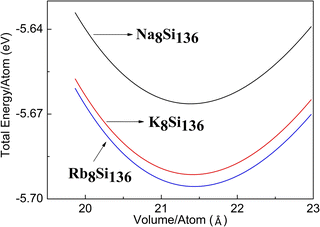
For the sake of capturing the optimized lattice constant, the energy versus volume curve is acquired by means of the 3^rd Birch–Murnaghan equation of state at first stage. Fig. 1 shows the energy versus volume curve for the different A₈Si₁₃₆ (A = Na, K, Rb) clathrates in the presence of P = 0 GPa. It is seen that the energy per atom is slightly less for Na₈Si₁₃₆ when compared to the other two compounds.

Fig. 1 Equation of state (E vs. V) of A_xSi₁₃₆ (A = Na, K, Rb).

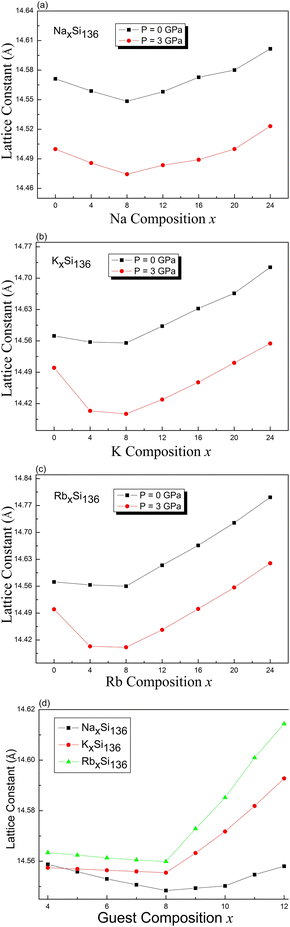
Using intuitive language, we determined the lattice constant for the cage-structured system A_xSi₁₃₆ under pressures of P = 0 GPa and P = 3 GPa, as shown in Fig. 2. The “guest-free” A₀Si₁₃₆ structure undergoes configurational compression at pressures greater than 0 GPa. Trends for the variation in the lattice constant have also been theoretically observed for each fixed alkaline composition in the subdiagrams labeled (a), (b), and (c). For the case of Na_xSi₁₃₆, lattice contraction as Na is introduced solely into the Si₂₈ cages for Na_xSi₁₃₆ (x = 4, 8) repeatedly occurs at nonzero pressure, which is analogous to our previous calculations obtained at P = 0 GPa.²⁰ As seen from the numerical results in Fig. 2(a), our computed minimum lattice constant for Na_xSi₁₃₆ is 14.548 Å at P = 0 GPa and 14.474 Å at P = 3 GPa. Early experimental report has pointed out the occupancies of Na@Si₂₀ and Na@Si₂₈, motivating us to perform our current calculational work.¹⁸ This is to say, the oversized cages are filled first when x < 8 and the smaller cages are then filled when x > 8. Specifically, sodium occupancy of Si₂₀ cages remains to be zero as total Na content is between 0 and about 6.8 according to such report.¹⁸ Meanwhile, a strong preferred occupation by Na of the oversized Si₂₈ cages is observed as the normalized Na occupancy rises to about 0.96 with increased total Na content from 0 to 8. Meanwhile, almost all Si₂₀ cages remain to be empty. Consequently, we conduct our computational work on determining the lattice parameter variation as a function of guest content, while assuming all the Si₂₈ cages should be preferentially occupied before the Na atoms fill into Si₂₀ cages.

Fig. 2 Predicted x dependence of the lattice constant for the type-II clathrate-based compounds (a) Na_xSi₁₃₆ (b) K_xSi₁₃₆ (c) Rb_xSi₁₃₆ under different pressures with 0 ≤ x ≤ 24 and (d) A_xSi₁₃₆ (A = Na, K, Rb; 4 ≤ x ≤ 12) at P = 0 GPa.

Once the sodium atoms are entirely substituted by potassium or rubidium, the lattice contraction shows no prominent feature compared with the lattice variation at P = 3 GPa for a composition of x = 4, 8, as shown in Fig. 2(b) and (c). In other words, the increased atomic weight and expanded volume of guest impurities might significantly weaken the attractive interactions between the guest and Si framework as x is tuned from 0 to 4 and to 8. Fig. 2(d) illustrates the trends for the variation in the lattice constant calculated at zero pressure, in the presence of increased composition value from 4 to 12 in a detailed manner. The minimum lattice parameter for each material is still found when x equals to 8. In addition to these, our calculated lattice parameter of Rb₁₂Si₁₃₆ at zero pressure remains at 14.6144 Å, which is slightly lower than the experimental value (14.7142 Å) for Rb_11.1(1)Si₁₃₆.³⁹ The equilibrium volume of Si₁₃₆ at zero pressure gives a cubic lattice constant of 14.5712 Å, about 0.38% smaller than the experimental value of 14.6269 Å.⁴⁰

To quantitatively verify the preferential occupation of hexakaidecahedron cages by guests upon gradual filling (Δx = 4), the formation energy per unit cell (E_f) for A_xSi₁₃₆ (4 ≤ x ≤ 12) at zero pressure is listed in Table 1. This quantity has the following format:

E_f(A_xSi₁₃₆) = E_AxSi136 − 4E_A − E_Ax−4Si136

where E_A is the energy per alkaline atom in its metal phase, and the definition is similar for the other constituents. From the calculated results for A_xSi₁₃₆ (A = K, Rb), we found that the clathrates in which the large cages are partially or entirely occupied by guests are more thermodynamically stable than the A₁₂Si₁₃₆ clathrate. Furthermore, the minimum formation energies are −8.0464 eV and −8.4220 eV for K₈Si₁₃₆ and Rb₈Si₁₃₆, respectively. For the case of Na_xSi₁₃₆ (x = 4, 8, 12), the formation energy per conventional unit cell continues to decrease when preferential filling of large cages with Na is available. This is consistent with an experimental study that verified that Si₂₀ cages start to encapsulate Na atoms after all Si₂₈ cages are fully occupied by guests.¹⁸ Once the guest choice is tuned from Na to K and to Rb, the value of E_f still decreases because the guest is solely inserted into the empty hexakaidecahedron of Si₁₃₆ with increased composition x (0 < x ≤ 8). Moreover, it is speculated that the unusual lattice response shown in Fig. 2 at P = 0 GPa might be quantitatively associated with the decreased formation energy E_f in A_xSi₁₃₆ (A = K, Rb; x = 4, 8). More details on the guest–framework interaction will be discussed in the next section.

Table 1 Calculated formation energy per conventional unit cell in A_xSi₁₃₆ (A = Na, K, Rb; x = 4, 8, 12) under designated pressure

Compound	Pressure (GPa)	A = Na	A = K	A = Rb
A4Si136	0 GPa	−4.3632	−7.3544	−8.2292
A8Si136	0 GPa	−5.3408	−8.0464	−8.4220
A12Si136	0 GPa	−5.5072	−5.4392	−4.5584

---

B. Electronic band structure

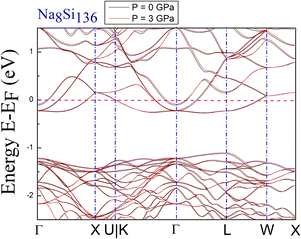
DFT calculations of the band structure at nonzero pressure were performed to examine the impact of high pressure on the electronic properties of Na₈Si₁₃₆. Fig. 2 shows the pressure impact of the reduced atomic volume for the clathrate series Na_xSi₁₃₆, while an unusual structural response still exists according to the associated XRD experiment.¹⁸ For Fig. 3, the symmetric points of the Brillouin zone (BZ) are given by Γ, X, U|K, L and W. The Fermi level is chosen to remain at 0 eV as an energy reference. The overall structure of Na₈Si₁₃₆ at P = 0 GPa is extremely similar to that of Na₈Si₁₃₆ at P = 3 GPa on an energy scale between −2.5 eV and 1.5 eV. The pressure of 3 GPa nearly causes the top of the valence band (VB) to change invariably compared to that of the P = 0 GPa case. However, a small exception exists in the L–W and W–X directions, where the trivial energy discrepancy at the top of the VB is more prominent than that in the other directions. Moreover, the bottom part of the conduction band (CB) between approximately −0.25 eV and 0 eV is almost unaffected by the pressure variation. In addition, the calculated band character is always metallic because the Fermi level lies in the CB for the P = 0 GPa and P = 3 GPa cases.

Fig. 3 Predicted electronic band structures of Na₈Si₁₃₆ under P = 0 GPa and P = 3 GPa conditions.

Each subdiagram labeled (a)–(d) in Fig. 4 shows the band structure of stoichiometric A₈Si₁₃₆ (A = K, Rb) under zero- and high-pressure conditions. Analogous to previous BS characteristics for Na₈Si₁₃₆, the Fermi level is also crossed by several dispersive bands arising from the CB along the Γ–X, Γ–L and Γ–U|K lines in Fig. 4.

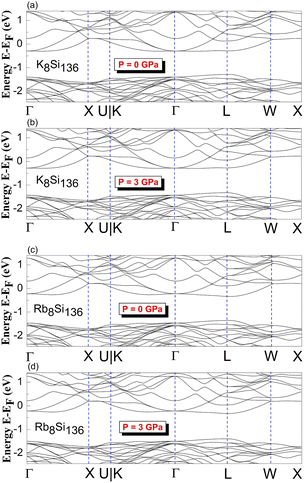Fig. 4 Predicted electronic band structures of (a) and (b) K₈Si₁₃₆ and (c) and (d) Rb₈Si₁₃₆ between P = 0 GPa and P = 3 GPa.

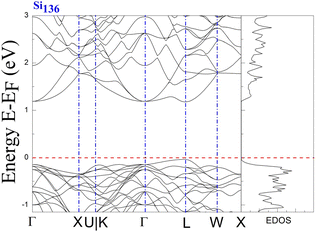
The results clearly demonstrate the metallic character of the compound, whose features are not affected by changes in the external pressure. In addition, our BS calculations indicate that the antibonding states of the pure silicon framework Si₁₃₆ are above the bandgap, as shown in Fig. 5. In contrast, the presence of encapsulated Na atoms in Na₈Si₁₃₆ (see Fig. 3) plays no prominent role in varying the VB structure, leading to qualitative agreement with the so-called “rigid band model”.⁴¹ In other words, the band behavior of guest-containing binary clathrate remains nearly the same as that of its “parent” Si₁₃₆ framework. It is intriguing to investigate how “doped” guests influence the occupation of antibonding states due to the presence of the outermost electrons of alkaline metals under various pressure conditions. Specifically, we present in more detail the calculations to determine to what extent the guest atoms donate to the Si framework with respect to A₈Si₁₃₆ (A = K, Rb) under the designated pressure conditions. Furthermore, the A₈Si₁₃₆ clathrates were found to be metallic with a “pseudogap” that connects the top of the VB to the bottom of the CB, as shown in Fig. 3 and 4. The calculated “pseudogap” is approximately 1.06 eV for K₈Si₁₃₆ at P = 0 GPa and approximately 1.01 eV at P = 3 GPa. For Rb₈Si₁₃₆, the calculated “pseudogap” remains at approximately 1.08 eV at zero pressure and approximately 1.05 eV at 3 GPa. Fig. 5 also shows that the direct band gap of Si₁₃₆ is approximately 1.21 eV. Moreover, the location of the valence band maximum along with the location of the conduction band minimum is found to be at the same site, which is denoted by the high symmetry point L.

Fig. 5 Predicted electronic band structure and electronic density of states of Si₁₃₆ at P = 0 GPa.

C. Electronic density of states

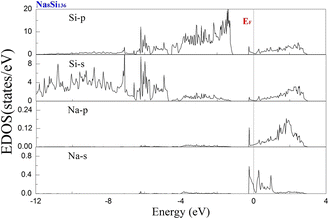
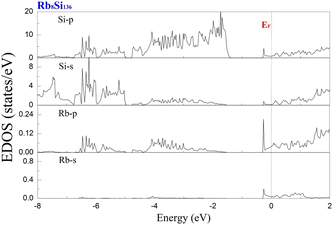
To examine the effect of guest filling on dissimilar guest–host interactions, we show in Fig. 6–9 the total and projected electronic density of states of A_xSi₁₃₆ (A = Na, K, Rb; 0 ≤ x ≤ 16) obtained at T = 0 K. It is widely noted that the crystal structure and chemical stoichiometry of such silicon-based binary clathrates can be described by the Zintl concept. Metallic behavior might be macroscopically manifested by excess electrons originating from guest atoms when coping with the chemical notation of A_xSi₁₃₆. One widely recognized fact that needs to be mentioned here is that the multiatomic interactions between the alkaline guest and the “oversized” Si₂₈ cage are basically repulsive. This is because the radius of the incorporated guest element is close to the cage radius of the Si₂₈ cavity. In other words, the separation between the guest atom and the cage framework atom is always smaller than the atomic radius of the encapsulated atom. When the distance between neighboring atoms is smaller than approximately 0.4 nanometers, the forces are repulsive in nature. The radius of the Si₂₈ cage in Si₁₃₆ is approximately 2.72 Å, while the atomic radius of the alkaline element (Na, K, Rb) ranges from 1.91 Å to 2.38 Å and to 2.55 Å.^42,43 Furthermore, the ionic radius of cation A⁺ (A = Na, K, Rb) is in the range of 0.97 Å and 1.48 Å.⁴³ It is known that multiatomic interactions depend on how tight-fitting a guest atom is inside the cage cavity. For instance, there appears to be less repulsive interaction for Na@Si₂₈ than for Rb@Si₂₈. Similarly, the Si₂₀ cage cavity is significantly repelled by encapsulated alkaline metal atoms such as Na, K, and Rb compared to the same guest incorporated into the “oversized” cage counterpart when considering A_xSi₁₃₆ (x = 12, 16, 20, 24). However, the net guest–host interaction becomes repulsive at the current stage in these materials. In other words, the resultant competition between repulsive multiatomic bonding and attractive ionic bonding causes the Si₂₀ cage to expand, leading to the expansion of the whole lattice of A_xSi₁₃₆ (x = 12, 16, 20, 24). It is also well known that the van der Waals-like repulsive force increases rapidly as the separation between guest atoms and cage framework atoms is gradually reduced.

In general, multiatomic interactions between guest atoms and silicon framework constituents are always repulsive. On the other hand, ionic bonds constructed due to charge transfer between guest and network atoms tend to deflate the relevant cage geometry. Consequently, the competition between ionic and multiatomic Na–Si (or K–Si, Rb–Si) interactions within the identical cage cavity (Si₂₀, Si₂₈) of the framework plays an essential role in affecting the whole lattice volume change. Fig. 6 shows the electronic density of states (EDOS) and p-orbital projected density of states (p-PDOS) for Si₁₃₆, Na₈Si₁₃₆, and Rb₈Si₁₃₆ in the lower portion of the conduction band. The EDOS profiles can be qualitatively described in the context of the rigid-band model. The EDOS profiles for the guest-containing clathrates are nearly the same as those of the empty framework when considering the lower portion of the CB. A small exception can be identified by the sharp peak found around the tail of the CB. This rigid-band behavior means that the guest–framework interaction is predominantly ionic in nature. The multiatomic repulsion between guest atoms and cage cavities is outweighed by such ionicity. Furthermore, there is charge transfer from the guests into the host conduction states. Specifically, the nonzero EDOS at the Fermi level in guest-containing materials is mainly attributed to the p-orbital of Si, indicating charge transfer from the alkaline metal to the framework. In the case of Rb₈Si₁₃₆, the extent of charge transfer seems to be less significant than that in Na₈Si₁₃₆. This is also verified in Fig. 7 and 8, where the s-orbital PDOS for Rb is strongly suppressed in the vicinity of the Fermi level in contrast to the s-orbital PDOS for Na in a similar region. Additionally, the p-orbital PDOS of the silicon framework at the Fermi level is more strongly increased in the Rb₈Si₁₃₆ case than in the Na₈Si₁₃₆ case. In general, Fig. 7–9 show the total electronic density of states along with the projected density of states for Na₈Si₁₃₆, Rb₈Si₁₃₆, and Na₁₆Si₁₃₆ at P = 0 GPa. From Fig. 7, the VB can be divided into two typical parts. First, the density of states corresponding to the energy window between −12 and −7 eV is predominantly attributed to the 3s orbital states of silicon atoms. Second, the contribution stemming from the 3p states of Si seems to be nonnegligible in the same energy interval. The increase in the EDOS from approximately −5 to −1.2 eV is mainly attributed to the 3p states of Si rather than the 3s states. Moreover, the lower part of the CB is composed of 3s and 3p states of Na as well as 3p states of Si.

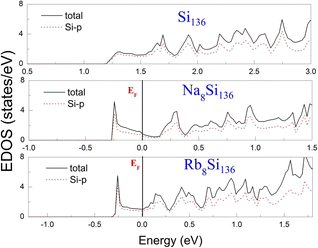Fig. 6 Predicted total EDOS and p-orbital projected EDOS of Si₁₃₆, Na₈Si₁₃₆ and Rb₈Si₁₃₆ at P = 0 GPa.

Fig. 7 Predicted projected EDOS of Na₈Si₁₃₆ at P = 0 GPa.

Fig. 8 Predicted projected EDOS of Rb₈Si₁₃₆ at P = 0 GPa.

Unlike in the case of Na₈Si₁₃₆, Fig. 8 shows that the charge transfer from guests to silicon framework atoms is weakened due to the considerably reduced s-orbital PDOS for Rb at the Fermi level compared to the s-orbital PDOS for Na in Fig. 7. Although the ionic attraction between Rb cations and negatively charged framework atoms is believed to cause the lattice volume to collapse, the rapidly decreased size difference may cause the “oversized” Si₂₈ cage voids to expand in a more significant manner due to the encapsulation of rubidium rather than sodium. In comparison with Na_xSi₁₃₆ (0 ≤ x ≤ 8), the resultant guest–framework interaction, which is attractive in nature, is believed to hinder the extent of lattice volume collapse, leading to a slight decrease in the lattice constant for Rb_xSi₁₃₆ (0 ≤ x ≤ 8) with increasing composition x as a whole (see Fig. 2(c)). Generally, unit cell contraction accompanied by an increase in composition (0 < x ≤ 8) can be attributed to an overall attractive interaction that arises from competition between ionic interactions and multiatomic interactions in A_xSi₁₃₆ (A = Na, K, Rb).

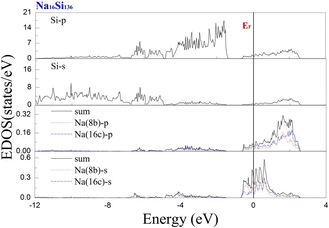
To investigate the guest–host interaction behavior in Si₂₀ cages, the calculated electronic DOS of Na₁₆Si₁₃₆ is shown in Fig. 9. The EDOS profile concerning the lower part of the CB can thus be clearly divided into contributions from Na guests residing at the 8b Wyckoff sites and contributions from equal amounts of Na atoms situated at the 16c Wyckoff sites. The notation “sum” in Fig. 9 yields the summation of the above mentioned contributions from Na guests residing inside different types of cage polyhedra. In the vicinity of the Fermi level, the EDOS contributions due to the incorporation of the s-orbital of Na atoms into Si₂₀ cages remain much lower than those of Na inside “oversized” cages. In other words, the local effect of Na was more pronounced in the Si₂₀ cages than in the Si₂₈ cages. In other words, significant charge transfer occurs from the guest to framework atoms of Si₂₈ cage cavities. The free radius of the Si₂₀ cage is approximately equal to 1.99 Å, which is considerably smaller than that of the Si₂₈ cage.⁴¹ In other words, a significantly decreased size difference between the Na atom and cage cavity may result in extremely strong repulsion. Compared with the resultant attractive interaction between Na and the Si₂₈ cage cavity, the net guest–host interaction involving the Si₂₀ cage becomes repulsive. Similarly, our subsequent computed work also verified that significant charge transfer from K to Si₂₈ framework atoms occurs in comparison with the extent of charge transfer in the Si₂₀ cage of K₁₆Si₁₃₆. The extremely reduced size difference between the Rb atom and Si₂₀ cavity is believed to be the main factor that causes prominent lattice expansion to occur, which can be quantitatively observed in Fig. 2(b) and (c). It is also speculated that the ability of a guest atom to fit inside its cage may help to affect the extent of charge transfer from the guest to framework atoms. The smaller the size difference between the guest and cage cavity is, the weaker the intensity of charge transfer from the guest to framework atoms.

Fig. 9 Predicted projected EDOS of Na₁₆Si₁₃₆ at P = 0 GPa.

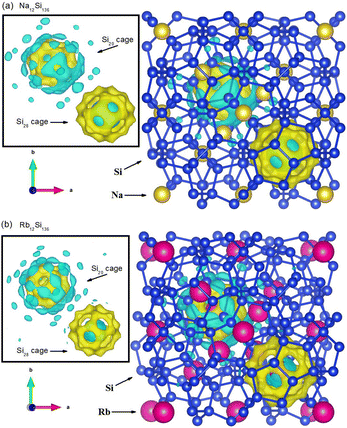
In order to reveal the real-space information when taking guest–framework interaction into consideration, we extract the charge density difference at P = 0 GPa in Fig. 10 from our DFT calculation regarding Na₁₂Si₁₃₆ and Rb₁₂Si₁₃₆, respectively. The inset figure of each subdiagram indirectly demonstrates the charge distribution between the single guest atom and its surrounding cage framework. Also, two distinct colors have been utilized to explain such issue in a qualitative manner. In the presence of Si₂₈ cage, the zone manifested by blue color remains to be the region where the central guest atom lose the electrons. Meanwhile, the zone manifested by yellow color remains to be the region where the cage framework atoms acquire the transferred electrons. This is to say, the ionic bonding nature can be detected when considering Na(or Rb)@Si₂₈ case. In contrast to this, the somewhat covalent bonding formation due to resultant competition between multiatomic repulsive interaction and Coulomb attractive force is observed, when dealing with Na(or Rb)@Si₂₀ case. In order words, the charges arising from the central metallic atom along with the cage framework atoms accumulate in the vicinity between the guest and the edge of Si₂₀ cage cavity. It is also seen that the ionic bonding strength is slightly weakened for Rb residing in the Si₂₈ cage, in contrast to Na encapsulated in the Si₂₈ cage. This correlates with the fact that smaller size difference between the guest and cage cavity leads to weaker intensity of charge transfer from the guest to framework atoms.

Fig. 10 Contour of charge density difference for (a) Na₁₂Si₁₃₆ and (b) Rb₁₂Si₁₃₆.

To determine the effect of elevated pressure on guest–framework interactions in different cage cavities, we implemented calculations to reveal the electronic structures of A₁₆Si₁₃₆ (A = Na, Rb) at P = 3 GPa and T = 0 K. The DFT-determined projected electronic density of states under nonzero pressure are clearly illustrated in Fig. 11. Additionally, the projected EDOS for Rb₁₆Si₁₃₆ at zero pressure is given for comparison. There is no apparent difference in the EDOS profiles of Na₁₆Si₁₃₆ and Rb₁₆Si₁₃₆ at different pressures (see Fig. 9 and 11) when taking the p-orbital contributions of Si atoms to the top of the valence band (−4 to −1.2 eV) structure into account. The influence of elevated pressure on the s-orbital projected density of states for Na atoms is negligibly small. The extent of charge transfer from Na to the Si₂₈ cage framework atoms is greater than that from Na to the Si₂₀ cage constituents at P = 3 GPa. The s-orbital projected EDOS profile at the Fermi level for Rb₁₆Si₁₃₆ in Fig. 11 indicates essential characteristics. Specifically, the contributions to the projected EDOS due to guests localized in different cage polyhedra remain almost the same under the two pressure conditions. This is, however, contrary to the s-orbital projected EDOS at E_F for Na₁₆Si₁₃₆ under both pressure conditions. Finally, Table 2 lists the quantitative calculations of the total and projected EDOS at E_F with respect to the A_xSi₁₃₆ (x = 4, 8, 12) clathrates.

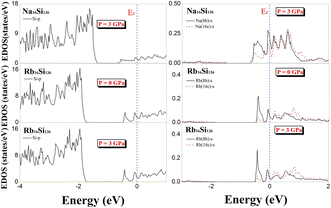Fig. 11 Predicted projected EDOS of Na₁₆Si₁₃₆, Rb₁₆Si₁₃₆ at P = 3 GPa and projected EDOS of Rb₁₆Si₁₃₆ at P = 0 GPa for comparison.

Table 2 Atomic orbital contributions to EDOS at Fermi level in A_xSi₁₃₆ (A = Na, K, Rb; x = 4, 8, 12) under different pressure conditions

EDOS	P = 0 GPa						P = 3 GPa
	NaxSi136		KxSi136		RbxSi136		NaxSi136		KxSi136		RbxSi136
A-s (states per eV)	x = 4	0.58	x = 4	0.168	x = 4	0.046	x = 4	0.535	x = 4	0.156	x = 4	0.043
	x = 8	0.123	x = 8	0.138	x = 8	0.036	x = 8	0.112	x = 8	0.129	x = 8	0.033
	x = 12	0.259	x = 12	0.115	x = 12	0.041	x = 12	0.267	x = 12	0.074	x = 12	0.044
Si-p (states per eV)	x = 4	2.093	x = 4	1.234	x = 4	1.193	x = 4	2.094	x = 4	1.213	x = 4	1.216
	x = 8	0.536	x = 8	0.836	x = 8	0.807	x = 8	0.526	x = 8	0.834	x = 8	0.809
	x = 12	1.136	x = 12	0.945	x = 12	1.538	x = 12	1.197	x = 12	0.846	x = 12	1.679
N(EF)	x = 4	3.176	x = 4	1.712	x = 4	1.516	x = 4	3.116	x = 4	1.666	x = 4	1.459
	x = 8	0.801	x = 8	1.215	x = 8	1.029	x = 8	0.768	x = 8	1.199	x = 8	1.024
	x = 12	1.827	x = 12	1.776	x = 12	2.535	x = 12	1.855	x = 12	1.457	x = 12	2.544

---

Table 2 shows the total density of states at the Fermi level N(E_F) for each A_xSi₁₃₆ (x = 4, 8, 12) under zero pressure. These values are similar to those of the same compositional material, A_xSi₁₃₆, at P = 3 GPa. Additionally, the contributions of the guest atom s states and Si p states to the EDOS at the Fermi level are also evaluated in Table 2. By considering the ratio of the contribution of Si p states to the contribution of guest s states of each binary compound at the two given pressures, we conclude that the strength of the charge transfer from the guest to the Si₂₀ framework decreases to a certain extent in the presence of A₁₂Si₁₃₆ compared to that in the cases of A₄Si₁₃₆ and A₈Si₁₃₆. Similarly, the ratio of the Si p state contribution to N(E_F), which is the total EDOS, experiences a large increase as the compositional value x varies from 4 to 8. Moreover, such characteristics have a weak dependence on external pressure changes. This also indicates that significant charge transfer occurs in the presence of guest atoms, which are incorporated into large cages (Si₂₈).

IV. Conclusions

We used LDA to study the mechanism of guest–framework bonding interactions by investigating the structural and electronic properties of A_xSi₁₃₆ clathrates. We noted that ionic attraction dominates the guest–framework bonding interactions in “oversized” Si₂₈ cage polyhedra. Moreover, significant charge transfer from the guest to framework atoms is believed to increase the extent of ionic bonding, causing the cage framework to contract in a certain manner. For the same alkaline metal, such as Na or K, the extent of charge transfer is normally greater in the 28-atom cage than in the 20-atom cage. These characteristics are also irrelevant to elevated pressure (from P = 0 GPa to P = 3 GPa). Considering the Na guests that are entirely substituted by heavier Rb atoms in Na₈Si₁₃₆ as an example, we have found that less significant charge transfer from Rb to Si framework constituents is available. Moreover, the size difference between the effective guest and cage volume begins to decrease, resulting in a much stronger repulsion between Rb and the Si₂₈ cage. Compared with the lattice constant of “guest-free” Si₁₃₆, ionic and repulsive multiatomic interactions found in the Rb₄Si₁₃₆ and Rb₈Si₁₃₆ cases can lead to a slight decrease in the lattice parameter. In other words, the size difference between the effective guest and cage volume, along with the ionicity due to charge transfer, has a combined impact on the guest–framework bonding interaction. Specifically, the repulsive interaction originating from the size difference between the alkaline metal radius and the Si₂₀ cage radius outweighs the ionic bonding due to charge transfer. Consequently, the whole lattice of A_xSi₁₃₆ (x = 12, 16, 20, 24) clathrates expands with continuously increasing composition value x. From the theoretical point of view, the replacement of Na by heavy guest atoms (K or Rb) in A_xSi₁₃₆ (x = 12, 16, 20, 24) can increase the strength of repulsive multiatomic interactions, while slightly weakening the strength of ionic attraction when taking the fixed composition into account. Moreover, the repulsion due to the decreased size difference between the encapsulated guest and Si₂₀ cage increases more rapidly than the decreased ionic attraction due to weakened charge transfer, resulting in prominent lattice expansion. In addition, the role of pressure and the effect of guest atom character on the structural stability and electronic structures of these clathrates are intensively discussed. It should be emphasized that the band structure, EDOS, and PDOS corresponding to the top portion of the valence band have a very weak dependence on the guest filling and pressure (0 ≤ P ≤ 3 GPa) of the same series of A_xSi₁₃₆ clathrates.

Data availability

The datasets used and analysed during the current study are available from the corresponding author on reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The equipment of the “Milky Way II” at Supercomputer Center in Lvliang is acknowledged for providing access to high performance computing technologies. This work was supported in part by the PhD & Postdoc Research Starup Foundation of Langfang Normal University (XBQ202122).

References

1. M. Christensen, S. Johnsen, F. Juranyi and B. B. Iversen, J. Appl. Phys., 2009, 105, 073508.
2. A. R. Khabibullin, T. D. Huan, G. Nolas and L. M. Woods, Acta Mater., 2017, 131, 475–481.
3. G. S. Nolas, J. L. Cohn, G. A. Slack and S. B. Schujman, Appl. Phys. Lett., 1998, 73, 178.
4. Y. Imai and M. Imai, J. Alloys Compd., 2011, 509, 3924–3930.
5. A. M. Guloy, R. Ramlau, Z. Tang, W. Schnelle, M. Baitinger and Y. Grin, Nature, 2006, 43, 320–323.
6. G. S. Nolas, G. A. Slack and S. B. Schujman, Semicond. Semimetals, 2000, 69, 255–300.
7. G. S. Nolas, B. C. Chakoumakos, B. Mahieu, G. J. Long and T. J. R. Weakley, Chem. Mater., 2000, 12, 1947–1953.
8. L. Qiu, I. P. Swainson, G. S. Nolas and M. A. White, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 035208.
9. K. Suekuni, T. Takasu, T. Hasegawa, N. Ogita, M. Udagawa, M. A. Avila and T. Takabatake, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205207.
10. T. Tadano, Y. Gohda and S. Tsuneyuki, Phys. Rev. Lett., 2015, 114, 095501.
11. M. C. Schäfer and S. Bobev, J. Am. Chem. Soc., 2013, 135, 1696–1699.
12. K. Wei, X. Zeng, T. M. Tritt, A. R. Khabibullin, L. M. Woods and G. S. Nolas, Materials, 2016, 9, 732.
13. M. Beekman and G. S. Nolas, J. Mater. Chem., 2008, 8, 842–851.
14. J. Hubner, Y. Prots, W. Schnelle, M. Bobnar, M. Konig, M. Baitinger, P. Simon, W. Carrillo-Cabrera, A. Ormeci, E. Svanidze, Y. Grin and U. Schwarz, Chem.–Eur. J., 2019, 25, 1–10.
15. J. Chen, A. S. Arvij, X. Zheng, S. Y. Rodriguez and J. H. Ross, J. Alloys Compd., 2014, 593, 261.
16. M. Jing and S. Dong, J. Nat. Gas Chem., 2005, 14, 238–242.
17. X. Connetable and X. Blase, Appl. Surf. Sci., 2004, 226, 289–297.
18. M. Beekman, E. N. Nenghabi, K. Biswas and C. W. Myles, Inorg. Chem., 2010, 49, 5338–5340.
19. Y. Li, J. C. T. Garcia, N. Chen and L. Liu, J. Appl. Phys., 2013, 113, 203908.
20. D. Xue, C. W. Myles and C. Higgins, Materials, 2016, 9, 691.
21. J. Lipkowski and H. Schneider, J. Coord. Chem., 2021, 74, 1–16.
22. S. Yamanaka, Springer Ser. Mater., 2014, vol. 199, pp. 193–226.
23. H. Kawaji, H. Horie, S. Yamanaka and M. Ishikawa, Phys. Rev. Lett., 1995, 74, 1427.
24. G. K. Ramachandran, P. F. McMillan, S. K. Deb, M. Somayazulu, J. Gryko, J. Dong and O. F. Sankey, J. Phys.: Condens.Matter, 2000, 12, 4013.
25. J. S. Kaspe, P. Hagenmuller, M. Pouchard and C. Cros, Science, 1965, 1713–1714.
26. V. I. Smelyansky and J. S. Tse, Chem. Phys. Lett., 1997, 264, 459–465.
27. Y. Kono, N. Ohya, T. Taguchi, K. Suekuni, T. Takabatake, S. Yamamoto and K. Akai, J. Appl. Phys., 2010, 107, 123720.
28. S. Bobev, J. Meyers, V. Fritsch and Y. Yamasaki, 25th International Conference on Thermoelectrics, 2006.
29. K. Biswas and C. W. Myles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245205.
30. S. Bobev and S. Sevov, J. Solid State Chem., 2000, 153, 92–105.
31. S. Stefanoski, C. D. Malliakas, M. G. Kanatzidis and G. S. Nolas, Inorg. Chem., 2012, 51, 8686–8692.
32. S. Stefanoski and G. S. Nolas, Cryst. Growth Des., 2011, 11, 4533–4537.
33. H. Morito, H. Yamane, R. Y. Umetsu and K. Fujiwara, Crystals, 2021, 11, 808.
34. S. Paschen, V. Pacheco, A. Bentien and A. Sanchez, Phys. B, 2003, 328, 39–43.
35. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
36. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
37. K. Laasonen, R. Car, C. Lee and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6796.
38. K. Biswas, C. W. Myles, M. Sanati and G. S. Nolas, J. Appl. Phys., 2008, 104, 033535.
39. I. Veremchuk, M. Beekman, I. Antonyshyn and W. Schnelle, Materials, 2016, 9, 593.
40. K. Biswas and C. W. Myles, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115113.
41. G. K. Ramachandran, J. Dong, O. F. Sankey and P. F. McMillan, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 033102.
42. E. Reny, P. Gravereau, C. Cros and M. Pouchard, J. Mater. Chem., 1998, 8, 2839–2844.
43. C. W. Myles, J. Dong and O. F. Sankey, Phys. Status Solidi B, 2003, 239, 26–34.

---