Open Access Article
Open Access ArticleThermal transport properties of gas-filled silica aerogels
Shuheng Xua and
Jieren Song *b
*b
aChifeng University, Chifeng 024000, China
bSchool of Mechanical and Materials Engineering, North China University of Technology, Beijing 100144, China. E-mail: songjr_2008@126.com
First published on 26th June 2024
Abstract
Silica aerogel (SA), recognized as an efficient insulating material, is characterized by its extremely low thermal conductivity (TC) and high porosity, presenting extensive application potential in aerospace and building energy conservation. In this study, the thermal transport properties of gas-filled SA are explored using molecular dynamics (MD) methods. It is found that an increase in porosity leads to a significant decrease in TC, primarily due to enhanced phonon scattering and reduced material stiffness. Additionally, the TC of SA influenced by gas exhibits a pattern of initial decrease, followed by an increase, and then a decrease again, driven by complex interactions between gas molecules and pore walls, phonon localization, and scattering mechanisms. At a gas concentration of 80%, the TC in confined spaces is significantly increased by nitrogen, attributed to enhanced intermolecular interactions and increased collision frequency. The impact of gases on the TC of gas–solid coupled composite materials is also investigated, revealing that gas molecules serve as a “bridge” for phonons, playing a crucial role in reducing interfacial scattering and enhancing low-frequency vibrational modes, thus further enhancing heat transfer efficiency. The TC of these composite materials is primarily regulated by the gas-phase TC in response to temperature, while the response to strain is predominantly governed by variations in the solid-phase TC. These results provide essential theoretical support and design guidelines for the development and design of new high-efficiency insulating materials.
1. Introduction
In the context of rapid technological development and increasing energy demands, the development of efficient thermal insulation materials has become a critical challenge, particularly in the fields of aerospace,1 electric power energy,2 energy-efficient construction,3 and the petrochemical industry.4 Silica aerogel (SA),5 with its extremely low thermal conductivity (TC), high porosity, lightweight nature, and good chemical stability, shows immense potential in various applications, including thermal insulation,6 acoustic isolation,7 and optics.8 The complex nanostructure of this material triggers intricate thermal transport phenomena, including gas molecule collisions, phonon transport, external radiation absorption, and their coupling effects, making the study and optimization of these thermal transport mechanisms crucial for enhancing the performance of nanoporous thermal insulating materials.9In the study of the thermal transport mechanisms of SA, methods such as experimental measurements, theoretical deductions, and numerical simulations are predominantly used. Researchers have successfully determined the TC of aerogels through various experimental techniques. For instance, Rettelbach et al. explored the effect of temperature and carbon load on the effective TC of carbon-doped aerogel powders using the hot plate method.10 It was found that as the load increased, the contact area between powder particles expanded, leading to an increase in TC. Lu et al. measured the TC of aerogels of different densities using the hot-wire method, revealing the impact of density on the TC of aerogels.11 Wei et al. used the transient hot strip method to measure the TC of SAs under various temperatures and pressures, finding that the TC significantly decreased as pressure decreased; the TC was directly proportional to the cube of temperature, and a density range corresponding to the lowest TC was identified.12 These studies have clarified the direct impacts of parameters such as particle size, porosity, density, temperature, and pressure on the TC of SA. However, these studies have yet to delve deeply into the micro-nature of heat transfer mechanisms, and there remains a lack of sufficient data to understand the thermal transport processes at the microscopic level and their fundamental influencing factors. Therefore, further theoretical and numerical studies are essential for a comprehensive understanding of the thermal transport properties and mechanisms of SA, as well as for improving its thermal management performance.
In early studies, Fricke et al. experimentally determined the relationship between the TC of SA and its density, establishing an empirical model based on gas-phase, solid-phase, and radiative TCs.13 Although subsequent studies by various scholars proposed diverse empirical models, these models were often built under specific conditions, limiting their applicability and predictive accuracy across different operating conditions. To overcome this limitation and enhance the accuracy of theoretical models, researchers have turned to developing theoretical models based on typical structural units. For instance, Zeng et al. introduced three types of structural units, such as crossed rods, crossed cylindrical rods, and crossed spherical rods, to describe the nanoporous network structure of SAs and theoretically calculated the effective TC of SAs under a one-dimensional heat transfer assumption.14 Additionally, Wei et al. proposed a theoretical model for the effective TC of SA composites based on the crossed spherical rod model.12 Lu et al.15 and Zhao et al.16 also used the crossed spherical rod model to describe the nanoporous structure of SA and proposed theoretical models for the effective TC of SA composites, incorporating micron-scale typical structural units of additives.
Additionally, research on numerical calculation models has been initiated. Spagnol et al. used periodic two-dimensional regular fractal Von Koch snowflake structures and irregular random structures generated by a finite diffusion packing model to represent the complex structure of SA, estimating the effective TC under different density conditions.17 Zhao et al. further generated a three-dimensional random particle packing structure to simulate the typical structure of nanoporous aerogel materials, using numerical methods to calculate the material's radiative heat conduction coupling effects.18 Bi et al. calculated the TC of SAs using the finite volume method based on a three-dimensional physical model, employing geometric shapes such as regular triangular prisms, cubes, octahedra, and regular hexagonal prisms to represent the structure of SA.19 While these methods simplify or assume the complex structure of SA to some extent, the establishment and calculation of models still rely on experimental data to determine specific parameters, limiting the predictive power and general applicability of the models.
In the field of TC research for SA, molecular dynamics (MD) methods provide a means to deeply explore the microscopic structure and properties of materials based on the computational simulation of atomic or molecular interaction potentials. This method can accurately simulate complex actual conditions, including porosity, density, and doping, thus authentically reflecting the microscopic behavior of materials. For instance, Ng et al. analyzed the TC of SA using MD simulations, focusing on the specific effects of porosity and density on TC.20 Patil et al. studied the TC of glass fiber-reinforced SA nanocomposites, revealing the influence mechanisms of glass fiber aspect ratio and composite density on TC.21 Yang et al. focused on the impact of graphene doping on the TC of SA, finding that the addition of graphene effectively reduces collisions between gas phases, thereby lowering heat transfer efficiency.22 Additionally, they investigated the effect of water molecules on the TC of SA, discovering that the adsorption of water molecules can fill molecular-level defects, reducing phonon scattering and thus enhancing TC.23 However, despite the significant progress made by the MD method in revealing the TC mechanisms of SA, current research still has limitations. For example, intuitive characterization methods for the pore structure in aerogels are not yet mature, and the specific impact of porosity on thermal conduction mechanisms is not fully understood. In terms of gas filling, existing studies have not yet clearly revealed the differences in the impact of various gases like oxygen and nitrogen on the thermal conductive behavior of SA. The mechanism of temperature and strain regulation on the TC of gas-filled SA has not been explored yet. Therefore, a deeper exploration of the thermal transport characteristics of gas-filled SA and the development of effective control strategies are crucial for designing and preparing SA with superior performance and broader application ranges.
In this study, the thermal transport control mechanisms of gas-filled SA are systematically investigated using MD methods. Initially, the impact of porosity on the TC of SA is thoroughly analyzed. Subsequently, the effects of gas filling on the thermal transport of SA are studied, with a deep exploration of the TC of gases at different concentrations within SA, examining the thermal transport properties of gas-filled SA. Finally, the regulatory effects of temperature and strain on the TC of gas-filled SA are investigated. The findings provide significant theoretical support for understanding and optimizing the thermal transport mechanisms of SA and its gas–solid coupled composite materials.
2. Methods
The atomic model of SA is created based on the β-cristobalite silica crystal model, with crystal parameters provided by Wyckoff.24 Fig. 1a illustrates the three stages involved in the transition from β-cristobalite silica crystal to SA. In stage 1, the β-cristobalite silica crystal model is relaxed at 300 K for 50 ps using the NVT ensemble, followed by an instantaneous expansion to achieve the desired density. In stage 2, the expanded model is heated from 300 K to the target temperature over 50 ps. Subsequently, the model that reaches the target temperature is cooled back to 300 K over another 50 ps, during which the silica–oxygen network forms as the temperature changes. Notably, the target temperature is used in the simulation process to induce the transition from β-cristobalite silica crystal to SA, where high temperatures facilitate the breaking and reorganization of the silica–oxygen network, thereby forming a porous structure.25 In stage 3, the silica–oxygen network model undergoes energy minimization to ultimately form the SA model. In constructing the gas-filled SA model, the functionality of the PACKMOL software package is utilized,26 distributing oxygen molecules randomly within SA according to predefined molar fractions of 20%, 40%, 60%, and 80%. The energy minimization process eliminates potential instabilities introduced by molecular insertion, ensuring the reliability of the model. The filling with nitrogen is achieved by replacing the corresponding oxygen molecules to maintain the consistency of the initial distribution.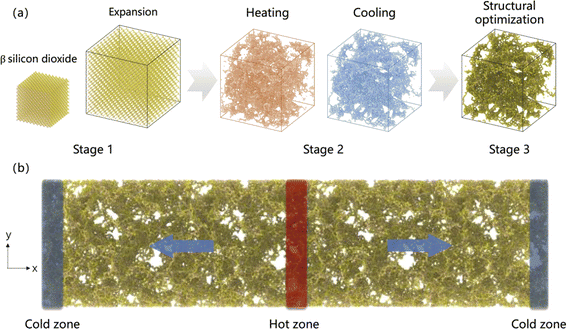 | ||
| Fig. 1 (a) Three stages of the transformation from β-phase silicon dioxide crystal to SA. (b) Computational model of SA. | ||
LAMMPS is used to run all molecular dynamics simulations,27 and OVITO is utilized to visualize the atomic simulation data.28 The Tersoff potential is employed to describe the interactions among Si–Si, Si–O, and O–O atoms.29 Yeo et al. used this potential function to study the thermal transport properties of SAs, with computational results closely matching those reported in experimental studies.30 The IFF force field parameters describe oxygen and nitrogen molecules, combining harmonic bond stretching potentials with Lennard-Jones (LJ) parameters to achieve simulation errors under 5%, as shown in Tables 1 and 2.31 The 12–6 LJ potential is used to describe the non-bonded interactions between SA and gases. The force field parameters for silicon and oxygen atoms in silica are extracted from the universal force field,32 with distance parameters of 4.295 Å for silicon and 3.5 Å for oxygen and energy parameters of 17.46 meV and 2.61 meV, respectively. The force field parameters for interacting atom pairs are obtained from the arithmetic mean of the distance parameters and the geometric mean of the energy parameters. The global cutoff distance for the LJ potential is set to 12 Å.
| Parameter | Values | Unit |
|---|---|---|
| Kr | 71.2551 | eV Å−2 |
| r0 | 1.2074 | Å |
| εOO | 4.5479 | meV |
| σOO | 3.297 | Å |
| Parameter | Values | Unit |
|---|---|---|
| Kr | 138.5661 | eV Å−2 |
| r0 | 1.0977 | Å |
| εNN | 3.4620 | meV |
| σNN | 3.614 | Å |
The Müller-Plathe method is employed to predict the TC of SA at room temperature.33 The simulation time increment is set to 0.5 fs, and periodic boundary conditions are applied in all three directions. Initially, the starting structure is equilibrated at 300 K using the NVT ensemble for 50 ps. The model is divided along the x-axis into several slabs, each 2 Å thick, with the central slab designated as the hot region and the slabs at both ends as cold regions, as illustrated in Fig. 1b. In this step, simulations are conducted using the NVE ensemble, and the heat flux Jx is obtained by swapping the velocity vectors of the “hottest” atom in the cold slab with the “coldest” atom in the hot slab every 200 time steps:
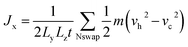 | (1) |
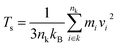 | (2) |
In MD, the Von Mises stress of each atom can be calculated to provide a detailed description of the atom's state under stress. The formula for Von Mises stress is as follows:34
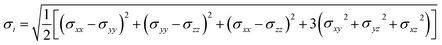 | (3) |
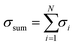 , and the average atomic stress is σavg = σsum/N, where N is the total number of atoms.
, and the average atomic stress is σavg = σsum/N, where N is the total number of atoms.
The calculation of atomic heat flow involves the difference between the energy flow and the stress power flow, reflecting the net energy transport due to atomic movement, and thus describing the contribution of the atom to the heat flow. The expression for atomic heat flow is:
| Ji = |eivi − σivi| | (4) |
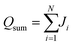 .
.
3. Results and discussion
3.1 Thermal conductivity of silica aerogel
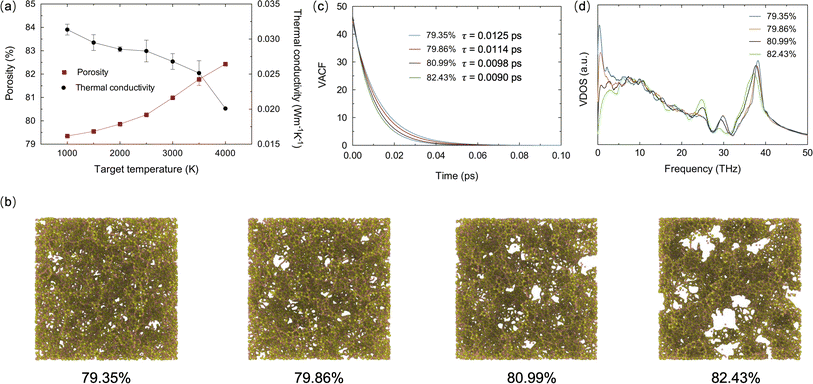
The influence of porosity on the thermal transport properties of SA at various target temperatures is explored. All models start with an initial density of 0.38 g cm−3 and a fixed volume of 2.1 × 106 Å3. By heating and subsequently rapidly cooling from 1000 K to 4000 K, SA models with porosities ranging from 79.35% to 82.43% are generated. It is noteworthy that in practical engineering applications, the porosity of SAs often exceeds 90%. However, in MD models, excessively high porosity may lead to structural instability, hence porosity is typically maintained around 80%. The calculation of porosity employs the atomic configuration analysis tool developed by Joshi et al.,35 effectively reflecting the material's microstructural characteristics. As shown in Fig. 2a, as the target temperature increases, the overall porosity of the SA tends to rise, whereas the TC shows the opposite trend, decreasing with increasing porosity. This trend illustrates the significant impact of porosity on TC. As porosity increases, the effective path for heat flow reduces, more pores mean more interface scattering of phonons, thereby lowering thermal transport efficiency. Fig. 2b displays the microstructure of SAs at different porosities. As porosity gradually increases from 79.35% to 82.43%, the size of the pores enlarges, and the distribution transitions from uniform to clustered, with enhanced connectivity between pores, while the solid framework becomes sparser and more fragmented. These microstructural changes indicate a reduction in TC. The velocity autocorrelation function (VACF) is a crucial tool for calculating phonon lifetimes τ, providing information on the decay of atomic vibrations over time and thus insights into phonon scattering mechanisms. Fig. 2c shows the VACF decay curves for SA models at different porosities, with the average phonon lifetimes calculated by integrating the VACF curves. It is observed that as porosity increases, the VACF decays faster, and the average phonon lifetime decreases, indicating an increase in phonon scattering due to pores, which further reduces TC. The phonon vibrational density of states (VDOS) obtained from the Fourier transform of the VACF further elucidates the impact of porosity on TC:36,37
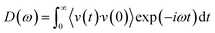 | (5) |
3.2 Thermal conductivity of gas-filled silica aerogels
The thermal transport properties of SA filled with varying concentrations of oxygen and nitrogen are investigated. The SA model used has an initial porosity of 80.99%. SA filled with oxygen and nitrogen is named OFSA and NFSA, respectively, with filling concentrations ranging from 20% to 80% molar fractions. As shown in Fig. 3, as the gas concentration increases, the distribution of oxygen and nitrogen molecules within SA becomes increasingly dense, particularly at 80%, where the gases are observed to almost fill the entire porous structure. To understand the specific impact of the two gases on the porosity volume, calculations of porosity are conducted. The results indicate that porosity significantly decreases as gas concentration increases. From 20% to 60% concentration, the impact of oxygen and nitrogen on the pore volume tends to be consistent. However, when the filling concentration reaches 80%, the porosity of OFSA is slightly higher than that of NFSA. This difference is due to the relatively larger effective size of oxygen molecules, leading to more pronounced repulsion effects among oxygen molecules at high filling states, thereby leaving more unoccupied pore space.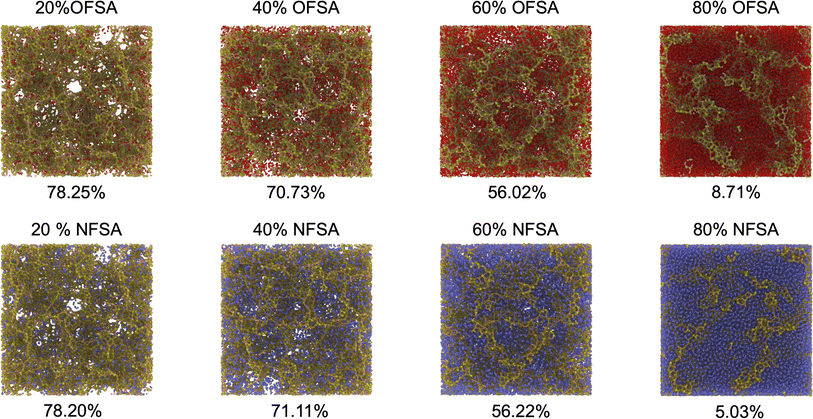 | ||
| Fig. 3 Models of OFSA and NFSA at different filling concentrations, along with their porosity, where red represents oxygen atoms and blue represents nitrogen atoms. | ||
Fig. 4a shows the impact of gas filling from 0% to 80% concentration on the TC of SA. The TC of SA under the influence of oxygen and nitrogen gases experiences a trend of initial decrease, followed by an increase, and then another decrease. This non-monotonic behavior indicates a complex thermal conduction process at different gas concentrations. To investigate the underlying mechanisms, the effects of gas filling on the structural characteristics of SA, atomic vibrational properties, and atomic stress are studied. Fig. 4b–d respectively show the porosity, VDOS, and average atomic stress at different gas concentrations. Given the nearly identical impact of nitrogen and oxygen on the TC, only nitrogen filling is shown in Fig. 4c for the study. In the initial stages of gas filling, the porosity of SA significantly increases, mainly due to the initial adsorption of a small number of gas molecules on the internal surfaces of SA. These adsorbed molecules cause minor movements of surface atoms and create a slight “stretching” effect on the pore walls. This adjustment in the pore structure results in a redshift in VDOS, a decrease in phonon frequency, and an increase in localized phonon scattering due to the uneven interactions between the adsorbed gas molecules and the pore walls, thereby reducing the TC. As the gas concentration increases to 40%, the porosity slightly decreases, mainly due to the strengthening of the interactions between the gas molecules and the pore walls, which induces changes in the internal stresses of the pore walls, leading to a reduction in some pore wall spacings. The subsequent adsorption of more gas molecules further reduces the atomic vibration frequency of SA, slows down the phonon transmission speed, and further decreases the TC. When the gas concentration reaches 60%, adsorption sites near saturation, especially the accessible parts of surfaces and larger pores. At this stage, additional gas molecules primarily occupy previously unfilled micro-pores, causing a slight increase in overall porosity. The peak height in the VDOS increases during this phase, indicating a significant increase in phonon state density at that frequency, more concentrated phonon vibration modes, and enhanced phonon localization, thereby restricting effective energy transfer. However, as the filling of gas increases, the gas molecules form a more uniform distribution within the pores, reducing localized scattering and increasing the transmission efficiency of specific phonon modes. This adjustment in phonon behavior effectively overcomes the negative effects of phonon localization, leading to an increase in TC. When the gas concentration reaches 80%, the gas molecules in the pores exert greater pressure on the pore walls, pushing them outward and thereby increasing the pore volume. The peak height in the VDOS further increases at this stage, indicating more pronounced phonon localization at that frequency. Despite a more uniform molecular distribution and further weakened localized scattering, the significantly increased interactions cause stronger stress scattering. Ultimately, the combined effects of stress scattering and phonon localization lead to a further decrease in TC. The aforementioned phenomena reflect the complex interplay of interactions between gas molecules and pore walls, phonon localization, and scattering mechanisms.
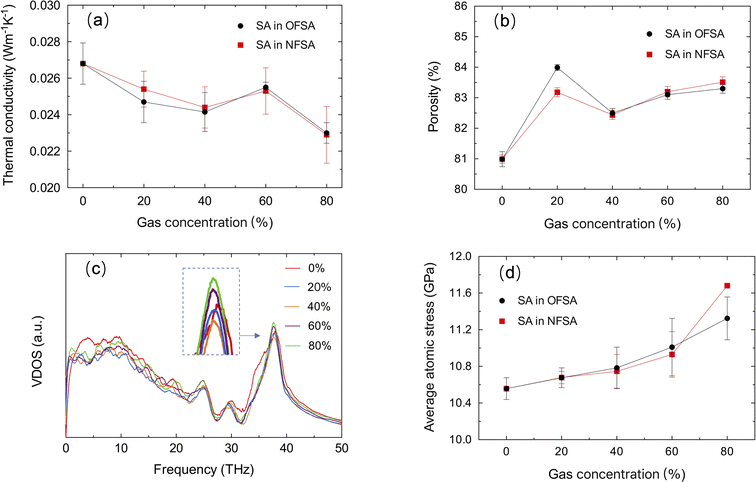 | ||
| Fig. 4 (a) TC, (b) porosity, (c) VDOS, and (d) average atomic stress changes of SA at varying gas concentrations. | ||
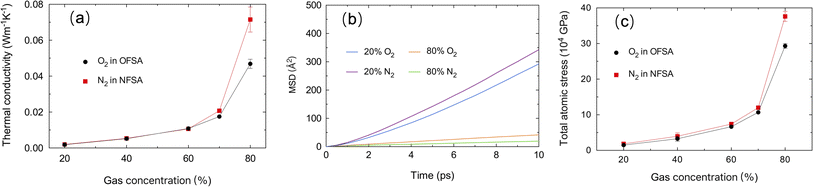
Fig. 5a displays the TC of gases in the porous structure of SA. It is observed that the TC of both oxygen and nitrogen in SA increases with the increase in gas concentration, with nitrogen showing a more significant increase at 80% concentration. To further explore the differences in TC trends, the diffusion characteristics of the two gases at different concentrations in confined spaces are studied. Fig. 5b illustrates the change over time in the mean square displacement (MSD) of oxygen and nitrogen at 20% and 80% concentrations. At 20%, the MSD curves for both oxygen and nitrogen show a clear linear increasing trend, indicating significant diffusion behavior at this concentration, with nitrogen diffusing slightly faster than oxygen, primarily due to nitrogen molecules being lighter than oxygen molecules, which diffuse faster at the same temperature according to the Maxwell–Boltzmann distribution.38 However, TC is influenced not only by molecular speed but also by collision efficiency and energy transfer mechanisms. At lower concentrations, the distance between gas molecules is greater, leading to lower collision frequencies, and despite their different diffusion speeds, the TC of nitrogen and oxygen remains similar. As the gas concentration increases to 80%, the MSD curves for both oxygen and nitrogen become very flat, indicating that diffusion is significantly restricted at higher concentrations. Oxygen's diffusion speed relative to nitrogen is higher, directly related to the larger pore structure,39 as shown in Fig. 3. In this structure, the larger pore network provides more pathways for oxygen, facilitating its diffusion behavior at high concentrations. As the gas concentration increases, the average distance between molecules decreases, leading to significantly increased collisions. This frequent collision in a high-concentration environment enhances the efficiency of heat transfer, thereby increasing TC. Compared to oxygen, nitrogen in a structure with smaller pore rates has less room to move, and the intense collisions between molecules are more pronounced, resulting in a higher TC for nitrogen in confined spaces. Fig. 5c shows the changes in total atomic stress at different gas concentrations in SA. It is found that at lower concentrations, the stress of both gases is relatively low, but as the concentration increases, the stress begins to rise, especially at 80% concentrations, where there is a significant increase in stress. This stress trend shows a significant correlation with changes in TC. As the concentration increases from 20% to 70%, the decreased distance between molecules significantly enhances their interactions, thereby increasing the frequency of molecular collisions and energy exchange, further leading to an increase in TC. As the molecular concentration further increases, the interactions between molecules strengthen, and collisions become more frequent, effectively enhancing the efficiency of heat transfer. Additionally, at 80% concentration, the total atomic stress of nitrogen is significantly higher than that of oxygen. This indicates that at higher molecular concentrations, the interactions between nitrogen molecules are stronger and molecular collisions are more frequent, thereby achieving more efficient heat transfer. Therefore, in this porous medium, the TC of nitrogen is higher than that of oxygen.
Fig. 6a shows the variations in TC for OFSA and NFSA under different gas concentrations. It is observed that TC increases with the increase in gas concentration, with OFSA and NFSA exhibiting significant increases, especially beyond a 70% concentration, with NFSA showing a more pronounced increase. To gain deeper insights into the impact of gas filling on the thermal transport properties of OFSA and NFSA, the effect of gas filling on the heat flow is quantified by comparing the total atomic heat flow in filled versus unfilled conditions. This atomic heat flow ratio, R, is defined as:
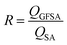 | (6) |
 | ||
| Fig. 6 Changes in (a) TC and (b) atomic heat flow ratio for OFSA and NFSA at different gas concentrations, (c) comparison of the VDOS for SA, OFSA and NFSA at 20% and 80% concentrations. | ||
3.3 Regulation of thermal conductivity in gas-filled silica aerogels
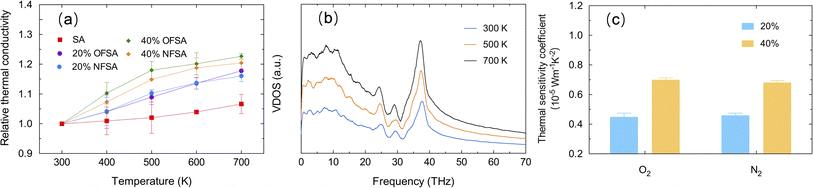
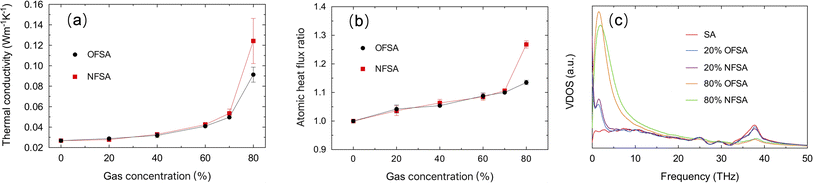
Fig. 7a presents the relative TC of SA, OFSA, and NFSA from 300 to 700 K, where the relative TC is defined as the ratio of the TC at a specific temperature to that at the baseline temperature of 300 K. The results show that the relative TC of SA, OFSA, and NFSA increases with rising temperatures. To further explore this phenomenon, the VDOS at different temperatures for SA is calculated, as shown in Fig. 7b. As the temperature increases, a significant rise in the peak of the VDOS curve is observed, indicating that higher temperatures excite more phonons to participate in vibration, thereby significantly increasing the vibrational state density of phonons. Simultaneously, a redshift to lower frequencies in the high-frequency peaks is observed with rising temperatures, due to increased phonon–phonon scattering caused by anharmonic vibrations at higher temperatures,41,42 leading to a decrease in phonon frequency. Among these two competing phenomena, the increase in the number of phonons at higher temperatures plays a dominant role in thermal transport, leading to an increase in TC. Additionally, it is found that with rising temperatures, OFSA and NFSA with higher concentrations exhibit faster growth in relative TC, indicating that the TC of high-concentration OFSA and NFSA is more sensitive to temperature. To quantify the temperature sensitivity of TC, a temperature sensitivity coefficient C = Δk/ΔT is defined, where Δk is the change in TC and ΔT is the temperature difference from the baseline temperature of 300 K. As depicted in Fig. 7c, at 500 K, the temperature sensitivity of TC in OFSA with oxygen and NFSA with nitrogen significantly increases as the gas concentration rises from 20% to 40%. This enhancement in temperature sensitivity is primarily due to the intensified thermal motion of gas molecules at high temperatures and the increased gas concentration, which lead to higher frequency and intensity of molecular collisions. Consequently, this effectively enhances the efficiency of heat transfer. As a result, when OFSA and NFSA contain higher concentrations of gas, the relative rate of increase in TC is faster, making the temperature sensitivity of TC stronger.The impact of compressive strain on the TC of OFSA and NFSA is studied, with SA often required to maintain excellent insulating performance even under pressure or compression. Therefore, understanding how compressive strain affects TC is crucial for the design and use of SA. Compressive strain is applied in the y-direction at a strain rate of 1 × 108 s−1. To mitigate the impact of high strain rates on the obtained characteristics, it is necessary to suppress the temperature rise caused by high loading strain rates by performing the NVT ensemble during the loading step.43 Fig. 8a shows the changes in TC of SA, OFSA, and NFSA at 20% and 40% concentrations under different compressive strains. It is observed that as the compressive strain increases, the TC of SA, as well as OFSA and NFSA at 20% and 40%, shows a significant rising trend. This phenomenon is attributed to the internal structural rearrangement caused by compression. As the compressive strain increases, the porosity of SA, OFSA, and NFSA significantly decreases, and the contact area between the frameworks of SA increases, thereby enhancing the TC of the SA framework, and thus, OFSA and NFSA also increase overall. Moreover, through linear regression analysis, it is found that the relationship between TC and compressive strain for SA, OFSA, and NFSA exhibits a high linear correlation, with little variation in the slope values, indicating that the sensitivity of these models' TC to compressive strain is similar, and thus the sensitivity of TC to compressive strain is primarily contributed by SA. Although OFSA and NFSA introduce gases, these gases have a minimal effect on altering the response of TC to compressive strain. Fig. 8b and c respectively show the changes in VDOS of SA and 40% OFSA under different compressive strains. It can be seen that as the compressive strain increases, there are no significant changes in the high and low-frequency peaks, while a notable blue shift occurs near the mid-frequency peak around 30 THz. This phenomenon is due to the compressive strain causing the atomic arrangement to become tighter, thus increasing the overall stiffness of the material. When the stiffness increases, the frequency of phonon modes correspondingly rises, an effect that is particularly pronounced around 30 THz. In summary, it can be concluded that temperature and strain are effective factors in regulating the TC of OFSA and NFSA. The temperature dependency of the TC of OFSA and NFSA is primarily controlled by the gas-phase TC, while the strain dependency is mainly driven by changes in the solid-phase TC.
 | ||
| Fig. 8 (a) Changes in TC of SA, as well as OFSA and NFSA at 20% and 40% concentrations under different compressive strains, VDOS of (b) SA and (c) 40% OFSA under various compressive strains. | ||
4. Conclusion
The thermal transport properties of gas-filled SA have been systematically studied using MD methods. It has been found that an increase in the porosity of SA leads to a significant reduction in TC, an effect primarily resulting from increased phonon scattering due to the porous structure and the consequent reduction in material stiffness. The redshift phenomenon in the VDOS further confirms the impact of reduced stiffness on phonon propagation characteristics. As the gas concentration increases, the dense distribution of gas molecules within SA leads to a decrease in porosity. At an 80% concentration, oxygen, having larger molecules, exhibits more significant repulsion effects, resulting in a slightly higher porosity compared to nitrogen. Due to the complex interplay between gas molecules and pore walls, phonon localization, and scattering mechanisms, the TC of SA under the influence of oxygen and nitrogen experiences an initial decline, followed by a rise, and then a decline again. Within SA, as the gas concentration increases, the TC of both oxygen and nitrogen improves, particularly at 80% concentration, where nitrogen shows a significant increase due to more frequent molecular collisions and stronger intermolecular interactions. Furthermore, as the filling gas concentration increases, the TC of OFSA and NFSA significantly improves, as gas molecules serve as “bridges” for phonons, reducing interfacial scattering and enhancing low-frequency vibration modes. The temperature dependency of the TC of OFSA and NFSA is primarily controlled by the gas-phase TC, while the dependency on strain is mainly driven by changes in the solid-phase TC. These research results provide valuable perspectives for further understanding and utilizing the thermal transport properties of aerogel materials.Data availability
The data that support the findings of this study are included in the figures and tables within this article. For further details, please refer to the relevant sections of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by Research Startup Fund Project of North China University of Technology, Science Foundation of the National Key Laboratory of Science and Technology on Advanced Composites in Special Environments (JCKYS2022603C022), and China Postdoctoral Science Foundation (2022M721783).References
- M. Koebel, A. Rigacci and P. Achard, J. Sol-Gel Sci. Technol., 2012, 63, 315–339 CrossRef CAS.
- R. Singh, S. Tundee and A. Akbarzadeh, Sol. Energy, 2011, 85, 371–378 CrossRef.
- W. Jezierski, B. Sadowska and K. Pawłowski, Energies, 2021, 14, 1 CrossRef.
- A. Bahadori, Thermal Insulation Handbook for the Oil, Gas, and Petrochemical Industries, Gulf Professional Publishing, 2014 Search PubMed.
- A. Soleimani Dorcheh and M. H. Abbasi, J. Mater. Process. Technol., 2008, 199, 10–26 CrossRef CAS.
- R. H. Nosrati and U. Berardi, Energy Build., 2018, 158, 698–711 CrossRef.
- Z. Mazrouei-Sebdani, H. Begum, S. Schoenwald, K. V. Horoshenkov and W. J. Malfait, J. Non-Cryst. Solids, 2021, 562, 120770 CrossRef CAS.
- X. Ji, Y. Du and X. Zhang, Adv. Mater., 2022, 34, 2107168 CrossRef CAS PubMed.
- C.-Y. Zhu, H.-B. Xu, X.-P. Zhao, L. Gong and Z.-Y. Li, Energy Storage Sav., 2022, 1, 217–240 CrossRef CAS.
- T. Rettelbach, J. Säuberlich, S. Korder and J. Fricke, J. Non-Cryst. Solids, 1995, 186, 278–284 CrossRef CAS.
- X. Lu, M. C. Arduini-Schuster, J. Kuhn, O. Nilsson, J. Fricke and R. W. Pekala, Science, 1992, 255, 971–972 CrossRef CAS PubMed.
- G. Wei, Y. Liu, X. Zhang, F. Yu and X. Du, Int. J. Heat Mass Transfer, 2011, 54, 2355–2366 CrossRef CAS.
- J. Fricke, X. Lu, P. Wang, D. Büttner and U. Heinemann, Int. J. Heat Mass Transfer, 1992, 35, 2305–2309 CrossRef CAS.
- S. Zeng, A. Hunt and R. Greif, J. Heat Transfer, 1995, 117, 4 Search PubMed.
- G. Lu, X.-D. Wang, Y.-Y. Duan and X.-W. Li, J. Non-Cryst. Solids, 2011, 357, 3822–3829 CrossRef CAS.
- J.-J. Zhao, Y.-Y. Duan, X.-D. Wang and B.-X. Wang, J. Non-Cryst. Solids, 2012, 358, 1303–1312 CrossRef CAS.
- S. Spagnol, B. Lartigue, A. Trombe and V. Gibiat, Europhys. Lett., 2007, 78, 46005 CrossRef.
- J.-J. Zhao, Y.-Y. Duan, X.-D. Wang and B.-X. Wang, J. Non-Cryst. Solids, 2012, 358, 1287–1297 CrossRef CAS.
- C. Bi, G. H. Tang, Z. J. Hu, H. L. Yang and J. N. Li, Int. J. Heat Mass Transfer, 2014, 79, 126–136 CrossRef.
- T. Y. Ng, J. J. Yeo and Z. S. Liu, J. Non-Cryst. Solids, 2012, 358, 1350–1355 CrossRef CAS.
- S. P. Patil, B. S. Bachhav and B. Markert, Ceram. Int., 2022, 48, 2250–2256 CrossRef CAS.
- M. Yang, Q. Sheng, L. Guo, H. Zhang and G. Tang, Langmuir, 2022, 38, 2238–2247 CrossRef CAS PubMed.
- M. Y. Yang, Q. Sheng, H. Zhang and G. H. Tang, J. Mol. Liq., 2022, 349, 118176 CrossRef CAS.
- R. W. G. Wyckoff, The Structure of Crystals, Chemical Catalog Company, Incorporated, 1924 Search PubMed.
- J. Song, X. Xu and X. Liang, Phys. Chem. Chem. Phys., 2024, 26, 2025–2034 RSC.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Stukowski, Model. Simulat. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- S. Munetoh, T. Motooka, K. Moriguchi and A. Shintani, Comput. Mater. Sci., 2007, 39, 334–339 CrossRef CAS.
- J. J. Yeo, Z. S. Liu and T. Y. Ng, Model. Simulat. Mater. Sci. Eng., 2013, 21, 075004 CrossRef CAS.
- S. Wang, K. Hou and H. Heinz, J. Chem. Theory Comput., 2021, 17, 5198–5213 CrossRef CAS PubMed.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- J. Song, Z. Xu, X. He and X. Liang, Phys. Chem. Chem. Phys., 2022, 24, 9648–9658 RSC.
- K. Joshi, M. I. Arefev and L. V. Zhigilei, Carbon, 2019, 152, 396–408 CrossRef CAS.
- J. Chen, J. Phys. Chem. Lett., 2020, 11, 4298–4304 CrossRef CAS PubMed.
- J. Wang and J. Chen, Phys. Rev. E, 2020, 101, 042207 CrossRef CAS PubMed.
- J. S. Rowlinson, Mol. Phys., 2005, 103, 2821–2828 CrossRef CAS.
- Z. Zhan, J. Xiao, Y. Zhang, M. Pan and R. Yuan, Int. J. Hydrogen Energy, 2007, 32, 4443–4451 CrossRef CAS.
- J. Song, Z. Xu, X. Xu, X. Liang and X. He, ACS Appl. Mater. Interfaces, 2023, 15, 1817–1826 CrossRef CAS PubMed.
- J. Song, Z. Xu and X. He, Int. J. Heat Mass Transfer, 2020, 157, 119954 CrossRef CAS.
- J. Song, Z. Xu, X. He, Y. Bai, L. Miao, C. Cai and R. Wang, Phys. Chem. Chem. Phys., 2019, 21, 12977–12985 RSC.
- J. Song, Z. Xu, X. Liang and X. He, J. Phys. Chem. C, 2022, 126, 9482–9492 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |