Open Access Article
Open Access ArticleSynthesis, structural and magnetic properties of cobalt(II) complexes with pyridine-based macrocyclic ligand containing two pyridine pendant arms†
Eva Zahradníková a,
Céline Pichon
a,
Céline Pichon b,
Carine Duhayonb,
Jean-Pascal Sutter
b,
Carine Duhayonb,
Jean-Pascal Sutter *b,
Petr Halaša and
Bohuslav Drahoš
*b,
Petr Halaša and
Bohuslav Drahoš *a
*a
aDepartment of Inorganic Chemistry, Faculty of Science, Palacký University Olomouc, 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic. E-mail: bohuslav.drahos@upol.cz; Tel: +420 585 634 954 Tel: +420 585 634 429
bLaboratoire de Chimie de Coordination du CNRS (LCC-CNRS), Université de Toulouse, CNRS, Toulouse, France. E-mail: jean-pascal.sutter@lcc-toulouse.fr
First published on 3rd September 2024
Abstract
With the aim of tuning the magnetic anisotropy, a series of Co(II) complexes with the general formula of complex cations [Co(L)X]+, where X = Br− (1); I− (2); NCO− (3); NCS− (4a); N3− (5), and [Co(L)(NCS)2] (4b), (L = a 17-membered pyridine-based N3O2-macrocyclic ligand containing two pyridin-2-ylmethyl pendant arms) were prepared and thoroughly characterized. The molecular structures for all complexes showed strongly distorted geometry in between octahedral and trigonal prismatic. The magnetic studies confirmed substantial magnetic anisotropy with positive values of D, the axial zero-field splitting parameter, but E/D ratios close to 1/3. This was supported by theoretical CASSCF calculations showing no significant effect of the co-ligands. Complex 4b was found to behave as a field-induced SMM.
Introduction
Magnetoactive complexes, especially single-molecule magnets (SMMs), represent an interesting family of compounds, where a slow relaxation of the magnetization of purely molecular origin occurs below a blocking temperature.1,2 SMMs do not rely on magnetic ordering unlike “classical” magnets, thus they are potential materials for ultra-dense information storage, quantum computing, molecular switches, or spintronics.3–5 SMMs are characterized by an energy barrier, U, between two states corresponding to the opposite direction of the magnetic moment. This barrier depends both on the spin of the system S, and on the value of the axial zero-field splitting parameter D. The original efforts to increase the value of U were based on increasing the number of total spin, however, this turned out to be at the expense of the overall magnetic anisotropy.6,7 On the other hand, tuning the magnetic anisotropy of individual magnetic centers by appropriate ligand design and modulation of the coordination sphere has been more successful.8,9 Macrocyclic ligands appear particularly interesting because they can induce less frequent coordination numbers or maintain specific/required coordination geometry of the central atom, and lead to interesting magnetic behaviors.10–12Co(II) complexes represent the second most studied group of SMMs13 after Dy(III) complexes.14,15 Various structures based mainly on acyclic ligands (Schiff bases, heterocycles, polypyridines) have been intensively investigated,16 whereas those with macrocyclic ligands are rather scarce. Furthermore, the coordination sphere, i.e. the geometry and strength of the ligand field, has a crucial effect on magnetic anisotropy and consequently on the relaxation of magnetization as well,17–19 which is valid not only for Co(II) compounds, but also for all other complexes including Dy(III)-based SMMs.
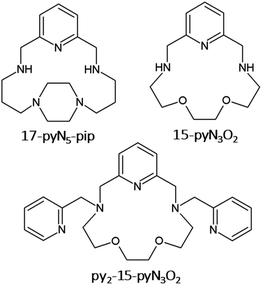
The synthesis of 15-membered pyridine-based macrocyclic ligand 15-pyN3O2 (see Fig. 1) was described more than 30 years ago,20 and complexes with 3d transition metals have been studied mainly in the field of molecular magnetism and medicine. The first study concerned Mn(II) complexes as potential MRI contrast agents.21 Furthermore, a series of complexes with M = Mn, Fe, Co, Ni, Cu, and Zn was prepared. As the radius of the central atom decreased, a decrease in coordination number was observed from 7 for Mn(II), Fe(III), Co(II), through 5 + 2 for Ni(II), 4 + 1 for Cu(II) to 5 for Zn(II). In the case of the Co(II) and Ni(II) complexes, a large axial ZFS component with D(Co) ≈ 40 cm−1, D(Ni) = −6.0 cm−1, was found.11
Since the Co(II) complex showed an intriguing magnetic behavior, a series of [Co(15-pyN3O2)X2], where X = Cl−, Br−, I−, was subsequently prepared and studied.22 All three complexes had coordination number 7 and the shape of the coordination polyhedron corresponded to distorted pentagonal bipyramid and exhibited the behaviour of field-induced SMMs. For this geometry of the coordination polyhedron, Co(II) is anticipated to possess a positive D parameter, which was subsequently confirmed in all cases with D(Cl) = 38 cm−1; D(Br) = 41 cm−1; D(I) = 35 cm−1.22 The correlation between the values of D parameter and the Mayer bond order (decreasing in order Co–I > Co–Cl > Co–Br) was understood as a consequence of the ligand field splitting and the decreasing covalency of the Co–X bond. Whether associated to a Cl, Br, or I anion, all complexes behaved as field-induced SMMs.22
Moreover, several derivatives of 15-pyN3O2 decorated with two pendant arms with different functional groups (e.g. pyridine,10 carboxylate,23 benzimidazol)24 were prepared. Among them the pyridine derivative py2-15-pyN3O2 (Fig. 1) was the most interesting as a decrease in coordination number from 7 (MnII, FeII, CoII), to 6 + 1 (NiII), to 5 (CuII) was observed.10 For the 7-coordinated complexes, all donor atoms of the macrocyclic ligand were coordinated to the central metal atom and the geometry of the coordination sphere was close to pentagonal bipyramid. In case of Ni(II) complex, the length of Ni–Oaliph bond was prolonged to 2.653(3) Å, and for the Cu(II) complex, one pyridine pendant arm and one oxygen atom were not coordinated. Substantial magnetic anisotropy was evidenced for Fe(II), Co(II) and Ni(II) complexes, with D(Fe) = −7.4(2) cm−1, D(Co) = +34(1) cm−1, and D(Ni) = −12.8(1) cm−1.10 Despite its positive D parameter, the Co(II) complex exhibited slow relaxation of magnetization below 8 K.10
On the other hand, for a series of Co(II) complexes with 17-membered pyridine/piperazine-based macrocycle 17-pyN5-pip (Fig. 1), [Co(17-pyN5-pip)X]+ (where X = Cl−, Br−, N3−, NCO−, NCS−, NCSe−) with distorted trigonal prismatic geometry, a negative D parameter was found with values ranging from −20 to −41 cm−1, and all showed field-induced SMM behavior.25
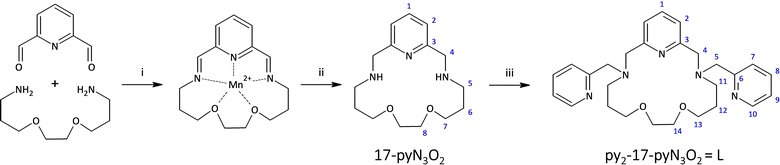
Thus, motivated by the above-mentioned studies, we synthesized a structurally new macrocyclic ligand py2-17-pyN3O2 = L (Fig. 2) as a structural analogue of py2-15-pyN3O2 with an enlarged macrocyclic cavity and its Co(II) complexes with different monovalent halido-/pseudohalido coligands. We investigated the effect of enlarged 17-membered macrocyclic cavity on the molecular structure and coordination geometry of Co(II) centers and compare the coordination ability of this ligand L with its 15-membered analogue. Moreover, the effect of coligand exchange on the structural properties as well as on the magnetic behavior of all Co(II) complexes were examined.
Experimental
Materials and methods
All the solvents (VWR International, Fontenay-sous-Blois, France) and other chemicals were purchased from commercial sources (Acros Organics, Geel, Belgium and Sigma-Aldrich, St. Louis, MO, USA) and used as received. Silica gel for column chromatography was purchased from Penta, Prague, Czech Republic (Silica gel 100; 0.063–0.2 mm). A one channel just infusion™ linear pump NE 300 (New Era Pump Systems, Inc., Farmingdale, NY, USA) and HSW Norm-Ject 20 mL syringes were employed during the ligand synthesis (infusion rate 1 mL min−1). 1H and 13C NMR spectra were measured at laboratory temperature on 400 MHz NMR spectrometer Varian MR-400 for high-resolution solution-state NMR (Varian, Palo Alto, CA, USA): 1H 399.95 MHz, (CDCl3, tetramethylsilane) δ = 0.00 ppm, 13C 100.60 MHz, (CDCl3, residual solvent peak) δ = 77.0 ppm. Multiplicity of the signals was indicated as follows: s – singlet, d – doublet, t – triplet, quin – quintet, m – multiplet, br – broad. Deuterated solvent CDCl3, containing 0.03% of TMS, from Sigma-Aldrich was used as received. The atom numbering scheme used for NMR data interpretation is shown in Fig. 2. The carbon as well as hydrogen atoms were assigned according to the spectra obtained from two-dimensional correlation experiments 1H–1H gs-COSY, 1H–13C gs-HMQC and 1H–13C gs-HMBC (see ESI Fig. S1–S5†). The mass spectra were collected on an LCQ Fleet mass spectrometer (Thermo Scientific, Waltham, MA, USA) equipped with an electrospray ion source and three-dimensional (3D) ion-trap detector in the positive mode (see ESI Fig. S6–S10†). IR spectra were measured on Jasco FT/IR-4700 spectrometer (Jasco, Easton, MD, USA) using the ATR technique on a diamond plate in the spectral range 4000–400 cm−1 (see ESI Fig. S11†). Elemental analysis (C, H, N) was realized on a Flash 2000 CHNO–S analyzer (Thermo Scientific, Waltham, MA, USA).Magnetic measurements for all the samples were carried out with a Quantum Design MPMS 5S SQUID magnetometer in the temperature range 2–300 K. The measurements were performed on polycrystalline samples mixed with grease and put in gelatin capsules. The temperature dependences of the magnetic susceptibility was obtained in an applied field of 1 kOe and the isothermal field dependence of the magnetizations were collected up to 5 T at temperatures between 2 and 8 K. The molar susceptibility (χM) was corrected for sample holder, grease and for the diamagnetic contribution of all the atoms by using Pascal's tables.26 AC susceptibility data were collected in the frequency range 1–1500 Hz. Assessment of the ZFS parameters have been done considering an S = 3/2 spin for Co(II), the software PHI27 was used for fitting the χMT = f(T) and M = f(H) behaviors. The powder X-ray diffraction (PXRD) patterns were measured on Rigaku Miniflex600 diffractometer in reflection mode with λ(CuKα1,Kα2) = 1.54059 and 1.54439 Å radiations (see ESI Fig. S12†).
Crystal data refinement
Single crystals of 1–5 suitable for X-ray structure analysis were prepared as described in the section Synthesis. X-ray diffraction data were collected on XtaLAB (Synergy-i or Synergy-s) Rigaku diffractometers (CuKα radiation source, λ = 1.54184 Å) at 293(2) K or at 100 K. The molecular structures of studied complexes were solved by direct methods or SHELXT and refined by full-matrix least-squares based on F2 (SHELXL 2014/07).28 Program Olex2 1.3 and CRYSTALS_15.4.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 were used for the final refinement.30 The hydrogen atoms on carbon atoms were fixed into idealized positions (riding model) and assigned temperature factors either Hiso(H) = 1.2 Ueq. (pivot atom) for CH and CH2 moieties or Hiso(H) = 1.5 Ueq. (pivot atom) for CH3 groups. The molecular and crystal structures of the studied complexes, depicted in Fig. 3 and S13–S23† were drawn using the Mercury software.31 Solvent mask procedure had to be applied to treat the co-crystallized disordered solvent molecules (one CH3OH molecule for complexes 1, 2, 3, 5 and 0.25 CH3OH molecule for complexes 4a). Other positional disorders were found in obtained molecular structures – complex 3: perchlorate anion (occupancy factors 0.39 and 0.61), complex 4a: uncoordinated NCS- anion (occupancy factors 0.48 and 0.52) and O2–C12–C13 part of the macrocycle (occupancy factors 0.23 and 0.77), complex 5: perchlorate anion (occupancy factors 0.20 and 0.80) and C11–O2–C12 part of the macrocycle (occupancy factors 0.27 and 0.73).
29 were used for the final refinement.30 The hydrogen atoms on carbon atoms were fixed into idealized positions (riding model) and assigned temperature factors either Hiso(H) = 1.2 Ueq. (pivot atom) for CH and CH2 moieties or Hiso(H) = 1.5 Ueq. (pivot atom) for CH3 groups. The molecular and crystal structures of the studied complexes, depicted in Fig. 3 and S13–S23† were drawn using the Mercury software.31 Solvent mask procedure had to be applied to treat the co-crystallized disordered solvent molecules (one CH3OH molecule for complexes 1, 2, 3, 5 and 0.25 CH3OH molecule for complexes 4a). Other positional disorders were found in obtained molecular structures – complex 3: perchlorate anion (occupancy factors 0.39 and 0.61), complex 4a: uncoordinated NCS- anion (occupancy factors 0.48 and 0.52) and O2–C12–C13 part of the macrocycle (occupancy factors 0.23 and 0.77), complex 5: perchlorate anion (occupancy factors 0.20 and 0.80) and C11–O2–C12 part of the macrocycle (occupancy factors 0.27 and 0.73).
Synthesis of ligands
Complexes preparation and characterization
Caution! Perchlorate salts of complexes are hazardous, heating or scratching them in solid form can lead to an explosion.Co(II) complexes 1 and 4a were prepared in the same way. Equimolar amounts of metal salt (71 mg of CoBr2·6H2O or 45 mg of Co(SCN)2·2H2O) and ligand L (100 mg; 0.217 mmol) were mixed in methanol (3 mL). The complexes were crystallized by vapor diffusion of diethyl ether into the resulting methanolic solution at 7 °C and the single crystals suitable for X-ray analysis were separated by decantation after three weeks. 4b was obtained from 4a after leaving the crystallisation mixture at RT for several days.
Co(II) complexes 2, 3 and 5 were prepared similarly. Co(ClO4)2·6H2O (79 mg; 0.217 mmol) was dissolved in methanol (2 mL) and tetrabutylammonium iodide (200 mg; 0.541 mmol), NaNCO (70 mg; 1.08 mmol) or NaN3 (56 mg; 1.08 mmol) were added. The solution was filtered and the filtrate was added dropwise to methanolic solution (2 mL) of L (100 mg; 0.217 mmol). The complexes were crystallized as mentioned above.
[CoLBr]Br·CH3OH (1·CH3OH): Dark green crystals, yield 100 mg (68%). MS m/z(+): 484.31 (calcd. 484.27) [CoL + Na]+; 599.20 (calcd. 599.13) [CoL + Br]+; C28H39Br2CoN5O3; Mr = 712.38, found (calcd.): C 46.87 (47.21); H 5.45 (5.52); N 9.68 (9.83); IR (ATR, cm−1): 1606, 1579, 1442 [ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)py + ν(C
C)py + ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)py].
N)py].
[CoLI]I0.5(ClO4)0.5·CH3OH (2·CH3OH): Dark violet crystals, yield 72 mg (44%). MS m/z(+): 484.32 (calcd. 484.27) [CoL + Na]+; 619.17 (calcd. 619.16) [CoL + ClO4]+; 647.11 (calcd. 647.12) [CoL + I]+; C28H39Cl0.5CoN5O5I1.5; Mr = 792.66, found (calcd.): C 42.68 (42.43); H 4.84 (4.96); N 8.66 (8.84); IR (ATR, cm−1): 1605, 1578, 1444 [ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)py + ν(C
C)py + ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)py]; 1091, 622 [ν(ClO4)−].
N)py]; 1091, 622 [ν(ClO4)−].
[CoL(NCO)]ClO4·CH3OH (3·CH3OH): dark violet crystals, yield 92 mg (61%). MS m/z(+): 519.19 (calcd. 519.20) [CoL − H]+; 562.20 (calcd. 562.21) [CoL + NCO]+; C29H39ClCoN6O8; Mr = 694.04, found (calcd.): C 51.03 (50.19); H 5.59 (5.66); N 12.14 (12.11); IR (ATR, cm−1): 2205 [ν(NCO)−]; 1605, 1583, 1444 [ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)py + ν(C
C)py + ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)py]; 1077, 621 [ν(ClO4)−].
N)py]; 1077, 621 [ν(ClO4)−].
[CoL(NCS)]NCS·0.25CH3OH (4a·0.25CH3OH): violet crystals, yield 60 mg (43%). MS m/z(+): 484.32 (calcd. 484.27) [CoL + Na]+; 578.19 (calcd. 578.19) [CoL + NCS]+; C29.25H36CoN7O2.25S2; Mr = 644.71, found (calcd.): C 53.61 (53.49); H 5.67 (5.63); N 15.01 (15.21); IR (ATR, cm−1): 2050 [ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S)−] 1605, 1570, 1467 [ν(C
S)−] 1605, 1570, 1467 [ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)py + ν(C
C)py + ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)py].
N)py].
[CoLN3]ClO4·CH3OH (5·CH3OH): dark blue crystals, yield 53 mg (35%). MS m/z(+): 484.32 (calcd. 484.27) [CoL + Na]+; 562.17 (calcd. 562.22) [CoL + N3]+; C28H39ClCoN8O7; Mr = 694.04, found (calcd.): C 47.96 (48.46); H 5.38 (5.66); N 16.58 (16.15); IR (ATR, cm−1): 2068 [ν(N3)−]; 1605, 1580, 1444 [ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)py + ν(C
C)py + ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)py]; 1076, 621 [ν(ClO4)−].
N)py]; 1076, 621 [ν(ClO4)−].
Computation details
ORCA 5.0.4 software package33 was utilized for all computations. First, complex cations were extracted from crystal structures and positions of hydrogen atoms were optimized using DFT with BP86 functional34 and def2-TZVP basis set for all atoms except for carbon and hydrogen where less demanding def2-SVP basis set was chosen35 together with resolution of identity (RI) approximation36 and def2/J auxiliary basis set.37 For complex 2, DKH2 was turned on together with relativistically recontracted DKH2-def2-SVP and TZVP basis sets similarly as before except for iodine where SARC-DKH-TZVP basis set38 was chosen together with SARC/J auxiliary basis set for Coulomb fitting. Subsequent CASSCF(7,5)/NEVPT2 calculations were performed utilizing the same basis sets as for the optimization calculations with the addition of RIJCOSX approximation39 and def2-TZVP/C basis set40 for correlation calculation.Results and discussion
Synthesis and general characterization of the ligand L
Ligand L represents a structurally new compound, and it is a two-carbon longer analogue to the previously prepared ligand py2-15-pyN3O2 (Fig. 1). The synthesis of the parent macrocycle proceeded analogously to the previously described 17-membered pyridine/piperazine-based ligand 17-pyN5-pip.32 For the cyclization step a linear pump was used, which ensures continuous addition of reactants, leading to a significant increase in the reaction yield. In this case 73% yield was achieved. In addition, an optimization of the cyclization reaction was performed on this system and the results are the subject of a forthcoming publication. The next step was a simple substitution reaction with pre-neutralized 2-(chloromethyl)pyridine. After purification of the crude product by column chromatography, the desired product was obtained and subsequently used for the preparation of complexes with selected Co(II) salts.Synthesis and general characterization of complexes 1–5
Complexes 1 and 4a were prepared by mixing the Co(II) salt with the ligand in methanol. Complex 4a transformed to 4b. The synthesis of complexes 2, 3 and 5 was divided in two steps: methanolic solution of Co(II) perchlorate was mixed with tetrabutylammonium iodide, NaNCO or NaN3 respectively, then the resulting solution was filtered and the filtrate was then mixed with the methanolic solution of ligand. After diffusion of diethyl ether was finished, highly crystalline solids were obtained for all complexes. The formation of all complexes was subsequently confirmed by mass spectrometry, infrared spectroscopy, elemental analysis and single crystal X-ray analysis. No inert conditions were required as all compounds are air-stable.IR spectra of all complexes were very similar (see ESI, Fig. S11†). Vibrations corresponding to the macrocyclic ligand can be observed in the positions ∼1600, ∼1580 and ∼1460 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N aromatic vibrations). For complexes 3–5, stretching vibrations of the coordinated anions 2068 cm−1 (N
N aromatic vibrations). For complexes 3–5, stretching vibrations of the coordinated anions 2068 cm−1 (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), 2205 cm−1, (N
N), 2205 cm−1, (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), ∼2050 cm−1 (N
O), ∼2050 cm−1 (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S) or perchlorate anion ∼1080 and ∼620 cm−1 were observed as well. Signals in mass spectra (positive mode) always very well corresponded to the [Co(L)X]+ cation, where X = Br− (1); I− (2); NCO− (3); NCS− (4a); and N3− (5). In case of complexes containing perchlorate counter anions, signal of [Co(L)(ClO4)]+ cations was observed as well.
S) or perchlorate anion ∼1080 and ∼620 cm−1 were observed as well. Signals in mass spectra (positive mode) always very well corresponded to the [Co(L)X]+ cation, where X = Br− (1); I− (2); NCO− (3); NCS− (4a); and N3− (5). In case of complexes containing perchlorate counter anions, signal of [Co(L)(ClO4)]+ cations was observed as well.
The phase purity of the samples was confirmed by the measurement of X-ray powder diffraction patterns which are comparable to those calculated from cif files for each complex (see ESI Fig. S12†).
X-ray diffraction analysis
All complexes crystallized in the space groups P21/c except for, complexes 4a and 4b which crystallized respectively in the space groups P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and Pna21. Other crystal data and structure refinements for studied complexes 1–5 are listed in Table 1. The molecular structures of complexes 1–5 are depicted in Fig. 3, S13 and S14.† For 1–3, 4a, and 5 the macrocyclic ligand is coordinated to the central Co(II) cation by three nitrogen donor atoms of the macrocyclic cavity and two nitrogen donor atoms belonging to the methylpyridine pendant arms and the last sixth coordination position is occupied by an anionic halido/pseudohalido coligand (Fig. 3). The distances for coordination bonds of all complexes 1–5 are listed in Table 2, selected bond angles are listed in Table S1.† There is no bond between the central metal atom and the two oxygen atoms in the aliphatic part of the macrocycle (interatomic distance ∼5.7 Å). The shortest bonds within the coordination sphere are between Co(II) and the N-donor coligand (NCO, N3) in the range of 2.015–2.044 Å. The length of the bonds to the macrocyclic pyridine ring N1 ranges between 2.059–2.068 Å, followed by slightly longer bonds to the nitrogen atoms N4 and N5 in the pendant arms (2.090–2.210 Å). In contrast, the bonds between the central atom and the aliphatic nitrogen atoms are significantly extended (2.330–2.438 Å), and the longest distance is between the central atom and the halogen anions (2.563 and 2.822 Å for 1 and 2, respectively).
and Pna21. Other crystal data and structure refinements for studied complexes 1–5 are listed in Table 1. The molecular structures of complexes 1–5 are depicted in Fig. 3, S13 and S14.† For 1–3, 4a, and 5 the macrocyclic ligand is coordinated to the central Co(II) cation by three nitrogen donor atoms of the macrocyclic cavity and two nitrogen donor atoms belonging to the methylpyridine pendant arms and the last sixth coordination position is occupied by an anionic halido/pseudohalido coligand (Fig. 3). The distances for coordination bonds of all complexes 1–5 are listed in Table 2, selected bond angles are listed in Table S1.† There is no bond between the central metal atom and the two oxygen atoms in the aliphatic part of the macrocycle (interatomic distance ∼5.7 Å). The shortest bonds within the coordination sphere are between Co(II) and the N-donor coligand (NCO, N3) in the range of 2.015–2.044 Å. The length of the bonds to the macrocyclic pyridine ring N1 ranges between 2.059–2.068 Å, followed by slightly longer bonds to the nitrogen atoms N4 and N5 in the pendant arms (2.090–2.210 Å). In contrast, the bonds between the central atom and the aliphatic nitrogen atoms are significantly extended (2.330–2.438 Å), and the longest distance is between the central atom and the halogen anions (2.563 and 2.822 Å for 1 and 2, respectively).
| a Rint = ∑|Fo2 − Fo,mean2|/∑Fo2.b R1 = ∑(|·|Fo| − |Fc|·|)/∑|Fo|; wR2 = [∑wR2(Fo − Fo2)2/∑w(Fo2)2]1/2. | ||||||
|---|---|---|---|---|---|---|
| Compound | 1·MeOH | 2·MeOH | 3·MeOH | 4a·0.25MeOH | 4b | 5·MeOH |
| Formula | C28H39Br2CoN5O3 | C28H39Cl0.5CoI1.5N5O5 | C29H39ClCoN6O8 | C29.25H36CoN7O2.25S2 | C29H35CoN7O2S2 | C28H39ClCoN8O7 |
| Mr | 712.38 | 792.66 | 694.04 | 644.71 | 636.71 | 694.04 |
| Temperature (K) | 293(2) | 293(2) | 100.0(1) | 100.0(1) | 100.0(1) | 100.0(1) |
| Wavelength (Å) | 1.54184 | 1.54184 | 1.54184 | 1.54184 | 1.54184 | 1.54184 |
| Crystal system | Monoclinic | Monoclinic | Monoclinic | Triclinic | Orthorhombic | Monoclinic |
| Space group | P21/c | P21/c | P21/c | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Pna21 | P21/c |
| a (Å) | 9.5063(2) | 9.8084(2) | 10.1831(3) | 9.4553(3) | 9.20980(10) | 10.2781(4) |
| b (Å) | 16.1542(6) | 16.5786(3) | 15.8178(4) | 9.5655(3) | 32.9484(3) | 15.7954(4) |
| c (Å) | 19.9926(7) | 20.3177(3) | 19.9190(6) | 18.0521(5) | 9.78030(10) | 19.6987(5) |
| α (°) | 90 | 90 | 90 | 84.509(2) | 90 | 90 |
| β (°) | 95.610(3) | 92.489(2) | 93.777(3) | 85.684(2) | 90 | 95.297(3) |
| γ (°) | 90 | 90 | 90 | 69.475(3) | 90 | 90 |
| V, Å3 | 3055.49(17) | 3300.73(10) | 3201.46(17) | 1520.53(8) | 2967.81(5) | 3184.36(17) |
| Z | 4 | 4 | 4 | 2 | 4 | 4 |
| Dcalc, g cm−3 | 1.479 | 1.530 | 1.373 | 1.391 | 1.425 | 1.381 |
| μ, mm−1 | 7.714 | 15.686 | 5.416 | 6.023 | 6.171 | 5.439 |
| F(000) | 1380 | 1516 | 1380 | 666 | 1332 | 1380 |
| θ range for data collection (°) | 3.524–67.684 | 3.442–67.684 | 3.571–67.684 | 4.927–67.684 | 2.682–73.823 | 3.593–57.684 |
| Refl. Collected | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103 103 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118 118 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 483 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 491 |
| Independent refl. | 5591 | 5979 | 5926 | 5523 | 6088 | 5884 |
| R(int)a | 0.0524 | 0.0422 | 0.0507 | 0.0403 | 0.0340 | 0.0417 |
| Data/restrains/parameters | 4030/0/334 | 5013/0/380 | 4687/60/434 | 4906/36/402 | 5642/1/371 | 4143/78/462 |
| Completeness to θ (%) | 98.8 | 98.3 | 98.2 | 99.0 | 99.2 | 97.7 |
| Goodness-of-fit on F2 | 1.037 | 1.032 | 1.106 | 1.030 | 0.953 | 1.033 |
| R1, wR2 (I > 2σ(I)b) | 0.0538/0.1440 | 0.0473/0.1282 | 0.0567/0.1562 | 0.0624/0.1597 | 0.0268/0.0730 | 0.0639/0.1708 |
| R1, wR2 (all data)b | 0.0754/0.1591 | 0.0561/0.1340 | 0.0710/0.1641 | 0.0697/0.1647 | 0.0274/0.0733 | 0.0881/0.1869 |
| Largest diff. peak and hole/A−3 | 1.215/−0.667 | 0.724/-0.638 | 0.791/-0.524 | 1.465/-0.484 | 0.180/-0.250 | 0.901/-0.766 |
| CCDC number | 2344172 | 2344178 | 2344177 | 2344175 | 2371458 | 2344176 |
| 1 | 2 | 3 | 4 | 4a | 4b | 5 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Co1–N1 | 2.059(4) | Co1–N1 | 2.064(4) | Co1–N1 | 2.068(3) | Co1–N1 | 2.059(3) | 2.069(1) | Co1–N1 | 2.065(3) |
| Co1–N2 | 2.439(4) | Co1–N2 | 2.339(4) | Co1–N2 | 2.433(3) | Co1–N2 | 2.361(2) | 2.280(2) | Co1–N2 | 2.344(3) |
| Co1–N3 | 2.364(4) | Co1–N3 | 2.409(4) | Co1–N3 | 2.350(3) | Co1–N3 | 2.338(4) | 2.703(2) | Co1–N3 | 2.400(4) |
| Co1–N4 | 2.099(3) | Co1–N4 | 2.209(4) | Co1–N4 | 2.108(3) | Co1–N4 | 2.090(3) | 2.162(2) | Co1–N4 | 2.159(4) |
| Co1–N5 | 2.196(4) | Co1–N5 | 2.106(3) | Co1–N5 | 2.166(3) | Co1–N5 | 2.204(3) | 5.455(2) | Co1–N5 | 2.103(3) |
| Co1–Br1 | 2.5635(9) | Co1–I1 | 2.8222(7) | Co1–N6 | 2.015(3) | Co1–N6 | 2.064(3) | 2.002(2) | Co1–N6 | 2.044(3) |
| Co1–N7 | — | 2.032(2) | ||||||||
| τ6 | 0.46 | 0.48 | 0.47 | 0.47 | 0.49 | 0.49 | ||||
Complex 4a underwent a rather scarce crystal-to-crystal transformation to a structurally different new compound 4b, which was evidenced by measured PXRD patterns (Fig. S12†). The coordination sphere of 4b (Fig. 3 and S23†) is strikingly different from that of 4a. Two thiocyanate anions coordinate the central Co(II) atom and only one pyridine pendant-arm is linked to the metal center whereas the second pyridine pendant-arm is uncoordinated. Moreover, the Co–N3 (macrocycle) distance is significantly elongated to ∼2.7 Å, suggesting semi-coordination of N3 and final coordination number 5 + 1.
In order to elucidate the nature of Co1–N3 interaction, we performed QT-AIM41 analysis in the vicinity of these atoms utilizing MultiWFN 3.7 software,42 as our co-workers utilized this method in previous work.43 Negative sign(λ2)ρ value (Fig. S15†) in this region suggests that the interaction should be indeed attractive.44 This is also supported by electron localization function plot (Fig. S16†) which shows orientation of the nitrogen lone electron pair towards the metal ion.45 QT-AIM analysis revealed a presence of the bond critical point (BCP) of type (3,−1) between Co1–N3 (Fig. S15†) in which the real space function values were analysed. Coordination bonds usually exhibit positive values of Laplacian of electron density (∇2ρ(r)) and negative values of energy density (H(r)) whereas both should be positive in the case of non-covalent interaction.46 For Co1–N3 interaction, the values are 0.061 and −0.0013, respectively. Additionally, ratio |V(r)|/G(r), where V(r) represents potential energy density and G(r) represents Lagrangian kinetic energy, should be higher than 1 for bonds possessing a degree of covalency.47 For the studied BCP, ratio |V(r)|/G(r) equals 1.076 and thus can be concluded that the bond is coordination covalent, albeit weaker, based on the aforementioned descriptors.
All complexes showed very distorted geometry of the coordination sphere between octahedral and trigonal prismatic ones as was confirmed by a continuous shape measures (deviation between the real and ideal polyhedron geometry) calculated by using the program Shape 2.1 (Table S2†).48,49 For complexes 1–4 the coordination sphere has distorted octahedral geometry, and for complex 5 it has distorted trigonal prism shape. In all cases the deviations from ideal geometry are large (∼7) and the differences in Shape parameters for the octahedral and trigonal prismatic geometry are quite small (∼0.2–0.5 for complexes 3–5, ∼2 for complexes 1 and 2, Table S2†). Thus, the coordination sphere of these complexes is strongly distorted and lies in between these two geometries. The distortion of the polyhedron decreases in order 1 → 4a → 3 → 4b → 5 → 2.
The coordination geometry was also investigated by using the newly proposed structural parameter τ6, which is defined as follows (angles α, β and γ are the three greatest valence angles of the coordination center):50
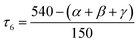 | (1) |
This geometry index ranging from 0 (ideal octahedron) to 1 (ideal trigonal prismatic shape) is analogous to previously published τ5 and τ4 indices for five- and four-coordinate complexes, respectively. The τ6 value for studied complexes 1–5 is very close to 0.5 (Table 2), which is in agreement with the parameter obtained with Shape and confirms an actual shape of the coordination polyhedron between octahedral and prismatic trigonal.
The macrocyclic ligand is significantly bent. To express the degree of the bending, two planes have been interleaved through the system – the first one through the central atom, the pyridine nitrogen atom N1 and the two nitrogen atoms bearing the pendant arms N2 and N3, and the second plane through the central atom and the two macrocyclic oxygen atoms O1 and O2 (blue and red, respectively in Fig. 4). The angle between these two planes ranges from 75.7° (4a) to 77.8° (1).
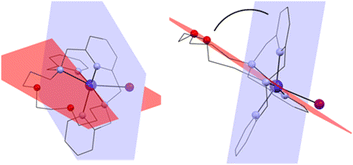 | ||
| Fig. 4 Two planes interleaved through the complex cation showing the bending of the macrocyclic ligand. Front view (left) and side view (right). | ||
These molecular structures of Co(II) complexes differ significantly from those obtained with py2-15-pyN3O2, in which all seven donor atoms of the macrocycle were coordinated to the central metal atom leading to a pentagonal bipyramidal coordination sphere. This structural difference most probably arises from (i) the higher flexibility of the macrocyclic scaffold of L, induced by longer propylene bridges between O and NH groups and (ii) formation of less stable six-membered chelate rings for L in comparison with more stable five-membered chelate rings in case of py2-15-pyN3O2. This is a typical example of the fact that the size of the macrocyclic cavity plays a crucial role in the coordination number and the geometry of the coordination sphere as well.
In the crystal packing, complexes 1 and 2 formed supramolecular 1D chains through hydrogen bonds between the two oxygen atoms of the aliphatic part of the molecule and the main pyridine ring –O⋯H–Carom (Fig. 5, S17 and S18†). These systems are further strengthened via π–π stacking interactions (Cg⋯Cg distance is 4.203 Å for 1, Fig. 5 and 4.302 Å for 2) between the individual pyridine nuclei. The individual molecules are then linked via a system of additional hydrogen bonds involving the bromide anions. The main pyridine ring is thus linked to the pendant arms via uncoordinated bromide anions Carom–H⋯Br⋯H–Carom. In case of complex 2 the uncoordinated anion is half perchlorate and half iodide (Fig. S19†).
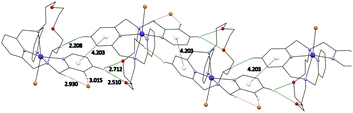 | ||
| Fig. 5 Visualization of π–π stacking interactions with a centroids (white balls) distance between two pyridine rings and hydrogen bonds discussed in the text for complex 1. | ||
1D chains were also found in the structure of complexes 3, 4a/b and 5 along the b-axis (Cg⋯Cg distance is 4.209 Å, 4.258/4.026 Å and 4.211 Å, respectively, see Fig. S20 and S23†). The molecules of complex 3 are oriented in antiparallel directions and they are stabilized by hydrogen bonds via the isocyanate anions with aliphatic –CH2– bonds bearing pyridine rings (Fig. S21†). In the case of complexes 3 and 5, an uncoordinated perchlorate anion is present in the structure, which further extends the chains into a 3D network through the formation of Carom–H⋯O–Cl–O⋯H–Carom hydrogen bonds (Fig. S22†). The thiocyanate anion in the structure of complex 4a occupies a site in the center of symmetry at two positions in the crystallographically independent unit. In addition, π–π stacking interaction between the pyridine nuclei of the pendant arms (Cg⋯Cg distance is 3.632 Å) was observed in the complex 4a (Fig. S20†). A different situation is observed for complex 4b, in which one of the methylpyridine pendant arms is uncoordinated and oriented in opposite direction. A 1D stacking is formed due to above-mention π–π stacking interaction however it involves the uncoordinated pendant arm and a macrocyclic pyridine ring (see Fig. S23†).
Magnetic studies
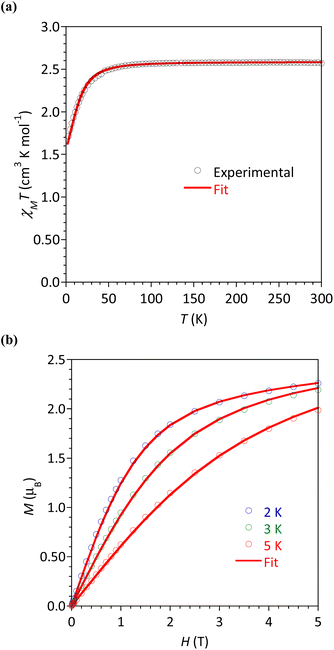
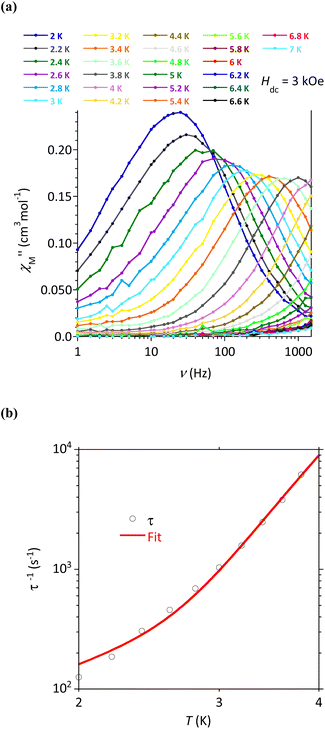
The magnetic susceptibility χM (defined as M/H per mole of complex with M the magnetization and H the magnetic field) between 2 and 300 K, and the field dependence of the magnetization were studied for all the complexes. The respective plots are given in Fig. 6 for 4b and Fig. S24–S27† for the other complexes. The possibility of slow relaxation of the magnetization was tested by AC susceptibility.The temperature dependences of the χMT product are very similar in this series of compounds. The main features will be described taking 4b as an example (Fig. 6a) and some characteristic values are summarized in Table 3. For 4b, the value of χMT at 300 K was 2.33 cm3 K mol−1, in agreement with the calculated value of 2.48 cm3 K mol−1 for a Co(II) center with spin 3/2 and g = 2.3. Upon cooling, the χMT product decreased slowly until 30 K before a more rapid diminution to a minimum value of 1.71 cm3 K mol−1 at 2 K. This behavior is typical of Co(II) systems with second-order spin–orbit coupling (i.e. magnetic anisotropy), and, possibly intermolecular interactions that are also expected to operate at low temperatures.
| Compound | χT (300 K) | M (μB) (2 K) | D (cm−1) | E (cm−1) | E/D | g |
|---|---|---|---|---|---|---|
| a By CASSCF/NEVPT2.b No satisfactory fit could be obtained for 5. | ||||||
| 1·MeOH | 2.42 | 2.15 | 16.17 ± 0.4 | 4.9 ± 0.2 | 0.30 | 2.272 ± 0.001 |
| Calculateda | −17.38 | −5.44 | 0.31 | 2.265 | ||
| 2·MeOH | 2.59 | 2.15 | −17.4 ± 0.4 | 5.3 ± 0.4 | 0.30 | 2.354 ± 0.002 |
| Calculateda | −23.61 | −6.35 | 0.27 | 2.278 | ||
| 3·MeOH | 2.58 | 2.26 | 12.8 ± 0.3 | 2.8 ± 0.3 | 0.22 | 2.231 ± 0.001 |
| Calculateda | −14.96 | −4.73 | 0.31 | 2.256 | ||
| 4a.0.25 MeOH | — | — | — | — | — | — |
| Calculateda | −19.29 | −5.37 | 0.28 | 2.264 | ||
| 4b | 2.33 | 2.14 | 17.0 ± 0.3 | 3.4 ± 0.2 | 0.20 | 2.348 ± 0.001 |
| Calculateda | −17.40 | −5.63 | 0.32 | 2.264 | ||
| 5·MeOH | 2.47 | 2.23 | b | b | b | b |
| Calculateda | −15.34 | −4.18 | 0.27 | 2.250 | ||
The field dependences of the magnetization were measured at temperatures ranging between 2 and 5 K (Fig. 6b and S24–S27†). The observed values at 2 K and 5 T (highest field) are between 2.14 and 2.26 μB, significantly lower than the expected value of 3 μB for a spin-only contribution for an S = 3/2 system. This is the consequence of the magnetic anisotropy resulting from ZFS for Co(II). To quantify this anisotropy the χMT vs. T and M vs. H curves were simultaneously analyzed using the program PHI.27 For all complexes, positive D values were obtained but it must be stressed that the E/D ratio is large and close to 1/3. Attempts made to fit with negative values for D gave even worse E/D ratio (except for 2). This is in agreement with geometries closer to octahedral (vide supra) known to promote D > 0.9 For complex 5 we could not obtain a satisfactory modeling, even taking into account intermolecular interactions (zj′), suggested by the marked drop of χMT at 2 K. The absolute D and E values are in good agreement with those obtained by theoretical calculations (vide infra), the difference of sign is not relevant for system with large rhombicity (E/D ratio close to the maximal value 1/3).51
In order to confirm obtained experimental D and E values, the post-Hartree–Fock CASSCF(7,5)/NEVPT2 calculations were performed. Results are given in Table 3. The D values for all the complexes are negative and found between −24 and −15 cm−1. The calculated individual non-zero contributions to D-tensor for complexes 1–5 are given in Table S3† and it is clear that the contribution of the first excited state has always the largest negative value, thus represents the main contribution to D-tensor and therefore the overall D-values are negative in sign.
The absolute D-values are in good agreement with the experimental ones including also large values of rhombic parameter E or E/D ratio close to the maximal value 1/3. On the other hand, they differ in sign which is not relevant for systems with a large rhombicity. In such a case the system has uniaxial magnetic anisotropy regardless the sign of D-value.51 It is worth noting that norms of projected states of the effective Hamiltonian are near 1, suggesting that the results obtained from calculations should be reliable as there are no low-lying 2nd excited states.
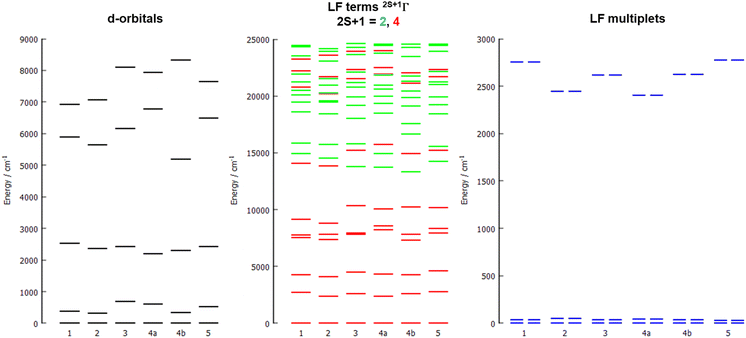
The energy diagrams of the d-orbital splitting, ligand-field terms and ligand-field multiplets are shown in Fig. 7. The splitting of d-orbitals is far from that of an ideal octahedral or trigonal prismatic ligand field, which is in accordance with strongly distorted coordination geometry in between octahedral and trigonal prismatic.
The d-orbital splitting resembles the splitting obtained for previously studied trigonal prismatic Co(II) complexes with 17-pyN5-pip,25 especially those with NCO−, NCS− and NCSe− coligands. Moreover, calculated D-values were in a similar range (ca. 30–50% larger, i.e. −31 to −35 cm−1) in comparison with studied complexes 1–5.
AC susceptibility responses have been investigated for each complex but a maximum for 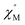 above 2 K was only detected for complex 4b when applying a dc field. The field dependence of the AC signal at 2 K indicated an optimal field of 3 kOe (Fig. S28†). Subsequently, the AC signals for 4b in HDC = 3 kOe were measured scanning frequencies from 1 to 1500 Hz every 0.2 K between 2 and 7 K (Fig. 8a and S29†). The relaxation time, τ, was obtained by analyzing the
above 2 K was only detected for complex 4b when applying a dc field. The field dependence of the AC signal at 2 K indicated an optimal field of 3 kOe (Fig. S28†). Subsequently, the AC signals for 4b in HDC = 3 kOe were measured scanning frequencies from 1 to 1500 Hz every 0.2 K between 2 and 7 K (Fig. 8a and S29†). The relaxation time, τ, was obtained by analyzing the 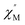 versus ν data for each temperature with the generalized Debye model,52 results are plotted as 1/τ (log scale) versus T in Fig. 8b. This behavior was well reproduced until 2.6 K considering Raman and direct relaxation mechanisms (eqn (2)), best fit gave C = 0.02 ± 0.01 K−n s−1, n = 9.3 ± 0.4 and B = 14
versus ν data for each temperature with the generalized Debye model,52 results are plotted as 1/τ (log scale) versus T in Fig. 8b. This behavior was well reproduced until 2.6 K considering Raman and direct relaxation mechanisms (eqn (2)), best fit gave C = 0.02 ± 0.01 K−n s−1, n = 9.3 ± 0.4 and B = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 3000 K−1 T−4 s−1. Attempts considering Raman and QTM processes gave poor quality fits, and an Orbach mechanism is excluded for a system with positive D.53
000 ± 3000 K−1 T−4 s−1. Attempts considering Raman and QTM processes gave poor quality fits, and an Orbach mechanism is excluded for a system with positive D.53
| τ−1 = CTn + BH4T | (2) |
Conclusion
A new macrocyclic ligand containing two 2-methylpyridine pendant arms was prepared and involved in the preparation of a series of Co(II) complex with one monovalent coligand (X = Br−, I−, NCO−, NCS− and N3−). All complexes are six-coordinate with a strongly distorted coordination sphere lying in between octahedral and trigonal prismatic geometry. Although the macrocyclic ligand is potentially heptadentate, only its nitrogen atoms are involved in the coordination to Co(II), the two oxygen donor atoms are not due to a large flexibility of the 17-membered macrocycle. These complexes show modest magnetic anisotropy with positive D-values but with E/D ratio close to 1/3, regardless the different coligand. Interestingly, complex 4b was found to behave as a field-induced SMM with magnetization relaxation driven by a direct and Raman mechanisms.Data availability
The data supporting this article have been included as part of the ESI.† Crystallographic data for 1, 2, 3, 4a, 4b and 5 has been deposited at the CCDC database under deposition numbers 2344172, 2344178, 2344177, 2344175, 2371458, and 2344176.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Palacký University Olomouc projects IGA_PrF_2023_007 and IGA_PrF_2024_009. Authors are grateful to M. J.-F. Meunier (LCC) for technical assistance in magnetic data collections and to P. Richterová for measurement of elemental analyses.References
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, U.K., 2006 Search PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia and D. Gatteschi, Nat. Mater., 2009, 8, 194 CrossRef CAS PubMed.
- R. E. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 7992 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef CAS PubMed.
- A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., 2006, 118, 229 Search PubMed.
- F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229 RSC.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- V. Vieru, S. Gómez-Coca, E. Ruiz and L. F. Chibotaru, Angew. Chem., Int. Ed., 2024, 63, e202303146 CrossRef CAS PubMed.
- P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2016, 55(12), 5957 CrossRef CAS PubMed.
- B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2015, 54(7), 3352 CrossRef PubMed.
- J.-P. Sutter, V. Béreau, V. Jubault, K. Bretosh, C. Pichon and C. Duhayon, Chem. Soc. Rev., 2022, 51, 3280–3313 RSC.
- P. Kumar Sahu, R. Kharel, S. Shome, S. Goswami and S. Konar, Coord. Chem. Rev., 2023, 475, 214871 CrossRef CAS.
- T. G. Ashebr, H. Li, X. Ying, X.-L. Li, C. Zhao, S. Liu and J. Tang, ACS Mater. Lett., 2022, 4, 307–319 CrossRef CAS.
- J. Li, Y. Yang, Q. Yu, G. Su and W. Liu, J. Phys. Chem. C, 2024, 128, 4882–4890 CrossRef CAS.
- J. Juráková and I. Šalitroš, Monatsh. Chem., 2022, 153, 1001–1036 CrossRef PubMed.
- A. Sarkar, S. Dey and G. Rajaraman, Chem.–Eur. J., 2020, 26, 14036–14058 CrossRef CAS PubMed.
- S. Ghosh, S. Kamilya, M. Das, S. Mehta, M.-E. Boulon, I. Nemec, M. Rouzières, R. Herchel and A. Mondal, Inorg. Chem., 2020, 59, 7067–7081 CrossRef CAS PubMed.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- U. Luening, Liebigs Ann. Chem., 1987, 11, 949–955 CrossRef.
- B. Drahoš, J. Kotek, P. Hermann, I. Lukeš and É. Tóth, Inorg. Chem., 2010, 49, 3224–3238 CrossRef PubMed.
- B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2017, 56, 5076–5088 CrossRef PubMed.
- P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Eur. J. Inorg. Chem., 2018, 2018, 4286–4297 CrossRef CAS.
- B. Drahoš, I. Císařová, O. Laguta, V. T. Santana, P. Neugebauer and R. Herchel, Dalton Trans., 2020, 49, 4425–4440 RSC.
- E. Zahradníková, J.-P. Sutter, P. Halaš and B. Drahoš, Dalton Trans., 2023, 52, 18513–18524 RSC.
- O. Kahn, Molecular Magnetism, VCH, Weinheim, 1993 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- P. W. Betteridge, J. R. Carruthers, R. I. Cooper, K. Prout and D. J. Watkin, J. Appl. Crystallogr., 2003, 36, 1487 CrossRef CAS.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- E. Zahradníková, R. Herchel, I. Šalitroš, I. Císařová and B. Drahoš, Dalton Trans., 2020, 49, 9057–9069 RSC.
- (a) F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152(22), 224108 CrossRef CAS PubMed; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1606 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297 RSC.
- F. Neese, J. Comput. Chem., 2003, 24(14), 1740 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8(9), 1057 RSC.
- J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41(20), 1842 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356(1–3), 98 CrossRef CAS.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117(4), 587 Search PubMed.
- R. F. Bader, Acc. Chem. Res., 1985, 18(1), 9–15 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed.
- L. Havlíček, R. Herchel, I. Nemec and P. Neugebauer, Polyhedron, 2022, 223, 115962 CrossRef.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132(18), 6498–6506 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92(9), 5397–5403 CrossRef CAS.
- I. V. Ananyev, N. A. Bokach and V. Y. Kukushkin, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76(3), 436–449 CrossRef CAS PubMed.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117(12), 5529–5542 CrossRef CAS.
- D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Chem.–Eur. J., 2003, 9(6), 1281–1295 CrossRef CAS PubMed.
- S. Alvarez, Dalton Trans., 2005,(13), 2209–2233 RSC.
- J. Moncol, Czech Chem. Soc. Symp. Ser., 2023, 21, 147 Search PubMed.
- I. Nemec, R. Herchel, M. Kern, P. Neugebauer, J. van Slageren and Z. Travnicek, Materials, 2017, 10, 249 CrossRef PubMed.
- C. Dekker, A. F. M. Arts, H. W. de Wijn, A. J. van Duyneveldt and J. A. Mydosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 11243 CrossRef CAS PubMed.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 5300 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2344172, 2344175–2344178 and 2371458. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ra02387k |
| This journal is © The Royal Society of Chemistry 2024 |