Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermophysical properties of polyethylene glycol oligomers via molecular dynamics simulations†
Thi H. Ho *ab,
Tong Duy Hien
*ab,
Tong Duy Hien c,
Øivind Wilhelmsend and
Thuat T. Trinh
c,
Øivind Wilhelmsend and
Thuat T. Trinh *d
*d
aLaboratory for Computational Physics, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: thi.hohuynh@vlu.edu.vn
bFaculty of Mechanical – Electrical and Computer Engineering, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
cFaculty of Engineering, Vietnamese-German University (VGU), Thu Dau Mot City, Binh Duong Province 75000, Vietnam
dDepartment of Chemistry, Porelab, Norwegian University of Science and Technology, Trondheim, Norway. E-mail: thuat.trinh@ntnu.no
First published on 3rd September 2024
Abstract
Polyethylene glycol (PEG) is a versatile chemical with numerous applications in various fields, including biomedical research, pharmaceutical development, and industrial manufacturing. Molecular dynamics (MD) is a powerful tool for investigating the thermophysical properties of PEG molecules. In this study, we employ the General AMBER force field (GAFF) to perform MD simulations on various PEG oligomers, focusing on the calculation of density, self-diffusion coefficients, shear viscosity, and thermal conductivity. The results demonstrate excellent agreement with experimental data, where GAFF outperforms other force fields in reproducing thermophysical properties. For a PEG tetramer, the GAFF force field reproduces experimental data within 5% for the density, 5% for the diffusion coefficient, and 10% for the viscosity. In comparison, the OPLS force field displays significant deviations exceeding 80% for the diffusion coefficient and 400% for the viscosity. A detailed analysis of partial charge distributions and dihedral angles reveals that they significantly impact the structural behavior of PEG oligomers. The findings highlight the GAFF force field as one of the most accurate and reliable options for simulating systems with PEGs.
Introduction
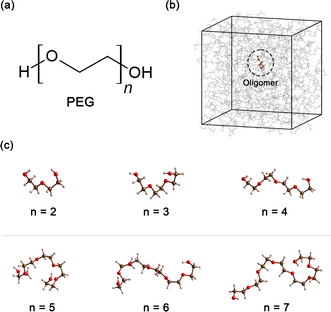
Polyethylene glycol (PEG), a compound of significant versatility, holds a pivotal role across diverse industries. Its chemical structure is represented as H–[O–CH2–CH2]n–OH, as depicted in Fig. 1(a). With an annual production order of approximately 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons,1 this compound has garnered considerable attention due to its wide-ranging uses in the chemical and healthcare industries.2 For example, in the medical field, PEG is often used as an excipient in pharmaceutical products, serving as a base for various dosage forms, including oral, topical, and parenteral medications.3,4 Its role in enhancing the solubility and stability of drugs makes it a crucial component in pharmaceutical products. In the cosmetic industry, PEG is known for its multiple functions, such as a humectant that helps retain moisture, a solvent that aids in the dissolution of other substances, or a softener that contributes to the texture and feel of cosmetic products.5,6 In the manufacturing sector, PEG is utilized for its properties as an anti-foaming agent and plasticizer, and in the production of ceramics.7–9 Furthermore, PEG can also function as a heat transfer medium10 or a chemical solvent11 when PEG is present as a major component in the system.
000 tons,1 this compound has garnered considerable attention due to its wide-ranging uses in the chemical and healthcare industries.2 For example, in the medical field, PEG is often used as an excipient in pharmaceutical products, serving as a base for various dosage forms, including oral, topical, and parenteral medications.3,4 Its role in enhancing the solubility and stability of drugs makes it a crucial component in pharmaceutical products. In the cosmetic industry, PEG is known for its multiple functions, such as a humectant that helps retain moisture, a solvent that aids in the dissolution of other substances, or a softener that contributes to the texture and feel of cosmetic products.5,6 In the manufacturing sector, PEG is utilized for its properties as an anti-foaming agent and plasticizer, and in the production of ceramics.7–9 Furthermore, PEG can also function as a heat transfer medium10 or a chemical solvent11 when PEG is present as a major component in the system.
The vast applications of PEG can be attributed to its unique physical and chemical properties. Considering safety aspects, PEG is environmentally benign and non-toxic, possesses a low vapor pressure, thereby minimizing the risk of inhalation exposure.12 Its biodegradable nature further enhances its ecological compatibility, making it a preferred choice in green chemistry.13 In addition to its advantageous properties as a green chemical solvent, PEG is appealing due to its cost-effectiveness and superior solvent capabilities compared to ionic liquids for certain solutes.14 This enables its usage as a solvent for various mineral salts15 and also allows PEG to be used as a medium to fabricate metal organic frameworks (MOFs).16,17 Recently, the interest in PEG as a solvent for chemical synthesis and separations has increased, as shown by recent studies.12,18,19 This highlights the ongoing exploration of the potential for PEG in various fields and its importance in future scientific advancements.
PEG is commercially available as a polydisperse mixture, where the average molar weight of these mixtures is indicated by the product name. For example, PEG200 indicates that the average molar weight is approximately 200 g mol−1. In recent years, the physical properties of PEG, such as its density, velocity, self-diffusion coefficient, and thermal conductivity, have become the focus of extensive research. These properties are crucial for understanding the behavior of PEG in different applications. Numerous investigations have reported the densities20–36 viscosities,20–24,28,30,32–34,37,38 and thermal conductivities39–44 of PEG. However, a comprehensive understanding of these properties remains an ongoing subject for both experimental and theoretical studies. In experimental studies, the values of the thermophysical properties of neat (pure) PEG are typically obtained from extrapolations to zero content of water or other solvents.11,38 Consequently, these properties may vary from vendor to vendor and batch to batch for PEG, posing challenges for accurate determination of these properties for neat PEG.
Employing molecular dynamics (MD) simulations to calculate thermophysical properties is a powerful and widely used methodology, offering insights into the behavior of materials at the molecular level.11,45–48 However, the selection of appropriate force fields, which accurately represent the interatomic interactions in the system, poses a significant challenge. A review of the literature reveals that while there are numerous force fields available for glymes, which are structurally similar to PEGs, there are only a limited number of force fields specifically designed for PEGs.49 These include GAFF/AMBER,50,51 CGenFF/CHARMM,52,53 GROMOS,54 OPLS,55 Martini,56 and a specific force field from the Müller–Plathe group.57 These force-fields were frequently created and examined for aqueous solutions containing PEG, but not for neat PEG. Furthermore, each of these force fields has its own strengths and limitations, and the choice of force field can significantly impact the results from MD simulations.
Recently, Hoffmann et al.45 conducted MD simulations to evaluate the accuracy of available force fields for neat PEG200, focusing on replication of experimental properties, particularly the density and self-diffusion coefficients. Their findings show that there are discrepancies in the results between various force fields and simulation specifications, and suitable modifications to the force field could improve the simulation results. The authors claimed that OPLS is currently the best force field for simulating PEG oligomer properties.45 However, there remain significant differences between simulation results and experimental data.45 Therefore, further development and testing of force-fields for neat PEG is necessary to enhance the understanding of PEG and its suitability for different applications.
In this study, we investigate neat PEG oligomers by use of MD simulations with the General AMBER force field (GAFF). The accuracy of the GAFF force field is assessed by comparing the MD result to existing experimental data, focusing on density, self-diffusion coefficients, viscosity, and thermal conductivity. Our results demonstrate excellent agreement with the existing data from the literature for all ethylene glycol oligomers. Furthermore, we analyze the results from the MD simulations to delve deeper into the effects of bonding behavior, elucidating and interpreting the origins of changes in the radial distribution functions, as well as structural and thermophysical properties. In an attempt to improve the results, we adjust the electrical charge of the atoms. The modifications reveal strong correlations between the charge balance and the properties of PEG molecules.
The structure of the paper is as follows. The Methods section elucidates the details of the MD simulations and the analyses derived from the obtained MD trajectories. The Results and discussion section provides a summary of the MD simulation results and a comparison with the existing literature data. This is followed by a presentation of the results from the modifications of the GAFF force field by altering the electrical charge of atoms. Important structural measures, including average end-to-end distances, radii of gyration, hydrogen, bonding, and dihedral angle distribution were analyzed to find relationships between oligomer size and the properties of PEG oligomer. Finally, the Conclusions section encapsulates the key findings.
Computational methods
Simulation details
All simulations of neat ethylene glycol oligomers with n = 2–7, illustrated in Fig. 1(c), were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) code.58,59 The simulation temperature was 328 K, which is in the middle range (298–358 K) of available experimental data.37,38,60 In this work, the GAFF50,51 force field was utilized to describe the molecular interactions.For oligomers of PEG200, where no improper torsions are applied, the potential function is:
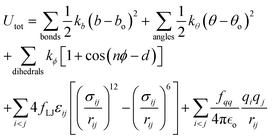 | (1) |
The Lennard-Jones (LJ) interaction parameters contact distance σ, and well-depth ε, between two atoms are calculated according to geometric mean combination rules 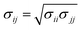 and
and 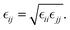 The fudge factors fLJ and fqq for Lennard-Jones and Coulomb interactions, respectively, are zero for nonbonding interactions between 1–2 and 1–3 atom pairs, 0.5 for 1–4 pairs, and 1 for all other atom pairs. This means that the non-bonding interactions are only computed between atoms if they are located more than three covalent bonds apart or are present on different molecules. We present the non-bonding interactions between atom pairs in Table 1. The parameters for bonding interactions, which include bond stretching, angle bending, and dihedral torsion, are listed in Tables S1–S3 in the ESI.†
The fudge factors fLJ and fqq for Lennard-Jones and Coulomb interactions, respectively, are zero for nonbonding interactions between 1–2 and 1–3 atom pairs, 0.5 for 1–4 pairs, and 1 for all other atom pairs. This means that the non-bonding interactions are only computed between atoms if they are located more than three covalent bonds apart or are present on different molecules. We present the non-bonding interactions between atom pairs in Table 1. The parameters for bonding interactions, which include bond stretching, angle bending, and dihedral torsion, are listed in Tables S1–S3 in the ESI.†
| Chemical group | Atom | ε (K) | σ (Å) | q (e) |
|---|---|---|---|---|
| Hydroxyl (–O–H) | O | 105.85 | 3.07 | −0.65 |
| H | 0.00 | 0.00 | 0.42 | |
| Ether (–CH2–O–) | C | 55.05 | 3.40 | 0.05 |
| H | 7.90 | 2.47 | 0.09 | |
| O | 85.55 | 3.00 | −0.34 |
For atomic charge modification, density functional theory (DFT) calculations were performed using the Gaussian 09 software suite.61 The B3LYP hybrid functional,62–64 in conjunction with the 6-311+G(d,p) basis set, was utilized to derive the atomic charges from four distinct charge models: CM5, Hirshfeld, Mulliken, and ESP. The general AMBER force field (GAFF) charge and atomic charges obtained from these models are presented in Table 2.
| Chemical group | Atom | GAFF | CM5 | Hirshfield | Mulliken | ESP |
|---|---|---|---|---|---|---|
| Hydroxyl (–O–H) | O | −0.65 | −0.46 | −0.25 | −0.32 | −0.75 |
| H | 0.42 | 0.34 | 0.17 | 0.24 | 0.44 | |
| Ether (–CH2–O–) | C | 0.05 | −0.06 | 0.01 | −0.18 | 0.36 |
| H | 0.09 | 0.1 | 0.4 | 0.14 | −0.02 | |
| O | −0.34 | −0.28 | −0.18 | −0.21 | −0.66 |
Neat PEG systems were prepared by randomly inserting a total of 250, 500 or 1000 PEG oligomer molecules into a cubic box using the Packmol code,65 schematically shown in Fig. 1(b). Following preparation, the systems were subjected to energy minimization using the conjugate gradient algorithm66 to eliminate high-energy contacts that were generated during system preparation. The minimization continued until the system reached a local energy minimum or until a maximum of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps had elapsed. A distance of 1.4 nm was chosen for the cut-off of all non-bonding interactions, including electrostatics and LJ interactions. For the treatment of long-range electrostatic interactions, the Edward summation method was employed. During the energy minimization, no long-range analytic tail dispersion corrections for the energy and pressure were applied.
000 steps had elapsed. A distance of 1.4 nm was chosen for the cut-off of all non-bonding interactions, including electrostatics and LJ interactions. For the treatment of long-range electrostatic interactions, the Edward summation method was employed. During the energy minimization, no long-range analytic tail dispersion corrections for the energy and pressure were applied.
After the energy minimization, each system was simulated in the isothermal-isobaric (NPT) ensemble. The simulation temperature and pressure were set to 328 K and 1 atm, with a time step of 2 fs. Initial velocities were generated for each atom using a random number generator. The NPT simulations were conducted for 10 million time steps (20 ns), a duration sufficient for the system density to converge. In every time step of the simulation, all hydrogen bonds in the PEG oligomer molecules were constrained using the SHAKE algorithm.67 The numerical integration of Newton's equations of motion was performed using the Stoermer–Verlet time integration algorithm.68 The non-bonding interactions were treated similarly to the energy minimization process, which included a 1.4 nm cutoff distance and the long-range treatment of electrostatic interaction. The system temperature was regulated using the Nose–Hoover temperature thermostat, and pressure was controlled using the Nose–Hoover pressure barostat.
After the NPT simulation, the average density from the converged region was selected to scale the system size to the average volume. Next, simulations in the canonical ensemble (NVT) were conducted at a temperature of 328 K. All parameters from the preceding NPT simulation were retained, with the exception of pressure coupling, which was deactivated. Each simulation was set to run for 50 million time steps (equivalent to 100 ns), a duration that allows the system to achieve numerical convergence. In addition, for the thermal conductivity, the total MD time was doubled. A minimum of 5000 position frames were recorded, and the energy frames were recorded every 25 fs to accurately obtain self-diffusion, shear viscosities, and thermal conductivity via the Green–Kubo (GK) integral time decomposition method,69 which is further elaborated in the next subsection.
Details about the analysis
All analysis was performed using modules available in the LAMMPS code or the OCTP plugin,70 a tool for on-the-fly calculation of transport properties of fluids with the order-n algorithm for LAMMPS. The density was obtained from NPT simulations, while self-diffusion coefficients, shear viscosity, radial distribution functions, hydrogen bonding numbers, and dihedral angle analyses were obtained from NVT simulations.The density was calculated from averaging instantaneous densities over the specific time frames of the trajectory from the NPT simulation. The instantaneous density is computed as follows:
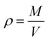 | (2) |
Self-diffusion coefficients were obtained from the NVT simulation using the Einstein-relation71 as follows:
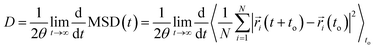 | (3) |
The analytic correction by Yeh and Hummer was used to calculate the self-diffusion coefficient at infinite box size:72
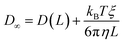 | (4) |
The shear viscosity (η) was computed from the time integral over the auto-correlation function of the off-diagonal components of the pressure tensor (Posαβ):70
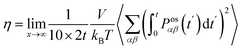 | (5) |
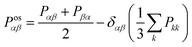 | (6) |
The thermal conductivity (λ) was calculated from the components of the energy current/heat flux (Jα) as follows:70
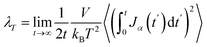 | (7) |
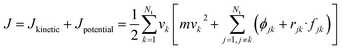 | (8) |
The radial distribution function (RDF), or pair correlation function between particles A and B with particle A as the central reference atom is computed as follows,
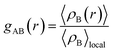 | (9) |
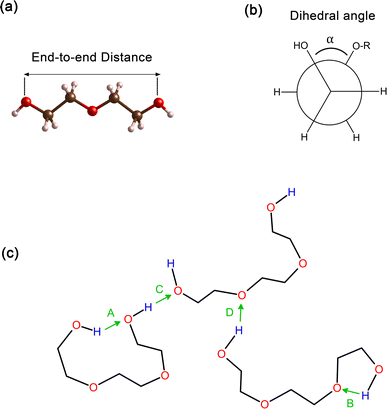
In order to obtain comprehensive understanding of the size and compactness of the PEG structure, we will analyze the average end-to-end distances and average radii of gyration. These statistical measures provide valuable insights into the physical dimensions and spatial configuration of the PEG molecule. The end-to-end distance of a PEG molecule was calculated as the straight-line distance between two terminal hydroxy oxygen atoms, as shown in Fig. 2(a). The average end-to-end distance is then obtained by averaging distances over all PEG molecules and over time in the MD trajectory. The radius of gyration was calculated as the root mean square distance of the atoms of the PEG chain from its center of mass,
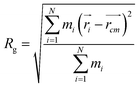 | (10) |
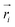 and
and 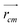 are position vector of atom i and center of mass of the polymer chain, respectively, and mi is the mass of atom i. The average radius of gyration is then obtained by averaging radii over all PEG chains and over time in the MD trajectory.
are position vector of atom i and center of mass of the polymer chain, respectively, and mi is the mass of atom i. The average radius of gyration is then obtained by averaging radii over all PEG chains and over time in the MD trajectory.
In addition, the distribution of proper dihedral angles was calculated to assess the conformational flexibility of molecules and to validate the accuracy of the force fields used in MD simulations. The dihedral angle α is defined as the angle formed by (HO)–C–C–(OR) segment, as shown in Fig. 2(b).
Hydrogen bonds serve as a crucial non-covalent structural force within molecular systems. In order to delve deeper into the strength and characteristics of the hydrogen bonding in the PEG structure, we performed an analysis of hydrogen bonding. The different types of hydrogen bonds are illustrated in Fig. 2(c). The H bonds plugin in the VMD program73 was utilized to calculate the number of hydrogen bonds at instantaneous points in time. Hydrogen bonding donor and acceptor groups were tabulated to determine the number of hydrogen bonds between a donor atom (D) and an acceptor atom (A) at any given point in time. The number of hydrogen bonds at an instantaneous point in time was then defined as the number of A–D pairs that met the criteria of the A–D distance being ≤0.35 nm and the angle A–H–D being ≤120°. The average number of hydrogen bonds was subsequently computed by averaging all the instantaneous hydrogen bond numbers over all trajectory frames.
Results and discussion
Thermophysical properties
Table 3 compares the calculated and experimental values for the thermophysical properties of PEG oligomers at T = 328 K. The calculated properties, which include the density, the self-diffusion coefficient (D), the viscosity (η), the product Dη, and the thermal conductivity (λ), were obtained using the GAFF force field. Each of these properties were obtained as a function of the oligomer size, denoted by n, which was varied from 2 to 7. Overall, the GAFF force field has a good ability to replicate the trends of the experimental data in the literature.| N = 250 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 |
|---|---|---|---|---|---|---|
| Density in kg m−3 | ||||||
| Exp37 | 1091.7 ± 0.1 | 1097.1 ± 0.1 | 1096.0 ± 0.1 | 1097.4 ± 0.2 | 1099.3 ± 0.9 | 1097.0 ± 1.0 |
| This work | 1143.1 ± 0.2 | 1137.7 ± 0.2 | 1143.3 ± 0.1 | 1145.1 ± 0.1 | 1147.5 ± 0.1 | 1149.9 ± 0.1 |
| (%) | 5% | 4% | 4% | 4% | 4% | 5% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Self-diffusion coefficient, D, in 10−11 m2 s−1 | ||||||
| Exp37 | 17.4 ± 0.5 | 12.5 ± 0.1 | 10.0 ± 1.0 | 8.6 ± 0.1 | 6.6 ± 0.2 | 5.7 ± 0.1 |
| This work | 20.7 ± 0.2 | 17.2 ± 0.4 | 9.6 ± 0.2 | 7.1 ± 0.1 | 5.7 ± 0.7 | 4.4 ± 0.2 |
| (%) | 19% | 38% | 4% | 17% | 14% | 23% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Shear viscosity η, in mPa s | ||||||
| Exp37 | 9.0 ± 0.3 | 11.2 ± 0.2 | 13.2 ± 0.3 | 15.8 ± 0.1 | 18.3 ± 0.4 | 20.6 ± 0.5 |
| This work | 7.3 ± 0.5 | 8.0 ± 1.0 | 14.4 ± 0.6 | 17.9 ± 2.0 | 19.9 ± 2.0 | 20.3 ± 2.2 |
| (%) | 19% | 29% | 9% | 13% | 9% | 2% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Dη (10−14 N) | ||||||
| Exp37 | 156.6 | 140.0 | 132.0 | 135.9 | 120.8 | 117.4 |
| This work | 151.1 | 137.6 | 138.2 | 127.1 | 113.4 | 89.3 |
| (%) | 4% | 2% | 5% | 7% | 6% | 24% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Thermal conductivity λ (W (m−1 K−1)) | ||||||
| Exp (mixture)44 | 0.191 ± 0.003 | 0.191 ± 0.003 | 0.191 ± 0.003 | 0.191 ± 0.003 | 0.191 ± 0.003 | 0.191 ± 0.003 |
| This work | 0.233 ± 0.014 | 0.228 ± 0.021 | 0.208 ± 0.010 | 0.205 ± 0.003 | 0.219 ± 0.010 | 0.193 ± 0.022 |
| (%) | 22% | 19% | 9% | 7% | 15% | 1% |
With a number of molecules of N = 250, the deviations between simulated and experimental values of shear viscosity and thermal conductivity show a striking trend. As the oligomer size increases from n = 2 to n = 7, the deviation decreases significantly. In particular, the deviation for small oligomers (n = 2) is around 20%, while for larger oligomers (n = 7), it drops to 1–2% (Table 3). This suggests that as the oligomer size grows, the simulations become increasingly accurate in predicting these thermophysical properties. The situation is different for the density and self-diffusion coefficient, where the deviations with respect to experimental data are relatively insensitive to oligomer size. The deviation for density remains around 5% across all oligomer sizes (n = 2–7), indicating that the simulations accurately capture the density for all considered oligomer sizes. Similarly, the self-diffusion coefficient shows a consistent deviation of approximately 20%, suggesting that this property is also relatively unaffected by a change in oligomer size.
For an oligomer size of n = 4, the calculated results exhibit good agreements with the experimental data, highlighting the accuracy of the force field for this particular molecular configuration. A closer look at the self-diffusion coefficients reveals a noticeable decrease as n increases, suggesting a decrease in molecular mobility for larger oligomers. This trend aligns with the anticipated increase in molecular interactions and entanglements as the chain length grows. Conversely, the viscosities exhibit an inverse relationship, with values increasing with oligomer size. This pattern implies a direct correlation between molecular size and the viscous resistance in the system. The calculated values for the product of Dη and thermal conductivity λ also provide useful information. Dη serves as an indicator of the system's dynamic behavior, while λ reflects the ability to conduct heat.
Furthermore, the finite-size effects70 for self-diffusion coefficients were taken into account to understand the influence of the simulation box size on the computed results. The simulation results are summarized in Table 4, including density, self-diffusion coefficient D, interpolated D∞ using eqn (4), shear viscosity η, the product Dη, and the thermal conductivity λ for different system sizes (250, 500, and 100 PEG molecules) at n = 2. Overall, the finite-size effects do not significantly influence the simulated thermophysical properties. According to the Stokes–Einstein relation presented in eqn (4), D∞ remains nearly unchanged beyond the system sizes considered in this work. This observation indicates that finite-size effects do not strongly influence the simulated thermophysical properties for this oligomer.
| Properties (n = 2) | Exp. | N = 250 | N = 500 | N = 1000 |
|---|---|---|---|---|
| Density in kg m−3 | 1091.7 ± 0.1 (ref. 37) | 1143.1 ± 0.2 | 1143.0 ± 0.1 | 1143.2 ± 0.1 |
| (5%) | (5%) | (5%) | ||
| Self-diffusion coefficient, D, in 10−11 m2 s−1 | 17.4 ± 0.5 (ref. 37) | 20.7 ± 0.2 | 21.0 ± 0.2 | 20.6 ± 0.1 |
| (19%) | (21%) | (18%) | ||
| D∞ | — | 21.0 | 21.2 | 20.8 |
| Viscosities η, in mPa s | 9.0 ± 0.3 (ref. 37) | 7.3 ± 0.5 | 7.2 ± 0.6 | 7.1 ± 0.3 |
| (19%) | (20%) | (21%) | ||
| Dη (10−14 N) | 156.6 (ref. 37) | 151.1 | 151.2 | 146.3 |
| (4%) | (4%) | (7%) | ||
| Thermal conductivity λ (W (m−1 K−1)) | 0.191 ± 0.003 (ref. 44) | 0.233 ± 0.014 | 0.250 ± 0.018 | 0.245 ± 0.010 |
| (22%) | (31%) | (28%) |
Table 5 compares the experimental and simulated properties of tetraethylene glycol (TeEG) at 328 K with different force fields. The GAFF force field simulations reported in this work demonstrate good agreement with experimental values for various thermophysical properties. Specifically, the simulated density shows a small deviation of approximately 4% from the experimental value. Similarly, the self-diffusion coefficient (D) and viscosity (η) exhibit deviations of 4% and 9%, respectively, from their corresponding experimental values. Notably, the product of these two properties, Dη, also shows a deviation of around 5%. These results indicate that the GAFF force field simulation is capable of accurately predicting various thermophysical properties of the PEG tetramer.
| Force field | Density (kg m−3) | Self-diffusion coefficient D (10−11 m2 s−1) | Viscosities η (mPa) | Dη (10−14 N) |
|---|---|---|---|---|
| GAFF (this work) | 1143.3 (4%) | 9.6 (4%) | 14.4 (9%) | 138.5 (5%) |
| Exp37 | 1096.0 | 10.0 | 13.2 | 132.0 |
| GROMOS45 | 1034.2 (6%) | 5.9 (41%) | 23.9 (81%) | 141.0 (7%) |
| CGenFF45 | 1084.9 (1%) | 2.7 (73%) | 50.4 (282%) | 136.1 (3%) |
| CZMP45 | 883.7 (19%) | 35.1 (251%) | 3.1 (77%) | 108.8 (18%) |
| Martini45 | 951.6 (13%) | 86.9 (769%) | 2.4 (82%) | 208.6 (58%) |
| OPLS45 | 1103.4 (<1%) | 1.56 (84%) | 65.5 (396%) | 102.2 (23%) |
We have compared our results to those reported earlier using various force fields such as GROMOS, CGenFF, CZMP, Martini, and OPLS in capturing the properties of PEG oligomer at n = 4. For the density, both CGenFF and OPLS are in excellent agreement with experimental values, with errors below 1% (Table 5). However, the excellent performance in predicting the density comes at the cost of significant deviations in other properties. In particular, CGenFF and OPLS exhibit large errors of around 80% for the self-diffusion coefficient and 300–400% for the viscosity, indicating that these force fields are not well-suited for predicting transport properties.
For the self-diffusion coefficient, the results using the GAFF force field show the lowest deviation from experimental data, with an error of only 4%. This is significantly better than other force fields, where GROMOS reports a deviation of 41% and MARTINI shows a huge deviation of nearly 800%, making it the least suitable force field in this regard. For the viscosity, the results with the GAFF force field show a significant improvement with respect to other force fields, with an error of only 9%. This is followed by the CZMP model, which reports a deviation of 77%, while OPLS shows the largest deviation of almost 400% (Table 5).
It is also interesting to analyse the product Dη, however, it can be missleading of not examined carefully. For instance, the CGenFF force field reported an impressive 3% deviation for the product Dη, but upon closer inspection, it is evident that D is underestimated by 73%, while the viscosity η is overestimated by 282%. Similarly, the GROMOS force field shows an acceptable 7% deviation, but this is also despite of large errors in D and η. Therefore, we recommend that this indicator should be thoroughly analyzed to avoid incorrect conclusions about the suitability of a force field to reproduce transport properties from experiments.
Atomic charge modifications to the GAFF force field
In an effort to improve the agreement with experimental data, we have modified the GAFF force field by adjusting the GAFF charge. To this end, four different charge models were evaluated: CM5, Hirshfield, Mulliken, and ESP. Table 2 provides a detailed overview of the atomic charges for each atom, carbon (C), oxygen (O), and hydrogen (H), within the hydroxyl and ether chemical groups of oligomers. In the hydroxyl group, the charge of the O atom varies much with the model, with the GAFF model suggesting a negative charge of −0.65, while the Hirshfeld model has −0.25. The charge of the H atom also shows a considerable variation, with the highest positive charge being 0.44 in the ESP model, and the lowest positive charge being 0.17. In the ether group, similar to the hydroxyl group, the atomic charges of the C, H, and O atoms vary much with the model. The atomic charge of the C atoms ranges from a positive value of 0.36 for the ESP model to a negative value of −0.18 for the Mulliken charge model. Meanwhile, the C atoms are almost neutral for the GAFF, CM5, and Hirshfeld models. The charge models seem to agree on the atomic charges of the H atoms, except for the Hirshfeld charge model that has a value of 0.4. The atomic charges of O atoms vary much, with the highest negative value being −0.66 for the ESP model to the smallest value of −0.18 for the Hirshfeld model.Table 6 compares the simulated and experimental values for the thermophysical properties of PEG200 at T = 328 K. The properties are simulated using the GAFF force field, both in its original form and with charge modifications. The experimental density of 1096.0 kg m−3 aligns closely with the GAFF force field when the Mulliken charge modification is applied, yielding a value of 1096.3 kg m−3. However, the GAFF, GAFF, CM5, and ESP models slightly overestimate the density, while the Hirshfeld model slightly underestimates it. In addition, the self-diffusion coefficient, experimentally determined to be 16.8 × 10−11 m2 s−1, is well approximated only when the GAFF charge model is used. It is overestimated with the CM5, Hirshfeld, and Mulliken charge models, and underestimated with the ESP charge model. The viscosity, experimentally measured to be 9.25 mPa s, is accurately approximated with both the GAFF and ESP charge models. Lastly, the thermal conductivity, with an experimental value of 0.21 W (m−1 K−1), aligns perfectly with the ESP charge modification, while the Hirshfeld modification leads to an underestimation. Overall, the CM5 and Mulliken charge models enhance the agreement with experimental data for the density. However, other charge modifications do not improve the result for the self-diffusion coefficient and the viscosity. The thermal conductivity remains nearly unchanged with the charge modifications.
| Properties/charge | Exp. | GAFF | CM5 | Hirshfield | Mulliken | ESP |
|---|---|---|---|---|---|---|
| Density, kg m−3 | 1096.0 ± 0.1 | 1143.3 ± 0.1 | 1107.2 ± 0.1 | 1047.6 ± 0.1 | 1096.3 ± 0.1 | 1143.2 ± 0.2 |
| (4%) | (1%) | (4%) | (<1%) | (4%) | ||
| Self-diffusion coefficient, D, in 10−11 m2 s−1 | 10.0 ± 1.0 | 9.6 ± 0.2 | 28.0 ± 0.9 | 68.1 ± 0.4 | 36.6 ± 0.7 | 9.8 ± 0.1 |
| (4%) | (180%) | (581%) | (266%) | (2%) | ||
| Viscosity η, in mPa s | 13.2 ± 0.3 | 14.4 ± 0.6 | 4.1 ± 0.5 | 1.7 ± 0.1 | 3.4 ± 0.4 | 12.8 ± 0.9 |
| (9%) | (69%) | (87%) | (74%) | (3%) | ||
| Dη (10−14 N) | 132.0 | 138.2 | 114.8 | 115.8 | 124.4 | 125.4 |
| (5%) | (13%) | (12%) | (6%) | (5%) | ||
| Thermal conductivity λ (W (m−1 K−1)) | 0.191 ± 0.003 | 0.208 ± 0.010 | 0.185 ± 0.016 | 0.162 ± 0.008 | 0.168 ± 0.008 | 0.208 ± 0.007 |
| (9%) | (3%) | (15%) | (12%) | (9%) |
Interestingly, we observe that the hydroxyl group exhibits a less negative charge, whereas the ether group tends to be more positive, especially for the Hirshfield and Mulliken charge models. This could lead to a reduction in density, aligning it more closely with experimental values. However, such variations may cause an overestimation of the self-diffusion coefficient and an underestimation of viscosity, as shown in Table 6. This analysis highlights the critical impact of atomic charge on determining properties of PEG oligomers. In the next sections, we analyze how charge modifications affect the simulation results.
It is crucial to acknowledge that altering atomic charges fundamentally modifies the underlying force fields. Each force field employs a default method for determining atomic charges. For example, GAFF utilizes the restrained electrostatic potential (RESP) approach. By adjusting charge assignment methods, we can achieve better agreement with experimental data for certain properties; however, this customization may also impact other properties. As demonstrated in our work, modifying atomic charges did not lead to improved thermophysical properties of PEG oligomers.
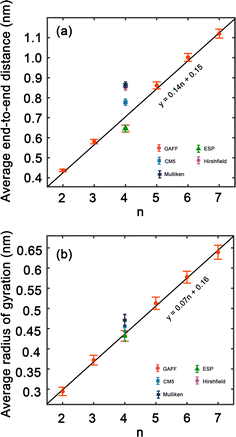
Structural properties of PEG
In order to improve the understanding of the dimensions and compactness of the PEG structure, we focus the analysis on oligomers with the sizes n = 2–7. Two key statistical measures will be discussed: the average end-to-end distances and the average radii of gyration, as depicted in Fig. 3. Fig. 3(a) reveals a linear correlation between the end-to-end distance of a PEG molecule and the oligomer size n. In Fig. 3(b), we observe a close to linear relationship between the radius of gyration and n, indicating a decrease in the compactness of the PEG molecule with an increase in n. An intriguing observation is the increase in standard deviation with n, which can be rationalized by the expansion of the structural configuration space as the length of the ethylene glycol oligomer increases. Large variations of average end-to-end distance of different charge models indicate a significant impact on the structural compactness of PEG molecules, giving insight into the differences in the predicted properties of PEG molecules shown in Table 6.By comparing the behavior of PEG oligomer using GAFF force field in this work and the OPLS obtained by Hoffmann et al.,45 we observe a consistent trend in the average end-to-end distance and radius of gyration as a function of oligomer size. As the oligomer size increases, both properties exhibit a linear rise, which is indicative of the elongation and swelling of the polymer chain. The GAFF force field predicts a slightly lower average end-to-end distance for PEG oligomers compared to OPLS, suggesting that GAFF may describe the system with slightly stiffer chains. This discrepancy could be attributed to the inherent characteristics and parameterizations of each force field, which may influence their respective representations of chain stiffness and conformational behavior.
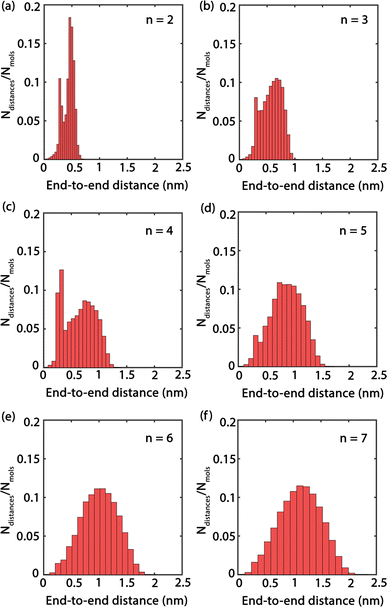
Fig. 4 presents histograms showing the end-to-end distances of PEG oligomers. A clear trend can be observed, where the histograms progressively shift towards right and broaden as n increases, indicating a correlation between oligomer size and spatial conformation. Specifically, the histogram for n = 2 in Fig. 4(a) reveals a large peak with a confined distribution, signifying the restricted conformational flexibility of the dimer and its tendency towards a compact structure. In contrast, the histogram for the trimer n = 3, shown in Fig. 4(b), displays a slight expansion and rightward shift of the peak, reflecting an increased average end-to-end distance and a broader molecular conformation. This pattern of broadening distribution persists for larger oligomer sizes n = 4 to n = 7, demonstrating the increased conformational diversity by the elongated PEG molecules that span from densely packed to extensively stretched structures.
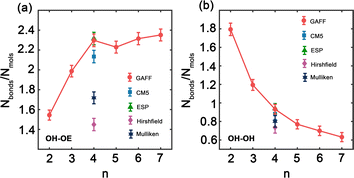
Hydrogen bonds are fundamental aspects of the intermolecular forces in PEG. Hence, to analyze how the GAFF force field and its charge modifications characterize these interactions in PEG simulations is crucial. Such investigations will shed light on the implications of hydrogen bonding for the thermophysical properties observed for PEG oligomers, presented in Tables 3 and 6. Fig. 5 illustrates the variation in the number of hydrogen bonds involving hydroxy hydrogen with ether oxygen (OH–OE) and hydroxy oxygen (OH–OH) per PEG molecule, across different oligomer sizes n, as obtained by both the original and the charge-modified GAFF force fields.
Fig. 5(a) illustrates a significant increase in the number of OH–OE hydrogen bonds up to an oligomer size of n = 4. Beyond this size, the trend continues to rise but at a slower rate. In contrast, Fig. 5(b) shows a decrease in the number of OH–OH hydrogen bonds, with a significant drop observed after n = 2. Different charge modifications, namely CM5, ESP, Hirshfield, and Mulliken, within the GAFF force field, markedly influence the number of hydrogen bonds. These variations in hydrogen bonding play a crucial role in determining the properties of PEG oligomers, as detailed in Table 6. The more pronounced variation in OH–OE hydrogen bonds compared to OH–OH bonds suggests that interactions involving hydroxy hydrogen and ether oxygen are more significant in determining the properties of PEG.
In addition to our own simulations, we compare the hydrogen bond interaction results obtained using GAFF and OPLS force fields with those reported in the literature.45 For OH–OE interactions, both GAFF and OPLS demonstrate an initial increase in hydrogen bonding with rising oligomer size. Nevertheless, the rate of this increase differs between the two force fields. GAFF exhibits a more gradual peak at n = 4, followed by a slower and continuous rise, whereas OPLS displays a steeper ascent throughout the entire range of oligomer sizes.45 This difference suggests that the two force fields may describe the OH–OE hydrogen bonding behavior with varying degrees of accuracy or specificity.
In contrast, for OH–OH interactions, GAFF and OPLS predict significantly different rates of hydrogen bond formation as a function of oligomer size. GAFF depicts a relatively steep trend compared to OPLS,45 indicating that fewer hydrogen bonds are formed between hydroxy oxygen atoms with increasing oligomer size. This disparity underscores the potential discrepancies in representing the intramolecular hydrogen bonding within PEG oligomers when using different force fields.
Fig. 6 presents the probability distributions of dihedral angles (HO)–C–C–O–(OR) in tetraethylene glycol (TeEG), using five different charge models: GAFF, CM5, Hirshfield, ESP, and Mulliken. Each curve exhibits a bimodal distribution with prominent peaks around ±140°, indicating that these angles are energetically favorable. Notably, the GAFF and ESP models display the largest peaks, suggesting that these charge assignments favor conformations with dihedral angles close to ±140° more strongly than the other models. In contrast, the CM5, Hirshfield, and Mulliken models show slightly smaller peaks, indicating a more moderate preference for these angles and allowing for smaller dihedral angles. This variation among the models underscores the sensitivity of dihedral angle distributions to the charge modification, reflecting how different electrostatic interactions can influence molecular conformations and, consequently, the thermophysical properties of the PEG oligomers.
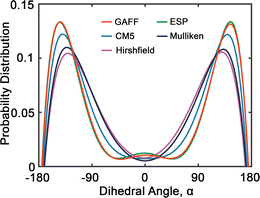 | ||
| Fig. 6 Probability distribution of dihedral angles (HO)–C–C–O–(OR) (see Fig. 2(b)) in tetraethylene glycol. Red, blue, purple, green and dark blue lines represent GAFF, CM5, Hirshfield, ESP, and Mulliken charges, respectively. | ||
Upon comparing the results obtained using GAFF and OPLS45 force fields, we observe several similarities and differences in their predictions. Both force fields predict similar preferred dihedral angles, as evidenced by the presence of two uphill peaks in their respective distributions. However, a notable difference between GAFF and OPLS lies in the positions of these peaks. For example, GAFF predicts peak positions approximately at ±140°, while OPLS suggests peak positions around ±60°.45 This discrepancy could imply variations in the predicted energy barriers or conformational flexibility between the two models.
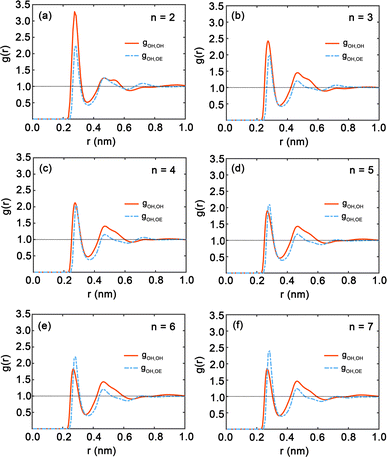
Fig. 7 presents the radial distribution functions (RDFs), offering a statistical view of the spatial relationships between hydroxy and ether oxygen atoms within PEG oligomers. The RDFs are depicted by red and blue curves, representing hydroxy–hydroxy and hydroxy–ether oxygen pairings, respectively. A clear trend is observed as the oligomer length extends from n = 2 to n = 7; the peaks in the RDFs shift in position and grow in intensity, indicating a shift in atomic interactions and spatial configurations. Here, both first peaks in Fig. 7 are near 0.3 nm. The shapes of the gOH,OH and gOH,OE at distances exceeding 0.5 nm do not show significant difference. In particular, Fig. 7(a) for n = 2 displays large peaks in the red curve, signifying strong local ordering and a high probability of finding another hydroxy oxygen atom at certain distances. Conversely, the peak of the blue curve for hydroxyl–ether oxygen atoms is lower, suggesting weaker interactions or a more dispersed distribution. This pattern aligns with the compact nature of the PEG dimer as seen in Fig. 4(a). In Fig. 7(b) and (c) for oligomers with n = 3 and n = 4, the peaks in both RDFs become sharper, reflecting an increasingly ordered atomic arrangement. The first peak in the red and blue curves is particularly sharp, highlighting a strong preference for specific interatomic distances. For longer chains, n = 5 to n = 7, as illustrated in Fig. 7(d) through Fig. 7(f), the peaks in the blue curve are more prominent compared to those in shorter oligomers, suggesting that the interactions between hydroxy and ether oxygen atoms intensify with increasing chain length.
The observed differences in structural properties between OPLS and GAFF force fields for PEG oligomers can be attributed to their development focuses. Notably, OPLS was specifically optimized for capturing molecular properties in liquid-phase environments. Consequently, this focus may result in suboptimal performance for transport properties like self-diffusion coefficients and shear viscosity, as these sensitive properties are highly dependent on the intricate molecular dynamics and the underlying potential energy landscape of the polymeric PEG system.
Conclusion
In this study, molecular dynamics simulations have been used to investigate the thermophysical properties of ethylene glycol oligomers, focusing on oligomer sizes ranging n = 2–7. Utilizing the GAFF force field, we systematically calculated the density, self-diffusion coefficients, shear viscosity, and thermal conductivity of these oligomers.The results revealed that the GAFF force field provides a robust framework for accurately predicting the behavior of ethylene glycol oligomers, aligning well with experimental data and outperforming other commonly used force fields. The GAFF force field demonstrates significant improvement in predicting self-diffusion and viscosity, with deviations with respect to experimental data below 10%. Other commonly used force fields, such as OPLS, CGenFF and GROMOS, report errors in the range 40–400%. The study reports, for the first time, thermal conductivities of polyethylene glycol (PEG) oligomers that are in good agreement with experimental data, demonstrating deviations below 20%. While our results demonstrate excellent agreement with experimental data at 328 K, it is essential to note that future studies should investigate the temperature dependence of PEG oligomer properties to fully understand the behavior of these molecules. Furthermore, investigations of charge modifications to the GAFF force field provided valuable insights into the influence of charge balance on the properties of PEG oligomers.
From the analyses of key measures such as average end-to-end distances, radii of gyration, and hydrogen bonding, correlations between oligomer size and thermophysical properties of PEG were highlighted. The analyses revealed a linear trend in the average end-to-end distances and radii of gyration as a function of oligomer size, indicating that larger oligomers adopt more extended conformations. This increase in size correlates with a higher molecular flexibility, as evidenced by the broadening distribution of end-to-end distances.
We found that subtle modifications to the charge distribution within the GAFF force field can significantly impact the bonding formation, which in turn affects the thermophysical properties of the PEG oligomers. This emphasizes the critical role of accurate charge modeling in molecular dynamics simulations and its implications for understanding the behavior of complex molecular systems such as PEG oligomers.
In summary, this study demonstrated an excellent performance of the GAFF force field for simulating the thermophysical properties of PEG oligomers, providing an alternative force field for such systems. While modifications to the atomic partial charges were discussed, a conclusion is that the original GAFF force field is preferred. Future research can build upon these findings by employing a combined AMBER/GAFF force field to study PEG–water interactions and explore the behavior of PEG oligomers in complex systems with other molecules.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Van Lang University, Vietnamese-German University, and the Norwegian University of Science and Technology. ØW and TTT acknowledge funding from the Research Council of Norway (RCN), the Center of Excellence Funding Scheme, Project No. 262644, PoreLab.References
- Polyethylene Glycol Market Size, Share & Trends Analysis Report By Application (Medical, Personal Care, Industrial, Others), By Region, And Segment Forecasts, 2023–2030, https://www.grandviewresearch.com/industry-analysis/polyethylene-glycol-peg-market, accessed Mar 04, 2024.
- F. R. Mansour, L. Zhou and N. D. Danielson, Applications of poly (ethylene) glycol (PEG) in separation science, Chromatographia, 2015, 78, 1427–1442 CrossRef CAS.
- R. P. Gullapalli and C. L. Mazzitelli, Polyethylene glycols in oral and parenteral formulations—A critical review, Int. J. Pharm., 2015, 496, 219–239 CrossRef CAS PubMed.
- D. Shi, D. Beasock, A. Fessler, J. Szebeni, J. Y. Ljubimova, K. A. Afonin and M. A. Dobrovolskaia, To PEGylate or not to PEGylate: Immunological properties of nanomedicine's most popular component, polyethylene glycol and its alternatives, Adv. Drug Delivery Rev., 2022, 180, 114079 CrossRef CAS PubMed.
- H.-J. Jang, C. Y. Shin and K.-B. Kim, Safety evaluation of polyethylene glycol (PEG) compounds for cosmetic use, Toxicol. Res., 2015, 31, 105–136 CrossRef CAS PubMed.
- A. A. D’souza and R. Shegokar, Polyethylene glycol (PEG): a versatile polymer for pharmaceutical applications, Expert Opin. Drug Delivery, 2016, 13, 1257–1275 CrossRef PubMed.
- B. Kekevi, H. Berber and H. Yıldırım, Synthesis and characterization of silicone-based surfactants as anti-foaming agents, J. Surfactants Deterg., 2012, 15, 73–81 CrossRef CAS.
- F. Hassouna, J.-M. Raquez, F. Addiego, P. Dubois, V. Toniazzo and D. Ruch, New approach on the development of plasticized polylactide (PLA): Grafting of poly (ethylene glycol)(PEG) via reactive extrusion, Eur. Polym. J., 2011, 47, 2134–2144 CrossRef CAS.
- M. Amin, A. M. Zeyad, B. A. Tayeh and I. S. Agwa, Engineering properties of self-cured normal and high strength concrete produced using polyethylene glycol and porous ceramic waste as coarse aggregate, Constr. Build. Mater., 2021, 299, 124243 CrossRef CAS.
- A. A. Minea, State of the art in PEG-based heat transfer fluids and their suspensions with nanoparticles, Nanomaterials, 2021, 11, 86 CrossRef CAS PubMed.
- M. M. Hoffmann, Polyethylene glycol as a green chemical solvent, Curr. Opin. Colloid Interface Sci., 2022, 57, 101537 CrossRef CAS.
- J. Soni, N. Sahiba, A. Sethiya and S. Agarwal, Polyethylene glycol: A promising approach for sustainable organic synthesis, J. Mol. Liq., 2020, 315, 113766 CrossRef CAS.
- F. G. Calvo-Flores, M. J. Monteagudo-Arrebola, J. A. Dobado and J. Isac-García, Green and bio-based solvents, Top. Curr. Chem., 2018, 376, 1–40 CrossRef CAS PubMed.
- Z. P. Visak, M. S. Calado, J. M. Vuksanovic, G. R. Ivanis, A. S. Branco, N. D. Grozdanic, M. L. Kijevcanin and S. P. Serbanovic, Solutions of ionic liquids with diverse aliphatic and aromatic solutes–Phase behavior and potentials for applications: A review article, Arab. J. Chem., 2019, 12, 1628–1640 CrossRef CAS.
- P. W. McGarvey and M. M. Hoffmann, Solubility of some mineral salts in polyethylene glycol and related surfactants, Tenside, Surfactants, Deterg., 2018, 55, 203–209 CAS.
- W.-W. Xiong and Q. Zhang, Surfactants as promising media for the preparation of crystalline inorganic materials, Angew. Chem., Int. Ed., 2015, 54, 11616–11623 CrossRef CAS PubMed.
- C. Forsyth, T. Taras, A. Johnson, J. Zagari, C. Collado, M. M. Hoffmann and C. R. Reed, Microwave assisted surfactant-thermal synthesis of metal-organic framework materials, Appl. Sci., 2020, 10, 4563 CrossRef CAS.
- R. Kardooni and A. R. Kiasat, Polyethylene glycol as a green and biocompatible reaction media for the catalyst free synthesis of organic compounds, Curr. Org. Chem., 2020, 24, 1275–1314 CrossRef CAS.
- J. F. Campos and S. Berteina-Raboin, Greener synthesis of nitrogen-containing heterocycles in water, PEG, and bio-based solvents, Catalysts, 2020, 10, 429 CrossRef CAS.
- R. Francesconi, A. Bigi, K. Rubini and F. Comelli, Molar heat capacities, densities, viscosities, and refractive indices of poly (ethylene glycols)+ 2-methyltetrahydrofuran at (293.15, 303.15, and 313.15) K, J. Chem. Eng. Data, 2007, 52, 2020–2025 CrossRef CAS.
- F. Comelli, S. Ottani, R. Francesconi and C. Castellari, Densities, viscosities, refractive indices, and excess molar enthalpies of binary mixtures containing poly (ethylene glycol) 200 and 400+ dimethoxymethane and+ 1, 2-dimethoxyethane at 298.15 K, J. Chem. Eng. Data, 2002, 47, 1226–1231 CrossRef CAS.
- N. V. Zivkovic, S. S. Serbanovic, M. L. Kijevcanin and E. Zivkovic, Volumetric and viscometric behavior of binary systems 2-butanol+ PEG 200,+ PEG 400,+ tetraethylene glycol dimethyl ether, and+ N-methyl-2-pyrrolidone, J. Chem. Eng. Data, 2013, 58, 3332–3341 CrossRef CAS.
- F. Comelli and S. Ottani, Excess enthalpies, densities, viscosities, and refractive indices of binary mixtures involving some poly (glycols)+ diethyl carbonate at 308.15 K, J. Chem. Eng. Data, 2004, 49, 970–975 CrossRef CAS.
- T.-Y. Wu, B.-K. Chen, L. Hao, K.-F. Lin and I.-W. Sun, Thermophysical properties of a room temperature ionic liquid (1-methyl-3-pentyl-imidazolium hexafluorophosphate) with poly (ethylene glycol), J. Taiwan Inst. Chem. Eng., 2011, 42, 914–921 CrossRef CAS.
- T.-Y. Wu, B.-K. Chen, L. Hao, Y.-C. Lin, H. P. Wang, C.-W. Kuo and I.-W. Sun, Physicochemical properties of glycine-based ionic liquid [QuatGly-OEt][EtOSO3](2-ethoxy-1-ethyl-1, 1-dimethyl-2-oxoethanaminium ethyl sulfate) and its binary mixtures with poly (ethylene glycol)(Mw= 200) at various temperatures, Int. J. Mol. Sci., 2011, 12, 8750–8772 CrossRef CAS PubMed.
- A. Ali, S. Ansari and A. K. Nain, Densities, refractive indices and excess properties of binary mixtures of dimethylsulphoxide with some poly (ethylene glycol) s at different temperatures, J. Mol. Liq., 2013, 178, 178–184 CrossRef CAS.
- N. Chaudhary and A. K. Nain, Densities, speeds of sound, refractive indices, excess and partial molar properties of polyethylene glycol 200+ methyl acrylate or ethyl acrylate or n-butyl acrylate binary mixtures at temperatures from 293.15 to 318.15 K, J. Mol. Liq., 2018, 271, 501–513 CrossRef CAS.
- M. Hemmat, M. Moosavi, M. Dehghan, E. Mousavi and A. A. Rostami, Thermodynamic, transport and optical properties of formamide+ 1, 2-ethanediol, 1, 3-propanediol and poly (ethylene glycol) 200 binary liquid mixtures, J. Mol. Liq., 2017, 233, 222–235 CrossRef CAS.
- A. K. Nain, S. Ansari and A. Ali, Densities, refractive indices, ultrasonic speeds and excess properties of acetonitrile+ poly (ethylene glycol) binary mixtures at temperatures from 298.15 to 313.15 K, J. Solution Chem., 2014, 43, 1032–1054 CrossRef CAS.
- M. Yasmin and M. Gupta, Density, viscosity, velocity and refractive index of binary mixtures of poly (ethylene glycol) 200 with ethanolamine, m-cresol and aniline at 298.15 K, J. Sol. Chem., 2011, 40, 1458–1472 CrossRef CAS.
- H. Patel, Z. S. Vaid, U. U. More, S. P. Ijardar and N. I. Malek, Thermophysical, acoustic and optical properties of binary mixtures of imidazolium based ionic liquids+ polyethylene glycol, J. Chem. Thermodyn., 2016, 99, 40–53 CrossRef CAS.
- M. Moosavi, A. Motahari, A. Omrani and A. A. Rostami, Investigation on some thermophysical properties of poly (ethylene glycol) binary mixtures at different temperatures, J. Chem. Thermodyn., 2013, 58, 340–350 CrossRef CAS.
- M. Moosavi, A. Omrani, A. A. Rostami and A. I. Motahari, isothermal theoretical investigation and examination of different prediction equations on some physicochemical properties in PEG liquid polymer system, J. Chem. Thermodyn., 2014, 68, 205–215 CrossRef CAS.
- E. M. Živković, N. V. Živković, D. M. Majstorović, A. M. Stanimirović and M. L. Kijevčanin, Volumetric and transport properties of binary liquid mixtures with 1-ethyl-3-methylimidazolium ethyl sulfate as candidate solvents for regenerative flue gas desulfurization processes, J. Chem. Thermodyn., 2018, 119, 135–154 CrossRef.
- C. Aucouturier, G. Roux-Desgranges and A. Roux, Excess molar volumes and excess molar heat capacities of (polyethylene glycols+ water) at temperatures betweenT= 278 K andT= 328 K, J. Chem. Thermodyn., 1999, 31, 289–300 CrossRef CAS.
- O. E.-A. A. Adam and A. A. Hassan, Volumetric properties of binary mixtures of o-cresol+ poly (ethylene glycols) in the temperature range 288.15–308.15 K and atmospheric pressure, Phys. Chem. Liq., 2018, 56, 55–68 CrossRef CAS.
- M. M. Hoffmann, R. H. Horowitz, T. Gutmann and G. Buntkowsky, Densities, viscosities, and self-diffusion coefficients of ethylene glycol oligomers, J. Chem. Eng. Data, 2021, 66, 2480–2500 CrossRef CAS.
- M. M. Hoffmann, J. D. Kealy, T. Gutmann and G. Buntkowsky, Densities, viscosities, and self-diffusion coefficients of several polyethylene glycols, J. Chem. Eng. Data, 2021, 67, 88–103 CrossRef.
- M. Chereches, A. Vardaru, G. Huminic, E. I. Chereches, A. A. Minea and A. Huminic, Thermal conductivity of stabilized PEG 400 based nanofluids: An experimental approach, Int. Commun. Heat Mass Transfer, 2022, 130, 105798 CrossRef CAS.
- Y. Kou, S. Wang, J. Luo, K. Sun, J. Zhang, Z. Tan and Q. Shi, Thermal analysis and heat capacity study of polyethylene glycol (PEG) phase change materials for thermal energy storage applications, J. Chem. Thermodyn., 2019, 128, 259–274 CrossRef CAS.
- D. Lou, T. Grablander, M. Mao, H. Hong and G. Peterson, Improved thermal conductivity of PEG-based fluids using hydrogen bonding and long chain of nanoparticle, J. Nanopart. Res., 2021, 23, 1–10 CrossRef.
- X. Cui, Y. Wang, J. Tang, J. Wang, Q. Jiang, L. Huang, J. Liu, Y. Wang, H. Li and L. A. Belfiore, Enhanced thermal conductivity and thermal performance of polyethylene glycol (PEG)/modified SiO2 composite phase change material, Sci. Adv. Mater., 2018, 10, 309–314 CrossRef CAS.
- M. Cherecheş, D. Bejan, C. Ibanescu, M. Danu, E. I. Cherecheş and A. A. Minea, Viscosity and isobaric heat capacity of PEG 400-based phase change materials nano-enhanced with ZnO nanoparticles, J. Therm. Anal. Calorim., 2022, 147, 8815–8826 CrossRef.
- A. Gómez-Merino, J. Jiménez-Galea, F. Rubio-Hernández, J. Arjona-Escudero and I. Santos-Ráez, Heat Transfer and Rheological Behavior of Fumed Silica Nanofluids, Processes, 2020, 8, 1535 CrossRef.
- M. M. Hoffmann, M. D. Too, N. A. Paddock, R. Horstmann, S. Kloth, M. Vogel and G. Buntkowsky, On the behavior of the ethylene glycol components of polydisperse polyethylene glycol PEG200, J. Phys. Chem. B, 2023, 127, 1178–1196 CrossRef CAS PubMed.
- T. T. Trinh, T. J. Vlugt and S. Kjelstrup, Thermal conductivity of carbon dioxide from non-equilibrium molecular dynamics: A systematic study of several common force fields, J. Chem. Phys., 2014, 141, 134504 CrossRef PubMed.
- Ø. Wilhelmsen, T. T. Trinh, S. Kjelstrup, T. S. Van Erp and D. Bedeaux, Heat and mass transfer across interfaces in complex nanogeometries, Phys. Rev. Lett., 2015, 114, 65901 CrossRef PubMed.
- D. T. Ha, H. D. Tong, K.-Q. Tran and T. T. Trinh, The role of chemical functional groups in dewaterability of hydrochar: A molecular simulation study, J. Mol. Liq., 2024, 400, 124482 CrossRef CAS.
- K. Yellam, R. S. Katiyar and P. K. Jha, in Forcefields for Atomistic-Scale Simulations: Materials and Applications, ed. Verma, A., Mavinkere Rangappa, S., Ogata, S. and Siengchin, S., Springer Nature Singapore, Singapore, 2022, pp. 51–79 Search PubMed.
- J. P. Jambeck and A. P. Lyubartsev, Update to the general amber force field for small solutes with an emphasis on free energies of hydration, J. Phys. Chem. B, 2014, 118, 3793–3804 CrossRef PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- I. S. Gutiérrez, F.-Y. Lin, K. Vanommeslaeghe, J. A. Lemkul, K. A. Armacost, C. L. Brooks III and A. D. MacKerell, Parametrization of halogen bonds in the CHARMM general force field: Improved treatment of ligand–protein interactions, Bioorg. Med. Chem., 2016, 24, 4812–4825 CrossRef PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, et al., CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed.
- B. A. Horta, P. T. Merz, P. F. Fuchs, J. Dolenc, S. Riniker and P. H. Hunenberger, A GROMOS-compatible force field for small organic molecules in the condensed phase: The 2016H66 parameter set, J. Chem. Theory Comput., 2016, 12, 3825–3850 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- F. Grunewald, G. Rossi, A. H. De Vries, S. J. Marrink and L. Monticelli, Transferable MARTINI model of poly (ethylene oxide), J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef CAS PubMed.
- R. M. Cordeiro, F. Zschunke and F. Muller-Plathe, Mesoscale molecular dynamics simulations of the force between surfaces with grafted poly (ethylene oxide) chains derived from atomistic simulations, Macromolecules, 2010, 43, 1583–1591 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. Aktulga, J. Fogarty, S. Pandit and A. Grama, Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques, Parallel Computing, 2012, 38, 245–259 CrossRef.
- A. A. Minea, State of the art in PEG-based heat transfer fluids and their suspensions with nanoparticles, Nanomaterials, 2021, 11, 86 CrossRef CAS PubMed.
- M. Frisch, Gaussian 09, Revision D. 01, Gaussian. Inc, Wallingford CT, 2009, vol. 201 Search PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- L. Martinez, R. Andrade, E. Birgin and J. Martínez, PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- G. Yuan, Z. Wei and G. Li, A modified Polak–Ribière–Polyak conjugate gradient algorithm for nonsmooth convex programs, J. Comput. Appl. Math., 2014, 255, 86–96 CrossRef.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- J. Gibson, A. N. Goland, M. Milgram and G. Vineyard, Dynamics of radiation damage, Phys. Rev., 1960, 120, 1229 CrossRef CAS.
- D. J. Evans and G. P. Morriss, Statistical Mechanics of Nonequilbrium Liquids, ANU Press, 2007 Search PubMed.
- S. H. Jamali, L. Wolff, T. M. Becker, M. De Groen, M. Ramdin, R. Hartkamp, A. Bardow, T. J. Vlugt and O. A. Moultos, OCTP: A tool for on-the-fly calculation of transport properties of fluids with the order-n algorithm in LAMMPS, J. Chem. Inf. Model., 2019, 59, 1290–1294 CrossRef CAS PubMed.
- M. T. Allen, DJ Computer Simulation of Liquids, 1987 Search PubMed.
- I.-C. Yeh and G. Hummer, System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD – Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Force field coefficients for bond stretching (Fig. S1), angle bending (Fig. S2), and dihedral torsion (Fig. S3). See DOI: https://doi.org/10.1039/d4ra04898a |
| This journal is © The Royal Society of Chemistry 2024 |