Open Access Article
Open Access ArticleSuperalkali nature of the Si9M5 (M = Li, Na, and K) Zintl clusters: a theoretical study on electronic structure and dynamic nonlinear optical properties†
Atazaz Ahsin‡
ae,
Aamna Qamar‡be,
S. Muthu c,
V. Vetriveland,
Jianwei Cao
c,
V. Vetriveland,
Jianwei Cao *a and
Wensheng Bian
*a and
Wensheng Bian *ae
*ae
aBeijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: caojw@iccas.ac.cn; bian@iccas.ac.cn
bBeijing National Laboratory for Molecular Sciences, State Key Laboratory of Polymer Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, China
cDepartment of Physics, Arignar Anna Government Arts College, Cheyyar 604407, Tamil Nadu, India
dDepartment of Physics, Government College of Engineering, Srirangam, Thiruchirappalli 620012, Tamil Nadu, India
eSchool of Chemical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
First published on 28th May 2024
Abstract
Zintl clusters have attracted widespread attention because of their intriguing bonding and unusual physical properties. We explore the Si9 and Si9M5 (where M = Li, Na, and K) Zintl clusters using the density functional theory combined with other methods. The exothermic nature of the Si9M5 cluster formation is disclosed, and the interactions of alkali metals with pristine Si9 are shown to be noncovalent. The reduced density gradient analysis is performed, in which increased van der Waals interactions are observed with the enlargement of the size of alkali metals. The influence of the implicit solvent model is considered, where the hyperpolarizability (βo) in the solvent is found to be about 83 times larger than that in the gas phase for Si9K5. The frequency-dependent nonlinear optical (NLO) response for the dc-Kerr effect is observed up to 1.3 × 1011 au, indicating an excellent change in refractive index by an externally applied electric field. In addition, natural bonding orbitals obtained from the second-order perturbation analysis show the charge transfer with the donor–acceptor orbitals. Electron localization function and localized orbital locator analyses are also performed to better understand the bonding electrons in designed clusters. The studied Zintl clusters demonstrate the superalkali character in addition to their remarkable optical and nonlinear optical properties.
1 Introduction
Designing novel materials with excellent nonlinear optical (NLO) properties has gained significant interest in the last three decades because of their potential applications in various optical and electrical devices.1–4 As a prerequisite for nonlinear media, materials must be in noncentrosymmetric structures in order to generate effective non-equilibrium spontaneous electron polarization.5 Literature reveals that not only the hyperpolarizability but also third-rank NLO responses are equally contributing to achieving modern-day optical technologies such as optical data storage, optical communication, biological imaging, and signal processing.6–8 For obtaining exceptional NLO features in molecule systems, numerous techniques have been proposed in the literature, such as utilizing the push–pull mechanism,9 creating the metal–organic framework,10 introducing diradical character in the conjugated system,11 designing multidecker sandwich complexes,12 and induction of excess electrons in molecules.13Since Dye et al. carried out an innovative study of excess electron compounds based on cryptand and crown ether,14 the significant impact of excess electrons on the hyperpolarizability of molecules and clusters gives rise to new prospects for designing and exploring high-performance NLO materials.15 Almost two decades ago, Li et al. first reported the NLO properties of systems with excess electrons and uncovered the pivotal role of loosely bound electrons in amplifying the first hyperpolarizability (βo).16 Up until now, several molecular systems that exhibited the nature of excess electrons have been designed for optical and optoelectronic applications.17–19 The role of excess electrons in triggering the hyperpolarizability response has been revealed, and these electrons remarkably reduce excitation energies (transition energies), which would result in rapid excitation of electrons to virtual orbitals.13 The theory is evident that excitation energy (ΔE) has an inverse relation with βo of molecules from the conventional two-level model.20
In the development of excess electron molecules, alkali-like superatom clusters are frontline and emerging as building blocks for constructing the three-dimensional periodic table.21,22 As an intriguing subset of the superatom family, superalkalis has characteristics similar to the alkali metals.23 Generally, the superalkali nature of clusters is usually described by their reduced ionization potential (IPs) as compared to alkali metals (3.9–5.4 eV).24 A series of experiments on molecular species as superalkali clusters were reported such as XLi2 (X = F, Cl, Br, and I),25 OM3 (M = Li, Na, and K),26 NLi4,27 BLin (n = 1–7)28 and a variety of superalkali cluster were designed theoretically, such as bimetallic, uninuclear, and polynuclear ones.29–31 Very recently, Ayub et al. reported the superalkali (Li3O) and alkali metals doped crown ether complexes Li3O[12-crown-4] for optoelectronic properties,32 where dynamic third-order Kerr effect increased up to 2.75 × 1012 au. The alkali anion (superalkalide nature) and reduced excitation energy were observed for these complexes. Likewise, a class of bimetallic superalkali clusters was investigated for dynamic NLO properties, where a substantial hyperpolarizability value was assigned to the presence of excess electrons. Likewise, M2OCN and oxacarbon (C3X3Y3) superalkali clusters show tremendously enhanced NLO properties owing to the nature of excess electrons.33–35 The exceptional charge transfer from superalkali clusters to complexant and their superior reducing properties make them ideal candidates for constructing high-performance molecular NLO materials. The prospective applications can be seen in the synthesis of unusual charge-transfer salts (supersalts), cluster-assembled nanomaterial in the reduction of carbon dioxide as storage materials, and noble-gas-trapping hosts.23,36
Since the discovery by Eduard Zintl in 1930, groups 14, 15, and Zintl superatom clusters have drawn much curiosity and have been considered as potential antecedents for material design.37 It is also suggested that Zintl clusters can be connected via transition metal, alkali metal, non-metal atoms, or organic linkers to construct nanonetworks or materials with novel and tunable electronic properties. As far as we know, the study of the Zintl clusters based on Si-atom is very limited. Very recently, Zintl clusters [Si9R2]2− and [Si9R3]− [R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SiH(tBu)2, SnCy3, Si (TMS)3] have been synthesized experimentally.38 Later, Sinha et al.39 investigated the superhalogens nature of Si9R3 clusters theoretically, in which Zintl anion (Si92−) is functionalized with electronegative ligands such as –CF3, –CN, –BO, and –NO2.
SiH(tBu)2, SnCy3, Si (TMS)3] have been synthesized experimentally.38 Later, Sinha et al.39 investigated the superhalogens nature of Si9R3 clusters theoretically, in which Zintl anion (Si92−) is functionalized with electronegative ligands such as –CF3, –CN, –BO, and –NO2.
The present study mainly focuses on exploring superalkali and excess electron nature through noncovalent interactions of 1st group metals with pure Si9 cluster. In the designed clusters Si9M5 (M = Li, Na, and K), loosely bound alkali electrons are actively transferring charge and are crucial for activating the NLO of responses. In addition, van der Waals (vdW) interaction is very important in numerous chemical processes,40–44 and its role in the formation and properties of clusters is of great interest. The present work also uncovers the nature and magnitude of vdW forces in tuning the optoelectronic properties in the designed clusters. This paper is organized as follows. The computational details are given in Section 2. The results are presented and discussed in Section 3. Finally, a brief conclusion is given in Section 4.
2 Methods and computational details
For the designed Si9M5 (M = Li, Na, and K) clusters, ab initio molecular dynamics (AIMD) simulations were performed using the ORCA 5.0 package,45 and other quantum chemical simulations were performed by Gaussian 16.46 To make the results reliable, the method and basis set should be chosen carefully.47–51 The initial-guess structure for the pure Si9 cluster is obtained from literature, and the present geometry of Si9 is in good consistent with those reported in literature,52 which justifies that it is a global minimum. As for Si9M5, considering that the geometry of Si9 is not altered or distorted greatly during the adsorption of alkali metals by vdW interactions, we performed initial optimization in dozens of designed initial-guess structures, and then find the structure that has lowest potential energy. Our AIMD calculations justify that the present structures are the global minima, and it should be noted that a global optimization procedure53–56 would have better efficiency in searching global minimum on a potential energy surface (PES). Initial optimization is carried out using the B3LYP/6-31G level of theory. The stable molecular geometries were reoptimized, and the final optimization and the following entire electronic and NLO properties were computed using the ωb97xd/def2-qzvp level. Infrared and Raman frequencies are also computed using the same method. The thermodynamic stability of studied clusters was validated via binding energy (cohesive energy) per atom, which can be expressed as:| EB = [ESi9M5 − E(X)]/n | (1) |
Superalkali nature and reactivity were identified and illustrated through global reactivity parameters. Frontier molecular orbital (FMO) and natural population analysis (NPA) were chosen to get the orbital energies and charge transfer in Si9M5. A second-order Fock matrix study using the NBO tool was considered for the donor–acceptor atoms and type of electronic transition. The reactivity and topological properties were further examined using molecular electrostatic potential (MESP). The bonding nature of alkali metals to Si-atoms and vdW interactions were outlined through the quantum theory of atom in molecules (QTAIM) and noncovalent interaction (NCI) study. Additionally, the electron localization function (ELF) and localized orbital locator (LOL) analyses were performed to determine the nature of bonding (localized) and delocalized (lone pair) electrons within clusters. The chemical potential (μ) and electronegativity can be calculated using the equation:
| μ = −(IP + EA)/2 | (2) |
For the optical and NLO characteristics, dipole moment (μo), polarizability (αo), first-order hyperpolarizability (βo), and static second hyperpolarizability (γo) were calculated with the help of the following equations:
| μo = (μx2 + μy2 + μz2)1/2 | (3) |
| αo = 1/3(αxx + αyy + αzz) | (4) |
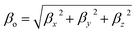 | (5) |
| βx = βxxx + βxyy + βxzz, βy = βyyy + βyzz + βyxx and βz = βzzz + βzxx + βzyy, | (6) |
| 〈γ〉 = 1/5(γxxxx + γyyyy + γzzzz + γxxyy + γxxzz + γyyxx + γyyzz + γzzxx) | (7) |
Furthermore, the density of states (DOS) spectral study was carried out to get a comprehensible picture of orbital energies and HOMO–LUMO gaps for clusters using the GaussSum software.58 TD-DFT study was also carried out by considering forty excited states for singlet and triplet. In this analysis, we calculated various excited state parameters and absorbance of clusters. Scattering hyperpolarizability (βHRS) was calculated by using the following relation:
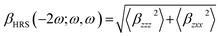 | (8) |
| DR = 〈βzzz2〉/〈βzxx2〉 | (9) |
Moreover, the frequency-dependent (dynamic) nonlinear optical parameters were calculated at the 532 and 1064 nm wavelength. The frequency-dependent β(−ω;ω,0) electro-optic Pockel's effect (EOPE) and β(−2ω;ω,ω) electric field-induced second harmonic generation (ESHG) were calculated. The second hyperpolarizability γ(ω), dc-Kerr γdc-Kerr (ω) = γ(−ω;ω,0,0) and second harmonic generation γESHG(ω) = γ(−2ω;ω,ω,0) were also obtained.
In the NBO analysis, donor (i)–acceptor (j) interactions between filled Lewis orbitals and empty non-Lewis orbitals are explored to further enrich the structural-reactivity relationship. For this purpose, a second-order Fock matrix is considered, where only high stabilization energy (E(2)) interactions are considered:59
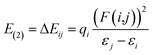 | (10) |
3 Results and discussion
3.1 Electronic structure and thermodynamic stability
We begin the neutral Zintl cluster (Si9) geometry as core, which is decorated with alkali metals (M = Li, Na, and K) for creating Zintl-superatom clusters with superalkali nature. The pure Si9 cluster shown in Fig. 1 has a bicapped pentagonal pyramid geometry, whereas the Si92− and Si94− clusters have different geometries (see Fig. S1†). The geometries of Si9M5 are consistent with previously reported clusters60 which are also trigonal prismatic, and the obtained bond distances are given in Fig. 1 and Table S2 of the ESI.† In Si9Li5, the interaction distance between Si and alkali metals ranged from 2.77 to 2.92 Å, while for Si9Na5 increased up to 3.02 Å. The highest interaction distance (3.79 Å) is observed between the Si–K bonds in the Si9K5 cluster. The calculated results at the ωb97xd/def2-qzvp level are given in Table 1. As seen, the binding energy per atom (EB) is higher for pure Si9 cluster as compared to Si9M5. A monotonic reduction EB for Si9M5 with the increased alkali metal size and interaction distance (dSi–M) are observed. The binding energies at the ωb97xd/def2-qzvp level are −4.42, −3.66, −4.25, and −3.53 eV for Si9, Si9Li5, Si9Na5, and Si9K5, respectively. These values are higher than those reported for the Ge9AM5 and P7M2 (M = Li, Na, and K) clusters,60,61 indicating that the present Si-based Zintl clusters have better thermodynamic stabilities. The computed mean dipole moment (μo) increase with the enlargement of the size of alkali metals. The μo value of Si9K5 is 20.42 D, which is 27 times higher than that of the pristine Si9 cluster (0.73 D). In addition, we can also see from Table 1 that, the chemical hardness of Si9 is 2.92 eV, higher than those of the Si9M5 clusters, and the chemical softness of Si9M5 increases with the increased metal size.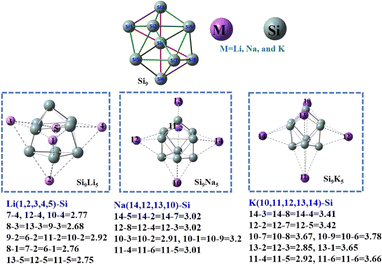 | ||
| Fig. 1 The optimized structure of the Si9, and Si9M5 clusters at the ωb97xd/def2-qzvp level of theory. The Si atom is in green and the alkali metal atoms are in pink. The important interaction distances (in Å) of alkali metals with silicon are given below the geometries. The corresponding Cartesian coordinates are given in Table S1.† | ||
| Properties | Si9 | Si9Li5 | Si9Na5 | Si9K5 |
|---|---|---|---|---|
| μo (D) | 0.73 | 2.61 | 4.46 | 20.42 |
| NBO on Si (e) | −0.17/0.11 | −0.60 | −0.52 | −0.48 |
| NBO charges (e) | — | 0.87 | 0.89 | 0.95 |
| Ionization potential (eV) | 7.58 | 4.35 | 4.10 | 2.41 |
| Electron affinity (eV) | 1.75 | 0.18 | 0.06 | 0.03 |
| EHOMO (eV) | −7.58 | −4.35 | −4.10 | −2.41 |
| ELUMO (eV) | −1.75 | −0.18 | −0.06 | −0.03 |
| Eg (eV) | 5.83 | 4.17 | 4.06 | 2.37 |
| Chemical potential (eV) | −4.66 | −2.27 | −2.08 | −1.22 |
| Hardness (eV) | 2.92 | 2.09 | 2.02 | 1.19 |
| Softness (eV) | 0.34 | 0.48 | 0.49 | 0.84 |
| Electronegativity (χ) | 4.66 | 2.27 | 2.08 | 1.22 |
| Electrophilicity index (eV) | 3.73 | 1.23 | 1.07 | 0.63 |
| Eb (eV) | −4.42 | −3.66 | 4.25 | −3.54 |
The superalkali nature of examined clusters can be monitored by their minimized ionization potential (IP) and electron affinity (EA) values. Pristine Si9 has an IP value of 7.58 eV, higher than the designed Si9M5, while its EA value is 1.75 eV. Table 1 shows that the interaction of alkali metals with the Si9 cluster has significantly lowered the IP and EA values. For instance, the obtained IP values are 4.35, 4.10, and 2.41 eV for Si9Li5, Si9Na5, and Si9K5, respectively. A similar trend of decreasing IP by doping alkali metals can also be found in the literature.62 EA value also decreased to 0.03 eV, which is much smaller than previously reported P7M2 clusters. The smaller EA values declare the electropositive nature and excellent reducing properties of the Si9M5 clusters. Furthermore, the superalkali character of these clusters can be observed by their reduced IP values compared to alkali metals. The IPs of Si9Li5 and Si9Na5 are lower than that of the Li atom, and the IP of Si9K5 has even lower than that of the Cs atom (3.89 eV), demonstrating that these clusters manifest superalkali characteristics.27 Due electropositive nature, alkali metals become electron deficient after sharing their valence electrons ns1 to np of Si-atoms within clusters. On the other hand, the Si9 cluster acquires electronic charge from alkali due to its comparatively higher electronegativity. The electronic stability of Si9M5 can also be correlated to the famous Jellium model. The core Zintl cluster Si9 contains 36 electrons, and after interactions with alkali metals, there are 41 electrons in total. Hence, after losing one electron, these clusters may become stable by attaining the electronic shell closure configuration of 40 electrons. The presence of loosely bound (excitable) electrons in these clusters mimics the chemistry of the first group metals.
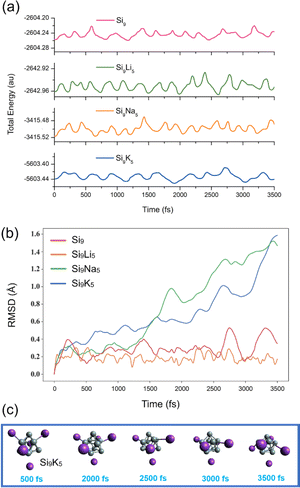
To investigate the kinetic and thermodynamic stability of the studied clusters, a total of 3500 different geometries for each cluster are obtained during the AIMD simulations at the B3LYP-D3/def2-SVP level of theory. The snapshots are taken at every 500 fs to ensure their structural integrity. Fig. 2a displays the fluctuation curves of total energy, indicating that the designed clusters are kinetically stable with steady fluctuations in energy. In addition, the changes in root-mean-square deviation (RMSD) of the geometries within the simulations are shown in Fig. 2b. As seen, the fluctuations are more pronounced for the Si9K5 cluster than the other three clusters, and the RMSD value for Si9K5 increases up to 1.5 Å near the 3500 fs. Although RMSD curves for both Na and K-based clusters are increasing, no isomerization or dissociation is observed in the geometries of clusters (see Fig. 2c and S2†). The larger deviations in the RMSD of Si9Na5 and Si9K5 may be due to their big size of metals and interaction distances. Hence, the present designed Zintl clusters are kinetically stable at room temperature, and can be further probed for optoelectronic applications.
Manipulating the FMO analysis, it is attainable to uncover complex interactions between two components in a system based on the HOMO–LUMO band gap (Eg). For the pure Zintl Si9, the Eg value is 5.83 eV, according to our FMO analysis. The orbital energies are presented in Table 1. As can be seen, due to the doping/interactions of alkali metals on Si9, the energy gaps (between HOMO and LUMO orbitals) of the present Si9M5 clusters are reduced. This is reasonable since the delocalized electrons of alkali (loosely held) would influence the valence electrons in the Si9 Zintl cluster, and then a diffuse excess electron system is generated, resulting in a reduced Eg gap. The HOMO–LUMO gaps of Si9Li5, Si9Na5, and Si9K5 are 4.17, 4.06 and 2.37 eV, respectively. The decreasing values have a periodic trend with the enlargement of the size of metals. In addition, the doping of alkali metals led to an increase in the energy of HOMO orbitals because of the residing excess electrons which lead to the generation of new HOMOs. The HOMO–LUMO gaps of Si9M5 are slightly higher than those of Ge9AM5 (ref. 60) and much lower than those of the P7M2 Zintl clusters.61 Fig. 3 shows the FMOs of the present clusters. As seen, the shape of LUMO of Si9Na5 and Si9K5 is spherical (similar to s-orbital) in shape. In the case of Si9Li5, the shape is more diffused, and the electronic density of the orbital is still higher around alkali metals than other places.
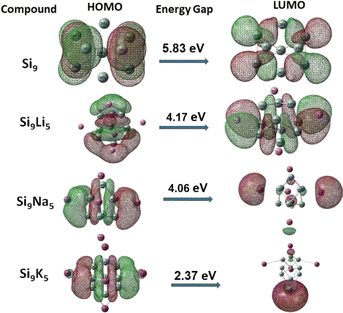 | ||
| Fig. 3 Representation of frontier molecular orbitals (FMOs) at the ωb97xd/def2-qzvp level (isovalue = 0.025). | ||
To visualize intra-and intermolecular charge transfer, we simulated the natural bonding orbital (NBO) charges on Si9M5, and the values are also given in Table 1. NBO charges on Si-atoms (QSi) have both positive and negative in magnitude. After alkali metals interaction, the Si-atoms get significant negative NBO charges, whereas partial charges on alkali metal (QM) atoms become positive as compared to silicon atoms. The highest magnitude (0.95 |e|) of NBO charge (positive) is displayed by the K-atom in the Si9K5 cluster, indicating excellent charge transfer. Such charge transfer from alkali metals to Si-atoms would result in asymmetric charge distribution within designed clusters.
Furthermore, charge transfer and delocalization can be explained using the interactions between bonds and different properties (such as stability, reactivity, and the relationship between donor and acceptor), as well as the relationship between donors (i) and acceptors (j). Table S3† lists the values from our NBO analysis, from which a number of electronic transitions are observed and the most significant transition with a major stabilization (E(2)) contribution is reported. Evidently, molecular interactions between the investigated system are mainly by σ–σ* and π–π* electronic transitions between Si–Si atoms. In Table S3,† we can also observe that, some bonds are very strong in Si9 due to strong interaction between Si–Si atoms. The most important maximum energy associated with the present clusters is to donate electrons from σ (Si4–Si6) to σ (Si4–Si9) in Si9, from σ* (Si9–Si11) to σ* (Si9–Si13) in Si9Li5, from π (Si7–Si9) to π* (Si1–Si2) in Si9Na5 and from σ* (Si4–Si8) to σ* (Si3–Si8) in Si9K5, with stable energies being 80.41, 44.86, 45.66 and 50.04 kcal mol−1, respectively.
3.2 Noncovalent interactions
The noncovalent interaction plays a very important role in many chemical processes.63–65 To investigate the nature of interactions between Si9 and alkali metals, we carried out a reduced density gradient (RDG) analysis based on the noncovalent interaction (NCI) method. Fig. 4 displays the RDG scatter graph, where the λ2 sign is exploited to differentiate between the bonded (λ2 < 0) and non-bonded (λ2 > 0) interactions. As seen in Fig. 4, for the present clusters, λ2 sign ρ function ranges from −0.05 to 0.05 au. The red peaks in the range of λ2 > 0 correspond to the effect of steric repulsion, green spikes appearing in the region of λ2 = 0 represent the dipole–dipole or London dispersion forces,13 blue-colored spikes in the regions ρ > 0 and λ2 < 0 represent the electrostatic interactions. In addition, Fig. 4 shows a significant increase in weak vdW attractions after the doping of alkali metals to the pure Si9 cluster. The strong, attractive interaction appears between −0.035 and −0.025 au. Hence, the isosurface plot indicates the presence of vdW interactions between the alkali metals and the pristine Si9 cluster, in which the dispersion interaction may play an important role. A significant increase in the magnitude of noncovalent can be seen with the increased atomic number of alkali metals, which may cause a strong impact on the NLO properties of the designed Si9M5 Zintl cluster.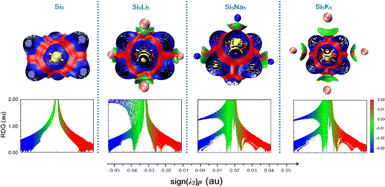 | ||
| Fig. 4 Representation of reduced density gradient (RGD) spectra and three-dimensional surfaces for non-covalent interactions analysis (NCI) at the ωb97xd/def2-qzvp level. | ||
We also performed the QTAIM analysis to identify the nature of bonding within the present clusters, and values are given in Table 2. The generated bond critical points (BCP) at (3, −1) appear in Fig. S3.† The interaction energies between alkali and silicon atoms (M–Si) are relatively weaker than the interaction between Si–Si in pure Si9, which demonstrates the presence of non-bonding interactions in present clusters. The Laplacian of electronic density (∇2ρ(r)) and total energy density (H(r)) values at BCP (3, −1) between Si–Si bond are negative, while positive for Si–M (where M = Li, Na, and K), which further suggests the non-covalent nature of bonds. Alkali metal interactions with silicon (M–Si) have a smaller value of total electronic density (ρ(r) < 0.1) and a positive magnitude of ∇2ρ(r), indicating the weak interactions are operational in the present Si9M5 clusters. Similarly, G(r)/|V(r)| ratios are close to or larger than unity for M–Si interactions, which also demonstrates the presence of vdW forces between Si and alkali metals in the present clusters.
| Cluster | Interaction | ρ(r) | Δ2ρ(r) | G(r) | V(r) | G(r)/|V(r)| | H(r) |
|---|---|---|---|---|---|---|---|
| Si9 | Si1–Si4 | 0.047 | 0.0040 | 0.0144 | −0.0280 | 0.5124 | −0.0136 |
| Si4–Si5 | 0.051 | −0.0041 | 0.0155 | −0.0323 | 0.4798 | −0.0168 | |
| Si4–Si9 | 0.047 | 0.0042 | 0.0143 | −0.0279 | 0.5125 | −0.0136 | |
| Si5–Si8 | 0.062 | −0.0292 | 0.0168 | −0.0417 | 0.4028 | −0.0248 | |
| Si9Li5 | Li1–Si8 | 0.016 | 0.0723 | 0.0153 | −0.0126 | 1.2142 | 0.0027 |
| Li2–Si12 | 0.016 | 0.0745 | 0.0159 | −0.0131 | 1.2137 | 0.0024 | |
| Li3–Si8 | −0.016 | 0.0725 | 0.0154 | −0.0127 | 0.4494 | 0.0027 | |
| Li4–Si2 | 0.055 | −0.0121 | 0.0160 | −0.0356 | 1.2126 | 0.0027 | |
| Li5–Si13 | 0.016 | 0.0729 | 0.0154 | −0.0127 | 0.8717 | 0.0027 | |
| Si9Na5 | Na10–Si3 | 0.012 | 0.0489 | 0.0034 | −0.0039 | 0.0903 | −0.0004 |
| Na11–Si5 | 0.011 | 0.0419 | 0.0027 | −0.0299 | 0.8571 | −0.0003 | |
| Na12–Si4 | 0.012 | 0.0400 | 0.0030 | −0.0035 | 0.9285 | −0.0004 | |
| Na13–Si6 | 0.010 | 0.0407 | 0.0026 | −0.0028 | 0.8571 | −0.0001 | |
| Na14–Si2 | 0.012 | 0.0418 | 0.0030 | −0.0035 | 1.2258 | −0.0005 | |
| Si9K5 | K10–Si7 | 0.006 | 0.0179 | 0.0038 | −0.0031 | 1.2258 | 0.0007 |
| K11–Si4 | 0.061 | −0.0282 | 0.0169 | −0.0418 | 0.4043 | 0.0007 | |
| K12–Si7 | 0.011 | 0.0332 | 0.0076 | −0.0069 | 1.1014 | 0.0006 | |
| K13–Si2 | 0.011 | 0.0345 | 0.0079 | −0.0071 | 1.1126 | 0.0007 | |
| K14–Si8 | 0.011 | 0.0332 | 0.0076 | −0.0069 | 1.1014 | 0.0006 |
3.3 Static nonlinear optical properties
It is rather beneficial for the NLO response of the superatom clusters that there is adequate electronic communication across their various moieties. As a new addition to the family of loosely bound excess electron compounds, the Si9M5 clusters designed in this work have superalkali characteristics and contain excess electrons, further prompting us to investigate their optoelectronic properties. Literature is also evident for crucial role of excess electrons and vdW interactions in triggering NLO response of molecules and clusters.66–68 The optical and NLO responses can be characterized through polarizability, hyperpolarizability, and static second hyperpolarizability. The obtained values are given in Table 3. The determined values of polarizability (αo) and μo are higher as compared to that of the urea, revealing excellent polarizability and charge separation. Overall, μo and αo response decreases in the order of Si9K5 > Si9Na5 > Si9Li5 > Si9. The highest value of αo can be seen for the Si9K5 cluster, while the lowest is observed for the pristine Si9 cluster. The substantial value of polarizability indicates the polarizable nature, which may be due to the presence of soft-nature alkali metals.| Properties | Si9 | Si9Li5 | Si9Na5 | Si9K5 |
|---|---|---|---|---|
| αo (au) | 268.82 | 403.913 | 578.84 | 1017.67 |
| βo (au) | 1.58 × 102 | 2.22 × 103 | 1.41 × 104 | 6.66 × 104 |
| βvec (au) | 1.44 × 102 | 1.01 × 103 | 1.19 × 104 | 4.72 × 104 |
| βHRS (au) | 1.44 × 102 | 1.01 × 103 | 1.19 × 104 | 4.72 × 104 |
| γo (au) | 5.94 × 104 | 6.01 × 105 | 2.37 × 106 | 7.67 × 107 |
| 〈βJ=1〉 | 122.92 | 1721.66 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246.21 246.21 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345.58 345.58 |
| 〈βJ=3〉 | 430.277 | 1898.84 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106.19 106.19 |
126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518.78 518.78 |
| ϕ〈βJ=1〉 | 22% | 47% | 50% | 30% |
| DR | 1.84 | 3.93 | 4.28 | 0.69 |
Hyperpolarizability (βo) is an approach for identifying nonlinear optical features of present clusters. The obtained βo values for Si9, Si9Li5, Si9Na5, and Si9K5 are 1.58 × 102, 2.22 × 103, 1.41 × 104, and 6.66 × 104 au, respectively. The βo value of the designed Si9M5 clusters is significantly increased compared to that of the pristine Si9, indicating the crucial role of excess electrons and non-covalent interactions. For example, the βo values of Si9Li5 and Si9K5 are 140 and 421 times larger than that of Si9, and the highest βo value of 6.66 × 104 au can be found in the Si9K5 cluster. Formulating excess electrons after the interaction of alkali metals might cause a significant reduction in excitation energies (ΔE), and excess electrons have a dominant role in triggering hyperpolarizability values. Fig. 5 displays ΔE of the crucial state and obtained βo of Si9 and Si9M5 clusters. As seen, there is an inverse relation of ΔE and βo. The calculated values of αo and βo of the present cluster are higher than those of urea and p-nitroaniline.69 The γo values range from 5.94 × 104 to 7.67 × 107 au, and a monotonic increase is observed from Li to K. Noncovalent interactions are also crucial in promoting the optical and NLO properties of designed clusters. The uptrend in values of hyperpolarizabilities is observed with the increased vdW interactions, as revealed by NCI analysis.
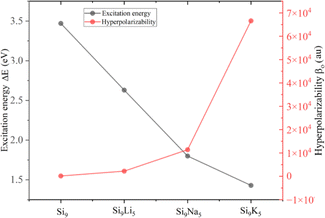 | ||
| Fig. 5 Plotted excitation energy (ΔE) of crucial state and obtained hyperpolarizability (βo) of Si9 and Si9M5 clusters at the ωb97xd/def2-qzvp level. | ||
In addition, the effect of solvent on αo and βo is also considered at the ωb97xd/def2-qzvp level, by employing the implicit, namely the universal solvent model based on solute electron density (SMD). Calculated values are presented in Table S4.† Obtained second-order NLO parameters in solvent media are better than those of vacuum-based results. It is worthy of note that computed values of βo using four different solvents are broadly consistent and in the same tendency. Using water as a solvent leads to slightly larger βo values. For instance, the calculated β value (5.5 × 106 au) for Si9K5 is found to be 83 times higher as compared to β in the gas phase. The altered electronic density and change in electronic properties due to the presence of solvent may influence the electric field, which would result in increased βo. The presence of solvent has introduced a strong polarization effect to the applied electric field. Thus, controlling the polarizable environment around studied clusters can be seen as an effective way to adjust the NLO response.
To get deep insight into nonlinear optical features, we disclose the second-order electric susceptibility response of the present clusters theoretically by Hyper-Rayleigh scattering (HRS) simulation, and the results are listed in Table 3. As seen, the obtained βHRS values of Si9, Si9Li5, Si9Na5, and Si9K5 are 1.44 × 102, 1.01 × 103, 1.19 × 104, and 4.72 × 104 au, respectively. From Si9 to Si9K5, βHRS values have the same trend as βo values, indicating the excellent NLO characteristics of the present clusters. In particular, the βHRS value of Si9K5 is 328 times larger than that of Si9. Furthermore, the average dipolar hyperpolarizability 〈βJ=1〉 and octupolar 〈βJ=3〉 values of the Si9M5 clusters are higher than those of Si9. The maximum dipolar contribution is 50% for the Si9K5, while the remaining clusters exhibit an octupolar-like nature. Compared with the previously reported clusters,47 the present clusters exhibit greater γo values.
3.4 Dynamic nonlinear optical properties
We also examined the frequency-dependent hyperpolarizability β(ω) theoretically considering the externally applied frequency of 532 and 1900 nm, and the obtained results are summarized in Table 4. β(ω) consists of two parts, i.e., electro-optical Pockel's effect (EOPE) with β(−ω,ω,0) and second harmonic generation phenomena (SHG) with β(−2ω,ω,ω). The choice of wavelengths also relevant to Nd:YAG laser functioning, which frequently emits invisible light in at longer wavelength and serves in laser-based devices.70 The electro-optical effect (Pockel's effect) is an essential nonlinear effect used in many applications. As shown in Table 4, for all four clusters, the values of β(−ω;ω,0) and β(−2ω,ω,ω) at ω = 0.0240 are higher than the corresponding values at ω = 0.0856. Hence, the frequency-dependent first hyperpolarizability β(ω) response dominates at smaller dispersion frequency (at longer wavelength). From Si9 to Si9K5, both β(−ω;ω,0) and β(−2ω,ω,ω) show increasing trends. Obviously, the dynamic first hyperpolarizability β(ω) values of Si9M5 are immensely better than the pristine Si9 cluster, indicating their excellent dynamic nonlinear optical features.| Frequency-dependent first hyperpolarizability β(ω) | ||||
|---|---|---|---|---|
| ω = 0.0856 (532 nm) | ω = 0.0240 (1900 nm) | |||
| β(−ω;ω,0) | β(−2ω;ω,ω) | β(−ω;ω,0) | β(−2ω;ω,ω) | |
| Si9 | 2.79 × 102 | 2.03 × 103 | 1.61 × 102 | 1.25 × 102 |
| Si9Li5 | 3.39 × 104 | 1.11 × 105 | 2.41 × 103 | 2.80 × 103 |
| Si9Na5 | 7.62 × 106 | 1.32 × 106 | 3.83 × 104 | 4.45 × 105 |
| Si9K5 | 2.65 × 106 | 3.05 × 105 | 2.65 × 108 | 1.05 × 108 |
| Frequency-dependent second hyperpolarizability γ(ω) | ||||
|---|---|---|---|---|
| γ(−ω;ω,0,0) | γ(−2ω;ω,ω,0) | γ(−ω;ω,0,0) | γ(−2ω;ω,ω,0) | |
| Si9 | 8.53 × 104 | 1.86 × 105 | 6.10 × 104 | 6.42 × 104 |
| Si9Li5 | 1.10 × 1010 | 3.30 × 109 | 6.81 × 105 | 1.83 × 106 |
| Si9Na5 | 3.67 × 109 | 3.90 × 108 | 3.48 × 106 | 2.44 × 108 |
| Si9K5 | 1.18 × 109 | 1.24 × 109 | 5.86 × 1011 | 1.30 × 1011 |
Table 4 also lists the dynamic second hyperpolarizability γ(ω) values. As seen, the obtained the dc-Kerr effect γ(−ω,ω,0,0) and second harmonic generation SHG γ(−2ω,ω,ω,ω) values are much better than those of static γo. The calculated highest response is indicated regarding the Kerr effect with a value up to 5.86 × 1011 au. Additionally, the frequency-dependent SHG and Kerr effect are much more prominent at 1900 nm (small dispersion frequency) than those of at 532 nm. Within the present designed clusters, an uptrend can be seen in both γ(−2ω;ω,ω,0) and γ(−ω,ω,0,0) values with increased metal size at 1900 nm, while at 532 nm Si9Li5 has the highest value of γ(−2ω;ω,ω,0) and γ(−ω,ω,0,0). The Kerr effect is caused by the instantaneous change in its refractive index in response to the applied electric field. Also, the change in the refractive index is directly related to the square of electric field strength. Hence, the applied smaller frequency (ω = 0.024) has significantly enhanced values of the Kerr effect as compared to a higher frequency. Fig. S4† reveals the variational trend frequency-dependent β(ω) and γ(ω) at 532 and 1900 nm, respectively, where the SHG and dc-Kerr effects exhibit the same increasing trend from Li to K at 1900 nm.
3.5 Spectroscopic study and bonding analysis
Fig. S5† depicts the obtained absorption spectra of the present Si9M5 clusters by our TD-DFT calculations. As seen, the absorbance maxima are shifted to longer wavelength (bathochromic shift), where the highest absorbance wavelength (866 nm) is seen for the Si9K5 cluster. The atomic number of alkali metals is the main influencing factor in the absorbance properties where increased-sized metals decrease the excitation energy. The values of excitation energies (ΔE), absorbance maxima (λmax), and oscillator strength (O.S.) are given in Table 5. The excitation (transition) energy (ΔE) of the Si9 cluster is higher than those with alkali metal decorated, and a gradual decrease in ΔE is observed from Si9Li5 to Si9K5 for designed clusters. The above results demonstrate that the higher size metals in Si9 clusters enable them to harvest light at comparatively longer wavelengths.| Clusters | ΔE (eV) | λmax (nm) | fos (au) |
|---|---|---|---|
| Si9 | 3.47 | 356 | 0.0091 |
| Si9Li5 | 2.63 | 469 | 0.0203 |
| Si9Na5 | 1.80 | 685 | 0.1620 |
| Si9K5 | 1.43 | 866 | 0.4689 |
In addition, we examined the total density of states (TDOS), and the obtained spectra are given in Fig. S6.† It is known that the different kinds of states inhabited by electrons at a discrete energy level are expressed by electronic states per unit of energy. For the pristine Si9, the wide energy gap can be seen where HOMO is located at −8 eV. After interacting with alkali metals, the HOMO–LUMO gap became narrow, where HOMO has a further increase in energy. Furthermore, the vibrational frequencies of Si9 and Si9M5 are listed in Table S5,† and the spectra of FT-IR and Raman are shown in Fig. S7.† The vibrational and Raman frequencies are simulated at the ωb97Xd/def2-qzvp level. In both Si9 and Si9M5 cases, the Si–Si stretching vibrations agree well with experimental values. The most dominant peaks of stretching vibrations of silicon in Si9 are ranging from 533 to 317 cm−1 (Table S5†). The increased vibrational frequency of Si9M5 reveals the structural change after introducing alkali metals.
Fig. 6 displays the results of ELF and LOL analysis, which further justifies the nature of boning and the presence of loosely bound electrons in present clusters. The color scale of the ELF and LOL maps varies from blue to red in the range of 0 to 1.0, respectively. The area colored in red and blue corresponds to the maximum and minimum Pauli repulsion with the unity and zero values, respectively. However, the highest repulsive interaction (most localized electron state) is shown in red. The strong localization of electrons (ELF > 0.5) corresponds to the covalent bond, lone pair, or inner shells. From the ELF analysis, the Si9Li5 cluster shows strong electron localization after interactions with alkali metals, where a concentrated red color can be seen with alkali metals. The blue spots (ELF < 0.5) show charge delocalization regions, indicating the existence of noncovalent interactions. The electrons are highly localized when ELF is one and delocalized when ELF is zero. The high level of ELF and LOL values are indicated by the red color near alkali metals. A delocalized electron cloud can be seen as a blue color on the outer surface of the Si9 cluster and also in the Si9M5 cluster. In addition, the green regions on the ELF surface and LOL colour-filled maps point out the presence of vdW interactions.
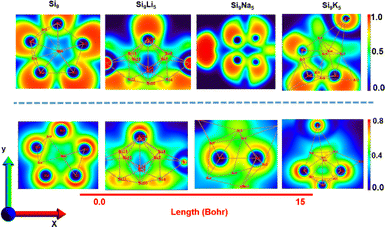 | ||
| Fig. 6 Electron localization function (ELF) (upper panel) and 2D localized orbital locator (LOL) spectra (lower panel) of the present clusters. The planes that are used to plot the ELF and LOL patterns are shown in Fig. S8.† | ||
4 Conclusions
In the concluding summary, we investigate the Zintl-based superalkali-excess electron clusters theoretically using various calculations. The designed Si9M5 (M = Li, Na, and K) clusters are thermodynamically stable, as indicated by the binding energies and AIMD simulations. Also, Si–M interactions are shown to be weak and dominated by vdW interactions, which contribute to optical and NLO properties. Excess electron nature, bonding structures, and partial atomic charges are calculated through FMO and NBO studies. IR and Raman frequencies are calculated to examine the amplitude of vibrations after doping. The HOMO–LUMO gap for Si9K5 is much reduced as compared to the pristine Si9 cluster. Remarkable static polarizability (αo) and hyperpolarizability (βo) values are obtained up to 1.02 × 104 au and 6.66 × 104 au for the Si9K5 cluster. The influence of the implicit solvent model has been considered, where βo increased 83 times as compared to the corresponding value in the gas phase for the Si9K5 cluster. The frequency-dependent NLO response for the dc-Kerr effect is observed up to 1.3 × 1011 au, indicating the excellent change in refractive index by an externally applied electric field. Electron localization (ELF) and localized orbital locator (LOL) further reveal the bonding nature in these clusters.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 22320102004, 22133003) and the Beijing National Laboratory for Molecular Sciences. Furthermore, author A. A. also acknowledges support from Alliance of National and International Science Organization (ANSO).References
- G. de la Torre, P. Vázquez, F. Agulló-López and T. Torres, Role of Structural Factors in the Nonlinear Optical Properties of Phthalocyanines and Related Compounds, Chem. Rev., 2004, 104, 3723–3750 CrossRef CAS PubMed.
- H. T. Uyeda, Y. Zhao, K. Wostyn, I. Asselberghs, K. Clays, A. Persoons and M. J. Therien, Unusual Frequency Dispersion Effects of the Nonlinear Optical Response in Highly Conjugated (Polypyridyl)metal–(Porphinato)zinc(II) Chromophores, J. Am. Chem. Soc., 2002, 124, 13806–13813 CrossRef CAS PubMed.
- D. Xiao, F. A. Bulat, W. Yang and D. N. Beratan, A Donor–Nanotube Paradigm for Nonlinear Optical Materials, Nano Lett., 2008, 8, 2814 CrossRef CAS PubMed.
- D. Cornelis, E. Franz, I. Asselberghs, K. Clays, T. Verbiest and G. Koeckelberghs, Interchromophoric Interactions in Chiral X-type π-Conjugated Oligomers: A Linear and Nonlinear Optical Study, J. Am. Chem. Soc., 2011, 133, 1317–1327 CrossRef CAS PubMed.
- K. M. Ok, Toward the Rational Design of Novel Noncentrosymmetric Materials: Factors Influencing the Framework Structures, Acc. Chem. Res., 2016, 49, 2774–2785 CrossRef CAS PubMed.
- H. Sun and J. Autschbach, Electronic Energy Gaps for π-Conjugated Oligomers and Polymers Calculated with Density Functional Theory, J. Chem. Theory Comput., 2014, 10, 1035–1047 CrossRef CAS PubMed.
- M. C. Lucking, K. Beach and H. Terrones, Large second harmonic generation in alloyed TMDs and boron nitride nanostructures, Sci. Rep., 2018, 8, 10118 CrossRef PubMed.
- N. Ma, W. Guo, Z. Zhu and G. Zhang, Third-order nonlinear optical property contrast as self-assembly recognition for nanorings C60, New J. Chem., 2022, 46, 4927–4935 RSC.
- T. Guerrero, P. G. Lacroix, H. García-Ortega, O. G. Morales-Saavedra, D. Agustin and N. Farfán, Enhanced NLO properties of molybdenum push-pull coordination compounds with tridentate ONO organic ligands, Inorg. Chim. Acta, 2016, 442, 10–15 CrossRef CAS.
- S. Van Cleuvenbergen, Z. J. Smith, O. Deschaume, C. Bartic, S. Wachsmann-Hogiu, T. Verbiest and M. A. van der Veen, Morphology and structure of ZIF-8 during crystallisation measured by dynamic angle-resolved second harmonic scattering, Nat. Commun., 2018, 9, 3418 CrossRef.
- K. Fukuda, N. Matsushita, Y. Minamida, H. Matsui, T. Nagami, S. Takamuku, Y. Kitagawa and M. Nakano, Impact of Diradical/Ionic Character on Third-Order Nonlinear Optical Property in Asymmetric Phenalenyl Dimers, ChemistrySelect, 2017, 2, 2084 CrossRef CAS.
- S.-J. Wang, Y.-F. Wang and C. Cai, Multidecker Sandwich Complexes VnBenn+1 (n = 1, 2, 3) as Stronger Electron Donor Relative to Ferrocene for Designing High-Performance Organometallic Second-Order NLO Chromophores: Evident Layer Effect on the First Hyperpolarizability and Two-Dimensional N, J. Phys. Chem. C, 2015, 119, 5589–5595 CrossRef CAS.
- R.-L. Zhong, H.-L. Xu, Z.-R. Li and Z.-M. Su, Role of Excess Electrons in Nonlinear Optical Response, J. Phys. Chem. Lett., 2015, 6, 612–619 CrossRef CAS PubMed.
- J. M. Ceraso and J. L. Dye, 23Na NMR spectrum of the sodium anion, J. Chem. Phys., 2003, 61, 1585–1587 CrossRef.
- R. L. Zhong, H. L. Xu, Z. R. Li and Z. M. Su, Role of excess electrons in nonlinear optical response, J. Phys. Chem. Lett., 2015, 6, 612–619 CrossRef CAS PubMed.
- Y. Li, Z.-R. Li, D. Wu, R.-Y. Li, X.-Y. Hao and C.-C. Sun, An Ab Initio Prediction of the Extraordinary Static First Hyperpolarizability for the Electron-Solvated Cluster (FH)2{e}(HF), J. Phys. Chem. B, 2004, 108, 3145 CrossRef CAS.
- N. Ma, J. Gong, S. Li, J. Zhang, Y. Qiu and G. Zhang, Second-order NLO responses of two-cavity inorganic electrides Lin@B20H26 (n = 1, 2): evolutions with increasing excess electron number and various B–B connection sites of B20H26, Phys. Chem. Chem. Phys., 2017, 19, 2557–2566 RSC.
- J.-J. Wang, Z.-J. Zhou, Y. Bai, Z.-B. Liu, Y. Li, D. Wu, W. Chen, Z.-R. Li and C.-C. Sun, The Interaction Between Superalkalis (M3O, M = Na, K) and a C20F20 Cage Forming Superalkali Electride Salt Molecules with Excess Electrons Inside the C20F20 Cage: Dramatic Superalkali Effect on the Nonlinear Optical Property, J. Mater. Chem., 2012, 22, 9652 RSC.
- S. Muhammad, H. Xu, Y. Liao, Y. Kan and Z. Su, Quantum Mechanical Design and Structure of the Li@B10H14 Basket with a Remarkably Enhanced Electro-Optical Response, J. Am. Chem. Soc., 2009, 131, 11833 CrossRef CAS PubMed.
- A. Ahsin and K. Ayub, Extremely large static and dynamic nonlinear optical response of small superalkali clusters NM3M′ (M, M′ = Li, Na, K), J. Mol. Graphics Modell., 2021, 109, 108031 CrossRef CAS.
- A. C. Reber, S. N. Khanna and A. W. Castleman, Superatom Compounds, Clusters, and Assemblies: Ultra Alkali Motifs and Architectures, J. Am. Chem. Soc., 2007, 129, 10189–10194 CrossRef CAS.
- F. Ullah, N. Kosar, K. Ayub and T. Mahmood, Superalkalis as a source of diffuse excess electrons in newly designed inorganic electrides with remarkable nonlinear response and deep ultraviolet transparency: a DFT study, Appl. Surf. Sci., 2019, 483, 1118–1128 CrossRef CAS.
- W.-M. Sun and D. Wu, Recent Progress on the Design, Characterization, and Application of Superalkalis, Chem.–Eur. J., 2019, 25, 9568–9579 CrossRef CAS.
- P. Jena and S. N. Khanna, Physics of cluster assembled materials, Mater. Sci. Eng., A, 1996, 217–218, 218–222 CrossRef.
- K. Yokoyama, N. Haketa, H. Tanaka, K. Furukawa and H. Kudo, Ionization energies of hyperlithiated Li2F molecule and LinFn−1 (n = 3, 4) clusters, Chem. Phys. Lett., 2000, 330, 339–346 CrossRef CAS.
- P. D. Dao, K. I. Peterson and A. W. Castleman Jr, The photoionization of oxidized metal clusters, J. Chem. Phys., 1984, 80, 563–564 CrossRef CAS.
- E. Rehm, A. I. Boldyrev and P. v. R. Schleyer, Ab initio study of superalkalis. First ionization potentials and thermodynamic stability, Inorg. Chem., 1992, 31, 4834–4842 CrossRef CAS.
- T. B. Tai, P. V. Nhat, M. T. Nguyen, S. Li and D. A. Dixon, Electronic Structure and Thermochemical Properties of Small Neutral and Cationic Lithium Clusters and Boron-Doped Lithium Clusters: Lin0/+ and LinB0/+ (n = 1–8), J. Phys. Chem. A, 2011, 115, 7673–7686 CrossRef CAS PubMed.
- A. K. Srivastava, Ab initio investigations on bimetallic mononuclear superalkali clusters, Chem. Phys. Lett., 2020, 759, 138049 CrossRef CAS.
- J. Tong, Y. Li, D. Wu, Z.-R. Li and X.-R. Huang, Ab Initio Investigation on a New Class of Binuclear Superalkali Cations M2Li2k+1+ (F2Li3+, O2Li5+, N2Li7+, and C2Li9+), J. Phys. Chem. A, 2011, 115, 2041–2046 CrossRef CAS PubMed.
- S. K. Pandey, Novel and Polynuclear K- and Na-Based Superalkali Hydroxides as Superbases Better Than Li-Related Species and Their Enhanced Properties: An Ab Initio Exploration, ACS Omega, 2021, 6, 31077–31092 CrossRef CAS.
- A. Ahsin and K. Ayub, Superalkali-based alkalides Li3O@[12-crown-4]M (where M = Li, Na, and K) with remarkable static and dynamic NLO properties; a DFT study, Mater. Sci. Semicond. Process., 2022, 138, 106254 CrossRef CAS.
- A. Ahsin and K. Ayub, Remarkable electronic and NLO properties of bimetallic superalkali clusters: a DFT study, J. Nanostruct. Chem., 2022, 12, 529–545 CrossRef CAS.
- A. Ahsin and K. Ayub, Theoretical investigation of superalkali clusters M2OCN and M2NCO (where M = Li, Na, K) as excess electron system with significant static and dynamic nonlinear optical response, Optik, 2021, 227, 166037 CrossRef CAS.
- A. Ahsin and K. Ayub, Oxacarbon superalkali C3X3Y3 (X = O, S and Y = Li, Na, K) clusters as excess electron compounds for remarkable static and dynamic NLO response, J. Mol. Graphics Modell., 2021, 106, 107922 CrossRef CAS PubMed.
- L. Saedi, M. Dodangi, A. Mohammadpanaardakan and M. Eghtedari, Superalkali–Superhalogen Complexes as Versatile Materials for Hydrogen Storage: A Theoretical Study, J. Cluster Sci., 2020, 31, 71–78 CrossRef CAS.
- R. B. King, in Structure and Bonding in Zintl Ions and Related Main Group Element Clusters BT – Zintl Ions: Principles and Recent Developments, ed. T. F. Fässler, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 1–24 Search PubMed.
- L. J. Schiegerl, A. J. Karttunen, W. Klein and T. F. Fässler, Silicon clusters with six and seven unsubstituted vertices via a two-step reaction from elemental silicon, Chem. Sci., 2019, 10, 9130–9139 RSC.
- S. Sinha, P. Jena and S. Giri, Functionalized nona-silicide [Si9R3] Zintl clusters: a new class of superhalogens, Phys. Chem. Chem. Phys., 2022, 24, 21105–21111 RSC.
- J. Cao, F. Li, W. Xia and W. Bian, van der Waals interactions in bimolecular reactions, Chin. J. Chem. Phys., 2019, 32, 157–166 CrossRef CAS.
- Z. Shen, H. Ma, C. Zhang, M. Fu, Y. Wu, W. Bian and J. Cao, Dynamical importance of van der Waals saddle and excited potential surface in C(1D) + D2 complex-forming reaction, Nat. Commun., 2017, 8, 14094 CrossRef CAS.
- D. Skouteris, D. E. Manolopoulos, W. Bian, H. J. Werner, L. H. Lai and K. Liu, Van der Waals interactions in the Cl + HD reaction, Science, 1999, 286, 1713–1716 CrossRef CAS PubMed.
- J. Cao, Y. Wu and W. Bian, Ring polymer molecular dynamics of the C(1D) + H2 reaction on the most recent potential energy surfaces, Chin. J. Chem. Phys., 2021, 34, 833–842 CrossRef CAS.
- Y. Wu, J. Cao, H. Ma, C. Zhang, W. Bian, D. Nunez-Reyes and K. M. Hickson, Conical intersection–regulated intermediates in bimolecular reactions: Insights from C(1D) + HD dynamics, Sci. Adv., 2019, 5, eaaw0446 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. a. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. a. Petersson, H. Nakatsuji, X. Li, M. Caricato, a. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, a. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. a. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. a. Keith, R. Kobayashi, J. Normand, K. Raghavachari, a. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, G16_C01, Gaussian 16, Revision C.01, Gaussian, Inc., Wallin, 2016 Search PubMed.
- Y. Ren and W. Bian, Mode-Specific Tunneling Splittings for a Sequential Double-Hydrogen Transfer Case: An Accurate Quantum Mechanical Scheme, J. Phys. Chem. Lett., 2015, 6, 1824–1829 CrossRef CAS PubMed.
- F. Li, X. Yang, X. Liu, J. Cao and W. Bian, An Ab Initio Neural Network Potential Energy Surface for the Dimer of Formic Acid and Further Quantum Tunneling Dynamics, ACS Omega, 2023, 8, 17296–17303 CrossRef CAS PubMed.
- J. Luo, J. Cao, H. Liu and W. Bian, Accurate quantum dynamics of the simplest isomerization system involving double-H transfer, Chin. J. Chem. Phys., 2022, 35, 185–192 CrossRef CAS.
- J. Cao, Z. Zhang, C. Zhang, K. Liu, M. Wang and W. Bian, Quasiclassical trajectory study of H+SiH4 reactions in full-dimensionality reveals atomic-level mechanisms, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13180–13185 CrossRef CAS PubMed.
- W. Xia, J. Cao, Q. Lu and W. Bian, Production of ultracold polyatomic molecules with strong polarity by laser cooling: a detailed theoretical study on CaNC and SrNC, Front. Chem., 2022, 10, 1009986 CrossRef CAS PubMed.
- L. J. Schiegerl, A. J. Karttunen, J. Tillmann, S. Geier, G. Raudaschl-Sieber, M. Waibel and T. F. Fässler, Charged Si9 Clusters in Neat Solids and the Detection of [H2Si9]2− in Solution: A Combined NMR, Raman, Mass Spectrometric, and Quantum Chemical Investigation, Angew. Chem., Int. Ed., 2018, 57, 12950–12955 CrossRef CAS PubMed.
- J. Zhang and M. Dolg, ABCluster: the artificial bee colony algorithm for cluster global optimization, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- H. Zhai and A. N. Alexandrova, Ensemble-Average Representation of Pt Clusters in Conditions of Catalysis Accessed through GPU Accelerated Deep Neural Network Fitting Global Optimization, J. Chem. Theory Comput., 2016, 12, 6213–6226 CrossRef CAS PubMed.
- J. Zhang and V. A. Glezakou, Global optimization of chemical cluster structures: Methods, applications, and challenges, Int. J. Quantum Chem., 2021, 121, 1–18 Search PubMed.
- K. Yu, X. Wang, L. Chen and L. Wang, Unbiased fuzzyglobal optimization of Lennard-Jones clusters for N ≤ 1000, J. Chem. Phys., 2019, 151, 214105 CrossRef PubMed.
- F. Neese, The ORCA program system, WIREs, Comput, Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- A. L. Tenderholt and K. M. Langner, cclib: a library for package independent computational chemistry algorithms, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- H. Singh, A DFT insight into structure, NBO, NCI, QTAIM, vibrational, and NLO properties of cationic amino acid ionic liquid [Pro-H]+BF4−, Struct. Chem., 2024, 35, 471–483 CrossRef CAS.
- A. Ahsin, A. B. Shah and K. Ayub, Germanium-based superatom clusters as excess electron compounds with significant static and dynamic NLO response; a DFT study, RSC Adv., 2022, 12, 365–377 RSC.
- A. Ahsin and K. Ayub, Zintl based superatom P7M2 (M = Li, Na, K & Be, Mg, Ca) clusters with excellent second and third-order nonlinear optical response, Mater. Sci. Semicond. Process., 2021, 134, 105986 CrossRef CAS.
- K. Ayub, Are phosphide nano-cages better than nitride nano-cages? A kinetic, thermodynamic and non-linear optical properties study of alkali metal encapsulated X12Y12 nano-cages, J. Mater. Chem. C, 2016, 4, 10919–10934 RSC.
- Q. Lu and W. Bian, The Decay of Dispersion Interaction and Its Remarkable Effects on the Kinetics of Activation Reactions Involving Alkyl Chains, J. Phys. Chem. Lett., 2023, 14, 10642–10647 CrossRef CAS PubMed.
- X. Yang, H. Ma, Q. Lu and W. Bian, Efficient Method for Numerical Calculations of Molecular Vibrational Frequencies by Exploiting Sparseness of Hessian Matrix, J. Phys. Chem. A, 2024, 128, 3024–3032 CrossRef CAS PubMed.
- W. Bian and H.-J. Werner, Global ab initio potential energy surfaces for the ClH2 reactive system, J. Chem. Phys., 2000, 112, 220–229 CrossRef CAS.
- A. Ahsin, A. Ali and K. Ayub, Transition metals based metalides TM-Janus-TM (where TM = Sc–Zn and Janus = F6C6H6); a theoretical study of nonconventional metalides with excellent static and dynamic nonlinear optical properties, Mater. Sci. Semicond. Process., 2023, 162, 107506 CrossRef CAS.
- A. Ahsin, I. Ejaz, S. Sarfaraz, K. Ayub and H. Ma, Polaron Formation in Conducting Polymers: A Novel Approach to Designing Materials with a Larger NLO Response, ACS Omega, 2024, 9, 14043–14053 CrossRef CAS PubMed.
- A. Ahsin, T. Jadoon and K. Ayub, M@[12-crown-4] and M@[15-crown-5] where (M = Li, Na, and K); the very first examples of non-conventional one alkali metal-containing alkalides with remarkable static and dynamic NLO response, Phys. E, 2022, 140, 115170 CrossRef CAS.
- S. P. Karna, P. N. Prasad and M. Dupuis, Nonlinear optical properties of p-nitroaniline: an ab initio time-dependent coupled perturbed Hartree-Fock study, J. Chem. Phys., 1991, 94, 1171–1181 CrossRef CAS.
- M. R. Maina, Y. Okamoto, K. Hamada, A. Okada, S. ichi Nakashiba and N. Nishi, Effects of superposition of 532 nm and 1064 nm wavelengths in copper micro-welding by pulsed Nd:YAG laser, J. Mater. Process. Technol., 2022, 299, 117388 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02396j |
| ‡ The authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |