Open Access Article
Open Access ArticleOptically compatible infrared camouflage performance of ITO ink†
Xiao Feifei *,
Xu Weidong,
Liu Heng,
Li Hao,
Yu Haibao and
Hao Bentian
*,
Xu Weidong,
Liu Heng,
Li Hao,
Yu Haibao and
Hao Bentian
Field Engineering College, Army Engineering University of PLA, Nanjing 210014, China. E-mail: xiaofeieif8719@126.com
First published on 29th May 2024
Abstract
With the rapid development of military reconnaissance technology, reconnaissance devices have been equipped with wideband reconnaissance ability, which imposes increased requirements on camouflage. Developing multiband camouflage materials with good compatibility has become increasingly important. Indium tin oxide (ITO), a transparent conductive oxide with good comprehensive photoelectric properties, exhibits different absorption, reflectivity, and transmission characteristics in different bands of electromagnetic waves. Therefore, ITO might be able to solve broadband and multiband camouflage problems effectively. In this paper, ITO is expressed as In32−xSnxO48. The energy band structure, optical properties, and infrared absorption spectra at different doping ratios of Sn (x = 0, 1, 2, 3) were obtained on the basis of first principle theory, and the camouflage mechanism of ITO in different electromagnetic wavebands was explored. Results demonstrated that when x = 3, specifically, when the doping ratio of Sn atoms was 9.375%, ITO had high transmission in the visible light band and infrared band reflectivity and can realize optically compatible infrared camouflage. In accordance with calculation results, ITO nanodispersion liquid (x = 3) was mixed with green camouflage coating added with some additives to prepare green ITO camouflage ink for silkscreen printing. The ink formed a camouflage protective ink coating after it was coated onto the surface of fabric through silkscreen printing. Results showed that the emissivity of the ITO ink coating decreased by more than 0.13 when its solid content reached 20%, and its camouflage performance in the visible light band was barely affected. The results of this research can guide the application of ITO materials in the field of camouflage.
1. Introduction
Under modern war conditions and severe threats from high-technology reconnaissance and surveillance, good camouflage protection is particularly important for sudden attacks and maintaining target survival on the battlefield. Developing multispectral camouflage materials covering optics, infrared, and radar wavebands on the basis of existing camouflage materials is necessary. Camouflage blankets and covers should be fabricated on the basis of camouflage fabrics and in accordance with the typical geological background and camouflage needs of targets. Through the adjustment of multiple technologies and combined design of multispectral camouflage, targets can be easily hidden and their importance can be reduced, thus providing technological support for the comprehensive camouflage of targets.1–3 Camouflage fabrics have the characteristics of strong flexibility, light weight, and easy transportability. However, existing camouflage fabrics have poor adaptation to different environments and are insufficiently light. Existing camouflage fabrics should be changed continuously in accordance with the war environment to improve camouflage efficacy.4,5 The real-time production of camouflage patterns that integrate well with the background environment and coating of optically compatible infrared camouflage ink onto the surfaces of camouflage fabric through silkscreen printing can make targets blend with the background color and surface tissue structure, develop deformation in the infrared band, and realize optical and infrared camouflage functions.6,7 The key material of optically compatible infrared camouflage ink is the functional fillers that can reduce the emissivity of the coating without damaging its optical camouflage function.Indium tin oxide (ITO), a transparent conductive oxide with good comprehensive photoelectric properties, can absorb, reflect, and transmit different bands of electromagnetic waves. ITO, which has the potential for multispectral camouflage, is expected to be used as a functional filler in multispectral compatible inks. ITO is mainly applied in the form of thin films in various industries. In 1984, Schott Glaswerke demonstrated that ITO film formed on a PET base has high reflectivity at 9.5 μm, high visible light permeability, good adhesion force with glass on base plates, high anti-scratching property, and good weather resistance.8 Similar conclusions have been drawn in subsequent studies. The preparation of ITO thin film faces great challenges and incurs a high cost, which restricts its application in camouflage projects. The application of ITO as a camouflage ink might be suitable for camouflage protection projects. Some studies on the applications of ITO in transparent thermal insulation coating and nanoprinting ink have been reported. Although relevant studies have demonstrated that ITO has good transparency in the optical band, its absorption, reflectivity, and transmission mechanisms of infrared electromagnetic waves have different interpretations.9–11 ITO is obtained by doping In2O3 with Sn. The addition of Sn influences the physical properties of materials remarkably and determines the performance of ITO. Given that each Sn atom can only provide a maximum of one excessive electron to In2O3, a sufficiently high Sn density is required to obtain numerous charge carriers (electrons).10 Thus far, ITO has been applied in practical engineering through heavy doping.
In2O3 has a ferromanganese structure that contains 80 atoms, including 32 indium atoms and 48 oxygen atoms. The chemical formula of In2O3 after being doped with Sn can be defined as In32−xSnxO48, where x represents the number of added Sn atoms. The material structure can influence the basic physical and chemical properties of In32−xSnxO48. In this study, the geometric structure of the dominant crystal of In32−xSnxO48, which contains 80 atoms, was optimized on the basis of first principle theory. In addition, the energy band structure, optical properties, and infrared adsorption spectra of the crystal when x = 0, 1, 2, 3 (representing Sn atom doping ratios of 0%, 3.125%, 6.25%, and 9.375%) were calculated to characterize the properties of ITO materials. This study aims to explore the camouflage mechanism of ITO in different electromagnetic bands. Additionally, ITO with the optimal comprehensive performance was chosen in accordance with calculation results. The nanodispersion liquid of the chosen ITO was mixed with green optical camouflage coating to prepare ink film on high-strength polyester fabric surfaces through silkscreen printing. The camouflage performances of the ink film compatible with the visible light and infrared bands were investigated.
2. Methods
2.1 Calculation in accordance with first principle theory
In this study, first principle theory based on density functional theory (DFT) was chosen and applied by using the CASTEP calculation program.12 The crystal structure used in this study contained 80 atoms. Geometric structural optimization and property calculation require considerable calculation loads. We first conducted a convergence test on the K point and truncation energy of the plane wave to balance calculation loads and accuracy. In the test, the K point was 4 × 4 × 4, the truncation energy of the plane wave was 600 eV, and the convergence standard was 10 meV per atom.13,14The first step of calculation has to optimize the geometric structure of crystals to guarantee the accuracy of subsequent calculations. In this study, LBFGS was employed as the geometric optimization algorithm, and the DFT method was based on generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE).15 The dispersion correction method used TS. Spin and spin–orbit coupling were open during the geometric structural optimization of crystals.16 The judgment criteria for ion step convergence were set as follows: an energy of 5.0 × 10−6 eV per atom, a max.force of 0.01 eV A−1, a max.stress of 0.01 GPa, and a max.displacement of 5.0 × 10−4 A. Crystal optimization used full mode. At electron step convergence, pseudopotentials used norm conserving.17 The convergence standards were set as an SCF tolerance of 5.0 × 10−7 eV per atom and max.SCF cycles of 100.
For the optimized crystal structure, spin tended to be 0 and was ignored in the subsequent calculation of properties. The energy band structure and optical properties of crystals along the four high symmetric point paths in the Brillouin zone were calculated with the GGA and HSE06 hybrid functions.18–20 The infrared absorption spectra of crystals were obtained by using the original crystal structure and involved the strict optimization of geometric structures. In this case, the criteria for ion step convergence were stricter than those of ordinary geometric structural optimization, as follows: an energy of 2.0 × 10−6 eV per atom, a max.force of 0.002 eV A−1, a max.stress of 0.004 GPa, and a max.displacement of 2.0 × 10−4 A. The other convergence criteria were consistent with the convergence criteria used during geometric structure optimization.
For In32−xSnxO48, all calculations focused on the In2O3 structure when x = 0. Calculation was implemented in accordance with the above methods. When x = 1, 2, 3, the calculation focused on the ITO structure with different Sn doping ratios. Doping processing was performed with the disorder script (See Appendix – Disorder script) by using the optimized In2O3 as the input structure. After doping, another geometric structural optimization was conducted on the structure added with Sn. As a result of heavy doping, the doping ratio of Sn was high, and the point O was ignored during calculation.21 Sn atoms were added into defect-free crystals to simulate In2O3 with different point defects caused by various doping ratios.22 The dominant crystals of In32−xSnxO48 containing 80 atoms had two Wyckoff sites of 8b and 24d. A total of 32 configurations existed when x = 1. Two different configurations were obtained after simplification. When x = 2, 496 configurations were present, and 18 different configurations were identified after simplification. When x = 3, 4312 configurations were present, and 100 different configurations were identified after simplification. The single-point energy of different configurations when x = 1, 2, 3 was calculated. The three structures with the lowest single-point energy among all structures were identified for the optimization of geometric structures. Symmetry was not added during the geometric optimization of all configurations to avoid reducing symmetry. In accordance with the geometric optimization results, the structure with the lowest and the most stable energy among all structures was chosen as the final structure. The calculation method for ITO was consistent with that for In2O3.
2.2 Preparation and performance characterization of ITO silkscreen printing ink
In accordance with the calculation results, ITO nanodispersion liquid with the corresponding doping ratios were mixed with the same medium green camouflage coating (L = 39.58, a = −6.37, b = 17.01) at the ITO solid contents of 10%, 20%, and 30%. They were mixed mechanically for 1 h in a SDF400 laboratory multipurpose dispersion sand mill at the rate of 400 rpm. An appropriate amount of retarder (mass ratio of isohexadiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water = 1
water = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and thickener (mass ratio of PMA
1) and thickener (mass ratio of PMA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M240
M240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O = 1
H2O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were added to the coating in the uniform dispersion. The solution was adjusted to the state appropriate for silkscreen printing. The ITO silkscreen printing ink was prepared in this manner. The prepared ink was printed onto the surface of high-strength polyester fabric by using a customized scraper and 80-, 120-, and 200-mesh screen printing plates. The fabric was held still until the ink film dried and then dried in a drying oven at 50 °C for 1 h. The optical chromatic value and color difference of the ink film were tested with an UltraScan Pro spectrophotometer. The emissivity of the ink film at 8–14 μm was measured by using an IR-2 double-band emissivity meter.
1) were added to the coating in the uniform dispersion. The solution was adjusted to the state appropriate for silkscreen printing. The ITO silkscreen printing ink was prepared in this manner. The prepared ink was printed onto the surface of high-strength polyester fabric by using a customized scraper and 80-, 120-, and 200-mesh screen printing plates. The fabric was held still until the ink film dried and then dried in a drying oven at 50 °C for 1 h. The optical chromatic value and color difference of the ink film were tested with an UltraScan Pro spectrophotometer. The emissivity of the ink film at 8–14 μm was measured by using an IR-2 double-band emissivity meter.
3. Results and discussion
3.1 First principle theory calculation results
 | ||
| Fig. 1 Crystal structure of In32−xSnxO48 with (a) In2O3; (b) In31Sn1O48; (c) In30Sn2O48 and (d) In29Sn3O48. | ||
When x = 1, one Sn4+ replaces one In3+ site, and crystal distortion occurs when Sn is introduced into the In2O3 crystal; Sn4+ is prone to entering b+ sites with a low degree of distortion.23,24 Given the high doping content of Sn, the crystal structure remains unchanged. When x = 2, 3, the crystal structure of ITO remains consistent with that of c-ITO, as has been proved by calculations.25 ITO after geometric structural optimization at x = 1, 2, 3 is shown in Fig. 1(b)–(d), wherein the lake blue atoms are Sn atoms added into the In2O3 crystal.
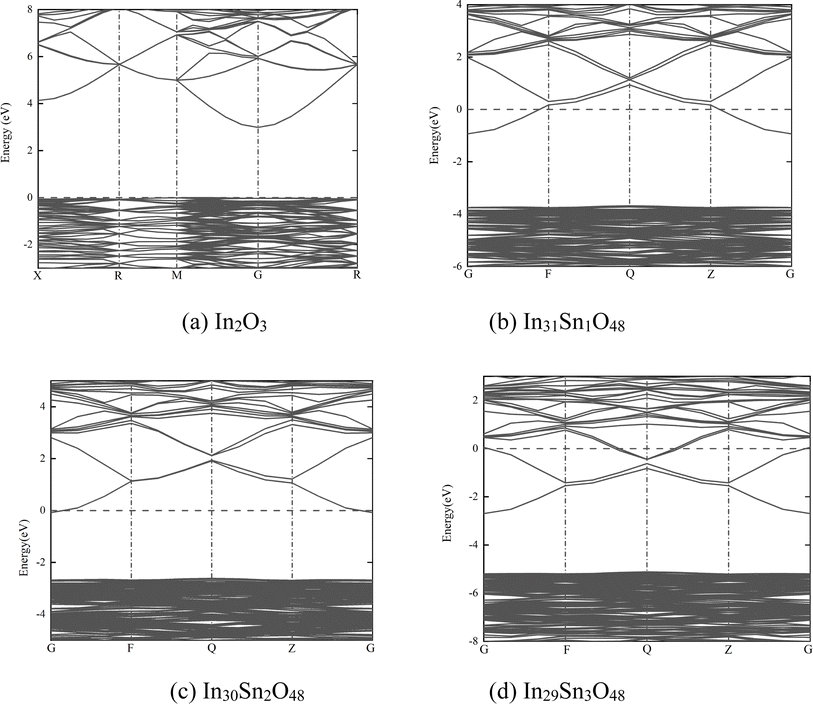 | ||
| Fig. 2 Band structure of In32−xSnxO48 with (a) In2O3; (b) In31Sn1O48; (c) In30Sn2O48 and (d) In29Sn3O48. | ||
In Fig. 2, the dotted line with the energy of 0 represents the Fermi level. The HSE06 hybrid function was applied for calculation before Sn doping. The energy band gap of In2O3 is the direct band gap and has a value of 2.985 eV. After doping with Sn at different ratios, the energy band structure of ITO negligibly changes. With the increase in doping ratio, the Fermi level moves deeply into the conduction band, whereas the optical band gap expands gradually. The maximum optical energy gap exceeds 4 eV when x = 3, which can guarantee the transparency of the whole visible spectra. The expansion width of the optical band gap could be interpreted in accordance with Burstein–Moss mobility theory.26
The high-valence Sn4+ in ITO replaces the In3+ site, thus increasing carrier concentration. The Fermi level enters the conduction band completely or partially. Some energy levels at the bottom of the conduction band are occupied by electrons. Therefore, electrons can only jump from a position in the valence band to the lowest energy state of the conduction band that has not been occupied by electrons. In other words, the effective optical energy gap of samples widens, thus making the practical absorption spectra move toward the short-wave direction. However, the electron wave function of impurity atoms exhibit considerable overlaps with the continuous increase in Sn content. The energy level of isolated impurities expands into an energy band that connects to the bottom of the conduction band to form a new degenerate conduction band with the tail extending into the forbidden band. This phenomenon narrows the original forbidden band.
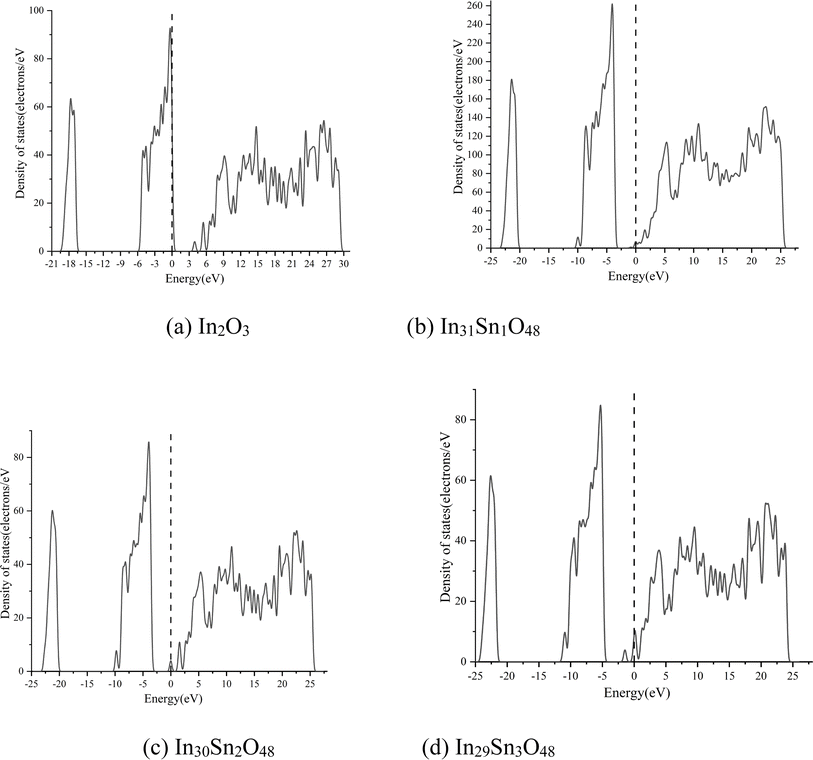
The macroscopic electrical properties of materials are mainly decided by the properties of the electrons near the Fermi surface. When x > 0, the Fermi level enters the conduction band, indicating that free electrons are present near the Fermi level. With the increase in doping ratio, the Fermi level increases gradually, as can be proven by the calculated state density (Fig. 3, wherein the dotted line with the energy of 0 is the Fermi level). The high Fermi level indicates the strong electrical conductivity of ITO. When x = 3, the Fermi level enters the conduction band deeply and is far from the bottom of the conduction band. Electrons near the Fermi level can only jump among dense energy levels in the conduction band but undergo forbidden transition among forbidden bands. All of these phenomena are similar to metal characteristics and may account for the low emissivity of ITO in the infrared band.
The real part of the dielectric function expresses polarization caused by external electromagnetic field and characterizes the contributions of media to light adsorption. The virtual part expresses media dissipation in the electric field. They are the most fundamental optical properties, and other properties can be calculated from the dielectric function. The calculation formulas for reflectivity R(ω), absorption coefficient α(ω), and electron energy loss function L(ω) are shown as eqn (1)–(3), respectively.
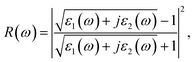 | (1) |
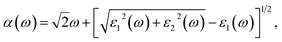 | (2) |
| L(ω) = ε2(ω)/[ε12(ω) + ε22(ω)]. | (3) |
The optical properties of In32−xSnxO48 obtained through calculation are shown in Fig. 4, wherein the x-axis has been transformed into wavelength (nm).
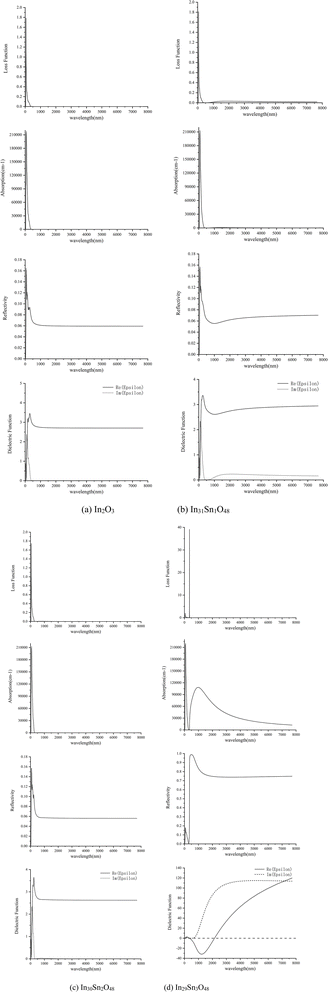 | ||
| Fig. 4 Optical properties of In32−xSnxO48 with (a) In2O3; (b) In31Sn1O48; (c) In30Sn2O48 and (d) In29Sn3O48. | ||
Fig. 4 shows that when x = 1, 2, the optical properties of In32−xSnxO48 change slightly relative to those of In2O3. When x = 3, Sn concentration increases and provides additional free electrons. Therefore, ITO becomes a high-density free electron gas material because it has a high concentration of free carriers, and its response to the electromagnetic field of light (light field) is closely related to the frequency of the light field (wavelength).27 At low frequencies, free electrons in each half cycle of the alternating light field are impacted in accelerating mode several times by the electric field along a direction. Such polarized free electron gas provides a strong shielding effect against the electromagnetism of the light field. Therefore, materials have strong reflectivity (R) in the low-frequency infrared zone. When the light frequency increases to the plasma frequency (ωp), the inertia of electrons cannot follow the light field of high-frequency changes. Such plasma electrons have weak absorption and reflectivity in the light field, thus making the material enter the transparency zone.
When the light frequency further increases to the intrinsic excitation absorption frequency (ωg), photons have sufficient energy to make the bound electrons of the material jump from the intrinsic band to the excitation state and become free electrons. The absorption of shortwaves with light frequency higher than ωg has strengthened dramatically, whereas the transmittance (T) and reflectivity (R) of these shortwaves have weakened considerably.
The wavelength corresponding to the plasma frequency (ωp) is the plasma wavelength (λp) and that corresponding to the intrinsic excitation (absorption) frequency (ωg) is the intrinsic excitation wavelength (λg). The former is the starting point for materials to enter the high infrared reflection (λ > λp) region and also the turning point for materials to enter the low absorption and high reflection regions gradually (λ < λp). The latter is the turning point for ITO material to enter the high absorption region (λ < λg). Fig. 4 shows that for ITO, λp ≈ 1200 nm and λg ≈ 303 nm. The λg–λp range of ITO covers the visible light band and guarantees the transmission of ITO materials in the visible light band. Moreover, the ITO material has strong absorption in the ultraviolet region and strong reflectivity in the infrared region.
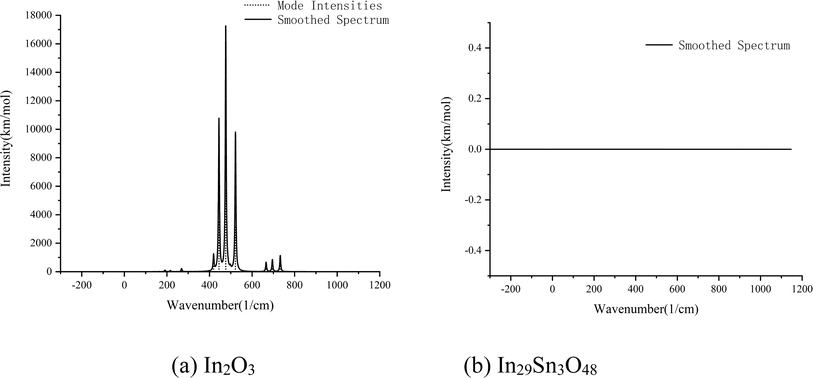
The spectral absorption characteristics of In2O3 and In29Sn3O48 in the waveband ranges of 111.50–769.90 and 104.05–742.54 cm−1, respectively, were calculated in accordance with first principle theory (Fig. 5). In2O3 has strong infrared adsorption at 444.38, 476.3, and 522.1 cm−1, whereas In29Sn3O48 has almost 0 absorption in the whole infrared waveband. Kirchhoff's radiation law states that the reflectivity and absorptivity of any object on a wavelength, an angle, and a polarization direction are equal under the balanced state.28 The calculation results in Fig. 5 confirm that ITO has low emissivity in the far infrared band.
3.2 Optical and infrared performances of ITO silkscreen printing ink
Color difference (ΔE) was used to characterize the color deviation degree between the ink film and standard color. ΔE ≤ 3 is usually required. The color difference formula in the CIE1976L*a*b* colorimeter system was applied to evaluate the optical camouflage performances of ITO ink. The formula for calculating color difference is29
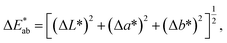 | (4) |
ITO screen printing ink was prepared in accordance with the method presented in Section 2.2. Its chromatic value and reflectivity at 8–14 μm are listed in Table 1.
| Num. | Mesh count | Solid content of ITO | L | a | b | ΔL | Δa | Δb | E (8–14 μm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 80 | 0 | 39.06 | −8.79 | 15.23 | 0.07 | 0.25 | −0.14 | 0.921 |
| 2 | 120 | 0 | 38.94 | −9.07 | 15.42 | −0.05 | −0.03 | 0.05 | 0.939 |
| 3 | 200 | 0 | 38.82 | −8.91 | 15.37 | −0.17 | 0.13 | 0.00 | 0.938 |
| 4 | 80 | 10% | 38.73 | −8.96 | 14.33 | −0.26 | 0.08 | −1.04 | 0.773 |
| 5 | 120 | 10% | 38.72 | −8.88 | 14.23 | −0.27 | 0.16 | −1.14 | 0.782 |
| 6 | 200 | 10% | 38.63 | −8.69 | 14.19 | −0.36 | 0.35 | −1.18 | 0.789 |
| 7 | 80 | 20% | 39.69 | −7.77 | 13.96 | 0.70 | 1.27 | −1.41 | 0.742 |
| 8 | 120 | 20% | 38.14 | −8.82 | 14.39 | −0.85 | 0.22 | −0.98 | 0.744 |
| 9 | 200 | 20% | 38.39 | −8.54 | 14.57 | −0.60 | 0.50 | −0.80 | 0.757 |
| 10 | 80 | 30% | 37.64 | −8.51 | 12.29 | −1.35 | 0.53 | −3.08 | 0.763 |
| 11 | 120 | 30% | 37.62 | −8.60 | 12.43 | −1.37 | 0.44 | −2.94 | 0.779 |
| 12 | 200 | 30% | 37.68 | −8.74 | 12.66 | −1.31 | 0.30 | −2.71 | 0.793 |
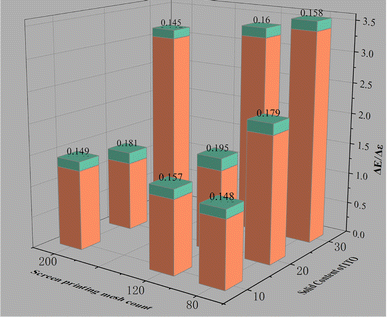
The above calculation results show that ITO and ITO film have low emissivities within the wavelength range of 8–14 μm.30,31 The data in Table 1 show that the emissivity of the prepared ITO ink is not excessively low likely due to the following two aspects: first, the ink is compatible with optical properties. The emissivity of the paint for optical camouflage is high, and adding ITO can reduce system emissivity. Meanwhile, obtaining the emissivity of ITO itself is difficult. Second, the physical and mechanical properties of the connection material should receive attention, and realizing complete infrared transparency is impossible. This study focuses on how ITO affects the optical camouflage performance of optical paints and reduction in infrared emissivity. The color differences between the ITO ink and medium green as well as the emissivity difference at 8–14 μm were calculated in accordance with the data in Table 1 and plotted in Fig. 6. After ITO ink was printed onto the surface of high-strength polyester fabric through 80-, 120-, and 200-mesh screen printing plates, the color difference with medium green is controlled within 3, and the emissivity reduction exceeds 0.13. The emissivity of the original medium green (L = 39.58, a = −6.37, b = 17.01) has decreased by one level. To summarize, the prepared ITO ink can be used as an optically compatible infrared camouflage ink.
4. Conclusions
The geometric structure of In2O3 that contains 80 atoms is first optimized on the basis of first principle theory. For the optimized dominant crystal In32−xSnxO48, different amounts of Sn atoms (x = 1, 2, 3) are added to the defect-free crystal to simulate ITO with different doping ratios of Sn atoms (3.125%, 6.25%, and 9.375%). The energy band structures, optical properties, and infrared absorption spectra of the crystal when x = 0, 1, 2, 3 are obtained. The results show that ITO retains its transparency in the waveband range of 303–1200 nm when x = 3 (Sn atom doping ratio of 9.375%). Moreover, it has strong absorptivity for the short waveband (wavelength < 303 nm) or ultraviolet band. It has high reflectivity for the long waveband (wavelength > 1200 nm) or infrared waveband. In accordance with calculation results, ITO with a Sn doping ratio of 9.375% is selected to prepare ink. ITO nanodispersion liquid (9.375%) is mixed with medium green optical camouflage coating to prepare ITO silkscreen printing ink for fabrics through modification. Later, the ink layer is prepared by coating the ITO ink onto the surface of high-strength polyester fabric through silkscreen printing. The experimental results show that the ink film can reduce the emissivity of the far infrared waveband at 8–14 μm by more than 0.13 without changing the optical properties of the medium green camouflage coating in the visible waveband.On the basis of the fundamental material structure, this study interprets the camouflage mechanism of ITO in different wavebands through the calculation results of first principle theory from the perspective of quantum mechanics. Furthermore, the camouflage mechanism of ITO is verified by coating the prepared ink onto the surface of fabric. The results of this research can guide the applications of ITO in the field of camouflage. Future studies will explore how to further decrease the emissivity of ITO ink and develop other colors of ITO ink.
Author contributions
Conceptualization: Feifei Xiao and Weidong Xu. Data curation: Feifei Xiao, Bentian Hao, and Haibao Yu. Methodology: Feifei Xiao and Heng Liu. Resources: Heng Liu and Hao Li. Writing – original draft: Feifei Xiao; writing – review & editing: Feifei Xiao and Weidong Xu.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This research was funded by “Development and Engineering Application of Multispectral Compatible Camouflage Materials” (grant number 62122062205).References
- L. Wang, Y. Yang and X. Tang, et al., Combined multi-band infrared camouflage and thermal management via a simple multilayer structure design, Opt. Lett., 2021, 46(20), 5224–5227 CrossRef CAS PubMed.
- H. Zhu, Q. Li and C. Tao, et al., Multispectral camouflage for infrared, visible, lasers and microwave with radiative cooling, Nat. Commun., 2021, 12(1), 1805 CrossRef CAS PubMed.
- G. Liang, Y. Xiao and J. Zhang, et al., Optimizing the emissivity regulation performance of a multilayer adaptive infrared camouflage structure based on transport ability control of an ionic liquid, Appl. Surf. Sci., 2023, 614, 156145 CrossRef CAS.
- G. C. Ispas, V. Raditoiu and A. Raditoiu, et al., Colored coating materials with spectrally selective reflectance for woodland camouflage textile fabrics, Proceedings, 2019, 29(1), 61 Search PubMed.
- J. Yu and Z. Y. Hu, Study on Tent Cloth Materials for Desert Type Camouflage, Adv. Mater. Res., 2012, 590, 134–137 Search PubMed.
- F. Bollino and M. Catauro, Sol-Gel Technology to Prepare Advanced Coatings, Photoenergy and Thin Film Materials, 2019, pp. 321–378 Search PubMed.
- M. Wegener, D. Eckert and A. Roosen, Manufacture of sub-μm thin, particulate-based ITO layers by roller coating, J. Eur. Ceram. Soc., 2015, 35(8), 2321–2332 CrossRef CAS.
- Z. Chen, X. Qin and T. Zhou, et al., Ethanolamine-assisted synthesis of size-controlled indium tin oxide nanoinks for low temperature solution deposited transparent conductive films, J. Mater. Chem. C, 2015, 3(43), 11464–11470 RSC.
- T. ChonanH. KunoFine particles of antimony tin oxide for sunscreen, dispersion thereof for sunscreen material formation, sunscreen material and transparent base material for sunscreenAU Pat., 2003246172A, 2004 Search PubMed.
- J. Xu, J. B. Liu and B. X. Liu, et al., Design of n-type transparent conducting oxides: the case of transition metal doping in In2O3, Adv. Electron. Mater., 2018, 4(3), 1700553 CrossRef.
- C. Freysoldt, B. Grabowski and T. Hickel, et al., First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86(1), 253 CrossRef.
- S. J. Clark, M. D. Segall and C. J. Pickard, et al., First principles methods using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220(5–6), 567–570 CrossRef CAS.
- P. Wisesa, K. A. McGill and T. Mueller, Efficient generation of generalized Monkhorst-Pack grids through the use of informatics, Phys. Rev. B, 2016, 93(15), 155109 CrossRef.
- R. Kingsbury, A. S. Gupta and C. J. Bartel, et al., Performance comparison of r2SCAN and SCAN metaGGA density functionals for solid materials via an automated, high-throughput computational workflow, Phys. Rev. Mater., 2022, 6(1), 013801 CrossRef CAS.
- J. P. Perdew, J. A. Chevary and S. H. Vosko, et al., Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671 CrossRef CAS.
- S. Grimme, J. Antony and S. Ehrlich, et al., A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- D. R. Hamann, M. Schlüter and C. Chiang, Norm-conserving pseudopotentials, Phys. Rev. Lett., 1979, 43(20), 1494 CrossRef CAS.
- R. R. Pela, M. Marques and L. K. Teles, Comparing LDA-1/2, HSE03, HSE06 and G0W0 approaches for band gap calculations of alloys, J. Phys.: Condens. Matter, 2015, 27(50), 505502 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- I. Hamberg and C. G. Granqvist, Evaporated Sn-doped In2O3 films: basic optical properties and applications to energy-efficient windows, J. Appl. Phys., 1986, 60(11), R123–R160 CrossRef CAS.
- A. I. Cocemasov, V. I. Brinzari and D. L. Nika, Energetic, structural and electronic features of Sn-, Ga-, O-based defect complexes in cubic In2O3, J. Phys.: Condens. Matter, 2020, 32(22), 225703 CrossRef CAS.
- G. B. González, et al., Neutron diffraction study on the defect structure of indium-tin-oxide, J. Appl. Phys., 2001, 89(5), 2550–2555 CrossRef.
- N. Nadaud, N. Lequeux and M. Nanot, et al., Structural studies of tin-doped indium oxide (ITO) and In4Sn3O12, J. Solid State Chem., 1998, 135(1), 140–148 CrossRef CAS.
- N. Balasubramanian and A. Subrahmanyam, Electrical and optical properties of reactively evaporated indium tin oxide (ITO) films-dependence on substrate temperature and tin concentration, J. Phys. D: Appl. Phys., 1989, 22(1), 206 CrossRef CAS.
- A. Klein, C. Körber and A. Wachau, et al., Transparent conducting oxides for photovoltaics: manipulation of Fermi level, work function and energy band alignment, Materials, 2010, 3(11), 4892–4914 CrossRef CAS.
- A. Klein, C. Körber and A. Wachau, et al., Transparent Conducting Oxides for Photovoltaics: Manipulation of Fermi Level, Work Function and Energy Band Alignment, Materials, 2010, 3, 1–2 CrossRef PubMed.
- F. C. Zhang, Z. Y. Zhang and W. H. Zhang, et al., The first-principle calculation of electronic structure and optical properties of In2O3, Acta Chim. Sin., 2008, 66(16), 1863 CAS.
- J. J. Greffet, P. Bouchon and G. Brucoli, et al., Generalized Kirchhoff law, arXiv, 2016, preprint, arXiv:1601.00312, DOI:10.48550/arXiv.1601.00312.
- W. S. Mokrzycki and M. Tatol, Colour difference ΔE-A survey, Mach. Graph. Vis., 2011, 20(4), 383–411 Search PubMed.
- S. C. Dixon, D. O. Scanlon and C. J. Carmalt, et al., n-Type doped transparent conducting binary oxides: an overview, J. Mater. Chem. C, 2016, 4(29), 6946–6961 RSC.
- A. S. A. C. Diniz, The effects of various annealing regimes on the microstructure and physical properties of ITO (In2O3:Sn) thin films deposited by electron beam evaporation for solar energy applications, Renewable Energy, 2011, 36(4), 1153–1165 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02784a |
| This journal is © The Royal Society of Chemistry 2024 |