Open Access Article
Open Access ArticleExploring the multifaceted properties: electronic, magnetic, Curie temperature, elastic, thermal, and thermoelectric characteristics of gadolinium-filled PtSb3 skutterudite
Poorva Nayak and
Dinesh C. Gupta
and
Dinesh C. Gupta *
*
Condensed Matter Theory Group, School of Studies in Physics, Jiwaji University, Gwalior 474 011, India. E-mail: poorvanayak11@gmail.com; sosfizix@gmail.com
First published on 29th May 2024
Abstract
The investigation of binary and filled skutterudite structures, particularly PtSb3 and GdPt4Sb12, has gained significant attention, becoming a focal point in scientific research. This comprehensive report delves into the intrinsic characteristics of these structures using Density Functional Theory (DFT). Initially, we assess the structural stability of PtSb3 and GdPt4Sb12 by examining their total ground state energy and cohesive energy, employing the Brich Murnaghan equation of state to determine stability in various configurations. Further insights are gained by exploring second-order elastic constants (SOEC's) to extend our understanding of structural stability. The electronic structures are then meticulously defined through a quantum mechanical treatment, employing a combination of two distinct spin-polarized approximation schemes: Perdew–Burke–Ernzerhof Generalised Gradient Approximation (PBE-GGA) and Tran–Blaha modified Becke–Johnson (TB-mBJ). The resulting band structures reveal a symmetry in electronic behavior, showcasing spin-magnetic moments of 3 μB and 7.58 μB per formula unit, with the primary contributions emanating from the Pt 3d and Pt4+ 3d-transition elements. To gauge thermal stability, we evaluate the phonon-dependent Grüneisen parameter (γ) across specific temperature ranges. The study extends to exploring transport properties as a function of chemical potential (μ − EF) at various temperatures. The findings suggest that these designed materials hold substantial potential for diverse applications, particularly in conventional spin-based and thermoelectric technologies. The comprehensive insights obtained through this investigation pave the way for a deeper understanding and broader implications in various technological domains.
1. Introduction
Thermoelectric materials have revolutionized the way we think about energy conversion; with the ability to convert temperature gradients into productive electric energy, making them ideal for sustainable technologies. These materials offer reliable, pollution-free, and enduring solutions for power generation, refrigeration, and temperature control.1,2 However, the widespread commercialization of these materials is hindered by the low energy-conversion efficiency they offer. To overcome this challenge, we need to focus on the properties of thermoelectric materials. The figure of merit, zT = S2σT/κ, is a critical tool used to evaluate the performance of thermoelectric devices. The evaluation considers the Seebeck coefficient, electrical conductivity, and total thermal conductivity and is conducted at the absolute temperature, T. By improving the properties of thermoelectric materials, we can unlock their full potential and make them viable options for sustainable technologies.The zT, a crucial metric for thermoelectric efficiency, is intricately tied to the electronic and crystallographic characteristics of materials. Achieving optimal performance involves a comprehensive approach, delving into intrinsic properties derived from atomic structures and extrinsic effects related to the morphology of polycrystalline materials.3–6 In the 90s, theoretical studies delineated the key parameters influencing the electrical performance of thermoelectric materials.7 Concepts like the density of states, band degeneracy, and effective mass have gained significance for their correlation with the Seebeck coefficient and electrical conductivity, playing pivotal roles in enhancing these properties.8–12 Consequently, strategies employing band engineering, especially band convergence, have been extensively explored for thermoelectric efficiency improvements, evident in systems like PbTe13–15 and Mg2Si.16–18 Analyzing electronic band changes in terms of crystallographic structure provides valuable insights into the connection between lattice bonding interactions and electronic parameters. This exploration guides the selection of suitable dopants and substitutions to achieve desired outcomes.19
There is a notable resurgence of interest in thermoelectrics, driven by the availability of new materials and emerging needs. Among these materials, the skutterudite system has garnered attention. Iridium triantimonide (IrSb3), a semiconducting compound with the skutterudite or CoAs3 structure, stands out in this group.20–25 This material meets the essential criteria for achieving high zT, including a large unit cell, heavy constituent atom masses, and substantial carrier mobility, as outlined by Slack.26,27 Preliminary studies suggest that IrSb3 holds promise as a potential thermoelectric material.20,28 Skutterudites, characterized by their unique structure, feature sizable voids that can be filled or doped to manipulate thermal conductivity. However, comprehensive experimental studies on skutterudite properties have only recently been initiated.20,29,30 Additionally, band structure calculations by Singh and Pickett indicate that CoSb3, CoAs3, and IrSb3 are narrow-gap semiconductors, adding further insights into the potential of these materials.31
The binary skutterudites exhibit a cubic Im3 (Th5) structure, following the AB3 format, where A signifies a metal atom and B represents a pnicogen atom. The cubic unit cell accommodates eight formula units, and the structure includes two large voids per unit cell. Skutterudites establish covalent structures characterized by low coordination numbers for the constituent atoms, allowing the incorporation of additional atoms into these voids. Utilizing X-ray crystallographic data, we have computed the void radii for nine binary semiconducting skutterudite compounds.20,23,32,33 The B atom's radius (rB) is determined as half of the average B–B separation. The vacancy radius is then calculated as the distance (d) from the center of the void to any one of the twelve surrounding B atoms, minus r(B).
| r(vacancy) = d − r(B) |
Filled skutterudites, denoted as TM4B12, have been synthesized.34–46 In these structures, the voids, originally surrounded by pnicogen atoms (B) in the unfilled configuration, are now occupied by T, typically a rare-earth element. The composition includes M as the transition metal (Fe, Os, or Ru) and B as the pnicogen (P, As, or Sb). Remarkably, substantial X-ray thermal parameters have been noted for the filler atoms within these filled skutterudite structures.34,35,38,42
This study involves the formulation of a set of PtSb3 and RPt4Sb12-filled skutterudite, incorporating diverse filler (R = Gd). The thermoelectric properties of these materials were systematically measured across the temperature range of 300 to 900 K. The research includes a comprehensive assessment and discussion, focusing on the impact of these fillers on both the crystal structure and thermoelectric properties of the materials.
2. Material design approch
At the atomic scale, the computational methodology for studying systems, whether molecules or solids, has found extensive applications, particularly in data analysis to establish a foundation for experimental outcomes. In this study, we employed the WIEN2k simulation package,47 incorporating the linearized augmented plane wave (FP-LAPW) method48 to compute various fundamental properties of the PtSb3 and GdPt4Sb12 skutterudite system.The simulation process for these compounds was initiated with the application of the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA).49 Within the GGA formalism, the exchange correlation (Exc) is defined as the derivative of the local charge density and its associated gradient. However, GGA encounters challenges in accurately interpreting the electronic structure of systems containing d/f electrons. This limitation arises from the self-interaction of the electron and insufficient potential for highly localized states, resulting in reported errors of approximately 20–30% in previous studies.50 Consequently, a supplementary method is required to enhance precision in expressing the properties of such systems.
To address this, we adopted the TB-mBJ51 method, known for its reliability, simplicity, and ab initio nature, providing a more accurate treatment of highly correlated d/f electron systems within the framework of density functional theory (DFT). Within DFT, the FP-LAPW method defines the crystal space of PtSb3 and GdPt4Sb12 into non-overlapping muffin tin (MT) spheres and an interstitial region subjected to a plane-wave basis set for eigenvalue convergence. The linearized augmented plane-wave basis set, with lmax = 10 and KmaxRMT = 7 (where Kmax denotes the highest possible k-value and RMT is the radius of the smallest sphere), was employed for non-overlapping atomic spheres to ensure charge and energy convergence.
The Fourier series expansion of charge density and potential within the interstitial region was performed with a wave vector up to Gmax = 12 a.u−1. A tetrahedral method, coupled with a dense k-mesh of 2000 k-points following the Monkhorst and Pack convention scheme, was utilized. A threshold energy of −6.0 Ry was chosen between core and valence states for accurate self-consistent calculations, with convergence tolerances set at 10−4 e for charge and 10−4 Ry for energy. Subsequently, the mechanical behavior of the compounds was analyzed using the cubic-elastic package,52 while the thermoelectric response was explored through the semi-classical Boltzmann theory embedded in the BoltzTraP code.53 Finally, thermal properties were assessed using the Gibbs2 (ref. 54) package in conjunction with the WIEN2k code.
3. Result and discussion
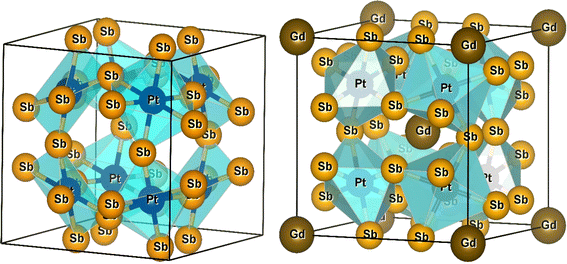
3.1 Crystalline structure of CoSb3 and RT4X12
As discussed earlier, the atomic positions of the transition metals and filled Gd atoms remain fixed. However, to achieve convergence of atomic forces to the order of 1 mRy a.u.−1, a relaxation process was applied to the atomic positions of the Pnictogen atoms within the unit cell structure. This relaxation resulted in the determination of coordinates (0, y, z) for the Pnictogen atoms. The unit cell structures of PtSb3 and GdPt4Sb12 are illustrated in Fig. 1. Within binary skutterudites PtSb3, the transition metal is situated at the Wyckoff position 8c (0.25, 0.25, 0.25), while Pnictogen atoms occupy the 24 g (0, y, z) site. It is imperative to determine the values for coordinates y and z to facilitate the relaxation of atomic positions within the unit cell. Notably, binary skutterudites feature two voids at the Wyckoff position 2a (0, 0, 0). In the context of Gd-filled skutterudites GdPt4Sb12, the Gd atom is positioned at the void Wyckoff position 2a (0, 0, 0), with the transition metal occupying the same Wyckoff position 8c (0.25, 0.25, 0.25). Simultaneously, Pnictogen atoms are located at the 24 g (0, y, z) site. The determination of coordinates y and z becomes crucial for the relaxation of atomic positions within the unit cell in this scenario as well. The optimized values of the y and z coordinates for Pnictogen atoms in both binary skutterudite PtSb3 and ternary skutterudite GdPt4Sb12 are presented in Table 1. Additionally, the table provides detailed information on the obtained lattice constants (a0) and bulk moduli (B0) corresponding to the equilibrium unit cell volume (V0). The lattice constants represent the dimensions of the unit cell, providing insights into the crystal structure and spacing of atoms within the material. The bulk modulus quantifies the material's resistance to uniform compression, indicating its ability to withstand changes in volume under applied pressure. These parameters are crucial for understanding the structural stability and mechanical properties of the compounds. Furthermore, the table includes the energy of formation and cohesive energy for all the compounds, offering valuable insights into their stability and bonding characteristics. The energy of formation represents the energy change accompanying the formation of a compound from its constituent elements, providing information about the compound's thermodynamic stability. On the other hand, cohesive energy measures the energy required to separate the atoms within a compound into isolated atoms, reflecting the strength of chemical bonds and interatomic interactions. These parameters are essential for predicting material stability, chemical reactivity, and potential applications in various fields, including catalysis, materials science, and solid-state chemistry. Overall, the comprehensive information presented in the table enhances our understanding of the structural, mechanical, and thermodynamic properties of the compounds, facilitating further exploration and potential applications in diverse scientific and technological domains. The optimization of structural parameters was conducted under zero pressure conditions, utilizing the generalized gradient approximation GGA-PBE for calculating total energy. The computations encompassed both ferromagnetic (FM) and non-magnetic (NM) states within two cubic structures PtSb3 and GdPt4Sb12. The total energy values, dependent on cell volume for our compound, were fitted to Birch–Murnaghan's equation of states55,56 and graphically represented in Fig. 2. It is evident from the results that the ferromagnetic (FM) configuration within the PtSb3 and GdPt4Sb12 structure exhibits lower energy, establishing its energetic preference over the other configurations.| Materials | Phase | a | V | B | B′ | E0 | Ecoh | EFor |
|---|---|---|---|---|---|---|---|---|
| PtSb3 | FM | 0.786 | 0.24 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348.17 348.17 |
5.0 | −4123206.52 | 3.0 | −0.18 |
| NM | 0.786 | 0.86 | 1737.91 | 5.0 | −4123188.30 | |||
| GdPt4Sb12 | FM | 0.769 | 0.42 | 84.62 | 5.0 | −2871263.28 | 2.6 | −0.62 |
| NM | 0.769 | 0.41 | 100.70 | 5.0 | −2871261.38 |
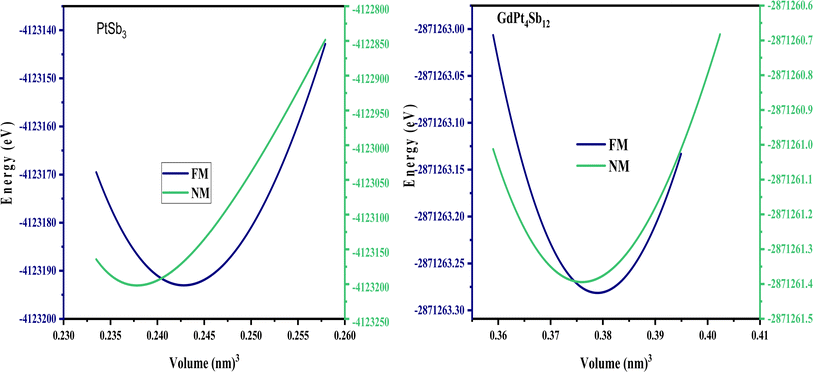 | ||
| Fig. 2 Optimizing the ground state of PtSb3 and GdPt4Sb12 compounds in ferromagnetic and non-ferromagnetic structural configurations. | ||
3.2 Electronic properties
Examining the energy band structure of materials is crucial for gaining deeper insights into their properties before considering them for potential technological uses. Consequently, the dispersion of electronic energy bands is employed to classify materials into categories such as insulators, semiconductors, semi-metals, and metals. To analyze the electronic characteristics of PtSb3 and GdPt4Sb12, we computed their band structures and density of states (DOS) using various exchange–correlation schemes. In this ongoing study, we have specifically applied the PBE-GGA and TB-mBJ approximations to predict the electronic properties of the PtSb3 and GdPt4Sb12 compounds. The electronic properties of the materials were analyzed by computing the band structure and Density of States (DOS) using both Generalized Gradient Approximation (GGA) and GGA + mBJ. Fig. 3 present the metallic band characteristics of the unfilled and filled skutterudites for both spin channels. The overlapping valence band (above the Fermi level) and conduction band (below the Fermi level) in both materials indicate their metallic nature. Even with the use of the mBJ potential, there is no observable shift in energy levels from the Fermi level in both materials, emphasizing their metallic character. The absence of a forbidden gap in both approaches further confirms their metallic nature. Fig. 4 and 5 illustrates the total density of states, highlighting the variation in the electronic profile with the incorporation of the mBJ potential. The metallic nature is evident in this representation as well. To delve deeper into the band formation and Fermi level occupancy, the projected density of states (pDOS) was executed, as depicted in Fig. 5 and 6. The pDOS of PtSb3 and GdPt4Sb12 reveals a strong hybridization of Gd-f and Sb-p states, occupying the Fermi level and contributing to the metallic behavior in both spin states. Additionally, the partial density of states emphasizes that Sb-p and Gd-f states are predominant in these materials, while the low-lying states mainly consist of sharp peaks from Pt-d states.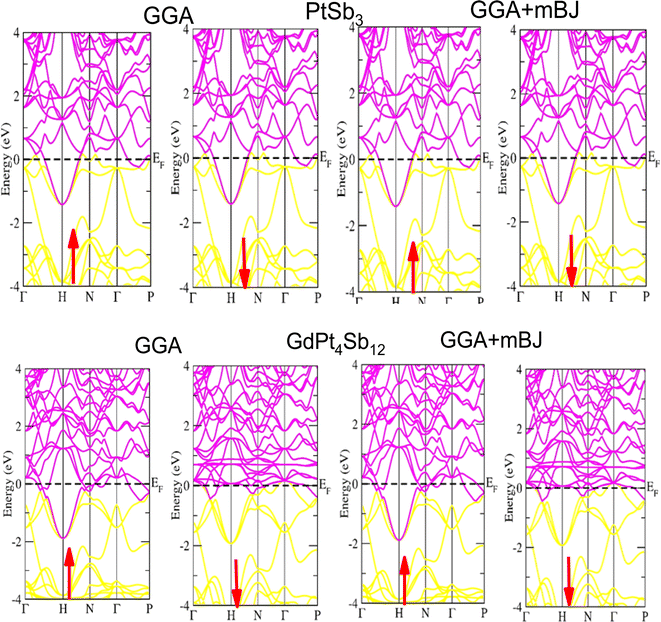 | ||
| Fig. 3 Performing DFT calculations, band profiles of PtSb3 and GdPt4Sb12 within GGA, and GGA + mBJ are presented, with arrows indicating potential spin-up and spin-down orientations. | ||
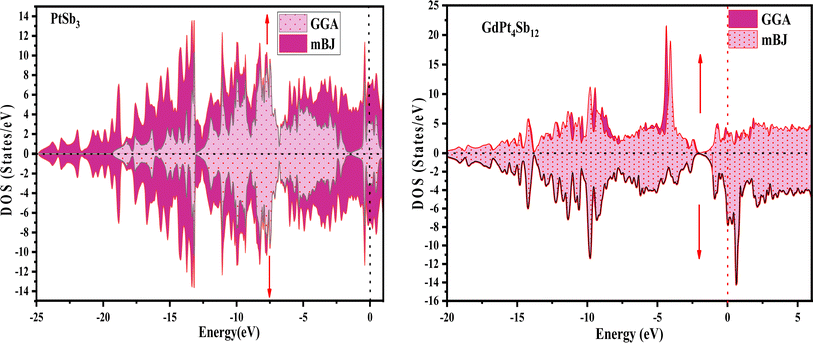 | ||
| Fig. 4 Spin-polarized total density of states (DOS) for PtSb3 and GdPt4Sb12 skutterudite is depicted in GGA and GGA + mBJ calculations. | ||
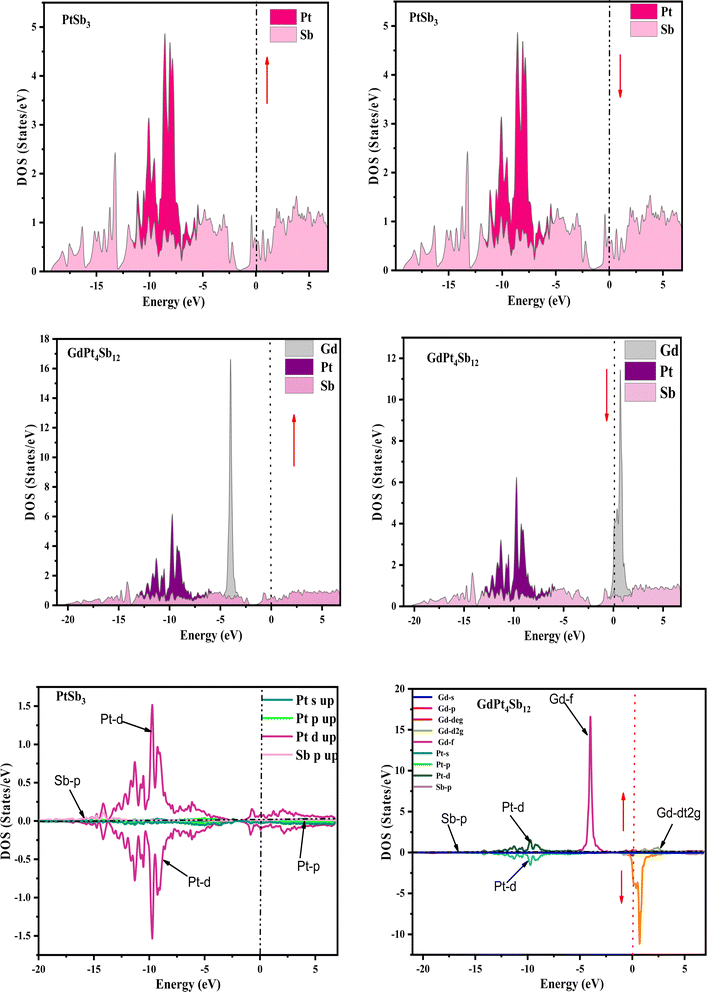 | ||
| Fig. 5 Spin-polarized atomic and partial density of states (pDOS) for PtSb3 and GdPt4Sb12 are illustrated using the GGA + mBJ potential scheme, where zero on the x-axis denotes the Fermi-level (EF). | ||
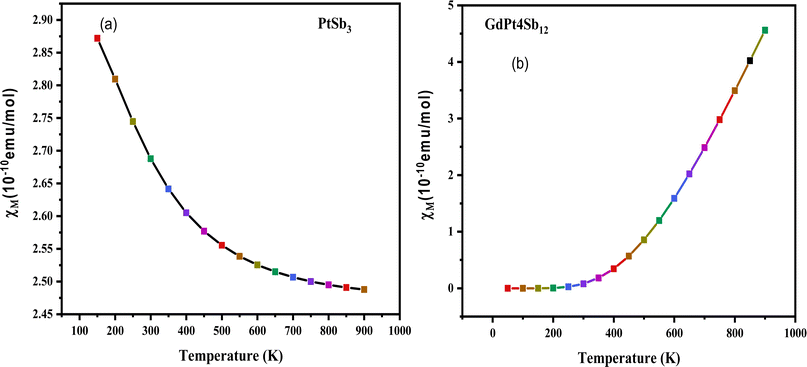 | ||
| Fig. 6 Temperature dependence of magnetic susceptibility (χ) for (a) PtSb3 and (b) GdPt4Sb12 compound. | ||
3.3 Magnetism
In this exploration of magnetism, the focus is on understanding how the electronic structure and arrangement of electrons in molecular orbitals influence magnetic properties. Two exchange–correlation approximations, namely Generalized Gradient Approximation (GGA) and GGA + mBJ, are utilized for this study. The aim is to develop a detailed understanding of the interactions between different components within compounds, allowing for a comprehensive explanation of their magnetic behavior. The magnetic moment per formula unit is calculated to be 3.00 and 7.58 μB for PtSb3 and GdPt4Sb12, respectively. These values closely match previously reported magnetic moments for similar compounds like SmFe4Sb12 and GdFe4P12, which were 4.88 and 6.80 μB, as per a ref. 57. This consistency indicates the reliability of the findings. In these material systems, the contribution of f-electrons is found to be significant in determining their overall magnetic nature. The positive values obtained for the magnetic moment of various atoms suggest a parallel alignment of spins, indicating a ferromagnetic (FM) interaction. This alignment implies that the spins tend to align in the same direction, thereby enhancing the overall magnetism of the materials. The observed high spin polarization and substantial magnetism in these compounds make them promising candidates for applications in emerging spin-based technologies. This suggests that these materials have potential applications in advanced technological fields that rely on magnetic properties, highlighting their importance in future technological advancements. To analyze the magnetism of these representative-filled skutterudites, we conducted through studies using the Wien2k simulation software. The analysis employed the GGA, and GGA+mBJ, functional schemes, as shown in Table 2.| Material | Methods | Curie temperature | |
|---|---|---|---|
| GGA | GGA + mBJ | ||
| PtSb3 | 2.5 | 3.00 | 518 |
| GdPt4Sb12 | 6.29 | 7.58 | 537 |
The validation of the ferromagnetic ground state, as established through structural optimization plots, is further substantiated by an in-depth examination of the magnetic susceptibility (χ) in the cubic structure of PtSb3 and GdPt4Sb12 compounds. Adhering to the Curie–Weiss law,71 which describes the behavior of paramagnetic materials at high temperatures, a positive Curie–Weiss constant indicates the presence of ferromagnetic interactions, while a negative value suggests antiferromagnetic interactions. Fig. 6(a) and (b) depict graphical representations of the magnetic susceptibility, showcasing the temperature-dependent behavior of these materials. The calculated Curie–Weiss constant values for PtSb3 and GdPt4Sb12 are determined to be 100 K and 150 K, respectively. These positive Curie–Weiss constant values, significantly exceeding zero, serve as strong evidence supporting the ferromagnetic ground state of the investigated compounds. The graphical representations in Fig. 6(a) and (b) highlight the variations in magnetic susceptibility with temperature for PtSb3 and GdPt4Sb12 compounds, offering valuable insights into their magnetic properties and behavior across different temperature regimes. This detailed analysis further solidifies our understanding of the magnetic behavior of these materials and underscores their potential applications in various fields, including spintronics, magnetic data storage, and magnetic sensing.
3.4 Curie temperature
The determination of the Curie temperature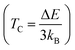 for the compounds under investigation involves utilizing a specific equation derived from the Heisenberg model, as detailed in ref. 58 and 59. This equation incorporates the energy difference (ΔE) between the non-magnetic and ferromagnetic states of the materials. For both PtSb3 and GdPt4Sb12 substances, ΔE is calculated as the difference between the total energy of the non-magnetic state (ENM) and the total energy of the ferromagnetic state (EFM). The inclusion of the Boltzmann constant (kB) in this equation is crucial, as it relates the energy difference to temperature. The Curie temperature (TC) is defined as ΔE/3kB, where ΔE represents the energy barrier that must be overcome for the transition from the non-magnetic to the ferromagnetic state to occur. At the Curie temperature, the thermal energy available becomes sufficient to disrupt the ferromagnetic alignment of magnetic moments within the material. Therefore, the difference in total energies (ΔE) between the non-magnetic and ferromagnetic states serves as a crucial parameter for determining TC. It provides insights into the temperature at which the material's magnetic properties are expected to change and helps in understanding the thermal energy required to influence the magnetic behavior of these substances. Based on these calculations, the predicted Curie temperature values are found to be 518 K and 537 K for PtSb3 and GdPt4Sb12, respectively. It's noteworthy that these assessed TC values are lower than room temperature, indicating the suitability of these compounds for applications that require operation at lower temperatures. This information is valuable for understanding the thermal behavior and potential applications of these materials, particularly in contexts where controlled magnetic properties are essential. In Table 2, estimated values of the Curie temperature (TC) are provided.
for the compounds under investigation involves utilizing a specific equation derived from the Heisenberg model, as detailed in ref. 58 and 59. This equation incorporates the energy difference (ΔE) between the non-magnetic and ferromagnetic states of the materials. For both PtSb3 and GdPt4Sb12 substances, ΔE is calculated as the difference between the total energy of the non-magnetic state (ENM) and the total energy of the ferromagnetic state (EFM). The inclusion of the Boltzmann constant (kB) in this equation is crucial, as it relates the energy difference to temperature. The Curie temperature (TC) is defined as ΔE/3kB, where ΔE represents the energy barrier that must be overcome for the transition from the non-magnetic to the ferromagnetic state to occur. At the Curie temperature, the thermal energy available becomes sufficient to disrupt the ferromagnetic alignment of magnetic moments within the material. Therefore, the difference in total energies (ΔE) between the non-magnetic and ferromagnetic states serves as a crucial parameter for determining TC. It provides insights into the temperature at which the material's magnetic properties are expected to change and helps in understanding the thermal energy required to influence the magnetic behavior of these substances. Based on these calculations, the predicted Curie temperature values are found to be 518 K and 537 K for PtSb3 and GdPt4Sb12, respectively. It's noteworthy that these assessed TC values are lower than room temperature, indicating the suitability of these compounds for applications that require operation at lower temperatures. This information is valuable for understanding the thermal behavior and potential applications of these materials, particularly in contexts where controlled magnetic properties are essential. In Table 2, estimated values of the Curie temperature (TC) are provided.
3.5 Mechanical properties
The study of elastic properties delves into understanding how materials respond to mechanical stresses and deformations. It's a captivating field that offers profound insights into various material characteristics, impacting disciplines like physics, chemistry, and materials science. Elastic properties influence critical material attributes such as specific heat capacity, melting point, and equation of state, underscoring their significance in diverse scientific domains. One of the key parameters in understanding elastic properties is the elasticity modulus. This modulus provides valuable information about the strength of atomic bonding within a crystal lattice, thereby determining the material's resistance to deformation. Essentially, it tells us how much force is needed to deform the material. Additionally, an analysis of elastic constants allows us to uncover the crystal's anisotropy, which refers to the directional dependence of material properties. In cubic crystals, which possess a high degree of symmetry, three independent elastic constants—C11, C12, and C44—are typically used to describe the elastic behavior of the system.60 These constants capture the response of the crystal to different types of stress and strain. By employing Voigt–Reuss–Hill's approximations, which are methods used to estimate bulk and shear moduli, we can derive essential material properties such as bulk modulus (B) and shear modulus (G). The bulk modulus represents the material's resistance to volume changes under pressure, while the shear modulus describes its resistance to shape deformation caused by shear stress. Understanding these moduli provides valuable insights into the mechanical behavior of materials under various conditions. It enables researchers to predict how materials will respond to external forces and tailor their properties for specific applications. Overall, the study of elastic properties enriches our comprehension of material behavior and enhances our ability to design and engineer advanced materials with desired functionalities.
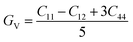 | (1) |
The Reuss approximation is a fundamental concept in the study of elastic properties of materials, particularly in the context of determining bulk and shear moduli. This approximation assumes ideal conditions where the material is considered perfectly homogeneous, meaning that its properties are uniform throughout its structure. Additionally, it assumes perfect bonding between each constituent material within the structure. When applying the Reuss approximation, it is assumed that the material behaves as if it were composed of many small identical regions, each with identical properties. In this idealized scenario, the material responds uniformly to external stresses, and there are no defects or irregularities in its structure. The assumption of perfect bonding between constituents implies that there is no relative motion or slippage between atoms or molecules within the material. This assumption is particularly relevant when considering the response of materials to shear stress, as shear deformation involves the relative displacement of adjacent planes of atoms.61
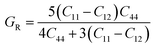 | (2) |
Hill's62 theoretical expression for the shear modulus in polycrystalline materials is a significant contribution to our understanding of material behavior, particularly in heterogeneous structures composed of multiple crystalline grains. This expression takes into account the elastic properties of individual grains, as well as their orientation and distribution within the material. In polycrystalline materials, each grain possesses its own set of elastic properties due to variations in crystallographic orientation, defects, and local microstructure. Hill's model considers these individual grain properties and their arrangement within the material to predict the overall mechanical behavior. By incorporating information about grain size, shape, and orientation distribution, Hill's model provides a more comprehensive understanding of how polycrystalline materials respond to external loads. This is particularly relevant in practical applications where materials experience complex loading conditions. The shear modulus, a key parameter in Hill's model, quantifies the material's resistance to deformation under shear stress. It reflects the material's ability to maintain its shape when subjected to parallel forces acting in opposite directions. Understanding the shear modulus is crucial for engineers and materials scientists as it directly influences material performance in various applications, such as structural design, manufacturing processes, and material selection. By accurately predicting the shear modulus using Hill's model, researchers can optimize material properties and design materials with enhanced mechanical strength and durability. Overall, Hill's theoretical expression for the shear modulus has become a widely used tool in the field of materials science and engineering, enabling researchers to predict and analyze the mechanical behavior of polycrystalline materials with greater accuracy and reliability.
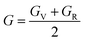 | (3) |
In the case of a cubic crystal, when the pressure (P) is 0 GPa, the relationship between the bulk elastic modulus and the elastic constants is detailed in ref. 63.
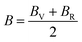 | (4) |
The mechanical stability criteria for cubic crystals are dictated by the following conditions, as outlined in ref. 64.
| C11 − C12 > 0; C44 > 0; +2C12 > 0 | (5) |
The research presented in Table 3 is a testament to the power of scientific exploration. Using GGA-PBE, we can unravel the multifaceted properties of PtSb3 and GdPt4Sb12 at zero temperature and zero pressure. The calculated values of crystal constants, bulk modulus, elastic constants, and shear modulus, provide crucial insights into the behavior of these compounds. By comparing our findings with prior research, we can appreciate the remarkable consistency and reliability of scientific investigations. This study is an inspiration to all those who seek to unlock the secrets of the universe through rigorous experimentation and analysis.
| Parameter | C11 | C12 | C44 | C′′ | B | Y | B/G | ν | A | θD | Tm |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PtSb3 | 180.07 | 30 | 68.25 | −38.25 | 80.02 | 164.18 | 1.12 | 0.15 | 0.90 | 385 | 2326 |
| GdPt4Sb12 | 300 | 95.25 | 120.86 | −26.61 | 163.5 | 275.70 | 1.44 | 0.21 | 1.18 | 458 | 1616 |
| GdFe4P12 (ref. 69) | 328.00 | 59.98 | 115.81 | — | 149.02 | 289.21 | — | 0.17 | 0.87 | — | |
| GdRu4P12 (ref. 69) | 337.23 | 96.37 | 128.05 | — | 176.66 | 303.42 | — | 0.21 | 1.06 | — | |
| GdOs4P12 (ref. 69) | 368.97 | 104.52 | 136.21 | — | 192.67 | 327.57 | — | 0.22 | 1.03 | — |
Following Pugh's criteria for crystal mechanical behavior, the bulk modulus-to-shear modulus (B/G) ratio65,66 serves as a key indicator, with high values suggesting material extensibility and low values indicating brittleness, with a critical threshold set at 1.75. In the case of PtSb3 and GdPt4Sb12 compounds, calculations yield B/G values of 1.12 and 1.44 at zero temperature and pressure, respectively, surpassing the critical threshold. Consequently, both materials demonstrate characteristics of good brittleness, implying they are more prone to fracture or failure under applied stresses that induce shape deformation rather than volume compression. This assessment provides crucial insights into the mechanical behavior of PtSb3 and GdPt4Sb12, aiding in their classification and understanding of their response to external loading conditions.
The anisotropy factor expressed as A = 2C44/(C11 − C12), plays a crucial role in assessing material anisotropy, with a value of 1 indicating complete isotropy and other values suggesting varying degrees of anisotropic behavior. For PtSb3 and GdPt4Sb12 compounds, the calculated anisotropy factors are reported as 0.9 and 1.18, respectively, utilizing a specific method. These values affirm the anisotropic nature of both materials, indicating that their mechanical properties exhibit directional dependence. Such an assessment is essential for understanding how these materials behave under different loading conditions and for designing components or structures where the directional variability of material properties must be considered for optimal performance.
The Debye temperature is determined by employing the average sound velocity, denoted as νm.
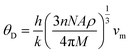 | (6) |
The velocity νm is defined as the average of the transverse velocity (νt) and the longitudinal velocity (νl), and it is expressed by the following equation:
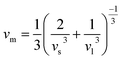 | (7) |
In our study, we determined the Debye temperature (θD) values for PtSb3 and GdPt4Sb12 by evaluating essential parameters, resulting in 385 K and 458 K, respectively. This determination is crucial as the Debye temperature reflects the characteristic vibrational energy of atoms in a solid material, providing insights into its thermal behavior. Interestingly, we observed an increasing trend in θD as Gd is incorporated into the PtSb3 structure, suggesting alterations in the lattice dynamics and atomic vibrations due to the presence of Gd. To further explore the thermal characteristics of these materials, we employed Fine's relation, utilizing the elastic constant C11 to estimate their respective melting temperatures. This approach offers valuable insights into the temperature-dependent behavior of PtSb3 and GdPt4Sb12, shedding light on their thermal properties and potential applications in various fields, such as thermoelectrics or high-temperature materials.
| Tm (K) = [553 + (5.911) C11] ± 300 K | (8) |
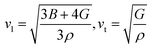 | (9) |
To delve into the mechanical properties, we conducted calculations of sound phase velocities for both longitudinal and transverse modes based on elastic constants. In cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 204m symmetry, only three directions of elastic waves exist [111], [110], and [100].68 Waves traveling in other directions exhibit quasi-transverse or longitudinal characteristics. Additionally, we determined the average velocity or Debye velocity (νD) using the following relation:
204m symmetry, only three directions of elastic waves exist [111], [110], and [100].68 Waves traveling in other directions exhibit quasi-transverse or longitudinal characteristics. Additionally, we determined the average velocity or Debye velocity (νD) using the following relation:
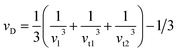 | (10) |
This exploration into sound velocities and Debye velocity not only provides insights into the mechanical behavior of PtSb3 and GdPt4Sb12 but also hints at their stability across different temperature conditions.
The tabulated results of all computed phase velocities are presented in Table 4 for reference and public dissemination.
| Planes | Sound velocities | PtSb3 | GdPt4Sb12 |
|---|---|---|---|
| [100] | νl = √C11/ρ | 3295.01 | 3970.56 |
| νt1 = √C44/ρ | 1326.23 | 1465.02 | |
| νt2 = √C44/ρ | 1326.85 | 1465.23 | |
| νD | 1855.20 | 2065.74 | |
| [110] | νl = √C11 + C12 + C44/2ρ | 3052.01 | 3590.91 |
| νt1 = √C11 – C12/ρ | 2538.38 | 2652.20 | |
| νt2 = √C44/ρ | 2537.51 | 2652.44 | |
| νD | 2730.80 | 2931.21 | |
| [111] | νl = √C11 + 2C12 + 4C44/3ρ | 2821.00 | 3027.00 |
| νt1 = √C11 – C12 + C44/3ρ | 1532.34 | 2018.54 | |
| νt2 = √C11 – C12 + C44/3ρ | 1520.45 | 2018.69 | |
| νD | 1858.90 | 2436.01 |
3.6 Thermoelectric properties
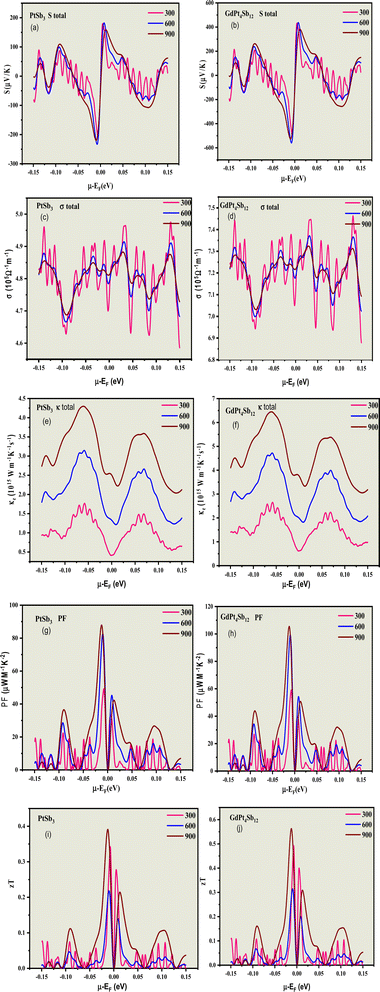
The transport properties are determined by employing the Boltzmann transport theory under the constant relaxation time approximation (with a fixed relaxation time of 5.9 × 10−15 s). This calculation is conducted irrespective of the compound and considers the spin effect of thermoelectrics. In simpler terms, we assess how materials conduct heat and electricity by using a theoretical framework that accounts for constant relaxation time and incorporates the impact of spin on thermoelectric properties. The constant relaxation time approximation relies on the assumption that electrical conductivity is primarily governed by relaxation time, which is believed to exhibit minimal variation within the energy scale of kBT. This implies that at the thermal energy scale (kBT), the behavior of electrical conductivity is considered relatively consistent. In simpler terms, we assume that the time it takes for a material to return to equilibrium after an applied electric field (relaxation time) plays a crucial role in determining electrical conductivity, and this relationship is assumed to hold across the energy scale of kBT. The impact of temperature on different transport coefficients and the power factor (PF) (S2σ) concerning the chemical potential (μ) has been thoroughly examined. This exploration delves into how temperature changes affect various factors governing the movement of charge carriers and contribute to the overall power factor, which is a key parameter in assessing the efficiency of thermoelectric materials. Understanding how the chemical potential behaves as temperature changes is crucial when choosing the right doping element to enhance the thermoelectric response. This consideration is significant in tailoring the properties of materials for optimal thermoelectric performance. By comprehending the relationship between chemical potential and temperature fluctuations, one can make informed decisions in the selection of doping elements, ultimately aiming to maximize the thermoelectric response of the material.
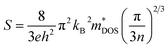 | (11) |
The Seebeck coefficient stands out as a crucial parameter for comprehending how a material responds to an applied temperature gradient. When considering the Seebeck coefficient about the chemical potential, it is negative for n-doped systems and positive for p-doped systems. The chemical potential serves as a defining factor for the doping level or carrier concentration in a material, playing a pivotal role in enhancing the thermoelectric properties of the material for practical applications.
It's essential to note that the magnitude of the charge carrier concentration associated with the chemical potential is contingent on the actual band structure. This aspect is not precisely predicted by single-particle Density Functional Theory (DFT) calculations. Despite the invaluable insights provided by DFT, it's important to acknowledge potential limitations in precisely predicting the charge carrier concentration based on the chemical potential due to the complexities inherent in the actual band structure of the material. The Seebeck coefficients (S) for the spin-up and spin-down states of the two considered compounds have been graphed against the chemical potential at three different temperatures, as illustrated in Fig. 7(a) and (b). Upon comparing these figures, a notable observation emerges: for both compounds in both the p-type and n-type regions.
This phenomenon can be explained by the significantly higher values of spin-down Density of States (DOSs) for all compounds in comparison to the spin-up DOSs near the Fermi level. In simpler terms, the increased Seebeck coefficient for carriers with a spin-down orientation is a consequence of the elevated spin-down DOS's relative to spin-up DOSs near the Fermi level. In the p-type region, GdPt4Sb12 exhibits a higher Seebeck coefficient than PtSb3 and GdPt4Sb12 for both spin-up and spin-down states, indicating an equal contribution of holes and electrons for GdPt4Sb12. Specifically, in the p-type region, the highest Seebeck coefficient for PtSb3 is 200 μV K−1, and GdPt4Sb12 with a peak value of 600 μV K−1. These results provide valuable insights into the distinctive thermoelectric properties of both compounds, particularly about spin orientation and doping.
In a parallel fashion, analogous trends in the characteristics of the Seebeck coefficient values emerge in the n-type region. The compounds exhibit a preference for low doping in this region as well. Notably, equal Seebeck coefficient values are attained in the n-type region compared to the p-type region, underscoring the prominence of n-type doping in these materials.
For the both spin-up and spin-down states in the n-type region, the maximal calculated Seebeck coefficient values are as follows: −300 μV K−1, and −600 μV K−1 for PtSb3 and GdPt4Sb12, respectively. The noteworthy high values of the Seebeck coefficient in our calculations can be attributed to the parabolic band structures resulting from the presence of Pt-3d states near the Fermi level (EF) with a high effective mass, a characteristic more pronounced in GdPt4Sb12. This insight provides a deeper understanding of the materials' thermoelectric behavior, particularly in the context of doping and spin orientation.
Fig. 7(e) and (f) illustrate the electronic thermal conductivity per relaxation time (κ/τ) versus chemical potential at a temperature of 300, 600, 900 K for both spin-up and spin-down states. In the p-type region, the materials exhibit a direct response to the chemical potential, with κ/τ sharply increasing as the chemical potential rises. The increase in κ/τ is notably higher for PtSb3 reaching a peak value of 4.5 × 1014 W m−1 K−1 s−1 (spin up & down), while GdPt4Sb12 achieves a maximum value of 7.0× 1014 W m−1 K−1 s−1 (spin up & down).
In the n-type region at 300 K, κ/τ exhibits a more significant response compared to the p-type region. Like the p-type region, there is an abrupt increase in κ/τ as the chemical potential rises in the n-type region for all materials, namely PtSb3, and GdPt4Sb12. These results provide valuable insights into the thermal conductivity characteristics of the materials, particularly under different temperature conditions and spin orientations.
Fig. 7(g) and (h) illustrate the chemical potential dependence of PF/τ for both spin-up and spin-down states of PtSb3 and GdPt4Sb12, presented in units of 1014 μW m−1 K−2. The PF/τ reaches its maximum in the chemical potential interval of [−0.15, 0.15 eV], establishing this range as critical for achieving high performance in alkaline-rare earth-based thermoelectric materials PtSb3 and GdPt4Sb12.
In the p-type region, PF/τ is negligible for chemical potentials close to −0.15 eV in all studied materials. This small value persists until the chemical potential reaches approximately −0.05 eV, after which PF starts to fluctuate. GdPt4Sb12 exhibits a higher PF/τ value than PtSb3. The highest PF values in the p-type region are observed for PtSb3, reaching 100 × 1014 μW m−1 K−2 (spin up & down). The maximum PF/τ for (spin up & down) in GdPt4Sb12 is 120 × 1014 μW m−1 K−2 (spin up & down). Similarly, in the n-type region, a comparable trend in PF/τ values is observed.
These efficiency measurements suggest that both compounds exhibit promising potential as TE materials, particularly at elevated temperatures. This information serves as a valuable guide for experimentalists in synthesizing and exploring these materials for practical thermoelectric applications.
3.7 Thermodynamic properties
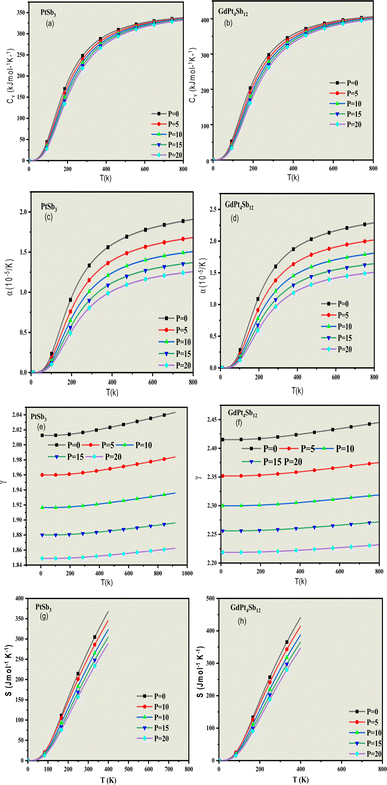
To assess and understand the influence of pressure and temperature characteristics, we have implemented a modified version of the quasi-harmonic approximation (QHA).70–72 This approach is employed to govern the importance of these factors on the materials in question. Unfortunately, there is a lack of existing results that demonstrate how these compounds behave under different and varying pressure and temperature conditions. Further investigation and experimentation are necessary to fill this knowledge gap and gain insights into the compounds' behavior across a range of environmental conditions. Hence, our investigation holds significance for experimentalists aiming to synthesize PtSb3 and GdPt4Sb12 compounds. Thermodynamic properties play a crucial role in establishing the material's carrier capability and establishing the cause-and-effect relationship between the dynamics and microstructure of the material.To precisely determine the temperature variation of thermodynamic properties, we consider the quantization of lattice vibrations. Our calculations focus on the deviation of heat capacity (Cv), Grüneisen parameter (γ), thermal expansion coefficient (α), and entropy (S) across a range of temperatures (0–800 K) and pressures (0–20 GPa). Heat capacity (Cv) is a critical metric indicating a material's ability to store heat as temperature changes. This parameter provides insights into various properties such as lattice vibration. As solids typically exhibit minimal volume changes with temperature, we present specific heat at constant volume (CV) in Fig. 8(a) and (b). The graph illustrates that CV increases with temperature, reflecting the rise in atomic vibrations. At higher temperatures, CV approaches a constant value, aligning with the Dulong and Petit limits.71 However, at lower temperatures, CV undergoes abrupt changes, adhering to the Debye T3 law. This comprehensive analysis sheds light on the intricate thermodynamic behavior of PtSb3 and GdPt4Sb12 compounds under diverse temperature and pressure conditions.
Thermal expansion (α) is the inherent tendency of matter to alter its shape, area, volume, and density in response to fluctuations in temperature. Fig. 8(c) and (d) provides a visual representation of this phenomenon concerning temperature and pressure variations for the skutterudite compounds under investigation. The graphical depiction reveals a distinct pattern in the thermal expansion coefficient (α). At lower temperatures, there is a noticeable and sharp increase in the (α) values. However, as the temperature rises, (α) gradually reaches a constant value, suggesting a stabilization in the material's response to temperature changes at higher temperature ranges. This graphical representation offers valuable insights into the thermal expansion characteristics of the present skutterudite compounds under different temperature and pressure conditions.
The Grüneisen parameter (γ) serves as a crucial indicator of thermo-mechanical properties, elucidating the connection between changes in volume for crystals and the frequency associated with phonons. It holds significant importance as a dynamical property that quantifies the relationship between the elastic and thermal descriptions of solids, establishing a direct connection between them. In the current context, the Grüneisen parameter (γ) exhibits an upward trend with increasing temperature. This indicates a progressive incline in its values as the temperature rises. Conversely, a noteworthy observation is the significant decrease in the Grüneisen parameter (γ) as pressure increases. This implies that, under varying pressure conditions, the Grüneisen parameter (γ) experiences a radical decline. To illustrate, the calculated values of the Grüneisen parameter at a pressure of 0 GPa and a temperature of 300 K for PtSb3 and GdPt4Sb12 are 2.02 and 2.43, respectively, as depicted in Fig. 8(e) and (f). This information provides valuable insights into how the Grüneisen parameter responds to temperature and pressure variations, contributing to a comprehensive understanding of the dynamic properties of the materials under investigation.
The entropy of a material provides crucial insights into its vibrational properties, playing a vital role in understanding various dispositions such as heat pumps, heat engines, and refrigerators. Fig. 8(g) and (h) illustrates the entropy at ambient conditions under fixed pressures. Examining the plots reveals a consistent increase in entropy from 0 K to 500 K. Furthermore, the entropy values obtained are noteworthy, with PtSb3 registering a value of 45.33 J mol−1 K−1 and GdPt4Sb12 showing 47.04 J mol−1 K−1 at ambient conditions. This implies that, at these conditions, PtSb3 exhibits a lower degree of order compared to GdPt4Sb12 Beyond the temperature of 400 K and 500 K, the extensive property of entropy experiences a considerable rise. This heightened value can be attributed to the increased vibrational entropy of the material as temperature rises. Interestingly, there is a subsequent declining trend with the increase in cohesive energy. These findings contribute significantly to our understanding of the dynamic behavior of the materials, particularly in relation to vibrational entropy and cohesive energy at varying temperatures.
4. Conclusion
In conclusion, our comprehensive exploration of rare-earth-based filled skutterudite, specifically PtSb3 and GdPt4Sb12, through the application of density functional theory has provided valuable insights into their electronic structures, establishing the foundation for further investigations. Our focus on assessing total ground state energies has ensured the structural stability of these compounds, while positive values obtained for second-order elastic constants and related mechanical parameters substantiate their ductile nature, suggesting potential applications in structural materials. Moreover, the examination of cohesive energies reinforces the extension of bond stability, augmenting their suitability for various engineering applications. Calibrated functionals, particularly in the context of exchange–correlation signatures, affirm their well-known metallic nature, providing a basis for understanding their electronic behavior. Additionally, the intrinsic magnetic character confirmed through band structures, certifying a significant magnetic moment, opens avenues for magnetic materials research and applications. Furthermore, the estimated values of the Seebeck coefficient (S) and the satisfactory figure of merit (zT) at different temperatures indicate their promising applicability in power technology and nanoengineering applications, suggesting their potential as thermoelectric materials for energy harvesting and conversion. These intriguing properties position specifically PtSb3 and GdPt4Sb12, as potential candidates in multifunctional or smart materials, paving the way for future advancements in material science and technology.Data availability
The computational work has been done by using the Wein 2K software package. Output data is available with the corresponding author. It will be provided to readers on a requirement basis.Author contributions
Poorva Nayak contributed to the theoretical investigation, analysis, and writing original draft, and Dinesh C. Gupta contributed to supervision, software, validation, review, editing, and modification. Both authors significantly contributed to the completion of this work. There is no funding received from anywhere for this research work.Conflicts of interest
All authors declare that no known financial or personal interest has been involved that may come forward at a later stage to influence the work reported in this manuscript.Acknowledgements
The authors would like to sincerely thank Jiwaji University Gwalior for providing the necessary facilities to conduct this research.References
- L. E. Bell, Cooling, heating, generating power, and recovering waste heat with thermoelectric systems, Science, 2008, 321(5895), 1457–1461 CrossRef CAS PubMed.
- E. Ghafari, F. Severgnini, S. Ghahari, Y. Feng, E. J. Lee, C. Zhang and Y. Chen, Thermoelectric nanocomposite for energy harvesting, Multifunctional Nanocomposites for Energy and Environmental Applications, 2018, vol. 1, pp. 173–202 Search PubMed.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7(2), 105–114 CrossRef CAS PubMed.
- X. Zhang and L. D. Zhao, Thermoelectric materials: Energy conversion between heat and electricity, J Materiomics, 2015, 1(2), 92–105 CrossRef CAS.
- J. He and T. M. Tritt, Advances in thermoelectric materials research: Looking back and moving forward, Sci., 2017, 357(6358), 9997 CrossRef PubMed.
- S. Twaha, J. Zhu, Y. Yan and B. Li, A comprehensive review of thermoelectric technology: Materials, applications, modeling, and performance improvement, Renewable Sustainable Energy Rev., 2016, 65, 698–726 CrossRef CAS.
- G. D. Mahan and J. O. Sofo, The best thermoelectric, Proc. Natl. Acad. Sci. U. S. A., 1996, 93(15), 7436–7439 CrossRef CAS PubMed.
- M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, Perspectives on thermoelectrics: from fundamentals to device applications, Energy Environ. Sci., 2012, 5(1), 5147–5162 RSC.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Compromise, and synergy in high-efficiency thermoelectric materials, Adv. Mater., 2017, 29(14), 1605884 CrossRef PubMed.
- E. Witkoske, X. Wang, M. Lundstrom, V. Askarpour and J. Maassen, Thermoelectric band engineering: The role of carrier scattering, J. Appl. Phys., 2017, 122(17), 5612–5645 CrossRef.
- J. Mao, Z. Liu, J. Zhou, H. Zhu, Q. Zhang, G. Chen and Z. Ren, Advances in thermoelectrics, J. Appl. Phys., 2018, 67(2), 69–147 Search PubMed.
- X. Su, P. Wei, H. Li, W. Liu, Y. Yan, P. Li and C. Uher, Multi-scale microstructural thermoelectric materials: transport behavior, non-equilibrium preparation, and applications, Adv. Mater., 2017, 29(20), 1602013 CrossRef PubMed.
- J. P. Heremans, B. Wiendlocha and A. M. Chamoire, Resonant levels in bulk thermoelectric semiconductors, Energy Environ. Sci., 2012, 5(2), 5510–5530 RSC.
- G. Tan, F. Shi, S. Hao, L. D. Zhao, H. Chi, X. Zhang and M. G. Kanatzidis, Non-equilibrium processing leads to a record high thermoelectric figure of merit in PbTe–SrTe, Nat. Commun., 2016, 7(1), 12167 CrossRef CAS PubMed.
- T. Fu, X. Yue, H. Wu, C. Fu, T. Zhu, X. Liu and X. Zhao, Enhanced thermoelectric performance of PbTe bulk materials with figure of merit zT> 2 by multi-functional alloying, J. Materiomics, 2016, 2(2), 141–149 CrossRef.
- W. Liu, X. Tan, K. Yin, H. Liu, X. Tang, J. Shi and C. Uher, Convergence of conduction bands as a means of enhancing the thermoelectric performance of n-type Mg2Si1− x Snx solid solutions, Phys. Rev. Lett., 2012, 108(16), 166601 CrossRef PubMed.
- J. Mao, H. S. Kim, J. Shuai, Z. Liu, R. He, U. Saparamadu and Z. Ren, Thermoelectric properties of materials near the band crossing line in Mg2Sn–Mg2Ge–Mg2Si system, Acta Mater., 2016, 103, 633–642 CrossRef CAS.
- H. Kamila, P. Sahu, A. Sankhla, M. Yasseri, H. N. Pham, T. Dasgupta and J. de Boor, Analyzing transport properties of p-type Mg 2 Si–Mg 2 Sn solid solutions: optimization of thermoelectric performance and insight into the electronic band structure, j. Mater. Chem. A, 2019, 7(3), 1045–1054 RSC.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Thinking like a chemist: intuition in thermoelectric materials, Angew. Chem., Int. Ed., 2016, 55(24), 6826–6841 CrossRef CAS PubMed.
- H. J. Goldsmid, Introduction to Thermoelectricity, Springer, Berlin, 2010, vol. 121, p. 46 Search PubMed.
- T. M. Tritt and V. M. Browning, Overview of measurement and characterization techniques for thermoelectric materials, Semicond. Semimetals, 2001, 69, 25–49 CAS.
- C. Wood, Materials for thermoelectric energy conversion, Rep. Prog. Phys., 1988, 51(4), 459 CrossRef CAS.
- G. A. Slack and V. G. Tsoukala, Some properties of semiconducting IrSb3, J. Appl. Phys., 1994, 76(3), 1665–1671 CrossRef CAS.
- A. Kjekshus and G. Pedersen, The crystal structures of IrAs3 and IrSb3, Acta Crystallogr., 1961, 14(10), 1065–1070 CrossRef CAS.
- N. N. Zhuravlev, X-ray Diffraction Determination of the Structure of CoSb3, RhSb3, and IrSb_3, Sov. Phys. Crystallogr., 1956, 15, 404–406 Search PubMed.
- V. V. Udalova and Z. G. Pinsker, Electron diffraction study of the structure of ammonium sulfate, Sov. Phys. Crystallogr., 1963, 8, 433 Search PubMed.
- A. Kjekshus, T. Rakke, S. Rundqvist, T. Østvold, A. Bjørseth and D. L. Powell, Compounds with the skutterudite-type crystal structure. III. structural data for arsenides and antimonides, Acta Chem. Scand., Ser. A, 1974, 28, 99–103 CrossRef CAS.
- A. R. N. E. Kjekshus, High-temperature x-ray study of the thermal expansion of IrAs3 and IrSb3, Acta Chem. Scand., 1961, 15(3), 678–681 CrossRef CAS.
- F. Hulliger, Halbleitende Verbindungen mit Skutterudit-Struktur, Helv. Phys. Acta, 1961, 34, 782 CAS.
- P. Nayak, P. Srivastava and D. C. Gupta, Theoretical exploration of inherent electronic, structural, mechanical, thermoelectric, and thermophysical response of KRu4Z12 (Z= As12, Sb 12) filled skutterudite materials, RSC Adv., 2023, 13(40), 27873–27886 RSC.
- R. Bruls, H. T. Hintzen and R. Metselaar, On the Debye temperature in the Slack approximation for an estimation of the thermal conductivity of non-metallic compounds, J. Appl. Phys., 2005, 98(12), 362 CrossRef.
- G. S. Nolas, G. A. Slack, T. Caillat and G. P. Meisner, Raman scattering study of antimony-based skutterudites, J. Appl. Phys., 1996, 79(5), 2622–2626 CrossRef CAS.
- D. T. Morelli, T. Caillat, J. P. Fleurial, A. Borshchevskv, J. Vandersande, B. Chen and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 9622 CrossRef CAS PubMed.
- J. W. Sharp, E. C. Jones, R. K. Williams, P. M. Martin and B. C. Sales, Thermoelectric properties of CoSb3 and related alloys, J. Appl. Phys., 1995, 78(2), 1013–1018 CrossRef CAS.
- J. Singh, N. Itoh, Y. Nakai, J. Kanasaki and A. Okano, Defect-excitation processes involved in laser-induced atomic emission and laser ablation of non-metallic solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(16), 11730 CrossRef CAS PubMed.
- T. Lundstrom and N. O. Ersson, Refinement of the crystal structure of hf 2 p, Acta Chem. Scand., 1968, 22(6), 1801–1808 CrossRef CAS.
- T. Schmidt, G. Kliche and H. D. Lutz, Structure refinement of skutterudite-type cobalt triantimonide, CoSb3, Acta Crystallogr., Sect. A, 1987, 43(9), 1678–1679 Search PubMed.
- L. E. DeLong and G. P. Meisner, The pressure dependence of the superconducting transition temperature of LaT4P12 (T= Fe, Ru, Os), J. Solid State Chem., 1985, 53(2), 119–123 CAS.
- D. J. Braun and W. Jeitschko, Preparation, and structural investigations of antimonides with the LaFe4P12 structure, J. Less-Common Met., 1980, 72(1), 147–156 CrossRef CAS.
- D. J. Braun and W. Jeitschko, Ternary arsenides with LaFe4P12-type structure, J. Solid State Chem., 1980, 32(3), 357–363 CrossRef CAS.
- W. Jeitschko and D. Braun, LaFe4P12 with filled CoAs3-type structure and isotypic lanthanoid–transition metal polyphosphates, Acta Crystallogr., Sect. A, 1977, 33(11), 3401–3406 CrossRef.
- C. B. Evers, W. Jeitschko, L. Boonk, D. J. Braun, T. Ebel and U. D. Scholz, Rare earth, and uranium transition metal pnictides with LaFe4P12 structure, J. Alloys Compd., 1995, 224(2), 184–189 CrossRef CAS.
- S. Zemni, D. Tranqui, P. Chaudouet, R. Madar and J. P. Senateur, Synthesis, and crystal structure of a new series of ternary phosphides in the systems TrCoP (Tr: rare earth), J. Solid State Chem., 1986, 65(1), 1–5 CrossRef CAS.
- D. J. Braun and W. Jeitschko, Thorium-containing pnictides with the LaFe4P12 structure, J. Less-Common Met., 1980, 76(1–2), 33–40 CrossRef CAS.
- N. T. Stetson, S. M. Kauzlarich and H. Hope, The synthesis, and structure of two filled skutterudite compounds: BaFe4Sb12 and BaRu4Sb12, J. Solid State Chem., 1991, 91(1), 140–147 CrossRef CAS.
- C. B. Evers, L. Boonk and W. Jeitschko, Alkaline Earth Transition Metal Antimonides AT4Sb12 (A= Ca, Sr, Ba; T= Fe, Ru, Os) with LaFe4P12-Structure, Adv. Inorg. Chem., 1994, 620(6), 1028–1032 CAS.
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Full-potential, linearized augmented plane wave programs for crystalline systems, Comput. Phys. Commun., 1990, 59(2), 399–415 CrossRef CAS.
- G. K. Madsen, P. Blaha, K. Schwarz, E. Sjöstedt and L. Nordström, Efficient linearization of the augmented plane-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(19), 195134 CrossRef.
- P. Kumari, C. Ashwathkumaran and V. Srivastava, DFT calculations on heat capacity and Debye temperature of Cs2GeF6 perovskite under high temperature and pressure, AIP Conf. Proc., 2023, 2800, 1 Search PubMed.
- S. A. Khandy and D. C. Gupta, New isostructural halide double perovskites Cs2GeNiX6 (X= Cl, Br) for semiconductor spintronics and thermoelectric advancements, J. Solid State Chem., 2021, 300, 122196 CrossRef CAS.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102(22), 226401 CrossRef PubMed.
- P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka and J. Luitz, wien2k: An augmented plane wave+ local orbitals program for calculating crystal properties, Karlheinz Schwarz (Austria): Techn. Universität Wien, 2001, vol. 60, 1, p. 70 Search PubMed.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- A. Otero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features, and implementation, Comput. Phys. Commun., 2011, 182(10), 2232–2248 CrossRef CAS.
- F. Birch, Phys. Rev., 1947, 71(11), 809 CrossRef CAS.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247 CrossRef CAS PubMed.
- W. Jeitschko, A. J. Foecker, D. Paschke, M. V. Dewalsky, C. B. Evers, B. Künnen and M. H. Möller, Crystal structure and properties of some filled and unfilled skutterudites: GdFe4P12, SmFe4P12, NdFe4As12, Eu0. 54Co4Sb12, Fe0. 5Ni0. 5P3, CoP3, and NiP3, Adv. Inorg. Chem., 2000, 626(5), 1112–1120 CAS.
- X. P. Wei, W. Sun, Y. L. Zhang, X. W. Sun, T. Song, T. Wang and X. F. Zhu, Investigations on electronic, Fermi surface, Curie temperature, and optical properties of Zr2CoAl, J. Solid State Chem., 2017, 247, 97–104 CrossRef CAS.
- P. L. Yan, J. M. Zhang, B. Zhou and K. W. Xu, The structural, electronic, magnetic, and mechanical properties of quaternary Heusler alloys ZrTiCrZ (Z= Al, Ga, In, Si, Ge, Sn): a first-principles study, J. Phys. D: Appl. Phys., 2016, 49(25), 255002 CrossRef.
- Z. L. Lv, H. L. Cui, H. Wang, X. H. Li and G. F. Ji, Electronic and elastic properties of BaLiF3 with pressure effects: First-principles study, Phys. Status Solidi B, 2016, 253(9), 1788–1794 CrossRef CAS.
- L. Li, Y. J. Wang, D. X. Liu, C. G. Ma, M. G. Brik, A. Suchocki and A. H. Reshak, Comparative first-principles calculations of the electronic, optical, elastic, and thermodynamic properties of XCaF3 (X= K, Rb, Cs) cubic perovskites, Mater. Chem. Phys., 2017, 188, 39–48 CrossRef CAS.
- N. Erum and M. A. Iqbal, First-principles investigation of fluorine-based strontium series of perovskites, Commun. Theor. Phys., 2016, 66(5), 571 CrossRef CAS.
- A. Moussali, M. B. Amina, B. Fassi, I. Ameri, M. Ameri and Y. Al-Douri, First-principles calculations to investigate structural and thermodynamic properties of Ni 2 LaZ (Z= As, Sb, and Bi) Heusler alloys, Indian J. Phys., 2020, 94, 1733–1747 CrossRef CAS.
- D. C. Wallace and H. Callen, Thermodynamics of crystals, Am. J. Phys., 1972, 40(11), 1718–1719 CrossRef.
- Z. Jin, Y. Wu, S. Li, Q. Wu, S. Chen, Y. Chen and C. Zhang, Electronic structure, elastic, optical and thermodynamic properties of cubic perovskite NaBaF3 with pressure effects: first-principles calculations, Results Phys., 2021, 22, 103860 CrossRef.
- S. Hadji, A. Bouhemadou, K. Haddadi, D. Cherrad, R. Khenata, S. Bin-Omran and Y. Al-Douri, Elastic, electronic, optical, and thermodynamic properties of Ba3Ca2Si2N6 semiconductor: First-principles predictions, Phys. Rev. B, 2020, 589, 412213 CrossRef CAS.
- T. M. Bhat, M. Nabi and D. C. Gupta, Electronic, elastic, and thermoelectric performance in n-type Sr-filled brittle skutterudite, Phys. Rev. B, 2020, 592, 412209 CrossRef CAS.
- R. L. Fleischer, D. M. Dimiduk and H. A. Lipsitt, Intermetallic compounds for strong high-temperature materials: status and potential, Annu. Rev. Mater. Sci., 1989, 19(1), 231–263 CrossRef CAS.
- S. Nautiyal, P. Yadav and U. P. Verma, Effect of filled Gd on structural, elastic, and electronic properties of skutterudite structure (TP3; T= Fe, Ru or Os) compounds: a first-principles study, J. Phys. Chem. Solids, 2019, 135, 109087 CrossRef CAS.
- A. Otero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features, and implementation, Comput. Phys. Commun., 2011, 182(10), 2232–2248 CrossRef CAS.
- F. Peng, H. Z. Fu and X. L. Cheng, First-principles calculations of thermodynamic properties of TiB2 at high pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 400(1–2), 83–87 CrossRef CAS.
- M. Y. Sofi and D. C. Gupta, Scrutinized the inherent spin half-metallicity and the thermoelectric response of f-electron-based RbMO3 (M= Np, Pu) perovskites: a computational assessment, Sci. Rep., 2022, 12(1), 19476 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |