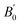Open Access Article
Open Access ArticleOrthorhombic lead-free hybrid perovskite CH3NH3SnI3 under strain: an ab initio study†
Amina Dendanea,
Benali Rerbal *a,
Tarik Ouahrani
*a,
Tarik Ouahrani bc,
Alejandro Molina-Sanchez
bc,
Alejandro Molina-Sanchez d,
Alfonso Muñoz
d,
Alfonso Muñoz e and
Daniel Errandonea
e and
Daniel Errandonea *f
*f
aLaboratory of Materials Discovery, Unit of Research Materials and Renewable Energies, LEPM-URMER, Université de Tlemcen, 13000 Algeria, Algeria. E-mail: ben.rerbal@gmail.com
bÉcole supérieure en sciences appliquées, ESSA-Tlemcen, BB 165 RP Bel Horizon, Tlemcen 13000, Algeria
cLaboratoire de Physique Théorique, Université de Tlemcen, BP 119, 13000, Algeria
dInstitute of Materials Science (ICMUV), University of Valencia, Catedrático Beltrán 2, E-46980 Valencia, Spain
eDepartamento de Física, MALTA-Consolider Team, Universidad de La Laguna, San Cristóbal de La Laguna, E38200 Tenerife, Spain
fDepartamento de Física Aplicada - Instituto de Ciencia de Materiales, Matter at High Pressure (MALTA) Consolider Team, Universidad de Valencia, Edificio de Investigación, C/Dr Moliner 50, Burjassot, 46100, Valencia, Spain. E-mail: daniel.errandonea@uv.es
First published on 20th June 2024
Abstract
We report a computational study where we explore the possibility of tuning the electronic properties of orthorhombic methylammonium tin iodide CH3NH3SnI3 using strains. According to our findings, a moderate [001] strain, smaller than 2%, would open the band gap up to 1.25 eV and enhance the exciton binding energy, opening up new possibilities for the use of CH3NH3SnI3 in technological applications. To better understand the impact of strain, we also examined its influence on bonding properties. The results reveal that the directional pnictogen and the hydrogen bonding are not altered by strains and that the tuning of the electronic properties is the result of changes induced in the orbital contributions to states near the Fermi level and the tilting of the SnI6 octahedral units.
Introduction
In recent years, the advent of perovskite solar cells based on hybrid halide perovskites has revolutionized the field of photovoltaic (PV) solar cells.1,2 In particular the synthesis3–5 of lead-free methylammonium tin iodide CH3NH3SnI3 opened new avenues for photovoltaic materials. To be efficiently used in PV applications, a semiconductor material should have a high light absorption (∼105 cm−1 for >1.4 eV).6,7 A low carrier recombination loss and an efficient carrier collection efficiency are also requisites, together with a long optical path to promote photon recycling.8 Recent experiments5 showed that CH3NH3SnI3 has a direct band gap of 1.2–1.3 eV. Thus, it would be beneficial to modify its band-gap energy to meet the ideal PV conditions. One possibility to modify the band-gap energy of hybrid perovskites is the application of external strain/stresses.9–11 In our case, we will focus on the orthorhombic structure (space group Pnma) which is observed at low temperatures below 200 K.12 Regarding the influence of strain in this structure, there are two important characteristics of CH3NH3SnI3. First, the methylammonium (MA) ion (CH3NH3)+ is an asymmetric and positively charged organic unit with a permanent dipole. Second, the low-temperature orthorhombic structure is formed by a framework of SnI6 corner-sharing octahedral framework. The MA molecules are within cages formed by six SnI6 octahedra. The interaction of the MA molecule with iodine atoms, forming and hydrogen bonding, induces a distortion of the SnI6 octahedra. Strains will affect both the MA molecule and the interaction with SnI6 units affecting therefore the physical properties of CH3NH3SnI3.Strain engineering is a very helpful technique for fine-tuning the electronic properties of materials by adjusting their band structure.13 It has been shown14 that hybrid perovskite crystals can be exposed to strains, which are usually created by deposition on substrates with a lattice mismatch with the hybrid perovskite.14 It is known that the strains should be small to not cause a non-periodicity on the crystal lattice and to avoid crystal instabilities.15 Thus, a careful balance is needed to achieve the desired outcomes when applying external stresses. Density-functional theory (DFT) calculations can be a very useful tool for deeply understanding the effects of strain in the properties of hybrid perovskites and for a rational design of composing multilayers including them.16 In this work, we have used DFT simulations to predict the most important properties of CH3NH3SnI3 and to explore how strains can be used for tailoring the band-gap energy of this compound. We will show that small controlled strains can modify the electronic in a way that could be beneficial for photoelectronic applications. In contrast with previous DFT studies,17–20 we will report the first study, in which by including van der Waals interactions, an accurate description of the crystal structure is provided and the dynamical stability of orthorhombic CH3NH3SnI3 is supported.21 The band-gap energy and exciton binding energies22,23 have been calculated under different strain conditions. We have found that a tensile [001] strain in the range of +2% is enough to open the band gap in ∼1.25 eV. Additionally, since lattice instabilities may result from changes in the bonding pattern, particularly from the hydrogen bonds in the methylammonium ion, we have characterized the strength of hydrogen bonds and other interactions using the non-covalent interactions (NCI) index.24 Previous to calculations under strain, we tested our method by performing calculations of mechanical, vibrational, and electronic properties of CH3NH3SnI3 at normal conditions. These results will also be reported for completeness.
Computational details
We have performed DFT calculations using the Vienna ab initio simulation package (VASP).26–28 The projector-augmented wave (PAW) scheme has been utilized.28 A kinetic energy cut-off of 700 eV was used for the plane-wave basis (see Fig. S1 in ESI† for the convergence test). We have employed the DFT-D2 weighted exchange potential of Perdew–Burke–Ernzerhof (PBE),29 which includes the van der Waals (vdW) dispersion as a correction to the ground state energy.30,31 Furthermore, since PBE tends to underestimate band-gap energy, we have used the modified Becke and Johnson (mBJ)32 and Heyd–Scuseria–Ernzerhof (HSE) hybrid density functional (HSE06)33 to calculate the electronic density of state (DOS) and the band structure. Additionally, Phonopy34 interfaced to VASP have been used to perform lattice-dynamics calculations.35 The direct force constant approach has been employed.36,37 We have used (2 × 2 × 2) supercells to obtain the phonon dispersion curves. The phonon density of states (PDOS) has been obtained by integrating the phonon frequencies with a large number of k-points (14 × 14 × 14 grid). The exciton binding energy (Eb) was estimated by the mean of the two-band model of Wannier–Mott.22,23 Additionally, because the effect of spin–orbit coupling (SOC) is significant for hybrid perovskite due to the presence of Sn atoms, we also checked the effect of SOC on the band gap value. This task was taken into account in the band structure calculations, using a second variational method.38 The binding energy of the first exciton is given by Eb = Rμ/m0ε∞2, where R is the Rydberg unit of energy, ε∞ is the macroscopic dielectric constant,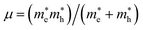 is the reduced mass of the electron and hole, and m0 is the electron rest mass.
is the reduced mass of the electron and hole, and m0 is the electron rest mass. 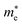 and
and 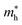 represent respectively the effective mass of the electron and hole.
represent respectively the effective mass of the electron and hole.
We have used the Non-covalent Interactions Index (NCI) as a descriptor39,40 to analyze the covalent and ionic bonding character. The NCI has been computed using the reduced density gradient of the electron density (ρ), where the density varies gradually. This characterization has been carried out within the parameters of QTAIM, which are specified by.41
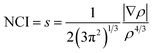 | (1) |
In the question, the parameter s is dimensionless, which is ensured by the 4/3 density exponent. Critical points of s(r) isosurfaces define their characteristics.39,40 The sign of the second eigenvalue of the Hessian (λ2) multiplied by the electron density of rho determines the significance of the NCI isosurface. If the outcome is negative, the isosurface is colored blue and the interactions are considered attractive. If it is positive, the corresponding domains are colored red and the interactions are deemed as repulsive. Weak interactions, such as hydrogen bonds or van der Waals interactions, are activated when (λ2) × ρ is close to zero, and the isosurfaces are shown in green.42
Results and discussion
Stability and mechanical properties of orthorhombic CH3NH3SnI3
We began our simulations with the geometry optimization of orthorhombic CH3NH3SnI3, including the dispersion forces (An overview of this structure is given in Fig. S2 of the ESI†). These interactions become increasingly important in systems with large and polarized electron clouds, such as organic molecules. For this reason, some difference is found between our lattice parameters and those previously calculated without dispersion corrections17–20 (see Table 1). On the other hand, our results are similar to recent results of ref. 17 conducted with the same approximation. The differences between both studies are related to the use of a smaller (400 eV cutoff energy in ref. 17. Our results show the best agreement with experiments25 showing the importance of using a large energy cut-off and including dispersion forces in calculations. We are aware that the cation (CH3NH3)+ tends to have rotational dynamics, however, this phenomenon is not relevant to our study. We used in simulations the position and configuration of the cation (CH3NH3)+ that minimizes the total energy.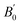 ), and elastic constants (Cij). The table also contains the average mechanical properties of bulk polycrystals like the bulk modulus B (in GPa), shear modulus G (in GPa), Young modulus E (in GPa), vickers hardness HV (in GPa) obtained from the elastic constants using Voigt (V), Reuss (R), and Hill (H) approximations are also included. Results are compared with the literature
), and elastic constants (Cij). The table also contains the average mechanical properties of bulk polycrystals like the bulk modulus B (in GPa), shear modulus G (in GPa), Young modulus E (in GPa), vickers hardness HV (in GPa) obtained from the elastic constants using Voigt (V), Reuss (R), and Hill (H) approximations are also included. Results are compared with the literature
| a (Å) | b (Å) | c (Å) | B0 | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PBE + D2 (this work) | 8.34 | 12.63 | 8.93 | 19.28 | 4.47 | 31.85 | 12.91 | 13.99 | 38.83 | 11.85 | 26.53 | 6.05 | 13.13 | 5.15 |
| Experiment ref. 25 | 8.75 | 12.35 | 8.53 | — | — | — | — | — | — | — | — | — | — | — |
| PBE + D2 17 | 8.37 | 12.72 | 9.05 | — | — | — | — | — | — | — | — | — | — | — |
| Ref. 18 | 9.03 | 12.94 | 8.56 | — | — | — | — | — | — | — | — | — | — | — |
| Ref. 19 | 8.49 | 12.72 | 9.19 | 21.89 | — | 35.83 | 13.54 | 17.13 | 44.88 | 14.12 | 28.73 | 5.85 | 15.72 | 5.03 |
| Ref. 20 | 9.059 | 12.496 | 8.394 | — | 30.48 | 14.69 | 11.08 | 26.08 | 10.51 | 39.67 | 6.04 | 13.70 | 4.85 |
| BV | BR | BH | EV | ER | EH | GV | GR | GH | VHV | VHR | VHH | |||
| 19.413 | 19.046 | 19.229 | 22.849 | 20.227 | 21.546 | 8.762 | 7.644 | 8.203 | 1.731 | 1.375 | 1.550 |
We also calculated the phonon dispersion including the D2 correction. So, in contrast to the study done in ref. 20, which found that orthorhombic CH3NH3SnI3 the structure is dynamically unstable for pressure smaller than 0.7 GPa, our zero-pressure phonon dispersion does not show any imaginary mode; signature of its dynamical stability (see Fig. 1). This shows that incorporating the weak dispersive interactions is fundamental for describing the studied compound. Fig. 1 shows the entire phonon spectrum in (a) and a zoom of the low-frequency region in (b). The zoom facilitates the identification of low-frequency vibrations associated with the inorganic part of the compound. The high-frequency vibrations corresponding to the inorganic part of the compound can be clearly seen in Fig. 1(b). The phonon modes of orthorhombic CH3NH3SnI3 obey to the following mechanical representation: Γ = 19 Ag + 17 Au + 14 B1g + 22 B1u + 19 B2g + 17 B2u + 14 B3g + 22 B3u. Where there are 22 B1u + 17 B2u + 22 B3u = 61 infrared modes 19 Ag + 14 B1g +19 B2g + 14 B3g = 66 Raman modes and 17 Au Silent modes. The calculated mode as well as their assignment and activity are reported in Table 2. Vibrations of the inorganic molecule are identified in Fig. 1(b). All modes reported below 200 cm−1 arise from internal stretching, libration, and bending vibrations of the SnI6 octahedron as well as to vibrations where the octahedra and the organic molecule vibrate as rigid units. The high-frequency modes are mainly associated with internal vibrations of the methylammonium molecule involving vibrations of the C–H and N–H bonds. We have used the tools on the Bilbao Crystallographic Server to extract the activity of each mode. With these tools, using the point group symmetry as well as the selection rules for IR and Raman activities, the specific symmetry and activity of each vibrational mode is obtained. The results are displayed in Table 2.
| ω (cm−1) | Silent | ω (cm−1) | Raman | ω (cm−1) | Infrared |
|---|---|---|---|---|---|
| 15.71 | Au | 15.11 | B1g | 7.80 | B2u |
| 27.95 | Au | 16.81 | A1g | 20.91 | B1u |
| 31.49 | Au | 30.79 | B2g | 23.18 | B2u |
| 32.52 | Au | 31.55 | A1g | 24.52 | B3u |
| 41.33 | Au | 34.82 | B2g | 29.55 | B1u |
| 61.24 | Au | 35.49 | B3g | 31.19 | B2u |
| 92.76 | Au | 37.13 | A1g | 33.92 | B3u |
| 97.83 | Au | 37.59 | B2g | 39.03 | B3u |
| 105.67 | Au | 40.26 | B1g | 42.29 | B1u |
| 136.16 | Au | 51.03 | B3g | 42.56 | B3u |
| 329.12 | Au | 51.87 | A1g | 44.63 | B2u |
| 898.24 | Au | 57.17 | B2g | 48.17 | B1u |
| 1245.68 | Au | 78.45 | B1g | 52.30 | B2u |
| 1440.45 | Au | 82.26 | A1g | 53.70 | B3u |
| 1570.10 | Au | 85.83 | B2g | 64.68 | B1u |
| 3105.28 | Au | 90.36 | B3g | 82.46 | B3u |
| 3211.72 | Au | 93.53 | B3g | 84.22 | B1u |
| 94.83 | B1g | 85.69 | B1u | ||
| 96.27 | A1g | 89.33 | B2u | ||
| 98.03 | A1g | 92.33 | B3u | ||
| 100.20 | B3g | 96.33 | B1u | ||
| 101.53 | B2g | 98.93 | B3u | ||
| 102.04 | B1g | 101.24 | B2u | ||
| 110.61 | B2g | 102.77 | B1u | ||
| 116.35 | B3g | 109.17 | B3u | ||
| 131.09 | B1g | 122.35 | B2u | ||
| 133.29 | B3g | 131.19 | B2u | ||
| 138.53 | Ag | 143.53 | B3u | ||
| 144.23 | B2g | 150.97 | B1u | ||
| 145.97 | B1g | 330.32 | B2u | ||
| 331.16 | B3g | 899.28 | B2u | ||
| 332.43 | B1g | 906.82 | B3u | ||
| 899.91 | B3g | 907.02 | B1u | ||
| 903.05 | B2g | 978.27 | B1u | ||
| 904.05 | Ag | 978.37 | B3u | ||
| 905.68 | B1g | 1245.85 | B2u | ||
| 977.89 | A1g | 1247.41 | B3u | ||
| 978.93 | B2g | 1247.68 | B1u | ||
| 1245.08 | B1g | 1394.88 | B3u | ||
| 1245.85 | B3g | 1395.51 | B1u | ||
| 1247.71 | Ag | 1438.24 | B2u | ||
| 1247.85 | B2g | 1438.54 | B3u | ||
| 1396.12 | A1g | 1440.05 | B1u | ||
| 1397.12 | B2g | 1440.08 | B3u | ||
| 1438.54 | B3g | 1445.45 | B1u | ||
| 1438.54 | A1g | 1561.89 | B2u | ||
| 1438.68 | B1g | 1579.34 | B3u | ||
| 1438.91 | B2g | 1581.14 | B1u | ||
| 1439.54 | Ag | 2996.77 | B3u | ||
| 1450.92 | B2g | 2997.14 | B1u | ||
| 1563.06 | B1g | 3099.21 | B1u | ||
| 1565.46 | B3g | 3099.24 | B3u | ||
| 1580.34 | B2g | 3104.88 | B2u | ||
| 1580.94 | A1g | 3128.96 | B3u | ||
| 2997.47 | B2g | 3133.00 | B1u | ||
| 2998.77 | A1g | 3192.84 | B1u | ||
| 3099.27 | B2g | 3195.91 | B3u | ||
| 3099.37 | Ag | 3213.22 | B2u | ||
| 3104.41 | B1g | ||||
| 3104.84 | B3g | ||||
| 3130.09 | A1g | ||||
| 3133.96 | B2g | ||||
| 3192.67 | B2g | ||||
| 3193.70 | A1g | ||||
| 3212.18 | B3g | ||||
| 3221.52 | B1g |
We have also analyzed the mechanical properties of the studied compound. We have fitted the energy versus volume results with a third-order Birch–Murnaghan equation of state44 to determine the bulk modulus (B0) and its pressure derivative, and we have calculated elastic constants 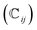 and their related elastic moduli. Results are shown in Table 1. The elastic moduli have been obtained under the Voigt (V), Reuss (R), and Hill (H) approximations45 and the hardness has been calculated using the model proposed by Mazhnik and Oganov.46 We have evaluated the Born stability criteria,47 which allows us to determine the elastic stability of the crystal. For an orthorhombic system, they are:43
and their related elastic moduli. Results are shown in Table 1. The elastic moduli have been obtained under the Voigt (V), Reuss (R), and Hill (H) approximations45 and the hardness has been calculated using the model proposed by Mazhnik and Oganov.46 We have evaluated the Born stability criteria,47 which allows us to determine the elastic stability of the crystal. For an orthorhombic system, they are:43
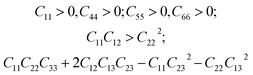 | (2) |
The mechanical stability of the orthorhombic phase of CH3NH3SnI3 is demonstrated here by the fulfillment of the stability criteria. The elastic constants summarized in Table 1 agree with results reported in Refs 19 and 20. According to the bulk modulus B0 obtained from the equation of states fit and from elastic constants B, we can state that the studied hybrid perovskite is highly compressible. The bulk modulus is comparable to that of MAPbBr3 (ref. 9) metalorganic framework48 and rare-gas solids.49 This can be attributed to the presence of organic components, specifically large organic MA cations, which are highly compressible. Additionally, given the low Vickers hardness of the material (see Table 1), we can conclude that its resistance to deformation is weak. This means that in a structure of this type, strains should only be applied very moderately. Interestingly, the bulk and Young modulus are similar, which indicates that the resistance to volumetric compression is similar to the tensile or compressive stiffness. In contrast, the shear modulus is approximately one-third of the other two moduli, indicating a preference for shear deformations.
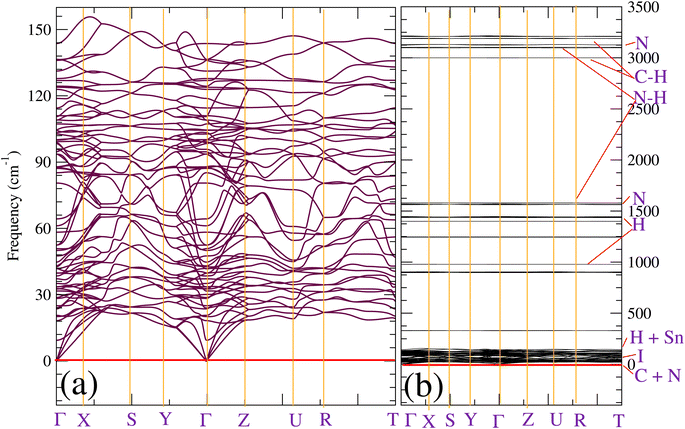
Bonding properties of orthorhombic CH3NH3SnI3
We will now discuss the bonding pattern of CH3NH3SnI3. We will start by performing a topological analysis of bounded atomic basins using the electron localization function (ELF).50 This tool provides an alternative and complementary analysis to QTAIM in terms of electron-pair localization regions.51–53 It was successfully utilized to shed light on the chemical interactions found in molecules, molecular complexes, and crystals. It provides a bond path topology, which is the graphical representation of atomic domains bonded to each other. In addition to ELF, we will also use other indexes like the charge density (ρb), the sign and magnitude of the charge density's Laplacian (∇2ρb), and the bond critical points, which are reliable markers for identifying inter- and intra-molecular interactions. Indeed, ∇2ρb > 0 can serve as a sign of polar covalent bonds, while ∇2ρb < 0 or ∇2ρb > 0, refers to whether an interaction between atomic basins has an open-shell (region with charge concentration) or a closed-shell (region with charge depletion) character.51 After partitioning the structure into topological ELF attractors, we have determined the different basins which are summarized in Table 3. As the PAW method used by VASP incorporates the influence of core electrons without explicitly including them in the wavefunction calculations, no core basins exist for our partition. Instead, the focus is on valence electrons, with the core-electron effects being incorporated through pseudopotentials or PAW potentials.55,56 Therefore, only the electron pairs that form closed atomic electronic shells around the nuclei are of interest to the current ELF analysis. Examples of these are the protonic or hydrogen V(H) lone-pair (valence) basins, as well as the synaptic (V(C), V(N), V(Sn), and V(I)) basins, and the disynaptic (V(H, N) and V(H, C)) basins.55,57 The first outstanding feature of the current ELF analysis shows that the overall geometric stability of CH3NH3SnI3 arises from an environment consisting of an interplay between hydrogen, carbon, and pnictogen-bonded interactions. The appearance of N-centered bonding (V(N)) is accompanied by hydrogen bonds (V(H)). The high value of ellipticity of our ELF attractors indicates that the electrons of the V(C) basin are strongly localized,55 whereas the negative sign of ∇2ρb indicates the covalent nature of most bonds (see Fig. 2). On the other hand, low ellipticity found for V(H, C) and V(H, N) implies that the electrons of these basins are more isotropic or spherical in their electronic domains.55 Additionally, as the density between I and N/C atoms is small, we can stipulate that the pnictogen bonds present between [NH3NH3]2+ and [I]2+ in their ion-pair form are weaker, but we note an important number of hydrogenated V(H) basins. Lastly, we observe that there is a hint of ionic bonding character from the V(Sn) basin.54| Bassin | V (Ω) (Bohr3) | q (electrons) | ELF | η | ∇2ρb | ρb (atomic units) |
|---|---|---|---|---|---|---|
| V(H,C) | 129.249 | −3.001 | 0.999 | 0.014 | −3.427 | 0.294 |
| V(H,N) | 45.823 | −1.123 | 0.996 | 0.003 | −3.042 | 0.273 |
| V(H) | 33.333 | 0.163 | 0.999 | 0.043 | −3.482 | 0.295 |
| V(C) | 31.978 | −0.952 | 0.999 | 0.364 | −0.908 | 0.177 |
| V(N) | 18.319 | −0.223 | 0.984 | 5.060 | −0.143 | 0.056 |
| V(I) | 242.577 | −4.974 | 0.906 | 1.471 | −0.212 | 0.093 |
| V(Sn) | 145.264 | −2.761 | 0.890 | 2.146 | −0.213 | 0.093 |
As we could not extract all weak interactions by using the ELF partition, we also used the reduced density gradient (RDG, s) approach to analyze the existing non-covalent interactions. Fig. 2 displays the 3D isosurface of the RDG. As we can see from Fig. 2, the plot does not show any red domains but rather green weak ones in the direction of N–H⋯I bonds. We also see significantly more delocalization of the electron density at the Sn and I critical bonding regions, which is reflected in the RDG isosurface, which is significantly more blue-green than green. This trend indicates that, even though the nature of these interactions comes from hydrogen atoms, they remain very weak, and more interactions are involved to describe the bonding pattern of the investigated compound. This finding does not match what was already proposed in Ref. 58 for tetragonal CH3NH3PbI3, but is in good concordance with the conclusions given in the recent work of Ref. 59. At the same time, they indicate that this interaction is too small to affect the orthorhombic structure of MASnI3.
Electronic properties of orthorhombic CH3NH3SnI3
To get an accurate band gap value, we have used two approaches in addition to the PBE-GGA functional, namely the mBJ-GGA and HSE06 potentials. PBE-GGA yields a result of 0.7123 eV, while mBJ-GGA and HSE06 yield very similar results of 1.13 eV and 1.11 eV, respectively. Consequently, due to the high computational costs of the HSE06 calculation and the similarity of the results with mBJ-GGA; the analysis of electronic properties will be conducted using the latter method. Our calculated band gap values agree well with the 1.21–1.30 eV value reported in experiments4 and the theoretical values obtained using mBJ (1.12 eV) in ref. 20. Due to the presence of heavy elements such as the Sn atom the relativistic effects could be important. Consequently, the effect of SOC was also estimated and found to be equal to 0.24 eV. We have shown the occurrence of splitting occurring at the low level of the conduction band. The SOC lifts the degeneracy of electronic states with the same energy but different spin orientations. This trend impacts electron transport and affects the band gap value (see Fig. S3 in the ESI† file). We present in Fig. 3 the band structure along the high symmetry points of the Pnma Brillouin zone. According to the band structure, CH3NH3SnI3 has a direct band gap at the Γ point. The direct band gap is often considered advantageous for efficient light absorption and electron–hole pair generation as well as valuable for a range of photonic and electronic devices beyond solar cells.60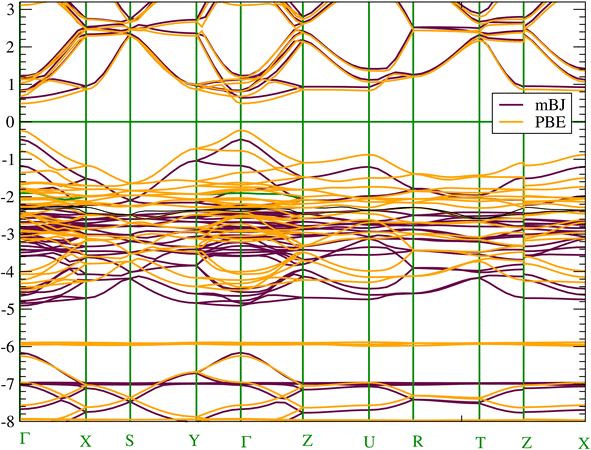 | ||
| Fig. 3 (Color online) Electronic band structure of CH3NH3SnI3 calculated with (a) at mBJ-GGA and (b) PBE-GGA. | ||
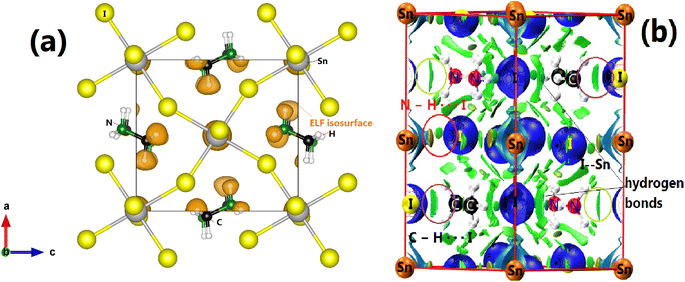
Concerning the topology of the band structure, we observed that the valence band appears to be significantly less dispersive than the conduction band. This characteristic suggests that the compound here studied might be a semiconductor of the p type.61 In fact, the organic cations contribute delocalized π-electrons to the valence band, while the metal cations and halide anions contribute more localized orbitals. To check such a conclusion, we have additionally plotted the projected electronic density of states (PDOS) to obtain insights into the electron orbital contribution of each atom. As shown in Fig. 4, the primary components of the conduction band minimum (CBM) are the 5p states of the Sn atoms, whereas the primary contribution of the Valence band maximum (VBM) is the 5p states of the I atoms with an overlap of the Sn 5s states. Additionally, our findings demonstrate that the organic (CH3NH3)+ cation had a negligible impact on the formation of the CBM and VBM near the Fermi energy level. The topology of the electronic orbital analyzed below suggests that the band gap can be engineered more efficiently by applying an external field to the SnI6 units rather than by replacing the ionic cation (CH3NH3)+ with a different one. This confirms the hypothesis made by Walsh.62
CH3NH3SnI3 under [001] strain
We will discuss how the influence of strain on the bonding and electronic properties of orthorhombic CH3NH3SnI3. We have considered strains along [100], [010], and [001] and found that only the last one does not destabilize the orthorhombic crystal structure. The strain applied along [001] direction is calculated as follows:
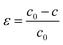 | (3) |
To determine the distortion of the SnI6 octahedron, we estimated the distortion index (ID) using Bauer's definition.63 In untrained orthorhombic CH3NH3SnI3 ID is equal to 0.24%. A negative strain of ε = 0.2% changes the distortion index to 0.3% and the maximum one of tensile ε = +2% changes it to ID = 2%.13 So, the range of applied strain that we used does not exceed 2.2%. This moderate distortion may be regarded as within an acceptable range, maintaining the stability of the octahedral networks so that the Pnma symmetry is preserved.13 These slight distortions do not substantially modify bond lengths and angles of SnI6 but are rather enough to affect the overlap of atomic orbitals, which changes the electronic band structure as well as the value of the band gap.64
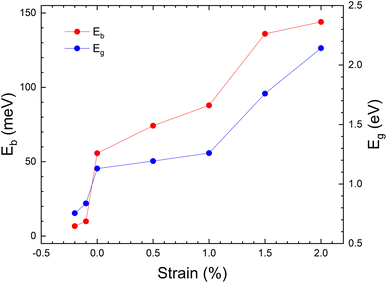
The evolution of band gap as a function of applied strain is shown in Fig. 5. These results are calculated using the PBE-GGA approximation to minimize computational time. This approximation gives an underestimated value for the band gap but describes correctly the changes induced by strain.65,66 The band gap changes from 0.7 to ∼2 eV. Also, due to the importance of excitons in PV applications, the binding energy of excitons (Eb) was calculated. The un-strained structure has a value of Eb = 66 meV, which is similar to the value calculated in ref. 17 (Eb = 60 meV) for MASnI3, for CsPbCl3 (ref. 67) (Eb = 65 meV) and the value measured for MAPbI3 (Eb = 55 meV).68 Fig. 5 shows the evolution of Eb vs. strain. We should keep in mind that the band gap of the material is 1.3 eV, so this value needs to be pushed down to achieve maximum power conversion efficiency (PCE). Our results show that with a moderate tensile strain, the band gap value of CH3NH3SnI3 can be considerably tuned to values where it can be used for PV devices, with high power conversion efficiencies.69 We have also found that for a tensile strain of +2%, the exciton binding energy is enhanced reaching a value of 144 meV. Tailoring the band structure and excitonic levels offers an efficient way to optimize exciton dissociation and improve the overall performance of photovoltaic devices. The strained structure with ε = +2%, thus, can enhance the absorption of photons and the generation of photo-carriers, opening the way to enhancing PV efficiency.
To further understand how strains affect CH3NH3SnI3, we have performed an NCI analysis on the strained structure with ε = +2%. For the sake of comparison, the results of both un-strained and strained structures are shown in Fig. 6a and b. In this case, we used the 2D map at the PBE level sign(λ)2 × ρ vs. RDG plots. As we already mentioned in the description given in the computational detail section, the interactions are classified according to their position on the (sign(λ2) × ρ(r)) scale, where (sign(λ2)) is the sign of the second eigenvalue of the Hessian matrix of ρ.70 Such a sign is used in conjunction with ρ to distinguish between attractive and repulsive interactions. According to the color code described above, we can notice the existence of three RDG regions, the first one corresponds to the region (1) for −0.03(a.u) <sign(λ2) × ρ(r) < −0.02 (a.u.), the second region (2) to −0.01 (a.u.) <sign(λ2) × ρ(r) < +0.01 (a.u) and the last one corresponds to the region (3) around sign(λ2) × ρ(r) = +0.03 (a.u). Region (1) corresponds to both I⋯I non-covalent interactions and Sn–I ionic bonds. They are the inherent geometrical features of the organic and inorganic systems and are dispersive. We can observe that applying tensile strain does not affect region I, indicating that the structure's bonding pattern, which maintains the strained structure's stability, has not changed. The intermolecular interactions of this region are compatible with the isosurface of the bi-colored disk shown in Fig. 2. Region (2) corresponds to the N–H⋯I bonds with values of 3.11 and 3.15 Å for respectively, un-strained and +2% strained structures. The green color and the region around sign(λ2) × ρ(r) = 0 indicates that there are hydrogen bonds, which are described as somewhat depleted between the I and H atoms.71 A similar value of sign(λ2) × ρ(r) = −0.01 (a.u.) was noticed while this bond was analyzed in the O-CD3ND3PbI3 compounds.71 We can see that applying tensile strain enhances region (2), but it appears to be concentrated around the non-covalent region, suggesting that the tilting effect is not caused by the hydrogen or the carbon- and pnictogen bond changes. Finally, region (3) stands for the methylammonium ion (CH3NH3)+ which has a pronounced covalent bonding. It is seen that the application of strain does not weaken these bonds. However, the effect of the out-of-plane strains on the ionic Sn–I bond should not be overlooked, as they partly contribute to determining the overall structure of CH3NH3SnI3.
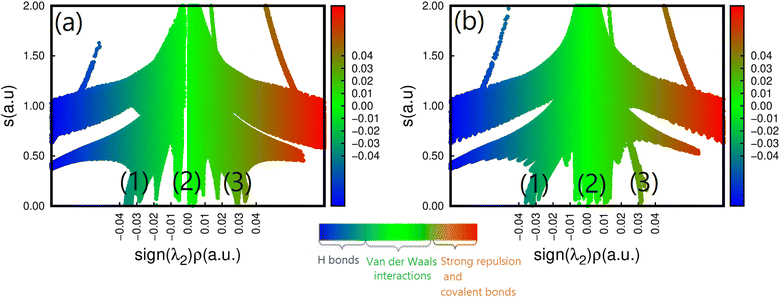 | ||
| Fig. 6 Reduced density gradient S(r) vs. sign(λ2)ρ(r) for the (a) un-strained and (b) strained structure (ε = +2%) of CH3NH3SnI3. | ||
Conclusions
We have reported a theoretical study of CH3NH3SnI3 including both ab initio calculations and an analysis based on the topology of the electron localization function and the reduced form of the density. We present here a first attempt to analyze the bonding of un-strained and strained hybrid CH3NH3SnI3. We found that including ver der Waals interations improved the description of the crystal structure of the studied compound, First, we have analyzed the un-strained crystal structure. We have found that the structure of CH3NH3SnI3 is dynamically and mechanically stable in the orthorhombic Pnma phase structure. This conclusion is supported by the phonon dispersion and elastic constants that fulfill the Born criteria. The study also contains a discussion of the main features of chemical bonding and routes to tuning the properties of CH3NH3SnI3 without altering its stability. Specifically, we have found that the H atoms form hydrogen bonding interactions with the bridging halogens, while the N atoms form directional pnictogen bonding interactions with the halogen sites of the SnI6 octahedra of the inorganic counterpart.We have also shown that the band-gap energy of orthorhombic CH3NH3SnI3 can be tuned using strains. A 2% strain induces a change in the band gap of 1.25 eV and, at the same time, increases the exciton binding energy, which enhances the possibility of going beyond the use of this material for near-infrared light emitter applications. The examination of the chemical interactions that govern the bonding pattern reveals that these strains only slightly modify the global ionic and covalent bonding, leaving the hydrogen and strong bonds unaffected. We consider that the reported results contribute to open new avenues for the use of CH3NH3SnI3 in technological applications. Strains of the order of 2% can be achieved by depositing thin films of CH3NH3SnI3 on wide band-gap substrates like indium tin oxide. The selection of different substrates with the appropriate mismatch strain with CH3NH3SnI3 stipulated by our calculations will allow the use of CH3NH3SnI3 in applications with band gaps ranging from 0.7 to 2.2 eV.
Data availability
The data that support the findings of this study are available on request from the corresponding author.Author contributions
A. D. investigation, writing – original draft, R. B. writing – review & editing, Supervision. T. O.: conceptualization, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing. A. M.: formal analysis, resources, investigation, writing – review & editing. A. M.-S: resources, validation, formal analysis, writing – review & editing. D. E.: validation, formal analysis, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
T. O. thanks for the financial support obtained through PRFU B00L02EP130220230001. D. E. and A. M. thanks the financial support of the Spanish Ministry of Science and Innovation (MCIN/AEI/10.13039/501100011033) under grants number PID2022-138076NB-C41/44, and RED2022-134388-T. D.E. thanks the support from the Generalitat Valenciana (GV) under grants CIPROM/2021/075 and MFA/2022/007. A. M. S. acknowledges the funding of Ministerio de Ciencia e Innovacion, which is part of Agencia Estatal de Investigacion (AEI), through the project PID2020-112507GB-I00 QUANTA-2DMAT (Novel quantum states in heterostructures of 2D materials) and the Generalitat Valenciana through the Grant PROMETEO/2021/082 (ENIGMA) and the projects SEJIGENT/2021/034 and MFA/2022/009. This study is part of the Advanced Materials program supported by MCIN and GV with funding from the European Union NextGenerationEU (PRTR-C17.I1). The authors thank Dr Pablo P. Boix from Instituto de Tecnología Química (ITQ, UPV-CSIC) for enlightening comments.References
- I. Fernandez-Guillen, C. A. Aranda, P. F. Betancur, M. Vallés-Pelarda, C. Momblona, T. S. Ripolles, R. Abargues and P. P. Boix, Perovskite Thin Single Crystal for a High Performance and Long Endurance Memristor, Adv. Electron. Mater., 2024, 2300475, DOI:10.1002/aelm.202300475.
- P. Serafini, P. P. Boix, E. M. Barea, T. Edvinson, S. Sánchez and I. Mora-Seró, Photonic Processing of MAPbI3 Films by Flash Annealing and Rapid Growth for High-Performance Perovskite Solar Cells, Sol. RRL, 2023, 7, 2201102, DOI:10.1002/solr.202200641.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties, Inorg. Chem., 2013, 52, 9019–9038, DOI:10.1021/ic401215x.
- F. Hao, C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Lead-free solid-state organic-inorganic halide perovskite solar cells, Nat. Photonics, 2014, 8, 489–494, DOI:10.1038/nphoton.2014.82.
- I. Mohanty, S. Mangal, S. Jana and U. P. Singh, Synthesis and characterization of Methylammonium tin iodide (CH3NH3SnI3) absorber layer for photovoltaic applications, Mater. Today: Proc., 2023 DOI:10.1016/j.matpr.2023.05.677.
- A. Ennaoui, S. Fiechter, Ch. Pettenkofer, N. Alonso-Vante, K. Büker, M. Bronold, Ch. Höpfner and H. Tributsch, Iron disulfide for solar energy conversion, Sol. Energy Mater., 1993, 29, 289–370, DOI:10.1016/0927-0248(93)90095-K.
- R. Murphy and D. R. Strongin, Surface reactivity of pyrite and related sulfides, Surf. Sci. Rep., 2009, 64, 1–45, DOI:10.1016/j.surfrep.2008.09.002.
- A. Zunger, S. Wagner and P. M. Petroff, New materials and structures for photovoltaics, J. Electron. Mater., 1993, 22, 3–16, DOI:10.1007/BF02665719.
- A. Liang, J. Gonzalez-Platas, R. Turnbull, C. Popescu, I. Fernandez-Guillen, R. Abargues, P. P. Boix, L.-T. Shi and D. Errandonea, Reassigning the Pressure-Induced Phase Transitions of Methylammonium Lead Bromide Perovskite, J. Am. Chem. Soc., 2022, 144(43), 20099–20108, DOI:10.1021/jacs.2c09457.
- A. Liang, R. Turnbull, C. Popescu, I. Fernandez-Guillen, R. Abargues, P. P. Boix and D. Errandonea, Pressure-Induced Phase Transition versus Amorphization in Hybrid Methylammonium Lead Bromide Perovskite, J. Phys. Chem. C, 2023, 127(26), 12821–12826, DOI:10.1021/acs.jpcc.3c03263.
- X. Lu, W. Yang, Q. Jia and H. Xu, Pressure-induced dramatic changes in organic-inorganic halide perovskites, Chem. Sci., 2017, 8, 6764, 10.1039/C7SC01845B.
- Y. Q. Huang, J. Su, Q. F. Li, D. Wang, L. H. Xu and Y. Bai, Structure, optical and electrical properties of CH3NH3SnI3 single crystal, Physica B, 2019, 563, 107–112, DOI:10.1016/j.physb.2019.03.035.
- H.-S. Kim and N.-G. Park, Importance of tailoring lattice strain in halide perovskite crystals, NPG Asia Mater., 2020, 12, 78, DOI:10.1038/s41427-020-00265-w.
- U. W. Pohl, Epitaxy of Semiconductors: Introduction to Physical Principles, Springer, 2013 Search PubMed.
- O. V. Oyelade, O. K. Oyewole, D. O. Oyewole, S. A. Adeniji, R. Ichwani, D. M. Sanni and W. O. Soboyejo, Pressure-Assisted Fabrication of Perovskite Solar Cells, Sci. Rep., 2020, 10, 7183, DOI:10.1038/s41598-020-64090-5.
- Z. Liu, B. Wang and C. Cazorla, Mechanical and electronic properties of CeO2 under uniaxial tensile loading: A DFT study, Materialia, 2021, 15, 101050, DOI:10.1016/j.mtla.2021.101050.
- N. T. Han, V. K. Dien and M.-F. Lin, Electronic and Optical Properties of CH3NH3SnI3 and CH(NH2)2SnI3 Perovskite Solar Cell, Phys. Status Solidi RRL, 2023, 17, 2300020, DOI:10.1002/pssr.202300020.
- N. Suhaili, M. F. M. Taib, M. K. Yaakob, O. H. Hassan and M. Z. A. Yahya, Properties of Lead-Free Hybrid Organic-Inorganic Halide Perovskite CH3NH3BX3 Using Density Functional Theory, Mater. Today: Proc., 2017, 4, 5154–5160, DOI:10.1016/j.matpr.2017.05.021.
- V. K. Sharma, V. Kanchana, M. K. Gupta and R. Mittal, Ultra-low thermal conductivity of orthorhombic CH3NH3SnI3: A first-principles investigation, J. Solid State Chem., 2020, 290, 121541, DOI:10.1016/j.jssc.2020.121541.
- I. O. Abdallah-Ali, D. P. Joubert and M. S. H. Suleiman, First-principles study of structural, mechanical, dynamical stability, electronic and optical properties of orthorhombic CH3NH3SnI3 under pressure, Eur. Phys. J. B, 2019, 92, 202, DOI:10.1140/epjb/e2019-100101-1.
- M. Fox and G. F. Bertsch, Optical Properties of Solids, Am. J. Phys., 2002, 70, 1269–1270, DOI:10.1119/1.1691372.
- F. Bassani, G. P. Parravicini, R. A. Ballinger and J. L. Birman, Electronic States and Optical Transitions in Solids, Phys. Today, 1976, 29, 58, DOI:10.1063/1.3023374.
- M. Fox and G. F. Bertsch, Optical properties of solids, Am. J. Phys., 2002, 70, 1269, DOI:10.1119/1.1691372.
- A. Otero-de-la-Roza, E. R. Johnson and J. Contreras-Garcıa, Revealing non-covalent interactions in solids: NCI plots revisited, Phys. Chem. Chem. Phys., 2012, 14, 12165–12172, 10.1039/C2CP41395G.
- Y. Takahashi, R. Obara, Z. Z. Lin, Y. Takahashi, T. Naito, T. Inabe, S. Ishibashi and K. Terakura, Dalton Trans., 2011, 40, 5563, 10.1039/D3DT03772J.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50, DOI:10.1103/PhysRevB.47.558.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561, DOI:10.1103/PhysRevB.47.558.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/physrevlett.77.3865.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT − D) for the 94 elements H − Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465, DOI:10.1002/jcc.21759.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102, 226401, DOI:10.1103/PhysRevLett.102.226401.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215, DOI:10.1063/1.1564060.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- P. Liu, B. Kim, X.-Q. Chen, D. D. Sarma, G. Kresse and C. Franchini, Relativistic GW+BSE study of the optical properties of Ruddlesden-Popper iridates, Phys. Rev. Mater., 2018, 2, 075003, DOI:10.1103/PhysRevMaterials.2.075003.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355, DOI:10.1103/PhysRevB.55.10355.
- P. Giannozzi, S. de Gironcoli, P. Pavone and S. Baroni, Phys. Rev. B, 1991, 43, 7231, DOI:10.1103/PhysRevB.43.7231.
- S. Steiner, S. Khmelevskyi, M. Marsman and G. Kresse, Calculation of the magnetic anisotropy with projected-augmented-wave methodology and the case study of disordered Fe1−xCox alloys, Phys, Rev. B, 2018, 93, 224425, DOI:10.1103/PhysRevB.93.224425.
- R. A Boto, J.-P. Piquemal and J. Contreras-García, Revealing strong interactions with the reduced density gradient: a benchmark for covalent, ionic, and charge-shift bonds, Theoretical Chemistry Accounts: Theory, Computation, and Modeling, 2017, 136, 139 CrossRef . https://hal.archives-ouvertes.fr/hal-01636270.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506, DOI:10.1021/ja100936w.
- H. Z. Guedda, T. Ouahrani, A. Morales-García, R. Franco, M. A. Salvadó, P. Pertierra and J. M. Recio, Computer simulations of 3C-SiC under hydrostatic and non-hydrostatic stresses, Phys. Chem. Chem. Phys., 2016, 18, 8132–8139, 10.1039/C6CP00081A.
- T. Ouahrani, R. Khenata, B. Lasri, A. H Reshak, A. Bouhemadou and S. Bin-Omran, First and second harmonic generation of the XAl2Se4 (X= Zn, Cd, Hg) defect chalcopyrite compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 407, 3760–3766, DOI:10.1016/j.physb.2012.05.057.
- T. Ouahrani, F.-Z. Medjdoub, S. Gueddida, Á. Lobato-Fernandez, R. Franco, N.-E. Benkhettou, M. Badawi, A. Liang, J. Gonzalez and D. Errandonea, Understanding the Pressure Effect on the Elastic, Electronic, Vibrational, and Bonding Properties of the CeScO3 Perovskite, J. Phys. Chem. C, 2021, 125(1), 107–119, DOI:10.1021/acs.jpcc.0c08641.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- D. H. Chung and W. R. Buessem, J. Appl. Phys., 1967, 38, 2535–2540 CrossRef CAS.
- E. Mazhnik and A. R. Oganov, A model of hardness and fracture toughness of solids, J. Appl. Phys., 2019, 126, 125109 CrossRef.
- Dynamical Theory and Experiment, ed. M. Born and K. Huang, Springer, Berlin, 1982, vol. 1. DOI:10.1007/bf02645493.
- J. Navarro-Sánchez, I. Mullor-Ruíz, C. Popescu, D. Santamaría-Pérez, A. Segura, D. Errandonea, J. González-Platas and C. Martí-Gastaldo, Peptide metal-organic frameworks under pressure: flexible linkers for cooperative compression, Dalton Trans., 2018, 47, 10654–10659, 10.1039/C8DT01765D.
- D. Errandonea, R. Boehler, S. Japel, M. Mezouar and L. R. Benedetti, Structural transformation of compressed solid Ar: An x-ray diffraction study to 114 GPa, Phys. Rev. B, 2006, 73, 092106, DOI:10.1103/PhysRevB.73.092106.
- A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5404, DOI:10.1063/1.458517.
- R. F. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- P. L. A. Popelier, Atoms in Molecules: An Introduction, Pearson Education, Harlow, UK, 2000 Search PubMed.
- S. Belarouci, T. Ouahrani, N. Benabdallah, A. Morales-García and I. Belabbas, Two-dimensional silicon carbide structure under uniaxial strains, electronic and bonding analysis Comp, Mater. Sci., 2018, 151, 288–295, DOI:10.1016/j.commatsci.2018.05.020.
- T. Ouahrani, I. Merad-Boudia, H. Baltache, R. Khenata and Z. Bentalha, Effect of pressure on the global and local properties of cubic perovskite crystals, Phys. Scr., 2011, 84, 025704, DOI:10.1088/0031-8949/84/02/025704.
- R. J. Gillespie and R. S. Nyholm, Inorganic stereochemistry, Quarterly Reviews, Chem. Soc. Rev., 1957, 11, 339–380, 10.1039/QR9571100339.
- T. Ouahrani, R. Franco, J. M. Menéndez, M. Marqués and J. M. Recio, Microscopic partition of pressure and elastic constants in CdTe polymorphs, J. Alloys Compd., 2014, 592(15), 150–156, DOI:10.1016/j.jallcom.2013.12.153.
- A. Savin, O. Jepsen, J. Flad, L. K. Anderson, H. Preuss and H. G. von Schnering, Electron localization in solid-state structures of the elements: the diamond structure, Angew Chem. Int. Ed. Engl., 1992, 32, 187–188, DOI:10.1002/anie.199201871.
- F. El-Mellouhi, A. Marzouk, E. T. Bentria, S. N. Rashkeev, S. Kais and F. H. Alharbi, Hydrogen Bonding and Stability of Hybrid Organic– Inorganic Perovskites, ChemSusChem, 2016, 9, 1–9, DOI:10.1002/cssc.201600864.
- A. Varadwaj, P. R. Varadwaj and H. M. Marques, The Pnictogen Bond, Together with Other Non-Covalent Interactions, in the Rational Design of One-, Two- and Three-Dimensional Organic-Inorganic Hybrid Metal Halide Perovskite Semiconducting Materials, and Beyond, Int. J. Mol. Sci., 2022, 23, 8816, DOI:10.3390/ijms23158816.
- E. Mosconi, A. Amat, M. D. K. Nazeeruddin, M. Grätzel and F. De Angelis, First-principles modeling of mixed halide organometal perovskites for photovoltaic applications, J. Phys. Chem. C, 2013, 117, 13902–13913, DOI:10.1021/jp4048659.
- R. Shukla, A. Arya and A. K. Tyag, Interconversion of perovskite and fluorite structures in Ce-Sc-O system, Inorg. Chem., 2010, 49, 1152–1157, DOI:10.1021/ic9020096.
- A. Walsh, Principles of Chemical Bonding and Band Gap Engineering in Hybrid Organic-Inorganic Halide Perovskites, J. Phys. Chem. C, 2015, 119, 5755–5760, DOI:10.1021/jp512420b.
- W. H. Baur, The geometry of polyhedral distortions. Predictive relationships for the phosphate group, Acta Crystallogr., Sect. B: Struct. Sci., 1974, 30, 1195, DOI:10.1107/S0567740874004560.
- T. Ouahrani, R. M. Boufatah, M. Benaissa, Á. Á. Morales-García, M. Badawi and D. Errandonea, Effect of intrinsic point defects on the catalytic and electronic properties of Cu2WS4 single layer: Ab initio calculations, Phys. Rev. Mater., 2023, 7, 025403, DOI:10.1103/PhysRevMaterials.7.025403.
- S. López-Moreno, J. Sánchez-Martín, E. Bandiello, M. Bettinelli, C. L. Bull, C. Ridley and D. Errandonea, The effect of pressure on the band-gap energy in FePO4 and FeVO4, J. Phys. Chem. Solids, 2023, 183, 111604, DOI:10.1016/j.jpcs.2023.111604.
- D. Errandonea, F. Rodriguez, R. Vilaplana, D. Vie, S. Garg, B. Nayak, N. Garg, J. Singh, V. Kanchana and G. Vaitheeswaran, Band-Gap Energy and Electronic d–d Transitions of NiWO4 Studied under High-Pressure Conditions, J. Phys. Chem. C, 2023, 127(31), 15630–15640, DOI:10.1021/acs.jpcc.3c03512.
- M. Baranowski, P. Plochocka, R. Su, L. Legrand, T. Barisien, F. Bernardot, Q. Xiong, C. Testelin and M. Chamarro, Exciton binding energy and effective mass of CsPbCl3: a magneto-optical study, Photonics Res., 2020, 8, A50–A55, DOI:10.1364/PRJ.401872.
- K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. Tse-Wei Wang, T. Stergiopoulos, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Determination of the exciton binding energy and effective masses for methylammonium and formamidinium lead tri-halide perovskite semiconductors, Energy Environ. Sci., 2016, 9, 962–970, 10.1039/C5EE03435C.
- K. Galkowski, A. Surrente, M. Baranowski, B. Zhao, Z. Yang, A. Sadhanala, S. Mackowski, S. D Stranks and P. Plochocka, Excitonic Properties of Low Bandgap Lead-Tin Halide Perovskites, ACS Energy Lett., 2019, 4(3), 615–621, DOI:10.1021/acsenergylett.8b02243.
- S. Bouguima, T. Ouahrani, A. Bouheddadj, M. Le Roux, D. Errandonea and M. Badawi, Understanding the optical and bonding properties of hybrid metal-halide (C5H16NP) PbX4 (X= Cl, Br, I) perovskite: A density-functional theory study, Inorg. Chem. Commun., 2021, 130, 108721, DOI:10.1016/j.inoche.2021.108721.
- P. R. Varadwaj, A. Varadwaj, H. M. Marques and K. Yamashita, Significance of hydrogen bonding and other noncovalent interactions in determining octahedral tilting in the CH3NH3PbI3 hybrid organic-inorganic halide perovskite solar cell semiconductor, Sci. Rep., 2019, 9, 50, DOI:10.1038/s41598-018-36218-1.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02804j |
| This journal is © The Royal Society of Chemistry 2024 |