Open Access Article
Open Access ArticleHydrogen storage in M(BDC)(TED)0.5 metal–organic framework: physical insights and capacities†
Nguyen Thi Xuan Huynh *a,
Vu Thi Ngana,
Nguyen Thi Yen Ngocbc,
Viorel Chihaia
*a,
Vu Thi Ngana,
Nguyen Thi Yen Ngocbc,
Viorel Chihaia d and
Do Ngoc Son
d and
Do Ngoc Son *bc
*bc
aLaboratory of Computational Chemistry and Modelling (LCCM) – Faculty of Natural Sciences, Quy Nhon University, 170 An Duong Vuong, Quy Nhon City, Binh Dinh Province, Vietnam. E-mail: nguyenthixuanhuynh@qnu.edu.vn
bHo Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam. E-mail: dnson@hcmut.edu.vn
cVietnam National University Ho Chi Minh City, Linh Trung Ward, Ho Chi Minh City, Vietnam
dInstitute of Physical Chemistry “Ilie Murgulescu” of the Romanian Academy, Splaiul Independentei 202, Sector 6, 060021 Bucharest, Romania
First published on 20th June 2024
Abstract
Finding renewable energy sources to replace fossil energy has been an essential demand in recent years. Hydrogen gas has been becoming a research hotspot for its clean and free-carbon energy. However, hydrogen storage technology is challenging for mobile and automotive applications. Metal–organic frameworks (MOFs) have emerged as one of the most advanced materials for hydrogen storage due to their exceptionally high surface area, ultra-large and tuneable pore size. Recently, computer simulations allowed the designing of new MOF structures with significant hydrogen storage capacity. However, no studies are available to elucidate the hydrogen storage in M(BDC)(TED)0.5, where M = metal, BDC = 1,4-benzene dicarboxylate, and TED = triethylenediamine. In this report, we used van der Waals-dispersion corrected density functional theory and grand canonical Monte Carlo methods to explore the electronic structure properties, adsorption energies, and gravimetric and volumetric hydrogen loadings in M(BDC)(TED)0.5 (M = Mg, V, Co, Ni, and Cu). Our results showed that the most favourable adsorption site of H2 in M(BDC)(TED)0.5 is the metal cluster–TED intersection region, in which Ni offers the strongest binding strength with the adsorption energy of −16.9 kJ mol−1. Besides, the H2@M(BDC)(TED)0.5 interaction is physisorption, which mainly stems from the contribution of the d orbitals of the metal atoms for M = Ni, V, Cu, and Co and the p orbitals of the O, C, N atoms for M = Mg interacting with the σ* state of the adsorbed hydrogen molecule. Noticeably, the alkaline-earth metal Mg strongly enhanced the specific surface area and pore size of the M(BDC)(TED)0.5 MOF, leading to an enormous increase in hydrogen storage with the highest absolute (excess) gravimetric and volumetric uptakes of 1.05 (0.36) wt% and 7.47 (2.59) g L−1 at 298 K and 7.42 (5.80) wt% and 52.77 (41.26) g L−1 at 77 K, respectively. The results are comparable to the other MOFs found in the literature.
1 Introduction
The energy demands for industrialization based on fossil fuels have been causing an enormous increase in global warming. Finding clean and renewable energy alternatives to fossil fuels is an urgent need for a sustainable environment and the development of the global economy.1,2 Hydrogen gas has attracted much attention due to its high energy density, non-toxicity, and high abundance on Earth.3–5 Compared to other renewable energy sources, such as solar and wind turbines, hydrogen energy is unaffected by season, temperature, geology, etc.3,6 However, storing hydrogen gas is challenging because hydrogen gas is very mobile and occupies an extensive volume. Besides, its high energy density contains potentially explosive risks when applying pressure-tank storage, which also require heavy equipment incompatible with mobile solutions. Therefore, searching for advanced storage materials plays a crucial role in the success of hydrogen energy technology.7–9 Metal–organic frameworks (MOFs) are promising H2 adsorbents with their exceptionally high specific surface area, ultra-large pore size, high porosity, good chemical stability, tuneable porous structure, and reproducible and facile synthesis.6,9–14 Although thousands of MOFs have been synthesized, only a few have been investigated for H2 storage, specifically at room temperatures and low pressures.15,16 The 2025 main criteria set by the US Department of Energy (DOE) are 55 mg H2 per g [MOF + H2] system or 5.5 wt% (1.8 kW h kg−1) for gravimetric storage and 40 g H2 per L [MOF + H2] (1.3 kW h L−1) for volumetric storage under moderate temperatures (from −40 °C to 60 °C) and low pressures (below 100 bar).7,17 Besides, the ultimate DOE targets are 6.5 wt% and 50 g H2 per L.At cryogenic temperatures (∼77 K), MOFs have achieved reasonable hydrogen capacities to meet the DOE storage targets.9 So far, the experimental data have recorded very high H2 adsorption capacity for MOF-210 with 17.6 wt% (total uptake) and 8.6 wt% (excess uptake) at 80 bar and 77 K,18 NU-100 with 9.95 wt% at 56 bar and 16.4 wt% at 70 bar for excess capacity,19 MOF-200 with 16.3 wt% (total uptake) and 7.4 wt% (excess uptake) at 100 bar,19 MOF-205 with 12.0 wt% and 7.0 wt% for total and excess uptakes at 80 bar,18 MOF-177 with 11.0 total wt% and 7.5 excess wt% at 70 bar,20 Be12(OH)12(BTB)4 with 9.2 total wt% (43 g H2 per L) and 6.0 excess wt%,21 and 5.46 MOF-5 with 5.1 wt% at 65 bar.22 Nevertheless, due to weak interaction with H2 at ambient temperatures, MOFs store rather low H2 uptake, below 2.0 wt% or 20 mg g−1.9,23,24 In our knowledge, at the room temperature (298 K), the highest H2 storage was found for Be12(OH)12(BTB)4 about 1.0 excess wt% and 2.3 total wt% at 95 bar and Mn3[(Mn4Cl)3(BTT)8(MeOH)10]2 with 1.5 wt% (12 g L−1) at 90 bar.21 Besides, most MOFs have low isosteric heats of H2 adsorption (Qst), often from −4 to −13 kJ mol−1.25 As suggested, for efficient H2 storage in fuel cells using adsorption material-based hydrogen storage technology at room temperatures, the ideal Qst of H2 for MOFs should be from −15 and −25 kJ mol−1.15 Therefore, temperatures must decrease to cryogenic range to improve hydrogen capacities and provide a satisfactory drive range in automotive applications. On the other hand, practical strategies have been proposed to strengthen H2 adsorption at room temperatures to enhance the H2@MOFs interaction via substituting metal centres, organic ligands, and counter-ions.11 These strategies showed that Qst and the H2 uptakes significantly improved at ambient temperatures and low pressures below 100 bar.9
Recently, M(BDC)(TED)0.5 with the paddle-wheel structure of the metal clusters has been of great interest due to its high porosity and thermal stability.26,27 Ni and Zn(BDC)(TED)0.5 are excellent SO2 capture materials,28 Ni(BDC)(TED)0.5 for CO2 and SO2 co-adsorption,29 and also other toxic gases.15 It is also well-known for highly selective separation of CH3OH/H2O and CO2/CH4 mixtures in Zn(BDC)(TED)0.5 (ref. 30) and C2H6/C2H4 in M(BDC)(TED)0.5 (M = Co, Cu, Ni, Zn).31 A study showed good adsorption/desorption of argon, hydrogen, and hydrocarbons in Zn and Cu(BDC)(TED)0.5.30,32 Combining experiment and simulation, Liu and co-workers showed Zn(BDC)(TED)0.5 had good hydrogen adsorption loadings at 77 K with the maximum excess uptake of ca. 4.2 wt% at 20 bar, and at 298 K, ca. 0.23 wt% (by UFF), 0.28 wt% (by Buch potential), and 0.21 wt% (by experiment).33 We find that M(BDC)(TED)0.5 is very promising for hydrogen storage. However, no works are available to elucidate the influences of metal substitutions (M = Mg, V, Co, Ni, and Cu) in M(BDC)(TED)0.5 on hydrogen adsorption and storage. Therefore, this work is devoted to solving the research topic with the aid of vdW-DF density functional theory and grand canonical Monte Carlo simulations. In the past, computer simulations allowed the prediction and design of new MOF structures with significant gas storage capacity.12,13,34 Here, we used the density functional theory approach to explore physical insights into the H2 adsorption sites and the interaction nature between H2 and M(BDC)(TED)0.5. We then used grand canonical Monte Carlo simulations to obtain hydrogen loadings via adsorption isotherms. To improve the H2 adsorption ability of M(BDC)(TED)0.5, the metal M(II) ions (alkaline earth and transition metals) are of concern, i.e., magnesium (Mg), vanadium (V), cobalt (Co), nickel (Ni), and copper (Cu). These metals have been selected because, based on experimental and theoretical research, the first-row transition metals such as Ni, V, Co, and Cu are common connectors in MOFs.12,35–37 Also, Mg-based MOFs exhibited a good adsorption ability to H2 and other small gases.7,36,38 Various factors can influence the hydrogen storage capacity of MOFs. However, this work focused only on the ideal structure of M(BDC)(TED)0.5 and ignored other factors, such as humidity, flexibility, defects, etc., on the H2 storage capacity and the H2 interaction with M(BDC)(TED)0.5.
2 Computational approaches
2.1 The density functional theory calculations
We used the van der Waals dispersion-corrected density functional theory (vdW-DF)39 via the Vienna ab initio simulation package (VASP).40,41 The vdW-DF calculations were established with cut-off energy of 700 eV for expanding the plane wave basis set, the revised Perdew–Burke–Ernzerhof functional for the exchange–correlation energy,42,43 the projector-augmented-wave method for the electron–ion interaction,44,45 and Monkhorst and Pack k-points sampling of 5 × 5 × 5 mesh grid for optimizing structure, calculating total energy, and investigating electronic properties.46 The geometric structure of all designed H2@M(BDC)(TED)0.5 systems was fully relaxed before computing the total energy. For analyzing the electronic properties of H2@M(BDC)(TED)0.5 systems, we calculated the atomic point charges using the Bader partition technique,47,48 charge density difference (CDD), and the electronic density of states.49 The adsorption energy ΔE of the hydrogen molecule in M(BDC)(TED)0.5 is defined as| ΔE = E[MOF+H2] − EMOF − EH2. | (1) |
The charge density difference (CDD) is calculated by
| Δρ = ρ[M-MOF+H2] − ρM-MOF − ρH2, | (2) |
2.2 Grand canonical Monte Carlo simulations
The pair interactions between the ith atom and the jth atom of the H2 molecule with M(BDC)(TED)0.5 were described by the van der Waals interactions in the Lennard-Jones (LJ) 6–12 model (ULJij) with the cut-off radius of 20 Å and the electrostatic interactions or Coulomb interactions (UCLij) with the cut-off radius of 13 Å as follows
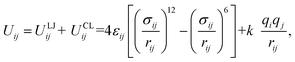 | (3) |
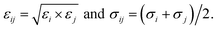 | (4) |
In the GCMC simulations, the hydrogen molecule can move freely by inserting, deleting, translating, and rotating operations to reach an equilibrium state, whereas the MOF atoms were kept fixed. The hydrogen uptake capacities in wt% are calculated by
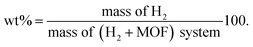 | (5) |
We calculated the absolute uptake (nabs) and excess uptake (nexc) of hydrogen gas for gravimetric and volumetric loadings at temperatures of 77 K and 298 K and pressures up to 100 bar using the RASPA package. The relationship between absolute and excess uptakes is
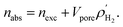 | (6) |
 and Vpore are the molar density of the bulk H2 in the gas phase and the pore volume of M(BDC)(TED)0.5, respectively.
and Vpore are the molar density of the bulk H2 in the gas phase and the pore volume of M(BDC)(TED)0.5, respectively.
3 Results and discussion
3.1 Geometry optimization for M(BDC)(TED)0.5
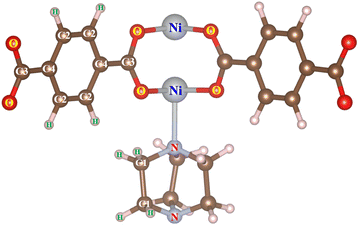
We designed the geometry structure of M(BDC)(TED)0.5 based on experimental data,28,29 where M = (Mg, V, Co, Ni, Cu), BDC = 1,4-benzene dicarboxylate, and TED = triethylenediamine, with the parameters for a primitive unit cell α = β = γ = 90° and a = b ≠ c, as shown in Fig. 1. The MOF has the secondary building units of metal–oxygen–carbon clusters in the paddle-wheel shape at the node of the network.28,31 The unit cell contains 54 atoms, including two metal (M), eight oxygen, two nitrogen, twenty-two carbon, and twenty hydrogen atoms. Two metal atoms combine with four surrounding O atoms to form the metal cluster, connecting to BDC linkers and TED groups.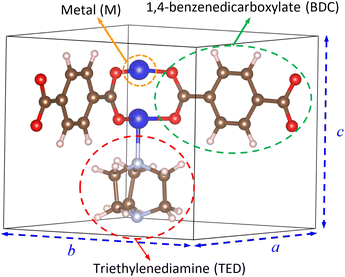 | ||
| Fig. 1 The primitive unit cell of M(BDC)(TED)0.5. Light pink (H), brown (C), light grey (N), red (O), and blue (M). | ||
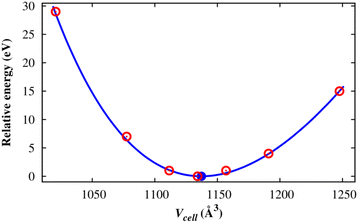
After designing the unit cell geometry, we fully optimized the atomic positions and the unit cell size of the M(BDC)(TED)0.5 using the vdW-DF calculations. The unit cell size of structures was optimized by fitting to the Murnaghan equation of state when presenting the DFT total energy as a function of the unit cell volume (Vcell) or the lattice constants (Fig. 2).55,56 From now on, we will use M-MOF to denote the short name of M(BDC)(TED)0.5. The optimized parameters for the unit cell of the M-MOF structure are presented in Table 1. The average distance from two metal atoms to their nearest oxygen atoms is about 2.0 Å. The pore volume (Vpore) and specific surface area (SSA), obtained using the RASPA code,53 are the parameters featuring the porosity of the M-MOF. Our obtained parameters for Ni-MOF are a = b = 10.979 Å, c = 9.384 Å, and Vpore = 0.761 cm3 g−1, which are in good agreement with the experimental results a = b = 11.15 Å, c = 9.53 Å,57 and Vpore = 0.76 cm3 g−1.31 The optimized parameters for the remaining M-MOFs also agreed with the available experimental data.31,57 The SSA and Vpore of the primitive unit cell are in the order Mg-MOF > V-MOF > Ni-MOF > Co-MOF > Cu-MOF, which is reasonable compared to the experimental data,31 i.e., Ni-MOF > Co-MOF ≈ Cu-MOF for Vpore and Ni-MOF > Co-MOF > Cu-MOF for SSA.
| M-MOF | dM–O (Å) | Lattice constants (Å) | Unit cell volume, Vcell (Å3) | Pore volume, Vpore (cm3 g−1) | Specific surface area, SSA (g cm−2) | |
|---|---|---|---|---|---|---|
| a = b | c | |||||
| Mg-MOF | 2.040 | 10.989 | 9.393 | 1134.28 | 0.874 | 1931.34 |
| V-MOF | 2.022 | 10.969 | 9.375 | 1127.99 | 0.782 | 1727.54 |
| Co-MOF | 1.947 | 10.901 | 9.317 | 1107.16 | 0.741 | 1627.64 |
| Ni-MOF | 1.994 | 10.979 | 9.384 | 1131.13 | 0.761 | 1685.63 |
| Cu-MOF | 2.023 | 10.845 | 9.270 | 1090.28 | 0.709 | 1560.67 |
| Co-MOF31 | 0.619 | 1708 | ||||
| Ni-MOF31,57 | 11.15 | 9.53 | 1184 | 0.757 | 1905 | |
| Cu-MOF31 | 0.627 | 1631 | ||||
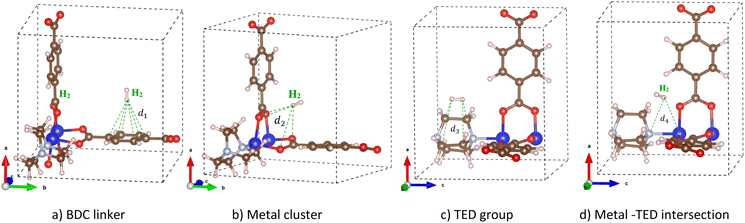
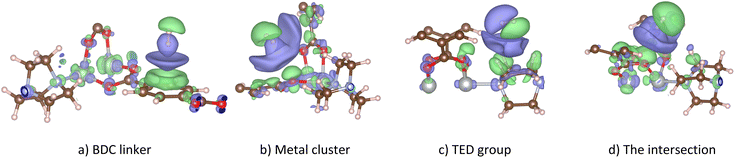
3.2 Favourable H2 adsorption sites
We added a hydrogen molecule to the optimized unit cell of M-MOF, then fully relaxed the geometric structure of the H2@M-MOF system. Hydrogen molecules can adsorb on four possible regions: the metal cluster, BDC linker, TED group, and the intersection of the metal cluster and the TED group (the metal cluster–TED intersection). The favourable order of the adsorption sites was investigated via the adsorption energy (in kJ mol−1) of the H2 molecule, which was calculated via eqn (1). The more negative the adsorption energy ΔE, the more favourable the adsorption site for the H2 molecule will be. The most favourable H2 adsorption configuration, the one with the most negative adsorption energy for each region, is shown in Fig. 3. The detailed values for the H2 adsorption energy and structural parameters are listed in Table 2. Here, d1 and d2 are the average distances from the nearest H atom of the H2 molecule to six C atoms of the BDC linker and four O atoms of the metal cluster, respectively. The average distance from the nearest H atom of the H2 molecule to the C atoms of the TED group is d3. The average distance from the nearest H atom to one metal atom (Mg, V, Co, Ni, or Cu) of the metal cluster and the N atom of the TED is d4. See Fig. 3 for the explanation of the distance from H2 to the M-MOF.| M-MOF | BDC linker | Metal cluster | TED group | Metal cluster–TED intersection | |
|---|---|---|---|---|---|
| Ni-MOF | ΔE (kJ mol−1) | −12.428 | −13.730 | −15.457 | −16.930 |
| d (Å) | 3.209 (d1) | 3.466 (d2) | 3.444 (d3) | 4.156 (d4) | |
| Mg-MOF | ΔE (kJ mol−1) | −8.700 | −10.008 | −10.990 | −12.435 |
| d (Å) | 3.326 (d1) | 3.534 (d2) | 3.470 (d3) | 4.177 (d4) | |
| V-MOF | ΔE (kJ mol−1) | −7.744 | −10.015 | −10.634 | −11.713 |
| d (Å) | 3.256 (d1) | 3.314 (d2) | 3.479 (d3) | 4.060 (d4) | |
| Co-MOF | ΔE (kJ mol−1) | −6.448 | −9.436 | −9.190 | −10.264 |
| d (Å) | 3.084 (d1) | 3.294 (d2) | 3.483 (d3) | 3.770 (d4) | |
| Cu-MOF | ΔE (kJ mol−1) | −5.999 | −8.591 | −8.634 | −9.828 |
| d (Å) | 3.300 (d1) | 3.536 (d2) | 3.417 (d3) | 4.140 (d4) | |
Table 2 exhibits that the magnitude of the H2 adsorption energy, ΔE, of M-MOF is in the following order of the adsorption sites: metal–TED intersection > TED group > metal cluster > BDC linker, except for M = Co, it is the intersection > metal cluster > TED group > BDC linker. On the other hand, the absolute value of ΔE is in decreasing order: Ni-MOF > Mg-MOF > V-MOF > Co-MOF > Cu-MOF for all adsorption sites of BDC linker, TED group, and metal–TED intersection, except for the metal node, the order between Mg-MOF and V-MOF is approximately the same. Notably, the H2 adsorption strength of Ni-MOF and Cu-MOF is always the best and the worst among the considered metal substitutions, respectively. The most and second most negative H2 adsorption energy of −16.930 kJ mol−1 on Ni-MOF and −12.435 kJ mol−1 on Mg-MOF is around the criterion (−15 kJ mol−1) for the heat of adsorption. Therefore, Ni-MOF and Mg-MOF are expected to offer significant hydrogen adsorption capacity.58 The obtained adsorption energies imply that the M(BDC)(TED)0.5 has a great potential for H2 storage, where the intersection region between the metal cluster and the TED group is predicted to attract hydrogen gas the most. Note that our obtained adsorption energies include only the electronic effects of the interaction between the H2 molecule and the M-MOFs, which are different compared to adsorption enthalpy values that include not only the electronic effects but also other factors such as coverage, temperature, and pressure.59 Furthermore, the adsorption of a single H2 molecule in the unit cell of the M-MOFs gave rise to the highest adsorption energy (Table 2). Simultaneous adsorption of many H2 molecules in the unit cell will lower the average adsorption energy per H2 molecule compared to the single site model. However, we can approximately estimate the average adsorption energies from various single site contributions (BDC linker, metal cluster, TED group, and metal cluster–TED intersection), i.e., in the magnitude order: Ni-MOF (−14.64 kJ mol−1) > Mg-MOF (−10.53 kJ mol−1) > V-MOF (−10.03 kJ mol−1) > Co-MOF (−8.83 kJ mol−1) > Cu-MOF (−8.26 kJ mol−1).
The average distance from the nearest H atom of the H2 molecule to M-MOF (Table 2) shows that, on the BDC linker, the H2 molecule is almost perpendicular to the BDC plane (the end-on configuration of H2, see Fig. 3a) with the average distance from the nearest H atom of H2 to the C atoms d1 = 3.0–3.3 Å. On the metal cluster, the most stable adsorption site for H2 is in the central region of the metal cluster (see Fig. 3b) with an average distance to four O atoms d2 = 3.3–3.5 Å for different M-MOFs. On the TED group (Fig. 3c), H2 is nearly parallel to the C–C bonds of TED (the side-on configuration) with the average distance d3 = 3.4–3.5 Å from the nearest H atoms to the nearest C atoms. In the intersection region between the metal cluster and the TED group, H2 is more favourable in the middle of the intersection with the H–H bond towards the metal cluster (see Fig. 3d). The average distance from the nearest H atom of H2 to the nearest N atom and the nearest metal atom is in the range of d4 = 3.8–4.2 Å. The actual distance from the nearest H atom to M-MOF is that from this H atom to the nearest O atom, which is 2.70 Å.
3.3 Electronic structure properties of H2@M(BDC)(TED)0.5 systems
The total charge of the adsorbed hydrogen molecule calculated by the Bader partition method,47,48 in Table 3, shows that the H2 molecule can gain the charge from M-MOF and lose the charge to M-MOF with the positive and negative values, respectively. However, the charge gain and loss are ignorable because their magnitude is the same as the error (0.005e−) of charge calculation. Therefore, the interaction between the H2 molecule and the M-MOF is dominated by the charge attraction instead of the charge exchange. Therefore, the interaction between them is physisorption. This result supports the obtained adsorption energies, as shown in Table 2.| M-MOF | BDC linker | Metal cluster | TED group | Metal–TED intersection |
|---|---|---|---|---|
| Ni-MOF | 0.0070 | 0.0048 | −0.0003 | 0.0053 |
| Mg-MOF | 0.0054 | 0.0034 | −0.0011 | 0.0053 |
| V-MOF | 0.0048 | 0.0027 | −0.0004 | 0.0008 |
| Co-MOF | 0.0061 | 0.0043 | −0.0001 | 0.0031 |
| Cu-MOF | 0.0052 | 0.0109 | −0.0005 | 0.0059 |
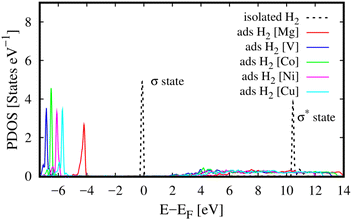
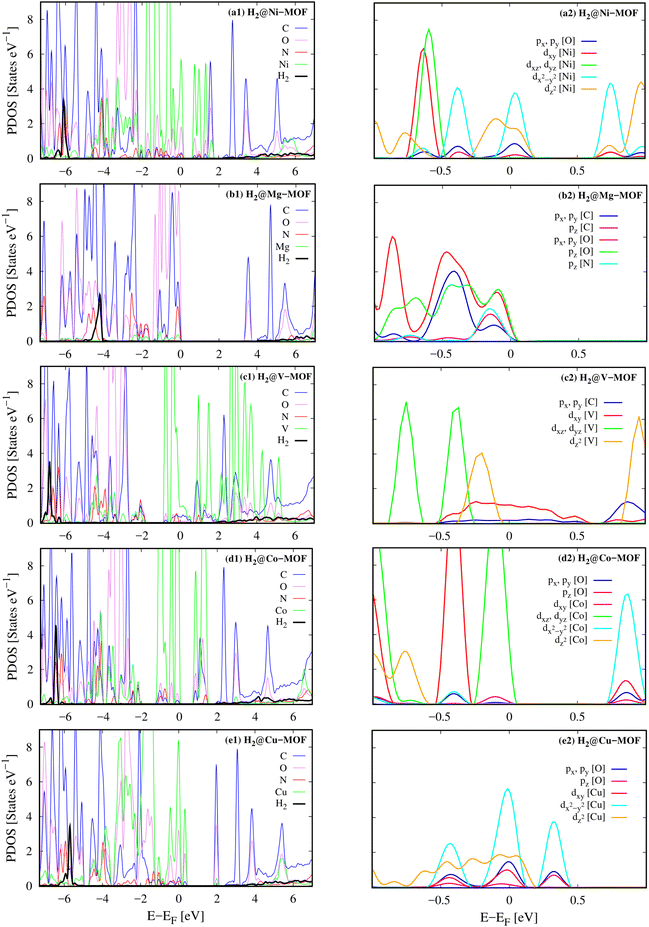
Besides, we can reveal the physical insights with more details into the interaction between the H2 molecule and M-MOF via analysing the electronic density of states of the H2@M(BDC)(TED)0.5 (M = Mg, V, Co, Ni, and Cu) systems. To answer the question of what state of the H2 molecule participates in the interaction, we plotted the total DOS of the H2 molecule before and after its adsorption on the substrate surface (Fig. 4). We found that the isolated H2 molecule has two peaks, i.e., the occupied σ and unoccupied σ* states locating at the negative and positive energies, respectively. The first peak is at the Fermi level, while the second one is about 10 eV away from the Fermi level. When adsorbing in the M-MOF, the σ* state becomes broadened and simultaneously reduced the height; however, it is still in the range of positive energies. Whilst, the peak of the σ state is shifted to a more negative energy level with a slight modification in the shape of the peak. This shift is not due to the charge exchange with the M-MOF because the Bader charge exchange is ignorable, but it is due to the Coulomb attractive interaction between the H2 molecule and the M-MOF (as analysed above). We know that an adsorbate and an adsorbent can combine into a system because the occupied states of the adsorbate can attract the unoccupied states of the adsorbent and vice versa. Therefore, we have to analyse the DOS of the adsorbed-state M-MOF and the adsorbed H2 molecule to understand the contributions of each component of the M-MOF to the interaction with the H2 molecule. As shown in Fig. 5a1–e1 for the metal cluster–TED intersection adsorption site, the atom-projected DOS around the Fermi level is dominated by the states of the N and O atoms for the cases M = Ni, Co, and Cu (Fig. 5a1, d1 and e1), by those of the V and C atoms for M = V (Fig. 5c1), and by the O, C, and N atoms for M = Mg (Fig. 5b1). We found that the metal component (the green line) is dominated around the Fermi level for the considered M-MOFs except for M = Mg. The occupied states of the M-MOFs just below the Fermi level attract and broaden the unoccupied σ* state of the H2 molecule, while the unoccupied states of the M-MOFs, just above the Fermi level for M = Ni, V, Co, and Cu, and at 3.5 eV for M = Mg, attract the occupied σ state of the H2 molecule. However, this attractive interaction is not strong enough to bring the peaks of the H2 molecule to cross the Fermi level. Therefore, no significant charge exchange was found between the adsorbate (H2) and adsorbent (M-MOF), resulting in the physisorption between H2 and M(BDC)(TED)0.5. We have to emphasise that similar characteristics of the DOS were also found for the other adsorption sites (BDC linker, metal cluster, and TED group) of the H2@M-MOF systems. Therefore, we have just focused on the DOS analysis for the metal cluster–TED intersection region. This selection becomes representative because it is the most favourable adsorption site for the H2 molecule, and it is not only close to the metal cluster but also the TED group and the BDC linker.
The close-up view around the Femi level of the orbital-projected DOS, Fig. 5a2–e2, explained the contribution of the different orbitals of the adsorbed-state M-MOFs. We found that the main contributors at the Femi level are the dx2−y2 and dz2 orbitals of the metal atoms for M = Ni and Cu (Fig. 5a1 and e2), the dxy orbital for M = V (Fig. 5c2), and the dxz and dyz orbitals for M = Co (Fig. 5d2). The other portions also come from the O px, py orbitals (Fig. 5a, b2 and e2) and the C px, py orbitals (Fig. 5c2). Besides, the O pz orbital also made a significant contribution at the Fermi level for the Mg-MOF (Fig. 5b2).
Fig. 6 shows the charge density difference for the H2@Ni(BDC)(TED)0.5 system at various adsorption sites. Charge accumulation and donation (in the e− unit) are presented in purple and green colours, respectively. We found that the H2 molecule exhibits the antibonding (σ*) state, showing by two different colours for two H atoms with the node in the middle region of the H–H bond length, for all cases disregarding the end-on configuration (Fig. 6a, b and d) or the side-on configuration (Fig. 6d) of the H2 molecule. One H atom accumulates and the other H atom donates the negative charge. However, the accumulation and donation of the H atoms should not come from the charge exchange with the M-MOF (as mentioned above), but it should stem from the charge rearrangement between two H atoms. This rearrangement creates the charge dipole that, in turn, induces the rearrangement in the charge clouds of the M-MOF to collaborate with the dipole of the H2 molecule. Interestingly, the σ* state of the H2 molecule in the side-on configuration on the TED region is arranged strangely, with the symmetry axis not perpendicular to but made an angle with the H–H bond.
3.4 Gravimetric and volumetric hydrogen storage capacities of M(BDC)(TED)0.5 MOFs
Before calculating the hydrogen storage capacities, we have to obtain the point charge for the atoms of the M-MOF in terms of the DDEC6 framework, where the point charge of hidden atoms is also calculated with better accuracy compared to the Bader partition method. The unit cell size and the geometric structure of M(BDC)(TED)0.5 were first optimized by the vdW-DF density functional theory calculations and the charge density of the obtained structure was exported. The atomic point charge was then computed with the DDEC6 package, which is listed in Table 4 for Ni(BDC)(TED)0.5. The atomic indices are shown in Fig. 7. For the substitutions of the other metals, calculating their partial charges is also performed using the same methodology and steps.| Atoms | q (e) | Atoms | q (e) | Atoms | q (e) | Atoms | q (e) | Atoms | q (e) |
|---|---|---|---|---|---|---|---|---|---|
| H | 0.093277 | H | 0.074371 | C2 | −0.06467 | C2 | −0.06565 | O | −0.53948 |
| H | 0.093177 | H | 0.074219 | C2 | −0.07018 | C3 | 0.638866 | O | −0.51495 |
| H | 0.094422 | H | 0.064973 | C2 | −0.06689 | C4 | −0.081851 | O | −0.53399 |
| H | 0.092604 | H | 0.06552 | C2 | −0.0655 | C3 | 0.634135 | O | −0.52034 |
| H | 0.092547 | H | 0.074004 | C3 | 0.637809 | C4 | −0.075996 | O | −0.53516 |
| H | 0.093763 | H | 0.067559 | C4 | −0.08061 | C1 | −0.026607 | O | −0.52142 |
| H | 0.094164 | H | 0.071051 | C3 | 0.634733 | C1 | −0.029119 | O | −0.53036 |
| H | 0.092883 | H | 0.076798 | C4 | −0.07643 | C1 | −0.019935 | O | −0.52943 |
| H | 0.067228 | H | 0.06806 | C2 | −0.06137 | C1 | −0.024998 | Ni | 0.667318 |
| H | 0.074921 | C1 | −0.02552 | C2 | −0.06856 | N | −0.115297 | Ni | 0.653275 |
| H | 0.068644 | C1 | −0.02485 | C2 | −0.06969 | N | −0.121477 |
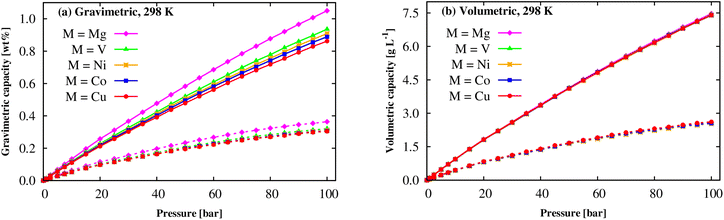
By GCMC simulations for the system repeating by 3 × 3 × 3 times of the DFT unit cell, this work studies the H2 uptake capacity for excess adsorption (nexc) and absolute adsorption (nabs) per the unit mass and volume at cryogenic (77 K) and room (298 K) temperatures, where nabs is calculated via nexc using the expression (6).60 Before officially computing the H2 uptake capacities of M(BDC)(TED)0.5, we are going to validate our model within a rigid M-MOF structure and the selected LJ force field parameters (Subsection 2.2). Although we do not intend to study Zn(BDC)(TED)0.5, the experimental isotherms of this M-MOF are available and shown in the full range of 0–50 bar pressures and at temperatures of 298 K and 77 K. As shown in Fig. S1 and Table S1 of ESI,† our obtained results, with the same model as Subsection 2.2, are in good agreement, particularly for 298 K, with the experiment with an error of well below 20% for the gravimetric excess loadings. Using flexible and new parameterized force fields perhaps solves the discrepancies. However, such force fields are not available in the present work. For gravimetric loadings at 298 K, Fig. 8a shows that the nabs and nexc quantities monotonically increase as the pressures increase up to 100 bar. Mg can significantly enhance the isotherms over the other metals, and the absolute amount increases relatively faster than the excess quantity. In a close-up view, for each pressure, the gravimetric adsorption capacity is in the order: Cu-MOF < Co-MOF < Ni-MOF < V-MOF < Mg-MOF. Here, the Mg(BDC)(TED)0.5 achieves the highest H2 uptake capacity among the studied M-MOFs with nexc = 0.36 wt% and nabs = 1.05 wt%, see Table 5. However, the gravimetric excess and absolute capacities are slightly different for the other metals at room temperature and pressure of 100 bar. The results exhibited that gravimetric H2 uptakes of M(BDC)(TED)0.5 are an acceptable agreement with the experiments for Co(BDC)(DABCO)0.5,61,62 Cu(BDC)(DABCO)0.5 (ref. 62) (DABCO = TED), and comparable to those of well-known MOFs such as MIL-101 (Cr),63 but lower than those of the best MOFs so far, i.e., MOF-74 (Mg),64 Be12(OH)12(BTB)4,21 and MOF-5,65 and slightly higher than MIL-88A (M).13 Note that the best MOFs only achieved 1–2 wt% absolute H2 uptake at ambient conditions.11–13,23,24 A monotonic behaviour (Fig. 8b) is also found for the volumetric excess and absolute uptakes for all the cases of metals. Also, the metal substitution negligibly impacts volumetric H2 storage capacity at ambient conditions. The maximum values for the volumetric excess and absolute loadings are about 2.55 and 7.40 g L−1 (i.e., 29.0 and 83.5 cm3 (STP) cm−3, STP = standard temperature and pressure) at 298 K and the pressure of 100 bar. These values are the same as those of MIL-88A (M);13 however, the maximum absolute capacity of M-MOF is lower than the best MOF, Be12(OH)12(BTB)4.21 We can also decrease the temperature to cryogenic condition to significantly increase the hydrogen uptake capacities.11,60
| MOFs | Pressure (bar) | Excess (absolute) uptakes | |
|---|---|---|---|
| Gravimetric in wt% | Volumetric in g L−1 | ||
| Mg-MOF | 100 | 0.36 (1.05) | 2.59 (7.47) |
| V-MOF | 100 | 0.32 (0.94) | 2.55 (7.42) |
| Ni-MOF | 100 | 0.31 (0.91) | 2.53 (7.39) |
| Co-MOF | 100 | 0.31 (0.90) | 2.55 (7.39) |
| Cu-MOF | 100 | 0.30 (0.86) | 2.62 (7.40) |
| Co(BDC)(DABCO)0.5 | 100 | 0.32 (293 K)62 | |
| Cu(BDC)(DABCO)0.5 | 100 | 0.42 (293 K)62 | |
| MIL-101 (Cr) | 80 | 0.43 (ref. 63) | |
| MOF-74 (Mg) | 100 | 0.80 (ref. 64) | |
| Be12(OH)12(BTB)4 | 95 | 1.0 (2.3)21 | (11)21 |
| MOF-5 | 48 | 1.65 (ref. 65) | |
| MIL-88A (M) (M = Co, Fe, Ni, Mn, Cr, V, Ti, Sc) (simulation) | 100 | 0.22–0.29 (0.63–0.72)12 | 2.44–2.83 (6.94–7.08)12 |
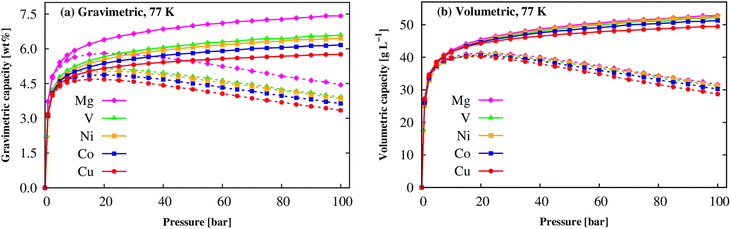
At the cryogenic temperature of 77 K, Fig. 9 shows that a similar behaviour was found for the gravimetric and volumetric uptake capacities, where the absolute and excess curves increase quickly at low pressures, and then the excess uptakes approach the maximum values at the pressure of 20 bar for M = Mg, V, Co, Cu and of 25 bar for M = Ni, while the absolute values continue increasing until 100 bar. The maximum values are shown in Table 6. We found that Mg(BDC)(TED)0.5 also obtains the best gravimetric and volumetric H2 adsorption capacities at 77 K, nexc = 5.80 wt% and nabs = 7.42 wt% followed by V-MOF > Ni-MOF > Co-MOF > Cu-MOF for gravimetric uptake, 41.26 g L−1 and 52.77 g L−1 and slightly higher than the other M-MOFs. Although the gravimetric H2 storage capacity of the M-MOFs is still lower than that of the best MOFs such as MOF-177, MOF-210, and NU-100, comparable to that of MOF-5 and Be12(OH)12(BTB)4, but significantly higher than that of MOF-74, MIL-53 (M), Zn(BDC)(TED)0.5, and MIL-88A (M) (Table 6). Remarkedly, our result for Co-MOF shows a reasonable agreement with the experimental data, 4.87 vs. 4.11 wt%.62 To date, much attention has been paid to gravimetric capacities and less volumetric capacities to reach DOE's target. Our results indicated that M-MOFs exhibit comparable volumetric uptakes to MIL-88A (M) and significantly higher than those 43 g L−1 at 100 bar of Be12(OH)12(BTB)4.21 We also found that the adsorbed H2 amounts at 77 K are much higher than those at 298 K, also meeting the DOE targets. Therefore, the M(BDC)(TED)0.5 MOFs are promising for hydrogen storage at low temperatures.
| MOFs | Pressure for excess (absolute) uptakes, bar | Excess (absolute) uptakes | |
|---|---|---|---|
| Gravimetric, wt% | Volumetric, g L−1 | ||
| Mg-MOF | 20 (100) | 5.80 (7.42) | 41.26 (52.77) |
| V-MOF | 20 (100) | 5.13 (6.59) | 40.71 (52.23) |
| Ni-MOF | 25 (100) | 5.03 (6.42) | 40.91 (52.52) |
| Co-MOF | 20 (100) | 4.87 (6.17) | 40.55 (51.29) |
| 4.11 (ref. 62) | |||
| Cu-MOF | 20 (100) | 4.68 (5.76) | 40.20 (49.47) |
| MOF-74 | 30 | 2.8 (ref. 70) | |
| MIL-53 (M) (M = Al, Cr) | 16 | 3.8 (Al), 3.1 (Cr)71 | |
| Zn(BDC)(TED)0.5 | 20 | ∼4.06 (UFF), ∼4.38 (Buch potential),33 ∼4.28 (experiment)33 | |
| MIL-88A (M) (M = Co, Fe, Ni, Mn, Cr, V, Ti, Sc) (simulation) | 10–15 (100) | 4.00–4.63 (4.60–5.30)12 | 43.78–45.51 (50.57–51.99)11 |
| MOF-5 | 65 | 5.1 (ref. 22) | |
| Be12(OH)12(BTB)4 | 20 (100) | 6.0 (9.2)21 | (43)21 |
| MOF-177 | 70 | 7.5 (11)20 | |
| MOF-210 | 80 | 8.6 (17.6)18 | |
| NU-100 | 56 (70) | 9.95 (16.4)19 | |
As shown in the above parts, we observed that the Ni and Mg substitutions displayed the best and the second-best enhancements of the H2 adsorption energy at the adsorption sites. However, their order is opposite for the gravimetric and volumetric storage capacities. The order of their adsorption energies can be explained via the differences in their electronic structure properties, as discussed in the upper section. We now have to study the effects of structural characteristics such as specific surface area (SSA) and pore volume (Vpore) of M-MOFs to see whether there are any influences of these factors on the H2 adsorption capacity, particularly for the gravimetric uptake because of more significant variations found for the metal substitutions. The data are visualized in Fig. 10, which shows a correlation between the maximum gravimetric uptake versus SSA and Vpore at 298 K (Fig. 10a and b) and 77 K (Fig. 10c and d). It shows that the correlations are almost linear. Compared to 298 K, the linear dependences of the adsorption amount at 77 K on SSA and Vpore are also more obvious. This behaviour was also found for several MOFs in the literature,12,66,67 higher than Chahine's rule that was widely accepted in many previous works that every 500 m2 g−1 of SSA obtains ca. 1.0 wt% saturated H2 loading at 77 K and the pressure ≥ 20 bar.67–69
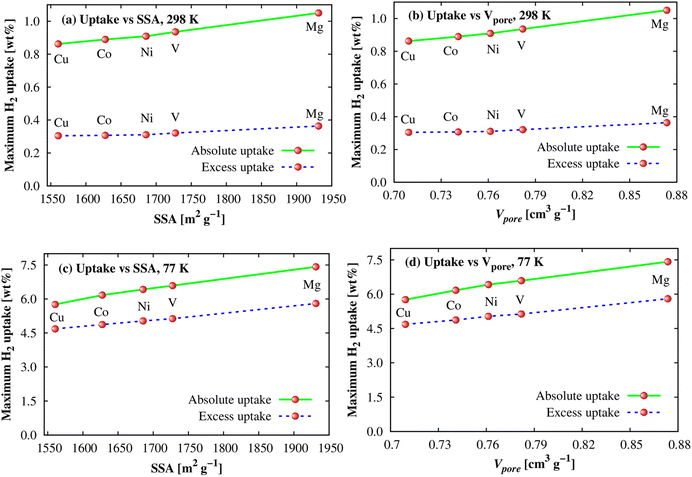 | ||
| Fig. 10 The dependence of the H2 gravimetric uptakes on SSA and pore volume of M-MOFs at 298 K (a and b) and 77 K (c and d). | ||
4 Conclusions
We investigated the hydrogen storage in M(BDC)(TED)0.5 metal–organic framework (M = Mg, V, Co, Ni, and Cu) by the combination of the vdW-DF density functional theory calculations and the grand canonical Monte Carlo simulations. We obtained the most favourable adsorption sites and configurations for the hydrogen molecule in M(BDC)(TED)0.5. The favourable order for the H2 adsorption sites is the metal cluster–TED intersection > TED group > metal cluster > BDC linker for M = Mg, V, Ni, and Cu, but the metal cluster–TED intersection > metal cluster > TED group > BDC linker for M = Co. The constructive order for enhancing the H2 adsorption strength is Ni > Mg > V > Co > Cu. The H2 molecule uses its σ* antibonding state, while M(BDC)(TED)0.5 mainly uses the d orbital of the metal atoms for M = Ni, V, Cu, and Co and the p orbital of the O, C, N atoms for M = Mg, to participate in the interaction between the H2 molecule and M(BDC)(TED)0.5. This interaction is physisorption with the local rearrangement of charge dipoles without charge exchange crossing the adsorbate and the adsorbent. Considering the effects of temperature and pressure, we obtained the gravimetric and volumetric H2 uptake capacities and found that the adsorption ability of M(BDC)(TED)0.5 with M = Mg is the best one among the considered metal substitutions. The Mg atoms bring not only the differences in the characteristics of DOS but also the largest specific surface area and pore volume to facilitate hydrogen storage.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Conceptualization (DNS, NTXH), formal analysis (DNS, NTXH, NTYN), investigation (NTXH, DNS), resources (DNS, NTXH, VTN, VC), supervision (DNS, VC), validation (NTXH, DNS, VTN), visualization (NTXH, NTYN), writing of original draft (DNS, NTXH), reviewing and editing (DNS, NTXH, VC).Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research is funded by Vietnam Ministry of Education and Training (MOET) under grant number B2022-DQN-05.References
- S. Y. Lee, J. H. Lee, Y. H. Kim, J. W. Kim, K. J. Lee and S. J. Park, Processes, 2022, 10, 304 CrossRef CAS.
- A. Li, J. Phys.: Conf. Ser., 2022, 2403, 012022 CrossRef CAS.
- X. Zhang, P. Liu and Y. Zhang, Inorg. Chim. Acta, 2023, 557, 121683 CrossRef CAS.
- M. Momirlan and T. N. Veziroglu, Int. J. Hydrogen Energy, 2005, 30, 795–802 CrossRef CAS.
- R. Li, X. Han, Q. Liu, A. Qian, F. Zhu, J. Hu, J. Fan, H. Shen, J. Liu, X. Pu, H. Xu and B. Mu, ACS Omega, 2022, 7, 20081–20091 CrossRef CAS PubMed.
- Z. A. Sandhu, M. A. Raza, N. S. Awwad, H. A. Ibrahium, U. Farwa, S. Ashraf, A. Dildar, E. Fatima, S. Ashraf and F. Ali, Mater. Adv., 2024, 5, 30–50 RSC.
- M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. S. Cho, H. Furukawa, M. Haranczyk, M. Head-gordon, S. Jeong, A. Karkamkar, D. Liu, J. R. Long, K. R. Meihaus, I. H. Nayyar, R. Nazarov, D. J. Siegel, V. Stavila, J. J. Urban, P. S. Veccham and B. C. Wood, Energy Environ. Sci., 2018, 11, 2784–2812 RSC.
- C. Liu, F. Li, L. P. Ma and H. M. Cheng, Adv. Mater., 2010, 22, E28–E62 CAS.
- Z. Chen, K. O. Kirlikovali, K. B. Idrees, M. C. Wasson and O. K. Farha, Chem, 2022, 8, 693–716 CAS.
- N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS PubMed.
- V. Zeleňák and I. Saldan, Nanomaterials, 2021, 11, 1638 CrossRef PubMed.
- N. T. X. Huynh, V. Chihaia and D. N. Son, Adsorption, 2020, 26, 509–519 CrossRef CAS.
- N. T. X. Huynh, V. Chihaia and D. N. Son, J. Mater. Sci., 2019, 54, 3994–4010 CrossRef.
- Z. Zhang, Y. Wang, H. Wang, X. Xue and Q. Lin, Front. Mater., 2021, 8, 766288 CrossRef.
- T. T. T. Huong, P. N. Thanh, N. T. X. Huynh and D. N. Son, VNU Journal of Science: Mathematics - Physics, 2016, 32, 67–85 Search PubMed.
- S. Meduri and J. Nandanavanam, Mater. Today Proc., 2023, 72, 1–8 CrossRef CAS.
- J. A. Gómez and D. M. F. Santos, Designs, 2023, 7, 97 CrossRef.
- H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. O. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428 CrossRef CAS PubMed.
- O. K. Farha, A. Ö. Yazaydın, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948 CrossRef CAS PubMed.
- H. Furukawa, M. A. Miller and O. M. Yaghi, J. Mater. Chem., 2007, 17, 3197–3204 RSC.
- K. Sumida, M. R. Hill, S. Horike, A. Dailly and J. R. Long, J. Am. Chem. Soc., 2009, 131, 15120–15121 CrossRef CAS PubMed.
- B. Panella, M. Hirscher, H. Putter and U. Muller, Adv. Funct. Mater., 2006, 16, 520–524 CrossRef CAS.
- Y. Liu, D. Shen, Z. Tu, L. Xing, Y. G. Chung and S. Li, Int. J. Hydrogen Energy, 2022, 47, 41055–41068 CrossRef CAS.
- X. Zhang, Q. r. Zheng and H. z. He, J. Taiwan Inst. Chem. Eng., 2022, 138, 104479 CrossRef CAS.
- M. S. Shannon, A. C. Irvin, H. Liu, J. D. Moon, M. S. Hindman, C. H. Turner and J. E. Bara, Ind. Eng. Chem. Res., 2015, 54, 462–471 CrossRef CAS.
- A. Schoedel, Z. Ji and O. M. Yaghi, Nat. Energy, 2016, 1, 16034 CrossRef CAS.
- L. Peng, S. Wu, X. Yang, J. Hu, X. Fu, Q. Huo and J. Guan, RSC Adv., 2016, 6, 72433–72438 RSC.
- K. Tan, P. Canepa, Q. Gong, J. Liu, D. H. Johnson, A. Dyevoich, P. K. Thallapally, T. Thonhauser, J. Li and Y. J. Chabal, Chem. Mater., 2013, 25, 4653–4662 CrossRef CAS.
- D. N. Son, T. T. T. Huong and V. Chihaia, RSC Adv., 2018, 8, 38648–38655 RSC.
- Y. F. Chen, J. Y. Lee, R. Babarao, J. Li and J. W. Jiang, J. Phys. Chem. C, 2010, 114, 6602–6609 CrossRef CAS.
- H. Xiang, A. Ameen, P. Gorgojo, F. R. Siperstein, S. M. Holmes and X. Fan, Microporous Mesoporous Mater., 2020, 292, 109724 CrossRef CAS.
- J. Y. Lee, D. H. Olson, L. Pan, T. J. Emge and J. Li, Adv. Funct. Mater., 2007, 17, 1255–1262 CrossRef CAS.
- J. Liu, J. Y. Lee, L. Pan, R. T. Obermyer, S. Simizu, B. Zande, J. Li, S. G. Sankar and J. K. Johnson, J. Phys. Chem. C, 2008, 112, 2911–2917 CrossRef CAS.
- N. T. X. Huynh, O. K. Le, T. P. Dung, V. Chihaia and D. N. Son, RSC Adv., 2023, 13, 15606–15615 RSC.
- J. H. Bak, V.-D. Le, J. Kang, S. Wei and Y.-H. Kim, J. Phys. Chem. C, 2012, 116, 7386–7392 CrossRef CAS.
- T. Pham, K. A. Forrest, R. Banerjee, G. Orcajo, J. Eckert and B. Space, J. Phys. Chem. C, 2015, 119, 1078–1090 CrossRef CAS.
- K. Lee, J. D. Howe, L. C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668–678 CrossRef CAS.
- K. Pareek, R. Rohan, Z. Chen, D. Zhao and H. Cheng, Int. J. Hydrogen Energy, 2017, 42, 6801–6809 CrossRef CAS.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, J. Chevary, S. Vosko, K. Jackson, M. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens.Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- J. Kohanoff, Electronic Structure Calculations for Solids and Molecules: Theory and Computational Methods, Cambridge University Press, Cambridge, 2006 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- D. Levesque, A. Gicquel, F. L. Darkrim and S. B. Kayiran, J. Phys.: Condens.Matter, 2002, 14, 9285–9293 CrossRef CAS.
- V. G. Tyuterev and N. Vast, Comput. Mater. Sci., 2006, 38, 350–353 CrossRef CAS.
- N. T. X. Huynh, O. M. Na, V. Chihaia and D. N. Son, RSC Adv., 2017, 7, 39583–39593 RSC.
- K. Tan, N. Nijem, P. Canepa, Q. Gong, J. Li, T. Thonhauser and Y. J. Chabal, Chem. Mater., 2012, 24, 3153–3167 CrossRef CAS.
- S. K. Bhatia and A. L. Myers, Langmuir, 2006, 22, 1688–1700 CrossRef CAS PubMed.
- D. Dubbeldam, S. Calero, T. J. H. Vlugt, R. Krishna, T. L. M. Maesen and B. Smit, J. Phys. Chem. B, 2004, 108, 12301–12313 CrossRef CAS.
- J. A. Mason, M. Veenstra and J. R. Long, Chem. Sci., 2014, 5, 32–51 RSC.
- L. G. Zhu and H. P. Xiao, Z. Anorg. Allg. Chem., 2008, 634, 845–847 CrossRef CAS.
- T. Takei, J. Kawashima, T. Ii, A. Maeda, M. Hasegawa, T. Kitagawa, T. Ohmura, M. Ichikawa, M. Hosoe, I. Kanoya and W. Mori, Bull. Chem. Soc. Jpn., 2008, 81, 847–856 CrossRef CAS.
- M. Latroche, S. Surblé, C. Serre, C. Mellot-Draznieks, P. L. Llewellyn, J. H. Lee, J. S. Chang, H. J. Sung and G. Férey, Angew. Chem., Int. Ed., 2006, 45, 8227–8231 CrossRef CAS PubMed.
- K. Sumida, C. M. Brown, Z. R. Herm, S. Chavan, S. Bordiga and J. R. Long, Chem. Commun., 2011, 47, 1157–1159 RSC.
- L. Pan, M. B. Sander, X. Huang, J. Li, M. Smith, E. Bittner, B. Bockrath and J. K. Johnson, J. Am. Chem. Soc., 2004, 126, 1308–1309 CrossRef CAS PubMed.
- D. Fairen-Jimenez, Y. J. Colón, O. K. Farha, Y.-S. Bae, J. T. Hupp and R. Q. Snurr, Chem. Commun., 2012, 48, 10496–10498 RSC.
- L. Zhang, M. D. Allendorf, R. Balderas-Xicohténcatl, D. P. Broom, G. S. Fanourgakis, G. E. Froudakis, T. Gennett, K. E. Hurst, S. Ling, C. Milanese, P. A. Parilla, D. Pontiroli, M. Riccò, S. Shulda, V. Stavila, T. A. Steriotis, C. J. Webb, M. Witman and M. Hirscher, Prog. Energy, 2022, 4, 042013 CrossRef.
- J. S. Camp, V. Stavila, M. D. Allendorf, D. Prendergast and M. Haranczyk, J. Phys. Chem. C, 2018, 122, 18957–18967 CrossRef CAS.
- M. Hirscher, V. A. Yartys, M. Baricco, J. Bellosta von Colbe, D. Blanchard, R. C. Bowman, D. P. Broom, C. E. Buckley, F. Chang, P. Chen, Y. W. Cho, J. C. Crivello, F. Cuevas, W. I. F. David, P. E. de Jongh, R. V. Denys, M. Dornheim, M. Felderhoff, Y. Filinchuk, G. E. Froudakis, D. M. Grant, E. M. A. Gray, B. C. Hauback, T. He, T. D. Humphries, T. R. Jensen, S. Kim, Y. Kojima, M. Latroche, H. W. Li, M. V. Lototskyy, J. W. Makepeace, K. T. Møller, L. Naheed, P. Ngene, D. Noréus, M. M. Nygård, S. i. Orimo, M. Paskevicius, L. Pasquini, D. B. Ravnsbæk, M. V. Sofianos, T. J. Udovic, T. Vegge, G. S. Walker, C. J. Webb, C. Weidenthaler and C. Zlotea, J. Alloys Compd., 2020, 827, 153548 CrossRef CAS.
- A. G. Wong-Foy, A. J. Matzger and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 3494–3495 CrossRef CAS PubMed.
- G. Ferey, M. Latroche, C. Serre, F. Millange, T. Loiseau and A. Percheron-Guegan, Chem. Commun., 2003, 2976–2977 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Hydrogen storage in M(BDC)(TED)0.5 metal–organic framework: physical insights and capacities. See DOI: https://doi.org/10.1039/d4ra02697g |
| This journal is © The Royal Society of Chemistry 2024 |