Open Access Article
Open Access ArticleThe Li2Ti6O13 and Li2Zr6O13 composite as a high-performance anode for alkali-ion batteries: a molecular dynamics study†
Yohandys A. Zulueta a,
Minh Tho Nguyen
a,
Minh Tho Nguyen *bc and
My Phuong Pham-Ho
*bc and
My Phuong Pham-Ho de
de
aDepartamento de Física, Facultad de Ciencias Naturales y Exactas, Universidad de Oriente, Santiago de Cuba, CP 90500, Cuba
bLaboratory for Chemical Computation and Modeling, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: minhtho.nguyen@vlu.edu.vn
cFaculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
dFaculty of Chemical Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam
eVietnam National University Ho Chi Minh City, Linh Trung Ward, Thu Duc City, Ho Chi Minh City, Vietnam
First published on 19th July 2024
Abstract
The current development of technology has highlighted the necessity of compounds that enhance the durability and performance of alkali-ion batteries. The anodes of these batteries need to overcome the challenges of low dc-conductivity at ambient temperatures and interfacial resistance between the solid-state electrolyte. By conducting large-scale molecular dynamics simulations, we investigated the transport properties of Li2Ti6O13 and Li2Zr6O13 mono- and bi-crystals, as well as Li2Ti6O13@Li2Zr6O13 composites. While the monocrystalline and bi-crystalline Li2Zr6O13 show similar transport properties, the composite materials, combining both compounds, exhibit the highest diffusion coefficients and dc-conductivity. The transport properties of the composite materials are found to be significantly higher than those mono- and bi-crystalline samples due to the Li interstitial mechanism and the presence of grain boundaries. Our study offers valuable insights for the development of high-performance energy storage materials.
1. Introduction
Lithium hexatitanate (Li2Ti6O13) is one of the materials that can be used as a negative electrode in lithium ion batteries (LIBs). Li2Ti6O13 has a tunnel structure with a large surface area, a theoretical capacity of 170 mA h g−1, open cell voltage of 1.5–1.7 V and dc conductivity at 25 °C of 5.6 × 10−6 S cm−1. These structural and electrochemical properties make this compound an intriguing anode material.1–5 Despite such intrinsic properties, many experimental strategies were considered to improve the anode performance, and it appears that Li2Ti6O13 is less promising than lithium pentatitanate (Li4Ti5O12) for use as a anode.1–6In a previous work, a new compound, lithium hexazirconate (Li2Zr6O13), and its anode performance were studied by using density functional theory computations.5 The Li2Zr6O13 possesses the lattice structure of Li2Ti6O13, including the lattice, electronic and mechanical properties. The open cell voltage of Li2Zr6O13 is close to the reported value for Li2Ti6O13 and other anode materials.1–5,7 Various experimental strategies have been devoted to improve the performance of similarly active materials for anodes.1–12 For instance, Li2TiO3 was used as a co-material to stabilize the structure and enhance the electrode material with better electrochemical performance of the combined Li4Ti5O12–Li2TiO3 whose ionic conductivity is higher than that of Li4Ti5O12.8,9 Carbon-coating free, β-Li2TiO3 delivers a specific capacity of 200 mA h g−1 within 100 cycles and 170 mA h g−1 after 500 cycles preserving a coulombic efficiency above 97%.10 Graphene supported Li2SiO3/Li2SnO3 prepared through a hydrothermal method has an initial specific capacity of 1016.5 mA h g−1 and its specific capacity amounts to 440.8 mA h g−1 after 200 cycles. The enhancement of lithium storage of this composite was explained by the synergy among the composite components.11 In addition, the temperature dependence of electrical properties of composites formed by biphasic sodium titanate and poly(o-methoxyaniline) (Na2Ti3O7/Na2Ti6O13/POMA) with different concentrations of POMA was determined from complex impedance measurements.12 Differences on the electrical properties between the composite and individual components were reported.12
In this context we set out to search for a co-material which can be combined with Li2Ti6O13 using molecular dynamics simulations. In fact, atomistic simulation is a powerful tool to investigate structure–property relations and for theoretical design of new materials.13–16 In particular, classical molecular dynamics computations provide us with relevant information concerning the transport properties in large systems.13–16
The nudged elastic band (NEB) method and molecular dynamics (MD) simulations are popular computational methods used to investigate the behaviour of molecules and materials at the atomic level. The main difference between the two methods consists in the fact that NEB computations are used to evaluate the energy barriers and reaction pathways between different stable states, whereas MD is used to probe the behaviour of materials over time and their dynamic behaviour. In addition, MD computations allow the investigation of very large molecular systems including the polycrystalline materials.
Various theoretical studies on Li2Ti6O13 have been reported, disclosing its thermodynamic stability, lattice properties, doping effect, and partially diffusion process.5,7,17–19 To our knowledge, full molecular dynamics simulations disclosing the transport properties of Li2Ti6O13 have not been reported yet. To further understand the factors influencing the electrochemical behaviour, the transport properties are essential keys for determine the Li insertion/de-insertion rates.
Transport properties depend not only on the atomic mass and net charge of the mobile, but also on the migration path and the proper structure of the system. It is well-known that the effect of grain boundary is important on transport properties in polycrystalline materials.20–22 In the present study, we conduct large-scale MD computations with the aim to disclose transport properties of both mono- and bi-crystalline Li2B6O13 with the metal B = Ti, Zr, and as mentioned above, of a new ceramic composite materials combining for the first time both Li2Ti6O13 and Li2Zr6O13 compounds. In particular, the influence of the grain boundary on transport properties are disseminated, providing us with some relevant strategies stimulating future experimental investigations.
2. Computational protocols
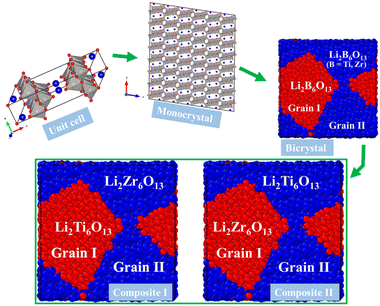
Fig. 1 displays the unit cell of the hexa-metaloxide Li2B6O13 with B = Ti and Zr in the conventional representation. The monoclinic Li2B6O13 crystal structure consists of a corner-sharing [BO6] octahedron and a [LiO4] tetrahedron. The [BO6] octahedron forms chains along the b-axis of the crystal, which are connected by the [LiO4] tetrahedron to form a three-dimensional (3D) structure. The tunnels running along the b-axis serve as ion channels for lithium ion diffusion.1–5,7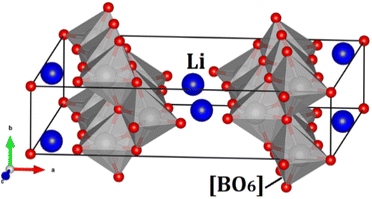 | ||
| Fig. 1 Conventional representation of the hexa-metal-oxide Li2B6O13 (B = Ti, Zr) unit cell in the C2/m. Blue balls represent the Li ions and the grey polyhedron the [BO6] octahedron. | ||
High diffusion coefficient and high dc-conductivity, complemented by low activation energies at operative temperatures, are crucial parameters for evaluating potential battery materials as they ensure fast Li transport properties. In fact, the exceptional ion transport properties enable the desirable anode to exhibit better cycling performance, preventing a certain chemical reactivity between the anode and the solid-state electrolyte.23–27 In this study, the Large-Scale Atomic-Molecular Massively Parallel Simulator (LAMMPS)28 code is used to perform large-scale MD simulations with periodic boundary conditions to disclose Li+ transport properties. The potential parameters employed, also known as force fields, are taken from previous reports.18,29 The Buckingham approximation is used for the short-range interactions, while long-range are purely coulombic describing the long-range potential energy.
Fig. 2 displays the workflow followed in this study. The mono- and bi-crystalline structures of the hexa metal-oxide Li2B6O13 for both metals B = Ti, Zr, as well as the Li2Ti6O13@Li2Zr6O13 and Li2Zr6O13@Li2Ti6O13 composite samples, are constructed by using the Voronoi tessellation method as compiled in the Atomsk code.30 For monocrystalline Li2Ti6O13 (Li2Zr6O13) samples, we use a supercell containing 360 unit cells (4 × 15 × 6 unit cells). In this sense, monocrystalline samples consist of a single grain. In contrast, bi-crystalline Li2Ti6O13 (Li2Zr6O13) have two randomly oriented grains shown as Grain I and Grain II in Fig. 2.
Regarding composite materials, Li2Ti6O13@Li2Zr6O13 and Li2Zr6O13@Li2Ti6O13, they are constructed from the template of their bi-crystalline simulation boxes. The label (Grain I)@(Grain II) indicates that in Li2Ti6O13@Li2Zr6O13, Grain I consists of Li2Ti6O13, while Grain II comprises Li2Zr6O13. Similarly, for Li2Zr6O13@Li2Ti6O13, Grain I is Li2Zr6O13, and Grain II is Li2Ti6O13. In this paper, the term composition refers hereafter to the Li2B6O13 (B = Ti, Zr) structure present in each grain.
Simulation boxes of 60 × 60 × 60 Å3 are used for modelling the bi-crystalline and composite samples. To probe the Li+ migration, we introduce low concentration (0.09) of Li+ vacancies compensated by O2− vacancies (in accordance with the Li2O Schottky defect) inside the simulation boxes. The size of simulation boxes for monocrystalline samples, resulting in a 61.71 × 56.63 × 55.94 Å3, close to the bi-crystalline and composite samples.
During the tessellation process, certain ions are placed too close to each other or even superimposed. As a result, these ions are either removed or separated prior to introducing defects into the bi-crystalline sample. Any extra charge which may arise due to the introduction of defect concentration is compensated by Li+ vacancies.
To ensure the accuracy of the simulation results, the simulation boxes undergo equilibration using an isothermal–isobaric ensemble (NPT). Once equilibrated, constant volume–temperature NVT ensemble is used for production, with the mean square displacement (MSD) for the Li+ ions being saved to calculate their diffusion coefficient (D).
The slope of the MSD plots is used to obtain the diffusion coefficient as follows:
| MSD = 6Dt | (1) |
In the ESI,† a sample of LAMMPS input files of mono-, bi-crystalline Li2Zr6O13 samples, and Li2Zr6O13@Li2Ti6O13 composite are included for reproducibility providing further simulation details for use by the readers.
The diffusion data computed are then converted to the dc-conductivity by using the Nernst–Einstein equation:
| σ(T) = HVNq2D(T)/kBT | (2) |
We assume HV = 1 due to the lack of experimental measurements of diffusion and conduction processes in these materials, in particular for Li2Zr6O13. Both the diffusion and conduction processes are thermally activated; it implies that the relevant kinetics follow the conventional Arrhenius equation Δ(T) = Δ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−EΔa/kBT), where kB represents the Boltzman constant, T the temperature, Δ0 the pre-exponential factor (Δ(T) → Δ0, T → ∞) and EΔa the activation energy, with Δ = D the Arrhenius dependence for diffusion can be obtained, while for Δ = σ, the conduction process is determined.
exp(−EΔa/kBT), where kB represents the Boltzman constant, T the temperature, Δ0 the pre-exponential factor (Δ(T) → Δ0, T → ∞) and EΔa the activation energy, with Δ = D the Arrhenius dependence for diffusion can be obtained, while for Δ = σ, the conduction process is determined.
Together with the activation energy, the diffusion and dc-conductivity at 25 °C are the magnitudes characterizing the transport properties in ionic materials.13,15,22,29
3. Results and discussion
3.1 Tracking Li+-ion in mono-, bi-crystalline Li2B6O13 (B = Ti, Zr) and Li2Ti6O13@Li2Zr6O13 composite samples
The temporal evolution of MSDs with respect to the temperature of Li2Ti6O13 and Li2Zr6O13 are depicted in Fig. 3. As it is shown, the slope of all MSD plots increases with the increment of the temperature, indicating the presence of a thermally activated process. Another interesting finding is that the MSD plots for Li2Ti6O13 are placed higher than that for Li2Zr6O13.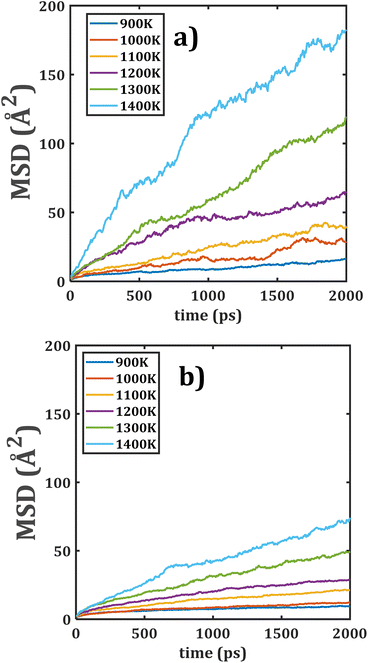 | ||
| Fig. 3 Mean square displacement (MSD) versus simulation time of monocrystalline (a) Li2Ti6O13 and (b) Li2Zr6O13. | ||
The diffusion coefficient, obtained from eqn (1), are thus larger in Li2Ti6O13 as compared to the monocrystalline Li2Zr6O13. It can be attributed to the ionic radius difference of 0.115 Å between the Zr4+ and Ti4+ ions with direct implications on the structural characteristics such as lattice parameters the [LiO4] space channels, the Li–Li distance, the [BO6] octahedral volume, bond angle variance and average O–O distance.5,31
The Li–Li distance is related to the diffusion jump distance where the diffusion mechanism strongly depends on the diffusion jump distance. Li2Zr6O13 has longer Li–Li distance as compared to their isostructural Li2Ti6O13,5 in such a way that lower Li+ diffusion coefficients are expected in monocrystalline Li2Zr6O13.
Fig. 4 shows the temporal evolution of MSD of the bi-crystalline Li2Ti6O13 and Li2Zr6O13 samples. In this case, the linear dependence of MSD with respect to time is more appreciable in the entire range of the simulation time; it is ascribed to the presence of grain boundaries.
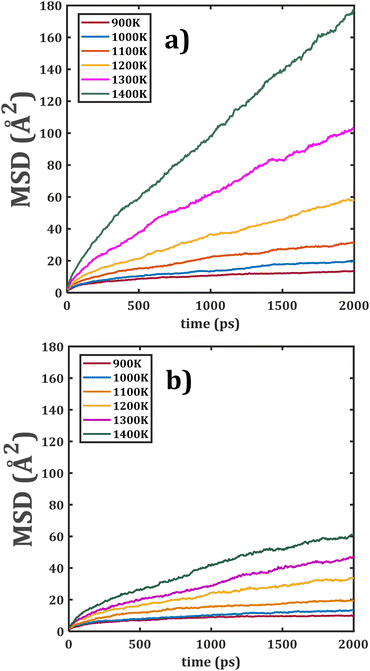 | ||
| Fig. 4 Mean square displacement (MSD) versus simulation time of bi-crystalline (a) Li2Ti6O13 and (b) Li2Zr6O13. | ||
The grain boundary affects the transport properties introducing additional Li+ vacancies in the sample, thereby favouring the Li+ migration. Analogously, the diffusion characteristic in Li2Ti6O13 is better than the one in its Zr counterpart. The effect of [BO6] octahedral distortion, together with the grain boundaries, are the sources of better transport properties in bi- against monocrystalline samples. 5,20–22
The next step deals with the Li+ transport properties of the target Li2Ti6O13@Li2Zr6O13 and Li2Zr6O13@Li2Ti6O13 composite samples. As was described in Section 2 (and depicted in Fig. 2), the Li2Ti6O13@Li2Zr6O13 composite consists in a bi-crystal where Grain I contains Li2Ti6O13 and Grain II, Li2Zr6O13 (denoted as LTZO), while the Li2Zr6O13@Li2Ti6O13 composite is the inverse: the Grain II contain Li2Ti6O13 and Grain I is constituted by Li2Zr6O13 (denoted as LZTO).
Fig. 5 displays the MSD plots of both composite materials. Comparison of both MSD versus time points out appreciable similarities between the slopes of each temperature and better linear dependence as compared to the individual monocrystalline samples. These results suggest that a change in the grain composition does not affect the Li+ transport properties in these composite materials.
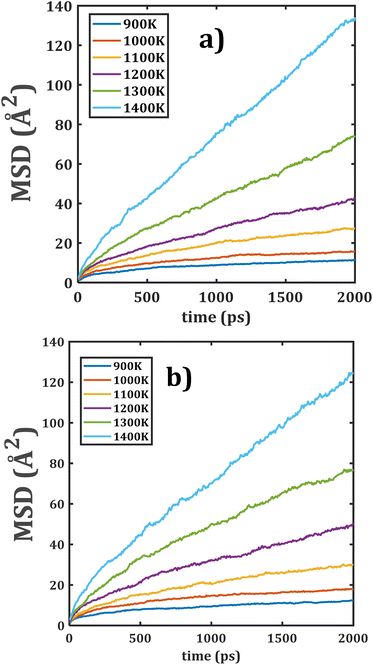 | ||
| Fig. 5 Mean displacement (MSD) versus simulation time of composite Li2Ti6O13@Li2Zr6O13 materials: (a) LTZO and (b) LZTO. | ||
3.2 Transport properties of Li+-ion in mono-, bi-crystalline Li2B6O13 and composite Li2Ti6O13@Li2Zr6O13 samples
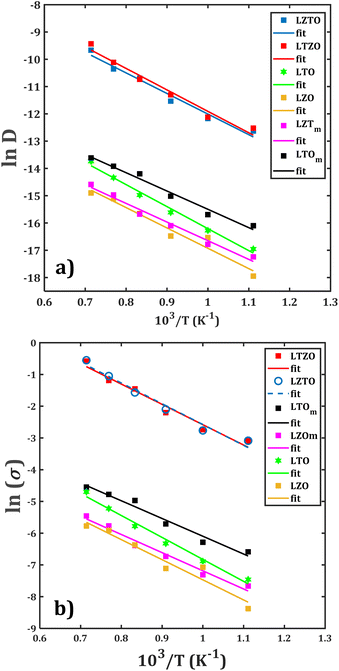
In order to quantitatively measure the Li+ transport properties of the compounds of interest, the Arrhenius dependence of both diffusion and conduction processes is performed. With the collected diffusion data in each sample, the dc-conductivity at each temperature is obtained by using eqn (2). Fig. 6 displays the Arrhenius dependence of the diffusion and conduction data for each sample. There are various findings concerning the diffusion/conduction behaviour:• The monocrystalline Li2Zr6O13 sample exhibits transport properties similar to those of the bi-crystalline Li2Zr6O13 sample.
• Both the largest diffusion coefficients and dc-conductivity are observed in the composite materials, followed by monocrystalline and bi-crystalline Li2Ti6O13 samples.
• The diffusion coefficients and dc-conductivity for the composite materials are found to be about two orders of magnitude higher as compared to the rest of the samples.
From such a first conclusion, one can assume an insignificant contribution of the grain boundary on the Li+ transport properties of Li2Zr6O13. As a matter of fact, the additional Li+ migration sites created by the grain boundaries do not considerably affect the overall Li+ diffusion within the structure. On the other hands, introduction of grain boundary, together with the composition of the composite, tends to improve the Li+ transport properties as compared to those of mono and bi-crystalline samples. In this case, the additional migration sites generated by the grain boundaries result in an alternative Li+ migration paths with shorter diffusion jump distances, thus favouring the diffusion through the composite materials.
Another interesting observation is that the composite has similar values of diffusion coefficient and dc-conductivity upon temperature change, indicating that the composition, i.e., the grain characteristics, does not affect significantly the Li+ mobility. From the results of the Arrhenius fitting, the diffusion activation energy (EDa) and the diffusion coefficient at 25 °C (![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ), together with the conduction activation energy (Eσa) and conductivity at ambient temperature (σ
), together with the conduction activation energy (Eσa) and conductivity at ambient temperature (σ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) are determined. Table 1 collects these data calculated for each sample. The obtained activation energy lies between 0.58–0.70 and 0.48–0.56 eV for both diffusion and conduction, respectively. These low values are beneficial for their use as anode materials.1–12
) are determined. Table 1 collects these data calculated for each sample. The obtained activation energy lies between 0.58–0.70 and 0.48–0.56 eV for both diffusion and conduction, respectively. These low values are beneficial for their use as anode materials.1–12
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) and conductivity (σ
) and conductivity (σ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) at 25 °C of each compounds
) at 25 °C of each compounds
| Compound | EDa (eV) | ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (cm2 s−1) (cm2 s−1) |
Eσa (eV) | σ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) (S cm−1) (S cm−1) |
|---|---|---|---|---|
| LTOm | 0.58 | 2.96 × 10−14 | 0.48 | 4.84 × 10−9 |
| LZTm | 0.65 | 1.23 × 10−15 | 0.49 | 1.22 × 10−9 |
| LTO | 0.70 | 6.10 × 10−16 | 0.60 | 1.05 × 10−10 |
| LZO | 0.64 | 1.25 × 10−15 | 0.55 | 2.16 × 10−10 |
| LZTO | 0.65 | 1.20 × 10−13 | 0.55 | 2.43 × 10−8 |
| LTZO | 0.66 | 1.02 × 10−13 | 0.56 | 1.77 × 10−8 |
The lowest and highest diffusion/conduction activation energy are found for monocrystalline and bi-crystalline Li2Ti6O13 samples. The difference of EDa and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (Eσa and σ
(Eσa and σ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) between mono- and bi-crystalline Li2Zr6O13 is low. In addition, composite materials have similar activation energy and
) between mono- and bi-crystalline Li2Zr6O13 is low. In addition, composite materials have similar activation energy and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (σ
(σ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) at ambient temperature. These results consolidate the previous analysis pointing out no influence of grain boundary on the transport properties of Li2Zr6O13 as well as the grain composition in the targeted composite materials.
) at ambient temperature. These results consolidate the previous analysis pointing out no influence of grain boundary on the transport properties of Li2Zr6O13 as well as the grain composition in the targeted composite materials.
The results of transport properties obtained in this study are in line with those reported in the literature. For instance, values of ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ranging between 10−9 to 10−12 cm2 s−1 have been reported for the knowing anodes Li4Ti5O12, Na2Ti3O7 and Na2Ti6O13 compounds.32 Values ranging between 10−17 to 10−15 cm2 s−1, in Na2Li2Ti6O14 result in a poor performance at high charge–discharge rates were reported.33–35 Value of conduction activation energy of 0.65 eV was found in a comparative study.36 Even a lower value of Li+ diffusion activation energy (0.47 eV) had been reported with a different theoretical approach.17
ranging between 10−9 to 10−12 cm2 s−1 have been reported for the knowing anodes Li4Ti5O12, Na2Ti3O7 and Na2Ti6O13 compounds.32 Values ranging between 10−17 to 10−15 cm2 s−1, in Na2Li2Ti6O14 result in a poor performance at high charge–discharge rates were reported.33–35 Value of conduction activation energy of 0.65 eV was found in a comparative study.36 Even a lower value of Li+ diffusion activation energy (0.47 eV) had been reported with a different theoretical approach.17
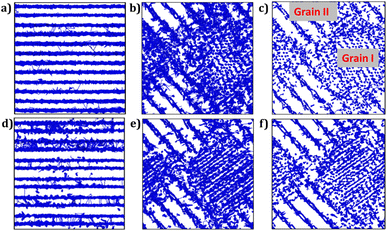
Fig. 7 illustrates the trajectory density plots of each sample at 900 K for monoclinic and bi-crystalline samples, and for the composite material, the trajectory density plots are recorded at 500 K to better observe the role of the composition at lower temperatures. From Fig. 7a and d, it is observed that the Li+ migration occurs along the [LiO4] channels in monoclinic Li2Ti6O13 and Li2Zr6O13 samples, including migration between layers. Higher density plot is observed in monocrystalline Li2Zr6O13 as compared to Li2Ti6O13. In addition, Li+ ions migrate via an interstitial mechanism, as evidenced by density plots between [LiO4] layers in agreement with the lower diffusion activation energy in monocrystalline Li2Zr6O13.
For bi-crystalline samples (Fig. 7b and e), larger density plots are observed, including migration between grain boundaries.
The trajectory density plots of composite materials are very similar to each other, which is also confirmed by their activation energies. In this case, the most relevant findings consist of the evidence of large-scale Li+ migration across the entire composite, irrespective of the grain composition. After all, the presence of grain boundaries and interstitial mechanism improve the transport properties of these materials.
4. Concluding remarks
Large-scale molecular dynamics simulations are performed to explore the transport properties of mono- and bi-crystalline Li2B6O13 (B = Ti, Zr) and the composite Li2Ti6O13@Li2Zr6O13. Calculated results demonstrate that the monocrystalline Li2Zr6O13 exhibits similar transport properties as the bi-crystalline Li2Zr6O13 sample. The highest diffusion coefficients and dc-conductivity are obtained in the composite material, followed by monocrystalline and bi-crystalline Li2Ti6O13 samples. The obtained activation energies amount to the range of 0.58–0.70 and 0.48–0.56 eV for both diffusion and conduction, respectively.The diffusion coefficients and dc-conductivity for the composite material are found to be about two orders of magnitude higher as compared to the rest of the samples. The trajectory density maps indicate that the Li interstitial mechanism, together with the presence of grain boundaries, are the sources for improvement of transport properties of the composite material.
Considering the much improved transport properties revealed in this study, further experimental verification is highly recommended to assess the potential of these compounds, especially the new composites, as active materials for anodes in the current and future energy storage devices. This also suggests a more general strategy for improvement making use of composite materials.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
YAZ: conception, data acquisition and interpretation, original draft preparation, editing, review. MTN: conception, project supervision, manuscript editing, review. MPPH: data analysis, editing, review. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MTN thanks Van Lang University for support.Notes and references
- J. C. Pérez-Flores, F. García-Alvarado, M. Hoelzel, I. Sobrados, J. Sanz and A. Kuhn, Dalton Trans., 2012, 41, 14633–14642 RSC.
- J. C. Pérez-Flores, C. Baehtz, M. Hoelzel, A. Kuhn and F. García-Alvarado, Phys. Chem. Chem. Phys., 2012, 14, 2892–2899 RSC.
- J. C. Pérez Flores, M. Hoelzel, A. Kuhn and F. García Alvarado, ECS Trans., 2012, 41, 195–206 CrossRef CAS; J. Zheng, Y. Wu, Y. Sun, J. Rong, H. Li and L. Niu, Nano-Micro Lett., 2021, 13, 1–37 CrossRef.
- K. Kataoka, J. Awaka, N. Kijima, H. Hayakawa, K. I. Ohshima and J. Akimoto, Chem. Mater., 2011, 23, 2344–2352 CrossRef CAS.
- J. R. Fernández-Gamboa, F. Tielens and Y. A. Zulueta, Mater. Sci. Semicond. Process., 2024, 173, 108144 CrossRef.
- B. Vikram Babu, K. Vijaya Babu, G. Tewodros Aregai, L. Seeta Devi, B. Madhavi Latha, M. Sushma Reddi, K. Samatha and V. Veeraiah, Results Phys., 2018, 9, 284–289 CrossRef.
- J. R. Fernández-Gamboa, F. Tielens and Y. A. Zulueta, Mater. Sci. Semicond. Process., 2022, 152, 107074 CrossRef.
- Y. Wang, A. Zhou, X. Dai, L. Feng, J. Lie and J. Li, J. Power Sources, 2014, 266, 114–120 CrossRef CAS.
- A. Kozlova, N. Uvarov, M. Sharafutdinov, E. Gerasimov and Y. Mateyshina, J. Solid State Chem., 2022, 313, 123302 CrossRef CAS.
- Y. Xie, Q. Wang, F. Gu, K. Dai, M. Shui and J. Shu, J. Alloys Compd., 2022, 893, 162348 CrossRef CAS.
- Q. Wang, S. Yang, J. Miao, Y. Zhang, D. Zhang, Y. Chen and Z. Li, Appl. Surf. Sci., 2019, 469, 253–261 CrossRef CAS.
- S. Dos Santos Costa, J. Pereira da Silva, M. Moraes Biondo, E. A. Sanches, M. M. Da Silva Paula, F. Xavier Nobre, J. Anglada Rivera, Y. Alexis Zulueta, M. S. Torikachvili, D. Vieira Sampaio, M. Vinicius Dias Vermelho, Ş. Ţălu, L. Aguilera Dominguez and Y. Leyet, Molecules, 2022, 27, 5756 CrossRef CAS PubMed.
- Y. A. Zulueta and M. T. Nguyen, Phys. Chem. Chem. Phys., 2023, 25, 27926–27935 RSC.
- B. A. Goldmann, M. J. Clarke, J. A. Dawson and M. S. Islam, J. Mater. Chem. A, 2022, 10, 2249–2255 RSC.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS.
- Y. Huang, B. Cao, Z. Geng and H. Li, Acc. Mater. Res., 2024, 5(2), 184–193 CrossRef CAS.
- Y. A. Zulueta, P. Geerlings, F. Tielens and M. T. Nguyen, J. Solid State Chem., 2019, 279, 120930 CrossRef CAS.
- N. Kuganathan, S. Ganeshalingam and A. Chroneos, Materials, 2019, 12, 2851 CrossRef CAS.
- Y. A. Zulueta and M. T. Nguyen, Phys. Status Solidi B, 2018, 255, 1700669 CrossRef.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef CAS.
- J. A. Dawson, H. Chen and M. Saiful Islam, J. Phys. Chem. C, 2018, 122, 23978–23984 CrossRef CAS.
- L. Van Duong, M. T. Nguyen and Y. A. Zulueta, RSC Adv., 2022, 12, 20029–20036 RSC.
- A. Ahniyaz, I. de Meatza, A. Kvasha, O. Garcia-Calvo, I. Ahmed, M. F. Sgroi, M. Giuliano, M. Dotoli, M. A. Dumitrescu, M. Jahn and N. Zhang, Adv. Appl. Energy, 2021, 4, 100070 CrossRef CAS.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- Z. H. Fu, X. Chen and Q. Zhang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1621 CAS.
- H. Cheng, J. G. Shapter, Y. Li and G. Gao, J. Energy Chem., 2021, 57, 451–468 CrossRef CAS.
- P. U. Nzereogu, A. D. Omah, F. I. Ezema, E. I. Iwuoha and A. C. Nwanya, Appl. Surf. Sci. Adv., 2022, 9, 100233 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- Y. A. Zulueta and M. T. Nguyen, Dalton Trans., 2021, 50, 3020–3026 RSC.
- P. Hirel, Comput. Phys. Commun., 2015, 197, 212–219 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- S. Chauque, C. B. Robledo, E. P. M. Leiva, F. Y. Oliva and O. R. Cámara, ECS Trans., 2014, 63, 113–128 CrossRef CAS.
- P. Wang, P. Li, T. F. Yi, X. Lin, H. Yu, Y. R. Zhu, S. Qian, M. Shui and J. Shu, J. Power Sources, 2015, 297, 283–294 CrossRef CAS.
- K. Wu, D. Wang, X. Lin, L. Shao, M. Shui, X. Jiang, N. Long, Y. Ren and J. Shu, J. Electroanal. Chem., 2014, 717–718, 10–16 CrossRef CAS.
- P. Wang, P. Li, T. F. Yi, X. Lin, Y. R. Zhu, L. Shao, M. Shui, N. Long and J. Shu, J. Power Sources, 2015, 293, 33–41 CrossRef CAS.
- O. Skurikhina, M. Gombotz, M. Senna, M. Fabián, M. Baláz, K. L. Da Silva, M. Achimovičová, H. M. R. Wilkening and B. Gadermaier, Z. Phys. Chem., 2022, 236, 1077–1088 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: LAMMPS input files of mono, bi-crystalline Li2Zr6O13 samples, and Li2Zr6O13@Li2Ti6O13 composite for reproducibility providing further simulation details for the readers. See DOI: https://doi.org/10.1039/d4ra02998d |
| This journal is © The Royal Society of Chemistry 2024 |