Open Access Article
Open Access ArticleOn the use OF 1H-NMR chemical shifts and thermodynamic data for the prediction of the predominant conformation of organic molecules in solution: the example of the flavonoid rutin†
Haroldo C. Da Silva ab and
Wagner B. De Almeida
ab and
Wagner B. De Almeida *a
*a
aLaboratório de Química Computacional e Modelagem Molecular (LQC-MM), Departamento de Química Inorgânica, Instituto de Química, Universidade Federal Fluminense (UFF), Outeiro de São João Batista s/n, Campus do Valonguinho, Centro, 24020-141, Niterói, RJ, Brazil. E-mail: wbdealmeida@gmail.com
bDepartamento de Físico-Química, Instituto de Química, Pavilhão Haroldo Lisboa da Cunha, Universidade do Estado do Rio de Janeiro (UERJ), Rua São Francisco Xavier, 524, Maracanã, 20550-013, Rio de Janeiro, RJ, Brazil. E-mail: haroldo.candal@uerj.br
First published on 18th June 2024
Abstract
Conformational analyses of organic compounds in solution still represent a challenge to be overcome. The traditional methodology uses the relative energies of the conformations to decide which one is most likely to exist in the experimental sample. The goal of this work was to deepen the approach of conformational analysis of flavonoid rutin (a well-known antioxidant agent) in DMSO solution. The methodology we used in this paper involves expanding the sample configuration space to a total of 44 possible geometries, using Molecular Dynamics (MD) simulations, which accesses structures that would hardly be considered with our chemical perception, followed by DFT geometry optimizations using the ωB97X-D/6-31G(d,p) – PCM level of theory. Spectroscopic and thermodynamic analyses were done, by calculating the relative energies and nuclear magnetic resonance (1H-NMR) chemical shifts, comparing the theoretical and experimental 1H-NMR spectra (DMSO-d6) and evaluating Mean Absolute Error (MAE). The essence of this procedure lies in searching for patterns, like those found in traditional DNA tests common in healthcare. Here, the theoretical spectrum plays the role of the analyzed human sample, while the experimental spectrum acts as the reference standard. In solution, it is natural for the solute to dynamically alter its geometry, going through various conformations (simulated here by MD). However, our DFT/PCM results show that a structure named 32 with torsion angles ϕ1 and ϕ2 manually rotated by approx. 20° showed the best theoretical-experimental agreement of 1H-NMR spectra (in DMSO-d6). Relative energies benchmarking involving 16 DFT functionals revealed that the ωB97X-D is very adequate for estimating energies of organic compounds with dispersion of charge (MAE < 1.0 kcal mol−1, using ab initio post–Hartree–Fock MP2 method as reference). To describe the stability of the conformations, calculations of Natural Bonding Orbitals (NBO) were made, aiming to reveal possible intramolecular hydrogen bonds that stabilize the structures. Since van der Waals (vdW) interactions are difficult to be identified by NBO donations, the Reduced Density Gradient (RDG) were calculated, which provides 2D plots and 3D surfaces that describe Non-Covalent Interactions (NCI). These data allowed us to analyze the effect of dispersion interactions on the relative stability of the rutin conformations. Our results strongly indicate that a combination of DFT (ωB97X-D)-PCM relative energies and NMR spectroscopic criterion is a more efficient strategy in conformational analysis of organic compounds in solution.
1 Introduction
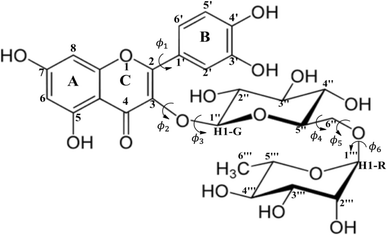
The importance of the knowledge of the molecular structure of chemical compounds has been recognized all over the years, with more emphasis on biological activity (see for example ref. 1–4). As mentioned in ref. 1, it would be of great value to be able to describe exactly what happens in the interaction of a drug with a reactive cellular constituent. According to the authors in their 1966 article (ref. 1), theories and explanations prove their worth only if they permit predictions and extrapolations. Many developments in this area of research have been achieved since then. The list of scientific publications related to structure–activity relationship is enormous and the works reported in ref. 2–4 are cited only to show the development of the area in the last forty years. Although in ref. 2–4 the drug molecular structure and theoretical calculations of chemical properties are used in attempt to understand biological activity, no emphasis was placed on the determination of the molecular geometry in solution. In the light of these studies, it became clear that a precise information on the molecular conformations plays an important role. For samples in the solid and gas phases, experimental structural determination can be accomplished through X-ray and electron diffraction experiment respectively. However, in solution there is no way to acquire accurate information on the molecular conformations directly from experimental procedures (spectroscopy for example).Flexible organic molecules may assume several conformations due to rotation of moiety units and functional groups. Therefore, finding the predominant molecular conformation of organic compounds in solution is a hard task for experimentalists. Then, quantum chemical calculations can be an important tool when combined with experimental data in solution. Among many relevant organic molecules possessing biological activity, the flavonoid rutin (a flexible molecule represented in Scheme 1) called our attention some years ago. According to the literature, flavonoids have antitumor,5–8 antimicrobial,9 antioxidant10–12 and anti-inflammatory13 activities. However, it is proven that most of the biological properties of these polyphenols are associated with its high antioxidant potential.11,14
In a previous work15 we carried out a structural investigation of the flavonoid rutin, through a search for possible minimum energy structures on the Potential Energy Surface (PES) using the Density Functional Theory (DFT) methodology,16 with the B3LYP functional17,18 and 6-31G(d,p) basis set.19 In that first work, all structures were optimized in the vacuum. Through scan calculations involving six inter-ring torsion angles, ϕ1, ϕ2, ϕ3, ϕ4, ϕ5 and ϕ6 (defined in Scheme 1), 34 distinct optimized structures were located, named structures 1 to 34. Experimental 1H-NMR spectrum (in DMSO-d6)20 was used as reference data to assist in the conformational elucidation in solution, along with DFT calculations of NMR chemical shifts and thermodynamic quantities using standard statistical thermodynamics formalism.21 The Polarizable Continuum Model (PCM)22 was used to simulate the solvent effect in single point DFT calculations (vacuum optimized geometries). The best match between experimental (in DMSO-d6) and DFT-PCM 1H-NMR spectra, calculated for all 34 optimized structures, were used as a criterion to determine the preferred rutin conformation in DMSO solution.
The goal of this work is to expand and improve the conformational analysis of the flavonoid rutin, incorporating molecular dynamics as a source of new conformations, using 16 DFT functional and post–Hartree–Fock method to make a more accurate evaluation of relative energies and to describe the intramolecular interactions that influence the energies of the conformations in DMSO solution through Natural Bonding Orbitals (NBO) analysis.
2 Calculations
B3LYP/6-31G(d,p) vacuum-optimized molecular structures of rutin (Scheme 1) were reoptimized at the DFT level16 with the ωB97X-D functional,23 which carries a dispersion correction and has been found very satisfactory for the description of thermochemistry and non-covalent interactions, using the 6-31G(d,p) basis set,19 and including solvent effects (DMSO solvent, ε = 46.826) through the polarizable continuum model (PCM).22 This is a more accurate computational procedure than the previous one. In the present work we investigate how a deepening of the methodology can affect the determination of the most probable structure in solution, with the inclusion of 16 DFT functional and the post–Hartree–Fock MP2 (Møller–Plesset second-order perturbation theory)24,25 level of theory, using flavonoid rutin as a working example. To improve our search for possible conformation of rutin present in solution we performed Molecular Dynamics (MD)26 simulation in DMSO allowing a sample on distinct areas of the energy hypersurface. Ten sequential frames out of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 were used as input for DFT geometry optimization yielding ten new true minimum energy structures on the PES for rutin (named structures 35 to 44). We can now consider that a truly comprehensive search for minimum energy structures on the PES was accurately accomplished using an adequate level of calculation for geometry optimization (ωB97X-D/6-31G(d,p)-PCM), with 44 distinct conformers of rutin being located.
000 were used as input for DFT geometry optimization yielding ten new true minimum energy structures on the PES for rutin (named structures 35 to 44). We can now consider that a truly comprehensive search for minimum energy structures on the PES was accurately accomplished using an adequate level of calculation for geometry optimization (ωB97X-D/6-31G(d,p)-PCM), with 44 distinct conformers of rutin being located.
The question now is how to select among 44 conformers the best candidate structures to be present in DMSO solution. It may be thought that as rutin is a very flexible molecule (Scheme 1) there is a dynamic process in solution with various conformations been accessible as a function of time. A Boltzmann-type conformational population (using ΔG relative energy values) would be a common criterion to select relevant conformations, naturally favoring the global minimum energy structure. The spectroscopic criterion is based on the best match between experimental and DFT calculated 1H-NMR chemical shifts. In this case there are two strategies: identifying the lowest DFT NMR statistical indices and the best match between theoretical and experimental 1H-NMR spectrum.
Harmonic frequency calculations were performed for ωB97X-D/6-31G(d,p)-PCM-DMSO optimized geometries to characterize them as true minima on the PES (all frequencies are real). In this study, conformational analysis of rutin was improved by MD simulations, using a simulation box with a side length of 3.913 nm, filled with a single rutin molecule and 500 dimethyl sulfoxide (DMSO) molecules using the Packmol software.27 Initially, the system underwent an energy minimization simulation in 3000 steps to eliminate initial repulsive interactions. The system with minimized energy was subjected to a 1 nm NpT equilibration step at room temperature (298.15 K) and pressure (1 atm), using Berendsen thermostat and barostat.28 Subsequently, the equilibration protocol was extended for an additional 2 nm, using the Parrinello–Rahman barostat,29 aiming to enhance system density equilibration. In a last step, 10 nm NpT production simulation was performed. It provided the extraction of the final frame, which was subsequently incorporated into the conformational analysis. To augment the exploration of the conformational space, nine extra conformations were extracted from the production simulation, every 1 nm of simulation a conformation was collected, generating the following geometries, named #1000, #2000, #3000, #4000, #5000, #6000, #7000, #8000, and #9000, in addition to the last frame (#10000).
The molecular interactions within the system were described using the General Amber Force Field (GAFF), with parameters for both rutin and DMSO molecules being generated via the Antechamber software.30,31 These parameters were then formatted for compatibility with the GROMACS 2020.2 (ref. 32) simulation software using ACPYPE program.33 Bond lengths involving hydrogen atoms were constrained using the Parallel Linear Constraint Solver (P-LINCS),34,35 and the equations of motion were integrated employing Verlet leapfrog algorithm.36–38
Intramolecular interactions (hydrogen bonds and dispersive interactions) were initially characterized by the measurement of interatomic distances. However, the description of the hydrogen bonds was also addressed through the calculation of the natural bond orbitals (using the NBO software39–45), which allows the analysis of the donations of electronic density from localized orbitals for oxygen lone pairs electrons to localized σ orbitals for OH bonds (interaction O⋯HO). In addition, the intramolecular hydrogen bonds were identified by the generation of the NCI (Non-Covalent Interactions) graphs and surfaces, analyzing the values of sign(λ2)ρ(a.u), where λ2 is the second eigenvalue of the Hessian matrix and ρ is the electronic density. NCI data were calculated by the Multiwfn program.46
DFT-PCM NMR calculations of shielding constants (σ) with chemical shifts (δ) determined on a δ-scale relative to tetramethylsilane (TMS) internal reference was done using the Gauge-Independent Atomic Orbital (GIAO) method47 with the B3LYP functional17,18 and 6-31G(d,p) basis set (named B3LYP/6-31G(d,p)//ωB97X-D/6-31G(d,p), where the double slash means that geometries were optimized with the ωB97X-D functional), which has been shown to be adequate for organic molecules (see for example ref. 48 and 49). All quantum chemical calculations were done with the Gaussian 09 package.50
3 Results and discussions
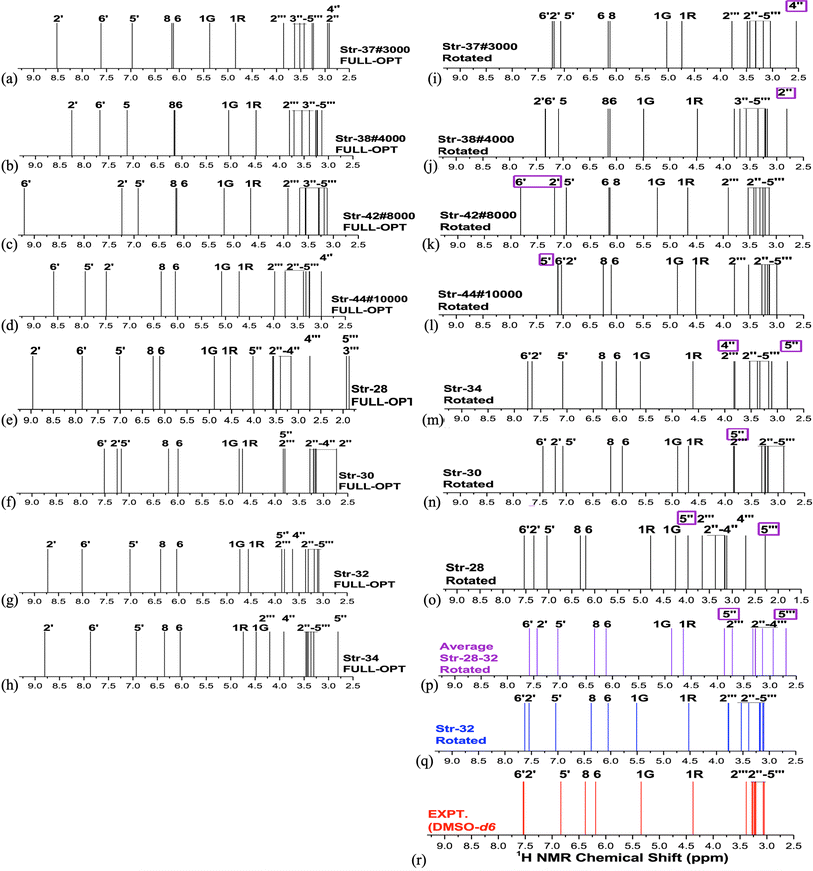
B3LYP/6-31G(d,p)-PCM-DMSO relative energies with respect to the global minimum (ΔErel, in kcal mol−1) and the Mean Absolute Deviation (MAD, in ppm), evaluated using 1H-NMR data (in DMSO-d6) as reference experimental data are shown in Fig. 1 (values for structures 1–34 were taken from our previous work15) for all 44 B3LYP/6-31G(d,p) optimized structures (in the vacuum) located on the PES for rutin (named structures 1 to 44). The last ten new structures (named 35–44) were obtained using MD simulation frames as input for DFT geometry optimization (see Fig. S1 and S2, ESI,† respectively for optimized structures and 1H-NMR spectra). It can be seen from Fig. 1a that the first 30 structures (1–30) are more than 10 kcal mol−1 above the global minimum (34) as well as all new MD optimized structures, with the lowest energy MD structure being last-frame optimized geometry 44 which is still 9.4 kcal mol−1 energetically disfavored. The statistical indices data from Fig. 1b show that structure 30 exhibit low MAD values as well as most of the new MD optimized ones (structure 32 previously predicted as the preferred conformer also have small MAD). Combining all data reported in Fig. 1, we could select structures 30, 32, 34, 37, 38, 42 and 44 (having low relative energy values among all ten MD structures) as the best candidate rutin structures to be present in DMSO solution. In addition, we found that structure 28 is predicted to be relatively stable by others DFT functional having dispersion contribution (to be discussed later), not B3LYP. Although structure named 34 was the undisputed global minimum on the PES, it was not predicted to be the predominant structure in solution according to the 1H-NMR spectroscopic criterion.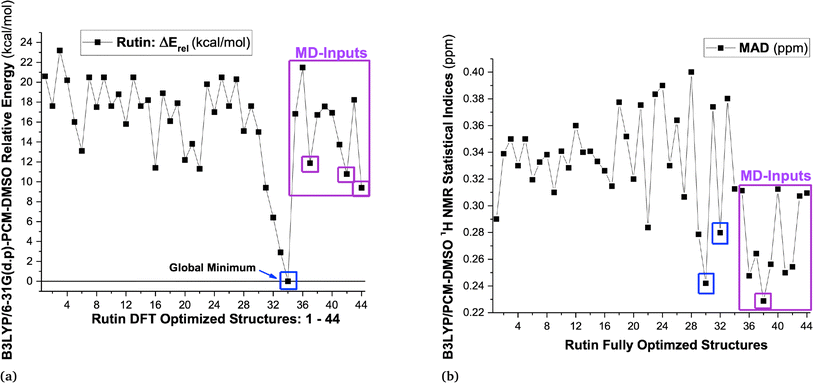 | ||
| Fig. 1 (a) B3LYP/6-31G(d,p)-PCM-DMSO relative energies (in kcal mol−1) for 34 optimized structures previously located on the PES for rutin15 and ten new structures obtained using MD frames as input for DFT geometry optimization, highlighted in pink rectangle (structures 35 to 44), totalizing 44 DFT fully optimized structures of rutin. (b) B3LYP/6-31G(d,p)-PCM-DMSO statistical indices (MAD in ppm) for all 44 optimized structures located on the PES for rutin. | ||
These selected rutin structures (28, 30, 32, 34, 37, 38, 42 and 44) were reoptimized including solvent effects using the PCM model and long-range corrected functional (ωB97X-D/6-31G(d,p)-PCM-DMSO level). All structures are true minima on the PES (no imaginary frequencies). Then the ϕ1 and ϕ2 torsion angles were rotated (artisanal manner) in small steps aiming to find an agreement between theoretical and experimental NMR data. A summary of relative energies (in kcal mol−1) and DFT-PCM 1H-NMR statistical indices results (in ppm), MAE (mean absolute error), are shown in Fig. 2 and torsional angles are given in Table 1. ΔErel and ΔGrel values yield a very similar trend (see Fig. S3, ESI†) and we can use ΔErel to select the most energetically favored structures, which is computationally less demanding. Also, in Table 1 are torsion angle values optimized in the vacuum and the deviation from DFT-PCM optimized values are not very substantial. Two sets of MAE data are shown in Fig. 2a, including all protons and only sugar moiety protons where the respective conformation changes can be assessed. Three rotated structures showed the lowest MAE values (in parenthesis): 32 (0.19 ppm), 38 (0.22 ppm) and 42 (0.22 ppm). The rotated DM last-frame structure 44 (DM#10000) have a large MAE value (0.25 ppm). Among the eight ϕ1, ϕ2 rotated structures conformer 32 is the global minimum by more than 3 kcal mol−1, while for fully optimized structures conformer 34 is the preferred one by more than 7 kcal mol−1. The B-ring orientation with ϕ1 larger than ±120° leads to better agreement with experimental 1H-NMR data (lower MAE values). Spatial orientations with smaller ϕ1 values are not favored.
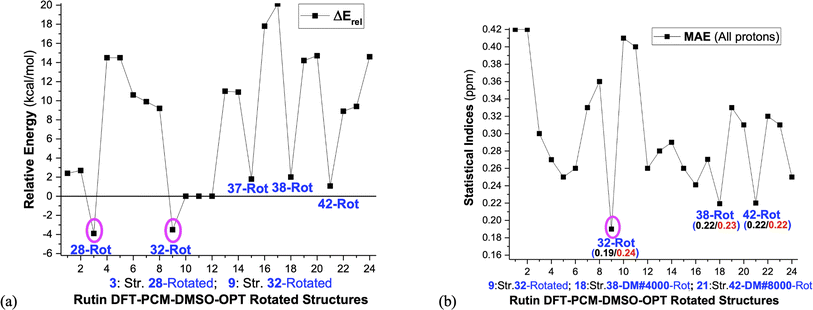 | ||
| Fig. 2 (a) ωB97X-D/6-31G(d,p)-PCM-DMSO relative energies (ΔErel and ΔGrel in kcal mol−1) with respect to structure 34 (b) B3LYP/6-31G(d,p)-PCM-DMSO statistical indices (MAE in ppm) values with all protons included and using only the sugar moiety protons are given. ΔGrel was estimated using thermal corrections for DFT fully optimized structures (the ϕ1, ϕ2 rotated structures are not true minimum on the PES, so harmonic frequency calculations, needed for evaluation of thermal correction, are meaningless). The torsion angles for ϕ1, ϕ2 rotated structures are given in Table 1. 1: Str-28-PCM-OPT; 2: Str-28 Vacuum-OPT; 3: Str-28-PCM-OPT-Rotated; 4: Str-30-PCM-OPT; 5: Str-30 Vacuum-OPT; 6: Str-30-PCM-OPT-Rotated; 7: Str-32-PCM-OPT; 8: Str-32 Vacuum-OPT; 9: Str-32-PCM-OPT-Rotated; 10: Str-34-PCM-OPT; 11: Str-34 Vacuum-OPT; 12: Str-34-PCM-OPT-Rotated; 13: Str-37-PCM-OPT; 14: Str-37 Vacuum-OPT; 15: Str-37-PCM-OPT-Rotated; 16: Str-38-PCM-OPT; 17: Str-38 Vacuum-OPT; 18: Str-38-PCM-OPT-Rotated; 19: Str-42-PCM-OPT; 20: Str-42 Vacuum-OPT; 21: Str-42-PCM-OPT-Rotated; 22: Str-44-PCM-OPT; 23: Str-44 Vacuum-OPT; 24: Str-44-PCM-OPT-Rotated. | ||
| Structures | ϕ1: [O-C2-C1′-C2′] | ϕ2: [C1′′-O-C3-C2] | ϕ3: [C2′′-C1′′-O-C3] | ϕ4: [O-C6′′-C5′′-O] | ϕ5: [C1′′′-O-C6′′-C5′′] | ϕ6: [C1′′′-O-C6′′-C5′] |
|---|---|---|---|---|---|---|
a Minimum energy structure located on the DFT PES (torsion angles scan) reported previously.15b DFT optimized structure using as input selected MD frames (#) among a total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 named #3000, #8000 and #10000.c ϕ1 and ϕ2 rotated structures, keeping the other geometrical parameters at their optimized values.d DFT-Vacuum optimized angles. 000 named #3000, #8000 and #10000.c ϕ1 and ϕ2 rotated structures, keeping the other geometrical parameters at their optimized values.d DFT-Vacuum optimized angles. |
||||||
| 28-Vacuum-OPTd | 168.6 | −85.4 | 177.3 | 86.9 | −51.0 | −153.0 |
| 28 PCM-DMSO-OPT (PES-Scan)a | 168.6 | −83.9 | 174.1 | 87.1 | −50.9 | −153.6 |
| 28 – rotatedc | 147.0 | −95.0 | ||||
| 30-Vacuum-OPTd | −142.2 | 101.5 | −82.8 | −165.1 | −93.8 | 175.0 |
| 30 PCM-DMSO-OPT (PES-Scan)a | −135.4 | 97.2 | −81.6 | −165.2 | −93.7 | 176.3 |
| 30 – rotatedc | −138.0 | 120.0 | ||||
| 32-Vacuum-OPTd | −168.9 | 104.2 | 140.4 | −163.2 | −92.1 | 173.9 |
| 32 PCM-DMSO-OPT (PES-Scan)a | −173.0 | 113.5 | 140.4 | −168.1 | −89.4 | −179.0 |
| 32 – rotatedc | −150.0 | 126.0 | ||||
| 34-Vacuum-OPTd | −160.8 | 99.5 | 141.9 | −60.4 | −121.0 | −173.7 |
| 34 PCM-DMSO-OPT (PES-Scan)a | −166.8 | 99.2 | 140.4 | −56.7 | −117.4 | −177.8 |
| 34 – rotatedc | −152.0 | 124.0 | ||||
| 37-Vacuum-OPTd | 158.4 | −92.8 | 16.3 | 56.1 | −167.4 | 171.5 |
| 37 PCM-DMSO-OPT (DM-#3000)b | 158.3 | −92.5 | 14.3 | 57.9 | −166.2 | 168.1 |
| 37 (DM-#3000)-Rotc | 135.0 | −80.0 | ||||
| 38-Vacuum-OPTd | 146.0 | −113.2 | 69.5 | 76.6 | 175.2 | −175.1 |
| 38 PCM-DMSO-OPT (DM-#4000)b | 153.2 | −113.8 | 93.0 | 69.4 | 170.8 | −175.2 |
| 38 (DM-#4000)-Rotc | 138.0 | −120.0 | ||||
| 42-Vacuum-OPTd | 30.3 | −147.0 | 136.7 | 68.1 | −155.0 | 164.7 |
| 42 PCM-DMSO-OPT (DM-#8000)b | 29.3 | −141.2 | 134.3 | 67.5 | −169.8 | 175.3 |
| 42 (DM-#8000)-Rotc | −40.0 | −145.0 | ||||
| 44-Vacuum-OPTd | −27.3 | −91.5 | −29.1 | 64.9 | 172.4 | 172.4 |
| 44 PCM-DMSO-OPT (DM-#10000)b | −20.9 | −92.0 | −37.7 | 68.8 | 165.6 | −179.8 |
| 44 (DM-#10000)-Rotc | 128.0 | |||||
The ϕ1, ϕ2 torsion angle rotated structures, optimized at the ωB97X-D/6-31G(d,p)-PCM-DMSO level, are given in Table 1 and indicated in Fig. 3. The relevant protons for 1H-NMR analysis (H6, H8, H2′, H5′, H6′, H1G (H1′′), H1R (H1′′′), H2′′, H3′′, H4′′, H5′′, H2′′′, H3′′′, H4′′′ and H5′′′) are also highlighted. From the relative protons position, it can be clearly seen that the effect on the NMR spectrum will be quite visible, once it is very sensitive to local chemical environment. All eight structures shown in Fig. 3 are completely dissimilar and can be considered a good sampling of the most probable conformers of rutin to be present in DMSO solution.
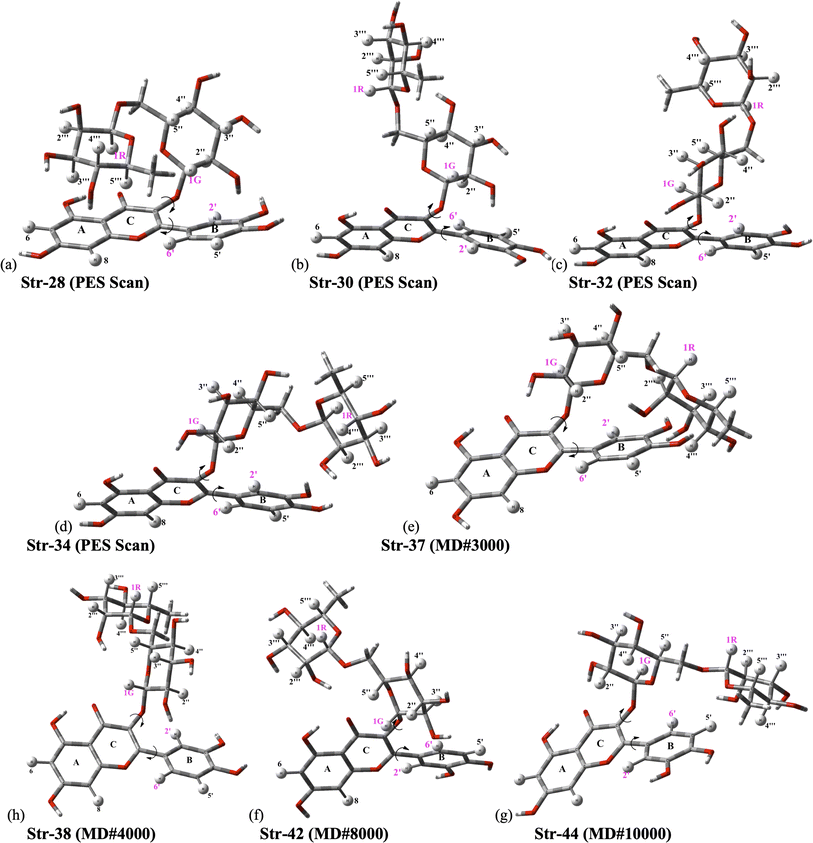 | ||
| Fig. 3 ωB97X-D/6-31G(d,p)-PCM-DMSO fully optimized structures located on B3LYP/6-31G(d,p) PES for rutin (ϕ1, ϕ2 torsion angles were rotated to reach agreement with experimental 1H-NMR spectrum in DMSO-d6 as explained in the text). (a–d) Previously located on B3LYP/6-31G(d,p) PES for rutin;15 (e–h) new fully optimized structures of rutin (ϕ1, ϕ2 torsion angles were rotated) using as input sequential frames obtained from MD simulation in DMSO (named #3000, #8000, #9000 and #10000; the last frame is named #10000). | ||
Analysis of NMR spectrum complements the MAE and thermodynamic data. In Fig. 4, experimental (in DMSO-d6)20 and B3LYP/6-31G(d,p)-PCM-DMSO 1H-NMR profile for the eight structures reported in Fig. 3 are shown. The calculated spectra for all fully optimized structures (Fig. 4a–h) are in significant disagreement with experimental data. As mentioned previously, the virtually degenerate signal for H2′, H6′ protons observed in the experimental spectrum can only be obtained through the rotation of the rutin B-ring through the torsion angle ϕ1. This was successfully achieved by the rotated structures 32 (Fig. 4q), 34 (Fig. 4m) and 37 (Fig. 4i). The rotated (DFT-optimized) MD Last-Frame H5′ in the wrong swapped position (as can also be seen in Fig. 4l). A closer analysis of Fig. 4i, m and r (Exp.), revealed that structure 37 has proton 4′′ in total wrong position and 34 has both 4′′ and 5′′ protons also in disagreement with experimental 1H-NMR pattern.
As can be seen from Fig. 2b if only MAE data were considered we were inclined to say that both structures 32 and 42 would likely to exist in DMSO solution. However, independent of the analysis of NMR spectrum in Fig. 4, structure 42 is around 10 kcal mol−1 above 32, being quite disfavored energetically. This leaves the rotated structure 32 as the only one with a good agreement with experimental NMR profile for all CHn protons. Our results show that a joint analysis of thermodynamics, statistical indices and 1H-NMR spectra is essential to reach a sound prediction on the predominant structures of organic compounds present in solution. Analysis of MAE alone can be misleading.
In the light of the many structures possible to exist for rutin (44 true minimum energy structures) it may be thought that a mixture of conformations should be observed in DMSO solution. In the case of the rutin conformers, the average chemical shift can be calculated using eqn (1) and (2), with the aid of the thermodynamic eqn (3), with ΔGrel (ΔErel) obtained from Fig. 2 (T = 298.15 K; R is the ideal gas constant). In these equations, [i] is the concentration of the conformation i, δi is the 1H-NMR chemical shift of the conformation i.
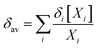 | (1) |
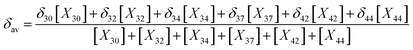 | (2) |
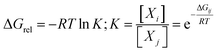 | (3) |
For fully optimized structures [34] 100%, so δav = δav,34. For rotated structures there is a competition between structures 32 and 28 depending on the use of ΔErel and ΔGrel in the Boltzmann type distribution. As our ΔGrel values for rotated structures are only estimates we may consider both structures as equally probable on energetic grounds. So, we may write, δav (δ32 + δ28)/2. This spectrum is also shown in Fig. 4n, where a disagreement with experiment is observed. Therefore, only 1H-NMR signals of a single structure (32 or 34) should be observed in DMSO solution, not a signal due to a mixture of conformations. The best agreement with experimental NMR data is obtained only for the ϕ1, ϕ2 rotated structure 32 (not 34), making it predominant in solution.
To corroborate our argument that the absence of an unambiguously assigned 1H-NMR signal (predicted in the DFT calculations of 1H-NMR chemical shifts) in the experimental spectrum is a proof that such molecular structures should be present in an undetectable concentration in the experimental sample we analyze below the well-known example of histidine. Experimental (high pH neutral and low pH protonated form) data and theoretical (DFT-PCM) 1H-NMR chemical shift (proton H2) for histidine model structures (Fig. 5) are given in Table 2. These results provide a good example of the existence of a single structure in the two extremes pH values. An average chemical shift value (δav(H2)) due to a mixture of two structures (eqn (1)) could easily be detected experimentally by analyzing the NMR data, if both neutral and protonated forms coexisted in solution.
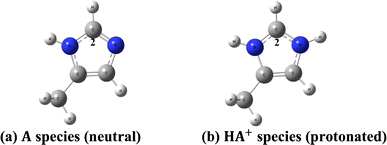 | ||
| Fig. 5 DFT optimized model histidine structures. (a) Neutral structure (A) (b) protonated structure (HA+). | ||
| Histidine model structure | Neutral species: high pH | Protonated species: low pH |
|---|---|---|
a Experimental data from ref. 51. At any pH the observed chemical shift is a weighted average of the two extreme values δH2(HA+) and δH2(A): 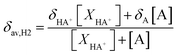 ; (XHA+ and XA are respectively the concentration of protonated and neutral species). ; (XHA+ and XA are respectively the concentration of protonated and neutral species). |
||
| B3LYP/6-31G(d,p)-PCM-chloroform | 7.3 | 8.3 |
| B3LYP/6-31G(d,p)-PCM-DMSO | 7.3 | 8.3 |
| B3LYP/6-31G(d,p)-PCM-water | 7.4 [∼7.7] a[HA+] = 0 | 8.4 [∼8.7] a[A] = 0 |
The apparent disagreement between thermodynamics and spectroscopic predictions not properly explained in our previous work15 can now be clearly understood. The relative ΔG calculated with DFT fully optimized structures does not represent the reality, since good agreement with experimental 1H-NMR profile (spectroscopic criterion) is achieved only for ϕ1, ϕ2 rotated structures (which are not true minimum on the PES). To be consistent we must evaluate relative energies for ϕ1, ϕ2 rotated structures, not fully optimized geometries. These results are also shown in Fig. 2a where ϕ1, ϕ2 rotated structure 32 is predicted to be the global minimum among all ϕ1, ϕ2 rotated structures, in perfect harmony with the spectroscopic prediction. Our results provide strong evidence that the molecular structure present in the experimental sample handled in the NMR experiment differ from the stationary point located on the DFT-PCM PES for rutin. When ϕ1 and ϕ2 torsion angles are rotated respectively by 23° and 12.5° with respect to the optimized values (see Table 1) the agreement between theoretical and experimental 1H-NMR profile is almost perfect. The same did not happen with structure 34 (global minimum fully optimized structure on the PES).
The procedure for finding the best ϕ1 and ϕ2 torsion angles is artisanal, where ϕ1 and ϕ2 were arbitrarily varied within a certain range and DFT-PCM NMR calculations performed for each pair of angles until a reasonable agreement with experimental 1H-NMR data (in DMSO-d6) is obtained. This procedure was carried out previously for various optimized structures, but only for structure 32 produced the best accordance with experimental 1H-NMR pattern. Perhaps the use of an improved description of the solvent effect beyond the continuum PCM model, using explicit DMSO solvent molecules in the geometry optimization procedure, would result in an DFT optimized structure close to the artisanal rotated structure 32 providing an agreement with experiment. However, as rutin has many polar groups that can explicitly interact with the polar DMSO solvent molecule (mainly O–H), in addition to conformational flexibility, such quantum chemical calculations would be a very hard computational task. Our results strongly indicate that the combination between thermodynamics and NMR spectroscopic analysis (statistical indices and 1H-NMR profile) seems to be an adequate strategy for the elucidation of the predominant structure of organic molecules in solution.
We should explain properly the nature of the PCM-DMSO-optimized-ϕ1-ϕ2-rotated structures, which may seem somewhat arbitrary. The motivation to create these rotated structures, which deviate from the fully optimized geometries, is to reach an agreement with experimental 1H-NMR profile obtained for rutin in DMSO solution. The DFT-PCM-DMSO fully optimized structures cannot correctly reproduce the NMR pattern. Therefore, it seems to us that the structure present in solution is distorted from the theoretical ones and a strategy to find the correct structure is to use the experimental NMR data as a reference and vary manually, in an artisanal way, some torsion angles (see Scheme 1) until an agreement with experimental data is found. Of course, this procedure can be questioned, but it works. At the end we could find a rotated structure that reproduce almost perfectly the experimental 1H-NMR spectrum of rutin in DMSO-d6 solution. And this structure (32) should be close enough to the one present in solution. NMR chemical shifts are very sensitive to local chemical environment and so only the correct molecular spatial arrangement present in solution can reproduce faithfully the experimental 1H-NMR profile. Experimental NMR data can be directly compared with theoretical values.
We believe that experimental NMR chemical shift can be used as a guide in the DFT-PCM geometry optimization procedure to correctly locate the molecular structure which resemble better the conformation present in solution. If we based only on energetic criterion (lowest minimum energy structure) through DFT-PCM calculations we may not succeed, since the theoretical models we used to describe the solute in the presence of solvent molecules are far away from the real experimental conditions. Inducing a molecular structure that can reproduce correctly the 1H-NMR profile seems a much more efficient approach. We think that once we have found the correct molecular structures which should be present in solution, the experimental NMR spectrum will be correctly predicted using a DFT-PCM methodology.
In classical simulation methods energy is evaluated using a force field, containing empirical equations and parameters, while in quantum chemistry calculations a chosen Hamiltonian operator (and basis set), that can be Hartree–Fock (HF), post-HF or DFT, is used in computer simulations. Therefore, relative energy values are directly dependent on the approximate theoretical method chosen for their evaluation. In the case of DFT methods which are applied to large organic molecules, the choice of the exchange–correlation function is important and depending on the type of intramolecular interactions present it may affect substantially the predictions of the predominant structure to be present in solution. To illustrate this last statement above we used 16 DFT functional (ωB97X-D,23 B3LYP,17,18 M062x,52 B97D,53 B3LYP-D3,54 SVWN,55,56 CAM-B3LYP,57 BLYP,18,58 BHANDHLYP,59 PBE,60 PBE0,61 BP86,58,62 PW91,63 B3PW91,17,64 TPSS65 and X3LYP66) to calculate relative energies, which may be considered a representative set and can provide a general view of the DFT performance for the evaluation of relative stability of conformers of organic molecules. In addition, the ab initio post-HF MP2 level of theory was used to calculate relative energy values for the eight rutin structures shown in Fig. 3, using ωB97X-D/6-31G(d,p)-PCM-DMSO optimized geometries. The MP2 correlated level of theory describe satisfactorily dispersion effects and can be used as reference to assess the performance of DFT functional. Of course, a highly post-HF correlated level of theory such as coupled cluster with single, doubled and triples excitations (CCSD(T))67 would be desirable, but it is computationally unfeasible for a large molecule such as rutin.
The results are show in Fig. 6, where it is clearly seen that dispersion effects can play a fundamental role in conformational analysis of rutin. Noncovalent intramolecular H-bond and van der Waals (vdW) type interactions are taking place. Only the DFT functional that carry dispersion effects yielded a good agreement with MP2 results for all distinct rutin structures, especially for structure 28, which is substantially stabilized by van der Waals (vdW) type noncovalent interactions (see Fig. 3a). In fact, this remarkable feature of DFT functional is quite visible in Fig. 6a–d, where only the ωB97X-D, M062x and B3LYP-D3 functional show MAE values below 1 kcal mol−1. The functional having no dispersion contribution yielded MAE values larger than approximately 3 kcal mol−1. However, the ϕ1, ϕ2 rotated structures 32, which does not contain explicit noncovalent vdW interactions, is predicted to be the global minimum energy, among all seven rotated structures, using all sixteen functional used here (change in the torsion angle Δϕ from the DFT-PCM optimized value due to ϕ1, ϕ2 rotation is given in Table 3). An exception is the B97D functional that favors slightly the rotated structure 28 (Fig. 6c). Just to mention the ωB97X-D and B3LYP (PCM values) 1H-NMR chemical shifts are quite similar with average MAE of 0.1 ppm (see Table S1 and Fig. S4, ESI†) for all rutin structures, strongly indicating that the ωB97X-D functional is also adequate for NMR calculations besides relative energies.
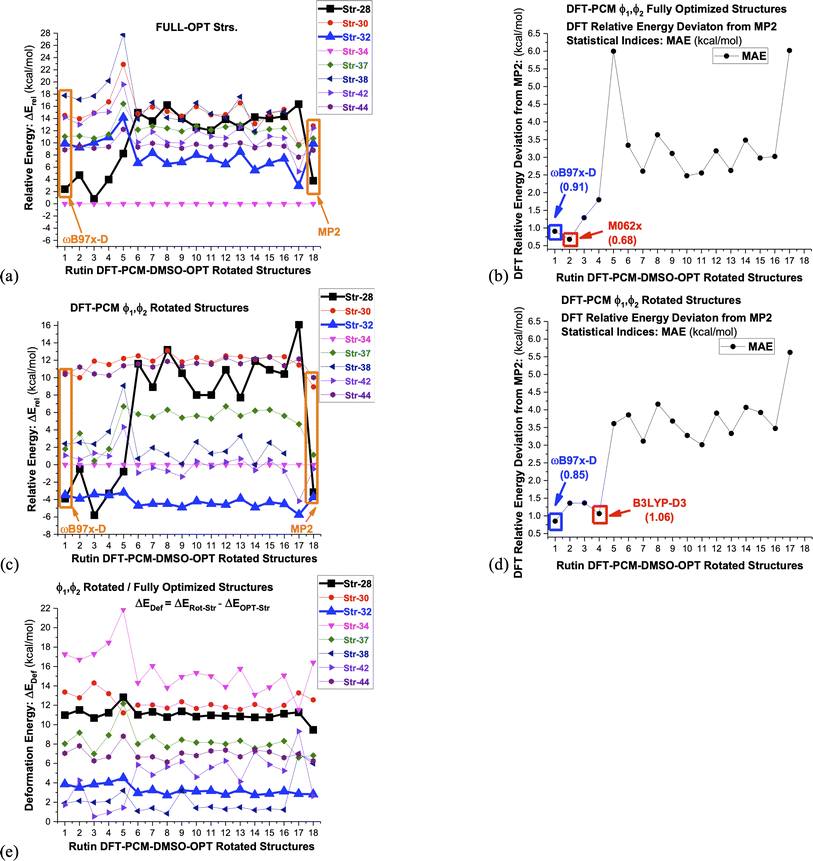 | ||
| Fig. 6 DFT/6-31G(d,p)-PCM-DMSO//ωB97X-D/6-31G(d,p)-PCM-DMSO single-point relative energies (ΔErel in kcal mol−1) with respect to structure 34, evaluated for seven chosen ωB97X-D/6-31G(d,p)-PCM-DMSO optimized-rotated structures from Fig. 3 (28, 30, 32, 34, 37-MD#3000, 38-MD#4000, 42-MD#8000, 44-MD#10000), using sixteen functional and the Pos-HF level (MP2) specified below. The torsion angles for rotated structures are given in Table 1. (a) ΔErel for fully-optimized structures (b) MAE: deviation from ΔErel-MP2 (fully-optimized structures) (c) ΔErel for ϕ1, ϕ2 rotated structures (d) MAE: deviation from ΔErel-MP2 (ϕ1, ϕ2 rotated structures) (e) DFT/6-31G(d,p)-PCM-DMSO deformation energy due to ϕ1, ϕ2 rotation evaluated with respect to fully-optimized structures. The deformation energy is defined as the difference between ΔErel evaluated for rotated and optimized structures 1: ωB97X-D; 2: M062x; 3: B97D; 4: B3LYP-D3; 5: SVWN; 6: B3LYP; 7: CAM-B3LYP; 8: BLYP; 9: BHANDHLYP; 10: PBE; 11: PBE0; 12: BP86; 13: PW91; 14: B3PW91; 15: TPSS; 16: X3LYP; 17: HF; 18: MP2. | ||
| Str-28 | Str-30 | Str-32 | Str-34 | 37-MD#3000 | 42-MD#8000 | 44-MD#10000 | |
|---|---|---|---|---|---|---|---|
| Δϕ (°) | −21.6 | −2.6 | +23.0 | +14.8 | −23.3 | −69.3 | +148.9 |
| Δϕ (°) | −11.1 | +22.8 | +12.5 | +24.8 | +12.5 | −3.8 | 0 |
Lastly in Fig. 6c deformation energy (ΔEDef), defined as the difference between ΔErel evaluated for ϕ1, ϕ2 rotated and fully optimized structures, is shown. This can be seen as a measure of the energy cost to reach a conformation that produce chemical shift values in close agreement with 1H-NMR experimental data in DMSO-d6 solution. It can be seen that structure 32 has the lowest ΔEDef values (followed closely by structure 42), while the previous global minimum structure 34 has the largest value, with structure 28 having also large ΔEDef. We believe that it is natural to associate the lowest ΔEDef value predicted for structure 32 to its favoritism to be experimentally observed as strongly indicated by the analysis of the 1H-NMR spectrum. Change in the torsion angle (Δϕ) from the DFT-PCM optimized value due to ϕ1, ϕ2 rotation is given in Table 3, where relatively small values are found for structure 32, implying that only slight torsion on the optimized structure (around 20°) is necessary to reach agreement with experimental spectroscopic data in solution.
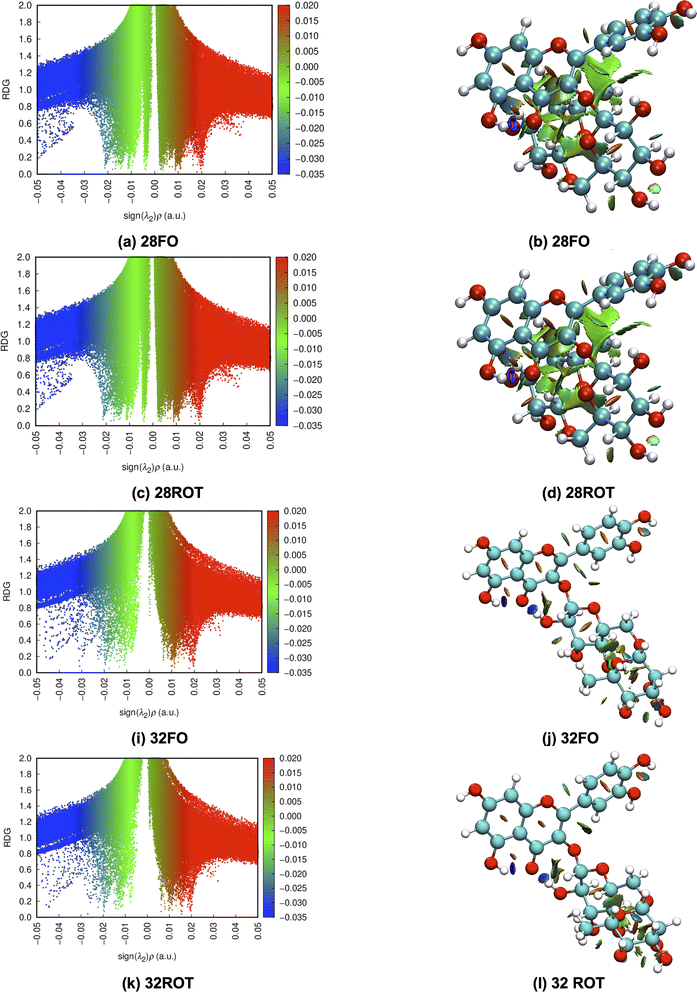
To better understand the relative stability of rutin conformers, interatomic distances related to intramolecular hydrogen bonds, as well as the respective electron density donations identified by NBO analysis are provided in the following tables. The first point to note is that the procedure of analyzing only interatomic distances can lead to the identification of interactions not confirmed in the NBO analysis. These interactions are marked as ND (non-detected) in Tables 4–7. For dispersive interactions (vdW), calculations of Non-Covalent Interactions (NCI) were carried out and the two-dimensional graphs of the Reduced Density Gradient (RDG) and the respective three-dimensional surfaces are shown in Fig. S5.† Dots with reduced density in blue represent hydrogen bonds (with expressively negative values for sign(λ2)ρ) and appear on the surface as well-defined disks with the same blue color. Points in green represent dispersive interactions (with less negative values for sign(λ2)ρ) and are represented three-dimensionally as large green surfaces. Dots with reduced density in red represent bad contacts, especially repulsions between internal groups of the molecule.
The NBO data for structures 28 and 30 (optimized and manually rotated) is shown in the Table 4. It is possible to see that there are no major changes in the intensities of intramolecular hydrogen bonds when the rotation is done. This can be confirmed by the very little variation in the lengths of the hydrogen bonds, in the respective stabilization energies (E2), and by the imperceptible change in the blue dots when comparing Fig. S5a with S5c (structure 28) and S5e with S5g (structure 30).† It is also possible to notice that structure 28 has fewer intramolecular hydrogen bonds than structure 30, suggesting that the stabilization of the conformation 28 (rotated) using the functionals with dispersion terms occurs due to vdW interactions. This confirmation can be made by the appearance of a greater number of green dots in the range −0.02 < sign(λ2)ρ < −0.01 of the RDG plot for structure 28. The importance of these dispersion interactions for rutin has already been pointed out in an article about their solubility in different solvents68 and it is confirmed here for conformational analyses.
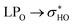 donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
| Interaction | Structure 28 | Interaction | Structure 30 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fully optimized | ϕ1, ϕ2 rotated | Fully optimized | ϕ1, ϕ2 rotated | ||||||
| d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | ||
| OH5-O4 | 1.66 | 38.4 | 1.66 | 38.35 | OH5-O4 | 1.67 | 37.46 | 1.67 | 37.19 |
| OH3′-OH3′′ | 2.07 | ND | 2.82 | ND | OH4′-OH3′ | 2.10 | 3.53 | 2.10 | 3.49 |
| OH4′-OH3′ | 2.15 | 2.76 | 2.15 | 2.62 | OH3′′′-OH4′′′ | 2.21 | 3.37 | 2.21 | 3.41 |
| OH2′′′-OH3′′′ | 2.37 | 1.39 | 2.37 | 1.4 | OH4′′-O-CH2 | 2.10 | 5.81 | 2.10 | 5.8 |
| OH3′′′-OH4′′′ | 2.41 | 1.44 | 2.41 | 1.34 | OH4′′-OH2′′′ | 2.11 | 7.62 | 2.11 | 7.62 |
| H3′′′-OH4′′′ | 2.34 | 2.06 | 2.34 | 2.06 | |||||
| H2′′′-OH3′′′ | 2.14 | 3.67 | 2.14 | 3.67 | |||||
For structures 32 and 34, the NBO data are shown in the Table 5 and the NCI plots are shown in Fig. S5i–p.† Unlike the first pair of structures previously described structures 32 and 34 undergo a clear weakening of the same intramolecular hydrogen bond: OH2′′-O4. This fact is confirmed by the elongation of the interaction, but it is much clearer by the decrease in the stabilization energy to almost 50% of the values of these optimized structures. This weakening is the cause of the disappearance of blue dots when comparing the RDG graphs for structures 32 and 34 (E(2) → rotated optimized). However, one point deserves attention. The rotation of the ring B of structure 34 breaks a hydrogen bond that existed in the optimized form: OH3′-O4, not detected (ND) in the NBO donations in the rotated structure.
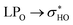 donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
| Interaction | Structure 32 | Interaction | Structure 34 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fully optimized | ϕ1, ϕ2 rotated | Fully optimized | ϕ1, ϕ2 rotated | ||||||
| d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | ||
| OH5-O4 | 1.72 | 29.17 | 1.72 | 29.50 | OH5-O4 | 1.71 | 30.48 | 1.71 | 30.84 |
| OH2′′-O4 | 1.85 | 19.56 | 1.93 | 13.07 | OH2′′-O4 | 1.90 | 15.97 | 1.99 | 8.02 |
| OH4′-OH3′ | 2.10 | 3.56 | 2.10 | 3.55 | OH4′-OH3′ | 2.04 | 4.84 | 2.04 | 4.59 |
| OH2′′-OH3′′ | 2.30 | 2.05 | 2.30 | 2.02 | OH2′′-OH3′′ | 2.35 | 1.09 | 2.35 | 1.08 |
| OH4′′-OCH2 | 2.04 | 7.29 | 2.04 | 7.29 | OH4′′-O6′′′ | 1.97 | 11.15 | 1.97 | 11.23 |
| OH2′′′-OH3′′′ | 2.14 | 4.67 | 2.14 | 4.67 | OH2′′′-OH3′′′ | 2.10 | 5.59 | 2.10 | 5.43 |
| OH3′′′-OH4′′′ | 2.31 | 2.35 | 2.31 | 2.35 | OH3′′′-OH4′′′ | 2.32 | 2.24 | 2.32 | 2.25 |
| OH3′-OH2′′′ | 1.82 | 20.53 | 3.28 | ND | |||||
The weakening of interactions between the ABC rings of rutin and its glycosidic part due the rotation can also be demonstrated in the structure 37 using the data given in Table 6. In conformation 37, rotation causes the weakening of two important hydrogen bonds: OH3′-O6′′′ and OH4′-O6′′′. This fact can be easily confirmed by the disappearing of the blue disk in the NCI surface (Fig. S5r and t†). For structure 38 the rotation of the ring B does not affect the interaction between the ABC rings and the glycosidic part because in both (fully optimized and rotated structures) the rhamnose and glucose rings are too far from ABC rings.
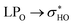 donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
| Interaction | Structure 37 | Interaction | Structure 38 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fully optimized | ϕ1, ϕ2 rotated | Fully optimized | ϕ1, ϕ2 rotated | ||||||
| d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | ||
| OH5-O4 | 1.69 | 34.60 | 1.69 | 34.64 | OH5-O4 | 1.69 | 34.58 | 1.69 | 34.45 |
| OH3′-O6′′′ | 1.94 | 12.30 | 2.51 | 1.26 | OH4′-OH3′ | 2.11 | 3.36 | 2.11 | 3.36 |
| OH4′-OH3′ | 2.06 | 4.47 | 2.06 | 4.41 | OH2′′-OH3′′ | 2.36 | 1.58 | 2.36 | 1.57 |
| OH3′′-OH4′′ | 2.34 | 1.55 | 2.34 | 1.55 | OH3′′-OH4′′ | 2.37 | 1.30 | 2.37 | 1.30 |
| OH2′′-OH3′′ | 2.35 | 1.63 | 2.35 | 1.63 | OH3′′′-OH4′′′ | 2.25 | 2.90 | 2.25 | 2.90 |
| OH2′′′-OH3′′′ | 2.24 | 1.80 | 2.24 | 1.80 | OH3′′′-O-CH2 | 2.18 | 2.82 | 2.18 | 2.82 |
| OH3′′′-OH4′′′ | 2.33 | 2.06 | 2.33 | 2.07 | |||||
| OH3′-O-CH2 | 2.12 | 3.99 | 2.12 | 3.99 | |||||
| OH4′-O6′′′ | 1.94 | 12.30 | 2.51 | 1.26 | |||||
Data for structures 42 and 44 are given in Table 7. The geometry 42, when rotated, approximates its glycosidic chain to the other side of the molecule (from the A ring to the B ring). This rotation, despite completely changing the orientation of glucose and rhamnose, does not considerably affect the hydrogen bonds and dispersive interactions of the molecule. In a similar way, for structure 44, the rotation of the ring B did not cause major changes in the orientation of the glycosidic chain. The NCI plots for these two structures are shown in Fig. S5ac–af.†
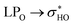 donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
donations at the ωB97X-D/6-31G(d,p) – PCM DMSO level of theory. ND = non detected by NBO analysis
| Interaction | Structure 42 | Interaction | Structure 44 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fully optimized | ϕ1, ϕ2 rotated | Fully optimized | ϕ1, ϕ2 rotated | ||||||
| d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | d (Å) | E(2) (kJ mol−1) | ||
| OH5-O4 | 1.71 | 31.25 | 1.71 | 31.38 | OH5-O4 | 1.70 | 34.42 | 1.70 | 32.34 |
| OH4′-OH3′ | 2.10 | 3.46 | 2.10 | 3.46 | OH2′′-O4 | 1.75 | 17.31 | 1.75 | 17.26 |
| OH2′′-OH3′′ | 2.37 | 1.40 | 2.37 | 1.41 | OH4′-OH3′ | 2.09 | 3.60 | 2.09 | 3.81 |
| OH3′′-OH4′′ | 2.41 | 1.28 | 2.41 | 1.28 | OH3′′-OH4′′ | 2.34 | 1.74 | 2.34 | 1.74 |
| OH2′′′-OH3′′′ | 2.22 | 2.52 | 2.22 | 2.53 | OH2′′-OH3′′ | 2.45 | 1.07 | 2.45 | 1.07 |
| OH3′′′-OH4′′′ | 2.33 | 2.01 | 2.33 | 2.01 | OH2′′′-OH3′′′ | 2.18 | 2.43 | 2.18 | 2.87 |
| OH3′-O-CH2 | 2.19 | 3.30 | 2.19 | 3.45 | OH3′′′-OH4′′′ | 2.33 | 2.06 | 2.33 | 2.06 |
| OH2′′′-OC4 | 2.00 | 7.14 | 2.11 | 4.43 | OH3′-O-CH2 | 2.12 | 3.34 | 2.12 | 3.34 |
To illustrate the discussion above. Bi and tridimensional NCI plots calculated at ωB97X-D/6-31G(d,p) – PCM DMSO level of theory are shown in Fig. 7 for fully optimized (FO) and ϕ1, ϕ2 rotated (ROT) structures 28 and 32. In particular for structure 28 relative energy value is quite sensitive to the chosen DFT functional, being remarkably stabilized by dispersion effects.
Substantial changes in intramolecular distances related to vdW interactions are observed for all structures (see Table 8). The rotated structure 28 has three vdW distances substantially shorter than the corresponding fully optimized structures causing an increase in the relative stabilization due to vdW type interactions. Rotated structures 32 and 34 have also one intramolecular vdW distance shorter than the fully optimized structures, while rotated structures 37, 38, 42 and 44 have longer vdW distances than respective fully optimized structures not contributing to energy stabilization. This analysis of intramolecular non-covalent interaction distances for ϕ1, ϕ2 rotated and fully optimized rutin structures is in line with the relative energy profile shown in Fig. 6a and c, providing a qualitative explanation for the larger stability of the structure 28 highly influenced by vdW type intramolecular interactions.
| van der Waals (vdW) type interactions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Str. 28 | ROT | OPT | Str. 30 | ROT | OPT | Str. 32 | ROT | OPT | Str. 34 | ROT | OPT |
| OH4′′′-C8 | 2.26 | 2.25 | OH2′′-C2′ | 2.97 | 2.20 | H1G-O4 | 2.20 | 2.56 | H1G-O4 | 2.19 | 2.91 |
| H5′′′-C10 | 2.42 | 2.64 | H2′-OC3 | 2.54 | 2.60 | CH2-H1R | 2.34 | 2.34 | CH2-H1R | 2.42 | 2.42 |
| H3′′′-C5 | 2.14 | 2.61 | H6′-O1 | 2.54 | 2.57 | H4′′-CH2 | 2.61 | 2.61 | |||
| H1R-O4 | 2.44 | 2.90 | H2′′-C1′ | 3.53 | 2.74 | ||||||
| CH3-H6′ | 2.44 | 2.47 | CH2-H1R | 2.39 | 2.39 | ||||||
| H1G-CH3 | 2.44 | 2.44 | H4′′-CH2 | 2.59 | 2.59 | ||||||
| H1R-O4 | 2.44 | 2.90 | H1G-H5′′ | 2.53 | 2.53 | ||||||
| H1R-H5′′′ | 2.37 | 2.37 | |||||||||
| Str. 37 | ROT | OPT | Str. 38 | ROT | OPT | Str. 42 | ROT | OPT | Str. 44 | ROT | OPT |
|---|---|---|---|---|---|---|---|---|---|---|---|
| H2′-OC3 | 2.73 | 2.27 | H2′-OC3 | 2.56 | 2.25 | H2′-OC3 | 2.51 | 2.39 | H6′-O1 | 2.80 | 2.28 |
| OH2′′-C3 | 2.58 | 2.58 | OH2′′-C3 | 2.99 | 2.99 | H1R-CH2 | 2.68 | 2.68 | H2′-OC3 | 2.79 | 2.39 |
| H1R-CH2 | 2.80 | 2.80 | H1R-CH2 | 2.31 | 2.34 | CH2-O6′′′ | 2.41 | 2.41 | OH2′′-C3 | 2.95 | 2.95 |
| CH2-O6′′′ | 2.80 | 2.37 | CH2-O6′′′ | 2.53 | 2.53 | H6′-OH2′′ | — | 2.14 | H2′′-C3 | 2.63 | 2.63 |
| CH3-OC3′ | 2.18 | 2.45 | CH3-OHC4′′′ | 2.62 | 2.62 | H1G-OC4 | — | 2.44 | H1R-CH2 | 2.42 | 2.42 |
| OH3′-CH2 | 2.83 | 2.24 | OH3′-CH2 | NO | NO | CH2-O6′′ | 2.55 | 2.55 | CH2-O6′′′ | 2.61 | 2.61 |
| H1G-C4 | 2.59 | 2.68 | H1G-OC3 | 2.47 | 2.47 | CH3-OC3′ | 2.09 | 2.25 | |||
| H6′-O1 | 2.56 | 2.39 | H6′-OH2′′ | 2.39 | — | H5′-OH2′′′ | 6.12 | 2.37 | |||
| H1G-OC4 | 2.35 | — |
The results reported in Fig. 2 and 6, and Tables 4–7, regarding rutin structures 28, 30, 32, 34, 37, 38, 42 and 44 shown in Fig. 3, provide a good example of how distinct conformers of the same organic molecule can be stabilized by dissimilar intramolecular interactions, and intermolecular interactions with solvent molecules or other molecules present in biological media. And an adequate choice of DFT functional can be crucial for the correct prediction of the relative energy profile. A comparison between selected MD frames named #3000, #4000, #8000 and #10000 (not optimized structures) and corresponding DFT-PCM optimized geometries is presented in Table S2† (torsion angles and relative energies) and Fig. S6† (1H-NMR spectra). The large differences observed in DM and DFT-PCM optimized torsion angles provide a good example of very dissimilar molecular structures resulting from the use of a force field and DFT exchange–correlation functional to minimize the molecular energies, as reflected by the relative energy values given in the last column of Table S2.† This is totally supported by the very distinct DFT-PCM 1H-NMR spectra calculated using the non-optimized MD frames and corresponding fully optimized DFF-PCM structures (Fig. S6†), illustrating the distinction between MD and DFT outcomes. None of DFT-PCM 1H-NMR spectra calculated using the MD frames (non-optimized geometries) yield a good agreement with experimental NMR profile (Fig. S6†) providing an indication that the molecular structures originating from MD simulation are substantially different from the predominant rutin conformer present in DMSO solution according to the spectroscopic analysis.
We use the flavonoid rutin in this work, but the essence of the methodology can be extended to any organic compound of interest, with some changes and limitations, such as: experimental data are necessary to compare with those obtained experimentally, which leads the researcher to carry out the experiment itself or find data already obtained by other research groups; the complexity of the organic molecule of interest (which may be even greater than the rutin), which would make the calculations computationally difficult, and an adjustment of the level of theory for possible particularities of other organic systems.
The current understanding of molecular conformation is based on the minimization of energy. However, the measurement made on the experimental sample is not of energy, but a magnetic measurement, which reveals details about the chemical environment of the nuclei. Predicting experimental chemical shifts theoretically is synonymous with predicting the most likely conformation of the molecule in solution.
4 Conclusions
In this paper we analyzed three theoretical procedures used in the elucidation of the predominant structure of organic molecules in solution, which is a hard task for experimentalists, using the flavonoid rutin as a working example: thermodynamic analysis (relative energy values), evaluation of statistical indices with respect to experimental NMR chemical shift data and analysis of 1H-NMR profile in solution (best match between theoretical and experimental NMR pattern). The thermodynamic and spectroscopic criterion do not always go in the same direction, as expected, and we provided here an explanation using as an example the conformers of rutin. It is natural to think that for large and flexible molecules, such as rutin, there is a dynamic process in solution with various conformations been accessible as a function of time, and the experimentally observed NMR signal for each proton, should be a weighted average (usually Boltzmann population) of all structures according to the eqn (1), where the concentration of each conformer is obtained using the well-known thermodynamic equation (relative energy values are given in Fig. 2).The interaction of the experimental sample with external magnetic field (NMR spectroscopy) can be considered as a reliable source of information on the molecular structure in solution. The sensitivity of 1H-NMR chemical shifts to local chemical environments (molecular structure) is of fundamental importance in the elucidation of the preferred conformer in solution, with the NMR spectrum being a faithful representation of the plausible molecular structures. Therefore, using quantum chemical methods we can perform an extensive search for local minimum energy structures on the PES and then carry out NMR chemical shifts calculation for each structure. A comparison with experimental NMR data (spectroscopic criterion) would allow us to eliminate improbable conformers which we expected to be also energetically disfavored (thermodynamic criterion).
The effect of the level of theory on the relative energy predictions for conformers of organic molecules was investigated using a series of distinct structures of rutin which can be considered representative of the type of relevant intramolecular interactions usually present in chemical compounds. The ab initio Pos-HF MP2/6-31G(d,p)-PCM-DMSO level of theory was used as reference and sixteen DFT exchange–correlation functional was employed in our analysis with the geometries optimized at the ωB97X-D/6-31G(d,p)-PCM-DMSO level of calculation. The MP2 correlated level of theory describe satisfactorily dispersion effects and can be used as reference to assess the performance of DFT functional. It came as no surprise that only the DFT functional carrying some type of dispersion correction were able to reproduce correctly the MP2 energy profile for all rutin conformers. Specifically, structure 28 was substantially stabilized by vdW type intramolecular interactions and only the relative energy results calculated with the ωB97X-D, M062x, B3LYP-D3 and B97D functional (using the 6-31G(d,p) basis set and PCM solvent model) were in good agreement with MP2/6-31G(d,p)-PCM-DMSO values. The ωB97X-D functional was the only one having MAE value (with respect to MP2) below 1 kcal mol−1 for the full series of rutin structures and therefore it seems adequate for studies of organic molecules. Regarding DFT calculation of NMR chemical shifts it has already been shown that the B3LYP/6-31G(d,p)-PCM//ωB97X-D/6-31G(d,p)-PCM level of calculation produce good agreement with experimental data in solution.49 Rutin structure 28 provided a good example where the use of a DFT functional including dispersion effects, such as ωB97X-D, is crucial for the correct prediction of relative energies of distinct conformers of the same molecule. And this may happen with any organic molecule where intramolecular vdW interactions are relevant.
Due to the effect of intramolecular interactions on the conformations, NCI/NBO analyses were performed in order to characterize the dispersive interactions and hydrogen bonds. The data showed that, in conformation 28, the presence of vdW forces is higher than in the other conformations, which justifies the extra stabilization predicted by functionals with dispersion terms. In addition, the NCI data reveal that ϕ1, ϕ2 rotation of the optimized structure 32 leads to new vdW interactions, producing a conformation with thermodynamic/spectroscopic preference and revealing the importance of describing dispersive interactions in rutin.
Before we proceed one thing should be clear in our mind. When the experimental 1H-NMR spectrum is well resolved with peaks well separated and clearly defined, there is a small probability that distinct conformers of the same molecule (having protons in a very different chemical environment) will be detected at equilibrium in appreciable concentrations in solution. And that is the case of the flavonoid rutin. Among 44 distinct conformations located on the PES (34 obtained using standard scan procedures varying six torsion angles, and 10 structures optimized using as input MD simulations frames) none of them could reproduce correctly the experimental 1H-NMR profile in DMSO-d6 solution (including the global minimum structures named 34). Only when two torsion angles (ϕ1, ϕ2 see Scheme 1) were rotated in an artisanal manner (by a maximum of +23° in structure 32), keeping all remaining geometrical parameters at their DFT optimized values, an agreement with experiment was attained. Eight selected structures using a sound criterion, named 28, 30, 32, 34, 37, 42 and 44 (MD last frame), were rotated and the NMR spectra calculated. According to relative energy values structure 32 is the global minimum among all rotated structures, which also reproduce almost perfectly the experimental 1H-NMR profile, but in the light the MAE data (NMR) both structures 32 and 42 were predicted to exist in solution, what does not seem correct. These results indicate that although statistical indices are very useful, analysis of them alone may yield misleading predictions. The list of possible conformers of rutin in solution can be more than the 44 reported here, but our analysis revealed that the concentration of a single structure 32 should be predominantly larger than other conformers that can be present in DMSO solution.
Our results show that the desired harmony between thermodynamic and spectroscopic criterion is only achieved when we consider a molecular structure with ϕ1 and ϕ2 torsion angles deviating by a small amount from the DFT-PCM-DMSO fully optimized values (true minimum energy structure on the PES). The common procedure of using the last frame of MD simulation (structure 44 in the present work) as a good candidate input for DFT/PCM geometry optimization procedure did not work well for rutin. Improving the solvent effect model used here (PCM) through inclusion of explicit DMSO solvent molecules in the geometry optimization procedure could probably lead us to the correct rotated structure (obtained in an artisanal manner). However, as rutin has many polar groups that can explicitly interact with the polar DMSO molecule (mainly O–H), in addition to conformational flexibility, such quantum chemical calculations would be a very hard computational task. Our results strongly indicate that the combination between thermodynamics and NMR spectroscopic analysis can be an adequate strategy for the elucidation of the predominant structure of organic molecules in solution. We may think about an NMR-constrained DFT geometry optimization procedure as more appropriate for the prediction of molecular structures in solution than the conventional approach.
It is worth mentioning that there are various interesting computational procedures available for sampling local minimum energy structures on the PES for large organic molecules, some based on classical and quantum/classical hybrid approaches, which can provide a comprehensive search for distinct conformers of the same molecule. Such computational approaches can locate molecular structures situated in far regions of the PES, which can be relevant and not easily detected by DFT torsion angles scan procedure. Although molecular structures obtained by other computational tools can be fine, relative energies may not be trusted since depending on specific molecular structure (as happened for rutin) non-covalent vdW type intermolecular interactions can take place and the choice of DFT functional can be crucial. Therefore, computational schemes designed for conformational search should use functional carrying dispersion correction, to contemplate more faithfully the diversity of intramolecular interactions present in organic compounds.
The comparison we report here, between the calculated 1H-NMR chemical shifts and the experimentally measured spectra, involves a search for patterns, a common approach in scientific research (as seen in the health field with DNA tests). Ultimately, we seek a strong match between the two sets of data (theoretical and experimental), which provides compelling evidence that the predominant molecular structure of the solute present in the solution has been accurately identified.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
W. B. De Almeida would like to thank the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for a research fellowship (Proc. No. 309269/2021-0) and Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) for support (Proc. No. E-26/201.163/2021).Notes and references
- A. Burger and A. P. Parulkar, Annu. Rev. Pharmacol., 1966, 6, 19–47 CrossRef CAS PubMed.
- W. J. Dunn and S. Wold, Bioorg. Chem., 1980, 9, 505–523 CrossRef CAS.
- W. Lewandowski, H. Lewandowska, A. Golonko, G. widerski, R. wisocka and M. Kalinowska, PLoS One, 2020, 15, e0229477 CrossRef PubMed.
- I. Koss-Mikoajczyk and A. Bartoszek, Molecules, 2023, 28, 6156 CrossRef PubMed.
- L. Naso, E. G. Ferrer, L. Lezama, T. Rojo, S. B. Etcheverry and P. Williams, JBIC, J. Biol. Inorg. Chem., 2010, 15, 889–902 CrossRef CAS PubMed.
- N. E. A. Ikeda, E. M. Novak, D. A. Maria, A. S. Velosa and R. M. S. Pereira, Chem.-Biol. Interact., 2015, 239, 184–191 CrossRef CAS PubMed.
- A.-M. J. Boerboom, M. Vermeulen, H. van der Woude, B. I. Bremer, Y. Y. Lee-Hilz, E. Kampman, P. J. van Bladeren, I. M. Rietjens and J. M. Aarts, Biochem. Pharmacol., 2006, 72, 217–226 CrossRef CAS PubMed.
- P. Thangavel, B. Viswanath and S. Kim, Mater. Sci. Eng. C., 2018, 89, 87–94 CrossRef CAS PubMed.
- K. R. Ng, X. Lyu, R. Mark and W. N. Chen, Food Chem., 2019, 270, 123–129 CrossRef CAS PubMed.
- A. Nowicka, A. Z. Kucharska, A. Sokó-towska and I. Fecka, Food Chem., 2019, 270, 32–46 CrossRef CAS PubMed.
- D. Sanna, V. Ugone, A. Fadda, G. Micera and E. Garribba, J. Inorg. Biochem., 2016, 161, 18–26 CrossRef CAS PubMed.
- Y.-C. Tsai, Y.-H. Wang, C.-C. Liou, Y.-C. Lin, H. Huang and Y.-C. Liu, Chem. Res. Toxicol., 2011, 25, 191–196 Search PubMed.
- R. Feng, Z. K. Guo, C. M. Yan, E. G. Li, R. X. Tan and H. M. Ge, Phytochemistry, 2012, 76, 98–105 CrossRef CAS PubMed.
- O. Farkas, J. Jakus and K. Héberger, Molecules, 2004, 9, 1079–1088 CrossRef CAS PubMed.
- L. A. De Souza, H. C. Da Silva and W. B. De Almeida, ChemistryOpen, 2018, 7, 902–913 CrossRef CAS PubMed.
- R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1995 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- Ab Initio Molecular Orbital Theory, ed. W. J. Hehre, Wiley, New York, 1986 Search PubMed.
- J. G. Napolitano, D. C. Lankin, S. Chen and G. F. Pauli, Magn. Reson. Chem., 2012, 50, 569–575 CrossRef CAS PubMed.
- D. A. McQuarrie, Statistical Thermodynamics, Univ. Science Books, Mill Valley, Calif, 1976 Search PubMed.
- B. Mennucci, E. Cancès and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506–10517 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- A. Szabo, Modern Quantum Chemistry, Dover Publications, Inc., Mineola, New York, 2012 Search PubMed.
- S. A. Adcock and J. A. McCammon, Chem. Rev., 2006, 106, 1589–1615 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- H. J. C. Berendsen, Simulating the Physical World: Hierarchical Modeling from Quantum Mechanics to Fluid Dynamics, Cambridge University Press, 2007 Search PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graph. Model., 2006, 25, 247–260 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, year Search PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- B. Hess, J. Chem. Theory Comput., 2007, 4, 116–122 CrossRef PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Acad. Press, San Diego, 2nd edn, 2011 Search PubMed.
- A. R. Leach, Molecular Modelling, Pearson/Prentice Hall, Harlow, 2nd edn, 2009 Search PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- R. Naaman and Z. Vager, The Structure of Small Molecules and Ions, Springer US, 1988 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1740 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- J. Carpenter and F. Weinhold, J. Mol. Struct., 1988, 169, 41–62 CrossRef.
- T. Lu and F. Chen, J. Comput. Chem., 2011, 33, 580–592 CrossRef PubMed.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- M. V. De Almeida, M. R. C. Couri, J. V. De Assis, C. P. A. Anconi, H. F. Dos Santos and W. B. De Almeida, Magn. Reson. Chem., 2012, 50, 608–614 CrossRef CAS PubMed.
- H. C. Da Silva and W. B. De Almeida, Chem. Phys., 2020, 528, 110479 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels. O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- P. J. Hore, Nuclear Magnetic Resonance, Oxford University Press, Oxford, 2nd edn, 2015 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410 RSC.
- J. C. Slater and J. C. Phillips, Phys. Today, 1974, 27, 49–50 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef PubMed.
- J. P. Perdew, P. Ziesche and H. Eschrig, Electronic structure of solids, 1991, vol. 91 Search PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677 CrossRef CAS PubMed.
- R. J. Bartlett and J. F. Stanton, Applications of PostHartree—Fock Methods: A Tutorial, 1994 Search PubMed.
- H. C. Da Silva, A. S. Paluch, L. T. Costa and W. B. De Almeida, J. Mol. Liq., 2021, 341, 117214 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03430a |
| This journal is © The Royal Society of Chemistry 2024 |