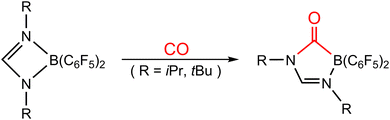Understanding the CO capture reaction through electronic structure analysis of four-membered-ring group-13/N- and B/group-15-based Lewis acid–base pairs

Abstract

Incomplete combustion yields a significant byproduct, known for its high toxicity to humans: gas phase carbon monoxide (CO). This study utilized several advanced theoretical methods to examine the factors contributing to the activation energy involved in CO capture by a frustrated Lewis pair (FLP) and to forecast the potential success of the CO capture reaction. The current theoretical findings indicate that among the four-membered-ring Group-13/N-FLP and B/Group-15-FLP molecules, only the B/N-based FLP-type molecule effectively captures CO, considering both thermodynamics and kinetics. According to the results obtained through energy decomposition analysis-natural orbitals for chemical valence (EDA-NOCV), it can be concluded that the donor–acceptor (singlet–singlet) model, rather than the electron-sharing (triplet–triplet) model, effectively characterizes the electronic structures in the CO trapping reaction involving four-membered-ring G13/G15-FLPs. Theoretical findings, derived from EDA-NOCV and frontier molecular orbital theory, demonstrate that the CO capture reaction by G13/G15-FLP involves two distinct bonding interactions. The first interaction is characterized by FLP-to-CO forward bonding, with the lone pair of G15 (G13/G15-FLP) donating to the empty p–π* orbital of carbon (CO), which predominates. The second interaction involves CO-to-FLP backward bonding, where the empty σ* orbital of G13 (G13/G15-FLP) accepts the lone pair of carbon (CO), albeit to a lesser extent. In summary, our theoretical findings indicate that the G13–C and G15–C bonds in the G15/G15-TS species with a four-membered ring can be classified as two dative single bonds. The importance of the interaction between Lewis bases and CO surpasses that of the interaction between Lewis acids and CO. Theoretical evidences in this study demonstrate a linear connection between the G13–G15 bond length within the four-membered-ring G13/G15-FLP and the activation barrier linked to CO capture. The activation strain model analysis in this study suggests that the activation energy required for bond formation primarily depends on the geometric deformation energy of G13/G15-FLP in capturing CO. Our DFT investigation shows that Hammond's postulate is obeyed by the CO catching reaction of the four-membered-ring G13/N-FLP, meaning that an earlier transition state is associated with a lower activation barrier, but not with the CO catching reaction of the four-membered-ring B/G15-FLP.

---

1. Introduction

Carbon monoxide (CO) is an inorganic compound gas that lacks color, odor, and taste. It is slightly lighter than air and poses a significant risk to human health when inhaled. When CO binds to hemoglobin, it forms carboxyhemoglobin, which obstructs the delivery of oxygen to body tissues.^1–7 The particular danger of CO lies in its imperceptible nature and non-specific symptoms, causing individuals to become sick or die without realizing their exposure. Unlike its inert isoelectronic analogue, N₂, CO is a reactive and highly poisonous gas. Nonetheless, it is intriguing to observe that despite its apparent polarity, this molecule exhibits a normal boiling point of −192 °C, a value that is remarkably similar to the boiling point of the nonpolar N2 (−196 °C).⁸ Like N₂, CO features a triple bond. However, the C–O bond in CO is exceptionally strong, boasting a dissociation energy of around 257.3 kcal mol⁻¹, thereby placing it among the strongest bonds in neutral diatomic molecules.⁹ Surprisingly, the C≡O triple bond exhibits greater stability than N₂, with a dissociation energy of 225.8 kcal mol⁻¹.⁹ Additionally, the presence of a lone pair of electrons on the C atom in CO is a significant attribute that accounts for its reactivity towards electron-seeking metal species,¹⁰ such as the Ni atom involved in the formation of Ni(CO)₄.^11–13 At present, atmospheric CO is particularly important due to its involvement in the intricate oxidation mechanism of many atmospheric hydrocarbon species. The conversion of CO to CO₂ by the hydroxyl radical is a significant step in this process.⁹ Moreover, CO contributes significantly to forest and crop damage, ecosystem acidification, stratospheric ozone depletion, and global climate change.¹⁴

Describing a reagent used in chemistry, a frustrated Lewis pair (FLP) is composed of a Lewis acid (LA) and a Lewis base (LB), which act as the electron acceptor and donor, respectively.¹⁵ The word “frustrated” means that the interaction between these two centers is hindered so that a polar covalent bond cannot be formed between them.¹⁵ This hindered condition can be generated by bulky substituents or intramolecular steric confinement. Principally, FLPs can have two interesting structures, namely, intramolecular and intermolecular frameworks. In this way, an FLP reagent has two functions of LA and LB at the same time, providing it with new reaction opportunities. Traditionally, chemists have used transition metal elements or organometallic complexes as catalysts. However, generally speaking, transition metals are usually more expensive, and most of them are toxic. Specifically, the latter characteristic will have negative impacts on both human health and the natural environment. Moreover, most of the newly identified FLP-associated molecules are free from transition metal elements, making them non-hazardous and more economical to fabricate. These exceptional bases make FLPs an enticing reagent for various captivating chemical reactions.^16–18 Over the past fifteen years, experimental chemists have created and produced various fascinating and useful FLP reagents, which function as catalysts for activating small molecules.^16–18 Consequently, FLP chemistry is now widely employed across different chemical disciplines, such as heterogeneous catalysis, solid-state chemistry, bioorganic and bioinorganic syntheses, and polymer chemistry.^19–34

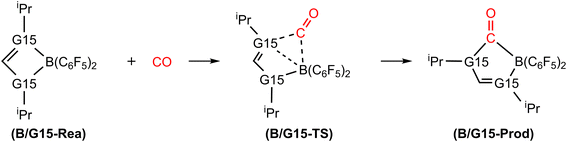
Catching CO with an FLP has been one of the various research topics of interest in FLP chemistry. Around a decade ago, Dureen and Stephan published findings on the reaction between the B/N-based FLP-type molecule (HC(RN)₂B(C₆F₅)₂; R = iPr and tBu) and 1 atm of CO, leading to the formation of the insertion product HC(RN)₂(CO)B(C₆F₅)₂,³⁵ as shown in Scheme 1. Despite previous reports on CO insertion into B–C bonds of boranes,³⁶ this study provides the first instance of CO insertion into B–N bonds. Subsequently, relevant experimental results of CO being captured by different types of FLP-assisted molecules were reported successively.^37–42 However, theoretical study on the capture reaction of CO by FLP-related molecules is comparatively rare.⁴³ Thus, the bonding nature and related information concerning CO sequestration by FLPs remain rather poorly understood. Therefore, in this work, we take the first experimental work reported by Dureen and Stephan³⁵ as the object of theoretical research. We will use advanced theoretical methods and models to explore the relative reactivity of this type of intramolecular FLP when the same group of elements occupies the LA or LB site of an FLP and to comprehend the basic cause of their activation barriers. By utilizing theoretical research methods, we have gained a deeper understanding of the intrinsic bonding nature and chemical reactions of various intramolecular FLP-related molecules and small molecules, such as H₂,^44,45 CO₂,^46,47 CS₂,⁴⁸ tetrahydrofuran,⁴⁹ and ketones.⁵⁰ The primary purpose of this work is to investigate the bonding nature and activation energy in the chemical reaction between the four-membered FLP-associated molecule and CO. Based on our current understanding, this theoretical article is groundbreaking in its application of computational chemistry to explore the bonding nature and activation energy of the CO molecule captured by FLP.

Scheme 1 Reactions of boron amidinates HC(RN)₂B(C₆F₅)₂ (R = iPr and tBu) with CO.

2. Methodology

The Gaussian 16 program package⁵¹ was utilized to perform molecular geometry optimizations at the M06-2X⁵²-D3 (ref. 53–55)/def2-TZVP⁵⁶ level of theory, without imposing symmetry constraints. Confirmation of energy minima for the stationary points on the potential energy surface was achieved through frequency calculations.

The ADF 2017.112 program package⁵⁷ was utilized to perform the energy decomposition analyses (EDAs)^58–65 at the M06-2X-D3 level, employing a triple-ζ-quality basis set. Uncontracted Slater-type orbitals augmented by two sets of polarization functions were used, with a frozen-core approximation for the core electrons (TZ2P).⁶⁶ Relativistic effects are incorporated in this single-point calculation by employing the zero-order regular approximation (ZORA).^67,68 The EDA calculations utilize the optimized geometries obtained from M06-2X-D3/def2-TZVP. This theoretical framework is denoted as ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP.

The EDA method was employed to quantitatively analyze the bonding interactions between the intramolecular FLP fragments and CO. The ΔE_INT, representing the instantaneous interaction energy between fragments A and B (namely G13/N-FLP or B/G15-FLP and CO), was further dissected into multiple contributions with physical significance.

ΔE_INT = ΔE_Elstat + ΔE_Pauli + ΔE_Disper + ΔE_Orb (1)

The electrostatic interaction energy between the density distribution of A and B in the transition state geometry, G13/G15 TS (see below), is denoted as ΔE_Elstat. The repulsive interaction between fragments A and B caused by the exclusion principle, which prohibits the co-occupation of the same region in space by two electrons with the same spin, is referred to as ΔE_Pauli. The dispersion interaction between A and B is considered in ΔE_Disper. ΔE_Orb represents the term responsible for stabilizing orbital interaction, which is calculated during the last phase of EDA when the Kohn–Sham orbitals reach their optimal state. This term can be additionally partitioned into contributions from orbitals that belong to different irreducible representations of the interacting system. Additionally, the visual examination of the deformation density (Δρ) using natural orbitals for chemical valence (NOCV)^69–72 analysis allows for the assignment of the ΔE_Orb term to a specific bond type. This term serves as an indicator of the charge deformation magnitude and visually represents the flow of charge associated with the pairwise orbital interaction. Consequently, the EDA-NOCV scheme provides both quantitative and qualitative information regarding the strength of orbital interactions in chemical bonds.

Moreover, in order to obtain a thorough comprehension of the factors that govern the CO catching reactions by FLPs, an analysis was carried out on the energies required for distorting the reactant fragments to the geometry of the transition state (ΔE_DEF), as well as the energies associated with the interaction between these distorted reactants at the transition state (ΔE_INT). This analytical framework is commonly referred to as the activation strain model (ASM),^73–78 which builds upon the distortion/interaction method pioneered by Ess and Houk and has been successfully applied to several chemical systems.^79–81

3. Bonding models

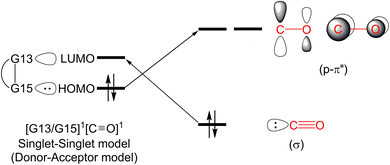
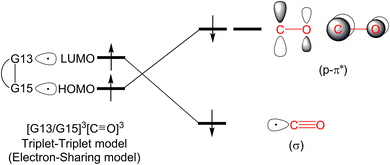
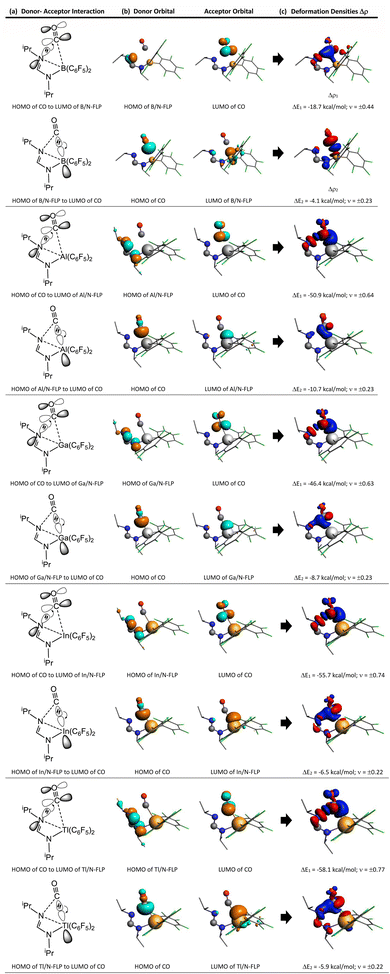
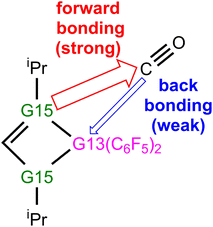
In this section, we will discuss the electronic structure model of the CO molecule captured by the G13/G15-based (G13 = Group 13 element and G15 = Group 15 element) molecule. In principle, we will disassemble their transition state structure (G13/G15-TS) into two fragments, i.e., CO and G13/G15-FLP. In other words, when G13/G15-FLP and CO bond together, their HOMOs (the highest occupied molecular orbitals) and LUMOs (the lowest unoccupied molecular orbitals) interact with each other. This interaction has two possible chemical bonding models: the singlet–singlet (S–S) interaction model and the triplet–triplet (T–T) interaction model. Notably, the total spin states of both models are singlets. In the S–S model, the HOMO of G13/G15-FLP, whose two electrons are situated on the relatively more electronegative G15 atom, interacts with the LUMO of CO, whose vacant p–π* orbitals are mainly located on the C atom of CO.¹⁰ That is, HOMO (the lone pair of G15) → LUMO (the vacant p–π* orbital of CO). Meanwhile, the lone pair electrons on the carbon atom of CO (HOMO) form an interaction with the LUMO of G13/G15-FLP, located on the G13 atom, which is comparatively more electropositive. In this case, LUMO (the empty σ* of G13) ← HOMO (the lone pair of C). CO generally acts as a σ-donor and a π-acceptor. The interactions mentioned above, denoted as the “donor–acceptor model”, are visually represented in Fig. 1.

Fig. 1 The singlet–singlet model or the donor–acceptor model.

On the other hand, within the T–T model, the single-electron orbitals of G15 and G13 from the G13/G15-based FLP-related molecule interact with the single-electron orbital of the CO molecule, resulting in the formation of two chemical bonds: G13–C and G15–C. The orbital interacting diagram, as shown in Fig. 2, visually illustrates this process. In simpler terms, the T–T model, or the electron-sharing model, can be represented as [G13/G15-FLP]³ + CO³ → [G13/G15-TS]¹.

Fig. 2 The triplet–triplet model or the electron-sharing model.

It is noteworthy that the bonding models employed in the reaction between the FLP-related molecule and CO exhibit a striking resemblance to the electronic structure descriptions of Fischer carbene⁸² and Schrock carbene,⁸³ which hold significant prominence in the realm of transition metal organometallic chemistry. In the ensuing discussion, we will employ these bonding models to delve into the electronic structure of the CO molecule upon its capture by G13/G15-FLP.

4. Results and discussion

4.1 Catching reactions of CO by G13/N-based FLPs

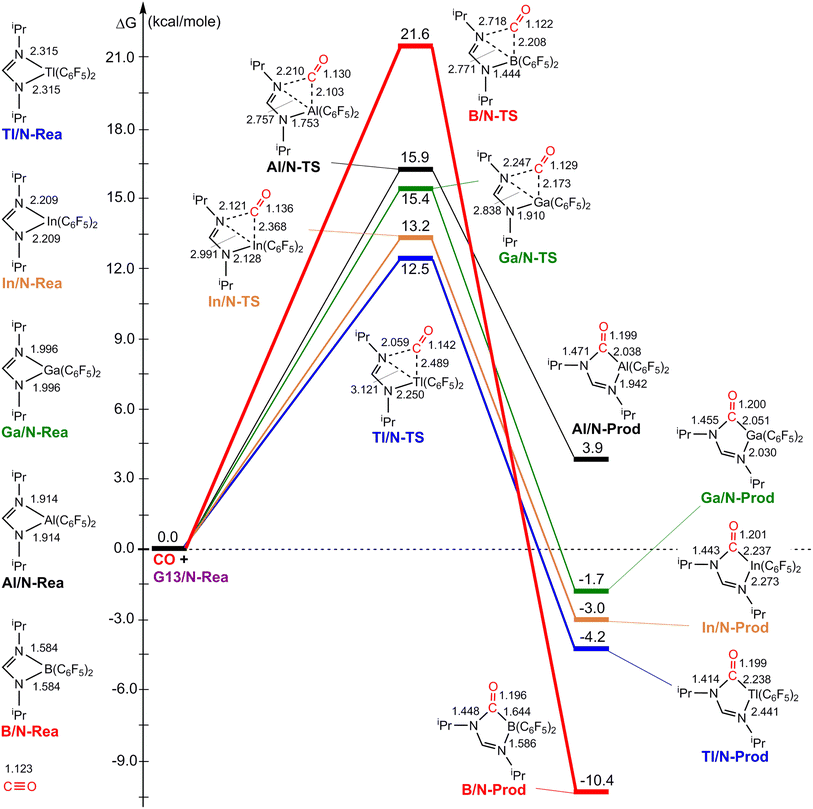
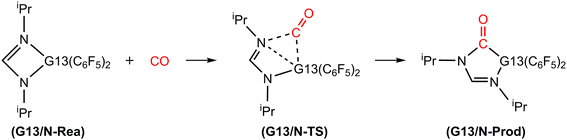
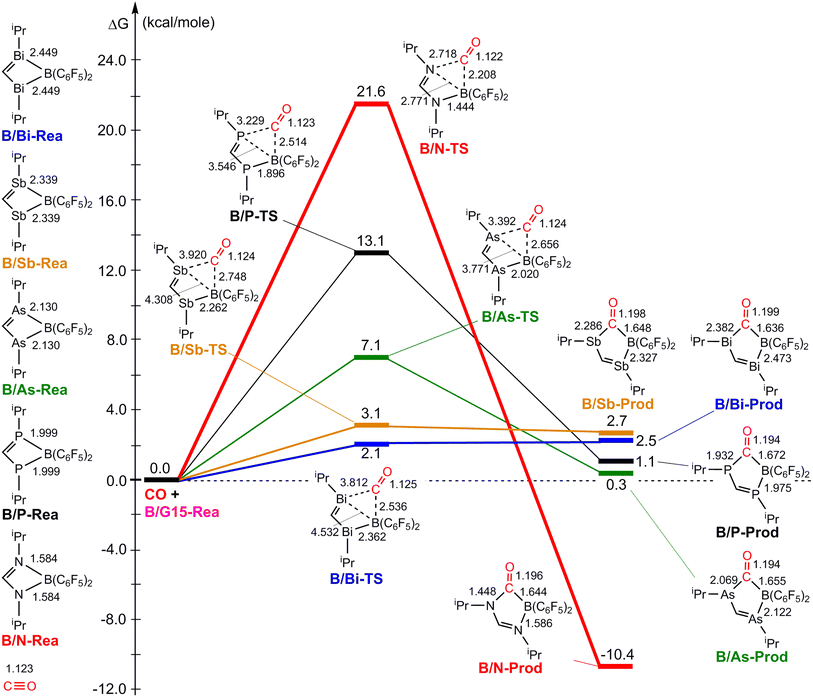
Fig. 3 illustrates the stationary points on the free energy surfaces of the CO capturing reactions by G13/N-Rea FLP-associated molecules (Scheme 2). These points include G13/N-Rea (reactant), G13/N-TS (transition state), and the final product (G13/N-Prod). Based on our calculations, we have not discovered their reaction precursors. Let us first focus on the G13/N-based FLP-type reactants. Fig. 3 clearly indicates that the G13–N bond length (Å) in G13/N-Rea is in order of 1.584 (B/N-Rea) < 1.914 (Al/N-Rea) < 1.996 (Ga/N-Rea) < 2.209 (In/N-Rea) < 2.315 (Tl/N-Rea), which is in the same order as the atomic radius (pm) of the LA center G13, that is, B (84) < Al (121) < Ga (122) < In (142) < Tl (145).⁸⁴ Additionally, Fig. 3 presents results indicating a decline in the activation free energy ΔG_ACT (kcal mol⁻¹) for the CO capture reaction by the G13/N-based FLP-assisted molecule in the following sequence: B/N-TS (21.6) > Al/N-TS (15.9) > Ga/N-TS (15.4) > In/N-TS (13.2) > Tl/N-TS (12.5). This demonstrates an opposite trend to the atomic radius of the G13 atom occupying the LA site of B/N-Rea. Consequently, the provided theoretical evidence reveals that a larger atomic radius of G13 situated at the LA site of G13/N-Rea corresponds to an increased G13–N bond length and a weakened bond strength of the G13–N bond. Therefore, CO can readily insert into a G13–N bond of G13/N-Rea using small activation energy, making CO easily captured by G13/N-Rea. Indeed, according to Fig. 4, the G13–N bond length and ΔG_ACT values are strongly correlated (R² = 0.963).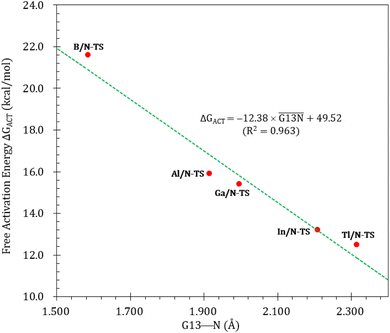

Fig. 3 The M06-2X-D3/def2-TZVP free energy surfaces for CO catching reactions by G13/N-FLPs. The stationary points include reactant (G13/N-Rea), transition state (G13/N-TS) and final product (G13/N-Prod). All bond lengths and energies are in Å and in kcal mol⁻¹, respectively.

Scheme 2 Mechanism for catching reaction of CO by G13/N-based FLP.

Fig. 4 Linear relationship between the G13–N bond length (Å) and ΔG_ACT of G13/N-TS (kcal mol⁻¹) values.

Nonetheless, our reaction free energy ΔG_RXN shown in Fig. 3 indicates that only the B/N-Rea catching reaction with CO, producing five-membered Al/N-Prod, is endergonic (3.9 kcal mol⁻¹). Among the four remaining exergonic reactions, the B/N-Prod molecule with a five-membered ring exhibits the highest heat of formation (−10.4 kcal mol⁻¹), while the Ga/N-Prod molecule with a five-membered ring exhibits the lowest heat of formation (−1.7 kcal mol⁻¹). The remaining four reactions are exergonic, among which the B/N-Prod molecule bearing a five-membered ring had the largest heat of formation (−10.4 kcal mol⁻¹) and the Ga/N-Prod molecule bearing a five-membered ring had the smallest heat of formation (−1.7 kcal mol⁻¹). From the theoretical analyses, it is clear that among four-membered-ring G13/N-based FLPs, only Al/N-Rea cannot undergo the CO catching reaction. The others (B/N-Rea, Ga/N-Rea, In/N-Rea, and Tl/N-Rea) can do so readily from both kinetic and thermodynamic viewpoints. In fact, our theoretical prediction agrees well with the available experimental result reported by Dureen and Stephan (Scheme 1).³⁵

Next, let us understand the electronic structure behind the four-membered-ring G13/N-Rea capturing the CO molecule. The HOMOs and LUMOs of G13/N-Rea and CO are graphically represented in Fig. 5. Fig. 5 shows that G13/N-Rea has a HOMO that is mostly located at the LB site, i.e., the N element, and a LUMO that is mainly situated at the LA site, i.e., the G13 element. On the other hand, the right-hand side of Fig. 5 shows that CO has a HOMO that is a lone pair orbital chiefly concentrated on the carbon atom¹⁰ and a LUMO that is a degenerate p–π* orbital mostly centered on the carbon atom.

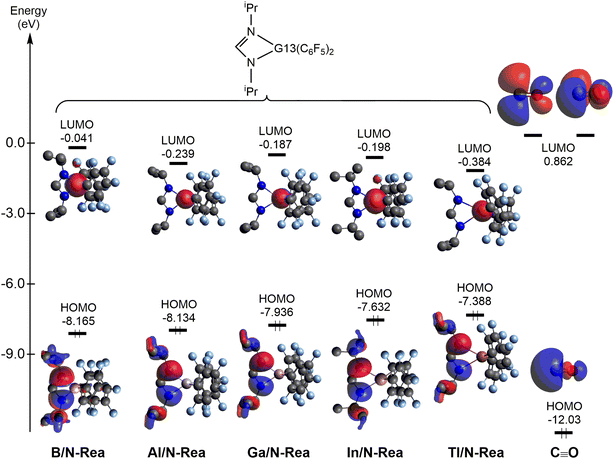Fig. 5 Energies of the frontier orbitals (HOMO and LUMO) of the model molecules G13/N-Rea and CO for comparison, computed at the M06-2X-D3/def2-TZVP level.

We then calculated the energy difference between the HOMO of G13/N-Rea and the LUMO of CO and the energy difference between the HOMO of CO and the LUMO of G13/N-Rea, which are collected in Table 1. Table 1 shows that the former energy difference is much smaller than the latter energy difference. According to the FMO theory,⁸⁵ the interaction between two orbitals will be stronger with a small energy gap than with a large energy gap. Therefore, our FMO evidence listed in Table 1 strongly suggests that the forward bonding, G13/N-Rea (HOMO) → CO (LUMO) interaction plays a substantial role in determining the bonding condition between G13/N-Rea and CO, whereas the back-bonding is the G13/N-Rea (HOMO) ← CO (LUMO) interaction, which contributes relatively little to the bonding pattern. We will confirm this finding again in the calculation results of EDA-NOCV discussed below.

Table 1 The energy difference between the HOMO of G13/N-Rea and the LUMO of CO, as well as the energy difference between the HOMO of CO and the LUMO of G13/N-Rea. The energy values (in eV) see Fig. 5

System	Energy difference∣CO (LUMO) − FLP (HOMO)∣	Energy difference∣FLP (LUMO) − CO (HOMO)∣
B/N-Rea + CO	9.027	11.99
Al/N-Rea + CO	8.996	11.80
Ga/N-Rea + CO	8.798	11.85
In/N-Rea + CO	8.494	11.84
Tl/N-Rea + CO	8.250	11.65

---

To gain a better understanding of the bonding interaction between G13/N-Rea and CO in G13/N-TS, EDA-NOCV was utilized, whose numerical results are given in Table 2. We performed EDA-NOCV calculations on G13/N-TS using the fragments G13/N-Rea and CO with the frozen geometries of the compound, but with different spin states. One calculation uses singlet fragments as reference states (the singlet–singlet model or the donor–acceptor model). The other calculation employs the electronic triplet states of G13/N-Rea and CO (the triplet–triplet model or the electron-sharing model). Previous works^86,87 have verified that the calculated values for the total orbital interaction (ΔE_Orb) can be used to indicate the best description of bonding interactions between two fragments. This reason is that the least alteration of the electronic charge distribution is required to yield the electronic structure of the molecule.^86,87 Hence, the EDA calculations that give the smallest ΔE_Orb value indicate which bonding model is the best choice for describing the bonding situation. Table 2 shows that the absolute values of ΔE_Orb were 27.8–75.9 and 222.6–271.0 kcal mol⁻¹ for the S–S model and the T–T model, respectively. Accordingly, our EDA analyses demonstrate that the donor–acceptor model faithfully describes the bonding interaction in G13/N-TS. Moreover, our EDA evidences strongly suggest that two connecting bonds (G13–C and N–C) in G13/N-TS are two dative single bonds.

Table 2 EDA-NOCV results (kcal mol⁻¹) of G13/N-TS using both singlet–singlet and triplet–triplet models at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level^a

Fragments	B/N-TS		Al/N-TS		Ga/N-TS		In/N-TS		Tl/N-TS
	B/N-Rea (S) + CO (S)	B/N-Rea (T) + CO(T)	Al/N-Rea (S) + CO (S)	Al/N-Rea (T) + CO (T)	Ga/N-Rea (S) + CO (S)	Ga/N-Rea (T) + CO (T)	In/N-Rea (S) + CO (S)	In/N-Rea (T) + CO (T)	Tl/N-Rea (S) + CO (S)	Tl/N-Rea (T) + CO (T)
a All energy values are given in kcal mol^−1.b ΔEINT = ΔEElstat + ΔEPauli + ΔEOrb + ΔEDisper.c The values, shown in parentheses, reflect the percentage contribution of attractive interactions to the overall total (ΔEElstat + ΔEOrb + ΔEDisper).d The percentages shown in parentheses denote the contribution of each value to the overall orbital interactions (ΔEOrb).
ΔEINT^b	−6.6	−215.6	−7.5	−231.0	−8.2	−220.5	−7.9	−212.4	−7.6	−203.5
ΔEPauli	59.1	49.4	140.4	89.4	133.3	81.0	144.4	89.3	146.0	142.8
ΔEElstat^c	−30.2 (45.9%)	−34.7 (13.1%)	−68.8 (46.5%)	−70.2 (21.9%)	−67.0 (47.4%)	−65.4 (21.7%)	−71.4 (46.9%)	−68.3 (22.6%)	−70.8 (46.1%)	−68.5 (19.8%)
ΔEOrb^c	−27.8 (42.3%)	−222.6 (84.0%)	−72.1 (48.8%)	−243.2 (75.9%)	−67.6 (47.8%)	−229.3 (76.0%)	−74.3 (48.8%)	−226.7 (75.2%)	−75.9 (49.4%)	−271.0 (78.2%)
ΔEOrb (1)^d	−18.7 (67.2%)	−209.8 (94.2%)	−50.9 (70.6%)	−208.4 (85.7%)	−46.4 (68.6%)	−197.9 (86.3%)	−55.7 (75.0%)	−190.1 (83.8%)	−58.1 (76.6%)	−207.7 (76.7%)
ΔEOrb (2)^d	−4.1 (14.7%)	−7.6 (3.4%)	−10.7 (14.8%)	−24.5 (10.1%)	−8.7 (12.9%)	−21.3 (9.3%)	−6.5 (8.8%)	−27.6 (12.2%)	−5.9 (7.8%)	−27.3 (10.1%)
ΔERest^d	−5.0 (18.1%)	−5.2 (2.3%)	−10.5 (14.6%)	−10.3 (4.2%)	−12.5 (18.5%)	−10.0 (4.4%)	−12.1 (16.2%)	−9.0 (4.0%)	−11.9 (15.6%)	−35.9 (13.3%)
ΔEDisper^c	−7.7 (11.7%)	−7.7 (2.9%)	−7.0 (4.7%)	−7.0 (2.2%)	−6.9 (4.9%)	−6.9 (2.3%)	−6.6 (4.3%)	−6.6 (2.2%)	−6.9 (4.5%)	−6.9 (2.0%)

---

Moreover, Table 2 indicates that ΔE_Orb between singlet fragments in G13/N-TS has two major components, i.e., ΔE_Orb(1) and ΔE_Orb(2). The former component was calculated to be −58.1 to −18.7 kcal mol⁻¹, accounting for 67.2%–76.6% of the contribution to ΔE_Orb. However, the latter component was computed to be only −10.7 to −4.1 kcal mol⁻¹, approximately 7.8–14.8% of the contribution to ΔE_Orb. In addition, the EDA-NOCV method not only provides numerical outcomes for orbital interactions but also visually represents the changes in electronic structures using deformation densities. These colorful images offer detailed insights into alterations in the electronic structure of the fragments caused by bond formation. Consequently, Fig. 6 displays the corresponding graphical presentation of the deformation densities Δρ₍₁₎ and Δρ₍₂₎.

Fig. 6 The analysis of G13/N-TS using EDA-NOCV involved the following components: (a) a qualitative illustration of the orbital interactions between G13/N-Rea and CO; (b) the shape of the most significant interaction between occupied and empty orbitals of G13/N-Rea and CO; (c) a plot indicating the deformation densities (Δρ₍₁₎ and Δρ₍₂₎) of the pairwise orbital interactions between the two fragments in their closed-shell state, along with the corresponding interaction energies (kcal mol⁻¹) ΔE_Orb(1) and ΔE_Orb(2), respectively. The deformation densities show the direction of charge flow from red to blue.

The left-hand side of Fig. 6 shows that the strongest orbital stabilization ΔE_Orb(1) comes from the donation of the lone pair of one nitrogen atom (LB) in G13/N-Rea to the vacant p–π* molecular orbital of the carbon atom of CO. This interaction can be represented by the lone pair of N (G13/N-based FLP) → the empty p–π* orbital of C (CO). The other orbital stabilization is the smaller contribution ΔE_Orb(2), which is derived from the back donation of the lone pair of the C atom in CO into the vacant σ* orbital of the G13 atom (LA) in G13/N-Rea. This interaction can be considered the vacant σ* orbital of G13 (G13/N-based FLP) ← the lone pair of C (CO). From these qualitative representations, it is noted that the NOCV evidence schematized in Fig. 6 is consistent with the FMO observations shown in Table 1.

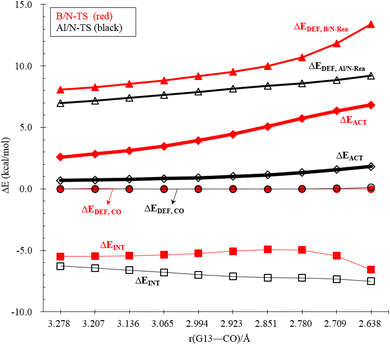
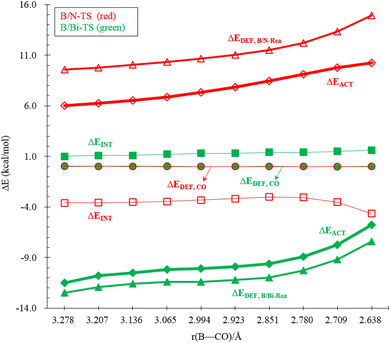
To reasonably explain how the barrier height of the four-membered-ring G13/N-based FLP CO capture reaction is generated, we applied the ASM to G13/N-TS using G13/N-Rea and CO as the fragments. Fig. 7 and Table 3 reveal that the activation energy (ΔE_ACT) receives a large contribution from the deformation energy of G13/N-Rea (ΔE_DEF,G13/N-Rea) and a relatively small amount from the deformation energy of CO (ΔE_DEF,CO) and the interaction energy (ΔE_INT) in G13/N-TS. In fact, according to the earlier theoretical results demonstrated in Fig. 3, we have already concluded that the ΔE_ACT of the reaction of G13/N-Rea to capture CO will decrease as the atomic number of G13 increases. This result is obtained because the larger the atomic number of the G13 element (LA) in the G13/N-Rea FLP-assisted molecule is, the larger its atomic radius.⁸⁴ This result, in turn, increases the bond length of the G13–N bond in G13/N-Rea (Fig. 3), resulting in the smaller bond energy of the G13–N bond. In this way, the carbon atom of CO can easily insert into one G13–N bond, decreasing the activation energy of this reaction. Therefore, the four-membered-ring G13/N-Rea FLP-type molecule bearing a heavier G13 element as the LA center can readily catch CO.

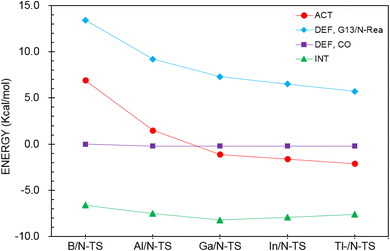Fig. 7 Activation strain analysis plot of ΔE_ACT (kcal mol⁻¹) for the reaction of G13/N-Rea with CO. Values extracted from Table 3.

Table 3 Activation strain analysis of G13/N-TS for the catching reaction of CO by four-membered G13/N-Rea^a,b

Entry	B/N-TS	Al/N-TS	Ga/N-TS	In/N-TS	Tl/N-TS
a At the level of ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP.b All values are in kcal mol^−1.c ΔEACT = ΔEDEF,CO + ΔEDEF,G13/N-Rea + ΔEINT.
ΔEACT^b^,^c	6.9	1.5	−1.1	−1.6	−2.1
ΔEDEF,CO	0.0	−0.2	−0.2	−0.2	−0.2
ΔEDEF,G13/N-Rea	13.4	9.2	7.3	6.5	5.7
ΔEINT	−6.6	−7.5	−8.2	−7.9	−7.6

---

Furthermore, according to the structural data shown in Fig. 3, the bond length of the breaking G13–N bond in G13/N-TS decreases according to B/N-TS (74.9%) > Al/N-TS (44.0%) > Ga/N-TS (42.2%) > In/N-TS (35.4%) > Tl/N-TS (34.8%), relative to the initial G13–N bond length in G13/N-Rea. In addition, the bond length of the unbroken G13–N bond in G13/N-TS decreases according to B/N-TS (8.8%) > Al/N-TS (8.4%) > Ga/N-TS (4.3%) > In/N-TS (3.7%) > Tl/N-TS (2.8%), with respect to the initial G13–N bond length in G13/N-Rea. The above theoretical information verifies the well-known Hammond's postulate;⁸⁸ that is, if the structure of the transition state is closer to that of the reactant, then its corresponding activation energy will be smaller. This prediction is consistent with the calculation results given in Fig. 3 and 4.

An in-depth ASM analysis of two representative systems, B/N-Rea and Al/N-Rea, can provide a quantitative understanding of the LA site's role in the CO catching process. Fig. 8 illustrates that both systems exhibit similar ASM features. A detailed examination of Fig. 8 suggests that only the deformation energies of B/N-FLP (ΔE_DEF,B/N-Rea) and Al/N-FLP (ΔE_DEF,Al/N-Rea) play a decisive role in the contrasting reactivity between B/N-Rea and Al/N-Rea. On the other hand, Fig. 8 shows that the ΔE_DEF,CO and ΔE_INT remain almost constant for both B/N-Rea and Al/N-Rea. For instance, at an G13–CO distance of 2.709 Å, B/N-TS exhibits a ΔE_DEF,B/N-Rea value of 11.8 kcal mol⁻¹, while Al/N-TS features a higher ΔE_DEF,Al/N-Rea value of 8.8 kcal mol⁻¹. Thus, the greater activation barrier in B/N-TS can be attributed to its higher ΔE_DEF,B/N-Rea value throughout the entire reaction pathway.

Fig. 8 ASM diagrams were employed to analyze the reactions of B/N-Rea (red lines) and Tl/N-Rea (green lines) FLP-type molecules with CO along the intrinsic reaction coordinate. The calculations were performed using the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level of theory.

4.2 Catching reactions of CO by B/G15-based FLPs

Fig. 9 summarizes the potential energy surfaces of the catching reaction of CO by B/G15-Rea (Scheme 3). Similar to the previous results shown in Fig. 3 and 9 indicates that the B–G15 bond length in B/G15-Rea increases with the atomic number and the atomic radius of the G15 atom occupying the LB site from small to large. In the case of G15, the reported atomic radius (pm) demonstrates a progression in the following order: N (71) < P (107) < As (119) < Sb (139) < Bi (148)⁸⁴ In the B/G15-Rea FLP-associated molecule, the bond lengths follow the order: 1.584 Å (B/N-Rea) < 1.999 Å (B/P-Rea) < 2.130 Å (B/As-Rea) < 2.339 Å (B/Sb-Rea) < 2.449 Å (B/Bi-Rea). However, our M06-2X results given in Fig. 7 show that the activation free energy ΔG_ACT (kcal mol⁻¹) of the CO capture reaction by B/G15-Rea follows the reverse order of 21.6 (B/N-TS) > 13.1 (B/P-TS) > 7.1 (B/As-TS) > 3.1 (B/Sb-TS) > 2.1 (B/Bi-TS). In other words, the greater the atomic number of G15 is, the larger the atomic radius of G15, the longer the B–G15 bond length in B/G15-Rea, and the smaller the activation energy of the four-membered-ring B/G15-FLP to capture CO. Notably, this interpretation is quite similar to the previous G13/N-TS cases discussed earlier. Again, a good linear relationship between the B–G15 bond length and ΔG_ACT is found, as shown in Fig. 10 (R² = 0.979).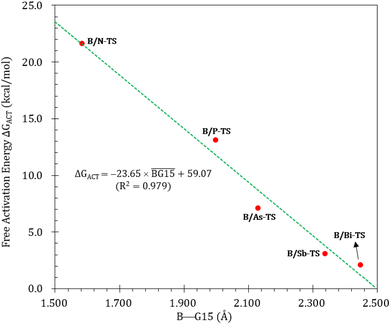

Fig. 9 The M06-2X-D3/def2-TZVP free energy surfaces for catching reactions of CO by G13/N-FLPs. The stationary points include reactant (B/G15-Rea), transition state (B/G15-TS) and final product (B/G15-Prod). All bond lengths and energies are in Å and in kcal mol⁻¹, respectively.

Scheme 3 Mechanism for catching reaction of CO by B/G15-based FLP.

Fig. 10 Linear relationship between the B–G15 bond length (Å) and ΔG_ACT of B/G15-TS (kcal mol⁻¹) values. Interestingly, from Fig. 9, we also observed that except for the case of B/N-Rea, the B/G15′-Rea FLP-mediated molecules possessing a heavy G15 atom (G15′ = P, As, Sb, and Bi) are expected to undergo endogonic reactions to catch a CO molecule. Namely, their free reaction energy ΔG_RXN (kcal mol⁻¹) was estimated to be 2.7 (B/Sb-Prod) > 2.5 (B/Bi-Prod) > 1.1 (B/P-Prod) > 0.3 (B/As-Prod) > −10.4 (B/N-Prod). Accordingly, the above theoretical evidence suggests that these four B/G15′-Rea FLP-assisted molecules bearing a heavy G15 atom as an LB center cannot capture CO effectively, and only the four-membered-ring B/N-Rea FLP-type molecule can readily capture CO, which was confirmed by the available experimental work.³⁵

To gain insight into the origin of reaction barriers for CO catching reactions by B/G15-FLPs, we also analyze the electronic structures of B/G15-Rea and CO. The pictures and corresponding energies of the HOMOs and LUMOs are summarized in Fig. S1.† Based on the information provided in Fig. S1,† it can be concluded that the LB site, representing the G15 element, is the main location of the HOMO in B/G15-Rea, whereas the LUMO primarily occupies the LA site, corresponding to the B element. Table S1† (ESI) shows the energy difference between the HOMO of B/G15-Rea and the LUMO of CO and the energy difference between the HOMO of CO and the LUMO of B/G15-Rea. The former energy gap (7.892–9.027 kcal mol⁻¹) is smaller than the latter energy gap (9.306–11.99 kcal mol⁻¹). According to the FMO theory,⁷⁸ we can clearly judge that when B/G15-Rea and CO interact with each other, the former plays a dominant role in the bonding interaction between B/G15-Rea and CO, while the latter contributes less. That is, the B/G15-Rea (HOMO) → CO (LUMO) interaction predominates. However, the contribution arising from the B/G15-Rea (HOMO) ← CO (LUMO) interaction is relatively small. The above FMO prediction will be further confirmed in the following EDA-NOCV results.

Table S2† (ESI) displays the EDA-NOCV results of B/G15-TS for both the singlet–singlet and triplet–triplet models. As mentioned earlier,^86,87 the crucial component of EDA-NOCV is ΔE_Orb since it is associated with the change in the total orbital interactions of the fragments. The numerical results in Table S2† show that for B/G15-TS, the absolute value of ΔE_Orb is much smaller for the singlet–singlet model (9.2–27.8 kcal mol⁻¹) than for the triplet–triplet model (180.6–222.6 kcal mol⁻¹). Therefore, our above EDA results demonstrate that during the CO catching reactions by the B/G15-Rea FLP-type molecules, the S–S model is more suitable for describing the electronic interaction. Similar to the G13/N-TS case, our above EDA information indicate that two connecting bonds (B–C and G15–C) in B/G15-TS are two dative single bonds.

Fig. S2† displays the deformation densities of the two most important pairwise orbital interactions (Δρ₍₁₎ and Δρ₍₂₎)_, along with the interacting orbitals of the fragments and the resulting molecular orbitals of the transition state. Similar to the NOCV evidence of G13/N-TS schematized in Fig. 6, the strongest interaction ΔE_Orb(1) (−58.1 to −18.7 kcal mol⁻¹), which contributes 67.2–76.6% to ΔE_Orb, comes from donating the lone pair of the G15 element to the LUMO of CO. Thus, this interaction can be written as the lone pair of G15 (B/G15-Rea) → the empty p-π* orbital of C (CO). ΔE_Orb(2) is a weaker interaction, estimated as −4.1 to −1.8 kcal mol⁻¹, and its contribution to ΔE_Orb is only approximately 14.7–14.7%. Fig. S2† shows that this weaker orbital interaction involves a σ donation from a lone pair on the carbon atom of CO to the empty σ* orbital located on the boron element of B/G15-Rea, which can be considered the vacant σ* orbital of B (B/G15-Rea) ← the lone pair of C(CO). Again, the above EDA-NOCV findings for the electronic interactions between B/G15-Rea and CO agree well with the FMO information presented in Table S1.†

Next, the ASM was applied to gain a more quantitative insight into the physical factor controlling the theoretically observed reactivity in the CO catching reactions of the four-membered-ring B/G15-Rea FLP-related molecules, whose calculated results are collected in Table 4 and sketched in Fig. 11. As seen in Fig. 11, the CO deformation energy (ΔE_DEF,CO) and the interaction energies between B/G15-Rea and CO (ΔE_INT) show nearly flat curves along the B/G15-TS species. Instead, the deformation energy of B/G15-Rea (ΔE_{DEF,B/G15-Rea}) makes the main contribution to the trend in the activation barriers. This phenomenon was rationalized earlier. In short, as the atomic number of the G15 element in the LB site of B/G15-Rea becomes larger, the atomic radius becomes larger as well, which makes the B–G15 bond length of B/G15-Rea longer, and its bond strength becomes smaller. Thus, one CO molecule can easily insert into one B–G15 bond of B/G15-Rea, leading to a smaller activation barrier. In the end, CO is readily captured by the four-membered-ring B/G15-Rea FLP-associated molecule and generates the final five-membered-ring insertion product.

Table 4 Activation strain analysis for the catching reaction of CO by four-membered B/G15-TS^a,b

Entry	B/N-TS	B/P-TS	B/As-TS	B/Sb-TS	B/Bi-TS
a At the level of ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP.b All values are in kcal mol^−1.c ΔEACT = ΔEDEF,CO + ΔEDEF,B/G15-Rea + ΔEINT.
ΔEACT^b^,^c	6.9	5.1	2.1	−0.4	−4.0
ΔEDEF,CO	0.0	0.0	0.0	0.0	0.0
ΔEDEF,B/G15-Rea	13.4	11.6	8.3	4.6	1.6
ΔEINT	−6.6	−6.5	−6.2	−6.0	−5.6

---

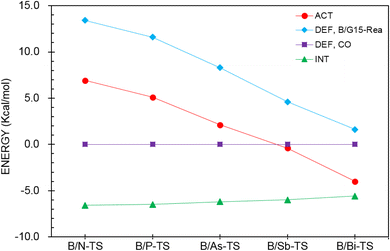Fig. 11 Activation strain analysis plot of ΔE_ACT (kcal mol⁻¹) for the reaction of B/G15-Rea with CO. Values extracted from Table 4.

We also examined the structural changes of two B–G15 bonds of B/G15-TS in such CO catching reactions. For the B–G15 bond in B/G15-TS shown in Fig. 9, the bond length is shortened by 8.8% (B/N-TS) > 5.2% (B/P-TS) ≈ 5.2% (B/As-TS) > 3.6% (B/Bi-TS) > 3.6% (B/Sb-TS) compared to the corresponding B–G15 bond length in B/G15-Rea. Additionally, for the B–G15 bond in B/G15-TS displayed in Fig. 9, the bond length is increased by 74.9% (B/N-TS) < 77.0% (B/As-TS) < 77.4% (B/P-TS) < 84.2% (B/Sb-TS) < 85.1% (B/Bi-TS) relative to the corresponding initial B–G15 bond length. From the above analyses, the structural changes of B/G15-TS unfortunately do not obey Hammond's postulate.⁸⁸

Performing a detailed ASM analysis on two representative systems, B/N-Rea and B/Bi-Rea, allows us to obtain a quantitative insight into the role of the LB site in the CO catching process. As shown in Fig. 12, both FLPs exhibit similar ASM characteristics. Upon careful examination of Fig. 12, it becomes evident that the reactivity difference between B/N-Rea and B/Bi-Rea is solely influenced by the deformation energy of the FLP-type molecule itself (i.e., ΔE_DEF,B/N-Rea and ΔE_DEF,B/Bi-Rea). However, as seen in Fig. 12, the ΔE_DEF,CO and ΔE_INT terms remain nearly constant for both B/N-Rea and B/Bi-Rea. For example, at an B–CO distance of 2.851 Å, B/N-TS demonstrates a ΔE_DEF,B/N-Rea value of 11.5 kcal mol⁻¹, whereas B/Bi-TS features a lower ΔE_DEF,B/P-Rea value of 11.0 kcal mol⁻¹. Hence, the lower activation barrier in B/Bi-TS can be attributed to its lower ΔE_DEF,B/Bi-Rea value along the entire reaction pathway.

Fig. 12 ASM diagrams were employed to analyze the reactions of B/N-Rea (red lines) and B/Bi-Rea (green lines) FLP-type molecules with CO along the intrinsic reaction coordinate. The calculations were performed using the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level of theory.

5. Conclusion

From the research results, several crucial conclusions can be summarized as follows:

(1) Based on our theoretical observations, it appears that the utilization of Group 13 elements or Group 15 elements in FLP-type molecules to replace the LA site of G13/N-Rea or the LB site of B/G15-Rea, respectively, results in successful CO capture exclusively by the four-membered-ring B/N-Rea FLP-associated molecule, without encountering any difficulties from both kinetic and thermodynamic viewpoints.

(2) Our theoretical findings reveal that a linear relationship exists between the G13–G15 bond length in the four-membered-ring G13/G15-FLP and the corresponding activation barrier for CO capture. In other words, the G13–G15 bond length in the four-membered-ring G13/G15-FLP molecule can be a good indicator of the barrier height of the CO catching reaction by the G13/G15-FLP.

(3) Our EDA-NOCV evidence indicates that the singlet–singlet (i.e., donor–acceptor) model rather than the triplet–triplet (i.e., electron-sharing) model can adequately describe the electronic structure of the transition state of the four-membered-ring G13/G15-based FLP capturing CO. In other words, two dative single bonds (G13–C and G15–C) take place in G13/G15-TS during the bonding process.

(4) Our EDA-NOCV findings demonstrate that during the reaction process of four-membered-ring G13/G15-based FLP catching CO, two major bonding interactions can occur, as graphically represented in Scheme 4. One is the forward FLP-to-CO donation, that is, LP(G15) → an empty p–π*(C), which dominates bonding between G13/G15-FLP and CO. The other interaction is the backward CO-to-FLP donation, that is, empty σ*(G13) ← LP(C), which plays a minor role in bonding between G13/G15-FLP and CO. In brief, the interaction of Lewis bases with CO is more crucial compared to the interaction of Lewis acids with CO.

Scheme 4 Two types of bonding effects between four-membered G13/G15-FLP and CO.

(5) Our ASM analyses indicate that the activation energy of the CO catching reaction by the four-membered-ring G13/G15-FLP is due to the structural deformation energy of G13/G15-FLP itself. Namely, the heavier the atomic weight of G13 (LA) or G15 (LB) of the four-membered-ring G13/G15-FLP is, the larger its atomic radius, the longer the G13–G15 bond length in the G13/G15-FLP, the smaller the bond strength of the G13–G15 bond, and the easier the CO insertion into a G13/G15-bond to yield a five-membered-ring product. Accordingly, the barrier height of this CO catching reaction becomes smaller.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the National Center for High-Performance Computing of Taiwan for generous amounts of computing time, and the National Science and Technology Council of Taiwan for the financial support. Our gratitude also goes to reviewers 1 and 2 for their very helpful suggestions and comments.

References

1. G. Lr, R. Rg and A. Kb, Aviat., Space Environ. Med., 1975, 46, 1289–1291.
2. R. F. Coburn, Prev. Med., 1979, 8, 310–322.
3. A. Ernst and J. D. Zibrak, N. Engl. J. Med., 1998, 339, 1603–1608.
4. L. D. Prockop and R. I. Chichkova, J. Neurol. Sci., 2007, 262, 122–130.
5. G. M. Turino, Circulation, 1981, 63, 253A–259A.
6. A. L. Horowitz, R. Kaplan and G. Sarpel, Radiology, 1987, 162, 787–788.
7. K. Sircar, J. Clower, M. k. Shin, C. Bailey, M. King and F. Yip, Am. J. Emerg. Med., 2015, 33, 1140–1145.
8. United States Environmental Protection Agency, An Introduction to Indoor Air Quality (IAQ), Carbon Monoxide (CO), http://www.epa.gov/iaq/co.html.
9. R. E. Weston Jr, J. Phys. Chem. A, 2001, 105, 1656–1661.
10. T. J. Venanzi, J. Chem. Educ., 1981, 56, 423.
11. J. N. Murrell, S. F. Kettle and J. M. Tedder, in The Chemical Bond, John Weley & Sons, New York, 2nd edn, 1985, p 96.
12. A. G. Whittaker, A. R. Mount and M. R. Heal, Instant Notes Physical Chemistry, Oxford: BIOS Scientific, United Kingdom, 2000, p 223.
13. P. A. Cox, Instant Notes Inorganic Chemistry, Oxford: BIOS Scientific, United Kingdom, 2000, p 59.
14. D. Bolze, Environ. Sci. Technol., 1988, 22, 596–597.
15. R. Kalescky, E. Kraka and D. Cremer, J. Phys. Chem. A, 2013, 117, 8981–8995.
16. G. C. Welch, R. R. S. Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126.
17. J. S. J. McCahill, G. C. Welch and D. W. Stephan, Angew. Chem., Int. Ed., 2007, 46, 4968–4971.
18. P. A. Chase, G. C. Welch, T. Jurca and D. W. Stephan, Angew. Chem., Int. Ed., 2007, 46, 8050–8053.
19. D. W. Stephan, Org. Biomol. Chem., 2008, 6, 1535–1539.
20. D. W. Stephan, Dalton Trans., 2009, 38, 3129–3136.
21. C. M. Mömming, E. Otten, G. Kehr, R. Fröhlich, S. Grimme, D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2009, 48, 6643–6646.
22. D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2010, 49, 46–76.
23. G. Erker, Pure Appl. Chem., 2012, 84, 2203–2217.
24. D. W. Stephan and G. Erker, Chem. Sci., 2014, 5, 2625–2641.
25. D. W. Stephan, Acc. Chem. Res., 2015, 48, 306–316.
26. D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2015, 54, 2–44.
27. D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2015, 54, 6400–6441.
28. D. W. Stephan, J. Am. Chem. Soc., 2015, 137, 10018–10032.
29. D. W. Stephan, Acc. Chem. Res., 2015, 48, 306–316.
30. S. A. Weicker and D. W. Stephan, Bull. Chem. Soc. Jpn., 2015, 88, 1003–1016.
31. D. W. Stephan, Science, 2016, 354, aaf7229.
32. G. Kehr and G. Erker, Chem. Rec., 2017, 17, 803–815.
33. A. R. Jupp and D. W. Stephan, Trends Chem., 2019, 1, 35–48.
34. D. W. Stephan, Chem, 2020, 6, 1520–1526.
35. M. A. Dureen and D. W. Stephan, J. Am. Chem. Soc., 2010, 132, 13559–13568.
36. A. Fukazawa, J. L. Dutton, C. Fan, L. G. Mercier, A. Y. Houghton, Q. Wu, W. E. Piers and M. Parvez, Chem. Sci., 2012, 3, 1814–1818.
37. R. Dobrovetsky and D. W. Stephan, J. Am. Chem. Soc., 2013, 135, 4974–4977.
38. C. P. Manankandayalage, D. K. Unruh and C. Krempner, Chem. Commun., 2021, 57, 12528–12531.
39. A. R. Cabrera, R. S. Rojas, M. Valderrama, P. Plüss, H. Berke, C. G. Daniliuc, G. Kehr and G. Erker, Dalton Trans., 2015, 44, 19606–19614.
40. A. Ramos, A. Antiñolo, F. Carrillo-Hermosilla, R. Fernández-Galán, M. del P. Montero-Rama, E. Villaseñor, A. Rodríguez-Diéguez and D. García-Vivó, Dalton Trans., 2017, 46, 10281–10299.
41. D. Ghosh, S. Sinhababu, B. D. Santarsiero and N. P. Mankad, J. Am. Chem. Soc., 2020, 142, 12635–12642.
42. O. E. Palomero and R. A. Jones, Dalton Trans., 2022, 51, 6275–6284.
43. M. Ríos-Gutiérrez, L. R. Domingo, R. S. Rojas, A. Toro-Labbé and P. Pérez, Dalton Trans., 2019, 48, 9214–9224.
44. Z.-F. Zhang, M.-C. Yang and M.-D. Su, Inorg. Chem., 2021, 60, 15253–15269.
45. M.-C. Yang, Z.-F. Zhang and M.-D. Su, Organometallics, 2022, 41, 374–389.
46. Z.-F. Zhang and M.-D. Su, J. Phys. Chem. A, 2022, 126, 5534–5544.
47. Z.-F. Zhang and M.-D. Su, Organometallics, 2022, 41, 3664–3678.
48. M.-C. Yang, Z.-F. Zhang and M.-D. Su, Inorg. Chem., 2022, 61, 12959–12976.
49. M.-C. Yang, Z.-F. Zhang and M.-D. Su, ACS Omega, 2023, 8, 863–870.
50. M.-C. Yang, Z.-F. Zhang and M.-D. Su, Phys. Chem. Chem. Phys., 2023, 25, 7423–7435.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
52. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868.
53. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154122.
54. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
55. D. G. A. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197–2203.
56. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
57. Computer code ADF2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
58. K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244.
59. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
60. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565.
61. F. M. Bickelhaupt and T. Ziegler, Organometallics, 1995, 14, 2288–2296.
62. F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128.
63. F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1–86.
64. G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, J. A. Van Gisbergen, J. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
65. A. Diefenbach, G. T. de Jong and F. M. Bickelhaupt, J. Chem. Theory Comput., 2005, 1, 286–298.
66. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
67. Ch. Chang, M. Pelissier and Ph. Durand, Phys. Scr., 1986, 34, 394–404.
68. J.-L. Heullyt, I. Lindgrent, E. Lindrothi, S. Lundqvist and A.-M. MHrtensson-Pendrill, J. Phys. B: At. Mol. Phys., 1986, 19, 2799–2815.
69. M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347–355.
70. M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580.
71. A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939.
72. M. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
73. F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128.
74. W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127.
75. I. Fernańdez and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967.
76. I. Fernańdez, Phys. Chem. Chem. Phys., 2014, 16, 7662–7671.
77. L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343.
78. I. Fernańdez, In Discoveringthe Future of Molecular Sciences, ed. B. Pignataro, Wiley-VCH, Weinheim, 2014, pp 165–187.
79. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647.
80. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198.
81. D. H. Ess, G. O. Jones and K. N. Houk, Org. Lett., 2008, 10, 1633–1636.
82. K. H. Dötz and J. Jr. Stendel, Chem. Rev., 2009, 109, 3227–3274.
83. R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, Wiley, New York, 4th edn, 2005, pp 310–311.
84. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 37, 2832–2838.
85. K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369.
86. A. Krapp, K. K. Pandey and G. Frenking, J. Am. Chem. Soc., 2007, 129, 7596–7610.
87. But another view was reported as follows: M. Gimferrer, S. Danés, E. Vos, I. Corral, A. Jana, P. Salvador and D. M. Andrada, Chem. Sci., 2023, 14, 384–392.
88. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03568b

---