Open Access Article
Open Access Articleσ-Hole, lone-pair-hole, and π-hole site-based interactions in aerogen-comprising complexes: a comparative study†
Mahmoud A. A. Ibrahim *ab,
Hassan A. A. Abuelliela,
Nayra A. M. Moussa
*ab,
Hassan A. A. Abuelliela,
Nayra A. M. Moussa ac,
Al-shimaa S. M. Radya,
Shaban R. M. Sayedd,
Mohamed A. El-Tayebd,
Muhammad Naeem Ahmed
ac,
Al-shimaa S. M. Radya,
Shaban R. M. Sayedd,
Mohamed A. El-Tayebd,
Muhammad Naeem Ahmed e,
Mohamed Khaled Abd El-Rahmanf and
Tamer Shoeib
e,
Mohamed Khaled Abd El-Rahmanf and
Tamer Shoeib *g
*g
aComputational Chemistry Laboratory, Chemistry Department, Faculty of Science, Minia University, Minia 61519, Egypt. E-mail: m.ibrahim@compchem.net
bSchool of Health Sciences, University of KwaZulu-Natal, Westville Campus, Durban 4000, South Africa
cBasic and Clinical Medical Science Department, Faculty of Dentistry, Deraya University, New Minya 61768, Egypt
dDepartment of Botany and Microbiology, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia
eDepartment of Chemistry, The University of Azad Jammu and Kashmir, Muzaffarabad 13100, Pakistan
fDepartment of Chemistry and Chemical Biology, Harvard University, 12 Oxford Street, Cambridge, MA 02138, USA
gDepartment of Chemistry, The American University in Cairo, New Cairo 11835, Egypt. E-mail: t.shoeib@aucegypt.edu
First published on 15th July 2024
Abstract
Herein, the potential of ZO3 and ZF2 aerogen-comprising molecules (where Z = Ar, Kr, and Xe) to engage in σ-, lp-, and π-hole site-based interactions was comparatively studied using various ab initio computations. For the first time, a premier in-depth elucidation of the external electric field (EEF) influence on the strength of the σ-, lp-, and π-hole site-based interactions within the ZO3/ZF2⋯NH3 and ⋯NCH complexes was addressed using oriented EEF with disparate magnitude. Upon the energetic features, σ-hole site-based interactions were noticed with the most prominent preferability in comparison to lp- and π-hole analogs. This finding was ensured by the negative interaction energy values of −11.65, −3.50, and −2.74 kcal mol−1 in the case of σ-, lp-, and π-hole site-based interactions within the XeO3⋯ and XeF2⋯NH3 complexes, respectively. Detailedly, the strength of the σ- and lp-hole site-based interactions directly correlated with the atomic size of the aerogen atoms and the magnitude of the positively oriented EEF. Unexpectedly, an irregular correlation was noticed for the interaction energies of the π-hole site-based interactions with the size of the π-hole. Interestingly, the π-hole site-based interactions within Kr-comprising complexes exhibited higher negative interaction energies than the Ar- and Xe-comprising counterparts. Notwithstanding, a direct proportion between the interaction energies of the π-hole site-based interactions and π-hole size was obtained by employing EEF along the positive orientation with high strength. The present outcomes would be a fundamental basis for forthcoming progress in studying the σ-, lp-, and π-hole site-based interactions within aerogen-comprising complexes and their pertinent applications in materials science and crystal engineering.
1. Introduction
Noncovalent interactions are indispensable in scientific research, enabling a deeper understanding of molecular behavior,1,2 biomolecular processes,3–5 and the design of advanced materials.6,7 The extensive study of these interactions has provided valuable insights into their fundamental nature and essential features, contributing to advancements in multiple scientific fields. Among noncovalent interactions, hole interactions have gathered impressive interest due to their superior contributions in various fields including anion recognition,8 ligand–acceptor interactions,9,10 materials science,11–13 drug discovery,14,15 and supramolecular chemistry.16–18In the literature, hole interactions can be categorized into several types, namely, σ-hole,19 π-hole,20 lone-pair (lp)-hole,21 and radical (R˙)-hole.22 In detail, the concept of σ-hole was initially introduced to describe a region of positive or less negative electrostatic potential that extended along the σ-bond of covalently bonded elements. Subsequent research expanded this concept to include π-hole interactions, which involve the interactions between the Lewis bases and the positive electrostatic potential regions located almost perpendicular to the molecular entity of the chemical system. In parallel, extensive studies were conducted on the interactions of the Lewis bases with the positive molecular electrostatic potential of lp- and R˙-holes, which refers to electron-deficient regions located nearly opposite to the lp and R˙, respectively. These categories of interactions were basically labelled based on the element involved in the bond donation, corresponding to its placement in the periodic table, as triel (Group III),23–25 tetrel (Group IV),26–29 pnicogen (Group V),30–33 chalcogen (Group VI),34,35 halogen (Group VII),19,35–38 and aerogen (Group VIII)39–41 bonds.
In recent years, immense theoretical and experimental studies have been performed to thoroughly unveil the features of aerogen (i.e., noble gas)-comprising complexes. Upon exploring the Inorganic Crystal Structure Database (ICSD), Gomila and Frontera documented the existence of interactions of xenon fluorides with several electron donors.42 Carvalho et al. adequately ensured the occurrence of aerogen bonds in the gas phase with disparate favorability that proportionally correlated with the atomic size of the interacted aerogen atom.43
Noble gas oxides are deemed one of the most common aerogen bond donors that were employed to divulge the aerogen interactions. Accordingly, their geometries and spectral characteristics were thoroughly investigated.44–47 In a landmark study, Esrafili et al. reported the effect of the substituent on the strength of the aerogen bond interactions of ZO3 (Z = Kr and Xe) with different nitrogen bases using a wide range of quantum mechanical calculations.41 It was declared that the low reactive ArO3, KrO3, XeO3, and XeF2O molecules exhibited preferential potentiality to interact with various electron donors (NH3, CH3CN, Cl−, and Br−) with interaction energies of up to −37.2 kcal mol−1.39
According to the literature, various types of holes could coexist within individual molecular entities, appearing throughout the molecular structure either on the same atom or in different atoms. While previous studies have reported the presence of multiple holes on different atoms within the same molecular entity,48–53 researchers have recently focused their investigations on characterizing the specific attributes of various hole interactions occurring on a single atom. In this context, the σ-hole and π-hole interactions in the case of KrF2O and XeF2O molecules have been extensively studied and outlined the electrostatic term as the most predominant contributor to the total interaction energies of their corresponding complexes.46,54 On the other hand, in molecules such as NF3/PF3 (ref. 55) and XeO3,47 researchers comparatively examined the σ- and lp-hole site-based interactions occurring on the same atom, demonstrating the higher preference for σ-hole interactions when interacting with Lewis bases, as compared to other types of holes.
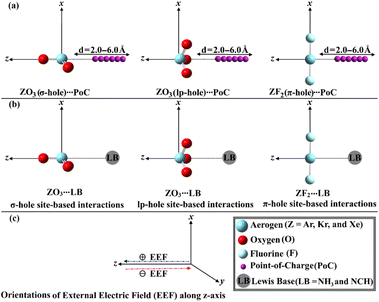
For the first time, this investigation would unveil the potentiality of aerogen-comprising molecules to engage in σ-, lp- and π-hole site-based interactions with Lewis bases (LB) within the ZO3⋯ and ZF2⋯LB complexes, respectively, as illustrated in Fig. 1. To pursue the research purpose, sundry quantum computations involving geometry optimization, point of charge (PoC) approach, electrostatic potential (ESP) analysis, and interaction energy were herein executed. To elucidate the physical force that dominates the interactions under investigation, the symmetry-adapted perturbation theory (SAPT) analysis was performed. Topological features of the studied interactions were also unveiled in the context of the quantum theory of atoms in molecules (QTAIM) and noncovalent interaction (NCI) index analyses. A premier insight into the oriented external electric field (EEF) influence on the strength of the σ-, lp-, and π-hole site-based interactions was announced (Fig. 1). The emerging findings would be a substantial base for the forthcoming studies relevant to σ-, lp-, and π-hole site-based interactions and their utilization in materials science and crystal engineering research.
2. Results and discussion
2.1. ESP analysis
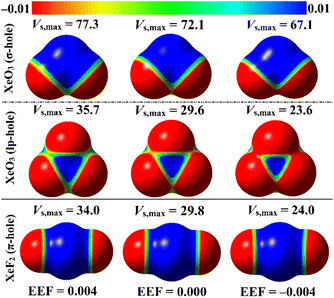
ESP analysis was herein executed on the optimized monomers to unveil the nature of the chemical systems, either nucleophilic or electrophilic, by generating MEP maps and assessing the Vs,max values. MEP maps and the Vs,max values are shown in Fig. 2.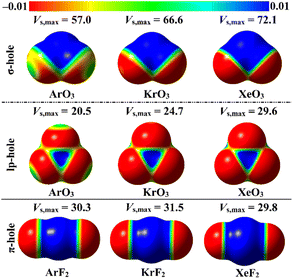 | ||
| Fig. 2 MEP maps of the optimized ZO3 and ZF2 monomers (where Z = Ar, Kr, and Xe) graphed utilizing 0.002 au electron density contours. Vs,max values are in kcal mol−1. | ||
Inspecting Fig. 2, σ-/lp- and π-holes were obviously noticed over the molecular entities of the studied ZO3 and ZF2 monomers, respectively. Apparently, the most prominent blue positive region over the surface of the aerogen-comprising molecules was ascribed to the σ-hole that also showed the largest Vs,max values. As a numerical illustration, the Vs,max surrounding the Xe's σ-, lp-, and π-holes were 72.1, 29.6, and 29.8 kcal mol−1, respectively.
Concerning the ZO3 molecules, a proportional correlation was noticed for the size and magnitude of the σ- and lp-holes with the aerogen-atomic size. For instance, the σ-hole of the aerogen atom in the ArO3, KrO3, and XeO3 molecules showed Vs,max quantities of 57.0, 66.6, and 72.1 kcal mol−1, respectively. This trend was also confirmed in the literature.56 While the π-hole of the ZF2 monomers enlarged according to the successive XeF2 < ArF2 < KrF2 pattern. This finding reflected the irregular correlation of the π-hole size and magnitude with the aerogen atomic size. As quantitative evidence, the aerogen π-hole in the ArF2, KrF2, and XeF2 molecules exhibited Vs,max with values of 30.3, 31.5, and 29.8 kcal mol−1, respectively.
2.2. PoC calculations
The PoC methodology, a recently announced approach, is established as an efficient way for conducting a comprehensive analysis of noncovalent interactions from an electrostatic standpoint.57 In accordance with this approach, negative PoCs with values of −0.25, −0.50, −0.75, and −1.0 au were adopted to simulate the effect of Lewis basicity on the examined interactions. The evaluation of the Estabilization of the ZO3⋯ and ZF2⋯PoC systems was conducted by examining the Z⋯PoC distances within the scope of 2.5–6.0 Å (Fig. 3). Estabilization of the ZO3⋯ and ZF2⋯PoC systems at the σ-, lp-, and π-hole⋯PoC distances of 2.5 Å are shown in Table 1.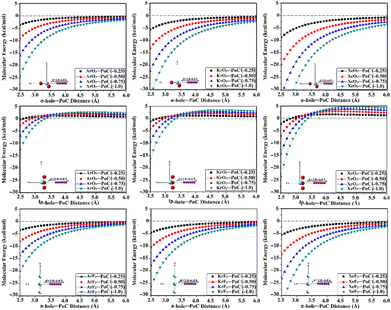 | ||
| Fig. 3 Curves of molecular energy (in kcal mol−1) of ZO3⋯ and ZF2⋯PoC systems (where Z = Ar, Kr, and Xe) at the σ-/lp- and π-hole⋯PoC distances ranging from 2.5 to 6.0 Å. | ||
| Site | System | Estabilization | |||
|---|---|---|---|---|---|
| PoC = −0.25 au | PoC = −0.50 au | PoC = −0.75 au | PoC = −1.0 au | ||
| σ-Hole | ArO3⋯PoC | −3.65 | −9.00 | −15.92 | −24.35 |
| KrO3⋯PoC | −5.62 | −13.14 | −22.42 | −33.36 | |
| XeO3⋯PoC | −8.78 | −19.86 | −33.07 | −48.25 | |
| Lp-hole | ArO3⋯PoC | −0.59 | −2.99 | −7.08 | −12.76 |
| KrO3⋯PoC | −1.06 | −4.22 | −9.31 | −16.24 | |
| XeO3⋯PoC | −2.26 | −7.08 | −14.29 | −23.73 | |
| π-Hole | ArF2⋯PoC | −3.56 | −8.14 | −13.70 | −20.21 |
| KrF2⋯PoC | −4.61 | −10.60 | −17.88 | −26.38 | |
| XeF2⋯PoC | −5.63 | −13.40 | −23.11 | −34.61 | |
As illustrated in Fig. 3, the stabilization energy of the ZO3⋯ and ZF2⋯PoC systems boosted as the σ-/lp- and π-hole⋯PoC intermolecular distance diminished, respectively. Apparently, destabilization energies were noticed in the case of the ZO3⋯PoC systems at the most extended lp-hole⋯PoC distances only. This exceptional case could be mainly ascribed to the lowest positive lp-holes of the aerogen bond donor and the role of the repulsive forces of the oxygen atoms with the negative PoC in the overall interactions. The obtained proportional and reverse correlations, in successive, of the destabilization and stabilization energies with the σ-/lp-/π-hole⋯PoC intermolecular distances, announced the opulent effect of the Z⋯PoC intermolecular distances on the aerogen⋯Lewis base interactions.
The quantitative data listed in Table 1 unveiled that all the ZO3⋯ and ZF2⋯PoC systems showed towering Estabilization values at a distance of 2.5 Å, with the following order: π-hole < lp-hole < σ-hole. As a numerical illustration, Estabilization values of the Xe-comprising molecule⋯PoC system at the σ-, lp-, and π-hole⋯PoC distance of 2.5 Å were −8.78, −2.26, and −5.63 kcal mol−1, respectively. Generally, the PoC energetic outcomes declared the synchronization of Estabilization with the aerogen atomic size. For instance, ArO3⋯, KrO3⋯, and XeO3⋯PoC systems showed Estabilization of −3.65, −5.62, and −8.78 kcal mol−1, respectively, employing −0.25 au PoC at the σ-hole⋯PoC distance of 2.5 Å. It is worth mentioning that evident amelioration of the Estabilization values was noticed by boosting the adopted PoC negativity (i.e., Lewis basicity). Numerically, the XeO3⋯PoC system at σ-hole⋯PoC of 2.5 Å exhibited Estabilization values of −8.78, −19.86, −33.07, and −48.25 kcal mol−1 using PoC with values of −0.25, −0.50, −0.75, and −1.0 au, respectively.
2.3. Interaction energy
In order to assess the propensity of aerogen-comprising molecules to establish σ-/lp- and π-hole site-based interactions, ZO3⋯ and ZF2⋯LB complexes were herein investigated in a detailed manner, respectively. Geometry optimization calculations were first executed for the scouted complexes (Fig. 4). Interaction energies were calculated relying on the optimized geometries at the same level of theory and then benchmarked at the CCDS(T)/CBS level of theory (Table 2).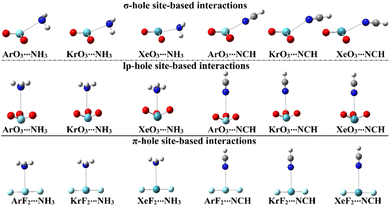 | ||
| Fig. 4 Optimized structures of the σ-/lp- and π-hole site-based interactions within the ZO3⋯ and ZF2⋯LB complexes, respectively (where Z = Ar, Kr, and Xe; LB = NH3 and NCH). | ||
| Site | Complex | Complexation parameters | Interaction energy | ||
|---|---|---|---|---|---|
| Da (Å) | θb (degree) | EMP2/aug-cc-pVTZ(PP) (kcal mol−1) | ECCSD(T)/CBS (kcal mol−1) | ||
| a D refers to Z⋯N bond distance.b θ refers to ∠O/F-Z⋯N bond angle in the σ-/π-hole site-based interactions and ∠Z-center⋯N bond angle in the lp-hole site-based interactions. | |||||
| σ-Hole | ArO3⋯NH3 | 2.86 | 147.2 | −6.56 | −6.07 |
| KrO3⋯NH3 | 2.80 | 158.7 | −8.87 | −8.34 | |
| XeO3⋯NH3 | 2.77 | 170.6 | −11.65 | −10.92 | |
| Lp-hole | ArO3⋯NH3 | 3.56 | 180.0 | −0.30 | −0.58 |
| KrO3⋯NH3 | 3.38 | 179.9 | −0.92 | −1.30 | |
| XeO3⋯NH3 | 3.01 | 179.9 | −3.50 | −3.76 | |
| π-Hole | ArF2⋯NH3 | 3.17 | 90.4 | −2.76 | −2.83 |
| KrF2⋯NH3 | 3.27 | 90.3 | −3.01 | −3.23 | |
| XeF2⋯NH3 | 3.48 | 90.3 | −2.74 | −3.03 | |
| σ-Hole | ArO3⋯NCH | 2.88 | 139.0 | −5.10 | −4.45 |
| KrO3⋯NCH | 2.88 | 150.3 | −6.42 | −5.76 | |
| XeO3⋯NCH | 2.93 | 162.5 | −7.67 | −6.87 | |
| Lp-hole | ArO3⋯NCH | 3.52 | 179.9 | −0.17 | −0.24 |
| KrO3⋯NCH | 3.42 | 179.9 | −0.36 | −0.43 | |
| XeO3⋯NCH | 3.30 | 179.8 | −0.93 | −0.96 | |
| π-Hole | ArF2⋯NCH | 3.12 | 90.4 | −2.28 | −2.15 |
| KrF2⋯NCH | 3.22 | 90.3 | −2.48 | −2.45 | |
| XeF2⋯NCH | 3.44 | 90.4 | −2.33 | −2.36 | |
As evident in Fig. 4, the aerogen-comprising molecules under investigation potentially interacted with Lewis bases, forming σ-/lp- and π-hole site-based interactions within the ZO3⋯ and ZF2⋯LB complexes, respectively. The occurrence of the abovementioned interactions was confirmed by the resulting negative interaction energy values, as compiled in Table 2.
Concerning the σ- and lp-hole site-based interactions, towering negative interaction energy values were denoted for the ZO3⋯LB complexes by boosting the aerogen atomic size, which is in line with the EP and PoC affirmations. For instance, the σ-/lp-hole site-based interaction showed EMP2/aug-cc-pVTZ(PP) values of −6.07/–0.58, −8.34/–1.30, and −10.92/–3.76 kcal mol−1 for the ArO3⋯, KrO3⋯, and XeO3⋯NH3 complexes, respectively. While the π-hole site-based interactions energetic quantities indicated that the Kr-comprising complexes exhibited higher negative values than their Ar- and Xe-comprising counterparts, indicating an irregular correlation with the size of the π-hole. For example, the π-hole site-based interactions within the ArF2⋯, KrF2⋯, and XeF2⋯NH3 complexes were observed with EMP2/aug-cc-pVTZ(PP) of −2.83, −3.23, and −3.03 kcal mol−1, respectively.
Furthermore, the studied aerogen-comprising complexes were denoted with higher preferability in the case of NH3-involved complexes in comparison to the NCH-based analogs. As a numerical evidence, the σ-hole site-based interactions within the XeO3⋯NH3 and ⋯NCH complexes had EMP2/aug-cc-pVTZ(PP) values of −11.65 and −7.67 kcal mol−1, respectively.
Among the studied interactions, the highest negative interaction energy values were ascribed to the σ-hole site-based interactions, which was in line with the ESP affirmations. For example, the σ-/lp- and π-hole site-based interactions were found in the XeO3⋯ and XeF2⋯NH3 complexes with MP2 energetic values of −11.65/–3.50 and −2.74 kcal mol−1 along with positive σ-/lp- and π-hole Vs,max values of 72.1/29.6 and 29.8 kcal mol−1 for the XeO3 and XeF2 monomers, respectively. Moreover, a nearly similar pattern was detected between the EMP2/aug-cc-pVTZ(PP) and ECCSD(T)/CBS values, confirming the precision of the opted MP2/aug-cc-PVTZ level of theory in the executed computations.
2.4. SAPT analysis
To divulge the physical nature of the σ-/lp- and π-hole site-based interactions, SAPT analysis was performed on the optimized ZO3⋯ and ZF2⋯LB complexes, respectively. Table 3 compiles total SAPT2+(3)dMP2 energy and its principal physical energetic components. The energy differences (ΔΔE) between the EMP2/aug-cc-pVTZ(PP) and ESAPT values were also evaluated and are listed in Table 3.| Site | Complex | Eelst (kcal mol−1) | Edisp (kcal mol−1) | Eexch (kcal mol−1) | Eind (kcal mol−1) | ESAPTa (kcal mol−1) | ΔΔEb |
|---|---|---|---|---|---|---|---|
| a ESAPT = Eelst + Eexch + Edisp + Eind.b ΔΔE = EMP2/aug-cc-pVTZ(PP) − ESAPT. | |||||||
| σ-Hole | ArO3⋯NH3 | −11.80 | −3.93 | 10.35 | −1.49 | −6.86 | −0.30 |
| KrO3⋯NH3 | −16.43 | −5.46 | 16.59 | −3.75 | −9.05 | −0.18 | |
| XeO3⋯NH3 | −24.25 | −7.61 | 27.88 | −7.84 | −11.82 | −0.17 | |
| Lp-hole | ArO3⋯NH3 | −1.41 | −2.29 | 3.38 | −0.07 | −0.39 | −0.09 |
| KrO3⋯NH3 | −3.72 | −3.51 | 6.33 | −0.19 | −1.10 | −0.18 | |
| XeO3⋯NH3 | −14.41 | −7.08 | 19.91 | −2.14 | −3.72 | −0.22 | |
| π-Hole | ArF2⋯NH3 | −4.50 | −1.93 | 3.68 | −0.21 | −2.97 | −0.21 |
| KrF2⋯NH3 | −4.79 | −2.02 | 4.01 | −0.44 | −3.23 | −0.22 | |
| XeF2⋯NH3 | −4.46 | −1.98 | 4.09 | −0.55 | −2.91 | −0.17 | |
| σ-Hole | ArO3⋯NCH | −6.72 | −3.05 | 5.49 | −0.87 | −5.15 | −0.05 |
| KrO3⋯NCH | −8.69 | −3.88 | 8.18 | −1.90 | −6.30 | −0.02 | |
| XeO3⋯NCH | −11.14 | −4.89 | 11.8 | −3.24 | −7.47 | 0.20 | |
| Lp-hole | ArO3⋯NCH | −0.26 | −2.02 | 2.19 | −0.02 | −0.11 | −0.04 |
| KrO3⋯NCH | −0.95 | −2.76 | 3.45 | −0.06 | −0.32 | −0.3 | |
| XeO3⋯NCH | −2.78 | −3.96 | 6.15 | −0.27 | −0.88 | 0.05 | |
| π-Hole | ArF2⋯NCH | −2.81 | −1.74 | 2.32 | −0.09 | −2.32 | −0.04 |
| KrF2⋯NCH | −3.15 | −1.83 | 2.74 | −0.27 | −2.50 | −0.3 | |
| XeF2⋯NCH | −3.06 | −1.80 | 2.92 | −0.37 | −2.31 | 0.02 | |
Based on the collected data in Table 3, negative values of Eelst, Edisp and Eind components were observed, outlining their appreciable contributions to the σ-/lp- and π-hole site-based attractive interactions in all the considered ZO3⋯ and ZF2⋯LB complexes, respectively. Illustratively, the σ-hole site-based interaction within the XeO3⋯NH3 complex had Eelst, Edisp, and Eind values of −24.25, −3.93, and −1.49 kcal mol−1, respectively. On the contrary, positive Eexch values unveiled the unpreferable impact of exchange forces on all the studied interactions.
SAPT findings generally demonstrated the substantial contributions of Eelst to all the considered interactions, with an exception for the weak lp-hole site-based interactions. For the latter exceptional interactions, the Edisp showed the highest dominance amplitude toward the attractive forces with values up to −3.96 in the case of the XeO3⋯NCH complex.
It is worth noting that the adopted SAPT calculations showed tiny ΔΔE values, ensuring the apparent accuracy of the utilized SAPT level of the theory. In general, the negative Eelst, Edisp, and Eind values exhibited a proportional correlation with the interaction energy pattern. As numerical evidence, Eelst values of the σ-hole site-based interactions in the XeO3⋯NH3 and ⋯NCH complexes were −24.25 and −11.14 kcal mol−1 along with MP2 energetic quantities of −11.65 and −7.67 kcal mol−1, respectively.
2.5. QTAIM calculations
Using QTAIM theory, bond critical points (BCPs) and bond baths (BPs) were extracted and are shown in Fig. 5. Besides, Laplacian (∇2ρb), total energy density (Hb), and electron density (ρb) were assessed and are gathered in Table 4.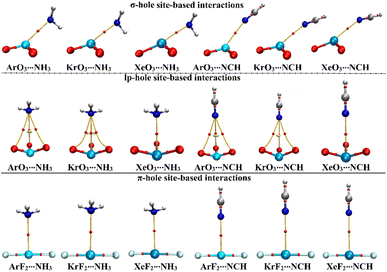 | ||
| Fig. 5 QTAIM plots of the σ-/lp- and π-hole site-based interactions within the ZO3⋯ and ZF2⋯LB complexes, respectively (where Z = Ar, Kr, and Xe; LB = NH3 and NCH). | ||
| Site | Complex | ρb (au) | ∇2ρb (au) | Hb (au) |
|---|---|---|---|---|
| σ-Hole | ArO3⋯NH3 | 0.01729 | 0.06579 | 0.00197 |
| KrO3⋯NH3 | 0.02361 | 0.07577 | 0.00087 | |
| XeO3⋯NH3 | 0.03166 | 0.08007 | −0.00147 | |
| Lp-hole | ArO3⋯NH3 | 0.00495 | 0.01580 | 0.00072 |
| KrO3⋯NH3 | 0.00741 | 0.02900 | 0.00124 | |
| XeO3⋯NH3 | 0.01909 | 0.05595 | 0.00081 | |
| π-Hole | ArF2⋯NH3 | 0.00916 | 0.03510 | 0.00186 |
| KrF2⋯NH3 | 0.00985 | 0.03306 | 0.00142 | |
| XeF2⋯NH3 | 0.00918 | 0.02687 | 0.00108 | |
| σ-Hole | ArO3⋯NCH | 0.01438 | 0.06288 | 0.00262 |
| KrO3⋯NCH | 0.01747 | 0.06696 | 0.00201 | |
| XeO3⋯NCH | 0.02015 | 0.06727 | 0.00146 | |
| Lp-hole | ArO3⋯NCH | 0.00442 | 0.01598 | 0.00085 |
| KrO3⋯NCH | 0.00579 | 0.02181 | 0.00110 | |
| XeO3⋯NCH | 0.00886 | 0.03520 | 0.00165 | |
| π-Hole | ArF2⋯NCH | 0.00845 | 0.03784 | 0.00228 |
| KrF2⋯NCH | 0.00906 | 0.03563 | 0.00183 | |
| XeF2⋯NCH | 0.00834 | 0.02883 | 0.00144 |
According to the displayed data in Fig. 5, one BP and BCP were observed between the aerogen-comprising molecules and the NH3 and NCH Lewis bases within the σ- and π-hole site-based interactions. This finding assured the potential of the ZO3 and ZF2 molecules to form σ- and π-hole site-based interactions, respectively. While three BPs and BCPs were noticed in the lp-hole site-based interactions of all studied complexes other than Xe-comprising complexes. This observation outlined the predominant contributions of the oxygen atoms to the interactions within Ar- and Kr-comprising complexes. The occurrence of sole BP within the Xe-comprising complexes unveils the domination of the attractive forces between the positive hole and the negative Lewis base.
From the recorded data in Table 4, small values of ρb and positive values of ∇2ρb and Hb were denoted for almost all the inspected complexes, unveiling that the interactions understudy have a closed-shell nature except for the σ-hole site-based interaction within the XeO3⋯NH3 complex. The latter interaction was detected by a negative Hb value, outlining its partially covalent nature. In general, the ρb, ∇2ρb, and Hb trends directly correlated with the interaction energy trend. For instance, the σ-hole site-based interactions of the ArO3⋯, KrO3⋯, and XeO3⋯NH3 complexes had ρb with values of 0.01729, 0.02361, and 0.22483 au accompanied by EMP2/aug-cc-pVTZ(PP) values of −6.07, −8.34, and −10.92, kcal mol−1, respectively.
2.6. NCI calculations
NCI index analysis unveils either the attractive or repulsive forces of the noncovalent interactions between the chemical species.58,59 In this regard, NCI plots were generated using a 0.50 au reduced density gradient with a colored scale ranging from blue (sign(λ2)ρ = −0.035 au) to red (sign(λ2)ρ = +0.020 au) and are displayed in Fig. 6.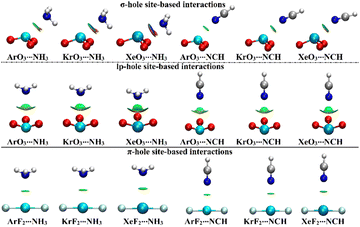 | ||
| Fig. 6 NCI plots of the σ-/lp- and π-hole site-based interactions within the ZO3⋯ and ZF2⋯LB complexes, respectively (where Z = Ar, Kr, and Xe; LB = NH3 and NCH). | ||
As delineated in Fig. 6, the occurrence of the σ-/lp- and π-hole site-based interactions within the ZO3⋯ and ZF2⋯LB complexes, respectively, was affirmed by the existence of the green isosurfaces between the interacted species. Conspicuously, blue-colored isosurfaces were found in the σ-hole site-based interactions of the Xe-comprising complexes, reflecting their partially covalent nature. For lp-hole site-based interactions, NCI plots were in line with the affirmations of the QTAIM, which demonstrated the contributions of the substituents to the interactions within all the considered complexes.
2.7. EEF effect
EEF was earlier reported to have an immense effect on the nature and strength of noncovalent interactions.60–62 In this regard, the EEF effect on the σ-, lp-, and π-hole site-based interactions was thoroughly assessed (Fig. 1). The geometrical optimization and MEP computations were initially performed for the aerogen-comprising molecules employing ±0.004, ±0.008, and ±0.016 au EEF (Fig. S1–S3†). Fig. 7 shows the visualized MEP maps of the optimized Xe-comprising molecules in the presence of ±0.004 au EEF.According to Fig. 7, applying a positively oriented EEF increased the σ-, lp-, and π-hole size on the examined molecules, whereas using a negatively oriented EEF lowered it. For example, the σ-hole magnitudes of the XeO3 molecule were noticed with Vs,max values of 77.3, 67.1, and 72.1 kcal mol−1 in the presence of +0.004, −0.004, and 0.000 au EEF, respectively. Based on the displayed data in Fig. S1–S3,† the preferable contribution of the EEF was obviously denoted by boosting the magnitude of the positively oriented EEF. Numerically, the Vs,max values of the σ-hole of the XeO3 molecule were 77.3, 82.6, and 93.5 kcal mol−1 under the effect of 0.004, 0.008, and 0.016 au EEF, respectively. Therefore, the subsequent analyses of the examined interactions were conducted solely under the conditions of the positively oriented EEF.
Under the positively oriented EEF influence, geometrical optimization calculations were executed using variant EEF magnitudes ranging from 0.004 to 0.016 au for the complexes under study. Based on the optimized geometries of the investigated complexes, the interaction energy computations were performed using +0.004, +0.008, and +0.016 au EEF (Table 5).
| Complexes | EEF (au) | ZO3/ZF2⋯NH3 | ZO3/ZF2⋯NCH | |||||
|---|---|---|---|---|---|---|---|---|
| Da (Å) | θb (degree) | E (kcal mol−1) | Da (Å) | θb (degree) | E (kcal mol−1) | |||
| a D refers to Z⋯N bond distance.b θ refers to the ∠O/F-Z⋯N bond angle in the σ-/π-hole site-based interactions and ∠Z-center⋯N bond angle in the lp-hole site-based interactions. | ||||||||
| σ-Hole | ArO3⋯LB | 0.004 | 2.83 | 150.1 | −7.23 | 2.85 | 146.2 | −5.69 |
| 0.008 | 2.81 | 152.1 | −7.94 | 2.82 | 148.8 | −6.39 | ||
| 0.016 | 2.75 | 155.8 | −9.72 | 2.77 | 152.7 | −8.12 | ||
| KrO3⋯LB | 0.004 | 2.76 | 160.3 | −10.08 | 2.84 | 153.8 | −7.36 | |
| 0.008 | 2.73 | 161.6 | −11.40 | 2.81 | 155.8 | −8.45 | ||
| 0.016 | 2.62 | 165.3 | −14.93 | 2.73 | 159.1 | −11.12 | ||
| XeO3⋯LB | 0.004 | 2.73 | 171.9 | −13.78 | 2.88 | 163.7 | −9.05 | |
| 0.008 | 2.66 | 173.4 | −15.98 | 2.84 | 165.1 | −10.67 | ||
| 0.016 | 2.56 | 176.4 | −22.07 | 2.73 | 168.4 | −14.78 | ||
| Lp-hole | ArO3⋯LB | 0.004 | 3.51 | 179.9 | −0.57 | 3.47 | 179.9 | −0.42 |
| 0.008 | 3.47 | 179.9 | −0.89 | 3.42 | 179.8 | −0.72 | ||
| 0.016 | 3.39 | 179.9 | −1.65 | 3.34 | 179.9 | −1.48 | ||
| KrO3⋯LB | 0.004 | 3.31 | 179.1 | −1.47 | 3.36 | 179.9 | −0.76 | |
| 0.008 | 3.24 | 179.6 | −2.05 | 3.30 | 179.9 | −1.24 | ||
| 0.016 | 3.10 | 179.7 | −3.71 | 3.19 | 180.0 | −2.48 | ||
| XeO3⋯LB | 0.004 | 2.78 | 179.9 | −6.81 | 3.21 | 179.9 | −1.73 | |
| 0.008 | 2.49 | 179.8 | −14.17 | 3.11 | 179.9 | −2.77 | ||
| 0.016 | 2.34 | 179.7 | −26.85 | 2.90 | 179.9 | −5.99 | ||
| π-Hole | ArF2⋯LB | 0.004 | 3.16 | 179.6 | −3.14 | 3.10 | 179.9 | −2.67 |
| 0.008 | 3.14 | 91.9 | −3.55 | 3.08 | 91.8 | −3.11 | ||
| 0.016 | 3.12 | 93.1 | −4.46 | 3.04 | 93.2 | −4.10 | ||
| KrF2⋯LB | 0.004 | 3.25 | 90.8 | −3.49 | 3.20 | 90.9 | −2.96 | |
| 0.008 | 3.23 | 91.5 | −4.01 | 3.17 | 91.6 | −3.50 | ||
| 0.016 | 3.18 | 92.9 | −5.17 | 3.11 | 93.0 | −4.74 | ||
| XeF2⋯LB | 0.004 | 3.44 | 90.7 | −3.32 | 3.40 | 91.6 | −2.90 | |
| 0.008 | 3.41 | 91.6 | −3.97 | 3.36 | 92.5 | −3.56 | ||
| 0.016 | 3.35 | 93.3 | −5.46 | 3.28 | 94.2 | −5.12 | ||
As summarized in Table 5, negative interaction energy values of the examined complexes increased as the strength of the positively oriented EEF expanded. Illustratively, interaction energy values of −13.78, −15.98, and −22.07 kcal mol−1 were observed for the σ-hole site-based interaction within the XeO3⋯NH3 complexes by utilizing +0.004, +0.008, and +0.016 au EEF, respectively.
Concerning π-hole site-based interactions, there was a remarkable direct correlation between the aerogen atomic size and the preferability of the interactions under investigation, particularly under the influence of the positively oriented EEF with the highest magnitude (i.e., 0.016 au EEF). For instance, the π-hole site-based interactions within ArF2⋯, KrF2⋯, and XeF2⋯NH3 complexes in the presence of EEF with a magnitude of 0.016 au showed interaction energy of −4.46, −5.17, and −5.46 kcal mol−1, respectively. In comparison, the π-hole site-based interactions within the ArF2⋯, KrF2⋯, and XeF2⋯NH3 complexes in the absence of the EEF had interaction energy values of −2.83, −3.23, and −3.03 kcal mol−1, respectively (Table 2). Such observations confirmed the predominant role of the EEF in controlling the interactions under investigation.
3. Computational methods
The potentiality of ZO3 and ZF2 aerogen-comprising molecules to form σ-/lp- and π-hole site-based interactions, respectively, was herein unveiled using NH3 and NCH Lewis bases. In this regard, all the adopted monomers and complexes were first subjected to geometry optimization using the MP2 method63 accompanied by the aug-cc-pVTZ basis set64,65 for all the employed atoms except Kr and Xe. The relativistic effects of the latter atoms were considered by incorporating the pseudopotentials (PP).65,66On the optimized monomers, ESP analysis was performed to demonstrate the nucleophilic and electrophilic nature of the systems under investigation. Subsequently, molecular electrostatic potential (MEP) maps were graphed by employing 0.002 au electron density envelopes in accordance with the literature suggestions.67 As well, the maximum positive electrostatic potential (Vs,max) values were assessed with the aid of Multiwfn 3.7 software.68
The PoC method was invoked as a dependable tool for studying the potentiality of the chemical systems to engage in σ-,57,69 lp-,55 and π-hole70 site-based interactions from an electrostatic perspective. Using PoC terminology, the influence of Lewis basicity on the stabilization energy (Estabilization) of the ZO3⋯ and ZF2⋯PoC systems was divulged using −0.25, −0.50, −0.75, and −1.0 au, as demonstrated in eqn (1). Detailedly, the ZO3 and ZF2 monomers were subjected to negative PoC via three distinct interaction sites, namely the σ-, lp-, and π-hole sites (see Fig. 1). The σ-, lp-, and π-hole⋯PoC distances were set using a range starting from 2.5 Å to 6.0 Å with a step size of 0.1 Å.
| Estabilization = Eaerogen-comprising molecule⋯PoC − Eaerogen-comprising molecule | (1) |
On the optimized structures of the investigated complexes, interaction energies were computed and then corrected from the basis set superposition error (BSSE) by incorporating the counterpoise (CP) correction procedure.71 Subsequently, the obtained energetic values were benchmarked at the CCSD/CBS level of theory, as given in the following eqns:72,73
| ECCSD(T)/CBS = ΔEMP2/CBS + ΔECCSD(T) | (2) |
| ΔEMP2/CBS = (64EMP2/aug-cc-pVQZ(PP) − 27EMP2/aug-cc-pVTZ(PP))/37 | (3) |
| ΔECCSD(T) = ECCSD(T)/aug-cc-pVdZ(PP) − EMP2/aug-cc-pVDZ(PP) | (4) |
SAPT analysis74 was performed using the PSI4 code75 to unveil the force beyond the occurrence of the investigated interactions within the complexes understudy. The total SAPT2+(3)dMP2 interaction energy (ESAPT) was computed by summing its main four physical components, namely dispersion (Edisp), exchange (Eexch), induction (Eind), and electrostatic (Eelst), as illustrated in eqn (5)–(9).76
| ESAPT = Eelst + Eexch + Eind + Edisp | (5) |
| Eelst = E(10)elst + E(12)elst + E(13)elst | (6) |
| Eexch = E(10)exch + E(11)exch + E(12)exch | (7) |
| Eind = E(20)ind,resp + E(20)exch-ind,resp + E(22)ind,resp + E(22)exch-ind,resp + δE(2)HF + δE(2)MP2 | (8) |
| Edisp = E(20)disp + E(20)exch-disp + E(21)disp + E(22)disp(SDQ) + E(22)dispT + E(30)disp | (9) |
4. Conclusions
In the current research, the ability of ZO3 and ZF2 aerogen-comprising molecules to form σ-/lp- and π-hole, respectively, with NH3 and NCH Lewis bases was comparatively investigated. Sundry ab initio computations involving ESP, PoC, interaction energy, QTAIM, NCI, and SAPT were performed. A premier understanding of the EEF influence on the complexation and energetic features of the σ-, lp-, and π-hole site-based interactions was obtained utilizing the oriented EEF with disparate magnitudes. The ESP outcomes confirmed the existence of positive σ-/lp- and π-hole over the ZO3 and ZF2 molecular structures, respectively, with observable appearance for σ-hole. The computed interaction energy quantities announced σ-hole site-based interactions with higher preferability than the other ones. Interestingly, the strength of the σ- and lp-hole site-based interactions directly correlated with the aerogen atomic size and the magnitude of the positively oriented EEF. In comparison, the strength of the π-hole site-based interaction showed an irregular correlation with the aerogen atomic size. Nevertheless, by applying the positively oriented EEF with high strength, a direct proportion between the strength of the latter interactions and aerogen atomic size was obtained. The emerging outcomes would be beneficial for forthcoming studies pertinent to the characterization of the σ-, lp-, and π-hole site-based interactions within aerogen-comprising complexes and their analogical applications.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Conceptualization, Mahmoud A. A. Ibrahim and Tamer Shoeib; methodology, Mahmoud A. A. Ibrahim, Nayra A. M. Moussa, and Mohamed Khaled Abd El-Rahman; software, Mahmoud A. A. Ibrahim; formal analysis, Hassan A. A. Abuelliel; investigation, Hassan A. A. Abuelliel and Nayra A. M. Moussa; resources, Mahmoud A. A. Ibrahim, Shaban R. M. Sayed, Mohamed A. El-Tayeb and Tamer Shoeib; data curation, Hassan A. A. Abuelliel; writing—original draft preparation, Hassan A. A. Abuelliel and Al-shimaa S. M. Rady; writing—review and editing, Mahmoud A. A. Ibrahim, Nayra A. M. Moussa, Mohamed A. El-Tayeb, Shaban R. M. Sayed, Muhammad Naeem Ahmed, Mohamed Khaled Abd El-Rahman, and Tamer Shoeib; visualization, Hassan A. A. Abuelliel and Muhammad Naeem Ahmed; supervision, Mahmoud A. A. Ibrahim; project administration, Mahmoud A. A. Ibrahim, Nayra A. M. Moussa and Tamer Shoeib. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project number (RSPD2024R678), King Saud University, Riyadh, Saudi Arabia, for funding this work. The computational work was completed with resources provided by the CompChem Lab (Minia University, Egypt, http://hpc.compchem.net), Center for High-Performance Computing (Cape Town, South Africa, http://www.chpc.ac.za), Bibliotheca Alexandrina (http://hpc.bibalex.org), and the American University in Cairo.References
- I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180–208 CrossRef CAS.
- P. R. Varadwaj, A. Varadwaj, H. M. Marques and K. Yamashita, Sci. Rep., 2019, 9, 50 CrossRef.
- K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17 CAS.
- E. Frieden, J. Chem. Educ., 1975, 52, 754–756 CrossRef CAS PubMed.
- X. de la Cruz, J. Reverter and I. Fita, J. Mol. Graphics, 1992, 10, 96–100 CrossRef CAS.
- D. Braga and F. Grepioni, Acc. Chem. Res., 2000, 33, 601–608 CrossRef CAS.
- J. M. A. Robinson, D. Philp, K. D. M. Harris and B. M. Kariuki, New J. Chem., 2000, 24, 799–806 RSC.
- J. Y. C. Lim and P. D. Beer, Chem, 2018, 4, 731–783 CAS.
- D. Mani and E. Arunan, J. Phys. Chem. A, 2014, 118, 10081–10089 CrossRef CAS PubMed.
- G. Mahmoudi, A. Bauza, M. Amini, E. Molins, J. T. Mague and A. Frontera, Dalton Trans., 2016, 45, 10708–10716 RSC.
- W. J. Vickaryous, R. Herges and D. W. Johnson, Angew. Chem., Int. Ed., 2004, 43, 5831–5833 CrossRef CAS.
- K. Muller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168 CrossRef CAS.
- L. P. Wolters, P. Schyman, M. J. Pavan, W. L. Jorgensen, F. M. Bickelhaupt and S. Kozuch, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 523–540 CAS.
- Y. Lu, Y. Wang and W. Zhu, Phys. Chem. Chem. Phys., 2010, 12, 4543–4551 RSC.
- Y. Lu, Y. Liu, Z. Xu, H. Li, H. Liu and W. Zhu, Expert Opin. Drug Discovery, 2012, 7, 375–383 CrossRef CAS PubMed.
- D. A. Uhlenheuer, K. Petkau and L. Brunsveld, Chem. Soc. Rev., 2010, 39, 2817–2826 RSC.
- D. K. Smith, J. Chem. Educ., 2005, 82, 393–400 CrossRef CAS.
- A. Bauza, T. J. Mooibroek and A. Frontera, Chem. Commun., 2014, 50, 12626–12629 RSC.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548 CrossRef CAS.
- M. A. A. Ibrahim, R. R. A. Saeed, M. N. I. Shehata, N. A. M. Moussa, A. M. Tawfeek, M. N. Ahmed, M. K. Abd El-Rahman and T. Shoeib, ACS Omega, 2023, 8, 32828–32837 CrossRef CAS PubMed.
- M. A. A. Ibrahim, Y. A. M. Mohamed, H. S. M. Abd Elhafez, M. N. I. Shehata, M. E. S. Soliman, M. N. Ahmed, H. R. Abd El-Mageed and N. A. M. Moussa, J. Mol. Graphics Modell., 2022, 111, 108097 CrossRef CAS.
- S. J. Grabowski, ChemPhysChem, 2014, 15, 2985–2993 CrossRef CAS PubMed.
- S. J. Grabowski, Molecules, 2015, 20, 11297–11316 CrossRef CAS.
- L. Gao, Y. Zeng, X. Zhang and L. Meng, J. Comput. Chem., 2016, 37, 1321–1327 CrossRef CAS.
- A. Bauza, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef CAS.
- W. Zierkiewicz, M. Michalczyk and S. Scheiner, Molecules, 2018, 23, 1416 CrossRef PubMed.
- A. Grabarz, M. Michalczyk, W. Zierkiewicz and S. Scheiner, ChemPhysChem, 2020, 21, 1934–1944 CrossRef CAS.
- M. Hou, Z. Liu and Q. Li, Int. J. Quantum Chem., 2020, 120, e26251 CrossRef CAS.
- I. Alkorta, J. Elguero and J. E. Del Bene, J. Phys. Chem. A, 2013, 117, 10497–10503 CrossRef CAS.
- S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288 CrossRef CAS PubMed.
- A. Bauza, R. Ramis and A. Frontera, J. Phys. Chem. A, 2014, 118, 2827–2834 CrossRef CAS.
- A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2016, 17, 1608–1614 CrossRef CAS PubMed.
- M. D. Esrafili and R. Nurazar, Mol. Phys., 2015, 114, 276–282 CrossRef.
- C. B. Aakeroy, D. L. Bryce, G. Desiraju, A. Frontera, A. C. Legon, F. Nicotra, K. Rissanen, S. Scheiner, G. Terraneo, P. Metrangolo and G. Resnati, Pure Appl. Chem., 2019, 91, 1889–1892 CrossRef CAS.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757 RSC.
- M. A. A. Ibrahim and A. A. M. Hasb, Theor. Chem. Acc., 2019, 138, 2–13 Search PubMed.
- H. Wang, W. Wang and W. J. Jin, Chem. Rev., 2016, 116, 5072–5104 CrossRef CAS PubMed.
- A. Bauza and A. Frontera, Angew. Chem., 2015, 54, 7340–7343 CrossRef CAS PubMed.
- A. Bauza and A. Frontera, Phys. Chem. Chem. Phys., 2015, 17, 24748–24753 RSC.
- M. D. Esrafili, S. Asadollahi and M. Vakili, Int. J. Quantum Chem., 2016, 116, 1254–1260 CrossRef CAS.
- R. M. Gomila and A. Frontera, Front. Chem., 2020, 8, 395 CrossRef CAS.
- F. M. Carvalho, A. S. Kiametis, A. L. de Araujo Oliveira, F. Pirani and R. Gargano, Spectrochim. Acta, Part A, 2021, 246, 119049 CrossRef CAS PubMed.
- M. D. Esrafili, F. Mohammadian-Sabet and M. Solimannejad, Chem. Phys. Lett., 2016, 659, 196–202 CrossRef CAS.
- M. D. Esrafili and E. Vessally, Chem. Phys. Lett., 2016, 662, 80–85 CrossRef CAS.
- W. Zierkiewicz, M. Michalczyk and S. Scheiner, Phys. Chem. Chem. Phys., 2018, 20, 4676–4687 RSC.
- J. Miao, Z. Xiong and Y. Gao, J. Phys.: Condens.Matter, 2018, 30, 444001 CrossRef.
- T. Lang, X. Li, L. Meng, S. Zheng and Y. Zeng, Struct. Chem., 2014, 26, 213–221 CrossRef.
- M. Solimannejad, N. Nassirinia and S. Amani, Struct. Chem., 2012, 24, 651–659 CrossRef.
- M. Solimannejad, V. Ramezani, C. Trujillo, I. Alkorta, G. Sanchez-Sanz and J. Elguero, J. Phys. Chem. A, 2012, 116, 5199–5206 CrossRef CAS PubMed.
- S. A. C. McDowell and J. A. Joseph, Mol. Phys., 2014, 113, 16–21 CrossRef.
- A. Bauza and A. Frontera, ChemPhysChem, 2016, 17, 3181–3186 CrossRef CAS PubMed.
- M. E. Alikhani, J. Mol. Model., 2020, 26, 94 CrossRef CAS.
- Y. Deng, Zanzhang, W. Cao, Y. Liu, B. Zheng and Z. Wang, J. Mol. Model., 2022, 28, 339 CrossRef CAS PubMed.
- M. A. A. Ibrahim, S. M. A. Saad, J. H. Al-Fahemi, G. A. H. Mekhemer, S. A. Ahmed, A. M. Shawky and N. A. M. Moussa, RSC Adv., 2021, 11, 4022–4034 RSC.
- M. Kolar, J. Hostas and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 9987–9996 RSC.
- M. A. A. Ibrahim, M. N. I. Shehata, M. E. S. Soliman, M. F. Moustafa, H. R. A. El-Mageed and N. A. M. Moussa, Phys. Chem. Chem. Phys., 2022, 24, 3386–3399 RSC.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS.
- J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef CAS PubMed.
- B. J. Dutta and P. K. Bhattacharyya, Int. J. Quantum Chem., 2015, 115, 1459–1466 CrossRef CAS.
- M. A. A. Ibrahim, N. A. M. Moussa, A. A. K. Kamel, M. N. I. Shehata, M. N. Ahmed, F. Taha, M. A. S. Abourehab, A. M. Shawky, E. B. Elkaeed and M. E. S. Soliman, Molecules, 2022, 27, 2963 CrossRef CAS.
- M. A. A. Ibrahim, N. A. M. Moussa, S. M. A. Saad, M. N. Ahmed, A. M. Shawky, M. E. S. Soliman, G. A. H. Mekhemer and A. S. M. Rady, ACS Omega, 2022, 7, 11264–11275 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- M. A. A. Ibrahim, J. Mol. Model., 2012, 18, 4625–4638 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. A. A. Ibrahim, R. R. A. Saeed, M. N. I. Shehata, M. N. Ahmed, A. M. Shawky, M. M. Khowdiary, E. B. Elkaeed, M. E. S. Soliman and N. A. M. Moussa, Int. J. Mol. Sci., 2022, 23, 3114 CrossRef CAS PubMed.
- M. A. A. Ibrahim, R. R. A. Saeed, M. N. I. Shehata, E. E. B. Mohamed, M. E. S. Soliman, J. H. Al-Fahemi, H. R. A. El-Mageed, M. N. Ahmed, A. M. Shawky and N. A. M. Moussa, J. Mol. Struct., 2022, 1265, 133232 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- B. K. Mishra, S. Karthikeyan and V. Ramanathan, J. Chem. Theory Comput., 2012, 8, 1935–1942 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 132, 184111–184120 CrossRef.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565 CAS.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E01, Gaussian09, Gaussian Inc., Wallingford CT, USA Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03614j |
| This journal is © The Royal Society of Chemistry 2024 |