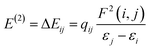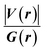Open Access Article
Open Access ArticleDeciphering the influence of PdII and PdIV oxidation states on non-standard chemical bonds within bis(jN-heterocyclic carbene) complexes: insights from DFT†
Jean Ongagna Moto *a,
Abel Idrice Adjieufack
*a,
Abel Idrice Adjieufack *b,
Simon Claude Ndika Ngomba,
Gaël Mouzong D'ambassaa,
Suzane Leonie Djendo Maziaa and
Désiré Mama Bikele*a
*b,
Simon Claude Ndika Ngomba,
Gaël Mouzong D'ambassaa,
Suzane Leonie Djendo Maziaa and
Désiré Mama Bikele*a
aComputational and Theoretical Chemistry Unit, Department of Chemistry, Faculty of Science, University of Douala, P.O. Box 24157, Douala, Cameroon. E-mail: jean.monfils@yahoo.fr
bPhysical and Theoretical Chemistry Laboratory, University of Yaoundé I, P.O. Box 812, Yaoundé, Cameroon. E-mail: adjieufack21@gmail.com
First published on 3rd July 2024
Abstract
Bis-N-heterocyclic carbene ligands (bis(NHC)) have introduced a new approach to designing homogeneous and heterogeneous catalysts, demonstrating the versatility of ligand concepts in catalysis. This study presents a computational analysis of palladium (+II and +IV) complexes containing either a normally (bis(nNHC)) or an abnormally (bis(aNHC)) bound CH2-bridged bis-N-heterocyclic carbene ligand; in addition, ancillary ligands are permuted from chlorides (X = Cl) to bromides (X = Br). Density functional theory at the B3PW91/6-31G(d)/Lanl2DZ level in the gas phase was used to investigate the electronic structure and bonding properties of bis(NHC)PdIIX2 and bis(NHC)PdIVX4 for bis(NHC) palladium(II) dihalide and palladium(IV) tetrachloride complexes, respectively. Results indicate that all of the palladium complex structures prefer a flexible boat-type conformation with an average C2v symmetry, according to bond property (Ccarbene–Pd and Pd–Cl[Br]) analysis. The strength of these bonds depends on coordinating halide ions (Cl− and Br−), the type of ligand (bis(nNHC) and bis(aNHC)), and the palladium oxidation state (+II and +IV). Analysis of thermodynamic parameters (ΔH0, ΔG0, and ΔEbind) shows an increase in values from an abnormal to normal chelating mode in tetrahalides, whereas the opposite is observed for dihalide complexes. The lower π-backbonding ability of the metal, which is influenced by the quantity and size of halide ions involved, could be one possible explanation for this deficiency.
1 Introduction
Petroleum feedstocks (oil and gas), estimated at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 300
000 and 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 barrels per year, currently represent the main source of fuel, chemicals, and materials in the world, although the exploitation and valorization of biomass (renewable source) are in full expansion.1 Despite the fact that this resource is expected to be exploited for 50 years,2 research on alternative uses of natural gas is aimed at limiting some of its effects and the gas emissions resulting from its use on the environment. Methane (60%), one of the main components of natural gas, is the main target because of its greater warming potential than carbon dioxide (CO2) on the global warming potential (GWP) scale.3 This gas and other lower hydrocarbons (C2H6, C3H6, etc.) are potential raw materials for the chemical industry. In fact, these compounds could be permanently converted into their corresponding chemical liquid products through efficient processes. From an economic perspective, the oxidation approaches for the functionalization of lower alkanes (n ≤ 3) offer an attractive alternative compared to conventional gas-to-liquid processes because they do not rely on the intensive energy formation of syngas.4 However, due to low reactivity, the selective conversion of alkane to alcohol is particularly difficult. A potential solution for this challenge resides in the design and materialization of a discrete molecular catalyst that activates and functionalizes C–H bonds of the corresponding alkane. Since the emergence of Shilov's approaches based on the activation and catalytic reactions of saturated hydrocarbons in the presence of transition metal (TM) complexes, the reactivity of alkanes has received much attention, and at the same time, the coordination of ligands to these TMs has also facilitated various spectacular catalytic transformations (Suzuki, Miyaura, and Heck cross-coupling reactions).5,6 In modern organometallic chemistry, the knowledge of ligand tuning remains one of the most powerful concepts for regulating the catalytic properties of TM centers and predicting catalytic activity. Since the synthesis and the isolation of the first free N-heterocyclic carbene (NHC) by Arduengo, these compounds have become universal ligands in coordination chemistry.7 They easily bind to all TMs with a low or high oxidation degree. Due to their specific coordination chemistry, NHC stabilizes and activates metal centers in key areas (medicinal,8 luminescent,8 functional material applications8 and catalysis9–11…). Despite this great interest in NHCs, detailed knowledge of the molecular mechanism and factors underlying their catalytic activity of hydrocarbon oxidation is still limited. In addition, the improvement of catalysts, therefore, remains in the test procedure, which can be done with multiple errors after the modification of the structure, and the resulting catalyst induces multiple steps until the reaction takes place. Such a fact is not adequate for a concept that is increasingly required by the scientific community: green chemistry. However, these trends have favored the development of diimidazolium salts as a precursor of the chelating bis-N-heterocyclic carbene (bis(NHC)) ligand. The corresponding complexation strategies allow the synthesis of a wide range of chelating bis(NHC) ligand metal complexes with variable structural and electronic properties. These properties offer the unique reactivity not found in their monodentate homologues for the activation and functionalization of the C–H bond (oxidation) of alkanes. Among these bidentate bis(NHC) ligands, the CH2-bridged bis-N-heterocyclic carbene ligands of bis(imidazole-2-ylidene) unit is the most common.
000 barrels per year, currently represent the main source of fuel, chemicals, and materials in the world, although the exploitation and valorization of biomass (renewable source) are in full expansion.1 Despite the fact that this resource is expected to be exploited for 50 years,2 research on alternative uses of natural gas is aimed at limiting some of its effects and the gas emissions resulting from its use on the environment. Methane (60%), one of the main components of natural gas, is the main target because of its greater warming potential than carbon dioxide (CO2) on the global warming potential (GWP) scale.3 This gas and other lower hydrocarbons (C2H6, C3H6, etc.) are potential raw materials for the chemical industry. In fact, these compounds could be permanently converted into their corresponding chemical liquid products through efficient processes. From an economic perspective, the oxidation approaches for the functionalization of lower alkanes (n ≤ 3) offer an attractive alternative compared to conventional gas-to-liquid processes because they do not rely on the intensive energy formation of syngas.4 However, due to low reactivity, the selective conversion of alkane to alcohol is particularly difficult. A potential solution for this challenge resides in the design and materialization of a discrete molecular catalyst that activates and functionalizes C–H bonds of the corresponding alkane. Since the emergence of Shilov's approaches based on the activation and catalytic reactions of saturated hydrocarbons in the presence of transition metal (TM) complexes, the reactivity of alkanes has received much attention, and at the same time, the coordination of ligands to these TMs has also facilitated various spectacular catalytic transformations (Suzuki, Miyaura, and Heck cross-coupling reactions).5,6 In modern organometallic chemistry, the knowledge of ligand tuning remains one of the most powerful concepts for regulating the catalytic properties of TM centers and predicting catalytic activity. Since the synthesis and the isolation of the first free N-heterocyclic carbene (NHC) by Arduengo, these compounds have become universal ligands in coordination chemistry.7 They easily bind to all TMs with a low or high oxidation degree. Due to their specific coordination chemistry, NHC stabilizes and activates metal centers in key areas (medicinal,8 luminescent,8 functional material applications8 and catalysis9–11…). Despite this great interest in NHCs, detailed knowledge of the molecular mechanism and factors underlying their catalytic activity of hydrocarbon oxidation is still limited. In addition, the improvement of catalysts, therefore, remains in the test procedure, which can be done with multiple errors after the modification of the structure, and the resulting catalyst induces multiple steps until the reaction takes place. Such a fact is not adequate for a concept that is increasingly required by the scientific community: green chemistry. However, these trends have favored the development of diimidazolium salts as a precursor of the chelating bis-N-heterocyclic carbene (bis(NHC)) ligand. The corresponding complexation strategies allow the synthesis of a wide range of chelating bis(NHC) ligand metal complexes with variable structural and electronic properties. These properties offer the unique reactivity not found in their monodentate homologues for the activation and functionalization of the C–H bond (oxidation) of alkanes. Among these bidentate bis(NHC) ligands, the CH2-bridged bis-N-heterocyclic carbene ligands of bis(imidazole-2-ylidene) unit is the most common.
The pioneering work on the generation of chelating dicarbene stabilized metal complexes with well-defined structures was carried out by Herrmann and co-workers.12,13 Subsequently, a wide range of chelating metal dicarbene complexes has been prepared from diimidazolium salts. Palladium is a metal exploited in a plethora of C–C coupling reactions (Mizoroki–Heck reaction, Suzuki–Miyaura reaction, Sonogashira coupling reaction), and many works related to palladium are summarized in these reviews.13–16 In addition, more than two decades ago, the Strassner group contributed to the conversion of methane and propane into liquid products by catalytic activation with an efficient functionalization of their C–H bond in the presence of palladium(II) complexes [Pd(II)bis(NHC)] and trifluoroacetic acid (HOTFA).17 These complexes lead to higher reactivity and catalyst stability compared to palladium(II) catalysts without NHC ligands.18
Furthermore, a sub-class of bis(NHC) ligands, so-called abnormal dicarbenes, which bind the metal through the imidazole C4 or C5 (CaNHC) site (Scheme 1(a)), has been investigated recently by Khlebnikov and co-workers.19 Their experimental studies have suggested that the heavy metal center was a stronger Lewis base when coordinated by the CaNHC site of C4-bound bis-N-heterocyclic carbene (bis(aNHC)) ligand20 compared to CnNHC (Scheme 1(b)) ones. However, the contribution of iodide ions has not been clearly elucidated, as well as their involvement in the reactivity of the complexes in the same works. Independent of the exact bond description between CaNHC of bis(aNHC) ligand with TM, the substantially higher donor strength of the CaNHC–metal bond is expected to have a strong impact on the catalytic activity of the coordinated metal center. This fact may disclose new applications in the catalysis field. It is, therefore, of utmost importance to combine the specific metal with the appropriate halide ions. Thus, Strassner's work on the influence of the counter-ion in the catalytic methane C–H bond activation mechanism by successively combining the halides Cl−, Br−, and I− with the Pd normal complex showed that for iodide, no activation could be observed.21 This point of view initiated by Strassner, and thus the authorship of the normal chelating complex is conceded to him, has given rise to a lot of hype concerning the emanation of the reactivity of the complex, which would be closely related to the combination of the metal, type of ligand and halide adopted.12–22 However, in the case of platinum metal, for example, normal and abnormal complexes, overall, acquired in practical applications have the effect of spurring a remarkable amount of experimental and theoretical works focused on the understanding Pt–CNHC and Pt–X bonds.19 A cumulative extension to this study has also highlighted other transition metals.19–22 The initial hypothesis based on the simple σ-donor character of bis(NHC) is now abandoned. To understand the electronic details and bonding properties of the M–CHNC bond and their role in catalysis, both d → π*M to NHC π*-back donation as well as π → dNHC to M π-donation must be considered. To date, actual comprehension of the structural architecture of these complexes necessary to explain the catalytic properties of reactions remains an incongruous topic. Our recent investigations indicate that the stability and reactivity of the metal–bis(NHC) complexes are not only related to their electronic properties but also to the coordination mode adopted23 and the oxidation state involved, M0/MII/MIV.24 Whereas for their monodentate counterparts benefiting from Tolman's studies,9 topological properties have been clarified. The idea of increasing the oxidation number of palladium from +2 to +4 in different complexes can be an informative index to inspect the favoured complexation process contributing to the bond activation mechanism. Exhibiting the exponential reactivity and given their ability to operate as catalysts for alkane C–H activation, we chose Strassner's complexes as a starting point for our explorations.
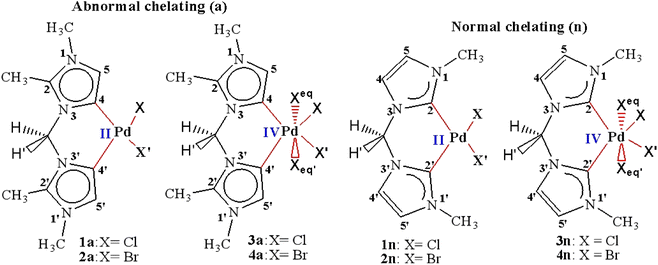 | ||
| Scheme 1 Palladium(II and IV) CH2-bridged bis-N-heterocyclic carbene complexes featuring abnormal (1a, 2a, 3a, and 4a) and normal bonding (1n, 2n, 3n, and 4n). | ||
The aim of this study is to investigate the impact of the ligand's coordination mode and the palladium's oxidation state on the chemical bond between the bis(NHC) ligand and palladium. Additionally, the study aims to establish design criteria for new catalysts of bis(NHC)PdIVX4 complexes based on electronic parameters using density functional theory analysis. This study is motivated by the fact that many similar normal-type complexes (Strassner's chelating type complex) have been reported to date, but the nature of the Ccarbene–Pd and Pd–halogen bonds, the oxidation state of palladium and their role in catalytic reactivity have not been clearly understood. In addition, the study of these properties in the case of abnormal-type complexes is unprecedented.
2 Computational details and background theory
2.1 Computational details
The geometry of different complexes was optimized using Gaussian 16 program25 at the Density Functional Theory (DFT) using the B3PW91 functional,23,26 LANL2DZ basis set for Pd, Cl, and Br, and the 6-31G(d) basis set for H, C, and N atoms. Frequency calculations were carried out at T = 298.15 K and P = 1 atm, in which all vibrational frequencies exhibited a real mode, confirming that these complexes are minima on the potential energy surface. To explain the rationality of the B3PW91 functional, additional calculations were carried out by employing the ωB97X-D with def2-TZVP basis set. Each thermodynamic state function (enthalpy, entropy, Gibbs free energy, and binding energy) was evaluated at T = 298.15 K and P = 1 atm (standard conditions). The QTAIM analysis and ELF electron population were carried out with the aid of Multiwfn 3.3.8 program26 to examine the nature of bonds in terms of electronic structure and bonding properties. To quantify the binding interactions around the metal centre, NBO, as implemented in the Gaussian 16 program,25 was developed at the B3PW91/6-31G(d)/Lanl2DZ level on optimised complexes. Finally, to obtain the density of states (DOS), partial density of states (PDOS) and overlap population density of states (OPDOS) spectra based on MOs, Multiwfn 3.3.8 program26 was used.2.2 Background theory
Conceptual DFT (CDFT) measures the reactivity and stability of molecular systems by extracting chemically relevant concepts from the DFT in terms of global reactivity descriptors (GRDs).27 The global electrophilicity ω, was estimated by applying the following formulas linked to the electronic chemical potentials (μ) and chemical hardness (η) of the studied complexes;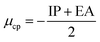 and
and 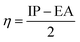 . The values of μ and η were then used for the calculation of ω via the formula
. The values of μ and η were then used for the calculation of ω via the formula 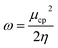 .27 Electronic parameters, IP (−εHOMO) and EA (−εLUMO), defined as the first vertical ionization potential and electronic affinity, respectively, and Egap (εLUMO–εHOMO) are used to discuss the chemical stability through electron transfer within the complexes according to Koopmans' theorem.28,29 In quantum chemical topology, the properties of one-density scalar functions are used to discuss the strength and nature of chemical bonding in molecules.30,31 This approach provides a partition of the function into non-overlapping atomic regions, so-called basins. The gradient field is characterized by its critical points (CPs) (where ρ(r) = 0) and their connectivity. CP can be either local maxima, minima or saddle points. In the QTAIM approach, the topological atom is defined as the union of a nucleus and its basin. Among the saddle points, a bond critical point (BCP) has a crucial role because the values of some descriptors at the BCP are related to the nature of the chemical bond. The electron density ρ(r) at the BCP is typically larger than 0.20 e bohr−3 in shared-shell interactions, in other words, covalent bonds, and smaller than 0.10 e bohr−3 in closed-shell (ionic) interactions. When the Laplacian of the density (∇2ρ(r)) at the BCP is negative, the local concentration of charge indicates a shared-shell interaction. In contrast, if ∇2ρ(r) is positive, there is a depletion of charge typically characterizing a closed-shell interaction. Due to the complexity of the nature of bonding interactions, another descriptor often used in QTAIM to distinguish shared-shell, closed-shell and intermediate bonding regimes is the ratio (|V(r)|/(G(r))), based on the potential energy density (V(r)) and the kinetic energy density (G(r)) at the BCP. When this ratio is smaller than 1, the kinetic energy density is the leading term, and electrons are destabilized close to the BCP; thus, no covalency is expected (pure ionic bond). The intermediate bond regime can be observed when the ratio is greater than 1 and less than 2 (1 < |V(r)|/(G(r) < 2). The energy density H(r) summarizes the mechanics of a bonding interaction. H(r) is negative for interactions with significant electron sharing, with its magnitude reflecting the covalence of the interaction.32 In line with this topological analysis, the bonding interaction between atoms was examined using the natural bond orbital (NBO) analysis.33 The second-order perturbation energy stabilization (E2) for each donor NBO(i) and acceptor NBO(j) estimated data is defined as follows:33
.27 Electronic parameters, IP (−εHOMO) and EA (−εLUMO), defined as the first vertical ionization potential and electronic affinity, respectively, and Egap (εLUMO–εHOMO) are used to discuss the chemical stability through electron transfer within the complexes according to Koopmans' theorem.28,29 In quantum chemical topology, the properties of one-density scalar functions are used to discuss the strength and nature of chemical bonding in molecules.30,31 This approach provides a partition of the function into non-overlapping atomic regions, so-called basins. The gradient field is characterized by its critical points (CPs) (where ρ(r) = 0) and their connectivity. CP can be either local maxima, minima or saddle points. In the QTAIM approach, the topological atom is defined as the union of a nucleus and its basin. Among the saddle points, a bond critical point (BCP) has a crucial role because the values of some descriptors at the BCP are related to the nature of the chemical bond. The electron density ρ(r) at the BCP is typically larger than 0.20 e bohr−3 in shared-shell interactions, in other words, covalent bonds, and smaller than 0.10 e bohr−3 in closed-shell (ionic) interactions. When the Laplacian of the density (∇2ρ(r)) at the BCP is negative, the local concentration of charge indicates a shared-shell interaction. In contrast, if ∇2ρ(r) is positive, there is a depletion of charge typically characterizing a closed-shell interaction. Due to the complexity of the nature of bonding interactions, another descriptor often used in QTAIM to distinguish shared-shell, closed-shell and intermediate bonding regimes is the ratio (|V(r)|/(G(r))), based on the potential energy density (V(r)) and the kinetic energy density (G(r)) at the BCP. When this ratio is smaller than 1, the kinetic energy density is the leading term, and electrons are destabilized close to the BCP; thus, no covalency is expected (pure ionic bond). The intermediate bond regime can be observed when the ratio is greater than 1 and less than 2 (1 < |V(r)|/(G(r) < 2). The energy density H(r) summarizes the mechanics of a bonding interaction. H(r) is negative for interactions with significant electron sharing, with its magnitude reflecting the covalence of the interaction.32 In line with this topological analysis, the bonding interaction between atoms was examined using the natural bond orbital (NBO) analysis.33 The second-order perturbation energy stabilization (E2) for each donor NBO(i) and acceptor NBO(j) estimated data is defined as follows:33where, qij represents the donor orbital occupancy, εj and εi are diagonal elements, and F2(i, j) is the off-diagonal NBO Fock matrix elements.
3 Results and discussion
3.1. Geometrical analysis
In order to predict the chemical reactivity of chelating bis(NHC) complexes towards the C–H bond activation of organic compounds, it is necessary to perform calculations at an appropriate theoretical level. Scheme 1 shows the eight bis(NHC) complexes, while Table 1 summarizes some key structural parameters (bond distances, valence, and dihedral angles) evaluated at the B3PW91//LANL2DZ/6-31G(d) level. Two chelating modes, normal (1n, 2n, 3n, and 4n) and abnormal (1a, 2a, 3a, and 4a), which correspond to different oxidation states (+2 and +4) of palladium are chosen for this investigation.| Chelating-type | Palladium(II) | Palladium(IV) | ||||||
|---|---|---|---|---|---|---|---|---|
| Normal | Abnormal | Normal | Abnormal | |||||
| Complexes | 1n | 2n | 1a | 2a | 3n | 4n | 3a | 4a |
| Cj–Pd | 1.993 | 2.003 | 1.997 | 2.009 | 2.064 | 2.092 | 2.019 | 2.039 |
| 1.993 | 1.996 | 1.981 | 1.990 | 2.034 | 2.055 | 1.994 | 2.010 | |
| Cj′–Pd | 1.993 | 2.003 | 1.997 | 2.009 | 2.064 | 2.092 | 2.019 | 2.039 |
| 1.993 | 1.996 | 1.981 | 1.990 | 2.034 | 2.055 | 1.994 | 2.010 | |
| Pd–X′ | 2.412 | 2.549 | 2.452 | 2.593 | 2.436 | 2.595 | 2.451 | 2.603 |
| Pd–Xeq′ | 2.342 | 2.478 | 2.363 | 2.499 | 2.350 | 2.498 | 2.371 | 2.519 |
| — | — | — | — | 2.443 | 2.611 | 2.460 | 2.621 | |
| — | — | — | — | 2.333 | 2.494 | 2.325 | 2.484 | |
| Pd–X′ | 2.412 | 2.549 | 2.452 | 2.593 | 2.436 | 2.595 | 2.451 | 2.603 |
| Pd–Xeq′ | 2.342 | 2.478 | 2.363 | 2.499 | 2.350 | 2.498 | 2.371 | 2.519 |
| — | — | — | — | 2.439 | 2.611 | 2.431 | 2.596 | |
| — | — | — | — | 2.336 | 2.501 | 2.354 | 2.508 | |
| Cj–Pd–Cj′ | 86.1 | 85.7 | 88.9 | 88.3 | 86.5 | 86.3 | 89.6 | 89.1 |
| 85.6 | 85.2 | 88.5 | 87.9 | 86.1 | 86.8 | 89.2 | 89.1 | |
| X–Pd–X′ | 93.2 | 92.8 | 96.5 | 95.4 | 88.8 | 87.0 | 89.6 | 92.9 |
| Xeq–Pd–Xeq′ | 92.8 | 93.9 | 95.4 | 95.2 | 88.9 | 88.0 | 94.1 | 92.5 |
| — | — | — | — | 177.5 | 180.0 | 172.6 | 174.7 | |
| — | — | — | — | 177.4 | 177.9 | 173.3 | 173.4 | |
| X–X′–Cj′–Cj | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Xeq–Xeq′–Cj′–Cj | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| — | — | — | — | 53.4 | 54.2 | 48.8 | 49.4 | |
| — | — | — | — | 53.3 | 54.2 | 49.6 | 49.4 | |
| Hendo–C–Hexo–Pd | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 |
| 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | ||||
From Table 1, the distance of CnNHC–Pd (2.064 Å) and CaNHC–Pd (2.019 Å) bonds are 0.071 and 0.022 Å greater in tetrachloride complexes (3n and 3a) compared to the dichloride (1n and 1a) ones. A similar trend is observed in the case of bromide complexes in which the Ccarbene–Pd distance [CnNHC–Pd; 2.092 Å (4n) and CaNHC–Pd; 2.039 Å (4a)] experienced a bond lengthening of 0.089 and 0.003 Å as compared to 2n and 2a, respectively. In addition, the distance of CnNHC–Pd and CaNHC–Pd bonds are longer in bromide than chloride complexes, with a slight increase occurring when passing from normal to abnormal complexes. All these observations suggest that the palladium (II and IV) center is a stronger Lewis or Brønsted base when coordinated by bis(aNHC) abnormal ligands as opposed to bis(nNHC) normal. This may be attributed to a more pronounced zwitterionic bonding of bin(aNHC), comprising an anionic vinyl-type fragment (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) for palladium coordination and a cationic NCN amidinium residue for intramolecular charge compensation.19 Irrespective of the exact Ccarbene–Pd bond description, the substantially higher donor power of bis(aNHC) is expected to have a strong impact on the catalytic activity of the coordinated palladium center.
C) for palladium coordination and a cationic NCN amidinium residue for intramolecular charge compensation.19 Irrespective of the exact Ccarbene–Pd bond description, the substantially higher donor power of bis(aNHC) is expected to have a strong impact on the catalytic activity of the coordinated palladium center.
With regard to the Pd–X bonds for dihalide complexes, the Pd–Br bond (2.549 Å in 2n and 2.593 Å in 2a) is notably longer than the Pd–Cl bond in the 1n and 1a complexes by approximately 0.137 and 0.141 Å, respectively (see, Table 1). Collectively, this Pd–X bond length analysis may hence point to a virtually different trans influence of the two chelating bis(NHC) ligands, although steric factors need to be considered as well, and a slightly greater trans influence coupled to the large size nuclei of bromide compared to chloride. This means that the repulsion of the halide from the palladium(II) coordination sphere due to the presence of a CH3 substituent at peripheral nitrogens (Scheme 1) is expected to be more pronounced in the bis(nNHC) than in the bis(aNHC) ligand. The same trends are observed for tetrahalide complexes for which the Pd–Xeq equatorial bond in 3n and 3a (Pd–Cleq close to 2.44 Å) and 4n and 4a (Pd–Breq close to 2.60 Å) remains nearly unchanged when switching from the normal to the abnormal model. However, these equatorial bonds are longer compared to the axial ones (Pd–X) within PdIV complexes (Table 1).
In order to guarantee the accuracy and validity of our geometric results and the level of theory adopted, we have initially compared the Pd–X and Ccarbene–Pd bond distances within the complexes from the available experimental data for the analogues. In agreement with the experimental data, the computations reproduced the strong chelating bond between the ligand and metal. Most of our calculated geometric data of the CnNHC–Pd, Pd–Cl bonds agree very well with the experimental data for the 1n complex.21 The maximum differences between X-ray data and our results for 3n complex in CnNHC–Pd, Pd–Cl, and Pd–Cleq bond lengths are just 0.045, 0.055, and 0.127 Å,24 respectively. This discrepancy could justify either the difference between the solid (X-ray data) and gas (our work) phases or the level of calculation. However, the lack of data from other complexes means that this comparison is limited to 1n and 3n. Otherwise, to more accurately reflect our findings in relation to the discrepancy observed in previous comparisons of CnNHC–Pd, Pd–Cl, and Pd–Cleq bond distances with experimental values on the 3n complex, we have implemented a revised calculation methodology. This employs the B3PW91/def2TZVP approach in the same gas phase. So, it is particularly instructive to compare the geometric data at the B3PW91/LanL2DZ/6-31G(d) level of theory with B3PW91/def2TZVP for all the complexes. Table 1 shows that the Ccarbene–Pd bond distance is identical within standard deviations in both approaches, averaging to 1.99 (1n) and 2.00 Å(2n) in normal and 1.99 (1a) and 2.00 Å(2a) in abnormal dihalide complexes. Similarly, the Pd–X bond distances are statistically equal, averaging 2.38 (Pd–Cl:1n) and 2.51 Å (Pd–Br:2n) in normal and 2.41 (Pd–Cl:1a) and 2.55 Å (Pd–Br:2a) in abnormal. Similar results were found for tetrahalide complexes but with much longer bond distances (see Table 1). This analysis of bond lengths indicates that the two levels of theory exhibit virtually identical geometric data, thereby highlighting a relative choice of level of theory to adopt. Beyond all considerations, we finally adopted the 6-31G (d) basis, which is more sophisticated and better suited to optimising the geometry of transition metal complexes, to the detriment of the def2TZVP basis, although the latter is more efficient in terms of calculation time.
Focusing on the angles, the pallado-chelation of the bis(aNHC) and bis(nNHC) ligands coupled to both halides (Cl− or Br−) forms a six-membered metallacycle in all complexes. Table 1 shows the angles of the computed complexes. From Table 1, we can see that the Cj–Pd–Cj′ bite angle and X–Pd–X′ of the chelating dicarbene around the Pd center are slightly smaller than 90°. This makes them well-suited for stabilising square-planar and octahedral coordination geometries for Pd(II) and Pd(IV), respectively. The X–X′–Cj′–Cj (0.0°) and H′–C–H–Pd (180.0°) dihedral angles form two perpendicular planes as an indicator for a bisector symmetry containing a C2v pseudo-symmetry axe, which keeps the Pd, Cbridged, H′, and H atoms invariant in PdII complexes or the Xeq, Xeq′, Pd, and Cbridged atoms in the PdIV ones (Fig. 1).
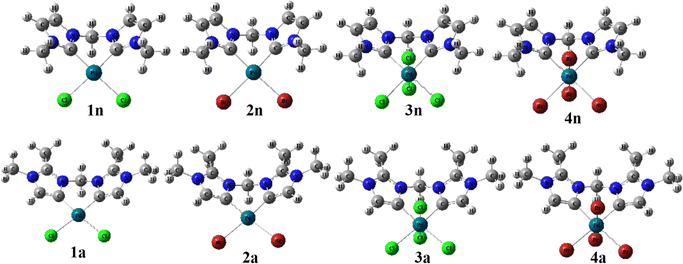 | ||
| Fig. 1 B3PW91//LANL2DZ/6-31G(d) optimized geometries of abnormal (1a, 2a, 3a, and 4a) and normal (1n, 2n, 3n, and 4n) complexes. | ||
3.2. Reactivity and thermodynamic stability evaluation
The analysis of the reactivity indices defined within the framework of the conceptual DFT (CDFT) is an important tool for evaluating the reactivity of chemical species. Table 2 presents the electronic chemical potential (μ), chemical hardness (η), and global electrophilicity (ω). As can be seen from Table 2, the ω values of the dihalide complexes (1n, 2n, 1a, and 2a) are smaller than those of the tetrahalide complexes (3n, 4n, 3a, and 4a), which range from 10.11 to 15.51 eV. From this, it can be inferred that the LaPdIVX4 or LnPdIVX4 tetrahalide palladium complexes exhibit preferential electrophilic behavior for the C–H bond activation processes in the following order: 3a > 3n > 4a > 4n. This justifies the good electrophilic character of the tetrachloride complex for the catalytic C–H bond activation, as experimentally explored by McCall.24 All these complexes are strong electrophiles according to the electrophilicity scale, which divides chemical compounds into strong (ω > 1.5 eV) and moderate (ω > 0.8 eV) electrophiles.34 Based on this electrophilic criterion, 3a would have the highest catalytic activity.| Complex | μ (eV) | η (eV) | ω (eV) | ΔG0 (kcal mol−1) | ΔH0 (kcal mol−1) | ΔS0 (kcal mol−1) | Ebind (kcal mol−1) |
|---|---|---|---|---|---|---|---|
| 1n | −3.40 | 2.24 | 2.59 | −45.20 | −59.0 | −0.046 | −58.4 |
| 2n | −3.30 | 1.95 | 5.59 | −38.8 | −25.0 | −0.05 | −20.8 |
| 1a | −2.94 | 1.74 | 2.48 | −44.6 | −57.7 | −0.044 | −57.1 |
| 2a | −2.86 | 1.60 | 2.56 | −33.9 | −46.4 | −0.042 | −45.8 |
| 3n | −3.69 | 0.51 | 13.37 | −102.3 | −118.6 | −0.055 | −118.0 |
| 4n | −3.96 | 0.78 | 10.11 | −80.6 | −96.9 | −0.067 | −96.3 |
| 3a | −3.77 | 0.46 | 15.51 | −111.7 | −126.8 | −0.050 | −126.1 |
| 4a | −4.04 | 0.72 | 11.29 | −92.2 | −107.9 | −0.052 | −107.3 |
Regarding the thermodynamic stability, the values of ΔEbind are negative in all cases, and therefore, indicate that bis(NHC) ligand stabilizes the Ccarbene–Pd bond. In addition, this value of ΔEbind increases from abnormal to normal chelating mode complexes due to the less π-backbonding ability of the metal. It is also important to note that the halide ions affect the strength of the Ccarbene–Pd bond. Concerning the Gibbs free energies, their negative values reveal that all these complexes exist and are stable (Table 2). Furthermore, the highest value of Gibbs free energy (−33.9 kcal mol−1) is recorded for 2a, while the smallest one (−111.7 kcal mol−1) is noted for 3a (more stable than the others, see Table 2).
3.3. Frontier orbitals and density of state analysis
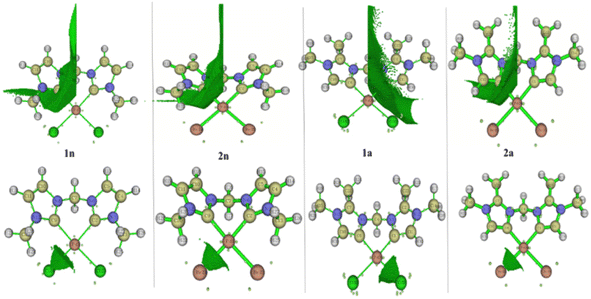
To better achieve the catalytic activity of all complexes through their intrinsic electronic bond properties, it is important to study the effective influence of CnNHC–Pd, CaNHC–Pd, and Pd–X bonds since the reactivity and stability discussed above (see Section 3.2) are affected by the presence of molecular bond orbital interactions. For that, we resorted to boundary orbital analysis in which each complex is divided into Pdi+ cation, halide ion (X−), and carbenic carbon (CnNHC or CaNHC), respectively. The atom contributions and the frontier molecular overlap compositions in each complex are given in Fig. 2 and 3. The analysis of HOMO clearly presents an electron density distribution preferentially located on the PdII center with a moderate HOMO energy close to −5.40 and −4.50 eV (Fig. 2) for the PdII normal and abnormal (except 2a, −4.46 eV) chelating models, respectively. Whereas, in the case of PdIV complexes, this electron density distribution entirely affects the first coordination sphere with almost the same HOMO energy as PdII. Following these previous observations, LUMO presents a high contribution deallocated preferentially on both imidazole rings with an energy close to −1.20 and −3.250 eV in PdII and PdIV complexes, respectively (Fig. 2 and 3). In addition, the ELUMO–HOMO gap of 2n (3.90 eV) and 2a (3.20 eV) PdII bromide complexes is low compared to that of PdII chloride counterparts (1n, 4.47 eV and 1a, 3.47 eV). In line with this analysis, the reversible fact was obtained upon the PdIV complexes for which the lower ELUMO–HOMO values were observed for 3n (1.01 eV) and 3a (0.91 eV) chloride complexes compared to bromide ones (Fig. 3). These observations highlight the lower kinetic stability of bromide PdII and chloride PdIV complexes, which correspond to greater preferential reactivity of each complex group. The preferential reactivity observed for bromide PdII and chloride PdIV complexes could explain the choice of their use as catalysts for the direct C–H bond activation and functionalization reactions of alkane,10,11,21 aromatic, alkene and benzylic aliphatic.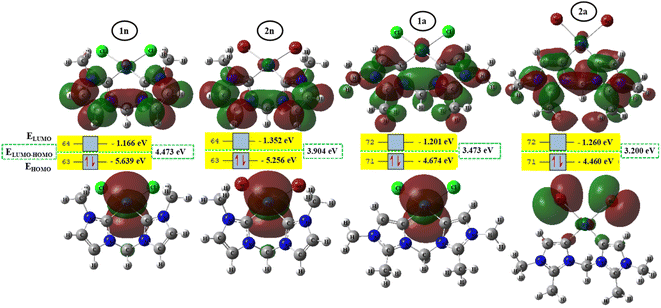 | ||
| Fig. 2 HOMO and LUMO isosurfaces (isovalue:0.02) of normal (1n, 2n, 3n, and 4n) complexes at B3PW91//LANL2DZ/6-31G(d) level of theory. | ||
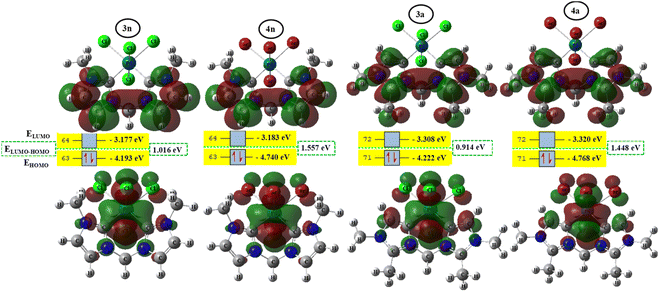 | ||
| Fig. 3 HOMO and LUMO isosurfaces (isovalue: 0.02) of abnormal (1a, 2a, 3a, and 4a) complexes at B3PW91//LANL2DZ/6-31G(d) level of theory. | ||
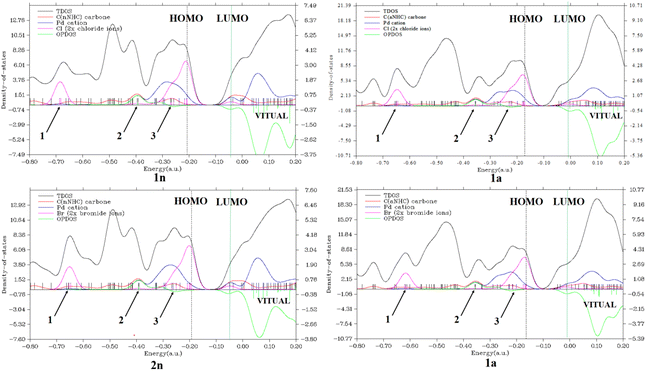
Secondly, considering the DOS map displayed in Fig. 4 and 1S,† it is important to know that each discrete vertical line corresponds to a molecular orbital (MO) energy level.35 In our case, the red, blue, and magenta curves represent the PDOS of CnNHC or CaNHC carbon, PdII or PdIV cation and Cl or Br ion, respectively. As can be seen from Fig. 4, the TDOS, PDOS and OPDOS information analysis of the energy levels allows us to observe three similar positions in each complex. The magenta PDOS curve, which is linked to the energetic density of states of halides (Cl− in 1n, 1a and Br− in 2n, 2a complexes), closely follows the black line (TDOS) in the regions ranging from −0.75 to −0.65 a.u (arrow 1 point) and from −0.35 to −0.15 a.u (arrow 3 points). These regions correspond to σ* (3 s) and π*(3p) orbitals, respectively, in all complexes. The fact that OPDOS (green curve) in these regions (arrow 1 and 3 points) is almost zero indicates a nonbonding interaction character35 between the Pd2+ cation and any halide in the corresponding complex. Furthermore, according to OPDOS diagrams, in their positive region close to −0.40 a.u (arrow 2 points) for 1n, 2n, 1a and 2a dihalide complexes, a π-bonding interaction character is established between CnNHC and Pd2+ for normal complexes and CaNHC and Pd2+ for abnormal ones.
Concerning the PdIV tetrahalide complexes, Fig. 1S† clearly shows the orbital characteristics in different energy ranges. Two main compositions of the MOs around −0.37 a.u (arrow 1 point) and −0.18 a.u (arrow 2 point) would be the bonding orbitals of the Cl−vBr−(magenta curve) with the Pd4+ atoms (blue curve) and the π-orbitals of CnNHC or CaNHC with Pd4+ elements, respectively. Inspection of the green OPDOS curve in these sites, which expresses the bonding character between Cl− (in 3n and 3a) or Br− (in 4n and 4a) halides with Pd4+ cation, and CnNHC or CaNHC atoms with Pd4+, on the other hand, suggest that their orbitals are very important for the stabilisation of CaNHC⋯Pd, CaNHC⋯Pd and Pd⋯X interactions. This observation is related to the fact that OPDOS has a positive value in these ranges (Fig. 1S†). For all virtual MOs, the OPDOS curve lies in the negative region and shows an anti-bonding character in this region. This is due to the unfavourable overlap in the orbital phase, as can be seen on the LUMO isosurface (Fig. 4 and 1S†).
3.4. Electronic and bonding properties
| Comp. | Occu. | Polarizability | Hybridization | |||
|---|---|---|---|---|---|---|
| Pd | CjNHC | Pd | CjNHC | |||
| 1 | n | 1.82 | 23.13% | 76.87% | s(25.23%), p(46.79%), d(27.98%) | s(40.98%), p(59.02%) |
| a | 1.81 | 23.46% | 76.54% | s(25.26%), p(45.91%), d(28.83%) | s(37.80%), p(62.20%) | |
| 2 | n | 1.82 | 23.18% | 76.82% | s(25.58%), p(46.00%), d(28.42%) | s(41.24%),p(58.76%) |
| a | 1.81 | 23.52% | 76.48% | (25.59%), p(45.17%), d(29.24%) | s(37.97%), p(62.03%) | |
| 3 | n | 1.80 | 31.08% | 68.92% | s(18.64%), p(46.79%), d(34.57%) | s(37.26%), p(62.73%) |
| a | 1.78 | 32.38% | 67.62% | s(18.41%), p(45.20%), d(36.38%) | s(34.04%), p(65.95%) | |
| 4 | n | 1.82 | 30.45% | 69.55% | s(18.73%), p(46.11%), d(35.16%) | s(38.16%), p(61.83%) |
| a | 1.80 | 32.08% | 67.92% | s(18.22%), p(44.53%), d(37.24%) | s(34.69%), p(65.31%) | |
| Mol. | Bond | ρ(r) (a.u) | ∇2ρ(r) (a.u) | ELF | V(r) (a.u) | G(r) (a.u) | H(r) (a.u) | Eint (kcal mol−1) | ε (a.u) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | Pd⋯CNHC | 0.117 | 0.475 | 2.280 | −0.182 | 0.151 | 1.210 | −0.032 | −57.133 | 0.163 |
| Pd⋯Cl | 0.053 | 0.233 | 0.687 | −0.069 | 0.064 | 1.085 | −0.005 | −21.648 | 0.537 | |
| 2n | Pd⋯CNHC | 0.116 | 0.450 | 2.271 | −0.769 | 0.145 | 5.311 | −0.032 | −241.273 | 0.129 |
| Pd⋯Br | 0.051 | 0.167 | 0.629 | −0.061 | 0.051 | 1.183 | −0.009 | −19.045 | 0.505 | |
| 1a | Pd⋯CNHC | 0.128 | 0.302 | 2.204 | −0.183 | 0.129 | 1.416 | −0.054 | −57.385 | 0.028 |
| Pd⋯Cl | 0.059 | 0.183 | 0.731 | −0.065 | 0.055 | 1.172 | −0.010 | −20.300 | 0.058 | |
| 2a | Pd⋯CNHC | 0.125 | 0.295 | 2.197 | −0.773 | 0.126 | 6.159 | −0.052 | −242.529 | 0.031 |
| Pd⋯Br | 0.054 | 0.125 | 0.679 | −0.053 | 0.042 | 1.255 | −0.011 | −16.503 | 0.050 | |
| 3n | Pd⋯CNHC | 0.097 | 0.441 | 2.110 | −0.148 | 0.129 | 1.147 | −0.019 | −46.435 | 0.386 |
| Pd⋯Cl | 0.048 | 0.232 | 0.537 | −0.063 | 0.061 | 1.045 | −0.003 | −19.829 | 1.090 | |
| Pd⋯ClEq | 0.047 | 0.219 | 0.445 | −0.061 | 0.058 | 1.052 | −0.003 | −19.045 | 0.947 | |
| Pd⋯Cl’Eq | 0.047 | 0.231 | 0.472 | −0.062 | 0.060 | 1.033 | −0.002 | −19.390 | 0.405 | |
| 4n | Pd⋯CNHC | 0.092 | 0.340 | 2.137 | −0.138 | 0.119 | 1.159 | −0.019 | −43.235 | 0.337 |
| Pd⋯Br | 0.045 | 0.165 | 0.536 | −0.054 | 0.048 | 1.136 | −0.007 | −17.037 | 2.313 | |
| Pd⋯BrEq | 0.044 | 0.138 | 0.421 | −0.049 | 0.042 | 1.173 | −0.007 | −15.342 | 1.194 | |
| Pd⋯Br’Eq | 0.043 | 0.159 | 0.369 | −0.052 | 0.046 | 1.131 | −0.006 | −16.252 | 1.204 | |
| 3a | Pd⋯CNHC | 0.101 | 0.491 | 1.943 | −0.169 | 0.146 | 1.158 | −0.023 | −52.961 | 0.120 |
| Pd⋯Cl | 0.047 | 0.217 | 0.584 | −0.061 | 0.058 | 1.060 | −0.004 | −19.264 | 0.155 | |
| Pd⋯ClEq | 0.049 | 0.223 | 0.491 | −0.063 | 0.059 | 1.059 | −0.004 | −19.641 | 0.690 | |
| Pd⋯Cl’Eq | 0.046 | 0.203 | 0.501 | −0.058 | 0.054 | 1.068 | −0.004 | −18.229 | 0.254 | |
| 4a | Pd⋯CNHC | 0.104 | 0.452 | 1.982 | −0.160 | 0.137 | 1.171 | −0.023 | −50.169 | 0.140 |
| Pd⋯Br | — | — | — | — | — | — | — | — | ||
| Pd⋯BrEq | 0.045 | 0.159 | 0.434 | −0.054 | 0.047 | 1.148 | −0.007 | −16.817 | 0.871 | |
| Pd⋯Br’Eq | 0.043 | 0.157 | 0.436 | −0.051 | 0.045 | 1.131 | −0.006 | −16.001 | 0.313 |
Since some covalency is witnessed by 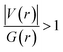 (the potential energy density V(r) dominates and electrons are stabilized at the BCP),37 we have integrated this descriptor to obtain further information about the Pd⋯X and CNHC⋯Pd interaction at BCP. So, the AIM analysis provides evidence in the series of PdII and PdIV complexes, by going from the normal chelating prototype complexes to the abnormal ones, that the Pd⋯X and CNHC⋯Pd are partial covalence characters. For example, the covalent character of the Pd⋯X interaction is strengthened since the average values of
(the potential energy density V(r) dominates and electrons are stabilized at the BCP),37 we have integrated this descriptor to obtain further information about the Pd⋯X and CNHC⋯Pd interaction at BCP. So, the AIM analysis provides evidence in the series of PdII and PdIV complexes, by going from the normal chelating prototype complexes to the abnormal ones, that the Pd⋯X and CNHC⋯Pd are partial covalence characters. For example, the covalent character of the Pd⋯X interaction is strengthened since the average values of 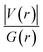 close successively to 1.134 (1n and 2n), 1.214 (1a and 2a), 1.095 (3n and 4n) and 1.093 (3a and 4a), increase in the following order Pd⋯Cl < Pd⋯Br while those of ∇2ρ(r) tend to decrease (Table 4). Then, we also integrated with the overall space of bonds, the total energy density (H(r)) defined by H(r) = G(r) + V(r) according to Roza criteria37 and ellipticity (ε) to obtain the ideal behaviour of the electron at BCP. Regardless of chelating model consideration, the negative H(r) values for both interactions (see Table 4) indicate an interaction with significant sharing of electrons. Its magnitude reflects the bond covalency interaction that increases according to the order, CNCH–Pd > Pd–X. Unfortunately, we note the most surprising results unexplained, which come from the 4a complex for which Table 4 shows the non-existence of BCP in one of Pd⋯Breq. Focusing on the ellipticity that depends on the instability of the bond, it has the property of determining the presence of a π-like character of the bonding up to the limit of the double bond for which the ellipticity reaches a maximum.38 Table 4 also shows that, regardless of Pd in its oxidation states (+2 and +4) and bis(jNHC) type complexes consideration, the ellipticity's collective positive values range from 0.1202 to 2.3131 a.u in CjNCH–Pd and from 0.3127 to 1.1943 a.u. in Pd–X bonding interactions. Such values well above zero highlighted a formal double bond and exhibited higher instability of these interactions.39 Although these values reflect a large perturbation from an ideal double bond, they are significantly greater than other corresponding values reported for 1a and 2a abnormal complexes in which values of ellipticity obtained, ranging from 0.028 to 0.058 a.u for CaNCH–Pd and Pd–X bonds, close to 0.0 a.u (see, Table 4) indicated a cylindrically symmetrical (simple bond) form.38 Therefore, the ellipticity data do not clearly corroborate with the results of the analyses. This could possibly be due to the highly polarised nature of the σ-bonding previously mentioned.
close successively to 1.134 (1n and 2n), 1.214 (1a and 2a), 1.095 (3n and 4n) and 1.093 (3a and 4a), increase in the following order Pd⋯Cl < Pd⋯Br while those of ∇2ρ(r) tend to decrease (Table 4). Then, we also integrated with the overall space of bonds, the total energy density (H(r)) defined by H(r) = G(r) + V(r) according to Roza criteria37 and ellipticity (ε) to obtain the ideal behaviour of the electron at BCP. Regardless of chelating model consideration, the negative H(r) values for both interactions (see Table 4) indicate an interaction with significant sharing of electrons. Its magnitude reflects the bond covalency interaction that increases according to the order, CNCH–Pd > Pd–X. Unfortunately, we note the most surprising results unexplained, which come from the 4a complex for which Table 4 shows the non-existence of BCP in one of Pd⋯Breq. Focusing on the ellipticity that depends on the instability of the bond, it has the property of determining the presence of a π-like character of the bonding up to the limit of the double bond for which the ellipticity reaches a maximum.38 Table 4 also shows that, regardless of Pd in its oxidation states (+2 and +4) and bis(jNHC) type complexes consideration, the ellipticity's collective positive values range from 0.1202 to 2.3131 a.u in CjNCH–Pd and from 0.3127 to 1.1943 a.u. in Pd–X bonding interactions. Such values well above zero highlighted a formal double bond and exhibited higher instability of these interactions.39 Although these values reflect a large perturbation from an ideal double bond, they are significantly greater than other corresponding values reported for 1a and 2a abnormal complexes in which values of ellipticity obtained, ranging from 0.028 to 0.058 a.u for CaNCH–Pd and Pd–X bonds, close to 0.0 a.u (see, Table 4) indicated a cylindrically symmetrical (simple bond) form.38 Therefore, the ellipticity data do not clearly corroborate with the results of the analyses. This could possibly be due to the highly polarised nature of the σ-bonding previously mentioned.
We have again evaluated the strengths of these bonds by using instantaneous interaction energy (Eint) defined by the formula 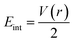 at BCPs according to Espinosa–Molins–Lecomte criteria. The calculated values have been gathered in Table 4. Higher Eint values (241.3 and 242.5 kcal mol−1) exhibited by 2n and 2a (bromide complexes), respectively, in the PdII type indicate stronger CjNCH–Pd interaction. The reverse fact is observed in PdIV type complexes for which the Eint of CjNCH–Pd in 3n (46.4 kcal mol−1) and 3a (53.0 kcal mol−1) chloride complexes are strengthened (Table 4). Such observations suggest a preferential catalytic activity of chloride complexes in the high Pd oxidation state over bromide complexes and reciprocally, based on the strength of the ligand⋯palladium interaction. These probably justified the choice of high Pd oxidation state (+4) for chloride complexes by Scott McCall24 and low Pd oxidation state (+2) for bromide complexes by Munz40 as catalyst for direct C–H bond functionalization reactions respectively of alkenes, alkynes, and alkanes. For the Pd–X bonds, the Eint values ranging from 15.3 to 21.6 kcal mol−1 fall within the range of typical halogen-bond energies (2.4–47.9 kcal mol−1),41 which indicated weak bond interaction forms. In addition, Table 4 also shows that the quantity Eint is inversely proportional to the size of the halide (Cl < Br) in each chelation mode of complexes independent of the Pd oxidation state form adopted. In the end, at this stage, the interpretation of the AIM data of these bonds is delicate since they describe an intermediate situation.
at BCPs according to Espinosa–Molins–Lecomte criteria. The calculated values have been gathered in Table 4. Higher Eint values (241.3 and 242.5 kcal mol−1) exhibited by 2n and 2a (bromide complexes), respectively, in the PdII type indicate stronger CjNCH–Pd interaction. The reverse fact is observed in PdIV type complexes for which the Eint of CjNCH–Pd in 3n (46.4 kcal mol−1) and 3a (53.0 kcal mol−1) chloride complexes are strengthened (Table 4). Such observations suggest a preferential catalytic activity of chloride complexes in the high Pd oxidation state over bromide complexes and reciprocally, based on the strength of the ligand⋯palladium interaction. These probably justified the choice of high Pd oxidation state (+4) for chloride complexes by Scott McCall24 and low Pd oxidation state (+2) for bromide complexes by Munz40 as catalyst for direct C–H bond functionalization reactions respectively of alkenes, alkynes, and alkanes. For the Pd–X bonds, the Eint values ranging from 15.3 to 21.6 kcal mol−1 fall within the range of typical halogen-bond energies (2.4–47.9 kcal mol−1),41 which indicated weak bond interaction forms. In addition, Table 4 also shows that the quantity Eint is inversely proportional to the size of the halide (Cl < Br) in each chelation mode of complexes independent of the Pd oxidation state form adopted. In the end, at this stage, the interpretation of the AIM data of these bonds is delicate since they describe an intermediate situation.
For a better prediction of the chemical bond properties of all complexes, we combined the AIM study with ELF population analysis. Fig. 6 and 4S† show the presence of ELF basin attractor on CjNHC–Pd and Pd–X at BCPs, meaning that the electrons are shared by the two elements involved. According to the well-known ELF basin symbolic method, the presence of these basins should be identified as V(CjNHC,Pd) and V(Pd,X). Table 4 depicts some integrals, namely the average electron population number in each basin. The result shows that the average integral of electron density in V(Pd, X) and V(CjCNH, Pd) are 1.0 and 2.1e, respectively. Evidently, the bonding between CNHC–Pd is much stronger than Pd – X; this is why the bond length of the former (close to 2.0 Å) is shorter than the latter (close to 2.5 Å). Note that the greater electron population number in V(CjNHC, Pd) of PdII compared to PdIV prototype complexes are 2.28 (1n), 2.27(2n), 2.20 (1a) and 2.20 (2a) (Table 4); therefore, it can be expected generally that Ccarbene–Pd bonds of dihalide complexes are stronger than tetrahalides ones. The ELF population number in V(CjCNH, Pd) and V(Pd, X) approximately reflecting that there is a pair of electrons shared between CjCNH and Pd and an ionic bond interaction between Pd and X.
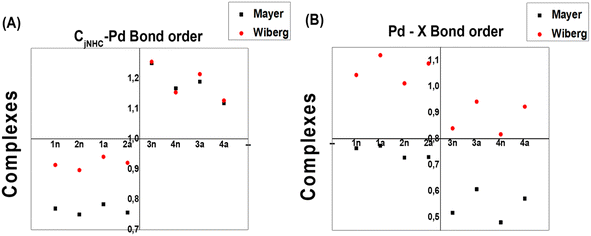
To measure both CjCNH–Pd and Pd–X bond strengths, which represent the combined covalent and ionic bond, Wiberg (WI) and Mayer (MI) bond orders are reported to be very well correlated with their description. Note that the Mayer bond order can be seen as a generalization of the Wiberg bond order for a restricted close-shell system.42 In our study, the WI and MI of both bonds on all the complexes were computed. The WI and MI values in Fig. 7 indicate that all the PdIV complexes present a CjCNH–Pd bond order (1.118–1.250 for WI and 1.127–1.255 for MI) greater than 1.0 a.u compared with those for all PdII complexes (0.750–0.784 for WI and for 0.897–0.914 for MI) and less than 1.0 a.u indicated that the former are stronger covalent bonds. The reverse fact is observed for the Pd–X bond order for which greater WI values close to 1.1 for PdII complexes could exhibited a slightly covalent bond compared with PdIV complexes (close to 0.89) (see Fig. 7b). From this previous Figure, although the WI values slightly increase from PdIV to PdII complexes, they are significantly greater than the MI values reported for Pd–X bonds in all complexes, which range from 0.45 to 0.75. These observations mainly suggest the marginally larger trans influence of bromide vs. chloride and confirmed by geometrical analysis (see Section 3.1).
3.5. Molecular electrostatic potential (MEP) surfaces
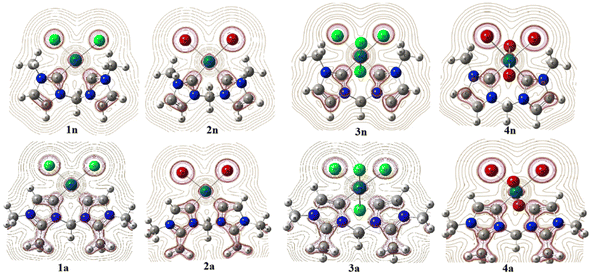
To investigate the reactive sites for electrophilic and nucleophilic attacks, the MEP surfaces for PdII and PdIV complexes have been plotted (Fig. 8). MEP surface is an electron density isosurface from SCF density mapped with an electrostatic potential surface (ESP). It is used to determine their sizes, shapes, and reactive sites on complexes in the case of eventual catalytic reactions. According to the literature, negative (red and yellow) and positive (light and dark blue) regions of the MEP surfaces are related to electrophilic and nucleophilic reactivity, respectively, while the green or white region corresponds to the limitation between negative and positive regions (zero electrostatic potential). The obtained results from MEP are mapped in Fig. 8(A), which shows that the red region of the MEP surface for PdII complexes is mainly localized over the different halide atoms, suggesting the most suitable atomic sites for a possible electrophilic attack. Moreover, in 1n and 2n complexes, the maximum blue region is localized on the CnNHC–Pd, and N3–C bonds that form the pallado-cycle and C–H of the CH2 bridged, showing that they are possible sites for attack by nucleophiles heavily weighted on CH2 methylene bridged. From the MEP maps in Fig. 8(B), it is also clear that the regions of 3n, 4n, 3a and 4a with the most negative V(r) are associated with the all-chloride ions. Hence, the most favourable atomic site for the electrophilic attack on these complexes is the PdX4 metallic moiety.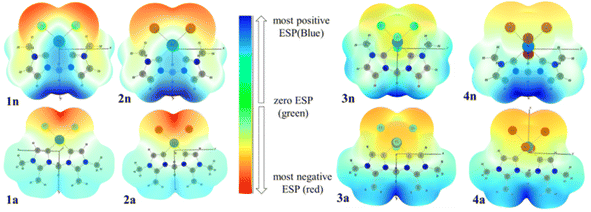 | ||
| Fig. 8 3D MEP surfaces of PdII (1n, 2n, 1a and 2a) and PdIV (3n, 4n, 3a and 3a) complexes, mapped onto electron density isosurfaces of value 0.02 a.u., using GaussView. | ||
4 Conclusion
Although several existing bis(NHC) palladium complexes have been reported to have successful catalytic efficiency in C–H bond activation, their intrinsic binding properties on the efficacy of catalytic activity are currently under increasing investigation. This has motivated an urgent search to understand the factors underlying this catalytic activity. In this regard, the present work has used Density Functional Theory calculations to elucidate more about the nature of CaCNH–Pdor CnCNH–Pd and Pd–X (X= Cl or Br) bond interactions, which have been found to play a key role based on the design criteria. The results of this work have conclusively demonstrated that thermodynamically favourable interactions can exist between bis(aNHC) or bis(nNHC) and Cl or Br halide ions with PdII and PdIV oxidation state, respectively, for the complex formation process. The calculated results show that both bis(aNHC) or bis(nNHC) ligands and the coordinating halides influence the strength of the CaCNH–Pdor CnCNH–Pd bonds. NBO methods clearly reveal the extent of σ-donation and π-backdonation for these bonds and help to understand the tunability of the complex structures. The σ-donation and π-backdonation are highest in the chlorine complexes and lowest in the bromine complexes. In addition, AIM analysis revealed that the greater covalent nature and strength of the CjNHC–Pd bond than Pd–X bonds depend on the nature of the oxidation state of palladium as well as the coordinating halide ion. The geometric aspect reveals the presence of C2v pseudo-symmetry and suggests that bromide is the weakly coordinating ligand compared to chlorides. Overall, the results show that bis(aNHC) and bis(nNHC) ligands appeared to be a suitable choice as ancillary support for PdIV due to their known propensity to stabilize highly oxidized metal centers without ligand dissociation. Thus, the resulting complexes can be made better catalyst precursors with preferred normal or abnormal coordination mode ligands on palladium and choosing a weakly coordinating halide.Data availability
Data will be made available on request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the results reported in this paper.Acknowledgements
This work was supported by the Ministry of Higher Education of Cameroon. The calculations were performed on the computers of the Consortium des Equipments de Calcul Intensif (CECI, http://www.ceci-hpc.be/) and particularly those of the Technological Platform of High-Performance Computing, for which the authors gratefully acknowledge the financial support of the FNRS-FRFC, of the Walloon Region, and of the University of Namur (Conventions No. 2.5020.11, GEQ U.G006.15, 1610468, and RW/GEQ2016).References
- «Le pétrole n’est pas renouvelable», 2020https://www.connaissancedesenergies.org/le-petrole-nestpas-renouvelable150513#notes. Accessed August 26.
- BP, BP Statistical Review of World Energy 2016, 2016 Search PubMed.
- https://gazissimo.fr/conseils/conso-energie.
- B. L. Conley, W. J. Tenn III, K. J. H. Young, S. K. Ganesh, S. K. Meier, J. Oxgaard, J. Gonzales, W. A. Gaddard III and R. A. Periana, Activation of Small Molecules: Organometallic and Bioinorganic Perspectives, Wiley-VCH, Weinheim, 2006, p. 235 Search PubMed.
- A. E. Shilov and G. B. Shulpin, Chem. Rev., 1997, 97, 2879 CrossRef CAS PubMed.
- N. F. Goldshleger, V. V. Eskova, A. E. Shilov and A. A. Shteinman, Zh. Fiz. Khim., 1972, 46, 1353 CAS.
- A. J. Arduengo, R. L. Harlow and M. Kline, J. Am. Chem. Soc., 1991, 113, 361 CrossRef CAS.
- L. Mercsa and M. Albrecht, Chem. Soc. Rev., 2010, 39, 1903 RSC.
- H. Jacobsen, A. Correa, A. Poater, C. Costabile and L. Cavallo, Coord. Chem. Rev., 2009, 253, 687 CrossRef CAS.
- D. Munz and T. Strassner, Angew. Chem., Int. Ed., 2014, 53, 2485 CrossRef CAS PubMed.
- D. Munz, D. Meyer and T. Strassner, Organometallics, 2013, 32, 3469 CrossRef CAS.
- W. A. Herrmann, J. Schwarz and M. G. Gardiner, Organometallics, 1999, 18, 4082 CrossRef CAS.
- J.-Q. Liu, X.-X. Gou and Y.-F. Han, Chem.–Asian J., 2018, 13, 2257 CrossRef CAS PubMed.
- J. A. Mata, M. Poyatos and E. Peris, Coord. Chem. Rev., 2007, 251, 841 CrossRef CAS.
- X. Hu and K. Meyer, J. Organomet. Chem., 2005, 690, 5474 CrossRef CAS.
- M. G. Gardiner and C. C. Ho, Coord. Chem. Rev., 2018, 375, 373 CrossRef CAS.
- T. Yagyu, A. Tsubouchi and Y. Nishimura, J. Organomet. Chem., 2014, 767, 1 CrossRef CAS.
- (a) A. Krüger and M. Albrecht, Aust. J. Chem., 2011, 64, 1113 CrossRef; (b) G. Guisado-Barrios, J. Bouffard, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2010, 49, 4759 CrossRef CAS PubMed.
- V. Khlebnikov, M. Heckenroth, H. Müller-Bunz and M. Albrecht, Dalton Trans., 2013, 42, 4197 RSC.
- M. Heckenroth, E. Kluser, A. Neels and M. Albrecht, Dalton Trans., 2008, 44, 6242 RSC.
- T. Strassner, M. Muehlhofer, A. Zeller, E. Herdtweck and W. A. Herrmann, J. Organomet. Chem., 2004, 689, 1418 CrossRef CAS.
- R. Jagadeesan, G. Velmurugan and P. Venuvanalingam, RSC Adv., 2015, 5, 80661 RSC.
- J. M. Ongagna, A. D. T. Fouegue, B. A. Ateba, G. D. Mouzong, J. Z. Mfomo, L. M. Mbaze and D. M. Bikele, J. Mol. Model., 2020, 246, 9 Search PubMed.
- A. S. McCall, H. Wang, J. M. Desper and S. Kraft, J. Am. Chem. Soc., 2011, 133, 1832 CrossRef CAS PubMed.
- M. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 16, Revision A. 03, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793 CrossRef CAS PubMed.
- R. Shankar, K. Senthilkumar and P. Kolandaivel, Int. J. Quantum Chem., 2009, 109, 764 CrossRef CAS.
- J. Martínez, Local reactivity descriptors from degenerate frontier molecular orbitals, Chem. Phys. Lett., 2009, 478, 310–322 CrossRef.
- R. Chauvin, C. Lepetit, B. Silvi and E. Alikhani, "Applications of Topological Methods in Molecular Chemistry, Springer, Berlin. 2016 Search PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- D. Cremer and E. Kraka, Angew Chem. Int. Ed. Engl., 1984, 23, 627 CrossRef.
- F. Weinhold and C. R. Landis, Chem. Educ. Res. Pract., 2001, 2, 91 RSC.
- L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, Tetrahedron, 2002, 58, 4417 CrossRef CAS.
- S. I. Gorelsky, S. Ghosh and E. I. Solomon, Mechanism of N2O Reduction by the μ4-S Tetranuclear CuZCluster of Nitrous Oxide Reductase, J. Am. Chem. Soc., 2006, 128, 278–290 CrossRef CAS PubMed.
- J. Haller, N. Kaltsoyannis, M. J. Sarsfield, I. May, S. Cornet, M. Redmond and M. Helliwell, Inorg. Chem., 2007, 46, 4868 CrossRef PubMed.
- D. Cremer and E. Kraka, Angew Chem. Int. Ed. Engl., 1984, 23, 627 CrossRef.
- The Quantum Theory of Atoms in Molecules, ed. Che’rif F. Matta and J. Boyd Russell, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007, Copyright 8, ISBN: 978-3-527-30748-7 Search PubMed.
- M. K. Samantaray, D. Roy, A. Patra, M. Saikh, R. B. Sunoj and P. Ghosh, J. Organomet. Chem., 2006, 691, 3797 CrossRef CAS.
- D. Munz and T. Strassner, Top. Catal., 2014, 57, 1372 CrossRef CAS.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., 2008, 47, 6114 CrossRef CAS PubMed.
- W. Su, S. Pan, X. Sun, S. Wang, L. Zhao, G. Frenking and C. Zhu, Nat. Commun., 2018, 9, 4997 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03893b |
| This journal is © The Royal Society of Chemistry 2024 |