Open Access Article
Open Access ArticleA machine learning-assisted study of the formation of oxygen vacancies in anatase titanium dioxide†
Dan Wang‡
a,
Ronghua Zan‡b,
Xiaorong Zhu *c,
Yuwei Zhanga,
Yu Wang
*c,
Yuwei Zhanga,
Yu Wang a,
Yanhui Gu*b and
Yafei Li
a,
Yanhui Gu*b and
Yafei Li *a
*a
aJiangsu Key Laboratory of New Power Batteries, Jiangsu Collaborative Innovation Centre of Biomedical Functional Materials, School of Chemistry and Materials Science, Nanjing Normal University, Nanjing 210023, P. R. China. E-mail: liyafei@njnu.edu.cn
bSchool of Computer Science and Technology, Nanjing Normal University, Nanjing 210023, P. R. China. E-mail: gu@njnu.edu.cn
cCollege of Chemistry and Chemical Engineering, Nantong University, Nantong 226019, P. R. China. E-mail: xiaorongzhu@ntu.edu.cn
First published on 21st October 2024
Abstract
Defect engineering of semiconductor photocatalysts is critical in reducing the reaction barriers. The generation of surface oxygen vacancies allows substantial tuning of the electronic structure of anatase titanium dioxide (TiO2), but disclosing the vacancy formation at the atomic level remains complex or time-consuming. Herein, we combine density functional theory calculations with machine learning to identify the main factors affecting the formation of oxygen defects and accelerate the prediction of vacancy formation. The results show that the first two-layer oxygen atoms on the typical surfaces of TiO2, including (100), (110), and (211) facets, are more likely to be activated when the gas is more reduced, the pressure is higher, and the reduction temperature is increased. Through machine learning, we can conveniently predict the formation of oxygen defects with high accuracy. Furthermore, we present an equation with acceptable accuracy for quantitatively describing the formation of oxygen vacancies in different chemical environments. Our work provides a fast and efficient strategy for characterizing the surface structure with atomic defects.
Introduction
Anatase titanium dioxide (TiO2) is a semiconductor material that is versatile, low-cost, stable, and non-toxic.1,2 Since its discovery as a photocatalyst for water splitting,3 there has been a strong interest in the photocatalytic application. However, its ability to capture light is hampered by the large band gap, which greatly limits the efficiency of solar energy conversion.4–8 Much effort has been made to improve the performance of TiO2, including defect engineering,9,10 surface modification,11 precious metal deposition12,13 and doping.14,15 Among these strategies, manipulating oxygen vacancies has drawn widespread attention and plays an important role in regulating the electronic properties of TiO2-based photocatalysts.16–18 Meanwhile, the preparation of TiO2 with different oxygen vacancy concentrations is a cheap and effective strategy that can control the absorbance and photocatalytic performance. For example, the oxygen vacancy can substantially lower the barrier for photocatalytic CO2 reduction via the fast-hydrogenation pathway.19 The optimal concentration ratio of single-electron-trapped oxygen vacancies to surface oxygen vacancies leads to the best activity in photocatalytic hydrogen production.20 Nonetheless, the basic factors that influence the oxygen vacancies' formation of TiO2 remain unclear, which requires a fundamental understanding of the oxygen vacancies at varying concentrations under experimental conditions.Currently, the identification of crystal structures with vacancies under given pressure (p) and temperature (T) is one of the most challenging problems in establishing structure–property relationships. Accurate first-principles computational techniques, such as density-functional theory (DFT), have facilitated the understanding of the structure and composition of a defective surface from the atomic level, such as vacancy formation energy (Ef)-based surface phase diagram.21 However, the higher computational cost and poor scalability limit their effectiveness in materials exploration.22 In recent years, machine learning (ML) has emerged as an effective way to screen materials.23–29 For example, Fung et al. used the ML approach to automatically derive key features from the electronic density of states (DOS) to predict adsorption energies with high accuracy, which provides physical insights into the response of adsorption energies to external perturbations of electronic structure.30 Zhong et al. used DFT to simulate optimal active sites to provide more training data for machine learning models; an automated framework was generated to systematically search for surfaces and adsorption sites with near-optimal CO adsorption energies.31 In view of the advantages of the ML approach, we are curious about whether we can use this approach to study factors affecting the formation of oxygen vacancies of TiO2.
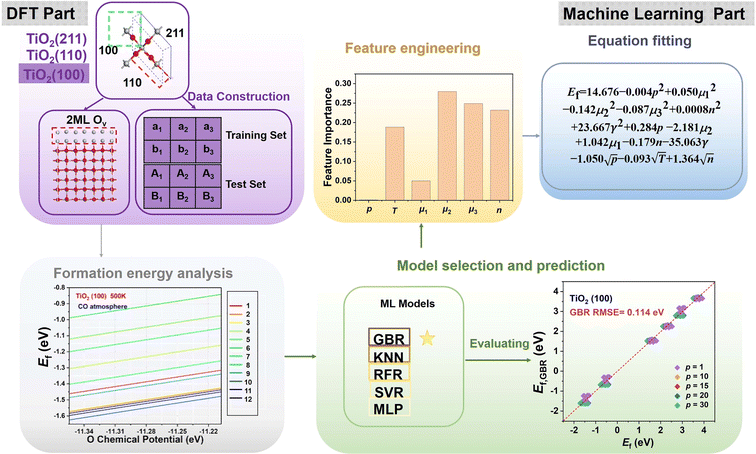
In this work, using DFT calculations and ML, we evaluated the formation of oxygen vacancies on three typical surfaces of TiO2 under H2, CO, and NO atmospheres. Our working flow contains the following five distinct stages: database construction, formation energy analysis, feature engineering, model selection and prediction, and equation fitting (Scheme 1). We first studied the oxygen vacancies' formation in the top two layers through high-throughput calculations (136 cases in total). These results were then related to reaction atmosphere, temperature, and pressure, resulting in 4080 formation energy data sets. The important factors affecting the formation of oxygen vacancies are further obtained by the machine learning analysis, and they are used as features to construct the model to predict the Ef of a given defective surface. Finally, by fitting the features, we proposed an equation for predicting the Ef values with acceptable accuracy.
Computational methods
DFT calculations
All DFT calculations were performed using the VASP code.32 The exchange–correlation interactions were described by the Perdew–Burke–Ernzerhof (PBE) functional,33 the projector augmented wave (PAW)34 pseudo-potentials were applied to treat the core-electron interactions. Electronic energies were computed with the tolerance of 5 × 10−5, and total forces were converged to less than 0.05 eV Å−1. A Gamma k-point was used to sample the Brillouin zone with an energy cut-off of 420 eV. The lattice parameters of TiO2 were calculated to be a = b = 3.71 Å and c = 9.54 Å, in agreement with previous experimental values.35 For the (100), (110), and (211) slabs, we constructed a 3 × 2, 4 × 4, and 2 × 4 supercell containing 12, 32, and 24 surface O atoms per layer to simulate the periodic TiO2 surface.A vacuum region of 20 Å was adopted to separate adjacent slabs. The bottom two layers were fixed, and the other layers were relaxed during the geometry optimization. The Ef on the first two layers of TiO2 were elucidated by high-throughput DFT calculations.
The surface energy (γ) is calculated as follows:
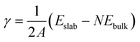 | (1) |
The energy of formation of oxygen vacancies (Ef) on TiO2 is calculated as:
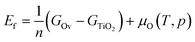 | (2) |
The chemical potential of species A in the gas phase with respect to vacuum at a specific temperature and pressure is represented by:21
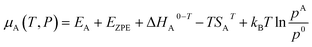 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A0–T is the enthalpy change from 0 K to a certain T, TSAT is the entropy, and p0 is taken as 1 bar.
A0–T is the enthalpy change from 0 K to a certain T, TSAT is the entropy, and p0 is taken as 1 bar.
The removal of surface oxygen atoms under H2 atmosphere conditions (H2 + O → H2O) is accomplished by reducing the surface oxygen atoms to water. The μO(T, p) is calculated as:
| μO(T, p) = μH2O(T, p) − μH2(T, p) | (4) |
The removal of surface oxygen atoms under CO atmospheric conditions (CO + O → CO2) is accomplished by reducing the surface oxygen atoms to carbon dioxide. The μO(T, p) is calculated as:
| μO(T, p) = μCO2(T, p) − μCO(T, p) | (5) |
The removal of surface oxygen atoms under NO atmosphere conditions (NO + O → NO2) is accomplished by reducing the surface oxygen atoms to nitrogen dioxide. The μO(T, p) is calculated as:
| μO(T, p) = μNO2(T, p) − μNO(T, p) | (6) |
Machine learning methods
The five common algorithms in the Scikit-learn module36 we used are K-nearest neighbors (KNN), linear support vector regression (Linear SVR), multilayer perceptron (MLP), gradient boosting regression (GBR) and random forest regression (RFR).In the above algorithms, KNN works by selecting K nearest neighbors for prediction based on Euclidean distance or Manhattan distance. In the case of regression, predictions are made by averaging the nearest target values.37 Additionally, KNN models built using this algorithm are straightforward to interpret and are well-suited for datasets with a limited number of features and samples.
Linear SVR is a regression algorithm based on Support Vector Machines,38 which fits the data by finding a hyperplane in the high-dimensional space so that the distance from all data points to that hyperplane is as small as possible.39 Compared to other algorithms, the SVR model developed using this approach demonstrates superior performance on high-dimensional datasets with numerous features and samples.
MLP, also known as a neural network, consists of an input layer, one or more hidden layers, and an output layer.40 Neurons are the basic units of a neural network and can be used to receive input signals and produce outputs. Weights are used to determine the strength of connections between neurons.41 After calculating the weighted sum of each hidden unit, the model applies a nonlinear function to the result, so neural networks can learn more complex functions than linear models.
RFR is a ML algorithm based on decision trees. It predicts the output values by constructing several different decision trees and taking the average of these values as the final prediction. This prediction way is able to reduce overfitting and maintain the predictive performance of the tree.42,43
Although both GBR and RFR are commonly used integrated learning algorithms, there are some differences between GBR and RFR. Each tree constructed by GBR tries to correct the errors of the previous tree, which enables GBR to convert weak learners into strong learners.44–47 In addition, the current learners are trained on the previous learner, which makes the GBR algorithm robust.48
Our ML model was trained based on the first layer and 5% of the second layer of oxygen-vacancy data. We used the untrained data obtained from the second O atomic layer in TiO2 as the test set to analyze the predictive ability of the model. To avoid the overfitting of the model, the performance of the machine learning model can be evaluated using the root mean square error (RMSE). We used the Pearson correlation coefficient to investigate the relevance of features and the coefficient of determination to characterize the accuracy of the model.
Results and discussion
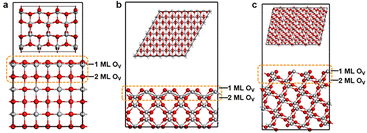
Fig. 1 shows the geometric structures of three typical TiO2 facets, (100), (110) and (211). Previous studies have found that the outer oxygen atoms of TiO2 can be readily removed during the catalytic process, and this removal of oxygen can also occur in the near-surface region of the TiO2 as the temperature increases.49–51 In this regard, we investigated the defective TiO2 facets with different oxygen concentrations in the data construction stage, with focusing on the upper two layers as a demonstration. This step produced 136 cases, which were characterized by high-throughput computation.High-pressure and high-temperature annealing can facilitate the generation of oxygen vacancies.52 It is notable that CO2 and nitrate reduction occur in an H2-rich atmosphere, producing reducing gases such as CO and NO, which would accelerate surface O depletion on TiO2 surfaces. Therefore, to guide the design of catalysts, it is necessary to determine the surface structure of TiO2 under reaction conditions and to study the relationship between activity and structure. To this end, based on eqn (2), we explored the formation of oxygen vacancies at temperatures of 298 K and 500 K, different pressure ratios (1, 10, 15, 20, and 30), as well as different atmospheres (H2, CO, and NO). The first two layers of oxygen vacancies, of which (100), (110), and (211) facets account for 720, 1920, and 1440 data sets, respectively.
Fig. 2 displays the formation energies of oxygen vacancies on the TiO2(100) surface calculated at 298 K and 500 K for CO, H2, and NO atmospheres. Please note that the pressure ratios of reductant to reduction products were 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 10
1, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 15
1, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 20
1, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 30
1, and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the differences in pressure and reduction atmospheres were reflected in differences in chemical potentials. The corresponding results of TiO2(110) and TiO2(211) are shown in Fig. S1–S4.† At 298 K, the formation of oxygen vacancies on relatively stable (100) and (110) surfaces is unfavorable regardless of the different atmospheres (Fig. 2a–c and S1†), and only a small number of oxygen atom vacancies on TiO2(211) are thermodynamically feasible (Fig. S2†). These results imply that the formation of oxygen vacancies is generally difficult, which is in agreement with the observed high stability of TiO2
1, and the differences in pressure and reduction atmospheres were reflected in differences in chemical potentials. The corresponding results of TiO2(110) and TiO2(211) are shown in Fig. S1–S4.† At 298 K, the formation of oxygen vacancies on relatively stable (100) and (110) surfaces is unfavorable regardless of the different atmospheres (Fig. 2a–c and S1†), and only a small number of oxygen atom vacancies on TiO2(211) are thermodynamically feasible (Fig. S2†). These results imply that the formation of oxygen vacancies is generally difficult, which is in agreement with the observed high stability of TiO2
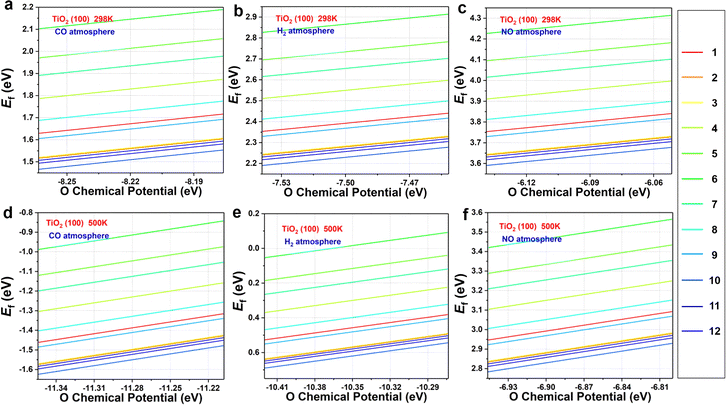 | ||
| Fig. 2 The formation energy of topmost O atoms on TiO2 surfaces with CO, H2, and NO as reducing agents at (a–c) 298 K and (d–f) 500 K. The red to blue lines are marked in the number of the O atoms. | ||
When the temperature is increased to 500 K, the values of Ef of the TiO2(100) surface become more negative (especially under CO and H2 atmospheres) (Fig. 2d–f). The similar situation can be observed in TiO2(110) and TiO2(211) (Fig. S3 and S4†). Therefore, oxygen vacancies are more likely to be formed at elevated temperatures, rationalizing previous experimental observations. Among the three reducing atmospheres, the CO atmosphere can best promote the formation of oxygen defects, followed by the H2 atmosphere. In addition, NO gas cannot easily reduce surface oxygen, and TiO2 maintains its structural integrity in the presence of NO.
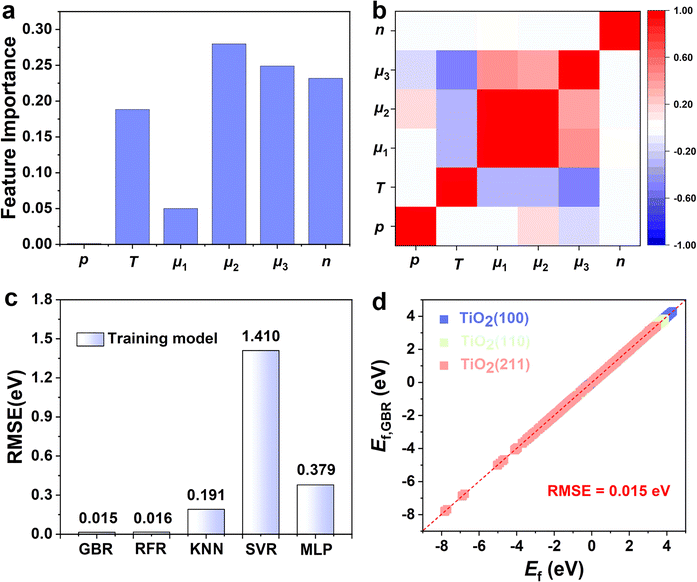
Choosing the right features can promote the model's prediction of the Ef of oxygen vacancy. The number of oxygen vacancies (n), the pressure ratio of the reducing agent to reducing product (p), the temperature (T), the surface energy (γ), the chemical potentials of reduction products (μ1) and the reducing gases (μ2), and the oxygen chemical potential (μ3) are considered as the factors affecting the Ef of oxygen vacancy. According to the analysis of the importance of the features, chemical potential, temperature, and the number of oxygen defects are all important factors affecting vacancy formation (Fig. 3a). Therefore, we use these factors as input parameters for training the ML model. Fig. 3b shows the Pearson correlation coefficient matrix, and the distribution of the six features has obvious differences in dimension and range, indicating that the relationship between these features and O vacancy formation energy is complex. The low correlation between the features indicates that the features are independent of each other and that a single feature does not accurately describe the formation pattern. Therefore, several key factors were chosen as the input parameters in the subsequent ML study.
An appropriate selection of algorithms is a critical part of designing an appropriate catalyst. Our ML models were trained based on the first layer of Ef data and 5% of the second layer of data (training set). The remaining 95% of the data from the second layer (test set) was then used to analyze the predictive ability of the model. Since some algorithms are very sensitive to data scaling, it is common practice to tune the features to make the algorithms more suitable for these data. Therefore, we performed data scaling and then constructed models using each of the five ML algorithms. To evaluate the learning performance of the five ML models, we compare the error between the actual and predicted values using RMSE as the key criterion (Fig. 3c). We found that the RFR and GBR models exhibit extremely high accuracy with lower errors of RMSE 0.015 eV and 0.016 eV, respectively (Fig. 3d). The actual values of the Ef based on DFT calculations are in high agreement with the ML predictions, which indicates that the hidden information in the raw data can be precisely extracted. In contrast, the three algorithms (i.e., KNN, SVR and MLP) have relatively high RMSE values (Fig. S5†); the significant difference between the predictions of Ef by DFT and ML suggests the lack of learning ability of the three models for TiO2.
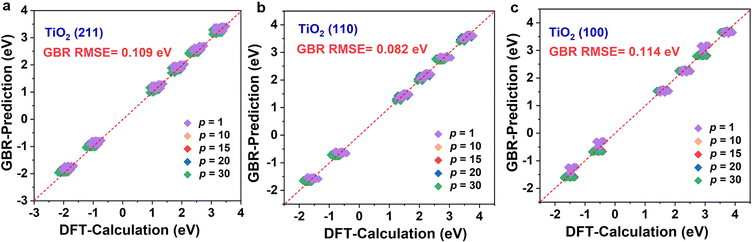
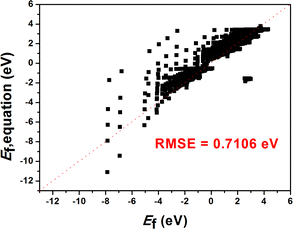
The above results clearly show that the GBR model is best suited for the TiO2 dataset. However, the RMSE of the RFR model is similar to that of the GBR model, so we predicted the formation energy of the second layer of oxygen vacancies using each of the two models and compared the model predictions with the Ef calculated based on DFT. Fig. 4 and S7† show the performance metrics of the GBR and RFR models for the test sets on the (100), (110), and (211) surfaces, respectively. The RFR model shows a slightly higher error value than the GBR model (RMSE = 0.098 eV) with an overall RMSE of 0.100 eV. In the process of constructing the model, we also employed classic linear such as ordinary least squares (OLS) and ridge regression for predictive purposes. Nevertheless, we encountered an abnormally negative R2 value for the linear model (Fig. S6†), suggesting that the relationship between the target energy and the features is not merely linear. GBR is an ensemble learning technique that sequentially enhances model performance by constructing a series of weak learners, typically in the form of decision trees. It works by minimizing the error of the preceding model at each step, thereby iteratively refining the prediction accuracy.53,54 GBR outperforms KNN, SVR, MLP, and RFR in forecasting the formation energy of oxygen defects. This superior performance can be attributed to several factors: (i) differences in model principles. KNN predicts based on the distances between samples, primarily relying on information from local neighbors.55 KNN is sensitive to the local structure of data and may not perform well in complex high-dimensional data or in the presence of significant noise. SVR uses the idea of support vector machines to maximize the number of samples within the regression error range by finding a hyperplane.56 While SVR excels at handling linear and a few nonlinear problems, it may not be as efficient as GBR when dealing with highly complex nonlinear data. MLP, a neural network, models complex nonlinear relationships through its neural connections.57,58 Although MLP is capable of handling complex data, it is highly sensitive to hyperparameter tuning (such as the number of layers, nodes, and activation functions), which may necessitate more time for tuning and training, particularly with small and medium-sized datasets. RFR is an ensemble learning algorithm that is based on decision trees.59,60 RFR is effective in handling nonlinear relationships; however, its predictions for each tree are independent and do not gradually correct errors like GBR can, which may result in some inaccuracies in certain cases. (ii) Capture complex data structures. GBR typically excels at capturing complex nonlinear relationships compared to KNN, SVR, MLP, and RFR,61 largely due to its use of a sequential, iterative approach involving multiple trees to more deeply conform to the data's subtle patterns. Other models might not effectively grasp these nuances, particularly when dealing with highly nonlinear data. (iii) Overfitting control. GBR effectively manages overfitting by adjusting the depth of the trees, the learning rate, and the number of weak learners, thereby typically achieving a good balance between bias and variance.53 SVR and MLP might overly depend on parameter tuning.62 KNN can be prone to overfitting local noise. While RFR has some capability to control overfitting, it lacks the mechanism of progressively reducing errors that GBR employs.63 Therefore, the GBR model's advantage often lies in its proficiency at dealing with complex nonlinear data, its capacity for incremental error correction, and its ability to maintain a balance between bias and variance. It is particularly well-suited for datasets characterized by complex relationships, nonlinear structures, and noise, which could explain its superior performance compared to other models in our study. Briefly, the training model shows the best model generalization performance and the lowest RMSE for our constructed GBR model (0.114 eV for TiO2(100) surface, 0.082 eV for TiO2(110) surface, and 0.109 eV for TiO2(211) surface), which fits well with the Ef values based on the DFT calculations. Please note that these data are scattered because of the effect of temperature. In addition, we examine the scalability of the GBR regression model by comparing the RMSE of 0.015 eV for the training set with the overall RMSE of 0.098 eV for the test set. The small difference between the RMSE of the training and test sets suggests that the overfitting is negligible. Hence, the ML using the GBR model is expected to be extended to the study of the N-layer structure of TiO2. The ability to directly detect the process of oxygen vacancy change is essential for realizing its further applications in related fields (Fig. 5).
We constructed eqn (7) using six distinct sets of features based on the feature importance ranking derived from the GBR model. The results of the SISSO algorithm indicate that the final eqn (7) can be utilized with only four features, n, p, γ, and μ3, that is, the lowest error value is obtained (Table S1†). To further explain why this occurs, a Pearson correlation analysis was conducted on the original seven features as well as the prediction targets. The results show that μ1, μ2, T, and μ3 have high correlations (0.62, 0.25, 0.63), which may lead to feature redundancy. In contrast, the correlation between μ3 and the prediction target is as high as 0.89. Such a result suggests that μ1, μ2, and T may be eliminable, which is consistent with the results obtained by SISSO. Finally, the equation can be expressed as:
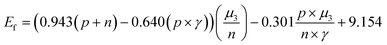 | (7) |
Conclusions
In summary, we reported a joint study of DFT calculations and ML for the rapid prediction of the surface oxygen vacancy formation on TiO2(100), (110) and (211) surfaces. The surface oxygen vacancies are sensitive to temperature and reducing gas, and the degree of reduction of oxygen atoms on different crystal surfaces varies under the same conditions. The extremely low error values indicate that the ML based on the GBR model can learn the hidden information behind the formation of TiO2 oxygen vacancies very skillfully. In addition, we proposed an equation for predicting the Ef with acceptable accuracy. Our work provides a fast and efficient analytical solution for relatively accurate prediction of oxygen vacancy formation in TiO2 under experimental conditions and facilitates the optimization of defect engineering in catalyst design.Data availability
The authors confirm that the data supporting the findings of this study are available within the article.Author contributions
Dan Wang, Ronghua Zan, Xiaorong Zhu: conceptualization and methodology. Dan Wang, Xiaorong Zhu: writing and draft preparation. Yuwei Zhang, Yu Wang, Yanhui Gu, Yafei Li: review and editing. All authors discussed and cowrite the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for funding support from the National Key R&D Program of China (2019YFA0308000), the Natural Science Foundation of China (No. 22173048), and the Priority Academic Program Development of Jiangsu Higher Education Institutions.Notes and references
- A. Meng, L. Zhang, B. Cheng and J. Yu, Adv. Mater., 2019, 31, 1807660 CrossRef PubMed.
- Y. Nam, J. H. Lim, K. C. Ko and J. Y. Lee, J. Mater. Chem. A, 2019, 7, 13833–13859 RSC.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef PubMed.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed.
- Z. Li, S. Wang, J. Wu and W. Zhou, Renewable Sustainable Energy Rev., 2022, 156, 111980 CrossRef.
- Q. Guo, C. Zhou, Z. Ma and X. Yang, Adv. Mater., 2019, 31, 1901997 CrossRef CAS PubMed.
- H. Chen, C. E. Nanayakkara and V. H. Grassian, Chem. Rev., 2012, 112, 5919–5948 CrossRef CAS PubMed.
- X. Chen, L. Liu, P. Y. Yu and S. S. Mao, Science, 2011, 331, 746–750 CrossRef CAS PubMed.
- S. Zhang, Z. Liu, D. Chen, Z. Guo and M. Ruan, Chem. Eng. J., 2020, 395, 125101 CrossRef.
- Y. Wang, Y. Zhang, X. zhu, Y. Liu and Z. Wu, Appl. Catal., B, 2022, 316, 121610 CrossRef.
- W. Hu, S. Yang and S. Yang, Trends Chem., 2020, 2, 148–162 CrossRef.
- G. J. Xia, M. S. Lee, V. A. Glezakou, R. Rousseau and Y. Wang, ACS Catal., 2020, 12, 4455–4464 CrossRef.
- L. Kuai, Z. Chen, S. Liu, E. Kan, N. Yu, Y. Ren, C. Fang, X. Li, Y. Li and B. Geng, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- J. Chen, S. K. Iyemperumal, T. Fenton, A. Carl, R. Grimm, G. Li and N. A. Deskins, ACS Catal., 2018, 8, 10464–10478 CrossRef.
- H. Choi, D. Shin, B. C. Yeo, T. Song, S. S. Han, N. Park and S. Kim, ACS Catal., 2016, 6, 2745–2753 CrossRef.
- Y. Nosaka and A. Y. Nosaka, Chem. Rev., 2017, 117, 11302–11336 CrossRef CAS.
- Z. Han, C. Choi, S. Hong, T. Wu, Y. Soo, Y. Jung, J. Qiu and Z. Sun, Appl. Catal. B Environ., 2019, 257, 117896 CrossRef CAS.
- F. Li, G. Liu, F. Liu, J. Wu and S. Yang, J. Hazard. Mater., 2023, 452, 131237 CrossRef CAS.
- Y. Ji and Y. Luo, J. Am. Chem. Soc., 2016, 138, 15896–15902 CrossRef CAS.
- L. Hou, Z. Guan, M. Zhang, C. He, Q. Li and J. Yang, Catal. Sci. Technol., 2018, 8, 2809–2817 RSC.
- A. Cao, Z. Wang, H. Li and J. K. Nørskov, ACS Catal., 2021, 11, 1780–1786 CrossRef CAS.
- S. Bhandari, S. Rangarajan and M. Mavrikakis, Acc. Chem. Res., 2020, 53, 1893–1904 CrossRef CAS PubMed.
- D. Roy, S. Mandal and B. Pathak, ACS Appl. Mater. Interfaces, 2021, 13, 56151–56163 CrossRef CAS PubMed.
- S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Nat. Commun., 2018, 9, 3405 CrossRef PubMed.
- M. Ducamp and F. Coudert, J. Phys. Chem. C, 2022, 126, 1651–1660 CrossRef CAS.
- L. Zhang, M. He and S. Shao, Nano Energy, 2020, 78, 105380 CrossRef CAS.
- X. Zhang, B. Ding, Y. Wang, Y. Liu, G. Zhang, L. Zeng, L. Yang, G. Yang, M. K. Nazeeruddin and B. Chen, Adv. Funct. Mater., 2024, 2314529 CrossRef CAS.
- Y. Jiao, H. Li, Y. Jiao and S. Qiao, J. Am. Chem. Soc., 2023, 145, 15572–15580 CrossRef CAS.
- Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, J. Phys. Chem. Lett., 2018, 9, 1668–1673 CrossRef CAS PubMed.
- V. Fung, G. Hu, P. Ganesh and B. G. Sumpter, Nat. Commun., 2021, 12, 88 CrossRef CAS PubMed.
- M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C. Dinh, P. D. Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Nature, 2020, 581, 178–183 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, A. Mülller, J. Nothman, G. Louppe, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- N. Saha, R. Heim, A. Mazumdar, G. Banerjee and O. Sarkar, Environ. Model. Assess., 2024, 1573–2967 Search PubMed.
- R. Zhang, J. Yang, S. Wu, H. Sun and W. Yang, Steel Res. Int., 2023, 94, 2200682 CrossRef CAS.
- R. Piraei, M. Niazkar, S. H. Afzali and A. Menapace, Water, 2023, 15, 2187 CrossRef.
- F. P. V. Ferreira, R. Shamass, V. Limbachiya, K. D. Tsav daridis and C. H. Martins, Thin-Walled Struct., 2022, 170, 108592 CrossRef.
- M. W. Gardner and S. R. Dorling, Atmos. Environ., 1998, 32, 2627–2636 CrossRef.
- H. Lu and X. Ma, Chemosphere, 2020, 249, 126169 CrossRef PubMed.
- S. Baharvand and H. Ahmari, Water Resour. Manag., 2024, 38, 2905–2934 CrossRef.
- A. Sharafati, S. B. Haji Seyed Asadollah, D. Motta and Z. M. Yaseen, Hydrol. Sci. J., 2020, 65, 2022–2042 CrossRef.
- J. H. Friedman, Annu. Stat., 2001, 29, 1189–1232 CrossRef.
- H. Nguyen, T. Vu, T. P. Vo and H. Thai, Constr. Build. Mater., 2021, 266, 120950 CrossRef.
- J. H. Friedman, Ann. Stat., 2001, 29, 1189–1232 Search PubMed.
- L. Yu, W. Zhang, Z. Nie, J. Duan and S. Chen, RSC Adv., 2024, 14, 9032 RSC.
- Y. Zhang, Z. Xu, G. Li, X. Huang, W. Hao and Y. Bi, Angew. Chem., Int. Ed., 2019, 58, 14229 CrossRef CAS PubMed.
- Y. Ji and Y. Luo, J. Am. Chem. Soc., 2016, 138, 15896–15902 CrossRef PubMed.
- Y. Zhao, Y. Zhao, R. Shi, B. Wang, G. I. N. Waterhouse, L. Wu, C. Tung and T. Zhang, Adv. Mater., 2019, 31, 1806482 CrossRef PubMed.
- A. M. Pennington, R. A. Yang, D. T. Munoz and F. E. Celik, Int. J. Hydrogen Energy, 2018, 43, 15176–15190 CrossRef.
- G. Díaz, J. Coto and J. Gómez-Aleixandre, Appl. Energy, 2019, 239, 610–625 CrossRef.
- M. A. Hassan, A. Khalil, S. Kaseb and M. A. Kassem, Appl. Energy, 2017, 203, 897–916 CrossRef.
- K. Beyer, J. Goldstein, R. Ramakrishnan and U. Shaft, When Is “Nearest Neighbor” Meaningful?, Springer, Berlin Heidelberg, 1999 Search PubMed.
- A. J. Smola and B. Schölkopf, Stat. Comput., 2004, 14, 199–222 CrossRef.
- J. L. Bernier, J. Ortega, E. Ros, I. Rojas and A. Prieto, Int. J. Neural Syst., 2003, 9, 511–521 CrossRef PubMed.
- Y. Tian, S. Xu and M. Li, Neural Networks, 2024, 179, 106567 CrossRef PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- U. Grömping, Am. Stat., 2009, 63, 308–319 CrossRef.
- X. Hao, X. Hu, T. Liu, C. Wang and L. Wang, Urban Clim., 2022, 44, 101172 CrossRef.
- L. Jinlong, H. Qiao, U. Christopher and E. D. Cosmin, Appl. Energy, 2021, 300, 117413 CrossRef.
- J. Guo, X. Zan, L. Wang, L. Lei, C. Ou and S. Bai, Eng. Fract. Mech., 2023, 293, 109714 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra04422c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |