Aromatic stabilization energies in excited states at the multiconfigurational level: assessment in archetypal organic rings

Abstract

In this study, the excited state (anti)aromaticity of archetypal rings: benzene, cyclobutadiene, and cyclooctatetraene, was investigated using the energetic criterion by calculating aromatic stabilization energies. Calculations were performed at the multiconfigurational level, including dynamic correlation effect corrections using the N-electron valence state perturbation theory (NEVPT2) method. Results were compared with previously published data based on the magnetic and delocalization criteria. Aromaticity was assessed for the ground state, singlet excited states (S₁, S₂, and S₃), and triplet excited states (T₁, T₂, T₃, and T₄). (Anti)aromaticity assignments using the energetic criterion demonstrate both agreement and discrepancies with the other criteria, particularly for higher energy electronic states demonstrating the complexity of aromaticity assignment beyond the ground state. Finally, an approximate equation is proposed for the calculation of aromatic stabilization energies in excited states using experimental data such as formation enthalpies and well-resolved absorption spectra.

---

Introduction

The modulation of (anti)aromaticity in the ground and excited states has gained much attention in recent years as it opens the door to the intelligent design of new chemical compounds. The modification of ground-state aromaticity has an impact on excited-state antiaromaticity and vice versa. Moreover, the assembly between aromatic and antiaromatic units in the ground state has a clear effect on the electronic structure, which allows to obtain antiaromatic–aromatic species in excited states that can exhibit interesting photochemical properties.^1–6

For the assignment of aromaticity, Hückel⁷ and Baird⁸ rules are the cornerstone. These rules via a simple electron (π for organic species) count determine whether a compound will be aromatic or antiaromatic. For more complex species such as polycyclic systems, we have other rules such as the Platt's perimeter⁹ model, Clar's rules^10,11 for benzenoids and the Glidewell–Lloyd rule for systems containing non-benzenoid rings.^12–14

More recently, several criteria have been developed to assign (anti)aromatic behavior and to quantify this property. These include magnetic,¹⁵ delocalization,^16,17 energetic,¹⁸ and other criteria.^19–23 The first two are the ones that have shown the greatest development and popularity owing to their effectiveness in quantification and because of the simplicity of their computation due to the development of different programs.^24–28

(Anti)aromaticity assignment in excited states is often complicated beyond the lowest energy excited states (beyond T₁ or S₁) mostly owing to the multiconfigurational character of electronic states, which requires the use of methods to account for these features, such as the complete active space self-consistent field (CASSCF) method.²⁹ Magnetic and delocalization criteria have had success since some indicators can be obtained using these multiconfigurational methods;^30–32 however, they have some disagreements concerning (anti)aromaticity assignments.^30,33

The energetic criterion is probably the oldest quantitative criterion for the study of aromaticity, dating back to 1933 when Pauling and Wheland calculated the aromatic stabilization energy for benzene.³⁴ However, in many cases, the quantification of (anti)aromaticity using this criterion can be a non-trivial exercise, and in some cases, it only allows the study of the low-lying excited state.^35,36 This is primarily due to the need to use reference reactions that avoid the occurrence of effects unrelated to aromaticity and due to the complexity of calculations that need to be performed.^{18,23,35,37–40}

Recently, the fulvenization approach⁴¹ was proposed as a simple and reliable method for the calculation of isomerization stabilization energies (ISEs) originally proposed by Schleyer in 2002.³⁷ This approach uses as reference the fulvenic isomer of the N-membered ring to be studied. It is just as simple to obtain as the original but has certain advantages. For example, it allows the calculation of systems that the original method could not calculate due to problems with the reference isomer. Additionally, the non-aromatic reference in the fulvenization (Fulv-ISE) approach is a planar conjugated system, which avoids the appearance of possible effects not related to (anti)aromaticity.

In this work, it is shown that this approach also allows assigning and quantifying the aromaticity in excited states through the use of multiconfigurational tools. For this purpose, the author quantified the (anti)aromaticity using the isomerization stabilization energies of the low-lying excited states of organic archetypes, namely, benzene, cyclobutadiene and cyclooctatetraene. The choice of multi-configurational methods over less computationally expensive techniques, such as time-dependent density functional theory (TD-DFT), stems from the limitations of the latter in accurately describing excited states. Different functionals can yield highly variable results, requiring comparison with experimental data. Moreover, the presence of ghost states in TD-DFT can lead to erroneous energy predictions. Although these ghost states can be mitigated using functionals with a high Hartree–Fock exchange component, there are instances where the predicted excitation energies still do not align closely with the experimental values.^42–44 Additionally, the main objective of this study is to quantify for the first time the (anti)aromaticity in electronic states beyond the first excited state as well as to compare the assignments delivered by this method with other (anti)aromaticity criteria in order to evaluate its performance. Therefore, it is advisable to use more robust tools when available.

Computational methods

Geometrical optimizations have been carried out using Gaussian16 (ref. 45) at the PBE0 (ref. 46)/def2-TZVP⁴⁷ level. The cases of cyclobutadiene (C₄H₄) and cyclooctatetraene (C₈H₈) were optimized at two different symmetries. D_4h and D_2h symmetries were used for the former, while geometries in D_8h and D_4h symmetries were used for the latter. For the case of benzene, the D_6h symmetry was preserved. The CASSCF calculations were then performed with the PBE0 geometries (Franck–Condon approximation) using the ORCA program.⁴⁸ The active space used corresponds to all the π-electrons and orbitals possessed by each of the systems: (6,6) for C₆H₆, (4,4) for C₄H₄, and (8,8) for C₈H₈ and for their respective fulvene isomers (for this, the rotate command was used so that the π-orbitals correspond to active space, see Fig. S1–S16 in the ESI†). State-average approach was employed (all electronic states contribute equally) and the resolution of identity approximation in conjunction with the def2-TZVP basis, which includes auxiliary functions for a reduction in the computational cost. The calculated states correspond to the fundamental S₀ and the vertical S₁, S₂, S₃, T₁, T₂, T₃, and T₄ states, which have been made separately according to their multiplicities, and the weights were assigned equally.

Energy corrections due to the inclusion of dynamic correlation effects have been made following the N-electron valence state perturbation theory (NEVPT2).⁴⁹ The calculation of the aromatic stabilization energies under the fulvenization approach are obtained from the isomerization energy when an N-atom ring converts into its fulvenic isomer. The equation for obtaining the energies is shown below

ΔE^Fulv-ISE = E^Fulv-Isomer − E^N-Ring (1)

where E^Fulv-Isomer refers to the electronic energy of the fulvenic isomer in the required electronic state and E^N-Ring is the electronic energy of the ring to be studied in its respective electronic state. A positive value means that a system exhibits aromatic behavior, negative values and values close to zero, which indicates anti-aromaticity and non-aromaticity, respectively.

Results and discussion

The results obtained through the application of the fulvenization approach have been compared with those obtained with the magnetic and delocalization criteria reported in the literature. The reference reactions used for the quantification of aromaticity using isomerization stabilization energies through the fulvenization approach of the ground state and the vertical excited states correspond to those presented in Scheme 1. Excited state energies including corrections for dynamic correlation effects (NEVPT2) offer better agreement with the available experimental/computational data^{31,32,50–52} with respect to CASSCF (see Tables S1 and S3 in the ESI†). For this reason, the quantification of (anti)aromatic (de)stabilization was calculated at this level.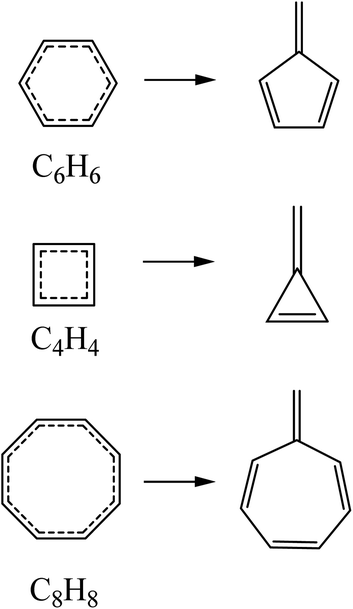

Scheme 1 Reference reactions used for the calculation of aromatic stabilization energies using the fulvenization approach.

Initially, the values of Fulv-ISE for benzene and its respective electronic states configurations can be found in Table 1. For the case of S₀, the value is similar to that reported previously, indicating an aromatic behavior, while for the case of T₁, the value is different from that reported at the DFT level;⁴¹ however, since it is a negative value, it is consistent with the antiaromatic character. For the case of S₁, the values reported by Karadakov et al.³³ and Feixas et al.³⁰ using the magnetic and delocalization criteria respectively indicate antiaromaticity; however, the value obtained under the fulvenization approach is −5.2 kcal mol⁻¹, suggesting a slightly antiaromatic or even non-aromatic behaviour. In the original article where the fulvenization approach was proposed, calculations of non-aromatic systems were not performed; however, in this work, it is shown that the aromatic stabilization energies obtained under this approach present values of −3.4 and −0.4 kcal mol⁻¹ for cyclohexene and cyclohexadiene, respectively (see Fig. S17 in ESI†), thus providing a small range (−4.7 to 0.0 kcal mol⁻¹) for the recognition of non-aromatic compounds at the DFT level.

Table 1 Aromatic stabilization energies under the fulvenization approach (in kcal mol⁻¹) and electronic state occupations for benzene at the NEVPT2/def2-TZVP//PBE0/def2-TZVP level

C6H6 (D6h)
State	Configuration	Fulv-ISE
S0	π^21π^22π^23π^04π^05π^06	34.5
S1	π^21π^12π^23π^14π^05π^06	−5.2
	π^21π^22π^13π^04π^15π^06
S2	π^21π^22π^13π^14π^05π^06	35.5
	π^21π^12π^23π^04π^15π^06
S3	π^11π^22π^23π^14π^05π^06	−22.4
	π^21π^22π^03π^24π^05π^06
	π^21π^22π^13π^04π^05π^16
	π^21π^02π^23π^24π^05π^06
T1	π^21π^22π^13π^14π^05π^06	−8.5
	π^21π^12π^23π^04π^15π^06
	π^11π^22π^23π^04π^05π^16
T2	π^21π^12π^23π^04π^15π^06	−5.5
	π^21π^22π^13π^14π^05π^06
	π^11π^12π^23π^14π^15π^06
T3	π^21π^22π^13π^04π^15π^06	51.2
	π^21π^12π^23π^14π^05π^06
T4	π^21π^12π^23π^14π^05π^06	62.5
	π^21π^22π^13π^04π^15π^06

---

Regarding S₂, the magnetic criteria indicates that in this state, benzene is aromatic, while the delocalization criterion indicates antiaromaticity. Using Fulv-ISE, a value of 35.5 kcal mol⁻¹ is obtained; thus, this electronic state would present an aromatic behavior in agreement with the magnetic criterion. It is necessary to mention that the delocalization criterion indicates that S₂ and S₃ are antiaromatic because the CASSCF calculations reported by Feixas et al.³⁰ indicate that both states are degenerate; however, the calculations obtained in this work at the CASSCF level show a difference of 0.2 eV between S₂ and S₃, which becomes even more noticeable when the dynamic correlation effects are included (1.7 eV). In the case of S₃, a value of −22.4 kcal mol⁻¹ is obtained; thus, it would be an antiaromatic state. This assignment is in agreement with Feixas et al. under the delocalization criteria while for the magnetic criterion, no values have been reported. The electronic delocalization indices also indicate that the T₂, T₃ and T₄ states are antiaromatic.

Special attention must be paid to the case of T₂ and T₃, which are degenerate states with excitation energies of 5.1 eV at the NEVPT2 level. The fulvenization approach indicates that despite this degeneracy, the assignments are antiaromatic/non-aromatic for the case of S₂ and aromatic for the case of S₃ (see Table 1). These differences can be attributed to the non-degenerate electronic states of the reference fulvene; thus, it is possible that under this criterion, one has different (anti)aromaticity assignments, which could result in a limitation of the method in highly symmetric systems. The same pattern will be observed later for the case of cyclooctatetraene. For the case of T₄, the value obtained is 62.4 kcal mol⁻¹, which indicates an aromatic behavior; however, due to the results and the possible degeneracies between the electronic states, it is recommended that for the assignment of (anti)aromaticity of N electronic states, at least N + 1 states should be calculated.

The Fulv-ISE values for the S₀ and T₁ states of C₄H₄ reported in Table 2 are in agreement with the Hückel and Baird rules; on the other hand, the singlet excited states in all cases indicate aromaticity for both D_4h and D_2h symmetry. Some discrepancies are observed when compared with the magnetic and delocalization criteria. The states S₁, S₂ and S₃ present aromatic behavior according to Fulv-ISE; however, Karadakov et al.³³ indicated aromaticity for S₁ and antiaromaticity for S₂ (they do not report values for S₃). On the other hand, the study by Feixas et al.³⁰ indicates that there is antiaromaticity for S₁ and S₃ and aromaticity for S₂.

Table 2 Aromatic stabilization energies under the fulvenization approach (in kcal mol⁻¹) and electronic state occupations for cyclobutadiene at the NEVPT2/def2-TZVP//PBE0/def2-TZVP level

C4H4
D4h			D2h
State	Fulv-ISE	Configuration	State	Fulv-ISE	Configuration
S0	−30.7	π^21π^12π^13π^04	S0	−14.1	π^21π^22π^03π^04
S1	49.8	π^21π^22π^03π^04	S1	29.1	π^21π^12π^13π^04
		π^21π^02π^23π^04
S2	98.8	π^21π^02π^23π^04	S2	47.7	π^21π^02π^23π^04
		π^21π^22π^03π^04
S3	38.2	π^21π^12π^03π^14	S3	54.3	π^21π^12π^03π^14
		π^11π^12π^23π^04			π^11π^22π^13π^04
T1	50.7	π^21π^12π^13π^04	T1	31.7	π^21π^12π^13π^04
T2	−22.8	π^21π^12π^03π^14	T2	−17.3	π^21π^12π^03π^14
		π^11π^12π^23π^04			π^11π^12π^23π^04
T3	8.0	π^11π^22π^13π^04	T3	−17.3	π^21π^02π^13π^14
		π^21π^02π^13π^14			π^11π^12π^23π^04
T4	18.6	π^21π^02π^13π^14	T4	16.1	π^11π^22π^13π^04
		π^11π^22π^13π^04			π^21π^12π^03π^14

---

For the case of triplet excited states, the Fulv-ISE values and delocalization indices coincide in an antiaromatic assignment for T₂. For the case of T₃ and T₄, the delocalization criterion indicates antiaromaticity, while the energy criterion applied in this work indicates aromaticity. However, when switching from D_4h to D_2h symmetry, curiously, the T₃ state becomes antiaromatic, coinciding with the delocalization criterion whose values were obtained at this symmetry. This switch from aromaticity to antiaromaticity in T₃ is due to different electronic transitions. However, due to the inclusion of dynamic correlation effects, the occupancies of the states obtained in this work with respect to the one performed by Feixas et al. are different, which may explain the differences with respect to the aromaticity assignment.

The case of C₈H₈ is less controversial since the D_8h symmetry coincides perfectly with the magnetic criterion. The S₀ state is antiaromatic while the T₁, S₁ and S₂ states are aromatic; indeed, Karadakov et al.⁵³ report that S₂ is much more aromatic than T₁ and S₁ and the Fulv-ISE value for S₂ is much higher when compared to the other two electronic states with D_8h symmetry. The delocalization criterion indicates that S₁ as well as T₂ and T₃ are antiaromatic (no values are reported for T₄ in Karadakov et al.'s work). The results with Fulv-ISE agree with the assignment given for T₂ and T₃; however, for the case of T₃, the value for D_8h symmetry is close to zero; therefore, in this symmetry, it could be considered non-aromatic, but if we reduce the symmetry to D_4h, the value becomes more negative. The opposite case is presented in T₁ wherein on reducing the symmetry to D_4h, the value obtained indicates a non-aromatic behavior. T₄ is an electronic state that presents antiaromaticity, becoming even more antiaromatic when going from D_8h to D_4h symmetry (Table 3).

Table 3 Aromatic stabilization energies under the fulvenization approach (in kcal mol⁻¹) and electronic state occupations for cyclooctatetraene at the NEVPT2/def2-TZVP//PBE0/def2-TZVP level

C8H8
D8h			D4h
State	Fulv-ISE	Configuration	State	Fulv-ISE	Configuration
S0	−31.5	π^21π^22π^23π^14π^15π^06π^07π^08	S0	−23.3	π^21π^22π^23π^24π^05π^06π^07π^08
S1	24.5	π^21π^22π^23π^24π^05π^06π^07π^08	S1	11.4	π^21π^22π^23π^04π^25π^06π^07π^08
		π^21π^22π^23π^04π^25π^06π^07π^08			π^21π^22π^23π^24π^05π^06π^07π^08
S2	66.5	π^21π^22π^23π^04π^25π^06π^07π^08	S2	30.7	π^21π^22π^23π^14π^15π^06π^07π^08
		π^21π^22π^23π^24π^05π^06π^07π^08
S3	−3.8	π^21π^22π^13π^24π^15π^06π^07π^08	S3	−15.8	π^21π^22π^13π^24π^15π^06π^07π^08
		π^21π^12π^23π^14π^25π^06π^07π^08			π^21π^12π^23π^14π^25π^06π^07π^08
		π^21π^22π^23π^04π^15π^06π^17π^08			π^21π^22π^23π^14π^05π^16π^07π^08
		π^21π^22π^23π^14π^05π^16π^07π^08			π^21π^22π^23π^04π^15π^06π^17π^08
T1	13.6	π^21π^22π^23π^14π^15π^06π^07π^08	T1	−0.3	π^21π^22π^23π^14π^15π^06π^07π^08
T2	−43.6	π^21π^12π^23π^24π^15π^06π^07π^08	T2	−45.8	π^21π^22π^13π^24π^15π^06π^07π^08
		π^21π^22π^13π^14π^25π^06π^07π^08
		π^21π^22π^23π^04π^15π^06π^17π^08			π^21π^22π^23π^14π^05π^16π^07π^08
		π^21π^22π^23π^14π^05π^16π^07π^08
T3	−0.9	π^21π^22π^13π^24π^15π^06π^07π^08	T3	−3.1	π^21π^12π^23π^24π^15π^06π^07π^08
		π^21π^12π^23π^14π^25π^06π^07π^08
		π^21π^22π^23π^04π^15π^16π^07π^08			π^21π^22π^23π^14π^05π^06π^17π^08
		π^21π^22π^23π^14π^05π^06π^17π^08
T4	−2.6	π^21π^22π^13π^14π^25π^06π^07π^08	T4	−28.4	π^21π^22π^13π^14π^25π^06π^07π^08
		π^21π^12π^23π^24π^15π^06π^07π^08
		π^21π^22π^23π^14π^05π^16π^07π^08			π^21π^22π^23π^04π^15π^16π^07π^08
		π^21π^22π^23π^04π^15π^06π^17π^08

---

A relationship between the aromatic stabilization energies derived from the fulvenization approach and experimental data is proposed. Initially, it was suggested that the aromatic stabilization energy in the ground state could be estimated using experimental enthalpies of formation. For benzene in its ground state, this approach yields a value of 33.7 kcal mol⁻¹, which is in excellent agreement with the energy calculated at the PBE0/def2-TZVP level (33.2 kcal mol⁻¹). Consequently, eqn (1) can be approximated as follows.

ΔE^Fulv-ISE ≈ ΔH^Fulv-isomer_f − ΔH^N-ring_f (2)

Additionally, the energies of the excited electronic states can be obtained from

E_state = E₀ + ΔE_exc (3)

where E₀ is the ground state energy and ΔE_exc refers to the excitation energy. The aromatic stabilization energy in the excited states under the fulvenization approach can be approximated as follows.

ΔE^Fulv-ISE_exc ≈ (ΔH^Fulv-isomer_f − ΔH^N-ring_f) + (ΔE^Fulv-isomer_exc − ΔE^N-isomer_exc) (4)

where the excitation energies could be taken from the well-resolved absorption spectra of the ring to be studied and its respective fulvenic isomer. As an example, we will calculate the ΔE^Fulv-ISE values for benzene. The enthalpies of formation were obtained from the NIST database, while the excitation energies for both benzene and fulvene were sourced from a literature review of well-resolved spectra.^{50,51,54–56} These experimental energies, along with the results obtained using eqn (4), are summarized in Table 4. As shown, the experimental data follow the same trends as the calculations, although there are differences in the absolute values. These discrepancies can be attributed to several factors, including experimental conditions and instrument resolution. This demonstrates that estimating (anti)aromaticity in excited states using experimental data is feasible, but it should be approached with caution. Ideally, such experiments should be performed under same conditions to minimize potential variations.

Table 4 Experimental enthalpies of formation (ΔH_f) and excited state energies (in kcal mol⁻¹) for benzene and fulvene

Compound	ΔHf	S1	S2	T1	T2
Benzene	19.8	119.9	143.0	92.2	110.7
Fulvene	53.5	79.3	121.8	54.2	71.5
Eqn (4)	33.7	−6.9	12.5	−4.3	−5.5

---

Conclusions

The capacity of the recently proposed fulvenization approach for calculating the aromatic stabilization energies (Fulv-ISE) and assigning (anti)aromaticity in vertical excited states has been tested using three archetypal rings, namely, benzene, cyclobutadiene and cyclooctatetraene. The calculated energies were obtained through multiconfigurational calculations including dynamic correlation effect corrections (NEVPT2). In all cases, there are agreements and differences with the magnetic and delocalization states, the latter especially in the case of higher energy electronic states due to the inclusion of dynamic correction effects and the occupancies of the electronic states being different. Additionally, this work once again shows the complexity of aromaticity assignment when going beyond the ground state.

Results indicate that benzene shows aromaticity in the S₀, S₂, T₃ and T₄ vertical states, while the other computed states show antiaromatic behavior. Regarding the degenerate states T₂ and T₃, different assignments are given since fulvene does not show degeneracy in these states, resulting in a limitation of the method due to the use of reference isomers. Additionally, it is recommended that if the N electronic states are to be analyzed, at least N + 1 states should be calculated to confirm that the states do not exhibit degeneracy.

In the case of cyclobutadiene, all the calculated states present aromaticity with the exception of S₀ and T₂; however, the T₃ state, which presents aromaticity in D_4h symmetry, becomes antiaromatic in D_2h symmetry. Cyclooctatetraene, on the other hand, presents an aromatic character only in the S₁ and S₂ states, in agreement with the magnetic criterion, while the rest of the results at D_8h symmetry present antiaromaticity. In addition, it is shown that the aromatic stabilization energies under this approach can be obtained from the experimental data such as formation enthalpies and absorption peaks in well-resolved absorption spectra.

These results extend the capability of the energy criterion for aromaticity assignment beyond the first excited states. In addition, the aromatic stabilization energies for higher energy electronic states can be calculated in a straightforward manner.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author thanks the financial support of the National Agency for Research and Development (ANID) through FONDECYT Project 1230571.

References

1. H. Ottosson, Nat. Chem., 2012, 4(12), 969–971.
2. M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114(10), 5379–5425.
3. W. Zeng, D. W. Szczepanik and H. Bronstein, J. Phys. Org. Chem., 2023, 36(1), e4441.
4. J. Kim, J. Oh, A. Osuka and D. Kim, Chem. Soc. Rev., 2022, 51(1), 268–292.
5. J. Yan, T. Slanina, J. Bergman and H. Ottosson, Chem.–Eur. J., 2023, 29(19), e202203748.
6. D. Dunlop, L. Ludvíková, A. Banerjee, H. Ottosson and T. Slanina, J. Am. Chem. Soc., 2023, 145(39), 21569–21575.
7. E. Hückel, Z. Phys., 1931, 70(3), 204–286.
8. N. C. Baird, J. Am. Chem. Soc., 1972, 94(14), 4941–4948.
9. J. R. Platt, J. Chem. Phys., 1949, 17(5), 484–495.
10. E. Clar, The Aromatic Sextet, J. Wiley, 1972.
11. M. Solà, Front. Chem., 2013, 1, 1–8.
12. C. Glidewell and D. Lloyd, Tetrahedron, 1984, 40(21), 4455–4472.
13. R. Pino-Rios and M. Solà, J. Phys. Chem. A, 2021, 125(1), 230–234.
14. R. Báez-Grez and R. Pino-Rios, Phys. Chem. Chem. Phys., 2024, 12162–12167.
15. R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44(18), 6597–6615.
16. F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44(18), 6434–6451.
17. I. Casademont-Reig, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, in Aromaticity, ed. I. Fernandez, Elsevier, 2021, pp. 235–259.
18. M. Alonso and I. Fernández, in Aromaticity, ed. I. Fernandez, Elsevier, 2021, pp. 195–235.
19. H. Szatylowicz, P. A. Wieczorkiewicz and T. M. Krygowski, in Aromaticity, ed. I. Fernandez, Elsevier, 2021, pp. 71–99.
20. D. R. Roy and P. K. Chattaraj, in Aromaticity, ed. I. Fernandez, Elsevier, 2021, pp. 285–319.
21. D. Yu, T. Stuyver, C. Rong, M. Alonso, T. Lu, F. De Proft, P. Geerlings and S. Liu, Phys. Chem. Chem. Phys., 2019, 21(33), 18195–18210.
22. R. Báez-Grez and R. Pino-Rios, ACS Omega, 2022, 7(25), 21939–21945.
23. H. Szatylowicz, P. A. Wieczorkiewicz and T. M. Krygowski, Sci, 2022, 1–22.
24. T. Lu and F. Chen, J. Comput. Chem., 2012, 33(5), 580–592.
25. T. A. Keith, AIMAll (Version 190213), Overland Park KS, USA, 2019, https://aim.tkgristmill.com.
26. D. Inostroza, V. García, O. Yañez, J. J. Torres-Vega, A. Vásquez-Espinal, R. Pino-Rios, R. Báez-Grez and W. Tiznado, New J. Chem., 2021, 45(18), 8345–8351.
27. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, Cinvestav-Mérida, Mérida, Mexico, 2016.
28. E. Matito, ESI-3D: Electron Sharing Indices Program for 3D Molecular Space Partitioning, Institute of Computational Chemistry and Catalysis (IQCC), University of Girona, 2006.
29. J. W. Park, R. Al-Saadon, M. K. MacLeod, T. Shiozaki and B. Vlaisavljevich, Chem. Rev., 2020, 120(13), 5878–5909.
30. F. Feixas, J. Vandenbussche, P. Bultinck, E. Matito and M. Solà, Phys. Chem. Chem. Phys., 2011, 13(46), 20690–20703.
31. P. B. Karadakov, J. Phys. Chem. A, 2008, 112(31), 7303–7309.
32. P. B. Karadakov, J. Phys. Chem. A, 2008, 112(49), 12707–12713.
33. P. B. Karadakov, P. Hearnshaw and K. E. Horner, J. Org. Chem., 2016, 81(22), 11346–11352.
34. L. Pauling and G. W. Wheland, J. Chem. Phys., 1933, 1(6), 362–374.
35. Y. Mo and P. v. R. Schleyer, Chem.–Eur. J., 2006, 12(7), 2009–2020.
36. I. Fernández and G. Frenking, Faraday Discuss., 2007, 135(0), 403–421.
37. P. v. R. Schleyer and F. Pühlhofer, Org. Lett., 2002, 4(17), 2873–2876.
38. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101(5), 1385–1420.
39. Y. García-Rodeja and M. Solà, in Exploring Chemical Concepts through Theory and Computation, 2024, pp. 223–250.
40. A. R. Katritzky, K. Jug and D. C. Oniciu, Chem. Rev., 2001, 101(5), 1421–1450.
41. L. Leyva-Parra and R. Pino-Rios, ACS Omega, 2024, 9(1), 1436–1442.
42. F. Furche and D. Rappoport, in Theoretical and Computational Chemistry, ed. M. Olivucci, Elsevier, 2005, pp. 93–128.
43. C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42(3), 845–856.
44. M. Campetella, F. Maschietto, M. J. Frisch, G. Scalmani, I. Ciofini and C. Adamo, J. Comput. Chem., 2017, 38(25), 2151–2156.
45. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.02, Gaussian, Inc., Wallingford, CT, 2016.
46. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110(13), 6158–6170.
47. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
48. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152(22), 224108.
49. C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350(3), 297–305.
50. E. N. Lassettre, A. Skerbele, M. A. Dillon and K. J. Ross, J. Chem. Phys., 1968, 48(11), 5066–5096.
51. J. P. Doering, J. Chem. Phys., 1969, 51(7), 2866–2870.
52. M. H. Palmer, S. V. Hoffmann, N. C. Jones, M. Coreno, M. de Simone and C. Grazioli, J. Chem. Phys., 2019, 151(8), 084304.
53. P. B. Karadakov and N. Preston, Phys. Chem. Chem. Phys., 2021, 23(43), 24750–24756.
54. R. D. Brown, P. J. Domaille and J. E. Kent, Aust. J. Chem., 1970, 23(9), 1707–1720.
55. F. Negri and M. Z. Zgierski, J. Chem. Phys., 1995, 102(13), 5165–5173.
56. K. R. Asmis, M. Allan, O. Schafer and M. Fülscher, J. Phys. Chem. A, 1997, 101(11), 2089–2095.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05147e

---