Anisotropic half-metallicity in zigzag edge SiP₃ nanoribbons

Abstract

We investigate magnetic and spin-transport properties of the zigzag-edge nanoribbon structures of two-dimensional (2D) SiP₃ system within first-principle calculations. Based on the edge terminations, the nanoribbons can be categorized in three subclasses, two of them with even number of silicon (Si) atoms and one of them with odd number of Si atoms in the one-dimensional unitcell with antiferromagnetic bulk spin-ordering, analogous to their 2D counterpart. All the ribbons exhibit indirect band-gap semiconducting behavior and the gap decreases with increase in width of the ribbons. The nanoribbon with only phosphorus (P) atoms at least along one of the edges show half-metallic behavior over a small bias window, when probed with cross-ribbon external electric field. Especially, the nanoribbon with odd number of Si atoms stabilizes in a ground state with net non-zero magnetization and exhibits half-metallicity only under forward bias. Such anisotropic half-metallicity along with the precise control of the electronic properties in terms of edge and external bias manipulation hold immense potential for spintronic and switching device applications.

---

Introduction

Magnetic ordering in two-dimensional (2D) systems has been of sustained interest from both fundamental and application perspective.^1–3 Recently the 2D van der Waals systems, e.g., transition metal trichalcogenides and trihalides have been reported to host magnetic ordering.^4–9 The uniaxial magnetic anisotropy opens up a spin-wave gap that supports the spin ordering at non-zero temperature.² However, such magnetic ordering has been mostly elusive in 2D materials made of p-block elements.¹⁰ The most widely studied 2D material, graphene does not support any localized spin moment unless introduced with defects, such as vacancy, grain boundary and edges.^11–13

Finite termination of 2D graphene along the zigzag crystallographic direction results in quasi-one-dimensional nanoribbon (NR) structures that exhibit distinct electronic properties due to the quantum confinement and edge effects.^14–23 In graphene zigzag NRs, the spin arrangement of edge geometries follows Lieb's theorem, which states that two sub-lattice points in a bipartite lattice tend to align their electronic spins in an antiferromagnetic manner.²⁴ Along one zigzag edge, the atoms belong to the same sub-lattice, leading to ferromagnetic coupling along that edge. Conversely, the atoms along the other edge are also ferromagnetically coupled, but with opposite spins.¹⁸ These magnetic edges play a significant role in shaping the band structures of NRs.¹⁹ The localized spin moments along the edges lead to a splitting of the partial flat band at the Fermi energy as obtained in non-magnetic ground state and eliminate the Fermi instability arising from the diverging density of states (DOS) by opening up a band gap.¹⁹ This has been confirmed experimentally through scanning tunnelling spectroscopy measurements.²⁵ Due to such magnetic ground state, zigzag graphene NRs exhibit half-metallic behavior in presence of in-plane cross-ribbon electric field, resulting in totally spin polarized current for electrons with one spin orientation and an insulating or semiconducting band gap for the opposite spin.²⁶

Such intriguing property with potential spintronics applications has motivated us to investigate the zigzag edge NRs of recently reported monolayer of SiP₃, a Si substituted blue phosphorene, that hosts the domain fragmented antiferromagnetic (AFM) spin-ordering in 2D.²⁷ Monolayer SiP₃ is a 8 atoms unit cell that consists of Si and P atoms (see Fig. 1a). Each phosphorous hexagon in the unit cell is uniformly encircled by six Si atoms. The spin density of SiP₃ (see Fig. 1b) shows each Si atom's local magnetic moment is ferromagnetically coupled with the three neighbouring P atoms. The phosphorous hexagons, on the other hand, exhibit fully bipartite nature, that is, opposite spin alignments between nearest P neighbours, which results into an overall AFM ground state of SiP₃. The AFM ground state emerges as a consequence of the Fermi instability in the non-magnetic ground state.^28–31 Here we explore the interplay of such bulk magnetization with the localized zigzag edge states and the influence of in-plane cross-ribbon electric field in the NR structures of SiP₃.

Fig. 1 (a) Top and side views of lattice structure of 2D SiP₃. Small shaded hexagon denotes the P hexagon which is surrounded by six Si atoms, shown by the bigger shaded hexagon. The dotted rhombus depicts the unit cell. (b) Schematic representation of spin density of 2D SiP₃. The spin-up and spin-down density are shown by red and green colored circles, respectively. Radius of the circles is proportional to the magnitude of the spin density. (c) The phonon dispersion of 2D SiP₃ in the first Brillouin zone. (d) The electronic band structure and DOS of 2D SiP₃ in antiferromagnetic ground state. The horizontal and vertical dotted lines represent the Fermi energy and the high-symmetric points, shown in the hexagonal first Brillouin zone (inset), respectively. The atomic orbitals projected DOS are depicted with different colors.

In this study, using density functional theory, we investigate the electronic, magnetic and transport properties of zigzag edge NRs of 2D SiP₃, termed as SiP₃-ZNR. We define three types of SiP₃-ZNRs based on distinct combinations of edge atoms i.e., Si and P. A single edge can be constructed either by taking two P atoms (PP-edge) or by considering one Si and one P atom (SiP or PSi-edge). Identical edges in either side of the NRs stabilize the ground state with AFM spin-ordering, whereas two different edge types in a NR give rise to net non-zero magnetization. This variation in magnetic ground states is attributed to the odd number of Si atoms in the unit cell of the NRs. Moreover, the NRs with at least one PP-edge exhibit half-metallicity within a window of cross-ribbon electric field strength. However, the NRs with one PP and one SiP-edge show anisotropic half-metallicity only under the forward bias. At larger bias all the NRs turn metallic. Such edge and bias dependent broad range of electronic properties can have significant and diverse spintronics applications.

Computational details

We calculate the structural and electronic properties of all NRs, using density functional theory (DFT) as implemented in the Spanish Initiative for Electronic Simulations with Thousands of Atoms (SIESTA) computational package.³² The total energy-convergence requirement is set at 10⁻⁵ eV and a double-ζ polarized basis set with a 400 Ry energy cutoff is employed. We investigate norm conserving pseudopotentials in the fully nonlocal Kleinman–Bylander scheme to handle electron-ion interactions.³³ For all the spin-polarized calculations, we use the Perdew–Burke–Ernzerhof exchange and correlation functional within a generalized gradient approximation.³⁴ The lattice parameters along with the atomic positions are relaxed within conjugate-gradient method, until the force on each atom becomes less than 0.01 eV Å⁻¹. We use a 9 × 1 × 1 Monkhorst–Pack³⁵ k-grid for geometrical optimization and a 90 × 1 × 1 grid for electronic calculations of SiP₃-ZNRs. A vacuum separation of 15 Å is considered to prevent any interactions between neighbouring unitcells. We further model the external electric field as ramp potential applied along the cross-ribbon direction.

Results and discussions

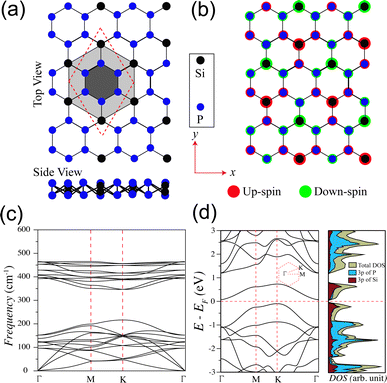
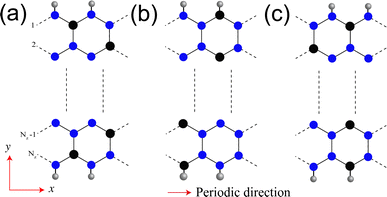
We start our discussion with structural, magnetic and electronic properties of 2D monolayer SiP₃. Fig. 1a shows the structure of SiP₃, where P hexagons (smaller shaded hexagon) are symmetrically surrounded by six Si atoms (bigger shaded hexagon) to form a 8 atom unit cell. We find relaxed lattice constant of monolayer SiP₃ is 6.296 Å. Note that the SiP₃ system is a buckled structure, as can be seen from the side view. Since the ground state of monolayer SiP₃ is AFM, we illustrate the spin density distribution in Fig. 1b. It shows each Si atom's local magnetic moment is ferromagnetically coupled to the three neighboring P atoms. However, the P hexagons preserve a fully bipartite character with opposing spin alignments between nearest P neighbors. The average spin moments on P and Si atoms are found to be 0.041μ_B and 0.389μ_B, respectively.²⁷ Next, we have checked the dynamical stability of 2D SiP₃ via phonon calculations and plotted the phonon dispersion in Fig. 1c. The absence of any imaginary frequencies in the phonon spectra confirms the stability of 2D SiP₃. We calculate the degenerate up and down-spin electronic band structures and DOS of SiP₃ and present them in Fig. 1d. Two less dispersive bands near the Fermi energy lead to an indirect band gap of 0.17 eV. Additionally, investigation of the projected DOS originating from the 3p orbitals of both P and Si atoms reveals a hybridized nature of these frontier bands.²⁷

Next, we create the SiP₃-ZNRs by finite termination along the zigzag crystallographic direction of 2D SiP₃. The fabrication of these NRs can experimentally be achieved by mechanically cutting the 2D sheet by lithographic patterning or by electrode patterning on 2D material by photo-lithography or laser-induced materials deposition (LIMD) techniques.^36–41 Depending on edge termination of NRs, we can generate three different classes of zigzag edge combinations: (i) P atoms along both the edges (PP–PP), (ii) alternating P and Si atoms along both the edges (PSi–SiP), and (iii) P atoms along one edge and alternating P and Si atoms along the other edge (PP–PSi), as shown in Fig. 2a–c, respectively. Similar types of edge geometries have been reported in case of BC₃ system as well.⁴² The number of zigzag lines (N_z) along the cross-ribbon direction determines the ribbons' overall width. All the zigzag ribbons are represented by N_z-PP–PP, N_z-PSi–SiP and N_z-PP–PSi. Note that, in case of both PP–PP and PSi–SiP edge SiP₃-ZNRs, the N_z is even, while it is odd for the PP–PSi NRs. We vary the widths as N_z = 6, 8, 10, and 12 in case of PP–PP and PSi–SiP edges and N_z = 7, 9, and 11 in case of PP–PSi edge. To saturate the dangling bonds, all the NRs are passivated with hydrogen (H) atoms. The lattice constants of all quasi-one-dimensional PP–PP, PSi–SiP and PP–PSi edge NRs of different widths show almost identical value of ∼6.92 Å. The Si–P and P–P bond lengths along the edges remain unaltered as compared to the bulk.

Fig. 2 The unit cells of three types of zigzag edge SiP₃ NRs terminated with (a) PP–PP, (b) PSi–SiP and (c) PP–PSi edges. The edge atoms are passivated by hydrogen atoms (white color balls). The number of zigzag chains, i.e., N_z determines the width of the NRs along the y-direction. The periodicity is considered along the x-direction.

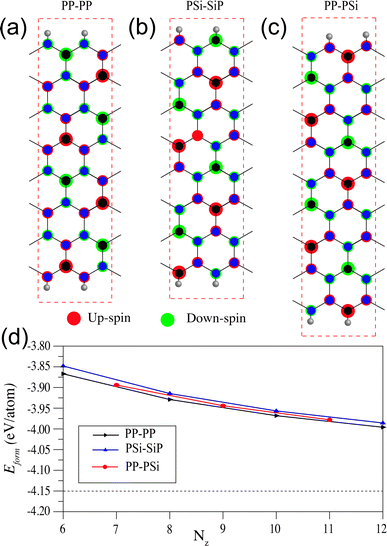
We calculate the spin density of all the NRs in order to analyze their magnetic ground state and present them in Fig. 3. The spin orderings of the NRs are identical to the 2D SiP₃.²⁷ The edge spin moments are negligible different as compared to the bulk spin moments, which is in stark contrast with that of graphene nanoribbons which shows predominantly edge spin localization. Two Si atoms in the unit cell of 2D SiP₃ localize up and down spin moments, giving rise to net zero magnetic moment. Firstly, in the case of PP–PP edge, the ground state is AFM irrespective of their width (N_z = 6, 8, 10 and 12). Total spin moment remains zero, owing to even number of Si atoms in the unit cell. In Fig. 3a, we show the unit cell along with the spin density of N_z = 8. As can be seen, there is four Si atoms with up-spin moment (red circles) and four Si atoms with down-spin moments (green circles). All the phosphorus atoms preserve bipartite nature, resulting in AFM ground state for the PP–PP edge SiP₃-ZNRs. Note that, each edge of the PP–PP edge NRs localizes either up or down-spin. Similarly, in the case of PSi–SiP edge SiP₃-ZNRs, the ground state stabilizes in AFM state for all widths, owing to the even number of Si atoms in the unit cell, as can be seen in Fig. 3b for N_z = 8. However, unlike the previous system, the PSi–SiP edge NRs show alternating up and down-spin localization along the same edge. On the contrary, the PP–PSi edge SiP₃-ZNRs contain odd number of Si atoms in their unit cell, creating imbalance between up and down-spins and consequently stabilize in a ferromagnetic ground state. In Fig. 3c, we show the unit cell and spin density of the NR with N_z = 9. This class of zigzag edge NRs show 1μ_B magnetic moment per unit cell, irrespective of their width. Particularly, one edge of PP–PSi NRs contains all P atoms with parallel spin alignment, whereas the other edge shows alternating up and down-spin localization, owing to alternating Si and P atoms along the edge. This observation remains consistent for all the NRs with odd N_z.

Fig. 3 Spin density plot of (a) 8-PP–PP, (b) 8-PSi–SiP, (c) 9-PP–PSi edge SiP₃-ZNRs. The dotted rectangular boxes show the unit cell of corresponding system. The spin-up and spin-down density are shown by red and green colored circles, respectively. Radius of the circles is proportional to the magnitude of the spin density. (d) The formation energy scaled with respect to the number of atoms in the unit cell of all the three types of ribbons in their respective magnetic ground states. The dashed horizontal line shows the scaled formation energy of 2D SiP₃.

To investigate the stability, then we calculate the formation energy of all the NRs, scaled with respect to the total number of atoms in the unit cell, using the following formula: 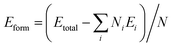, where E_total is the total energy of the ribbon, E_i and N_i are the energy and number of i-th element and N is the total number of atoms within the unit cell. The formation energies as a function of varying width of all different types of NRs are shown in Fig. 3d. Note that, higher negative energy emphasizes higher stability. The NRs show less stability as compared to the 2D SiP₃ which shows formation energy of −4.15 eV per atom. The stability of the ribbons enhances with increasing width and approaches towards the 2D limit, as shown by the dashed horizontal line. The stability of different classes of zigzag NRs increases in the order: PSi–SiP < PP–PSi < PP–PP, although the differences are quite small. This shows that the NRs terminated with P atoms are more stable as compared to the Si atoms.

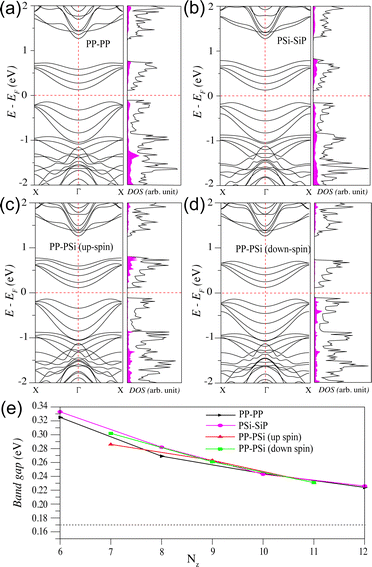
We further calculate the electronic band structures of all the SiP₃-ZNRs and present them in Fig. 4. In case of the PP–PP edge NR with N_z = 8, the AFM ground state results in degenerate up and down-spin electronic dispersions with a narrow indirect band gap (see Fig. 4a). The PSi–SiP edge NR of same width also exhibits degenerate up and down-spin bands, owing to the AFM ground state, with a narrow indirect band gap (see Fig. 4b). For both these classes of NRs the bands near the Fermi energy show small contribution from the edge atoms and predominant contribution from the bulk atoms, as reflected from their respective projected DOS plots. However, the PP–PSi edge NRs show non-degenerate up and down-spin bands, owing to its ferromagnetic ground state. We plot the spin-polarized electronic band structures of 9-PP–PSi in Fig. 4c and d, for the up and down-spins, respectively. As can be seen, irrespective of their distinct band dispersions, the up and down-spin band gaps show very small difference. In this case also the bands near the Fermi energy arise majorly from the bulk atoms. Notably, the edge contribution near the Fermi energy appears in the conduction bands of the up-spins and valence bands of the down-spins. This indicates the possibility of up-spin hole and down-spin electron mobility along the edges.

Fig. 4 Degenerate up and down-spin band structures and DOS of (a) 8-PP–PP edge and (b) 8-PSi–SiP edge SiP₃-ZNRs. The non-degenerate (c) up-spin and (d) down-spin band structures of 9-PP–PSi edge SiP₃-ZNR. The shaded regions in the DOS plots show the projected DOS from the edge atoms. The horizontal dashed lines in each plot represent the Fermi energy. (e) The variation of band gap for different edge geometries of the SiP₃-ZNRs as a function of their width, i.e., N_z. The dashed horizontal black line represents the band gap of 2D SiP₃.

Next, we investigate the variation of the band gap with the change of the width of all the three classes of the zigzag edge NRs and present the same in Fig. 4e. As can be seen, the band gap for all the ribbons decreases with the increase in width and approaches towards the bulk band gap, as shown by the dashed horizontal line. In case of ferromagnetic PP–PSi edge NRs of narrow width (N_z = 7), the up and down-spin gaps are different. However, they tend to merge together with gradual increase in width. Since, the zigzag NRs of all possible edge terminations exhibit narrow band gap, they can be considered for transport channels under the application of external electric field.

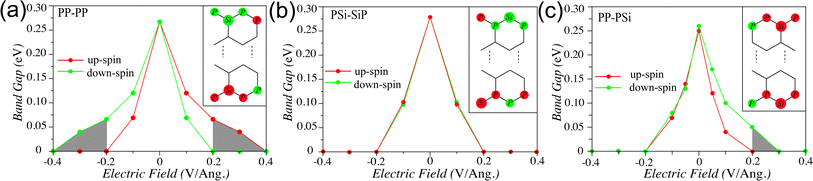
That is why, we further explore their electronic transport properties under the external electric field along the cross-ribbon direction, modelled as transverse ramp potential. We vary the electric field from −0.4 V Å⁻¹ to 0.4 V Å⁻¹ in the interval of 0.1 V Å⁻¹. First we explore the effect of an applied electric field on the spin polarized band gap of 8-PP–PP edge NR and present the results in Fig. 5a. As can be seen, at zero applied field, the up and down-spins show identical band gap due to their degenerate band structure. The increase of electric field not only reduces the band gap but also breaks their spin degeneracy. Along the +ve bias direction the down-spin band gap decreases more rapidly than that of the up-spin. Beyond 0.2 V Å⁻¹, the down-spin gap completely closes while the up-spin gap remains open, resulting in only conducting down-spin channel. Therefore, at this critical electric field strength, the PP–PP edge NR show half-metallic behavior. On the contrary, this NR show half-metallic behavior with conducting up-spin channel when the applied field direction is reversed, i.e., at −0.2 V Å⁻¹. However, further increase in field strength makes both the up and down-spin channels conducting. Therefore, the half-metallicity can be achieved over a small bias window that is conducive within the experimental set-up.

Fig. 5 The variation of up- and down-spin band gaps as a function of the applied electric field along the cross-ribbon direction of (a) 8-PP–PP, (b) 8-PSi–SiP and (c) 9-PP–PSi edge SiP₃-ZNRs. The positive and negative electric field depict the forward and reverse biases. The shaded areas show the range of half-metallicity. The inset in each figure shows the schematic edge spin configuration of the corresponding ribbon with up and down spins denoted by red and green color circles, respectively.

To understand the reason behind this observed half-metallicity, we schematically depict the spin configuration of the PP–PP edge NR in the inset of Fig. 5a. The P atoms on each edge exhibit the same spin orientation, i.e., one edge has all down-spin moments (top edge in the inset) and the other edge has all up-spin moments (bottom edge in the inset). Under the +ve ramp potential applied from top to bottom direction, the down-spins experience major drive and consequently the down-spin gap reduces rapidly as compared to the up-spin. However, the existence of bulk polarization ensures the decrease of the up-spin gaps, albeit slowly. The spin gap variation reverses when the field is applied in −ve direction, i.e., from bottom to top direction, owing to the up-spin localization along the bottom edge. The half-metallic behavior does not sustain over a large electric field range, since beyond a certain field strength, both the spins start conducting due to significant bulk polarization of these NRs. Note that, in case of zigzag edge graphene NRs, the applied transverse electric field also results in half-metallic behavior beyond a certain field strength.⁴³ But in that case, on application of ramp potential, one of the spin gaps reduces and the other increases in a small range of field strength. This difference in spin gap variation as compared to the present case can be attributed to the predominant edge spin localization and no bulk polarization in zigzag edge graphene NRs.

Fig. 5b shows the band gap variation of 8-PSi–SiP as a function of applied electric field along the cross-ribbon direction. Due to its AFM ground state, it shows degenerate up and down-spin band gaps at zero bias. On application of external bias, both the spin gaps reduces simultaneously and close at 0.2 V Å⁻¹ and −0.2 V Å⁻¹ field strengths. Therefore, this system shows semiconducting to metallic transition under applied bias. The identical responses by the up and down-spins towards the applied bias can be attributed to the identical AFM spin alignments with alternating up and down-spins along both the edges, as can be seen in the inset. The transverse bias in forward and reverse directions drives both the spins in similar way, resulting in metallic ground state beyond a critical field strength.

The PP–PSi edge NRs, however, present a specific edge spin arrangements. In this case, the top PP edge (see inset of Fig. 5c) localizes the up-spin, leading to a ferrimagnetic spin-ordering. But the bottom PSi edge localizes alternating up and down-spins in consecutive P and Si edge atoms. Therefore, the forward (i.e., +ve) bias from the top to bottom edge direction is expected to drive the up-spins more strongly than the down-spins. This is reflected in the steep decrease in the up-spin band gap as compared to that of the down-spin, resulting in a half-metallic ground state beyond 0.2 V Å⁻¹. However, the reverse (i.e., −ve) bias affects both the spins in the bottom edge almost identically, leading to a decrease in up and down-spin band gaps simultaneously. The little difference in the up and down-spin band gaps under −ve bias can be attributed to the unequal spin moments on alternating Si and P atoms along the bottom edge. Therefore, this system is capable of exhibiting half-metallic behavior under forward bias and metallic behavior under reverse bias, beyond a critical field strength. This presents an unprecedented feature of controlling spin transport behavior based on the polarity of the source-drain electrodes, paving new avenues of designing memory storage devices.

Conclusions

In conclusion, we study the quantum confinement effect on 2D SiP₃ by creating the quasi-one-dimensional zigzag NRs. Depending upon the edge termination we classify the SiP₃ NRs in three categories, namely, PP–PP, PSi–SiP, and PP–PSi edge NRs. The unit cell with an even number of Si atoms, shows the antiferromagnetic ground state for both zigzag PP–PP and PSi–SiP NRs. The unit cell with an odd number of Si atoms with PP–PSi zigzag edge NRs exhibit the ferromagnetic ground state with 1μ_B magnetic moment per unit cell. All the SiP₃-ZNRs show indirect band gap, which decreases with increase in the width of the NRs. The contribution of edge atoms near the Fermi level is minimal, emphasizing the dominance of bulk bands in deciding the electronic properties of these NRs. Further, PP–PP edge zigzag NRs exhibit half-metallicity under the influence of applied transverse electric field, owing to their ferrimagnetic spin configurations along the edges. On the other hand, PSi–SiP zigzag edge NRs exhibit semiconductor to metallic transition under both forward and backward biases. The PP–PSi zigzag edge NRs show the anisotropic half-metallicity under only forward bias, due to the ferrimagnetic PP edge. The observation of half-metallicity and its tunability based on the edge termination can find potential applications in spintronic and memory storage devices. Moreover, due to the buckled structure of SiP₃ system, the application of strain can alter the magnetic moments on Si and P atoms, thereby affecting the electronic band dispersion, and consequent half-metallic properties.^44–48 Therefore, the strain-dependent electronic and magnetic properties of these SiP₃ nanoribbons can provide valuable insights for the experimental device engineering.

Data availability

The calculations have been carried out using SIESTA package,³² version 4.1 https://siesta.icmab.es/siesta/CodeAccess/.

Author contributions

SD define the project. SA performs all the computational calculations. SA and SD have written, reviewed & edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

SA and SD thank IISER Tirupati for Intramural Funding and Science and Engineering Research Board, Dept. of Science and Technology, Govt. of India for research grant (CRG/2021/001731). The authors acknowledge National Supercomputing Mission (NSM) for providing computing resources of ‘PARAM Brahma’ at IISER Pune, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and DST, Govt. of India.

References

1. K. S. Burch, D. Mandrus and J.-G. Park, Nature, 2018, 563, 47–52.
2. M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419.
3. C. Gong and X. Zhang, Science, 2019, 363, eaav4450.
4. S. Jiang, J. Shan and K. F. Mak, Nat. Mater., 2018, 17, 406–410.
5. K. Kim, S. Y. Lim, J. Kim, J.-U. Lee, S. Lee, P. Kim, K. Park, S. Son, C.-H. Park and J.-G. Park, et al., 2D Mater., 2019, 6, 041001.
6. C. Tan, J. Lee, S.-G. Jung, T. Park, S. Albarakati, J. Partridge, M. R. Field, D. G. McCulloch, L. Wang and C. Lee, Nat. Commun., 2018, 9, 1554.
7. S. Tian, J.-F. Zhang, C. Li, T. Ying, S. Li, X. Zhang, K. Liu and H. Lei, J. Am. Chem. Soc., 2019, 141, 5326–5333.
8. G. Zhang, F. Guo, H. Wu, X. Wen, L. Yang, W. Jin, W. Zhang and H. Chang, Nat. Commun., 2022, 13, 5067.
9. J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002.
10. S. Dutta, S. R. Das and S. Adhikary, in Recent Advances in Graphene and Graphene-Based Technologies, IOP Publishing Bristol, UK, 2023, p. 16, https://iopscience.iop.org/book/edit/978-0-7503-3999-5/chapter/bk978-0-7503-3999-5ch16.
11. S. Dutta and K. Wakabayashi, Sci. Rep., 2015, 5, 11744.
12. S. Dutta and K. Wakabayashi, AIP Conf. Proc., 2013, 153–154.
13. S. Dutta and S. K. Pati, J. Mater. Chem., 2010, 20, 8207–8223.
14. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
15. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
16. S. Dutta and S. K. Pati, J. Mater. Chem., 2010, 20, 8207–8223.
17. P. De Padova, P. Perfetti, B. Olivieri, C. Quaresima, C. Ottaviani and G. Le Lay, J. Phys.: Condens. Matter, 2012, 24, 223001.
18. K. Wakabayashi, M. Fujita, H. Ajiki and M. Sigrist, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8271.
19. M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920–1923.
20. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
21. C. Tao, L. Jiao, O. V. Yazyev, Y.-C. Chen, J. Feng, X. Zhang, R. B. Capaz, J. M. Tour, A. Zettl and S. G. Louie, et al., Nat. Phys., 2011, 7, 616–620.
22. X. Zhang, O. V. Yazyev, J. Feng, L. Xie, C. Tao, Y.-C. Chen, L. Jiao, Z. Pedramrazi, A. Zettl and S. G. Louie, et al., ACS Nano, 2013, 7, 198–202.
23. S. Dutta, A. K. Manna and S. K. Pati, Phys. Rev. Lett., 2009, 102, 096601.
24. E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201.
25. C. Tao, L. Jiao, O. V. Yazyev, Y.-C. Chen, J. Feng, X. Zhang, R. B. Capaz, J. M. Tour, A. Zettl and S. G. Louie, et al., Nat. Phys., 2011, 7, 616–620.
26. Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349.
27. S. Adhikary, S. Dutta and S. Mohakud, Nanoscale Adv., 2021, 3, 2217–2221.
28. Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802.
29. J. Xie, M. Si, D. Yang, Z. Zhang and D. Xue, J. Appl. Phys., 2014, 116, 073704.
30. K. Wakabayashi and S. Dutta, Solid State Commun., 2012, 152, 1420–1430.
31. G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Hwang, L. P. Biro and L. Tapasztó, Nature, 2014, 514, 608–611.
32. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
33. L. Kleinman and D. Bylander, Phys. Rev. Lett., 1982, 48, 1425.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
36. L. Jiao, X. Wang, G. Diankov, H. Wang and H. Dai, Nat. Nanotechnol., 2010, 5, 321–325.
37. P. Ruffieux, S. Wang, B. Yang, C. Sánchez-Sánchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli and D. Passerone, et al., Nature, 2016, 531, 489–492.
38. T. Makita, A. Yamamura, J. Tsurumi, S. Kumagai, T. Kurosawa, T. Okamoto, M. Sasaki, S. Watanabe and J. Takeya, Sci. Rep., 2020, 10, 4702.
39. Y. Chen, S. F. Hung, W. K. Lo, Y. Chen, Y. Shen, K. Kafenda, J. Su, K. Xia and S. Yang, Nat. Commun., 2020, 11, 5334.
40. Y. Chen, F. Fang and N. Zhang, npj 2D Mater. Appl., 2024, 8, 17.
41. H. Kim, C. S. Chang, S. Lee, J. Jiang, J. Jeong, M. Park, Y. Meng, J. Ji, Y. Kwon and X. Sun, et al., Nat. Rev. Methods Primers, 2022, 2, 40.
42. S. Dutta and K. Wakabayashi, J. Mater. Chem. C, 2013, 1, 4854–4857.
43. E. Rudberg, P. Sałek and Y. Luo, Nano Lett., 2007, 7, 2211–2213.
44. W. Zhang, C. He, T. Li and S. Gong, RSC Adv., 2015, 5, 33407–33413.
45. L. Ao, A. Pham, X. Xiang, F. Klose, S. Li and X. Zu, RSC Adv., 2017, 7, 51935–51943.
46. J. Vahedi and R. Peters, Phys. Rev. B, 2021, 103, 075108.
47. V. K. Gudelli, N. Alaal and I. S. Roqan, ACS Appl. Eng. Mater., 2023, 1, 1292–1300.
48. Y. Li, X. Jiang, Z. Liu and Z. Liu, Nano Res., 2010, 3, 545–556.

---

Footnote

† Present address: Department of Nanotechnology for Sustainable Energy, School of Science and Technology, Kwansei Gakuin University, 1-Gakuen Uegahara, Sanda 669-1330, Hyogo, Japan.

---