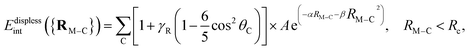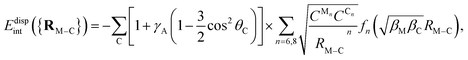A practical post-Hartree-Fock approach describing open-shell metal cluster-support interactions. Application to Cu₃ adsorption on benzene/coronene

Abstract

Current advances in synthesizing and characterizing atomically precise monodisperse metal clusters (AMCs) at the subnanometer scale have opened up fascinating possibilities in designing new heterogeneous (photo)catalysts as well as functional interfaces between AMCs and biologically relevant molecules. Understanding the nature of AMC–support interactions at molecular-level is essential for optimizing (photo)catalysts performance and designing novel ones with improved properties. Møller–Plesset second-order perturbation theory (MP2) is one of the most cost-efficient single-reference post-Hartree–Fock wave-function-based theories that can be applied to AMC–support interactions considering adequate molecular models of the support, and thus complementing state-of-the-art dispersion-corrected density functional theory. However, the resulting AMC–support interaction is typically overestimated with the MP2 method and must be corrected. The coupled MP2 (MP2C) scheme replacing the uncoupled Hartree–Fock dispersion energy by a coupled dispersion contribution, has been proven to describe accurately van-der-Waals (vdW)-dominated interactions between closed-shell AMCs and carbon-based supports. In this work, the accuracy of a MP2C-based scheme is evaluated in modelling open-shell AMC-cluster interactions that imply charge transfer or other strong attractive energy contributions beyond vdW forces. For this purpose, we consider the interaction of Cu₃ with molecular models of graphene of increasing size (benzene and coronene). In this way, it is shown that subchemical precision (within 0.1 kcal mol⁻¹) is achieved with the modified MP2C scheme, using the explicitly correlated coupled cluster theory with single, double, and perturbative triple excitations [CCSD(T)-F12] as a benchmark method. It is also revealed that the energy difference between uncoupled and coupled dispersion terms closely follows benchmark values of the repulsive intramonomer correlation contribution. The proposed open-shell MP2C-based approach is expected to be of general applicability to open-shell atomic or molecular species interacting with coronene for regions of the potential landscape where single-reference electronic structure descriptions suffice.

---

1 Introduction

Current advances in cutting-edge synthesis techniques are allowing to precisely control the size and chemical composition of metal clusters at atomic level, down to the subnanometer scale, in different environments (gas-phase, solution, within helium nanodroplets, and interacting with biologically relevant molecules) and various thermodynamical conditions (temperature and pressure).^1–4 These atomically precise monodisperse metal clusters (AMCs), typically made of less than 10 atoms, are paving the way for entirely new quantum materials with potential applications in catalysis,^5–11 photocatalysis,^2,12–14 energy conversion,¹⁵ bioimaging,^16,17 theranostics,^18–20 luminescence,²¹ and sensing²² (see, e.g., ref. 3 for an overview of applications of naked AMCs in catalysis). Naturally, the interaction between the AMCs and the support material significantly influences the stability, activity, and selectivity of AMC-based (photo)catalysts. The molecular-level understanding and manipulation of AMC–support interactions have the potential to boost their functionalities in (photo)catalysis, being at the forefront of modern subnanometer science at the bottom scale of nanotechnology.

On the theoretical side, tremendous progresses in the efficiency of state-of-the-art modelling, based on dispersion-corrected density functional theory (DFT), are making possible detailed characterizations of AMC–support interactions, including molecular dynamics (MD) simulations with machine-learned accelerators at long time scales and ‘operando’ conditions of AMC-based (photo)catalysts (see, e.g., ref. 4 for a perspective of the current state-of-the-art). For instance, ref. 23 presented DFT-based molecular dynamics simulations a few hundreds of picoseconds long, predicting that intrinsic defects of graphene surfaces, carbon vacancies, are capable of stabilizing individual AMCs through spatial confinement, avoiding their sintering upon diffusion. In the quest of complementing DFT-based descriptions, Møller–Plesset second-order perturbation theory (MP2) is probably the most cost-efficient single-reference post-Hartree–Fock wave-function-based theory that can be applied to AMC–support interactions. However, previous benchmarking of the van-der-Waals-dominated interaction between the Ag₂ cluster and molecular models of graphene of increasing size (benzene and coronene) has indicated a severe overestimation of the attractive AMC–support interaction with the MP2 method.²⁴ Fortunately, the benchmark results²⁴ also showed that the overestimation can be corrected by applying the coupled MP2 method (MP2C) of Heßelmann and Pitoňák^25,26 that replaces the uncoupled second-order dispersion contribution contained in the MP2 interaction energy with the coupled dispersion energy evaluated via linear-response time-dependent DFT.

An open question arises on the possibility of correcting the MP2 method similarly to describe AMC–support interactions that might imply charge transfer or other strong attractive contribution beyond van-der-Waals(vdW)-dominated interaction forces. For instance, polarization forces have been proven to be crucial in the stabilization of metal cation–benzene complexes.²⁷ Thus, it has been recently shown that the Ag⁺–benzene interaction is a factor of ten stronger than the vdW-dominated Ag–benzene interaction.²⁸ Likewise, open-shell AMC–support interactions are expected to be much stronger than their closed-shell counterparts. In fact, open-shell AMCs are more prone to participate in chemical bonding with the support either by sharing or transferring their outer unpaired electrons.²⁹ The previous study of the Ag⁺–benzene complex showed a remarkably good agreement between MP2 and coupled cluster theories with single, double, and perturbative triple excitations [CCSD(T)] when a smaller electronic basis set is applied in MP2 calculations to correct the overestimated attractive interaction.²⁸ In this work, we propose an open-shell extension of the MP2C scheme^25,26 instead, applying linear response time-dependent Hartree–Fock theory, allowing the consideration of open-shell AMC–support complexes with any electronic basis set and sensible molecular models of the support. Its accuracy is demonstrated by applying it to Cu₃–benzene and Cu₃–coronene complexes.

A possible issue when dealing with open-shell AMC–support interactions is the occurrence of conical intersections leading, e.g., to Jahn–Teller effects. As found in theoretical and experimental studies,^30–32 Cu₃ is a classical case of a Jahn–Teller fluxional cluster. This way, it experiences a conical intersection at equilateral triangular D_3h structures causing a Jahn–Teller distortion that removes the degeneracy of two electronic states of symmetry E′, lowering the D_3h symmetry to C_2v. However, a previous study³³ has shown that the Jahn–Teller distortion is lifted when the Cu₃ cluster collides with the benzene molecule in an orthogonal orientation of the cluster plane with respect to the benzene ring plane. In order to test the proposed single-reference MP2C-based scheme in comparison with the ‘gold standard’ CCSD(T) approach, we have considered the same C_2v structure of the Cu₃–benzene complex³³ in this work.

A second topic of this study is the fitting of the dispersion and dispersionless Cu₃–coronene interactions to an inter-atomic pairwise potential model (PPM).^34–39 This PPM was originally developed to provide a potential energy surface (PES) for a He atom colliding with a Mg surface³⁴ and further extended to a fullerene molecule,³⁵ as well as the interaction of He, N₂ and D₂ with carbon nanotubes (CNTs).^36,37 The PPM fitted very well with benchmark ab initio interaction energies for binding in the regions endohedral and exohedral to the CNTs and showed excellent transferability upon increasing the CNTs size. It has also been used to probe the embedding of single-walled CNTs into helium nanodroplets (HNDs),⁴⁰ and the HNDs-mediated soft-deposition and diffusion of silver clusters on amorphous carbon and graphene through large-scale molecular dynamics (MD) simulations on the nanoseconds scale.³⁸ Following the same procedure in this work, we deliver PPM parameters that are directly applicable in MD simulations of the diffusion process of copper clusters on carbon-based surfaces.

This article is structured as follows: in Section 2, the computational-theoretical approach and the details of our calculations are presented. Section 3 focuses on analyzing the intermolecular interactions featured by Cu₃–benzene and Cu₃–coronene complexes, the performance of the open-shell MP2C-based approach, as well as the fitting to an intermolecular potential model of the dispersion and dispersionless energy contributions. Finally, Section 4 closes with concluding remarks and future prospects.

2 Theoretical-computational methods

We have used the polarized correlation-consistent triple-ζ basis of Dunning and collaborators⁴¹ (cc-pVTZ) for C and H atoms, while the augmented aug-cc-pVTZ-PP basis set was employed for copper,⁴² including small-core (10- and 19-valence-electron) relativistic pseudopotentials.⁴² Test calculations have been also carried out using the quadruple-ζ cc-pVQZ basis for C and H atoms along with the aug-cc-pVQZ-PP basis set on copper atoms. These basis sets will collectively be denoted as (A)VTZ(-PP) and (A)VQZ(-PP). It has been shown that the aug-cc-pVTZ-PP basis set provides Cu–Cu distances in optimized geometries and spatial harmonic frequencies – in the normal modes approximation – of Cu₅ isomers differing by less than 0.02 Å and 1.4 cm⁻¹ (on average) from the values obtained with the aug-cc-pVQZ-PP basis set.³² Relative energies such as the Jahn–Teller stabilization energy and the energy barrier between minima and transition states were converged to better than 0.01 and 0.001 eV, respectively.³² Test calculations were carried out using the DFT-D3 approach on the Cu₃–benzene complex. They showed that the augmentation of the cc-pVTZ basis set for carbon and hydrogen atoms leave the interaction energy at the equilibrium Cu₃–benzene structure almost unmodified (within 0.6%), with values of −37.96 kcal mol⁻¹ using augmentation just for copper atoms and −38.14 kcal mol⁻¹ using augmentation for all atoms. To determine the errors arising from the use of the pseudopotentials, second-order Douglas–Kroll–Hess calculations^43–45 have previously been carried out for the Ag₂–benzene complex²⁴ using the aug-cc-pVTZ-DK basis set^46,47 at CCSD(T) level. The errors amounted to 0.01–0.02 kcal mol⁻¹ and 0.5% of the interaction energy only²⁴ and smaller errors can be expected for the lighter Cu₃–benzene system. The complete basis set (CBS) limit of the interaction energies at the equilibrium geometry of the Cu₃–benzene complex have also been estimated for post-Hartree–Fock methods as follows:^48,49 First, the correlation energies evaluated at post-Hartree–Fock levels using the (A)VTZ(-PP) and (A)VQZ(-PP) basis sets were extrapolated using the n⁻³ scheme of Helgaker and co-workers⁴⁸ with n = 3 and 4,

E^corr_n = E^corr_CBS + A n⁻³.

Next, the extrapolated CBS estimations for the correlation contributions were added to the CBS counterparts at Hartree–Fock (HF) level, using the empirical-based exponential,⁵⁰

E^HF_n = E^HF_CBS + α exp^−βn.

This exponential expression has been found to be effective in estimating CBS limit energies at the HF level for the Ag₂/benzene system,²⁴ working better than the power form (see also ref. 51). As discussed in ref. 49, however, the actual convergence rate with n is much slower than the exponential decay as the asymptotic limit is approached for the total energy due to the problem associated with obtaining a correct description of the Coulomb cusp with one-electron basis sets.

As a high-level single-reference ab initio method, we have applied the R/UCCSD(T) scheme where the restricted open-shell Hartree–Fock (ROHF) approach is used in a first step. The spin-constraint is relaxed in the subsequent coupled-cluster calculations as in ref. 32. The explicitly correlated CCSD(T)-F12 method has been used as a benchmark method as well.⁵² As the model treatment, we have applied the (unrestricted open shell) second-order Møller–Plesset perturbation theory (UMP2) approach. For comparison purposes, the DFT-D3 scheme has also been used by combining the Perdew–Burke–Ernzerhof (PBE) density functional,⁵³ using the restricted open-shell Kohn–Sham approach, with the Becke–Johnson (BJ) damping,⁵⁴ for the Grimme's D3 dispersion correction. Benchmark studies have previously shown that the DFT-D3 ansatz describes well the dispersion-dominated interactions between the closed-shell Ag₂ cluster and the surfaces of graphene and titanium dioxide (see ref. 24 and 29, respectively). We have verified in previous works^55,56 that the replacement of the D3(BJ) dispersion correction with the most recent D4's Grimme's parametrization⁵⁷ modifies very little the optimized structures the optimized structures of copper clusters⁵⁵ as well as the (p–T)-phase diagrams describing the interaction of these clusters with molecular oxygen at different conditions of temperature and pressure.⁵⁶ Actually, the experimental measurements were closer to the phase diagrams obtained with the D3(BJ) parametrization in ref. 58. Hence, in this study, we have decided to use the D3(J) parametrization. DFT-D3 calculations were carried out with the MOLPRO code.⁵⁹

The internal coordinates of Cu₃ and the benzene molecule were fixed to those found in a full optimizations of a C_2v Cu₃–benzene structure at CCSD(T) level of theory.³³ The DFT-D3 approach has been used in the optimization of the same C_2v structure but considering coronene. This ansatz is justified by the similarity of DFT-D3 and CCSD(T)-based optimized structures of the Cu₃–benzene complex. This way, the geometrical parameters differed by 0.02 Å and 0.2° at most. An analysis of the Mulliken charges⁶⁰ was accomplished for the two complexes using Kohn–Sham orbitals. All calculations of interaction energies within the supermolecular approach have been carried out using the last version of the MOLPRO code.⁵⁹ Specifically, the interaction energies (E_int) were calculated as,

E_int = {E_{Cu3–support}}_Min − {E_{Cu3–support}}_Asymp

where {E_{Cu3–support}}_Min is the energy at the minimum and {E_{Cu3–support}}_Asymp is the energy at the asymptotic limit of separated Cu₃ + support (benzene or coronene) fragments. The asymptotic limit was determined at a distance of 40 Å.

Dispersion energy contributions were obtained separately from Symmetry adapted Perturbation Theory (SAPT) calculations carried out using the Psi4 (see ref. 61) and the Psi4NumPy packages (see ref. 62). Specifically, the uncoupled Hartree–Fock dispersion term (E^UHF_disp) was computed at the SAPT0 level, using the unrestricted open-shell Hartree–Fock (UHF) approach for the monomers (i.e., the AMC and benzene or coronene). Subsequently, all relevant quantities were exported as NumPy arrays using the Psi4NumPy package,⁶² easing accessibility within the main Python script. The script was then utilized to compute the coupled dispersion term, using the frequency-integrated linear response function derived from unrestricted time-dependent Hartree–Fock theory E^TD-UHF_disp (see ref. 63 and 64 for details on the implementation to compute the coupled dispersion contributions). Additionally, multi-configurational self-consistent-field (CASSCF) calculations have been carried out. Specifically, coupled (SAPT-based) dispersion contributions were calculated using CASSCF descriptions of the monomers with the SAPT(CAS) method,^65–67 as implemented in the GAMMCOR code.⁶⁸

Treating Cu₃ and benzene fragments as single structureless pseudo-particles, nuclear bound-state energies were obtained by numerically solving the one-dimensional Schrödinger equation associated to the intermolecular Cu₃–benzene vibrational motion. For this purpose, we applied the discrete variable representation approach,⁶⁹ using sinc-DVR functions.⁶⁹ Since the interaction potential is diagonal in the DVR basis, it needed to be estimated just on the considered set of DVR grid points. To generate more points on the potential energy curves (PECs) and ensure a larger dataset, a cubic spline-type interpolation was applied.

3 Results and discussion

This section is organized as follows: first, in Section 3.1, we discuss the adequacy of a single-reference description of the Cu₃–benzene complex when considering the structure shown in Fig. 1. Next, in Section 3.2, the adsorption mechanisms of Cu₃ clusters to benzene and coronene are analyzed. Section 3.3 addresses the correction of the corresponding intermolecular potentials calculated at MP2 level with the open-shell MP2C-based approach, assessing its accuracy through benchmarking with coupled-cluster theory approaches. Finally, Section 3.4 focuses on the fitting of the dispersion and dispersionless interaction energies to an inter-atomic pairwise potential form.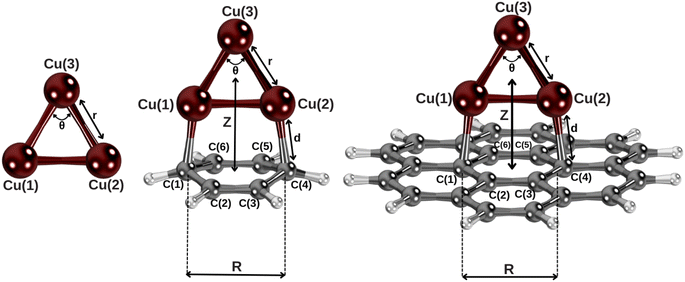

Fig. 1 Complexes under investigation at the equilibrium geometries (see Section 2 and the ESI† for the computational details). Z is defined as the distance between the centers of mass of Cu₃ and the benzene and coronene molecules, lying along the plotted axis.

3.1 Verification of the adequacy of single-reference electronic structure methods

As mentioned in the Introduction, when the interaction of a Jahn–Teller metal cluster with a given support is addressed, it is important to verify the adequacy of single-reference electronic structure methods for the considered region of the potential landscape. A previous study using the internally contracted multireference Rayleigh Schrödinger (second-order) perturbation theory RS2C method⁷⁰ has revealed that, considering the Cu₃–benzene structure shown in Fig. 1, the energies of the ground and excited electronic states differ by ∼1.1 eV, with the conical intersection located ∼1.5 eV above the associated chemisorption minimum. The adequacy of the single-reference CCSD(T) method has also been verified through the coupled cluster diagnostics⁷¹ (see also ref. 72). This study thus indicates the appropriateness of the single-reference approaches for the considered Cu₃–benzene structures. In contrast, the two electronic states are kept degenerate for a C_3v structure of the complex in which the plane of the Cu₃ cluster and the benzene ring plane are parallel to each other, thus requiring multi-configurational descriptions.³³

As an additional test, SAPT(CAS) calculations were carried out by considering an active space of nine electrons distributed in eleven orbitals [referred to us (9,11)]. This space involved the well-proven (3,5) active space of Cu₃ isolated in the gas-phase³² (i.e., three electrons distributed in five orbitals) and the standard valence π(6,6) active space of the benzene molecule (i.e., six electrons distributed in six π orbitals).⁷³ The similarity of coupled dispersion energies calculated with ROHF and CAS(9,11) wavefunctions (to within 1 kcal mol⁻¹ and 2%) indicated that a single-reference description suffices at the considered geometry. Besides it, we also tested a MP2C-based scheme on the optimized structure by replacing the uncoupled dispersion contribution by the coupled one from SAPT(ROHF) calculations. It was found that the interaction energy (−33.95 kcal mol⁻¹) agrees very well with that obtained with the CCSD(T) and DFT-D3 approaches (−33.08 and −35.57 kcal mol⁻¹, respectively).

3.2 Cu₃ adsorption mechanism on benzene and coronene

Let us now focus on the adsorption mechanism of the Cu₃ cluster in benzene and coronene. Fig. 1 shows the structures of the Cu₃–benzene and Cu₃–coronene complexes optimized with the CCSD(T) and DFT-D3 approaches, while Table 1 presents the corresponding geometrical parameters as well as the net charge of the copper cluster upon adsorption. As can be observed in Fig. 1, the Cu₃ cluster lies on a plane perpendicular to both benzene and coronene. The distance between carbon atoms directly bonded to copper atoms (R in Table 1) increases by 0.08 Å to accommodate the Cu₃ cluster. The interaction energy is ca. 36 kcal mol⁻¹ at CCSD(T)-F12 level, which can be compared with the value of ca. 8 kcal mol⁻¹ for the vdW-dominated Ag₂ interaction.²⁴ The net charge donated by the Cu₃ cluster to the benzene ring is very small (about 0.03 a.u., see Table 1). In fact, the Cu₃–benzene interaction is better characterized by a strong polarization that is summed to a long-range quadrupole–quadrupole energy contribution.⁷⁴ Thus, the Cu atom at the apex of the triangular structure (labelled as Cu(3) in Fig. 1) acquires a Mulliken charge (−0.37 a.u.) which is opposite in sign and above a factor of two larger in magnitude than those of Cu atoms at the base of the triangular Cu₃ structure (0.17 a.u.). To favor the induced dipole-quadrupole Cu₃–benzene interaction, the negative region of benzene's π cloud points towards the positive ends of the Cu₃ cluster.

Table 1 Geometrical parameters (see Fig. 1) characterizing Cu₃–benzene and Cu₃–coronene complexes. The best estimates (using the CCSD(T) method) have been marked in boldface. Values in parentheses have been obtained with the DFT-D3 approach. The value of the charge on the Cu₃ cluster is also presented, evaluated as a sum of the Mulliken charges on each Cu atom (see Section 2 and the ESI for the details)

System	Cu3–benzene	Cu3–coronene	Cu3	Benzene	Coronene
θ [°]	61.2 (61.1)	(62.0)	66.5 (66.7)	—	—
rmin [Å]	2.35 (2.36)	(2.32)	2.28 (2.28)	—	—
Zmin [Å]	2.80 (2.82)	(2.77)	—	—	—
Rmin [Å]	2.88 (2.86)	(2.88)	—	2.80 (2.82)	(2.85)
dmin [Å]	2.03 (2.04)	(2.07)	—	—	—
Cu3 charge	(−0.03)	(0.26)	(0.00)	—	—

---

It can be also observed from Table 1 that the DFT-D3 structural parameters of either the Cu₃–benzene complex or the separated Cu₃ and benzene fragments differ from the CCSD(T) counterparts very little (by 0.02 Å and 0.2° at most). Thus, the optimization of the Cu₃–coronene complex has been carried out at DFT-D3 level. This way, we can verify from Table 1 that the structures of Cu₃–benzene and Cu₃–coronene complexes are very similar. When going from benzene to coronene, the distance between the carbon atoms bonded to the Cu atoms increases by 0.02 Å, with the latter experiencing a shift upwards by 0.03 Å.

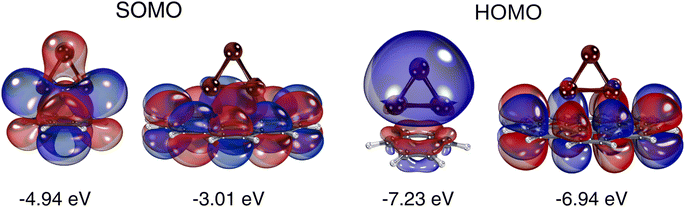
The essential difference between the Cu₃ adsorption mechanisms on benzene and coronene can be understood by simply considering that the Mulliken charges of carbon atoms in the former (−0.1 a.u.) are about 10 times larger than in the latter (−0.01 a.u.). As can be observed in the shape of the SOMO (see Fig. 2), the Cu₃–benzene interaction is marked by the formation of Cu(1)–C1 and Cu(2)–C4 bonds through the mixing of p-type [Cu(1) and Cu(2)] orbitals with π benzene orbitals along with a polarization of the electronic cloud the apex Cu(3) atom. The polarization is manifested in the weight of the s-type Cu(3) orbital in the SOMO, favoring an induced dipole–quadrupole Cu₃–benzene interaction. In contrast, the Cu₃–coronene interaction is marked by an ionic displacement of electronic charge. Thus, the SOMO is made of Cu(1) and Cu(2) orbitals of type p donating electronic charge to C atoms located in the central coronene ring. This effect is compensated for by the delocalization of the π orbitals on the entire coronene molecule. The HOMOs of the Cu₃–benzene and Cu₃–coronene complexes differ as well. In the Cu₃–benzene complex, there is notable polarization of the s orbitals of Cu atoms towards the π orbitals of benzene. In contrast, for the Cu₃–coronene complex, the d-type orbitals of Cu(1) and Cu(2) mix with the delocalized π cloud.

Fig. 2 Picture showing isosurfaces of the frontier ‘singly-occupied’ (or occupied only by a single spin component) molecular orbital (referred to as SOMO) as well as the highest-energy (or occupied by two spin components) molecular orbital (referred to as HOMO) in Cu₃–benzene and Cu₃–coronene complexes. The energies of the orbitals are also indicated.

3.3 Intermolecular interaction potentials. Correction of MP2 interaction energies

The supermolecular interaction energies between the Cu₃ cluster and benzene shown in Fig. 3 were obtained using three main different single-reference electronic structure methods: the single-reference ‘gold standard’ method (using both CCSD(T) and explicitly correlated CCSD(T)-F12 approaches), the unrestricted open-shell MP2(UMP2) method, and the coupled unrestricted open-shell (UMP2C) scheme. Specifically, UMP2 interaction energies (E^UMP2_int) are calculated following the coupled MP2 treatment of Pitoňák and Heßelmann.^25,26 This way, uncoupled MP2 dispersion contributions (E^UHF_disp) are replaced with those obtained via time-dependent Hartree–Fock (TD-UHF) response theory (E^TD-UHF_disp) (see ref. 63 and 64 and Methods section for details).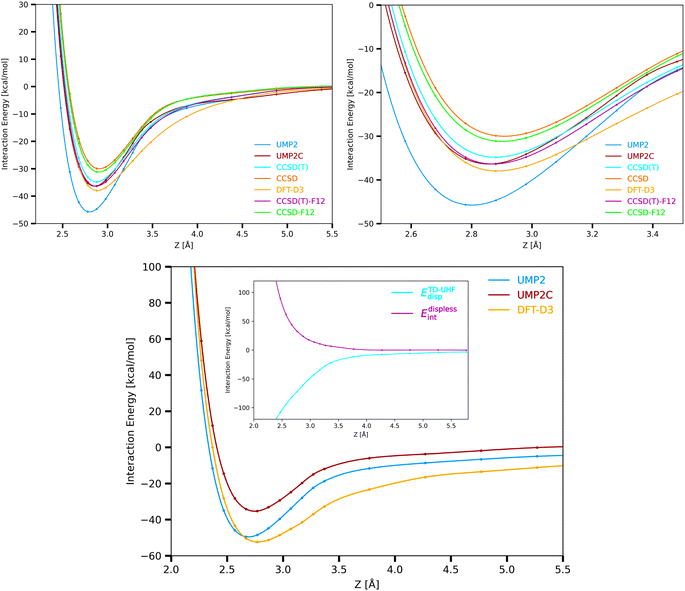

Fig. 3 Cu₃–benzene (upper panels) and Cu₃–coronene (bottom panel) interaction potentials and Cu₃ – coronene coupled dispersion (E^TD-UHF_disp) and dispersionless energy contribution (E^displess_int) (inset in the bottom panel). The interaction potentials have been evaluated at DFT-D3, CCSD, CCSD-F12, CCSD(T), CSSD(T)-F12, UMP2, and UMP2C levels with the (A)VTZ(-PP) basis set (see Section 2 and the ESI† for computational details). See Fig. 1 for the optimized structures. The coupled dispersion has been calculated using time-dependent unrestricted Hartree–Fock (TD-UHF) linear response function.

As in the original treatment,^25,26 the repulsive exchange-dispersion (E^UHF_exch-disp) term is kept at the HF level. Test calculations were also done by substituting it with a coupled exchange-dispersion contribution (E^exch-disp_TD-UHF) estimated on the basis of the treatment developed by Schäffer and Jansen.^75,76 These calculations showed (see Table 5 of the ESI†) that benchmark values of the intramonomer correlation contribution for the Ag₂–benzene interaction are better reproduced when the term E^exch-disp_TD-UHF is excluded in the correction.

In contrast with previous applications of the coupled MP2 method to complexes including metal clusters,^24,77 the localized HF method of Della Sala and Görling⁷⁸ has not been applied. Within the framework of the UMP2C scheme, the total interaction energy E^total_int is obtained as,

E^total_int(UMP2C) = E^UMP2_int − E^disp_UHF + E^disp_TD-UHF

As can be observed in Fig. 1 by comparing CCSD(T)-F12, UMP2, and UMP2C potential energy curves, the overestimated attractive Cu₃–benzene interaction and the underestimated intermolecular distance by the UMP2 method (by 30% and 0.1 Å, respectively, see Table 1 of the ESI†) are fully corrected with the UMP2C scheme. More conclusive numerical evidence of the excellent performance of the UMP2C approach is provided in Table 2 through the comparison of the interaction energy at the minimum, the equilibrium intermolecular distance and the energies of the nuclear bound states associated to the Cu₃–benzene intermolecular motion. These energies have been obtained by numerically solving the Schrödinger equation in a one-dimensional representation (see Methods section for the details). We have also verified that the interaction energies obtained at CCSD(T), CCSD(T)-F12, and UMP2C energy levels were well converged with the (A)VTZ(-PP) basis set. This way, the extrapolation of these energies to the CBS limit differed by less than 3% from those obtained with the (A)VTZ(-PP) basis (see Table 2). The DFT-D3-based value is converged with the (A)VQZ(-PP) basis to 1% instead. Counterpoise corrections⁷⁹ were also estimated, being less than 1% of the interaction energy (e.g., 14.96 meV at DFT-D3 level with the (A)VTZ(-PP) basis). It is interesting to note from Table 2 that the UPM2C scheme outperforms the CCSD(T) approach so that the CCSD(T)-F12-based energies of the nine lowest nuclear bound states are reproduced with subchemical accuracy (to within 0.1 kcal mol⁻¹ and 7 meV), with the values of equilibrium Cu₃–benzene distances and deep-well differing by just 0.01 Å and 0.5 meV, respectively.

Table 2 Interaction energy at the minimum (E_min, in meV), equilibrium intermolecular distance between Cu₃ and benzene centers of mass (Z_min, in Å), zero-point energy (ZPE, in meV) and nuclear bound-state energies (ε_n, in meV) associated to the Cu₃–benzene intermolecular degree of freedom as function of the vibrational quantum number n at CCSD(T), CCSD(T)-F12, UMP2C, and DFT-D3 levels of theory with the (A)VTZ-PP basis set. The best estimates (using the CCSD(T)-F12 approach) have been marked in boldface. For the sake of comparison, the values of E_min obtained with the (A)VQZ-PP basis are presented in parentheses, while the extrapolated values to the complete basis set (CBS) limit are shown as E^CBS_min terms, with all of them having been calculated at the CCSD(T)-based equilibrium structure with the (A)VTZ-PP basis set

Method	CCSD(T)	CCSD(T)-F12	UMP2C	DFT-D3
Emin [meV]	−1497.62 (−1523.90)	−1564.03 (−1593.21)	−1564.53 (−1591.74)	−1632.39 (−1649.37)
E^CBSmin [meV]	−1543.09	−1614.50	−1611.59	—
Zmin [Å]	2.88	2.87	2.86	2.88
ZPE [meV]	7.17	7.29	7.85	6.86
ε1 [meV]	−1475.94	−1542.15	−1541.06	−1611.70
ε2 [meV]	−1461.46	−1527.58	−1525.54	−1597.90
ε3 [meV]	−1447.02	−1513.06	−1510.14	−1584.18
ε4 [meV]	−1432.63	−1498.57	−1494.86	−1570.52
ε5 [meV]	−1418.29	−1484.14	−1479.69	−1556.93
ε6 [meV]	−1404.01	−1469.76	−1464.62	−1543.42
ε7 [meV]	−1389.78	−1455.43	−1449.65	−1529.96
ε8 [meV]	−1375.59	−1441.15	−1434.77	−1516.57
ε9 [meV]	−1361.46	−1426.91	−1419.97	−1503.24

---

For the sake of comparison, the upper left-hand panel of Fig. 3 also presents the Cu₃–benzene interaction potential calculated at CCSD, CCSD-F12 and DFT-D3 levels, with the bound-state energies having been obtained with the DFT-D3 scheme as well (see Table 2). As expected from the electrostatic dipole–quadrupole contribution to the interaction, the UHF interaction energy is attractive. Interestingly, as in benchmark studies of Cu₃ and Cu₅ clusters isolated in the gas-phase,³² the DFT-D3 scheme clearly outperforms the CCSD method. While the CCSD and CCSD-F12 approaches significantly underestimate the intermolecular interaction (by 18% and 14%, respectively), the value of the CCSD(T)-F12 deep well is reproduced to within 4% with the DFT-D3 approach, with the equilibrium Cu₃–benzene distance differing by just 0.01 Å. Yet, the lowest-energy bound states supported by the Cu₃–benzene interaction potential are overestimated by up 76 meV (5.5%) with the DFT-D3 scheme.

It is important to stress that the positive energy difference between coupled and uncoupled dispersion contributions can be attributed to the repulsive nature of the intramonomer correlation for cluster–support interactions. This contribution was accurately calculated via the usage of the method of increments⁸⁰ at CCSD(T) level for the Ag₂–benzene interaction.²⁴ The application of the UPM2C scheme to the same complex in this work (see Table 5 of the ESI†) has confirmed that the energy difference between coupled and uncoupled dispersion contribution as function of the intermolecular distance closely follow those reported in ref. 24, explaining the reasons of the excellent performance of the UMP2C approach. The main drawback of the MP2 method is in fact the lack of intramonomer correlation contributions to the interaction (see, e.g., ref. 81). As assessed by applying the method of increments at CCSD(T) level to Ag₂–benzene,²⁴ the intramonomer correlation contribution is repulsive due to the correlation space truncation that the monomers cause in each other:^24,82 In free benzene, the electrons occupying the carbon rings orbitals are correlated through their excitations to all virtual orbitals. Part of the available virtual orbital space becomes blocked by the metal cluster occupied orbitals. As typically found,^24,80,82,83 this contribution decays exponentially as the intermolecular distance increases.

Focusing on the intermolecular potentials of the Cu₃–coronene complex shown in Fig. 3, which have been calculated at computationally feasible UMP2, UMP2C, and DFT-D3 levels, it can be observed that both DFT-D3 and UMP2C methods correct the underestimation of the intermolecular distance by the UMP2 approach. However, the DFT-D3 approach is clearly overestimating the attractive interaction, with the potential dwell being 8% deeper than the UMP2 counterpart (see Table 2 of the ESI†). The overestimation of the interaction by the DFT-D3 scheme is even more clear in the middle- and long-range region. Interestingly, the correction brought by the replacement of the uncoupled dispersion by the coupled counterpart with the UPM2C approach is larger in the Cu₃–coronene complex than in the Cu₃–benzene system (14.2 and 8.4 kcal mol⁻¹ in the corresponding minima, see Tables 3 and 4 of the ESI†). This difference is attributed to a major role of the repulsive intramonomer correlation contribution to the interaction energy for the Cu₃–coronene complex. In fact, the application of the method of increments⁸⁰ at CCSD(T) level to the Ag₂–benzene complex in ref. 24 revealed that the intramonomer correlation contribution can be essentially estimated as a sum of one-body and two-body intramonomer increment modifications arising from the metal cluster and the C–C (either single or double) bonds, with all of them being overly repulsive. Thus, the larger number of C–C bonds in coronene seems to cause an increase of the total intramonomer correlation contribution even if the increment modifications should vary when going from benzene to coronene. Moreover, similarly to Ag₂–coronene,²⁴ the enhanced exchange-repulsion for the Cu₃–coronene interaction also contributes to make the dwell depth very similar in Cu₃–benzene and Cu₃–coronene complexes (to within 1 kcal mol⁻¹, see Tables 1 and 2 of the ESI†).

For the sake of completeness, we have proven the adequacy of the same dispersion correction but applied to the RS2C multireference treatment using a (9,11) active space (see Fig. 1 of the ESI†). For these test calculations, the same computational set-up described in previous studies^32,33 has been followed. It can be clearly seen from Fig. 1 of the ESI† that the dispersion correction brings the RS2C(9,11) interaction potential in almost perfect agreement with the single-reference CCSD(T)-F12 counterpart. This outcome is consistent with the single-reference character of the wavefunctions in the considered region of the potential energy landscape. Thus, the main configuration of the reference (CASSCF) wavefunction has a coefficient of 0.89 at the potential minimum. If the dispersion correction is factorized with the weight of the main configuration, the resulting potential energy curve appears just slightly below the CCSD(T)-F12 interaction potential, which is once again consistent with the single-reference nature of the wavefunction at the considered Cu₃–benzene structure in this work.

3.4 Partition of the interaction energies. Fitting to a pairwise potential model of dispersionless and dispersion contributions

When addressing the modeling of intermolecular interaction potentials, it is crucial to distinguish between short-range (almost repulsive) and long-range attractive (dispersion) contributions. One essential advantage of the UMP2C scheme is that it allows to dissect the interaction energy in dispersion-like and dispersionless contributions. Specifically, since the main (coupled) dispersion contribution is subtracted, the magnitude E^UPM2C_int − E^disp_TD-UHF can be associated to with the dispersionless-like term. In this work, we numerically demonstrate that this contribution is overly repulsive for both Cu₃–benzene and Cu₃–coronene complexes in contrast with the coupled dispersion contribution (see inset in right-hand panel of Fig. 3, Tables 3 and 4 of the ESI†). As discussed in previous works of atom/molecule–support interactions (see, e.g., ref. 4), the total dispersionless contribution is typically short-range and its magnitude depends on the chemical environment. The dispersion contribution is naturally long-range and the parameters modeling their analytical form have been found to be highly transferable between cluster models of a given support (see, e.g., ref. 84).

Once ensured the characteristics of the dispersionless and dispersion contributions for a given cluster–support interaction, they can be fitted to an additive inter-atomic pairwise potential model (PPM),^35,85 which is a modified version of that proposed by Carlos and Cole.^86,87 The PPM functional form for the dispersionless energy contribution accounts for the typical exponential growth of the dominant dispersionless terms (e.g., the exchange-repulsion in SAPT-based decompositions⁸⁸) but also including a Gaussian-type ‘cushion’ to describe weakly attractive tails stemming from other dispersionless terms. For the case of benzene and coronene acting as the support of metal clusters,

where R_c is a cut-off distance, R_M–C stands for the distance between the metal cluster center-of-mass and one carbon atom of the benzene or coronene molecules acting as the support, and θ_C is the angle between the support normal and the vector R_M–C pointing from the metal cluster center-of-mass to the same C atom. The dimensionless factor γ_R in the first term accounts for the anisotropy of the C–C bonds. The sum in the second term runs over all carbon atoms. For the coupled dispersion contribution, we have applied the typical C₆/C₈ expansion with the damping functions of Tang and Toennies f_n (n = 6, 8)⁸⁹
where γ_A is also a dimensionless anisotropy parameter. It has been previously shown^35,36,85,90 that the inclusion of γ_A and γ_R anisotropy terms is important when modelling corrugation effects of the support. Without including the anisotropy γ_A term, the PPM for the dispersion is equivalent to the so-named D_as functional by Szalewicz and collaborators.^91,92 While these anisotropic terms have been found to be important when modeling the interaction of He atoms with several supports,^35,36,85,90 they were not necessary when fitting the Ag₂–coronene interaction energies to get effective pairwise C–Ag potential parameters.³⁸ Accordingly, as discussed in ref. 28, the Ag–graphene interaction depends very slightly on the particular adsorption site (see also ref. 93). This PPM for the dispersion term has also been used in ab initio-assisted determinations of pair He–Au and Ar–Au potentials for MD simulations of He and Ar atoms on Au surfaces (see ref. 94 and 95). As in the present study, these works highlighted that ab initio calculations using small cluster models of the support can be used to obtain the pair potentials necessary in MD simulations, having being validated with experimental-based determinations.^38,95

Table 3 presents the parameters derived for the dispersion contribution in pair C–Cu potentials with the UPM2C approach. The difference between the values on the C₆ coefficients for C–Cu and C–Ag inter-atomic pairs (43.434 eV·Å⁻⁶ from Table 3 and 54.102 eV·Å⁻⁶ from ref. 38) can simply be explained by considering that the static polarizability of Cu atoms is smaller than for Ag atoms (46.5 ± 0.5 vs. and 55 ± 8 a.u. from ref. 96). The inclusion of γ_A anisotropy terms in the fitting procedure has not affected the values of the dispersion coefficients. Similarly to previous work on the interaction of rare-gas atoms with coronene,⁸⁴ the parametrization including the dispersion interaction with the terminal C–H bonds have a negligible influence on the values of the optimized parameters. In fact, the difference between the parameters with and without considering C–H bonds in the parametrization is a diagnostic of convergence with respect to the size of the cluster model and the possible role of edge effects. Similar findings are found for the dispersionless parameters presented in Table 4. In short, our results indicate that coronene is a good model of graphene to characterize the Cu₃–graphene interaction.

Table 3 Parameters defining the dispersion contributions to the Cu₃–coronene interaction energies using the additive pairwise potential model (PPM) considering hydrogen atoms and without considering hydrogen atoms (in parentheses)

	Cu	C	C–Cu
C6 [eV·Å^−6]	88.347 (88.347)	21.354 (21.358)	43.434 (43.439)
C8 [eV·Å^−8]	2898.629 (2898.995)	13.254 (13.254)	196.006 (196.018)
β [Å^−1]	0.573 (0.568)	3.660 (3.561)	2.097 (2.023)

---

Table 4 Parameters defining the dispersionless contributions to the Cu₃–coronene interaction energies using the additive pairwise potential model (PPM) considering hydrogen atoms and without considering hydrogen atoms (in parentheses)

A [eV]	α [Å^−1]	β [Å^−2]	γR
1508.005 (1508.005)	2.146 (2.145)	0.200 (0.199)	−0.99 (−1.00)

---

Let us now analyze the dispersionless parameters tabulated in Table 4. It is interesting to note that the inclusion of γ_R is necessary to get a good fitting. Otherwise, the errors amount to at least 50%. As discussed in ref. 85, this dimensionless factor modulates the corrugation amplitude. For ‘anti-corrugated cases’, the interaction energy would be less repulsive directly above the surface C atoms, with cos(θ_C) adopting a value close to unity. This would be translated in positive γ_R, as found for the He–Mg(0001) interaction.⁸⁵ The opposite holds when the interaction becomes less repulsive for adsorption on top of ‘hollow’ sites. This is the case of the He–graphite interaction, for which a γ_R value of −0.54 has been reported.^86,87 A corrugation is also found for Cu₃ adsorption, which is reflected in the negative value of the γ_R parameter (−0.99). In contrast, for the case of the Ag–C pair,³⁸ it was not necessary to add the corrugation amplitude in the functional form. By comparing the dispersionless C–Ag and C–Cu pair potentials, we have verified that the former is more repulsive, as expected from steric considerations.

Summarizing this section, the parameters tabulated in Tables 3 and 4 can be used in MD simulations on, e.g., the diffusion of Cu₃ clusters on graphene as a function of temperature, similarly to a previous study on the deposition and diffusion of silver clusters on carbon-based surfaces.³⁸ The application of the UMP2C approach and the PPM to the Cu₃–Cu₃ interaction potential would allow to extend the dynamics calculations to the aggregation of copper clusters on graphene, and to compare with those reported through, e.g., ab initio MD (AIMD) simulations.²³

4 Concluding remarks and future prospects

Summarizing, the accurate characterization of cluster–support interactions is crucial to optimize the (photo)catalysts performance of atomically precise metal clusters of subnanometer size and to design new ones with improved properties. Møller–Plesset second-order (MP2) theory is one of the most successful post-Hartree–Fock wave-function-based theories that can be applied to sensible molecular models of the support such as coronene when considering graphene. However, MP2 interaction energies of cluster–support interactions are typically too attractive and must be corrected. In this work, we have proposed an extension of the MP2C approach,²⁶ previously applied to the vdW-type Ag₂–coronene interaction,²⁴ to open-shell cluster–support interactions implying highly attractive energy contributions beyond vdW forces. The excellent performance of the newly MP2C-based approach has been ensured by applying it to correct the MP2 intermolecular potential characterizing the interaction of Cu₃ clusters with benzene and coronene, having achieved subchemical accuracy when considering the CCSD(T)-F12 method as the reference.

Importantly, we have also found that DFT-D3 delivers an optimized structure of the Cu₃–benzene complexe agreeing very well with the CCSD(T)-based one. The same holds for optimized structures of Cu_n clusters (n = 3, 5, 10),^23,32 with the DFT-D3 scheme even outperforming the CCSD approach.³² Similarly, it has been found that the DFT-D3-based structure of coronene is consistent with that experimentally determined to within 0.01 Å for the C–C bond lengths (see Fig. 2 of the ESI†). Therefore, a practical approach would consist in applying the open-shell MP2C-based method in single-point calculations on top of structures optimized at DFT-D3 level or extracted from AIMD simulations as a function of temperature.²³

It should be stressed that the applicability of the proposed open-shell UMP2C approach is beyond the specific case of AMC–support interactions. It is functional for any open-shell atom, molecule, or cluster interacting with molecular models of the carbon-based support such as coronene. In particular, our goal is to use this UMP2C approach in getting accurate interaction energies between astrochemically relevant open-shell molecules and coronene in the quest of identifying the role that polycyclic aromatic hydrocarbons (PAHs) might play in interstellar chemistry by forming complexes with other atoms/molecules/clusters. Another direction for future prospect is the extension of the single-reference open-shell UMP2C scheme to cluster–support structures featuring multi-reference character in the corresponding wavefunctions. Preliminary tests have shown that the same dispersion corrections embedded in the newly developed open-shell MP2C-based scheme serve to curate the overestimated attractive interaction with the RS2C method. However, further work is necessary to test the correction scheme in RS2C-based calculations of excited electronic states and regions of the potential landscape near to conical intersections.³³

Besides proving the excellent performance of the open-shell MP2C-based approach, the parameters of an inter-atomic pairwise potential model for the dispersionless and dispersion contributions to the Cu₃–coronene interaction have been provided. Since coronene is a sensible cluster model of graphene, it is expected that these parameters can be used in MD simulations of the dynamics of subnanometric copper clusters onto graphene sheets. The feasibility of such approach has already been verified in MD calculations of the deposition and diffusion of silver clusters on carbon-based surfaces,³⁸ having delivered a good agreement with experimental measurements. We hope that our practical approach to cluster–support interactions, combining DFT- and post-Hartree–Fock-based methods, might motivate efforts to further advance in the young field of subnanometer science.

Data availability

The data supporting the findings of this study are available in the ESI† of this article.

Author contributions

Conceptualization: M. P. d. L.-C., investigation; K. M. K, A. K., and M. P. d. L.-C. methodology: K. M. K, A. K., and M. P. d. L.-C.; supervision: M. P. d. L.-C.; project administration: M. P. d. L.-C.; funding acquisition: M. P. d. L.-C.; software: K. M. K., A. K., and M. P. d. L.-C. formal analysis: K. M. K., M. P. d. L.-C.; data curation: K. M. K., M. P. d. L.-C.; visualization: K. M. K., M. P. d. L.-C.; validation: K. M. K., M. P. d. L.-C. writing – original draft: K. M. K and M. P. d. L.-C.; writing – review and editing: K. M. K. and M. P. d. L.-C.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Filip Brzęk and Piotr Żuchowski for having provided an updated version of the code to calculate dispersion and exchange-dispersion energy contributions. This work has been partially supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00/AEI/10.13039/501100011033 and the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01). This publication is also based upon the work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). The CESGA supercomputer center, the CTI at CSIC (Spain), and Nicolaus Copernicus University in Toruń (Poland) are acknowledged for providing the computational resources.

Notes and references

1. M. P. de Lara-Castells, C. Puzzarini, V. Bonačić-Koutecký, M. A. López-Quintela and S. Vajda, Phys. Chem. Chem. Phys., 2023, 25, 15081–15084.
2. J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115.
3. Z. Luo and A. Shehzad, ChemPhysChem, 2024, e202300715.
4. M. P. de Lara-Castells, Small Struct., 2024, 2400147.
5. A. Halder, C. Lenardi, J. Timoshenko, A. Mravak, B. Yang, L. K. Kolipaka, C. Piazzoni, S. Seifert, V. Bonačić-Koutecký, A. I. Frenkel, P. Milani and S. Vajda, ACS Catal., 2021, 11, 6210–6224.
6. H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911.
7. R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088.
8. L. Vega, H. A. Aleksandrov, R. Farris, A. Bruix, F. Viñes and K. M. Neyman, Mater. Adv., 2021, 2, 6589–6602.
9. E. Fernández and M. Boronat, J. Phys. Condens. Matter, 2019, 31, 013002.
10. S. Sharma and A. Ansari, Results Chem., 2023, 5, 100982.
11. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
12. M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500.
13. P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074.
14. M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759.
15. M. A. Abbas, P. V. Kamat and J. H. Bang, ACS Energy Lett., 2018, 3, 840–854.
16. V. Bonačić-Koutecký and R. Antoine, Nanoscale, 2019, 11, 12436–12448.
17. M. V. Romeo, E. López-Martínez, J. Berganza-Granda, F. Goñi-de Cerio and A. L. Cortajarena, Nanoscale Adv., 2021, 3, 1331–1341.
18. G. F. Combes, A.-M. Vučković, M. Perić Bakulić, R. Antoine, V. Bonačić-Koutecky and K. Trajković, Cancers, 2021, 13, 4206.
19. K. Zheng and J. Xie, Trends Chem., 2020, 2, 665–679.
20. Q. Zhang, M. Yang, Y. Zhu and C. Ma, Curr. Med. Chem., 2018, 25, 1379–1396.
21. H.-T. Sun and Y. Sakka, Sci. Technol. Adv. Mater., 2014, 15, 014205.
22. L. Zhang and E. Wang, Nano Today, 2014, 9, 132–157.
23. L. L. Carroll, L. V. Moskaleva and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2023, 25, 15729–15743.
24. M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804.
25. A. Heßelmann, J. Chem. Phys., 2008, 128, 144112.
26. M. Pitoňák and A. Heßelmann, J. Chem. Theory Comput., 2010, 6, 168–178.
27. I. Soteras, M. Orozco and F. J. Luque, Phys. Chem. Chem. Phys., 2008, 10, 2616–2624.
28. B. Fernández, M. Pi and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2023, 25, 16699–16706.
29. M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119.
30. S. R. Langhoff, C. W. Bauschlicher, S. P. Walch and B. C. Laskowski, J. Chem. Phys., 1986, 85, 7211–7215.
31. R. R. Persaud, M. Chen, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2019, 123, 1198–1207.
32. A. O. Mitrushchenkov and M. P. de Lara-Castells, ChemPhysChem, 2023, 24, e202300317.
33. K. M. Krupka and M. P. de Lara-Castells, 2024, in peer review.
34. M. P. de Lara-Castells, R. Fernández-Perea, F. Madzharova and E. Voloshina, J. Chem. Phys., 2016, 144, 244707.
35. A. W. Hauser and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2017, 19, 1342–1351.
36. A. W. Hauser, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 3807–3821.
37. M. P. de Lara-Castells, A. W. Hauser, A. O. Mitrushchenkov and R. Fernández-Perea, Phys. Chem. Chem. Phys., 2017, 19, 28621–28629.
38. R. Fernández-Perea, L. F. Gómez, C. Cabrillo, M. Pi, A. O. Mitrushchenkov, A. F. Vilesov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 22248–22257.
39. M. Liao, R. Grenier, Q.-D. To, M. P. de Lara-Castells and C. Léonard, J. Phys. Chem. C, 2018, 122, 14606–14614.
40. A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. Lett., 2016, 7, 4929–4935.
41. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
42. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
43. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
44. B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748.
45. G. Jansen and B. A. Hess, Phys. Rev. A, 1989, 39, 6016–6017.
46. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
47. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53.
48. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
49. M. P. de Lara-Castells, R. V. Krems, A. A. Buchachenko, G. Delgado-Barrio and P. Villarreal, J. Chem. Phys., 2001, 115, 10438–10449.
50. D. Feller, J. Chem. Phys., 1993, 98, 7059–7071.
51. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
52. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
55. A. O. Mitrushchenkov, A. Zanchet, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. A, 2021, 125, 9143–9150.
56. J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822.
57. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
58. D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. López-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, Chem.–Eur. J., 2023, 29, e202301517.
59. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
60. R. S. Mulliken, J. Chem. Phys., 1962, 36, 3428–3439.
61. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197.
62. D. G. A. Smith, L. A. Burns, D. A. Sirianni, D. R. Nascimento, A. Kumar, A. M. James, J. B. Schriber, T. Zhang, B. Zhang, A. S. Abbott, E. J. Berquist, M. H. Lechner, L. A. Cunha, A. G. Heide, J. M. Waldrop, T. Y. Takeshita, A. Alenaizan, D. Neuhauser, R. A. King, A. C. Simmonett, J. M. Turney, H. F. Schaefer, F. A. Evangelista, A. E. DePrince, T. D. Crawford, K. Patkowski and C. D. Sherrill, J. Chem. Theory Comput., 2018, 14, 3504–3511.
63. M. Hapka, P. S. Żuchowski, M. M. Szczęśniak and G. Chałasiński, J. Chem. Phys., 2012, 137, 164104.
64. K. Madajczyk, P. S. Żuchowski, F. Brzęk, L. Rajchel, D. Kędziera, M. Modrzejewski and M. Hapka, J. Chem. Phys., 2021, 154, 134106.
65. M. Hapka, M. Przybytek and K. Pernal, J. Chem. Theory Comput., 2018, 15, 1016–1027.
66. M. Hapka, M. Przybytek and K. Pernal, J. Chem. Theory Comput., 2019, 15, 6712–6723.
67. M. Hapka, M. Przybytek and K. Pernal, J. Chem. Theory Comput., 2021, 17, 5538–5555.
68. K. Pernal, M. Hapka, M. Przybytek, M. Modrzejewski, A. Sokół and A. Tucholska, GammCor Code, 2023, https://github.com/pernalk/GAMMCOR.
69. Z. Bačić and J. C. Light, Annu. Rev. Phys. Chem., 1989, 40, 469–498.
70. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557.
71. W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468.
72. In order to assess the reliability of the single reference method, the coupled cluster diagnostics⁷¹ have been examined for the CCSD(T)-based equilibrium geometry of Cu₃–benzene structures: T₁ < 0.05, D₁ < 0.15, and |%TAE| < 10%, with %TAE being the percent total atomization energy (see ref. 71). This way, for the Cu₃–benzene complex, we found that T₁ = 0.03, D₁ = 0.1, and |%TAE| = 2%.
73. M. Boggio-Pasqua and G. Groenhof, Comput. Theor. Chem., 2014, 1040–1041, 6–13.
74. V. Hänninen, M. Korpinen, Q. Ren, R. Hinde and L. Halonen, J. Phys. Chem. A, 2011, 115, 2332–2339.
75. R. Schäffer and G. Jansen, Theor. Chem. Acc., 2012, 131, 1235.
76. R. Schäffer and G. Jansen, Mol. Phys., 2013, 111, 2570–2584.
77. M. P. de Lara-Castells, R. Fernández-Perea, F. Madzharova and E. Voloshina, J. Chem. Phys., 2016, 144, 244707.
78. F. Della Sala and A. Görling, J. Chem. Phys., 2001, 115, 5718–5732.
79. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
80. H. Stoll, J. Chem. Phys., 1992, 97, 8449–8454.
81. S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154.
82. V. Staemmler, J. Phys. Chem. A, 2011, 115, 7153–7160.
83. M. P. de Lara-Castells, H. Stoll and A. O. Mitrushchenkov, J. Phys. Chem. A, 2014, 118, 6367–6384.
84. M. P. de Lara-Castells, M. Bartolomei, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 194701.
85. M. P. de Lara-Castells, R. Fernández-Perea, F. Madzharova and E. Voloshina, J. Chem. Phys., 2016, 144, 244707.
86. W. E. Carlos and M. W. Cole, Surf. Sci., 1980, 91, 339.
87. L. W. Brunch, M. C. Cole and E. Zaremba, Physical Adsorption: Forces and Phenomena, Clarendon Press, Oxford, 1997.
88. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
89. K. T. Tang and J. P. Toennies, J. Chem. Phys., 1984, 80, 3726–3741.
90. A. W. Hauser and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2017, 19, 1342–1351.
91. R. Podeszwa and K. Szalewicz, J. Chem. Phys., 2012, 136, 161102.
92. R. Podeszwa, K. Pernal, K. Patkowski and K. Szalewicz, J. Phys. Chem. Lett., 2010, 1, 550–555.
93. J. Granatier, P. Lazar, M. Otyepka and P. Hobza, J. Chem. Theory Comput., 2011, 7, 3743–3755.
94. R. Grenier, Q.-D. To, M. P. d. Lara-Castells and C. Léonard, J. Phys. Chem. A, 2015, 119, 6897–6908.
95. M. Liao, R. Grenier, Q.-D. To, M. P. de Lara-Castells and C. Léonard, J. Phys. Chem. C, 2018, 122, 14606–14614.
96. P. Schwerdtfeger and J. K. Nagle, Mol. Phys., 2019, 117, 1200–1225.

---

Footnote

† Electronic supplementary information (ESI) available: Plot of Cu₃–benzene interaction potentials at CCSD(T)-F12, UMP2C, RS2C(9,11), ‘RS2CC(9,11)’, and ‘RS2CC(9,11) weighted’ levels, additional details on the calculations: numerical values of interaction energies, dispersion and dispersionless energy contributions, intramonomer correlation energies, coronene structure with theoretical and experimental values of the bond lengths. See DOI: https://doi.org/10.1039/d4ra05401f

---