Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio study of electronic, elastic, thermodynamic, photocatalytic properties of double antiperovskite, Cs6AgBiX2 (X = Cl, Br, I)
Laraib Sajida,
M. Usman Saeeda,
S. H. Mashadib,
S. Sheryar Abidc,
Shamiala Pervaiza,
Zeeshan Alia,
Yousef Mohammed Alanazid,
Aziz-Ur-Rahim Bacha e and
Y. Saeed
e and
Y. Saeed *a
*a
aDepartment of Physics, Abbottabad University of Science and Technology, Abbottabad, KPK, Pakistan. E-mail: yasir.saeed@kaust.edu.sa; yasirsaeedphy@aust.edu.pk; Tel: +(92)-3454041865
bDepartment of Computer Sciences, Abbottabad University of Science and Technology, Abbottabad, KPK, Pakistan
cDepartment of Electrical Engineering, University of Azad Jammu & Kashmir, Muzaffarabad, Pakistan
dCollege of Engineering, Chemical Engineering Department, King Saud University, Riyadh, Saudi Arabia
eState Key Laboratory of Urban Water Resource and Environment, Shenzhen Key Laboratory of Organic Pollution Prevention and Control, School of Civil and Environmental Engineering, Harbin Institute of Technology Shenzhen, Shenzhen 518055, P. R. China
First published on 5th November 2024
Abstract
In this paper, we use density functional theory (DFT) using full-potential linearized augmented plan wave plus local orbital method (FP-LAPW + lo). The structural, electronic, optical, photocatalytic, mechanical, vibrational, and thermodynamical behaviors of new double antiperovskite (DAP) Cs6AgBiX2 (X = Cl, Br, I) were studied. The band structure was calculated with and without spin orbit coupling (SOC). Using the TB-mBJ approach (Hybrid) revealed bandgap values of 1.504 eV, 1.491 eV, and 1.392 eV for Cs6AgBiCl2, Cs6AgBiBr2, and Cs6AgBiI2, respectively. Optical characteristics were studied to ascertain the light absorbing ability of Cs6AgBiX2. The elastic and vibrational (phonon) properties demonstrate that Cs6AgBiCl2 and Cs6AgBiBr2 are stable but Cs6AgBiI2 is not. The calculated optimal bandgap and high absorption coefficient of Cs6AgBiCl2 and Cs6AgBiBr2, suggest their potential for solar cell applications. Moreover, our photocatalytic results suggest that these materials have high oxidizing capacity that can be used to efficiently produce oxygen cheaply using solar water splitting.
1 Introduction
Growing industrialization and fossil fuel use has significantly contaminated the environment and there is now a global energy crisis. To address this, researchers are turning to renewable energy sources, with solar energy being a key focus due to its safety and eco-friendliness.1–3 Perovskite materials are gaining attention for solar energy use because of their great properties like effective light absorption and improving power conversion efficiency. Researchers have been studying these materials extensively.4–6Perovskite has the crystal structure CaTiO3 and the formula ABX3, it is used in different forms like antiperovskite X3BA and double perovskite A2B′B′′X6. These structures offer unique qualities, like easy synthesis and stability.7–9 A recent addition is the double antiperovskite X6B′′B′A2, showing promise for various applications.10 Hybrid halide perovskites, like CH3NH3PbX3 are widely studied for efficient solar cells but their sensitivity to moisture and use of toxic lead, pose challenges. Seeking stable, lead-free alternatives has led to the exploration of double perovskite halides, such as Cs2AgBiX6. These compounds, like Cs2AgBiCl6 and Cs2AgBiBr6, are non-toxic and stable, making them promising for solar applications compared to the lead-containing alternatives. The unique structure of halide double perovskites has gained attention as a potential replacement for lead-based perovskite materials.11–15
van der Waals (vdW) interactions have been shown to have a significant impact on the geometry optimization and electronic properties of inorganic CH3NH3(Pb,Sn)(I, Br, Cl)3 halide perovskites. Studies have focused on the effects of these interactions on the structural and electronic properties of these perovskites. A hydrogen/ionic link between the halogen atoms and an ordinary amine group (NH3+) creates the bonding between organic and inorganic components (van der Waals interaction).16,17 Wang et al.18 presented a PD with a hybrid vdW heterostructure made of graphene (Gr)/1D CH3NH3PbI3 and hexagonal boron nitride (h-BN).
However, vdW heterostructures based on double perovskites are still uncommon but are known to have a significant role on the properties of 2D perovskites. Gao et al. constructed different heterostructures made up of CsCl, NaInCl, CsNaInCl, and Cl interfaces of the inorganic double perovskite Cs2NaInCl6 and two-dimensional transition metal–sulfur complexes XS2 (X = Cr, Mo, and W).19 Using DFT calculations, properties of the 2D (C4H9NH3)2PbI4/black phosphorus (BP) vdW heterostructure have been investigated.20 Furthermore, density functional theory considering vdW, was used to calculate the electron structure and interface properties of inorganic perovskite (without organic cation), results show weak vdW forces between the interfaces of Cs2AgBiBr6 and Ti3C2Tx (to maintain its semiconductor characteristics).21 There is no study for vdW interactions in 3D inorganic double perovskites or double anti-perovskites as compared to 2D and heterostructures.
Recently, Rani et al. explored some new double antiperovskites Na6SOCl2, Na6SOBr2, Na6SOI2, K6SOCl2, K6SOBr2 and K6SOI2 with bandgaps of 4.34 eV, 3.71 eV, 3.33 eV, 3.99 eV, 3.38 eV and 2.90 eV, respectively, and show that they are good for thermoelectric applications.22 Yu et al. predict that Na6SOI2 is specifically appealing for solid sodium-ion battery applications at low temperatures.23 Mebrouki et al. examined the process by which temperature effects the BaVO3 elastic constants C11, C12, and C44, less progressively as temperature rises.24 Djebari et al. calculated the octahedral factor, the formation energy, the tolerance factor etc. to confirm the structural stability of A3+B4+(O2N)7− and A2+B5+(O2N)7−. Based on the computed bandgaps, photovoltaic and ferroelectric devices could find use for them.25 Gao et al. discovered that the coefficient of thermal expansion is negatively impacted by variations in pressure and temperature.26 Since the double antiperovskite has just recently been proposed, there are not many reports on tests or theoretical calculations, suggesting that this might be a new line of inquiry. Presently, we are examining the features of double antiperovskites Cs2AgBiX6 (X = Cl, Br, I). We are examining the expected material’s structural, electrical, elastic and optical properties, focusing on those with a bandgap similar to MAPI.27
2 Computational details
Using the Wien2k code, we ran our calculations using the full-potential linearized augmented plane wave plus local orbitals (FP-LAPW + lo) technique, which is a component of DFT.28 Using the more accurate exchange-correlation potential flavor of the generalized gradient approximation (WC-GGA), structural, electrical, and thermodynamic features are investigated.29 To acquire precise bandgap data, we implemented the modified Becke-Johnson (mBJ) scheme across the WC-GGA.30,31 In the past, the mBJ plan provided promising band structures and bandgap values for lead halide perovskites and other semiconductors when compared to experimental results.32–37 The scheme mBJ across WC-GGA gives results close to the experimental results for Cs6AgBiX2 (X = Cl, Br and I). The accuracy of our calculations is mainly affected by two factors: one is the total number of k points, so for the Brillouin zone (BZ) integration a k-mesh of 13 × 13 × 13 was used and a finer k-mesh of 24 × 24 × 24 for electronic and optical properties. Another factor is cutoff kinetic energy which determines the number of plane wave expansions inside the muffin-tin radii, here the cutoff energy is set to be −7.0 Ryd, which separates the valence states from the core states of electrons. The plane-wave expansion cutoff was expanded up to Gmax = 20 and the angular momentum of the sphere is lmax = 12. All structures were optimized with an energy convergence tolerance of up to 10−5 Ryd.38–413 Results and discussion
3.1 Structural properties
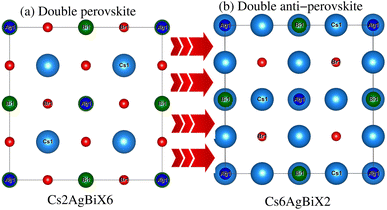
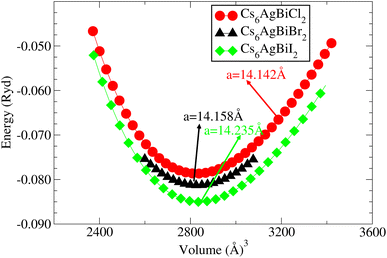
Understanding the different physical characteristics of a substance is crucial and understanding structural characteristics is essential for this. Fig. 1 shows the transformation of double perovskite into a double anti-perovskite crystal structure. The proposal aims to optimize the structural properties of Cs6AgBiX2 (X = Cl, Br, I) by reducing the energy to its ground state. The starting point for the optimization procedure is the lattice parameter of experimental Cs2AgBiCl6. The volume optimization curve, which represents the relationship between energy and volume, is plotted in Fig. 2 for Cs6AgBiX2 (X = Cl, Br, I). To fit the nonlinear plot of energy vs. volume we used the initial lattice parameter values for Cs2AgBiX6 (X = Cl and Br) as a reference. The volume optimization was used to calculate structural parameters such as bulk modulus B (GPa) and lattice constant a (Å), for Cs6AgBiX2 (X = Cl, Br, I). Table 1 shows the structural characteristics, which were determined by applying Birch–Murnaghan's equation of states.44 The optimized lattice constants for all compounds fall within the range 14.14 Å to 14.24 Å, closely aligning with experimentally synthesized double perovskites like Cs2AgBiCl6 and Cs2AgBiBr6, which have lattice constants of 10.77 Å and 11.27 Å.14 The optimized bulk modulus (B) ranges from 4.63 GPa to 5.16 GPa as presented in Table 1. Unfortunately, experimental or theoretical data for comparison with these optimized compounds is not available.| Materials | a = b = c (Å) | Bulk modulus B (GPa) | GGA Eg (eV) | GGA + SOC Eg (eV) | Hybrid Eg (eV) |
|---|---|---|---|---|---|
| Cs6AgBiCl2 | 14.14 | 4.63 | 0.91 | 0.72 | 1.50 |
| Cs6AgBiBr2 | 14.16 | 5.10 | 0.84 | 0.65 | 1.49 |
| Cs6AgBiI2 | 14.24 | 5.16 | 0.78 | 0.59 | 1.39 |
3.2 Electronic band structure
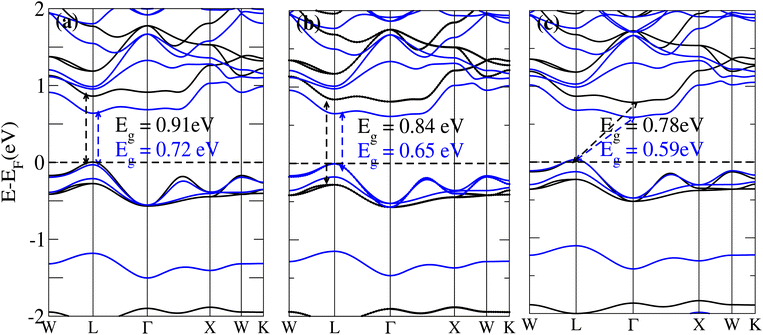
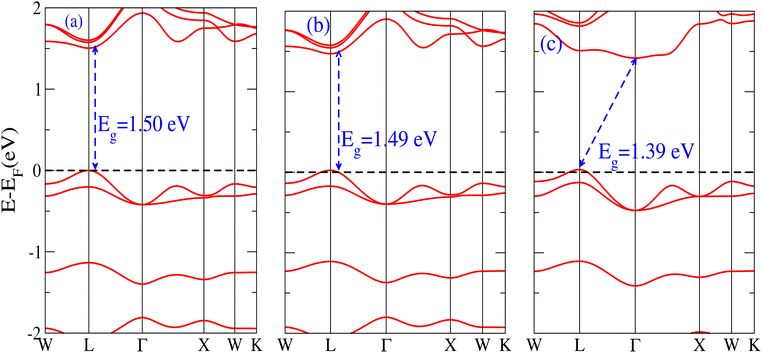
The behavior of a material is profoundly shaped by its band structure, a critical aspect for studying its properties. Analyzing the band structure, including determining its metallic or semiconducting nature, provides valuable insights into the electronic characteristics of the material. This electronic band structure is essential for understanding the optical behaviour and resistivity of solids, which are important for the design of solid-state electronics like solar cells and transistors. The band gap is either direct or indirect, the dispersion of bands informs us of the electronic behavior through which we can specify the physical properties of materials. Consequently, we conducted band structure calculations for Cs6AgBiX2 (X = Cl, Br, I) and examined their electronic conduct for further analysis. The initial bandgap calculations for each compound utilized a simple self-consistent field (SCF) approach without considering spin–orbit coupling (SOC). Similarly, this was also done in order to obtain bandgap values that nearly match the experimental bandgap value of MAPI (1.55 eV), producing a straight bandgap as a result at the symmetry point similar to MAPI.42 Additionally, mBJ + SOC (Hybrid) was utilized to modify the bandgap values in order to better correlate with the experimental MAPI, as a good solar cell absorber. The bandgap of CH3NH3PbCl3 is 3 eV, while the band gap of CH3NH3PbBr3 is 2.26 eV.43 The experimental (theoretical) bandgap values for Cs2AgBiCl6 and Cs2AgBiBr6, which were previously reported as 2.77 (2.62) eV and 2.19 (2.06) eV, respectively, were recalculated as a baseline with a similar approach.14,43 We computed bandgap values of 1.50 eV (Cl), 1.49 eV (Br), and 1.39 eV (I) for Cs6AgBiX2 (X = Cl, Br, I) with hybrid, respectively. These are close to MAPI, hence proving that anti-double perovskite could reduce the bandgap values substantially as compared to double perovskites. While with SOC, and without SOC, bandgap results are listed in Table 1 and are explained in Fig. 3 and 4.Our analysis leads to the conclusion that the FP-LAPW + lo technique, without considering mBJ + SOC, tends to substantially underestimate bandgap values in double antiperovskites. Consequently, our objective is to identify a lead-free material with a bandgap value approximately equal to 1.5 eV, serving as a potential replacement for MAPI at room temperature.45
The bandgap values for Cs6AgBiCl2, Cs6AgBiBr2 and Cs6AgBiI2 are 0.91 eV, 0.84 eV and 0.78 eV, in the absence of SOC. The bandgap values of these materials with and without SOC are depicted in Fig. 3a–c. The band structure of Cs6AgBiCl2 has a bandgap value of 0.91 eV in the absence of SOC and 0.72 eV in the presence of SOC. The band structure of Cs6AgBiBr2 has a bandgap value of 0.84 eV in the absence of SOC and 0.65 eV in the presence of SOC. These two materials have a direct bandgap as shown in Fig. 3a and b while the band structure of Cs6AgBiI2 has a bandgap value of 0.78 eV in the absence of SOC and 0.59 eV in the presence of SOC as shown in Fig. 3c.
It is observed that the bandgap values decreased slightly for Cs6AgBiX2 (X = Cl, Br, I) after applying SOC. The bandgap values of Cs6AgBiCl2 and Cs6AgBiBr2 align closely with the experimentally calculated values of CH3NH3PbI3 (1.55 eV). Within the bandgap of 1.39 to 1.50 eV (see Fig. 4), efficient semiconductor solar cells can be developed, enabling the release of electrons without generating a substantial amount of heat. While some recently investigated double antiperovskites have a direct bandgap, their values exceed this optimal range. Others within the mentioned range, although having an indirect bandgap, are not suitable for solar cell applications. Pressure-induced bandgap tuning could potentially bring the bandgap close to 1.5 eV.
3.3 Density of states (DOS)
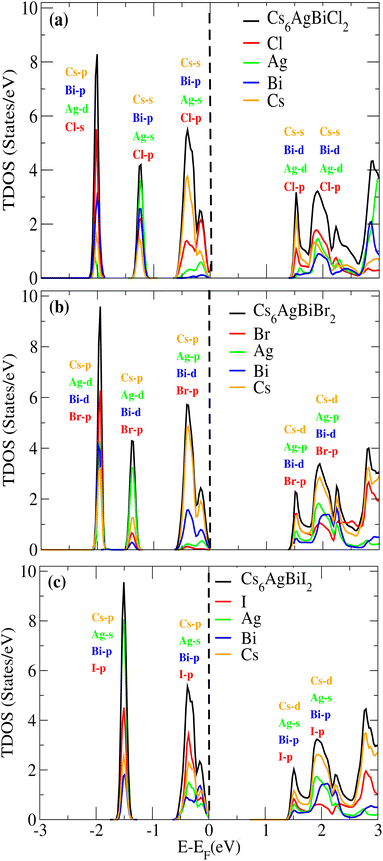
We examined the density of states (DOS) for Cs6AgBiX2 (X = Cl, Br, I) in order to evaluate the individual contributions of Cs, Ag, Bi, Cl, Br and I atoms to the valence band maxima (VBM) and conduction band minima (CBM), as depicted in Fig. 5a–c.In Fig. 5a and b, it is evident that the VBM is predominantly influenced by the Cs atom in both materials, while the CBM is shared between Cs and Cl/Br atoms. Notably, Br atoms significantly contribute to the bandgap value. Further insights into the orbital contributions of Cl and Br in the VBM and CBM were gained by examining the PDOS, which is also illustrated in Fig. 5 for Cs6AgBiX2 (Cl, Br, I).
The range of the valence band is −3 to 0 and the conduction band range is 0 to 3, and the 0 point represents the Fermi level. Fig. 5a reveals that the Cs-s orbital plays a dominant role in both CBM and VBM, while other atoms have a relatively small contribution compared to these two atoms. The p-orbital of Cl also exhibits significance in the CBM, whereas the contributions of d orbitals are minor in VBM. In VBM, the p-orbital of Bi plays a crucial role, with Cl's p-orbital occupying the entire VBM up to 2 eV, however Br's d-orbital does not contribute much to either the CBM or VBM. Also, compared to Ag and Bi, the effect of Cl's p-orbital on VBM is greater. According to Fig. 5b, comparable patterns are seen in the DOS: Br's p-orbital and Cs's d-orbital completely dominate the CBM and Cs's p-orbital completely dominates the VBM. According to Fig. 5c, similar patterns are seen in the DOS: I's p-orbital and Cs's p-orbital completely dominate the CBM and Cs's d-orbital completely dominates the VBM.
3.4 Optical properties
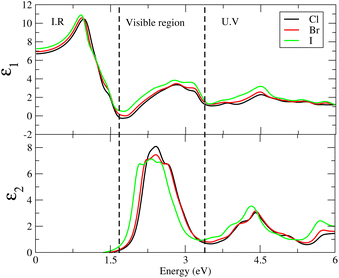
Studying the optical characteristics of materials is essential from the standpoint of the industrial manufacture of optical devices like sensors, lasers, modulators, solar calculators and optical coatings. One promising option for optical materials production is perovskite high-performing optoelectronic devices.45,46 The optical characteristics such as the complex dielectric function, ε(ω) = ε1(ω) + iε2(ω), can be utilized to describe a material's reaction to an external electromagnetic field,47 where ε1(ω) and ε2(ω) are the real and imaginary parts of ε(ω). In the relation ε1(ω), is the dielectric constant, which expresses the amount of material polarized by induced electric dipole formation in the presence of an electric field, whereas ε2(ω) indicates the capacity for electromagnetic waves to transmit and attenuate them. The dielectric characteristics ε(ω) are closely linked to the combined density of states (DOS) and transition momentum matrix components. The real part of the dielectric function, ε1(ω), can be obtained from ε2(ω) using Kramers–Kronig relationship.48 The wave is diminishing and cannot propagate if the value of ε < 0; if ε1(ω) > 0 light can propagate through the material.49,50The dispersion of the real and imaginary components of the dielectric characteristics can be analyzed to compute the refractive index, optical conductivity, reflection and absorption coefficients among other optical properties.
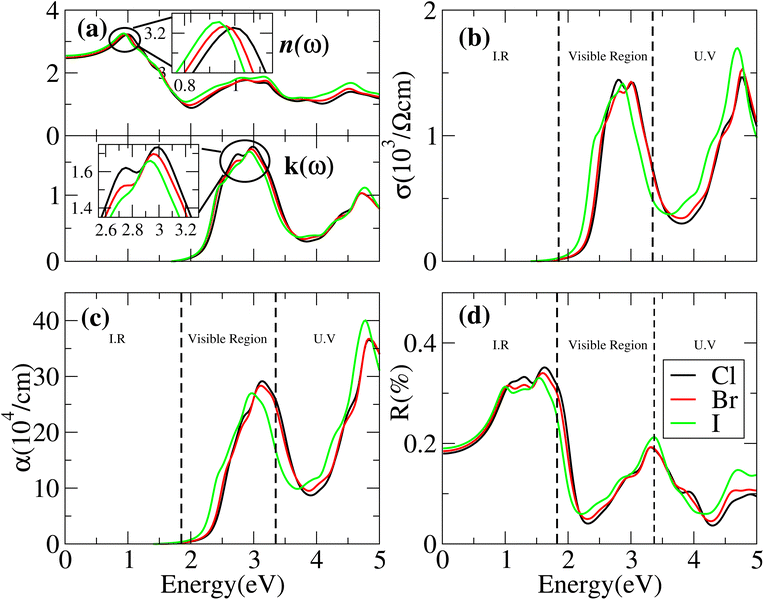
The optical properties of solids can be explained by the refractive index n(ω) and extinction co-efficients k(ω). In the case of n(ω) < k(ω) the incident rays are reflected and the behavior of materials is dielectric to metallic. It is more advantageous for materials with high dielectric constants to be used in solar cells since they often have low exciton binding energy.51
Cs6AgBiX2 (Cl, Br, I) have ε1 9.57, 9.75 and 10.19, respectively, which are greater than Cs2LiTlBr6 (1.6), Cs2NaTlBr6 (1.7), Cs2AgCrI6 (5.7), MAPbI3 (5.4) and FAPbI3 (5.7), other potential candidates for solar cell applications.51–56 It is important to reach maximum polarization characteristics, as indicated by the size of ε1(ω), in order to obtain optimal semiconductor performance. In the visible light range, ε1(ω) approaches peak polarization values of 11.96, 8.77 and 8.63 at 1.0 eV, 0.91 eV, and 0.90 eV, respectively; and ε2(ω) imaginary part shows the light absorption with ε2(ω) values 8.6, 7.9 and 7.5 at −3.0 eV, −3.8 eV, −4.3 eV. None of these compounds are in the visible region. Computations based on the distribution of the dielectric characteristics with real and imaginary parts are shown in Fig. 6, and provide important new information on the linear optical behavior of these materials. We calculated parameters such as the refractive index (n), extinction coefficient (k), absorption coefficient I(ω), optical conductivity σ(τ), and reflectivity R(ω), in order to analyze the optical properties of Cs6AgBiX2 (X = Cl, Br, I), as illustrated in Fig. 7. For Cs2LiTlBr6 and Cs2NaTlBr6, the static dielectric constants ε(0) are 1.6 eV and 1.7 eV, respectively.46 So here our study produced comparable findings. Looking at Fig. 7a, we can see that both materials, Cs6AgBiCl2 and Cs6AgBiBr2, have a static refractive index (n(ω)) with values of 3.2 and 3.1, respectively. In Cs2LiTlBr6 the highest values for n(ω) and k(ω) are 1.8 eV and 2.6 eV, while for Cs2NaTlBr6, these values are 2.5 eV for n(ω) and 3.2 eV for k(ω). The optical conductivity (σ) of Cs6AgBiCl2 peaks at 650 (Ω cm)−1 at 2.6 eV in Fig. 7b, whereas Cs6AgBiBr2 peaks at 500 (Ω cm)−1 at 3 eV. Because of this, Cs6AgBiCl2 has exceptionally high optical conductivity in the visible light spectrum (1.77 eV to 3.1 eV) which is important for solar cell applications. The efficiency of solar energy conversion is often described by the absorption coefficient, representing how specific light frequencies penetrate the material before absorption. For Cs6AgBiCl2 and Cs6AgBiBr2, the absorption coefficient spectrum I(ω) shows peaks of 12 × 104 cm−1 at 2.6 eV (477 nm) and 11 × 104 cm−1 at 3.2 eV, respectively (Fig. 7c). These values are comparable to those of MAPI (methylammonium lead iodide) at 104–105 cm−1. The absorption coefficient increases rapidly as incident photons approach the absorption edge, with Cs6AgBiCl2 exhibiting higher absorption in the visible region compared to Cs6AgBiBr2. Lastly, in Fig. 7d, the maximum reflectivity R(ω) for Cs6AgBiCl2 and Cs6AgBiBr2 is 13.5% at approximately 1.6 eV and 9% at 2.2 eV, respectively.
3.5 Photocatalytic properties
Suitable indirect bandgap semiconductors can be used to utilize solar energy to generate hydrogen by dissociating water.57,58 Therefore, clean renewable energy can be produced through photocatalytic water splitting.59,60 Water is oxidized by holes and reduced by electrons in the photocatalytic process.61The oxidation–reduction potential of O (1.23) eV for this operation needs to be smaller (higher) than the conduction (valence) band photocatalytic water splitting for all materials under consideration (Table 2).
| Compounds | χ (eV) | Eg (eV) | ECBM | EVBM |
|---|---|---|---|---|
| Cs6AgBiCl2 | 1.17 | 1.50 | −1.06 | −2.57 |
| Cs6AgBiBr2 | 1.16 | 1.49 | −1.10 | −2.59 |
| Cs6AgBiI2 | 1.14 | 1.39 | −1.26 | −2.65 |
Mullikan electronegativity is used to explore this:
| EVBM = χ − Eelec + 0.5Eg | (1) |
| ECBM = EVBM + Eg | (2) |
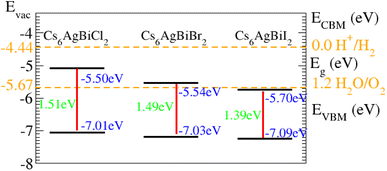
As displayed in Fig. 8, on the hydrogen scale the standard oxidation and reduction potentials for photocatalytic water splitting are (−4.44 eV) and (−5.67 eV), respectively.62 The Fermi level is set to (−4.44) eV in order to determine the band edge positions of the VB and CB with respect to standard oxidation.62 The CB and VB are set to (0 eV = −4.44 eV) and (1.23 eV = ¬5.67 eV).63 It is clear from the figure that all the materials show good responses for the oxidation of water but fail to produce hydrogen from water.
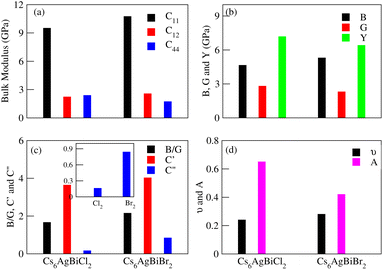
3.6 Elastic properties
The effective elastic constants are essential for determining a material's practical applications, providing information about its reactivity to outside influences and structural stability. The elastic constants C11, C12, C44, shear moduli G and Bulk moduli B are the key points of elastic properties. These properties help us to understand the material demand in industrial applications. In the case of Cs6AgBix2 (x = Cl, Br, I) the calculated elastic constants are detailed in Table 3 and graphical analysis is given in Fig. 9. The materials Cs6AgBiCl2 are Cs6AgBiBr2 meet the requirements of Born–Huang stability for cubic crystal stability, that is C11 > 0, C44 > 0, C11 + 2C12 > 0, C11 − C12 > 0 and C12 < B < C11 are satisfied64 while Cs6AgBiI2 does not meet the criteria. So it is unstable.| Constants | Cs6AgBiCl2 | Cs6AgBiBr2 | Cs6AgBiI2 |
|---|---|---|---|
| C11 | 9.5 | 10.74 | 9.15 |
| C12 | 2.22 | 2.56 | 3.17 |
| C44 | 2.38 | 1.72 | −3.65 |
| B | 4.64 | 5.10 | 5.16 |
| Gv | 2.8 | 2.67 | −0.99 |
| GR | 2.7 | 2.24 | −32.67 |
| GH | 2.8 | 2.45 | −16.83 |
| Y | 7.17 | 6.86 | −3.18 |
| B/G | 1.66 | 2.15 | 0.30 |
| C′′ | −0.16 | 0.84 | 6.82 |
| ν | 0.24 | 0.28 | 0.60 |
| A | 0.65 | 0.42 | −1.22 |
| C′ | 3.64 | 4.09 | 2.99 |
| Az | 1.73 | 1.55 | 0.54 |
| Au | 0.22 | 0.95 | −4.84 |
| ξ | 0.38 | 0.39 | 0.49 |
| T(m) | 609.15 | 616.48 | 607.08 |
 | ||
| Fig. 9 Graphical view of elastic properties for elastically stable Cs6AgBiCl2, Cs6AgBiBr2 and Cs6AgBiI2. | ||
The elastic constants can be calculated using the following Voigt–Reuss–Hill approximation where, in the formulas BV = BR = C11 + 2C12/3, GV = C11 − C12 + 3C44 and GR = 5C44(C11 − C12)/(4C44 + 3C11 − 3C12), subscripts V and R stand for Voigt bound and Reuss bound, respectively.65 In Table 3, we can see that the Gv of Cs6AgBiX2 (Cl, Br, I) decreases continuously which shows that the resistive behavior of these materials is in the order Cs6AgBiCl2 > Cs6AgBiBr2 > Cs6AgBiI2.
Poisson's ratio (ν) or Pugh's ratio (B/G) can be used to evaluate a material's toughness and brittleness. When ν is less than 0.26 or B/G is less than 1.75, the material is considered ductile.66 Here, only one material, Cs6AgBiCl2, is ductile while the other two are brittle as their ν and B/G values are greater than 0.26 and 1.75, respectively. Ionic materials typically have a ν range of 0.3–0.4, but the limit for pure ionic materials is 0.5. Covalent materials usually have ν values around 0.2 and for Cs6AgBiX2 (X = Cl, Br, I), they are 0.24, 0.28 and 0.59, indicating a greater ionic property than covalent property.67
Elastic anisotropy is associated with the development of microcracks during the use of a material, we computed this for Cs6AgBiX2 (X = Cl, Br, I) using the anisotropy index A = 2C44/(C11 − C12). A material is isotropic if A is either 0 or 1; otherwise, it exhibits anisotropy.68,69 The mechanical properties, given in Table 3, were analyzed using standard relations. Cs6AgBiCl2 shows greater shear modulus (GH) and Young's modulus (Y) values, indicating greater stiffness and resistance against plastic deformation compared to Cs6AgBiBr2.
Cauchy's pressure (C′′ = C12 − C44) values, whether positive or negative are presented in Table 3, further elucidate the ductile nature of Cs6AgBiCl2. The positive values of C′′ for Cs6AgBiBr2 and Cs6AgBiI2 reinforce the materials' brittleness. The shear constant (GH), determining a material's dynamic stability, has a positive value for Cs6AgBiCl2, Cs6AgBiBr2 and Cs6AgBiI2 in Table 3, affirming their mechanical stability.
In order to graphically portray the anisotropic and elastic behavior of the materials under study, three-dimensional (3-D) contour plots of the Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (ν) have been created using the Elate Code.70 Fig. 10 and 11, respectively, show the resulting 3-D visual representations for Cs6AgBiCl2 and Cs6AgBiBr2. Notably, all other constants show large deviations from a fully spherical (3-D) shape, with the exception of linear compressibility, highlighting the anisotropic character of these materials.
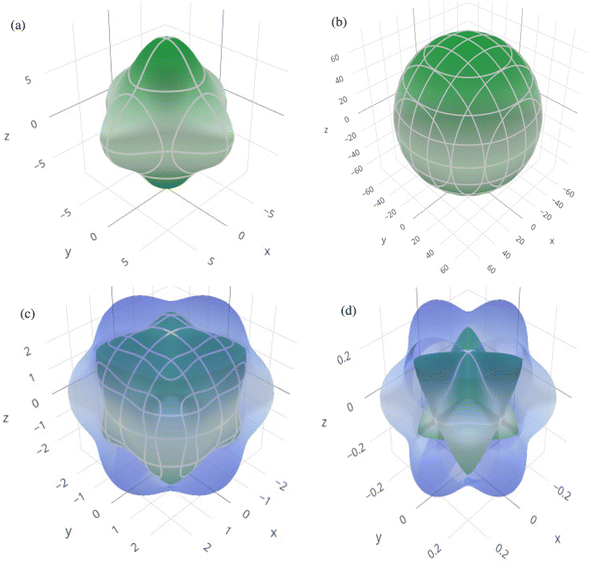 | ||
| Fig. 10 3D spatial dependence of (a) Young's modulus, (b) linear compressibility, (c) shear modulus and (d) Poisson's ratio for Cs6AgBiCl2. | ||
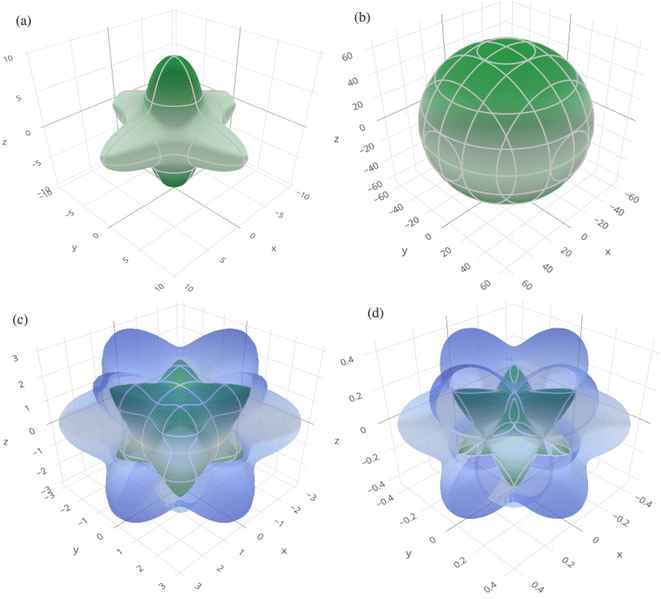 | ||
| Fig. 11 3D spatial dependence of (a) Young's modulus, (b) linear compressibility, (c) shear modulus and (d) Poisson's ratio for Cs6AgBiBr2. | ||
Additionally, anisotropic parameters, such as Zener (AZ) and Universal anisotropic parameters (AU), have been determined using the second-order elastic constants (SOECs).71,72 Table 3 presents the computed values for these parameters. In isotropic materials, the Zener elastic parameter, which is mainly related to shear anisotropy in materials, stays constant at 1. But any departure from unity, as we can observe in AU and AZ in Table 3, indicates that the material under study exhibits anisotropic behavior. The elastic constants have later been used to calculate the Kleiman parameter (ξ). Table 3 indicates that the materials have a higher resistance against bond angle distortions and bond bending due to the observed low value of ξ.
We determined the melting temperature using the following equation in order to assess their stability at high temperatures,73
| T(m) = [553 + 5.911C11] ± 300 | (3) |
The predicted melting temperatures are determined to be 609.15 ± 300 K for Cs6AgBiCl2, 616.48 ± 300 K for Cs6AgBiBr2 and 607.08 ± 300 K for Cs6AgBiI2. Notably, the high value of the melting temperature suggests that these materials exhibit stability even under extreme temperatures.
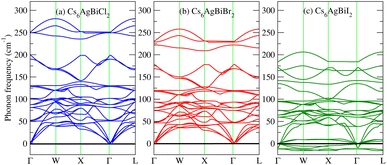
3.7 Phonon dispersion and thermal properties
To further confirm the stability, adding to the elastic constant results, we use a 2 × 2 × 2 supercell in the well -established PHONOPY package.74,75 The calculated phonon band structures of Cs6AgBiCl2, Cs6AgBiBr2 and Cs6AgBiI2 are shown in Fig. 12a–c. Cs6AgBiCl2 and Cs6AgBiBr2 are dynamically stable which also validates the elastic results, while Cs6AgBiI2 has negative phonon frequencies up to −25 cm−1. Hence, Cs6AgBiI2 has been shown to be unstable by elastic as well as vibrational analysis.Aside from these elastic constants, Debye temperature (ΘD) is an important thermal parameter that is closely linked to several physical properties such as a compound’s melting point and specific heat capacity. It is possible to calculate Debye temperature using average sound velocity vm.76
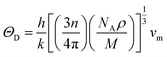 | (4) |
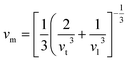 | (5) |
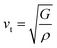 | (6) |
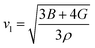 | (7) |
Table 4 displays the values of vt, vl, vm, and ΘD that were derived from the aforementioned relations. Cs6AgBiCl2 and Cs6AgBiBr2 have the highest Debye temperature indicating that these are thermally more conductive. These findings also provide insight into the bond strength hierarchy.
| Compound | Cs6AgBiCl2 | Cs6AgBiBr2 |
|---|---|---|
| vt (m s−1) | 1006.9 | 904.04 |
| vl (m s−1) | 1737.84 | 1670.64 |
| vm (m s−1) | 1086.32 | 985.35 |
| ΘD (K) | 473.6 | 451.3 |
| ωD (THz) | 61.9 | 58.9 |
4 Conclusion
In this work, structural, electronic, optical, photocatalytic, mechanical, vibrational, and thermodynamical behaviors were studied for new double antiperovskite (DAP) Cs6AgBiX2 (X = Cl, Br, I). Band structures were calculated with and without spin orbit coupling (SOC). Using the TB-mBJ approach (hybrid) reveals bandgap values of 1.504 eV, 1.491 eV, and 1.392 eV for Cs6AgBiCl2, Cs6AgBiBr2, and Cs6AgBiI2 respectively. To gain deeper insight into the orbital contributions of chlorine (Cl), bromine (Br), and iodine (I) near the Fermi level, analysis of the total density of states (TDOS) and partial density of states (PDOS) were studied. In addition to electronic properties, the investigation extended to optical properties, including real and fictitious refractive indexes, extinction coefficients, optical conductivities, absorption coefficient, and reflectivity. The elastic and phonon properties demonstrate that Cs6AgBiCl2 and Cs6AgBiBr2 are stable except Cs6AgBiI2. The calculated optimal bandgap (∼1.5 eV) and high absorption coefficient (∼30× 104 cm−1) of Cs6AgBiCl2 and Cs6AgBiBr2, suggest their potential for solar cell applications. In addition, our photocatalytic results suggest that these Cs6AgBiX2 have more oxidizing capacity due to good visible-light absorption capability that can be used for cheap oxygen production via solar water splitting.Data availability
Data will be made available upon request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors would like to acknowledge the Researcher's Supporting Project Number (RSP2024R511), King Saud University, Riyadh, Saudi Arabia. The author Y. Saeed would like to thank the Higher Education Commission (HEC) of Pakistan for providing a grant under NRPU-15844.References
- T. Wu, M. L. Yao and M. Q. Long, First principle calculations of interface interactions and photoelectric properties of perovskite CsPbX3 (X = Cl, Br, I) and penta-graphene van der Waals heterostructures, Acta Phys. Sin., 2021, 70, 056301 CrossRef.
- H. K. Ting, L. Ni, S. B. Ma, Y. Z. Ma, L. X. Xiao and Z. J. Chen, Progress in electron-transport materials in application of perovskite solar cells, Acta Phys. Sin., 2015, 64, 038802 CrossRef.
- P. Zhao, J. Su, Y. J. Guo, Z. H. Wang, Y. Lin, X. P. Hao, Ouyang and J. J. Chang, Cs2TiI6: a potential lead−free all−inorganic perovskite material for ultrahigh−performance photovoltaic cells and alpha-particle detection, Nano Res., 2022, 15, 2697–2705 CrossRef CAS.
- Y. Guo, Y. B. Xue and L. Q. Xu, Interfacial interactions and enhanced optoelectronic properties of GaN/perovskite heterostructures: insight from first-principles calculations”, J. Mater. Sci., 2021, 56, 11352–11363 CrossRef CAS.
- G. M. Sui, G. J. Yan, G. Yang, B. Zhang and Y. Q. Feng, Theoretical investigation on structure and optoelectronic performance of two-dimensional fluorbenzidine perovskites, Acta Phys. Sin., 2022, 71, 208801 CrossRef.
- D. Wang, H. M. Zhu, Z. M. Zhou, Z. W. Wang, S. L. Lv, S. P. Pang and G. L. Cui, Effect of solvent on the perovskite thin film morphology and crystallinity, Acta Phys. Sin., 2015, 64, 038403 CrossRef.
- Y. B. Fu, H. Wei, L. Wei, H. D. Zhang, X. P. Wang, B. Liu, Y. Y. Zhang, X. S. Lv, J. X. Zhou and H. J. Yu, Origin of the difference in thermal conductivity and anharmonic phonon scattering between LiNbO3 and LiTaO3, CrystEngComm, 2021, 23, 8572–8578 RSC.
- Y. N. Xiao, P. F. Sui, Y. C. Zhao, J. Ni, S. Meng and Z. H. Dai, Low lattice thermal conductivity of hydride-based cubic antiperovskites A3HB (A = Li, Na; B = S, Se, Te) with higher−order anharmonicity correction, Int. J. Energy Res., 2022, 46, 13687–13697 CrossRef CAS.
- Y. Liu, L. H. Ni, G. Xu, C. L. Song, G. R. Han and Y. Zheng, Phase transition in PbTiO3 under pressure studied by the first−principles method, Phys. B, 2008, 403, 3863–3866 CrossRef CAS.
- D. Han, C. B. Feng, M. H. Du, T. Zhang, S. Z. Wang, G. Tang, T. Bein and H. Ebert, Design of high−performance lead−free quaternary antiperovskites for photovoltaics via ion type inversion and anion ordering, J. Am. Chem. Soc., 2021, 143, 12369–12379 CrossRef CAS.
- J. Chen, X. Cai, D. Yang, D. Song, J. Wang, J. Jiang, A. Ma, S. Lv, M. Z. Hu and C. Ni, Recent progress in stabilizing hybrid perovskites for solar cell applications, J. Power Sources, 2017, 355, 98–133 CrossRef CAS.
- M. J. Fang, C. W. Tsao and Y. J. Hsu, Semiconductor nanoheterostructures for photoconversion applications, J. Phys. D: Appl. Phys., 2020, 53, 143001–143026 CrossRef CAS.
- Y. H. Chiu, T. H. Lai, M. Y. Kuo, P. Y. Hsieh and Y. J. Hsu, Photoelectrochemical cells for solar hydrogen production: Challenges and opportunities, APL Mater., 2019, 7, 080901–080911 CrossRef.
- Y. Saeed, B. Amin, H. Khalil, F. Rehman, H. Ali, M. I. Khan, A. Mahmood and M. Shafiq, Correction: Cs2NaGaBr6: a new lead-free and direct bandgap halide double perovskite, RSC Adv., 2020, 10, 17444–17451 RSC.
- M. Z. Rehman, S. A. M. Abdelmohsen, E. A. Mahmoud, M. U. Saeed, M. Idress, M. Shafiq, B. Amin and Y. Saeed, First principles study of structural, electronic, elastic and optical properties of Cs2LiTlBr6 and Cs2NaTlBr6, Mater. Sci. Semicond. Process., 2022, 151, 106993 CrossRef.
- N. Pandech, T. Kongnok, N. Palakawong, S. Limpijumnong, W. R. Lambrecht and S. Jungthawan, Effects of the van der Waals Interactions on Structural and Electronic Properties of CH3NH3(Pb, Sn)(I, Br, Cl)3 Halide Perovskites, ACS Omega, 2020, 5, 25723–25732 CrossRef CAS.
- H. Ferjani, Y. B. Smida and Y. Al-Douri, First-Principles Calculations to Investigate the Effect of Van der Waals Interactions on the Crystal and Electronic Structures of Tin-Based 0D Hybrid Perovskites, Inorganics, 2022, 10, 155 CrossRef CAS.
- G. Wang, B. Han, C. H. Mak, J. Liu, B. Liu, P. Liu, X. Hao, H. Wang, S. Ma, B. Xu and H.-Y. Hsu, Mixed-dimensional van der waals heterostructure for high-performance and air-stable perovskite nanowire photodetectors, ACS Appl. Mater. Interfaces, 2022, 14, 55183–55191 CrossRef CAS.
- S. Gao, W. Chen, E. Abduryim, C. Chen, C. Dong, Y. Kuai, X. Guan and P. Lu, Double-perovskite van der Waals heterostructure Cs2NaInCl6-XS2 (X=Cr, Mo, W) as great potential material in photovoltaic devices, Surf. Interfaces, 2023, 37, 102734 CrossRef CAS.
- D. Li, D. Li, A. Yang, H. Zhang, X. Lai and C. Liang, Electronic and Optical Properties of van der Waals Heterostructures Based on Two-Dimensional Perovskite (PEA)2PbI4 and Black Phosphorus, ACS Omega, 2021, 6, 20877–20886 CrossRef CAS PubMed.
- L. Yang, P. Hou, B. Wang, C. Dall'Agnese, Y. Dall'Agnese, G. Chen, Y. Gogotsi, X. Meng and X.-F. Wang, Performance improvement of dye-sensitized double perovskite solar cells by adding Ti3C2Tx MXene, Chem. Eng. J., 2022, 446, 136963 CrossRef CAS.
- U. Rani, P. K. Kamlesh, R. Agarwal, J. Kumari and A. S. Verma, Electronic and thermo-physical properties of double antiperovskites X6SOA2 (X = Na, K and A = Cl, Br, I): a non−toxic and efficient energy storage materials, Int. J. Quantum Chem., 2021, 121, 26759 CrossRef.
- Y. Yu, Z. Wang and G. S. Shao, Theoretical design of double anti-perovskite Na6SOI2 as a super−fast ion conductor for solid Na+ ion batteries, J. Mater. Chem. A, 2018, 6, 19843–19852 RSC.
- M. Mebrouki, T. Ouahrani and Y. O. Ciftci, Unraveling thermal and dynamical properties of the cubic BaVO3 perovskite from first−principles calculation, Int. J. Thermophys., 2016, 37, 71–80 CrossRef.
- K. Djebari, A. Dahani, M. Djermouni, K. Dine, A. Cherif, O. Arbouche, A. Zaoui and S. Kacimi, Spontaneous polarization study in A3+B4+(O2N)7− and A2+B5+(O2N)7− perovskite-type oxynitrides: a first principles investigation”, Appl. Phys. A: Mater. Sci. Process., 2022, 128, 398–410 CrossRef CAS.
- Q. Gao, R. Y. Ma, L. Li, H. H. Xie, J. B. Deng and X. R. Hu, First-principle study on compensated half metallic double perovskite compound Ba2PrVO6, J. Supercond. Novel Magn., 2017, 30, 545–554 CrossRef CAS.
- H. X. Gao, De-Y. Hu, T.-Yu Tang, Qi-Qi Liang, Qi Dai, S.-S. Wu and Y.-L. Tang, First-principles study on the structural, electronic, elastic, optical and thermodynamic properties of double antiperovskites X6BiSbN2 (X = Mg, Ca, Sr), J. Phys. Chem. Solids, 2004, 187, 111859 CrossRef.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k; an Augmented Plane Wave Plus Local Orbital Program for Calculating Crystal Properties, Vienna University of Technology, Austria, 2001 Search PubMed.
- Z. Wu and R. E. Cohen, More accurate generalized gradient approximation for solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- E. Engel and S. H. Vosko, Exact exchange-only potentials and the virial relation as microscopic criteria for generalized gradient approximations, Phys. Rev. B: Condens. Matter, 1993, 47, 13164 CrossRef CAS PubMed.
- Z. Ali, I. Ahmed, I. Khan and B. Amin, Electronic structure of cubic perovskite SnTaO3, Intermetallics, 2012, 31, 287 CrossRef CAS.
- G. Murtaza, I. Ahmed, B. Amin and M. Zahid, Investigation of structural and optoelectronic properties of BaThO3, Opt. Mater., 2011, 33, 553 CrossRef CAS.
- H. Jiang, Band gaps from the Tran-Blaha modified Becke-Johnson approach: A systematic investigation, J. Chem. Phys., 2013, 138, 134115 CrossRef.
- J. A. Camargo-Martinez and R. Baquero, Performance of the modified Becke-Johnson potential for semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195106 CrossRef.
- R. A. Jishi, O. B. Ta and A. A. Sharif, Modeling of lead halide perovskites for photovoltaic applications, J. Phys. Chem. C, 2014, 118, 28344–28349 CrossRef CAS.
- R. A. Jishi, Modified Becke-Johnson exchange potential: improved modelling of lead halides for solar cell applications, AIMS Mater. Sci., 2016, 3, 149–159 CAS.
- M. Z. ur Rehman, S. A. Abdelmohsen, E. A. Mahmoud, M. U. Saeed, M. Idress, M. Shafiq, B. Amin and Y. Saeed, First principles study of structural, electronic, elastic and optical properties of Cs2LiTlBr6 and Cs2NaTlBr0, Mater. Sci. Semicond. Process., 2022, 151, 106993 CrossRef.
- Y. Saeed, B. Amin, H. Khalil, F. Rehman, H. Ali, M. I. Khan, A. Mahmood and M. Shafiq, Cs2NaGaBr6 : a new lead-free and direct band gap halide double perovskite, RSC Adv., 2020, 10, 17444–17451 RSC.
- U. Khan, M. U. Saeed, H. O. Elansary, I. M. Moussa and Y. Saeed, A DFT study of bandgap tuning in chloro-fluoro silicene, RSC Adv., 2024, 14, 4844–4852 RSC.
- M. Usman Saeed, T. Usman, S. Pervaiz, Z. Ali, Y. Mohammed Alanazi, A. U. R. Bacha and Y. Saeed, DFT Analysis of Alkali Scandium Sulfides AScS 2 (A = K, Rb): Unveiling Structural, Electronic, and Optical Properties for Enhanced Photocatalysis”, ACS Appl. Opt. Mater., 2024, 2, 1955–1964 CrossRef.
- C. Y. Wang, S. R. Li, S. F. Wang, P. X. Zhao, R. S. Zhuo and B. Y. Yu, Effect of biaxial Pre-proof strain on monolayer MoS2 and its vacancy defect system: a first-principles study, J. Solid State Chem., 2023, 317, 123711 CrossRef CAS.
- J. Liang, C. Wang, Y. Wang, Z. Xu, Z. Lu, Y. Ma, H. Zhu, Y. Hu, C. Xiao, X. Yi, G. Zhu, H. Lv, L. Ma, T. Chen, Z. Tie, Z. Jin and J. Liu, All-Inorganic Perovskite Solar Cells, J. Am. Chem. Soc., 2017, 139, 2852 CrossRef CAS PubMed.
- E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Cs2AgBiX6 (X= Br, Cl): new visible light absorbing, lead-free halide perovskite semiconductors, Chem. Mater., 2016, 28, 1348 CrossRef CAS.
- J. Liang, C. Wang, Y. Wang, Z. Xu, Z. Lu, Y. Ma, H. Zhu, Y. Hu, C. Xiao, X. Yi, G. Zhu, H. Lv, L. Ma, T. Chen, Z. Tie, Z. Jin and J. Liu, All-inorganic perovskite solar cells, J. Am. Chem. Soc., 2016, 138, 15829–15832 CrossRef CAS PubMed.
- Z. Abbas, N. Jabeen, A. Hussain, F. Kabir, T. Alshahrani, H. H. Raza, S. Muhammad, S. Azam and I. Gorczyca, Effect of Nb, Ta and V replacements on electronic, optical and elastic properties of NbCu3Se4: a GGA+U study”, J. Solid State Chem., 2021, 301, 122338 CrossRef CAS.
- P. Mondal, N. A. Shahed, S. Khanom, M. K. Hossain and F. Ahmed, Effect of oxygen defects in tuning the half-metallic and optical nature of Sr2CoXO6 (X = Mo and W): a first-principles study, Mater. Chem. Phys., 2022, 277, 125429 CrossRef CAS.
- L. D. Whalley, J. M. Frost, Y. K. Jung and A. Walsh, Perspective: Theory and simulation of hybrid halide perovskites, J. Chem. Phys., 2017, 146, 220901 CrossRef PubMed.
- D. Y. Hu, X. H. Zhao, T. Y. Tang, L. Li, L. K. Gao and Y. L. Tang, First-principles calculations to investigate structural, elastic, electronic and optical properties of lead-free perovskite derivatives Cs2SeX6 (X = Cl, Br, I), Opt. Mater., 2021, 119, 111316 CrossRef CAS.
- L. Y. Gong, P. Zhang, Q. Chen, Z. H. Lou, J. Xu and F. Gao, First principles study of structure and property of Nb5+ doped SrTiO3, Acta Phys. Sin., 2021, 70, 227101 CrossRef.
- E. Oyeniyi, Electronic and optical properties of Mg3XN (X = P, As, Sb, Bi) antiperovskites: the GW/BSE approach”, Solid State Commun., 2022, 355, 114927 CrossRef CAS.
- W. F. Goh and W. E. Pickett, Topological and thermoelectric properties of double antiperovskite pnictides, J. Phys.: Condens. Matter, 2020, 32, 345502 CrossRef CAS.
- C. Y. Wang, S. R. Li, S. F. Wang, P. X. Zhao, R. S. Zhuo and B. Y. Yu, Effect of biaxial[110] strain on monolayer MoS2 and its vacancy defect system: a first-principles study”, J. Solid State Chem., 2023, 317, 123711 CrossRef CAS.
- Z. Abbas, N. Jabeen, A. Hussain, F. Kabir, T. Alshahrani, H. H. Raza, S. Muhammad, S. Azam and I. Gorczyca, Effect of Nb, Ta and V replacements on electronic, optical and elastic properties of NbCu3Se4: a GGA+U study”, J. Solid State Chem., 2021, 301, 122338 CrossRef CAS.
- P. Mondal, N. A. Shahed, S. Khanom, M. K. Hossain and F. Ahmed, Effect of oxygen defects in tuning the half-metallic and optical nature of Sr2CoXO6 (X = Mo and W): a first−principles study, Mater. Chem. Phys., 2022, 277, 125429 CrossRef CAS.
- S. Berri, Theoretical analysis of the structural, electronic and optical properties of tetragonal Sr2GaSbO6, Chin. J. Phys., 2017, 55, 2476–2483 CrossRef CAS.
- K. Maeda and K. Domen, Photocatalytic water splitting: recent progress and future challenges, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS.
- R. M. Navarro Yerga, M. C. Alvarez Galvan, F. Del Valle, J. A. Villoria de la Mano and J. L. Fierro, Water splitting on semiconductor catalysts under visible-light irradiation, Chem. Sustain. Ener. Mater., 2009, 2, 471–485 CAS.
- F. E. Osterloh, Inorganic materials as catalysts for photochemical splitting of water, Chem. Mater., 2008, 20, 35–54 CrossRef CAS.
- X. Hu, G. Li and J. C. Yu, Design, fabrication and modification of nanostructured semiconductor materials for environmental and energy applications, Langmuir, 2010, 26, 3031–3039 CrossRef CAS.
- A. Kudo, Photocatalysis and solar hydrogen production, Pure Appl. Chem., 2007, 79, 1917–1927 CrossRef CAS.
- J. Liu, X. Fu, S. Chen and Y. Zhu, Electronic structure and optical properties of Ag3PO4 photocatalyst calculated by hybrid density functional method, Appl. Phys. Lett., 2011, 99, 191903 CrossRef.
- M. Saeed, I. U. Haq, A. S. Saleemi, S. U. Rehman, B. U. Haq, A. R. Chaudhry and I. Khan, First-principles prediction of the ground-state crystal structure of double-perovskite halides Cs2AgCrX6 (X = Cl, Br, and I), J. Phys. Chem. Solids, 2022, 160, 110302 CrossRef CAS.
- J. Li and H. Chen, First-principles investigation of the mechanical and thermodynamic properties of the antiperovskite centrosymmetric platinum-based superconductors APt3P (A = Ca, Sr, La and Ce), Phys. B, 2020, 577, 411791 CrossRef CAS.
- M. Y. Rudysh, M. Piasecki, G. L. Myronchuk, P. A. Shchepanskyi, V. Y. Stadnyk, O. R. Onufriv and M. G. Brika, AgGaTe2 The thermoelectric and solar cell material: structure, electronic, optical, elastic and vibrational features, Infrared Phys. Technol., 2020, 111, 103476 CrossRef CAS.
- B. T. Wang, W. X. Zhang and W. D. Li, Mechanics, Lattice dynamics, and chemical bonding in ZrB2 and ZrB2 from first-principles calculations, Sci. Adv. Mater., 2013, 5, 1916–1921 CrossRef CAS.
- X. H. Zhao, Y. L. Tang, T. Y. Tang, X. F. Diao, L. K. Gao, Q. Xie, B. Shi, L. Yuan and L. M. Lu, Study on mechanical, electronic and optical properties of Pb-free double halide perovskites In2TiX6 (X = Cl, Br, I) for solar cells based on first-principles, Mater. Today Commun., 2021, 26, 102180 CrossRef CAS.
- L. K. Gao, X. H. Zhao, X. F. Diao, T. Y. Tang and Y. L. Tang, First-principles study of photoelectric properties of CsSnBr3 under hydrostatic pressure, Acta Phys. Sin., 2021, 70, 158801 CrossRef.
- J. Li and H. Chen, First-principles investigation of the mechanical and thermodynamic properties of the antiperovskite centrosymmetric platinum-based superconductors APt3P (A = Ca, Sr, La and Ce), Phys. B, 2020, 577, 411791 CrossRef CAS.
- R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: An open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28, 275201 CrossRef PubMed.
- S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101, 055504 CrossRef.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., Ser. 5, 1954, 45, 823 CrossRef CAS.
- M. Y. Sofi and D. C. Gupta, Scrutinized the inherent spin half-metallicity and thermoelectric response of ff-electron-based RbMO3 (M = Np, Pu) perovskites: A computational assessment, Sci. Rep., 2022, 12, 19476 CrossRef CAS PubMed.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35, 353001 CrossRef CAS.
- A. Togo, First-principles Phonon Calculations with Phonopy and Phono3py, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- Q. Mahmood, M. Yaseen, M. Hassan, M. S. Rashid, I. Tlili and A. Laref, The first-principle study of mechanical, optoelectronic and thermoelectric properties of CsGeBr3 and CsSnBr3 perovskites, Mater. Res. Express, 2019, 6, 045901 CrossRef.
- S. Kuma and M. M. Woldemariam, Structural, electronic, lattice dynamic, and elastic properties of SnTiO3 and PbTiO3 using density functional theory, Adv. Condens. Matter Phys., 2019, 2019, 1–12 CrossRef.
- Z. Sun, S. Li, R. Ahuja and J. M. Schneider, Calculated elastic properties of M2AlC (M = Ti, V, Cr, Nb and Ta), Solid State Commun., 2004, 129, 589–592 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |