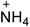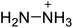Open Access Article
Open Access ArticleApplication of machine learning in developing a quantitative structure–property relationship model for predicting the thermal decomposition temperature of nitrogen-rich energetic ionic salts†
Yunling Zhanga,
Liang Fanb,
Chao Suc,
Zhenyu Shu*d and
Haijie Zhang *b
*b
aBeiyuan Campus, Beijing Vocational College of Agriculture, Beijing, 100012, China
bState Key Laboratory of Environmental Criteria and Risk Assessment, Chinese Research Academy of Environmental Sciences, Beijing 100012, China. E-mail: zhanghaijie@craes.org.cn
cTaiji Computer Co., Ltd, Beijing, 100012, China
dSchool of Information Science and Engineering, Ningbo Institute of Technology, Zhejiang University, Ningbo, 315100, China. E-mail: shuzhenyu@nit.zju.edu.cn
First published on 26th November 2024
Abstract
While thermal decomposition temperature (Td) is one of the most important indexes for energetic materials, the most common way of determining and evaluating Td requires laboratory experiments that are complicated, time-consuming and expensive. In the present study, the quantitative structure–property relationship (QSPR) model of Td for 21 nitrogen-rich energetic ionic salts was built and used for Td prediction through 13 descriptors and principal component analysis. The relatively small dataset of 21 samples may lead to overfitting. In the case of small datasets, possible overfitting was reduced by the support vector machine to derive the non-linear QSPR model. The obtained correlation coefficient (R2) of 96.31% and root-mean-square error (RMSE) of 15.72 indicate the relative reliability of the QSPR model developed in this work. Moreover, Td values of 6 newly designed nitrogen-rich energetic ionic salts were predicted using the new QSPR model. The predicted Td values range from 194 to 225 °C, which are better than that of 4-amino-3,5-dinitro-1H-pyrazole (LLM-116: 178 °C), and no. 1, 2 and 5 are comparable to that of the traditional explosive 1,3,5-trinitro-1,3,5-triazinane (RDX: 230 °C), indicating the excellent properties of the designed energetic ionic salts, which can be used for the preparation of potential energetic materials.
1. Introduction
Energetic materials, such as explosives, propellants, and pyrotechnics, are widely used in the civil industry and military applications. In addition to good detonation performance characterized by high detonation velocity and pressure and high heat of formation, energetic materials should exhibit good stability in order to ensure that they are stored and transported safely. Thermal stability is a particularly important property of energetic materials because the amount of energy released during the decomposition process is closely related to chemical reactivity.1 The thermal stability of energetic materials can be determined using calorimetric measurements to evaluate their temperature and heat of decomposition.1,2 Overall, thermal decomposition temperature (Td) is the most widely used parameter to characterize the thermal stability of energetic materials.Recently, nitrogen-rich energetic ionic salts have attracted more attention than their nonionic analogues. Unlike nonionic explosives, ionic salts are composed of cations and anions, both of which may participate in the decomposition and explosion process, possessing lower vapor pressure, higher density, and higher thermal stability.3–8 Nitrogen-rich heterocyclic compounds such as furazan (furoxan) and tetrazole are currently the focus of research activities in the field of energetic ionic salts, where multiple experimental3–5 and theoretical9 studies have been performed. Being energetic materials, nitrogen-rich energetic ionic salts possess good thermal stability in order to decrease the risk of a catastrophic explosion.10 Machine learning (ML), as a type of artificial intelligence, is a data-driven technology that uses algorithms to parse, learn, and predict data. The important advantage of ML is that once an algorithm learns how to process data, it can automatically complete the prediction work, avoiding hazardous, complicated, time-consuming and expensive experiments. Recently, ML, which is capable of overcoming the well-known shortcomings of the existing experimental methods and techniques, has attracted the attention of the wide research community working in chemistry, materials science, medicine and other related fields.11–18
The method of establishing a correlation between physical or chemical properties of a compound and its molecular structure via various descriptors, such as quantitative structure–property relationship (QSPR), is particularly good at modeling and predicting the properties of new energetic materials, such as impact sensitivity,11,19–22 density,12,23–25 melting point,26–28 decomposition enthalpy,1,2 detonation velocity,29,30 and decomposition temperature.31–39 For example, Fathollahi et al. employed Artificial Neural Networks (ANN) model and multiple linear regression (MLR) to predict the Td of cocrystals and obtained the correlation coefficient R2 of 0.9784 and 0.7438, respectively.31 Wang et al. developed two models by MLR and SVM for the prediction of self-accelerating Td of organic peroxides and obtained the correlation coefficient R2 of 0.727 and 0.952, respectively.32 Zohari et al. predicted the Td of azole-based energetic compounds via the MLR approach and obtained the correlation coefficient R2 of the model of 0.936.34 This means that the existing models for determining Td focus mainly on the aforementioned non-ionic molecules and that in the existing QSPR models for non-ionic molecules, most of the selected descriptors carry on limited amount of information on the chemical composition of these molecules such as the number of atoms, atomic groups and chemical bonds.33,35 A significant difference between energetic ionic salts and non-ionic molecules, such as the hydrogen-bonding interactions between the cations and anions, indicates that an improved QSPR model should be developed. Also, based on the literature review of our knowledge, such QSPR studies on the Td of energetic ionic salts are lacking. In order to improve the description of the internal structure of the energetic ionic salts, 12 quantitative descriptors along with oxygen balance of the 21 samples collected from the same research group, which are closely related to the thermal property of energetic materials, were chosen as descriptors to build the QSPR model of Td in this study.
It is important to note that the dataset used in this study is relatively small and, hence, a suitable ML algorithm for the small dataset is needed. With the development of ML, a variety of ML algorithms such as ANN, Support Vector Machines (SVM), Random Forest, and Decision Tree became available and commonly used in the development of various material QSPR models.13–15 Both ANN and MLR models have limitations when applied to nitrogen-rich energetic ionic salts. While ANN is capable of modeling nonlinear relationships, it typically requires large datasets for proper training, which may not be feasible in the case of complex energetic salts where experimental data are quite scarce. On the other hand, MLR, which is simple and easy to interpret, is often inefficient in capturing the nonlinear and multivariate dependencies of such compounds. SVM, which follows the structural risk minimization principle, offers a better balance to effectively handle small dataset and modeling nonlinear relationships, possessing a higher prediction accuracy and generalization.40–45 Due to the difficulties in preparing energetic ionic salts and the limited number of samples that can be collected, SVM is the most suitable model for building the Td QSPR of energetic ionic salts.
Moreover, to reduce the computational cost and complexity of machine learning algorithms, it is necessary to perform the descriptors data in reduced dimensions. Principal Component Analysis (PCA) and Least Absolute Shrinkage and Selection Operator (LASSO) are widely used for dimensionality reduction. PCA is an unsupervised method that does not rely on target variables (labels), which makes it suitable for extracting key features from the data in the case when no clear target variable is present. In contrast, LASSO is a supervised learning method that requires target variables for feature selection. This reliance on target variables can make LASSO prone to overfitting, especially with small sample sizes. Compared to LASSO, PCA can better mitigate overfitting. At the same time, cross validation was used for parameter selection during the training of the SVM model, which can effectively avoid overfitting. The developed QSPR model was further used to predict the Td values of 6 theoretically designed nitrogen-rich energetic ionic salts. It is important to note that while SVM is well-suited for small sample sizes, the relatively small dataset of 21 nitrogen-rich energetic ionic salts used in this study may still impose some limitations on the model generalization to a wider range of compounds. Further work should focus on expanding the dataset to improve the robustness and reliability of the model.
2. Computational details
2.1 Quantum chemical calculations
The density functional theory (DFT) proposed by Kohn et al.46 has been continuously developed and improved into a commonly used quantum chemistry method.47–50 It replaces the wave function with electron density as the fundamental quantity being studied and uses it to describe the properties of the entire system. In this paper, quantum chemical calculations were performed with the Gaussian 09 program.51 Geometric optimization and frequency calculations of the energetic ionic salts were carried out at the M06-2X/6-311++G(3df,3pd) level of theory. The ability of the highly parameterized, empirical exchange–correlation functional M06-2X to deliver excellent description of a variety of different properties and processes has been long known and is confirmed by a number of studies over the past few years.52–55 The basis set used here is the largest Pople basis set, which comprises relatively low computational costs with a very good performance. Computations were carried out with the convergence criteria set at tight levels. To confirm the minimum energy structures, frequency calculations were conducted and characterized by the absence of imaginary frequencies. The detailed calculation script has been presented in the (ESI).†Thirteen general descriptors, including oxygen balance (OB) and quantum chemical descriptors, were calculated to build a QSPR model for Td. These quantum chemical descriptors were the energy of the highest occupied molecular orbital (EHOMO), energy of the lowest unoccupied molecular orbital (ELUMO), energy gap (ΔE) between the highest occupied molecular orbital and the lowest unoccupied molecular orbital, total dipole moment (μ), polarizability (α), nucleus-independent chemical shift (NICS) for furazan (furoxan) ring, NICS for the tetrazole ring, available free space (ΔV), variance of electrostatic potential value on the van der Waals molecular surface (σ2), ionization potential (I), electron affinity (A), and Wiberg bond order (WBO) of the weakest chemical bond. The detailed description is as follows.
OB is an index used to measure the deficiency or excess of oxygen in a compound when all carbon is converted into carbon monoxide and all hydrogen is converted into water for the compound with the molecular formula of CaHbNcOd (without crystal water), OB = 1600[(d − 2a − b/2)/Mr] [%], in which Mr was the relative molecular mass. An OB value of zero indicates complete oxidation during the detonation. At this point, the most energy is released.56 Therefore, in addition to high density and a high heat of formation, a good oxygen balance is another important factor for designing nitrogen-rich five- or six-membered heterocycles as high-performance energetic materials.56–59
The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are the most important orbitals in a molecule, which play prominent roles in governing chemical reactions.60,61 EHOMO reflects the ability of a molecule to donate electrons and ELUMO reflects the ability of a molecule to accept electrons.61
ΔE is an important descriptor of energetic materials, which is obtained by calculating the difference between EHOMO and ELUMO, affects the kinetic stability, chemical reactivity, optical polarizability, and chemical hardness-softness of a molecule.62–64 Molecules with large ΔE values have been reported to have lower chemical reactivity.20,65 In other words, a larger HOMO–LUMO gap suggests a higher stability66 because a large gap is not beneficial for the transition of electrons from HOMO to LUMO.20
The polarity of a molecule is reflected by its total μ and α values. The value of μ indicates the polarity of a polar covalent bond,67 which is equal to the product of charge on the two bonded atoms and the distance between them. The total molecular dipole moment of a molecule is approximately equal to the vector sum of each bond dipole moment. Thus, the total value of μ reflects the global polarity of a molecule. Higher total μ and α values indicate a greater possibility of electrostatic interaction with other molecules.68
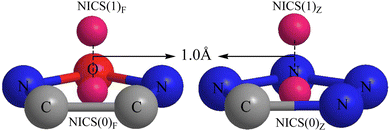
The NICS index proposed by Schleyer's team in 1996 (ref. 69 and 70) is based on absolute magnetic shielding and can be used to characterize aromaticity. Its physical meaning is the negative value of the magnetic shielding value set by a person that is not at the atomic nucleus position. The larger the negative value, the stronger the magnetic field shielding, indicating a stronger aromaticity. Aromaticity is highly relevant to electron delocalization in closed circuits and will lead to lower energy (often substantially lower) and a variety of unusual chemical and physical properties.70 Calculating NICS at the center of a ring describes σ aromaticity, while calculating the NICS out of the center of the ring describes π aromaticity.71,72 A more negative NICS value suggests a greater aromaticity. In this study, ΛNICS(0)F and ΛNICS(0)Z are the indexes of σ aromaticity at the mass center of the furazan (furoxan) and tetrazole rings, respectively. ΛNICS(1)F and ΛNICS(1)Z represent the NICS values calculated at 1.0 Å away from the mass center of the corresponding plane, and these terms describe the π aromaticity. A graphical representation of ΛNICS(0)F, ΛNICS(0)Z calculated at the center of the plane and ΛNICS(1)F, ΛNICS(1)Z calculated at 1.0 Å out of the plane is shown in Fig. 1. The Multiwfn software program73 was used to measure the center of mass of the furazan (furoxan) and tetrazole rings.
ΔV is the difference between Veff and V(int), as shown in eqn (1). Veff is the effective volume of a molecule that completely fills the unit cell and V(int) is the intrinsic gas-phase molecular volume. ΔV is an important descriptor because the availability of more space indicates that a molecule has a stronger ability to absorb and localize, vibrationally or translationally.74,75
| ΔV = Veff − Vint | (1) |
The 0.003 au contour has been reported to provide a range of packing coefficients and also an average value, both of which are very close to the crystallographic data.75
Electrostatic potential (ESP) has significant fundamental significance and is commonly used to analyze and predict noncovalent interactions. The total variance of the electrostatic potential value on the van der Waals molecular surface (σtot2), positive electrostatic potential variance (σ+2), and negative electrostatic potential variance (σ−2) are the means of statistically-defined quantities. These three indexes are usually used to characterize the surface potential.74 Among them, σtot2 is the sum of σ+2 and σ−2, which are defined as followed.
| σtot2 = σ+2 + σ−2 | (2) |
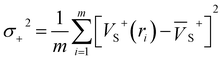 | (3) |
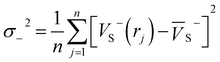 | (4) |
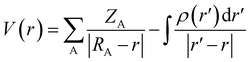 | (5) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) S+ is the average of the positive ESPs, and
S+ is the average of the positive ESPs, and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) S− is the average of the negative ESPs on the molecular surface. Eqn (5) can be used to calculate the electrostatic potential at any point r, where ZA is the charge on nucleus A, located at RA, and ρ(r′) is the electronic density.
S− is the average of the negative ESPs on the molecular surface. Eqn (5) can be used to calculate the electrostatic potential at any point r, where ZA is the charge on nucleus A, located at RA, and ρ(r′) is the electronic density.
I and A can be obtained via the calculations based on the energy difference of neutral and anionic or cationic species76
| I = Ecation − Eneutral | (6) |
| A = Eneutral − Eanion | (7) |
Bond order was first proposed by Pauling77 and can be used to characterize bond strength. A larger bond order value indicates a stronger chemical bond, while a smaller bond order indicates a weaker bond, which is easier to break up. Bond order is commonly represented by the phenomenological bond order and theoretical bond order.78 Determining the phenomenological bond order requires bond lengths and symmetrical stretching frequencies, which are experimentally measured. The theoretical bond order is unobservable and has no unique definition or physical basis.79 The WBO is a commonly used definition of theoretical bond order.80 Therefore, the weakest chemical bond can be found by calculating the WBO. A small value of WBO indicates a weak bond, which may work as a trigger bond.81 Since the breaking of the weakest chemical bond in energetic materials may lead to its decomposition and affect the stability of energetic materials,82–84 the WBO of the weakest chemical bond was chosen as a descriptor.85,86
Meanwhile, in order to generate a relatively reliable simulation result, additional simulations with different sets of descriptors (7, 8, 9, 10, 11, 12 and 13 descriptors) were performed, and their results are summarized in Table S1 (ESI).† RMSE presents a fluctuating downward tendency with the increase in the number of descriptors and reached the smallest value with 13 descriptors. However, the R2 does not present a simple linear dependence on the number of descriptors and reaches the largest value in the case 13 descriptors. As can be seen, the models with smallest number of descriptors, 7 or 8, perform poorly. In particular, the RMSE of 64.42 and R2 of 50.89% are obtained in the case of 8 descriptors. This indicates that these models failed to capture the necessary information about the molecular structure, which leads to underfitting, where the models were too simple to fully learn the underlying patterns. In order to comprehensively describe the key molecular structural features, the model with 13 descriptors was selected. These descriptors include most valuable information relevant directly on the stability and reactivity. However, since the largest descriptors (13) combined with a small dataset may lead to overfitting, dimensionality reduction techniques and cross-validation were employed to optimize the model. The correlation coefficients between each descriptor and Td are shown in Table S2,† with WBO, OB, ΛNICS(0)F and ΛNICS(0)Z being the most relevant to Td prediction.
2.2 Quantitative structure–property relationships
A nonlinear QSPR model was employed to study the relationship between the Td values and structures of nitrogen-rich energetic ionic salts. This model was developed by SVM approach with radial basis function (RBF) as the kernel function.87 The purpose of the kernel function is to map objects to a feature space, and RBF is one of the more commonly used kernel functions.88 Because the RBF kernel is nonlinear, the built QSPR model is also nonlinear.PCA89 was used for dimensional reduction. The principle of PCA involves the formation of a latent variable through the linear combination of original variables, which allows for the generation of new orthogonal axes to rationalize the maximum possible variance in only a few dimensions. Then, the QSPR of the Td values and descriptors processed in the reduced dimensions was built by SVM, which was freely available in the LIBSVM software.90 MATLAB 2013a was used to perform all simulations.
3. Discussion
3.1 Sample analysis
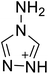
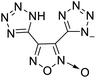
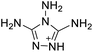
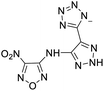
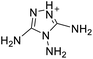
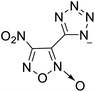
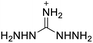
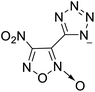
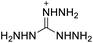
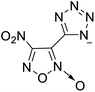
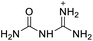
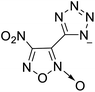
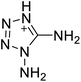
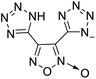
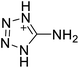
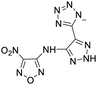
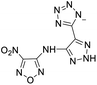
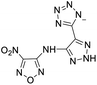
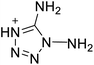
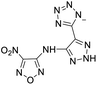
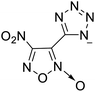
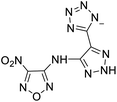
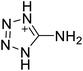
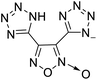
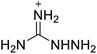
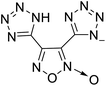
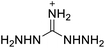
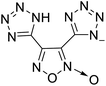
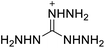
The selection of experimental data is an important part of QSPR studies because experimental conditions may have a strong effect on the studied target property. Thus, it is necessary to ensure that all experimental values were measured under the same conditions. In this study, 21 nitrogen-rich energetic ionic salts were chosen. These ionic salts were measured under the same conditions by the same research group,3–5 and their structures and Td values are shown in Table 1.The optimized geometries of the 21 nitrogen-rich energetic ionic salts at the M06-2X/6-311++G(3df,3pd) level of theory are shown in Fig. S1 (ESI).† The number (No.) of each energetic ionic salt is referenced in Table 1. All the anions of these nitrogen-rich energetic ionic salts have two common aromatic rings: a furazan (furoxan) ring and a tetrazole ring. These anions are paired with nitrogen-rich cations such as ammonium, hydrazinium, guanidinium, and azolium. As shown in Table 1, the nitrogen-rich energetic ionic salts based on bis-heterocycle-substituted 1,2,3-triazole (HTANFT) and 3,4-bis(1H-5-tetrazolyl)furoxan (H2BTF) all have Td values higher than 200 °C except for No. 11. These Td values are comparable to that of the traditional explosive 1,3,5-trinitro-1,3,5-triazinane (RDX; Td = 230 °C),3 suggesting that HTANFT and H2BTF show excellent promise for the design of thermally stable energetic ionic salts. In contrast, the nitrogen-rich energetic ionic salts based on 4-nitro-3-(5-tetrazole)-furoxan (HTNF) show relatively low Td values. Among them, the N-carbamoylguanidinium salt (No. 7) has the highest Td, indicating that N-carbamoylguanidinium shows good potential as the cation of thermally stable energetic ionic salts.
3.2 Local reactivity
The frontier molecular orbitals (HOMO and LUMO) are closely related to chemical reactions.60,61 Therefore, to investigate the reactivity of energetic ionic salts, the HOMO and LUMO distributions must be known. As shown in Fig. 2(a), the HOMO and LUMO of the 21 nitrogen-rich energetic ionic salts are mainly located in their anions, indicating that the anions are the main active region. Furthermore, the decomposition process of energetic materials is significantly influenced by the breaking of the weakest chemical bond.91,92 For example, the weakest C–N bond dissociation of nitro compounds is considered to be the rate-determining step of their decomposition process.91 The WBO of each salt is shown in Fig. 2(b). As can be seen, the N–H bond is usually the weakest bond of these energetic ionic salts. These N–H bonds are mainly located in the frontier molecular orbital. Thus, to further evaluate the decomposition process of the studied 21 energetic ionic salts, the WBO of the weakest chemical bond of each complex was determined.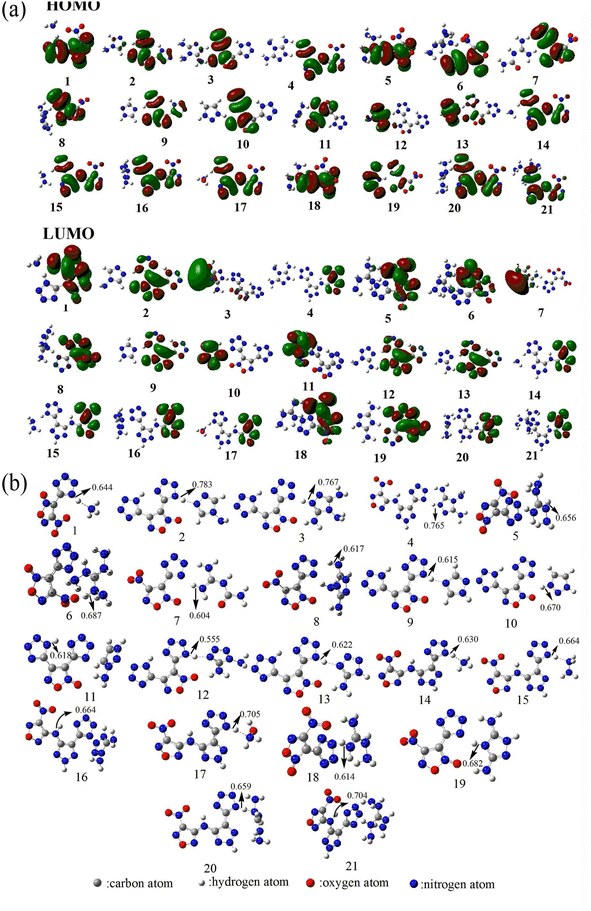 | ||
| Fig. 2 (a) The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). (b) Wiberg bond order of the weakest chemical bond of the 21 nitrogen-rich energetic ionic salts at the M06-2X/6-311++G(3df,3pd) level of theory. The number of each energetic ionic salt is referenced in Table 1. | ||
3.3 Descriptors calculated by quantum chemistry
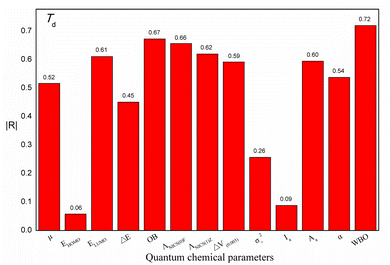
In this study, M06-2X combined with the 6-311++G(3df,3pd) basis set were used to obtain the quantum chemical parameters. Some quantum chemical parameters can be expressed in different ways. For example, NICS can be calculated at different positions on atomic rings, ESP values can be calculated for different regions on molecular surfaces, and I and A can be calculated with different methods. To develop a reliable model, suitable descriptors that are strongly correlated with Td need to be selected. In this section, the selection of these parameters will be discussed in detail. The values of these parameters are shown in Table S3,† and the absolute values of the correlation coefficients (|R|) between these parameters and Td are shown in Fig. 3.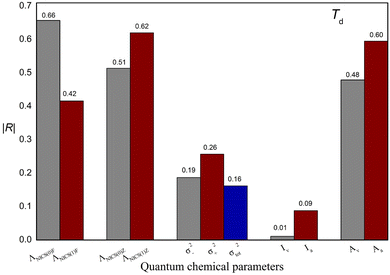 | ||
| Fig. 3 Absolute values of the correlation coefficient (|R|) between the quantum chemical parameters expressed in different ways and experimental thermal decomposition temperature (Td). | ||
Additionally, to study the relationships between each quantum chemical parameter and Td, linear models were built to obtain the |R| value between each parameter and Td. Fig. 4 shows a histogram of the |R| values of the linear models. These |R| values range from 0.06 to 0.72, indicating that the relationships between the individual parameters and Td are not simple or direct. In other words, a single parameter is correlated with Td but is not sufficient for predicting Td. For instance, the WBO descriptor has the largest |R| value of 0.72. However, the values of this descriptor are not in agreement with the change in Td. In addition, two ionic salts (No. 5 and No. 6) have the same WBO values but different Td values, indicating that Td is affected by multiple factors. Therefore, to better describe the relationship between these parameters and Td, these quantum chemical parameters of the energetic ionic salts and OB were fully used to construct a reliable model.
3.4 Quantitative structure–property relationship
In this study, SVM is the ideal approach for a small number of samples79 and hence used to develop a nonlinear QSPR model. All quantum chemical parameter calculations were performed under the M06-2X/6-311++G(3df,3pd) level of theory, and all the parameters were taken as descriptors (Table 2).| No. | μ/Debye | EHOMO/eV | ELUMO/eV | ΔE/eV | OB | ΛNICS(0)F | ΛNICS(1)Z | ΔV(0.003)/Å3 | σ+2/(kcal mol−1)2 | Ia/eV | Aa/eV | α/Bohr3 | WBO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a μ/Debye: dipole moment EHOMO/ev: energy of the highest occupied molecular orbital ELUMO/ev: energy of the lowest unoccupied molecular orbital ΔE: energy gap between the HOMO and LUMO OB: oxygen balance ΛNICS(0)F: index of aromaticity calculated at the central of the furazan (furoxan) ΛNICS(1)Z: index of aromaticity calculated at 1.0 Å out of the tetrazole ΔV(0.003)/Å3: available free space per molecule in the unit cell σ+2/(kcal mol−1)2: positive ESP variance Ia/ev: adiabatic ionization potential Aa/ev: adiabatic electron affinity α/bohr3: polarizability WBO: Wiberg bond order of the weakest chemical bond. | |||||||||||||
| 1 | 6.25 | −9.16 | −2.77 | −6.39 | −29.6 | −13.33 | −13.35 | 53.04 | 221.08 | 8.98 | 2.63 | 116.30 | 0.64 |
| 2 | 13.62 | −9.16 | −1.88 | −7.28 | −67.9 | −10.95 | −13.23 | 75.94 | 293.53 | 8.88 | 1.78 | 179.84 | 0.62 |
| 3 | 20.37 | −8.49 | −1.46 | −7.03 | −66.6 | −11.26 | −13.92 | 82.04 | 495.31 | 8.45 | 1.82 | 201.92 | 0.56 |
| 4 | 18.36 | −7.38 | −1.61 | −5.77 | −65.4 | −12.32 | −13.22 | 92.30 | 489.94 | 7.68 | 1.86 | 228.61 | 0.61 |
| 5 | 6.81 | −8.37 | −2.46 | −5.91 | −44.4 | −13.34 | −14.73 | 65.55 | 234.41 | 8.48 | 2.70 | 158.41 | 0.77 |
| 6 | 11.49 | −8.05 | −2.39 | −5.66 | −44.8 | −13.78 | −14.31 | 69.40 | 259.24 | 8.24 | 2.67 | 167.70 | 0.77 |
| 7 | 16.61 | −8.17 | −1.46 | −6.70 | −45.1 | −13.70 | −14.16 | 72.86 | 614.82 | 8.30 | 1.46 | 168.05 | 0.66 |
| 8 | 10.74 | −8.35 | −1.64 | −6.72 | −48.5 | −13.81 | −14.05 | 72.48 | 415.25 | 8.35 | 1.93 | 172.70 | 0.69 |
| 9 | 9.25 | −9.37 | −2.07 | −7.30 | −68.7 | −11.11 | −13.15 | 71.61 | 240.87 | 9.17 | 1.95 | 168.94 | 0.62 |
| 10 | 18.89 | −8.47 | −1.83 | −6.64 | −68.7 | −11.38 | −13.88 | 70.24 | 651.07 | 8.55 | 1.68 | 171.40 | 0.61 |
| 11 | 17.48 | −8.26 | −1.72 | −6.54 | −67.9 | −11.29 | −14.48 | 72.97 | 656.95 | 8.41 | 1.78 | 176.84 | 0.67 |
| 12 | 11.49 | −9.25 | −2.13 | −7.11 | −54.6 | −11.10 | −13.23 | 77.50 | 254.36 | 9.41 | 2.14 | 185.74 | 0.62 |
| 13 | 10.74 | −9.43 | −2.21 | −7.22 | −54.7 | −11.18 | −13.17 | 73.53 | 350.53 | 9.23 | 2.21 | 175.38 | 0.63 |
| 14 | 10.05 | −8.33 | −2.10 | −6.23 | −56.7 | −12.13 | −12.63 | 69.78 | 237.42 | 8.70 | 1.83 | 163.81 | 0.66 |
| 15 | 10.26 | −8.33 | −2.10 | −6.23 | −56.5 | −12.13 | −12.64 | 73.95 | 253.29 | 8.74 | 1.84 | 172.84 | 0.66 |
| 16 | 13.26 | −7.62 | −1.77 | −5.84 | −54.7 | −12.26 | −13.75 | 84.30 | 436.67 | 7.81 | 2.98 | 207.73 | 0.70 |
| 17 | 8.35 | −8.43 | −2.17 | −6.26 | −48.3 | −12.10 | −12.48 | 72.25 | 264.09 | 8.75 | 1.89 | 167.87 | 0.68 |
| 18 | 7.69 | −8.32 | −2.47 | −5.85 | −43.9 | −13.33 | −14.96 | 62.58 | 338.45 | 8.47 | 2.66 | 149.79 | 0.78 |
| 19 | 10.41 | −8.41 | −1.74 | −6.67 | −48.3 | −13.89 | −14.19 | 70.14 | 369.49 | 7.77 | 2.23 | 167.02 | 0.60 |
| 20 | 9.26 | −8.41 | −2.16 | −6.25 | −63.2 | −12.21 | −12.68 | 85.32 | 249.80 | 7.95 | 2.44 | 206.10 | 0.66 |
| 21 | 7.67 | −7.80 | −2.13 | −5.66 | −62.8 | −12.18 | −14.14 | 86.80 | 320.33 | 7.84 | 2.91 | 213.89 | 0.70 |
The main steps for constructing the QSPR model were as follows. The first step, 21 ionic salts, were divided into training set (numbers 5–21) and testing set (numbers 1–4). PCA was used to extract a descriptor data matrix from the multidimensional space to obtain a more accurate model. It should be noted that PCA does not directly remove the descriptors. Instead, PCA summarizes the information of the original data matrix and displays this information in a reduced dimensional space.97,98 The procedure can be expressed as shown in Scheme 1.
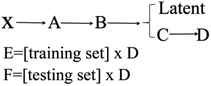 | ||
| Scheme 1 The main dimension reduction process of the model construction for 21 nitrogen-rich energetic ion salts with 13 descriptor data. | ||
X (17 × 13) is the original matrix, consisting of 13 descriptors for each of the 17 energetic ionic salts in the training set. The average value of each column from X was subtracted to obtain matrix A (17 × 13). The covariance matrix B (13 × 13) was then obtained from matrix A. The latent (13 × 1) was obtained by arranging the eigenvalues of the covariance matrix B in descending order. The matrix C (13 × 13) is eigenvectors, which have the same order as the eigenvalues in the latent. The eigenvalues and the proportions of matrix C described by the first four components are shown in Table 3. These four components can contain 99.99% of the total information of the energetic ionic salts. Next, the first four volumes of matrix C were extracted to form matrix D (13 × 4). Matrix D was multiplied by the training set matrix (17 × 13) to obtain matrix E (17 × 4). Additionally, matrix D was multiplied by the testing set matrix (4 × 13) to obtain matrix F (4 × 4). Thus, the dimension reduction of the descriptor matrix was achieved. Finally, matrix E, matrix F, and the four important components were used to develop the nonlinear QSPR. All the matrices and latent are reported in the ESI.†
| Component | Eigenvalue | Proportion (%) | Accumulation (%) |
|---|---|---|---|
| 1 | 21762.47 | 98.05 | 98.05 |
| 2 | 371.19 | 1.67 | 99.73 |
| 3 | 55.51 | 0.25 | 99.98 |
| 4 | 2.83 | 0.01 | 99.99 |
As shown in Table 3, the proportion described by the first principal component is 98.05%, which means that the first principal component can explain 98.05% of the total information. However, the specific relationship between the first principal component and the descriptors of the energetic ionic salts is uncertain. This is because the first principal component was obtained by transforming the original data matrix.
The second step for constructing the QSPR model was the optimization of SVM parameters. The selection of the kernel function parameters is crucial for SVM regression performance. In this study, the most important parameters for the SVM model are the regularization parameter c and the kernel parameter g. The value of c controls the trade-off between maximizing the margin and minimizing the training error, while the value of g determines the generalization ability of the SVM approach. Therefore, it is necessary to find the global optimal values of c and g. The global optimal values of c and g were evaluated by applying the “leave-one-out cross-validation” method to the training set data. The global optimal values of c and g were respectively determined to be 0.93 and 0.35 when the minimum mean square error value was obtained by “leave-one-out cross-validation”. Additionally, leave-p-out99 and k-fold cross-validation100 are also suitable for the QSPR studies of the small sample data to provide a robust model performance and generalize well to the unseen data.
The final step for constructing the QSPR model is to evaluate the model. The root-mean-square error (RMSE) and correlation coefficient (R2) values were used to evaluate the performance of the model. The values of RMSE101 and R2 (ref. 102) were calculated with the following equations.
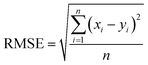 | (8) |
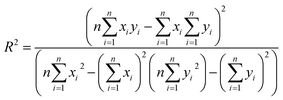 | (9) |
| No. | Expa | Pred | Residue | Number | Expa | Pred | Residue |
|---|---|---|---|---|---|---|---|
| a Thermal decomposition temperatures were taken from ref. 3–5.b The molecules in the training set.c The molecules in the testing set. | |||||||
| 1c | 142 | 161 | −19 | 12b | 204 | 221 | −17 |
| 2c | 225 | 243 | −18 | 13b | 218 | 206 | 12 |
| 3c | 251 | 247 | 4 | 14b | 224 | 217 | 7 |
| 4c | 228 | 242 | −14 | 15b | 219 | 218 | 1 |
| 5b | 122 | 161 | −39 | 16b | 217 | 212 | 5 |
| 6b | 133 | 198 | −65 | 17b | 224 | 194 | 30 |
| 7b | 213 | 212 | 1 | 18b | 153 | 152 | 1 |
| 8b | 180 | 183 | −3 | 19b | 182 | 183 | −1 |
| 9b | 225 | 224 | 1 | 20b | 214 | 215 | −1 |
| 10b | 223 | 222 | 1 | 21b | 187 | 188 | −1 |
| 11b | 177 | 211 | −34 | ||||
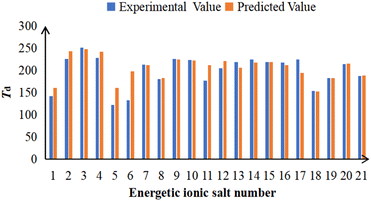 | ||
| Fig. 5 The comparison between the experimental and predicted Td for 21 energetic ionic salts. The number of energetic ionic salt is referenced in Table 1. | ||
3.5 The potential limitations of the model
Except for the leave-one-out cross-validation with the R2 of 96.31% and RMSE of 15.72, which indicates the reliability of the developed QSPR model, k-fold cross-validation (k = 8 and 10) were performed in order to ensure the predictive power of our model. At k = 8, the RMSE and R2 are 16.38 and 93.87%, respectively. At k = 10, the RMSE and R2 are 15.82 and 96.03%, respectively, also indicating that the developed QSPR model is quite reliable. Moreover, the reliability of the QSPR model verified by leave-one-out cross-validation is relatively higher than that of k-fold cross validation for the small dataset of energetic ionic salts considered in the present study. Due to the difficulty in preparing energetic ionic salts and measuring their Td, the number of similar ionic salts prepared and measured at the same experiment conditions was limited. Hence, only 21 samples were selected in this study to maintain the accuracy and consistency of the samples. The relatively small dataset may raise a potential risk of overfitting, where the model may perform well on the training set but poorly on new data. Hence, cross-validation techniques, such as leave-one-out cross-validation and k-fold cross-validation, were employed to mitigate this risk. However, the limited dataset size may still be an issue in the case of the model application to a broader set of data. Moreover, the lack of validation on a broader set of compounds, including those outside the class of nitrogen-rich energetic ionic salts, may affect the conclusions about the applicability of this model to other materials and larger datasets. Further research is needed in order to evaluate the model performance on different energetic materials and larger data sets.3.6 Nitrogen-rich energetic ionic salts design and prediction
Based on the analysis of the structural characteristics of the nitrogen-rich energetic ionic salts with relatively high Td values, 6 new energetic ionic salts were further designed. The anions of these salts are based on HTANFT or H2BTF. Among the energetic ionic salts based on H2BTF, ionic salt No. 10 shows a relatively high Td, indicating that ionic salts prepared with 1H-1,2,3-triazolium as the cation may exhibit high Td values. Among the energetic ionic salts based on HTNF, ionic salt No. 7 has the highest Td, indicating that N-carbamoylguanidinium may be an excellent functional group. In addition, the salts containing aminoguanidinium derivatives as the cation (such as No. 5 and No. 20) have different Td values. This shows that the derivatives of aminoguanidinium can be potentially used for the design of thermally stable energetic ionic salts paired with suitable anions. As a result, the designed nitrogen-rich energetic ionic salts with anions based on HTANFT were paired with 1H-1,2,3-triazolium, 5-amino-tetrazolium, and N-carbamoylguanidinium. The nitrogen-rich energetic ionic salts based on H2BTF were paired with aminoguanidinium, diaminoguanidinium, and triaminoguanidinium.The 6 designed energetic ionic salts were optimized at the M06-2X/6-311++G(3df,3pd) level of theory, and all descriptors are collected in Table S4† to predict Td. As shown in Table 5, the predicted Td values of these new nitrogen-rich energetic ionic salts are relatively high, ranging from 194 to 225 °C. These Td values are higher than that of 4-amino-3,5-dinitro-1H-pyrazole (LLM-116:178 °C) and Nos. 1, 2 and 5 are comparable to that of the RDX (230 °C), indicating that the designed energetic ionic salts show good promise for the preparation of thermally stable energetic materials, which may be used in special materials such as rockets, spacecraft, and devices for high-altitude aircraft in the future.
4. Conclusions
In this study, quantitative structure–property relationship (QSPR) model of the Td of nitrogen-rich energetic ionic salts was built based on the SVM approach. The Td of 21 nitrogen-rich energetic ionic salts were firstly analyzed using the QSPR model, in which EHOMO, ELUMO, ΔE, μ, α, OB, ΛNICS(0)F, ΛNICS(1)Z, ΔV, σ2, Ia, Aa, and WBO of the weakest chemical bond were comprehensively taken as descriptors. Also, all the descriptors were chosen by PCA for dimensional reduction. The correlation coefficient (R2) of the testing set is 96.31%, and the root-mean-square error (RMSE) of the testing set is 15.72 for the built QSPR model, indicating a reliable performance. Furthermore, 6 new energetic ionic salts were designed, and their Td were predicted with the built QSPR model. The predicted Td ranged from 194 to 225 °C, which are better than LLM-116 (178 °C), and the designed No. 1, 2 and 5 are similar to that of RDX (230 °C), indicating the excellent potential of these designed energetic ionic salts.The optimized QSPR model has been used to predict the Td of nitrogen-rich energetic ionic salts and has shown good predictive ability. It could provide effective method support for the design and preparation of energetic materials where laboratory synthesis research is usually costly, time-consuming, expensive and dangerous to quickly and effectively obtain stable explosive materials. Due to the diverse and complex structures of energetic ionic salt explosives, this model has the potential to be applied in further predicting the thermodynamic characteristics of different types of energetic ionic salts and guiding the development of related experimental research. It would be fair to admit that despite applying dimensionality reduction techniques, such as PCA, and cross-validation to optimize the model, there still exists the possibility of overfitting. Further research is needed to address this issue by expanding the dataset and by exploring simpler models that may offer a better balance between the model complexity and its generalizability.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors thank the National Natural Science Foundation of China (No. 22306179) for support of this research.References
- G. Fayet, P. Rotureau and L. Joubert, et al., Predicting Explosibility Properties of Chemicals from Quantitative Structure-Property Relationships, Process Saf. Prog., 2010, 29, 359–371 CrossRef CAS.
- G. Fayet, P. Rotureau and L. Joubert, et al., On the prediction of thermal stability of nitroaromatic compounds using quantum chemical calculations, J. Hazard. Mater., 2009, 171, 845–850 CrossRef CAS PubMed.
- H. Huang, Z. Zhou and L. Liang, et al., Nitrogen-Rich Energetic Monoanionic Salts of 3,4-Bis(1H-5-tetrazolyl)furoxan, Chem.–Asian J., 2012, 7, 707–714 CrossRef CAS PubMed.
- C. Bian, K. Wang and L. Liang, et al., Nitrogen-Rich Energetic Salts of Bis-Heterocycle-Substituted 1,2,3-Triazole (HTANFT), Eur. J. Inorg. Chem., 2014, 35, 6022–6030 CrossRef.
- L. Liang, K. Wang and C. Bian, et al., 4-Nitro-3-(5-tetrazole)furoxan and Its Salts: Synthesis, Characterization, and Energetic Properties, Chem.–Eur. J., 2013, 19, 14902–14910 CrossRef CAS PubMed.
- J. Song, K. Wang and L. Liang, et al., High-energy-density materials based on 1-nitramino-2,4-dinitroimidazole, RSC Adv., 2013, 3, 10859–10866 RSC.
- V. Thottempudi, J. Zhang and C. He, et al., Azo substituted 1,2,4-oxadiazoles as insensitive energetic materials, RSC Adv., 2014, 4, 50361–50364 RSC.
- D. Fischer, T. M. Klapötke and J. Stierstorfer, 1,5-Di(nitramino)tetrazole: High Sensitivity and Superior Explosive Performance, Angew. Chem., Int. Ed., 2015, 54, 10299–10302 CrossRef CAS PubMed.
- Y. Shao, W. Zhu and H. Xiao, Structure-property relationships of energetic nitrogen-rich salts composed of triaminoguanidinium or ammonium cation and tetrazole-based anions, J. Mol. Graph. Model., 2013, 40, 54–63 CrossRef CAS PubMed.
- A. K. Sikder and N. Sikder, A review of advanced high performance, insensitive and thermally stable energetic materials emerging for military and space applications, J. Hazard. Mater., 2004, 112, 1–15 CrossRef CAS PubMed.
- M. J. Kamlet and H. G. Adolph, The relationship of impact sensitivity with structure of organic high explosives II. Polynitroaromatic explosives, Propellants, Explos. Pyrotech., 1979, 4, 30–34 CrossRef CAS.
- F. Luan, H. Liu and Y. Wen, et al., QSPR Study for Estimation of Density of Some Aromatic Explosives by Multiple Linear Regression Approach, Propellants, Explos. Pyrotech., 2010, 35, 169–174 CrossRef CAS.
- A. K. Chew, M. Sender and Z. Kaplan, et al., Advancing material property prediction: using physics-informed machine learning models for viscosity, J. Cheminf., 2024, 16(1), 31 Search PubMed.
- F. Cravero, M. F. Diaz and I. Ponzoni, Polymer informatics for QSPR prediction of tensile mechanical Properties case study:Strength at break, J. Chem. Phys., 2022, 156, 204903 CrossRef CAS PubMed.
- H. Zheng, W. Lv and Y. Wang, et al., Molecular kinematic viscosity prediction of natural ester insulating oil based on sparse Machine learning models, J. Mol. Liq., 2023, 385, 122355 CrossRef CAS.
- Q. Gou, J. Liu and H. Su, et al., Exploring an accurate machine learning model to quickly estimate stability of diverse energetic materials, Iscience, 2024, 27(4), 1–18 CrossRef PubMed.
- J. Feng, Z. Dong and Y. Ji, et al., Accelerating the Discovery of Metastable IrO2 for the Oxygen Evolution Reaction by the Self-Learning-Input Graph Neural Network, JACS Au, 2023, 3(4), 1131–1140 CrossRef CAS PubMed.
- J. Burés and I. Larrosa, Organic reaction mechanism classification using machine learning, Nature, 2023, 613, 689–695 CrossRef PubMed.
- J. Li, A multivariate relationship for the impact sensitivities of energetic N-nitrocompounds based on bond dissociation energy, J. Hazard. Mater., 2010, 174, 728–733 CrossRef CAS PubMed.
- N. R. Badders, C. Wei and A. A. Aldeeb, et al., Predicting the impact sensitivities of polynitro compounds using quantum chemical descriptors, J. Energ. Mater., 2006, 24, 17–33 CrossRef CAS.
- V. Prana, G. Fayet and P. Rotureau, et al., Development of validated QSPR models for impact sensitivity of nitroaliphatic compounds, J. Hazard. Mater., 2012, 235–236, 169–177 CrossRef CAS PubMed.
- J. Xu, L. Zhu and D. Fang, et al., QSPR Studies of impact sensitivity of nitro energetic compounds using three-dimensional descriptors, J. Mol. Graph. Model., 2012, 36, 10–19 CrossRef CAS PubMed.
- N. Zohari, F. Abrishami and V. Zeynali, Using the QSPR approach for estimating the density of azole-based energetic compounds, Z. Anorg. Allg. Chem., 2017, 643, 2124–2137 CrossRef CAS.
- M. Fathollahi and H. Sajady, Prediction of density of energetic cocrystals based on QSPR modeling using artificial neural network, Struct. Chem., 2018, 29, 1119–1128 CrossRef CAS.
- N. Zohari and F. G. Mohammadkhani, Prediction of the density of energetic Cocrystals: a way to design high performance energetic materials, Cent. Eur. J. Energ. Mater., 2020, 17, 31–48 CrossRef CAS PubMed.
- J. A. Morrill and E. F. C. Byrd, Development of quantitative structure property relationships for predicting the melting point of energetic materials, J. Mol. Graph. Model., 2015, 62, 190–201 CrossRef CAS PubMed.
- S. Trohalaki, R. Pachter and G. W. Drake, et al., Quantitative Structure-Property Relationships for Melting Points and Densities of Ionic Liquids, Energy Fuels, 2005, 19, 279–284 CrossRef CAS.
- A. M. Al-Fakih, Z. Y. Algamal and M. H. Lee, et al., A penalized quantitative structure-property relationship study on melting point of energetic carbocyclic nitroaromatic compounds using adaptive bridge penalty, SAR QSAR Environ. Res., 2018, 29, 339–353 CrossRef CAS PubMed.
- D. Wang, G. He and H. Chen, Prediction for the Detonation Velocity of the Nitrogenrich Energetic Compounds Based on Quantum Chemistry, Russ. J. Phys. Chem. A, 2014, 88, 2363–2369 CrossRef CAS.
- N. Zohari and F. G. Mohammadkhani, Detonation velocity assessment of energetic cocrystals using QSPR approach, Z. Anorg. Allg. Chem., 2020, 646, 30–35 CrossRef CAS.
- M. Fathollahi and H. Sajady, QSPR modeling of decomposition temperature of energetic cocrystals using artificial neural network, J. Therm. Anal. Calorim., 2018, 133, 1663–1672 CrossRef CAS.
- B. Wang, H. Yi and K. Xu, et al., Prediction of the self-accelerating decomposition temperature of organic peroxides using QSPR models, J. Therm. Anal. Calorim., 2017, 128(1), 399–406 CrossRef CAS.
- N. Zohari, N. Sheibani and H. Z. Chavoshi, Investigation of the most effective molecular descriptors on the thermal behaviour of energetic azido-ester plasticizers through QSPR approach, J. Therm. Anal. Calorim., 2018, 131, 3157–3167 CrossRef CAS.
- N. Zohari, F. Abrishami and V. Zeynali, Prediction of decomposition temperature of azole-based energetic compounds in order to assess of their thermal stability, J. Therm. Anal. Calorim., 2020, 141, 1453–1463 CrossRef CAS.
- N. Zohari, M. H. Keshavarz and Z. Dalaei, Prediction of decomposition onset temperature and heat of decomposition of organic peroxides using simple approaches, J. Therm. Anal. Calorim., 2016, 125, 887–896 CrossRef CAS.
- A. Mousaviazar, Z. Shirazi and M. H. Keshavarz, et al., A novel approach for prediction of exothermic decomposition temperature of energetic complexes through additive and non-additive descriptors, J. Therm. Anal. Calorim., 2022, 147, 12907–12917 CrossRef CAS.
- S. Lotfi, S. Ahmadi and P. Kumar, A hybrid descriptor based QSPR model to predict the thermal decomposition temperature of imidazolium ionic liquids using Monte Carlo approach, J. Mol. Liq., 2021, 338, 116465 CrossRef CAS.
- Z. Zhang, C. Chen and Y. Cao, et al., Descriptors applicability in machine learning-assisted prediction of thermal decomposition temperatures for energetic materials: Insights from model evaluation and outlier analysis, Thermochim. Acta, 2024, 735, 179717 CrossRef CAS.
- M. Xiao, X. Zhang and K. Xiao, et al., Prediction of thermal decomposition temperatures of binary imidazolium ionic liquid mixtures using improved E-state index descriptors, J. Loss Prev. Process, 2023, 84, 105111 CrossRef CAS.
- V. Cherkassky and Y. Ma, Practical selection of SVM parameters and noise estimation for SVM regression, Neural Network., 2004, 17, 113–126 CrossRef PubMed.
- L. Tang, Y. Zhou and J. Jiang, et al., Radial Basis Function Network-Based Transform for a Nonlinear Support Vector Machine as Optimized by a Particle Swarm Optimization Algorithm with Application to QSAR Studies, J. Chem. Inf. Model., 2007, 47, 1438–1445 CrossRef CAS PubMed.
- Y. Li, Z. Dai and D. Cao, et al., Chi-MIC-share: A new feature selection algorithm for quantitative structure-activity relationship models, RSC Adv., 2020, 10(34), 19852–19860 RSC.
- P. Xu, X. Ji and M. Li, et al., Small data machine learning in materials science, npj Comput. Mater., 2023, 9(1), 42 CrossRef.
- T. R. Noviandy, G. M. Idroes and T. E. Tallei, et al., QSAR Modeling for Predicting Beta-Secretase 1 Inhibitory Activity in Alzheimer's Disease with Support Vector Regression, Malacca Pharm., 2024, 2(2), 79–85 CrossRef.
- M. S. Abubakar, K. O. Aremu and M. Aphane, et al., A QSPR analysis of physical properties of antituberculosis drugs using neighbourhood degree-based topological indices and support vector regression, Heliyon, 2024, 10(7), 1–27 CrossRef PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140(4A), A1133–A1138 CrossRef.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for density functional theory, Chem. Rev., 2012, 112(1), 289–320 CrossRef CAS PubMed.
- A. D. Becke, Perspective: Fifty years of density-functional theory in chemical physics, J. Chem. Phys., 2014, 140(18), 1–18 CrossRef PubMed.
- K. Burke, Perspective on density functional theory, J. Chem. Phys., 2012, 136(15), 150901 CrossRef PubMed.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, et al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, Assessment of the Performance of the M05-2X and M06-2X Exchange-Correlation Functionals for Noncovalent Interactions in Biomolecules, J. Chem. Theory Comput., 2008, 4, 1996–2000 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Applications and validations of the Minnesota density functionals, Chem. Phys. Lett., 2011, 502, 1–13 CrossRef CAS.
- S. Zhang, G. Wang and Y. Lu, et al., The Interactions between Imidazolium-Based Ionic Liquids and Stable Nitroxide Radical Species: A Theoretical Study, J. Phys. Chem. A, 2016, 120, 6089–6102 CrossRef CAS PubMed.
- J. Zhang, Q. Zhang and T. V. Thao, et al., Energetic Salts with π-Stacking and Hydrogen-Bonding Interactions Lead the Way to Future Energetic Materials, J. Am. Chem. Soc., 2015, 137, 1697–1704 CrossRef CAS PubMed.
- J. Zhang, C. He and D. A. Parrish, et al., Nitramines with Varying Sensitivities: Functionalized Dipyrazolyl-N-nitromethanamines as Energetic Materials, Chem.–Eur. J., 2013, 19, 8929–8936 CrossRef CAS PubMed.
- J. Zhang and J. M. Shreeve, Nitroaminofurazans with Azo and Azoxy Linkages: A Comparative Study Of Structural, Electronic, Physicochemical, and Energetic Properties, J. Phys. Chem. C, 2015, 119, 12887–12895 CrossRef CAS.
- Q. Wu, W. Zhu and H. Xiao, A New Design Strategy for High-energy low-sensitivity explosives: combining cxygen balance equal to zero, a combination of nitro and amino groups, and N-oxide in one molecule of 1-Amino-5-nitrotetrazole-3N-oxide, J. Mater. Chem. A, 2014, 2, 13006–13015 RSC.
- M. Karelson, V. S. Lobanov and A. R. Katritzky, Quantum-Chemical Descriptors in QSAR/QSPR Studies, Chem. Rev., 1996, 96, 1027–1043 CrossRef CAS PubMed.
- G. Gece and S. Bilgic, Quantum chemical study of some cyclic nitrogen compounds as corrosion inhibitors of steel in NaCl media, Corros. Sci., 2009, 51, 1876–1878 CrossRef CAS.
- M. Tian, W. J. Chi and Q. S. Li, et al., Theoretical design of highly energetic poly-nitro cage compounds, RSC Adv., 2016, 6, 47607–47615 RSC.
- D. Zhai, C. Ma and P. Ma, et al., Theoretical insight into different energetic groups on the performance of energetic materials featuring RDX ring, Fuel, 2021, 294, 120497 CrossRef CAS.
- C. Li, Z. Lu and S. Li, et al., The influence of the number of fluorine atoms on the properties of energetic materials, J. Mol. Struct., 2024, 1318, 139246 CrossRef CAS.
- X. Jin, B. Hu and W. Lu, et al., Theoretical study on a novel high-energy density material 4,6,10,12-tetranitro-5,11-bis(nitroimino)-2,8-dioxa-4,6,10,12-tetraaza-tricyclo[7,3,0,03,7] dodecane, RSC Adv., 2014, 4, 6471–6477 RSC.
- Z. Zhou and R. G. Parr, Activation Hardness: New Index for Describing the Orientation of Electrophilic Aromatic Substitution, J. Am. Chem. Soc., 1990, 112, 5720–5724 CrossRef CAS.
- G. Gece, The use of quantum chemical methods in corrosion inhibitor studies, Corros. Sci., 2008, 50, 2981–2992 CrossRef CAS.
- H. Zhao, X. Zhang and L. Ji, et al., Quantitative structure-activity relationship model for amino acids as corrosion inhibitors based on the support vector machine and molecular design, Corros. Sci., 2014, 83, 261–271 CrossRef CAS.
- P. V. R. Schleyer, C. Maerker and A. Dransfeld, et al., Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- Z. F. Chen, C. S. Wannere and C. Corminboeuf, et al., Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- C. Wang, X. Zhang and J. Lu, et al., Theoretical studies on all-metal binuclear sandwich-like complexes M2(η4-E4)2 (M=Al, Ga, In; E=Sb, Bi), J. Mol. Model., 2012, 18, 3577–3586 CrossRef CAS PubMed.
- C. Wang, X. Zhang and M. Ge, et al., The first nonmetal-centered binuclear sandwich-like complexes based on the tetraatomic species E42−(E = N, P, As, Sb, Bi) and boron atoms, New J. Chem., 2011, 35, 2527–2533 RSC.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. Pospíšil, P. Vávra and M. C. Concha, et al., A possible crystal volume factor in the impact sensitivities of some energetic compounds, J. Mol. Model., 2010, 16, 895–901 CrossRef PubMed.
- M. Pospíšil, P. Vávra and M. C. Concha, et al., Sensitivity and the available free space per molecule in the unit cell, J. Mol. Model., 2011, 17, 2569–2574 CrossRef PubMed.
- M. G. Elghalban, A. M. E Defarwy and R. K. Shah, et al., α-Furil Dioxime: DFT Exploration and its Experimental Application to the Determination of Palladium by Square Wave Voltammetry, Int. J. Electrochem. Sci., 2014, 9, 2379–2396 CrossRef.
- L. Pauling, Atomic Radii and Interatomic Distances in Metals, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- R. F. See, Which Method of Assigning Bond Orders in Lewis Structures Best Reflects Experimental Data? An Analysis of the Octet Rule and Formal Charge Systems for Period 2 and 3 Nonmetallic Compounds, J. Chem. Educ., 2009, 86, 1241–1247 CrossRef CAS.
- Z. Chen and H. Xiao, Quantum Chemistry Derived Criteria for Impact Sensitivity, Propellants, Explos. Pyrotech., 2014, 39, 487–495 CrossRef CAS.
- K. B. Wiberg, Application of the Pople-Santry-Segal CNDO Method to Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutyl, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- Y. Li, Y. Li and S. Jin, et al., Molecular design of energetic tetrazine-triazole derivatives, J. Mol. Model., 2021, 27, 1–8 CrossRef PubMed.
- S. R. Saraf, W. J. Rogers and M. S. Mannan, Application of transition state theory for thermal stability prediction, Ind. Eng. Chem. Res., 2003, 42, 1341–1346 CrossRef CAS.
- E. Theerlynck, D. Mathieu and P. Simonetti, Towards improved models to rationalize and estimate the decomposition temperatures of nitroalkanes, nitramines and nitric esters, Thermochim. Acta, 2005, 426(1), 123–129 CrossRef CAS.
- Z. Yu and E. R. Bernstein, On the decomposition mechanisms of new imidazole-based energetic materials, J. Phys. Chem. A, 2013, 117(8), 1756–1764 CrossRef CAS PubMed.
- L. Song, C. Zhang and C. Sun, et al., Stabilization mechanisms of three novel full-nitrogen molecules, Monatsh. Chem., 2021, 152, 421–430 CrossRef CAS.
- H. Liu, P. Chen and X. Huang, et al., A physical organic strategy to predict and interpret stabilities of chemical bonds in energetic compounds for the discovery of thermal-resistant properties, J. Mol. Model., 2024, 30(3), 84 CrossRef CAS PubMed.
- N. T. Renukadevi and P. Thangaraj, Performance Evaluation of SVM-RBF Kernel for Medical Image Classification, J. Comput. Sci. Technol., 2013, 13, 15–19 Search PubMed.
- R. Alwee, S. M. H Shamsuddin and R. Sallehuddin, Hybrid support vector regression and autoregressive integrated moving average models improved by particle swarm optimization for property crime rates forecasting with economic indicators, Sci. World J., 2013, 2013, 11 Search PubMed.
- M. Rusu, D. Rusu and C. Sârbu, Lipophilicity of metallic complexes of 4-methoxyphenyl-4'-chlorobenzoylhydrazine as estimated from principal component analysis of thin layer chromatographic retention data, Anal. Lett., 1999, 32, 2999–3011 CrossRef CAS.
- E. Byvatov, U. Fechner and J. Sadowski, et al., Comparison of Support Vector Machine and Artificial Neural Network Systems for Drug/Nondrug Classification, J. Chem. Inf. Comput. Sci., 2003, 43, 1882–1889 CrossRef CAS PubMed.
- S. R. Saraf, W. J. Rogers and M. S. Mannan, Application of transition state theory for thermal stability prediction, Ind. Eng. Chem. Res., 2003, 42, 1341–1346 CrossRef CAS.
- E. Theerlynck, D. Mathieu and P. Simonetti, Towards improved models to rationalize and estimate the decomposition temperatures of nitroalkanes, nitramines and nitric esters, Thermochim. Acta, 2005, 426(1), 123–129 CrossRef CAS.
- J. Cai, C. Xie and X. Jin, et al., High performance and heat-resistant pyrazole-1, 2, 4-triazole energetic materials: Tuning the thermal stability by asymmetric framework and azo-bistriazole bridge, Chem. Eng. J., 2022, 433, 134480 CrossRef CAS.
- X. Miao, X. Yang and Y. Li, et al., Thermal stability of azole-rich energetic compounds: their structure, density, enthalpy of formation and energetic properties, Phys. Chem. Chem. Phys., 2023, 25(28), 18523–18544 RSC.
- C. K. Kim, S. G. Cho and J. Li, et al., QSPR Studies on Impact Sensitivities of High Energy Density Molecules, Bull. Korean Chem. Soc., 2011, 32, 4341–4346 CrossRef CAS.
- J. S. Murray, M. C. Concha and P. Politzer, Links between surface electrostatic potentials of energetic molecules, impact sensitivities and C-NO2/N-NO2 bond dissociation energies, Mol. Phys., 2009, 107, 89–97 CrossRef CAS.
- C. Sârbu, T. Djaković-Sekulić and N. Perišić-Janjić, et al., Evaluation of lipophilicity of some benzimidazole and benztriazole derivatives by RP HPTLC and PCA, J. Pharm. Biomed. Anal., 2002, 30, 739–745 CrossRef PubMed.
- K. Polikreti, V. Argyropoulos and D. Charalambous, et al., Tracing correlations of corrosion products and microclimate data on outdoor bronze monuments by Principal Component Analysis, Corros. Sci., 2009, 51, 2416–2422 CrossRef CAS.
- J. Shao, Linear model selection by cross-validation, J. Am. Stat. Assoc., 1993, 88(422), 486–494 CrossRef.
- M. Stone, Cross-validatory choice and assessment of statistical predictions, J. R. Stat. Soc. Ser. B Methodol., 1974, 36(2), 111–133 CrossRef.
- P. Lind and T. Maltseva, Support Vector Machines for the Estimation of Aqueous Solubility, J. Chem. Inf. Comput. Sci., 2003, 43, 1855–1859 CrossRef CAS PubMed.
- C. C. Chang and C. J. Lin, LIBSVM: a library for support vector machines, ACM Trans. Intell. Syst. Technol., 2011, 2(3), 1–27 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05875e |
| This journal is © The Royal Society of Chemistry 2024 |