DOI:
10.1039/D4RA05886K
(Paper)
RSC Adv., 2024,
14, 33471-33488
Study of thermodynamic, transport and volumetric properties of nanofluids containing ZrO2 nanoparticles in polypropylene glycol, polyvinyl pyrrolidone and water†
Received
13th August 2024
, Accepted 2nd October 2024
First published on 22nd October 2024
Abstract
Zirconium dioxide (ZrO2) nanofluids are used in cooling systems, solar energy, and heat exchangers, offering improved heat transfer and efficiency across a wide temperature range. The aim of this work was to study the influence of polypropylene glycol (PPG) and polyvinyl pyrrolidone (PVP) and aqueous solutions of them as a base fluid on stability, volumetric properties, and viscosity of nanofluids containing Zirconium oxide (ZrO2) nanoparticles. The stability of these nanofluids has been confirmed using UV-Vis spectroscopy, and the particle size distribution of the systems using dynamic light scattering (DLS). Among these systems ZrO2–PPG and ZrO2–H2O–PVP30% have appropriate stability. The density, speed of sound and viscosity of these nanofluids have been measured at T = (293.15 to 318.15) K. From these data, the excess molar volume (VEm) and isentropic compressibility (κs) have been determined. The effects of ZrO2 nanoparticles and temperature have also been investigated on volumetric and transport properties of aqueous solutions of PPG and PVP. The (VEm) values were fitted to the Redlich–Kister, Ott et al., and polynomial equations. Also, the isentropic compressibility (κs) values were correlated with the polynomial equation. The Eyring-NRTL and Eyring-mNRF models have been used for correlating of the viscosity of the nanofluids with temperature dependency. The performance of the Einstein, Brinkman, Lundgren and Batchelor models in the prediction of viscosity of the nanofluids has also been analyzed.
1. Introduction
Technological advancements in the field of power generation cause an increment in the creation of heat during work processes. As a result, the need to reduce the generated heat becomes more essential.1 Nanofluids are one of the most promising cooling agent that transferring heat efficiently. These materials are suspensions of nanoparticles with the size of 1–100 nm, that possess specific characteristics such as high thermal conductivity that can make them potentially a suitable alternative to other coolers.2 The creation of nanofluids necessitates the utilization of nanoparticles and a base fluid; these materials can be characterized by their unique properties and can offer potential applications in various fields such as heat transfer, lubrication, and advanced materials science.3 One of the primary obstacles encountered in the utilization of nanofluids pertains to their inherent stability. The tendency of nanoparticles to agglomerate, driven by strong intermolecular forces, results in clotting and sedimentation within the channels through which nanofluids are passed. Consequently, their ability to effectively enhance thermal conductivity is hindered. As a result, increasing the stability of nanofluids can be considered a significant objective. Many researchers have applied various strategies to improve nanofluid stability; including the incorporation of surfactants, polymers, ultrasound, and mechanical agitation.4–6 One of the cost effective methods to improve the stability of nanoparticles in a base fluid is utilization of polymers.7
Polymers on the other hand unlike the other applicants can be categorized as cost-effective, more accessible, that makes them a favorable and robust ingredient in the industry. One of the most important features of a polymer is that they can improve the stability of nanofluids. There are several methods to enhance the stability of nanofluids, the initial method involves the creation of an adsorbed layer, where polymers possess the ability to be adsorbed onto the surface of nanoparticles, consequently forming a protective layer. This protective layer, serves the crucial function of inhibiting direct contact between nanoparticles, thereby preventing their aggregation and accumulation within the fluid medium.6 Furthermore, another strategy involves the generation of steric repulsion, where certain polymers exhibit functional groups that become ionized and charged when immersed in water. These electrically charged functional groups induce repulsive forces between nanoparticles, thereby preventing their aggregation and subsequent accumulation.8 Moreover, polymer leads to an increase in fluid viscosity as the concentration of polymer escalates. The elevation in viscosity levels plays a pivotal role in diminishing the Brownian motion (random motion of particles immersed in fluid) exhibited by nanoparticles, consequently reducing the likelihood of their collision and subsequent aggregation within the nanofluid.9 Lastly, polymers have the ability to induce alterations in surface energy exhibited by both nanoparticles and the base fluid. This modification in surface energy profiles exerts an influence on the intermolecular operative forces between nanoparticles and the surrounding fluid medium, consequently impacting the aggregation tendencies within the nanofluid system.10
PVP is a polymer that is widely utilized across various fields due to its remarkably intriguing characteristics.11,12 Polypropylene glycol (PPG) is less toxic than polyethylene glycol (PEG) and frequently used in the pharmaceutical and cosmetic fields as solvent, carrier, humectants, lubricant, binder, base and coupling agent and also for extraction, separation, and purification of biological materials.13,14 The utilization of (PPG) has been thoroughly examined in the presence of various fluid systems as a stabilizing agent.15,16 Metal nanoparticles, metal oxides, carbides, nitrides or carbon nanotubes with various shapes are used in the preparation of nanofluids.17 Among these materials, metal oxides as a nanostructure stand as a suitable candidate as they have been used in the manufacture of optical cells, electroluminescence, electrochromic windows, and chemical sensors.18 ZrO2 can be mentioned among these nanoparticles. ZrO2 nanoparticles possess high mechanical properties such as high strength and flexibility, also these nanoparticles possess interesting characteristics such as heat insulation that has been widely utilized in the industrial fields.19 Some research studies have been conducted on ZrO2 nanoparticles. Gustaman and co-workers,20 synthesized the ZrO2 nanoparticles through the sol–gel method and investigated the possibility of using nanofluid containing ZrO2 as a coolant in a nuclear reactor. They synthesized ZrO2 nanoparticles and studied the properties of nanofluid containing ZrO2 nanoparticles dispersed in water base fluid at different pH. The results show that the thermal conductivity of the studied nanofluid is about 4–9% higher than the base fluid. Recent studies have shown that nanofluids containing metal oxide nanoparticles dispersed in water as a fluid can increase thermal conductivity by 30–40%.21 Moghtaderi and colleagues,22 investigated the effect of anionic surfactants (Sodium dodecyl benzene sulfonate) on the stability and thermodynamic properties of metal oxide nanofluids containing Al2O3 and CuO nanoparticles.22 ZrO2 nanoparticles show significant physical properties, despite the excellent heat transfer properties of metal oxide nanoparticles, there are still issues to be investigated about nanofluids.23–26 One of the basic issues in this field is the agglomeration of oxide nanoparticles in aqueous solutions, which is due to high hydrophilicity and strong Van der Waals forces.27,28 Despite extensive measurements, the very important and practical property of nanofluids is thermal conductivity. The studies and models that have been investigated to fit thermodynamic quantities and viscosity of polymer solutions and nanofluids are often for a concentrated region, and fewer studies have been conducted in the field of thermodynamics of nanofluids in the dilute region.29–31
In this research, nanofluid systems including ZrO2 nanoparticles in water, PPG and aqueous PVP as base fluids have been investigated and the thermodynamic performance and interactions in these systems have been investigated. UV-Vis spectroscopy was adopted to observe the stability of nanofluid with the passage of time. The density, speed of sound and viscosity of nanofluids including ZrO2 nanoparticles dispersed in PPG, H2O–PVP and H2O have been measured up to semi-dilute concentration range at T = (293.15, 298.15, 308.15, 318.15) K. For elucidating the interactions occurring in biphasic heterogeneous colloids, the excess molar volume (VEm) and isentropic compressibility (κs) which are convenient for this aim determined.32 The VEm values were correlated with the Redlich–Kister,33 Ott et al.34 and polynomial equations. The κs values were fitted with the polynomial equation. The Eyring-NRTL35 and Eyring-mNRF36 models have successfully been used to correlate the viscosity reported data. Additionally, the Einstein, Brinkman, Lundgren, and Batchelor models was employed to predict the viscosity data.
2. Experimentation
2.1. Chemicals
The utilized chemicals in this work were ZrO2, PPG and PVP. The specification about the utilized chemicals are as follows:
The ZrO2 nanoparticles with an average diameter of 20 nm was purchased from Nanostructured & Amorphous Materials Inc., USA, polyvinylpyrrolidone (PVP) and polypropylene glycol (PPG) from Merck. The related approximate molar mass for ZrO2 was 123.218 g mol−1, for PPG was 400 and for PVP was 50 000. The utilized materials purity were >99% according to the supplier. Also, the related CAS. no. for ZrO2 was 1314-23-4, 9003-39-8 for PVP and 25322-69-4 for PPG. The utilized water in this study for preparation of the nanofluids was double distilled deionized with conductance about 1 μS cm−1.
2.2. Preparation of the nanofluids
Zirconium oxide (ZrO2) nanoparticles were dispersed in various base fluids, including polypropylene glycol (PPG), water, and binary mixtures of water–PPG and water–polyvinylpyrrolidone (PVP) with different mass fractions of polymers. The mole fractions of the base fluids has been provided in Tables S1 and S2.† To prepare these mixtures, an analytical balance (AND, GR-202, Japan) with a precision of ±1 × 10−4 g was employed. The resulting mixtures were subjected to ultrasonic treatment for one hour using an ultrasonic bath (Grant, England) followed by 30 minutes of exposure to an ultrasonic probe device (UP400S, 400 watts, 24 kHz).
2.3. Instruments and process
The whole measurements are illustrated in Fig. 1 to show the flow of the work to assess the stability of the nanofluids. The details of the measurements are described in the continuation.
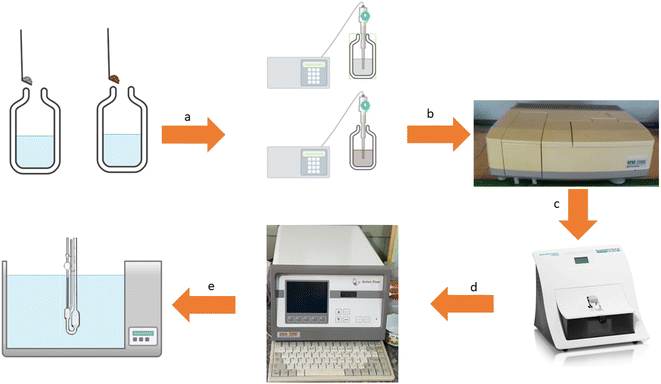 |
| | Fig. 1 The measurements diagram including preparation of mixtures and sonication (a), UV-Vis spectrophotometry (b), dynamic light scattering (c), density and speed of sound measurements (d), and viscosity measurement (e). | |
2.3.1. UV-Vis and dynamic light scattering studies (DLS). The UV-Vis spectra were measured with a spectrophotometer and (Analytic Jena, SPECORD-250, Germany) in the wavelength range from 200 to 600 nm. Particle size distribution and zeta potential are measured by a DLS device (DLS, Nanotrac wave model) for the studied system in terms of stability to obtain the nanoparticle size inside the nanofluid systems.
2.3.2. Density and speed of sound measurements. Density and speed of sound for the stable nanofluid system are measured at T = (293.15 to 318.15) K by a densimeter (Anton Paar, DSA 5000, Austria). This densimeter measures the density and speed of sound with a precision of 3 × 10−6 g cm−3 and 0.1 m s−1. The instrument was automatically thermostabilized within ±0.001 K (with a built-in Peltier temperature controller).
2.3.3. Viscosity. The viscosity of the stable nanofluid was measured by capillary viscometer, the dangling Ubbelohde-type viscometer (Julabo, MD-18V, Germany). In these viscometers, the temperature was controlled with an accuracy of 0.01 K. The passage of the time for nanofluid through the capillary tube was measured by a stopwatch. The precision of the used stopwatch was 0.01 s.| |
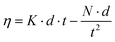 | (1) |
In these equations: t sample passage time through the capillary tube, N and K are viscometer constants, d is nanofluid density and θ is correction factor. In these research work θ was 1.
3. Result and discussion
3.1. Stability studies
The stability of nanofluids was investigated by UV-Vis spectroscopy. First, the nanoparticles of ZrO2 have been dispersed in PPG, water and aqueous solutions of PPG–H2O, PVP–H2O as base fluids. The prepared nanofluids were stirred for one hour by a magnetic stirrer, then they were respectively placed in an ultrasonic bath for 24 h, and after 24 h in an ultrasonic bath with a probe for 30 min. UV-Vis absorption spectroscopy for ZrO2–PPG, ZrO2–H2O and different ratios of ZrO2–PPG–H2O nanofluids at ZrO2 mole fraction of 0.00038 are shown in Fig. 2.
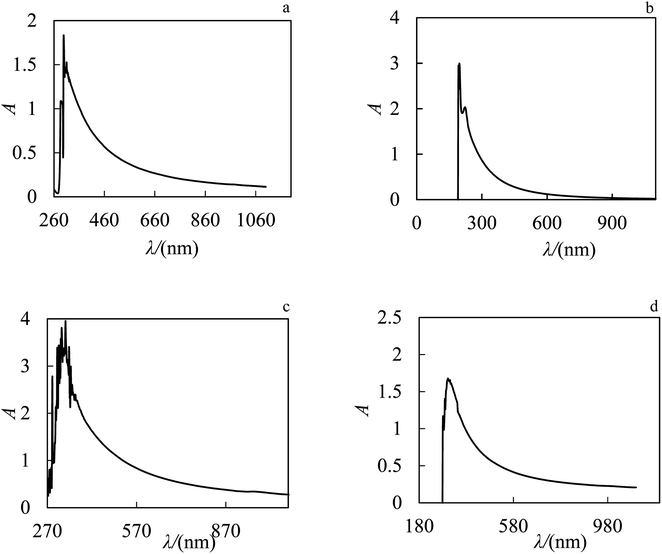 |
| | Fig. 2 UV-Vis absorption spectrum of nanofluids after ultrasonic bath (a) ZrO2–PPG, (b) ZrO2–H2O, (c) ZrO2–PPG–H2O with ratio (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and (d) ZrO2–PPG–H2O with ratio (3 1) and (d) ZrO2–PPG–H2O with ratio (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of PPG–H2O base fluid in molar fraction of ZrO2 equal to 0.00038. 1) of PPG–H2O base fluid in molar fraction of ZrO2 equal to 0.00038. | |
The UV-Vis analysis demonstrates the maximum absorption wavelength of ZrO2–PPG is 306 nm, ZrO2–PPG–H2O (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is 333 nm, ZrO2–PPG–H2O (3
1) is 333 nm, ZrO2–PPG–H2O (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is 309 nm and ZrO2–H2O have two sharp peaks in the region of 201 and 295 nm. Therefore, to check the stability of the prepared nanofluids, after sonication, their UV-Vis spectra were recorded over the time.37 These spectra over the time for ZrO2–PPG, ZrO2–H2O and different ratios of ZrO2–PPG–H2O nanofluids are shown in Fig. 3. As depicted in Fig. 3, the ZrO2–PPG system has a stability about one month, and with the time elaps, the nanoparticles were sedimented.
1) is 309 nm and ZrO2–H2O have two sharp peaks in the region of 201 and 295 nm. Therefore, to check the stability of the prepared nanofluids, after sonication, their UV-Vis spectra were recorded over the time.37 These spectra over the time for ZrO2–PPG, ZrO2–H2O and different ratios of ZrO2–PPG–H2O nanofluids are shown in Fig. 3. As depicted in Fig. 3, the ZrO2–PPG system has a stability about one month, and with the time elaps, the nanoparticles were sedimented.
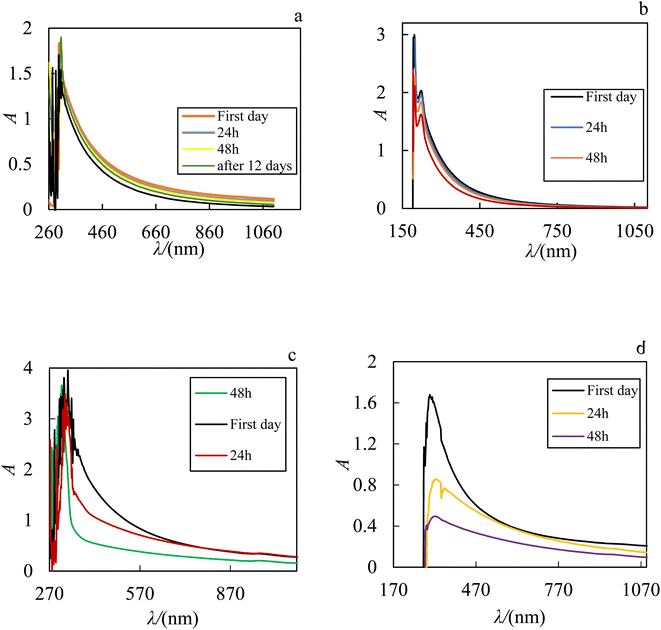 |
| | Fig. 3 UV-Vis absorption spectrum of (a) ZrO2–PPG, (b) ZrO2–H2O, (c) ZrO2–PPG–H2O with ratio (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and (d) ZrO2–PPG–H2O with ratio (3 1) and (d) ZrO2–PPG–H2O with ratio (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of PPG–H2O base fluid in molar fraction of ZrO2 equal to 0.00038. 1) of PPG–H2O base fluid in molar fraction of ZrO2 equal to 0.00038. | |
The ZrO2–PPG system is stable for about one month and as the times elapses, the nanoparticles begin to precipitate from the solution. The ZrO2–H2O system is stable for 24 h and after 24 h the intensity of absorption decreases and the sample is unstable due to the formation of clusters of ZrO2 nanoparticles. It can be seen in Fig. 3(c) and (d) that by adding water to the ZrO2–PPG mixture, the samples face a sharp decrease in absorption and are completely unstable, it can be concluded that the interactions between water molecules and PPG are more than the interaction between PPG and ZrO2 nanoparticles, and as a result, the percentage of water compared to PPG increases, the maximum absorption decreases and ZrO2 nanoparticles are deposited.38–40 Among the investigated systems, the ZrO2–PPG nanofluid exhibited satisfactory stability, as evidenced by both its intrinsic properties and thermodynamic analysis. Consequently, further thermodynamic studies can be conducted on this specific nanofluid. Fig. 4 presents the absorption–time profiles for the ZrO2–PPG and ZrO2–PPG–H2O nanofluids.38–40
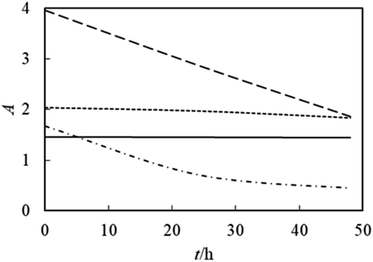 |
| | Fig. 4 UV-Vis absorption spectrum in terms of time for nanofluid ZrO2–PPG (—), ZrO2–H2O (…), ZrO2–PPG–H2O (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (----), ZrO2–PPG–H2O (3 1) (----), ZrO2–PPG–H2O (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (-.-.-.) in the molar fraction of ZrO2 equal to 0.00038. 1) (-.-.-.) in the molar fraction of ZrO2 equal to 0.00038. | |
According to the results reported in the studies by Zafarani and his colleagues, the research conducted on the ZnO–PPG nanofluid system, the studied nanofluid has stability for 7 days and then with the time elaps nanoparticles start to sediment.41 These results indicates that the ability of PPG in spreading ZrO2 nanoparticles can be justified by the fact that with the presence of an additional oxygen in ZrO2, more hydrogen bonds are formed with polymer molecules and the stability of the system increases. In this research, due to the instability of the ZrO2–PPG–H2O system, we must look for factors that increase the stability of these nanoparticles without having side effects. For this reason, PVP was used as a stabilizing agent and surfactant. In this research, in order to achieve a suitable system in terms of stability, different proportions of PVP–H2O were prepared and ZrO2 nanoparticles were dispersed in them. The prepared nanofluids were placed in an ultrasonic bath for 24 h and their stability over time was checked by UV-Vis and the results are shown in Fig. 5.
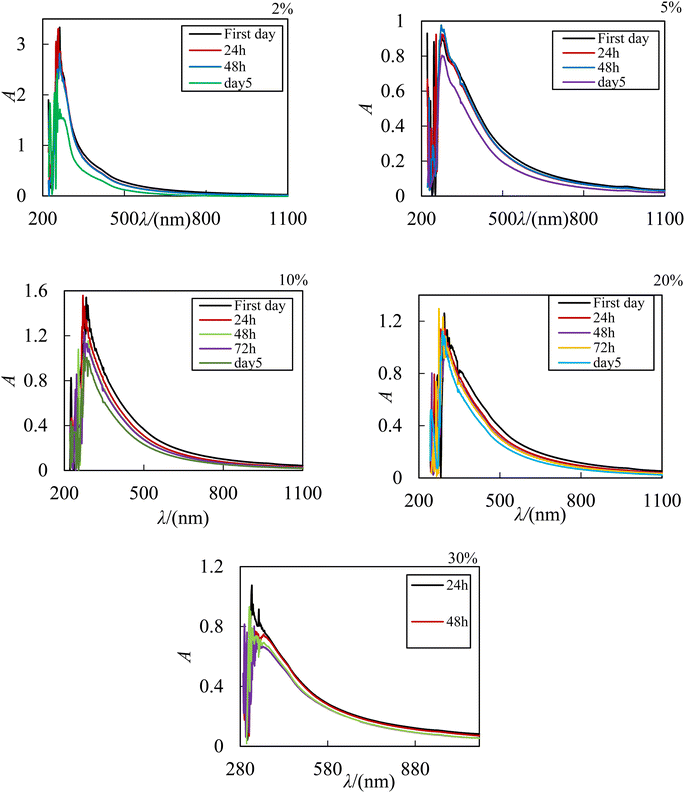 |
| | Fig. 5 UV-Vis absorption spectrum of ZrO2–H2O–PVP nanofluids with different ratios of PVP in ZrO2 mole fraction equal to 0.00038. | |
It is evident from Fig. 5, the absorption peak in the presence of PVP has become sharper and the maximum absorption has increased towards longer wavelengths, which indicates the larger particles, which can be attributed to the effect of PVP as a surfactant. The properties of the solvent in spectroscopy have an effect on the absorbed wavelength of the material. Therefore, the choice of solvent is important, it may be that hydrogen bonds produced by polar solvents with the ground state of polar molecules are easier than creating bonds with their excited states, as a result, the energy of electron transfers in these molecules will increase and the transfers will be towards the shorter wavelength. On the other hand, in some cases, the excited states may form stronger hydrogen bonds than the ground state, thus shifting the absorption to longer wavelengths because the electron energy decreases. By comparing the UV-Vis of ZrO2–H2O with ZrO2–PVP–H2O, it can be concluded that the systems become more stable in the presence of PVP. The interaction of PVP with ZrO2 in the ZrO2–H2O system causes the stabilization of the excited state, in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio of PVP
3 ratio of PVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, the stability is higher than the other ratios. PVP is a polymer with long chains and hollow spaces, nanoparticles can enter these empty spaces due to their small size, and water molecules can create strong hydrogen bonds with the polymer, and because of these strong bonds in this system, nanoparticles are more stable.
H2O, the stability is higher than the other ratios. PVP is a polymer with long chains and hollow spaces, nanoparticles can enter these empty spaces due to their small size, and water molecules can create strong hydrogen bonds with the polymer, and because of these strong bonds in this system, nanoparticles are more stable.
The analysis of the resulting spectra in Fig. 5 shows that by increasing the viscosity of the base fluid in the consequence of addition of polymer, the dispersion of nanoparticles improves. The UV-Vis of different ratios of ZrO2–H2O–PVP indicates that area under the curve in the proportions of 2%, 5%, 10% and 20% of PVP is stable for about 3 days and then decreases with the time elaps which shows the sedimentation of nanoparticles. The area under the peak decreases slowly with the increase in the amount of PVP. In the recorded UV-Vis spectrum with a ratio of 30% PVP, there is no noticeable change in the system for 5 days, and after this period of time, the amount of reduction in the area under the peak (the amount of deposition of nanoparticles) is very slow. According to these observations, the ZrO2–H2O–PVP system with a ratio of 30% PVP is more stable than other systems and can be introduced as an ideal fluid for ZrO2 nanoparticles.
3.2. Particle size distribution and zeta potential
After checking the stability of the studied nanofluid systems, the particle size distribution for the stable nanofluid system containing ZrO2 nanoparticles dispersed in PPG has been measured by DLS. The average particle size was 163.7 nm, according to the obtained results, the average size of the nanoparticles in the fluid were larger than the initial size of the nanoparticles. In Yu and collogues studies, increasing in the size of nanoparticles was attributed to the aggregation of nanoparticles.42 The large size of ZrO2 nanoparticles in the fluid can be caused by the presence of long polymer chains and the particles being surrounded by polymer chains. Of course, the particles can be placed in the spaces created by the polymer, which is called the polymer compaction effect, and even this phenomenon can be considered as an effective factor in the stability of nanofluids. In a study conducted on the ZrO2–H2O system, it was observed that the size of the nanoparticles in the nanofluid is about 200 nm, which is more than the initial size of the nanoparticles, which was 60 nm,43 the large size of nanoparticles in water is related to the clumping of ZrO2 nanoparticles in water.
The zeta potential for the stable nanofluid containing ZrO2 nanoparticles dispersed in PPG was measured and the value of +68 mV was obtained. In the study conducted on the ZrO2–H2O system, zeta potential for this nanofluid was +45 in acidic conditions and −41 in alkaline conditions.44 The results reported for the zeta potential of the system, according to the studies conducted and the results obtained in the literature, systems with a zeta potential greater than +30 and less than −30 have stability.45 Therefore, according to the size of the zeta potential, it can be concluded that PPG is a suitable fluid for spreading ZrO2 nanoparticles. These observations confirms the results of UV-Vis spectroscopy.
3.3. Density and speed of sound
In this research, ZrO2 nanoparticles were dispersed in PPG, H2O, PPG–H2O and PVP–H2O base fluids by applying ultrasonic waves. The experimental density, speed of sound and viscosity data for ZrO2 in PPG, aqueous solution of PVP and ZrO2 in water are collected in Table 1.
Table 1 Density (d), excess molar volume (VEm), viscosity (η), speed of sound (u), isentropic compressibility (κs), for nanofluid of ZrO2 nanoparticles dispersed in PPG, PVP–H2O, and H2O at different temperaturesa
| 100 × x1b |
100 × φ1c |
10−3 × d (kg m−3) |
u (m s−1) |
η (mPa s) |
106 × VEm (m3 mol−1) |
1012 × κs (T Pa−1) |
| The standard uncertainties for molality, temperature and pressure were u(m) = 0.001 mol kg−1, u(T) = 0.2 K, u(P) = 10.5 h Pa, respectively with level of confidence 0.95. The standard combined uncertainty for viscosity was about, uc(η) = 0.02 mPa s, for density were about, uc(d) = 0.06 × 10−3 g cm−3, and for speed of sound were about, uc(u) = 1.5 m s−1 (level of confidence 0.68). x1: mole fraction of ZrO2 nanoparticle. φ1: volume fraction of ZrO2 nanoparticle. |
| ZrO2 nanoparticles dispersed in PPG |
| T = 293.15 K |
| 0.2520 |
0.013 |
1.014337 |
1402.12 |
100.225 |
−0.038 |
501.473 |
| 0.5350 |
0.028 |
1.015157 |
1395.81 |
100.979 |
−0.068 |
505.608 |
| 0.9120 |
0.048 |
1.016418 |
1388.15 |
101.518 |
−0.172 |
510.569 |
| 1.2190 |
0.064 |
1.017508 |
1383.12 |
102.222 |
−0.278 |
513.739 |
| 1.6390 |
0.087 |
1.018998 |
1378.44 |
102.569 |
−0.417 |
516.477 |
| 3.5620 |
0.193 |
1.026107 |
1363.25 |
106.313 |
−1.100 |
524.392 |
| 5.7000 |
0.315 |
1.033569 |
1355.69 |
107.531 |
−1.574 |
526.429 |
| T = 298.15 K |
| 0.2520 |
0.013 |
1.010667 |
1386.51 |
71.994 |
−0.183 |
514.690 |
| 0.5350 |
0.028 |
1.011509 |
1380.56 |
72.517 |
−0.222 |
518.704 |
| 0.9820 |
0.052 |
1.012819 |
1374.55 |
72.990 |
−0.347 |
522.573 |
| 1.2190 |
0.064 |
1.013891 |
1371.75 |
73.426 |
−0.447 |
524.154 |
| 1.6390 |
0.087 |
1.015499 |
1368.44 |
75.561 |
−0.633 |
525.859 |
| 3.5620 |
0.192 |
1.022647 |
1355.21 |
77.342 |
−1.336 |
532.428 |
| 5.7000 |
0.314 |
1.030289 |
1349.55 |
78.989 |
−1.879 |
532.921 |
| T = 308.15 K |
| 0.2520 |
0.013 |
1.002978 |
1352.19 |
39.862 |
−0.496 |
545.297 |
| 0.5350 |
0.028 |
1.003792 |
1347.12 |
41.072 |
−0.526 |
548.964 |
| 0.9820 |
0.051 |
1.005127 |
1342.59 |
41.280 |
−0.664 |
551.940 |
| 1.2190 |
0.064 |
1.006219 |
1339.56 |
41.387 |
−0.774 |
553.839 |
| 1.6390 |
0.086 |
1.007790 |
1336.29 |
41.501 |
−0.950 |
555.685 |
| 3.5620 |
0.190 |
1.015008 |
1326.34 |
43.802 |
−1.696 |
560.042 |
| 5.7000 |
0.311 |
1.022781 |
1321.95 |
44.521 |
−2.301 |
559.484 |
| T = 318.15 K |
| 0.2520 |
0.013 |
0.996634 |
1318.48 |
24.623 |
−1.071 |
577.188 |
| 0.5350 |
0.028 |
0.997400 |
1314.80 |
25.272 |
−1.082 |
579.978 |
| 0.9820 |
0.051 |
0.998628 |
1310.39 |
25.398 |
−1.178 |
583.170 |
| 1.2190 |
0.063 |
0.999735 |
1307.59 |
25.538 |
−1.296 |
585.022 |
| 1.6390 |
0.085 |
1.001199 |
1304.88 |
25.775 |
−1.432 |
586.595 |
| 3.5620 |
0.189 |
1.008329 |
1298.21 |
27.065 |
−2.156 |
588.448 |
| 5.7000 |
0.309 |
1.015912 |
1291.16 |
27.964 |
−2.700 |
590.451 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| ZrO2 nanoparticles dispersed in PVP–H2O (30% w/w) |
| T = 293.15 K |
| 0.0031 |
0.003 |
1.062929 |
1639.58 |
60.502 |
−0.003 |
349.970 |
| 0.0071 |
0.006 |
1.063105 |
1638.85 |
61.162 |
−0.003 |
350.224 |
| 0.0100 |
0.009 |
1.063269 |
1638.44 |
61.322 |
−0.003 |
350.345 |
| 0.0130 |
0.011 |
1.063376 |
1638.25 |
61.621 |
−0.003 |
350.391 |
| 0.0180 |
0.015 |
1.063566 |
1637.98 |
61.745 |
−0.002 |
350.444 |
| 0.0260 |
0.022 |
1.063790 |
1637.65 |
62.069 |
0.000 |
350.511 |
| 0.0330 |
0.028 |
1.063999 |
1637.43 |
62.261 |
0.002 |
350.537 |
| T = 298.15 K |
| 0.0031 |
0.003 |
1.061314 |
1643.24 |
49.419 |
−0.004 |
348.943 |
| 0.0071 |
0.006 |
1.061497 |
1642.69 |
49.701 |
−0.004 |
349.116 |
| 0.0100 |
0.009 |
1.061663 |
1642.47 |
49.793 |
−0.004 |
349.155 |
| 0.0130 |
0.011 |
1.061780 |
1642.32 |
50.034 |
−0.004 |
349.180 |
| 0.0180 |
0.015 |
1.061979 |
1642.05 |
50.326 |
−0.004 |
349.230 |
| 0.0260 |
0.022 |
1.062225 |
1641.89 |
51.251 |
−0.002 |
349.217 |
| 0.0330 |
0.028 |
1.062436 |
1641.74 |
51.789 |
0.000 |
349.211 |
| T = 308.15 K |
| 0.0031 |
0.003 |
1.057130 |
1649.52 |
33.966 |
−0.005 |
347.661 |
| 0.0071 |
0.006 |
1.057316 |
1648.83 |
34.300 |
−0.005 |
347.891 |
| 0.0100 |
0.009 |
1.057479 |
1648.55 |
34.830 |
−0.005 |
347.956 |
| 0.0130 |
0.011 |
1.057591 |
1648.47 |
35.312 |
−0.005 |
347.953 |
| 0.0180 |
0.015 |
1.057796 |
1648.28 |
35.450 |
−0.005 |
347.965 |
| 0.0260 |
0.022 |
1.058056 |
1647.91 |
35.619 |
−0.003 |
348.036 |
| 0.0330 |
0.028 |
1.058285 |
1647.75 |
35.768 |
−0.002 |
348.028 |
| T = 318.15 K |
| 0.0031 |
0.003 |
1.052388 |
1655.65 |
25.836 |
−0.006 |
346.647 |
| 0.0071 |
0.006 |
1.052571 |
1655.25 |
25.943 |
−0.006 |
346.754 |
| 0.0100 |
0.009 |
1.052729 |
1654.90 |
26.106 |
−0.006 |
346.849 |
| 0.0130 |
0.011 |
1.052845 |
1654.73 |
26.267 |
−0.006 |
346.882 |
| 0.0180 |
0.015 |
1.053051 |
1654.48 |
26.422 |
−0.006 |
346.919 |
| 0.0260 |
0.022 |
1.053321 |
1654.16 |
26.541 |
−0.005 |
346.964 |
| 0.0330 |
0.028 |
1.053559 |
1653.88 |
26.677 |
−0.003 |
347.003 |
| 100 × x1b |
100 × φ1c |
10−3 × d (kg m−3) |
u (m s−1) |
106 × VEm (m3 mol−1) |
1012 × κs (T Pa−1) |
| ZrO2 nanoparticles dispersed in H2O |
| T = 293.15 K |
| 0.1700 |
0.194 |
0.998418 |
1482.95 |
−0.002 |
455.444 |
| 0.2920 |
0.333 |
0.998443 |
1482.90 |
−0.001 |
455.463 |
| 0.3650 |
0.417 |
0.998464 |
1482.78 |
−0.001 |
455.527 |
| 0.5110 |
0.583 |
0.998505 |
1482.79 |
0.000 |
455.502 |
| 0.6080 |
0.694 |
0.998534 |
1482.59 |
0.000 |
455.612 |
| 0.7290 |
0.832 |
0.998572 |
1482.89 |
0.001 |
455.410 |
| T = 298.15 K |
| 0.1700 |
0.194 |
0.997386 |
1496.98 |
−0.004 |
447.409 |
| 0.2920 |
0.333 |
0.997394 |
1497.08 |
−0.003 |
447.346 |
| 0.3650 |
0.417 |
0.997405 |
1496.92 |
−0.003 |
447.436 |
| 0.5110 |
0.583 |
0.997431 |
1496.87 |
−0.002 |
447.455 |
| 0.6080 |
0.694 |
0.997455 |
1496.70 |
−0.001 |
447.545 |
| 0.7290 |
0.832 |
0.997489 |
1496.91 |
−0.001 |
447.405 |
| T = 308.15 K |
| 0.1700 |
0.194 |
0.994495 |
1519.73 |
−0.007 |
435.376 |
| 0.2920 |
0.333 |
0.994490 |
1519.75 |
−0.005 |
435.367 |
| 0.3650 |
0.417 |
0.994494 |
1519.65 |
−0.005 |
435.422 |
| 0.5110 |
0.583 |
0.994499 |
1519.59 |
−0.003 |
435.455 |
| 0.6080 |
0.694 |
0.994519 |
1519.41 |
−0.003 |
435.549 |
| 0.7290 |
0.832 |
0.994558 |
1519.73 |
−0.002 |
435.348 |
| T = 318.15 K |
| 0.1700 |
0.194 |
0.990520 |
1536.19 |
−0.014 |
427.806 |
| 0.2920 |
0.333 |
0.990525 |
1536.33 |
−0.013 |
427.726 |
| 0.3650 |
0.417 |
0.990529 |
1536.12 |
−0.012 |
427.841 |
| 0.5110 |
0.583 |
0.990534 |
1535.98 |
−0.011 |
427.917 |
| 0.6080 |
0.694 |
0.990539 |
1535.85 |
−0.010 |
427.987 |
| 0.7290 |
0.832 |
0.990555 |
1536.02 |
−0.009 |
427.886 |
According to the results of UV-Vis spectroscopy, due to the instability of nanofluids containing ZrO2 nanoparticles dispersed in PPG-H2O base fluids, thermodynamic studies only on PPG and PVP–H2O fluids were done. To compare the studied systems, density and speed of sound were measured for the H2O–ZrO2 system. In order to understand the interactions inside the nanofluid, the excess molar volume (VEm) and isentropic compressibility (κs) were calculated using the experimental data of density and sound speed through the following equations:46,47
| |
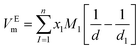 | (3) |
| |
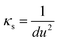 | (4) |
where
x is the mole fraction,
M is the molar mass, subscripts 1, 2 and 3 stand for ZrO
2 nanoparticles, polymer and water, respectively, while, density of the ZrO
2 nanoparticles the value of 5.98 kg m
−3 was taken from the literature.
48 Since the concentration of the investigated mixtures is dilute, the
VEm calculated at different temperatures are not very sensitive to this value. Accordingly, the value of 5.98 kg m
−3 at the four investigated temperatures was used. The calculated values of
VEm and
κs are also reported in
Table 1. It can be seen that, in all cases, the density decreased with increasing temperature, whereas the loading of nanoparticles implied higher density values, as expected.
The temperature dependency of VEm and κs for ZrO2–PPG, ZrO2–H2O–PVP and ZrO2–H2O systems are shown in Fig. 6. Density, viscosity and speed of sound for ZrO2–PPG and ZrO2–H2O–PVP nanofluid systems have been measured at different temperatures by capillary viscometer and densimeter device, the results are reported in Table 1.
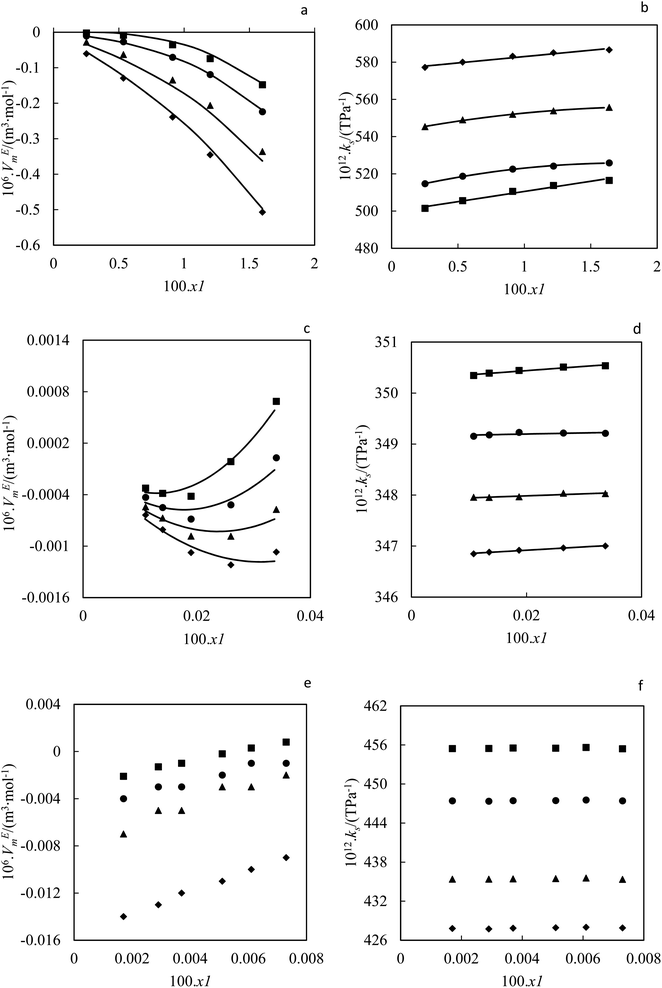 |
| | Fig. 6 Excess molar volume (a) and (b) isentropic compressibility in terms of nanoparticle mole fraction for ZrO2–PPG system at T = ((■) 293.15, (●) 298.15, (▲) 308.15, (♦) 318.15) K in comparison with (—) polynomial equation; excess molar volume (c) and (d) isentropic compressibility in terms of nanoparticle mole fraction for ZrO2–H2O–PVP system at T = ((■) 293.15, (●) 298.15, (▲) 308.15, (♦) 318.15) K compared to (—) polynomial equation; experimental data of (e) excess molar volume and (f) isentropic compressibility in terms of nanoparticle mole fraction for ZrO2–H2O system at T = ((■) 293.15, (●) 298.15, (▲) 308.15, (♦) 318.15) K. | |
As is evident from Table 1 and Fig. 6, VEm values are negative for ZrO2–PPG within the dilute concentration range and become more negative with increasing concentration. The effect of temperature on the VEm of ZrO2–PPG is not noticeable, however, with increasing temperature, the value of (VEm) becomes less negative. In the mixtures, negative VEm values can be due to the unlike interactions and also the placement of small molecules in spaces between polymer chains (compression effect). The positive values of VEm are characteristic of Van der Waals interactions between molecules. In the ZrO2–PPG nanofluid system, there are different interactions between unlike molecules (polymer molecules and nanoparticles), and Van der Waals interactions between (polymer–polymer) and (nanoparticle–nanoparticle), while the similar interactions of nanoparticles together cause the agglomeration phenomenon. In the ZrO2–PPG system, VEm is negative generally, so it can be concluded that the unlike interactions are dominant and also nanoparticles accommodation in the voids provided by the polymer.
According to Table 1 and Fig. 6(c) it can be seen that the VEm for the ZrO2–H2O–PVP is negative and becomes more negative in dilute areas and becomes positive with increasing the concentration of nanoparticles, which shows that there are interactions between nanoparticles and base fluid in the dilute regions, and with increasing in the concentration of nanoparticles, the amount of Van der Waals forces increases and the nanoparticles become agglomeration in the base fluid. The performance of the molar volume is related to the interactions between the hydrogen atoms of the H2O and the oxygen atoms of PVP, which has a nitrogen molecule in its structure and has the ability to form a strong hydrogen bond with H2O. It can also be seen that with the increasing in the temperature, the VEm value becomes more negative, which can be related to the effect of polymer compression, which breaks the long polymer chains and collapses its molecular structure with the increase in temperature. Nanoparticles come out of the compressed state and the interaction of nanoparticles with each other breaks down and they interact more with H2O and PVP.49–51
It is also evident from Table 1 and Fig. 6(e) that VEm is negative for ZrO2–H2O nanofluid system and increases and becomes positive with increasing the concentration of nanoparticles; it can be concluded that in the ZrO2–H2O nanofluid system, small H2O molecules create hydrogen bonds with each other and trap nanoparticles in the holes in the solution, but due to the high molecular mass of ZrO2 nanoparticles, the hydrogen bonds between H2O molecules is loosened and causes instability. By comparing the ZrO2–H2O and ZrO2–H2O–PVP systems, it can be indicated that VEm in the ZrO2–H2O system is negative and increases with the increase in the concentration of nanoparticles, while in the ZrO2–H2O–PVP system, it is negative and becomes more negative with increasing concentration in dilute regions and increases again with increasing nanoparticle concentration. In both systems, VEm becomes less negative with increasing the temperature. The effect of temperature in the ZrO2–H2O system is more noticeable than in the ZrO2–H2O–PVP system, and with increasing temperature, the amount of VEm decreases, which indicates that the number of weakened hydrogen bonds is more in the ZrO2–H2O system from ZrO2–H2O–PVP system.52–56
According to Table 1 and Fig. 6(d), the κs value for ZrO2–H2O–PVP system is positive in all concentrations and increases with increasing the concentration of nanoparticles and is almost constant in compact points. It decreases with increasing the temperature as it is evident from Table 1 and Fig. 6(f) that the κs for the ZrO2–H2O system increases with the increase in the concentration of nanoparticles and has almost a constant value in all areas and decreases with the increase in the temperature. In all studied nanofluids and at all temperatures, the isentropic compressibility has positive values, which indicates the existence of a regular molecular structure due to the presence of strong hydrogen bonds. At high temperatures, hydrogen bonds are weakened and the coherent molecular structure collapses. The isentropic compressibility performance of the studied nanofluids can be shown as follows:
| κs(ZrO2–PPG) > κs(ZrO2–H2O) > κs(ZrO2–H2O–PVP30%) |
The studies conducted on excess molar volume (VEm) and isentropic compressibility (κs) and the obtained results confirm the results of UV-vis spectroscopy.
3.4. Viscosity results
In order to ensure the accuracy of the data obtained from the capillary viscometer, the viscosity of ZrO2–PPG and ZrO2–H2O–PVP nanofluids was also measured over the time and the changes of η/ηbasefluid for these nanofluids are shown according to time in Fig. 7.
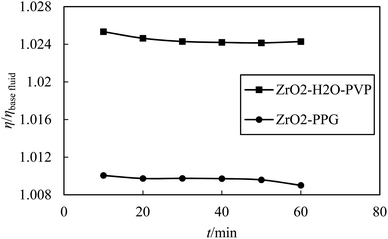 |
| | Fig. 7 Experimental viscosity ratio η/ηbasefluid plotted against time (t min−1) for of ZrO2 in PPG and H2O–PVP. | |
Fig. 7 shows the repeatability of viscosity data in terms of time, which is a confirmation of the suitability of capillary viscometers for these measurements. According to the Table 1, the viscosity of ZrO2–PPG and ZrO2–H2O–PVP nanofluids increased with increasing the concentration of nanoparticles and decreased with increasing temperature. It should be noted that, for both mentioned systems, the effect of temperature on the viscosity of nanofluids is more significant than the effect of increasing concentration. In the results reported in a study conducted on the viscosity of the ZrO2–H2O system, it has been observed that the viscosity of the mentioned nanofluid is affected by the concentration of nanoparticles and negligible change in viscosity is seen with the temperature change.
4. Correlation
The VEm values of nanofluid systems were correlated by Redlich–Kister, Ott57 and polynomial equation at each temperature. These equations listed respectively in eqn (5)–(7). In the polynomial eqn (7), Ah is the polynomial coefficient and h + 1 is the number of polynomial coefficients. In this research, the VEm values are fitted by the mentioned equations by two methods. Each of the equations are given a temperature dependence by writing each of the parameters as 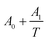 , and two methods are tried in fitting the data. In the first method, the usual fitting method was used, and in the second method, the fitting was done by dividing the main equation into x1x2 . The efficiency of the equations was studied by comparing the standard deviation obtained from the excess molar volumes and the density of the samples. Fitting the VEm values was done by using the mentioned equations and using two fitting methods in each equation. Due to the lack of acceptable results from the fitting of the VEm values for the ZrO2–H2O system, the fitting data of this system was not studied. In Table 2, the standard deviation related to fitting the VEm values and density data of the ZrO2–PPG and ZrO2–H2O–PVP using the mentioned equations are reported. According to the results of Table 2, it can be concluded that the standard deviation related to the polynomial eqn (7), in fitting the data in both systems are acceptable while the second method has a better efficiency in fitting than the first method.
, and two methods are tried in fitting the data. In the first method, the usual fitting method was used, and in the second method, the fitting was done by dividing the main equation into x1x2 . The efficiency of the equations was studied by comparing the standard deviation obtained from the excess molar volumes and the density of the samples. Fitting the VEm values was done by using the mentioned equations and using two fitting methods in each equation. Due to the lack of acceptable results from the fitting of the VEm values for the ZrO2–H2O system, the fitting data of this system was not studied. In Table 2, the standard deviation related to fitting the VEm values and density data of the ZrO2–PPG and ZrO2–H2O–PVP using the mentioned equations are reported. According to the results of Table 2, it can be concluded that the standard deviation related to the polynomial eqn (7), in fitting the data in both systems are acceptable while the second method has a better efficiency in fitting than the first method.
Table 2 Standard deviations (σ) from fitting the excess molar volume (VEm) values in eqn (5)–(7) for ZrO2–PPG and ZrO2–H2O–PVP at different temperatures
| |
Ott et al. |
Redlich–Kister |
Polynomial |
| Method 1 |
Method 2 |
Method 1 |
Method 2 |
Method 1 |
Method 2 |
| ZrO2–PPG |
| T = 293.15 K |
| 103 × σ (VEm/(cm3 mol−1)) |
8.7 |
1.8 |
20.4 |
10.0 |
7.4 |
1.7 |
| 104 × σ (d/g cm−3) |
6.1 |
4.8 |
6.1 |
5.0 |
6.1 |
4.8 |
| T = 298.15 K |
| 103 × σ (VEm/(cm3 mol−1)) |
5.8 |
0.9 |
95.5 |
26.2 |
21.9 |
0.8 |
| 104 × σ (d/g cm−3) |
10.2 |
7.9 |
10.2 |
7.2 |
10.2 |
7.9 |
| T = 308.15 K |
| 103 × σ (VEm/(cm3 mol−1)) |
7.4 |
1.7 |
65.0 |
5.2 |
64.5 |
1.6 |
| 104 × σ (d/g cm−3) |
17.6 |
13.8 |
17.6 |
13.8 |
17.6 |
13.8 |
| T = 318.15 K |
| 103 × σ (VEm/(cm3 mol−1)) |
4.9 |
3.0 |
553.7 |
5.6 |
142.0 |
2.9 |
| 104 × σ (d/g cm−3) |
30.5 |
24.2 |
30.0 |
24.2 |
30.2 |
24.2 |
| Overall (103 × σ (VEm/(cm3 mol−1))) |
6.7 |
1.9 |
178.7 |
11.8 |
58.9 |
1.8 |
| Overall (104 × σ (d/g cm−3)) |
16.1 |
12.7 |
16.0 |
12.6 |
16.0 |
12.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| ZrO2–H2O–PVP (30% w/w) |
| T = 293.15 K |
| 104 × σ (VEm/(cm3 mol−1)) |
8.8 |
0.3 |
4.7 |
2.3 |
4.0 |
0.7 |
| 104 × σ (d/g cm−3) |
1.0 |
0.8 |
1.3 |
0.8 |
1.0 |
0.8 |
| T = 298.15 K |
| 104 × σ (VEm/(cm3 mol−1)) |
3.6 |
4.2 |
3.9 |
2.0 |
3.9 |
0.9 |
| 104 × σ (d/g cm−3) |
1.4 |
1.1 |
1.4 |
1.2 |
1.4 |
1.2 |
| T = 308.15 K |
| 104 × σ (VEm/(cm3 mol−1)) |
1.4 |
1.4 |
6.4 |
1.2 |
5.2 |
0.7 |
| 104 × σ (d/g cm−3) |
1.8 |
1.5 |
1.8 |
1.5 |
40.5 |
1.5 |
| T = 318.15 K |
| 104 × σ (VEm/(cm3 mol−1)) |
0.9 |
1.0 |
8.9 |
0.7 |
6.2 |
0.6 |
| 104 × σ (d/g cm−3) |
2.3 |
1.9 |
2.3 |
1.9 |
2.3 |
1.9 |
| Overall (104 × σ (VEm/(cm3 mol−1))) |
3.6 |
1.7 |
5.9 |
1.5 |
4.8 |
0.7 |
| Overall (104 × σ (d/g cm−3)) |
1.6 |
1.3 |
1.7 |
1.3 |
11.3 |
1.3 |
In Table S3† the standard deviations obtained from fitting the VEm values and density data are reported for ZrO2–PPG and ZrO2–H2O–PVP systems, respectively, using temperature dependent equations. According to these tables, the efficiency of the polynomial equation with temperature dependency for both systems and using both methods is better than the Redlich–Keister and Ott equations with temperature dependency. Also, the efficiency of the second method in fitting of the VEm values and density data was better than the first method in all equations. Therefore, according to the results of the standard deviation of all systems and all temperatures, the efficiency of the polynomial equation with the second method and temperature dependency is better than other methods. The parameters of Redlich-Kister, Ott et al. and polynomial equations, using the first fitting method are also reported in Table 3.
Table 3 Excess molar volume (VEm) parameters of eqn (5)–(7) using the first fitting method for ZrO2–PPG and ZrO2–H2O–PVP systems at different temperatures
| ZrO2–PPG – eqn (5) |
| |
10−5 × A0 |
10−5 × A1 |
10−5 × A2 |
σ |
| T = 293.15 K |
| 106 × VEm/(m3 mol)−1 |
0.07845 |
0.166 |
0.08751 |
0.020 |
| T = 298.15 K |
| 106 × VEm/(m3 mol)−1 |
−0.5284 |
−1.083 |
−0.5554 |
0.095 |
| T = 308.15 K |
| 106 × VEm/(m3 mol)−1 |
−1.64 |
−3.376 |
−1.738 |
0.065 |
| T = 318.15 K |
| 106 × VEm/(m3 mol)−1 |
−3.881 |
−7.996 |
−4.12 |
0.553 |
| ZrO2–H2O–PVP30% – eqn (5) |
| |
10−4 × A0 |
10−7 × A1 |
10−4 × A2 |
σ × 104 |
| T = 293.15 K |
| 106 × VEm/(m3 mol)−1 |
3.431 |
−2.014 |
−3.435 |
4.70 |
| T = 298.15 K |
| 106 × VEm/(m3 mol)−1 |
3.8 |
−2.163 |
−3.805 |
3.90 |
| T = 308.15 K |
| 106 × VEm/(m3 mol)−1 |
4.031 |
2.072 |
−4.037 |
6.47 |
| T = 318.15 K |
| 106 × VEm/(m3 mol)−1 |
4.361 |
−2.884 |
−4.368 |
8.97 |
| ZrO2–PPG – eqn (6) |
| |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
σ |
| T = 293.15 K |
| 106 × VEm/(m3 mol)−1 |
1.164 |
−368.304 |
0.00074 |
−0.931 |
0.001375 |
359.181 |
0.008 |
| T = 298.15 K |
| 106 × VEm/(m3 mol)−1 |
607.679 |
−62.253 |
−112.654 |
−106.015 |
−25.958 |
97.299 |
0.005 |
| T = 308.15 K |
| 106 × VEm/(m3 mol)−1 |
545.88 |
−365.089 |
−104.117 |
283.253 |
−7.734 |
−358.568 |
0.007 |
| T = 318.15 K |
| 106 × VEm/(m3 mol)−1 |
492.221 |
−519.075 |
−445.575 |
40.94 |
1790 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 990![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.004 |
| ZrO2–H2O–PVP30% – eqn (6) |
| |
A0 |
A1 |
A2 |
10−4 × A3 |
A4 |
10−3 × A5 |
σ |
| T = 293.15 K |
| 106 × VEm/(m3 mol)−1 |
1.757 |
1.167 |
39.417 |
3.4 |
614.014 |
−3.469 |
8.87 |
| T = 298.15 K |
| 106 × VEm/(m3 mol)−1 |
334.554 |
−237.219 |
−248.974 |
0.0836299 |
40.959 |
−0.044249 |
3.64 |
| T = 308.15 K |
| 106 × VEm/(m3 mol)−1 |
8480 |
1896 |
−2007 |
0.495 |
−4.152 |
−0.4953 |
1.41 |
| T = 318.15 K |
| 106 × VEm/(m3 mol)−1 |
7742 |
1586 |
−1704 |
0.3406 |
−6.208 |
−0.3407 |
0.92 |
| ZrO2–PPG – eqn (7) |
| |
A0 |
10−4 × A1 |
10−6 × A2 |
σ |
| T = 293.15 K |
| 106 × VEm/(m3 mol)−1 |
−5.918 |
−0.18 |
0.03501 |
0.007 |
| T = 298.15 K |
| 106 × VEm/(m3 mol)−1 |
−70.656 |
0.5546 |
−0.2222 |
0.021 |
| T = 308.15 K |
| 106 × VEm/(m3 mol)−1 |
−200.6 |
1.999 |
−0.695 |
0.064 |
| T = 318.15 K |
| 106 × VEm/(m3 mol)−1 |
−445.801 |
4.866 |
−1.648 |
0.142 |
| ZrO2–H2O–PVP30% – eqn (7) |
| |
A0 |
10−5 × A1 |
10−8 × A2 |
104 σ |
| T = 293.15 K |
| 106 × VEm/(m3 mol)−1 |
−38.934 |
1.373 |
2.894 |
4.07 |
| T = 298.15 K |
| 106 × VEm/(m3 mol)−1 |
−49.989 |
1.521 |
3.363 |
3.90 |
| T = 308.15 K |
| 106 × VEm/(m3 mol)−1 |
−58.307 |
1.614 |
2.09 |
5.27 |
| T = 318.15 K |
| 106 × VEm/(m3 mol)−1 |
−67.084 |
1.746 |
1.796 |
6.21 |
Also, the parameters of the Redlich–Kister, Ott et al. and polynomial equations using the second fitting method are reported in Table 4.
Table 4 Excess molar volume (VEm) parameters of eqn (5)–(7) using the second fitting method for ZrO2–PPG and ZrO2–H2O–PVP through utilization of Redlich–Kister and Ott equations at different temperatures
| ZrO2–PPG – eqn (5) |
| |
10−3A0 |
A1 |
10−3A2 |
σ |
| T = 293.15 K |
| 106 × VEm/m3 mol−1 |
−6.097 |
−12090 |
−5.992 |
0.010 |
| T = 298.15 K |
| 106 × VEm/m3 mol−1 |
−7.758 |
−15410 |
−7.658 |
0.026 |
| T = 308.15 K |
| 106 × VEm/m3 mol−1 |
−0.206268 |
−0.0002367 |
0.197979 |
0.005 |
| T = 318.15 K |
| 106 × VEm/m3 mol−1 |
−7.764 |
−15450 |
−7.709 |
0.005 |
| ZrO2–H2O–PVP30% –eqn (5) |
| |
10−3A0 |
A1 |
10−3A2 |
104σ |
| T = 293.15 K |
| 106 × VEm/m3 mol−1 |
5.657 |
7.866 |
−5.656 |
2.36 |
| T = 298.15 K |
| 106 × VEm/m3 mol−1 |
4.57 |
7.637 |
−4.568 |
2.02 |
| T = 308.15 K |
| 106 × VEm/m3 mol−1 |
3.667 |
7.405 |
−3.667 |
1.25 |
| T = 318.15 K |
| 106 × VEm/m3 mol−1 |
3.044 |
7.439 |
−3.044 |
0.73 |
| ZrO2–PPG – eqn (6) |
| |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
σ |
| T = 293.15 K |
| 106 × VEm/m3 mol−1 |
−18.656 |
−703.285 |
772.435 |
−69.78 |
0.526 |
0.245 |
0.001 |
| T = 298.15 K |
| 106 × VEm/m3 mol−1 |
−69.882 |
−28.451 |
25.213 |
−1.785 |
0.686 |
1.38 |
0.000 |
| T = 308.15 K |
| 106 × VEm/m3 mol−1 |
−68.041 |
−13.028 |
8.654 |
−8.746 |
−1.871 |
5.232 |
0.001 |
| T = 318.15 K |
| 106 × VEm/m3 mol−1 |
−87.469 |
−1.385 |
−0.724 |
−17.796 |
−5.389 |
2.326 |
0.003 |
| ZrO2–H2O–PVP30% – eqn (6) |
| |
A0 |
A1 |
A2 |
10−4A3 |
A4 |
10−3A5 |
σ |
| T = 293.15 K |
| 106 × VEm/m3 mol−1 |
−3900 |
57.508 |
−53.281 |
−0.2153 |
−28.07 |
2.173 |
0.37 |
| T = 298.15 K |
| 106 × VEm/m3 mol−1 |
−1977 |
706.587 |
−681.511 |
−1.482 |
−20.593 |
14.81 |
4.26 |
| T = 308.15 K |
| 106 × VEm/m3 mol−1 |
0.222 |
223.192 |
−43.175 |
0.3742 |
−0.528 |
−3.659 |
1.45 |
| T = 318.15 K |
| 106 × VEm/m3 mol−1 |
0.558 |
−7.376 |
−10.963 |
0.305 |
0.133 |
−3.039 |
1.04 |
| ZrO2–PPG – eqn (7) |
| |
A0 |
A1 |
A2 |
σ |
| T = 293.15 K |
| 106 × VEm/m3 mol−1 |
−0.012 |
−210.271 |
−2.396.104 |
0.00179 |
| κs/(T Pa−1) |
4.999.10−7 |
1.188.10−6 |
−1.282.10−5 |
0.842 |
| T = 298.15 K |
| 106 × VEm/m3 mol−1 |
−3.324 |
−193.136 |
−3.063.104 |
0.00089 |
| κs/(T Pa−1) |
510.745 |
1.731.103 |
−4.975.104 |
0.177 |
| T = 308.15 K |
| 106 × VEm/m3 mol−1 |
−10.146 |
−242.146 |
−2.906.104 |
0.0045 |
| κs/(T Pa−1) |
542.137 |
1.41.103 |
−3.591.104 |
0.176 |
| T = 318.15 K |
| 106 × VEm/m3 mol−1 |
−23.497 |
−62.186 |
−3.084.104 |
0.00294 |
| κs/(T Pa−1) |
576.161 |
683.678 |
−1.012 |
0.630 |
| ZrO2–H2O–PVP30% – eqn (7) |
| |
A0 |
A1 |
A2 |
104 σ |
| T = 293.15 K |
| 106 × VEm/m3 mol−1 |
−5.892 |
2.263.104 |
11.283 |
0.72 |
| κs/(T Pa−1) |
350.274 |
832.154 |
3.125.10−4 |
0.015 |
| T = 298.15 K |
| 106 × VEm/m3 mol−1 |
−6.49 |
1.828.104 |
9.428 |
0.91 |
| κs/(T Pa−1) |
349.154 |
217.412 |
1.065 |
0.020 |
| T = 308.15 K |
| 106 × VEm/m3 mol−1 |
−6.98 |
1.468.104 |
7.762 |
0.73 |
| κs/(T Pa−1) |
347.905 |
400.153 |
1.122 |
0.015 |
| T = 318.15 K |
| 106 × VEm/m3 mol−1 |
−7.595 |
1.218.104 |
6.624 |
1.92 |
| κs/(T Pa−1) |
346.788 |
652.935 |
1.22 |
0.007 |
Continuous lines in Fig. 6(a) and (c) correspond to this equation. The parameters of the polynomial equation with temperature dependency and using the second fitting method, for ZrO2–PPG and ZrO2–H2O–PVP systems are reported in Table S4.† The continuous lines in Fig. S1(a) and (b)† for ZrO2–PPG and ZrO2–H2O–PVP systems are in accordance with this model, which is compared with the obtained experimental data. The parameters of Redlich–Kister,58,59 Ott57 and polynomial temperature dependent equations using the first fitting method, are reported in Tables S5, S6, and S7† respectively. Also, the parameters of the temperature dependent equations of Redlich–Kister58,59 and Ott57 using the second fitting method are reported in Tables S8 and S9.† The isentropic compressibility (κs) data of the considered systems were fitted by the polynomial equation. The parameters obtained from this equation are reported in Table 4 for ZrO2–PPG and ZrO2–H2O–PVP nanofluids. Continuous lines in Fig. 6(b) and (d) correspond to this equation. These figures and Table 4 show that the efficiency of the polynomial equation is acceptable.
| |
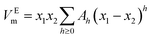 | (5) |
| |
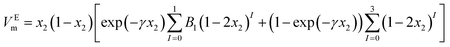 | (6) |
| |
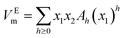 | (7) |
It is important to fit viscosity data of nanofluids by considering the dependence of concentration and temperature simultaneously. In some equations, the temperature dependency is only considered. The equations with only a concentration dependency are alternatively used for predicting the viscosity of nanofluids systems at each temperature. Models that altogether consider temperature and concentration dependence have many parameters. In recent years, the Eyring-NRTL model has been used with good efficiency in fitting the viscosity data. In this research, the effectiveness of the mentioned model and the new Eyring-mNRF model in fitting the viscosity data of ZrO2–PPG and ZrO2–H2O–PVP nanofluids systems have been investigated. The Eyring-NRTL equation is as follows:14,60–63
| |
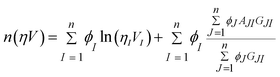 | (8) |
| |
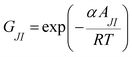 | (10) |
V and
VI are the molar volume of the nanofluid and component
I,
φI is the volume fraction of component
I, equal to
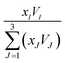
in which
xI is the mole fraction of component
I. The
T is temperature and
R is the universal constant of gases;
aJJ and
bJJ are empirical parameters of the Eyring-NRTL model. The
a is the non-randomness factor which was set to 0.2 in this work.The Eyring-mNRF model is represented by the following equation:
14,60–63| |
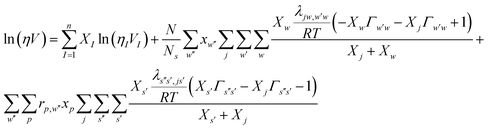 | (11) |
| |
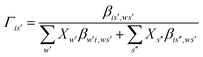 | (12) |
| |
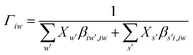 | (13) |
| | |
λij,kl = λij,lk = λji,kl = λji,lk = −λkl,ij = −λlk,ij = −λkl,ji = −λlk,ji
| (14) |
| | |
ωij,kl = ωij,lk = ωji,kl = ωji,lk = −ωkl,ij = −ωlk,ij = −ωkl,ji = −ωlk,ji
| (15) |
| |
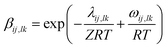 | (16) |
| |
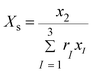 | (17) |
where,
rp,w′′ approximates the ratio of the molar volume of the polymer (
p) and corresponding solvent molecule (
w′′).
N is the total number of polymers, nanoparticles and solvents. Subscripts
s,
s′,
s′′ represented polymer monomers, nanoparticle and solvent moles,
w,
w′,
w′′ show the solvent molecules;
i,
j,
k and
l stand for segments of polymer chain, solvent molecules and nanoparticles. The
λij,lk and
wij,lk are the parameters of the Eyring-mNRF model.
Z is the non-random factor which was set to 8 in this work.
Parameters of the Eyring-mNRF model along with the standard deviation resulting from this model and also the Eyring-NRTL model resulting from fitting the viscosity data of the ZrO2–PPG and ZrO2–H2O–PVP nanofluids systems are shown in Table 5. In order to observe the performance of the Eyring-NRTL and Eyring-mNRF models in a better manner, the experimental and calculated viscosity values with these two models are shown in Fig. 8.
Table 5 Eyring-NRTL and Eyring-mNRF model parameters along with standard deviation (σ) for ZrO2–PPG and ZrO2–H2O–PVP
| ZrO2–PPG |
| Eyring-NRTL |
a12 |
b12 |
a21 |
b21 |
σ (η/mPa s) |
| −8168.231 |
−33.02 |
83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288.78 288.78 |
−7.639 |
0.001 |
| Eyring-mNRF |
λ1sss |
λ11s1 |
ω1sss |
ω11s1 |
σ (η/mPa s) |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397.892 397.892 |
−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248.059 248.059 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 382![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771.024 771.024 |
81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508.806 508.806 |
0.001 |
| ZrO2–H2O–PVP |
| Eyring-NRTL |
a12 |
b12 |
a21 |
b21 |
σ (η/mPa s) |
| −0.107 |
−37.986 |
242.359 |
94.6 |
0.001 |
| Eyring-mNRF |
λ1sss |
λ11s1 |
ω1sss |
ω11s1 |
σ (η/mPa s) |
−37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855.873 855.873 |
−65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583 583![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122.907 122.907 |
7443.86 |
−8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662.783 662.783 |
0.001 |
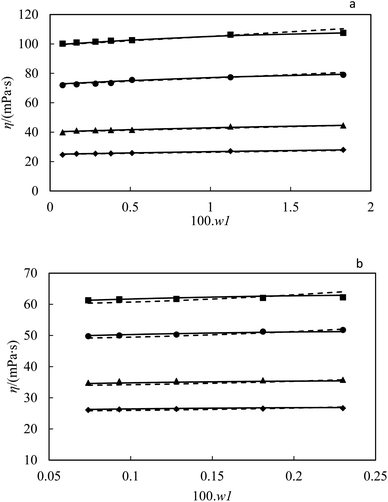 |
| | Fig. 8 Viscosity by weight fraction for nanofluid (a) ZrO2–PPG and (b) ZrO2–H2O–PVP at T = ((■) 293.15, (●) 298.15, (▲) 308.15, (♦) 318.15) K compared to (—) NRTL and (----) mNRF equation. | |
As can be seen from Table 5, the performance of both Eyring-NRTL and Eyring-mNRF models is good in fitting the viscosity data of both systems.
5. Prediction
The viscosity data of nanofluids containing two components can be predicted by well-known equations such as Einstein (18), Brinkman (19), Lundgren (20) and Batchelor (21) models. These equations are as follows:| |
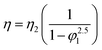 | (19) |
| |
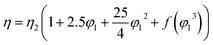 | (20) |
| | |
η = η2(1 + 2.5φ1 + 6.2φ12)
| (21) |
In eqn (18), the η and η2 are the viscosity of nanofluid and viscosity of base fluid, respectively and in eqn (20), f(φ13) is the Taylor series for volume fraction of nanofluid (φ1). The Taylor series is as follows eqn (22):14
| | |
f(φ13) = 0.01 + 0.0003(φ1 − 0.01) + 0.03(φ1 − 0.01)2 + (φ1 − 0.01)3
| (22) |
In this research, the viscosity data of ZrO
2–PPG and ZrO
2–H
2O–PVP nanofluids have been predicted by these equations at four temperatures; the results are reported in
Table 6. This table show the good performance of the mentioned models and especially the Lundgren model
eqn (20) in predicting the viscosity data of ZrO
2–PPG and ZrO
2–H
2O–PVP in the dilute concentration region.
Table 6 Standard deviations (σ (η/mPa s)) and absolute average relative deviations (AARD) obtained from prediction of viscosity values of nanofluid of ZrO2–PPG and ZrO2–H2O–PVP with Einstein64–66 (eqn (18)), Brinkman65,67 (eqn (19)), Lundgren68 (eqn (20)) and Batchelor69 (eqn (21)) models
| |
Einstein model |
Brinkman model |
Lundgren model |
Batchelor model |
| T/K |
σ |
100 AARD |
σ |
100 AARD |
σ |
100 AARD |
σ |
100 AARD |
| ZrO2–PPG |
| 293.15 |
4.227 |
3.371 |
4.584 |
3.624 |
3.440 |
2.406 |
4.225 |
3.369 |
| 298.15 |
3.032 |
2.553 |
3.292 |
2.807 |
2.615 |
1.580 |
3.030 |
2.552 |
| 308.15 |
2.159 |
3.763 |
2.304 |
4.013 |
1.875 |
2.802 |
2.159 |
3.762 |
| 318.15 |
1.416 |
3.681 |
1.507 |
3.930 |
1.254 |
2.719 |
1.416 |
3.680 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| ZrO2–H2O–PVP |
| 293.15 |
1.926 |
3.072 |
1.966 |
3.132 |
1.339 |
2.103 |
1.926 |
3.072 |
| 298.15 |
1.952 |
3.541 |
1.985 |
3.601 |
1.513 |
2.577 |
1.952 |
3.541 |
| 308.15 |
1.618 |
4.478 |
1.641 |
4.537 |
1.289 |
3.523 |
1.618 |
4.477 |
| 318.15 |
0.744 |
2.716 |
0.761 |
2.777 |
0.501 |
1.744 |
0.744 |
2.716 |
The good performance of the Lundgren model eqn (20) in predicting the viscosity data of ZrO2–PPG and ZrO2–H2O–PVP nanofluids, particularly in the dilute concentration region, can be attributed to several key factors. This model effectively accounts for the interaction between dispersed nanoparticles and the base fluid, making it highly suitable for capturing the behavior of nanofluids in dilute concentrations where particle–particle interactions are minimal. In this regard, viscosity is mainly influenced by individual nanoparticles, and the Lundgren model is specifically designed to handle such conditions. Additionally, the model likely considers the shear-thinning behavior of nanofluids like ZrO2–PPG and ZrO2–H2O–PVP, which further enhances its adaptability to different flow dynamics at low concentrations. Moreover, the model incorporates temperature sensitivity, enabling it to accurately reflect the temperature-dependent viscosity of nanofluids, which is crucial for predicting viscosity across various temperatures. These factors collectively explain the model's superior accuracy in predicting viscosity under these conditions.
6. Conclusions
In these research, ZrO2–PPG nanofluid was found to be the most stable among the studied nanofluids, remaining stable for over a month. ZrO2–H2O nanofluid was stable for 24 hours, while ZrO2–PPG–H2O nanofluid was unstable at different ratios. The addition of water to the ZrO2–PPG system increased interactions between the polymer and water, leading to nanoparticle agglomeration. The size of nanoparticles in the stable ZrO2–PPG nanofluid was found to be larger than the initial size. Excess molar volume and isentropic compressibility were calculated from density, speed of sound, and viscosity measurements. Negative excess molar volume values suggested unlike interactions and compression effects, while positive values indicated Van der Waals interactions. ZrO2–H2O nanofluid exhibited interactions between water molecules and nanoparticles. ZrO2–H2O–PVP nanofluid with 30% polymer was the most stable, with dominant unlike interactions in dilute and semi-dilute regions and Van der Waals forces in concentrated regions. Redlich-Kister, Ott, and polynomial equations were used to fit excess molar volume data, the polynomial equation with temperature dependence performing best. Eyring-NRTL and Eyring-mNRF models were used to correlate viscosity data, with both models showing good performance. Einstein, Brinkman, Lundgren, and Batchelor models were used to predict viscosity data of ZrO2–PPG and ZrO2–H2O–PVP nanofluids at four temperatures.
There is minimal limitation about the focus on potential industrial applications or scalability, which is critical for determining the real-world relevance of these findings. The findings may apply to other nanofluid systems that is not investigated yet. Future research on ZrO2-based nanofluids could focus on enhancing the stability of ZrO2–H2O and ZrO2–PPG–H2O systems by exploring additives or surface modifications to prevent nanoparticle agglomeration. Further studies on the interaction mechanisms, particularly in mixed fluid systems, can provide deeper insights into optimizing nanofluid properties for various applications. Advanced modeling approaches, integrating temperature dependence and particle dynamics, could refine predictions of viscosity and other thermophysical properties. Additionally, improving the stability and performance of these nanofluids could enhance their potential in heat transfer and industrial applications.
Data availability
Data are available upon request from the authors.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The Authors are grateful for the grant support of University of Tabriz.
References
- S. M. S. Murshed, Advanced Cooling Technologies and Applications, BoD – Books on Demand, 2019 Search PubMed.
- A. Ghadimi, R. Saidur and H. S. C. Metselaar, Int. J. Heat Mass Transfer, 2011, 54, 4051–4068 CrossRef CAS.
- J. E. Yumi, T. J. Moreno and G. C. Chango, Lat. Am. Appl. Res., 2023, 53, 77–88 Search PubMed.
- K. A. Jehhef and M. Siba, Acta Mech. Malaysia, 2019, 2, 1–19 CrossRef.
- S. N. M. Zainon and W. H. Azmi, Micromachines, 2021, 12, 176 CrossRef PubMed.
- J. Wang, X. Yang, J. J. Klemeš, K. Tian, T. Ma and B. Sunden, Renewable Sustainable Energy Rev., 2023, 188, 113854 CrossRef CAS.
- J. Silva-Yumi, T. M. Romero and G. C. Lescano, ESPOCH Congresses: The Ecuadorian Journal of STEAM, 2021, 998–1006 Search PubMed.
- S. Chakraborty and P. K. Panigrahi, Appl. Therm. Eng., 2020, 174, 115259 CrossRef CAS.
- J. Xu and B. Yang, Nanotechnol. Rev., 2013, 2, 289–306 CAS.
- L. Dan, K. Zhang, Q. Wang and N. Liu, J. Ind. Eng. Chem., 2024, 132, 518–528 CrossRef CAS.
- M. Teodorescu and M. Bercea, Polym.-Plast. Technol. Eng., 2015, 54, 923–943 CrossRef CAS.
- X. Zhi, H. Fang, C. Bao, G. Shen, J. Zhang, K. Wang, S. Guo, T. Wan and D. Cui, Biomaterials, 2013, 34, 5254–5261 CrossRef CAS PubMed.
- M. M. Fiume, W. F. Bergfeld, D. V Belsito, R. A. Hill, C. D. Klaassen, D. Liebler, J. G. Marks Jr, R. C. Shank, T. J. Slaga and P. W. Snyder, Int. J. Toxicol., 2012, 31, 245S–260S CrossRef CAS PubMed.
- M. T. Zafarani-Moattar, H. Shekaari, R. Munes-Rast and R. Majdan-Cegincara, Fluid Phase Equilib., 2015, 403, 136–144 CrossRef CAS.
- A. V Lebedev and S. N. Lysenko, Solid State Phenom., 2012, 190, 649–652 Search PubMed.
- B. Bai, L. Li, Y. Liu, H. Liu, Z. Wang and C. You, SPE Reservoir Eval. Eng., 2007, 10, 415–422 CrossRef CAS.
- A. A. Mohammed, H. I. Dawood and H. N. Onyeaka, IOP Conference Series: Earth and Environmental Science, IOP Publishing, 2023, vol. 1232, p. 12009 Search PubMed.
- H. Sui, L. Zhang, W. Zong, F. Zhang, R. Liu, C. Gao and C. Li, J. Dispersion Sci. Technol., 2007, 28, 1316–1324 CrossRef CAS.
- R. Mueller, R. Jossen, S. E. Pratsinis, M. Watson and M. K. Akhtar, J. Am. Ceram. Soc., 2004, 87, 197–202 CrossRef CAS.
- D. G. Syarif, Adv. Mater. Res., 2014, 896, 163–167 CAS.
- S. U. S. Choi, Z. G. Zhang, Wl. Yu, F. E. Lockwood and E. A. Grulke, Appl. Phys. Lett., 2001, 79, 2252–2254 CrossRef CAS.
- M. A. Khairul, K. Shah, E. Doroodchi, R. Azizian and B. Moghtaderi, Int. J. Heat Mass Transfer, 2016, 98, 778–787 CrossRef CAS.
- N. K. Gupta, S. Mishra, A. K. Tiwari and S. K. Ghosh, Mater. Today: Proc., 2019, 18, 968–978 Search PubMed.
- K.
H. Solangi, S. N. Kazi, M. R. Luhur, A. Badarudin, A. Amiri, R. Sadri, M. N. M. Zubir, S. Gharehkhani and andK. H. Teng, Energy, 2015, 89, 1065–1086 CrossRef CAS.
- S. J. Thrush, A. S. Comfort, J. S. Dusenbury, Y. Xiong, H. Qu, X. Han, J. D. Schall, G. C. Barber and X. Wang, Tribol. Trans., 2020, 63, 68–76 CrossRef CAS.
- Z. Said, L. S. Sundar, A. K. Tiwari, H. M. Ali, M. Sheikholeslami, E. Bellos and H. Babar, Phys. Rep., 2022, 946, 1–94 CrossRef CAS.
- S. Hussain, M. Salman, J. P. Youngblood, U. Farooq, S. Yasmeen, K. M. Al-Ahmary and M. Ahmed, J. Mol. Liq., 2024, 411, 125704 CrossRef CAS.
- U. M. Kakar, Z. Tauanov, S. Azat, N. A. Ahmadi, M. H. Hassand, A. Sarwari, A. W. Monib and P. Niazi, J. Chem. Stud., 2024, 3, 7–20 CrossRef.
- P. C. Mishra, S. K. Nayak and S. Mukherjee, Int. J. Eng. Res. Technol., 2013, 2, 734–745 Search PubMed.
- K. Apmann, R. Fulmer, A. Soto and S. Vafaei, Materials, 2021, 14, 1291 CrossRef CAS PubMed.
- I. Tavman and A. Turgut, Microfluidics Based Microsystems: Fundamentals and Applications, Springer, 2010, pp. 139–162 Search PubMed.
- M. T. Zafarani-Moattar and R. Majdan-Cegincara, J. Chem. Thermodyn., 2012, 54, 55–67 CrossRef CAS.
- O. Redlich and A. T. Kister, Ind. Eng. Chem., 1948, 40, 345–348 CrossRef.
- J. B. Ott, C. E. Stouffer, G. V. Cornett, B. F. Woodfield, R. C. Wirthlin, J. J. Christensen and U. K. Deiters, J. Chem. Thermodyn., 1986, 18, 1–12 CrossRef CAS.
- M. Hosseini and S. Ghader, J. Mol. Liq., 2010, 153, 139–145 CrossRef CAS.
- M. T. Zafarani-Moattar and R. Majdan-Cegincara, Ind. Eng. Chem. Res., 2011, 50, 8245–8262 CrossRef CAS.
- M. Šárpataky, J. Kurimský and M. Rajňák, Nanomaterials, 2021, 11, 2885 CrossRef PubMed.
- F. Ordóñez, F. Chejne, E. Pabón and K. Cacua, Ceram. Int., 2020, 46, 11970–11977 CrossRef.
- S. R. Kumar, H. O. Sharma, S. Kumar and D. K. Patel, Proc. Inst. Mech. Eng., Part E, 2023 DOI:10.1177/09544089231190223.
- G. K. Sidhu and R. Kumar, IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2018, vol. 360, p. 12038 Search PubMed.
- M. T. Zafarani-Moattar, H. Shekaari, R. Munes-Rast and R. Majdan-Cegincara, Fluid Phase Equilib., 2015, 403, 136–144 CrossRef CAS.
- W. Yu, H. Xie, L. Chen and Y. Li, Thermochim. Acta, 2009, 491, 92–96 CrossRef CAS.
- R. Taylor, S. Coulombe, T. Otanicar, P. Phelan, A. Gunawan, W. Lv, G. Rosengarten, R. Prasher and H. Tyagi, International Conference on Micro/Nanoscale Heat Transfer, American Society of Mechanical Engineers, 2012, vol. 54778, pp. 219–234 Search PubMed.
- L. Zhang, Y. Ding, M. Povey and D. York, Prog. Nat. Sci., 2008, 18, 939–944 CrossRef CAS.
- S. Wu, D. Zhu, X. Li, H. Li and J. Lei, Thermochim. Acta, 2009, 483, 73–77 CrossRef CAS.
- H. Shekaari and S. S. Mousavi, Fluid Phase Equilib., 2010, 291, 201–207 CrossRef CAS.
- H. Shekaari, M. T. Zafarani-Moattar, M. Mokhtarpour and S. Faraji, J. Mol. Liq., 2019, 289, 111077 CrossRef CAS.
- M. N. Roy, V. K. Dakua and B. Sinha, Int. J. Thermophys., 2007, 28, 1275–1284 CrossRef CAS.
- A. A. Minea, The Annals of “Dunarea de Jos” University of Galati. Fascicle IX, Metall. Mater. Sci., 2016, 39, 35–47 Search PubMed.
- S. Medhi, S. Chowdhury, A. Kumar, D. K. Gupta, Z. Aswal and J. S. Sangwai, J. Petrol. Sci. Eng., 2020, 187, 106826 CrossRef CAS.
- Y. Sun, W. Zhang, J. Li, R. Han and C. Lu, Molecules, 2023, 28, 4331 CrossRef CAS PubMed.
- J. Kim, Y. Tian and J. Wu, J. Phys. Chem. B, 2015, 119, 12108–12116 CrossRef CAS PubMed.
- A. Mondal and S. Ram, J. Am. Ceram. Soc., 2004, 87, 2187–2194 CrossRef CAS.
- A. J. Kemeakegha, G. A. Cookey and W.-A. L. Izonfuo, J. Thermodyn., 2015, 2015, 782138 Search PubMed.
- A. Serna, I. G. de la Fuente, J. A. González, J. C. Cobos and C. Casanova, Fluid Phase Equilib., 1995, 110, 361–367 CrossRef CAS.
- T. Otsuka and Y. Chujo, Polym. J., 2008, 40, 1157–1163 CrossRef CAS.
- J. B. Ott, P. R. Brown, J. D. Moore and A. C. Lewellen, J. Chem. Thermodyn., 1997, 29, 149–178 CrossRef CAS.
- D. J. Luning Prak, J. Chem. Eng. Data, 2023, 68, 1053–1066 CrossRef CAS.
- D. J. Luning Prak, J. Chem. Eng. Data, 2024, 69, 973–986 CrossRef CAS.
- M. Mokhtarpour, S. Homayoon-far, H. Shekaari and M. T. Zafarani-Moattar, J. Chem. Eng. Data, 2020, 65, 5369–5383 CrossRef CAS.
- M. T. Zafarani-Moattar and R. Majdan-Cegincara, Ind. Eng. Chem. Res., 2011, 50, 8245–8262 CrossRef CAS.
- M. T. Zafarani-Moattar and R. Majdan-Cegincara, J. Chem. Thermodyn., 2012, 54, 55–67 CrossRef CAS.
- M. T. Zafarani-Moattar and R. Majdan-Cegincara, Fluid Phase Equilib., 2013, 354, 102–108 CrossRef CAS.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho, B. Van Horn, H.-C. Kim and C. J. Hawker, Nat. Mater., 2003, 2, 762–766 CrossRef CAS PubMed.
- J. Ouyang, B. Han, G. Chen, L. Zhao and J. Ou, Constr. Build. Mater., 2018, 185, 293–301 CrossRef CAS.
- H. Saigo, D. B. Kc and N. Saito, Sci. Rep., 2022, 12, 6541 CrossRef PubMed.
- F. J. Valdes-Parada, J. A. Ochoa-Tapia and J. Alvarez-Ramirez, Phys. A, 2007, 385, 69–79 CrossRef.
- D. I. Pullin and P. G. Saffman, Phys. Fluids A, 1993, 5, 126–145 CrossRef.
- Z. An, Y. Zhang, Q. Li, H. Wang, Z. Guo and J. Zhu, Powder Technol., 2018, 328, 199–206 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Hemayat Shekaari
,
Hemayat Shekaari * and
Behrang Golmohammadi
* and
Behrang Golmohammadi
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is 333 nm, ZrO2–PPG–H2O (3
1) is 333 nm, ZrO2–PPG–H2O (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is 309 nm and ZrO2–H2O have two sharp peaks in the region of 201 and 295 nm. Therefore, to check the stability of the prepared nanofluids, after sonication, their UV-Vis spectra were recorded over the time.37 These spectra over the time for ZrO2–PPG, ZrO2–H2O and different ratios of ZrO2–PPG–H2O nanofluids are shown in Fig. 3. As depicted in Fig. 3, the ZrO2–PPG system has a stability about one month, and with the time elaps, the nanoparticles were sedimented.
1) is 309 nm and ZrO2–H2O have two sharp peaks in the region of 201 and 295 nm. Therefore, to check the stability of the prepared nanofluids, after sonication, their UV-Vis spectra were recorded over the time.37 These spectra over the time for ZrO2–PPG, ZrO2–H2O and different ratios of ZrO2–PPG–H2O nanofluids are shown in Fig. 3. As depicted in Fig. 3, the ZrO2–PPG system has a stability about one month, and with the time elaps, the nanoparticles were sedimented.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (----), ZrO2–PPG–H2O (3
1) (----), ZrO2–PPG–H2O (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (-.-.-.) in the molar fraction of ZrO2 equal to 0.00038.
1) (-.-.-.) in the molar fraction of ZrO2 equal to 0.00038.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio of PVP
3 ratio of PVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, the stability is higher than the other ratios. PVP is a polymer with long chains and hollow spaces, nanoparticles can enter these empty spaces due to their small size, and water molecules can create strong hydrogen bonds with the polymer, and because of these strong bonds in this system, nanoparticles are more stable.
H2O, the stability is higher than the other ratios. PVP is a polymer with long chains and hollow spaces, nanoparticles can enter these empty spaces due to their small size, and water molecules can create strong hydrogen bonds with the polymer, and because of these strong bonds in this system, nanoparticles are more stable.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
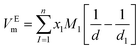
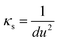

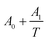 , and two methods are tried in fitting the data. In the first method, the usual fitting method was used, and in the second method, the fitting was done by dividing the main equation into x1x2 . The efficiency of the equations was studied by comparing the standard deviation obtained from the excess molar volumes and the density of the samples. Fitting the VEm values was done by using the mentioned equations and using two fitting methods in each equation. Due to the lack of acceptable results from the fitting of the VEm values for the ZrO2–H2O system, the fitting data of this system was not studied. In Table 2, the standard deviation related to fitting the VEm values and density data of the ZrO2–PPG and ZrO2–H2O–PVP using the mentioned equations are reported. According to the results of Table 2, it can be concluded that the standard deviation related to the polynomial eqn (7), in fitting the data in both systems are acceptable while the second method has a better efficiency in fitting than the first method.
, and two methods are tried in fitting the data. In the first method, the usual fitting method was used, and in the second method, the fitting was done by dividing the main equation into x1x2 . The efficiency of the equations was studied by comparing the standard deviation obtained from the excess molar volumes and the density of the samples. Fitting the VEm values was done by using the mentioned equations and using two fitting methods in each equation. Due to the lack of acceptable results from the fitting of the VEm values for the ZrO2–H2O system, the fitting data of this system was not studied. In Table 2, the standard deviation related to fitting the VEm values and density data of the ZrO2–PPG and ZrO2–H2O–PVP using the mentioned equations are reported. According to the results of Table 2, it can be concluded that the standard deviation related to the polynomial eqn (7), in fitting the data in both systems are acceptable while the second method has a better efficiency in fitting than the first method.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990
990![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000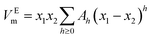
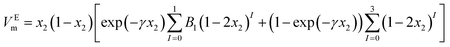
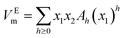
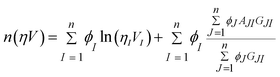
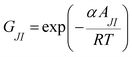
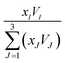 in which xI is the mole fraction of component I. The T is temperature and R is the universal constant of gases; aJJ and bJJ are empirical parameters of the Eyring-NRTL model. The a is the non-randomness factor which was set to 0.2 in this work.The Eyring-mNRF model is represented by the following equation:14,60–63
in which xI is the mole fraction of component I. The T is temperature and R is the universal constant of gases; aJJ and bJJ are empirical parameters of the Eyring-NRTL model. The a is the non-randomness factor which was set to 0.2 in this work.The Eyring-mNRF model is represented by the following equation:14,60–63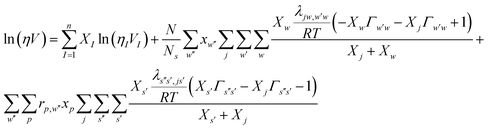
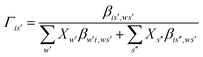
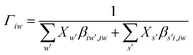
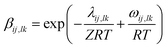
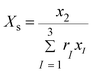
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288.78
288.78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078
078![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397.892
397.892![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187
187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248.059
248.059![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382
382![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771.024
771.024![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508.806
508.806![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855.873
855.873![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583
583![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122.907
122.907![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662.783
662.783
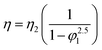
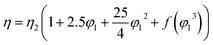
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)




