Open Access Article
Open Access ArticleUnraveling fundamental characteristics of Na2Mg3Cl8 as a solid-state electrolyte for Na-ion batteries†
Yohandys A. Zulueta a,
Jose R. Fernández-Gamboa
a,
Jose R. Fernández-Gamboa a,
Thi Viet Bac Phungb,
My Phuong Pham-Hocd and
Minh Tho Nguyen*ef
a,
Thi Viet Bac Phungb,
My Phuong Pham-Hocd and
Minh Tho Nguyen*ef
aDepartamento de Física, Facultad de Ciencias Naturales y Exactas, Universidad de Oriente, CP 90500, Santiago de Cuba, Cuba
bCenter for Environmental Intelligence, College of Engineering and Computer Science, VinUniversity, Hanoi, 10000 Vietnam
cFaculty of Chemical Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, 70000 Vietnam
dVietnam National University Ho Chi Minh City, Linh Trung, Thu Duc City, Ho Chi Minh City, 70000 Vietnam
eLaboratory for Chemical Computation and Modeling, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, 70000 Vietnam. E-mail: minhtho.nguyen@vlu.edu.vn
fFaculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, 70000 Vietnam
First published on 23rd October 2024
Abstract
In this theoretical study, we harnessed advanced atomistic computations to unravel several features of Na2Mg3Cl8, an unexplored but promising chloride compound for solid-state electrolytes in Na-batteries. First, Na2Mg3Cl8 exhibits an insulating behavior, characterized by an energy gap of ∼5 eV, arising from the hybridization of [NaCl] trigonal prismatic and [MgCl6] octahedral units. Second, the compound possesses mechanical stability and ductility, which render it suitable for practical fabrication. Improved electrolyte/electrode contact can reduce resistance and enhance battery performance. The electrochemical performance of Na2Mg3Cl8 involves an open cell voltage of 1.2 V and a theoretical capacity of 133 mA h g−1. Finally, its transport characteristics include low activation energy for diffusion and conduction as well as a remarkable room-temperature conductivity of 1.26 mS cm−1, comparable to those of current superionic conductors.
1. Introduction
Sodium-ion batteries (NIBs) currently hold significant importance owing to their cost-effectiveness, sustainability, safety, performance, scalability, and diverse applications.1–7 As an alternative to lithium-ion batteries, NIBs offer several advantages as they utilize abundant and low-cost materials, making them economically more viable.1–7 Additionally, NIBs exhibit energy-efficient power delivery, fast charging, stability across extreme temperatures, and safety against overheating or thermal runaway.1–9 Their emergence represents a key step toward efficient and sustainable energy storage.1–14Although NIBs have garnered attention as a cost-effective alternative to lithium-ion batteries (LIBs) for large-scale energy storage, their lower energy density than that of LIBs necessitates further intensive research and innovation.5–9 One critical component in NIBs is the solid electrolyte, which plays a pivotal role in transferring charge carriers between both positive and negative electrodes. Solid-state electrolytes (SSEs) offer a higher energy density than liquid counterparts, making them more suitable for NIBs. However, the current SSEs suffer from several limitations such as low ionic conductivity, narrow electrochemical stability window, and poor contact with electrodes.10–14
In this context, theoretical computations for discovering new solid-state electrolytes (SSEs) for sodium-ion batteries are pivotal.15–19 These computational methods provide us with insights into fundamental properties and mechanisms associated with SSEs, thereby accelerating their development and implementation. Current computational techniques include atomistic first-principles calculations, molecular dynamics simulations and force field approaches.15,20,21 Results derived from advanced atomistic simulations can guide the design of SSEs with high ion diffusivity, chemical stability, and a wide electrochemical stability window, ultimately advancing all-solid-state battery technology.15–19
As potential materials, halide-based sodium solid-state electrolytes offer several key benefits. First, they exhibit high voltage stability and air stability, which make them suitable for cell manufacturing. Additionally, these electrolytes possess decent room temperature ionic conductivity, which is crucial for efficient ion transport within batteries.22–25 They are also compatible with oxide cathode materials, ensuring good performance when paired with employed electrodes. Furthermore, halide solid electrolytes provide excellent chemical stability, an essential requirement for maintaining battery performance over multiple charge–discharge cycles. Their robustness helps prevent degradation and ensures long-term reliability. Lastly, their scalability makes them a viable option for large-scale battery manufacturing, which is advantageous for commercial applications. These considerations lead to the motivation for intensive ongoing research in this field.22–25
Advanced atomistic simulations were previously carried out to assess the key features of the Na6MgCl8 rock-salt material.25,26 It was found that Na6MgCl8 is an insulating material with an energy gap of ∼5 eV, and it exhibits mechanical stability and ductility. Theoretical simulations predicted that the Zn2+ ion is the most suitable divalent dopant that enhances the defect characteristics and transport properties of the Na6MgCl8 structure.26 Indeed, the Na transport properties were found to be notably improved upon the doping of Na6MgCl8 with Ba2+ and Zn2+ ions.26 Expanding the study to Na6MCl8 compounds, where M = Ca2+, Ba2+, Zn2+ and Sr2+, we observed some remarkable properties. These include lower energy gap than the reported values for Na6MgCl8 (which has an energy gap of 4.1–4.6 eV). All relevant structures are mechanically stable and ductile, ensuring compatibility with electrodes. Additionally, a three-dimensional migration pathway was predicted. The Na6BaCl8 structure possesses the lowest values of defect formation energies and the highest conductivity at 250 K.25
Na6MgCl8 compound having the same type of atoms (Na, Mg and Cl) was investigated in earlier studies as a Na2Mn3Cl8 isostructural motif in the search for the crystal structure of Na6MnCl8 and Na2Mn3Cl8 lattice structures.27 There are no previous works reporting the physicochemical properties and technological applications of Na2Mg3Cl8. In this context, an exploration of the inherent properties and thereby the possible application of Na2Mg3Cl8 compound in battery technology is of interest. Bearing in mind the importance of theoretical computations for the rapid delivery of properties of materials, the aim of the present work is to reveal the under-evaluated battery properties of the Na2Mg3Cl8 material with the aid of advanced atomistic simulations. In this work, by integrating density functional theory (DFT), static simulations, defect energetics, and bond valence site energy (BVSE) computations, for the first time, we have elucidated the structural, electronic, mechanical, and transport properties of the quasi-unexplored Na2Mg3Cl8 compound. The predicted properties suggest that Na2Mg3Cl8 is a promising candidate for use as a solid-state electrolyte in current or future sodium-ion batteries.
2. Computational methodology
DFT calculations were performed using the CASTEP code to determine the structural, electronic and mechanical properties of the Na2Mg3Cl8 compound.28 The GGA-PBESOL exchange–correlation functional within the generalized gradient approximation was employed.29 Ultrasoft pseudopotentials with a plane-wave energy cutoff of 830 eV were utilized. Specifically, the pseudoatomic functions for Na-2s22p63s1, Mg-2p63s2 and Cl-3s23p5 in reciprocal space represent the electronic configurations of the constituent atoms.For electronic structure computations and geometry optimizations, we set the convergence thresholds as follows: a total energy change of 5 × 10−6 eV per atom and maximum force, stress, and atomic displacements of 10−2 eV Å−1, 2 × 10−2 GPa, and 5 × 10−4 Å, respectively. Additionally, a 4 × 4 × 4 k-point mesh following the Monkhorst–Pack method samples the Brillouin zone.30
To perform force field-based computations, the General Utility Lattice Program (GULP) was employed,31 in which the potential parameters (force field) are derived from prior studies, describing both long-range and short-range interactions.26,32,33 Specifically, the Buckingham formulation governs short-range interactions, while long-range interactions are treated as coulombic forces, where only the charge and interatomic distance contribute to the long-range potential energy. Together with the force field (FF), the shell model accounts for ionic polarization, where each ion is approximated as a positively charged core connected to a negatively charged shell by a spring, and the sum of the core–shell charges yield the formal charge of the polarizable species.34
For defect calculations, the Mott–Littleton method was employed,35 in which the crystal structure is divided into two concentric spherical regions with radii R1 and R2, where R1 < R2. The inner sphere contains the isolated defect or defect cluster, positioned where the interaction with the local structure is strong. Meanwhile, region R2 is treated using a quasicontinuum approximation. We adopted specific values of R1 = 13 Å and R2 = 27 Å to ensure smooth convergence in simulations. Geometry optimizations and defect energetics computations utilized the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm,31,36 which is a widely applied technique to explore defect formation in various solid-state materials.15,20,21,32,37
Furthermore, the BVSE offers a straightforward and effective approach for determining diffusion paths and activation energies in diffusion and conduction processes.16–19 This method identifies mobile cations based on regions of low bond valence site energy. Specifically, the bond length between a cation A and an anion (LA–x) is evaluated using the tabulated empirical parameters L0,A–x and bA–x, which are related to individual bond valences (1).
| sA–x = exp[(L0,A–x − LA–x)/bA–x] | (1) |
The bond valence site energy of a cation A [EBVSE(A)] is evaluated in a similar way to the Morse empirical potentials16–19 by adding the coulombic repulsive term (Er) of the mobile A ion with respect to other immobile ions (eqn (2)).
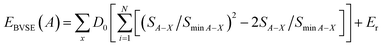 | (2) |
The softBV-GUI, code which serves as a bond valence pathway analyser, was employed for computing EBVSE(Na). The necessary parameters from eqn (2) were seamlessly integrated into the softBV-GUI code. Specifically, when analysing EBVSE(Na) coulombic repulsions between mobile sodium ions (Na+) and immobile Mg2+ cations were considered. Coulombic attraction interactions were included into the Morse-type attraction terms. For further insights into the bond valence approach, we refer readers to the recent relevant references.16–19,38
3. Results and discussion
3.1 Structural and electronic properties of the Na2Mg3Cl8 structure
Fig. 1 displays the unit cell in the hexagonal representation of the Na2Mg3Cl8 lattice structure. Compared to Na6MgCl8, while the chloride Na2Mg3Cl8 crystallizes into a hexagonal lattice structure (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), Na6MgCl8 adopts a cubic Fm
m), Na6MgCl8 adopts a cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group with a lattice parameter of a = 11.085 Å. Na6MgCl8 has a rock-salt structure with four primitive cells, whereas Na2Mg3Cl8 has lattice parameters of a = 7.355 Å and c = 19.511 Å, possessing three primitive cells in its hexagonal representation.27 In the Na2Mg3Cl8 structure, while Na+ ions are six-coordinated with Cl− ions, resulting in trigonal prismatic hybridization, Mg2+ cations are also six-coordinated with Cl− anions, forming an octahedron.27 Notably, Na2Mg3Cl8 offers more accessible sites for Na+ ions, making it interesting for Na+ storage and migration.27
m space group with a lattice parameter of a = 11.085 Å. Na6MgCl8 has a rock-salt structure with four primitive cells, whereas Na2Mg3Cl8 has lattice parameters of a = 7.355 Å and c = 19.511 Å, possessing three primitive cells in its hexagonal representation.27 In the Na2Mg3Cl8 structure, while Na+ ions are six-coordinated with Cl− ions, resulting in trigonal prismatic hybridization, Mg2+ cations are also six-coordinated with Cl− anions, forming an octahedron.27 Notably, Na2Mg3Cl8 offers more accessible sites for Na+ ions, making it interesting for Na+ storage and migration.27
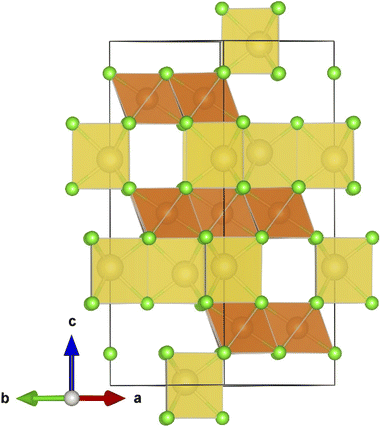 | ||
Fig. 1 Hexagonal representation of the Na2Mg3Cl8 lattice structure (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group). Yellow prisms represent the [NaCl] polyhedron, light brown the [MgCl6] octahedron and green balls Cl− ions. m space group). Yellow prisms represent the [NaCl] polyhedron, light brown the [MgCl6] octahedron and green balls Cl− ions. | ||
Table 1 shows the results of the cell parameters obtained by DFT and force field computations. We observed that the a-cell parameter obtained from the FF method was underestimated by 3.7%, while the c-parameter was underestimated by 2.6% with respect to available experimental data.27 Conversely, results from DFT computations exhibit a low overestimation as compared to the literature values.27 Commonly DFT computations tend to overestimate the lattice parameters, whereas the force field method tends to underestimate these values. In this study, the differences between the computed values with the experiment are small. Consequently, both approaches are suitable for reproducing the cell parameters of Na2Mg3Cl8.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group) derived from different approaches
m space group) derived from different approaches
| Cell parameters (Å) | Methods | ||
|---|---|---|---|
| Force fields | DFT | Experimental (ref. 27) | |
| a | 7.086 (−3.7%) | 7.377 (+0.3%) | 7.355 |
| c | 19.000 (−2.6%) | 19.601 (+0.5%) | 19.511 |
Exploration of electronic properties is of vital importance to decide the applicability of a compound as a battery material. An electrode material needs to be a good electric conductor to facilitate charge transfer during battery operation. Fig. 2 depicts the band structure of Na6Mg3Cl8 in the equilibrium ground state. The valence bands are located between −3.5 eV and the Fermi level (0 eV reference), while the conduction bands lie between 4.9 and 16 eV. Many electrons lie at the top valence bands at the Γ-point (G), which can be passed to the bottom of the conduction band along the Γ-point. The calculated energy gap value of Eg = 4.9 eV is similar to that of 5.1 eV previously reported for Na6MgCl8 compound.26 This closely aligns with the criteria for considering SSEs as these compounds exhibit minimal electronic conduction. In view of the usual underestimation of DFT calculations and the lack of experimental results, the value of Eg = 4.9 eV should be considered as a lower bound.39
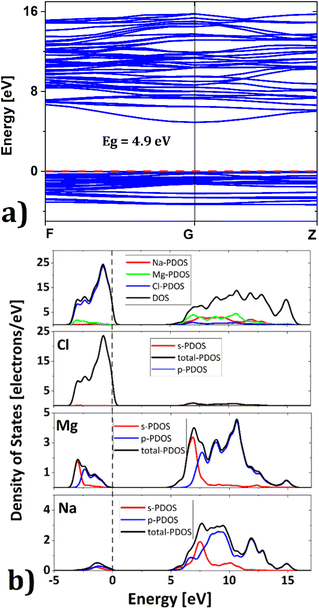 | ||
| Fig. 2 (a) Band gap and (b) density of states of the Na2Mg3Cl8 structure; red and black dashed lines represent the Fermi level. | ||
Fig. 2b shows the density of states of Na6Mg3Cl8. The valence band is dominated by Cl− ions and the conduction band by Mg2+ cations (Fig. 2b); Na+-DOS has lower contributions to both valence and conduction bands. These results agree well with the [NaCl] trigonal prismatic and [MgCl6] octahedral hybridization, defining the Na2Mg3Cl8 lattice structure.
3.2 Defect chemistry in Na2Mg3Cl8 structure
Intrinsic defects significantly influence the transport properties of materials. Notably, the Schottky defect type is prevalent in conducting materials. The Schottky formation mechanism is typically described using three distinct schemes. The first scheme, expressed in Kröger–Vink notation,40 is described by eqn (3)
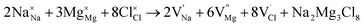 | (3) |
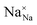 ,
, 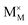 and
and 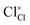 represent the host ions occupying its respective atomic position at the Na2Mg3Cl8 lattice structure, while
represent the host ions occupying its respective atomic position at the Na2Mg3Cl8 lattice structure, while 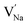 ,
, 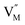 and
and 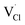 symbolize an Na-, Mg- and Cl-vacancy, respectively. In this sense, eqn (3) describes the full Schottky defect formation mechanism. The formation of NaCl Schottky defect is described by eqn (4),
symbolize an Na-, Mg- and Cl-vacancy, respectively. In this sense, eqn (3) describes the full Schottky defect formation mechanism. The formation of NaCl Schottky defect is described by eqn (4),
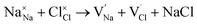 | (4) |
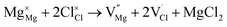 | (5) |
The solution energy (Es) is then computed as (eqn (6)–(8)) follows
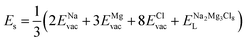 | (6) |
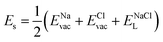 | (7) |
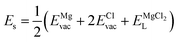 | (8) |
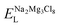 , ENaClL and
, ENaClL and 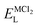 symbolize the lattice energy of Na2Mg3Cl8, NaCl and MgCl2 compounds, respectively.
symbolize the lattice energy of Na2Mg3Cl8, NaCl and MgCl2 compounds, respectively.
Table 2 collects the calculated results of defect energetics computations. The lowest vacancy formation energy corresponds to the Na+ vacancy of 5.2 eV per vacancy, followed by Cl− vacancy (5.9 eV per vacancy). Compared to the reported vacancy formation energy in Na6MgCl8 (5.2 and 5.4 eV per vacancy for Na+ and Cl− vacancy, respectively),26 the basic vacancy formation energies are comparable to each other between these chloride structures (including the Mg2+ vacancy formation energy). On the other hand, it has been reported that the Na+ and Cl− vacancies are the most common defect types that appear in chloride structures.23–26,32 This result confirms that the observation mentioned above is also valid for the Na2Mg3Cl8 structure.
| Schottky solution energy (eV per defect) | ||
|---|---|---|
| NaCl | MgCl2 | Na2Mg3Cl8 |
| 1.49 | 3.52 | 9.06 |
Table 2 also includes the results of Schottky solution energy obtained from eqn (6)–(8). The lowest Schottky formation energy corresponds to the NaCl defect type (1.49 eV per defect), followed by the MgCl2-Schottky and full Na2Mg3Cl8-Schottky schemes. Again, this result suggests that the most abundant defect type in this structure must be the NaCl-Schottky type, with a minor influence of the MgCl2-Schottky scheme. The NaCl-Schottky type involves 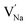 formation, which determines the conduction mechanism in this structure. In comparison to NaCl-Schottky in the Na6MgCl8 structure (being 1.26 eV per defect),26 the solution energy in Na2Mg3Cl8 appears to be similar, which seemingly confirms that this Schottky defect type is responsible for the transport properties in this material.
formation, which determines the conduction mechanism in this structure. In comparison to NaCl-Schottky in the Na6MgCl8 structure (being 1.26 eV per defect),26 the solution energy in Na2Mg3Cl8 appears to be similar, which seemingly confirms that this Schottky defect type is responsible for the transport properties in this material.
3.3 Mechanical properties of Na2Mg3Cl8 structure
Accurate information on mechanical properties is of crucial importance when selecting materials for use as electrodes or electrolytes in batteries.41–43 Ensuring mechanical stability involves achieving a moderate Young's modulus to facilitate desirable contact between a solid electrolyte and the electrodes, thereby preventing the formation of undesirable voids and cracks that could impact long-range transport properties and the battery life.41–43 The mechanical behavior of a crystalline structure follows Hooke's law and is described by the elastic constant matrix (Cij), eqn (9).
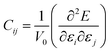 | (9) |
In eqn (9), E represents the total energy, V0 the equilibrium volume, and ε the strain load. From eqn (9), the total energy (E) can be expressed as in equation
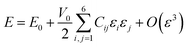 | (10) |
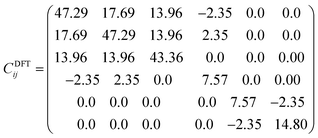 | (11) |
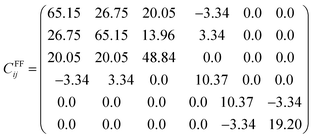 | (12) |
All the diagonal components are positive in both Cij matrices and the eigenvalues are λDFT1 = 9.25, λDFT2 = 9.60, λDFT3 = 20.32, λDFT4 = 34.76, λDFT5 = 39.17 and λDFT6 = 105.98 GPa; from the force field method, λFF1 = 6.88, λFF2 = 7.08, λFF3 = 15.50, λFF4 = 30.09, λFF5 = 31.65, λFF6 = 76.68 GPa. Despite the Cij (and consequently the eigenvalues) differences between the values derived from DFT computations and force field based (FF) methods, the Na2Mg3Cl8 structure is mechanically stable.
With the Cij elements, the other relevant mechanical magnitudes are computed. Table 3 collects the elastic modulus obtained by the DFT and FF approaches of Na2Mg3Cl8 structure. The values of Young modulus (E) are comparable to those of other battery materials.26 For instance, the bulk, shear and Young modulus of Na6MgCl8 amount to 26.57, 15.00 and 42.86 GPa, respectively, as reported in ref. 26. The bulk modulus, which is higher than shear modulus, indicates that Na2Mg3Cl8 is more susceptible to shape deformation than volume change. In addition, the Young's modulus is higher than the bulk modulus, indicating that Na2Mg3Cl8 is better against uniaxial compression or tension than hydrostatic pressure. The Li10GeP2S12 compound, which is used as an SSE in Li-ion batteries, has a Young's modulus of 37.20 GPa.52 The reported values of other Na-containing materials such as Na3OBr and Na3OCl of 55.70 and 60.50 GPa, respectively, are slightly larger.53 Overall, Na2Mg3Cl8 can be regarded as a promising SSE improving the contact with the electrodes.
| Mechanical properties | Method | Reuss | Voigt | Hill |
|---|---|---|---|---|
| Bulk (B) | DFT | 25.33 | 25.46 | 25.40 |
| FF | 33.69 | 34.76 | 34.22 | |
| Shear (G) | DFT | 10.36 | 12.14 | 11.25 |
| FF | 13.47 | 15.48 | 14.47 | |
| Young (E) | DFT | 37.45 | 37.45 | 37.36 |
| FF | 48.97 | 48.97 | 40.09 | |
| B/G | DFT | 2.45 | 2.10 | 2.26 |
| FF | 2.50 | 2.25 | 2.36 | |
| Universal anisotropy (AU) | DFT | 0.87 | ||
| FF | 0.78 | |||
| AB | DFT | 0.0027 | ||
| FF | 0.0157 | |||
| AG | DFT | 0.0795 | ||
| FF | 0.0692 | |||
The bulk (B), shear (G) and Young's (E) modulus derived by DFT computations are smaller than those obtained from the force field-based method. DFT computation tends to underestimate the mechanical properties.39 With the lack of experimental studies concerning the mechanical properties of this compounds, we would suggest considering these values as both lower and upper bounds. Despite the difference, the B/G ratio derived from both methods are similar to each other. According to Pugh's criteria, it can be noted that the B/G ratio is greater than 1.75, implying that Na2Mg3Cl8 is a ductile material, which can deform significantly under stress or when subjected to external forces without cracking.
In order to further explore the elastic anisotropy, the anisotropy regarding compressibility (AB) and shear (AG) is defined by eqn (13)
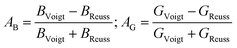 | (13) |
| AU = 5(GVoigt/GReuss) + (BVoigt/BReuss) − 6 | (14) |
In summary, the Na2Mg3Cl8 compound is determined to be mechanically stable and suitable for practical application as solid-state electrolyte.
3.4 Estimation of open cell voltage and capacity of Na2Mg3Cl8
To investigate the impact of Na vacancy concentration on the stability of the Na2Mg3Cl8 lattice structure, the distribution of sodium vacancies and their energetic cost were investigated. For this purpose, various distributions of sodium vacancies were generated maintaining inequivalent configurations within a 1 × 2 × 1 Na2Mg3Cl8 supercell. This study focuses on intermediate compositions of NaxMg3Cl8, with x ranging from 0 to 2.0. The site occupancy disorder (SOD) code was used to identify these configurations.55,56 This approach, which was effective in earlier studies,57 helps us describe how the Na+ ions are distributed over the crystal sites.55–57The process begins by generating all possible configurations within the supercell, each uniquely defined by specifying substitution sites in a parent structure. We then select and fully relax the atomic positions and volume of the inequivalent configurations from the complete canonical ensemble. Configurations are considered equivalent if an isometric transformation can convert one into the other.
The symmetry group of the parent structure and internal translations within the supercell provide a list of potential symmetry operations. To evaluate the thermodynamic stability of the pseudo-binary phases of NaxMg3Cl8, we used the above-hull energy.58 All computational analyses, including the construction of phase diagrams, were performed with the Python Materials Genomics (pymatgen) software library.59 This comprehensive approach allows an in-depth exploration of the thermodynamic landscape to be carried out, thus aiding with the identification of stable compositions and phases under different conditions.
The outstanding stability of the solid electrolyte materials is based on the widely reported electrochemical window of 0–5 V from cyclic voltammetry measurements. Solid electrolyte materials have a limited intrinsic electrochemical window, and the decomposition of most solid electrolyte materials is thermodynamically, favorable the formation of decomposition interphases. In solid electrolytes, stable phases can exist at intermediate ion concentrations that include ion-vacancy orderings in intercalation materials or different atomic orderings in alloys. Atomistic simulations can be used to determine all possible intermediate phases employing the convex hull formalism. However, the number of potential combinations to generate ion vacancies is quite large, making it impractical to be evaluated using atomistic simulations.58
The intermediate phases in the system share the same host structure, where sodium ions and vacancies occupy a common sublattice. Addressing the general problem of determining the distribution of Na-vacancy over the available lattice sites can be effectively achieved using the SOD approach, which identifies inequivalent configurations and significantly reduces the number of required calculations.55
Fig. 3 depicts the formation energies calculated using an FF-based method for the pseudo-binary phases of Na2Mg3Cl8 at temperatures of 0 and 300 K.
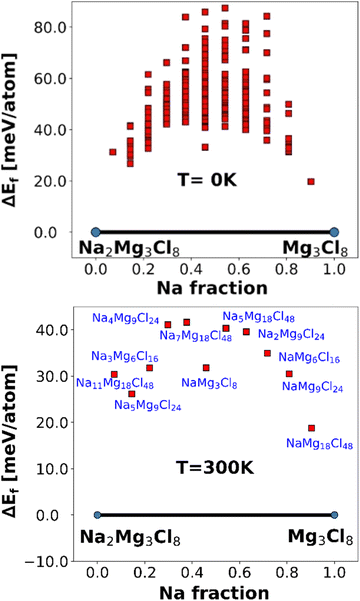 | ||
| Fig. 3 Formation energies of pseudo-binary phases of Na2Mg3Cl8 at 0 (top) and 300 K (bottom). The red point represents the unstable phases in Na+ vacancy generation. | ||
At both temperatures, Na2Mg3Cl8 and the derivative Mg3Cl8 without Na are identified as stable phases, indicated by the blue points on the convex hull. The intermediate compositions are unstable, as represented by red squares above the convex hull (Fig. 3). The formation of intermediate phases is energetically unfavorable. The consistent stability of Na2Mg3Cl8 and Mg3Cl8 is crucial for their use as solid electrolytes in Na-ion battery.
The stability window is determined by the voltages at which Na+ is extracted from the electrolyte to form an Na-deficient decomposition layer between the electrolyte and the cathode and at which sodium atom is inserted into the electrolyte, reducing another species and forming an Na-reduced decomposition layer. The open cell voltage (VOC) is an essential magnitude to determine the electrochemical window of the solid-state electrolyte.1–5 The VOC is estimated by the difference in the chemical potentials of Na+ ions in the cathode (μNAcath) and the anode (μNAan), as described by eqn (15):20,21
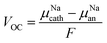 | (15) |
| VOC = −ΔE/xF | (16) |
To assess the energetic cost of an Na-intercalation and the change in the internal energy of the Na2Mg3Cl8 structure, a 1 × 2 × 1 supercell of Na2Mg3Cl8 was used to remove Na+-ions, and the total energy was obtained through FF calculations. The change in the reaction energy (ΔENa) of Na+ intercalation between both stable phases Na2Mg3Cl8 and Mg3Cl8 can be calculated using eqn (17).
| ΔENa = E(Na2Mg3Cl8) − [E(Mg3Cl8) + 2E(Na)] | (17) |
In addition, predictions of the theoretical capacity (Q) can be done using the Faraday equation
| Q = zFn/3.6M | (18) |
3.5. Transport properties of Na2Mg3Cl8 structure
Knowledge on the diffusion and conduction of alkali ions in a material is crucial when evaluating its potential.1–14,32,60 The sodium diffusion coefficient and conductivity within the electrode/electrolyte material directly impact the sodiation/desodiation rate during the charge and discharge cycles.1–14,32,60 The transport properties of candidate materials are essential for picking the one that achieves a high power output, energy density, and long cycle life in Na-ion batteries.1–14,32,60For this purpose, the BVSE was used for prompt predictions of Na+ transport properties in the Na2Mg3Cl8 structure. The first step in a BVSE approach that deals with an exploration of the migration path derived from the BVSE. Migration pathways for Na+ ions were determined by identifying the regions with low bond valence site energy within mesh grids of Na2Mg3Cl8 structure with a resolution of ±0.1 Å3.61
Fig. 4 depicts the energy profile against the reaction coordinates of the Na2Mg3Cl8 structure derived from BVSE computations. Archives containing the BVSE results are included in the ESI.† The respective energy landscape in Na2Mg3Cl8 is displayed in Fig. 5a. There are two intermediate sites denoted as i1 and i2, with minimum energies and six transition structures (saddle points labelled with s) with maximum energies, which determine the energy barriers. From Fig. 4 and the energy profile displayed in Fig. 5a, it can be noted that 2D migration paths located between the [MgCl6] octahedron is the predominant Na+ ion mechanism in Na2Mg3Cl8 with low migration energy barrier. The Na+ ion migration scheme can be explained by a Na+ interstitial mechanism: 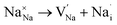 .
.
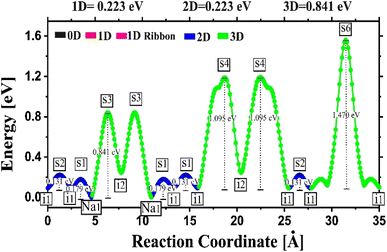 | ||
| Fig. 4 Energy vs. reaction coordinate profile of the Na2Mg3Cl8 structure derived from BV computations. | ||
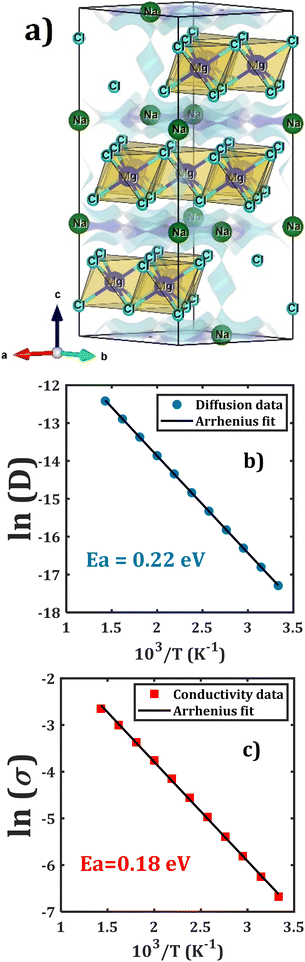 | ||
| Fig. 5 (a) Bond valence energy landscape in the Na2Mg3Cl8 structure (blue isosurfaces) calculated using BVSE and an Arrhenius plot for Na+; (b) diffusion and (c) conduction in the Na6MgCl8 structure. | ||
Fig. 5b and c collect the transport properties (diffusivity and conductivity) of Na2Mg3Cl8 in the temperature range of 300–700 K. An Arrhenius dependence of Na+ diffusivity and conductivity is observed. The conductivity data was obtained using the Nernst–Einstein equation, where the diffusion coefficient at each temperature is directly related to the Na+ ion conductivity.20,21,32
The calculated activation energy amounts to 0.22 and 0.18 eV for Na+ diffusion and conduction, respectively. The predicted results of activation energy suggests that there are effective jumps in the mass transport that contribute to the charge transport process, thus lowering the conduction activation energy. Low activation energy in a solid-state electrolyte significantly enhances ionic conductivity, which in turn boosts battery performance by enabling faster charge and discharge rates, improving energy efficiency, and extending the overall lifespan of the battery.1–10 This leads to more reliable and high-performing energy storage solutions, which crucial for applications ranging from portable electronics to electric vehicles and grid storage systems.1–11
Together with the low activation energies for diffusion and conduction, the Na2Mg3Cl8 structure possesses promising diffusion coefficient and conductivity at 300 K of 3.10 × 10−8 cm2 s−1 and 1.26 mS cm−1, respectively. The source of these outstanding properties can be explained by the crystal structure of Na2Mg3Cl8, specifically by the [NaCl] and [MgCl4] frameworks. As was mentioned in Section 3.1, Na2Mg3Cl8 has more Na+ accessible sites, favoring the migration through interstitial mechanism. The values of activation energy and transport properties at 300 K are equally comparable to those of the currently used solid state electrolytes in Na-ion battery technologies.62–67 For instance, in a recent study on Na3YBr6 solid-state electrolyte, which was prepared via a solid-state reaction, has an activation energy of 0.15 eV and promising electrochemical window, making this Na halide compound a good candidate for sodium all solid-state batteries.68 Another study on the tetragonal phase of Na3SbS4 (293–453 K) showed an activation energy of 0.22 eV and conductivity at 293 K of 0.6 mS cm−1.69 Recent advances significantly improved the room-temperature ionic conductivity of Na1+xZr2SixP3−xO12 (0 < x < 3) superionic conductors, reaching a remarkable value of 1 mS cm−1.70–75 The computed values of room-temperature conductivity and activation energy are competitive with those reported in current SSEs.
In this context, the Na2Mg3Cl8 compound, with its remarkably low activation energy of 0.18 eV and impressive room temperature conductivity of 1.26 mS cm−1, stands out as an exceptional candidate for solid-state electrolytes in both current and future Na-ion batteries. We are optimistic that the outstanding properties predicted in this theoretical study will motivate experimental synthesis efforts, paving the way for groundbreaking advancements in Na2Mg3Cl8 compounds and their applications in energy storage technologies.
4. Concluding remarks
Advanced atomistic computations were employed to investigate the structural, electronic, mechanical, and transport properties of an unexplored chloride compound, specifically Na2Mg3Cl8. The computed lattice parameters using density functional theory and force-field based methods closely match the values reported in the literature. The exploration of electronic properties reveals that the Na2Mg3Cl8 structure exhibits insulating characteristics, with an energy gap of ∼4.9 eV arising from the hybridization of [NaCl] trigonal prismatic and [MgCl6] octahedral units.The exploration of mechanical properties points out that Na2Mg3Cl8 is a ductile material and mechanically stable, which is beneficial for practical fabrication, improving the electrolyte/electrode contact, reducing the resistance and improving the performance of the battery device. On the other hand, Na2Mg3Cl8 has appropriate transport properties with low activation energies for both diffusion and conduction processes and an outstanding room-temperature conductivity of 1.26 mS cm−1 comparable to that of other superionic conductors.
In light of these remarkable properties, experimental synthesis efforts are highly desirable to validate our theoretical predictions regarding the Na2Mg3Cl8 compound as a solid electrolyte.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
YAZ: conception, data acquisition and interpretation, original draft preparation, editing, review. JRFG: data acquisition and interpretation, original draft preparation. TVBP: funding, editing, review. MPPH: data analysis, editing, review. MTN: conception, project supervision, manuscript editing and review. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support provided by the VinUniversity Center for Environmental Intelligence under Flagship Project VUNI.CEI.FS_0005. MTN thanks Van Lang University and MPPH acknowledges the Ho Chi Minh City University of Technology (HCMUT) and VNU-HCM for support.Notes and references
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J. N. Chotard, C. P. Grey, M. S. Islam and C. Masquelier, Chem. Mater., 2018, 30, 2618–2630 CrossRef CAS.
- H. Tian, S. Liu, L. Deng, L. Wang and L. Dai, Energy Storage Mater., 2021, 39, 232–238 CrossRef.
- K. Chayambuka, G. Mulder, D. L. Danilov and P. H. L. Notten, Adv. Energy Mater., 2018, 8, 1–49 Search PubMed.
- B. Singh, Z. Wang, S. Park, G. S. Gautam, J. N. Chotard, L. Croguennec, D. Carlier, A. K. Cheetham, C. Masquelier and P. Canepa, J. Mater. Chem. A, 2021, 9, 281–292 RSC.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Nano Mater. Sci., 2019, 1, 91–100 CrossRef.
- A. Emly, E. Kioupakis and A. Van Der Ven, Chem. Mater., 2013, 25, 4663–4670 CrossRef CAS.
- J. Xu, Y. Wang, S. Wu, Q. Yang, X. Fu, R. Xiao and H. Li, ACS Appl. Mater. Interfaces, 2023, 15, 21086–21096 CrossRef CAS PubMed.
- B. Tao, D. Zhong, H. Li, G. Wang and H. Chang, Chem. Sci., 2023, 14, 8693–8722 RSC.
- Z. Wei, L. F. Nazar and J. Janek, Batteries Supercaps, 2024, 7, e202400005 CrossRef CAS.
- Q. Zhao, S. Stalin, C. Z. Zhao and L. A. Archer, Nat. Rev. Mater., 2020, 5, 229–252 CrossRef CAS.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- Q. Ma and F. Tietz, ChemElectroChem, 2020, 7, 2693–2713 CrossRef CAS.
- H. Ahmad, K. T. Kubra, A. Butt, U. Nisar, F. J. Iftikhar and G. Ali, J. Power Sources, 2023, 581, 233518 CrossRef CAS.
- N. Aslfattahi, L. Samylingam, M. S. Kiai, K. Kadirgama, V. Kulish, M. Schmirler and Z. Said, J. Energy Storage, 2023, 72, 108781 CrossRef.
- A. A. Franco, A. Rucci, D. Brandell, C. Frayret, M. Gaberscek, P. Jankowski and P. Johansson, Chem. Rev., 2019, 119, 4569–4627 CrossRef CAS PubMed.
- L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Chem. Mater., 2021, 33, 625–641 CrossRef CAS.
- S. Adams, Solid State Ionics, 2006, 177, 1625–1630 CrossRef CAS.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 18–33 CrossRef CAS PubMed.
- Y. A. Zulueta and M. T. Nguyen, Phys. Chem. Chem. Phys., 2023, 25, 27926–27935 RSC.
- Y. A. Zulueta and M. T. Nguyen, in Annual Reports in Computational Chemistry, Elsevier, 2023, vol. 19, pp. 1–43 Search PubMed.
- J. Sung, J. Heo, D.-H. Kim, S. Jo, Y.-C. Ha, D. Kim, S. Ahn and J.-W. Park, Mater. Chem. Front., 2024, 8, 1861–1887 RSC.
- X. Nie, J. Hu and C. Li, Interdiscip. Mater., 2023, 2, 365–389 Search PubMed.
- C. Fu, Y. Li, W. Xu, X. Feng, W. Gu, J. Liu, W. Deng, W. Wang, A. M. M. Abeykoon, L. Su, L. Zhu, X. Wu and H. Xiang, Nat. Commun., 2024, 15, 4315 CrossRef CAS PubMed.
- Y. A. Zulueta, M. P. Pham-Ho and M. T. Nguyen, RSC Adv., 2024, 14, 21644–21652 RSC.
- Y. A. Zulueta, M. P. Pham-Ho and M. T. Nguyen, J. Phys. Chem. Solids, 2024, 188, 111916 CrossRef CAS.
- C. J. J. Loon and D. J. W. Ijdo, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 770–773 CrossRef.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- B. A. Goldmann, M. J. Clarke, J. A. Dawson and M. S. Islam, J. Mater. Chem. A, 2022, 10, 2249–2255 RSC.
- Computational Modelling of Zinc Oxide and Related Oxide Ceramics, University of Surrey, https://openresearch.surrey.ac.uk/esploro/outputs/doctoral/Computational-Modelling-of-Zinc-Oxide-and/99512944702346, (accessed 30 May 2024) Search PubMed.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485–499 RSC.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- L. Van Duong, M. T. Nguyen and Y. A. Zulueta, RSC Adv., 2022, 12, 20029–20036 RSC.
- L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Chem. Mater., 2021, 33, 625–641 CrossRef CAS.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- F. A. Kröger, The Chemistry of Imperfect Crystals, North-Holland Pub. Co., 1964 Search PubMed.
- Z. Ding, J. Li, J. Li and C. An, J. Electrochem. Soc., 2020, 167, 070541 CrossRef.
- X. Ke, Y. Wang, G. Ren and C. Yuan, Energy Storage Mater., 2020, 26, 313–324 CrossRef.
- M. Hou, F. Liang, K. Chen, Y. Dai and D. Xue, Nanotechnology, 2020, 31, 132003 CrossRef CAS PubMed.
- M. Born, K. Huang and M. Lax, Am. J. Phys., 1955, 23, 474 CrossRef.
- I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Naukova Dumka, Kiev, 1983, pp. 60–180 Search PubMed.
- F. I. Fedorov, Theory of Elastic Waves in Crystals, Springer US, Boston, MA, 1968 Search PubMed.
- W. Voigt Lehrbuch der Kristallphysik (BG Teubner Leipzig und 791 Berlin) 980 S; Reproduced 1966 Spring Fachmedien Wiesbaden GmbH, 1928 Search PubMed.
- A. Reuss, J. Appl. Math. Mech., 1929, 9, 49–58 CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- R. Hill, J. Mech. Phys. Solids, 1963, 11, 357–372 CrossRef.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- Z. Q. Wang, M. S. Wu, G. Liu, X. L. Lei, B. Xu and C. Y. Ouyang, Int. J. Electrochem. Sci., 2014, 9, 562–568 CrossRef.
- M. A. Sattar, M. Javed, M. Benkraouda and N. Amrane, Int. J. Energy Res., 2021, 45, 4793–4810 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. d. Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- V. Fotopoulos, R. Grau-Crespo and A. L. Shluger, Phys. Chem. Chem. Phys., 2023, 25, 9168–9175 RSC.
- J. R. Fernández-Gamboa, F. Tielens and Y. A. Zulueta, Mater. Sci. Semicond. Process., 2024, 173, 108144 CrossRef.
- C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- J. Zhu, Y. Wang, S. Li, J. W. Howard, J. Neuefeind, Y. Ren, H. Wang, C. Liang, W. Yang, R. Zou, C. Jin and Y. Zhao, Inorg. Chem., 2016, 55, 5993–5998 CrossRef CAS PubMed.
- J. Liang, X. Li, S. Wang, K. R. Adair, W. Li, Y. Zhao, C. Wang, Y. Hu, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, Y. Mo and X. Sun, J. Am. Chem. Soc., 2020, 142, 7012–7022 CrossRef CAS PubMed.
- N. Wang, K. Yang, L. Zhang, X. Yan, L. Wang and B. Xu, J. Mater. Sci., 2018, 53, 1987–1994 CrossRef CAS.
- Q. Zhang, C. Zhang, Z. D. Hood, M. Chi, C. Liang, N. H. Jalarvo, M. Yu and H. Wang, Chem. Mater., 2020, 32, 2264–2271 CrossRef CAS.
- R. Jalem, A. Hayashi, F. Tsuji, A. Sakuda and Y. Tateyama, Chem. Mater., 2020, 2020, 58 Search PubMed.
- X. Y. Niu, X. Y. Dou, C. Y. Fu, Y. C. Xu and X. Y. Feng, RSC Adv., 2024, 14, 14716–14721 RSC.
- J. A. Dawson, T. S. Attari, H. Chen, S. P. Emge, K. E. Johnston and M. S. Islam, Energy Environ. Sci., 2018, 11, 2993–3002 RSC.
- L. Wang, Z. Song, X. Lou, Y. Chen, T. Wang, Z. Wang, H. Chen, W. Yin, M. Avdeev, W. H. Kan, B. Hu and W. Luo, Small, 2024, 2400195 CrossRef CAS PubMed.
- X. Y. Niu, X. Y. Dou, C. Y. Fu, Y. C. Xu and X. Y. Feng, RSC Adv., 2024, 14, 14716–14721 RSC.
- R. Jalem, A. Hayashi, F. Tsuji, A. Sakuda and Y. Tateyama, Chem. Mater., 2020, 32, 8373–8381 CrossRef CAS.
- J. Luo, G. Zhao, W. Qiang and B. Huang, J. Am. Ceram. Soc., 2022, 105, 3428–3437 CrossRef CAS.
- J. F. Nonemacher, S. Naqash, F. Tietz and J. Malzbender, Ceram. Int., 2019, 45, 21308–21314 CrossRef CAS.
- B. Hitesh and A. Sil, J. Am. Ceram. Soc., 2023, 106, 6743–6754 CrossRef CAS.
- Z. Gao, J. Yang, G. Li, T. Ferber, J. Feng, Y. Li, H. Fu, W. Jaegermann, C. W. Monroe and Y. Huang, Adv. Energy Mater., 2022, 12, 2103607 CrossRef CAS.
- E. J. Cheng, T. Yang, Y. Liu, L. Chai, R. Garcia-Mendez, E. Kazyak, Z. Fu, G. Luo, F. Chen, R. Inada, V. Badilita, H. Duan, Z. Wang, J. Qin, H. Li, S. Orimo and H. Kato, Mater. Today Energy, 2024, 44, 101644 CrossRef CAS.
- N. Wang, K. Yang, L. Zhang, X. Yan, L. Wang and B. Xu, J. Mater. Sci., 2018, 53, 1987–1994 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra06490a |
| This journal is © The Royal Society of Chemistry 2024 |