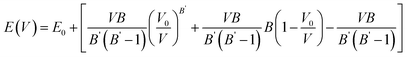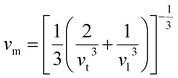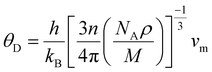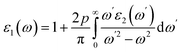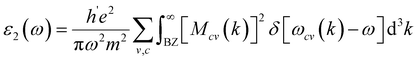DOI:
10.1039/D4RA06555G
(Paper)
RSC Adv., 2024,
14, 34679-34689
A spin-polarized analysis of the half-metallicity, mechanical, structural and optoelectronic attributes of full-Heusler XVCo2 (X = B and P) alloys
Received
11th September 2024
, Accepted 16th October 2024
First published on 30th October 2024
Abstract
Cobalt-based Heusler alloys possess high Curie temperatures with half-metallic characteristics, which make them excellent candidates for spintronic applications. These types of Heusler alloys are perfect for the fabrication of magnetic sensors and memory-based devices. Herein, an in-depth first principles analysis of the physical attributes of XVCo2 (X = B and P) was performed. The mBJ functional was employed to treat electron-ion interaction within their crystal structures. The crystal structure of XVCo2 (X = B and P) was optimized, and relaxation parameters for both alloys were analyzed. Their ground-state energies at minimum volume were also computed. The Thomas Charpin methodology was employed to compute elastic constants for XVCo2 (X = B and P), and mechanical properties of both alloys were obtained. For both alloys, metallic behavior was recorded in spin up channels, while indirect bandgaps of 0.38 eV and 1.73 eV were calculated in spin down channels for BVCo2 and PVCo2, respectively. Both studied alloys showed 100% polarization at the Fermi level. Furthermore, their bonding character was analyzed via electron density plots. The optical characteristic obtained from a complex dielectric equation revealed higher dispersion in the visible range for BVCo2 and PVCo2, making these materials excellent candidates for spintronics and optoelectronic devices.
1. Introduction
Presently, the rapidly increasing internet speed necessitates low switching and adaptable RAM technologies for PCs and smartphones.1 The existing approach to meet this need, which involves shrinking the size of chip cells while adding more transistors, will eventually become ineffective because of efficiency constraints and financial considerations.2–4 Thus, appropriate semiconductor materials are essential for the development and improvement of optoelectronic devices. The necessity for material design to fulfill particular specifications in optoelectronic devices is driving this change.5 Half-metallic compounds serve as foundational elements for reshaping the landscape of memory and spintronic devices, information technology and telecommunications.6–8 In 1983, half-metallic ferromagnetic materials were discovered, exhibiting metallic properties in one spin state and semiconductor traits in the other.9–11 The field that uses the spin of electrons for the storage and processing of information is termed as spintronics, and it is a fairly new area of technology that still requires significant work.12 Using single electron spins as sources and introducing spins into materials to produce and control electrical devices are two of the most researched applications in spintronics.13 Heusler alloys, which were discovered in 1903, have captured the attention of researchers owing to their exceptional multifunctional applications in magnetic shape memory devices.14–19 There are a variety of structures based on which these alloys are classified, such as full Heusler (X2YZ), half Heusler (XYZ) and quaternary Heusler alloys (XX′YZ).20,21 Each alloy with these distinct structural compositions has unique features, but full Heusler alloys continue to be appropriate for many magnetic-based applications because of their remarkable characteristics.22 Numerous Heusler alloys have been reported to exhibit 100% polarization at the Fermi level and investigated in the prior literature; e.g., half-metallic behavior was observed in FeRuVZ (Z = Si and Ge) Heusler alloys.23 The silver-based Heusler alloys Ag2XGa (X = Ti and V) have reported to be useful in spintronic applications.24 TiHfFeX (X = Al, Ga, and In) was reported to show half-metallic behaviour and considered a viable option for the construction of magnetic shape memory alloys.25 Nowadays, Co-based Heusler compounds have received significant interest because of their distinct and diverse features compared to other Heusler compounds.26 Cobalt-based Heusler alloys have been extensively studied and are particularly noteworthy as Heusler alloys possessing lower magnetization with the goal of producing high current-induced magnetic switching, ultimately leading to higher stability in the material.27–29 Additionally, various Co-based alloys such as Co2MnX (X = Al, Ge, Si, Ga),30 Co2VX (X = Al, Be),31 Co2MnX (X = Ge, Sn),32 Co2ScX (X = As, Sb, Bi),33 Co2CrX (X = Ga, Al),34 Co2YAl (Y = Fe, Ti),35 Co2ZrSi36 Co2YX (X = P, As, Sb, and Bi)37 and Co2YX (X = P, As, Sb, Bi)38 have been documented in the literature for their exceptional spintronic properties, while experimental investigations have been conducted on Co2MnxTi1−xSi, Co2MnGa1−xGex, and Co2TiZ (where Z = Sb, Sn, Ge, Si).39 Together with their magnetic properties, Heusler alloys are also known for their excellent performance in optoelectronic applications. For instance, prominent optical characteristics were observed in Ru2CrAl,40 Na2SrX (Si and Ge),41 CoFeXAs (X = Mn, Cr and V),42 and Co2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) –
–![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xVxFeGe.43 They are also well-suited for high-tech structural and functional uses because of their exceptional mechanical characteristics. Heusler alloys such as Co2YAl (Y = Fe, Ti),35 CrCoVSb44 and Co2TaZ (Z = Si, Sn)45 exhibit excellent mechanical characteristics. However, their physical properties are not well understood, despite their prospective applications in a variety of technology domains. Furthermore, the investigation of Co-based Heusler alloys, in particular XVCo2 (X = B, P), is still unexplored. Thus, to provide fundamental insights, this study attempts to explore these aspects using first principles analysis. Gaining this understanding is essential for advancements in the creation and use of these innovative materials.
xVxFeGe.43 They are also well-suited for high-tech structural and functional uses because of their exceptional mechanical characteristics. Heusler alloys such as Co2YAl (Y = Fe, Ti),35 CrCoVSb44 and Co2TaZ (Z = Si, Sn)45 exhibit excellent mechanical characteristics. However, their physical properties are not well understood, despite their prospective applications in a variety of technology domains. Furthermore, the investigation of Co-based Heusler alloys, in particular XVCo2 (X = B, P), is still unexplored. Thus, to provide fundamental insights, this study attempts to explore these aspects using first principles analysis. Gaining this understanding is essential for advancements in the creation and use of these innovative materials.
2. Computational analysis
For several years, researchers in the field of condensed matter physics have employed density functional theory to assess the electronic properties of atoms and molecules.46 The codes based on DFT have received significant attention in the past few years given that the results compiled through this software provide an easy way to evaluate the physical characteristics of a material without consuming a lot of time. Density functional theory employs different functionals to explain the energy of a system in the form of electron density.47 To evaluate the physical traits of the XVCo2 (X = B, P) full-Heusler alloys, we employed the Wien2K algorithm, which is a DFT-based code. For the expansion of the wave function, the FP-LAPW approach48 was employed, which is already built in the Wien2K code. In the muffin-tin region, the potential is variable, and in the interstitial region, the potential is constant, which are the two sections that the FP-LAPW approach separates the crystal structure into and the mathematical expressions are as follows:| |
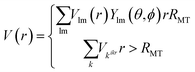 | (1) |
The expansion of the wave function in the unit cell was achieved by using a linear combination of the plane waves in the interstitial area and the spherical harmonics in the muffin-tin region. The GGA potential was used for the crystal relaxation, and the mBJ functional was used to evaluate the electrical and optical characteristics of XVCo2 (X = B, P). The mBJ functional is as follows:
| |
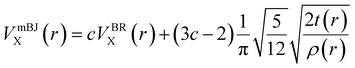 | (2) |
where
VBRX is the Becke Roussel potential and
c is mathematically stated as:
| |
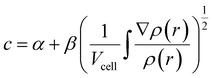 | (3) |
where
α and
β can be attuned according to our required calculations given that they are the free parameters in the Wien2K software. For accurate SCF calculations, several parameters were tuned such as the RMT ×
Kmax = 7,
lmax = 12 and
Gmax = 14 (a.u)
−1. The muffin-tin radii for “B”, “P”, “V” and “Co” were tuned as 1.80, 1.85, 2.06 and 2.17 (a.u)
−1, respectively. To avoid charge leakage
via overlapping spheres, the cut-off energy was selected as −8 Ry. To ensure accuracy in the SCF calculations, a large mesh of 2000K points was selected together with the energy convergence of 0.0001 Ry. The crystal structures and the relevant structural data for these structures were obtained through VESTA.
49 The optical interactions of the materials were evaluated using the Kramers–Kronig complex equations.
3. Results and discussion
3.1 Structure and stability
An in-depth analysis of crystal structures is critical because it gives information on the symmetry, atom arrangement, chemical reactions, and optimal performance of materials. Knowing the structural properties of a material reveals important information regarding its use in various applications. Our studied alloys possess cubic symmetry with the space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m225. In this three-dimensional structure of XVCo2 (X = B, P), each V atom is bonded to six equivalent “B” or “P” atoms and eight equivalent “Co” atoms, creating a body-centred cubic geometry. The atomic bond lengths were computed using the VESTA and observed to be 2.36 Å, 2.73 Å, and 2.73 Å for V–Co, V–B, and V–P, respectively. The crystal structures of XVCo2 (X = B, P) are plotted in Fig. 1. To assess the ground-state energies for both Heusler alloys, their crystal structures were optimized. The volume optimization curves were plotted for the non-magnetic and ferromagnetic phases. The volume optimization curves for BVCo2 and PVCo2 revealed that these alloys are more stable in the FM phase. Fig. 1(b) and (d) demonstrate the volume optimization curves for both alloys, respectively. After volume optimization, the optimized parameters for both Heusler alloys were analysed using the Birch–Murnaghan equation, as follows:
m225. In this three-dimensional structure of XVCo2 (X = B, P), each V atom is bonded to six equivalent “B” or “P” atoms and eight equivalent “Co” atoms, creating a body-centred cubic geometry. The atomic bond lengths were computed using the VESTA and observed to be 2.36 Å, 2.73 Å, and 2.73 Å for V–Co, V–B, and V–P, respectively. The crystal structures of XVCo2 (X = B, P) are plotted in Fig. 1. To assess the ground-state energies for both Heusler alloys, their crystal structures were optimized. The volume optimization curves were plotted for the non-magnetic and ferromagnetic phases. The volume optimization curves for BVCo2 and PVCo2 revealed that these alloys are more stable in the FM phase. Fig. 1(b) and (d) demonstrate the volume optimization curves for both alloys, respectively. After volume optimization, the optimized parameters for both Heusler alloys were analysed using the Birch–Murnaghan equation, as follows:| |
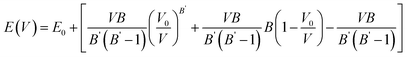 | (4) |
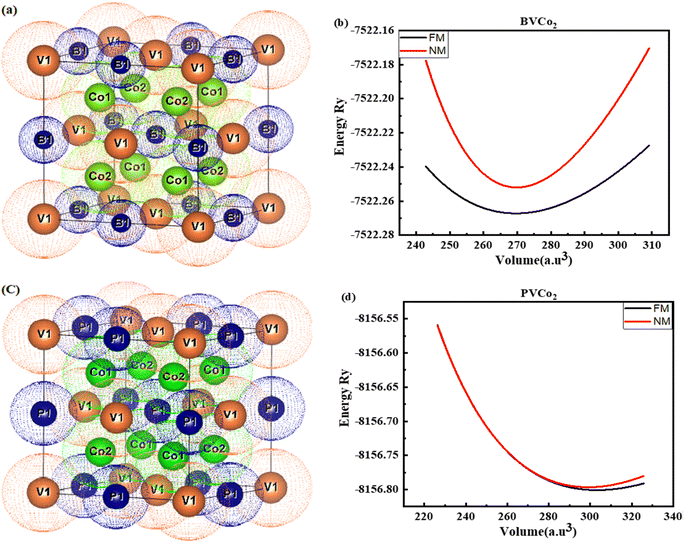 |
| | Fig. 1 (a and c) Unit cell structure and (b and d) volume optimization curves for BVCo2 and PVCo2. | |
In the Birch–Murnaghan equation, the first term corresponds to the optimized ground-state energy, which is the minimum energy of the alloy at which it is stable, while the second term defines the compressional changes in the structure caused by variations in the volume and bulk modulus. The optimized bulk modulus values for both alloys depict that these alloys are very hard to compress. All the optimized lattice constants for XVCo2 (X = B, P) are summarized in Table 1. After assessing the structural stability of both alloys, we assessed their thermo-dynamical stability by computing their respective formation energies. The formation energy of an alloy indicates the amount of energy that has been absorbed or released in its formation.50 An alloy is considered stable if its formation energy is computed to be negative, whereas the formation energy is positive for an unstable alloy.51 The formation energy for XVCo2 (X = B, P) was calculated as follows:
| | |
EF = Etotal − (2ECo + EV + EB/P)
| (5) |
where,
Etotal represents the ground-state energy for XVCo
2 (X = B, P) and
ECo,
EV and
EB/P are the energies of the discrete atoms Co, V and B/P, respectively. The computed formation energy for BVCo
2 is slightly lower than that of PVCo
2, which infers that it possesses slightly higher thermo-dynamical stability.
Table 1 Optimized lattice parameters for XVCo2 (X = B and P)
| Heusler alloy |
A0 |
V0 (a.u3) |
B (GPa) |
B′ |
E0 (Ry) |
EF |
| BVCo2 |
5.42 |
272.28 |
255.55 |
4.02 |
−7522.267 |
−2.73 |
| PVCo2 |
5.64 |
283.13 |
184.07 |
6.92 |
−8156.800 |
−2.79 |
3.2 Elastic attributes
The ability of these two materials to endure external stress and revert to their original form was assessed based on their mechanical properties.52,53 In the first principles calculations of a material, multiple methods can be employed to compute its elastic constant.54 The method we employed to evaluate the elastic constants of XVCo2 (X = B, P) is the Thomas Charpin method.55 This technique includes applying slight strains to a crystal in a systematic manner and computing its subsequent stress responses to determine the its elastic constants. Because the Heusler alloys under investigation have cubic symmetry, their mechanical properties could be adequately addressed using only three elastic constants (C11, C12, and C44). It is critical that these elastic constants fully justify Born's stability criterion, which requires that all computed elastic constants should be greater than zero. If Born's stability criterion fails to be satisfied, then further mechanical traits of the desired compound cannot be assessed. The evaluated elastic constants and the related properties for XVCo2 (X = B, P) are presented in Table 2. The C11 and C12 elastic constants define the directional changes in the materials, whereas C44 defines the forces that cause deformity in their shape. The bulk modulus is the most important term in the assessment of mechanical qualities given that it defines the ability of a material to resist volumetric changes with an increase in the external pressure.56 According to the computed results, it can be seen that PVCo2 possesses a larger bulk modulus than BVCo2, which implies that PVCo2 is more resistive to the volumetric changes caused via external stresses. The ability of a material to stretch or compress with the application of force is measured through its Young's modulus.57 The attained results of Young's modulus imply that PVCo2 is a rigid material in comparison BVCo2 and is not easily stretched or compressed. The deformation caused in the shape of materials can be analysed through the shear modulus.58 PVCo2 offers a higher shear modulus value than BVCo2, which indicates that causing an irregularity in the shape of PVCo2 is difficult compared to BVCo2. The anisotropy factor is computed to determine the directional dependency of the properties of a material. In the case of A = 1 or A = 0, the attributes of a material are not affected by the change in direction, which is referred to as an isotropic material. Deviation of the anisotropy factor from zero or unity results in anisotropic behavior, implying that the properties of a material may vary depending on the direction.59 The anisotropy value of both Heusler alloys implies anisotropic behaviour, as depicted by their anisotropy values. Brittle materials cannot tolerate tension and rapidly break, whereas ductile materials handle external stresses exceedingly well. The B/G ratio, referred to as “Pugh's ratio”, determines how ductile or brittle a material is. An alloy or a compound is considered brittle if B/G < 1.75, otherwise it is ductile. A larger B/G ratio denotes a greater capacity to tolerate deformation, whereas a lower ratio implies a propensity for fracture.60 Both XVCo2 (X = B, P) Heusler alloys showed B/G higher than 1.75, indicating that both alloys are ductile materials. Furthermore, Poisson's ratio can aid in determining if a material is brittle or ductile. According to Poisson's criteria, material brittleness is defined as v < 0.26, and ductility is defined as v > 0.26.61 The evaluated results of Poisson's ratio depicts that both alloys are ductile. The type of bonding between the atoms of a material can be judged by the Cauchy pressure. In the case of ionic bonding, the Cauchy pressure is evaluated to be positive, whereas for covalent bonding, the Cp value is negative.60 The reported Cauchy pressure values for both alloys revealed ionic bonding between their atoms. The hardness factor reflects the capacity of a material to withstand indentation and scratches. Higher hardness factor values indicate that a material is more resistant to scratching, whereas lower values indicate that it can be easily deformed.62 The computed hardness factor values for both studied alloys revealed their higher resistance to scratching. The ratio of the bulk modulus to shear deformation of a material, or machinability index, illustrates how easy or workable it is.63 Lower values of the machinability index show the difficulty in handling a material, whereas higher values imply that it is easy to handle. Both alloys revealed lower machinability index values. In the case of both Heusler alloys, we also evaluated elastic sound waves using their mechanical properties. Waves in a material can propagate in two different ways, i.e., transverse waves and compressional waves. Transverse waves move through materials perpendicularly, whereas compressional waves move parallel across the medium. In the case of both studied Heusler alloys, it is noticeable that the compressional waves were dominant compared to transverse waves. Furthermore, the mean velocities for XVCo2 (X = B, P) were also computed and mathematically stated as follows:| |
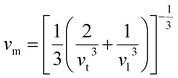 | (6) |
Table 2 Mechanical parameters of BVCo2 and PVCo2 alloys
| Mechanical properties |
BVCo2 |
PVCo2 |
| C11 |
340.33 |
389.2 |
| C12 |
239.09 |
230.1 |
| C44 |
142.022 |
110.34 |
| (Bulk modulus) B |
272.28 |
283.13 |
| (Young's modulus) Y |
252.85 |
260.6 |
| (Shear modulus) S |
93.96 |
96.7 |
| (Anisotropy factor) A |
2.80 |
1.38 |
| (Pugh's ratio) B/G |
2.90 |
2.92 |
| (Poisson's ratio) v |
0.33 |
0.34 |
| (Cauchy pressure) Cp |
97.06 |
119.76 |
| (Hardness factor) Hv |
10.77 |
10.37 |
| (Machinability index) μm |
1.92 |
2.56 |
| (Compressional waves) vl (m s−1) |
6553.53 |
6677.58 |
| (Transverse waves) vt (m s−1) |
3183.79 |
3235.79 |
| (Mean velocity)vm (m s−1) |
3577.43 |
3636.37 |
| (Melting temperature) Tm (K) |
2564.35 |
2853.17 |
| (Debye temperature) θD (K) |
575.21 |
561.87 |
The mean velocity defines the average speed at which a wave passes through a material. It provides significant information regarding the ability of a material to stretch, compress and revert to its original state. The temperature at which a material melts is referred to as the melting temperature.64 A material with stronger bonding between its atoms or molecules will have a greater melting temperature given that more heat energy is required to dissolve these tight connections, enabling the material to change from solid to liquid form. The calculated results of the melting temperature for XVCo2 (X = B, P) imply the strong bonding of their atoms with each other. The Debye temperature is an extremely important term in the field of solid-state physics given that it provides detailed insight about the specific heat, stiffness, thermal conductivity and phonons of materials65 and is computed as follows:
| |
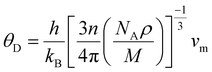 | (7) |
According to the Debye temperature results for XVCo2 (X = B, P), the specific heat capacity of these alloys will change very slowly below this temperature.
3.3 Electro-magnetic properties
The nature of a material and its uses in the field of optoelectronic devices can be assessed by its electronic properties. Magnetic materials, which behave like a conductor in one spin channel and insulator or a semiconductor in the other spin channel, are termed half-metallic materials.66 These half-metallic materials show significant potential in spintronic-related applications. The electronic properties of XVCo2 (X = B, P) such as band structure, TDOS and PDOS were computed using the mBJ approximation. The band structure profiles for XVCo2 (X = B, P) were analyzed for high symmetry point (W-L-Γ-X-W-K) in the first Brillion zone. The Fermi line, which separates the conduction and valence band, is represented by EF. Fig. 2(a) shows the band structure profile of BVCo2 for the spin-up channel and it is clearly seen that the dispersion curves in its conduction band overlap with the dispersion curves present in its valence band, revealing its metallic behavior. Fig. 2(b) shows the plot of the band structure of the spin-down channel for BVCo2. In the spin-down channel, a visible gap was observed in both intermediate bands with an indirect bandgap of 0.38 eV. In the case of PVCo2, metallic behavior was observed in the spin-up channel, as shown in Fig. 2(c), while a direct bandgap of 1.73 eV was observed in the spin-down state, as presented in Fig. 2(d). In the case of both studied alloys, half metallic behavior was observed, which implies that these alloys are perfect for efficiently generating and controlling the spin polarized currents.
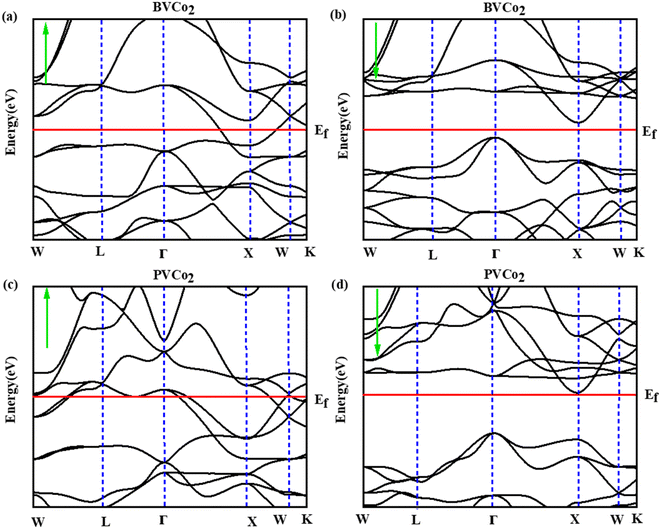 |
| | Fig. 2 Band structure profiles for BVCo2 (a and b) and PVCo2 (c and d). | |
On the contrary, we also obtained the TDOS plots for XVCo2 (X = B, P) in the energy range of −6 eV to 6 eV, as presented in Fig. 3. The total density of states corresponds to the different energy levels that electrons can occupy. Fig. 3(a) illustrates the TDOS plot of BVCo2 for both spin states. The TDOS plot in the spin-up channel indicates 100% polarization at the Fermi level, while a clear bandgap is noticed in the spin-down channel. In the case of the PVCo2 alloy, a bandgap in the spin-down channel was observed, while metallic character was observed in the spin-up state. Together with TDOS, we also assessed the PDOS for XVCo2 (X = B, P), as displayed in Fig. 4. It was observed that for BVCo2, the B-p state showed the highest involvement in the conduction band with small contributions from the V-d and Co-d states in both spin channels, while V-d and Co-d showed the highest contribution in the valence band, as presented in Fig. 4(a). In the case of PVCo2, the P-p and Co-d states show the highest contribution in the conduction band with the minor contribution of the V-d state in both spin channels. In the conduction band, V-d and Co-d states prominently contribute, with a small contribution from the P-p state, as depicted in Fig. 4(b).
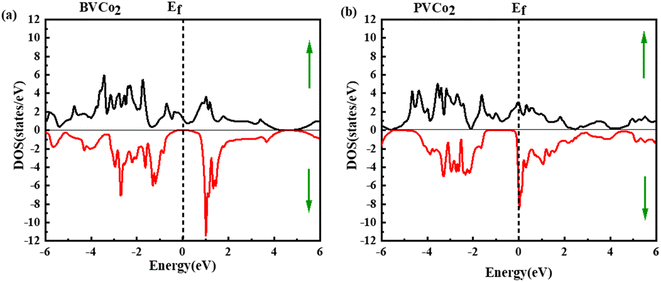 |
| | Fig. 3 Total DOS for (a) BVCo2 and (b) PVCo2. | |
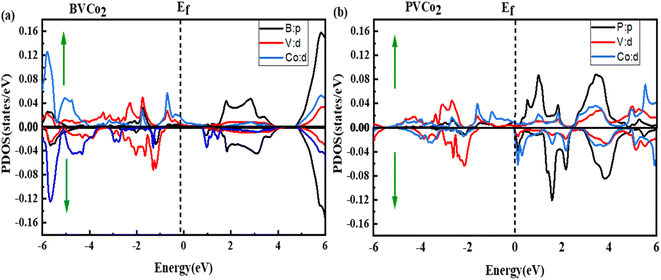 |
| | Fig. 4 Partial density of states for (a) BVCo2 and (b) PVCo2. | |
The response of a material when it interacts with an external magnetic field is analysed by its magnetic traits. The magnetic moments for XVCo2 (X = B, P) are listed in Table 3. In the case of the BVCo2 alloy, the major contribution was observed from its “Co” atom, whereas the contributions from the “B” and “V” atoms are extremely low. The magnetic moment in the interstitial region for BVCo2 is negative, which implies that the direction of the magnetic moment is opposite to the external magnetic field, and thus the collective magnetic moment for BVCo2 was computed as 2μB. In the case of the PVCo2 alloy, the major contribution was noticed from the “V” and “Co” atoms, while a very small contribution is noticed from the “P” atom. The total magnetic moment for PVCo2 was computed as 2.81μB.
Table 3 Calculated partial and total magnetic moments for BVCo2 and PVCo2
| Alloys |
Magnetic moment (μB) |
| B |
P |
V |
Co |
Interstitial |
Total |
| BVCo2 |
0.0251 |
— |
0.050 |
1.029 |
−0.134 |
2.00 |
| PVCo2 |
— |
0.049 |
0.795 |
0.957 |
0.056 |
2.81 |
3.4 Bonding nature
The atomic bonding of the studied BVCo2 and PVCo2 alloys for both spin channels is presented in Fig. 5. Their bonding nature was analysed for the [110] plane. The yellow and red regions indicate an increase in the electron density, while the blue and green regions imply a lower electron density. In the case of BVCo2, covalent bonding was observed in the V and B atoms in both spin channels, while for PVCo2, ionic bonding was observed in the P and V atoms in the spin up channel and covalent bonding was noticed between the P and V atoms in the spin down channel.
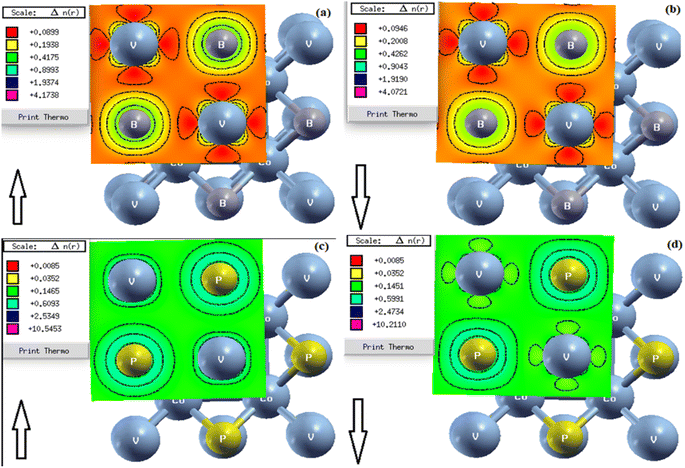 |
| | Fig. 5 Contour plots for (a and b) BVCo2 and (c and d) PVCo2. | |
3.5 Optical attributes
The optical traits of bulk materials can be analysed when they interact with external electromagnetic waves. This interaction results in a few important optical characteristics that make it simple to assess the potential of a material for use in the field of optoelectronics. The optical properties of the BVCo2 and PVCo2 alloys were examined through a set of complex equations known as the Kramers–Kronig equations. These equations are divided into two segments, real and imaginary parts, as follows:| |
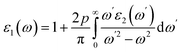 | (8) |
The real part elaborates the ability of a material to disperse or polarize incident light.67 The “P” in the mathematical expression of the real part is Cauchy's principle value. On the contrary, the imaginary part provides detailed information regarding the absorption and scattering power of a material,68 as follows:
| |
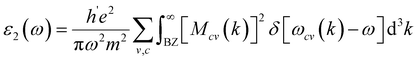 | (9) |
where
MCV is the dipole matrix. The optical characteristics of the BVCo
2 and PVCo
2 alloys were analysed in the energy range of 0 to 12 eV, and their real part is drawn in
Fig. 6(a). In both alloys, a declining trend was observed with an increase in the incident energy. The static value for BVCo
2 was observed to be 47.5, which gradually declined, and then increased to the peak at 1.89 eV in the visible region. After this peak value, a sharp decline was observed, which was followed by a linear trend as the energy increased. In the case of PVCo
2, the static value was noticed as 97.25, which then declined drastically and the peak was observed at 2.24 eV. With an increase in the photon energy, the real part of PVCo
2 showed a linear trend. In the case of both alloys, the maximum polarization was noticed in the visible region.
Fig. 6(b) shows the plot of the imaginary component of the dielectric function for both the PVCo
2 and BVCo
2 alloys. In the case of BVCo
2, the maximum scattering and absorption were observed in the visible region at 2.24 eV, which gradually declined when the energy increased, and another noticeable peak at 9.42 eV was detected in the UV region. The graphical pattern of the imaginary part for PVCo
2 showed the maximum value at 0.095 eV, followed by another peak at 0.55 eV, which declined in the visible region and prominent peaks appeared at 2.87 eV and 9.61 eV. The bending of light when it passes through a material is determined through the refractive index, as represented in
Fig. 6(c) for PVCo
2 and BVCo
2. In the case of BVCo
2, the static refractive index was observed to be 6.90, which showed a sharp decline, and a peak at 1.94 eV was noticed in the visible region. Several smaller peaks appeared as the photon energy increased and a minor peak in the UV region was observed at 9.12 eV. The refractive index for PVCo
2 has a static value of 10.01, which shows a drop. A peak was observed in the visible region at 1.94 eV, and another notable peak was detected in the UV region at 9.51 eV. The extinction coefficient, which is illustrated in
Fig. 6(d), indicates how strongly a material absorbs light or other electromagnetic radiation at a given wavelength. The maximum extinction coefficient peak for BVCo
2 was found to be in the visible region at 2.68 eV. After this peak value, the extinction coefficient displayed a decreasing behavior with an increase in the photon energy and another minor peak was observed at 9.80 eV. In the case of PVCo
2, significant extinction coefficient peaks were observed throughout the electromagnetic spectrum at 0.74 eV, 4.25 eV, 8.53 eV, and 9.80 eV with the maximum peak at 3.31 eV. In the case of BVCo
2, its extinction coefficient reveals the strong absorption of light in the visible spectrum, whereas for PVCo
2, the highest absorption occurs in the UV region.
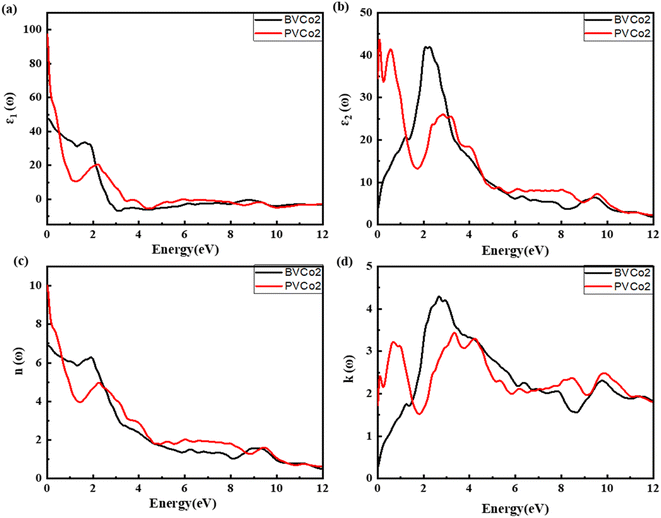 |
| | Fig. 6 (a) Real and (b) imaginary parts, (c) refractive index and (d) extinction coefficient for BVCo2 and PVCo2. | |
The energy loss for PVCo2 and BVCo2 is represented in Fig. 7(a), which corresponds to the amount of energy that is lost when electrons interact with a material. In the case of BVCo2, the important energy loss peaks were seen at 6.13 eV and 11.06 eV and the maximum energy loss peak was noticed at 8.42 eV. In the case of PVCo2, a minor energy loss peak was noticed at 1.40 eV. With an increase in energy, some major peaks appeared and the highest peak was detected at 9.07 eV. The absorption spectra of PVCo2 and BVCo2 are presented in Fig. 7(b), which provide information regarding their ability to absorb incident light when they interact with electromagnetic waves. The minor absorption peak for BVCo2 was noticed at 3.03 eV, while with an increase in energy, another peak at 7.85 eV emerged, and the maximum absorption was noticed in the UV region at 9.83 eV. In the case of PVCo2, peaks were visible at 1.12 eV, 4.34 eV, and 8.55 eV, and the highest absorption was noticed at 9.94 eV. Optical reflectivity is another crucial optical characteristic to assess given that it reveals the amount of light that is reflected or transmitted into a given material. The optical reflectivity of PVCo2 and BVCo2 is displayed in Fig. 7(c). The R(0) for BVCo2 was observed at 0.55, and with an increase in energy, several prominent peaks appeared at 3.38 eV, 4.36 eV, and 8.61 eV, and the maximum reflectivity was observed at 10.57 eV. In the case of PVCo2, the static value of the optical reflectivity was noticed at 0.67, which gradually declined in the visible region, and then increased to the peak at 3.00 eV. More prominent peaks appeared for PVCo2 at 7.95 eV and 10.08 eV with an increase in energy, while the maximum peak was seen at 11.95 eV. It can be concluded from the optical reflectivity plot for both alloys that these materials become highly reflective in the UV region, indicating that more light is reflected, and then transmitted. The optical conductivity for PVCo2 and BVCo2 is reported in Fig. 7(d), which corresponds to the quantity of electrons becoming conductive when they absorb the incident light. The maximum optical conductivity peaks for PVCo2 and BVCo2 were noticed at 3.25 eV and 2.65 eV, respectively, indicating that for PVCo2, the electrons become extremely conductive in the UV spectrum, whereas for BVCo2, they become extremely conductive in the visible region.
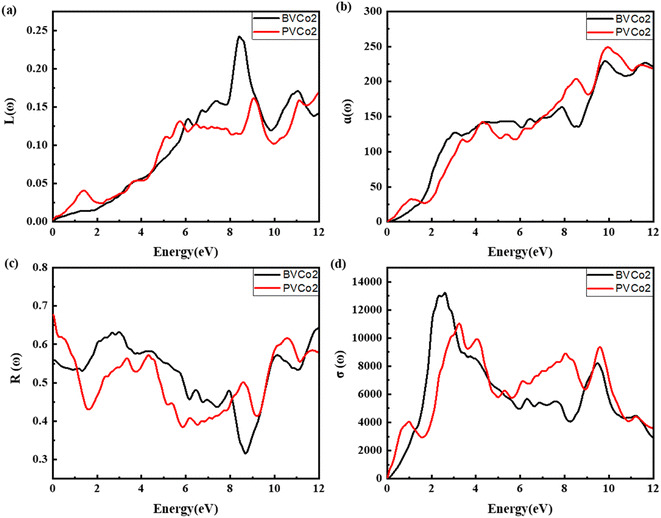 |
| | Fig. 7 (a) Energy loss, (b) absorption coefficient, (c) reflectivity and (d) optical conductivity of BVCo2 and PVCo2. | |
4. Conclusions
The half-metallic behavior of Heusler alloys has attracted significant attention in recent decades given that these materials have demonstrated an excellent output for magnetic shape memory devices. In this study, using the mBJ functional and FP-LAPW approach, the physical characteristics of PVCo2 and BVCo2 were determined. The volume optimization curves, ground-state energies and negative formation energies for both alloys revealed that they are completely stable in non-magnetic and magnetic phases. Also, their computed elastic constants and mechanical properties completely satisfy the mechanical stability criteria. The elastic properties of both alloys indicate that they are ductile and require a higher melting temperature for phase transitioning. The electronic properties revealed half-metallic behavior for both alloys, which is extremely desirable in spintronic applications. Also, high polarization and dispersion in the visible and UV spectrum were observed for BVCo2 and PVCo2. Thus, the optical traits of these materials revealed that they are suitable for application in optoelectronic and spintronic devices.
Data availability
Data will be available upon request.
Conflicts of interest
The authors have no competing conflict of interest.
References
- J. Li, et al., Task incremental learning-driven Digital-Twin predictive modeling for customized metal forming product manufacturing process, Robot. Comput.-Integr. Manuf., 2024, 85, 102647 CrossRef.
- M. Tariq, et al., Magnetoelectric, and dielectric based switching properties of co-doped BiFeO3 for low energy memory technology: A first-principles study, Phys. B, 2023, 650, 414489 CrossRef CAS.
- Y. Xiang, et al., Cross-sectional performance prediction of metal tubes bending with tangential variable boosting based on parameters-weight-adaptive CNN, Expert Syst. Appl., 2024, 237, 121465 CrossRef.
- D. Zhang, et al., Electromagnetic shocking induced fatigue improvement via tailoring the α-grain boundary in metastable β titanium alloy bolts, J. Alloys Compd., 2023, 966, 171536 CrossRef CAS.
- İ. K. Durukan, Y. O. Ciftci and H. Tekin, A new candidate for optoelectronic device applications: CoTiX (X: P, As, Sb) half-heusler compounds, Phys. B, 2024, 678, 415752 CrossRef.
- F. Casper, et al., Half-Heusler compounds: novel materials for energy and spintronic applications, Semicond. Sci. Technol., 2012, 27(6), 063001 CrossRef.
- S. A. Khandy and J.-D. Chai, Novel half-metallic L21 structured full-Heusler compound for promising spintronic applications: A DFT-based computer simulation, J. Magn. Magn. Mater., 2019, 487, 165289 CrossRef CAS.
- T. Aull, et al., Ab initio study of magnetic tunnel junctions based on half-metallic and spin-gapless semiconducting Heusler compounds: Reconfigurable diode and inverse tunnel-magnetoresistance effect, Phys. Rev. Appl., 2022, 18(3), 034024 CrossRef CAS.
- R. A. De Groot, et al., New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024 CrossRef CAS.
- S. E. Kulkova, et al., The electronic structure and magnetic properties of full-and half-Heusler alloys, Mater. Trans., 2006, 47(3), 599–606 CrossRef CAS.
- P. Brown, et al., The magnetization distributions in some Heusler alloys proposed as half-metallic ferromagnets, J. Phys.: Condens. Matter, 2000, 12(8), 1827 CrossRef CAS.
- M. Hariharan, et al., Structural, electronic, magnetic, and thermoelectric properties of full-Heusler alloys A2CoS (A= Cu, Zn) for spintronic application via conceptual DFT study, J. Phys. Chem. Solids, 2024, 187, 111858 CrossRef CAS.
- B. Gurunani, S. Ghosh and D. C. Gupta, Comprehensive investigation of half Heusler alloy: Unveiling structural, electronic, magnetic, mechanical, thermodynamic, and transport properties, Intermetallics, 2024, 170, 108311 CrossRef CAS.
- F. Firdous, et al., Half-metallicity, magnetic and optical attributes of mechanically stable half-Heusler VSnX (X= Pt, Pd) alloys for spintronics: a DFT study, Eur. Phys. J. Plus, 2023, 138(8), 699 CrossRef CAS.
- J. Munir, et al., Electronic, magnetic and optical properties of reduced hybrid layered complex Ni(pyz)V4O10 (pyz= C4H4N2) by first-principles, J. Magn. Magn. Mater., 2016, 416, 241–246 CrossRef CAS.
- F. Heusler, Über magnetische manganlegierungen, Verh. Dtsch. Phys. Ges., 1903, 5(12), 219 CAS.
- A. Zayak, et al., Anomalous vibrational effects in nonmagnetic and magnetic Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(5), 054113 CrossRef.
- R. Sunmonu, et al., DFT–GGA calculations of magnetic, elastic, thermodynamic and thermoelectric properties of Co2YAl (Y= Ti, V) full Heusler alloy systems, Mater. Sci. Eng., B, 2020, 262, 114739 CrossRef CAS.
- T. Graf, S. S. Parkin and C. Felser, Heusler compounds—A material class with exceptional properties, IEEE Trans. Magn., 2010, 47(2), 367–373 Search PubMed.
- S. Paul, et al., Griffiths phase like behaviour in CoCrVZ (Z= Al, Ga) Heusler alloys, J. Magn. Magn. Mater., 2024, 598, 172041 CrossRef CAS.
- S. Idrissi, et al., A DFT study of the equiatomic quaternary Heusler alloys ZnCdXMn (X= Pd, Ni or Pt), Solid State Commun., 2021, 331, 114292 CrossRef CAS.
- S. Chakraborty, et al., Rare coexistence of disorder-induced Griffiths phase and reentrant spin-glass state in a Heusler alloy Rh2FeAl with high Curie temperature, J. Alloys Compd., 2024, 976, 173215 CrossRef CAS.
- S. Paul, Structural, magnetic and transport properties of FeRuVZ (Z = Si, Ge) Heusler alloys: experiment and theory, J. Alloys Compd., 2024, 175020 CrossRef CAS.
- I. A. Elkoua and R. J. Masrour, A comparative study of physical and thermoelectrical characteristics of the new full-Heusler alloys Ag2TiGa and Ag2VGa with ab initio calculations, Int. J. Quantum Chem., 2024, 124(1), e27307 CrossRef CAS.
- I. Ait Elkoua and R. Masrour, Investigation of structural, electronic, magnetic, and mechanical stability of a non-trivial topology phase in compound full-Heusler alloys TiHfFe X (X= Al, Ga, In), Mod. Phys. Lett. B, 2024, 38(23), 2450187 CrossRef CAS.
- A. A. Musari, R. S. Sunmonu and S. O. Babajide, Investigation of electronic, elastic, dynamical, thermodynamic and thermoelectric properties of Cobalt based half-Heusler compounds, Comput. Condens. Matter, 2024, 39, e00890 CrossRef.
- R. Smith, et al., Effects of disorder on the magnetic properties of the Heusler alloy V2FeAl, Acta Mater., 2024, 267, 119733 CrossRef CAS.
- R. Shan, et al., Demonstration of half-metallicity in fermi-level-tuned Heusler alloy Co2FeAl0.5Si0.5 at room temperature, Phys. Rev. Lett., 2009, 102(24), 246601 CrossRef CAS PubMed.
- J. Hu, S. Granville and H. Yu, Spin-Dependent Thermoelectric Transport in Cobalt-Based Heusler Alloys, Ann. Phys., 2020, 532(11), 1900456 CrossRef CAS.
- F. Dahmane, et al., Investigations of the structural, electronic, magnetic, and half-metallic behavior of Co2MnZ (Z= Al, Ge, Si, Ga) Full-Heusler compounds, J. Supercond. Novel Magn., 2016, 29, 809–817 CrossRef CAS.
- J. Munir, et al., Spin-polarized electromagnetic and optical response of full-Heusler Co2VZ (Z= Al, Be) alloys for spintronic application, Eur. Phys. J. Plus, 2021, 136, 1–18 CrossRef.
- D. Rai and R. Thapa, Electronic structure and magnetic properties of X2YZ (X= Co, Y= Mn, Z= Ge, Sn) type Heusler compounds: a first principle study, Phase Transitions, 2012, 85(7), 608–618 CrossRef CAS.
- M. E. Amine Monir, et al., First-principles investigation of half-metallicity and ferrimagnet properties of Co2ScZ (Z= as, Sb, and Bi), J. Supercond. Novel Magn., 2016, 29, 501–508 CrossRef CAS.
- Y. Li, et al., First-principles study on structural, electronic, elastic and thermodynamic properties of the full-Heusler alloys Co2YZ (Y= Sc, Cr and Z= Al, Ga), Eur. Phys. J. Appl. Phys., 2015, 70(3), 31001 CrossRef.
- B. Fadila, et al., Structural, magnetic, electronic and mechanical properties of full-Heusler alloys Co2YAl (Y= Fe, Ti): first principles calculations with different exchange-correlation potentials, J. Magn. Magn. Mater., 2018, 448, 208–220 CrossRef CAS.
- J. Y. Jiu and J. I. Lee, A Prediction of Half-Metallicity in a Co2-Based Full Heusler Compound with the 4d Transition-Metal Element, Co2ZrSi: A First-Principles Study, J. Korean Phys. Soc., 2007, 51(1), 155 CrossRef CAS.
- O. Amrich, et al., Half-metallic ferrimagnetic characteristics of Co2YZ (Z= P, As, Sb, and Bi) new full-Heusler alloys: a DFT study, J. Supercond. Novel Magn., 2018, 31, 241–250 CrossRef CAS.
- O. Amrich, et al., Half-metallic ferrimagnetic characteristics of Co2YZ (Z= P, As, Sb, and Bi) new full-Heusler alloys: a DFT study, J. Supercond. Novel Magn., 2018, 31, 241–250 CrossRef CAS.
- P. Klaer, et al., Tailoring the electronic structure of half-metallic Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(14), 144405 CrossRef.
- A. Kumar, M. Kumar and R. P. Singh, Effect of spin orbit coupling on opto-electronic and magnetic properties of full Heusler alloy, Ru2CrAl for spintronic and optical devices: Theoretical investigations using DFT, Optik, 2022, 249, 168250 CrossRef CAS.
- C. Abbes, et al., Exploring the structural, electronic, optical properties and stability of Na2SrX (Si and Ge) full-Heusler alloys: A first principle investigation, Emergent Mater., 2023, 6(4), 1319–1327 CrossRef CAS.
- K. Bouferrache, et al., Structural stability, opto-electronic, magnetic and thermoelectric properties of half-metallic ferromagnets quaternary Heusler alloys CoFeXAs (X= Mn, Cr and V), Solid State Commun., 2024, 377, 115366 CrossRef CAS.
- A. Tahiri, et al., First-Principles Calculations Study of Structural, Elastic, Electronic and Optical Properties of Co2− xVxFeGe Full-Heusler Alloys, J. Electron. Mater., 2023, 52(10), 6919–6928 CrossRef CAS.
- C. Wu, et al., The structural, half-metal, magnetic, and mechanical properties of full Heusler alloy CrCoVSb: a first-principles study, Chin. J. Phys., 2020, 66, 436–443 CrossRef CAS.
- A. Mishra and A. Singh, A DFT study on structure, electronic, magnetic and mechanical properties of full Heusler alloys Co2TaZ (Z= Si and Sn), Bull. Mater. Sci., 2023, 46(4), 218 CrossRef CAS.
- R. Khare, et al., Coupled quantum mechanical/molecular mechanical modeling of the fracture of defective carbon nanotubes and graphene sheets, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(7), 075412 CrossRef.
- P. G. Mezey, The holographic electron density theorem and quantum similarity measures, Mol. Phys., 1999, 96(2), 169–178 CrossRef CAS.
- J. Munir, et al., A computational insight into the Zintl SZr2N2 and BaAg2S2 phases for optoelectronic thermoelectric applications, Phys. B, 2023, 671, 415403 CrossRef CAS.
- H. Murtaza, et al., First-principles analysis on the optoelectronic, structural, elastic and transport characteristics of novel fluoroperovskites Cs2TlAgF6 for green technology, ECS J. Solid State Sci. Technol., 2024, 13(3), 033006 CrossRef CAS.
- Y. Kurtulus, et al., Electronic structure and magnetic exchange coupling in ferromagnetic full Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(1), 014425 CrossRef.
- Y. El Krimi, R. Masrour and A. Jabar, Structural, electronic and magnetic properties of full-Heusler alloy Co2CrAl, Inorg. Chem. Commun., 2020, 121, 108207 CrossRef CAS.
- H. Murtaza, et al., Exploring the optoelectronic attributes, thermoelectric and photocatalytic potential of double perovskites Cs2BB'H6 (B= Al, Na and B'= Tl, In): A DFT study, Mater. Sci. Eng., B, 2024, 301, 117171 CrossRef CAS.
- L. Shao, et al., Why do cracks occur in the weld joint of Ti-22Al-25Nb alloy during post-weld heat treatment?, Front. Mater., 2023, 10, 1135407 CrossRef.
- Y. Zhao, et al., Applications of unified phase-field methods to designing microstructures and mechanical properties of alloys, MRS Bull., 2024, 1–13 Search PubMed.
- H. Murtaza, et al., Scrutinize the physical attributes of thermodynamically and elastically stable double perovskite oxides Ba2CdXO6 (X= Mo, U) for optoelectronics, photocatalytic and green technology, Comput. Mater. Sci., 2024, 232, 112674 CrossRef CAS.
- H. Murtaza, et al., Effect of bandgap tunability on the physical attributes of potassium-based K2CuBiX6 (X= I, Br, Cl) double perovskites for green technologies, Inorg. Chem. Commun., 2024, 162, 112206 CrossRef CAS.
- H. Murtaza, et al., Unveiling the mechanical, structural, thermoelectric, and optoelectronic potential of K2NaGaBr6 and K2RbTlBr6 double perovskites for sustainable technologies, Sol. Energy, 2024, 273, 112502 CrossRef CAS.
- H. Murtaza, et al., First-principles analysis to assess the solar water splitting and hydrogen storage capabilities of Cs2XGaH6 (X= Al, Na), Int. J. Hydrogen Energy, 2024, 83, 124–132 CrossRef CAS.
- S. M. Qaid, et al., A computational approach to correlate the physical attributes of lead-free Rb2XRhF6 (X= Li, Ag) double perovskite halides for optoelectronics and renewable energy applications, Phys. B, 2023, 671, 415416 CrossRef.
- H. Murtaza, et al., A DFT-based determination of the physical attributes of Cs2InBiF6 fluoroperovskite by using multiple potentials, Opt. Quantum Electron., 2024, 56(9), 1440 CrossRef CAS.
- H. Murtaza, et al., Spin-polarized analysis of the magneto-electronic, mechanical and optical response of double perovskites Cs2XCeI6 (X= Li, Na): A DFT study, Mater. Sci. Semicond. Process., 2024, 181, 108645 CrossRef CAS.
- Q. Ain, et al., First-principles analysis of the physical properties of XAcTe2 (X= Li, Na) Heusler alloys for optoelectronic and thermoelectric devices, Comput. Mater. Sci., 2023, 224, 112156 CrossRef CAS.
- M. Jamil, et al., Investigations of the structural, mechanical and optoelectronic attributes of Rb2TlB′I6 (B′= As, Ga) double perovskites for photovoltaics, J. Inorg. Organomet. Polym. Mater., 2024, 1–11 Search PubMed.
- S. M. Qaid, et al., A Theoretical Insight into the Physical Characteristics of Double Perovskite Rb2TlInBr6 for Renewable Energy Applications, Cryst. Res. Technol., 2024, 59(3), 2300329 CrossRef CAS.
- Q. Ain, et al., The screening of the potential features of potassium-based K2BGaI6 (B= Tl, Rb) double perovskites for eco-friendly technologies: a first-principles study, Opt. Quantum Electron., 2024, 56(7), 1164 CrossRef CAS.
- F. Firdous, et al., Half-metallicity, magnetic and optical attributes of mechanically stable half-Heusler VSnX (X= Pt, Pd) alloys for spintronics: a DFT study, Eur. Phys. J. Plus, 2023, 138(8), 699 CrossRef CAS.
- A. S. Jbara, et al., Density functional theory study of mixed halide influence on structures and optoelectronic attributes of CsPb(I/Br)3, Appl. Opt., 2020, 59(12), 3751–3759 CrossRef CAS PubMed.
- Q. Ain, et al., Structural, optoelectronic and thermal response of new stable MgBe2X2 (X= As, P) Zintl phases: First-principles calculation, Mater. Sci. Eng., B, 2023, 287, 116136 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Shams A. M. Issac,
Hesham M. H. Zakaly
b,
Shams A. M. Issac,
Hesham M. H. Zakaly def and
Junaid Munir
def and
Junaid Munir *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) –
–![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xVxFeGe.43 They are also well-suited for high-tech structural and functional uses because of their exceptional mechanical characteristics. Heusler alloys such as Co2YAl (Y = Fe, Ti),35 CrCoVSb44 and Co2TaZ (Z = Si, Sn)45 exhibit excellent mechanical characteristics. However, their physical properties are not well understood, despite their prospective applications in a variety of technology domains. Furthermore, the investigation of Co-based Heusler alloys, in particular XVCo2 (X = B, P), is still unexplored. Thus, to provide fundamental insights, this study attempts to explore these aspects using first principles analysis. Gaining this understanding is essential for advancements in the creation and use of these innovative materials.
xVxFeGe.43 They are also well-suited for high-tech structural and functional uses because of their exceptional mechanical characteristics. Heusler alloys such as Co2YAl (Y = Fe, Ti),35 CrCoVSb44 and Co2TaZ (Z = Si, Sn)45 exhibit excellent mechanical characteristics. However, their physical properties are not well understood, despite their prospective applications in a variety of technology domains. Furthermore, the investigation of Co-based Heusler alloys, in particular XVCo2 (X = B, P), is still unexplored. Thus, to provide fundamental insights, this study attempts to explore these aspects using first principles analysis. Gaining this understanding is essential for advancements in the creation and use of these innovative materials.
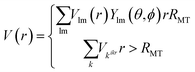
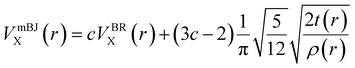
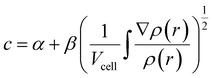
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m225. In this three-dimensional structure of XVCo2 (X = B, P), each V atom is bonded to six equivalent “B” or “P” atoms and eight equivalent “Co” atoms, creating a body-centred cubic geometry. The atomic bond lengths were computed using the VESTA and observed to be 2.36 Å, 2.73 Å, and 2.73 Å for V–Co, V–B, and V–P, respectively. The crystal structures of XVCo2 (X = B, P) are plotted in Fig. 1. To assess the ground-state energies for both Heusler alloys, their crystal structures were optimized. The volume optimization curves were plotted for the non-magnetic and ferromagnetic phases. The volume optimization curves for BVCo2 and PVCo2 revealed that these alloys are more stable in the FM phase. Fig. 1(b) and (d) demonstrate the volume optimization curves for both alloys, respectively. After volume optimization, the optimized parameters for both Heusler alloys were analysed using the Birch–Murnaghan equation, as follows:
m225. In this three-dimensional structure of XVCo2 (X = B, P), each V atom is bonded to six equivalent “B” or “P” atoms and eight equivalent “Co” atoms, creating a body-centred cubic geometry. The atomic bond lengths were computed using the VESTA and observed to be 2.36 Å, 2.73 Å, and 2.73 Å for V–Co, V–B, and V–P, respectively. The crystal structures of XVCo2 (X = B, P) are plotted in Fig. 1. To assess the ground-state energies for both Heusler alloys, their crystal structures were optimized. The volume optimization curves were plotted for the non-magnetic and ferromagnetic phases. The volume optimization curves for BVCo2 and PVCo2 revealed that these alloys are more stable in the FM phase. Fig. 1(b) and (d) demonstrate the volume optimization curves for both alloys, respectively. After volume optimization, the optimized parameters for both Heusler alloys were analysed using the Birch–Murnaghan equation, as follows: