Open Access Article
Open Access ArticleModeling the relative response factor of small molecules in positive electrospray ionization†
Dimitri Abrahamsson *ab,
Lelouda-Athanasia Koronaiou
*ab,
Lelouda-Athanasia Koronaiou cd,
Trevor Johnsona,
Junjie Yangb,
Xiaowen Jia and
Dimitra A. Lambropoulou
cd,
Trevor Johnsona,
Junjie Yangb,
Xiaowen Jia and
Dimitra A. Lambropoulou cd
cd
aDepartment of Pediatrics, New York University Grossman School of Medicine, New York 10016, USA. E-mail: dimitri.abrahamsson@gmail.com
bDepartment of Obstetrics, Gynecology and Reproductive Sciences, School of Medicine, University of California, San Francisco, California 94158, USA
cLaboratory of Environmental Pollution Control, Department of Chemistry, Aristotle University of Thessaloniki, University Campus, 54124 Thessaloniki, Greece
dCenter for Interdisciplinary Research and Innovation (CIRI-AUTH), Balkan Center, Thessaloniki 57001, Greece
First published on 22nd November 2024
Abstract
Technological advancements in liquid chromatography (LC) electrospray ionization (ESI) high-resolution mass spectrometry (HRMS) have made it an increasingly popular analytical technique in non-targeted analysis (NTA) of environmental and biological samples. One critical limitation of current methods in NTA is the lack of available analytical standards for many of the compounds detected in biological and environmental samples. Computational approaches can provide estimates of concentrations by modeling the relative response factor of a compound (RRF) expressed as the peak area of a given peak divided by its concentration. In this paper, we explore the application of molecular dynamics (MD) in the development of a computational workflow for predicting RRF. We obtained measurements of RRF for 48 compounds with LC – quadrupole time-of-flight (QTOF) MS and calculated their RRF. We used the CGenFF force field to generate the topologies and GROMACS to conduct the (MD) simulations. We calculated the Lennard-Jones and Coulomb interactions between the analytes and all other molecules in the ESI droplet, which were then sampled to construct a multilinear regression model for predicting RRF using Monte Carlo simulations. The best performing model showed a coefficient of determination (R2) of 0.82 and a mean absolute error (MAE) of 0.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. This performance is comparable to other predictive models including machine learning models. While there is a need for further evaluation of diverse chemical structures, our approach showed promise in predictions of RRF.
log units. This performance is comparable to other predictive models including machine learning models. While there is a need for further evaluation of diverse chemical structures, our approach showed promise in predictions of RRF.
Introduction
Recent technological breakthroughs in high-resolution mass spectrometry (HRMS) have made it an increasingly popular technology in environmental analysis,1 biomonitoring2,3 and metabolomics.4 Often combined with suspect screening (SS) and non-targeted analysis (NTA) workflows, HRMS has shown great promise in the discovery of lesser-known chemical structures and in comprehensively characterizing the chemical composition of complex mixtures.2,3,5 One critical challenge associated with the application of HRMS in SS or NTA is the limited availability of analytical standards for many anthropogenic/synthetic chemicals and many endogenously produced metabolites.6,7When it comes to endogenous metabolites, the lack of commercially available analytical standards is often due to certain compounds being less well-characterized and thus not yet synthesized or purified. For anthropogenic chemicals, one of the reasons is that chemical manufacturers in the U.S. are not required to produce analytical standards for the chemicals that they manufacture and release to the environment.7 One exception to this rule is pesticides.7 It is important to note at this stage that the requirement for analytical standards does not extend to the transformation and breakdown products of these chemicals. So even in a hypothetical scenario where manufacturers would be required to produce analytical standards, that would cover only the parent compounds and not all the transformation products. The U.S. Environmental Protection Agency (EPA) has prioritized about 1.2 million chemicals of environmental importance and has created a database called EPA's CompTox Chemicals Dashboard (henceforth referred to as “the dashboard”).8 Nuñez et al.6 estimated that out of the 1.2 million chemicals on EPA's Dashboard, less than 2% are available as analytical standards.
There is thus a need to develop computational approaches to confirm and quantify detected compounds without analytical standards.6,9,10 While detection and tentative confirmation can be achieved with MS/MS libraries, quantification remains a more challenging task.11,12 Liquid Chromatography (LC) – Electrospray Ionization (ESI) HRMS is one of the most commonly used HRMS techniques in SS and NTA studies. One critical challenge in ESI is that abundances expressed as peak areas or peak heights are not easily translatable to concentrations. Two compounds of the same concentration can exhibit peak areas that differ by 3 orders of magnitude because of differences in ionization.12,13 Abundances may be used as a surrogate for concentrations in certain situations when comparing the same chemical across different samples, however, they cannot be used to compare two chemicals to each other.14 We should note at this point that while we focus on HRMS in our paper, low-resolution MS such as triple-quadrupole instruments can also be used to study the ionization efficiency of chemicals. We focus primarily on HRMS and NTA because that is when one often meets with the lack of available analytical standards and when predictive models can help circumvent that problem.
While ESI is extensively used in mass spectrometry for the analysis of both small (e.g., metabolites) and large molecules (e.g., proteins), the precise mechanism has not been fully understood. Briefly, during ESI, the solution containing the analyte passes through a metal capillary that is charged at an electric potential of thousands of volts (kV). The solution forms a tip at the end of the capillary known as a Taylor cone that emits a spray of fine droplets. The droplets start in the μm range and shrink in size as they undergo evaporation often accelerated with heating of the capillary. The density of the charged ions in the droplet is controlled by repulsive coulombic forces between positively charged ions. The upper limit of that density is described as the Rayleigh stability limit:15,16
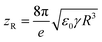 | (1) |
Conceptual models have been proposed to describe the process that molecules undergo to become ionized and transferred to the gas phase during ESI. We focus our discussion on the commonly used positive ESI under which positive ions are formed. Small molecules (<1000 Da) are thought to ionize and be transferred to the gas phase by the ion evaporation model (IEM).15 According to IEM, the analyte is protonated already while inside the droplet and eventually moves from the center towards the surface of the droplet. As the positively charged analyte meets the positively charged solvent molecules on the surface of the droplet, the ion is transferred to the gas phase through repulsive forces of positively charged ions and by the excess droplet charge.
Larger molecules such as globular proteins (natively folded proteins) are thought to ionize and be transferred to the gas phase by the Charged Residue Model (CRM).15,17 According to CRM, solvent droplets containing a single protein molecule gradually evaporate to dryness and as the solvent molecules evaporate, the charge is transferred to the analyte. The droplets remain close to the Rayleigh stability limit while evaporating, which indicates that the droplet loses some of the electric charge as it shrinks in size. This is supported by experimental observations where the size of solvent droplets positively correlated with the droplet charge following an exponential curve. Contrary to small molecules, the ejection of globular proteins is not kinetically favorable. The repulsive forces of the excess surface charge are not sufficiently strong for the molecule to be ejected and transferred to the gas phase. CRM is supported by experimental evidence where ionization of globular proteins produces ions with a charge of [M + zRH]zR+, where zR is the charge at the Rayleigh limit of water droplets of the same size as the globular protein.15
While these two models are considered distinct, both of these two processes could apply to small or medium-sized molecules, especially in the case of heated ESI where the evaporation of the water droplets is assisted through heating of the capillary. This is also supported by molecular dynamics (MD) simulations studies where native (unmodified) carbohydrates ionize through CRM, while their permethylated derivatives ionize through IEM.18
Ionization efficiency is a property that has proven to be difficult to predict from a small number of chemical descriptors or physicochemical properties. Numerous investigations have examined the correlation between ionization efficiencies and diverse physicochemical properties, including but not limited to their pKa, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, surface area, charge delocalization, and gas-phase proton affinity.19–24 These findings have led to the development of various predictive models for ionization efficiencies,22,25–28 utilizing both the physicochemical properties of analytes and solvent characteristics as fundamental inputs. These models commonly rely on parameters associated with the analyte's hydrophobicity (e.g., log
P, surface area, charge delocalization, and gas-phase proton affinity.19–24 These findings have led to the development of various predictive models for ionization efficiencies,22,25–28 utilizing both the physicochemical properties of analytes and solvent characteristics as fundamental inputs. These models commonly rely on parameters associated with the analyte's hydrophobicity (e.g., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, WAPS, WANS, C/H ratio) and ionizability (such as pKa and the degree of ionization).29 Data-driven approaches involving machine learning, such as random forest models, have shown great promise in providing predictions with reasonable uncertainties.11,12,30–32 It should be noted, however, that these approaches require large datasets in the order of hundreds of chemicals with diverse structures and properties, and the predictions are tied to a specific method and instrumentation.
P, WAPS, WANS, C/H ratio) and ionizability (such as pKa and the degree of ionization).29 Data-driven approaches involving machine learning, such as random forest models, have shown great promise in providing predictions with reasonable uncertainties.11,12,30–32 It should be noted, however, that these approaches require large datasets in the order of hundreds of chemicals with diverse structures and properties, and the predictions are tied to a specific method and instrumentation.
Theory-driven approaches that are based on quantum chemistry and computational chemistry principles could provide an alternative when large datasets are not available or are difficult to obtain. Molecular dynamic simulations (MD) have been previously applied in a number of studies to understand the mechanism of ionization in salt ions, peptides, and proteins33–37 and to a lesser extent in small molecules18,38 However, to the best of our knowledge, there appears to be little on the predictions of their ionization efficiency using MD simulations. Our study aims to fill this gap by employing molecular dynamics to model the behavior of chemicals in the ionization chamber and evaluate the potential of such theory-driven approaches to make predictions and assess their uncertainties.
Materials and methods
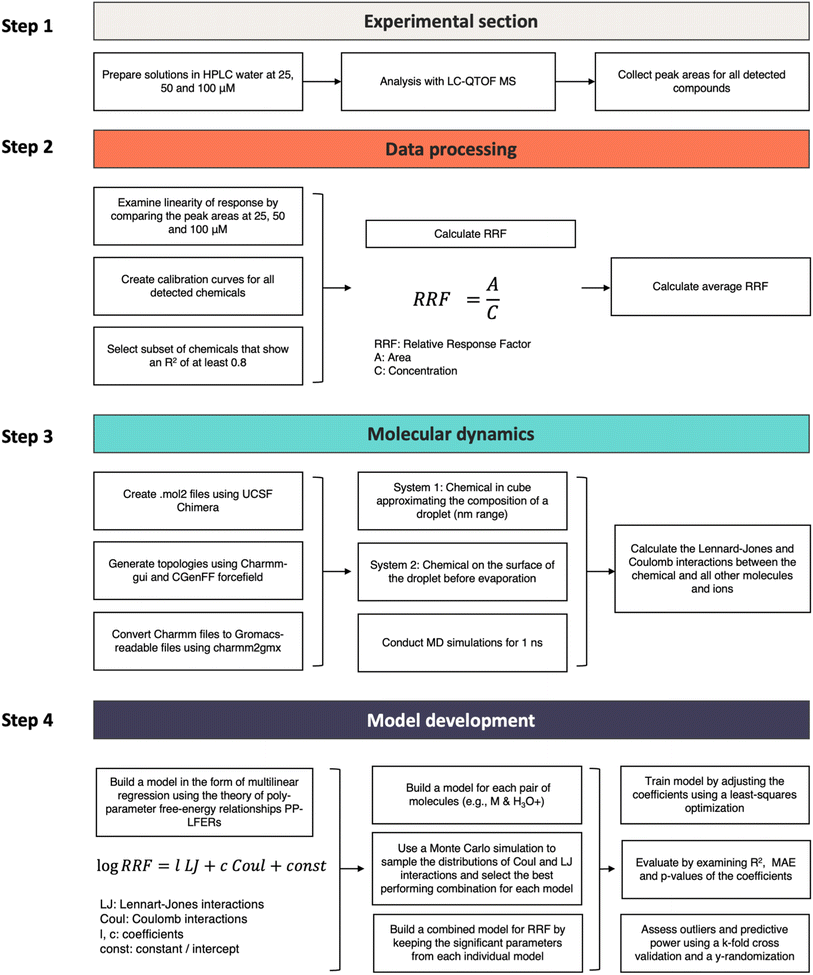
Workflow diagram
The individual steps of the experimental and computational aspects of the study are presented in Fig. 2.Experimental section
The instrument was operated in both positive electrospray ionization mode (ESI+) and full scan mass spectra (MS1) were acquired in the range of 100–1000 Da with a resolving power of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and a mass accuracy of <5 ppm. The instrument was calibrated before the analysis and the mass difference was corrected with reference standards using masses 121.050873 and 922.009798 for positive ionization mode.
000 and a mass accuracy of <5 ppm. The instrument was calibrated before the analysis and the mass difference was corrected with reference standards using masses 121.050873 and 922.009798 for positive ionization mode.
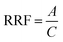 | (2) |
Molecular dynamics simulations
| H2O(l) ⇌ H(aq)+ + OH(aq)− | (3) |
| H2O(l) + H(aq)+ ⇌ H3O(aq)+ | (4) |
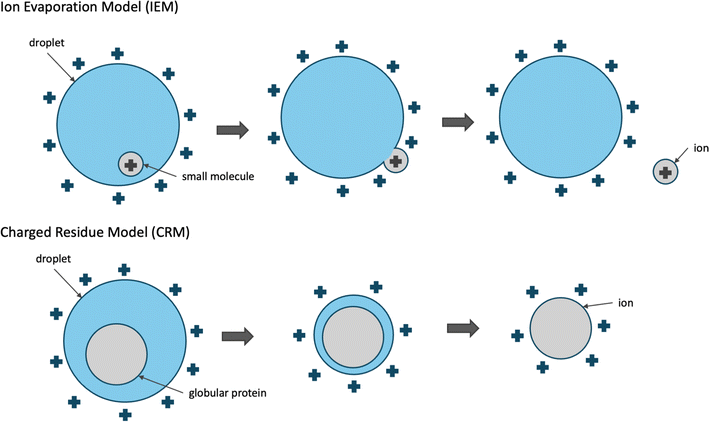 | ||
| Fig. 1 Conceptual models describing the mechanism of electrospray ionization. Small molecules are thought to be ionized through the ion evaporation model (IEM),15 while larger molecules, such as globular proteins are thought to ionize through the charged residue model (CRM).15 | ||
The numbers of water (TIP3P) and methanol molecules were determined based on the gradient mixing (Fig. S1†) of the two solvents during LC and based on the retention time of each chemical (ESI spreadsheet†). This means that for every chemical the number of water and methanol molecules was different depending on when it was eluted from the LC column. Previous MD studies46 on ESI droplets have also suggested that the amount of methanol in the droplet plays a critical role in the ionization efficiency of the analytes. As the volume of methanol increases, the evaporative rate increases, as does the ionization efficiency, for many molecules.46
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps as the maximum number of minimization steps to perform and <1000 kJ mol−1 nm−1 as the threshold at which the minimization process can stop. The minimization and subsequent simulation steps were run using Verlet as the cut-off scheme for neighbor searching and Fast Smooth Particle-Mesh Ewald electrostatics (FSPME or PME in GROMACS) for modeling the electrostatic interactions. The short-range electrostatic cut-off points for Coulomb and van der Waals interactions were set to 1.2 nm which is recommended for CGenFF.49 The temperature was set at 300 K and it was controlled with a Berendsen thermostat in NVT and a Parrinelo–Rahman barostat in NPT. System equilibration was conducted in two stages, the NVT stage where volume and temperature were kept constant, and the NPT stage where pressure and temperature were kept constant. The simulation step was set at 0.5 fs using a leapfrog integrator and the simulation length was 200 ps. The production step following equilibration was conducted using the same simulation step and integrator as previously but in this case, the simulation length was 1000 ps (1 ns). All the mdp files for the minimization, equilibration, and production steps with all the details are available on GitHub (https://github.com/dimitriabrahamsson/electro-spray).
000 steps as the maximum number of minimization steps to perform and <1000 kJ mol−1 nm−1 as the threshold at which the minimization process can stop. The minimization and subsequent simulation steps were run using Verlet as the cut-off scheme for neighbor searching and Fast Smooth Particle-Mesh Ewald electrostatics (FSPME or PME in GROMACS) for modeling the electrostatic interactions. The short-range electrostatic cut-off points for Coulomb and van der Waals interactions were set to 1.2 nm which is recommended for CGenFF.49 The temperature was set at 300 K and it was controlled with a Berendsen thermostat in NVT and a Parrinelo–Rahman barostat in NPT. System equilibration was conducted in two stages, the NVT stage where volume and temperature were kept constant, and the NPT stage where pressure and temperature were kept constant. The simulation step was set at 0.5 fs using a leapfrog integrator and the simulation length was 200 ps. The production step following equilibration was conducted using the same simulation step and integrator as previously but in this case, the simulation length was 1000 ps (1 ns). All the mdp files for the minimization, equilibration, and production steps with all the details are available on GitHub (https://github.com/dimitriabrahamsson/electro-spray).Our model is based on the idea that the RRF of a given compound in ESI+ can be described as a function of the Coulomb and Lennard-Jones interactions between the compound and all other molecules in the solution. RRF was expressed as a function of the Coulomb and Lennard-Jones using a multilinear regression model.
The model was as follows:
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF = lLJ + cCoul + const RRF = lLJ + cCoul + const
| (5) |
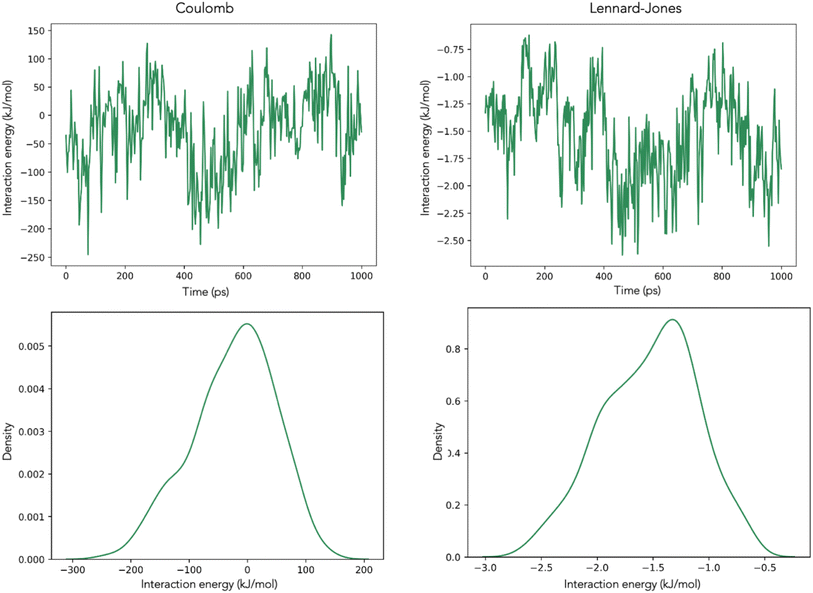
One critical challenge when incorporating these interactions into a model is finding which metrics are meaningful for the purposes of the model. We applied a Monte Carlo simulation approach to randomly sample the Coulomb and Lennard-Jones distributions (3 percentile points per distribution plus the standard deviation) 100 times for each set of molecules (i.e., System 1: (i) analyte and water, (ii) analyte and methanol, and (iii) analyte and H3O+ ions; System 2: analyte and H+ ions) and selected the best-performing model for each set.
Expanding the lLJ and cCoul terms of the equation we get:
| lLJ =l1LJp1 + l2LJp2 + l3LJp3 + l4LJstd | (6) |
| cCoul = c1Coulp1 + c2Coulp2 + c3Coulp3 + c4Coulstd | (7) |
The coefficients and the intercept of the model were determined through a least-squares minimization using the statsmodels package (version 0.14.0) in Python (version 3.10.11). The script is available on GitHub (https://github.com/dimitriabrahamsson/electro-spray). The model was evaluated by examining the R2, the mean absolute error (MAE), and the p-values of the coefficients. After selecting the best-performing model for each set of molecules from both systems, we built a composite model with the parameters whose p-values were lower than 0.1. We purposely chose a higher cutoff point at this stage in order to be more inclusive, however, in the final model, only the p-values below 0.05 were considered significant. The final model was evaluated based on its R2, the mean absolute error (MAE), and the p-values of the coefficients. We also tested whether the addition of other physicochemical properties, i.e. vapor pressure (PV), water solubility (SW), the equilibrium partitioning ratio between octanol and water (KOW), air and water (KAW), methanol and water (KMW), methanol and air (KMA), and the innate charge of the molecule improved the predictive accuracy of the model. PV and SW were calculated with OPERA 2.6 (ref. 50) available on the dashboard.8 KOW, KAW, KMW, and KMA were calculated with UFZ-LSER.51 The innate charge of the molecule was determined by examining the structure and its protonation state at pH 5 and noting 0 if it was neutral, +1 (or more) if it had a positive innate charge, and −1 (or less) if it had a negative innate charge. The properties were tested iteratively by adding each property to the model and recording its performance. Only one property was tested at a time and only the properties whose coefficient showed a p-value of less than 0.05 were considered significant and were included in the model. A parameter with a mere increase in R2 without a significant p-value would not be included in the model.
The predictive power of the model was further evaluated with a 10-fold cross-validation and a y-randomization. During the 10-fold cross-validation, the dataset was first divided into 10 equally sized sub-datasets. Then, during each fold one dataset was set as the testing set and the remaining sub-datasets were compiled into a training set. The model was trained on the training set and tested on the testing set. The process was repeated 10 times (10-fold). It is important to note at this point that when applying a k-fold cross-validation and when dividing the dataset into training and testing there is always a possibility of encountering compounds in the testing set that are outside the applicability domain of the trained model. In order to account for this discrepancy, if a prediction was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units higher than the highest value in the dataset or 2
log units higher than the highest value in the dataset or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units lower than the lowest value in the dataset it was considered outside the applicability domain and it was excluded from the evaluation. The compounds that were excluded from any particular fold of the cross-validation exercise were still included in the discussion section of the paper. The purpose of the k-fold cross-validation is to evaluate the predictive power of the model outside its training set and to identify outlier compounds in the dataset. These compounds are considered outliers in the sense that they represent physicochemical properties that are dissimilar to the ones in the training set and in order for the model to make accurate predictions, they have to be included in the training set.
log units lower than the lowest value in the dataset it was considered outside the applicability domain and it was excluded from the evaluation. The compounds that were excluded from any particular fold of the cross-validation exercise were still included in the discussion section of the paper. The purpose of the k-fold cross-validation is to evaluate the predictive power of the model outside its training set and to identify outlier compounds in the dataset. These compounds are considered outliers in the sense that they represent physicochemical properties that are dissimilar to the ones in the training set and in order for the model to make accurate predictions, they have to be included in the training set.
For the y-randomization, the y variable, in this case the RRF was randomly shuffled, and the model was developed as previously by dividing the dataset into training and testing sets. The process was repeated 5 times, and the predictions were averaged across the 5 iterations. The purpose of the y-randomization is to evaluate the extent to which the model predictions are different from random predictions. This helps to determine whether the model is making meaningful predictions and whether it has been overparametrized. The lower the R2 of the y-randomization and the more different it is from the R2 of the cross-validation, the higher the likelihood that the model is making meaningful predictions that are distinct from random predictions.
One of the challenges we encountered is that the generated CGenFF topologies often included high penalties (>50) for a charge, a bond, an angle, a dihedral, or an improper group. While high penalties do not necessarily mean large errors, they do denote a low similarity with the build-by-analogy structure in CGenFF and it is recommended to apply caution when using such structures because they may require further validation. This may be an important issue in the case of protein dynamics and ligand binding, however, in our case, it is unclear how these penalties or uncertainties may influence our calculations. To address this issue, we tested the robustness of the model by incrementally removing compounds with high penalties starting from the ones with the highest penalties to the ones with the lowest penalties. This resulted in 10 different models with a different cutoff point as the maximum acceptable penalty ranging from 500 to 50. We then examined the changes in the R2 of the model as the number and type of chemicals in the dataset changed. In order to avoid introducing errors in the first steps of the model development, we developed the first iteration of the model with chemicals that had a penalty of less than 300.
Results and discussion
Experimental measurements
The observed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF values for the chemicals in our dataset ranged from 1.73 to 3.17 with Cinchophen showing the lowest value and Thiabendazole showing the highest value (ESI spreadsheet†). As RRF is the ratio of abundance to concentration, higher RRF values indicate higher ionization efficiency (higher abundance at lower concentrations). This observation is in agreement with data from our previous study12 where Cinchophen showed a lower RRF compared to Thiabendazole. It should be noted that the two studies use the same mixtures (in part) but different methods and different instruments (same type – Agilent LC-QTOF-MS – but different instrument). Despite the differences in methods and instrumentation, the differences in the RRF values of the two chemicals are preserved. This observation is supportive of the ionization efficiency (IE) scale approach developed by Oss et al.25 where a set of RRF values can be represented as a scale of relative ionization efficiencies and that scale should in principle be transferable across different methods.
RRF values for the chemicals in our dataset ranged from 1.73 to 3.17 with Cinchophen showing the lowest value and Thiabendazole showing the highest value (ESI spreadsheet†). As RRF is the ratio of abundance to concentration, higher RRF values indicate higher ionization efficiency (higher abundance at lower concentrations). This observation is in agreement with data from our previous study12 where Cinchophen showed a lower RRF compared to Thiabendazole. It should be noted that the two studies use the same mixtures (in part) but different methods and different instruments (same type – Agilent LC-QTOF-MS – but different instrument). Despite the differences in methods and instrumentation, the differences in the RRF values of the two chemicals are preserved. This observation is supportive of the ionization efficiency (IE) scale approach developed by Oss et al.25 where a set of RRF values can be represented as a scale of relative ionization efficiencies and that scale should in principle be transferable across different methods.
Model development
From the models developed for System 1, the best-performing models for predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF showed an R2 of 0.42 when using the analyte–water interactions, 0.37 when using the analyte–methanol interactions, and 0.39 when using the analyte-H3O+ interactions (ESI spreadsheet†). From the models developed for System 2, the best-performing model for predicting log
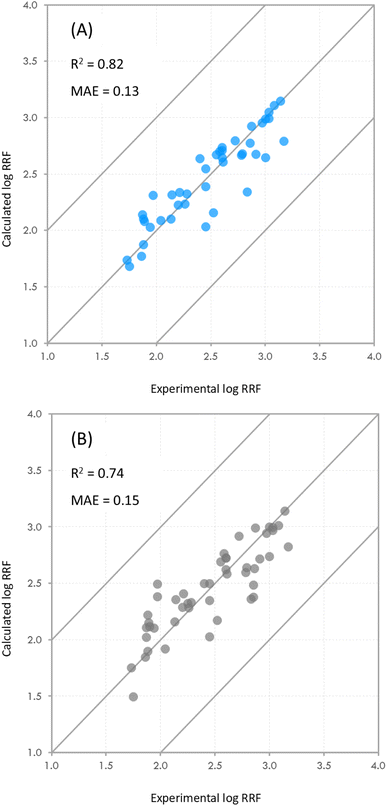
RRF showed an R2 of 0.42 when using the analyte–water interactions, 0.37 when using the analyte–methanol interactions, and 0.39 when using the analyte-H3O+ interactions (ESI spreadsheet†). From the models developed for System 2, the best-performing model for predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF showed an R2 of 0.71 (ESI spreadsheet†). This observation indicates that the final stage of ionization [M + H]+ is better described by the interactions of the analyte with the H+ ions on the surface of the droplet (Fig. 1 – step 2 of IEM) than by the interactions of the analyte with the other molecules while in the center of the droplet (Fig. 1 – step 1 of IEM). This is not to say that there is no predictive value in the interactions of the analyte with the solvent molecules. Previous studies have demonstrated the impacts of different solvents on the ionization efficiency of small molecules52,53 and this is in agreement with our calculations from System 1. This observation just indicates that the interactions of the analyte on the droplet are potentially more determining the ionization efficiency of the analyte. The final composite model consisted of the following parameters. System 1: p2, p3 and the standard deviation for Lennard-Jones interactions between the analyte and water; System 2: p1, p2, p3 and the standard deviations for Lennard-Jones and Coulomb interactions between the analyte and H+ ions. For system 1, p1 was not included because its p-value (p = 0.117) was higher than the 0.05 cutoff point. The derived coefficients for the abovementioned parameters showed p-values below 0.05 (Table S1†). Out of all the physicochemical properties that we tested, the only one that showed a statistically significant contribution was the water solubility of the analyte (SW). The final model showed an R2 of 0.82 and an MAE of 0.13.
RRF showed an R2 of 0.71 (ESI spreadsheet†). This observation indicates that the final stage of ionization [M + H]+ is better described by the interactions of the analyte with the H+ ions on the surface of the droplet (Fig. 1 – step 2 of IEM) than by the interactions of the analyte with the other molecules while in the center of the droplet (Fig. 1 – step 1 of IEM). This is not to say that there is no predictive value in the interactions of the analyte with the solvent molecules. Previous studies have demonstrated the impacts of different solvents on the ionization efficiency of small molecules52,53 and this is in agreement with our calculations from System 1. This observation just indicates that the interactions of the analyte on the droplet are potentially more determining the ionization efficiency of the analyte. The final composite model consisted of the following parameters. System 1: p2, p3 and the standard deviation for Lennard-Jones interactions between the analyte and water; System 2: p1, p2, p3 and the standard deviations for Lennard-Jones and Coulomb interactions between the analyte and H+ ions. For system 1, p1 was not included because its p-value (p = 0.117) was higher than the 0.05 cutoff point. The derived coefficients for the abovementioned parameters showed p-values below 0.05 (Table S1†). Out of all the physicochemical properties that we tested, the only one that showed a statistically significant contribution was the water solubility of the analyte (SW). The final model showed an R2 of 0.82 and an MAE of 0.13.
The coefficients and intercept of the developed model were determined to be as follows:
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF = lLJ + cCoul − 0.14SW + 2.51 RRF = lLJ + cCoul − 0.14SW + 2.51
| (8) |
| lLJ = 0.63LJHp1 − 5.80LJHp2 + 4.92LJHp3 + 3.49LJHstd + 0.21LJWp2 − 0.20LJWp3 + 0.35LJWstd | (9) |
| cCoul = −0.01CoulHp1 + 0.03CoulHp2 − 0.03CoulHp3 − 0.04CoulHstd | (10) |
The p-values of the coefficients and the intercept were all below 0.05 (Table S1†). The standard errors for the derived coefficients are presented in Tables S1 and S2.† The R2 and MAE of the model were comparable to those in the study of Oss et al.25 where they observed an R2 of 0.67 and a standard residual error of 0.86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. While the two studies are very different in the computational approaches, they both share datasets of similar size (48 vs. 62) and they both use multilinear regression models as their final predictive models thus allowing for meaningful comparisons.
log units. While the two studies are very different in the computational approaches, they both share datasets of similar size (48 vs. 62) and they both use multilinear regression models as their final predictive models thus allowing for meaningful comparisons.
We examined whether the differences between the experimental and modeled RRF (absolute errors) could be explained due to the different retention times (RT) of the chemicals and by extension due to the different ratios of water to methanol, but we did not observe a significant association between the two. Neither did we observe a significant association between RRF and RT (Fig. S6†).
Our modeling calculations showed that the interactions of the analyte with the water molecules in System 1 were similar but slightly more predictive than the interactions of the analyte with the H3O+ ions (R2: 0.42 vs. 0.39). Given the great collinearity of these two variables, including both of them in the model renders the coefficients for H3O+ insignificant (p > 0.05). This observation suggests that, at least in terms of interactions with the analyte, the H atoms in the H2O molecules are not distinguishable from the H atoms in the H3O+ ions.
As mentioned earlier in the methods, we examined the effect that compounds with high penalties may have on the predictive power of the model. Including all compounds with penalties over 300 resulted in a small decrease in R2 (0.82 vs. 0.74) and a small increase in the MAE (0.13 vs. 0.15) of the model (Fig. 4). After incrementally removing compounds with high penalties from the dataset, we observed that the R2 of the model appeared to be consistent with an increase around cutoff points of 250 and 300 (Fig. S7†), which confirmed our initial cut-off point of 300. We should note at this point that while in this particular case, the effect of including compounds with high penalties appears to be minimal, we do not know how that may manifest in other datasets with different compositions and with compounds with higher penalties.
The 10-fold cross-validation showed an R2 of 0.52 and an MAE of 0.25 for compounds that were not included in the training set (Fig. S8A†). This shows that the model can make reasonable predictions for chemicals that were not included in the training set. Two chemicals were shown to be outside of the applicability domain of the model (based on the definition in the Methods section). These two chemicals were Furalaxyl and Dicrotophos (Fig. S9†). During the cross-validation, Furalaxyl showed an absolute error of 10.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units, and Dicrotophos had an absolute error of 5.58
log units, and Dicrotophos had an absolute error of 5.58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. Both chemicals had penalties lower than 300 so it does not seem that their penalties would be a likely explanation (ESI spreadsheet†). Most likely, these two chemicals are structurally and physicochemically distinct from the other chemicals in the dataset. This is supported by the observation that when these two compounds are included in the dataset their absolute errors are 0.001
log units. Both chemicals had penalties lower than 300 so it does not seem that their penalties would be a likely explanation (ESI spreadsheet†). Most likely, these two chemicals are structurally and physicochemically distinct from the other chemicals in the dataset. This is supported by the observation that when these two compounds are included in the dataset their absolute errors are 0.001![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units for Furalaxyl and 0.03
log units for Furalaxyl and 0.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units for Dicrotophos (Fig. S10†).
log units for Dicrotophos (Fig. S10†).
The y-randomization showed that when the model is trained on random data the expected R2 is 0.03 (Fig. S8B†). This is substantially lower than both the R2 of the model with all the chemicals (0.74) and the R2 of the 10-fold cross-validation (0.52). This observation suggests that the model is making meaningful predictions that are distinct from random predictions.
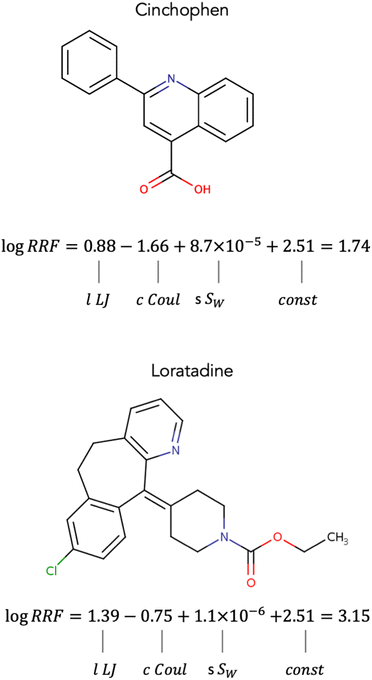
In trying to understand the contributions of the different interactions to RRF we examined the different terms of eqn (8) for two chemicals that showed near 0 differences between experimental and calculated values of RRF. The two chemicals were (1) Cinchophen with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF of 1.73 (calculated log
RRF of 1.73 (calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF = 1.74), and (2) Loratadine with a log
RRF = 1.74), and (2) Loratadine with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF of 3.14 (calculated log
RRF of 3.14 (calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF = 3.15). Both chemicals' log
RRF = 3.15). Both chemicals' log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RRF is determined to a larger extent by the Lennard-Jones and Coulomb interactions and to a smaller extent by their water solubility. For both chemicals, the Lennard-Jones interactions appear to have a positive contribution to RRF while the Coulomb interactions appear to have a negative contribution (Fig. 5). This is consistent for all chemicals in the dataset. When comparing Cinchophen and Loratadine, it appears that the lower RRF of Cinchophen is due to smaller lLJ and cCoul terms (Fig. 5). The Lennard-Jones potential approximates the van der Waals interactions and the Coulomb potential represents the ability to engage in hydrogen bonding. Previous studies have suggested that increased non-polar character, which would be represented by the Lennard-Jones potential is associated with higher RRF, while increased polar character which would be represented by the Coulomb potential is associated with a decrease in RRF.25,26,30,54,55 Our observations appear to be in agreement with the findings from previous studies.
RRF is determined to a larger extent by the Lennard-Jones and Coulomb interactions and to a smaller extent by their water solubility. For both chemicals, the Lennard-Jones interactions appear to have a positive contribution to RRF while the Coulomb interactions appear to have a negative contribution (Fig. 5). This is consistent for all chemicals in the dataset. When comparing Cinchophen and Loratadine, it appears that the lower RRF of Cinchophen is due to smaller lLJ and cCoul terms (Fig. 5). The Lennard-Jones potential approximates the van der Waals interactions and the Coulomb potential represents the ability to engage in hydrogen bonding. Previous studies have suggested that increased non-polar character, which would be represented by the Lennard-Jones potential is associated with higher RRF, while increased polar character which would be represented by the Coulomb potential is associated with a decrease in RRF.25,26,30,54,55 Our observations appear to be in agreement with the findings from previous studies.
Water solubility appears to play a small (Fig. 5) yet significant role (Tables S1 and S2†) in the model. For all compounds in the dataset, the sSW term has a positive contribution to RRF. Based on this observation, one would expect that compounds with higher water solubility would have a higher RRF. However, given that the term sSW is several orders of magnitude smaller than the lLJ and cCoul terms, the influence of sSW on RRF is minimal in comparison. In our developed model, sSW acts as a corrective factor rather than a determining factor. Furthermore, water solubility is known to decrease with increasing molecular weight,56 which is also what we observed in our dataset. The contribution of the sSW for Cinchophen is slightly larger than that of Loratadine which is in agreement with their molecular weights (Cinchophen: 249.26 g mol−1, Loratadine: 382.89 g mol−1).
Limitations and future considerations
One limitation that needs to be acknowledged is that while our model showed good accuracy (R2: 0.82) the computational cost of our approach is much higher than other approaches that rely on simpler descriptor generators like PaDEL57 or Mordred.58 Running one simulation on one system for one chemical takes approximately 13 min using an ASUS GeForce GTX 1080 TI 11 GB Turbo GPU. Conducting simulations for 48 chemicals, 2 systems, and 3 replicates each comes up to 62.4 h. This may limit the ability of the model to be used as an online application as it would require access to GPUs. The workflow is, however, applicable in PCs with NVIDIA GPUs.Another limitation that should be acknowledged is that, in this study, we examined only one type of force field (CGenFF). Future applications could examine whether using other types of force fields like gaff2 from AMBER and GROMOS from GROMACS can produce better predictions than CGenFF.
Finally, on the experimental side, it should be acknowledged that for the purposes of this study, we tested only two solvents for our LC gradient, HPLC water and methanol. As the ionization efficiency of chemicals is known to vary by different solvents,53 the effect of that variability on the modeling calculations is something that needs to be investigated further.
Conclusion
Our study presents a novel approach for modeling the ionization efficiency of organic molecules. Our approach can be used in combination with existing approaches for concentration estimates of chemical compounds in environmental and biological samples. While there is a variety of modeling approaches for RRF, our view is that these approaches are complementary rather than competing. When trying to estimate concentrations of chemicals in environmental or biological samples, combining the results of multiple different approaches can help establish multiple layers of evidence that can be used in support of a prediction when analytical standards are unavailable.Data availability
All code, ESI spreadsheets,† underlying datasets, and chemical structures used in this study are publicly available and can be accessed on GitHub under the following repository: https://github.com/dimitriabrahamsson/electro-spray. All Python scripts are accompanied by instructions on how to run them in order to replicate the findings of the study.Author contributions
D. A. co-wrote the manuscript, designed the study, conducted the lab experiments, ran part of the simulations, and worked on the modeling section. L.-A. K. co-wrote the manuscript, ran simulations, and assisted with the modeling section. T. J. assisted with writing the manuscript and proofreading. J. Y. helped with proofreading, providing expertise on the analytical side, and assisting with revisions. X. J. helped with proofreading, providing expertise on the analytical side, and assisting with revisions. D. L. co-wrote the manuscript, supervised the experimental part of the study, provided advice and expertise on designing and executing the experiments, and interpreting the findings.Conflicts of interest
The authors declare that they have no competing interests to report.Acknowledgements
This study was funded by NIH/NIEHS (Grant No. R00ES032892, K99ES032892, P30ES030284). We would like to thank Elin Ulrich from the U.S. EPA for assisting with providing the chemical mixtures that were used in this study. We would also like to thank June-Soo Park of the California EPA for providing lab space and equipment to support our experiments.References
- S. R. Newton, R. L. McMahen, J. R. Sobus, K. Mansouri, A. J. Williams, A. D. McEachran and M. J. Strynar, Suspect Screening and Non-Targeted Analysis of Drinking Water Using Point-of-Use Filters, Environ. Pollut., 2018, 234, 297–306, DOI:10.1016/j.envpol.2017.11.033.
- A. Wang, D. P. Abrahamsson, T. Jiang, M. Wang, R. Morello-Frosch, J.-S. Park, M. Sirota and T. J. Woodruff, Suspect Screening, Prioritization, and Confirmation of Environmental Chemicals in Maternal-Newborn Pairs from San Francisco, Environ. Sci. Technol., 2021, 55(8), 5037–5049, DOI:10.1021/acs.est.0c05984.
- D. Panagopoulos Abrahamsson, A. Wang, T. Jiang, M. Wang, A. Siddharth, R. Morello-Frosch, J.-S. Park, M. Sirota and T. J. Woodruff, A Comprehensive Non-Targeted Analysis Study of the Prenatal Exposome, Environ. Sci. Technol., 2021, 55(15), 10542–10557, DOI:10.1021/acs.est.1c01010.
- Y. Zhu, D. K. Barupal, A. L. Ngo, C. P. Quesenberry, J. Feng, O. Fiehn and A. Ferrara, Predictive Metabolomic Markers in Early to Mid-Pregnancy for Gestational Diabetes Mellitus: A Prospective Test and Validation Study, Diabetes, 2022, 71(8), 1807–1817, DOI:10.2337/db21-1093.
- C. Moschet, T. Anumol, B. M. Lew, D. H. Bennett and T. M. Young, Household Dust as a Repository of Chemical Accumulation: New Insights from a Comprehensive High-Resolution Mass Spectrometric Study, Environ. Sci. Technol., 2018, 52(5), 2878–2887, DOI:10.1021/acs.est.7b05767.
- J. R. Nuñez, S. M. Colby, D. G. Thomas, M. M. Tfaily, N. Tolic, E. M. Ulrich, J. R. Sobus, T. O. Metz, J. G. Teeguarden and R. S. Renslow, Evaluation of In Silico Multifeature Libraries for Providing Evidence for the Presence of Small Molecules in Synthetic Blinded Samples, J. Chem. Inf. Model., 2019, 59(9), 4052–4060, DOI:10.1021/acs.jcim.9b00444.
- Legal obstacles to toxic chemical research | Science, https://www.science.org/doi/10.1126/science.abl4383, accessed 2023-11-30.
- CompTox Chemicals Dashboard, https://comptox.epa.gov/dashboard/, accessed 2023-11-30.
- D. Abrahamsson, A. Siddharth, T. M. Young, M. Sirota, J.-S. Park, J. W. Martin and T. J. Woodruff, In Silico Structure Predictions for Non-Targeted Analysis: From Physicochemical Properties to Molecular Structures, J. Am. Soc. Mass Spectrom., 2022, 33(7), 1134–1147, DOI:10.1021/jasms.1c00386.
- D. Abrahamsson, C. L. Brueck, C. Prasse, D. A. Lambropoulou, L.-A. Koronaiou, M. Wang, J.-S. Park and T. J. Woodruff, Extracting Structural Information from Physicochemical Property Measurements Using Machine Learning – A New Approach for Structure Elucidation in Non-Targeted Analysis, Environ. Sci. Technol., 2023, 57(40), 14827–14838, DOI:10.1021/acs.est.3c03003.
- P. Liigand, J. Liigand, K. Kaupmees and A. Kruve, 30 Years of Research on ESI/MS Response: Trends, Contradictions and Applications, Anal. Chim. Acta, 2021, 1152, 238117, DOI:10.1016/j.aca.2020.11.049.
- D. Panagopoulos Abrahamsson, J.-S. Park, R. R. Singh, M. Sirota and T. J. Woodruff, Applications of Machine Learning to In Silico Quantification of Chemicals without Analytical Standards, J. Chem. Inf. Model., 2020, 60(6), 2718–2727, DOI:10.1021/acs.jcim.9b01096.
- L. C. Groff, J. N. Grossman, A. Kruve, J. M. Minucci, C. N. Lowe, J. P. McCord, D. F. Kapraun, K. A. Phillips, S. T. Purucker, A. Chao, C. L. Ring, A. J. Williams and J. R. Sobus, Uncertainty Estimation Strategies for Quantitative Non-Targeted Analysis, Anal. Bioanal. Chem., 2022, 414(17), 4919–4933, DOI:10.1007/s00216-022-04118-z.
- T. A. Johnson and D. P. Abrahamsson, Quantification of Chemicals in Non-Targeted Analysis without Analytical Standards – Understanding the Mechanism of Electrospray Ionization and Making Predictions, Curr. Opin. Environ. Sci. Health, 2023, 100529, DOI:10.1016/j.coesh.2023.100529.
- L. Konermann, E. Ahadi, A. D. Rodriguez and S. Vahidi, Unraveling the Mechanism of Electrospray Ionization, Anal. Chem., 2013, 85(1), 2–9, DOI:10.1021/ac302789c.
- L. X. X. Rayleigh, On the Equilibrium of Liquid Conducting Masses Charged with Electricity, London, Edinburgh Dublin Philos. Mag. J. Sci., 1882, 14(87), 184–186, DOI:10.1080/14786448208628425.
- M. Dole, L. L. Mack, R. L. Hines, R. C. Mobley, L. D. Ferguson and M. B. Alice, Molecular Beams of Macroions, J. Chem. Phys., 1968, 49(5), 2240–2249, DOI:10.1063/1.1670391.
- E. I. Calixte, O. T. Liyanage, H. J. Kim, E. D. Ziperman, A. J. Pearson and E. S. Gallagher, Release of Carbohydrate–Metal Adducts from Electrospray Droplets: Insight into Glycan Ionization by Electrospray, J. Phys. Chem. B, 2020, 124(3), 479–486, DOI:10.1021/acs.jpcb.9b10369.
- V. J. Mandra, M. G. Kouskoura and C. K. Markopoulou, Using the Partial Least Squares Method to Model the Electrospray Ionization Response Produced by Small Pharmaceutical Molecules in Positive Mode, Rapid Commun. Mass Spectrom., 2015, 29(18), 1661–1675, DOI:10.1002/rcm.7263.
- J. Golubović, C. Birkemeyer, A. Protić, B. Otašević and M. Zečević, Structure–Response Relationship in Electrospray Ionization-Mass Spectrometry of Sartans by Artificial Neural Networks, J. Chromatogr. A, 2016, 1438, 123–132, DOI:10.1016/j.chroma.2016.02.021.
- T. Henriksen, R. K. Juhler, B. Svensmark and N. B. Cech, The Relative Influences of Acidity and Polarity on Responsiveness of Small Organic Molecules to Analysis with Negative Ion Electrospray Ionization Mass Spectrometry (ESI-MS), J. Am. Soc. Mass Spectrom., 2005, 16(4), 446–455, DOI:10.1016/j.jasms.2004.11.021.
- A. Kruve, K. Kaupmees, J. Liigand and I. Leito, Negative Electrospray Ionization via Deprotonation: Predicting the Ionization Efficiency, Anal. Chem., 2014, 86(10), 4822–4830, DOI:10.1021/ac404066v.
- P. Liigand, K. Kaupmees, K. Haav, J. Liigand, I. Leito, M. Girod, R. Antoine and A. Kruve, Think Negative: Finding the Best Electrospray Ionization/MS Mode for Your Analyte, Anal. Chem., 2017, 89(11), 5665–5668, DOI:10.1021/acs.analchem.7b00096.
- C. M. Alymatiri, M. G. Kouskoura and C. K. Markopoulou, Decoding the Signal Response of Steroids in Electrospray Ionization Mode (ESI-MS), Anal. Methods, 2015, 7(24), 10433–10444, 10.1039/C5AY02839F.
- M. Oss, A. Kruve, K. Herodes and I. Leito, Electrospray Ionization Efficiency Scale of Organic Compounds, Anal. Chem., 2010, 82(7), 2865–2872, DOI:10.1021/ac902856t.
- A. Kruve and K. Kaupmees, Predicting ESI/MS Signal Change for Anions in Different Solvents, Anal. Chem., 2017, 89(9), 5079–5086, DOI:10.1021/acs.analchem.7b00595.
- T. B. Nguyen, S. A. Nizkorodov, A. Laskin and J. Laskin, An Approach toward Quantification of Organic Compounds in Complex Environmental Samples Using High-Resolution Electrospray Ionization Mass Spectrometry, Anal. Methods, 2012, 5(1), 72–80, 10.1039/C2AY25682G.
- L. Wu, Y. Wu, H. Shen, P. Gong, L. Cao, G. Wang and H. Hao, Quantitative Structure–Ion Intensity Relationship Strategy to the Prediction of Absolute Levels without Authentic Standards, Anal. Chim. Acta, 2013, 794, 67–75, DOI:10.1016/j.aca.2013.07.034.
- P. Liigand, J. Liigand, F. Cuyckens, R. J. Vreeken and A. Kruve, Ionisation Efficiencies Can Be Predicted in Complicated Biological Matrices: A Proof of Concept, Anal. Chim. Acta, 2018, 1032, 68–74, DOI:10.1016/j.aca.2018.05.072.
- S. Bieber, T. Letzel and A. Kruve, Electrospray Ionization Efficiency Predictions and Analytical Standard Free Quantification for SFC/ESI/HRMS, J. Am. Soc. Mass Spectrom., 2023, 34(7), 1511–1518, DOI:10.1021/jasms.3c00156.
- E. Palm and A. Kruve, Machine Learning for Absolute Quantification of Unidentified Compounds in Non-Targeted LC/HRMS, Molecules, 2022, 27(3), 1013, DOI:10.3390/molecules27031013.
- J. Liigand, T. Wang, J. Kellogg, J. Smedsgaard, N. Cech and A. Kruve, Quantification for Non-Targeted LC/MS Screening without Standard Substances, Sci. Rep., 2020, 10(1), 5808, DOI:10.1038/s41598-020-62573-z.
- C. D. Daub and N. M. Cann, How Are Completely Desolvated Ions Produced in Electrospray Ionization: Insights from Molecular Dynamics Simulations, Anal. Chem., 2011, 83(22), 8372–8376, DOI:10.1021/ac202103p.
- D. Kim, N. Wagner, K. Wooding, D. E. Clemmer and D. H. Russell, Ions from Solution to the Gas Phase: A Molecular Dynamics Simulation of the Structural Evolution of Substance P during Desolvation of Charged Nanodroplets Generated by Electrospray Ionization, J. Am. Chem. Soc., 2017, 139(8), 2981–2988, DOI:10.1021/jacs.6b10731.
- M. Luan, Z. Hou, B. Zhang, L. Ma, S. Yuan, Y. Liu and G. Huang, Inter-Domain Repulsion of Dumbbell-Shaped Calmodulin during Electrospray Ionization Revealed by Molecular Dynamics Simulations, Anal. Chem., 2023, 95(23), 8798–8806, DOI:10.1021/acs.analchem.2c05630.
- M. Luan, Z. Hou and G. Huang, Suppression of Protein Structural Perturbations in Native Electrospray Ionization during the Final Evaporation Stages Revealed by Molecular Dynamics Simulations, J. Phys. Chem. B, 2022, 126(1), 144–150, DOI:10.1021/acs.jpcb.1c09130.
- L. Konermann, H. Metwally, R. G. McAllister and V. Popa, How to Run Molecular Dynamics Simulations on Electrospray Droplets and Gas Phase Proteins: Basic Guidelines and Selected Applications, Methods, 2018, 144, 104–112, DOI:10.1016/j.ymeth.2018.04.010.
- K. Hanifi, P. M. Scrosati and L. Konermann, MD Simulations of Peptide-Containing Electrospray Droplets: Effects of Parameter Settings on the Predicted Mechanisms of Gas Phase Ion Formation, J. Phys. Chem. B, 2024, 128(25), 5973–5986, DOI:10.1021/acs.jpcb.4c01241.
- E. M. Ulrich, J. R. Sobus, C. M. Grulke, A. M. Richard, S. R. Newton, M. J. Strynar, K. Mansouri and A. J. Williams, EPA's Non-Targeted Analysis Collaborative Trial (ENTACT): Genesis, Design, and Initial Findings, Anal. Bioanal. Chem., 2019, 411(4), 853–866, DOI:10.1007/s00216-018-1435-6.
- Chemaxon, https://chemaxon.com/, accessed 2024-06-01.
- G. J. Van Berkel, F. Zhou and J. T. Aronson, Changes in Bulk Solution pH Caused by the Inherent Controlled-Current Electrolytic Process of an Electrospray Ion Source, Int. J. Mass Spectrom. Ion Processes, 1997, 162(1), 55–67, DOI:10.1016/S0168-1176(96)04476-X.
- CHARMM-GUI, https://www.charmm-gui.org/, accessed 2024-01-21.
- Periodic boundary conditions - GROMACS 2024.2 documentation, https://manual.gromacs.org/current/reference-manual/algorithms/periodic-boundary-conditions.html, accessed 2024-06-01.
- M. G. Wolf and G. Groenhof, Explicit Proton Transfer in Classical Molecular Dynamics Simulations, J. Comput. Chem., 2014, 35(8), 657–671, DOI:10.1002/jcc.23536.
- J. N. Smith, R. C. Flagan and J. L. Beauchamp, Droplet Evaporation and Discharge Dynamics in Electrospray Ionization, J. Phys. Chem. A, 2002, 106(42), 9957–9967, DOI:10.1021/jp025723e.
- E. I. Calixte, O. T. Liyanage, D. T. Gass and E. S. Gallagher, Formation of Carbohydrate–Metal Adducts from Solvent Mixtures during Electrospray: A Molecular Dynamics and ESI-MS Study, J. Am. Soc. Mass Spectrom., 2021, 32(12), 2738–2745, DOI:10.1021/jasms.1c00179.
- P. Atkins, J. de Paula, J. Keeler, Atkins' Physical Chemistry, Oxford University Press, 12th edn, 2022 Search PubMed.
- P. Kebarle, U. H. Verkerk, On the Mechanism of Electrospray Ionization Mass Spectrometry (ESIMS), in Electrospray and MALDI Mass Spectrometry, John Wiley & Sons, Ltd, 2010, pp 1–48, DOI:10.1002/9780470588901.ch1.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr, CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields, J. Comput. Chem., 2010, 31(4), 671–690, DOI:10.1002/jcc.21367.
- K. Mansouri, C. M. Grulke, R. S. Judson and A. J. Williams, OPERA Models for Predicting Physicochemical Properties and Environmental Fate Endpoints, J. Cheminf., 2018, 10(1), 10, DOI:10.1186/s13321-018-0263-1.
- UFZ – LSER Database, https://www.ufz.de/index.php?en=31698%26contentonly=1%26m=0%26lserd_data[mvc]=Public/start, accessed 2024-05-26.
- A. Kruve, Influence of Mobile Phase, Source Parameters and Source Type on Electrospray Ionization Efficiency in Negative Ion Mode, J. Mass Spectrom., 2016, 51(8), 596–601, DOI:10.1002/jms.3790.
- J. Liigand, A. Kruve, I. Leito, M. Girod and R. Antoine, Effect of Mobile Phase on Electrospray Ionization Efficiency, J. Am. Soc. Mass Spectrom., 2014, 25(11), 1853–1861, DOI:10.1007/s13361-014-0969-x.
- N. B. Cech and C. G. Enke, Relating Electrospray Ionization Response to Nonpolar Character of Small Peptides, Anal. Chem., 2000, 72(13), 2717–2723, DOI:10.1021/ac9914869.
- J. Hermans, S. Ongay, V. Markov and R. Bischoff, Physicochemical Parameters Affecting the Electrospray Ionization Efficiency of Amino Acids after Acylation, Anal. Chem., 2017, 89(17), 9159–9166, DOI:10.1021/acs.analchem.7b01899.
- J. Tolls, J. van Dijk, E. J. M. Verbruggen, J. L. M. Hermens, B. Loeprecht and G. Schüürmann, Aqueous Solubility–Molecular Size Relationships: A Mechanistic Case Study Using C10- to C19-Alkanes, J. Phys. Chem. A, 2002, 106(11), 2760–2765, DOI:10.1021/jp011755a.
- PaDEL-descriptor, An open source software to calculate molecular descriptors and fingerprints - Yap - 2011 - Journal of Computational Chemistry, Wiley Online Library, https://onlinelibrary.wiley.com/doi/full/10.1002/jcc.21707, accessed 2024-06-01 Search PubMed.
- H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, Mordred: A Molecular Descriptor Calculator, J. Cheminf., 2018, 10(1), 4, DOI:10.1186/s13321-018-0258-y.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra06695b |
| This journal is © The Royal Society of Chemistry 2024 |