Open Access Article
Open Access ArticleInfluence of ultrafast laser processing on amorphous structures – based on molecular dynamics simulation
Shijia Liua,
Jiaqi Liub,
Jialin Liub and
Jiuye Chen *c
*c
aSchool of OptoElectronic Engineering, Changchun University of Science and Technology, Changchun 130022, China
bHalifax Grammar School, Halifax B3H 2Y2, Canada
cSchool of Science, Changchun University of Science and Technology, Changchun 130022, China. E-mail: chenjiuye@mails.cust.edu.cn
First published on 9th December 2024
Abstract
Ultrafast laser processing technology exhibits exceptional precision and irreplaceable functionality in the fabrication of micron and nanometer-scale devices. However, its short action time presents challenges for observing and studying the interactions between ultrafast lasers and materials. This study employs molecular dynamics simulations to specifically investigate the application of ultrafast laser processing in treating amorphous structural defects on Ni–Fe alloy surfaces. The simulations reveal the impact of energy deposition on the material's crystallization behavior on a nanosecond timescale. It was found that the crystallization temperature increases with the rising rate of temperature change, although the final crystal structure remains unchanged. Enhanced energy deposition accelerates lattice formation, improves atomic ordering, and reduces the crystallization time from 4.5 ns to 3.2 ns. The lattice phase transition is completed within 0.5 ns, and an increased incubation temperature effectively minimizes the proportion of the amorphous phase. The simulation results clearly illustrate the fundamental nucleation and growth mechanisms, providing valuable insights into the effects of ultrafast laser processing on surface lattice structures and atomic dynamics. Moreover, these findings establish a theoretical foundation and offer data support for developing future material processing methods.
1. Introduction
In recent years, ultrafast lasers have garnered extensive attention due to their exceptionally high peak intensity and ultra-short pulse duration. These lasers have found applications across various fields, including the metal industry, micro-nano machining, and chip manufacturing.1–5 Compared to traditional long-pulse laser processing techniques, ultrafast laser pulses can interact with target materials on a much shorter timescale, thereby completing the processing before lattice disorder and thermal diffusion occur.6 This characteristic enables ultrafast lasers to induce localized melting phenomena in material processing, rather than ablation, leading to successful applications in surface processing of perovskite materials7 and ceramics welding.8 Additionally, ultrafast laser technology based on multiphoton absorption has been employed to fabricate 3D nanostructures, with reported minimum feature sizes of 180 nm for silver pillar structures.9 Ultrafast laser processing technology exhibits significant potential for diverse applications and plays an indispensable role in several ambitious research endeavors,10–12 providing potential opportunities for future innovations.However, despite the extensive application of ultrafast laser processing technology in material processing, studies on subtle structural changes in materials, particularly at the nanoscale, remain insufficient. The interaction time of ultrafast lasers with materials is on the order of nanoseconds (10−9 seconds), which poses challenges for accurately observing the entire processing process. During ultrafast laser irradiation, material surfaces may undergo nanosecond-scale melting and recrystallization processes,13 which directly affect the chemical composition, crystal structure, and morphology of the material surface.14 There is no doubt that different structures significantly influence the properties of materials. The mechanical properties of amorphous structures differ greatly from those of crystalline structures,15 the magneto crystalline anisotropy and saturation magnetization of alloys can change with variations in their crystalline phases.16 Therefore, it is crucial to observe and control the changes in various lattices during metal processing. Although theoretical models exist to explain the processing mechanism,17–19 there is still a lack of research on finer structures, particularly at the atomic level. Furthermore, research on nucleation behavior at ultrafast timescales is relatively scarce, making it particularly challenging to explore the interactions between ultrafast lasers and materials in depth. Fortunately, advancements in computational technology have made it possible to study atomic behavior at ultrafast timescales through computer simulations.20,21 Molecular dynamics (MD) simulations are commonly used to investigate phase transitions, especially the microscopic structural changes in metallic systems. Using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS), it is possible to directly track and simulate nucleation behavior, and analyze and visualize phase structural transformations and related dynamic processes in material systems, providing significant support for the study of atomic dynamics in ultrafast laser processing.
This paper employs molecular dynamics simulations to investigate the impact of ultrafast laser processing on the surface morphology of metals under different parameters, using a Ni3Fe1 alloy as the sample. Ni3Fe1 alloy, a widely used alloy also found in space meteorites,22 is characterized by its distinct lattice structure: a perfect face-centered cubic structure (γ phase) in the stable state, a body-centered cubic phase (δ phase) in the metastable state, and an amorphous state with disordered atomic arrangements when defects are present or the processing is inadequate.23 The stable Ni3Fe1 alloy exhibits excellent soft magnetic properties and an extremely low thermal expansion coefficient,24 making it an ideal material for magnetic recording media, information storage, as well as MEMS and radio frequency devices.25 It is evident that the amorphous structure significantly affects the performance of alloys, particularly in the study of structural transformations in Ni–Fe alloys. Additionally, the distinct and easily discernible structures of Ni–Fe alloys enable their effective application in simulation calculations. Thus, this study simulates the application of ultrafast laser processing technology in addressing amorphous structural defects on material surfaces, observes the transition from amorphous to crystalline states in the alloy structure, and calculates the factors influencing phase transitions. MD simulations utilize embedded atom potentials covering spatial scales from a few angstroms to several hundred angstroms on nanosecond timescales, making this approach suitable for simulating micro-nano scale structural morphologies. Through MD simulations, a comprehensive understanding of phase transition processes in ultrafast micro-nano processing can be achieved, offering deeper insights into the microscopic structure and properties of materials, and providing important guidance and support for optimizing ultrafast laser processing technology. Future work will extend this research to explore the micro-nano processing mechanisms of different material systems under ultrafast laser irradiation, aiming to provide more valuable information and insights for material processing development and applications.
2. Simulation methods
The traditional view considers ultrashort laser pulse processing a cold machining method. However, current research indicates the potential presence of surface overheating and melting phenomena during this process.26,27 To observe the thermal phenomena and thermomechanical effects more accurately in ultrafast laser–material interactions, we employed the open-source LAMMPS software for molecular dynamics (MD) simulations. Molecular dynamics simulations of the current Ni3Fe1 alloy system with an atomic ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, were conducted in a three-dimensional space. The initial simulated dimensions are about 14 × 14 × 14 lattice regions, and this size may change with temperature variations (some specific structural and perspective dimensions will be provided in the corresponding locations). The simulation operates under the isothermal–isobaric ensemble (NPT) with an initial external pressure of 0 Pa. Before the simulation, the velocities of all atoms are initialized using a Gaussian distribution with a random seed. The simulation uses a “metal” unit system, with a time step set to 0.005 picoseconds (5 femtoseconds). The total interaction duration is controlled by the number of computation steps, requiring 2 × 106 steps over a 10 ns simulation period. Thermodynamic data, including temperature, energy, and volume, is output every 1000 steps. The interaction results between the laser pulse and the material are primarily evaluated based on changes in temperature and energy. During the calculations, atomic coordinates are iteratively adjusted, and the system undergoes energy minimization using the steepest descent method. The calculation formula is as follows:
1, were conducted in a three-dimensional space. The initial simulated dimensions are about 14 × 14 × 14 lattice regions, and this size may change with temperature variations (some specific structural and perspective dimensions will be provided in the corresponding locations). The simulation operates under the isothermal–isobaric ensemble (NPT) with an initial external pressure of 0 Pa. Before the simulation, the velocities of all atoms are initialized using a Gaussian distribution with a random seed. The simulation uses a “metal” unit system, with a time step set to 0.005 picoseconds (5 femtoseconds). The total interaction duration is controlled by the number of computation steps, requiring 2 × 106 steps over a 10 ns simulation period. Thermodynamic data, including temperature, energy, and volume, is output every 1000 steps. The interaction results between the laser pulse and the material are primarily evaluated based on changes in temperature and energy. During the calculations, atomic coordinates are iteratively adjusted, and the system undergoes energy minimization using the steepest descent method. The calculation formula is as follows:
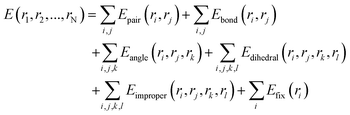 | (1) |
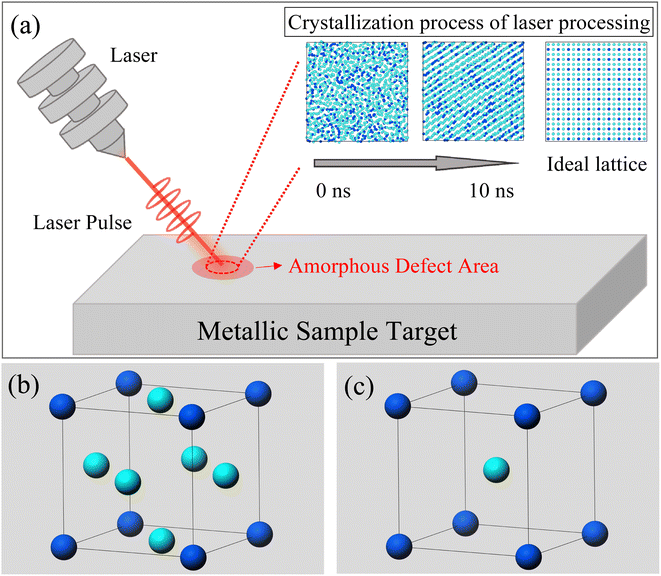
The OVITO (2.9.0) software was utilized for processing atomic images.28 As shown in Fig. 1, our simulation designated an amorphous region as the defect area to be processed. By injecting laser pulses into this region, we observed the evolution of the lattice. Throughout this process, we output atomic distribution images and temperature data at each step. Additionally, we calculated the radial distribution function (RDF) of the nuclear structure in the model, providing distribution data for body-centered cubic (BCC), face-centered cubic (FCC), and amorphous structures. These lattice structure data and RDF images served as criteria for evaluating surface morphology changes.
In addition, in this simulation, the Ni–Fe potential is constructed based on the Embedded Atom Method (EAM), which is highly efficient and effective in describing atomic interactions in transition metal systems, particularly suitable for body-centered cubic (BCC) and face-centered cubic (FCC) metals.29 The EAM treats each atom in the solid as embedded in a host solid composed of the remaining atoms. The energy functional is approximated through a potential function with two terms: (i) a sum of pairwise interactions ϕ(rij) between atoms i and j, and (ii) a sum of embedding energies F, which is a function of the atomic density rho. Alpha and Beta are the element types of atoms i and j:
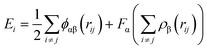 | (2) |
From eqn (2), it can be found that the atoms are brought to local minima of the potential energy surface, therefore avoiding potentials overcome limitations associated with simple pairwise interatomic potentials in simulations of metallic systems.
As we know, the Radial-Distribution-Function g(r) is commonly used to characterize whether a structure is crystalline or amorphous (hereafter referred to as RDF). It represents the distribution of other particles at a distance r from a given atom. To calculate the RDF, each atom is imagined to be at the center of a series of concentric spheres. RDF can then be obtained by the following formula:30
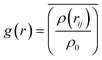 | (3) |
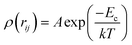 | (4) |
| ln(β/T2) = −Ec/RT + constant | (5) |
3. Results and discussion
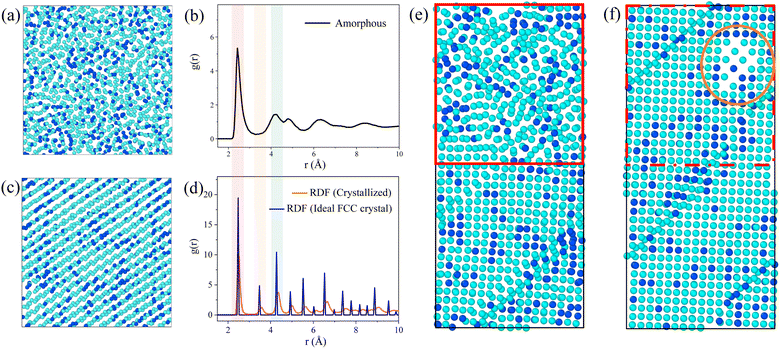
During the simulation, we observed the atomic projection images and the RDF for the Ni3Fe1 alloy. Fig. 2 shows the atomic projection and RDF for the simulated alloy at temperatures of 300 K and 1000 K, respectively. From Fig. 2a, it can be observed that the planar distribution of nickel and iron atoms is disordered at 300 K, which is confirmed by the typical amorphous structure of RDF in Fig. 2b. As the energy input increases and the temperature of the simulated alloy reaches 1000 K, it can be seen from Fig. 2c that the lattice becomes significantly ordered, which is verified by the typical crystalline structure of RDF in Fig. 2d.Based on the simulation results presented in Fig. 1, it is evident that the energy input during laser processing facilitates a transition of atoms from a disordered state to an ordered state. Molecular dynamics simulations provide valuable insights into the specific mechanisms underlying this transformation. The simulation data reveal that the resulting lattice structure aligns with findings from existing studies,23,33–35 particularly regarding the formation of the face-centered cubic (FCC) crystal structure. As shown in Fig. 2d, the radial distribution function of the crystal structure closely approximates that of the ideal FCC structure, exhibiting similar peak positions, which suggests successful FCC structure formation and indicates that laser processing effectively promotes the reorganization of the lattice structure in amorphous materials. However, although the crystallization results match well with the ideal outcome at the positions of the first few nearest-neighbor peaks, there are slight differences in the peak values of the distribution function, revealing some imperfection in the crystal structure. This phenomenon may be due to the inclusion of defect regions in the statistical process of the distribution function, leading to a decrease and broadening of the radial distribution function peaks. Interestingly, the energy input during the simulation was insufficient to cause sample melting. Our simulation data also show that the sample temperature did not reach the melting point, which is crucial for the application of laser processing. In molten metals, there are many disordered atoms, and the properties exhibited by this disordered state are significantly different from those of the desired stable face-centered cubic structure. Therefore, it is preferable to avoid the formation of a molten state as much as possible without introducing additional complex structures. Since the melting point was not reached, the local structure of the sample can change without complete melting, demonstrating the unique advantage of laser processing in surface defect repair. This processing method is akin to an “annealing” process, allowing for localized improvement of the material's structure without disrupting its overall properties, thus enhancing material performance and longevity. Atomic projection maps at the interface at 300 K and 1000 K are also constructed in Fig. 2e and f. It is evident that the amorphous region (red area in Fig. 2e) gradually becomes more ordered with increasing temperature, with atoms starting to rearrange into an ordered lattice (red area in Fig. 2f). Under the same processing conditions, the crystallized regions are minimally affected, and the existing energy input remains insufficient to damage the already-formed lattice structure. Therefore, this processing method primarily targets the amorphous regions and promotes their crystallization through localized heating.
Notably, a body-centered cubic (BCC) structure appears in the orange region at the upper right of Fig. 2f. This phenomenon can be attributed to the lower number of atoms in the amorphous region within the same volume, resulting in a lower atomic density. Due to the lower coordination number of the BCC structure, this region is more likely to form such a structure rather than the FCC structure. Although this region has shown some ordered state structurally, it is still considered a “defect” compared to the expected FCC structure. This observation indicates that structural transformation issues exist during laser processing, which requires further investigation to address these “defects”. Therefore, we plan to investigate the treatment of the amorphous regions by studying both isothermal and non-isothermal crystallization methods.
3.1 Crystallization processes under non-isothermal conditions
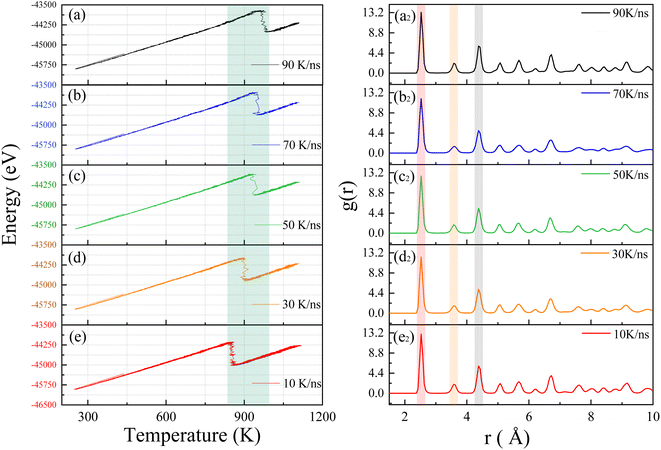
We will investigate the crystallization process of Ni–Fe alloy under non-isothermal conditions with varying input power levels. By adjusting the laser heating rates, we aim to explore their effects on crystallization temperature and lattice structure. Several heating rates were established for this study, considering that the laser induces a temperature change of approximately 1000 K within 10 nanoseconds in the model system. Consequently, starting from this temperature change rate, we extended the duration of the heating process to study the crystallization behavior under different heating rates, including 90 K ns−1, 70 K ns−1, 50 K ns−1, 30 K ns−1, and 10 K ns−1. Fig. 3 presents the total energy versus temperature curves for Ni–Fe alloys under these various heating rates. These curves illustrate the energy variations of the sample at different rates, providing a deeper understanding of the crystallization process.The simulation results reveal that all energy curves exhibit a single exothermic crystallization peak associated with the crystallization process around 900 K as shown by the green band in Fig. 3. As the heating rate increases, the crystallization temperature rises from 855.2 K to 975.1 K, as detailed in Table 1. Consistent with experimental results on the crystallization process of amorphous alloys,36 the simulation results demonstrate a relationship between crystallization temperature and heating rate. We believe that the crystallization behavior has significant kinetic characteristics.37,38 As the temperature increases from 250 K to 1100 K, the atomic system acquires sufficient thermal energy to overcome activation energy barriers, facilitating nucleation. When the system temperature reaches the crystallization temperature, the potential energy of atoms drops sharply, and atoms in the amorphous state begin to progressively transform into an ordered crystal structure. The simulation results show that an increase in heating rate leads to a rise in crystallization temperature, which is directly related to the increased activation energy barrier caused by lattice thermal fluctuations. Therefore, the crystallization temperature of the Ni–Fe alloy model increases significantly with rising heating rates. To further confirm the effect of heating rate on the crystallization of the Ni–Fe alloy model, atomic correlations at different heating rates were analyzed using the RDF. Fig. 3 shows the RDF of the Ni3Fe1 alloy at heating rates of (a2) 90 K ns−1, (b2) 70 K ns−1, (c2) 50 K ns−1, (d2) 30 K ns−1, and (e2) 10 K ns−1. From Fig. 3a2–e2, all curves exhibit the typical face-centered cubic (FCC) structure, with the atomic structure showing long-range ordered characteristics. The first peak is sharp and has a higher intensity (red band), while the second and third neighbor peaks (gray and yellow bands) have lower intensities, as observed in the Ni–Fe alloy,39 and are consistent with the RDF of the ideal FCC lattice shown in Fig. 2d. Although the heating rate significantly affects the crystallization temperature of the Ni–Fe alloy, it has a negligible effect on lattice formation. This indicates that while the heating rate significantly alters the crystallization temperature, it does not noticeably affect the distribution of atomic distances. This can also be clearly observed from Table 1, indicating that the stable lattice structure of the atoms is less affected by the heating rate.
| Heating rate (K ns−1) | FCC (%) | BCC (%) | Others (%) | Crystallization temperature (K) |
|---|---|---|---|---|
| 10 | 70.3 | 1.1 | 22.3 | 855.2 |
| 30 | 70.7 | 1.0 | 22.5 | 899.8 |
| 50 | 70.1 | 1.1 | 22.7 | 939.9 |
| 70 | 69.3 | 0.9 | 23.4 | 950.2 |
| 90 | 70.0 | 0.9 | 23.2 | 975.1 |
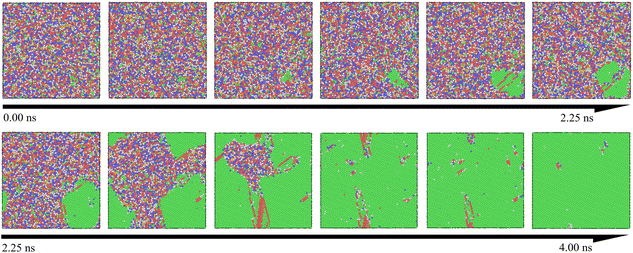
Table 1 presents the relationship between heating rate and lattice formation. The data indicate that the proportion of face-centered cubic (FCC) lattice remains relatively unchanged as the temperature change rate increases. This suggests that optimizing amorphous defects through adjustments to the heating rate at a fixed final temperature has limited efficacy. During the crystallization process, the atomic distribution in the simulation system remains disordered below the crystallization temperature. Upon reaching the crystallization point, several clusters with initial lattice structures emerge as nuclei, leading to a process akin to heterogeneous nucleation. As the temperature increases, these nuclei gradually grow via diffusion. To enhance visualization, we expanded the simulation view to a 35 × 35 lattice region. Fig. 4 illustrates this crystallization process over time, with atoms color-coded by their lattice structures, where the FCC structure is indicated in green. It is evident that clusters near the FCC nucleus in the lower right corner gradually expand until all grains coalesce. This transition marks the disappearance of the amorphous structure and the emergence of a crystalline structure, confirming that this processing method aligns with the conventional grain boundary nucleation mechanism.40,41
It is evident that the rate of temperature change has a certain impact on the activation energy of crystallization, which can lead to fluctuations in the crystallization temperature within a certain range. Specifically, the rate of temperature change affects the rate of heat transfer within the material and the uniformity of the local temperature. This results in uneven heat distribution and thermal gradients within the material, which may cause fluctuations in the local crystallization temperature. Such fluctuations can alter the conditions for crystal formation to some extent, leading to variations in the crystallization temperature. This simulation has shown that a faster heating rate results in a higher crystallization temperature. However, the impact of temperature change rate on the nucleation rate and lattice fraction is relatively minor. As illustrated by eqn (4), the variation in nucleation rate is primarily influenced directly by temperature. With increasing temperature, more nucleation sites can form within a shorter period. Therefore, although the rate of temperature change does influence activation energy, the nucleation and growth processes remain more directly governed by temperature.
It can be inferred that temperature regulation has a more significant effect on the nucleation rate and lattice structure than adjustments in the rate of temperature change. To gain a deeper understanding of this process, we will investigate the changes in the critical crystallization temperature starting from the minimum crystallization temperature of 850 K obtained from Table 1. This temperature is generally considered the critical threshold for the transition of the material from an amorphous to a crystalline state. Building on this, we will further examine the crystallization of the amorphous structure under different temperature conditions, particularly analyzing the dynamic process of crystallization and the effect of temperature on the uniformity of the crystal structure. Through these studies, we aim to achieve a more comprehensive understanding of the temperature dependence in the crystallization process, which will contribute to optimizing the performance and processing techniques of crystalline materials.
3.2 Crystallization processes under isothermal conditions
In this section, molecular dynamics simulations were performed to investigate the impact of different incubation temperatures on crystallization time and lattice structure distribution. These simulations provide critical insights into the crystallization mechanisms under varying energy inputs. The simulation conditions were consistent with previous setups but with precise adjustments to the terminal temperatures. Based on the results from Table 1, we believe that crystallization behavior will occur in the simulations at temperatures above 850 K. Therefore, we conducted calculations starting from the lowest crystallization temperature reported in Table 1, which is 850 K, and examined temperatures of 860 K, 850 K, 840 K, 830 K, and 820 K. By using lower temperatures, we aim to minimize the effects of atomic thermal motion at high temperatures on the study of the crystallization process, allowing for clearer observation of atomic behavior and crystallization near the critical temperature.Fig. 5a illustrates how the energy of the Ni–Fe alloy varies over time at temperatures of 820 K, 830 K, 840 K, 850 K, and 860 K. At 820 K, the energy remains nearly constant as incubation time increases, indicating that the alloy remains in an amorphous state due to insufficient atomic activation energy to transition from the disordered to the ordered phase.35 Consequently, the potential energy of the Ni–Fe alloy model is unaffected by incubation time at 820 K, suggesting there is a minimum threshold for laser energy input. Specifically, the laser energy must elevate the sample locally above 820 K to facilitate defect repair.
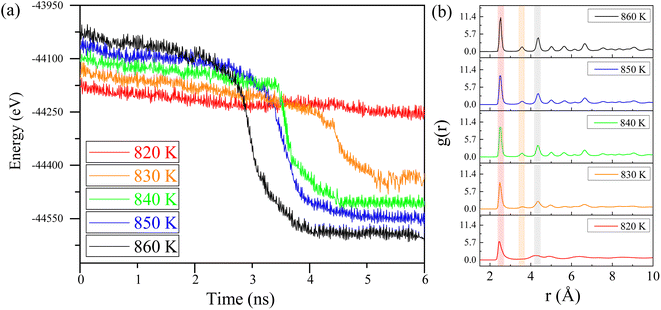 | ||
| Fig. 5 (a) Potential energy vs. time for Ni–Fe alloy at different isothermal temperatures. (b) The radial distribution function (RDF) of the Ni–Fe alloy at different temperatures. | ||
At an isothermal temperature of 830 K, however, the model's overall energy shows a marked decrease with longer incubation times. This decline in potential energy is attributed to the transition of the lattice structure from disordered to ordered. Crystallization appears to be complete around 4.5 nanoseconds, with the phase transition occurring in approximately 0.5 nanoseconds, assuming the incubation period is disregarded. Notably, as the isothermal temperature rises, the incubation time decreases from 4.5 nanoseconds to 3.2 nanoseconds, as indicated in Table 2. This observation suggests that the nucleation and growth of the Ni–Fe alloy are highly sensitive to temperature changes. The expansion of the nucleation and growth regions leads to greater atomic ordering, aligning with the findings presented in Fig. 4.
| Temperature (K) | FCC (%) | BCC (%) | Others (%) | Crystallization time (ns) |
|---|---|---|---|---|
| 820 | 53.0 | 2.2 | 33.7 | — |
| 830 | 60.9 | 2.2 | 26.3 | 4.5 |
| 840 | 66.8 | 1.3 | 23.8 | 3.8 |
| 850 | 65.7 | 1.1 | 24.0 | 3.6 |
| 860 | 67.6 | 1.4 | 23.9 | 3.2 |
Additionally, as shown in Table 2, with increasing incubation temperature, the proportion of the FCC lattice in the overall structure rises, and the proportion of face-centered cubic structure also increases from 60.9% to 67.6% with the increase in temperature, indicating a strong temperature dependency. This suggests that precise control of lattice growth via temperature is a feasible approach. To further confirm the effect of temperature on atomic ordering, the radial distribution function (RDF) of the isothermal crystallization of the Ni–Fe alloy model was examined, as illustrated in Fig. 5b. At 820 K, the structure of the Ni–Fe alloy model is amorphous, exhibiting short-range order with a clearly defined first-neighbor peak, while the second and third neighbor peaks are obscured. As the isothermal temperature increases from 830 K to 860 K, changes in the RDF pattern are observed: the first peak narrows (red band in Fig. 5), and the intensity of the second and third neighbor peaks increases (yellow and gray bands in Fig. 5). This indicates a transition from short-range to long-range order in the alloy, with noticeable crystallization behavior kinetically. The appearance and growth of critical nuclei play a crucial role in the crystallization process of the alloy model. Critical nuclei exhibit strong spatial correlation with surrounding nuclei before crystallization begins, potentially leading to rapid subsequent crystallization. Therefore, with increasing isothermal temperature, the increased intensity and reduced width of the second and third neighbor peaks in the Ni–Fe alloy model confirm the feasibility of using ultrafast laser processing. Appropriate energy input can induce crystallization in amorphous regions of the alloy, ensuring lattice structure consistency and avoiding melting or phase explosion phenomena, thus providing a potential method for non-destructive alloy surface processing.
4. Conclusion
Through molecular dynamics simulations, this study systematically investigates the impact of ultrafast laser processing on the crystallization behavior of the Ni3Fe1 alloy model in its amorphous state. The results demonstrate that laser processing allows for precise control over the crystallization process within amorphous regions, addressing the limitations of conventional annealing, which necessitates uniform heating of the entire sample. The simulations reveal that the temperature changes induced by energy input significantly affect the crystallization temperature, lattice structure, and radial distribution function. Specifically, with the same energy input, narrower laser pulse widths (faster temperature changes) lead to higher crystallization temperatures. While the rate of temperature change has a minor effect on lattice formation and proportion, these factors are strongly correlated with the final incubation temperature. Higher terminal temperatures reduce the proportion of amorphous structures and enhance the ordered lattice content. Furthermore, increased energy levels accelerate lattice formation, reducing the phase transition time of the Ni–Fe alloy model from 4.5 nanoseconds to 3.2 nanoseconds. These findings underscore the significant impact of ultrafast laser processing on both lattice structure and ultrafast atomic dynamics, offering insights into its effects on surface lattice structures and providing new perspectives for exploring material phase transition mechanisms.Data availability
Molecular Dynamics Simulations are performed via LAMMPS software. The authors will supply the relevant data in response to reasonable requests.Author contributions
Shijia Liu: writing – original draft and data curation. Jiaqi Liu: investigation, creation of models and conducting a research and investigation process. Jialin Liu: software, implementation of the computer code and supporting algorithms; testing of existing code components. Jiuye Chen: conceptualization and supervision.Conflicts of interest
The authors declare that there are no conflicts of interest related to this article.Notes and references
- J. Cui, L. Yang and Y. Wang, et al., Nanospot soldering polystyrene nanoparticles with an optical fiber probe laser irradiating a metallic AFM probe based on the near-field enhancement effect, ACS Appl. Mater. Interfaces, 2015, 7(4), 2294–2300 CAS.
- M. E. Fermann and I. Hartl, Ultrafast fibre lasers, Nat. Photonics, 2013, 7(11), 868–874 CrossRef CAS.
- K. Sugioka and Y. Cheng, Ultrafast lasers—reliable tools for advanced materials processing, Light: Sci. Appl., 2014, 3(4), e149 CAS.
- C. Momma, B. N. Chichkov and S. Nolte, et al., Short-pulse laser ablation of solid targets, Opt. Commun., 1996, 129(1–2), 134–142 CrossRef CAS.
- S. K. Das, K. Dasari and A. Rosenfeld, et al., Extended-area nanostructuring of TiO2 with femtosecond laser pulses at 400 nm using a line focus, Nanotechnology, 2010, 21(15), 155302 CrossRef.
- K. C. Phillips, H. H. Gandhi and E. Mazur, et al., Ultrafast laser processing of materials: a review, Adv. Opt. Photonics, 2015, 7(4), 684–712 CrossRef CAS.
- Y. Zhang, S. Zhu and J. Hu, et al., Femtosecond laser direct nanolithography of perovskite hydration for temporally programmable holograms, Nat. Commun., 2024, 15(1), 6661 CrossRef CAS.
- E. H. Penilla, L. F. Devia-Cruz and A. T. Wieg, et al., Ultrafast laser welding of ceramics, Science, 2019, 365(6455), 803–808 CrossRef CAS PubMed.
- A. Ishikawa, T. Tanaka and S. Kawata, Improvement in the reduction of silver ions in aqueous solution using two-photon sensitive dye, Appl. Phys. Lett., 2006, 89(11) CrossRef CAS.
- K. Sugioka, Progress in ultrafast laser processing and future prospects, Nanophotonics, 2017, 6(2), 393–413 CAS.
- F. H. Rajab, D. Whitehead and Z. Liu, et al., Characteristics of hierarchical micro/nano surface structure formation generated by picosecond laser processing in water and air, Appl. Phys. B, 2017, 123, 1–12 CrossRef CAS.
- P. K. Maroju, C. Grazioli and M. Di Fraia, et al., Attosecond pulse shaping using a seeded free-electron laser, Nature, 2020, 578(7795), 386–391 CrossRef CAS PubMed.
- Z. Zheng, C. Wu and S. Liu, et al., Analysis of energy occupying ratio of Coulomb explosion and thermal effect in picosecond pulse laser processing, Opt. Commun., 2018, 424, 190–197 CrossRef CAS.
- S. K. Sundaram and E. Mazur, Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses, Nat. Mater., 2002, 1(4), 217–224 CrossRef CAS PubMed.
- Z. Wang, J. Chen and Q. Zhou, et al., Molecular Dynamics Simulation and Mechanical Properties Analysis of Ni-Fe Alloy under Uniaxial Stretching, Integr. Ferroelectr., 2022, 228(1), 9–16 CrossRef CAS.
- J. Liu, L. J. Riddiford and C. Floristean, et al., Kinetics of order-disorder transformation of L12 FeNi3 in the Fe-Ni system, J. Alloys Compd., 2016, 689, 593–598 CrossRef CAS.
- A. F. Pan, W. J. Wang and X. S. Mei, et al., Laser thermal effect on silicon nitride ceramic based on thermo-chemical reaction with temperature-dependent thermo-physical parameters, Appl. Surf. Sci., 2016, 375, 90–100 CrossRef CAS.
- N. M. Bulgakova and I. M. Bourakov, Phase explosion under ultrashort pulsed laser ablation: modeling with analysis of metastable state of melt, Appl. Surf. Sci., 2002, 197, 41–44 CrossRef.
- J. K. Chen, J. E. Beraun and L. E. Grimes, et al., Modeling of femtosecond laser-induced non-equilibrium deformation in metal films, Int. J. Solids Struct., 2002, 39(12), 3199–3216 CrossRef.
- A. P. Thompson, H. M. Aktulga and R. Berger, et al., LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. Chen, W. Sun and N. Liu, et al., Dynamics simulation study on crystallization of amorphous Ni-Fe alloy, Ferroelectrics, 2019, 548(1), 82–88 CrossRef CAS.
- E. Poirier, F. E. Pinkerton and R. Kubic, et al., Intrinsic magnetic properties of L1 FeNi obtained from meteorite NWA 6259, J. Appl. Phys., 2015, 117(17) CrossRef CAS.
- J. F. Li, W. Q. Jie and G. C. Yang, et al., Solidification structure formation in undercooled Fe–Ni alloy, Acta Mater., 2002, 50(7), 1797–1807 CrossRef CAS.
- T. I. Zubar, S. A. Sharko, D. I. Tishkevich, N. N. Kovaleva, D. A. Vinnik, S. A. Gudkova, E. L. Trukhanova, E. A. Tromfimov, S. A. Chizhik, L. V. Panina, S. V. Trukhanov and A. V. Trukhanov, Anomalies in Ni-Fe nanogranular films growth, J. Alloys Compd., 2018, 748, 970–978 CrossRef CAS.
- N. Inaba, H. Asanuma, S. Lgarashi, S. Mori, F. Kirino, K. Koike and H. Morita, Damping Constants of Ni-Fe and Ni-Co Alloy Thin Films, IEEE Trans. Magn., 2006, 42(10), 2372–2374 CAS.
- H. Hakkinen and U. Landman, Superheating, melting, and annealing of copper surfaces, Phys. Rev. Lett., 1993, 71(7), 1023 CrossRef CAS PubMed.
- R. F. W. Herrmann, J. Gerlach and E. E. B. Campbell, Ultrashort pulse laser ablation of silicon: an MD simulation study, Appl. Phys. A: Mater. Sci. Process., 1998, 66(1) CrossRef CAS.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18(1), 015012 CrossRef.
- G. Bonny, R. C. Pasianot and L. Malerba, Fitting interatomic potentials consistent with thermodynamics: Fe, Cu, Ni and their alloys, Philos. Mag., 2009, 89(34–36), 3451–3464 CrossRef CAS.
- X. D. Dai, J. H. Li and B. X. Liu, Atomistic modeling of crystal-to-amorphous transition and associated Kinetics in the Ni–Nb System by Molecular Dynamics Simulations, J. Phys. Chem. B, 2005, 109(10), 4717–4725 CrossRef CAS.
- Y. C. Lei, H. J. Zhao, W. Cai, L. X. Gao and X. An, Crystallization kinetics and martensitic transformation of Ti 49 Ni 46.5 Ce 4.5 alloy thin film, Vacuum, 2010, 84(9), 1138–1141 CrossRef CAS.
- H. E. Kissinger, Reaction Kinetics in Differential Thermal Analysis, Anal. Chem., 1957, 29(11), 1702–1706 CrossRef CAS.
- K. Kadau, P. Entel, T. C. Germann, P. S. Lomdahl, B. L. Holian, K. Kadau, P. Entel and T. C. Germann, et al., Large-scale molecular-dynamics study of the nucleation process of martensite in Fe-Ni alloys, J. Phys. IV, 2001, 11(8), 8–17 Search PubMed.
- G. Bonny, R. C. Pasianot and L. Malerba, Fe–Ni many-body potential for metallurgical applications, Modell. Simul. Mater. Sci. Eng., 2009, 17(2), 025010 CrossRef.
- D. Janovszky, J. Sólyom, A. Roósz and Z. Czigány, Crystallization of Fe-Ni based amorphous alloy, Mater. Sci. Forum, 2007, 537, 185–190 Search PubMed.
- H. Chang and S. Sastri, Crystallization of a Fe-Ni base amorphous alloy, Metall. Trans. A, 1977, 8(7), 1063–1070 CrossRef.
- Z. H. Wang, E. J. Guo, C. L. Tan and X. H. Tian, Crystallization kinetics of Ni51Mn36Sn13 free-standing alloy thin films, Vacuum, 2016, 130, 124–129 CrossRef CAS.
- X. H. Tian, Z. H. Wang, J. C. Zhu, C. L. Tan, K. Zhang, Z. Yu and W. CAI, The effect of Fe doping on the crystallization kinetics of Ni-Mn-Sn freestanding alloy thin films, J. Non-Cryst. Solids, 2018, 495, 19–26 CrossRef CAS.
- O. Verners, Y. K. Shin and A. C. T. V. Duin, Molecular dynamics simulation of Al grain mixing in Fe/Ni matrices and its influence on oxidation, J. Appl. Phys., 2013, 114(2), 023501.1–023501.15 CrossRef.
- C. Ni, H. Ding and X. J. Jin, Grain size dependence of the martensitic transformation in a nano-grained Fe–Ni polycrystal–A molecular dynamics study, J. Alloys Compd., 2013, 546, 1–6 CrossRef CAS.
- J. M. Rickman, W. S. Tong and K. Barmak, Impact of heterogeneous boundary nucleation on transformation kinetics and microstructure, Acta Mater., 1997, 45(3), 1153–1166 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |