Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The radical scavenging activity of 1-methyl-1,4-dihydronicotinamide: theoretical insights into the mechanism, kinetics and solvent effects†
Quan V. Vo *a,
Nguyen Thi Hoaa and
Adam Mechler
*a,
Nguyen Thi Hoaa and
Adam Mechler *b
*b
aThe University of Danang – University of Technology and Education, Danang 550000, Vietnam. E-mail: vvquan@ute.udn.vn
bDepartment of Biochemistry and Chemistry, La Trobe University, Victoria 3086, Australia. E-mail: a.mechler@latrobe.edu.au
First published on 20th November 2024
Abstract
1,4-Dihydronicotinamide derivatives, including 1-methyl-1,4-dihydronicotinamide (MNAH), are derivatives of the active center of nicotinamide coenzyme (NADH) and are therefore potent radical scavengers. MNAH serves as a useful model of NADH that allows for modeling studies to address the activity of this important biomolecule. In this work, MNAH activity was evaluated against typical free radicals using quantum chemical calculations in physiological environments, with a secondary aim of comparing activity against two physiologically relevant radicals of markedly different stability, HO˙, and HOO˙, to establish which of these is a better model for assessing antioxidant capacity in physiological environments. The HO˙ + MNAH reaction exhibited diffusion-limited overall rate constants in all media, including the gas phase. The HOO˙ antiradical activity of MNAH was also good, with overall rate constants of 2.00 × 104 and 2.44 × 106 M−1 s−1, in lipid and aqueous media, respectively. The calculated rate constant in water (koverall(MNAH + HOO˙) = 3.84 × 105 M−1 s−1, pH = 5.6) is in good agreement with the experimental data (kexp(NADH + HOO˙) = (1.8 ± 0.2)×105 M−1 s−1). In terms of mechanism, the H-abstraction of the C4–H bond characterized the HOO˙ radical scavenging activity of MNAH, whereas HO˙ could react with MNAH at several sites and following either of SET (in polar media), RAF, and FHT reactions, which could be ascribed to the high reactivity of HO˙. For this reason the results suggest that activity against HOO˙ is a better basis for comparison of anti-radical potential. In the broader context, the HOO˙ scavanging activity of MNAH is better than that of reference antioxidants such as trans-resveratrol and ascorbic acid in the nonpolar environment, and Trolox in the aqueous physiological environment. Therefore, in the physiological environment, MNAH functions as a highly effective radical scavenger.
1. Introduction
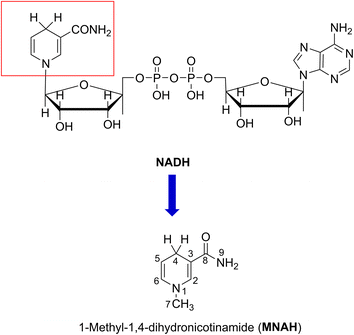
Reactive oxygen species (ROS) are molecules that are extremely reactive and are primarily produced by the mitochondrial electron transport chain.1 Under normal circumstances, ROS are generated as natural biproducts of normal metabolic processes and also serve a variety of functions in healthy physiological processes. For example, they activate signaling pathways to initiate biological processes as “secondary messengers”.2 Oxidative stress is the result of an imbalance between the antioxidant defense system and ROS production.3 It is also crucial to preserve the equilibrium of ROS in bone homeostasis and pathology.4 Nicotinamide coenzyme (NADH) is a natural redox factor that is crucial for the reduction of ROS; it is a ubiquitous hydride and electron source that participates in a diverse array of biochemical processes that occur in vivo.5–7 The mechanism of oxidoreductase primarily relies on the cycling of nicotinamide adenine dinucleotide (NAD) and its reduced form, NADH. The NAD redox pair (NAD+/NADH) serves as a coenzyme essential for oxidoreductase metabolism.8–12Since the active center of NADH is dihydronicotinamide (Fig. 1), which contains two weak C4–H bonds; the radical scavenging could occur directly there following the formal hydrogen transfer mechanism.13 The nicotinamide component may also react with highly-reactive ROS, such as HO˙ radicals, through the radical adduct formation (RAF) and either the hydrogen transfer pathway or single electron transfer (SET). Nevertheless, this matter has not yet been thoroughly investigated.
The hydroxyl radical is a prevalent and highly reactive species among free radicals. It is identified as the primary effector of tissue damage caused by ionizing radiation and oxidative damage to DNA.14,15 Because of its high reactivity its physiological lifetime is short, therefore the ideal way of reducing oxidative stress due to HO˙ would be to inhibit the production of hydroxyl radicals.16 Due to its dominant role in pathologic processes it is quite common in the literature to investigate radical scavenging activity against the hydroxyl radical, and it is indeed crucial if the focus is on evaluating the degradation of organic compounds.17–19 On the other hand, the HO˙ model may not be an effective way to compare the radical scavenging activity of organic compounds due to the inherent high reactivity of this radical. A more representative model of the typical less reactive radicals is the HOO˙ radical, and thus it is a better alternative for computational studies to evaluate the yet unknown free radical scavenging activity of compounds.16,17,19 To highlight this issue in this study we examine and compare activity against HO˙ and HOO˙.
Previous studies demonstrated that the HO˙/HOO˙ radical scavenging activity of organic compounds can be accurately modeled by quantum chemical methods.20–22 Using this method, we modeled the kinetics and mechanism of the HO˙/HOO˙ scavenging activity of 1-methyl-1,4-dihydronicotinamide (MNAH) (Fig. 1), the active center of NADH, in physiological environments.
2. Computational methods
The kinetic calculations in this study were conducted in accordance with the quantum mechanics-based test for overall free radical scavenging activity (QM-ORSA) protocol, combined with the SMD solvation model23 procedure for pentyl ethanoate and water solvents.17,24–27 The traditional transition state theory (TST) at a temperature of 298.15 K and a standard state of 1 M was used to compute the rate constant (k) as outlined in eqn (1) by using the Eyringpy code.26 (more information method in Table S1, ESI†):28–33
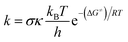 | (1) |
Gaussian 16 software37 was employed to conduct all calculations at the M06-2X/6-311++G(d,p) level of theory, which was previously identified as an appropriate model chemistry for this application.38,39
3. Results and discussions
3.1. The radical scavenging in the gas phase
| Mechanisms | Positions | BDE | ΔG° | |
|---|---|---|---|---|
| HO˙ | HOO˙ | |||
| FHT | C4–H | 71.2 | −45.8 | −14.6 |
| C7–H | 90.9 | −26.1 | 5.1 | |
| N9–H | 109.9 | −6.2 | 25.1 | |
| RAF | C2 | −23.1 | ||
| C3 | −17.4 | |||
| C5 | −25.7 | |||
| C6 | −20.2 | |||
| SET | 139.6 | 144.3 | ||
The findings revealed that most reactions between HO˙ and MNAH were thermodynamically favorable (ΔG° < 0), except for the SET reaction (ΔG° = 139.6 kcal mol−1). The MNAH + HOO˙ reaction was only spontaneous at the FHT (C4–H, ΔG° = −14.6 kcal mol−1), whereas those of other mechanisms, such as the SET and FHT (C7–H and N9–H), are not thermodynamically spontaneous (ΔG° = 5.1–144.3 kcal mol−1). The H-abstraction of C4–H is the most preferred thermodynamically MNAH + HO˙ reaction (ΔG° = −45.8 kcal mol−1, BDE = 71.2 kcal mol−1). Thus, this could make a significant contribution to the HO˙ radical scavenging activity of MNAH. Nevertheless, the MNAH + HO˙ reaction could also follow the RAF reactions at C2, C3, C5, and C6 and the FHT (C7–H) due to the low negative ΔG° values (ΔG° = −17.4 to −26.1 kcal mol−1). The HO˙/HOO˙ radical scavenging activity of MNAH may not involve the H-abstraction of N9–H due to the high BDE and ΔG° values (BDE = 109.9 kcal mol; ΔG° = −6.2 and 25.1 kcal mol−1 for HO˙ and HOO˙ radicals, respectively). Consequently, the kinetics of the HO˙/HOO˙ radicals scavenging activity of MNAH were evaluated at all of the sites of spontaneous reactions (ΔG° < 0).
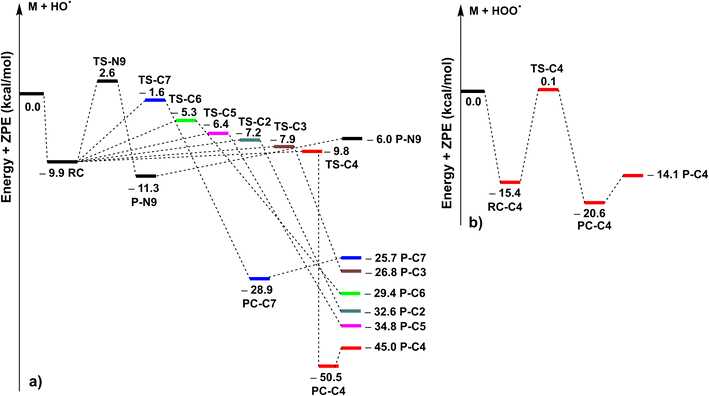 | ||
| Fig. 2 The PES of the MNAH + HO˙ (a)/HOO˙ (b) reactions at the spontaneous reactions (RC: pre-complex; TS: transition state; PC: post-complex; P: product). | ||
The kinetics of the MNAH + HO˙/HOO˙ reactions were calculated by using the QM-ORSA methodology.17 The results are presented in Table 2, whereas the optimized structures and the SOMO orbitals of transition states (TS) are shown in Fig. 3 and S1, ESI,† respectively. In the gas phase, the FHT reaction of the C4–H with HO˙ radicals was barrierless (ΔG≠ ≈ 0 kcal mol−1, kEck = 6.02 × 1012 M−1 s−1, Γ = 27.1%), whereas that of C7–H and N9–H bonds had no contribution to the radical scavenging activity with kEck = 1.39 × 1010 M−1 s−1 (Γ = 0.1%) and 5.60 × 107 M−1 s−1 (Γ = 0.0%), respectively. At the same time, the RAF reactions at C2, C3, and C5 form a substantial part of the overall MNAH + HO˙ reaction with ΔG≠ ≈ 0 kcal mol−1, kEck = 6.02 × 1012 M−1 s−1, Γ = 27.1% for each position. The addition reaction at the C6 location contributed only about 1.1% to the overall rate constant. Thus in the gas phase, the MNAH + HO˙ reaction was rapid and defined by the FHT(C4–H) and RAF(C2, C3, and C5) mechanisms with the overall rate constant koverall = 2.22 × 1013 M−1 s−1, whereas the MNAH + HOO˙ reaction was moderate and characterized by the FHT(C4–H) with koverall = 2.83 × 106 M−1 s−1. The main products of the MNAH + HO˙ reaction in the gas phase were P-C2 (27.1%), P-C3 (27.1%), P-C4 (27.1%), and P-C5 (17.6%), whereas for the MNAH + HOO˙ reaction P-C4(HOO) was the only product (100%) (Fig. 2 and Table 2).
| Radicals | Mechanisms | Positions | ΔG≠ | κ | kEck | Γ |
|---|---|---|---|---|---|---|
| a Γ = kEck·100/koverall. | ||||||
| HO˙ | FHT | C4–H | 0.0 | 1.0 | 6.02 × 1012 | 27.1 |
| C7–H | 3.9 | 1.6 | 1.39 × 1010 | 0.1 | ||
| N9–H | 8.9 | 30.2 | 5.60 × 107 | 0.0 | ||
| RAF | C2 | 0.0 | 1.0 | 6.02 × 1012 | 27.1 | |
| C3 | 0.0 | 1.0 | 6.02 × 1012 | 27.1 | ||
| C5 | 0.3 | 1.0 | 3.91 × 1012 | 17.6 | ||
| C6 | 2.0 | 1.0 | 2.35 × 1011 | 1.1 | ||
| koverall | 2.22 × 1013 | |||||
| HOO˙ | FHT | C4–H | 9.1 | 2.1 | 2.83 × 106 | 100.0 |
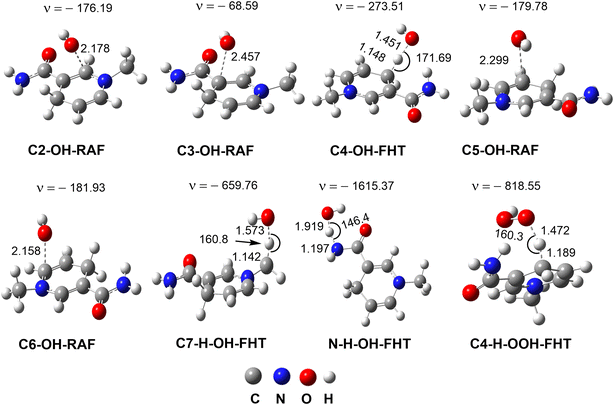 | ||
| Fig. 3 The optimized transition states of the RAF and FHT mechanisms in the MNAH + HO˙/HOO˙ reactions (ν in cm−1, bond length in Å). | ||
The extremely high theoretical rate constant for the MNAH + HO˙ reaction (koverall = 2.22 × 1013 M−1 s−1) suggests that the reaction is diffusion-limited even in the gas phase where the collision rate at the given temperature would limit the reaction to 109–1010 M−1 s−1. Hence the activity against HO˙ radical is not a useful basis for comparison. On the other hand, the HOO˙ radical scavenging activity of MNAH is comparable to the reference antioxidant Trolox (k(HOO˙ + Trolox) = 1.87 × 107 M−1 s−1).33 This suggests that MNAH may exhibit a good radical scavenging activity in the physiological environment that warrants further investigation.
3.2. The HO˙/HOO˙ scavenging activity of MNAH in the physiological environments
| Radicals | Mechanism | Pentyl ethanoate | Water | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔG≠ | κ | kapp | Γ | ΔG≠ | κ | kapp | kf | Γ | |||
| a The nuclear reorganization energy (λ, in kcal mol−1). | |||||||||||
| HO˙ | SET | 2.5 | 4.6a | 7.40 × 109 | 7.40 × 109 | 26.7 | |||||
| FHT | C4–H | ∼0 | 1.0 | 3.20 × 109 | 18.9 | ∼0 | 1.0 | 3.10 × 109 | 3.10 × 109 | 11.2 | |
| C7–H | 4.4 | 1.8 | 2.20 × 109 | 13.0 | ∼0 | 1.0 | 3.10 × 109 | 3.10 × 109 | 11.2 | ||
| N9–H | 12.0 | 37.6 | 3.80 × 105 | 0.0 | ∼0 | 1.0 | 2.90 × 109 | 2.90 × 109 | 10.5 | ||
| RAF | C2 | 1.7 | 1.0 | 2.60 × 109 | 15.4 | ∼0 | 1.0 | 2.60 × 109 | 2.60 × 109 | 9.4 | |
| C3 | 1.5 | 1.0 | 3.20 × 109 | 18.9 | ∼0 | 1.0 | 3.00 × 109 | 3.00 × 109 | 10.8 | ||
| C5 | 1.0 | 1.0 | 3.10 × 109 | 18.3 | ∼0 | 1.0 | 3.00 × 109 | 3.00 × 109 | 10.8 | ||
| C6 | 2.0 | 1.0 | 2.60 × 109 | 15.4 | ∼0 | 1.0 | 2.60 × 109 | 2.60 × 109 | 9.4 | ||
| koverall | 1.69 × 1010 | 2.77 × 1010 | |||||||||
| HOO˙ | SET | 11.1 | 16.6a | 4.30 × 104 | 4.30 × 104 | 1.8 | |||||
| FHT | C4–H | 11.9 | 1.6 | 2.00 × 104 | 9.3 | 2.4 | 2.40 × 106 | 2.40 × 106 | 98.2 | ||
| koverall | 2.00 × 104 | 2.44 × 106 | |||||||||
In pentyl ethanoate:
| koverall(HO˙) = Σkapp(RAF) + Σkapp(FHT) | (2) |
| koverall(HOO˙) = kapp(FHT(C4–H)) | (3) |
In water:
| koverall(HO˙) = kf(SET) + Σkf(RAF) + Σkf(FHT) | (4) |
| koverall(HOO˙) = kf(FHT) + kf(SET) | (5) |
The koverall values for the MNAH + HO˙ reaction in the nonpolar and aqueous environments were 1.69 × 1010 and 2.77 × 1010 M−1 s−1, respectively. The koverall of the MNAH + HOO˙ reaction is slower compared to the hydroxyl radical, with values of 2.00 × 104 and 2.44 × 106 M−1 s−1 in the pentyl ethanoate and water solvents, respectively. It is important to notice that the pKa value of the HOO˙ radical is 4.88. Consequently, the molar fraction of HOO˙ is 0.137 at pH = 5.6, resulting in a koverall(MNAH + HOO˙) of 3.84 × 105 M−1 s−1. This is in excellent agreement with the experimental data (kexp(NADH + HOO˙) = (1.8 ± 0.2)×105 M−1 s−1).45 It was found that the HO˙ scavenging activity of MNAH was defined by the FHT of C4–H and C7–H positions (31.9%) and RAF (68.0%) reactions in the nonpolar environment. Conversely, the H-abstraction of N9–H bond did not contribute to the MNAH + HO˙ reaction. On the other hand, the H-abstraction of the C4–H bond dominated the activity against HOO˙ (100%).
The HO˙ antiradical activity in the polar environment is a combination of all analyzed mechanisms (FHT (32.9%), SET (26.7%) and RAF (40.4%)). Formal hydrogen transfer was the driving force behind the activity against the HOO˙ radical, where the SET reaction contributed only 1.8% of the overall rate constant. Based on the findings, the FHT and RAF reactions with HO˙ radicals in the aqueous physiological environment were barrierless (ΔG≠ ≈ 0 kcal mol−1). Consequently, the kapp values of these processes were diffusion-limited (cannot exceed diffusion rates kD) and accounted for approximately 73.3% of the overall rate constant.
According to the results the MNAH + HO˙ reaction is practically diffusion-limited under all conditions, including the gas phase. On the other hand, the activity against HOO˙ was more nuanced. MNAH exhibits a higher HOO˙ antiradical activity in the lipid medium than trans-resveratrol (∼1.5 times, k = 1.31 × 104 M−1 s−1)46 and ascorbic acid (∼3.5 times, k = 5.71 × 103 M−1 s−1),17 but it is inferior to Trolox (∼5.0 times, k = 1.00 × 105 M−1 s−1).33 In the polar medium MNAH exhibits a higher activity than Trolox (∼18.5 times, k = 1.30 × 105 M−1 s−1),33 but it is weaker than ascorbic acid and trans-resveratrol. The markedly different activity against the two radicals is arguably the result of the high reactivity of HO˙ and not the exceptional specific activity of MNAH in targeting and eliminating HO˙. Thus our results underscore the importance of comparing antioxidant activity against the less reactive free radicals that have longer lifetimes under physiological conditions. Nevertheless, our results suggest that MNAH is an efficient radical scavenger in key physiological environments.
4. Conclusions
The radical scavenging activity of MNAH against HO˙ and HOO˙ was assessed through density functional theory calculations. In the lipid and water media, the koverall values of the HO˙ + MNAH reaction were 1.69 × 1010 and 2.77 × 1010 M−1 s−1, respectively. The HOO˙ radical scavenging activity was measured at 2.00 × 104 and 2.44 × 106 M−1 s−1. In water, at pH = 5.6, the calculated rate constant (koverall(MNAH + HOO˙) = 3.84 × 105 M−1 s−1) is in good agreement with the experimental data (kexp(NADH + HOO˙) = (1.8 ± 0.2)×105 M−1 s−1) and could verify the accuracy of the computing method. In both nonpolar and polar media, the HOO˙ antiradical activity of MNAH was defined by the H-abstraction of the C4–H bond, whereas the HO˙ antiradical activity was determined by a combination of the SET (in polar media), RAF, and FHT reactions. The hydroperoxyl radical scavenging activity of MNAH is greater than that of trans-resveratrol and ascorbic acid in the lipid medium, and Trolox in the aqueous physiological environment. The results have verified the potent radical scavenger role of MNAH in physiological environments, also highlighting that HOO˙ is a better model for comparing antiradical activity than the highly reactive HO˙.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Funds for Science and Technology Development of the University of Danang under project number B2021-DN01-01 (Q. V. V.).References
- A. A. Alfadda and R. M. Sallam, BioMed Res. Int., 2012, 2012, 936486 Search PubMed.
- R. L. Auten and J. M. Davis, Pediatr. Res., 2009, 66, 121–127 CrossRef CAS PubMed.
- J. S. Kimball, J. P. Johnson and D. A. Carlson, J. Bone Jt. Surg., 2021, 103, 1451–1461 CrossRef PubMed.
- R. S. Balaban, S. Nemoto and T. Finkel, Cell, 2005, 120, 483–495 CrossRef CAS PubMed.
- S. Immanuel, R. Sivasubramanian, R. Gul and M. A. Dar, Chem.–Asian J., 2020, 15, 4256–4270 CrossRef CAS PubMed.
- S. Zhang, J. Shi, Y. Chen, Q. Huo, W. Li, Y. Wu, Y. Sun, Y. Zhang, X. Wang and Z. Jiang, ACS Catal., 2020, 10, 4967–4972 CrossRef CAS.
- T. Knaus, C. E. Paul, C. W. Levy, S. De Vries, F. G. Mutti, F. Hollmann and N. S. Scrutton, J. Am. Chem. Soc., 2016, 138, 1033–1039 CrossRef CAS PubMed.
- H. Wu, C. Tian, X. Song, C. Liu, D. Yang and Z. Jiang, Green Chem., 2013, 15, 1773–1789 RSC.
- X. Wang, T. Saba, H. H. Yiu, R. F. Howe, J. A. Anderson and J. Shi, Chem, 2017, 2, 621–654 CAS.
- S.-J. Lin and L. Guarente, Curr. Opin. Cell Biol., 2003, 15, 241–246 CrossRef CAS PubMed.
- F. H. Ahmed, A. E. Mohamed, P. D. Carr, B. M. Lee, K. Condic-Jurkic, M. L. O'Mara and C. J. Jackson, Protein Sci., 2016, 25, 1692–1709 CrossRef CAS PubMed.
- T. Rawling, H. MacDermott-Opeskin, A. Roseblade, C. Pazderka, C. Clarke, K. Bourget, X. Wu, W. Lewis, B. Noble and P. A. Gale, Chem. Sci., 2020, 11, 12677–12685 RSC.
- Y.-H. Fu, Z. Wang, K. Wang, G.-B. Shen and X.-Q. Zhu, RSC Adv., 2022, 12, 27389–27395 RSC.
- L. P. Candeias and S. Steenken, Chem.–Eur. J., 2000, 6, 475–484 CrossRef CAS PubMed.
- C. Chatgilialoglu, M. D'Angelantonio, M. Guerra, P. Kaloudis and Q. G. Mulazzani, Angew. Chem., Int. Ed., 2009, 48, 2214–2217 CrossRef CAS PubMed.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed.
- T. Marino, A. Galano and N. Russo, J. Phys. Chem. B, 2014, 118, 10380–10389 CrossRef CAS PubMed.
- Q. V. Vo, M. V. Bay, P. C. Nam, D. T. Quang, M. Flavel, N. T. Hoa and A. Mechler, J. Org. Chem., 2020, 85, 15514–15520 CrossRef CAS PubMed.
- H. Boulebd, N. M. Tam, A. Mechler and Q. V. Vo, New J. Chem., 2020, 44, 16577–16583 RSC.
- F. Sarrami, L.-J. Yu and A. Karton, J. Comput.-Aided Mol. Des., 2017, 31, 905–913 CrossRef CAS PubMed.
- A. Karton, R. J. O'Reilly, D. I. Pattison, M. J. Davies and L. Radom, J. Am. Chem. Soc., 2012, 134, 19240–19245 CrossRef CAS PubMed.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 40, 2103–2110 CrossRef CAS PubMed.
- J. R. l. Alvarez-Idaboy and A. Galano, J. Phys. Chem. B, 2012, 116, 9316–9325 CrossRef CAS PubMed.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, Mérida, Yucatán, 2018 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS.
- E. Vélez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971–977 CrossRef.
- H. Boulebd, A. Mechler, N. T. Hoa and Q. Van Vo, New J. Chem., 2020, 44, 9863–9869 RSC.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. aramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095–1099 CrossRef CAS PubMed.
- K. U. Ingold and D. A. Pratt, Chem. Rev., 2014, 114, 9022–9046 CrossRef CAS PubMed.
- A. Galano, G. Mazzone, R. Alvarez-Diduk, T. Marino, J. R. Alvarez-Idaboy and N. Russo, Annu. Rev. Food Sci. Technol., 2016, 7, 335–352 CrossRef CAS PubMed.
- C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, J. Phys. Chem. B, 2011, 115, 12234–12246 CrossRef CAS PubMed.
- Q. V. Vo, N. T. Hoa, P. C. Nam, T. Q. Duong and A. Mechler, New J. Chem., 2023, 47, 10381–10390 RSC.
- A. Galano, A. Pérez-González, R. Castañeda-Arriaga, L. Muñoz-Rugeles, G. Mendoza-Sarmiento, A. Romero-Silva, A. Ibarra-Escutia, A. M. Rebollar-Zepeda, J. R. León-Carmona, M. A. Hernández-Olivares and J. R. Alvarez-Idaboy, J. Chem. Inf. Model., 2016, 56, 1714–1724 CrossRef CAS PubMed.
- A. Nadezhdin and H. Dunford, J. Phys. Chem., 1979, 83, 1957–1961 CrossRef CAS.
- M. Cordova-Gomez, A. Galano and J. R. Alvarez-Idaboy, RSC Adv., 2013, 3, 20209–20218 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07184k |
| This journal is © The Royal Society of Chemistry 2024 |