Open Access Article
Open Access ArticleEffect of catholyte in a single step electrochemical hydroiodic acid decomposition for hydrogen production using the iodine–sulfur thermochemical cycle
Ashwin Yashawanth Hegdea,
Saroj Chaudharyb,
Parvatalu Damarajub and
Pradeep Kumar Sow *a
*a
aDepartment of Chemical Engineering, BITS Pilani, K K Birla Goa Campus, Zuarinagar, Goa 403726, India. E-mail: pradeeps@goa.bits-pilani.ac.in
bOil and Natural Gas Corporation (ONGC) Energy Centre, India
First published on 19th December 2024
Abstract
This study identifies the most suitable catholyte for the electrochemical HI decomposition process, an emerging single-step alternative to the conventional multistep HI section of the I–S thermochemical cycle for hydrogen production. Four catholytes, H2O, H3PO4, H2SO4, and HI, were shortlisted based on compatibility with the I–S cycle and ability to support the hydrogen evolution. Polarization studies in a two-compartment electrochemical cell revealed a similar order of onset potentials for the electrochemical HI decomposition across all four catholyte electrolytes. However, the performance at higher overpotentials following the onset of the electrochemical HI decomposition followed the order H2SO4 > HI > H3PO4 > H2O. The polarization behavior was not found to vary significantly with the catholyte concentration. Model fitting revealed that the invariance in polarization behavior with the catholyte concentration arose from the compensation between the changes in activation overpotentials with the open-circuit voltage. The onset potential was predominantly influenced by the I2/HI ratio in the anolyte, with higher ratios resulting in an increase in the onset potentials for electrochemical HI decomposition. Polarization studies identified H2SO4 and HI as the most promising catholytes for further investigation. Consequently, continuous electrochemical HI decomposition and hydrogen production was demonstrated with H2SO4 and HI as the catholyte for three I2/HI ratios of 0.25, 0.5, and 1 at two different current densities, with an average current efficiency of ∼97%. Among the two acids, H2SO4 showed higher current efficiency and lower energy consumption per mole of hydrogen compared to HI under the similar anolyte configuration and current density.
1. Introduction
Hydrogen is an efficient energy carrier and, when derived from renewable energy sources such as solar, wind, or nuclear, has the potential to be a carbon-neutral fuel and thereby reduce greenhouse gas emissions. In addition to the direct water electrolysis, the thermochemical cycles, especially the iodine–sulfur (I–S) thermochemical cycle, has been considered a promising approach suitable for large-scale hydrogen production.1 The I–S thermochemical cycle is a promising green hydrogen production strategy that can integrate renewable energy sources like solar, wind, or nuclear power.2 Overall, the I–S thermochemical cycle comprises three primary reactions, namely the Bunsen reaction, the hydroiodic acid (HI) decomposition reaction, and the sulfuric acid (H2SO4) decomposition reaction, as given below:| Bunsen reaction: SO2 + I2 + 2H2O → H2SO4 + 2HI (290–390 K) | (1) |
| H2SO4 decomposition: H2SO4 → H2O + SO2 + 0.5O2 (970–1270 K) | (2) |
| HI decomposition: 2HI → H2 + I2 (570–770 K) | (3) |
Various studies and reports on the thermochemical cycles have consistently listed the I–S thermochemical cycle as one of the promising thermochemical cycle for large-scale hydrogen production.1,3–5 Studies have shown that the I–S thermochemical cycle can attain thermal efficiencies greater than 50%.6,7 The open-loop variant of the I–S thermochemical cycle offers a significant simplification by omitting the H2SO4 decomposition step. This elimination of the H2SO4 decomposition step not only simplifies the process but also yields H2SO4 as a valuable byproduct, which has considerable commercial significance.8 Sulfuric acid is in high demand across various sectors of the chemical industry, particularly in producing fertilizers, where it is required in substantial quantities. Additionally, this modification enhances the overall thermal efficiency of the open-loop I–S cycle, achieving values exceeding 81%.6 Nevertheless, the above process does involve multiple challenges, such as the need for high temperatures, holdup of materials, excess amount of iodine and water requirement, which increases the energy consumption in the HI section, high iodine (I2) losses, and the highly corrosive nature of the chemicals used.9,10 In addition to the above, the precipitation of iodine and the associated clogging of pipes also present significant challenges for the I–S cycle.11 Various recent studies have elaborated on the system modelling-based assessment of the thermochemical I–S cycle.12,13 Many of the I–S thermochemical cycle challenges are associated with the HI section, originating with the Bunsen reaction. The Bunsen reaction produces an HI–I2–H2O mixture, referred to as the HIx solution. The phase separation of the two acids phases, HI and H2SO4, produced in the Bunsen reaction is achieved when I2 is in excess.14 Furthermore, excess water is required to make the reaction thermodynamically favorable.15 The excess reactants are further required to reduce the side reactions associated with the Bunsen reaction.16 A significantly high amount of energy is required to process the excess water and iodine in the stream, resulting in a high energy demand for the HI section.17,18 It is to be noted that both the acids produced in the Bunsen reaction are required to be concentrated before the decomposition process. However, the concentration process for the HI produced in the Bunsen reaction is complicated by the formation of azeotrope, which renders the conventional distillation-based separation redundant. Consequently, alternative concentration strategies are employed, including electro-electrodialysis,8,9 extractive distillation,10 etc. Recently, pressure-swing distillation method has also been reported for the purification of HI from the HIx (HI–I2–H2O) mixture.19 In addition to the significant energy requirement of the HI section, the HIx solution is highly corrosive, requiring unique corrosion resistance materials, significantly increasing the associated capital costs.20 Specifically, it has been observed that the HIx present in the HI section is far more corrosive than HI alone.21 The need for multiple processing steps further exacerbates the high capital requirement for fabricating corrosion-resistant materials. The conventional thermal HI decomposition also suffers from low conversion efficiency, where most of the reported studies found the HI decomposition conversion to be within 20–30%.22 Advanced designs such as the use of U-shaped decomposer for the HI decomposition reaction have also been developed, where the HI conversion has been found up to ∼22%.23 For the scale up designs of the continuous HI decomposer using a Pt–Ir/C catalyst with the H2 production rate of 100 L h−1, the HI decomposition rate was approximately 22%.24 The lower conversion increases the quantity of recycled chemicals, thereby increasing the cycle energy demand.
As an alternative to the pre-concentration step followed by thermal HI decomposition, an electrochemical HI decomposition strategy can realize hydrogen production at lower temperatures without needing the above azeotropic composition of HI. The generalized scheme of electrochemical HI decomposition cell involves a two-compartment electrochemical cell, separated by an ion exchange membrane, with each compartment housing the cathode and the anode.25–30 The hydrogen evolution reaction (HER) occurs at the cathode through the proton reduction, while iodide and tri-iodide ion oxidation occurs at the anode.26,30 The output HIx from the Bunsen reaction serves as the anolyte. The effect of the HIx concentration in the anolyte on the performance of the electrochemical HI decomposition has been reported.27,30 Cation exchange membranes, including commercial Nafion membrane,26 and sulfonated (PVDF-co-HFP)–graphene oxide composite polymer electrolyte membrane,25 have been studied for their effectiveness in the process. In most of the reported studies, a constant hydrogen production rate has been demonstrated.26,27 Flowsheet development for the integrated electrochemical HI decomposition demonstrated thermal efficiencies ranging from 25–42%, depending on waste heat utilization, and 33.3% considering internal heat exchange.27 Additional simulation studies showed the energy and exergy efficiencies estimated to be 15.3–31.0% and 32.8%, respectively. Most exergy destruction occurred in the H2SO4 decomposer and condenser, accounting for 93.0% and 63.4%, respectively. The electrochemical HI decomposition has been shown to have a high exergy efficiency of 92.4% when integrated with I–S cycle.28 In most previously reported studies, water has been widely employed as the catholyte.25–29 In addition, HI and H2SO4 have also been reported as the catholytes for realizing electrochemical HI decomposition.30–32 However, the choice of catholyte and the impact of the catholyte concentration on the performance of electrochemical HI decomposition has not been reported. Since the catholyte contributes significantly towards the overpotential losses, it is crucial to investigate the influence of the catholyte on system performance.30
Here, we have shortlisted four potential electrolytes and have conducted a detailed analysis of the effect of catholyte and their concentration on the electrochemical interactions and the performance of the electrochemical HI decomposition system. The impact of electrolytes on HER was initially studied using a three-electrode setup, and the electrochemical HI decomposition system's performance was assessed through polarization (I–V) curves. Experimental data were modelled to identify overpotential components and understand variations in behavior. Additionally, we analyzed the emergent effects of I2/HI ratio changes in the anolyte for each catholyte. Based on these findings, we selected HI and H2SO4 for further continuous flow studies, where hydrogen production was successfully demonstrated, and performance parameters, including current efficiency and energy consumption, were evaluated. Among the studied catholytes, H2SO4 offers the best performance with the lowest energy requirement and highest current efficiency. The crucial insights gained from this research can assist in further scaleup studies and the operation of the new scheme for the I–S cycle with integrated electrochemical HI decomposition.
2. Experimental section
2.1 Materials
HI (57%; Loba Chemicals, India) and I2 (99.8%; Loba Chemicals, India) were utilized to prepare the anolyte solutions in deionized water with three different I2/HI ratios of 0.25, 0.5, and 1. Sulfuric acid (H2SO4) (98% extra pure; Loba Chemicals), phosphoric acid (H3PO4) (85% extra pure; Loba Chemicals), and hydroiodic acid (57%; Loba Chemicals, India) and deionized (DI) water were used for the preparation of the catholyte. The chemicals were used without any further processing or refinement procedures. Platinum electrodes (99.9%) procured from Fisher Scientific Pvt Ltd, measuring 25 mm × 25 mm and with a thickness of 0.25 mm, were utilized as electrodes for the two-compartment cell investigations. Nafion-117, procured from Fisher Scientific Pvt Ltd, was used as the proton exchange membrane (PEM) separator.2.2 Catholyte selection for electrochemical HI decomposition
In principle, any proton source can facilitate the HER and thus function as a catholyte. Consequently, there exists a multitude of potential candidates for catholyte, presenting a challenge in terms of selection and performance evaluation. To address this, we have first streamlined this extensive list by prioritizing electrolytes compatible with the I–S cycle, capable of HER drawing inferences from the previously reported studies. The rationale guiding the selection of these electrolytes is elaborated below. In addition to being the most widely reported catholyte for the electrochemical HI decomposition, water is present throughout the I–S cycle and thus possesses the least potential for contamination and impacting associated processes.25–29 The earlier studies on the electrochemical HI decomposition with water as a catholyte establish the feasibility of HER with water. Water has the lowest cost among all the catholytes considered here, thus amplifying its appeal as a catholyte for electrochemical HI decomposition.H3PO4 is a proton source and has been utilized as an electrolyte for the HER.33 The use of H3PO4 has been demonstrated in earlier schemes of the I–S cycle in the HI section.34,35 Furthermore, H3PO4 being extremely hygroscopic, has been used to purify the HIx solution from the Bunsen reaction by breaking an azeotropic mixture comprising HI and H2O. H3PO4 has also been used in the precipitating agent-based approach for conducting Bunsen reactions.36 Based on the established compatibility with the I–S cycle, we have shortlisted H3PO4 as a potential candidate for the catholyte section of the electrochemical HI decomposition.
H2SO4 is the most commonly reported electrolyte for HER studies and electrolysis experiments. Furthermore, H2SO4 is one of the existing chemical components within the traditional and current scheme of the I–S thermochemical cycle as a part of the sulfur section. During the Bunsen reaction, H2SO4 interacts with the HIx phase directly, as in the traditional Bunsen reaction scheme, or indirectly, as in the membrane-based Bunsen reaction strategy.37,38 Cross-contamination was also observed during the HIx and H2SO4 phase interactions across a Nafion 117 ion exchange membrane.39 However, the presence of H2SO4 in HI solution has not been found to affect the iodide electrooxidation occurring in the anodic section.31 Furthermore, the electrochemical HI decomposition has been demonstrated with H2SO4 as the catholyte.31,32 Based on the established compatibility and minimal effect on the iodine–iodide redox reactions, we have shortlisted H2SO4 as a potential catholyte for the electrochemical HI decomposition.
HI is the common component with the anolyte section of the electrochemical HI decomposition cell system and, therefore, has the least potential for foreign component contamination compared to all the above-discussed acids. Our earlier work demonstrated the potential for hydrogen production using HI as the catholyte in an electrochemical HI decomposition system, supporting the use of HI as the potential catholyte.30 Based on the above discussion the four potential catholytes selected for the electrochemical HI decomposition are: H2O, H3PO4, H2SO4 and HI.
2.3 Three-electrode studies
A standard three-electrode glass cell (ALS Co. Ltd) was used for the cyclic voltammetry (CV) studies. The three-electrode studies were conducted with a platinum disk (0.5 mm diameter) as the working electrode, Ag/AgCl as reference electrode, and platinum coil as a counter electrode, respectively. The platinum working electrode was cleaned by polishing on a polishing pad before each experiment using alumina powder (0.05 micron). The studies were conducted for four electrolytes: H2SO4, H3PO4, HI, and water. The concentration of the three acids used in this study was maintained at a constant 0.5 M.2.4 Electrochemical studies with small-volume two-compartment cell
A small size batch scale two-compartment cell was used for the polarization studies with the cell design described in our previous work.30 Reduced electrolyte requirements with the miniaturized cell significantly lowered both testing costs and the generation of waste electrolytes. Overall, the cell body coming in contact with the electrolyte was fabricated with Teflon. The two compartments were separated by Nafion 117 membrane, and each of the two compartments housed a platinum plate electrode with exposed circular area of 10 mm diameter. The volume of each compartment was 0.785 ml. Programmed chronoamperometry was used to evaluate the polarization data, where the current was evaluated at varying voltage values. The electrochemical studies for the two-compartment cell and the three-electrode system were conducted utilizing BioLogic SAS VSP electrochemical workstation.2.5 Model for the polarization curve studies
The total voltage (V) in the electrochemical system comprises the contribution from the open circuit voltage (OCV), voltage loss to realize the charge transfer, referred to as the activation overpotential (ΔVact), ohmic overpotential (ΔVohmic) and the mass transfer overpotential (ΔVMT) represented mathematically as:40,41| V = OCV + ΔVact + ΔVohmic + ΔVMT | (4) |
Asymmetric electrolyte composition in the anolyte and the catholyte section and the resulting difference in the activity of the electrochemical species give rise to the OCV. The OCV corresponds to the measured voltage when no current flows through the external circuit. The reaction kinetics corresponding to the anodic and cathodic section of the electrochemical cell results in the activation overpotential represented as ΔVact. The activation overpotential (ΔVact) is represented as the sum of anodic and cathodic activation overpotentials using a simplified Tafel equation:
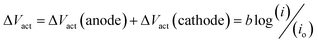 | (5) |
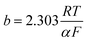 . Here, R is the ideal gas constant, T is the temperature, F is Faraday's constant, and α is the transfer coefficient. The ohmic overpotential loss can be described with a linear relationship between the current density and the voltage, given as:
. Here, R is the ideal gas constant, T is the temperature, F is Faraday's constant, and α is the transfer coefficient. The ohmic overpotential loss can be described with a linear relationship between the current density and the voltage, given as:| ΔVohmic = RΩ × i | (6) |
| ΔVMT = RMT × i | (7) |
Considering the activation overpotential losses, ohmic overpotential losses, and mass transfer overpotential losses, the total voltage V can be represented as
V = OCV − b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(io) + b log(io) + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(i) + RΩ × i + RMT × i = Vo + b log(i) + RΩ × i + RMT × i = Vo + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(i) + RT × i log(i) + RT × i
| (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(io), where Vo represents the current independent component. RT is referred to as the equivalent resistance corresponding to the resistive overpotential losses as (RT × i) and is the sum of the mass transfer and ohmic resistance given as RT = RΩ + RMT.44 The polarization curve providing current density (i) and the voltage (V) was fitted with the above equation using the non-linear least square method in MATLAB with the fitting parameters Vo, b, and RT. Post-fitting the experimentally obtained OCV was subtracted from the term Vo, and the evolution of the overall activation overpotential losses (Vo − OCV + b
log(io), where Vo represents the current independent component. RT is referred to as the equivalent resistance corresponding to the resistive overpotential losses as (RT × i) and is the sum of the mass transfer and ohmic resistance given as RT = RΩ + RMT.44 The polarization curve providing current density (i) and the voltage (V) was fitted with the above equation using the non-linear least square method in MATLAB with the fitting parameters Vo, b, and RT. Post-fitting the experimentally obtained OCV was subtracted from the term Vo, and the evolution of the overall activation overpotential losses (Vo − OCV + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(i)) were evaluated as a function of current density.
log(i)) were evaluated as a function of current density.
2.6 Continuous electrochemical HI decomposition
A symmetrical two-compartment electrochemical cell for HI decomposition was fabricated in-house, as shown in Fig. 1(a). Each of the two compartments of the electrochemical cell had a volume of 3.14 ml and was fabricated with Teflon considering its chemical resistance against HIx and other acids used in this study. Nafion 117 PEM divided the two compartments while providing an exposed circular area measuring 20 mm in diameter that allowed selective permeation of H+. Platinum electrodes were housed within each Teflon cell section at a distance of 10 mm from the membrane with a circular exposed area of 20 mm diameter. The overall design is similar to that used for the batch cell but with a higher electroactive area. All electrolysis experiments were conducted using a BioLogic SAS SP 200 electrochemical workstation.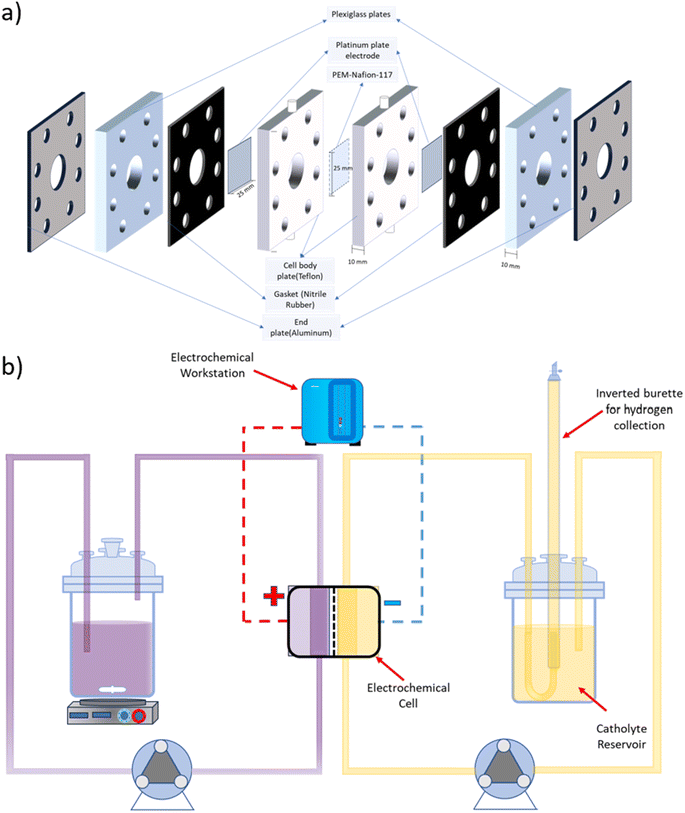 | ||
| Fig. 1 Schematic representation of (a) the two-compartment electrochemical HI decomposition cell and (b) the continuous flow system for electrochemical HI decomposition. | ||
A schematic representation of the experimental arrangement used for the continuous electrochemical HI decomposition is shown in Fig. 1(b). The setup comprised of the anolyte reservoir and the catholyte reservoir fitted with an inverted graduated burette as a gas collector with a U-type tube junction at the bottom of the burette to collect and simultaneously measure the gas volume by volume displacement method. The anolyte reservoir was placed on a magnetic stirrer to ensure the dissolution of iodine and homogenous concentration within the anolyte. Two peristaltic pumps, each for the anolyte and the catholyte section, were used to recirculate the electrolytes with the flow rates of 120 ml min−1. The electrochemical HI decomposition was conducted under constant current mode, and the volume of the hydrogen collected was quantified as a function of time.
The current efficiency was evaluated as the ratio of the experimentally observed hydrogen produced to the theoretical hydrogen production based on Faraday's law as:
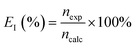 | (9) |
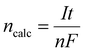 | (10) |
3. Results and discussion
3.1 Electrochemical behavior of catholyte in three-electrode system
The electrochemical behavior of four shortlisted catholytes has been studied using CV at varying scan rates, shown in Fig. 2. Here, the concentration of all the acids, HI, H2SO4, and H3PO4, were kept at 0.5 M. The CV analysis reveals similar features for H2SO4 and H3PO4 (Fig. 2(c) and (b)), whereas notable differences are observed in the CV profiles of H2O and HI. For H2SO4 and H3PO4, the positive potential region of the CV curves shows the presence of the platinum surface oxide formation–reduction reaction along with oxygen evolution. The middle zone of the CV corresponds to the double-layer effects on the platinum electrode. Since these electrolytes are to be used as the catholyte, the reduction potential regions become particularly important for the electrochemical HI decomposition process. In the negative potential CV region, features of hydrogen underpotential deposition and HER are observed in the forward scan, while desorption and hydrogen oxidation are seen in the reverse scan. Overall, the HER can be represented as:| 2H+ + 2e− → H2 | (11) |
 | ||
| Fig. 2 CV data obtained for the three-electrode system with Ag/AgCl reference at the scan rates of 20, 40, 60, 80, and 100 mV s−1 with the electrolytes (a) H2O (b) H3PO4 (c) H2SO4 and (d) HI. | ||
For all the acidic electrolytes H2SO4, H3PO4, and HI, the HER proceeds through the hydronium ion interactions. In particular, the HER is a multistep reaction that proceeds with either the Volmer–Heyrovsky or Volmer–Tafel pathway, where the elementary steps are given as:45–47
| H3O+ + e− + M → MHad + H2O (Volmer reaction step) | (12) |
| H3O+ + e− + MHad ↔ H2(g) + H2O + M (Heyrovsky reaction step) | (13) |
| 2MHad → H2(g) + 2M (Tafel Reaction step) | (14) |
Anions play a crucial role in various near-surface phenomena occurring within the electrode–electrolyte interface, affecting the electrochemical process through blocking of the active site, changes in the adsorption energy of the active sites neighbouring the absorbed anions, potential drop redistribution, surface restructuring.48 The anions have been shown to affect the platinum–hydrogen bonding and, consequently, the HER.49 The ability of the anion to affect the platinum–hydrogen surface bonding depends on the degree of solvation for the anion.48 Generally, a strongly solvated anion bonds weakly to the electrode surface, while a weakly solvated anion bonds strongly, with the possibility of direct chemical bonds.48 Furthermore, the anion in the electrolyte upon adsorbing on the platinum electrode surface can decrease the amount of adsorbed hydrogen or affect the energy distribution of absorbed hydrogen and the consequent HER process.49 For H2SO4 and H3PO4, the difference in the CV peak features indicates that the anionic species SO42− and PO43− affect the hydrogen adsorption process. Compared to the H2SO4 and H3PO4, iodide ions have been shown to absorb strongly on the platinum surface, reducing the hydrogen–platinum bond energy and the amount of absorbed hydrogen.49 In contrast to the SO42− and PO43− ions, the iodide ion contributed by the HI is electroactive within the electrochemical analysis window. Consequently, for the HI as the electrolyte, prominent anodic and cathodic peaks can be observed in Fig. 2(d) with significantly higher current values than the current values observed for all the other electrolytes. As the potential is scanned in the positive direction, the iodide ions present in the electrolyte get oxidized to tri-iodide and iodine as per the following reaction:
| 3I− ↔ I−3 + 2e− | (15) |
| 2I− ↔ I2 + 2e− | (16) |
| 2I3− ↔ 3I2 + 2e− | (17) |
Furthermore, the iodine produced as a result of the electrochemical reaction reacts homogeneously with the iodide ions to form tri-iodide ions given by the following equation:50
| I2 + I− ↔ I3−, Keq = 705–770 at 25 °C | (18) |
Upon reversing the potential scan, distinct electro-reduction peaks emerge, corresponding to the formation of iodide ions through the electro-reduction of the iodine and tri-iodide ions produced through the electrooxidation reaction during the forward cycle. After the iodide formation peak, the current increases again, corresponding to the HER process. It is to be noted that the typical underpotential hydrogen adsorption peaks are not prominently visible in the CV for HI, which are otherwise observable for the H2SO4 and H3PO4. This can be attributed to the reduced amount of absorbed hydrogen due to the strongly adsorbed I− ions on the platinum surface.49 Additionally, the higher magnitude of current associated with the iodine–iodide redox reaction also contributes to masking any CV features related to hydrogen adsorption–desorption. Nevertheless, the HER can be observed for all three acidic solutions studied here with varying anions.
Fig. 2(a) shows the CV for water as the electrolyte. The potential sweep in the positive direction shows the presence of oxygen evolution. Current peaks associated with the hydrogen adsorption–desorption can be observed for the negative potential scan. A similar two-step pathway comprising of Volmer–Heyrovsky or Volmer–Tafel pathway as that observed for the acidic system is expected for water. However, as a neutral electrolyte, water results in a lower number of available H+ ions than the acidic electrolyte. Consequently, the HER in the neutral solution proceeds through the water reduction process:47
| H2O + e− + M → MHad + OH− (Volmer reaction step) | (19) |
| H2O + e− + MHad ↔ H2(g) + M + OH− (Heyrovsky reaction step) | (20) |
| 2MHad → H2(g) + 2M (Tafel Reaction step) | (21) |
It is generally accepted that liberating a proton from water by dissociating H2O is kinetically difficult compared to acidic conditions where the proton is present as a hydronium ion.46,51 Furthermore, water dissociation introduces an additional energy barrier, contributing to the total energy barrier in the overall hydrogen evolution process from water.51 In contrast to the acidic electrolytes studied before, for neutral electrolytes such as water, the critical step that governs the rate of the HER involving the reduction of hydronium ions switches from being the Volmer–Tafel or Volmer–Heyrovsky step to the Volmer step, i.e., single-electron transfer to reduce H2O. The above results indicate that the pH and the anion present in the acid significantly affect the redox reaction mechanism and, therefore, are expected to affect the HER process for the electrochemical decomposition of HI. Overall, based on the CV studies, all four electrolytes selected for the studies can induce HER and, hence, can serve as the catholyte for the electrochemical HI decomposition process.
3.2 Polarization studies in two electrode cell system
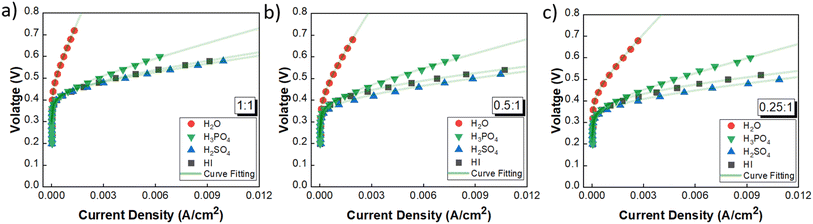
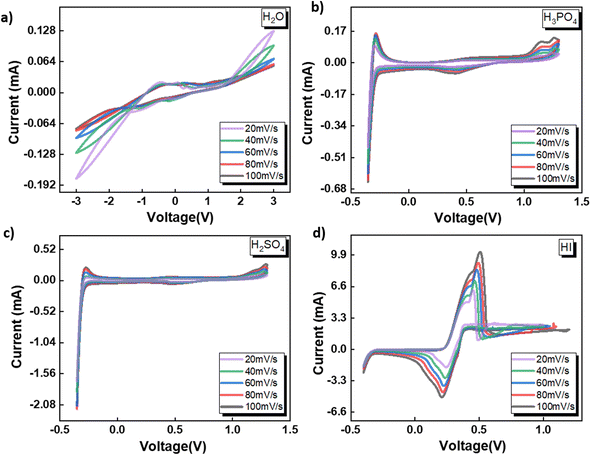
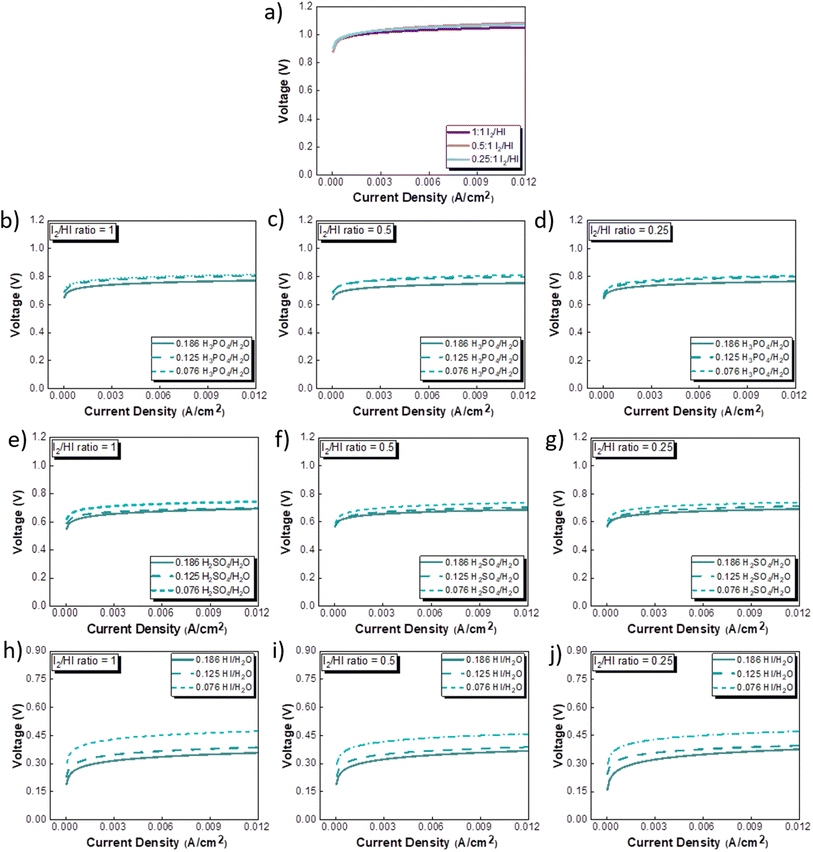
The CV studies emphasize the influence of anionic species in the electrolyte toward the HER occurring at the cathode. Here, we extend our analysis and derive a comprehensive system-level understanding of the electrochemical decomposition through polarization studies conducted in a two-compartment electrochemical cell. The investigations on the two-compartment cell targeted two specific aspects: (a) the effect of the catholyte type (H2O, H3PO4, H2SO4, and HI) and its concentration and (b) the emergent effect arising from the variation in the I2/HI ratio in the anolyte section. Fig. 3 shows the polarization curve obtained for varying catholytes (H2O, H3PO4, H2SO4, and HI) and their concentration as a function of the I2/HI ratio in the anolyte. The polarization curve for all the electrolyte variations obtained for the cell system shows a similar shape. The current density remains negligibly low at lower voltages and gradually starts increasing non-linearly with increasing voltage, representing the onset of the electrochemical HI decomposition and hydrogen production.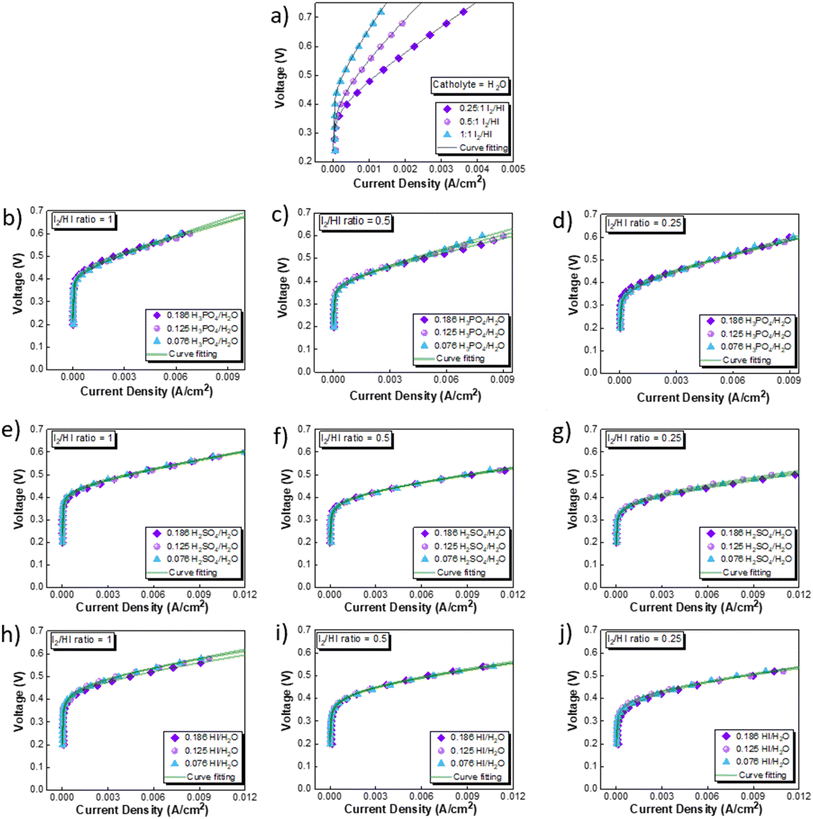 | ||
| Fig. 3 Two electrode polarisation curve studies corresponding to the three I2/HI ratios with respective catholytes, namely (a) H2O (b)–(d) H3PO4 (e)–(g) H2SO4, and (h)–(j) HI. | ||
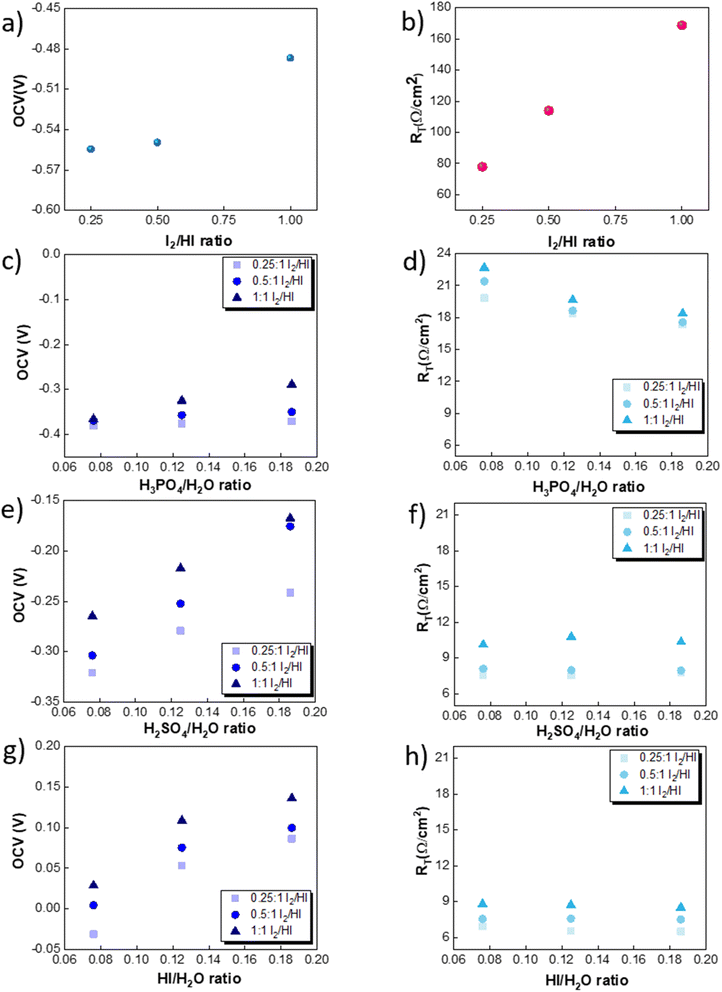
The onset potential increased with the I2/HI ratio, as observed in Fig. 3(a), with water as the catholyte. Similar behavior was observed for the other electrolytes used in this study. It is to be noted that the onset potential was found to be in the range of 0.3 to 0.4 V for all the cases. This increase in the onset potential aligns with the earlier reported studies, which can be attributed to the increase in the OCV for the cell with an increasing I2/HI ratio.30 Furthermore, it can be observed that at any given current density after the onset potential, the total voltage is lower for the lower I2/HI ratio, indicative of better performance. Interestingly, it can be observed that the polarization curve curves are nearly identical for the variation in the acid/H2O ratio in the catholyte at any given I2/HI ratio in the anolyte, featuring similar onset potentials in Fig. 3(b)–(j) for all the acids, H2SO4, H3PO4, and HI used in this study. The experimental data were fitted with the mathematical model outlined in Section 2.5 to deconvolute the overpotential contributions in the polarization behavior. The model equation described in eqn (8) was found to show a good fit for all the experimental polarization curve data, as shown in Fig. 3, with R2 values ∼0.99.
The OCV was evaluated experimentally before the experiment, and the data is shown in Fig. 4(a), (c), (e) and (g). For all the catholytes studied here, it was observed that the OCV became relatively more positive with an increase in the I2/HI ratios in the anolyte. Additionally, for the catholyte section, an increase in the acid/H2O ratio for all three acids resulted in the OCV attaining relatively more positive values. Positive OCV values were observed for HI as the catholyte, except for the HI/H2O ratio of 0.076 in the catholyte with an I2/HI ratio of 1 in the anolyte. This starkly contrasts the other acids studied here, where the OCV was found to have negative values. The OCV results from the asymmetric composition of the anolyte and catholyte sections.41 In a two-compartment PEM-separated cell system, the OCV is the combination of the electrode potentials for the anode and the cathode, the Donnan potential for the membrane, and the diffusion potential through the membrane.52 Consequently, changing the composition on either side of the membrane results in a variation of the OCV.
The RT corresponding to the resistive overpotential losses is a combination of the ohmic and mass transfer resistance and is shown in Fig. 4(b), (d), (f) and (h). While we can assume the resistance contribution from the electronic resistance from electrical connections and electrodes to be low and constant for the system, the ionic resistance and the mass transfer resistance component are expected to depend on the electrolyte composition. The RT of the cell was found to increase with increasing I2/HI ratio for fixed catholyte composition. With an increase in the iodine content in the anolyte, the concentration of tri-iodide ions increases. In comparison, the tri-iodide ion exhibits a larger solvated ion size (1.8 nm) compared to the iodide ion (0.39 nm). Consequently, this leads to reduced mobility of tri-iodide ions, resulting in a higher ionic resistance with increasing I2/HI ratio.53,54 This is in line with the earlier reported studies where the solution resistance was found to increase with an increase in the iodine content in the electrolyte solution.26,53,55,56 For the catholyte variation, the RT values for the four electrolytes follow the order: H2O > H3PO4 > H2SO4 > HI. Therefore, for the same anolyte composition, the difference in the RT can be attributed to the difference in the ionic species behavior in the catholyte. In general, increasing the concentration of the charged species reduces the electrolyte resistance. Water's exceptionally high RT can be attributed to the lower number of ionic species present and, hence, the lower number of charge carriers. For varying acids in the catholyte, the difference in the property of the anionic species contributes to the difference in the observed values of RT. For the three acids studied here, the phosphate ion (0.483 nm)57 presents with the largest hydrated ion size, followed by the sulfate ion (0.379 nm) and the iodide ion (0.331 nm).58 A higher hydrated ion radius reduces the mobility, contributing to the higher RT for H3PO4 while being the lowest for HI at similar acid/H2O ratios. Furthermore, it is to be noted that HI and H2SO4 are strong acids, while H3PO4 is a weak acid. As a result, H3PO4 is only weakly dissociated, producing relatively lower number of ions under equilibrium, which further contributes to the higher RT observed in the H3PO4 catholyte. In addition, when H3PO4 serves as the catholyte, an increase in the H3PO4/H2O ratio results in a reduction of the RT. On the other hand, for H2SO4 and HI, a change in the acid/H2O ratio does not significantly influence the RT. Increasing the number of ionic species in the electrolyte leads to two opposing effects on the solution resistance. Increasing the acid concentration increases the number of charged species, which can reduce the RT. However, the inter-ionic interactions also increase with the increasing number of charged species, which reduces the mobility of ions and hence can increase the RT. For HI and H2SO4, the relatively similar RT values indicate that the above two opposing effects emanating from the increasing acid concentration get balanced. However, H3PO4 is a weak acid, and the increase in conductivity due to the increased number of charged species dominates the overall effect, reducing the RT with an increase in the H3PO4/H2O ratio.
The activation overpotential contribution evaluated from the model fitting data is shown in Fig. 5 for all the studies. The activation overpotential losses were found to be of similar order for the same catholyte composition for all three I2/HI ratios. This aligns with the earlier studies that the activation overpotential losses in the anolyte section are negligibly low, and the overall activation losses emanate predominantly from the catholyte section.30 In contrast, the activation overpotential increases with a reducing acid/H2O ratio. Here, the activation overpotential components graphs are found to be shifted towards higher values while retaining a similar shape. The activation overpotential component is expressed with the Tafel equation as 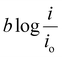 . A reduction in the acid/H2O ratio signifies a reduction in the H+ ion concentration, which results in the reduction of io values and increase in the cathodic transfer coefficient, causing the above observed increase in the activation overpotential losses.59 While the activation overpotential varies with the dilution of all acids, the polarization behavior for the cell remains similar for a given catholyte at varying dilutions. Such invariance in the polarization behavior can be attributed to the compensation of the change in the activation overpotential with the OCV change of the cell.
. A reduction in the acid/H2O ratio signifies a reduction in the H+ ion concentration, which results in the reduction of io values and increase in the cathodic transfer coefficient, causing the above observed increase in the activation overpotential losses.59 While the activation overpotential varies with the dilution of all acids, the polarization behavior for the cell remains similar for a given catholyte at varying dilutions. Such invariance in the polarization behavior can be attributed to the compensation of the change in the activation overpotential with the OCV change of the cell.
 | ||
| Fig. 5 Activation overpotential losses corresponding to the three I2/HI ratios of 0.25, 0.5 and 1 with the catholytes (a) H2O (b)–(d) H3PO4 (e)–(g) H2SO4, and (h)–(j) HI. | ||
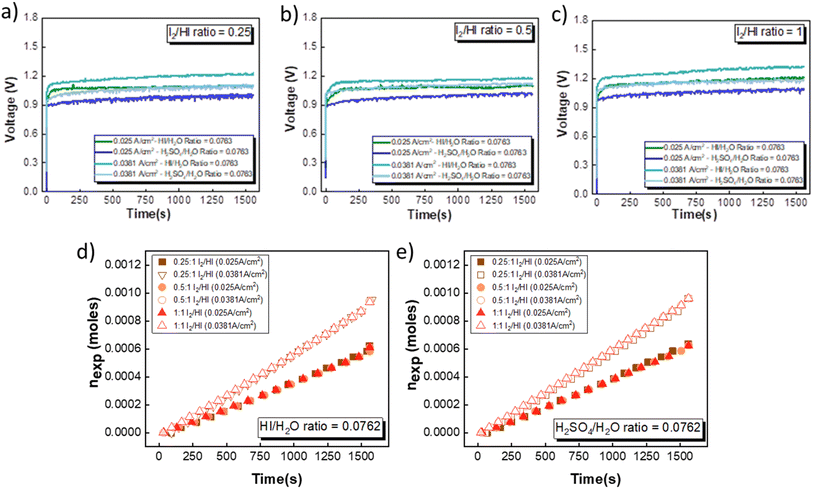
3.3 Continuous electrochemical HI decomposition
The electrochemical HI decomposition for hydrogen production with HI and H2SO4 as the catholyte has been carried out in a two-compartment cell system at two different current densities of 0.025 A cm−2 to 0.038 A cm−2. HIx solutions with I2/HI ratios of 1, 0.5, and 0.25 with a fixed HI/H2O ratio of 0.186 were employed in the anolyte section. For the catholyte section, investigations were conducted using HI/H2O and H2SO4/H2O ratios of 0.076. A total of nine continuous flow cell studies with hydrogen production have been presented. Upon the application of voltage, it was observed that hydrogen gas bubbles were transported to the inverted burette gas collector. Furthermore, the volume of collected hydrogen gas increased progressively over time, demonstrating the feasibility of continuous hydrogen production.Fig. 7(a)–(c) illustrates the evolution of the voltage over time during the electrochemical HI decomposition experiment for the electrolyte configurations discussed above at two different current densities. As expected, the voltage values are higher when operated at a higher current density for the same electrolyte composition. Furthermore, the voltage values recorded for the H2SO4 are consistently lower than those obtained for the HI for the same current density. This is in line with the polarization studies, where the performance of H2SO4 was slightly better than that of HI as the catholyte. The temporal evolution of the voltage exhibits noise-like fluctuations that can be attributed to the hydrogen bubble formation and detachment and the resulting changes in the electroactive area and hydrodynamic disturbances in the electrolyte during the bubble detachment and movement. The transient voltage is seen to show a gradual increase with time. As the electrochemical HI decomposition progresses, the iodide ion converts to iodine in the anolyte section, increasing the I2/HI ratio. The increase in the I2/HI ratio causes an increase in the OCV and the RT, which can be attributed to the gradual increase in the voltage with time during the electrochemical HI decomposition. The moles of hydrogen collected in the reservoir increased almost linearly with time for all the electrolyte combinations, as shown in Fig. 7(d) and (e). The above indicates that the hydrogen production rate remains nearly constant for the duration of the experiment. Furthermore, the hydrogen production rate is a function of the operating current density and remains unaffected by variations in the electrolyte composition, including the I2/HI ratio in the anolyte and variations in the catholyte.
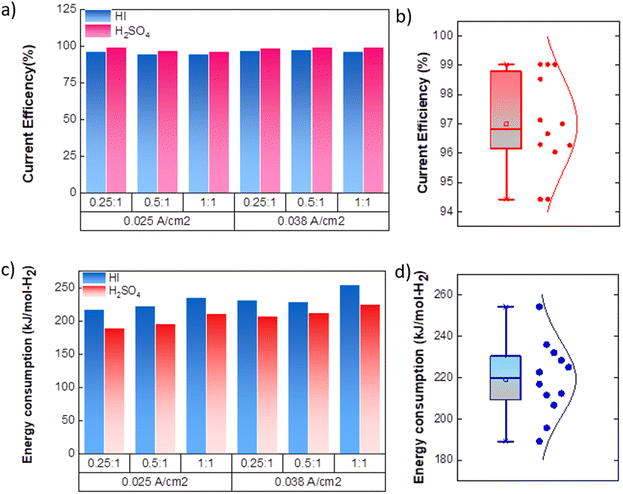
As expected, the hydrogen production rate is higher when the system operates at a higher current density, per Faraday's law. The hydrogen production rate was found to be ∼0.4 μmoles s−1 and ∼0.6 μmoles s−1 for the operating current density of 0.025 A cm−2 and 0.038 A cm−2, respectively. An initial lag between the start of the electrolysis and the collection of the first hydrogen bubble was observed due to the time required for the bubble to travel through the connecting pipelines. Therefore, after stopping the voltage supply, the pumps were run until all the bubbles within the pipeline were transferred to the gas collector to express the total hydrogen collected for the operation. The final data points in Fig. 7(d) and (e) correspond to the total volume of hydrogen collected after running the pumps for additional time. Based on the pressure within the inverted burette gas collection chamber, the corresponding moles of the hydrogen gas were evaluated. The final amount of the collected hydrogen gas was used to evaluate the overall current efficiency using eqn (9), as shown in Fig. 8(a), along with the normal distribution in Fig. 8(b). The recorded current efficiency values were above 94% across all experimental runs. Using H2SO4 as the catholyte yielded slightly higher current efficiency values than HI at similar anolyte composition and operating current density. An average current efficiency of approximately 97% was observed across all experimental runs. A current efficiency lower than 100% indicates side reactions other than HER. Specifically, the anolyte side is rich in iodine, while the catholyte is devoid of iodine. Consequently, the iodine from the anolyte side can permeate to the catholyte side during the electrochemical HI decomposition.26 In addition, the negatively charged iodide/tri-iodide ions can also permeate through the membrane, resulting in cross-contamination.39 For the HI as the catholyte, the iodine permeating through the membrane can further react homogeneously with the iodide ion to form tri-iodide ions. As seen in Fig. 2(d), the reduction of iodine and tri-iodide ions occurs at lower overpotentials as compared to the HER. Therefore, under reduction potentials, the iodine and tri-iodide ions, if present in the catholyte section, can undergo electro-reduction to form iodide ions preferentially over HER, thereby lowering the current efficiency. Additionally, a consistently higher current efficiency for H2SO4 compared to HI indicates that the iodine and tri-iodide permeation is relatively lower when H2SO4 is in the catholyte compared to HI. One of the possible reasons which can cause a higher permeation with HI as catholyte can be the higher solubility of the iodine in the electrolyte containing iodide ion through homogenous tri-iodide ion formation (eqn (18)). It is to be noted that the gradual contamination for the H2SO4 catholyte will occur during prolonged operations, which will essentially add ionic species in the electrolyte system.
The energy consumed per mole of hydrogen production (kJ mol-H2−1) based on the total energy consumed over the duration of the experiment and the total moles of hydrogen produced has been evaluated as: 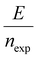 and is shown in Fig. 8(c). In the equation, nexp represents the experimentally quantified moles of hydrogen produced from the HI electrochemical decomposition. The net energy consumed (E) has been evaluated as the product of the area under the chronopotentiometry curve and the applied current, expressed as
and is shown in Fig. 8(c). In the equation, nexp represents the experimentally quantified moles of hydrogen produced from the HI electrochemical decomposition. The net energy consumed (E) has been evaluated as the product of the area under the chronopotentiometry curve and the applied current, expressed as 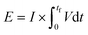 . The tf in the above case is the duration of the experiments in seconds, and I is the current in amperes, and V is in volt. The distribution of the energy consumption is shown in Fig. 8(d), and the mean energy consumption is ∼220 kJ mol-H2−1. For H2SO4, as the catholyte with the same current density and I2/HI ratio, the energy consumption is lower, which can be attributed to the lower overpotential losses coupled with higher current efficiencies. Additionally, H2SO4 also has a lower cost as compared to HI acid. Overall, H2SO4 results in higher performance, lower energy consumption, and lower cost than HI. Consequently, evaluating factors of performance, energy consumption, and cost, it becomes evident that H2SO4 emerges as a better choice for catholyte in electrochemical HI decomposition. A comparative assessment of the previously reported studies and the present study is shown in Table 1.
. The tf in the above case is the duration of the experiments in seconds, and I is the current in amperes, and V is in volt. The distribution of the energy consumption is shown in Fig. 8(d), and the mean energy consumption is ∼220 kJ mol-H2−1. For H2SO4, as the catholyte with the same current density and I2/HI ratio, the energy consumption is lower, which can be attributed to the lower overpotential losses coupled with higher current efficiencies. Additionally, H2SO4 also has a lower cost as compared to HI acid. Overall, H2SO4 results in higher performance, lower energy consumption, and lower cost than HI. Consequently, evaluating factors of performance, energy consumption, and cost, it becomes evident that H2SO4 emerges as a better choice for catholyte in electrochemical HI decomposition. A comparative assessment of the previously reported studies and the present study is shown in Table 1.
| References | Electrode material | Membrane | Anolyte | Catholyte | Performance parameter | Ref. |
|---|---|---|---|---|---|---|
| Xu et al. (2018) | Carbon papers | Nafion 117 and Nafion 115 | HI–I2–H2O | Deionized water | Current efficiency 93–87% | 26 |
| Hydrogen production rate: 6–12.5 ml min−1 | ||||||
| Ying et al. (2020) | Graphite electrodes | Nafion 117 | HI–I2–H2O | Deionized water | Hydrogen production rate: ∼4.5 ml min−1 | 29 |
| Ying et al. (2020) | Graphite electrodes | Nafion 117 | HI–I2–H2O | Deionized water | Hydrogen production rate: ∼4.5 ml min−1 | 27 |
| Shahi et al. (2021) | TiO2 expanded sheets coated with triple precious metal oxide (titanium–ruthenium–platinum) | Sulfonated copolymer of PVDF-co-HFP (SCP) and graphene oxide (SGO) | HI–H2O | Water | Current efficiency 93.4–81.3% | 25 |
| Energy required: 0.043–0.054 kW h mol-H2−1 (154.8–194.4 kJ mol-H2−1) | ||||||
| Nafion® 117 | Current efficiency 89.7% | |||||
| Energy required: 0.047 kW h mol-H2−1 (169.2 kJ mol-H2−1) | ||||||
| Zhang et al. (2022) | Platinum-coated titanium mesh as the anode and stainless-steel mesh as the cathode | Nafion 117 | HI + H2SO4 + H2O + toluene | H2SO4 + H2O | Current efficiency ∼ 100% | 32 |
| Hydrogen production rate: 6.78 × 10−5 to 44.1 × 10−5 mol l−1 s−1 | ||||||
| Current study | Platinum plate electrode for both anode and cathode | Nafion 117 | HI–I2–H2O | HI + H2O and H2SO4 + H2O | Current efficiency: 94–99% | |
| Hydrogen production rate: ∼0.4–0.6 μmoles s−1 | ||||||
| Energy required: 189–255 kJ mol-H2−1 |
The electrochemical decomposition of hydroiodic acid in the I–S thermochemical cycle is designed to operate in an integrated mode, either with the Bunsen reaction in an open-loop scheme or with both the Bunsen reaction and the sulfuric acid decomposition sections in a closed-loop scheme. In the standalone operation conducted in this study, an increase in the I2/HI ratio within the anolyte section leads to a rise in operating voltage. In contrast, an integrated system operating under steady-state conditions is expected to maintain a near-constant anolyte composition, resulting in stable and nearly constant voltage. Long-term stability evaluations in an integrated system are required, where the coupling of all process steps allows for a realistic assessment of potential component degradation and electrolyte stability under continuous operation. While this study provides insights into the short-term effects of varying the I2/HI ratio, further studies are required on exploring long-term performance and durability in such integrated setups.
4. Conclusions
In summary, we have presented a detailed study on the effect of the catholyte type and its concentration on the electrochemical HI decomposition process. From the CV behavior it is deduced that there were no parallel reactions in the catholyte when H2SO4, H3PO4, and H2O were used as an electrolyte. However, for HI as an electrolyte, a parallel reaction of reduction of iodine and tri-iodide ions occurs when iodine is present. The above can be eliminated by ensuring the catholyte is devoid of iodine. Polarization studies revealed that the onset potential for electrochemical HI decomposition remained comparable within the range of 0.3 to 0.4 V across various catholytes and their concentrations. However, a slight increase in the onset potential was observed with an increase in the I2/HI ratio from 0.25 to 1. The catholyte concentration was found to have minimal effect on the overall polarization behavior. Among all the electrolytes studied as catholytes, H2SO4 exhibited the highest performance, while H2O demonstrated the lowest performance. The nearly invariant polarization behavior for changing the catholyte concentration is attributed to the compensation of the activation overpotential with the changes in the OCV. Furthermore, the activation overpotential was similar for all three I2/HI ratios in the anolyte when catholyte composition was constant. Based on polarization curve analysis, HI and H2SO4 with the lowest acid/H2O ratio were chosen as catholytes for continuous flow hydrogen production studies. Hydrogen generation was achieved at current densities of 0.025 A cm−2 and 0.038 A cm−2 across three I2/HI ratios in the anolyte. Current efficiency remained high (∼97%), with an average energy requirement of ∼220 kJ mol-H2−1. Among the catholytes, H2SO4 exhibited the lowest energy requirement and higher current efficiency, making it the most promising choice for efficient electrochemical HI decomposition.Data availability
All the relevant data generated during this study have been included in the main article. Any additional data will be provided on request.Author contributions
Ashwin Y.: methodology, validation, formal analysis, investigation, writing – original draft, visualization, Saroj Chaudhary: resources, project administration, Parvatalu Damaraju: resources, project administration, Pradeep Kumar Sow: conceptualization, methodology, writing – review & editing, visualization, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank ONGC Energy Centre Trust (OECT, Agreement signing date: 2nd November 2021) for the financial support for conducting the research work. The authors would also like to thank Dr Richa Singhal for her support during this work. The authors acknowledge the assistance from the Mechanical Engineering workshop for their help with the fabrication of the cell components.References
- Y. Li, R. Lin, R. O'Shea, V. Thaore, D. Wall and J. D. Murphy, A perspective on three sustainable hydrogen production technologies with a focus on technology readiness level, cost of production and life cycle environmental impacts, Heliyon, 2024, 10, e26637, DOI:10.1016/j.heliyon.2024.e26637.
- C. Acar and I. Dincer, Comparative assessment of hydrogen production methods from renewable and non-renewable sources, Int. J. Hydrogen Energy, 2014, 39, 1–12, DOI:10.1016/j.ijhydene.2013.10.060.
- L. C. Brown, J. F. Funk and S. K. Showalter, Initial Screening of Thermochemical Water-Splitting Cycles for High Efficiency Generation of Hydrogen Fuels Using Nuclear Power, Oakland, CA, 1999, DOI:10.2172/761610.
- M. Ji and J. Wang, Review and comparison of various hydrogen production methods based on costs and life cycle impact assessment indicators, Int. J. Hydrogen Energy, 2021, 46, 38612–38635, DOI:10.1016/j.ijhydene.2021.09.142.
- R. Perret, Solar Thermochemical Hydrogen Production Research (STCH) Thermochemical Cycle Selection and Investment Priority, Sandia Reports, 2011, 1–117 Search PubMed.
- B. Ling, Z. Wang, J. Zhang, Y. He, Y. Zhu and K. Cen, Comprehensive comparative analysis of open-loop and closed-loop iodine-sulfur thermochemical cycle for hydrogen production, Int. J. Hydrogen Energy, 2023, 48, 14941–14953, DOI:10.1016/j.ijhydene.2023.01.051.
- S. Kasahara, Y. Imai, K. Suzuki, J. Iwatsuki, A. Terada and X. L. Yan, Conceptual design of the iodine–sulfur process flowsheet with more than 50% thermal efficiency for hydrogen production, Nucl. Eng. Des., 2018, 329, 213–222, DOI:10.1016/j.nucengdes.2017.11.046.
- J. Zhou, Y. Zhang, Z. Wang, W. Yang, Z. Zhou and J. Liu, et al., Thermal efficiency evaluation of open-loop SI thermochemical cycle for the production of hydrogen, sulfuric acid and electric power, Int. J. Hydrogen Energy, 2007, 32, 567–575, DOI:10.1016/j.ijhydene.2006.06.043.
- X. Vitart, P. Carles and P. Anzieu, A general survey of the potential and the main issues associated with the sulfur–iodine thermochemical cycle for hydrogen production using nuclear heat, Prog. Nucl. Energy, 2008, 50, 402–410, DOI:10.1016/j.pnucene.2007.11.023.
- R. Liberatore, P. Favuzza, C. Felici, P. Tarquini, G. Narducci and A. Borruto, Materials resistance to corrosion by I2–HI–H2O mixtures for the realization of a sulfur-iodine plant, Int. J. Hydrogen Energy, 2019, 44, 26816–26834, DOI:10.1016/j.ijhydene.2019.08.162.
- N. Hiroki, K. Yu, T. Nobuyuki, T. Hiroaki, I. Jin and K. Seiji, et al., Hydrogen production using thermochemical water-splitting iodine–sulfur process test facility made of industrial structural materials: engineering solutions to prevent iodine precipitation, Int. J. Hydrogen Energy, 2021, 46, 22328–22343, DOI:10.1016/j.ijhydene.2021.02.071.
- A. Yang, Z. Ying, M. Zhao, X. Zheng, B. Dou and G. Cui, Process modelling and assessment of thermochemical sulfur-iodine cycle for hydrogen production considering Bunsen reaction kinetics, Chem. Eng. Process., 2024, 195, 109624, DOI:10.1016/j.cep.2023.109624.
- J. Zeng, J. Zhang, B. Ling, Y. He, W. Weng and Z. Wang, Hydrogen production by sulfur-iodine thermochemical cycle — current status and recent advances, Int. J. Hydrogen Energy, 2024, 86, 677–702, DOI:10.1016/j.ijhydene.2024.08.446.
- H. S. Kim, Y. H. Kim, B. T. Ahn, J. G. Lee, C. S. Park and K. K. Bae, Phase separation characteristics of the Bunsen reaction when using HI solution (HI–I2–H2O) in the sulfur–iodine hydrogen production process, Int. J. Hydrogen Energy, 2014, 39, 692–701, DOI:10.1016/j.ijhydene.2013.10.098.
- Z. Ying, X. Zheng and G. Cui, Detailed kinetic study of the electrochemical Bunsen reaction in the sulfur-iodine cycle for hydrogen production, Energy Convers. Manage., 2016, 115, 26–31, DOI:10.1016/j.enconman.2016.02.046.
- M. Sakurai, Experimental study on side-reaction occurrence condition in the iodine–sulfur thermochemical hydrogen production process, Int. J. Hydrogen Energy, 2000, 25, 613–619, DOI:10.1016/S0360-3199(99)00074-9.
- S. Kasahara, S. Kubo, R. Hino, K. Onuki, M. Nomura and S. Nakao, Flowsheet study of the thermochemical water-splitting iodine–sulfur process for effective hydrogen production, Int. J. Hydrogen Energy, 2007, 32, 489–496, DOI:10.1016/j.ijhydene.2006.05.005.
- B. J. Lee, H. C. NO, H. J. Yoon, H. G. Jin, Y. S. Kim and J. I. Lee, Development of a flowsheet for iodine–sulfur thermo-chemical cycle based on optimized Bunsen reaction, Int. J. Hydrogen Energy, 2009, 34, 2133–2143, DOI:10.1016/j.ijhydene.2009.01.006.
- H. Liu, H. Ye, Q. Wang and H. Dong, Design and evaluation of a novel process for green hydrogen production in the iodine–sulfur cycle via pressure-swing distillation of HIx (HI-I2-H2O), Sep. Purif. Technol., 2024, 330, 125257, DOI:10.1016/j.seppur.2023.125257.
- B. Wong, R. T. Buckingham, L. C. Brown, B. E. Russ, G. E. Besenbruch and A. Kaiparambil, et al., Construction materials development in sulfur–iodine thermochemical water-splitting process for hydrogen production, Int. J. Hydrogen Energy, 2007, 32, 497–504, DOI:10.1016/j.ijhydene.2006.06.058.
- C. J. Orme and F. F. Stewart, Pervaporation of water from aqueous hydriodic acid and iodine mixtures using Nafion® membranes, J. Membr. Sci., 2007, 304, 156–162, DOI:10.1016/j.memsci.2007.07.028.
- A. Singhania and A. N. Bhaskarwar, Development of catalysts for hydrogen production from hydrogen iodide decomposition in thermo-chemical water-splitting sulfur-iodine cycle: a review, Catal. Rev., 2017, 59, 446–489, DOI:10.1080/01614940.2017.1366189.
- M. Zhao, Z. Ying, A. Yang, Z. Fang, X. Kong and X. Yu, et al., Development of a novel U-shaped decomposer for enhanced hydrogen production via HI decomposition in the sulfur-iodine cycle, Int. J. Hydrogen Energy, 2024, 91, 893–900, DOI:10.1016/j.ijhydene.2024.10.212.
- L. Wang, H. Liu, S. Chen and P. Zhang, HI decomposition over the HI-100 test apparatus at a hydrogen production rate over 100 L/h, Int. J. Hydrogen Energy, 2024, 55, 917–920, DOI:10.1016/j.ijhydene.2023.11.266.
- A. Shahi, C. Dwivedi, S. D. Manjare and V. Kulshrestha, Sulphonated (PVDF-co-HFP)-graphene oxide composite polymer electrolyte membrane for HI decomposition by electrolysis in thermochemical iodine-sulphur cycle for hydrogen production, Int. J. Hydrogen Energy, 2021, 46, 8852–8863, DOI:10.1016/j.ijhydene.2021.01.027.
- S. Xu, Y. He, B. Huang, Y. Zhang, Z. Wang and K. Cen, Decomposition of hydriodic acid by electrolysis in the thermochemical water sulfur–iodine splitting cycle, Int. J. Hydrogen Energy, 2018, 43, 3597–3604, DOI:10.1016/j.ijhydene.2017.12.177.
- Z. Ying, Y. Wang, X. Zheng, Z. Geng, B. Dou and G. Cui, Experimental study and development of an improved sulfur–iodine cycle integrated with HI electrolysis for hydrogen production, Int. J. Hydrogen Energy, 2020, 45, 13176–13188, DOI:10.1016/j.ijhydene.2020.03.037.
- Z. Ying, J. Yang, X. Zheng, Y. Wang and B. Dou, Energy and exergy analyses of a novel sulfur–iodine cycle assembled with HI–I2–H2O electrolysis for hydrogen production, Int. J. Hydrogen Energy, 2021, 46, 23139–23148, DOI:10.1016/j.ijhydene.2021.04.129.
- Z. Ying, Y. Wang, X. Zheng, Z. Geng, B. Dou and G. Cui, Modeling and experimental assessment of the novel HI-I2-H2O electrolysis for hydrogen generation in the sulfur-iodine cycle, Int. J. Energy Res., 2020, 44, 6285–6296, DOI:10.1002/er.5334.
- A. Y. Hegde, S. Chaudhary, P. Damaraju and P. K. Sow, Decoupling the anodic and cathodic behavior in asymmetric electrochemical hydroiodic acid decomposition cell for hydrogen production in the iodine–sulfur thermochemical cycle, Environ. Sci. Pollut. Res., 2023, 1–16, DOI:10.1007/s11356-023-30154-y.
- K. Zhang, X. Zhao, S. Chen, L. Chang, J. Wang and W. Bao, et al., Direct electrolysis of Bunsen reaction product HI/H2SO4/H2O/toluene mixture for hydrogen production: Pt electrode characterization, Int. J. Hydrogen Energy, 2018, 43, 13702–13710, DOI:10.1016/j.ijhydene.2018.02.079.
- K. Zhang, X. Li, L. Chang, W. Bao and H. Wang, Direct electrolysis of Bunsen reaction product for hydrogen production: the continuous-flow operation, Int. J. Hydrogen Energy, 2022, 47, 21923–21941, DOI:10.1016/j.ijhydene.2022.03.144.
- A. L. Tomás-García, J. O. Jensen, N. J. Bjerrum and Q. Li, Hydrogen evolution activity and electrochemical stability of selected transition metal carbides in concentrated phosphoric acid, Electrochim. Acta, 2014, 137, 639–646, DOI:10.1016/j.electacta.2014.06.087.
- J. H. Norman, G. E. Besenbruch, L. C. Brown, D. R. O'Keefe and C. L. Allen, Thermochemical water-splitting cycle, bench-scale investigations, and process engineering, Final report, February 1977–December 31, 1981, Oak Ridge, TN, 1982, DOI:10.2172/5063416.
- M. Lanchi, F. Laria, R. Liberatore, L. Marrelli, S. Sau and A. Spadoni, et al., HI extraction by H3PO4 in the sulfur–iodine thermochemical water splitting cycle: composition optimization of the HI/H2O/H3PO4/I2 biphasic quaternary system, Int. J. Hydrogen Energy, 2009, 34, 6120–6128, DOI:10.1016/j.ijhydene.2009.06.010.
- A. Giaconia, G. Caputo, S. Sau, P. P. Prosini, A. Pozio and M. De Francesco, et al., Survey of Bunsen reaction routes to improve the sulfur-iodine thermochemical water-splitting cycle, Int. J. Hydrogen Energy, 2009, 34, 4041–4048, DOI:10.1016/j.ijhydene.2008.11.009.
- Q. Zhu, Y. Zhang, Z. Ying, S. Wang, Z. Wang and J. Zhou, et al., Kinetic and thermodynamic studies of the Bunsen reaction in the sulfur-iodine thermochemical process, Int. J. Hydrogen Energy, 2013, 38, 8617–8624, DOI:10.1016/j.ijhydene.2013.04.110.
- Y. Zhang, Z. Ying, J. Zhou, J. Liu, Z. Wang and K. Cen, Electrolysis of the Bunsen Reaction and Properties of the Membrane in the Sulfur–Iodine Thermochemical Cycle, Ind. Eng. Chem. Res., 2014, 53, 13581–13588, DOI:10.1021/ie502275s.
- V. Immanuel, D. Parvatalu, A. Bhardwaj, B. N. Prabhu, A. N. Bhaskarwar and A. Shukla, Properties of Nafion 117 in highly acidic environment of Bunsen reaction of I-S cycle, J. Membr. Sci., 2012, 409–410, 137–144, DOI:10.1016/j.memsci.2012.03.046.
- B. Han, S. M. Steen, J. Mo and F. Y. Zhang, Electrochemical performance modeling of a proton exchange membrane electrolyzer cell for hydrogen energy, Int. J. Hydrogen Energy, 2015, 40, 7006–7016, DOI:10.1016/j.ijhydene.2015.03.164.
- P. K. Sow and A. Shukla, Effect of asymmetric variation of operating parameters on EED cell for HI concentration in I-S cycle for hydrogen production, Int. J. Hydrogen Energy, 2012, 37, 13958–13970, DOI:10.1016/j.ijhydene.2012.07.068.
- A. J. Bard and L. Faulkner, Electrochemical methods: fundamentals and applications, John Wiley & Sons, Hamilton, 2nd edn, 2001 Search PubMed.
- P. K. Sow and A. Shukla, A chronopotentiometry based identification of time-varying different transport resistances of electro-electrodialysis cell used for concentration of HIx solution, Int. J. Hydrogen Energy, 2013, 38, 3154–3165, DOI:10.1016/j.ijhydene.2012.12.129.
- Y. Zhang, Z. Ying, J. Zhou, J. Liu, Z. Wang and K. Cen, Electrolysis of the Bunsen Reaction and Properties of the Membrane in the Sulfur–Iodine Thermochemical Cycle, Ind. Eng. Chem. Res., 2014, 53(35), 13581–13588, DOI:10.1021/ie502275s.
- J. T. Bender, A. S. Petersen, F. C. Østergaard, M. A. Wood, S. M. J. Heffernan and D. J. Milliron, et al., Understanding Cation Effects on the Hydrogen Evolution Reaction, ACS Energy Lett., 2023, 8, 657–665, DOI:10.1021/acsenergylett.2c02500.
- P. S. Lamoureux, A. R. Singh and K. Chan, PH Effects on Hydrogen Evolution and Oxidation over Pt(111): Insights from First-Principles, ACS Catal., 2019, 9, 6194–6201, DOI:10.1021/acscatal.9b00268.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Mechanistic Switching by Hydronium Ion Activity for Hydrogen Evolution and Oxidation over Polycrystalline Platinum Disk and Platinum/Carbon Electrodes, ChemElectroChem, 2014, 1, 1497–1507, DOI:10.1002/celc.201402085.
- D. V. Tripkovic, D. Strmcnik, D. van der Vliet, V. Stamenkovic and N. M. Markovic, The role of anions in surface electrochemistry, Faraday Discuss., 2009, 140, 25–40, 10.1039/B803714K.
- V. S. Bagotzky, Y. B. Vassilyev, J. Weber and J. N. Pirtskhalava, Adsorption of anions on smooth platinum electrodes, J. Electroanal. Chem. Interfacial Electrochem., 1970, 27, 31–46, DOI:10.1016/S0022-0728(70)80200-5.
- D. A. Palmer, R. W. Ramette and R. E. Mesmer, Triiodide ion formation equilibrium and activity coefficients in aqueous solution, J. Solution Chem., 1984, 13, 673–683, DOI:10.1007/BF00650374.
- J. Rossmeisl, K. Chan, E. Skúlason, M. E. Björketun and V. Tripkovic, On the pH dependence of electrochemical proton transfer barriers, Catal. Today, 2016, 262, 36–40, DOI:10.1016/j.cattod.2015.08.016.
- N. Tanaka and K. Onuki, Equilibrium potential across cation exchange membrane in HI–I2–H2O solution, J. Membr. Sci., 2010, 357, 73–79, DOI:10.1016/j.memsci.2010.04.004.
- P. K. Sow, S. Sant and A. Shukla, EIS studies on electro-electrodialysis cell for concentration of hydriodic acid, Int. J. Hydrogen Energy, 2010, 35, 8868–8875, DOI:10.1016/j.ijhydene.2010.06.031.
- G. Lota, K. Fic and E. Frackowiak, Alkali metal iodide/carbon interface as a source of pseudocapacitance, Electrochem. Commun., 2011, 13, 38–41, DOI:10.1016/j.elecom.2010.11.007.
- Y. Zhang, Z. Ying, J. Liu, J. Zhou, Z. Wang and K. Cen, Electrochemical characterization of electrodes in the electrochemical Bunsen reaction of the sulfur-iodine cycle, Int. J. Hydrogen Energy, 2014, 39, 7216–7224, DOI:10.1016/j.ijhydene.2014.01.177.
- S.-D. Hong, J.-K. Kim, K.-K. Bae, S.-H. Lee, H.-S. Choi and G.-J. Hwang, Evaluation of the membrane properties with changing iodine molar ratio in HIx (HI–I2–H2O mixture) solution to concentrate HI by electro-electrodialysis, J. Membr. Sci., 2007, 291, 106–110, DOI:10.1016/j.memsci.2006.12.047.
- S. Verma and A. K. Pathak, Hydration of Phosphate Ion in Polarizable Water: Effect of Temperature and Concentration, Liquids, 2023, 3, 278–287, DOI:10.3390/liquids3030018.
- E. R. Nightingale, Phenomenological Theory of Ion Solvation. Effective Radii of Hydrated Ions, J. Phys. Chem., 1959, 63, 1381–1387, DOI:10.1021/j150579a011.
- G. M. Abd El-Hafez, N. H. Mahmoud, A. Walcarius and A. M. Fekry, Evaluation of the electrocatalytic properties of tungsten electrode towards hydrogen evolution reaction in acidic solutions, Int. J. Hydrogen Energy, 2019, 44, 16487–16496, DOI:10.1016/j.ijhydene.2019.04.223.
- S. Mitsushima, Y. Koizumi, S. Uzuka and K.-I. Ota, Dissolution of platinum in acidic media, Electrochim. Acta, 2008, 54, 455–460, DOI:10.1016/j.electacta.2008.07.052.
| This journal is © The Royal Society of Chemistry 2024 |