Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis of propoxylation with zinc–cobalt double metal cyanide catalysts with different active surfaces and particle sizes†
Sarah-Franziska
Stahl
and
Gerrit A.
Luinstra
 *
*
University of Hamburg, Institute for Technical and Macromolecular Chemistry, Bundesstr. 45, 20146 Hamburg, Germany. E-mail: luinstra@chemie.uni-hamburg.de
First published on 7th September 2023
Abstract
The action of three different Co/Zn double-metal-cyanide (DMC) catalysts in the propoxylation of polyols was compared in a kinetic study, using pulse-wise feeding of propylene oxide (PO). Key insights are that the catalysis proceeds by an external attack of hydroxyl chain ends on coordinated PO and that the different diffusion rates of PO and polyols result in the broadening of the distribution. This can be visualized by the introduction of finger printing. The initial [PO] decay had a first order dependence on the catalyst, PO and hydroxyl concentrations. The temperature dependence of the characteristic product ksK (ks: rate constant for ring-opening; K: equilibrium constant for PO coordination) showed that the rate determining step is most compatible with a PO ring-opening by a direct external nucleophilic attack of a hydroxyl group or one modulated by the diffusion rate of PO. Consideration of the number of crystallites per unit volume (related to the crystal size) and diffusion leads to a consistent description of the catalysis in terms of the rate and polydispersity of the product.
Introduction
Double metal cyanide (DMC) complexes were introduced in the early 1960s by General Tire Inc. as industrially viable potent Lewis acidic catalysts.1 They have become known (in particular to industry) as effective mediators for chain transfer polymerization under the ring-opening polymerization (ROP) of propylene oxide (PO) to generate polyether polyols from alcohol or acid starter molecules (Scheme 1).2–6 The high alkoxylation activity of DMC catalysts relative to traditional alkaline catalysts, like KOH, eliminates the need for neutralization and elaborate removal of catalyst residues from the product.7–10 The poly(propylene glycol) (PPG) products prepared with DMC catalysts profit from an almost perfect retention of the functionality of the starter, a low degree of unsaturation (absence of PO isomerization to allyl alcohol) and readily accessible narrow molecular weight distributions.11–15 These properties are advantageous for achieving the lowest possible viscosity for a particular chain length as higher molecular weight fractions, which tend to strongly increase the viscosity, are in small amounts or absent. Low viscosities are of particular importance in applications where mixing and wetting are essential, like in the predominant application of PPGs as soft-phase components in polyurethanes (PU). Application of a PPG with a narrow mass distribution is also advantageous for achieving a clear phase separation in segmented polymers.16 Challenges in the improvement of the catalyst's major action involve the reliable (robust) formation of narrowly dispersed products with compositions of precatalysts not claimed in current patents, and/or additionally enabling copolymerization with CO2,17 lactones18 or anhydrides.19 Advantageous are also higher value propoxylation products with molecular weights in the range of up to about 20 Da or over, prepared by catalysts with high turnover frequencies and sustained activity (for keeping the PO concentration low at high dosing rates), with no allyl formation and the functionality of starter entities being preserved. A low loading of catalyst is obviously most desirable.Addressing the challenges would profit from an in-depth knowledge of the alkoxylation in terms of the catalyst's action in connection to the process carried out. The current state of the art of catalyst and process development more or less relies on experience and on doing a large number of experiments (a Scifinder® search gives about 30 patents with similar titles).17 A number of efforts to systematically enhance the catalytic action through alternative catalyst synthesis is recognizable, however, general applicable principles have not been extracted yet. Indeed, the outcome of DMC complex synthesis is not very predictable and has many factors of influence, i.e. the coprecipitation of, in particular, the Co(CN)63− anion with zinc dichloride (or other sources of Zn2+)12,20,21 may yield several types of precatalyst depending on variables such as concentrations (ratios), solvent (mixtures), auxiliary reagents, temperature, mixing/stirring rate, application of mechanochemistry and post synthesis treatment (cf. ESI† Fig. S1–S3).2,5,17,22–36 In addition, the content and type of complexing agents and residual salts from the synthesis (KCl) may have an impact on the overall activity.29,37–42 Efforts for optimizing a catalyst are directed towards increasing the accessibility of active sites by radiation treatment, by trying to control the morphology e.g. using a reverse emulsion synthesis procedure or by supporting the active components and inducing the formation of layered structures.31,43–49 Other studies have been directed toward establishing a correlation between catalyst structure and activity – some experimental data point toward the importance of “non-crystalline” fractions of the catalyst for high activity as they may offer improved accessibility of active centers, but also here a convincing general case has not been built.50 Some evidence points to the favorable presence of more open “cubic” phases rather than coordinatively saturated hexagonal moieties, however, this was in fact rejected as the bulk phase is merely a hold for the active surface, and also reorganizes in contact with coordinating entities.17,29,51,52 Also, theoretical treatises are difficult to relate to general catalyst activities.34,53–55
Comparing the performance of individual DMC catalysts is limited by the diverging descriptions of catalytic action.13,28,42,56–58 Reported catalytic activity is mainly based on the resulting yield (kg per g of catalyst and/or per h) and/or the overall conversion of monomer.25,30,59 These numbers are not a good basis for an analysis or a targeted development. They are determined by manifold, difficult to assess factors such as the number of active sites, the average activity of the sites and diffusion kinetics (polymer/monomer) in heterogeneous catalysis.60
The activity of a heterogeneous catalyst needs to be considered in terms of “the seven steps” of heterogeneous catalysis, i.e., reflection of macro and microkinetic barriers, here in a fluid–solid system.61 Newer models attempt to break down the catalytic action in this context by treating the propoxylation as an insertion polymerization.62
The current description of propoxylation in terms of elementary chemical reaction (microkinetic) steps involves two competing and inherently different pathways: (1) insertion polymerization with a metal-bonded alkoxide as a key feature, and (2) stepwise chain growth with immediate release of the chain from the catalyst (Scheme 2). Most of the studies describe the catalyst's action as an insertion polymerization, like polyolefin formation.17,48,55,63–66 PO is treated as a pseudo-olefin that undergoes ring-opening and inserts into a metal alkoxide bond. The final step, giving the immortal polymerization characteristics, involves an acid–base reaction between ROH hydroxyl entities and metal-bound alkoxide.67 However, the Lewis-acid catalyzed ring-opening of PO involves a backside attack of a nucleophile, resulting in an anti-addition rather than a syn-addition, as observed e.g. in the ammonium chloride catalyzed formation of oxazolidinones from isocyanides and epoxides,68,69 or in the catalysis for the formation of poly(propylene carbonate) from PO and CO2.70–74 This observation is not directly consistent with the first mechanistic description. Only the ring-opening of PO by a strong Lewis acid generates a free carbocation that may lead to syn-addition, but its existence is unlikely in the presence of coordinating alcohols.7 An alternative mechanistic description involves the activation of PO by a moderate Lewis acid, followed by an external backside attack of an alcohol ROH and liberation of a propoxylated product in the form of ROPOH after a proton shift (Scheme 2, description 2).2
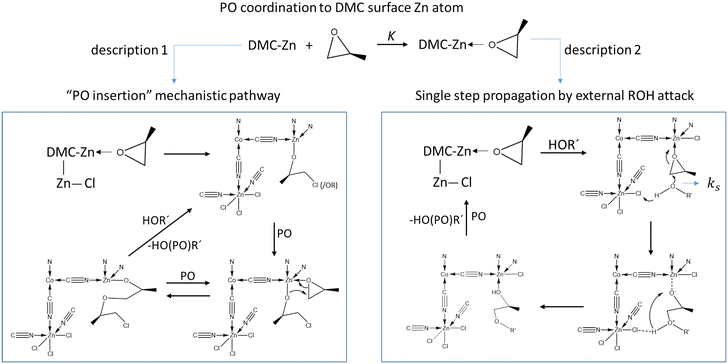 | ||
| Scheme 2 Competing mechanistic descriptions of the DMC mediated propoxylation of HOR, insertion polymerization (left) and stepwise addition by external nucleophilic attack (right). | ||
Kinetic studies of the propoxylation have the potential to distinguish between the alternatives presented in Scheme 2, (depending on the rate-determining step). One particularly comprehensive study, focusing on propoxylation in batch reactions, describes how the induction time and the subsequent propoxylation rate of a PPG diol starter (450 Da) is determined by the DMC content.7 It was found that the rate of PO is linearly dependent on the concentration of DMC and PO. The first-order dependence on the catalyst and PO concentration is consistent with both mechanisms in Scheme 2 and does not provide conclusive evidence. Note that this observation may only be taken as an indication, as the same dependence results from a reaction controlled by the rate of PO diffusion (flux of PO to a catalyst particle 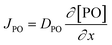 , where DPO represents the diffusion constant of PO in the medium, and x denotes the thickness of some film around the catalyst particle). The total flux is proportional to the surface area of the catalyst particles, and the time dependence of the gradient in the steady state
, where DPO represents the diffusion constant of PO in the medium, and x denotes the thickness of some film around the catalyst particle). The total flux is proportional to the surface area of the catalyst particles, and the time dependence of the gradient in the steady state 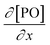 follows first-order kinetics in [PO] when using standard film theory. The more relevant dependence of the rate on the hydroxyl concentration was not determined in the study. The concentration of hydroxyl entities was almost constant in this study as a molar ratio of PPG to PO of 1
follows first-order kinetics in [PO] when using standard film theory. The more relevant dependence of the rate on the hydroxyl concentration was not determined in the study. The concentration of hydroxyl entities was almost constant in this study as a molar ratio of PPG to PO of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used, leading to only incremental chain growth (facilitating the evaluation and interpretation). A first-order dependence on the catalyst concentration was elaborated for the propoxylation in other cases too, however with a second other dependence on PO.63,75 The latter, however, may encompass effects that relate to the activation of the catalyst and the change of the hydroxyl concentration. The Arrhenius activation energy for the overall process was reported in the range of 60 kJ mol−1. An interpretation was not attempted on account of the complex rate law. Nevertheless, knowledge of the activation parameters can generally provide information about the mechanism.
1 was used, leading to only incremental chain growth (facilitating the evaluation and interpretation). A first-order dependence on the catalyst concentration was elaborated for the propoxylation in other cases too, however with a second other dependence on PO.63,75 The latter, however, may encompass effects that relate to the activation of the catalyst and the change of the hydroxyl concentration. The Arrhenius activation energy for the overall process was reported in the range of 60 kJ mol−1. An interpretation was not attempted on account of the complex rate law. Nevertheless, knowledge of the activation parameters can generally provide information about the mechanism.
The distribution of the masses of the products, PPGs, also contains information about the mechanism. The propoxylation of diols mediated by DMCs exhibits a phenomenon known as “catchup” kinetics.76 This term was introduced to describe the observation that low molecular weight diols are preferentially propoxylated in the presence of higher mass oligomers. This led to the development of the “continuous addition of starter” (CAOS) process, which enables the production of PPGs with narrow distributions in a continuous stirred tank reactor.77 The “catch-up” kinetics are explained in the context of mechanistic description 1 by assuming larger rate constants for the propoxylation of smaller diols.7,62 This explanation, however, contradicts the general assumption of equal reactivity of chain ends and is at least to be challenged for that reason.
Apart from the “catch up” kinetics, broad and multimodal distributions can arise during the propoxylation of diols with DMC catalysts. The undesired formation of these distributions is explained by the interpretation based on the PO-insertion mechanism (1) by suggesting the presence of different sites on the catalyst surface, similar to heterogeneous catalytic polyolefin formation.78 It should be noted, however, that the situation is different from polyolefin formation: both PO and ROH need to diffuse to the catalyst surface for chain growth. The self-diffusion of the PPG with slightly different molecular weights must thus keep pace with the rate of PO conversion to achieve balanced growth of an immortal polymerization (Scheme 3).79,80 The rate of PO conversion will fundamentally be dependent on its diffusion to the catalyst and the catalytic action, i.e. it is dependent on micro and macrokinetic factors of unknown magnitude.
 | ||
| Scheme 3 Propoxylation at DMC surfaces: concentration and mass transport of PO and PPG. Subscripts b and s refer to bulk and surface near species, respectively, and mt to mass transport. | ||
There is no doubt that DMC mediated propoxylation appears to be of high complexity, which is partly because of the open question of the microkinetic steps in the mechanism and the need for a global understanding of the factors that determine the rate and the mass distribution of the resulting PPGs. Generally, few kinetic data appear to be available on the action of DMCs in the industrial relevant regime of semi-batch operated reactors for the preparation of narrowly dispersed PPGs after the initial activation.7 A larger kinetic study was therefore carried out, using three similar DMCs prepared from hexacyano cobaltate and zinc cations, differing in particle size. Given the industrial importance of DMC catalyzed propoxylation and the promise of a knowledge driven optimization of the catalyst performance, a simple method for the mapping of the catalyst's action under relevant conditions seems also of value. The activation parameter characteristics are good indicators for the discrimination between the rate with micro (chemistry) and macro (diffusion) kinetic limitations. The option of performing measurements under temperature control was therefore included.
The results are interpreted in the context of heterogeneous catalysis and “polymer reaction” engineering, and yield an extended view of the “catch-up” kinetics.64,76,77,81–83 Evidence for rate-influencing diffusion and for a chemical reaction are found, showing the importance of micro and macro kinetic steps.60,84 The approach intends to decouple the discussion of a sub- or superior catalyst from the difficulty of determining the activity per unit mass, and to map the influence of polymer (PPG) and monomer (PO) diffusion in the context of the semi-batch feeding of PO.
Materials and methods
Materials
Argon (99.999% (5.0) purity, Praxair Deutschland GmbH), propylene oxide (PO) (99.9% purity, GHC Gerling, Holz & Co.) and Voranol™ 2000 L (PPG: poly(propylene glycol), Mn = 2400 g mol−1 against polystyrene standards, PDI = 1.10, DOW Chemical Company) were used as received. The DMCs used were gifts from industry with non-disclosure obligations with respect to their identity, some characterization is offered (ESI† Fig. S1–S3). They were formed from similar zinc and cobalt precursors, but differences in the conditions of synthesis (solvent/ligands, quality of mixing, temperature and concentration (gradients), effect of washing procedures, drying conditions and so on) typically lead to divergent morphologies, crystallinities and polarity (vide infra).20,30 Preparation methods of DMCs can e.g. be found in typical patents.6,85,86Semi-batch propoxylation
The catalytic chain transfer polymerization of PO was carried out in a 2 L-stainless steel autoclave (Parr Instrument GmbH, serial number 4524). The autoclave was charged with a specific amount of the chain transfer (starter) agent Voranol, usually 166 g, and DMC catalyst. It was closed, heated to 118 °C and held under a dynamic vacuum (5 × 10−2 mbar) for 1 h to remove volatiles. Thereafter, the vessel was pressurized with 6.5 bar argon (for reasons of pump operational liability) and a small amount of propylene oxide was added using a HPLC pump (Bischoff HDP PUMP Multitherm 200, 0.01–4.99 mL min−1) with a feeding rate of 0.83 mL min−1. A rapid increase in temperature and decrease in pressure indicated the activation of the catalyst after an induction period. Once the initial amount of propylene oxide was consumed, it was added continuously with a feeding rate of 0.94 mL min−1 until the desired molecular weight of the PPG was reached. The pressure and temperature were monitored throughout the experiments with the software ProfiSignal 2.2 (Delphin Technology). PO conversion was monitored by in-line FTIR-spectroscopy, using a ReactIR™ 45 m (Mettler Toledo) equipped with a probe having a diamond window. Spectra of 128 scans were recorded every minute between 650 and 2000 cm−1. The partial least squares (PLS) regression model for multivariate data analysis was used with The Unscrambler X 10.3 (Camo Software) to evaluate the data. The propoxylation temperature was kept constant at 120 °C and aliquots were taken at certain intervals through a rising pipe. After complete addition of the monomer, the autoclave was rapidly cooled to ambient temperature and depressurized. The reaction mixture was subsequently transferred to a drying oven and held under a dynamic vacuum at 50 °C until the weight was constant.Kinetic study
The experiments were conducted as above, only after completion of the activation of the catalyst, 10 wt% PO (with respect to the reactor content) was added with a feeding rate of 30 mL min−1 (Bischoff HDP PUMP Multitherm 200, 0.1–39.9). The rate of PO consumption was determined from the IR signature of the mixture.Polymer and catalyst characterization
The molecular weight distributions were obtained using size exclusion chromatography (MZ-gel SDplus linear column (5 μm, 300 × 8 mm), Schambeck RI 2012 detector and Flom Intelligent pump AI-12) with tetrahydrofuran as the eluent at 22 °C. The flow rate was 1 mL min−1 using an injection volume of 20 μm. Monodisperse PS standards (Polymer Standards Service GmbH) were used for calibration and the measured values were referenced against these standards. Data given are relative to these standards.The DMC catalysts were characterized by scanning electron microscopy (SEM, Zeiss Gemini Leo 1525 field emission microscope, EHT = 5 kV) using the software SmartSEM (Zeiss). Determination of the surface area was carried out by adsorption measurements using dinitrogen on a Surfer gas adsorption porosimeter (Thermo Fisher Scientific, Software Surfer Acquisition Ver. 1.7.10). The pore size was calculated using the BJH method.87 The powdery samples were prepared for measurement by degassing at 70 °C for 2 h. The surface area was calculated with the software Surfer Ver. 1.7.10 based on the BET method88 in the range of p/p0 = 0.05–0.3. The pore size distribution was calculated using the B.J.H. method in the range of p/p0 = 0.3054–1.003. Powder X-ray diffraction (XRD) measurements were carried out on a MPD X'Pert Pro Powder Diffractometer with Bragg–Brentano geometry (PANalytical, Cu-Kα: 0.154 nm). The sizes of the DMC primary particles were obtained from the SEM images by measuring the x,y,z, dimensions of randomly chosen examples.
Results and discussion
Catalyst characterization and propoxylation procedure
The precatalysts used, DMC A–C, are kindly provided samples based on hexacyano cobaltate and a zinc dication source. These DMCs will be treated as “black boxes” with a particular average size and surface area. This approach appears to be sufficient for building a further understanding of the catalysis. DMC A–C commonly show the usual plate-like habitus of these compounds at different dimensions (Fig. 1).30,51,89 DMC A seems to be the compound with the lowest order, and has the highest number of small primary particles, partly branching away from larger crystal platelets. DMC B and to a lesser extent DMC C have a more homogenous appearance. The X-ray powder diffraction pattern of DMC B displays mostly sharp and intense peaks, as expected, indicating a more ordered structure in comparison to DMC A and C (in accordance with the SEM images; Fig. S3†). The primary platelets of DMC C seem to have a higher state of agglomeration. The agglomerates of primary particles would be expected to break up in the initiation procedure of the propoxylation.A common issue when using a DMC as a catalyst is activation of the parent precursor solids for alkoxylation activity.90 This is usually achieved in a thermal process by heating the DMC solids with starter hydroxyl compounds and subsequent addition of a small amount of PO monomer. The activation procedure involves an induction period of unknown length,56 which depends on several factors such as the composition and preparation procedure of the DMC, temperature, contents of the coordinating entities, and so on.7,26,75,91,92 On an industrial, larger scale, usually in a semi-batch process, the PO monomer will only be added after the activation has been secured; the concentration of PO may not exceed certain limits as its ring-opening is highly exothermic and potentially dangerous situations may arise when leaving the intrinsically safe operation regime of the reactor.56 After the activation, the main part of the propoxylation can be carried out under the control of a PO feeding protocol.
It is a general understanding that coordinating entities (from the catalyst synthesis and/or from the starter and monomer) on the zinc atoms of the surface compete with PO coordination.93 PO is one of the most weakly coordinating agents and the activation procedure involves a displacement of such “blocking agents” from the surface.56,65,75,94,95 Neutral agents (like water and alcohols) may be physically removed and/or react with coordinated PO to become alkoxides, which may undergo protolysis if acidic hydrogen moieties are available to become (coordinated) alcohols (Scheme 2, right). The reaction of coordinated PO with decoordinating anionic nucleophiles (Cl−) present on the catalyst surface is tentatively also part of the activation process to yield basic, protonatable entities on the surface.55,65,75,96,97 The coordination of PO to the DMC surface becomes progressively more favorable with the increase in the chain length of the coadded starter alcohols in the reaction mixture.98,99 It is thus useful to apply alcohol starters as chain transfer agents with a molecular mass that does not effectively inhibit the catalyst.100 A PPG with a molecular weight of 2000 g mol−1 is satisfactory for this and was used in this study (Voranol 2000 L).
DMCs A–C could be activated for propoxylation reactions at about 120 °C after the dilution of the PPG with ∼4 mol eq. of PO. This initially added PO was consumed – dependent on the catalyst and conditions – in a time span below 120 min (the activation time). The decay of the PO concentration was monitored in situ with an FT-IR sensor. The induction time is defined as the time interval in which no substantial monomer conversion occurs and describes the phase between the addition of monomer and start of a time phase, where the consumption of PO starts to increase substantially.7 It can take up to 30 min. An exothermal peak and a pressure drop in the reactor indicate the beginning of the catalytic action. The temperature increase ΔT was always below 10 °C (Table 1). The latter is important for preventing thermal decomposition of the catalyst and possibly for preventing side reactions like the isomerization of PO to allyl alcohol (vide infra).
| Catalyst | Induction time/min | Activation phase/min | ΔT/°C |
|---|---|---|---|
| DMC A | 23 ± 4 | 47 ± 5 | 7 ± 1 |
| DMC B | 30 ± 1 | 117 ± 1 | 3 ± 1 |
| DMC C | 11 ± 5 | 27 ± 5 | 6 ± 2 |
Once the DMC precatalysts are activated, PO consumption at temperatures of 100 °C or higher is fast. Monitoring the PO concentration in-line while adding a small feed of PO (about 1 mL min−1 to a suspension of 50 mg DMC in 166 mL of PPG (2000 g mol−1)) shows that its conversion is always basically complete (98 ± 2%; Fig. 6). The low steady state concentration makes it challenging to obtain an accurate concentration dependent PO conversion profile. The small difference between the integrated feeding rate and a small, time dependent actual concentration would lead to pointless large errors in the consumption rate. It was therefore decided to add PO as repetitive larger pulses by using a relatively high feeding rate (30 mL min−1) and a significantly smaller amount of the DMC catalyst (approx. 5 mg in 166 mL of starter) to have enough time to observe the decline of the PO concentration. The pulses were kept at about 10 wt% of the total mass in the reactor. The actual feeding time added up to less than a minute. The measurements commenced after the PO was essentially mixed into the PPG, i.e., after 2–3 min, allowing the observation of most of the decay. The use of higher concentrations (than in industrial practice) of PO allows the observation of the action of the catalyst, as shown before.7 An approach of giving pulses of PO into a reactor was thus used in this study to create an extended map of the catalytic action.
The volume of the PPG starter after the propoxylation by the PO pulse increases in the experiment each pulse, leading to a dilution of the catalyst particles and hydroxyl groups (increasing molecular weight of the PPG). The pulses were accordingly adjusted, i.e., as the reaction volume increased, more PO was added to reach the 10 wt% of the reactor content. This approach limited the temperature increase by the propoxylation and allowed the reactor to be kept within safety limits. The average PPG chain growth at the first pulse was about 4 entities of PO, and it was about 8 for the 7th pulse.
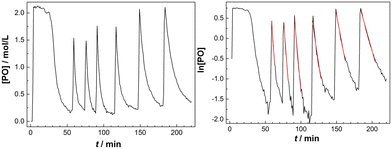
The decline of the PO concentration after the pulse can now easily be detected (Fig. 2). A rate coefficient for the decrease of the PO concentration shortly after the pulse was extracted from the earlier part of the profile with about constant temperature and presuming a first order decay. Plotting the time dependence of the [PO] indeed shows an initial exponential decrease and the linearity of a plot of ln[PO] versus time justifies the 1st order kinetics presumption (Fig. 2, right). A first order [PO] decay is observed in the majority of studies on DMC mediated propoxylation.7,60
The temperature in the reactor cannot (always) be held perfectly constant during the decay of a PO-pulse and increases because of the alkoxylation reaction (Fig. S4†). The observed rate coefficients kobs were consequently evaluated from the early part of the decay of the PO concentration, wherein the temperature was within a few degrees of the starting temperature. The tangent of ln[PO] in that specific interval was always constant within the resulting experimental error (R2 of linear regression >0.98). The time averaged (corrected) temperature in the reactor at the specific part of the linear decrease of the PO concentration was calculated and used for estimating the activation parameter. The standard deviations of the measured average temperatures for the pulsed additions were mostly below 2 °C (Tables S1–S3†), except for a few experiments with a temperature range of 7 °C in the first pulse (at higher catalyst concentrations). The temperature dependent rates are, as a consequence, only close approximations, leading to some (acceptable) scattering in the overall rate constants.
The initial first order fast decay of the PO concentration is generally followed by a much slower decay of changing rate. The moment of transition of the kinetics is dependent on the catalyst, its concentration, and the temperature. This observation of the slower than exponential decay at starving PO concentrations has been made before, and left undiscussed.7,75 A number of arguments, like locally decreasing [OH], change in PO mass transport as a function of molecular weight determined viscosity, change from transient to steady state film diffusion or the formation of a thicker film, may be put forward to account for this (vide infra). It indeed contains further information on the catalytic action and will be the topic of a further manuscript with more accurate data for that phase.
The next pulse was only given after the reactor content had reached its set temperature and the PO concentration was close to zero. The procedure also gives some time to allow a self-diffusion equilibration of the PPGs near the catalyst and the bulk, i.e. the molecular weights are not too high in the vicinity of the catalyst (Scheme 2).101 The pulse-induced increase of the temperature is larger for the early pulses as conversion is faster (higher [OH] and number of DMC particles/mL) than in later stages of experiments with a higher reactor content. The reaction rate decreases with the number of PO pulses in a run, i.e., with the increase of the molecular mass of the alcohols and the associated dilution with respect to hydroxyl and catalyst concentration (Fig. 2, S4 and Tables S1–S3†).
The observed rate constants kobs from the rate law 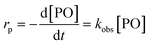 of the initial faster pulse decay at a given temperature were found to reduce to a single value after division by the theoretical bulk hydroxyl concentration and the DMC content (in mg per unit of volume) directly after the pulse. This fact suggests that the reaction order with respect to both the catalyst and the hydroxyl concentration is close to one. The constant resulting from the division of kobs by [OH] and [DMC] is denoted by the product ksK (in L2 s−1 mgDMC−1 mol−1), where ks (in L s−1 mgDMC−1) is understood as the rate constant for the ring-opening of surface coordinated PO per mg of DMC in a 1 L reaction volume and K (in L mol−1) as an equilibrium constant for the binding of PO to the catalyst's surface zinc atoms. These parameters are the outcome of a simple microkinetic mechanistic model for the catalyzed propoxylation as in description 2 (Scheme 2; vide infra).
of the initial faster pulse decay at a given temperature were found to reduce to a single value after division by the theoretical bulk hydroxyl concentration and the DMC content (in mg per unit of volume) directly after the pulse. This fact suggests that the reaction order with respect to both the catalyst and the hydroxyl concentration is close to one. The constant resulting from the division of kobs by [OH] and [DMC] is denoted by the product ksK (in L2 s−1 mgDMC−1 mol−1), where ks (in L s−1 mgDMC−1) is understood as the rate constant for the ring-opening of surface coordinated PO per mg of DMC in a 1 L reaction volume and K (in L mol−1) as an equilibrium constant for the binding of PO to the catalyst's surface zinc atoms. These parameters are the outcome of a simple microkinetic mechanistic model for the catalyzed propoxylation as in description 2 (Scheme 2; vide infra).
It is assumed that the alkoxylation of ROH is of an immortal type, and thus that the number of chain ends remains constant. NMR analysis of the products shows that indeed only traces of allylic or other end groups have formed. The pulsing addition of PO can thus easily be carried out at in situ formed PPGs of various molecular masses. The hydroxyl concentration [OH] in bulk corresponds to a particular molecular mass (cf. OH-number) and distribution with a specific viscosity, like in a typical situation in a propoxylation production plant operated in a semi-batch mode (but here at a higher PO concentration). Thus, extensive information is obtained on the action of the catalyst as function of [OH].
Kinetic parameter and mechanistic interpretation
The reaction pathway of the DMC-mediated propoxylation of alcohols is, based on the kinetics with first-order dependence on [OH], most compatible with description 2 (Scheme 2). The nucleophilic ring-opening of a coordinated PO (POcat) may be supposed to reach a pseudo-steady state (i.e., only dependent on the bulk [PO]) once the activation of the catalyst is completed. The kinetic data obtained at several concentrations of DMC particles and hydroxyls (starter ROH) and at various temperatures are of the activated catalyst. The microkinetics of chain growth by the ring-opening step in the mechanism (2) may be formulated as rp = ks[POcat][OH], with ks as the surface reaction constant. [OH] is the concentration of the ROH entities near the catalyst's surface. This concentration may become increasingly different from the concentration in the bulk during the pulse decay. PO will be faster to diffuse than the self-equilibration of the PPGs (Scheme 3; cf. ESI†). Hence, the PPGs close to the catalyst will grow in length faster, decreasing the local [OH] (at least temporarily at the end of a pulse; vide infra).The PO ring-opening by a nucleophile may be supposed to be the slowest of the chemical steps and thus a balanced preequilibrium PO coordination is presumed, involving coordination sites at the DMC surface, coordinated PO and surface-near PO dissolved in PPG.13 [POcat], the concentration of PO at the catalyst surface, expressed in mol PO per L and mgDMC, may as usual be treated in terms of the fraction of surface coverage, which is denoted by θPO. The equilibrium constant K for the PO coordination thus can be represented as  in L mol−1: PO is a weakly coordinating species, the relative coverage of the free coordination sites by it may be assumed to be small in relation to 1. The interpretation of a rate determining attack of ROH at a PO-surface entity gives the microkinetic propoxylation rate as
in L mol−1: PO is a weakly coordinating species, the relative coverage of the free coordination sites by it may be assumed to be small in relation to 1. The interpretation of a rate determining attack of ROH at a PO-surface entity gives the microkinetic propoxylation rate as 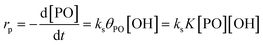 per unit of surface area of DMC with active sites in 1 L, which is proportional to [DMC] in mgDMC L−1. The separation of variables and integration from t = 0 to t = t gives ln([PO]t/[PO]0) = ksK[OH]t for every mgDMC per liter. The observed rate constant kobs divided by the concentration of DMC in mg L−1 and [OH] in mol L−1 thus gives ksK in L mol−1 per PO per s. The fact that within experimental error equal numbers for ksK are obtained under various conditions (DMC and ROH concentrations) indicates that the analysis may be valid. The same expressions would apply to the surface reaction when the rate is diffusion-influenced (i.e., with a non-zero PO concentration near the surface). The propoxylation rate thus appears not to be fully limited by PO mass transport, where no dependence on the hydroxyl group concentration is expected.102
per unit of surface area of DMC with active sites in 1 L, which is proportional to [DMC] in mgDMC L−1. The separation of variables and integration from t = 0 to t = t gives ln([PO]t/[PO]0) = ksK[OH]t for every mgDMC per liter. The observed rate constant kobs divided by the concentration of DMC in mg L−1 and [OH] in mol L−1 thus gives ksK in L mol−1 per PO per s. The fact that within experimental error equal numbers for ksK are obtained under various conditions (DMC and ROH concentrations) indicates that the analysis may be valid. The same expressions would apply to the surface reaction when the rate is diffusion-influenced (i.e., with a non-zero PO concentration near the surface). The propoxylation rate thus appears not to be fully limited by PO mass transport, where no dependence on the hydroxyl group concentration is expected.102
Categorization of the catalyst's action
The action of individual DMCs can be visualized by taking ksK as a measure. A fingerprint of the catalyst activity (in bulk) as a function of temperature and concentration of hydroxyl end groups can be constructed in the form of contour plots in which [OH] or the catalyst particle concentration is plotted against T (Fig. 3; Tables S1–S3†). Note that although the catalyst and hydroxyl concentrations are eliminated by the reduction of kobs to ksK, different conditions still apply and non-ideal conditions with respect to the “catalyst particle distance” become visible.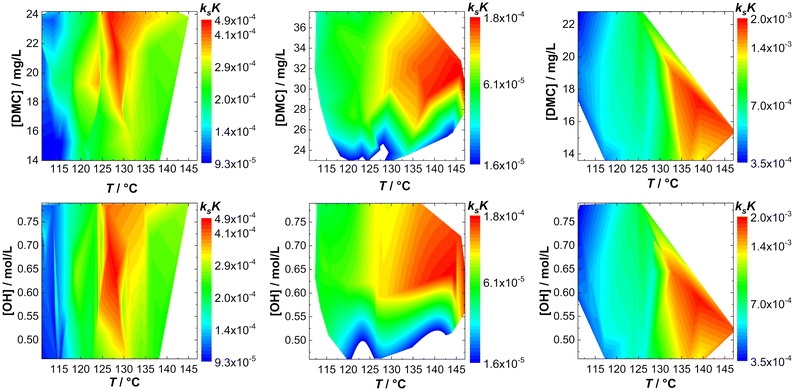 | ||
| Fig. 3 Fingerprints of bulk propoxylation with DMC A, DMC B and DMC C (left to right) with respect to catalyst (top) and calculated hydroxyl (bottom) concentration. | ||
The fingerprints are useful to show the difference in the action of the DMCs. The analysis for DMC C shows a straightforward increase in activity with increasing T and the rate constant is independent of the DMC and hydroxyl concentration. This is the expected behavior when the described catalysis applies under conditions where there are no influences from viscosity changes, deactivation, and other factors affecting the reaction rate. This independence is found only partly for DMC A; the rate is at a maximum at a temperature of about 130 °C. Deactivation of the catalyst at higher temperature explains this behavior.
DMC B is thermally robust like DMC C. Here, it is found that the effective ksK becomes more and more independent of the temperature and [OH] when the latter drops below about 0.55 mol L−1, when the DMC concentration is lower than about 26–28 mg L−1. Such a region in the fingerprint indicates a loss of control over the distribution, as semi-batch feeding experiments indicate (see the section Interpreting the action of DMC A–C). The fingerprinting of the dependence of the catalytic action on T and [DMC] thus enables descriptive catalyst characterization and categorizing. It also allows a global determination of the process conditions in terms of reaction rates (and the concomitant heat evolution) or indirectly on the molecular mass distribution and provides information on the thermal decomposition of the catalytic species.
Activation parameter, support for the Eley–Rideal mechanism 2
A fundamental insight into the catalyst action is gained by considering the apparent activation parameter obtained from the temperature dependence of ksK (Fig. 4). The analysis of the temperature dependence of ksK using the Arrhenius equation gives the apparent activation energy Ea (Table 2) as the slope with respect to 1/T after taking the natural logarithm as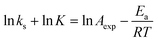 .103,104 The data were also interpreted in terms of the Eyring equation for transition state theory, ksK = exp(−ΔH‡/RT) × (kBT)/h × exp(ΔS‡/R) (Fig. S6†).105,106
.103,104 The data were also interpreted in terms of the Eyring equation for transition state theory, ksK = exp(−ΔH‡/RT) × (kBT)/h × exp(ΔS‡/R) (Fig. S6†).105,106
| (Pre)catalyst | DMC A | DMC B | DMC C |
|---|---|---|---|
| A exp and ΔS‡exp: pre-exponential factor and entropy of activation based on ksK, the “max” values are results when K is set to 10−4 L mol−1. | |||
| E a in kJ mol−1 | 120 ± 10 | 49 ± 4 | 59 ± 7 |
| A exp from ksK/s | 3.4 (± 0.3) × 1012 | 2.3 (±0.5) × 102 | 4.5 (±0.8) × 104 |
| max Aring-opening | 1016 | 106 | 108 |
| ΔH‡/kJ mol−1 | 120 ± 10 | 46 ± 4 | 56 ± 6 |
| ΔS‡exp from ksK in J K−1 mol−1 | −15 ± 2 | −2.1 (±1.5) × 102 | −1.7 (±0.9) × 102 |
| max ΔS‡ring-opening | −4 | −2 (±1.5) × 102 | −1.6 (±0.9) × 102 |
| V p/cm3 g−1 | 0.20 | 0.13 | 0.15 |
| D/nm | 75 | 230 | 110 |
| V mono/cm3 g−1 | 25 | 32 | 5.2 |
| S BET/m2 g−1 | 107 | 140 | 22.8 |
| V p(cum)/cm3 g−1 | 0.30 | 0.17 | 0.31 |
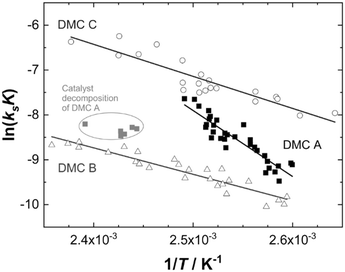
Evaluation of the relevant data with respect to the dependence of the initial fast PO consumption on the temperature indeed gives a linear plot with sufficiently high confidence to discriminate between the three types of DMC catalyst (Fig. 4, S5 and S6†). The uncertainty of the (average) temperature after the pulse gives some limitations with respect to the accuracy, i.e., possibly most of the scattering is from the non-isothermal propoxylation during the decay of the PO pulse in combination with the limited sampling speed of the spectrometer. It is higher for fast rates, however, the global linear dependence of ln(ksK) or 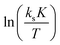 on 1/T for the data collected at varying [OH] and [DMC] shows that the pulse and decay method is adequate to reach consistent and meaningful values for Ea and ΔH‡ for the propoxylation (Table 2). The linearity indicates that a simple, uniform situation underlies the observations in the temperature range for the evaluation of the experimental data.
on 1/T for the data collected at varying [OH] and [DMC] shows that the pulse and decay method is adequate to reach consistent and meaningful values for Ea and ΔH‡ for the propoxylation (Table 2). The linearity indicates that a simple, uniform situation underlies the observations in the temperature range for the evaluation of the experimental data.
The data obtained when applying DMC A at temperatures above 130 °C are clearly outliers from the behavior observed below that temperature. The deviation is taken as evidence of substantial catalyst deactivation (e.g. simple extrapolation of the activation parameter indicates that more than 80% of the sites are lost at 140 °C). Data from these experiments were not considered in calculations of the kinetic parameters. In the case of DMC B, data obtained at molecular weights with [OH] below 0.55 mol L−1 were also not used in calculations of the general kinetic parameters. The effective [OH] near the catalyst is not known under conditions of strong PPG gradients between the bulk and the vicinity of the catalyst (Scheme 2), and no meaningful outcome of the calculation of ksK from kobs is obtained (see the section Interpreting the action of DMC A–C; see ESI† for data displayed and used for regression).
The temperature dependence of the product ksK may mainly originate from the temperature dependence of ks, i.e., the reaction step with the highest activation barrier. As noted before, PO is a weakly coordinating substrate,107,108 and the temperature dependence of K may thus be considered low as ΔH, and to an even greater extent ΔG, for coordination are quite small. The slope of the plots in Fig. 4 are thus effectively associated with the temperature dependence of ks of the ring-opening event.
A
exp and ΔS‡exp are based on the intercepts of the y-axes in the plots of ln(ksK) and 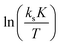 , respectively, against 1/T, where 1/T becomes zero. These numbers are, in contrast to the slope giving
, respectively, against 1/T, where 1/T becomes zero. These numbers are, in contrast to the slope giving 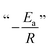 and
and 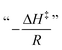 , quite dependent on K. An estimate for K is made from the consideration that propoxylation is evident under the conditions in which the coordination of PPG to the DMC surface will lead to a low number of free coordination sites. The coordination constant for the epoxide will be much smaller than 1, as epoxide adducts are not readily observed in the catalytic chemistry of epoxides and Zn2+. DFT calculations also show this; other entities like ester carbonyls coordinate more strongly.109
, quite dependent on K. An estimate for K is made from the consideration that propoxylation is evident under the conditions in which the coordination of PPG to the DMC surface will lead to a low number of free coordination sites. The coordination constant for the epoxide will be much smaller than 1, as epoxide adducts are not readily observed in the catalytic chemistry of epoxides and Zn2+. DFT calculations also show this; other entities like ester carbonyls coordinate more strongly.109
The presumed value of K is now set to the larger range down to a minimum of 10−4 L mol−1. In that scenario, the values for ΔS‡ from the ksK data will be a maximum of about 10 J K−1 mol−1 too low for the true value for the ring-opening. Concomitantly, the values of the pre-exponential factor of the Arrhenius equation would be higher by a maximum of a factor of 104. The largest pre-exponential factor for DMC A then ranges up to 1016 s−1, already a quite high number.
The activation parameters obtained show significant differences between the three catalysts and two classes may be distinguished (Table 2; Fig. 4). The values obtained for DMC A are in the range of a molecular reaction. The kinetic data of the experiments are likely to predominantly represent the elementary process of PO ring-opening at the catalyst surface by ROH. PO is a monomer with a rather high kinetic barrier for nucleophilic attack, and coordination to a Lewis acid is a prerequisite for reaction with weak nucleophiles like hydroxyl moieties.110–112 Also, the large pre-exponential factor A is typical for a two particle collision,113,114 and the negative value of ΔS‡ is in accordance with a two component reaction with a moderately early transition state.115,116 The activation energy and enthalpy of activation in the range of 120 kJ mol−1 indicate a partial (C–O) bond breakage towards the transition state. The action of DMC A is thus readily interpretable in terms of microkinetic chemical steps.
Chemical surface reactions can, descriptively, proceed either by a Langmuir–Hinshelwood mechanism, in which both reactants are assumed to be adsorbed at the catalyst surface, or an Eley–Rideal mechanism, where one reactant that is coordinated to the surface reacts with an external reactant molecule.61,113,117–120 The kinetics of the ring-opening of a coordinated PO molecule activated by DMC A are thus compatible with the external nucleophilic attack of a hydroxyl chain end OH in a transition state with a higher order of mechanistic description 2. The negative entropy of activation and the large pre-exponential factor found for the alkoxylation suggest that the propagation step is more along an Eley–Rideal type of mechanism, like the one depicted in Scheme 2 (right side). It is less likely that both reactants were first adsorbed at the catalyst surface (a syn ring-opening like for the insertion of an olefin Ziegler–Natta catalyst is considered not a viable reaction route).
The activation energies for propoxylation with DMC B and C are found somewhat below half of the value for DMC A, of the same order of magnitude as the reported value for the action of Zn–Co DMC in toluene of 59 kJ mol−1 (Table 2).63,121 The pre-exponential factors A(max) are atypically low for collisions in the fluid state. The entropies of activation appear as larger negative numbers that have no interpretation as an elementary chemical step. There is no reason to assume that the propoxylation mechanism is different from that at DMC A. The activation parameters rather indicate that the action of DMC B and C is influenced by the diffusion of at least one reagent (Scheme 3). This must be the monomer PO, although its mobility will potentially be higher than that of the hydroxyl chain ends.122 In contrast to simple chemical transformations, the polymerization not only yields a product in the form of a longer chain, but at the same time a new hydroxyl starting material at a marginally lower concentration. The diffusion of PPG with OH entities should thus not play a significant role as they would be ubiquitously available anywhere in the reaction mixture, i.e., also close to the DMC crystal surface.
The interpretation of the catalytic action should follow the basics of heterogeneous catalysis in the liquid phase for an immortal polymerization involving the dynamics of the PO monomer, polymer chains and their chain ends.123 The apparent activation energies of DMC B and C are at a level of 50% of that for DMC A, which may at first glance be reminiscent of the action of a porous heterogeneous catalyst in the intermediate “chemical and diffusion rate” regime (cf. ESI†).113 However, it seems inappropriate to treat the DMC catalyst as a porous particle system. Adsorption measurements with dinitrogen of the DMC precatalysts give type II van der Waals adsorption isotherms, typical for non-porous/macro-porous materials with a pore diameter larger than 50 nm (Table 2; Fig. S2†).124,125 The geometric surface extracted properties also do not hold obvious explanations for the differences in the diverse catalytic action. The measurements show that DMC A and DMC B have a comparable surface area, whereas the surface area of DMC C is about 15% of that of DMC B. The gross catalytic activity gives a very different order. The pores in the DMCs are in a similar range of 75–250 nm and the volumes of the pores are also similar. The pore volume in any of the DMCs makes up only a couple of percent of the monolayer, and since the DMCs are bulk solids, the surface outside the pores may contain most of the active centers.
An alternative, more appropriate kinetic description for the action of DMC B and C can be kept simple by assuming a pseudo-steady state flux of PO (proportional to the gradient) to the DMC surface, where it is converted (Schemes 3 and 4). The flux of PO to the surface is describable by Fick's first law as JPO = kmt([POb] − [POs]), with [POb] as the bulk (measurable) PO concentration, and [POs] the surface-near PO concentration (relevant to the PO coordination). The total amount of PO transport to the surface is JPO × A, with the total surface area A of DMC crystals in a reaction volume of 1 L. The product kmt × A can be replaced by a mass transport constant kmPO, with units of s−1, that relates to the total DMC surface area per liter, i.e. to the concentration of the DMC in mg L−1. The chemical reaction rate at the DMC surface with a preequilibrium coordination of PO and a concentration of ROH close to that of the bulk equals 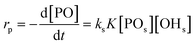 per total amount of DMC in 1 L. The latter should equal the mass transport to the catalyst's surface when
per total amount of DMC in 1 L. The latter should equal the mass transport to the catalyst's surface when 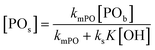 . The bulk concentration [POb] will be the average concentration of PO in the reactor. The observed rate for the total amount of DMC in 1 L is described by
. The bulk concentration [POb] will be the average concentration of PO in the reactor. The observed rate for the total amount of DMC in 1 L is described by 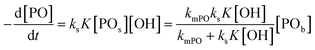 . The observed rate kobs for the total amount of DMC per L is therefore related to the more fundamental rate constants according to
. The observed rate kobs for the total amount of DMC per L is therefore related to the more fundamental rate constants according to 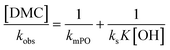 , or in the form of temperature dependencies as
, or in the form of temperature dependencies as 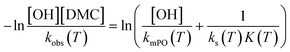 . The temperature dependencies of kobs and ks are clearly not connected simply anymore in the case of a diffusion-influenced rate of PO conversion. The temperature dependence of
. The temperature dependencies of kobs and ks are clearly not connected simply anymore in the case of a diffusion-influenced rate of PO conversion. The temperature dependence of 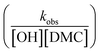 in the small interval of 30 K, however, may (deceptively) still show up with a linear dependence between ln
in the small interval of 30 K, however, may (deceptively) still show up with a linear dependence between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksK (and ln
ksK (and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksK/T) and 1/T (ESI†). An interpretation in terms of elementary reaction steps will, however, not be possible.7,63
ksK/T) and 1/T (ESI†). An interpretation in terms of elementary reaction steps will, however, not be possible.7,63
Interpreting the action of DMC A–C
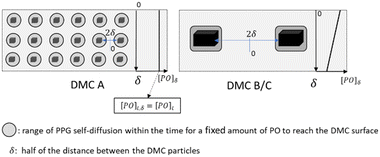
An explanation of the differences in the kinetics between DMC A on the one side, and DMC B and C on the other, results from a consideration of the PO diffusion path length under the conditions of an almost uniform distribution of PO in PPG that should arise within minutes after the pulse (Table 3). The measurement of the decay of the PO concentration reflects such a situation, i.e. the mixing of PO in PPG is considered complete at the start of the measurements. This seems viable: the action of DMC A is not limited by diffusion, and the overall rate for DMC B is lower, while that of DMC C is of the same order of magnitude as that of DMC A. The bulk [POb] may be assumed to be at a value given by the height of the pulse, the elapsed reaction time since the PO addition and the volume of the reaction mixture (Scheme 4). The DMC crystals can thus be treated as individual microreactors for the transformation of the immediate surrounding PO rich phase. This description has also been applied in a theoretical treatise of DMC catalyzed propoxylation, but with a metal bound alkoxide as the resting state and molecular weight dependent rate constants for propagation.62| DMC A | DMC B | DMC C | |
|---|---|---|---|
| a Calculated from an average crystallite as rectangular, cuboid with flat surfaces (see ESI†). b Error is in the range of 10%. c From all pulses of 2 separate runs. | |||
| Averaged crystal weight 10−12 ga | 0.05 | 4 | 0.4 |
| Pulse 1 (PPG 2250) | |||
| T (°C) | 124 | 121 | 126 |
| DMC in mg L−1 | 23.8 | 39.7 | 23.19 |
| d (cryst–cryst) in μm (= 2δ) | 13 | 46 | 26 |
| Relative time constant for diffusion over δ | 1 | 13 | 4 |
| TOF PO per crystal linear regime 10−14/s | 1.6 | 28 | 17 |
| Exponential PO consumptionb/% of decay | 93 | 58 | 76 |
| Pulse 3 (PPG 2800) | |||
| T (°C) | 125 | 122 | 128 |
| V p /cm 3 g −1 | 19.27 | 30.49 | 18.19 |
| DMC in mg L−1 | 14 | 49 | 28 |
| d (cryst–cryst) in μm | 76 | 34 | 67 |
| Exponential PO consumptionb/% of decay | 125 | 122 | 128 |
| Average exponential PO consumptionc/% of decay | 80 | 47 | 71 |
Based on the weight (= volume multiplied by density of 1.8 t m−3) of the primary catalyst particles, the number of particles per unit of reaction volume may be calculated under the premise of a complete dissociation of the aggregates of primary catalyst particles (Table 3). The break-up of the aggregates is expected when they are suspended in Voranol 2000 L with stirring shear and the (initial) polymerization reaction, pushing the primary particles away from each other as the polymer locally takes up more volume with PO consumption.
The minimum distance of PO diffusion may in a first approach be set to half of the distance between the crystals (Scheme 4). This allows the ranking of the length of the diffusion pathway for PO in the order DMC A, DMC C, DMC B, by choice of the experimental conditions and the composition of the catalysts (Table 3). First order estimates of the relative time constants for Brownian movements as mean squared displacement (〈x2〉 = 2D × t) over half the distance between the crystals indicate that diffusion to the surface of DMC B and C is half an order of magnitude slower than that to DMC A. This applies to the diffusion of PO and of the PPGs, the latter is of importance for the distribution of the molecular mass.
Taking the total amount of PO consumption per unit time (kobs) as a basis, the breakdown per crystallite shows that the number of molecules of PO converted by crystallites of DMC A is about one order of magnitude lower than for DMC C, and lower still than for DMC B (Table 3). The attainable flux of PO is thus clearly high enough to account for the absence of mass transport influences on the PO consumption in the action of DMC A with its shorter diffusion pathway and its lower propoxylation rate per crystal. The higher number of its crystallites per mg compensates with respect to the overall rate for the lower activity per particle over DMC B. The action of DMC B and C on the other hand is determined by sufficiently extensive PO activation and becomes influenced by PO mass transport. The much lower number of DMC B particles per L leads overall to a much lower overall activity than for DMC C.
It is worth returning to the change of the kinetic regime during the pulse decay from the initial exponential decay and put this into the perspective of the kinetics and the diffusion length for the PPGs. The change should be related to the “black box” of the catalyst, it seems not to be very dependent on the PO concentration (Table 3). The initial exponential decay is prolonged the longest for DMC A, followed by DMC C and B. This holds true for single evaluations under comparable conditions, but also for a gross average over a larger number of PO pulses (>10) at various OH and catalyst concentrations (Table 3, last entry). The order is in agreement with the distance between the crystals, and most probably is caused by an imbalance between the rate of PO diffusion and PPG self-diffusion as the width of the mass distribution also increases in the order DMC A to C to B. A straightforward argument for the decay in rate towards the end of a pulse would be a (n interpulse) formation of a lower concentration of hydroxyls near the surface by dilution from the propoxylation.
The “catch-up” kinetics, which help to keep the distribution of mass low, would only apply to the growth of PPGs in the range of the self-diffusion space given by the time PO needs to diffuse to the catalyst.126 Note that the observation of “catch-up” kinetics in DMC catalyzed propoxylation supports the interpretation of a rate determining ROH attack at an activated PO on the DMC surface. Thus, as long as the PPGs are “sufficiently” fast in self-diffusion (e.g., at low mass) and the distance between the catalyst particles is small, a sustained simple exponential decay of the PO pulse decay is expected. Accordingly, the linear regime is maintained the longest for DMC A, then for DMC C, with DMC B coming in last. Any loss of exponential decay in the limited chain growth of the pulse (growth of 4 to 7 units to the polymer with more than 40 to 55 units) indicates that the amount of DMC was not enough to keep the exchange of surface-near and -far PPGs within the same order as that of the frequency of propoxylation (Scheme 4). In other words, the distances between the particles were too large for the “catch-up” kinetics to be operative for the full bulk of the PPGs.
The percentage of the bulk PPGs outside the range of self-diffusion would be expected to be higher for large particles (at the same catalyst loading), leading to broader distributions tailing to higher masses. The PPG product distributions determined by SEC indeed show this global behavior, and with expected trends with respect to the catalysts and experimental conditions (Fig. 5). The products from DMC B mediated propoxylation even tend toward bimodality. The PPGs closer to the surface become propoxylated more extensively. The lower dynamics of the PPGs with longer chain lengths (eventually leading to entanglements) will result in a broadening of the distribution by a tailing at high mass.127–129 Concomitantly, the PDI will tend to increase progressively during the sequence of pulses as some longer chains are formed, and the pulse decay will deviate from exponential decay sooner. The effect is on the other hand somewhat compensated for by the fact that the overall rate of propoxylation decreases on account of the local lower [OH] (cf.Fig. 3 middle). Longer PPGs with a lower [OH] close to the DMC will pick up more PO per pulse for their fewer chain ends, which in turn are slower to equilibrate with the bulk. This self-enhancing behavior leads to the indifference to the global [OH] in the contour plots of DMC B.
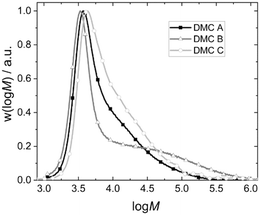 | ||
| Fig. 5 Exemplary molecular weight distributions of the final PPG products of pulse experiments with DMC A–C. | ||
As a result, the products from the propoxylation by DMC A tend to contain the lowest percentage of long chains. The fact that the initial exponential decay is lost at the end of the pulse indicates that also here the PPG self-diffusion cannot hold pace with the propoxylation rate, and that a broadening of the distribution occurs under the conditions of the measurements (relatively low catalyst concentration; Fig. 5). Note that the SECs in Fig. 5 are the result of products formed under conditions that are not comparable (number of pulses, temperature, catalysts loadings).
Semi-batch propoxylations with DMC A and DMC B
The analysis above pertains to conditions of relatively high PO concentrations with respect to conditions of standard semi-batch propoxylations. The latter would be more like the low PO concentration in the fading of the rate at the end of the pulse (after the first order decay), i.e., added PO is converted relatively fast to reach the low steady state concentration: a higher concentration cannot build up because of the limitations set to the feeding rate for safe operation. The flux of PO to the catalyst is lower because of the lower gradient and the propoxylation rate may be influenced by the mass transport for all DMCs. The resulting lower propoxylation rates should be favorable for the equilibration of PPGs between the bulk and catalyst near molecules by self-diffusion, and hence for keeping a low PDI in semi-batch reactions with a limited catalyst amount.A further set of experiments with DMC A and B was carried out at relatively low PO concentrations in semi-batch mode to assess the relevance of the pulse experiments. As rates and conversion are not useful discriminators under such conditions, the development of the molecular mass distribution was monitored.130 The self-diffusion of PPGs in relation to the PO diffusion should be a prominent factor for the outcome and with that the distance between the catalyst particles. It is shown that the insights from the pulse experiments for a good product can be transferred to the performance in semi-batch PO feeding experiments.
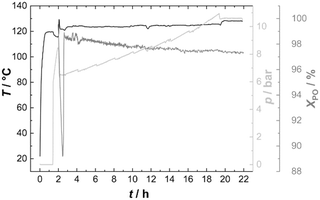
PO was thus fed continuously to the reactor at such a rate that the temperature could be held constant at 120 °C (Fig. 6). Starting from Voranol (2000 g mol−1; 2500 g mol−1 after activation against PS standards in the shown SEC traces), PO was admitted to give a final number average molecular mass of 20 kg mol−1 (against PS standards; Fig. 7). The increase in pressure (mainly of argon) is proportional to the increase in the volume of the reaction mixture (and decrease of the empty reactor volume). The small pressure drops at regular times giving rise to the “saw tooth” profile originating from the sampling of about 20 mL of the volume. In-line IR-spectra showed that the conversion of PO was always basically complete, i.e., the steady state PO concentration has almost no contribution to the pressure above the reaction mixture.
The pathway taken by PO after admittance to the reactor is macro-kinetically determined by the mixing to the smallest possible domain dictated by the reactor setup, and the subsequent diffusion into the medium and towards the catalyst particles. The setup with an anchor stirrer and the PO dosing rate fundamentally gives access to products with a low mass dispersion (Fig. S9†), showing that the mixing of PO is generally good enough for a low PDI of the PPG.
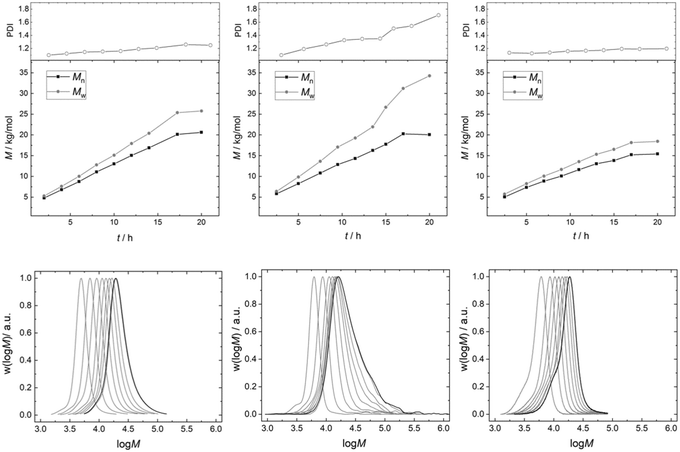
The PDI of the PPGs obtained with 50 mg of catalyst DMC A remains decisively lower than that for the product obtained from a reaction using 50 mg of DMC B (Fig. 7). The development of the PPG molecular mass distribution with PO consumption in the presence of DMC A is almost that of an ideal immortal polymerization. This observation is taken as further evidence of the importance of short diffusion distances. This is the regime of “catch-up” kinetics, where the end groups of lower molecular weight fractions with their higher hydroxyl concentrations are preferentially propoxylated, favorably enhanced by their higher diffusion constants.100,131 The narrow distribution is maintained almost up to the target molecular mass. Only a slight broadening of the distribution is observed. Thus, a PPG with Mn = 20 kg mol−1 (against PS) and a PDI of 1.2 could be achieved.
The PPG obtained under the same conditions (T and feeding rate) with DMC B (50 mg) shows a steadily increasing PDI to about 1.7 with the increase of the molecular mass in the reactor. The eventual formation of a multimodal distribution is indicated by tailing of the distributions at higher masses. The slower diffusion of the PPG chains relative to the rate of PO mobility and propoxylation results in a gradient between catalyst near, longer chains and those at half the distance between the DMC crystals. This gradient will be stronger the longer the diffusion pathway, i.e., the distance between the catalyst particles. The dilution of the catalyst in the experiment enhances the distance and the differences in PO and PPG mass transport. Additionally, the diffusion constant for the self-diffusion of PPG will progressively decrease with the molecular mass, whereas the PO mass transport rate may decrease less as this is probably mainly related to the segment dynamics (cf. ESI†).132 This increases the difference between the rate of self-diffusion and propoxylation. The effect of the “catch-up” kinetics would also become smaller (in the interpretation of mechanistic description 2) at higher masses of the PPGs (smaller differences of [OH] in products of higher molecular mass), and effectively a much broader distributed product is obtained: the formation during the feeding of even a second distribution is indicated.21,77 A low concentration of DMC crystals thus increases the PDI as has been noticed before.7
The broadening of the distribution with the degree of propoxylation is not a property of the surface (in terms of PO activation or polymer binding) of DMC B, but of the reaction conditions. If the propoxylation of PPG 2000 is carried out in the same setup with the use of 450 mg of DMC B, the broadening of the distribution is not found. The distance between the DMC crystals is then in the same ballpark as for DMC A in the pulse experiments. The product distribution in these experiments even has less tailing to higher mass than that for DMC A (a smaller shoulder at the low molecular weight side at about half the mass of the main product indicates that some polymers grow from one end only, possibly started from nucleophilic entities on the catalyst, vide supra).
The observations in the semi-batch propoxylation experiments mediated by DMC A and B as extremes in terms of small and large crystal sizes thus follow the insights from the pulse experiments. The outcome of the pulse experiments allows one to understand and predict the outcome of propoxylations with a DMC catalyst in industrial settings. A good catalyst for obtaining a narrowly distributed product will have a long phase of exponential decay of the PO pulse and will show a fingerprint like DMC C with a higher rate at higher temperature. Catalysts of smaller particle sizes will generally be favorable for propoxylations at low concentrations: the rate can be higher when the crystal sizes are smaller, keeping the distribution narrow. Effectively, the preparation of a supported DMC catalyst or the physical breaking up of the primary particles follows this strategy.31,48,74,89
Conclusions
The monitoring of the DMC mediated pulsed propoxylation of low molecular weight PPGs gives access to a set of characteristics of the catalyst's action. The outcome of the kinetic analysis is typical for heterogeneous catalysis with its known partitioning in macro – diffusion of reagent from and to the bulk phase – and microkinetics. Analyzing the kinetic data using Eyring and Arrhenius theories indicates that mass transport of PO is of importance to the propoxylation rate in the case of DMC B and DMC C, whereas the action of DMC A is determined by PO ring-opening. A derived rate of PO diffusion shows that the latter is feasible. The kinetic parameters are consistent with a propagation reaction according to an Eley–Rideal mechanism, i.e. a PO molecule coordinated to the catalyst surface reacts with an external polymer chain end. The catalytic action of the catalyst particles is more readily understood by considering them as individual “microreactors” than from surface geometry or morphology. Small crystallites give more “microreactors” at the same ppm level of catalyst loading and lead to small diffusion lengths.The imbalance between catalyst near and catalyst far PPG chain growth increases with the square of the distance between the catalyst particles, and should be kept within limits to keep the product distribution low. This distance lies in the range of 10 μm in the current study. The most suitable catalyst system for obtaining a narrowly dispersed product of higher molecular weight would have a rate of PO conversion balanced with the dynamics of the PPGs. DMC A, where PO ring-opening seems to be rate determining, gives narrow molecular weight distributions (PDI = 1.2 at Mn = 20 kg mol−1), provided that the reactor is well-mixed with an appropriate PO dosing protocol. The action of DMC B, where diffusion has a more prominent contribution to the reaction rate, leads to broader distributions, even with a PDI of up to 1.7, when propoxylation is carried out at the same rate of PO dosing as for DMC A.
A fingerprinting system was developed that allows description of the propoxylation reaction rate dependence on the temperature and concentration of chain ends [OH]. The catalyst activity is visualized in a T vs. [OH] or [DMC] rate constant ksK contour plot. This provides essential information on the catalyst's kinetic and thermal behavior and helps to identify essential parameters for preparing narrowly dispersed PPGs. A further consideration is the percentage of PO that can be converted in the exponential regime: this should be as high as possible. These insights are relevant to standard semi-batch propoxylations with a much lower steady state concentration of PO. The overall analysis shows that for the comparison of DMC catalysts and for directed catalyst development, insights into their specific action are necessary, and that the dependencies are relevant to catalyst and process development. It should also not be too surprising that no simple correlations between activity and overall catalyst composition exist.133–135
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. The authors want to acknowledge the efforts of Dr. Marbach in the early phase of the study (e.g., performing the first pulse experiments (some data in Fig. 3), establishing the distribution in the setup as a function of the dosing time) and of Dr. Szopinski, performing rheology at high temperature on PPGs of various masses and establishing general relationships between viscosity, temperatures, and mass. The expertise of Dr. Scheliga on size exclusion chromatography has been of high importance and his support is gratefully acknowledged.References
- J. Milgrom, US3278457, 1966.
- M. Ionescu, Chemistry and Technology of Polyols for Polyurethane, Rapra Technology, Shrewsbury, UK, 2005 Search PubMed.
- S. J. Yu, Y. Liu, S. J. Byeon, D. W. Park and I. Kim, Catal. Today, 2014, 232, 75 CrossRef CAS.
- G. Combs, EP1529566, 2005.
- B. Le-Khac, US5545601, 1996.
- B. Le-Khac, US5731407, 1998.
- A. Chruściel, W. Hreczuch, J. Janik, K. Czaja, K. Dziubek, Z. Flisak and A. Swinarew, Ind. Eng. Chem. Res., 2014, 53, 6636 CrossRef.
- K. G. McDaniel, M. Perry and J. E. Hayes, WO9914258, 1999.
- J. M. O'Connor, D. L. Lickei and R. L. Grieve, US6359101, 2002.
- P. F. Yang, J. Y. Li and T. D. Li, Acad. Manag. Rev., 2010, 160–162, 60 Search PubMed.
- Y. Gu, X. Dong and D. X. Sun, J. Macromol. Sci., Part A: Pure Appl. Chem., 2012, 49, 586 CrossRef CAS.
- S. Chen, P. Zhang and L. Chen, Prog. Org. Coat., 2004, 50, 269 CrossRef CAS.
- Y. J. Huang, G. R. Qi and Y. H. Wang, J. Polym. Sci., Part A: Polym. Chem., 2002, 40, 1142 CrossRef CAS.
- C. P. Smith, J. W. Reisch and J. M. Connor, J. Elastomers Plast., 1992, 24, 306 CrossRef CAS.
- L. R. Safina, K. E. Kharlampidi and D. K. Safin, Russ. J. Appl. Chem., 2012, 85, 1610 CrossRef CAS.
- P. Król, Linear Polyurethanes: Synthesis Methods, Chemical Structures, Properties and Applications, Leiden Boston, 2008 Search PubMed.
- N. An, Q. Li, N. Yin, M. Kang and J. Wang, Appl. Organomet. Chem., 2018, 32, e4509 CrossRef.
- M. Meuresch, A. Wolf and C. Guertler, WO2019121205A1, 2019.
- Z. Hua, G. Qi and S. Chen, J. Appl. Polym. Sci., 2004, 93, 1788 CrossRef CAS.
- S. Chen, X. Zhang, F. Lin and G. Qi, React. Kinet. Catal. Lett., 2007, 91, 69 CrossRef CAS.
- I. Kim, S. H. Byun and C. S. Ha, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 4393 CrossRef CAS.
- H. Liu, X. Wang, Y. Gu and W. Guo, Molecules, 2003, 8, 67 CrossRef CAS.
- B. Le-Khac, H. R. Hinney and P. T. Bowman, US5627122, 1997.
- J. Hofmann, S. Ehlers, B. Klinksiek, B. Klesczewski, C. Steinlein, L. Obendorf, H. Pielartzik and J. F. Pazos, WO02068502, 2002.
- Y. J. Huang, G. R. Qi and L. S. Chen, Appl. Catal., A, 2003, 240, 263 CrossRef CAS.
- S. Lee, S. T. Baek, K. Anas, C.-S. Ha, D.-W. Park, J. W. Lee and I. Kim, Polymer, 2007, 48, 4361 CrossRef CAS.
- M. Pinilla, C. Andrés-Iglesias, A. Fernández, T. Salmi, J. R. Galdámez and J. García-Serna, Eur. Polym. J., 2017, 88, 280 CrossRef.
- W. Zhang, L. Lu, Y. Cheng, N. Xu, L. Pan, Q. Lin and Y. Wang, Green Chem., 2011, 13, 2701 RSC.
- J. H. Yoon, I. K. Lee, H. Y. Choi, E. J. Choi, J. H. Yoon, S. E. Shim and I. Kim, Green Chem., 2011, 13, 631 RSC.
- J. Sebastian and S. Darbha, RSC Adv., 2015, 5, 18196 RSC.
- C. Marquez, M. Rivera-Torrente, P. P. Paalanen, B. M. Weckhuysen, F. G. Cirujano, D. de Vos and T. de Baerdemaeker, J. Catal., 2017, 354, 92 CrossRef CAS.
- Z. Guo and Q. Lin, J. Mol. Catal. A: Chem., 2014, 390, 63 CrossRef CAS.
- J. L. Garcia, E. J. Jang and H. Alper, J. Appl. Polym. Sci., 2002, 86, 1553 CrossRef CAS.
- C. H. Tran, L. T. T. Pham, Y. Lee, H. B. Jang, S. Kim and I. Kim, J. Catal., 2019, 372, 86 CrossRef CAS.
- G. H. Grosch, E. Bohres, R. Ruppel, K. Harre, E. Baum, M. Stosser, J. T. Miller and R. B. Prager, US20040044240A1, 2004.
- G. H. Grosch, H. Larbig, R. Lorenz, D. Junge, E. Gehrer and U. Treuling, DE19944762A1, 2001.
- S. Chen and L. Chen, Colloid Polym. Sci., 2004, 282, 1033 CrossRef CAS.
- I. K. Lee, J. Y. Ha, C. Cao, D.-W. Park, C.-S. Ha and I. Kim, Catal. Today, 2009, 148, 389 CrossRef CAS.
- Z. Guo, Q. Lin, X. Wang, C. Yu, J. Zhao, Y. Shao and T. Peng, Mater. Lett., 2014, 124, 184 CrossRef CAS.
- J. Sebastian and S. Darbha, J. Chem. Sci., 2014, 126, 499 CrossRef CAS.
- I. Kim, M. J. Yi, K. J. Lee, D.-W. Park, B. U. Kim and C.-S. Ha, Catal. Today, 2006, 111, 292 CrossRef CAS.
- X.-H. Zhang, Z.-J. Hua, S. Chen, F. Liu, X.-K. Sun and G.-R. Qi, Appl. Catal., A, 2007, 325, 91 CrossRef CAS.
- M. B. Eleveld, R. A. de Groot, R. A. W. Grotenbreg and J. P. Smit, WO2003008482A1, 2003.
- M. B. Eleveld, R. A. W. Grotenbreg and R. van Kempe, WO2003106025A1, 2003.
- A. Peeters, P. Valvekens, F. Vermoortele, R. Ameloot, C. Kirschhock and D. de Vos, Chem. Commun., 2011, 47, 4114 RSC.
- N. J. Robertson, Z. Qin, G. C. Dallinger, E. B. Lobkovsky, S. Lee and G. W. Coates, Dalton Trans., 2006, 5390 RSC.
- C. Marquez, A. Simonov, M. T. Wharmby, C. van Goethem, I. Vankelecom, B. Bueken, A. Krajnc, G. Mali, D. de Vos and T. de Baerdemaeker, Chem. Sci., 2019, 10, 4868 RSC.
- M. A. Subhani, C. Gürtler, W. Leitner and T. E. Müller, Eur. J. Inorg. Chem., 2016, 2016, 1944 CrossRef CAS.
- M. B. Eleveld and P. A. Schut, WO2006100219A1, 2006.
- J. Sebastian and D. Srinivas, Appl. Catal., A, 2013, 464-465, 51 CrossRef CAS.
- K. Lawniczak-Jablonska, E. Dynowska, W. Lisowski, J. W. Sobczak, A. Chruściel, W. Hreczuch, J. Libera and A. Reszka, X-Ray Spectrom., 2015, 44, 330 CrossRef CAS.
- J. Sebastian and D. Srinivas, Appl. Catal., A, 2015, 506, 163 CrossRef CAS.
- C. H. Tran, L. T. T. Pham, H. B. Jang, S. A. Kim and I. Kim, Catal. Today, 2021, 375, 429 CrossRef CAS.
- J. C. Wojdeł, S. T. Bromley, F. Illas and J. C. Jansen, J. Mol. Model., 2007, 13, 751 CrossRef.
- N. Almora-Barrios, S. Pogodin, L. Bellarosa, M. García-Melchor, G. Revilla-López, M. García-Ratés, A. B. Vázquez-García, P. Hernández-Ariznavarreta and N. López, ChemCatChem, 2015, 7, 928 CrossRef CAS.
- S. H. Lee, I. K. Lee, J. Y. Ha, J. K. Jo, I. Park, C.-S. Ha, H. Suh and I. Kim, Ind. Eng. Chem. Res., 2010, 49, 4107 CrossRef CAS.
- S. H. Lee, C.-S. Ha and I. Kim, Macromol. Res., 2007, 15, 202 CrossRef CAS.
- V. Šutinská, M. Pajtášová, D. Ondrušová, S. Ľalíková, A. Ferjancová, J. Paliesková and S. C. Mojumdar, J. Therm. Anal. Calorim., 2011, 104, 923 CrossRef.
- X. H. Zhang, S. Chen, X. M. Wu, X. K. Sun, F. Liu and G. R. Qi, Chin. Chem. Lett., 2007, 18, 887 CrossRef CAS.
- W. Reschetilowski, Einführung in die heterogene Katalyse, Berlin Heidelberg, 2015 Search PubMed.
- A. Jess and P. Wasserscheid, Chemical technology: An integral textbook, Wiley-VCH, Weinheim, 2013 Search PubMed.
- M. Klinger, R. Bachmann and A. Jupke, Macromol. Theory Simul., 2021, 30, 2100013 CrossRef CAS.
- L. Wu, A. Yu, M. Zhang and L. Chen, Gaofenzi Xuebao, 2003,(Band 6), 871 CAS.
- R. Bachmann, M. Klinger and A. Jupke, Macromol. Theory Simul., 2021, 30, 2100012 CrossRef CAS.
- Y.-J. Huang, X.-H. Zhang, Z.-J. Hua, S.-L. Chen and G.-R. Qi, Macromol. Chem. Phys., 2010, 211, 1229 CrossRef CAS.
- J. Zhao, B.-G. Li and H. Fan, Macromol. Theory Simul., 2021, 2000101 CrossRef CAS.
- J. Zhao, B.-G. Li, Z.-Y. Bu and H. Fan, Macromol. React. Eng., 2020, 14, 1900048 CrossRef CAS.
- T. Pelzer, B. Eling, H.-J. Thomas and G. A. Luinstra, Eur. Polym. J., 2018, 107, 1 CrossRef CAS.
- A. Prokofyeva, H. Laurenzen, D. J. Dijkstra, E. Frick, A. M. Schmidt, C. Guertler, C. Koopmans and A. Wolf, Polym. Int., 2017, 66, 399 CrossRef CAS.
- G. A. Luinstra, G. R. Haas, F. Molnar, V. Bernhart, R. Eberhardt and B. Rieger, Chem. – Eur. J., 2005, 11, 6298 CrossRef CAS.
- W.-M. Ren, Z.-W. Liu, Y.-Q. Wen, R. Zhang and X.-B. Lu, J. Am. Chem. Soc., 2009, 131, 11509 CrossRef CAS.
- M. I. Childers, J. M. Longo, N. J. van Zee, A. M. LaPointe and G. W. Coates, Chem. Rev., 2014, 114, 8129 CrossRef CAS PubMed.
- Z. Liu, M. Torrent and K. Morokuma, Organometallics, 2002, 21, 1056 CrossRef CAS.
- J. Shi, Z. Shi, H. Yan, X. Wang, X. Zhang, Q. Lin and L. Zhu, RSC Adv., 2018, 8, 6565 RSC.
- L.-C. Wu, A.-F. Yu, M. Zhang, B.-H. Liu and L.-B. Chen, J. Appl. Polym. Sci., 2004, 92, 1302 CrossRef CAS.
- J. Pazos and E. Browne, Polym. Prepr., 2008, 49, 434 CAS.
- IMPACT Technology – A Greener Polyether Process, ed. J. Reese, K. McDaniel, R. Lenahan, R. Gastinger and M. Morrison, 2009 Search PubMed.
- Handbook of transition metal polymerization catalysts, ed. R. E. Hoff, Wiley, Hoboken, N.J, 2010 Search PubMed.
- S. Asano, T. Aida and S. Inoue, J. Chem. Soc., Chem. Commun., 1985, 1148 RSC.
- S. Inoue, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 2861 CrossRef CAS.
- J. A. Dumesic, G. W. Huber and M. Boudart, in Handbook of Heterogeneous Catalysis, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2008, p. 1 Search PubMed.
- M. Pohl, Tailor-made Polyols for Sustainable Polyurethanes by Catalyzed Copolymerization of CO2 and Epoxides, Ph.D. Thesis, RWTH Aachen, 2017 Search PubMed.
- Catch Up and High Molecular Weight Tailing, Modeling Kinetics of DMC Catalyzed Polyol Preparation, 13th International Workshop on Polymer Reaction Engineering, ed. M. Klinger, R. Bachmann, A. Stute and A. Jupke, 2019 Search PubMed.
- C. H. Bartholomew and R. J. Farrauto, Fundamentals of Industrial Catalytic Processes, Hoboken, New Jersey, 2006 Search PubMed.
- E. Bohres, F. Hill, R. Ruppel and E. Baum, WO2004022227, 2004.
- S. Li, W. Qi, Y. Han, C. Chen, B. Hu, M. Yuan and G. Ding, CN1457928, 2003.
- E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309 CrossRef CAS.
- X.-K. Sun, X.-H. Zhang, F. Liu, S. Chen, B.-Y. Du, Q. Wang, Z.-Q. Fan and G.-R. Qi, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 3128 CrossRef CAS.
- J. Herzberger, K. Niederer, H. Pohlit, J. Seiwert, M. Worm, F. R. Wurm and H. Frey, Chem. Rev., 2016, 116, 2170 CrossRef CAS.
- I. Kim, J.-T. Ahn, C. S. Ha, C. S. Yang and I. Park, Polymer, 2003, 44, 3417 CrossRef CAS.
- I. Kim, J.-T. Ahn, S.-H. Lee, C.-S. Ha and D.-W. Park, Catal. Today, 2004, 93–95, 511 CrossRef CAS.
- A. Peeters, P. Valvekens, R. Ameloot, G. Sankar, C. E. A. Kirschhock and D. E. de Vos, ACS Catal., 2013, 3, 597 CrossRef CAS.
- Y.-Y. Zhang, G.-W. Yang, Y. Wang, X.-Y. Lu, G.-P. Wu, Z.-S. Zhang, K. Wang, R.-Y. Zhang, P. F. Nealey, D. J. Darensbourg and Z.-K. Xu, Macromolecules, 2018, 51, 791 CrossRef CAS.
- D. J. Darensbourg, J. R. Wildeson, S. J. Lewis and J. C. Yarbrough, J. Am. Chem. Soc., 2002, 124, 7075 CrossRef CAS PubMed.
- R. A. Livigni, R. J. Herold, O. C. Elmer and S. L. Aggarwal, in Polyethers, ed. E. J. Vandenberg, American Chemical Society, Washington, D. C., 1975, p. 20 Search PubMed.
- S.-F. Stahl and G. A. Luinstra, Catalysts, 2020, 10, 1066 CrossRef CAS.
- G. Wegener, M. Brandt, L. Duda, J. Hofmann, B. Klesczewski, D. Koch, R. J. Kumpf, H. Orzesek, H. G. Pirkl, C. Six, C. Steinlein and M. Weisbeck, Appl. Catal., A, 2001, 221, 303 CrossRef CAS.
- R. R. Sharifullin, L. R. Safina, A. S. Biktimerova, N. S. Gabdulkhakova and D. K. Safin, Catal. Ind., 2012, 4, 243 CrossRef.
- J. F. Pazos, US5777177, 1998.
- B. A. Smith, E. T. Samulski, L.-P. Yu and M. A. Winnik, Phys. Rev. Lett., 1984, 52, 45 CrossRef CAS.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, Wiley, New York, NY, 1962 Search PubMed.
- S. Arrhenius, Z. Phys. Chem., 1889, 4, 226 CrossRef.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- K. J. Laidler and M. C. King, J. Phys. Chem., 1983, 87, 2657 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- D. Darensbourg, Coord. Chem. Rev., 1996, 153, 155 CrossRef CAS.
- S. Penczek, P. Kubisa and K. Matyjaszewski, Cationic ring-opening polymerization, Springer, Berlin, 1980 Search PubMed.
- S. Kissling, P. T. Altenbuchner, M. W. Lehenmeier, E. Herdtweck, P. Deglmann, U. B. Seemann and B. Rieger, Chemistry, 2015, 21, 8148 CrossRef CAS.
- D. J. Darensbourg and J. C. Yarbrough, J. Am. Chem. Soc., 2002, 124, 6335 CrossRef CAS PubMed.
- D. J. Darensbourg, J. C. Yarbrough, C. Ortiz and C. C. Fang, J. Am. Chem. Soc., 2003, 125, 7586 CrossRef CAS PubMed.
- D. J. Darensbourg and A. D. Yeung, Macromolecules, 2013, 46, 83 CrossRef CAS.
- J. M. Thomas and W. J. Thomas, Principles and Practice of Heterogeneous Catalysis, Weinheim, 1997 Search PubMed.
- J. E. Leffler and E. Grunwald, Rates and equilibria of organic reactions: As treated by statistical, thermodynamic, and extrathermodynamic methods, Dover, New York, 1989 Search PubMed.
- R. A. Jones, Physical and mechanistic organic Chemistry, Cambridge Univ. Pr, Cambridge, 1985 Search PubMed.
- J. E. Leffler, J. Org. Chem., 1955, 20, 1202 CrossRef CAS.
- I. Langmuir, Trans. Faraday Soc., 1922, 17, 607 RSC.
- C. N. Hinselwood, Proc. R. Soc. London, Ser. A, 1926, 113, 230 Search PubMed.
- D. D. Eley and E. K. Rideal, Nature, 1940, 146, 401 CrossRef CAS.
- M. Boudart, in Interactions on Metal Surfaces, ed. R. Gomer, Springer-Verlag, Berlin/Heidelberg, 1975, p. 275 Search PubMed.
- T. Zhou, Z. Zou, J. Gan, L. Chen and M. Zhang, J. Polym. Res., 2011, 18, 2071 CrossRef CAS.
- C. M. Hansen, Polym. Eng. Sci., 1980, 20, 252 CrossRef CAS.
- M. Pohl, E. Danieli, M. Leven, W. Leitner, B. Blümich and T. E. Müller, Macromolecules, 2016, 49, 8995 CrossRef CAS.
- S. Brunauer, L. S. Deming, W. E. Deming and E. Teller, J. Am. Chem. Soc., 1940, 62, 1723 CrossRef CAS.
- K. S. W. Sing, Pure Appl. Chem., 1985, 57, 603 CrossRef CAS.
- J. R. Reese and P. Webb, WO2014159551A1, 2014.
- T. Cosgrove, Polymer, 1994, 35, 140 CrossRef CAS.
- C. Gainaru, W. Hiller and R. Böhmer, Macromolecules, 2010, 43, 1907 CrossRef CAS.
- G. Fleischer, M. Helmstedt and I. Alig, Polym. Commun., 1990, 31, 409 CAS.
- Identification and Optimization of Polymerization Processes Using Detailed Analysis of Molecular Weight Distributions, ed. R. Bachmann, S. Braun, M. Klinger and T. König, 2019 Search PubMed.
- K. G. McDaniel, EP1942126, 2008.
- A. Bormuth, M. Hofmann, P. Henritzi, M. Vogel and E. A. Rössler, Macromolecules, 2013, 46, 7805 CrossRef CAS.
- I. Kim, K. Anas, S. Lee, C.-S. Ha and D.-W. Park, Catal. Today, 2008, 131, 541 CrossRef CAS.
- Z. Li, Y. Qin, X. Zhao, F. Wang, S. Zhang and X. Wang, Eur. Polym. J., 2011, 47, 2152 CrossRef CAS.
- W. Zhang, Q. Lin, Y. Cheng, L. Lu, B. Lin, L. Pan and N. Xu, J. Appl. Polym. Sci., 2012, 123, 977 CrossRef CAS.
Footnote |
† Electronic supplementary information (ESI) available: Additional information on the reaction profile and experimental data for the pulse-decay experiments, reasoning for the Thiele modulus, diffusion and Mw dependent viscosity of the reaction mixture at 120 °C, data and discussion of the linearity of the relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksK (and ln ksK (and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksK/T) and 1/T under diffusion influenced rates, calculations of DMC crystals and data on the attainable PDIs in the setup. See DOI: https://doi.org/10.1039/d3re00313b ksK/T) and 1/T under diffusion influenced rates, calculations of DMC crystals and data on the attainable PDIs in the setup. See DOI: https://doi.org/10.1039/d3re00313b |
| This journal is © The Royal Society of Chemistry 2024 |