Open Access Article
Open Access ArticleInvestigation into the intersection between response process validity and answer-until-correct validity: development of the repeated attempt processing issue detection (RAPID) method
David G.
Schreurs
 a,
Jaclyn M.
Trate
a,
Jaclyn M.
Trate
 b,
Shalini
Srinivasan
c,
Melonie A.
Teichert
b,
Shalini
Srinivasan
c,
Melonie A.
Teichert
 d,
Cynthia J.
Luxford
d,
Cynthia J.
Luxford
 e,
Jamie L.
Schneider
e,
Jamie L.
Schneider
 f and
Kristen L.
Murphy
f and
Kristen L.
Murphy
 *a
*a
aUniversity of Wisconsin-Milwaukee, Milwaukee, Wisconsin 53211, USA. E-mail: kmurphy@uwm.edu
bUniversity of Wisconsin-Madison, Madison, Wisconsin 53706, USA
cMetropolitan State University of Denver, Denver, Colorado 80204, USA
dUnited States Naval Academy, Annapolis, Maryland 21402, USA
eTexas State University, San Marcos, Texas 78666, USA
fUniversity of Wisconsin-River Falls, River Falls, Wisconsin 54022, USA
First published on 22nd January 2024
Abstract
With the already widespread nature of multiple-choice assessments and the increasing popularity of answer-until-correct, it is important to have methods available for exploring the validity of these types of assessments as they are developed. This work analyzes a 20-question multiple choice assessment covering introductory undergraduate chemistry topics which was given to students in an answer-until-correct manner. Response process validity was investigated through one-on-one think-aloud interviews with undergraduate chemistry students. Answer-until-correct validity was also explored using an analysis of partial credit assignments. Results indicated the convenience of the quantitative partial credit method came at great cost to the precision of validity issue detection and is therefore not a valid shortcut to more rich qualitative approaches. The repeated attempt processing issue detection (RAPID) method is a novel method developed as a combination of response process and answer-until-correct validity. Results from this new method revealed validity issues that were undetected from the use of either approach individually or in concert.
Introduction
Assessment validity
One of many considerations that must be made when developing an assessment is ensuring the assessment produces data with evidence of high validity. Assessment validity is defined as “the degree to which evidence and theory support the interpretations of test scores entailed by proposed uses of tests” (American Educational Research Association, 1999; Arjoon et al., 2013). An assessment that produces data with evidence of high validity does an accurate job of measuring what it was designed to measure. Or, more alarmingly, an assessment with an abundance of validity issues does a poor job reflecting the students’ understanding. To minimize the risk of flawed assessment results, many types of validity investigation methods have been developed. Because these many methods exist, the optimal way of showing high assessment validity will vary based on the format, content, and context of the assessment (Wren and Barbera, 2013; Kreiter, 2015; Lewis, 2022; Lazenby et al., 2023).Response process
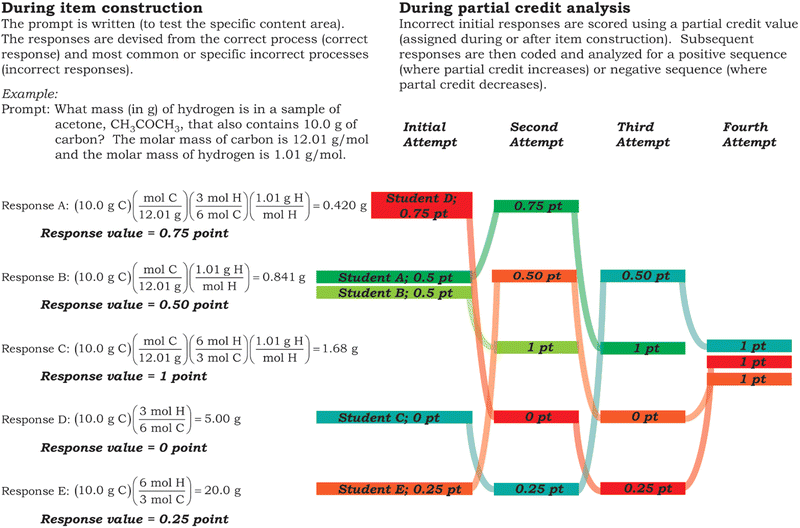
One method for investigating the validity of items within an assessment is the analysis of students’ response processes. Response process centres around the steps the student takes to arrive at their response and investigates the degree to which the student's process aligns with the response they choose (Kreiter, 2015; Deng et al., 2021). During forced-response item construction, the responses are formulated based on the correct process (correct answer) and specific, common incorrect processes (distractors). In research, these incorrect processes would ideally be determined by a qualitative analysis of common student mistakes as they engage with the item stem as an open-response question. However, in the typical classroom, it is more practical for incorrect distractors to be developed by utilizing the experience of an instructor who has worked with students and is familiar with the errors they tend to make.During a response process study, investigation into the process a student articulates within a single attempt when solving the item should reveal that only a student with a correct process and understanding will select the correct answer. Alternatively, students with incorrect processes and understandings will select the distractors. While this view of response process may suffice for some applications, it can also be explored more richly by not only ensuring students with an incorrect process and understanding select an incorrect response, but also that the incorrect process used by the student aligns with the process proposed during item construction (coined “enhanced response process validity” for differentiation here). The utilization of enhanced response process validity is particularly necessary if a deeper understanding of student misconceptions is desired. This is because traditional response process validity analysis only allows for claims of whether a mistake had been made; whereas enhanced response process validity allows for claims about what mistake had been made.
A fictitious example item showing item construction followed by examples of artificial student responses that might be collected during think-aloud interviews is shown in Fig. 1. This fictitious item was designed with five responses (as opposed to the four responses used for the actual study) to demonstrate the various validity threats more easily. Both the process assignment as well as the enhanced response process validity assignment are provided. These fictitious student responses are provided to illustrate the potential array of response process validity classifications; there are many other possible pathways (and other incorrect responses/processes) a student may follow.
As response process validity issues can arise from correct or incorrect responses, full response process analysis could require an analysis of all student responses. Coupling this with the time and resource investment to conduct and transcribe interviews, it is not surprising that response process validity investigations are less commonly used compared to other measures for validity. Examples of investigation into single-attempt response process validity can be found in the literature however, the reporting is relatively scarce compared to other validity methods (Adams et al., 2008; Stains et al., 2011; Wren and Barbera, 2013; Brandriet and Bretz, 2014; Schwartz and Barbera, 2014; Trate et al., 2019). It is possible that recent chemistry education publications regarding response process will lead to an increase in its popularity within the field (Deng et al., 2021; Balabanoff et al., 2022).
Answer-until-correct and partial credit analysis
An extension of multiple-choice assessments is answer-until-correct. Answer-until-correct methods use immediate feedback to allow students to reengage with a problem until they arrive at the correct answer (Pressey, 1926; Epstein et al., 2001). By allowing repeated attempts on each problem, students are given multiple opportunities to improve their process and learn the material (Bangert-Drowns et al., 1991; DiBattista, 2013). Answer-until-correct methods also allow an alternative approach to scoring where credit can be awarded to students based on how many attempts are required to arrive at the correct option (as opposed to assigning partial credit to each response). This immediate correction of students’ incorrect response choices can minimize the risks of students solidifying incorrect information (Skinner, 1974; Brown et al., 1999; Brosvic et al., 2005; Roediger and Marsh, 2005). Other work has found additional benefits of answer-until-correct methods including promotion of learning, student appreciation, and creation of assessments which have questions build off of one another because the correct answer to the previous questions can always be found (Epstein, 2002; Dibattista et al., 2004; Clariana and Koul, 2005; Slepkov and Shiell, 2014; Attali, 2015; Schneider et al., 2018; Pinhas, 2021). Another commonly cited advantage is that partial credit based on number of attempts can be awarded without making assumptions about the processes used by students to arrive at their response (Pressey, 1950; Epstein et al., 2002). However, while avoiding some assumptions about incorrect responses, answer-until-correct does rely on the assumption that as students engage with the immediate feedback, they are correcting their flawed thought processes. This means for an answer-until-correct assessment to be valid; students must use the immediate feedback to build a more complete understanding of the intended concepts ultimately arriving at the correct process and the correct response.A means to arrive at the sequential improvement of a student's process could be investigated through a merging of multiple responses for each item and a partial credit assignment for each response. Therefore, prior to completing this method of answer-until-correct validity, partial credit must be assigned to each response. This can be done during the test construction (when the process for each response is developed and justified) or following the test construction. When used for validity studies, it is also important to consider agreement between raters of partial credit assignment (Murphy et al., 2023a; 2023b). For the example used in Fig. 1 (and used again here), partial credit is assigned based on using a scale of full credit, ¾ credit, ½ credit, ¼ credit and no credit. As shown in Fig. 2, for an item to be valid using the sequential partial credit analysis method, a student would be expected to show a progressive increase in the assignment of partial credit for each response in sequence (noted in the figure for artificial students A–C in green/blue). An issue for validity would be cited when the sequence of responses did not show a progressive improvement in partial credit (shown in the figure for artificial students D and E in red/orange). What is not detected through this method is the incorporation of any processing and/or guessing. Assumptions can be made about student process (especially when using process-oriented assessment items), but the assumption of student process based on response selection may not always be valid (Ralph and Lewis, 2019). Because this type of analysis is conducted only using students’ response sets, not their think-aloud protocols of their processes, it does not account for details of the single-attempt response process which will be expanded upon in the next section.
 | ||
| Fig. 2 Possible pathways of partial credit analysis with valid response sets (green/blue) and invalid response sets (red/orange). | ||
The analysis that would then follow would consider the sequence of the responses based on expert assigned partial credit. Continuing with the example from Fig. 2, each response set is provided with the numeric analysis that would provide the assignment of valid vs. invalid processes using this partial credit analysis (Table 1).
| Student (color) | Response value | Change in values | Constant improvement | Valid partial credit process | |||||
|---|---|---|---|---|---|---|---|---|---|
| Initial response | Second response | Third response | Fourth response | Initial to second | Second to third | Third to fourth | |||
| A (green) | 0.50 | 0.75 | 1.00 | +0.25 | +0.25 | Yes | Valid | ||
| B (light green) | 0.50 | 1.00 | +0.50 | Yes | Valid | ||||
| C (blue) | 0.00 | 0.25 | 0.50 | 1.00 | +0.25 | +0.25 | +0.50 | Yes | Valid |
| D (red) | 0.75 | 0.00 | 0.25 | 1.00 | –0.75 | +0.25 | +0.75 | No | Invalid |
| E (orange) | 0.25 | 0.50 | 0.00 | 1.00 | 0.25 | –0.50 | 1.0 | No | Invalid |
Intersection of response process and partial credit analysis
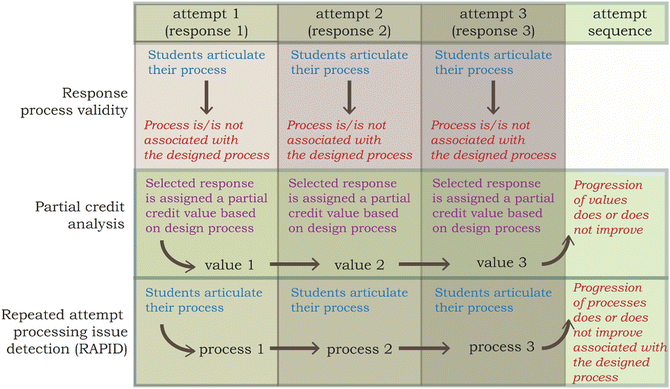
While previous work has made progress in validating the theory and implementation of answer-until-correct in general, and in methods for single-attempt response process validity on traditional multiple-choice assessments, no exploration of the relationship between these two concepts could be found (Towns, 2014; Slepkov et al., 2016). Now that the limitations of these methods have been discussed, the theoretical effect of merging these methods can be explored. As is shown in Fig. 3, a limitation with single-attempt response process validity is it only analyses individual attempts for potential threats. When a student engages with an item once (i.e., traditional, single response assessment), this method fulfils the purpose of this level of item validity. However, when students engage with an item multiple times, as when using answer-until-correct assessment, a set of responses or attempt sequences is generated (as shown in Fig. 3). A necessary element of an attempt sequence is the student is expected to reengage with the item between attempts. One example of a student not reengaging after an initial incorrect response is: “…Because I feel like earlier I was off by a little margin”. In this example the student selected the closest response to their initial attempt only because of the proximity to their first answer. This student did not utilize the knowledge of their initial incorrect response to reengage with the item. This issue of reengagement is expanded upon in Appendix 1.When students do reengage, attempt sequences still need to be evaluated for validity. This can potentially be accomplished by considering a partial credit analysis of each response and combined in the attempt sequence (as shown in Fig. 3). However, this method does not consider any student processing, only assumed processing through assigned partial credit value (assigned to the incorrect responses). Therefore, a new method was developed to examine the processing progression within an attempt sequence, which we called “Repeated Attempt Processing Issue Detection” or RAPID (also shown in Fig. 3).
To demonstrate the theoretical need for this new RAPID method Fig. 4 demonstrates an example process (used by Student I) which could result in missed validity issue detection. Student I would not have been flagged as an answer-until-correct validity issue despite an answer-until-correct validity issue being present. In this case the misdetection was caused by a response process issue present in the student's initial attempt which misaligned the student's process with the partial credit of their answer choice (as shown with a red outline). To correctly flag this answer-until-correct validity issue, a different method is required which overcomes the potential interaction between single-attempt response process and answer-until-correct validity issues.
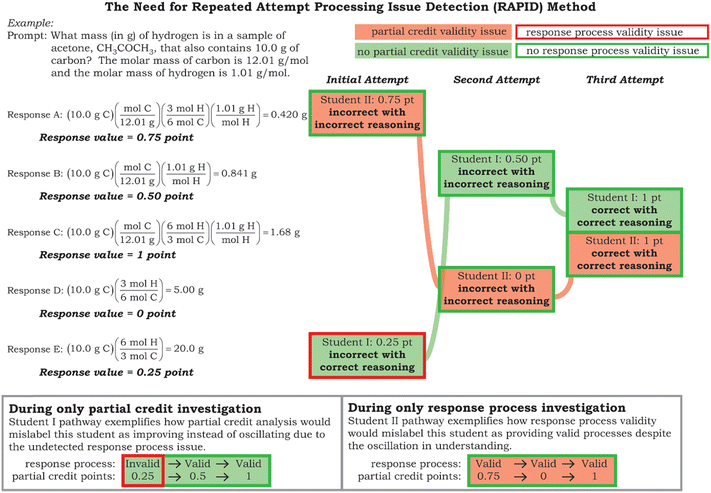 | ||
| Fig. 4 The need for the RAPID method (where answer-until-correct and single-attempt response process validity missed detection). | ||
Alternatively, the process used by Student II in Fig. 4 shows how a validity issue could be overlooked when using only single-attempt response process. For this student, each individual attempt has the students’ thought process align with their answer selection but how the student engaged with the answer-until-correct feedback constitutes a threat. The student's initial attempt is nearly correct with only a small mistake of inverting the mole ratio. However, once they discover this response is incorrect, rather than correcting their mistake, they move in the wrong direction and start making additional mistakes. In this case the feedback provided by the answer-until-correct format did not help the student and should be flagged as a validity issue. This shows the use of only single-attempt response process to search for validity issues within a multiple-attempt assessment is insufficient.
Both example misdetections using only traditional methods shows the need for a new method (like RAPID) which looks at the intersection of single-attempt response process validity and answer-until-correct validity and investigates the progression of students’ processes through multiple attempts of a single task.
Research questions
This project set out with the goal of answering the following research question:(1) How does the newly developed RAPID method perform in detecting validity issues compared to single-attempt response process validity and a quantitative approach to answer-until-correct validity?
Preamble
To properly compare the RAPID method against other validity issue detection methods, all three methods (response process, partial credit analysis, and RAPID) were conducted and will be discussed in this work. To present this work with a clear delineation between the methods, the full methods and results of response process validity and the partial credit analysis for answer-until-correct validity will first be discussed. These results served as the baseline against which the RAPID method would be compared. With these baselines being set, the “Methodology” and “Results” section strictly explore where the previous methods failed, how RAPID was conducted, and how RAPID compares against the other approaches. In order to understand the value and deficiencies of response process validity and partial credit analysis compared to the use of RAPID, and to ensure a reasonable comparison of results between methods, the same assessment was used for all methods. All of the compared results also shared the same sample.Sample
All of the methods conducted used data collected through think-aloud interviews where students worked through a 20-question assessment while verbalizing their thought processes. The assessment covered introductory chemistry concepts and was in a multiple-choice format with four responses. The students worked through the questions in an answer-until-correct style. Answer-until-correct was conducted by having students select their initial response followed by the interviewer telling them whether that response was correct or incorrect. If incorrect, the students reattempted the problem and selected another answer choice. This process was repeated until the student arrived at the correct answer at which point they moved on to the next question.Interviews were performed with 53 students at three different institutions. All students were current general chemistry students who were in the final weeks of their course. The first institution is classified as a large urban research-intensive institution and interviews were conducted in-person with 22 students. At the second institution (a Hispanic serving comprehensive university) and third institution (a small comprehensive university with bachelor level science programs), the interviews were conducted digitally over video-conference software (Trate et al., 2020). Participating students from the second and third institution worked through the same paper assessment as the students from the in-person institution with on-site assistance from one of the authors. Digital interview participants would verbalize their thought process and answer selection with the interviewer simply informing them whether they were correct or incorrect. Fourteen students were digitally interviewed from the second, and seventeen students were digitally interviewed from the third institution. Full details on the remote interviews and sample can be found in previous work (Trate et al., 2020). All interviews were digitally recorded and later transcribed for analysis. All students who participated consented to do so through an IRB approved consent form and protocol at each institution.
Response process validity
Response process method
Response process validity analysis for this work followed the process of think-aloud one-on-one interviews conducted with students so that the students’ thought processes could be collected and compared against their final answers. Further information on how this data was collected can be found in the “Sample” section. Investigation into response process was conducted on each of the attempts made by each student. Therefore, each attempt was assigned a single code and in the event of multiple codes being applicable the code most related to the students’ final answer selection was used. With 20 questions × 53 students, 1060 first attempts were initially analysed. However, because the assessment was taken as answer-until-correct, 251 second attempts and 113 third attempts were also investigated. Eight possible classifications were used in the analysis of the responses (described in Table 2). These codes are based on what has been previously reported in the literature (Trate et al., 2019). Of these codes, elimination, correct answer for the wrong reason, and wrong answer but had the right reason would all be classified as potential issues as they indicate the student was either using an incorrect process to arrive at the correct response or was using the correct process but not arriving at the correct response. Totally correct and totally incorrect both support item validity as the assessment correctly matches correct/incorrect answers with correct/incorrect processes respectively. Codes of guessing, incorrect but strategy cannot be determined, and correct but strategy cannot be determined were not used to support or refute response process validity as the student's process was either not present (guessing) or could not be determined. All codes were initially assigned by a single rater, and a sample consisting of eight questions were distributed to five raters to ensure reasonable code assignment. The questions distributed were specifically selected to represent a variety of codes. Each of the raters were chemistry content experts and part of the research project. Initially, a 71% agreement was found between raters. Following independent coding, codes were discussed until consensus was reached. As consensus always aligned with the original rater, no changes were made. Disagreements in initial assignment were primarily based on the primary rater being more likely to assign cannot be determined codes. It should also be noted that the enhanced response process validity was not conducted in this work as the scope of this work was only to look at whether students had made mistakes, and not at what mistakes had been made.| Code | Explanation |
|---|---|
| Totally correct | Selected correct answer with correct reasoning and correct conceptual understanding |
| Totally incorrect | Selected incorrect answer with incorrect reasoning and incorrect conceptual understanding |
| Guessed | Selected correct or incorrect answer by guessing, without any process |
| Elimination | Eliminated choices without any content knowledge |
| Correct answer for the wrong reason | Used a process that was wrong but that led them to a correct answer |
| Wrong answer but had the right reason | Used a process that was correct but selected an incorrect answer |
| Incorrect but strategy cannot be determined | Selected incorrect answer with a process which cannot be determined |
| Correct but strategy cannot be determined | Selected correct answer with a process that cannot be determined |
Response process results
Response process validity coding of the interviews revealed the distribution of codes shown in Table 3. These results indicate that response process validity issues represented a relatively small proportion of the overall attempts (2.1% + 1.4% = 3.5%). However, a proportion of attempts was not used to support or refute validity as 14.6% of attempts did not use a response process (coded as guessing) and in 4.3% (1.6% + 2.7%) the process used could not be determined (coded as correct/incorrect but strategy cannot be determined).| Response process validity issues | Count | Percent (%) | |
|---|---|---|---|
| Totally correct | No | 841 | 59.1 |
| Totally incorrect | No | 264 | 18.5 |
| Elimination | Yes | 30 | 2.1 |
| Correct answer for the wrong reason | Yes | 20 | 1.4 |
| Wrong answer but had the right reason | Yes | 0 | 0.0 |
| Guessed | Cannot determine | 208 | 14.6 |
| Incorrect but strategy cannot be determined | Cannot determine | 23 | 1.6 |
| Correct but strategy cannot be determined | Cannot determine | 38 | 2.7 |
While knowledge of the overall detection of response process codes is informative, it is more important to consider the concentration of potential issues by item. As shown in Table 4, only eight of the 20 questions showed any response process validity issues, however, questions 11 and 13 had a higher concentration (exceeding 10%) of the elimination code.
| Question | Totally correct | Totally incorrect | Correct answer for the wrong reason | Elimination | Correct but strategy cannot be determined | Incorrect but strategy cannot be determined | Guessed |
|---|---|---|---|---|---|---|---|
| 1 | 92 | 8 | |||||
| 2 | 79 | 17 | 2 | 2 | |||
| 3 | 70 | 26 | 4 | ||||
| 4 | 85 | 11 | 2 | 2 | |||
| 5 | 75 | 4 | 4 | 2 | 15 | ||
| 6 | 83 | 8 | 6 | 4 | |||
| 7 | 68 | 15 | 2 | 4 | 2 | 9 | |
| 8 | 79 | 4 | 2 | 4 | 2 | 9 | |
| 9 | 66 | 17 | 2 | 2 | 13 | ||
| 10 | 45 | 30 | 2 | 2 | 6 | 15 | |
| 11 | 64 | 8 | 23 | 2 | 4 | ||
| 12 | 64 | 28 | 4 | 4 | |||
| 13 | 47 | 36 | 11 | 2 | 4 | ||
| 14 | 75 | 19 | 4 | 2 | |||
| 15 | 60 | 25 | 2 | 2 | 4 | 8 | |
| 16 | 75 | 23 | 2 | ||||
| 17 | 79 | 15 | 6 | ||||
| 18 | 74 | 9 | 2 | 15 | |||
| 19 | 45 | 40 | 6 | 9 | |||
| 20 | 47 | 40 | 4 | 6 | 4 |
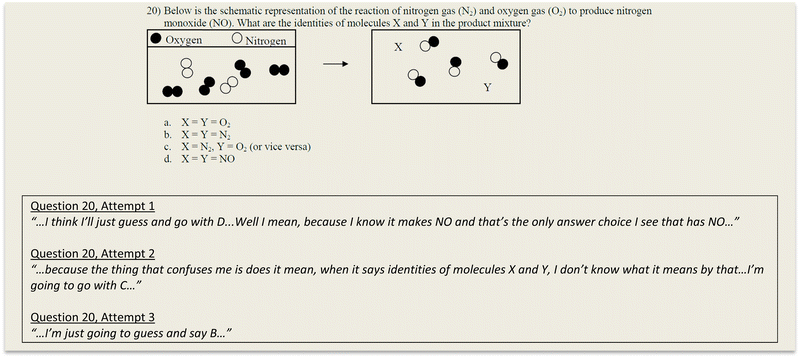
While not clear from the coding data, another item of note is question 20. In interviews it was observed that many students were unable to apply appropriate thought processes because they were confused by the question prompt and expected task. This perhaps could be seen in the first attempt data in the higher number of “cannot be determined” codes but was most evident in the interviews where students articulated not being sure what the question was asking and continued to guess for all of their attempts. One example of this is shown in Fig. 5.
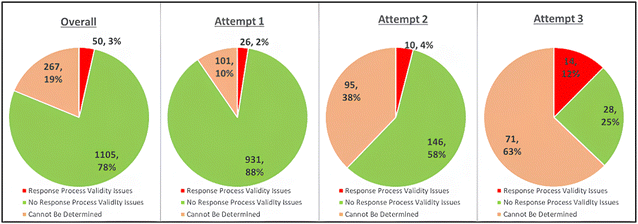
The analysis of students’ first attempts for response process validity on each item can be further expanded to look at how response process issues may evolve over multiple attempts. Although on the students’ first attempts, only 2% showed validity issues (Fig. 6), on the second attempt this increased to 4%, and by the third attempt it further increased to 12%. This shows that as the attempt number increases, issues become more prevalent which supports that an investigation of response process validity on answer-until-correct testing format could reveal valuable (and often missed) validity issues. Additionally, because the second and third attempts only include students who were incorrect initially, special attention should be paid to the prevalence of response process validity issues with lower performing students. This also suggests the impact could be even greater on more difficult assessments where more students may require second and third attempts, although this was outside of the scope of this work.
Of the attempts flagged for response process issues, all fell into “elimination” and “correct for the wrong reason”. The final response process validity issue which was searched for was “wrong answer but had the right reason”, which was not observed in this dataset. For an attempt to be flagged with the code of elimination, the student needed to arrive at their answer not based on articulated chemistry reasoning but rather by removing the other answer choices based on arbitrary reasoning.
One example of elimination which was observed in this sample is shown in Fig. 7 for a student's third attempt on question 3. Here the student eliminated the answer based on the response being larger than the other response options. It's important to note that this elimination required students to eliminate response options without articulating any chemistry reasoning. For example, had the student articulated that the molar mass for a compound this small could not reasonably be that large, they would not be coded as using elimination.
 | ||
| Fig. 7 Student using elimination on their third attempt to remove choice b and select choice a. Response choices c. and d. were previously selected on the first two attempts. | ||
An example of a response process validity issue based on a student selecting the correct answer for the wrong reason is also provided below (Fig. 8). Due to the algorithmic nature of this example, a mathematical representation of their verbalized thought process is also included to demonstrate this student's flawed reasoning leading them to the correct answer.
Despite the clear benefits of response process analysis, an important limitation is that this analysis only considers a single attempt at a time with no connection to other attempts on the item. Therefore, although response process can provide a valuable snapshot of processing validity, it has no mechanism to consider the larger picture of the student's progression in process and understanding over repeated attempts. Therefore, as indicated in the “Preamble” section, the response process analyses were only one part of this larger analysis seeking to compare this approach against alternate options.
Partial credit analysis for answer-until-correct validity
Partial credit analysis method
The partial credit analysis was conducted on attempts where students selected an incorrect answer on their first attempt and tracked their performance over subsequent attempts. This analysis was conducted on the same sample described previously and used for the qualitative response process validity analysis. Of the total 1424 attempts that were collected, only 615 were suitable for partial credit analysis (251 first attempts, 251 second attempts and 113 third attempts). More accurately, 138 two-attempt sequences and 113 three-attempt sequences were analysed, for a total of 251 attempt sequences.Because partial credit analysis requires partial credit assignment to all responses, for this work each of the four responses for each item was assigned a credit value of either 0, 0.25, 0.5, or 1 by expert raters based on how reasonable the inferred process associated with each response was. The correct answer would be 1, answers derived from close to the correct process would be 0.5 or 0.25 depending on how far they deviated from the correct process, and answer choices resulting from extremely flawed processes would be 0. Of the four possible credit values (0, 0.25, 0.5, 1), each could be assigned as frequently or infrequently as the raters felt appropriate. Five instructors from four institutions who regularly teach general chemistry I as well as one post-doc independently assigned partial credit and then discussed until consensus was reached. For numeric questions, raters were provided the mathematical process used to design each response. The mathematical steps served as the inferred process for students who selected that response.
Partial credit analysis results
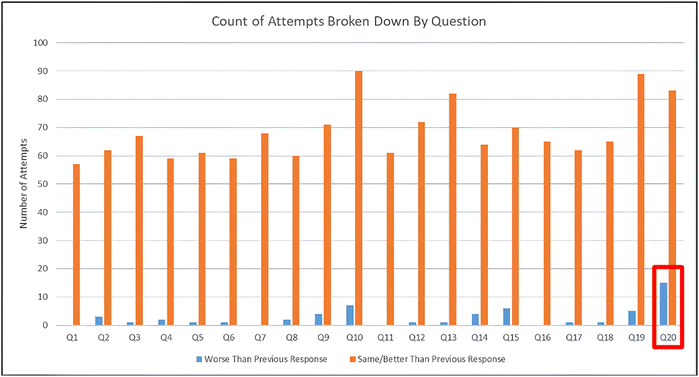
Using the partial credit values for each response, students whose answer selection suggested they were close to the correct answer, but the next selection indicated they were further from the correct answer were flagged as possible answer-until-correct validity issues following the method described in Fig. 2 and Table 1. Of the 364 individual attempt sets (251 from first to second attempt +113 from second to third attempt), only 55 (15.1%) showed a transition from a higher credit value to a lower credit value. This conclusion holds true on the question-level as well as is shown in Fig. 9 with each question being far more likely to have students perform the same or better on subsequent attempts. The question with the largest number of students performing worse on later attempts was question 20. This result was not surprising as the response process results previously indicated question 20 had some students struggle to understand what was being asked. With this confusion, many students resorted to guessing which increased the number of students who showed worse performance on later attempts. However, it is important once again to recognize the purpose of this work was not to investigate specific validity threats within this assessment, but rather compare detections between this method, response process, and the newly developed RAPID method.Methodology
The RAPID method implements a qualitative coding method similar to response process but applies the codes to attempt sequences (e.g., multiple attempts on a single item) instead of individual attempts. An important aspect of an attempt sequence is that students must reengage with the item following each attempt. One example was included prior where a student did not reengage after their initial incorrect response and instead opted to select the closest response to their initial answer. Another pathway a student may take to justify a response without reengagement is also included in Appendix 1. Any evidence for students not reengaging between attempts was flagged as a validity threat prior to RAPID coding.For RAPID coding, each of the attempt sequences was assigned a single code from Table 5. These codes focus on how the student's thought process evolved over multiple attempts on a single problem. As such, the development of these codes was based on all of the possible changes to student reasoning which could occur. Initially, coding was completed by a single rater that was then blindly checked with four chemistry content experts to ensure appropriate assignment. Any disagreement was resolved through discussion until consensus was reached and the coding scheme assignment was consistently applied.
| Code | Explanation |
|---|---|
| Progression | Student reasoning on the item improves over attempts |
| Stagnation | Student reasoning on the item does not change over attempts |
| Regression | Student reasoning on the item gets worse over attempts |
| Oscillation | Student reasoning on the item varies (with elements of both progression and regression) over attempts |
| Resort to guessing | Student has no process which could be tracked and guessed instead |
| Progression with guessing | Student reasoning on the item improves over attempts but guessed for one attempt |
| Stagnation with guessing | Student reasoning on the item does not change over attempts but guessed for one attempt |
| Regression with guessing | Student reasoning on the item gets worse over attempts but guessed for one attempt |
| Oscillation with guessing | Student reasoning on the item varies (with elements of both progression and regression) over attempts but guessed for one attempt |
| Only 1 attempt was needed | Student answered correctly on their first attempt so answer-until-correct validity cannot be investigated |
Examples of regression, stagnation, progression, and oscillation are shown below. Attempt sequences coded as guessing were not flagged as evidence for or against validity. Students who only articulated guessing for an entire attempt sequence were coded as guessing. However, if a student used two processes (for two attempts) and then resorted to guessing (for the final attempt), the initial attempt set (attempts 1 and 2) were coded but then included the additional component of “with guessing” to complete the attempt sequence code.
Regression: (Question 3, Attempt 1, 2 and 3)
“…Okay then I would do, so there's 3 moles of sodiums, so 3 times the molar mass of Na, 22.99 times 3, plus and then potassium is 30.97 plus, 4 times 16, plus 4 times 1.008, plus 16. So, I got 183.97. This is little bit off…That's the molar mass of sodium phosphate dihydrate….So, I’m just going to do it again, just make sure…2 times 22.99 plus 30.97 plus 5 times 16 plus 4 times 1.008. Okay still I got the same answer…So right then I’m gonna choose D.”“…So, I have to do is take the molar mass of just like sodium phosphate and may be the hydrate part…is not there…so it's 163…”
“Okay, now I know it's not C or D. But B is like extremely high. So, using elimination I choose A…”
Mathematical representation of verbalized thought process
(1) (22.99 × 3) + (30.97) + (4 × 16) + (4 × 1.008) + 16 = 183.97(2) (30.97) + (4 × 16) + (4 × 1.008) + 16 = 115.002
Stagnation: (Question 8, Attempt 1 and 2)
“…so, I’m going to go ahead and start with the 2.38 grams of the NH 3 and divide that by the molar mass for the NH 3 , 17.04 grams. That gives me 2.38 divided by 17.04, 0.14 moles. But that's still the NH 3 . So, since I have the 0.14 moles of NH 3 , I can multiply it by 3 moles of N 2 H 4 and then divide that by the molar mass of N 2 H 4 …I will plug in that to my calculator, and I get 0.013. Oh, I’m going to go back to this since I had 4, I have to multiply that by 4, so it gives me 0.56. Actually, this will still stay 3…so 32.06 grams times 0.56 multiply that by 3 divide by 32.06…so I got 0.052. So, it's very close to the 0.0557. So, I’m going to choose D…”“…maybe I will look at just the first step over here…the answer I got 0.14…so I go with answer A.”
Mathematical representation of verbalized thought process:
(1) 2.38/17.04 × 4 × 3/32.06 = 0.052(2) 2.38/17.04 × 3/32.06 = 0.013
Progression: (Question 3, Attempt 1 and 2)
“So first, I need to know the molar mass…3 times 22.99 plus phosphate, 30.97, 4 oxygens, 15.99 times 4…then 2H 2 O. So, 2 times 2 plus 16 times 2. So, 163.007 times 34.016, gives me 5544. So I think my answer will be B, because that's the closest I get to my answer. Just because alone sodium phosphate is already 163. Which is pretty close to the other 3 options, where we don’t have H 2 O, which is going to…when you multiply it's going to be way bigger.”“So, based on my interpretation, molar mass for this compound times by the other one. This star is a multiplication, so that's what I did. Maybe I should add them up. So…I think finding the molar mass of each of them is not my mistake. It's the multiplying them together, I should have added them up together. So, if I add them together, so, my new answer is A.”
Mathematical representation of verbalized thought process
(1) [(3 × 22.99) + (30.97) + (15.99 × 4)] × [(2 + 2 × 16)] = 5544(2) [(3 × 22.99) + (30.97) + (15.99 × 4)] + [(2 + 2 × 16)] = 197.9
Oscillation: (Question 3, attempt 1, 2 and 3)
“…is this supposed to be a plus or multiplication? So okay Na 3 PO 4 times 2H 2 O. I am going to get molar masses up here. Na is 22.990 times that by 3, gives 68.97. Then phosphate or phosphorus is 30.97 and there's only one of those. 99.94 is the total of those two so far. Oxygen is 16, and times 4, which is 64…And then 2H 2 O. H2O is…18.014, there's two of them so it's 36.028. And I will add this to this number here (99.94 + 64), 163.94…so the closest answer from that would be C”“…I am pretty sure that we had to multiply these two not add them. So, for that I did…which is 460…I will write, 15.99 times 4, which is 63, plus…no this is really off. Okay, 163.12 multiply by 36.028, which is close to the second answer…”
“So, I’m going to change my answer. I added these two (163.94 + 36.028) and got close to this one. It was 199.968, which is A.”
Mathematical representation of verbalized thought process
(1) (22.99 × 3) + (30.97) + (4 × 16) = 163.94(2) [(22.99 × 3) + (30.97) + (4 × 16)] × [2 × 18.014] = 5906.43
(3) [(22.99 × 3) + (30.97) + (4 × 16)] + [2 × 18.014] = 199.968
Results
RAPID method
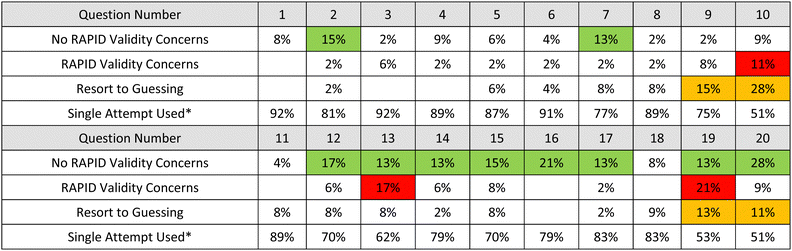
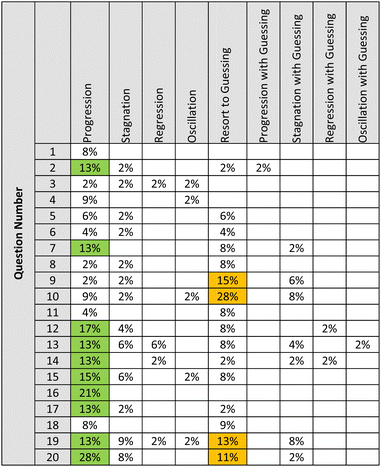
The RAPID coding revealed the counts and percentages shown below in Table 6. Of the students who required additional attempts, nearly half showed progression lending weight to the validity and fundamental tenets of answer-until-correct. Only fourteen total attempts (or about 5%) showed students’ processes regressing or oscillating. An additional 16% of student attempts showed stagnation, for which students did not show improvement or regression in their processing. All cases involving regression, oscillation, or stagnation were treated as validity threats as they violate the assumption that repeated attempts aid students in improving their process.| RAPID code | Count | Percent (%) |
|---|---|---|
| Expanded table can be found in Appendix 2. | ||
| Progression + progression with guessing | 123 | 49.00 |
| Stagnation + stagnation with guessing | 41 | 16.33 |
| Regression + regression with guessing | 8 | 3.19 |
| Oscillation + oscillation with guessing | 6 | 2.39 |
| Resort to guessing | 73 | 29.08 |
| Single attempt used | 807 | |
The question-level analysis of RAPID shows that half of the questions had >10% of students progressing in their reasoning over their attempt sequences (progression or progression with guessing) (green cells in Table 7). However, there were 3 questions of concern which had >10% of students raising RAPID concerns when including guessing (stagnation, stagnation with guessing, regression, regression with guessing, oscillation, oscillation with guessing) (red cells in Table 7). An important consideration when looking at the percentage of students on later attempts by question is the difficulty of the question (i.e., the number of students who needed a second/third attempt). Unsurprisingly, the three questions which had greater than 10% of students in two or more categories (questions 10, 13, and 19) also had some of the highest number of students requiring additional attempts.
Validity issue detection of RAPID versus response process and partial credit analysis
Using the results found from response process (both traditional and avoiding reengagement), partial credit analysis, and RAPID, comparisons were conducted to investigate the magnitude of differences in issue detection. To allow for an appropriate comparison, only attempts which were a part of an attempt sequence were compared because both the partial credit analysis and RAPID were not possible on a single attempt. Table 8 shows the attempt sequences that were flagged by at least one of the methods. Using this framework, Table 8 groups false-positive detection as any attempt sequences which were flagged by the partial credit analysis method, but the richer qualitative data used by RAPID suggested were not truly issues. The 29 sequences which were flagged only by partial credit are the result of students following response patterns that deeper investigation revealed students were progressing in understanding despite not aligning with partial credit assignments to distractors.| Detection classification | Validity issue detected | Attempt sequence count | Attempt sequence percent (%) | Detection classification percent (%) |
|---|---|---|---|---|
| False-positive (No RAPID Detection) | Partial credit analysis only | 29 | 29.9 | 32.0 |
| Partial credit analysis and response process | 2 | 2.1 | ||
| Correct detection (through suggested implementation using both RAPID and response process) | Response process only | 11 | 11.3 | 34.0 |
| Partial credit analysis and RAPID | 13 | 13.4 | ||
| Partial credit analysis, response process, and RAPID | 9 | 9.3 | ||
| False-negative (RAPID detection but missed by partial credit) | Response process and RAPID | 13 | 13.4 | 34.0 |
| RAPID only | 20 | 20.6 | ||
The final 2 false-positive attempt sequences again showed student progression not aligning with the partial credit which was assigned. However, these attempts were also flagged as containing response process issues. These response process issues led to students selecting their response for reasoning inconsistent with what was designed so the students’ response process skewed the partial credit analysis. Over all of the flagged attempt sequences, 32.0% constitute false-positive issue detection corrected through the use of response process and RAPID.
Using the implementation of both response process and RAPID, 34.0% of the attempt sequences were described as “Correct Detection”. These include sequences which were detected by either the attempt-level analysis (only response process) or both of the attempt sequence-level analyses (RAPID and partial credit analysis). One example of why coding is necessary at both the attempt and attempt-sequence level is the results seen with Q11. Q11 was not detected by RAPID but was detected by response process. This is because the validity threats were always contained within a single attempt and therefore unable to be detected when only coding attempt-sequences. This further revealed that 9.3% of the attempt sequences contained issues at both the attempt-level and the attempt sequence-level.
Furthermore, Table 8 also reveals a considerable percentage (34.0%) of false-negative issue detection. If attempt sequence-level detection was performed using only partial credit analysis, 33 (13 + 20) attempt sequences would have had their issues overlooked. Additionally, even if both response process and partial credit analyses would have been conducted, 20 sequences were not detected by any method besides RAPID.
Limitations
One limitation of this work is each question was treated individually and the effect that feedback from early questions played on performance on later questions was not investigated. This effect on later items that immediate feedback has is an important aspect of answer-until-correct and investigation into this area could reveal more issues through partial credit analysis or RAPID. However, an investigation into these answer-until-correct issues would further build off of, not detract from, the work done in this project.In addition, one interesting finding from this work was the poor performance of the partial credit assigned to distractors on students’ second and third attempts. This is a result which deserves further investigation, and a deeper understanding of this phenomenon may reveal an opportunity for developing a more efficient method for answer-until-correct validity issue detection.
Lastly, this new RAPID technique was only applied to one instrument of 20 questions on basic general chemistry knowledge. Employing the technique in additional contexts would allow for further understanding of its potential and/or limitations.
Implications
The results present an opportunity for both researchers and practitioners to evaluate assumptions made when considering the benefits of answer-until-correct assessments. The results of the RAPID coding align with the existing literature showing benefits of answer-until-correct assessments (Brown et al., 1999; Brosvic et al., 2005; Clariana and Koul, 2005; Slepkov, 2013; Attali, 2015; Pinhas, 2021). For this sample of students, 49% of those who required multiple attempts progressed in their reasoning suggesting answer-until-correct assessments are indeed helping students learn. However, to take advantage of the benefits offered through answer-until-correct assessments, steps must be taken to identify and minimize validity threats. To do this for studies where the improved problem-solving process is integral, researchers may want to consider studies incorporating both the response process and RAPID methods. Additionally, as was noted, when more complex items are included in the assessments, the rate of correct first responses will likely decrease, thus increasing the need for investigating the validity of the answer-until-correct assessment.For practitioners, the need for incorporating this level of validity studies is likely unnecessary. However, when developing items, considering the change in process associated with the various responses and the escalation of understanding expected by students may be considered. Additionally, when incorporating more challenging or complex items, practitioners may want to consider including more elaborate feedback (through a hint or similar feature) to provide students with additional scaffolding to progress to better understanding. Finally, the care that is taken during exam development for creating plausible distractors as well as incorporating the instructor's expert knowledge of their students and the processes they may use to solve problems is critical to note. This task taken on by instructors may often be overlooked or marginalized by outsiders and should be noted as important classroom work.
Finally, it is also hoped that the benefits cited and now further supported from this work of feedback using answer-until-correct formats would encourage course management system designers to include this feature in their quiz or testing platforms. As of the writing of this work, there are still widely used course management systems that do not allow answer-until-correct for each item (and instead require a student to use a second or third attempt on an entire assessment).
Discussion and conclusions
The findings discussed here demonstrate the benefit of using the RAPID method for detection of validity issues on answer-until-correct assessments. This is shown by the misalignment of the issue detection between methods and by the large number of attempts/attempt sequences which were flagged as having validity issues through only one approach. These results suggest that issues could be more reliably and accurately detected through the use of both an attempt-level (response process) and attempt-sequence-level (RAPID) in unison. It is advisable to conduct these codings simultaneously with attempt-level codes being assigned for each attempt within a single question of a single student, followed by a broader RAPID code for the sequence as a whole. This process would lead to only a marginal increase in time investment of the researcher.While the time investment is even smaller for partial credit analysis, the results presented here suggest that this procedure should not be used. Despite being unsurprising that the results generated from rich qualitative data outperformed the limited quantitative data of distractor selection, how poorly the partial credit approach performed was surprising. Concurrent research into this assessment has shown that the partial credit used in this work provides a reasonable estimate of student proficiency. One possible explanation for this unexpected result is the feedback from answer-until-correct invalidates the partial credit values that were previously assigned to each distractor and only the first response or attempt has a valid partial credit assignment, though this is an area where further investigation would be needed. Regardless of the reasoning behind this result, it must be made clear that these results do not suggest the assignment of partial credit is flawed, only that its use for validity issue detection may be problematic.
A consideration not directly addressed thus far is how validity threats should be handled once detected. While this is an important aspect, it was not addressed because how a test designer wishes to respond to items showing validity threats will depend on both the stakes of the assessment as well as the impact of validity threats. For low stakes assessments where the validity threat only had a modest impact on student ability estimation, no action may be required. However, with higher stakes assessments items may need to be omitted or rewritten. A brief example is included in Appendix 4 to show one possible approach to determine the impact of validity threats on the assessment.
While the results show clear advantages to using the RAPID method as opposed to a single traditional validity analysis, implementation of the method does still require a non-trivial time investment on the part of the researcher. However, as response process alone requires diligent analysis of transcripts from each response already, the added time investment to conduct RAPID coding as well is minimal. Further, if partial credit assignment to individual responses is desirable the completion of this coding can aid in determining appropriate credit values. Even if a response was derived by the test designer through a method which is close to the correct process, if the students who ended up selecting that response did so due to an unexpected pathway the partial credit assignment should be reconsidered. In other words, rather than relying on assumed student process, articulated student process can be used to determine partial credit.
Appendices
Appendix 1: avoiding reengagement cleaning
An important aspect of repeated-attempt assessments is students are presumed to be reengaging with the item on each attempt. However, two major classifications were found where students did not reengage: double-down or inverted reasoning. As the name suggests, double-down categorization was given to an attempt sequence where the knowledge of any previous incorrect attempt(s) did not lead the student to reevaluate their thought process, but rather the student continued to rely on their previous logic to select a new response. In the example below, this student initially answered 1.0 mol CCl4 (choice b) for question 7. After being told they were incorrect, the student still felt their process was correct and simply chose the closest answer to their previous attempt (1.5 mol CCl4).Double-down: (Question 7, Attempt 2)
“…Because I feel like earlier I was off by a little margin”
Alternatively, other students avoided reengagement with the task by simply inverting their previous reasoning. In other words, knowing their previous logic was incorrect, these students assumed that the opposite of their logic must therefore be correct. One example of this occurring is shown below.
Inverted reasoning: (Question 4, Attempt 1 and 2)
…so, I think it would be C, considering it has the lowest mass…”
“Okay, then I guess it would be the first one, because it would be the largest (mass).”
Of the 251 second attempts and 113 third attempts, only 12 attempts were found to have these engagement issues. Of these attempts, 5 showed students “double-down” and chose the closest response to their previous attempt. The remaining 7 students “inverted” their previous reasoning by choosing the response furthest from their initial attempt, again without reengagement with the problem. For this assessment with this sample, only 3% of the repeat attempts showed these issues which are unique to repeated-attempt assessments.
Appendix 2: RAPID method
The tables below represent expansions off of tables in the primary article. These tables show counts and percentages for each RAPID code prior to codes being binned together. Table 9 depicts the RAPID code distribution for each of the possible codes (rather than the collapse of a code with its “with Guessing” counterpart). Table 10 shows question-level percentages of the codes as opposed to the binning of the codes into RAPID validity concerns and non-answer-until-correct validity concerns.| RAPID code | Count | Percent (%) |
|---|---|---|
| Progression | 122 | 48.61 |
| Stagnation | 25 | 9.96 |
| Regression | 6 | 2.39 |
| Oscillation | 5 | 1.99 |
| Resort to guessing | 73 | 29.08 |
| Progression with guessing | 1 | 0.40 |
| Stagnation with guessing | 16 | 6.37 |
| Regression with guessing | 2 | 0.80 |
| Oscillation with guessing | 1 | 0.40 |
| Only 1 attempt was needed | 807 |
Appendix 3: comparison of response process validity and the RAPID method
Table 11 classifies all of the attempts used by students in this study by their response process validity and RAPID code. Further investigation is shown in Table 12 which specifically analyses sequences with response process validity issues and shows the type of RAPID code. This revealed no discerning pattern. Both of these tables align with the conclusion discussed in the primary article that RAPID validity and response process validity must each be investigated.| Response process validity issues | No response process validity issues | |
|---|---|---|
| Progression | 5 | 117 |
| Stagnation | 13 | 12 |
| Regression | 4 | 2 |
| Oscillation | 2 | 3 |
| Resort to guessing | 8 | 65 |
| Progression with guessing | 0 | 1 |
| Stagnation with guessing | 3 | 13 |
| Regression with guessing | 0 | 2 |
| Oscillation with guessing | 0 | 1 |
| Only 1 attempt | 24 | 783 |
| Attempts which exhibit response process validity issues | ||
|---|---|---|
| Count | Percent (%) | |
| Progression + progression with guessing | 5 | 8.47 |
| Stagnation + stagnation with guessing | 16 | 27.12 |
| Regression + regression with guessing | 4 | 6.78 |
| Oscillation + oscillation with guessing | 2 | 3.39 |
| Guessing | 8 | 13.56 |
| Only 1 attempt | 24 | 40.68 |
Appendix 4: assessing the impact of detected validity threats
Following the detection of validity threats within an assessment it may be desirable to better understand the impact the threats have on the assessment results. What follows is a brief example of one of many approaches which could be used to inform if the detected problematic items warrant remediation. This was done through a series of correlations between the assessment where validity threats were found, and assessments which are likely to be an accurate reflection of student chemistry proficiency (standardized national exams).Sample
The sample in the primary manuscript was composed of rich qualitative data which is limited in that the sample size being analysed scales with the time and resources needed for data analysis. This typically results in smaller sample sizes for the qualitative data making the results more susceptible to sampling errors. With this in mind, when assessing the impact of detected validity threats, it may be beneficial to take advantage of quantitative data which can be more efficiently collected. For this example, a class-wide sample was collected by providing the same 20-question assessment in written form to 284 students. All 284 students were from the first institution because this was the only institution for which final exam scores were available. To implement answer-until-correct to this many students, the commercially available Immediate Feedback Assessment Technique was utilized (Cogna Learn; Epstein Educational Enterprises; Epstein et al., 2001).Method
The score for each student in the class was calculated and subsequently compared against external measures (two different final exam scores) using R (Meng et al., 1992; Team, 2020). This correlation between the full assessment and external measures served as a baseline. Correlations were also calculated between these external measures and assessment scores calculated after the removal of items containing the most response process validity threats. The threshold for which items to remove was set as any item from the interview data with greater than 10% of any one of the validity issue codes. The external measures chosen were two standardize multiple-choice ACS Exams which together served as the students’ final exam (2005 General Chemistry Exam – Paired Questions, First Term | ACS Exams; 2008 General Chemistry Conceptual Exam – Full Year, First Term and Second Term | ACS Exams).Results
Based on the interview results, items Q11 and Q13 were flagged as the items with the most response process issues. The correlation was initially completed using the assessment score from all 20 items, then repeated using the assessment score without Q11 and Q13. If these correlations statistically differ from one another, that will indicate the two questions were contaminating the assessment score and were therefore harming the validity of the assessment. Correlations were checked for statistical differences using the referenced technique (Meng et al., 1992). As no significant differences were found (shown in Table 13), it was determined that the inclusion of Q11 and Q13 were not statistically having a negative impact on the accuracy of the assessment results. Therefore, it may be acceptable to leave these items in the assessment due to the small impact the response process validity threats had on the assessment overall.| r (Pearson product moment coefficient) | Z (p) | |
|---|---|---|
| Assessment (Full) and Paired ACS final | 0.640 | −0.535 (0.593) |
| Assessment (Q11 and Q13 removed) and Paired ACS final | 0.644 | |
| Assessment (Full) and Conceptual ACS final | 0.604 | −0.247 (0.805) |
| Assessment (Q11 and Q13 removed) and Conceptual ACS final | 0.606 |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from NSF TUES grant (DUE 1140914), lead-PI Jamie Schneider, and NSF IUSE Grant (DUE 1625233), PI Jamie Schneider. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. We are also grateful to Dr Panayiota Kendeou for her continued guidance and assessment of our project as the external evaluator on our recent NSF grant. A special thanks to Jordan Harshman for helping to create the exam used throughout this study as part of an undergraduate research project led by Jamie Schneider. Finally, we would like to show our appreciation to all the students who took the exams and the professors who aided in the distribution of the exam.References
- 2005 General Chemistry Exam – Paired Questions, First Term | ACS Exams.
- 2008 General Chemistry Conceptual Exam – Full Year, First Term and Second Term | ACS Exams.
- Adams W. K., Wieman C. E., Perkins K. K. and Barbera J., (2008), Modifying and Validating the Colorado Learning Attitudes about Science Survey for Use in Chemistry, J. Chem. Educ., 85(10), 1435 DOI:10.1021/ed085p1435.
- American Educational Research Association, (1999), Standards for educational and psychological testing, American Educational Research Association.
- Arjoon J. A., Xu X. and Lewis J. E., (2013), Understanding the State of the Art for Measurement in Chemistry Education Research: Examining the Psychometric Evidence, J. Chem. Educ., 90(5), 536–545 DOI:10.1021/ed3002013.
- Attali Y., (2015), Effects of multiple-try feedback and question type during mathematics problem solving on performance in similar problems, Comput. Educ., 86, 260–267 DOI:10.1016/j.compedu.2015.08.011.
- Balabanoff M., Al Fulaiti H., DeKorver B., Mack M. and Moon A., (2022), Development of the Water Instrument: a comprehensive measure of students’ knowledge of fundamental concepts in general chemistry, Chem. Educ. Res. Pract., 23(2), 348–360 10.1039/d1rp00270h.
- Bangert-Drowns R. L., Kulik C.-L. C., Kulik J. A. and Morgan M., (1991), The Instructional Effect of Feedback in Test-like Events, Rev. Educ. Res., 61(2), 213–238 DOI:10.3102/00346543061002213.
- Brandriet A. R. and Bretz S. L., (2014), The Development of the Redox Concept Inventory as a Measure of Students’ Symbolic and Particulate Redox Understandings and Confidence, J. Chem. Educ., 91(8), 1132–1144 DOI:10.1021/ed500051n.
- Brosvic G. M., Epstein M. L., Cook M. J. and Dihoff R. E., (2005), Efficacy of Error for the Correction of Initially Incorrect Assumptions and of Feedback for the Affirmation of Correct Responding: Learning in the Classroom, Psychol. Rec., 55(3), 401–418 DOI:10.1007/bf03395518.
- Brown A. S., Schilling H. E. H. and Hockensmith M. L., (1999), The Negative Suggestion Effect: Pondering Incorrect Alternatives May Be Hazardous to Your Knowledge, J. Educ. Psychol., 91(4), 756–764 DOI:10.1037/0022-0663.91.4.756.
- Clariana R. B. and Koul R., (2005), Multiple-try feedback and higher-order learning outcomes, Int. J. Instr. Media, 32(3), 239.
- Cogna Learn, IF-AT Forms.
- Deng J. M., Streja N. and Flynn A. B., (2021), Response Process Validity Evidence in Chemistry Education Research, J. Chem. Educ., 98(12), 3656–3666 DOI:10.1021/acs.jchemed.1c00749.
- DiBattista D., (2013), The Immediate Feedback Assessment Technique: A Learner-centered Multiple-choice Response Form, Canadian J. Higher Educ. (1975), 35(4), 111–131 DOI:10.47678/cjhe.v35i4.184475.
- Dibattista D., Mitterer J. O. and Gosse L., (2004), Acceptance by undergraduates of the immediate feedback assessment technique for multiple-choice testing, Teach. Higher Educ., 9(1), 17–28 DOI:10.1080/1356251032000155803.
- Epstein Educational Enterprises, Immediate Feedback Assessment Technique (IF-AT). Center for the Enhancement of Teaching & Learning, (Fig. 2), 1–3.
- Epstein M. L., (2002), Students Prefer the Immediate Feedback Assessment Technique, Psychol. Rep., 90(3), 1136 DOI:10.1177/003329410209000315.2.
- Epstein M. L., Epstein B. B. and Brosvic G. M., (2001), Immediate feedback during academic testing, Psychol. Rep., 88(3 PART 1), 889–894 DOI:10.2466/pr0.2001.88.3.889.
- Epstein M. L., Lazarus A. D., Calvano T. B., Matthews K. A., Hendel R. A., Epstein B. B. and Brosvic G. M., (2002), Immediate Feedback Assessment Technique Promotes Learning and Corrects Inaccurate first Responses, Psychol. Rec., 52(2), 187–201 DOI:10.1007/bf03395423.
- Kreiter C., (2015), When I say … response process validity, Med. Educ., 49(3), 247–248 DOI:10.1111/medu.12572.
- Lazenby K., Tenney K., Marcroft T. A. A. and Komperda R., (2023), Practices in instrument use and development in chemistry education research and practice 2010-2021, Chem. Educ. Res. Pract., 24(3), 882–895 10.1039/d2rp00275b.
- Lewis S. E., (2022), Considerations on validity for studies using quantitative data in chemistry education research and practice, Chem. Educ. Res. Pract., 23(4), 764–767 10.1039/d2rp90009b.
- Meng X. L., Rosenthal R. and Rubin D. B., (1992), Comparing correlated correlation coefficients, Psychol. Bull., 111(1), 172–175 DOI:10.1037/0033-2909.111.1.172.
- Murphy K., Schreurs D., Teichert M., Luxford C. and Schneider J., (2023a), Qualitative Scoring: An Alternate View into Student Proficiency, Chem. Educ. Res. Pract., manuscript in preparation.
- Murphy K., Schreurs D., Teichert M., Luxford C. and Schneider J., (2023b), A Comparison of Observed Scores, Partial Credit Schemes, and Modelled Scores Among Students of Different Ability Groupings, Chem. Educ. Res. Pract., manuscript in preparation.
- Pinhas A. R., (2021), Advantages and Disadvantages of Using the Answer-Until-Correct Multiple-Choice Test Format for a Class of Non-STEM Majors, J. Chem. Educ., 98, 2128–2131 DOI:10.1021/acs.jchemed.1c00090.
- Pressey S., (1926), A simple apparatus which gives tests and scores and teaches, School Soc., 23(586), 373–376.
- Pressey S. L., (1950), Development and Appraisal of Devices Providing Immediate Automatic Scoring of Objective Tests and Concomitant Self-Instruction, J. Psychol., 29(2), 417–447 DOI:10.1080/00223980.1950.9916043.
- Ralph V. R. and Lewis S. E., (2019), An explanative basis for the differential performance of students with low math aptitude in general chemistry, Chem. Educ. Res. Pract., 2(3), 57–593 10.1039/c9rp00068b.
- Roediger H. L. and Marsh E. J., (2005), The Positive and Negative Consequences of Multiple-Choice Testing, J. Exp. Psychol. Learn Mem. Cogn., 31(5), 1155–1159 DOI:10.1037/0278-7393.31.5.1155.
- Schneider J. L., Ruder S. M. and Bauer C. F., (2018), Student perceptions of immediate feedback testing in student centered chemistry classes, Chem. Educ. Res. Pract., 19(2), 442–451 10.1039/c7rp00183e.
- Schwartz P. and Barbera J., (2014), Evaluating the content and response process validity of data from the chemical concepts inventory, J. Chem. Educ., 91(5), 630–640 DOI:10.1021/ed400716p.
- Skinner B. F., (1974), About behaviorism, Alfred A. Knopf.
- Slepkov A. D., (2013), Integrated testlets and the immediate feedback assessment technique, Am. J. Phys., 81(10), 782–791 DOI:10.1119/1.4820241.
- Slepkov A. D. and Shiell R. C., (2014), Comparison of integrated testlet and constructed-response question formats, Phys. Rev. Spec. Top., Phys. Educ. Res., 10(2), 020120 DOI:10.1103/PhysRevSTPER.10.020120.
- Slepkov A. D., Vreugdenhil A. J. and Shiell R. C., (2016), Score Increase and Partial-Credit Validity When Administering Multiple-Choice Tests Using an Answer-Until-Correct Format, J. Chem. Educ., 93(11), 1839–1846 DOI:10.1021/acs.jchemed.6b00028.
- Stains M., Escriu-Sune M., de Santizo M. L. and Sevian H., (2011), Assessing Secondary and College Students’ Implicit Assumptions about the Particulate Nature of Matter: Development and Validation of the Structure and Motion of Matter Survey, J. Chem. Educ., 88(10), 1359–1365 DOI:10.1021/ed1002509.
- Team R. C., (2020), R: A Language and Environment for Statistical Computing.
- Towns M. H., (2014), Guide to developing high-quality, reliable, and valid multiple-choice assessments, J. Chem. Educ., 91(9), 1426–1431 DOI:10.1021/ed500076x.
- Trate J. M., Fisher V., Blecking A., Geissinger P. and Murphy K. L., (2019), Response Process Validity Studies of the Scale Literacy Skills Test, J. Chem. Educ., 96(7), 1351–1358 DOI:10.1021/acs.jchemed.8b00990.
- Trate J. M., Teichert M. A., Murphy K. L., Srinivasan S., Luxford C. J. and Schneider J. L., (2020), Remote Interview Methods in Chemical Education Research, J. Chem. Educ., 97(9), 2421–2429 DOI:10.1021/acs.jchemed.0c00680.
- Wren D. and Barbera J., (2013), Gathering evidence for validity during the design, development, and qualitative evaluation of Thermochemistry Concept Inventory items. J. Chem. Educ., 90(12), 1590–1601 DOI:10.1021/ed400384g.
| This journal is © The Royal Society of Chemistry 2024 |