Open Access Article
Open Access ArticleDecorrelated singlet and triplet exciton delocalization in acetylene-bridged Zn-porphyrin dimers†
Hasini
Medagedara‡
a,
Mandefro Y.
Teferi‡
b,
Sachithra T.
Wanasinghe‡
a,
Wade
Burson
a,
Shahad
Kizi
a,
Bradly
Zaslona
a,
Kristy L.
Mardis
 c,
Jens
Niklas
c,
Jens
Niklas
 b,
Oleg G.
Poluektov
b,
Oleg G.
Poluektov
 *b and
Aaron S.
Rury
*b and
Aaron S.
Rury
 *a
*a
aDepartment of Chemistry, Wayne State University, Detroit, MI 48202, USA. E-mail: arury@wayne.edu
bChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA. E-mail: oleg@anl.gov
cDepartment of Chemistry, Physics, and Engineering Sciences, Chicago State University, Chicago, IL 60628, USA
First published on 19th December 2023
Abstract
The controlled delocalization of molecular excitons remains an important goal towards the application of organic chromophores in processes ranging from light-initiated chemical transformations to classical and quantum information processing. In this study, we present a methodology to couple optical and magnetic spectroscopic techniques and assess the delocalization of singlet and triplet excitons in model molecular chromophores. By comparing the steady-state and time-resolved optical spectra of Zn-porphyrin monomers and weakly coupled dimers, we show that we can use the identity of substituents bound at specific positions of the macromolecules' rings to control the inter-ring delocalization of singlet excitons stemming from their B states through acetylene bridges. While broadened steady-state absorption spectra suggest the presence of delocalized B state excitons in mesityl-substituted Zn-tetraphenyl porphyrin dimers (Zn2U-D), we confirm this conclusion by measuring an enhanced ultrafast non-radiative relaxation from these inter-ring excitonic states to lower lying electronic states relative to their monomer. In contrast to the delocalized nature of singlet excitons, we use time-resolved EPR and ENDOR spectroscopies to show that the triplet states of the Zn-porphyrin dimers remain localized on one of the two macrocyclic sub-units. We use the analysis of EPR and ENDOR measurements on unmetallated model porphyrin monomers and dimers to support this conclusion. The results of DFT calculations also support the interpretation of localized triplet states. These results demonstrate researchers cannot conclude triplet excitons delocalize in macromolecular based on the presence of spatially extended singlet excitons, which can help in the design of chromophores for application in spin conversion and information processing technologies.
1 Introduction
Spin-polarized quantum states in molecules and materials possess many desirable properties such as accessibility/addressability using electromagnetic radiation at both optical and microwave wavelengths, weak interactions with their environments, and long lifetimes, which in favorable cases can approach seconds.1–8 These properties make spin polarized states excellent candidates for quantum information science (QIS), which is substantiated by their implementation in quantum computing and information processing protocols. While the spin-polarized states of semiconducting systems have been considered in more detail, the efficient formation and long lifetimes of triplet states in photo-excited molecules have recently attracted increasing attention for applications in quantum technologies.5–8 Molecular systems benefit from their amenability to chemical modifications that can control the lifetimes and angular momenta of their excited states. The ability to form excited states possessing well-defined angular momenta enables some molecular systems to undergo exotic non-radiative relaxation processes such as singlet fission,9–12 which can produce two triplet excitons from a singlet exciton formed through light absorption (exciton splitting).More important to the current study, research has shown that chemical binding of light absorbing molecules enables the formation of electronic states that can delocalize across distinct macromolecular sub-units. Towards this goal, Therien and co-workers have synthesized several types of porphyrin macromolecules linked by aromatic sub-units.13–16 The use of these aromatic units/moieties as directly bonded linking groups between the porphyrin sub-units leads to clear signatures of singlet exciton delocalization consistent with well-established theories.17 This delocalization manifests itself through the presence of multiple Soret transitions in their steady-state absorption spectra. These peaks in the absorption spectra correspond to different bright excitons formed through the coherent mixing of electronic density across the chemically bound porphyrin macrocycles. Additionally, the coherent delocalization of the singlet exciton density leads to complex changes in the ultrafast relaxation of the optically addressable excitons to lower lying excited electronic states, which include energy transfer between bright and dark excitons not possible in porphyrin monomers.18–22
As demonstrated in previous studies, coupling between light absorbing sub-units of macromolecular systems leads to important collective effects in the excited singlet states of these chromophores including enhanced exciton transport and radiative relaxation.23–25 Timmel and co-workers characterized triplet delocalization in directly bound porphyrin dimers and multimers using various techniques.26–31 Time-resolved electron paramagnetic resonance (tr-EPR) spectra following photo-excitation of the optically addressable ground singlet states of these macromolecules provide some indications that their spin densities may delocalize across the monomeric sub-units.27,28 These studies infer triplet delocalization as changes in tr-EPR spectra due to modulations of the three triplet energy levels, characterized by the components in the zero-field splitting (ZFS) tensor, D, which were consistent with a change in the spin density distribution from prolate to oblate resulting in a sign change of ZFS parameter D.31 These changes suggest that the spin densities of the triplet states delocalize across more than one of the porphyrin sub-units. Further studies using more advanced methods like pulsed electron-nuclear double resonance (ENDOR) techniques showed specific signatures of triplet delocalization in the hyperfine couplings stemming from electron-nuclear spin interactions.26,28,31 These more elaborate studies also demonstrated that triplet delocalization depends sensitively on the symmetry of the overall macromolecule.
While these are important conclusions regarding the correspondence of excited singlet and triplet delocalization in a small class of optically addressable molecules, significant gaps remain in researchers' ability to correlate the intramolecular coupling of singlet and triplet states in light harvesting molecules. For example, it remains unclear if the presence of delocalized singlet excitons in a macromolecules absorption spectra necessarily implies equal superpositions of monomers' orbitals characterizing the system's triplet states. Moreover, there are no data on correlations between the delocalization of singlet and triplet states with the electron withdrawing or donating abilities of different functional groups bound to light harvesting macromolecules. These gaps inhibit the rational design of molecules capable of delocalizing either singlet or triplet excitons controllably towards the synthesis of tunable systems for optically addressable qubits or spin-sensitive photochemistry.
In this study, we seek to expand the correlations between the delocalization of singlet and triplet excitons in a pair of Zn-porphyrin homodimers bound through acetylene bridges. By modulating the electron withdrawing ability of phenyl-derived substituents bound at the macrocycles' meso positions, we form two dimeric systems characterized by HOMO states localized on different ring-bound atoms. When the HOMO density is localized on atoms comprising the a2u orbital, we find polarized-intramolecular excitons delocalized over both monomeric units of a meso-substituted mesityl Zn-porphyrin dimer which can explain this molecule's UV-vis absorption spectrum. In contrast, substituting pentafluorophenyl groups on the same structures leads to UV-vis absorption spectra consistent with excitons localized on each sub-unit, which we propose stems from the molecule's HOMO state being the a1u orbital. We substantiate this physical picture using ultrafast transient absorption measurements of the internal conversion between each molecule's B and Q states. While we find this rate, kIC, decreases for the pentafluoro substituted dimers relative to their monomer, kIC increases for the mesityl substituted dimers relative to their monomers. We present a theoretical description of this effect as stemming from delocalized excitons in the B states of weakly bound Zn-porphyrin dimers.
In contrast to the differences in singlet delocalization discussed above as a function of the identity of the dimer's HOMO state, we find that the triplet states seem to be localized primarily on the macromolecular monomeric sub-units according to our EPR measurements. In the case of both macromolecules, the tr-EPR measurements show a slightly larger value for the ZFS parameter |D| for the monomeric system, which correlates with the overall spin density distribution. Additionally, we find no significant change in the time-resolved ENDOR spectra when comparing monomeric with dimeric systems, which is an unambiguous indication that the triplet spins remain similarly localized on one of the porphyrin sub-units independent of inter-ring chemical coupling. We discuss explanations for these results based on the orbital theory of metalloporphyrins and the results of DFT calculations of the dimer triplet spin densities. These results demonstrate that researchers must consider several facets of electronic and nuclear structure to control delocalized singlet and triplet excitons in molecular systems towards more effective screening of qubit candidates.
2 Experimental and computational methods
2.1 Synthesis of monomeric and dimeric porphyrin chromophores
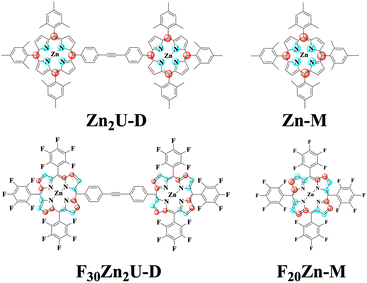
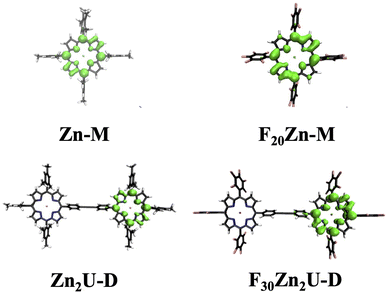
All the chemicals were purchased from Sigma Aldrich and Oakwood Chemical USA and used without further purification. 5,10,15,20-Tetrakis(pentafluorophenyl)porphyrin (F20Fb-M) molecules were purchased from TCI Chemicals USA. We synthesized the 5,10,15,20-(tetramesitly)porphyrin (Fb-M) using the methods described in the literature.32 Zinc substituted porphyrin monomers, zinc(II) 5,10,15,20-(tetramesitly)porphyrin (Zn-M) and zinc(II) 5,10,15,20 tetrakis(pentafluorophenyl)porphyrin (F20Zn-M), were synthesized by adding a solution containing excess zinc acetate in methanol and purified using column chromatography according to procedures reported previously.33,34 We used the Sonogashira coupling approach in the presence of a palladium catalyst to synthesize the required porphyrin dimers: 4,4′-bis[5,10,15-trimesityl-20-porphinyl]diphenylacetylene (Fb2U-D), 4-[zinc(II)5,10,15-trimesity1-20-porphiny1]-4-[5,10,15-trimesityl-20-porphny1]-diphenylacetylene (ZnFbU-D), 4,4′-bis[zinc(II)-5,10,15-trimesityl-20-porphinyl]diphenylacetylene (Zn2U-D), and 4,4′-bis[zinc(II)-5,10,15-pentafluoro-20-porphinyl]diphenylacetylene (F30Zn2U-D).35,36 All the synthesized molecules were characterized using MALDI-TOF mass spectrometry and 1H NMR spectroscopy. We show the structures of each molecular chromophore studied with both time-resolved optical and EPR spectroscopies in the panels of Fig. 1. Fig. S1† shows the structures of Fb-M, Fb2U-D, and ZnFbU-D, which were studied as models in time-resolved EPR and ENDOR measurements. We explain the synthesis of the model molecules in the ESI.†2.2 Steady-state and time-resolved optical spectroscopic measurements
0.2 mM stock solutions of zinc porphyrin monomers and 0.1 mM solutions of zinc homodimers were prepared in toluene. We acquired all the Q band spectra of zinc porphyrin monomers and homodimers using prepared stock solutions, which are shown in Fig. S2.† We diluted all stock solutions by a factor of ten to obtain the Soret absorption spectra of both monomers and homodimers. All sample solutions were placed into a 1 mm path length quartz cell and their absorption spectra were measured using a Jasco V-770 UV-vis/NIR spectrometer at room temperature (∼298 K).Transient optical transmission measurements were done using the output of a 1 kHz Ti:Sapphire regenerative amplifier (Spectra Physics Solstice Ace) possessing 40 fs pulses centered at 800 nm (1.57 eV). After splitting the output of this laser system, one arm was passed into an optical parametric amplifier (OPA, Light Conversion TOPAS Prime) to form 870 nm pulses from the second harmonic of the idler beam. We then passed these pulses to an external β-barium borate crystal to form pulses at 435 nm and separated the 870 nm fundamental using dichroic optics. We used an optical chopper to reduce the pump pulse repetition rate to 500 Hz and synchronized our detection to the chopping waveform with custom electronics. Using the other arm of 800 nm output from the regenerative amplifier, we formed white light continuum pulses by clipping the beam with an iris and focusing it into a 5 mm sapphire plate. Following collimation using an off-axis parabolic mirror, we steered the probe pulse to the sample where it was overlapped with the pump beam using a pinhole. We measured pump-induced transient transmission spectra on a shot-to-shot basis using customized triggering of a CCD camera (Andor Newton 920) affixed to a 0.3 m spectrograph (Andor Kymera). We made transient transmission measurements for each sample in which the pump and probe beams possess either parallel (ΔT‖/T) or perpendicular (ΔT⊥/T) linear polarization states.
The collected spectra were averaged, baseline corrected and plotted against probe time delay, as shown in Fig. S3.† To estimate time constants of ultrafast internal conversion imprinted onto excited state absorption (ESA) signals, we constructed isotropic kinetic traces by selecting probe energies (wavelengths) near 1.9 eV (640 nm) at which the ΔT/T reaches a minimal value, which would be consistent with ESA processes reduced by stimulated emission (SE), and calculated ΔTiso/T = ΔT‖/T + 2ΔT⊥/T. We then deconvoluted the instrumental response due to the temporal overlap of the pump and probe pulses using a Gaussian function of the form 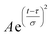 and estimated the time constants that characterize the dynamics of the photoexcited chromophores using two sets of exponential functions: A1[1 − e−t/τ1] for Zn-M and Zn2U-D and A1[1 − e−t/τ1]+ A2[1 − e−t/τ2] for F20Zn-M and F30Zn2U-D.
and estimated the time constants that characterize the dynamics of the photoexcited chromophores using two sets of exponential functions: A1[1 − e−t/τ1] for Zn-M and Zn2U-D and A1[1 − e−t/τ1]+ A2[1 − e−t/τ2] for F20Zn-M and F30Zn2U-D.
2.3 EPR and ENDOR measurements
Sample preparation for EPR measurements was performed in a N2 glove box. All the molecular chromophores studied with magnetic spectroscopy (Fb-M, Fb2U-D, ZnFbu-D, Zn-M, Zn2U-D, F20Zn-M, and F30Zn2U-D) were dissolved in deoxygenated toluene at a concentration of ∼3 mM. The solution was filled into an EPR quartz tube with an outer diameter of 4 mm, and the tube was sealed in a nitrogen glove box environment. The sample was then quickly frozen in liquid nitrogen, which resulted in transparent, glassy samples that were quickly transferred to the pre-cooled resonator.All EPR measurements were performed at X-band (9.7 GHz), using a commercial Bruker ELEXSYS E580 spectrometer (Bruker Biospin, Ettlingen, Germany) equipped with a dielectric ring ENDOR resonator (Bruker EN 4118X-MD4-W1). Light excitation was done in situ using an OPO (basiScan, GWU Lasertechnik, Germany) pumped with 355 nm ns pulsed Laser light (Nd:YAG Laser INDI, Spectra-Physics, operating at a rate of 20 Hz) at 560 nm, 580 nm, and 610 nm wavelengths directly in the resonator of the spectrometer through an optical fiber. Typical incident light intensities at the samples were ∼2 mJ per pulse. All EPR measurements were performed at a temperature of 20 K using a CF935 liquid helium gas-flow cryostat (Oxford Instruments, U.K.) and ITC temperature controller system (Oxford Instruments, U.K.). Data processing and simulations of EPR spectra were done using Matlab™ R2023a (The MathWorks Inc., Natick) and the Easyspin Matlab toolbox (version 6.0.0 dev.51).37,38
Time-resolved continuous wave EPR (transient EPR, tr-EPR) measurements were carried out by irradiating the samples continuously with low power microwave, at each particular magnetic field, and recording the resulting signal in direct detection mode without magnetic field modulation as a function of time after excitation with the laser pulse.39,40 The one-dimensional (non-derivative) EPR spectra were obtained by integrating the tr-EPR spectra between 400 ns and 1500 ns after a laser pulse as a function of magnetic field.
Field-swept echo-detected EPR spectra were recorded by monitoring the electron spin echo (ESE) intensity by using the conventional two microwave pulses Hahn echo sequence (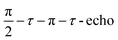 ) with a pulse length of π/2 = 16 ns, π = 32 ns, and τ = 280 ns, which followed a 7 ns laser pulse at a fixed delay after laser flash (DAF) time, as a function of magnetic field.41,42 Three pulse-echo-detected (3p ESE) field sweeps were done with a pulse sequence (
) with a pulse length of π/2 = 16 ns, π = 32 ns, and τ = 280 ns, which followed a 7 ns laser pulse at a fixed delay after laser flash (DAF) time, as a function of magnetic field.41,42 Three pulse-echo-detected (3p ESE) field sweeps were done with a pulse sequence (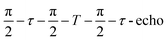 ) with time τ = 100 ns and time T = 20 μs.
) with time τ = 100 ns and time T = 20 μs.
Mims type TR-ENDOR measurements43 were performed at 20 K by employing a microwave pulse sequence of 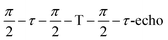 with a π/2-pulse length of 12 ns, τ = 100 ns, and T = 20 μs. For this ENDOR experiment, a high power 1 kW RF amplifier (TOMCO, Technologies, Stepney, Australia) was used to create a 15 μs RF π-pulse. The ENDOR spectra were recorded by monitoring ESE intensity as a function of the RF frequency.
with a π/2-pulse length of 12 ns, τ = 100 ns, and T = 20 μs. For this ENDOR experiment, a high power 1 kW RF amplifier (TOMCO, Technologies, Stepney, Australia) was used to create a 15 μs RF π-pulse. The ENDOR spectra were recorded by monitoring ESE intensity as a function of the RF frequency.
2.4 DFT calculations of triplet spin densities
Monomeric and dimeric structures were built in TmoleX19 (ref. 44) and optimized using density functional theory through TURBOMOLE v 7.4 employing the PBEh-3c functional45 and the associated def2-mSVP basis. Frequency calculations for all structures were performed to ensure that reported structures had no imaginary frequencies. EPR parameters were calculated using Orca v 5.0.3 (ref. 46) using the B3LYP functional, the Wachters + f47 basis for zinc, and the EPR-II basis48 for all other atoms.3 Results and discussion
3.1 Porphyrin electronic structure
In seminal work, Gouterman proposed that the excited state processes including optical absorption of porphyrin molecules could be described by a four-orbital model of two nearly degenerate occupied orbitals, a1u and a2u, and a doubly degenerate pair of unoccupied orbitals, e(x)g and e(y)g, which are related by a 90° rotation about an axis through the molecule's center.49,50 We show the spatial distributions of electron density in the occupied a1u and a2u orbitals in the panels of Fig. 1. Light absorption then leads to the formation of two possible excited state electronic configurations: eg(1)a1u(1) and eg(1)a2u(1). The near degeneracy of these states leads to a strong electron configuration interaction, which drives their mixing into equally weighted symmetric and antisymmetric linear superpositions known as the Bx,y and Qx,y states, respectively.51 The x and y subscripts on these states denote the fact that either one of the degenerate orbitals e(x)g or e(y)g can participate in the excitation process depending on the orientation of the porphyrin molecule relative to the polarization of light field.Since the B state corresponds to the symmetric superposition 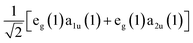 , one should expect this state to possess substantial oscillator strength in a light absorption process, which is substantiated by the presence of strong Soret bands in the linear UV-vis spectra of porphyrins. In contrast, given the Q state corresponds to the anti-symmetric superposition
, one should expect this state to possess substantial oscillator strength in a light absorption process, which is substantiated by the presence of strong Soret bands in the linear UV-vis spectra of porphyrins. In contrast, given the Q state corresponds to the anti-symmetric superposition 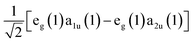 , one should expect negligible oscillator strength to exist in the transition to this state from the molecule's ground state. Despite this expectation, the Q state appears in linear absorption spectra with relatively large intensity due to the non-Condon vibronic coupling mechanism mediated by Herzberg–Teller coupling to the B state.50,52,53
, one should expect negligible oscillator strength to exist in the transition to this state from the molecule's ground state. Despite this expectation, the Q state appears in linear absorption spectra with relatively large intensity due to the non-Condon vibronic coupling mechanism mediated by Herzberg–Teller coupling to the B state.50,52,53
In addition to explaining the basic features of the porphyrin linear absorption spectra, the four-orbital model predicts that different ring substituents perturb the energetic ordering of the a1u and a2u orbitals by changing Coulomb integrals. For example, ring substituents bound at particular positions around the macrocycle that donate electron density to the porphyrin ring cause higher Coulomb repulsion effects in the orbitals located at those atomic sites. These increased Coulomb interactions destabilize the occupied orbital whose density lies on that ring site and drive its contribution to the spectroscopic B and Q states more substantially. In contrast, substituents that withdraw electron density reduce coulombic interactions, stabilize those occupied orbital energies, and reduce their contribution to the spectroscopic states. Thus, the perturbations caused by the electron donating/withdrawing ability of substituents bound at particular porphyrin ring positions can change the identity of the orbitals involved in the excited state processes of these molecules, including both light absorption and intermolecular energy transfer.54,55 However, connections between ring substitution, frontier orbital identity, and singlet and triplet exciton delocalization remain unclear. Making these connections necessitates correlation of optical and magnetic spectroscopic studies on appropriated model systems, as we show below.
3.2 Optical spectroscopy
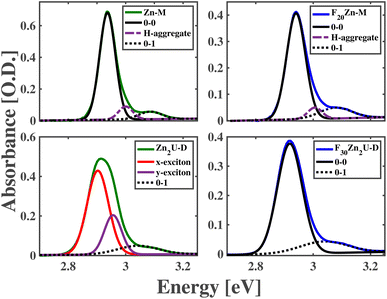
The panels of Fig. 2 compare measured and modeled steady-state absorption spectra of Zn-M, Zn2U-D, F20Zn-M, and F30Zn2U-D solutions in the region of these molecules' Soret resonances. These spectra show the presence of a single, inhomogeneously broadened peak in the spectra of Zn-M, F20Zn-M, and F30Zn2U-D corresponding to the 0–0 transitions between these molecules' S0 and S2 states. We assign lower intensity shoulders at higher energies from the main peaks as the 0–1 vibronic overtones stemming from the slight reorganization of the molecules' structures upon photoexcitation. We explain the routine we used to fit these spectra in the ESI.† In addition to the experimental absorption spectra we measure for these molecules, Fig. 2 also shows Gaussian models of the inhomogeneously broadened 0–0 and 0–1 vibronic transitions. Furthermore, we find we need to add one additional Gaussian peak in the absorption models to explain each spectrum completely, which we attribute to the formation of excitons in H-aggregates. We do not consider these intramolecular excitons further since the excitation pulses used in our ultrafast pump-probe measurements cannot drive these states resonantly. Table S1† details the results of modeling the spectra in Fig. 2.In contrast to these three molecules, the bottom left panel of Fig. 2 shows the 0–0 vibronic transition in the absorption spectrum of Zn2U-D necessitates the presence of two separate Gaussian peaks in our model to explain the peak shape and intensity adequately. The relative intensities and positions of these peaks are consistent with the presence of electronic coupling between the macromolecule's porphyrin sub-units. As shown schematically in the panels of Fig. 1, each porphyrin monomeric unit maintains nearly D4h symmetry, which causes the formation of equivalent transition dipoles along orthogonal molecular axes, as described above. Binding the molecules along the acetylene bridge breaks the overall symmetry of the dimer and leads to inter-ring coupling that differs for directions parallel and perpendicular to the bonding axes. Furthermore, ab initio electronic structure calculations suggest that the planes of each porphyrin macrocycle tilt by an angle of nearly 30° due to steric hindrance.56 Despite the complexities of these symmetries and structural considerations, we can use our model spectra and standard theories of intramolecular excitons to estimate coupling energies of Jxx = 36 meV and Jyy = 30 meV between the porphyrin subunits of Zn2U-D.
Unlike the case of Zn2U-D, we find that we need only a single Gaussian peak to model the 0–0 Soret resonance of F30Zn2U-D. We rationalize this difference in the steady-state absorption spectra using the electron withdrawing power of the different substituents bound at these molecules' meso positions. As considered in the case of hetero-dimeric systems developed and characterized by Lindsey et al.54,55 and explained above, we expect that the strong electronegativity of the F atoms in F30Zn2U-D will pull electron density away from the meso positions of the porphyrin ring that will stabilize the energy of the a2u orbital schematically in Fig. 1. This energy stabilization will result in the a1u orbital being the HOMO state, which does not contain significant electron density on the rings' meso positions. The lack of significant electron density on the meso positions reduces coupling between the Bx and By states in the distinct porphyrin sub-units of F30Zn2U-D. We propose that the opposite effect leads to the observed absorption spectra consistent with delocalized B-state excitons in Zn2U-D.
For the case of Zn2U-D, the relatively lower electronegativity of the meso-substituted mesityl groups leads to an overall electron donating effect at the binding sites around the porphyrin ring. This charge donation destabilizes the energy of the a2u orbital and causes it to become the HOMO state. Our binding of the porphyrin rings via the acetylene bridge at the meso position then leads to inter-ring coupling through HOMO density at these sites. However, the moderate coupling mediated by the acetylene bridge leads to a lack of clear separation between the energies of the coupled excitons in the absorption spectrum shown in the bottom left panel of Fig. 2, which impedes a firm conclusion that the spectral shape stems from exciton delocalization.
Despite the ability of theories developed by Spano to predict the properties of intermolecular excitons based on changes in the relative intensities of the vibronic peaks in an electronic progression,57 the small reorganization energy of the B state excitons in metalloporphyrins limits the intensity of the 0–1 vibronic overtone significantly, as shown in Fig. 2. This small relative intensity inhibits our ability to use the vibronic progressions of Zn2U-D to estimate exciton delocalization. Additionally, the non-trivial alignment of the transition dipole moments in Zn2U-D inhibits a straightforward application of Spano's theories to help assess exciton delocalization.
Previous studies elaborate on ground state electronic interactions present in Zn2U-D and F30Zn2U-D dimer models through their electrochemical studies.35,54,58 These studies allow us to compare the ground state properties of the two molecules based on the variation of the energy of their HOMO level induced by the electron donating/withdrawing ability of the meso-substituent groups. As reported by previous studies, both of these dimers show only weak interactions in the ground state.54,58 Hence, it can be inferred that despite the variations in the HOMO orbital energies in the dimer models, it does not employ a substantial influence on the electronic interactions in their ground-state configurations.
As demonstrated in previous studies, intra- and intermolecular coupling leads to important collective effects in the excited states of molecular chromophores including enhanced exciton transport and radiative relaxation.23–25 Clear estimates of increased rates of energy transfer and light emission necessitate strong coupling between the constituent chromophores manifest in linear optical spectra and long-lived radiative states. However, the moderate inter-ring coupling of excitons in Zn2U-D, which is consistent with the spectra in the bottom left panel of Fig. 2, and the short-lived nature of the Bx,y excitons in porphyrin sub-units do not meet these requirements. The clear delineation of inter-site coupling for a variety of macromolecular binding strengths necessitates further development of physical and chemical effects capable of sensing the formation of excitons delocalized over multiple chromophores. We propose that internal conversion can also assess the appearance and characteristics of inter-ring coupling between Zn-porphyrin sub-units in the moderate regime.
Several studies show that photo-excited B states in metalloporphyrins and free base porphyrin chromophores undergo rapid internal conversion to their respective Q states on time scales that vary between 30 fs to 1.5 ps depending on the identity of central metal cations and ring substituents.59–64 In the case of Zn-substituted porphyrins, this internal conversion process manifests both in the rise of fluorescence emission from the Q state as determined by time-resolved fluorescence measurements and the decay of the excited state absorption (ESA) signals to higher lying electronic states due to the onset of stimulated emission (SE).59,62 These studies demonstrate that the time scale of B to Q internal conversion depends sensitively on the chemical composition of the Zn-ligated chromophore.
When one considers a porphyrin macromolecule whose B state excitations can delocalize across different sub-units via chemical bonding, then one must amend standard equations characterizing internal conversion65 to include this coherent mixture in the non-radiative relaxation as
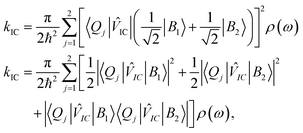 | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) IC|B2〉〈Q1|
IC|B2〉〈Q1|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) IC|B1〉| and |〈Q2|
IC|B1〉| and |〈Q2|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) IC|B2〉〈Q2|
IC|B2〉〈Q2|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) IC|B1〉|, which should be equal in the limit that the two porphyrin sub-units possess the same structure and the B excitons delocalize uniformly across them. Based on these assumptions, eqn (1) becomes,
IC|B1〉|, which should be equal in the limit that the two porphyrin sub-units possess the same structure and the B excitons delocalize uniformly across them. Based on these assumptions, eqn (1) becomes,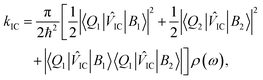 | (2) |
To substantiate this physical picture of the chemical effects on intramolecular coupling, we considered the dimers' ultrafast internal conversion between their B and Q states following photoexcitation of each chromophore. As shown by the absorption spectra in the bottom row of panels in Fig. 2, our 2.85 eV pump pulses excite each molecule on the lower energy edge of its respective 0–0 vibronic transition of the Soret resonance. Based on this energetic overlap, we propose that our pump pulses excite molecules into distinct B states containing no vibrational excitation.
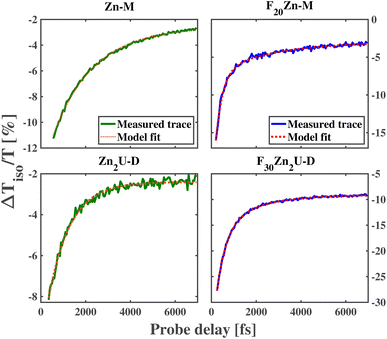
As shown in the top row of panels in Fig. 3, we observe a decay of the ESA features near 1.9 eV (630 nm) in the ultrafast dynamics of Zn-M and F20Zn-M with time constants of 1814 fs and 305 fs, respectively. These values for the B state lifetime qualitatively match those produced in previous, systematic time-resolved fluorescence measurements.60 The factor of 5 longer lifetime of the B state in Zn-M relative to the value we find in F20Zn-M stems from the difference in the identity of the HOMO state between the two chromophores. In addition to the difference in the internal conversion time constant, we find the need to model the ultrafast dynamics of F20Zn-M using two exponential functions, as explained in the Methods section. We propose that this longer time scale in the chromophore's dynamics stems from a structural reorganization within the Q state.
The bottom row of panels in Fig. 3 shows the dynamics of Zn-porphyrin dimers change relative to their monomeric counterparts. Through the analysis described in the Methods section, we find the initial ESA signature of Zn2U-D at 648 nm decays with a time constant of 973 fs, which is almost two times faster than the initial decay of the ESA signal for Zn-M. In contrast, we find the initial ESA signal at 640 nm for F30Zn2U-D decays with a longer time constant, 441 fs, than its monomeric counterpart F20Zn-M. We report the dynamical time scales for the ultrafast kinetics of each chromophore in Table 1 along with the associated 95% confidence intervals of these estimates.
| Chromphore | τ 1 [fs] | τ 2 [fs] | k IC [ps−1] |
|---|---|---|---|
| Zn-M | 1814 (1774, 1854) | — | 0.55 |
| F20Zn-M | 305 (274, 335) | 2577 (1953, 3201) | 3.28 |
| Zn2U-D | 973 (932, 1015) | — | 1.03 |
| F30Zn2U-D | 441 (407, 473) | 1775 (1510, 2040) | 2.27 |
Inverting the values of τ1 we extract from modeling the isotropic traces shown in Fig. 3 allows us to estimate kIC for each chromophore, which we report in Table 1. As expected from the relative values of τ1, we find that the internal conversion rate increases by nearly a factor of 2 when we compare kIC of Zn-M to that of Zn2U-D. Based on previous studies of the ultrafast internal conversion of Zn-ligated porphyrins, we propose that this increase in the internal conversion rate for Zn2U-D stems from quantum interference in the non-radiative relaxation of delocalized B state excitons. However, we must consider other chemical and structural explanations before concluding that this physical mechanism explains our results.
For example, as we noted above, we expect that the energetic ordering of the a1u and a2u porphyrin MOs affects the non-radiative relaxation of the photoexcited Bx,y states. While there will be some difference in the electron donating ability of the hydrogenated phenyl group that we bind to the acetylene bridge in Zn2U-D, we do not expect this change in the Hammett parameter of the functional group to explain the full change in the dimer's internal conversion rate. Previous ultrafast transient absorption and fluorescence upconversion measurements on Zn(II) tetraphenyl porphyrin (ZnTPP) show that the internal conversion time is nearly 1500 fs,59,60 which is 50% larger than the value we measured for Zn2U-D. If the lower electron donating ability of the fully hydrogenated phenyl groups relative to the mesityl groups caused the total difference in the internal conversion time constant going from Zn-M to Zn2U-D, then we would expect to observe an internal conversion time constant between 1500 fs and 1800 fs, which is significantly larger than the value of τ1 we observe experimentally for Zn2U-D. Based on these considerations, we propose that the vast majority of the near factor of two increases in the value of kIC found in our measurements stems from inter-ring quantum interference due to the delocalization of the B state excitons in Zn2U-D.
In addition to finding that the fast time scale slows when comparing the ultrafast dynamics of F20Zn-M to those of F30Zn2U-D, we find that the subsequent relaxation time increases when making the same comparison between the fluorinated derivatives. Given the fact that the fast time scale matches the values found from the increase of fluorescence from the Q state in F20Zn-M, we attribute the presence of slower dynamics in the transient spectra of both fluorinated chromophores to vibrational cooling within their Q states, which has been proposed to take place in iron-ligated porphyrin systems.61 We attribute the difference in the time scales of vibrational cooling between the two fluorinated derivatives to the larger number of atoms in the dimeric chromophore. In the presence of more atoms, we expect that the two-mode vibrational density of states will be larger in the spectral vicinity of low frequency modes capable of inducing Fermi resonance necessary to cause vibrational relaxation, as shown in previous studies of ground state structural dynamics.66,67
Despite the appearance of spectral features consistent with H-aggregates in our Zn-M and F20Zn-M samples, we do not expect that molecules participating in aggregate formation will participate in the observed ultrafast dynamics. For those molecules participating in aggregate formation to take part in the ultrafast dynamics, they must be excited by our pump pulse. Given our pump pulse possesses energy significantly below that of the H-aggregates in our samples, those molecules participating in aggregate formation will not be excited. Since they cannot be excited by our pump pulse, the excitons characteristic of H-aggregation will not participate in any of the observed dynamics.
As stated above, we expect that the term that describes interference between intra- and inter-ring internal conversion in eqn (2) must be a positive number. Therefore, this interference can only act to increase the internal conversion rate. Based on this idea, we argue that the change in the value of τ1 between F20Zn-M and F30Zn2U-D provides further evidence that the B states of the F-substituted macromolecule do not delocalize over the dimer's porphyrin sub-units. Instead, we propose that the decrease in the internal conversion rate of F30Zn2U-D relative to that of F20Zn-M stems from more significant changes in the electron withdrawing ability of the fully hydrogenated phenyl group that binds to the acetylene bridge chemically. The reduced electron withdrawing ability of the H atoms relative to F atoms drives a smaller energetic gap between the a1u and a2u porphyrin MOs, which causes kIC to increase relative to the monomeric systems that contain four fully fluorinated phenyl groups. Despite the clarity of this physical picture, it remains unclear how one can extend this analysis to understand the delocalization of triplet excitons. To establish this connection, we undertook time-resolved EPR and ENDOR spectroscopic studies.
3.3 Time-resolved EPR and ENDOR spectroscopy
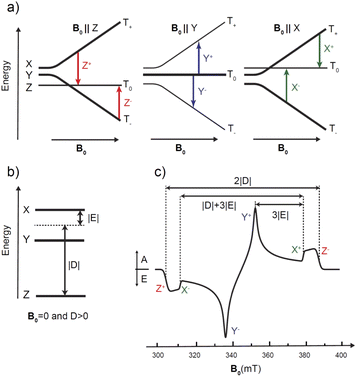
The photoexcited triplet state represents an important probe of the electronic structure of the various porphyrin monomers and dimers. The triplet state involves two strongly coupled unpaired electrons (S = 1) that are delocalized over the macrocycle and thereby probes the electron distribution of both the HOMO and the LUMO states i.e. the frontier orbitals important to chemical and optical properties of the chromophore. Knowledge of the distribution of the unpaired electrons over the frontier orbitals is of vital importance to understand delocalization in the triplet state and thus provides complementary knowledge to that gained about the photoexcited singlet state via stationary and time-resolved optical spectroscopy.The paramagnetic character of photoexcited triplet states makes time-resolved electron paramagnetic resonance spectroscopy coupled with a light source the most appropriate method for investigating the electronic structure of porphyrins in the triplet state.31,40,68–70 The “dark” nature of triplet states due to spin selection in light absorption makes the application of optical methods in triplet state characterization more challenging. Thus, time-resolved EPR techniques are frequently used to derive information on the magnitude and orientation of the traceless zero-field splitting (ZFS) tensor D of the triplet state. The two ZFS parameters D and E are sensitive indicators of the spatial extension and symmetry of the triplet exciton, as shown in Fig. 4. In addition, the spin-polarized triplet EPR spectra act as a fingerprint for understanding how this state forms while also providing larger signals compared to those in thermodynamic equilibrium.31,40,68–70 Additional and more specific information about the unpaired electron spin distribution can be obtained from the interaction of the electronic triplet state with the surrounding magnetic nuclei (I ≠ 0) of the molecule via the electron-nuclear hyperfine couplings (hfc). These hfcs reflect the unpaired electron spin density at the respective nucleus and in the close surrounding of the nucleus via the isotropic (Aiso) and anisotropic (Aaniso) contributions to the hyperfine coupling tensor. However, in the vast majority of cases, these hfcs are not resolved in the time-resolved EPR spectra of porphyrins. To determine the hfcs, more advanced methods like electron nuclear double resonance (ENDOR) experiments are required.43,71–73 If hfcs of several nuclei in different parts of the chromophore can be determined and assigned structurally, then the spin density distribution of the triplet state in the respective molecule can be revealed. Pulsed ENDOR spectroscopy combined with repetitive laser excitation at low temperatures is well suited to make these assignments since this method takes full advantage of the large electron spin polarization in the photoexcited triplet state. Furthermore, the large anisotropy of the triplet-state ZFS tensor in comparison to the magnitude of the hfcs allows one to perform orientation-selective ENDOR spectroscopy, which can provide the orientation and the sign of the hfc tensor components relative to the ZFS tensor axes under favorable conditions.
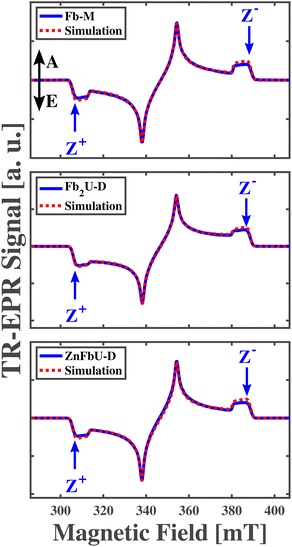
In the following, we will first briefly introduce the principles of time-resolved EPR and ENDOR performed on spin-polarized photoexcited porphyrin triplet states to provide a better understanding of the experiments and their analyses. For this reason, we choose the well-characterized free-base porphyrin monomer (Fb-M), the corresponding homodimer (Fb2U-D) and Zn-free base heterodimer (ZnFbU-D) as models to demonstrate our approach.
The measured and simulated time-resolved EPR (tr-EPR) spectra of Fb-M, Fb2U-D, and ZnFbU-D are shown in the panels of Fig. 5. Fig. S1† shows the structures of these molecules. The three spectra look very similar, all exhibiting the same polarization pattern, EAEAEA, which has been observed in previous EPR studies for free base porphyrins with different substituents.74 The ZFS parameters obtained from the simulation of the Fb-M spectra (|D| = 0.0390 cm−1(1170 MHz), |E| = 0.0080 cm−1 (239 MHz)) are very close to those obtained previously by pulse and transient EPR at X-band free base porphyrins.74–77 The other two porphyrins, the Fb homo- and Zn-Fb heterodimers, have ZFS parameters that are within ∼1% of each other. The g-tensor for all three complexes is highly isotropic and all principal g-values are close to the free electron g-value, 2.0023, as expected for organic molecules without heavy atoms. The ZFS parameters, g tensor values, and relative populations obtained from simulations of transient X-band EPR spectra are given in Table 2. The similarity of the polarization pattern and of both ZFS parameters |D| and |E| in the free base monomer and the two dimers suggests that the triplet exciton is localized on one half of the dimer, and on the free base porphyrin site in the case of the heterodimer, since the triplet spectra of Zn-porphyrin are quite different, as discussed below and shown in Fig. 7. However, the ZFS parameters might be very similar in spite of the strong triplet state delocalization, as in the case of a Frenkel-type triplet exciton. In this case only the comparison of hyperfine coupling constants between different complexes can provide definitive proof concerning localization/delocalization. We thus performed ENDOR spectroscopy to determine the unresolved 1H hyperfine coupling constants.
| Chromophore | |D| [MHz] | |E| [MHz] | g x (exp.) | g y (exp.) | g z (exp.) | g x (calc.) | g y (calc.) | g z (calc.) | p x | p y | p z |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fb-M | 1170 | 239 | 2.0032 | 2.0041 | 2.0023 | — | — | — | 0.25 | 0.69 | 0.06 |
| Fb2U-D | 1158 | 238 | 2.0037 | 2.0045 | 2.0025 | — | — | — | 0.30 | 0.63 | 0.08 |
| ZnFbU-D | 1165 | 237 | 2.0035 | 2.0042 | 2.0024 | — | — | — | 0.26 | 0.70 | 0.04 |
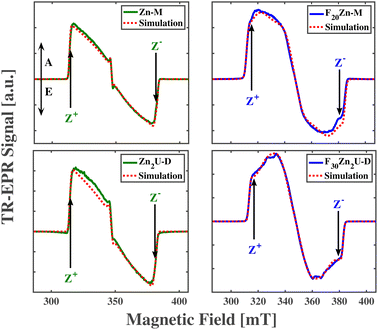
| Zn-M | 966 | 307 | 2.0033 | 2.0036 | 1.9969 | 2.0024 | 2.0028 | 1.9999 | 0.12 | 0.21 | 0.67 |
| Zn2U-D | 950 | 292 | 2.0012 | 2.0027 | 1.9973 | 2.0026 | 2.0030 | 2.0000 | 0.13 | 0.18 | 0.69 |
| F20Zn-M | 1021 | 230 | 2.0047 | 2.0022 | 1.9979 | 2.0025 | 2.0029 | 2.0000 | 0.30 | 0.30 | 0.40 |
| F30Zn2U-D | 968 | 138 | 2.0042 | 2.0027 | 1.9987 | 2.0025 | 2.0029 | 2.0004 | 0.20 | 0.20 | 0.60 |
For the triplet state, ENDOR transitions occur in agreement with the triplet ENDOR resonance condition:70,71
| 3νENDOR = |νL − msA|. | (3) |
This means that a strong and narrow line in ENDOR spectra is expected from the T0 manifold (mS = 0) at the Larmor frequency νL. Furthermore, it follows that those ENDOR transitions that do not stem from a nuclear transition in the mS = 0 manifold are either at the higher or lower frequency side with respect to the central νL transition. For the Z+ transition (T0 to T+1) of a triplet state with D > 0, the ENDOR lines occur on the low (if A > 0) or high (if A < 0) frequency side. The opposite situation is encountered for the Z− transition. Therefore, if the sign of the ZFS parameter D is known, the sign of the hfcs can be derived directly from the spectral position corresponding to the lines at higher/lower frequencies with respect to νL. If the sign of hyperfine coupling is known from previous studies, then the sign of D can be inferred immediately. It is sufficient to collect ENDOR spectra at just half of the field positions corresponding to the EPR spectrum turning points, one for each canonical orientation.
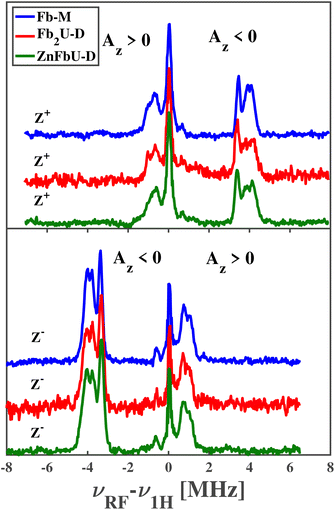
The pulsed Mims-type ENDOR spectra recorded at Z+ and Z− positions for free base porphyrin and its homo- and hetero-dimers are shown in the panels of Fig. 6. Note that for ease of comparison, all spectra have been corrected for the proton Larmor frequency at the respective magnetic field and are shown as absorptive. Mims-type ENDOR possesses a high sensitivity but suffers from so-called blind spots.43 However, for our relatively small hyperfine coupling constants, these blind spots are outside the recorded range and will not be considered further.
The deviations from the proton Larmor frequency and the hfcs correspond to the frequency shift between the ENDOR line and νH according to the triplet ENDOR resonance conditions and can be related directly to the principal component Az of the hyperfine coupling tensor using eqn (3), as long as this principal component is approximately parallel to the principal ZFS tensor axis. Since the Z axis of the ZFS tensor is perpendicular to the porphyrin plane and the methine protons attached directly to the π system remain in this plane, this is a reasonable approximation at least for Fb-M. As mentioned above, ENDOR signals at frequencies lower than the proton Larmor frequency are due to protons with positive hyperfine coupling constants and ENDOR signal frequencies higher than the proton Larmor frequency are due to protons with negative hyperfine coupling constants when measured on the Z+ EPR transition, i.e. the low field ENDOR spectrum. For the high field ENDOR spectrum exciting the Z− EPR transition, the physical situation is reversed. This assignment relies on the positive sign of D for the porphyrin triplet state. If D were negative, then the connections between ENDOR peaks and hfcs would be reversed. As stated above, emissive ENDOR spectra in Fig. 6 have been inverted to facilitate comparison.
The ENDOR spectra of Fb-M show remarkable similarities to the published results from tetraphenyl-phorphyrin (H2TPP) in toluene76 and are quite similar to a H2TPP derivative dissolved in a methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol mixture.74 These similarities allow us to assign the ENDOR signals to particular protons within the structure of Fb-M. The weakest negative coupling, slightly less than 1 MHz, can be assigned to the carbon-bound α-protons on the non-protonated pyrroles known as azomethine pyrroles. The three stronger negative couplings, partially overlapping between 3.3 and 4.3 MHz, are assigned to the carbon-bound α-protons on the protonated pyrroles, called imine pyrroles, and the nitrogen-bound protons. The good agreement with the published hyperfine couplings for H2TPP confirms that the spin density distribution in the porphyrin π systems is not significantly disturbed by the introduction of multiple methyl substituents to the phenyl groups, i.e. all these hfcs are negative.
ethanol mixture.74 These similarities allow us to assign the ENDOR signals to particular protons within the structure of Fb-M. The weakest negative coupling, slightly less than 1 MHz, can be assigned to the carbon-bound α-protons on the non-protonated pyrroles known as azomethine pyrroles. The three stronger negative couplings, partially overlapping between 3.3 and 4.3 MHz, are assigned to the carbon-bound α-protons on the protonated pyrroles, called imine pyrroles, and the nitrogen-bound protons. The good agreement with the published hyperfine couplings for H2TPP confirms that the spin density distribution in the porphyrin π systems is not significantly disturbed by the introduction of multiple methyl substituents to the phenyl groups, i.e. all these hfcs are negative.
The observed positive hyperfine couplings must arise from the phenyl groups and their methyl substituents. Here, we observe peaks up to 1.5 MHz from νL, which represents more pronounced hyperfine couplings than reported for H2TPP in toluene.76 The straightforward assignment is to the freely rotating methyl groups of the phenyl groups, which are absent in H2TPP.
When comparing the ENDOR spectra of the monomer Fb-M to homo- and hetero-dimers, almost complete agreement is found. If the triplet excitons were delocalized over both porphyrins or fast hopping between both porphyrins as in a Frenkel-type exciton, then the hfcs would be reduced to about half in the case of an equally shared triplet exciton in the homodimer. For unequal sharing, the total number of lines would increase and show smaller hfcs for one porphyrin and larger for the other porphyrin, reflecting the relative spin populations on the respective porphyrins. The sum of the hfcs from both porphyrins sub-units of the homodimer would approximately equal the one of the monomeric porphyrins. For the heterodimer, the situation would be a bit more complicated since hyperfine couplings in a Zn-porphyrin monomer are slightly different from the free base porphyrin. However, since we don't observe any clear difference in either the homo- or hetero-dimer from the free base porphyrin monomer, our initial conclusion from the time-resolved EPR spectra is completely confirmed: (i) in all cases the triplet exciton is fully localized on one free base porphyrin unit and (ii) the spin density distribution within this porphyrin is not disturbed by the presence of the covalently connected second porphyrin, even if this is another free base porphyrin or a Zn-containing porphyrin. We applied a similar experimental approach and analysis to assess the triplet state delocalized in the protonated and fluorinated Zn-porphyrin monomers and homodimers shown in Fig. 1.
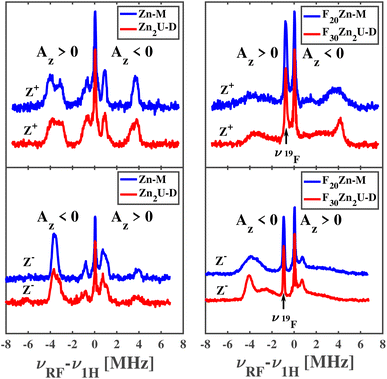
The top left and bottom left panels of Fig. 8 show the ENDOR of Zn-M and Zn2U-D with field settings corresponding to the canonical ZFS EPR transitions Z+ and Z−, respectively. ENDOR spectra in the left column of panels in Fig. 8 show signals from protons with positive and negative hfcs in addition to the narrow free proton line at the proton Larmor frequency. By comparing the top left and bottom left panels of Fig. 8, we find that the positions of the ENDOR lines with respect to νH are exchanged when exciting the corresponding low-field (Z+) or high-field (Z−) canonical EPR transition, as expected from our explanation above. The spectra are clearly different from those corresponding to the free base complexes in Fig. 6. The analysis of the ENDOR spectra is more complicated than for the free base porphyrin, since 3|E| ≈ |D|, and we thus excite another EPR transition (X−) in addition to the Z+ transition, with the same polarization, which leads to the appearance of additional ENDOR lines, as seen in Fig. S3.†
While the analysis is complicated, we can still compare the ENDOR spectra of the two different porphyrins, Zn-M and Zn2U-D, which appear almost identical. If the triplet exciton would be delocalized between two porphyrins sub-units, the hfcs would be reduced to about half in the case of an equally shared triplet exciton. Since we don't observe any clear difference between Zn-M and Zn2U-D, we confirmed our conclusion from the time-resolved EPR spectra that: (i) in both cases the triplet exciton is fully localized on one porphyrin unit and (ii) the spin density distribution within this porphyrin is not disturbed significantly by the presence of the covalently connected second porphyrin. However, it stills remains unclear if the same conclusions apply to the fluorinated Zn-porphyrin systems.
Pulsed Mims-type ENDOR spectra of F20Zn-M and F30Zn2U-D with field settings corresponding to the canonical ZFS EPR transitions Z+ and Z− are shown in the top right and bottom right panels of Fig. 8, respectively. In addition to ENDOR lines from protons shown at 0 MHz in Fig. 8, the ENDOR spectra of F20Zn-M and F30Zn2U-D also contain lines from 19F, which has a magnetic nuclear spin angular momentum 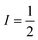 , appears with 100% abundance, and possesses a gyromagnetic ratio comparable to 1H. The narrow free fluorine line whose frequency is νF19 can be seen clearly at −0.75 MHz and −0.95 MHz relative to νH1 in the top right and bottom right columns of panels in Fig. 8, respectively.
, appears with 100% abundance, and possesses a gyromagnetic ratio comparable to 1H. The narrow free fluorine line whose frequency is νF19 can be seen clearly at −0.75 MHz and −0.95 MHz relative to νH1 in the top right and bottom right columns of panels in Fig. 8, respectively.
As expected from the discussion above, the positions of the ENDOR lines with respect to νH are exchanged when we excite the corresponding low-field (Z+) or high-field (Z−) canonical EPR transitions, as seen by comparing top right and bottom right panels of Fig. 8. The spectra are clearly different from the corresponding free base porphyrin shown in the panels of Fig. 6 and the methylated zinc porphyrin in the left panels of Fig. 8. While a detailed analysis of the ENDOR spectra is more complicated than in the cases discussed above due to overlap with 19F ENDOR signals and partial overlap of Z+ and X− EPR transitions of the monomer, we can still compare the ENDOR spectra of the two fluorinated porphyrins. In contrast to the non-fluorinated porphyrins, only partial agreement of the ENDOR spectra is found. In the case of fluorinated porphyrins the ENDOR lines are substantially broader. However, the positions of the strong lines around 4 MHz are very similar and in agreement with the similar lines in the protonated analogue. Broadening of the ENDOR lines can be explained by the presence of several conformers of the fluorinated dimer, which was reported in a previous theoretical study of a similar complex.56 Based on the close similarity in the positions of the ENDOR lines in all porphyrin systems reported here, we conclude that there is no substantial spin density delocalization between the two halves of the porphyrin dimers.
We use DFT calculations to aid in the interpretation of the tr-EPR and ENDOR spectra. The panels of Fig. 9 show the spin density iso-surfaces from the calculations detailed in the Methods section and provide a good visualization of the unpaired triplet electron spin distribution over the porphyrins. The top row of panels shows the Zn-M and F20Zn-M possess spin density distributions whose similarities and differences can be understood from the perspective of the electron donating or withdrawing ability of the rings' substituents. As examples of the similarities, we find that the triplet spin density spreads across all four of the interior N atoms and the C atoms at the rings' meso positions in both Zn-M and F20Zn-M. Additionally, we find that the triplet spin density spreads over the C atoms that bridge only two pyrroles on the exterior of the porphyrin rings. This non-symmetric spin polarization stems from the existence of two, degenerate eg LUMO states that possess electron density on two, non-adjacent pyrroles. The electron densities of these degenerate LUMO states are related by a 90° rotation.
As an example of differences in our DFT results, we find that the spin density delocalizes away from the meso positions of the F20Zn-M porphyrin ring. In contrast, spin localizes more completely on the meso position of the ring in Zn-M. This distinction in the localization of the meso position spin polarization can be rationalized in terms of the triplet state energy ordering controlled by the relative electron withdrawing/donating ability of the ring substituents. In the case of Zn-M, the electron donating ability of the mesityl phenyl groups stabilizes the energy of the excited state 3(a2ueg). Both the a2u and eg orbitals possess significant electron density on the meso position while only the eg orbital possesses density on the C atoms of the pyrrole skeleton. However, the electron withdrawing ability of the F atoms in the pentafluoro phenyl groups of F20Zn-M causes the excited state 3(a1ueg) to possess higher energy than its 3(a2ueg) counterpart.78 Since the a1u and eg orbitals possess substantial electron density on all the atoms in the pyrrole skeleton, populating these orbitals enables delocalization of the triplet spin polarization across more of the molecular structure than we find in the case of Zn-M.
Our DFT calculations support the main conclusion that triplet spin densities of the dimers Zn2U-D and F30Zn2U-D remain localized on one of the porphyrin sub-units, as seen in the bottom row of panels in Fig. 9. Additionally, we find that the differences in the delocalization triplet spin across the atoms in each porphyrin sub-unit in the dimeric systems resemble those we find in the monomers. The spin density delocalizes away from the porphyrin ring meso positions. This is more pronounced in the case of F30Zn2U-D than in Zn2U-D. We propose that the same mechanism that causes this difference in the monomers drives the relatively more delocalized triplet spin polarization in the case of the dimers: electron withdrawing F atoms in the pentafluoro phenyl group cause the excited state 3(a1ueg) to possess the highest energy. Since the orbitals of this state contain more population on the atoms of the pyrrole rings, the triplet spin can delocalize across these atoms more than in Zn2U-D.
The DFT calculations also help explain small changes in the ZFS parameter D between the Zn-porphyrin monomers and dimers. As seen in the bottom row of panels in Fig. 9, the triplet spin densities of the dimers extend to the para-position of the phenyl groups that bridge the two porphyrin sub-units. The spin density does not appear in these positions in the case of either one of the monomers. This extension of the spin density could account for the fact that we observe slightly smaller values of |D| in both Zn2U-D and F30Zn2U-D than in their respective monomers.
The EPR measurements were carried out at 20 K to extend the lifetimes of the triplet states in the different chromophores to values that enable good signal-to-noise ratios and subsequent data analysis to assess spin density delocalization. At higher temperatures, the lifetimes of the triplet states become limited by non-radiative relaxation to the molecules' ground state, which diminishes the signal we measure in the time-resolved EPR spectra. Given this temperature dependence of the triplet lifetime, we expect that the intersystem crossing rate between the triplet excited state and the singlet ground state depends sensitively on the populations of low frequency vibrations capable of mixing states possessing different spin configurations.
For example, computational studies predict that out-of-plane vibrations of fully hydrogenated free base porphyrin cause mixing between 1(ππ*) and 3(ππ*) that involve significant motions of meso-position C atoms.79,80 The excitation of these vibrations induces significant changes in the structure of the porphyrin ring that mix the 1(ππ*) and 3(ππ*) states with intermediate orbitals more localized on both the interior N atoms and meso C atoms. Second order perturbation theory predicts that these localized states mediate non-radiative relaxation from the excited 1(ππ*) state to the lower lying 3(ππ*) state by conserving angular momentum.80 Given the differences in their spin multiplicities, we expect similar vibrational coupling will control the rate of relaxation from the 3(ππ) state to the 1(ππ) ground state.
While the frequencies of the spin-coupling vibrations in free base porphyrin fall below 400 cm−1 when substituted with H atoms, our bonding mesityl or penta-fluoro-phenyl groups at the ring meso positions should increase the effective mass of these vibrational modes significantly. This change in the effective mass should reduce the out-of-plane vibrational frequencies below 200 cm−1.81,82 In that case, as we reduce the temperatures of the porphyrin samples used in EPR measurements, the populations of excited states along the low frequency vibrational modes will lower, which will result in less modulation of the porphyrin structure. The relatively suppressed structural modulations will cause smaller mixing between the ππ*/ππ states and their localized counterparts, which should reduce the ISC rate to the ground state.
In contrast to the temperature-dependent intersystem crossing rate, theoretical investigations propose that the rate of internal conversion from the porphyrin B state to its lower lying Q counterpart depends on the participation of dark states whose energies lie between those of the B and Q states.83 These predictions also propose that high-frequency, ring stretching vibrations can facilitate the mixing of the B and Q states, which would increase internal conversion between them. Based on the temperature-insensitivity of the energies of the involved dark states and the populations of the high frequency vibrations, there does not appear to be a clear hypothesis for a temperature-dependent internal conversion rate for our molecular systems based on a known or proposed physical mechanism.
4 Conclusions
We have studied signatures of singlet and triplet exciton delocalization in weakly bound Zn-porphyrin dimers using both optical and magnetic spectroscopic methods. In contrast to strongly bound porphyrin dimers whose significant intramolecular aromaticity induces clear features of singlet exciton delocalization in their linear optical spectra, the presence of inter-ring excitons in Zn-porphyrin dimers bound weakly by acetylene groups causes more subtle changes in these macromolecules' optical properties. To ameliorate the uncertainty in the extent of exciton delocalization stemming from the broad spectra moderately coupled dimeric porphyrins possess, we demonstrated a method to use non-radiative relaxation rates from photo-excited B states to lower lying Q states as a function of chemical substitution at the meso positions of the porphyrin rings. In the presence of sufficient electronic coupling between distinct light absorbing sites within a macromolecular structure, we propose researchers should find the rate of any non-radiative relaxation process will increase. We corroborated these predictions by showing an increased internal conversion rate when comparing the ultrafast dynamics of zinc(II) tetramesityl porphyrin monomer (Zn-M) to those of its associated dimer (Zn2U-D). This increased non-radiative relaxation supports our conclusion that the presence of delocalized B state excitons explains the complexities of the Zn2U-D linear absorption spectrum.In contrast to the observed increased internal conversion rate of Zn2U-D relative to its monomeric form, we find that the non-radiative relaxation of a fluorinated dimer derivative, F30Zn2U-D, decreases relative to its monomer. We rationalize this relatively decreased internal conversion rate of F30Zn2U-D by considering the fact that these dimeric macromolecules possess one less fluorinated phenyl group than on each porphyrin sub-unit less than the monomers. Hydrogenated sites on the bridging phenyl lead to a relatively smaller electron withdrawing from the meso positions of the dimer's porphyrin rings, which destabilizes the a2u MO and caused a slower internal conversion rate. We argue that these differences indicated the presence of B state excitons localized on each porphyrin sub-unit of F30Zn2U-D which is consistent with the structure of this macromolecule's absorption spectrum.
Unlike the differing delocalization of the singlet excitons in Zn2U-D and F30Zn2U-D, time-resolved EPR spectroscopic measurements show that the spin densities of these molecules' triplet states remain localized on one of the two porphyrin sub-units following intersystem crossing from the photo-excited singlet state. Notably, we find that these macromolecules' time-resolved EPR and Mims-type ENDOR spectra do not differ significantly from those of their respective monomeric forms. We use DFT calculations to rationalize this conclusion with the slightly smaller values of the ZFS parameter D that are consistent with simulations of the time-resolved EPR spectra of the dimers' photo-excited triplet states.
Despite the minimal delocalization of the triplet spin density in both Zn-porphyrin dimers, the EPR results suggest that molecules substituted differently at their meso positions possess spatially distinct triplet spin densities. Using the spin distributions predicted by DFT calculations, we motivate how one can connect the difference in the identity of the frontier orbitals to these distinctions in the triplet spin densities. We find that the triplet spin densities of the methylated monomer and dimer chromophores localize substantially on the meso positions of the porphyrin ring. In contrast, the triplet spin polarization of the fluorinated derivatives delocalizes away from the meso position more substantially, which we argue stems from the differences in the spatial distribution of electron density in the a1u and a2u porphyrin orbitals.
Our results demonstrate the care researchers need to take in assessing the delocalization of excitons across chemically bound chromophores. Most importantly, the delocalization of the singlet exciton in Zn2U-D does not guarantee that the triplet exciton of this molecule will also distribute its spin density across both porphyrin sub-units. Despite this issue, we demonstrate experimental methods to determine how both singlet and triplet excitons delocalize across bonded model chromophores. These methods will help researchers assess exciton delocalization in macromolecular systems central to future photochemical, photo-catalytic, and information processing technologies.
Data availability
Data used for this study can be made available by the corresponding authors upon reasonable request.Author contributions
H. M. made ultrafast optical spectroscopic measurements and analyzed the corresponding results, M. Y. T. and J. N. made the EPR measurements and analyzed the corresponding results, S. T. W. designed the synthetic methods, oversaw the production of zinc porphyrins by W. B., S. K., and B. Z., and made steady-state optical spectroscopic measurements, K. L. M. made the DFT calculations and analyzed the corresponding results, and O. G. P. and A. S. R. conceived of, designed, and garnered funding to support the study. J. N. and A. S. R. wrote the manuscript with substantive input from H. M., M. Y. T., S. T. W., K. L. M., and O. G. P.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Synthesis and EPR/ENDOR spectroscopic characterization of porphyrin molecules were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award number DE-SC-0022134. The EPR work at Argonne National Laboratory was supported by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, under Contract no. DE-AC-02-06CH11357. Ultrafast optical spectroscopic measurements were supported by the Air Force Office of Scientific Research through its Young Investigator Program by award number FA9550-19-1-0231 and the American Chemical Society Petroleum Research Fund through award number 60003-DNI6. STW thanks the Graduate School and Department of Chemistry at Wayne State University for support through a Schaap-Rumbles Graduate Fellowship.References
- X. Li, Y. Wu, D. Steel, D. Gammon, T. H. Stievater, D. S. Katzer, D. Park, C. Piermarocchi and L. J. Sham, Science, 2003, 301, 809–811 CrossRef CAS PubMed
.
- X. Xu, B. Sun, P. R. Berman, D. G. Steel, A. S. Bracker, D. Gammon and L. J. Sham, Science, 2007, 317, 929–932 CrossRef CAS PubMed
.
- X. Xu, B. Sun, P. R. Berman, D. G. Steel, A. S. Bracker, D. Gammon and L. J. Sham, Nat. Phys., 2008, 4, 692–695 Search PubMed
.
- J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. V. de Walle and D. D. Awschalom, Proc. Natl. Acad. Sci. U.S.A., 2010, 107, 8513–8518 CrossRef CAS
.
- C.-J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, Chem. Sci., 2019, 10, 1702–1708 RSC
.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Science, 2020, 370, 1309–1312 CrossRef CAS PubMed
.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem, 2020, 4, 490–504 CrossRef CAS PubMed
.
- C.-J. Yu, S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski and D. E. Freedman, Chem. Mater., 2020, 32, 10200–10206 CrossRef CAS
.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed
.
- J. J. Burdett and C. J. Bardeen, J. Am. Chem. Soc., 2012, 134, 8597–8607 CrossRef CAS PubMed
.
- J. J. Burdett and C. J. Bardeen, Acc. Chem. Res., 2013, 46, 1312–1320 CrossRef CAS PubMed
.
- C. J. Bardeen, J. Chem. Phys., 2019, 151, 124503 CrossRef PubMed
.
- V. S.-Y. Lin, S. G. DiMagno and M. J. Therien, Science, 1994, 264, 1105–1111 CrossRef CAS
.
- P. J. Angiolillo, V. S.-Y. Lin, J. M. Vanderkooi and M. J. Therien, J. Am. Chem. Soc., 1995, 117, 12514–12527 CrossRef CAS
.
- S. M. LeCours, S. G. DiMagno and M. J. Therien, J. Am. Chem. Soc., 1996, 118, 11854–11864 CrossRef CAS
.
- R. Shediac, M. H. B. Gray, H. T. Uyeda, R. C. Johnson, J. T. Hupp, P. J. Angiolillo and M. J. Therien, J. Am. Chem. Soc., 2000, 122, 7017–7033 CrossRef CAS
.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS
.
- C. Galli, K. Wynne, S. M. LeCours, M. Therien and R. Hochstrasser, Chem. Phys. Lett., 1993, 206, 493–499 CrossRef CAS
.
- K. Wynne and R. Hochstrasser, Chem. Phys., 1993, 171, 179–188 CrossRef CAS
.
- K. Wynne and R. M. Hochstrasser, J. Raman Spectrosc., 1995, 26, 561–569 CrossRef CAS
.
- C.-K. Min, T. Joo, M.-C. Yoon, C. M. Kim, Y. N. Hwang, D. Kim, N. Aratani, N. Yoshida and A. Osuka, J. Chem. Phys., 2001, 114, 6750–6758 CrossRef CAS
.
- M.-C. Yoon, D. H. Jeong, S. Cho, D. Kim, H. Rhee and T. Joo, J. Chem. Phys., 2003, 118, 164–171 CrossRef CAS
.
- V. Chernyak and S. Mukamel, Phys. Rev. B, 1993, 48, 2470–2478 CrossRef CAS PubMed
.
- S.-H. Lim, T. G. Bjorklund, F. C. Spano and C. J. Bardeen, Phys. Rev. Lett., 2004, 92, 107402 CrossRef PubMed
.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed
.
- C. E. Tait, P. Neuhaus, M. D. Peeks, H. L. Anderson and C. R. Timmel, Phys. Chem. Chem. Phys., 2016, 18, 5275–5280 RSC
.
- S. Richert, G. Bullard, J. Rawson, P. J. Angiolillo, M. J. Therien and C. R. Timmel, J. Am. Chem. Soc., 2017, 139, 5301–5304 CrossRef CAS PubMed
.
- S. Richert, B. Limburg, H. L. Anderson and C. R. Timmel, J. Am. Chem. Soc., 2017, 139, 12003–12008 CrossRef CAS PubMed
.
- G. Moise, L. Tejerina, M. Rickhaus, H. L. Anderson and C. R. Timmel, J. Phys. Chem. Lett., 2019, 10, 5708–5712 CrossRef CAS PubMed
.
- A. J. Redman, G. Moise, S. Richert, E. J. Peterson, W. K. Myers, M. J. Therien and C. R. Timmel, J. Phys. Chem. C, 2021, 125, 11782–11790 CrossRef CAS PubMed
.
- S. Richert, C. E. Tait and C. R. Timmel, J. Magn. Reson., 2017, 280, 103–116 CrossRef CAS
.
- J. S. Lindsey and R. W. Wagner, J. Org. Chem., 1989, 54, 828–836 CrossRef CAS
.
- Y. Wu, J. Jiang, Z. Weng, M. Wang, D. L. J. Broere, Y. Zhong, G. W. Brudvig, Z. Feng and H. Wang, ACS Cent. Sci., 2017, 3, 847–852 CrossRef CAS
.
- Z. Lin and J. Li, IUCrData, 2020, 5, x200877 CrossRef CAS
.
- J. S. Lindsey, S. Prathapan, T. E. Johnson and R. W. Wagner, Tetrahedron, 1994, 50, 8941–8968 CrossRef CAS
.
- R. W. Wagner, T. E. Johnson, F. Li and J. S. Lindsey, J. Org. Chem., 1995, 60, 5266–5273 CrossRef CAS
.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed
.
- C. E. Tait, M. D. Krzyaniak and S. Stoll, J. Magn. Reson., 2023, 349, 107410 CrossRef CAS PubMed
.
-
M. D. Forbes, L. E. Jarocha, S. Sim and V. F. Tarasov, in Advances in Physical Organic Chemistry, ed. I. H. Williams and N. H. Williams, Academic Press, 2013, Vol. 47, pp. 1–83 Search PubMed
.
-
S. Weber, in Transient EPR, ed. D. Goldfarb and S. Stoll, Wiley Weinheim, Germany, 2018, pp. 195–214 Search PubMed
.
- D. Stehlik and K. Möbius, Annu. Rev. Phys. Chem., 1997, 48, 745–784 CrossRef CAS PubMed
.
- H. Levanon and K. Möbius, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 495–540 CrossRef CAS
.
- C. Gemperle and A. Schweiger, Chem. Rev., 1991, 91, 1481–1505 CrossRef CAS
.
- C. Steffen, K. Thomas, U. Huniar, A. Hellweg, O. Rubner and A. Schroer, J. Comput. Chem., 2010, 31, 2967–2970 CrossRef CAS PubMed
.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033–1036 CrossRef CAS
.
-
V. Barone, in Recent advances in density functional methods, Part I, ed. D. P. Chong, World Scientific Publishing Company, Singapore, 1996 Search PubMed
.
- M. Gouterman, G. H. Wagnière and L. C. Snyder, J. Mol. Spectrosc., 1963, 11, 108–127 CrossRef CAS
.
- P. P. Roy, S. Kundu, N. Makri and G. R. Fleming, J. Phys. Chem. Lett., 2022, 13, 7413–7419 CrossRef CAS PubMed
.
- M. Gouterman, J. Chem. Phys., 1959, 30, 1139–1161 CrossRef CAS
.
- G. Orlandi and W. Siebrand, J. Chem. Phys., 1973, 58, 4513–4523 CrossRef CAS
.
- A. G. Avramenko and A. S. Rury, J. Phys. Chem. Lett., 2022, 13, 4036–4045 CrossRef CAS PubMed
.
- J.-P. Strachan, S. Gentemann, J. Seth, W. A. Kalsbeck, J. S. Lindsey, D. Holten and D. F. Bocian, J. Am. Chem. Soc., 1997, 119, 11191–11201 CrossRef CAS
.
- D. Holten, D. F. Bocian and J. S. Lindsey, Acc. Chem. Res., 2002, 35, 57–69 CrossRef CAS PubMed
.
- S. Caprasecca, C. Curutchet and B. Mennucci, J. Phys. Chem. C, 2013, 117, 12423–12431 CrossRef CAS
.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed
.
- J. Seth, V. Palaniappan, R. W. Wagner, T. E. Johnson, J. S. Lindsey and D. F. Bocian, J. Am. Chem. Soc., 1996, 118, 11194–11207 CrossRef CAS
.
- H.-Z. Yu, J. S. Baskin and A. H. Zewail, J. Phys. Chem. A, 2002, 106, 9845–9854 CrossRef CAS
.
- U. Tripathy, D. Kowalska, X. Liu, S. Velate and R. P. Steer, J. Phys. Chem. A, 2008, 112, 5824–5833 CrossRef CAS PubMed
.
- A. S. Rury and R. J. Sension, Chem. Phys., 2013, 422, 220–228 CrossRef CAS
.
- A. G. Avramenko and A. S. Rury, J. Phys. Chem. Lett., 2020, 11, 1013–1021 CrossRef CAS PubMed
.
- M.-H. Ha-Thi, N. Shafizadeh, L. Poisson and B. Soep, J. Phys. Chem. A, 2013, 117, 8111–8118 CrossRef CAS PubMed
.
- B. Abraham, J. Nieto-Pescador and L. Gundlach, J. Phys. Chem. Lett., 2016, 7, 3151–3156 CrossRef CAS PubMed
.
-
A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer, and Reactions in Condensed Molecular Systems, OUP, Oxford, 2013 Search PubMed
.
- S. N. Lavan, C. A. Saraza, K. Bhullar, S. Sabeyo-Yonta, A. M. Sanni and A. S. Rury, J. Phys. Chem. C, 2020, 124, 12933–12947 CrossRef CAS
.
- A. M. Sanni, S. N. Lavan and A. S. Rury, J. Phys. Chem. C, 2020, 124, 13942–13955 CrossRef CAS
.
- D. E. Budil and M. C. Thurnauer, Biochim. Biophys. Acta, Bioenerg., 1991, 1057, 1–41 CrossRef CAS PubMed
.
- W. Lubitz, F. Lendzian and R. Bittl, Acc. Chem. Res., 2002, 35, 313–320 CrossRef CAS PubMed
.
- W. Lubitz, Phys. Chem. Chem. Phys., 2002, 4, 5539–5545 RSC
.
-
M. D. Kemple, in ENDOR of Triplet State Systems in Solids, ed. M. M. Dorio and J. H. Freed, Springer US, Boston, MA, 1979, pp. 409–436 Search PubMed
.
- L. Kulik and W. Lubitz, Photosynth. Res., 2009, 102, 391–401 CrossRef CAS PubMed
.
-
J. R. Harmer, in Hyperfine Spectroscopy – ENDOR, ed. R. Harris and R. Wasylishen, John Wiley & Sons, Ltd, 2016, pp. 1493–1514 Search PubMed
.
- A. Barbon, M. G. Dal Farra, S. Ciuti, M. Albertini, L. Bolzonello, L. Orian and M. Di Valentin, J. Chem. Phys., 2020, 152, 034201 CrossRef CAS PubMed
.
- O. Gonen and H. Levanon, J. Chem. Phys., 1986, 84, 4132–4141 CrossRef CAS
.
- C. W. M. Kay, J. Am. Chem. Soc., 2003, 125, 13861–13867 CrossRef CAS PubMed
.
- C. E. Tait, P. Neuhaus, M. D. Peeks, H. L. Anderson and C. R. Timmel, J. Am. Chem. Soc., 2015, 137, 8284–8293 CrossRef CAS PubMed
.
- M. Asano, Y. Kaizu and H. Kobayashi, J. Chem. Phys., 1988, 89, 6567–6576 CrossRef CAS
.
- S. Perun, J. Tatchen and C. M. Marian, ChemPhysChem, 2008, 9, 282–292 CrossRef CAS PubMed
.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed
.
- Y.-H. Zhang, W.-J. Ruan, Z.-Y. Li, Y. Wu and J.-Y. Zheng, Chem. Phys., 2005, 315, 201–213 CrossRef CAS
.
- Y.-H. Zhang, W. Zhao, P. Jiang, L.-J. Zhang, T. Zhang and J. Wang, Spectrochim. Acta, Part A, 2010, 75, 880–890 CrossRef PubMed
.
- K. Falahati, C. Hamerla, M. Huix-Rotllant and I. Burghardt, Phys. Chem. Chem. Phys., 2018, 20, 12483–12492 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc03327a |
| ‡ These authors contributed equally to this study. |
| This journal is © The Royal Society of Chemistry 2024 |