Open Access Article
Open Access ArticlePredicting synthesis recipes of inorganic crystal materials using elementwise template formulation†
Seongmin
Kim
 a,
Juhwan
Noh
a,
Juhwan
Noh
 a,
Geun Ho
Gu
b,
Shuan
Chen
a,
Geun Ho
Gu
b,
Shuan
Chen
 a and
Yousung
Jung
a and
Yousung
Jung
 *ac
*ac
aDepartment of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), 291, Daehak-ro, Yuseong-gu, Daejeon, 34141, South Korea
bSchool of Energy Technology, Korea Institute of Energy Technology, 200 Hyuksin-ro, Naju, 58330, South Korea
cSchool of Chemical and Biological Engineering, Institute of Chemical Processes, Seoul National University, 1, Gwanak-ro, Gwanak-gu, Seoul, 08826, South Korea. E-mail: yousung.jung@snu.ac.kr
First published on 8th December 2023
Abstract
While advances in computational techniques have accelerated virtual materials design, the actual synthesis of predicted candidate materials is still an expensive and slow process. While a few initial studies attempted to predict the synthesis routes for inorganic crystals, the existing models do not yield the priority of predictions and could produce thermodynamically unrealistic precursor chemicals. Here, we propose an element-wise graph neural network to predict inorganic synthesis recipes. The trained model outperforms the popularity-based statistical baseline model for the top-k exact match accuracy test, showing the validity of our approach for inorganic solid-state synthesis. We further validate our model by the publication-year-split test, where the model trained based on the materials data until the year 2016 is shown to successfully predict synthetic precursors for the materials synthesized after 2016. The high correlation between the probability score and prediction accuracy suggests that the probability score can be interpreted as a measure of confidence levels, which can offer the priority of the predictions.
1 Introduction
Synthesizing new inorganic functional materials is a practical goal of materials science in various fields such as batteries,1–3 (photo-)electrochemical catalysts,4,5 and solar cells6 to name but a few. While advances in computational power and electronic structure calculation methods helped design new materials at a pace much faster than before,7–10 the actual synthesis of predicted candidate materials still remains a slow process due to the empirical nature of synthesis based on intuition and laboratory trial and error.Thus, to reduce the time and cost associated with failed syntheses, efforts to understand the chemistry of materials synthesizability have been made. For example, the use of Goldschmidt's tolerance factor, a heuristic stability metric based on the ratio of ionic radii, was suggested to approximate the stability of double halide perovskites.11 For NASICON-structured materials, machine-learning derived stability rules based on the Na content, elemental radii, and electronegativities were also suggested.12 In addition to these heuristic rules for synthetic accessibility that are domain specific, several thermodynamic quantities obtained from electronic structure calculations have been widely used as a helpful estimate of synthesizability.13 For example, the energy above the convex hull (ΔEhull) was used as an important criterion to identify synthesizable photocatalysts14 and metastable inorganic materials.15 Decomposition enthalpies (ΔHd) were also used as another metric to evaluate solid stability.16 Moreover, to address the computational costs of these first-principles calculations, machine learning (ML) models have been proposed to estimate the materials thermodynamics.17–19 More recently, data-driven approaches were proposed to predict the synthesizability of unknown inorganic crystals based on their structural similarity20–22 or chemical composition23 to the already synthesized materials.
Beyond the synthetic feasibility predictions as briefly described above, a few studies attempted to further suggest synthesis routes for inorganic materials. For example, in constructing the plausible reaction space for a target compound, a favorable synthetic pathway has been suggested based mainly on thermodynamic parameters and some kinetic heuristics.24 Nucleation barriers and phase competition metrics were also used, showing another approach to provide favorable paths for inorganic materials.25 In addition to these thermodynamic-based approaches, several data-driven models have also been proposed to generate precursors and synthetic conditions (e.g. heating temperature and time) to synthesize the target materials using text-mined meta-datasets.26–29 However, outcomes from generative models used in the latter studies29 can contain thermodynamically unstable precursors and do not generally present priority among the results, still remaining a question of which results should be tried experimentally first. In the same vein, they do not inform the measure of confidence for predicted reactions, requiring an additional process by domain experts to screen or rank the generated reaction recipes. While the previous study24 has shown the capability of suggesting intermediate reaction steps with priority for a net (overall) reaction (both target and starting materials are given), a prioritized retrosynthetic prediction of starting materials (precursors) is still under-studied.
This status of inorganic retrosynthetic reaction prediction can be contrasted with molecular synthesis planning where there are a number of models with promising prediction accuracy. Broadly, molecular retrosynthesis prediction models can be divided into two approaches, template-free30–32 and template-based33,34 methods. Using sequence-based or graph-based molecular representations, template-free methods have shown good performance without the requirement of a vast number of chemical reaction rules.30–32 On the other hand, template-based models use manually or automatically crafted reaction templates and rules extracted from reaction datasets.33,34 Since subtle changes in chemical environments can lead to very different reactivities and reaction outcomes, template-based approaches typically require a large number of reaction templates, of the order of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 20
000 to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, which still cannot cover and describe all the reactions. On the other hand, most solid-state inorganic syntheses are performed using a finite list of commercial precursors, and in that sense, synthesis planning in solid-state chemistry may be considered much simpler since the aim would then be to select appropriate precursors from commercially available compounds, only of the order of 100 precursors. This difference suggests that the concepts used in successful organic retrosynthesis models may be borrowed and adapted to address the inorganic retrosynthesis problem. In particular, by noting that most solid-state inorganic syntheses are performed using a finite list of commercial precursors, we envision that the set of popular inorganic precursors used in the literature can be seen as a “template” for inorganic solid-state synthesis, and a similar probability-based template selection model used in organic retrosynthesis can be used in inorganic synthesis planning. This template-based recommendation would remove the unwanted possibility of yielding unrealistic precursor chemicals that do not satisfy charge neutrality or have no CAS registry number, as in some of the existing template-free generative models for inorganic retrosynthesis predictions.29
000, which still cannot cover and describe all the reactions. On the other hand, most solid-state inorganic syntheses are performed using a finite list of commercial precursors, and in that sense, synthesis planning in solid-state chemistry may be considered much simpler since the aim would then be to select appropriate precursors from commercially available compounds, only of the order of 100 precursors. This difference suggests that the concepts used in successful organic retrosynthesis models may be borrowed and adapted to address the inorganic retrosynthesis problem. In particular, by noting that most solid-state inorganic syntheses are performed using a finite list of commercial precursors, we envision that the set of popular inorganic precursors used in the literature can be seen as a “template” for inorganic solid-state synthesis, and a similar probability-based template selection model used in organic retrosynthesis can be used in inorganic synthesis planning. This template-based recommendation would remove the unwanted possibility of yielding unrealistic precursor chemicals that do not satisfy charge neutrality or have no CAS registry number, as in some of the existing template-free generative models for inorganic retrosynthesis predictions.29
In this work, we introduce a template-based graph neural network for inorganic synthesis recipe prediction. The model is trained to predict a set of precursors for inorganic crystals by ranking the sets of precursors as probability scores. Temperature for the solid-state reaction is another important parameter in actual experimental synthesis, that is affected by both the target crystals and detailed precursors chosen. Thus, we additionally constructed a temperature prediction model that is sequentially connected to the precursor set prediction model. These two models combined then generate a set of precursors and temperature to produce a target solid compound. Due to the high correlation between the probability score and the prediction accuracy, the proposed model has the key advantage of quantifying confidence of the predictions, which could alleviate the exhausted experimental costs.
2 Results and discussion
2.1. Elementwise formulation of inorganic retrosynthesis
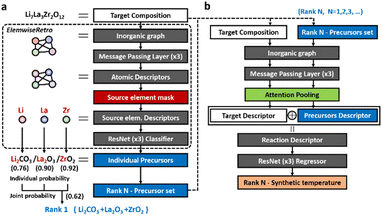
We formulated the retrosynthetic problems of inorganic materials by first dividing chemical elements in the target product into two types: elements that have to be provided as reaction precursors (denoted as “source elements”) and elements that can come from or leave reaction environments (denoted as “non-source elements”). After selecting source elements from the given target inorganic compositions, proper anionic frameworks (denoted as “precursor templates”) have to be attached to each source element to complete the actual precursor compounds. This formulation of the concept is summarized in Fig. 1a.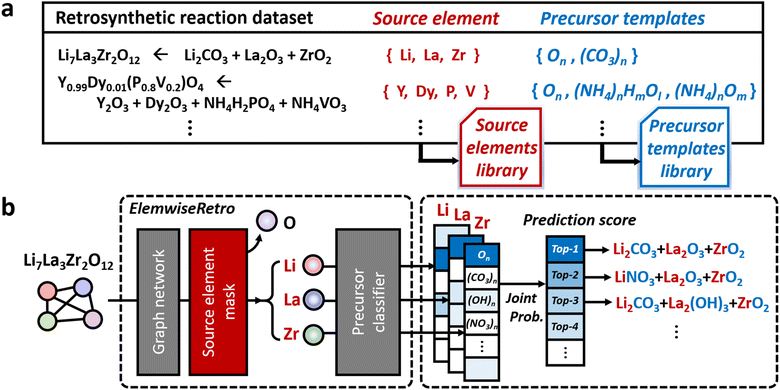 | ||
| Fig. 1 The overview of (a) the formulation of source elements and each precursor template library and (b) the inorganic retrosynthetic model architecture (see also Fig. 5 for more details on ElemwiseRetro) for top-scored based synthesis recipe prediction. | ||
To categorize the source and non-source elements, we examined the text-mined inorganic reaction database.35 To this end, we assigned metal groups (alkali, alkaline, transition, lanthanide, actinide, and post transition), metalloids, phosphorus, selenium, and sulfur as source elements and the others as environmental elements from the inorganic retrosynthetic point of view. Based on this formulation, we constructed a total of 60 precursor templates from the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 curated inorganic retrosynthetic datasets. The detailed procedures for the dataset selection and curation and the precursor template extraction are described in the Computational methods section.
477 curated inorganic retrosynthetic datasets. The detailed procedures for the dataset selection and curation and the precursor template extraction are described in the Computational methods section.
Based on this formulation, for a given target composition, the compound is encoded as a graph whose node features are obtained from a separate pretrained representation of inorganic compounds. Once the representation is fed into the model, the inorganic retrosynthetic model predicts the precursors that can provide all source elements contained in the given target composition using the source element mask, as shown in Fig. 1b. The formulated source element mask enables the model to discriminate the source element (Li, La, and Zr) information from the given compositions (Li7La3Zr2O12). Each source element is separately used in the following precursor classifier which predicts the precursor in the formulated template library. By calculating the joint probability of a set of precursors determined for each source element, the precursor-sets (synthesis “recipe”) are finally predicted as a probability score which can be ranked. The brief and detailed architecture of the proposed model, ElemwiseRetro, is described in Fig. 1b and 5, respectively.
2.2. Precursor set prediction
To demonstrate the ElemwiseRetro model performance, we calculated the top-k exact match accuracy for the test dataset as an evaluation metric, which measures the ratio that at least one valid recipe is included in one of the top-k highest scored precursor set predictions. Since the model might capture merely the popularity trend of literature-reported examples, as recently discussed for some organic retrosynthesis predictions,36 we constructed the template-popularity-based model as a baseline comparison. In this baseline, the prediction is made statistically based on the number of examples in which a particular template appears in the dataset. The results for the top-k exact match tests are shown in Table 1. The proposed ElemwiseRetro shows promising 78.6% top-1 and 96.1% top-5 accuracy, as compared to the popularity baseline model whose top-1 and top-5 accuracies are 50.4% and 79.2%, respectively. This result can be understood by the fact that ElemwiseRetro considers the combination and interaction of all elements in target compositions through message passing layers, whereas the baseline looks at only the individual source element types in the target composition and just randomly samples precursor recipes based on the popularity of each element's templates individually.| Top-k accuracy (%) | Model | ||
|---|---|---|---|
| ElemwiseRetro (RandSplit) | ElemwiseRetro (TimeSplit) | Baseline | |
| a The accuracies were obtained in a single run, but multiple runs yield similar results. | |||
| k = 1 | 78.6 | 80.4 | 50.4 |
| k = 2 | 87.7 | 89.4 | 70.5 |
| k = 3 | 92.9 | 92.9 | 75.1 |
| k = 4 | 94.6 | 94.3 | 77.6 |
| k = 5 | 96.1 | 95.8 | 79.2 |
2.3. Confidence level estimation
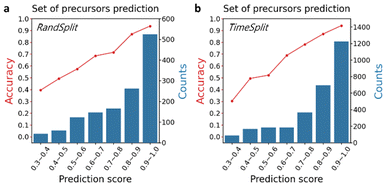
The reliability of the prediction is important to measure in order to prioritize and manage the cost of experimental environments. We split the top-1 exact match accuracy of precursor set prediction depending on their probability scores. As shown in Fig. 2a, a positive correlation between the probability score and the accuracy is clear. This means that the predictions with higher probability scores can be considered more reliable predictions.2.4. Publication-year-split validation
To further validate our model, we performed the publication-year-split test, for which we mined the published years of each dataset using the DOIs tagged in the inorganic reaction database. In this benchmark, instead of splitting the entire dataset between the training and test sets randomly as in the original ElemwiseRetro, we used the time sequence to split the dataset, the data before the year 2016 for training (∼75%) and the data after 2016 for testing (∼25%). As the accuracy results for this time split case is summarized in Table 1, both original ElemwiseRetro-RandSplit and ElemwiseRetro-TimeSplit yield consistent model performance. Furthermore, we split the top-1 exact match accuracy depending on their probability scores (Fig. 2b), and a positive correlation is still clear even though the test dataset was derived from the out of time domain. This result clearly suggests that our model can be used to discover undiscovered inorganic materials in the future.2.5. Synthetic temperature prediction
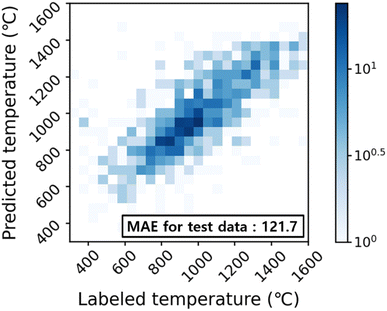
The synthetic temperature prediction model performance was investigated using the 2D parity heat map as shown in Fig. 3. The predicted temperatures from the model reproduce real temperatures qualitatively with a mean absolute error (MAE) of 121.7 °C, which outperforms the MAE (∼140 °C) of previous results.27,28 Nevertheless, a wide range of temperatures (300–1600 °C) used to synthesize a target crystal with a limited number of data points is potentially contributing to the relatively large MAE observed here.3 Computational methods
3.1. Dataset preparation
For preparing the dataset for training and testing, we started with the inorganic synthesis-related dataset35 which was text-mined from the literature published after the year 2000. The raw text-mined data contain some incomplete entries; thus we further refined the data. We removed the data with missing or incorrectly parsed elements and stoichiometry, which reduced the data size from 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782 to 25
782 to 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873. Next, the entries with inconsistency between the target crystal elements and the source elements in precursors were removed, resulting in 22
873. Next, the entries with inconsistency between the target crystal elements and the source elements in precursors were removed, resulting in 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837 datasets. Few cases of unstable or metastable precursors such as Li2O2 or precursors which have no CAS registry number were also filtered out or revised due to unmanageability in real synthetic environments. The data are further trimmed by selecting data where only one source element is present for each precursor, which is the case for most of the data (21
837 datasets. Few cases of unstable or metastable precursors such as Li2O2 or precursors which have no CAS registry number were also filtered out or revised due to unmanageability in real synthetic environments. The data are further trimmed by selecting data where only one source element is present for each precursor, which is the case for most of the data (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085) due to its affordability in real experimental synthesis for any type of inorganic synthesis. The duplicate cases were removed, ensuring that the final 13
085) due to its affordability in real experimental synthesis for any type of inorganic synthesis. The duplicate cases were removed, ensuring that the final 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 retrosynthetic curated datasets were derived.
477 retrosynthetic curated datasets were derived.
For the synthesis step with several experiments, the synthetic temperature was calculated by averaging. The data with the synthesis temperature less than 300 °C and more than 1600 °C were removed, as they are outliers. For multi-step reaction cases which have more than one heating step, we took the average temperature to represent the overall reaction. Those with high standard deviation data were removed. We note that several other reaction conditions (e.g. sequence of operations, type of mixing device, heating atmosphere, etc.) which might be up to each laboratorial standardized procedure would not be considered; incorporating these conditions is a topic of future work.
Through the aforementioned preprocessing, our final dataset size is 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 for the precursor set prediction from the targets and 9163 for the synthetic temperature prediction. The whole dataset was divided into training
477 for the precursor set prediction from the targets and 9163 for the synthetic temperature prediction. The whole dataset was divided into training![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) validation
validation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test (8
test (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
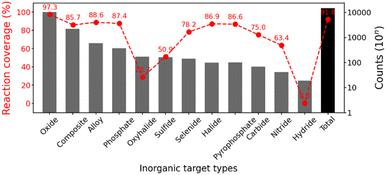
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to separate test data from the training process. Fig. 4 shows the coverage of the inorganic reaction data, which measures the ratio included in the final dataset after preprocessing the formulation of source elements and precursor templates, depending on the target types in the inorganic reaction dataset. The most frequent types (oxides, composites, alloys, and phosphates) are highly covered, which represents our inorganic reaction domain. The total reaction coverage from our template-based approach is 91.8%, which would be further developed in the future. Our formulated concepts have the possibility to handle reactions involving most elements and the broad types of popular inorganic materials (e.g. oxides, composites, alloys, phosphates, etc.).
1) to separate test data from the training process. Fig. 4 shows the coverage of the inorganic reaction data, which measures the ratio included in the final dataset after preprocessing the formulation of source elements and precursor templates, depending on the target types in the inorganic reaction dataset. The most frequent types (oxides, composites, alloys, and phosphates) are highly covered, which represents our inorganic reaction domain. The total reaction coverage from our template-based approach is 91.8%, which would be further developed in the future. Our formulated concepts have the possibility to handle reactions involving most elements and the broad types of popular inorganic materials (e.g. oxides, composites, alloys, phosphates, etc.).
In predicting the retrosynthetic precursors for given inorganic materials, we used source element-wise precursor templates to determine each type of precursor compounds. After thoroughly investigating the whole 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 inorganic synthetic dataset which was curated by the abovementioned preprocessing, we obtained the 60 lists of the precursor templates (e.g. –CO3 in Li2CO3, Na2CO3, and –OH in LiOH, Al(OH)3). Based on these precursor templates, our retrosynthetic model can predict each precursor per one source element within the pre-defined 60 template space.
477 inorganic synthetic dataset which was curated by the abovementioned preprocessing, we obtained the 60 lists of the precursor templates (e.g. –CO3 in Li2CO3, Na2CO3, and –OH in LiOH, Al(OH)3). Based on these precursor templates, our retrosynthetic model can predict each precursor per one source element within the pre-defined 60 template space.
3.2. Retrosynthetic model
We denote our retrosynthetic precursor prediction model as ElemwiseRetro, and the other is for the synthetic temperature prediction. The overall schematics of the two model architectures are illustrated in Fig. 5. In order to find a plausible set of precursors that could synthesize the target product, the composition of the inorganic target material was converted to a 2D graph, referred to as Roost,37 which is a kind of fully connected inorganic graph representation that has no edge attributes. The atomic feature vectors learned from ElemNet38 were embedded as the initial node states of the inorganic graph. We then apply the message passing neural network (MPNN)39 to the graph representation, which updates each atomic feature with the surrounding environmental information (the other atomic features). Typically, after passing the MPNN, the pooling operation is used to gather the updated node vectors in order to obtain a single inorganic descriptor as one-to-one mapping with a target input. Instead of using the pooling layer, however, we extracted the node vectors, which correspond to the source elements, from the updated atomic features to solve the retrosynthetic one-to-many (target-to-precursors) problem. Then the source element descriptors were separately entered into the prediction network (element-wise prediction) that consists of a residual network (ResNet)40 with three residual building blocks of 512-dimensional hidden layers. The residual building block is constructed to add feature vectors before and after passing the nonlinear activation function, known for contributing to the robustness of deeper neural networks.After training with the precursor templates, the retrosynthetic model classified each source element to infer their precursor template classes. At the end of the classifier, probability score distributions of the precursor templates for each source element were obtained using the SoftMax layer. Using this individual probability, we can automatically compute the joint probability, resulting in the set of precursor outcomes. The probability concept enables the model to derive the most synthetically probable precursors for inorganic retrosynthesis by ranking them as descending probability scores.
After predicting the set of precursors by ElemwiseRetro, both the target and precursors were inputted in the second model for predicting their synthetic temperature (Fig. 5b). The compositions of the target and precursors were converted to inorganic graphs by the aforementioned Roost. To distinguish information between the target and precursors, the atomic nodes in the inorganic graph were only intra-connected within the target and precursor sets, separately. Therefore, the target (or precursor) atomic features were updated only from the surrounding target (or precursor) information. After the MPNN, the attention pooling layer was applied to extract the target and precursor descriptors from the updated target and precursor graphs, respectively. Then the two descriptors were concatenated and fed into the regressor network to predict their synthetic temperature.
The atomic feature vectors learned from ElemNet38 were embedded as the initial node vectors of the inorganic graph. The atomic embedding dimension is 136, which is mapped to 63 dimensions by one linear layer. The stoichiometric weight is concatenated to each mapped atomic vector, resulting in an initial node dimension of 64. We used three MPNN layers to update the node features. The three hidden layers of the prediction network have 512/512/512 nodes. At the end of the prediction network, the SoftMax layer is used in ElemwiseRetro.
4 Conclusions
We proposed an element-wise template-based retrosynthetic model that enables a probabilistic prediction of the precursor set for inorganic crystals and the corresponding synthetic temperatures. Based on the concept of source elements, we derived a set of precursor templates of inorganic crystal compounds. We demonstrated a promising model performance by the top-k exact match accuracy test with the popularity baseline comparison. The observed positive correlation between the probability score and the prediction accuracy also allows us to estimate the confidence of the predictions. We further validated our model by the publication-year-split test, which suggests that our model has the possibility of covering up to the afterward time space where novel inorganic materials will be discovered or virtually proposed. While the current approach is the first and initial effort to use probabilistic modeling for inorganic solid-state retrosynthesis predictions, we expect that the concept of templates, source element decomposition, and element-wise prediction proposed here can be a promising direction to further develop inorganic retrosynthetic models with improved performance.Given that the field of inorganic retrosynthesis predictions is still in its early stage, it is important to acknowledge the limitations of our approach and identify opportunities for further improvement. Firstly, our model does not encompass inorganic reactions that involve catalytic compounds, as catalysts cannot be considered both as a source element and a non-source element within the framework of our model. This limitation restricts our ability to predict reactions that include catalytic processes. Secondly, our current model does not predict multi-step reaction pathways for inorganic crystals. This is due to the complexity of precursors that contain more than one source element, in compounds such as BaTi2O5, where two source elements exist within a single precursor. Our formulated approach is designed to handle one-step reactions, which aligns with the majority of the inorganic reaction data used for training. Thirdly, our model does not account for metastable and unstable precursor cases. For practical purposes, our study focuses only on commercially available compounds as starting materials, thereby excluding less stable compounds from consideration. Fourthly, certain types of inorganic crystal compounds, such as oxyhalides, sulfides, carbides, nitrides, and hydrides, are not well-covered by our model, as indicated in Fig. 4. This limitation arises from the definition of the source element space, which excludes carbon and nitrogen due to their overlapping presence in numerous precursor templates. In addition, even though the predicted recipes that do not exist in the dataset were evaluated as inaccurate in this work, they could still be valid. To deal with this, positive and unlabeled (PU) learning would be one solution by enumerating all other recipes that do not appear in the dataset as unlabeled training data in the future. Furthermore, our model can only handle the chemical formula of a target compound, which cannot distinguish the different structures of the same composition, i.e., polymorphs. Since the same composition can have diverse polymorphs in inorganic chemistry, a structure-based retrosynthetic model, as well as a polymorph prediction model, should also be studied. Moreover, since the current model is constructed by a template-based method that cannot predict or suggest the out-domain of the formulated templates, more developed formulations or template-free methods should be studied.
Nevertheless, we expect that the core concept of using element-wise and template-based prediction and the probabilistic method for the estimate of prediction confidence will be a prospective method to solve several future problems of inorganic materials retrosynthesis. In this work, only two element types, source elements and non-source elements, were considered. For further development, more concretized element types (more than three) from the inorganic retrosynthetic view could be a direction to cover the enlarged reaction space which includes catalytic compounds and complex types of precursors. To cover the multi-step reaction space, predicting the number of reaction and heating steps before predicting the precursors and synthetic temperature could be one way.
Data availability
All data and the code needed to reproduce the results and methods in this study are present in our group Github repository (https://github.com/kaist-amsg/ElemwiseRetro).Author contributions
Seongmin Kim – conceptualization, data curation, methodology, formal analysis, software, validation, investigation, visualization, writing-original draft. Juhwan Noh – investigation, writing-review & editing. Geun Ho Gu – investigation, writing-review & editing. Shuan Chen – investigation, writing-review & editing. Yousung Jung – supervision, funding acquisition, resources, writing-review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Institute of Information & Communications Technology Planning & Evaluation (IITP) of Korea grant (2021-0-02068, 2021-0-01343), National Research Foundation (NRF) of Korea grant (2019M3D1A1079303, RS-2023-00283902), and the LG Energy Solution-KAIST Frontier Research Laboratory (2021).Notes and references
- J. N. Reimers and J. Dahn, J. Electrochem. Soc., 1992, 139, 2091 CrossRef CAS.
- A. Manthiram, J. C. Knight, S. T. Myung, S. M. Oh and Y. K. Sun, Adv. Energy Mater., 2016, 6, 1501010 CrossRef.
- K. Mizushima, P. Jones, P. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- Y. Sun, C. Liu, D. C. Grauer, J. Yano, J. R. Long, P. Yang and C. J. Chang, J. Am. Chem. Soc., 2013, 135, 17699–17702 CrossRef CAS PubMed.
- J.-P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Science, 2017, 358, 739–744 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- T. Mueller, G. Hautier, A. Jain and G. Ceder, Chem. Mater., 2011, 23, 3854–3862 CrossRef CAS.
- G. Hautier, A. Jain, S. P. Ong, B. Kang, C. Moore, R. Doe and G. Ceder, Chem. Mater., 2011, 23, 3495–3508 CrossRef CAS.
- A. E. Fedorovskiy, N. A. Drigo and M. K. Nazeeruddin, Small Methods, 2020, 4, 1900426 CrossRef CAS.
- B. Ouyang, J. Wang, T. He, C. J. Bartel, H. Huo, Y. Wang, V. Lacivita, H. Kim and G. Ceder, Nat. Commun., 2021, 12, 5752 CrossRef CAS PubMed.
- C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498 CrossRef CAS.
- A. K. Singh, J. H. Montoya, J. M. Gregoire and K. A. Persson, Nat. Commun., 2019, 10, 443 CrossRef CAS PubMed.
- M. Aykol, S. S. Dwaraknath, W. Sun and K. A. Persson, Sci. Adv., 2018, 4, eaaq0148 CrossRef PubMed.
- C. J. Bartel, A. W. Weimer, S. Lany, C. B. Musgrave and A. M. Holder, npj Comput. Mater., 2019, 5, 4 CrossRef.
- W. Li, R. Jacobs and D. Morgan, Comput. Mater. Sci., 2018, 150, 454–463 CrossRef CAS.
- C. J. Bartel, A. Trewartha, Q. Wang, A. Dunn, A. Jain and G. Ceder, npj Comput. Mater., 2020, 6, 97 CrossRef.
- G. G. Peterson and J. Brgoch, J. Phys.: Energy, 2021, 3, 022002 CAS.
- J. Jang, G. H. Gu, J. Noh, J. Kim and Y. Jung, J. Am. Chem. Soc., 2020, 142, 18836–18843 CrossRef CAS PubMed.
- A. Davariashtiyani, Z. Kadkhodaie and S. Kadkhodaei, Commun. Mater., 2021, 2, 115 CrossRef.
- R. Zhu, S. I. P. Tian, Z. Ren, J. Li, T. Buonassisi and K. Hippalgaonkar, ACS Omega, 2023, 8, 8210–8218 CrossRef CAS PubMed.
- E. R. Antoniuk, G. Cheon, G. Wang, D. Bernstein, W. Cai and E. J. Reed, npj Comput. Mater., 2023, 9, 155 CrossRef.
- M. J. McDermott, S. S. Dwaraknath and K. A. Persson, Nat. Commun., 2021, 12, 3097 CrossRef CAS PubMed.
- M. Aykol, J. H. Montoya and J. Hummelshøj, J. Am. Chem. Soc., 2021, 143, 9244–9259 CrossRef CAS PubMed.
- E. Kim, K. Huang, S. Jegelka and E. Olivetti, npj Comput. Mater., 2017, 3, 53 CrossRef.
- C. Karpovich, Z. Jensen, V. Venugopal and E. Olivetti, arXiv, 2021, preprint, arXiv:2112.09612, DOI:10.48550/arXiv.2112.09612.
- H. Huo, C. J. Bartel, T. He, A. Trewartha, A. Dunn, B. Ouyang, A. Jain and G. Ceder, Chem. Mater., 2022, 34, 7323–7336 CrossRef CAS PubMed.
- E. Kim, Z. Jensen, A. van Grootel, K. Huang, M. Staib, S. Mysore, H.-S. Chang, E. Strubell, A. McCallum and S. Jegelka, J. Chem. Inf. Model., 2020, 60, 1194–1201 CrossRef CAS PubMed.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- B. Liu, B. Ramsundar, P. Kawthekar, J. Shi, J. Gomes, Q. Luu Nguyen, S. Ho, J. Sloane, P. Wender and V. Pande, ACS Cent. Sci., 2017, 3, 1103–1113 CrossRef CAS PubMed.
- K. Lin, Y. Xu, J. Pei and L. Lai, Chem. Sci., 2020, 11, 3355–3364 RSC.
- H. Dai, C. Li, C. Coley, B. Dai and L. Song, Advances in Neural Information Processing Systems, 2019, vol. 32 Search PubMed.
- S. Chen and Y. Jung, JACS Au, 2021, 1, 1612–1620 CrossRef CAS PubMed.
- O. Kononova, H. Huo, T. He, Z. Rong, T. Botari, W. Sun, V. Tshitoyan and G. Ceder, Sci. Data, 2019, 6, 203 CrossRef PubMed.
- W. Beker, R. Roszak, A. Wołos, N. H. Angello, V. Rathore, M. D. Burke and B. A. Grzybowski, J. Am. Chem. Soc., 2022, 144, 4819–4827 CrossRef CAS PubMed.
- R. E. Goodall and A. A. Lee, Nat. Commun., 2020, 11, 6280 CrossRef CAS PubMed.
- D. Jha, L. Ward, A. Paul, W.-k. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593 CrossRef PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural message passing for quantum chemistry, in International Conference on Machine Learning, PMLR, 2017, pp. 1263–1272 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Data distribution, ablation study, and the details of the computational methods. See DOI: https://doi.org/10.1039/d3sc03538g |
| This journal is © The Royal Society of Chemistry 2024 |