Open Access Article
Open Access ArticleMechanistic insights into radical formation and functionalization in copper/N-fluorobenzenesulfonimide radical-relay reactions†
Mukunda
Mandal‡
 *ab,
Joshua A.
Buss‡§
*ab,
Joshua A.
Buss‡§
 c,
Si-Jie
Chen¶
c,
Si-Jie
Chen¶
 c,
Christopher J.
Cramer||
c,
Christopher J.
Cramer||
 a and
Shannon S.
Stahl
a and
Shannon S.
Stahl
 *c
*c
aDepartment of Chemistry, Chemical Theory Center, and Supercomputing Institute, University of Minnesota, 207 Pleasant Street SE, Minneapolis, MN 55455, USA
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: mukunda.chem@gmail.com
cDepartment of Chemistry, University of Wisconsin–Madison, 1101 University Avenue, Madison, WI 53706, USA. E-mail: stahl@chem.wisc.edu
First published on 12th December 2023
Abstract
Copper-catalysed radical-relay reactions that employ N-fluorobenzenesulfonimide (NFSI) as the oxidant have emerged as highly effective methods for C(sp3)–H functionalization. Herein, computational studies are paired with experimental data to investigate a series of key mechanistic features of these reactions, with a focus on issues related to site-selectivity, enantioselectivity, and C–H substrate scope. (1) The full reaction energetics of enantioselective benzylic C–H cyanation are probed, and an adduct between Cu and the N-sulfonimidyl radical (˙NSI) is implicated as the species that promotes hydrogen-atom transfer (HAT) from the C–H substrate. (2) Benzylic versus 3° C–H site-selectivity is compared with different HAT reagents: Cu/˙NSI, ˙OtBu, and Cl˙, and the data provide insights into the high selectivity for benzylic C–H bonds in Cu/NFSI-catalyzed C–H functionalization reactions. (3) The energetics of three radical functionalization pathways are compared, including radical–polar crossover (RPC) to generate a carbocation intermediate, reductive elimination from a formal CuIII organometallic complex, and radical addition to a Cu-bound ligand. The preferred mechanism is shown to depend on the ligands bound to copper. (4) Finally, the energetics of three different pathways that convert benzylic C–H bonds into benzylic cations are compared, including HAT/ET (ET = electron transfer), relevant to the RPC mechanism with Cu/NFSI; hydride transfer, involved in reactions with high-potential quinones; and sequential ET/PT/ET (PT = proton transfer), involved in catalytic photoredox reactions. Collectively, the results provide mechanistic insights that establish a foundation for further advances in radical-relay C–H functionalization reactions.
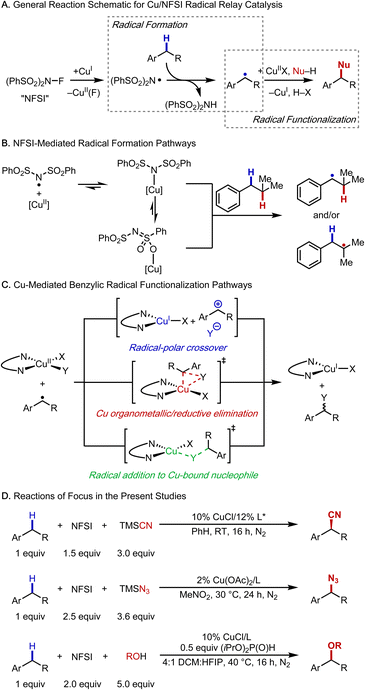
Introduction
Methods for selective functionalization of C–H bonds are highly appealing in organic synthesis as they enable streamlined preparation of complex molecules, including pharmaceuticals and agrochemicals.1–4 Copper-catalyzed radical-relay reactions are emerging as particularly effective methods for C–H functionalization and cross coupling.5,6 These methods conceptually build on reactions reported by Kharasch and Sosnovsky in the 1950s7,8 and later mechanistic studies,9 which introduced a strategy to generate carbon-centered radicals via hydrogen-atom transfer (HAT) and functionalization of the radicals with a CuII species. The Kharasch–Sosnovsky reactions employed peroxide-based oxidants, and subsequent adaptations of these reactions have been used to achieve selective functionalization of benzylic C–H bonds to afford new C–O,10,11 C–N,12,13 C–C,14 and C–F15 bonds. Analogous reactions, in which the peroxide oxidant is replaced by N-fluorobenzenesulfonimide (NFSI), proceed with high C–H site-selectivity, exhibit broad substrate scope, and use the C–H substrate as the limiting reagent (Fig. 1A).16–28Cu catalysts and NFSI appear to be privileged partners in radical-relay reactions with benzylic C–H bonds; however, important mechanistic questions remain unresolved, especially those related to the formation and functionalization of the organic radical. HAT is typically postulated to involve a free N-centered radical (cf.Fig. 1A), but alternative reactive species have been recently proposed in which an N-centered radical is coordinated to Cu (Fig. 1B).21 Understanding the nature of the active HAT mediator is important because this species directly influences reaction selectivity.
At least three different pathways have been proposed for functionalization of the organic radical to afford the product (Fig. 1C). These include (1) oxidation of the benzylic radical by CuII to form a benzylic cation, which can then react with an inner- or outer-sphere nucleophile, corresponding to a radical–polar crossover (RPC) mechanism; (2) radical addition to CuII, affording a benzylcopper(III) organometallic complex, followed by reductive elimination; and (3) a direct radical addition to a copper-bound nucleophile. Distinguishing among these reaction pathways has implications for enantioselectivity, which has been demonstrated in some cases,17–19,25 but not in others.22,27–30
The present study combines experimental and density functional theory (DFT) investigations to gain insight into the mechanistic features of three Cu/NFSI-mediated benzylic C–H functionalization reactions: cyanation, azidation and methoxylation (Fig. 1D). The complete reaction energetics for enantioselective benzylic cyanation are evaluated, with a focus on the benzylic radical formation and functionalization steps. We find that the N-centered sulfonimidyl radical (˙NSI) forms a thermodynamically favorable adduct with copper(II) that can promote HAT from the benzylic C–H bond. The regioselectivity of HAT by this Cu/˙NSI adduct is compared with that of ˙OtBu, and ˙Cl, species proposed to serve as the HAT reagent in other C–H functionalization methods. Comparison of experimental and computational data with these three reagents illuminates the unique benzylic site-selectivity evident in Cu/NFSI-mediated reactions. Attention is then given to the radical functionalization step, and the data show that the preferred pathway depends on the identity of the copper species. The nature of the nucleophile and ancillary ligands coordinated to CuII dictate whether the radical reacts via an inner-sphere or an outer-sphere electron-transfer (ET) pathway. The study concludes by comparing radical-relay reactions that involve a radical–polar crossover mechanism (i.e., HAT/ET) with other reactions that feature benzylic cation intermediates: hydride transfer (H−T) initiated by 2,3-dichloro-5,6-dicyanobenzoquinone (DDQ)31 and a multi-step photoredox-initiated pathway involving ET, proton-transfer (PT), and a second ET step (i.e., ET/PT/ET).32 The data here rationalize why the HAT/ET sequence in the corresponding radical-relay reactions exhibit broader C–H substrate scope relative to reactions involving H−T or ET/PT/ET pathways. Collectively, the results of this study provide a foundation for understanding previously reported reactions and guiding the development of new C–H functionalization methods.
Computational details
All calculations are done employing density functional theory (DFT) as implemented in the Gaussian 16 (Rev. B.01) electronic structure program.50 The hybrid meta-GGA density functional M06 was consistently used throughout the manuscript for our calculations, as it has been successfully applied in a closely related system21 and has demonstrated reliability in modelling copper-based molecular systems in general.40a,51 Geometry optimization and frequency calculations are done at the M06-D3(0)/basis-I level of theory,33,34 where basis-I refers to Ahlrichs' all-electron def2-SVPD basis for all atoms except for the C and H atoms, for which the def2-SVP basis was used.36 In all cases, an “ultrafine” grid was used for numerical integration in DFT. The natures of all stationary points are verified by calculating quasi-harmonic vibrational frequencies at the same level of theory. Low-frequency vibrational modes below 50 cm−1 are replaced with a value of 50 cm−1. For a more accurate estimation of Gibbs free energies (G), single-point electronic energies were re-calculated at the M06-D3(0)/basis-I geometries employing the same DFT functional but using a larger basis set: the def2-TZVPD basis for all atoms except for the C and H atoms, in which case the def2-TZVP basis was used (referred to as basis-II), and employing the SMD continuum solvation model35 with solvent parameters for dichloromethane (DCM). This electronic energy, calculated at the M06-D3(0)/basis-II/SMD(DCM) level, was added to thermal contributions to G calculated at the M06-D3(0)/basis-I level to obtain final G values. To account for the standard-state concentration change from 1 atm pressure in the gas phase to 1 M in the solution phase, an entropy “correction” term of 1.89 kcal mol−1 was added to the absolute free energies of all computed species. A more detailed discussion regarding this is provided in Section 3 of the ESI.†For the transition state (TS) structures involving crossing of potential energy surfaces (PES) of different spin multiplicity, e.g., the case of direct transformation of biradical CuII and the benzyl radical Ar(˙) into singlet CuI and Ar–X, TSs were located on the broken-symmetry (BS) singlet PES, and the approximate spin-projection scheme of Yamaguchi et al.52 was used for obtaining approximate spin-projected electronic energies of the lower-spin states using eqn (1).
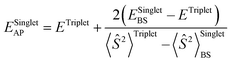 | (1) |
The intrinsic bond orbital (IBO) scheme39 was used for orbital localization to unravel the mechanistic details of the turnover-limiting hydrogen-atom abstraction step. In this case, wavefunctions at each point along the intrinsic reaction coordinate were obtained at the M06-D3(0)/basis-I level using ORCA 5.0.3. program,53 and these wavefunctions were then localized to produce the IBOs using the IboView program54 setting “iboexp = 2”.
Results and discussion
Computational analysis of Cu/NFSI-mediated benzylic cyanation
In a recent report, the Liu and Stahl groups disclosed a benzylic cyanation reaction that overcame several historical limitations associated with radical-relay reactions.17 The reaction employed limiting C–H substrates under mild conditions to afford benzylic cyanation products in high yields and with excellent enantioselectivities across a wide range of substrates, spanning simple building blocks to complex molecules. Preliminary computational analysis was conducted in this work,17 focusing on the steps associated with functionalization of the radical. Other steps of the reaction were not evaluated. Here, we expand the computational analysis to probe the full reaction energetics (Fig. 2) using DFT at the M06-D3(0)33,34/basis-II/SMD(CH2Cl2)35//M06-D3(0)/basis-I level of theory (see the Computational details section for basis-I and basis-II details). Computations were conducted using a bis(oxazoline)-bound copper(I) chloride pre-catalyst LCuI(Cl), which has been used in each of the three reactions examined in this study (Fig. 1D).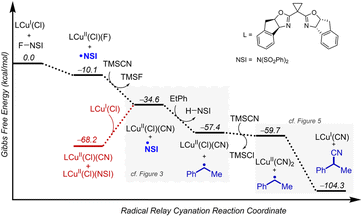 | ||
| Fig. 2 Full reaction thermodynamics for Cu/NFSI-catalysed benzylic cyanation. Gibbs free energies (kcal mol−1) are computed at M06-D3(0)/basis-II/SMD(CH2Cl2)//M06-D3(0)/basis-I level of theory. | ||
The reaction of NFSI with LCuI(Cl) is favourable both kinetically22,37 and thermodynamically (reaction free energy, ΔG° = −10.1 kcal mol−1, Fig. 2) and affords LCuII(Cl)(F) and the sulfonimidyl radical (˙NSI; Fig. 2).15,21,22 TMSCN (TMS = trimethylsilyl), employed as the cyanide source in the catalytic reactions, undergoes ligand exchange with LCuII(Cl)(F) to form LCuII(Cl)(CN) in a highly exergonic process (ΔG° = −24.5 kcal mol−1) that is driven by the formation of TMSF, with a strong Si–F bond.38 Another equivalent of TMSCN can react with LCuII(Cl)(CN) to replace the chloride with another cyanide, generating LCuII(CN)2 in a moderately exergonic process (ΔG° = −2.3 kcal mol−1). Reaction between ˙NSI and a second equivalent of CuI exhibits high thermodynamic favorability, as shown in Fig. 2 (red). Consequently, the resulting species, LCuII(Cl)(NSI), is anticipated to be present in the reaction equilibrium. In line with this expectation, a structurally analogous L′CuII(Cl)(NSI) species has been successfully isolated and characterized using X-ray crystallography, where L′ represents a bathophenanthroline ligand (for detailed X-ray crystal structure information, refer to Section 2 of the ESI†). However, this reaction will halt productive reactivity by quenching the active radical and sequestering the copper as a CuII species that does not promote efficient activation of NFSI (Fig. 2, red).22 Alternatively, ˙NSI can promote HAT from the benzylic C–H substrate to afford a benzylic radical (ΔG° = −22.8 kcal mol−1). The benzylic radical reacts with LCuII(CN)2 to afford the benzylic nitrile in a highly favorable process (ΔG° = −44.6 kcal mol−1; reaction of the benzylic radical with LCuII(Cl)(CN) is also highly favorable to afford the same cyanation product: ΔG° = −40.2 kcal mol−1).
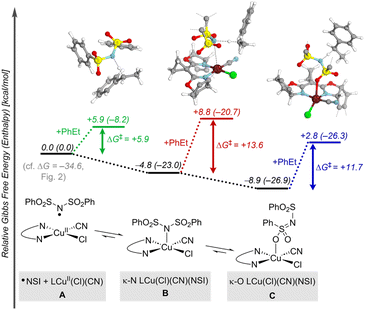
Formation of the benzylic radical is a crucial step in these reactions, prompting us to give further attention to the active species that promote HAT. In a complementary allylic cyanation reaction with a different N–F reagent, Liu and coworkers proposed that the N-centered radical coordinates to CuII.21 Similar behavior was identified here with ˙NSI, which can undergo favorable coordination to LCuII(Cl)(CN) through the sulfonimide nitrogen (κ-N isomer B, Fig. 3) or the sulfonyl oxygen atom (κ-O isomer C, Fig. 3). Both isomers form closed-shell Cu/NSI adducts (see ESI, Fig. S9† for structural details and Fig. S10† for spin–density plots of the spin-isomers), but the calculations indicate that generation of the κ-O isomer is thermodynamically more favorable 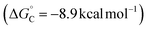 than the κ-N counterpart
than the κ-N counterpart  . The activation free energies (ΔG‡) for HAT from the 2° benzylic C–H bond in ethylbenzene were then computed for both of the isomeric Cu/NSI adducts as well as for free ˙NSI. Fig. 3 demonstrates that the HAT step involving free ˙NSI has a lower ΔG‡ (+5.9 kcal mol−1; green pathway) than the two Cu/NSI isomers (red and blue routes, with ΔG‡ = +13.6 and +11.7 kcal mol−1 for the κ-N and κ-O isomers, respectively). However, the greater stability of the κ-O Cu/NSI adduct dictates that this species will be the resting state, and it provides access to the lowest overall transition-state energy for HAT.
. The activation free energies (ΔG‡) for HAT from the 2° benzylic C–H bond in ethylbenzene were then computed for both of the isomeric Cu/NSI adducts as well as for free ˙NSI. Fig. 3 demonstrates that the HAT step involving free ˙NSI has a lower ΔG‡ (+5.9 kcal mol−1; green pathway) than the two Cu/NSI isomers (red and blue routes, with ΔG‡ = +13.6 and +11.7 kcal mol−1 for the κ-N and κ-O isomers, respectively). However, the greater stability of the κ-O Cu/NSI adduct dictates that this species will be the resting state, and it provides access to the lowest overall transition-state energy for HAT.
To gain a better understanding of the HAT mechanism with ˙NSI and the κ-O Cu/NSI adduct, the relevant intrinsic bond orbitals (IBOs) were analyzed. IBOs are a set of localized molecular orbitals that represent exact molecular wave functions.39 Analysis of the IBOs along the C–H reaction coordinate revealed that the HAT with free ˙NSI involves formal HAT between the carbon and nitrogen atoms, with synchronous transfer of electron and proton as a hydrogen atom. In contrast, the κ-O Cu/NSI species reacts via a proton-coupled electron transfer (PCET) pathway, whereby IBOs along the reaction coordinate reveal proton transfer to the proximal sulfonimide nitrogen and electron transfer from the alkylarene substrate to the lowest unoccupied molecular orbital (LUMO, dx2−y2) of Cu (for details, see Section 10 of the ESI†).40
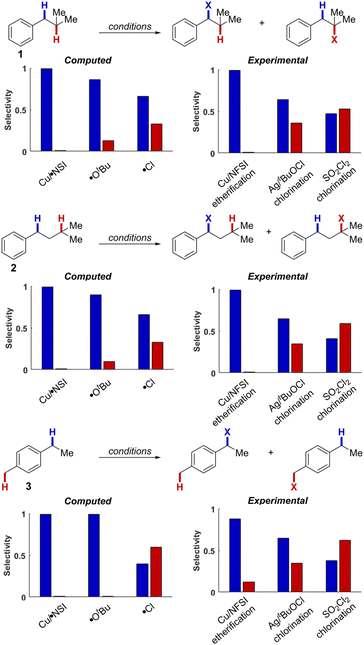
Experimental and computational comparison of HAT selectivities
Cu/NFSI-mediated C–H functionalization reactions appear to exhibit unique site-selectivity for benzylic C–H bonds. To gain insight into the reaction regioselectivity, we investigated HAT reactions of isobutylbenzene (1), isopentylbenzene (2) and 4-ethyltoluene (3) with κ-O Cu/NSI, tert-butoxyl radical (˙OtBu) and chlorine radical (˙Cl). Three synthetic methods in which these reactive species have been proposed as the HAT species include Cu/NFSI-catalyzed benzylic C–H methoxylation (κ-O Cu/NSI),22 Ag/tBuOCl-promoted C–H chlorination (˙OtBu),41 and SO2Cl2-mediated C–H chlorination (˙Cl).42The bond dissociation enthalpies (BDEs) of H–NSI, H–OtBu, and H–Cl were computed to be 107.0, 103.6 and 104.0 kcal mol−1, respectively, indicating that all three reactive species have a strong thermodynamic driving force for HAT from the relevant C–H bonds. Experimental data indicate that the substrate C–H BDEs are as follows:43 3° aliphatic C–H bonds in 1 and 2: 95.0 kcal mol−1, the 1° benzylic C–H bonds in 3: 90.0 kcal mol−1, and the 2° benzylic C–H bonds in all three substrates: 87 kcal mol−1. Computational BDEs for these substrates revealed similar values, with 2° benzylic C–H bonds generally showing lower values (85.2, 84.4, 83.5 kcal mol−1, for 1, 2, and 3 respectively; see ESI, Table S8†) compared to the 3° aliphatic (91.8 and 92.6 kcal mol−1, for 1 and 2, respectively) and the 1° benzylic C–H bonds (87.3 kcal mol−1, for 3). This distribution of C–H BDE values makes 1–3 an ideal set of compounds to interrogate site-selectivity.
We then evaluated the energy barriers for HAT (ΔG‡HAT) from the different C–H bonds in 1–3 to each of the reactive species: κ-O Cu/NSI, ˙OtBu, and ˙Cl (see Section 12 in the ESI† for calculated thermodynamic and activation energies for each of the different HAT reactions). The ΔG‡HAT values obtained with the κ-O Cu/NSI active species revealed that the activation energies for HAT from the 2° benzylic C–H bonds in 1 and 2 (ΔG‡b = 10.9 and 10.1 kcal mol−1, respectively; b = benzylic) are lower than those for the corresponding 3° aliphatic C–H bonds (ΔG‡a = 15.7 and 15.5 kcal mol−1; a = aliphatic). This preference for benzylic C–H activation (ΔΔG‡b–a ∼ 5 kcal mol−1 for the 2° benzylic and 3° aliphatic C–H sites) aligns with the experimental observation of excellent benzylic site-selectivity in the reactions of 1 and 2 with Cu/NFSI (Fig. 4). Reactions of ˙OtBu with 1 and 2 still favor HAT from the benzylic position but are calculated to be less selective, with ΔΔG‡b–a values of only 1.1 and 1.3 kcal mol−1 for 1 and 2, respectively. These energy differences correspond to 2° benzylic : 3° aliphatic C–H selectivities ranging from 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–9
1–9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In the reaction of 3, which contains 1° and 2° benzylic C–H bonds, both κ-O Cu/NSI and ˙OtBu are calculated to strongly favor reaction at the weaker 2° site (ΔΔG‡1°−2° ∼ 2.5 kcal mol−1). Reaction of the chlorine radical with both benzylic and 3° aliphatic sites is calculated to be barrierless,44 and selectivity with this species simply reflects the statistical ratio of the corresponding C–H bonds in 1, 2, and 3.
1. In the reaction of 3, which contains 1° and 2° benzylic C–H bonds, both κ-O Cu/NSI and ˙OtBu are calculated to strongly favor reaction at the weaker 2° site (ΔΔG‡1°−2° ∼ 2.5 kcal mol−1). Reaction of the chlorine radical with both benzylic and 3° aliphatic sites is calculated to be barrierless,44 and selectivity with this species simply reflects the statistical ratio of the corresponding C–H bonds in 1, 2, and 3.
These DFT results were benchmarked with experimental analyses of the same substrates 1–3, using the catalytic reaction systems proposed to involve the κ-O Cu/NSI,22 ˙OtBu,41 and ˙Cl42 as the reactive species (Fig. 4, right charts). Under the Cu/NFSI and SOCl2 reaction conditions, the experimental observations and computational predictions show strong agreement. Specifically, Cu/NFSI exhibits near-exclusive selectivity for reaction at the benzylic sites relative to the 3° aliphatic positions in 1 and 2 and high selectivity for 2° over 1° benzylic sites in 3. Meanwhile, both experimental and computational analysis of the reactions involving ˙Cl show poor selectivity with all three substrates, as significant reactivity is observed or predicted at both sites. Under the Ag/tBuOCl conditions, the observed selectivity in the reactions with 1–3 is lower than that predicted for ˙OtBu, suggesting that the tBuOCl oxidant may generate other competent HAT species, such as ˙Cl, in situ that erode the selectivity. Overall, these data highlight the excellent site-selectivity accessible with the Cu/NSI species, which may be attributed to the interplay of two effects. Steric factors arising from the Cu–NSI adduct should favor reactivity at the 2° benzylic over the 3° aliphatic sites (see Fig. S15 of the ESI† for a representative steric map plot). In addition, the attenuated reactivity of the ˙NSI radical upon binding to Cu lowers the thermodynamic driving force for HAT, resulting in a later transition state that is more sensitive to the stability of the carbon-centered radical being formed.
Analysis of radical functionalization pathways
In Cu/NFSI reactions, the carbon-centred radical generated via HAT is proposed to undergo functionalization by a CuII species. Three different radical-functionalization pathways have been considered in these reactions, as depicted in Fig. 1C: (1) radical–polar crossover (RPC) with subsequent trapping of the resulting carbocation by a nucleophile, (2) radical addition to copper and reductive elimination from an organometallic copper intermediate, and (3) direct addition of the radical to a copper-bound nucleophile. Computational modelling techniques were used to examine the dependence of the various reaction pathways on the Cu coordination environment.Experimental studies have shown that copper(I) and NFSI react rapidly in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, upon mixing in organic solvent.24 This reaction is expected to afford LCuII(Cl)(F) and LCuII(Cl)(NSI) as products (L = bis(oxazoline) ligand shown in Fig. 2), and these complexes served as the initial reference points for calculating the ligand-exchange energies shown in Fig. 5. The bis(sulfonimidyl) anion (NSI–) is expected to be a rather weakly coordinating ligand; however, an X-ray crystal structure of L′CuII(Cl)(NSI) (L′ = bathophenanthroline) was obtained during the course of this study (see Section 2 of the ESI† for details). Relative energies were compared for the different LCuII(X)(Y) species that are relevant to cyanation, azidation, and methoxylation reactions (X, Y = Cl, F, NSI, CN, N3, OMe; Fig. 5). A comprehensive tabulation of energies is provided in Table S5 of the ESI.†
1 stoichiometry, upon mixing in organic solvent.24 This reaction is expected to afford LCuII(Cl)(F) and LCuII(Cl)(NSI) as products (L = bis(oxazoline) ligand shown in Fig. 2), and these complexes served as the initial reference points for calculating the ligand-exchange energies shown in Fig. 5. The bis(sulfonimidyl) anion (NSI–) is expected to be a rather weakly coordinating ligand; however, an X-ray crystal structure of L′CuII(Cl)(NSI) (L′ = bathophenanthroline) was obtained during the course of this study (see Section 2 of the ESI† for details). Relative energies were compared for the different LCuII(X)(Y) species that are relevant to cyanation, azidation, and methoxylation reactions (X, Y = Cl, F, NSI, CN, N3, OMe; Fig. 5). A comprehensive tabulation of energies is provided in Table S5 of the ESI.†
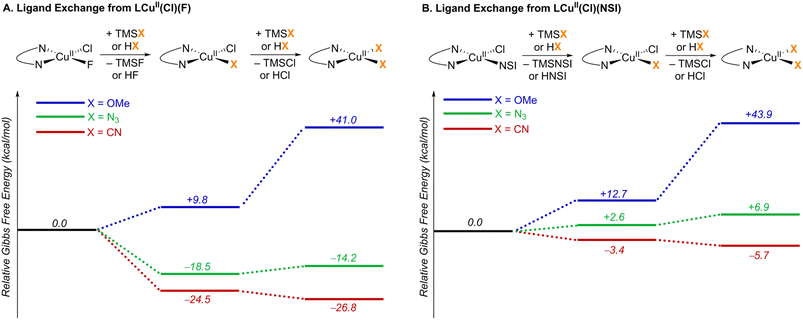 | ||
| Fig. 5 Ligand exchange thermodynamics starting from two key CuII resting states: (A) LCuII(Cl)(F) and (B) LCuII(Cl)(NSI). L = bis(oxazoline) ligand shown in Fig. 2. Gibbs free energies (kcal mol−1) are computed at 298.15 K at the M06-D3(0)/basis-II/SMD(CH2Cl2)//M06-D3(0)/basis-I level of theory. | ||
TMS-substituted nucleophiles undergo highly exergonic ligand exchange with the fluoride of LCuII(Cl)(F), affording copper chloride/cyanide and chloride/azide complexes and TMSF (first step in Fig. 5A). Subsequent exchange of the chloride ligand with an azide is unfavourable (ΔG° = +4.3 kcal mol−1), whereas exchange with a cyanide is favourable (ΔG° = −2.3 kcal mol−1). Cyanide also demonstrates favourable exchange with the anionic ligands in LCuII(Cl)(NSI) (ΔG° = −3.4 and −2.3 kcal mol−1 for exchange with NSI and Cl ligands, respectively), whereas azide exchange is endergonic with this complex (Fig. 5B). Formation of a Cu–OMe species from the reaction of MeOH with either of these reference compounds is calculated to be very unfavourable (ΔG° = +9.8 − +43.9 kcal mol−1), reflecting the weak basicity of the anionic ligands. Taken together, these results suggest that the most relevant CuII species for the different functionalization reactions consist of LCuII(CN)2 for cyanation, LCuII(Cl)(NSI) and LCuII(Cl)(N3) for azidation, and LCuII(Cl)(NSI) and LCuII(Cl)(F) for methoxylation.
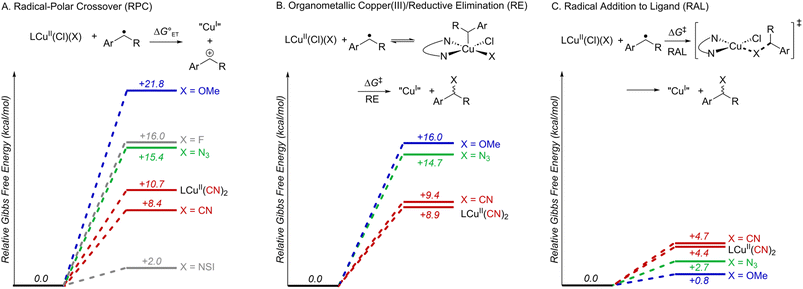
Subsequent calculations explored how the identity of the copper species influences the energetics of the different radical functionalization pathways (Fig. 6). RPC is initiated by one-electron oxidation of the benzylic radical by CuII to form a carbocation, which is then trapped by a nucleophile to afford a racemic coupling product. The energetics of electron transfer (ET) from the benzylic radical to the various LCuII(Cl)(X) species were calculated, and the reaction is endergonic in all cases (Fig. 6A; see Table S6 in the ESI†),45 albeit only slightly uphill with LCuII(Cl)(NSI)  , a CuII species expected to be present in the azidation and methoxylation reactions (cf.Fig. 5). Coordination of CN, N3, and OMe nucleophiles to CuII in place of NSI lowers the CuII/I redox potential relative to LCuII(Cl)(NSI) and increases the energy of ET, with
, a CuII species expected to be present in the azidation and methoxylation reactions (cf.Fig. 5). Coordination of CN, N3, and OMe nucleophiles to CuII in place of NSI lowers the CuII/I redox potential relative to LCuII(Cl)(NSI) and increases the energy of ET, with  values ranging from +8.4 to +21.8 kcal mol−1.
values ranging from +8.4 to +21.8 kcal mol−1.
Alternatively, the benzylic radical could react with the CuII species via addition, either at the CuII center (Fig. 6B) or at the coordinated ligand (Fig. 6C). Addition of the benzylic radical to the metal center is followed by rate-limiting reductive elimination (RE) to afford the coupling product. The computed activation free energies for the RE step reveal that the barriers are the lowest for the CN complexes (+8.9 − +9.4 kcal mol−1), followed by N3 (+14.7 kcal mol−1) and OMe complexes (+16.0 kcal mol−1) (Fig. 6B). In contrast, the energy barriers for radical addition to a Cu-bound ligand (RAL) in LCuII(Cl)(X) complexes are significantly lower and exhibit the opposite relative order: X = OMe (ΔG‡RAL = +0.8 kcal mol−1), N3 (ΔG‡RAL = +2.7 kcal mol−1), and CN (ΔG‡RAL = +4.4 − +4.7 kcal mol−1) (Fig. 6C). The ditopic nature of the azide ligand complicates direct comparisons, since prior work has raised the possibility of both terminal and bridging Cu–azide complexes and radical addition to the proximal and distal N atom of the azide.46 The favored pathway for the azide RAL pathway presented here corresponds to radical addition to the proximal N-atom (i.e., coordinated to Cu), which resembles addition to the CN and OMe ligands.
The combined data from Fig. 5 and 6 allow a comparison of the inner- versus outer-sphere pathways for each of the different nucleophiles (Fig. 7). Favourable coordination of cyanide to copper generates CuII–CN species that are less oxidizing than LCuII(Cl)(NSI) and support low-barrier inner-sphere pathways. The favoured pathway involves addition of a benzylic radical to the cyanide of the LCuII(CN)2 species (Fig. 7A). The initial report on this reactivity17 proposed radical addition to Cu followed by reductive elimination, which also has a relatively low barrier (ΔG‡RE = +8.9 kcal mol−1). Both the RAL and RE mechanisms position the benzylic radical in close proximity to the chiral Cu centre and rationalize the high enantioselectivity observed experimentally (see Fig. S17 in the ESI† for a comparison between computed activation barriers for R- and S-isomers in RE and RAL pathways during cyanation of ethylbenzene). The less favourable coordination of azide and methoxide nucleophiles to CuII, relative to cyanide (cf.Fig. 5) will contribute to the presence of LCuII(Cl)(NSI) in the azidation and methoxylation reaction mixtures. This relatively strong oxidant lowers the energy for electron transfer from the benzylic radical and favors the RPC pathway with N3 and OMe nucleophiles (Fig. 7B and C). This conclusion is consistent with experimental data for these reactions, which generate racemic products, even when using chiral ligands.
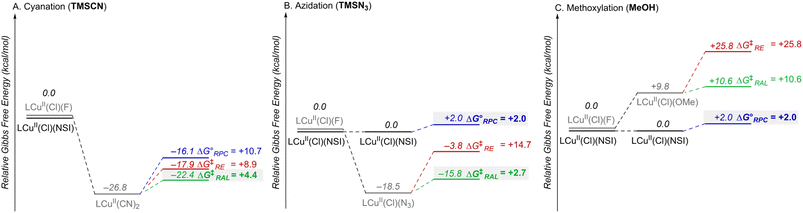 | ||
| Fig. 7 Combination of the data in Fig. 5 and 6, showing the relative Gibbs free energies (kcal mol−1) for the different CuII species and the mechanistic pathways (RPC, RE, RAL) for each of the three radical functionalization reactions, cyanation (A), azidation (B), and methoxylation (C). The RPC, RE and RAL pathways are depicted in blue, red, and green, respectively. | ||
Comparing different pathways for benzylic cation formation
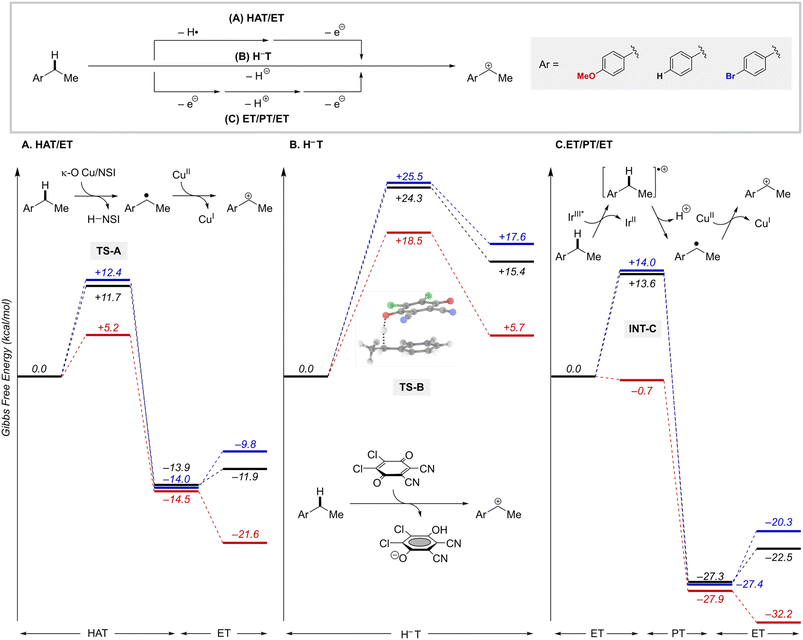
The likely participation of the RPC pathway in some of these reactions highlights a relationship between these radical-relay reactions and other benzylic C–H functionalization reactions that proceed through benzylic cation intermediates. In the present reactions, the RPC mechanism arises from an HAT/ET sequence. Alternative pathways to access benzylic cations include concerted hydride transfer (H−T), as in reactions with DDQ or other high-potential quinones,31 or sequential ET/PT/ET, such as those involved in some photoredox reactions.32 Results from these different approaches suggest that the HAT/ET reactions tolerate a wider range of benzylic substrates, not limited to those bearing electron-donating substituents. We sought to gain insights into this behaviour.Computational studies were conducted to analyse the energetics of representative HAT/ET, H−T, and ET/PT/ET reaction pathways using three different ethylbenzene derivatives, with –OMe, –H, and –Br groups as para substituents (Fig. 8). Analysis of the HAT step shows that the thermodynamics of HAT by the Cu/NSI species are highly favourable for all three substrates and largely unaffected by the para substituents (Fig. 8A). The kinetic barriers for the HAT steps are relatively low (ΔG‡ = +5.2 − +12.4 kcal mol−1) and show some electronic differentiation, with the lowest barrier evident for the electron-rich p-MeO derivative (TS-A, Fig. 8A): ΔΔG‡OMe/X = 6.5 and 7.2 kcal mol−1, for the p-H and p-Br derivatives, respectively. Subsequent oxidation of the radical intermediates to the corresponding cations by LCuII(Cl)(NSI) is affected by the para substitution of the substrate, although the impact of this sensitivity on reactivity is minimal because these ET steps are energetically less-demanding compared to the rate-limiting HAT steps. These observations explain why an HAT/ET method can accommodate a broad range of benzylic substrates. Trapping of the cations by the different nucleophiles to afford the coupling product is very exergonic in all cases (by >35 kcal mol−1; Fig. S20†). Hydride transfer (H−T) was investigated for the same series of ethylbenzene derivatives, using DDQ as the hydride acceptor.47,48 The concerted H−T steps to form the three carbocations show large kinetic barriers (Fig. 8B; TS-B, ΔG‡ = +18.5 − +25.5 kcal mol−1) compared to the HAT steps depicted in Fig. 8A. Moreover, formation of the cations is calculated to be endergonic (ΔG° = +5.7 − +17.6 kcal mol−1), contrasting the energetically favorable HAT step. These features are consistent with experimental data showing that synthetically useful reactions with DDQ are mostly limited to electron-rich substrates.31
Finally, we analysed a photoredox method for benzylic C–H methoxylation reaction that uses an Ir-based photoredox catalyst ([Ir(dF(CF3)ppy)2(5,5′-dCF3bpy)]PF6; see Fig. S18†) and proceeds via an ET/PT/ET sequence (Fig. 8C).32 Similar to the DDQ-promoted reactions, this method is primarily effective with electron-rich alkylarenes, such as those bearing p-OMe substituents. One-electron oxidation of the ethylbenzene derivatives considered here by triplet IrIII complex (IrIII*) yields the arene radical cation INT-C. For the p-OMe ethylbenzene derivative, this process is slightly exergonic 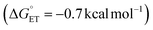 . The favourable nature of this initial ET step is expected to facilitate progression through the subsequent PT/ET steps, which are also exergonic for the p-OMe derivative. In contrast, ET from the p-H and p-Br substrates by the same IrIII* oxidant is thermodynamically unfavourable (ΔG° = +13.6 and 14.0 kcal mol−1, respectively), suggesting that back-electron transfer from the reduced Ir complex to the radical cation could compete with deprotonation of the radical cation and hinder progression through the subsequent steps.
. The favourable nature of this initial ET step is expected to facilitate progression through the subsequent PT/ET steps, which are also exergonic for the p-OMe derivative. In contrast, ET from the p-H and p-Br substrates by the same IrIII* oxidant is thermodynamically unfavourable (ΔG° = +13.6 and 14.0 kcal mol−1, respectively), suggesting that back-electron transfer from the reduced Ir complex to the radical cation could compete with deprotonation of the radical cation and hinder progression through the subsequent steps.
Overall, this analysis highlights important distinctions between benzylic C–H functionalization reactions that proceed via an HAT/ET pathway relative to those involving H−T or ET/PT/ET pathways. The ability of HAT/ET methods to tolerate substrates spanning electron-rich to electron-deficient derivatives is not limited to the Cu/NFSI reactions evaluated here. Similar behavior is evident in a number of HAT-initiated photochemical reactions that proceed via an RPC pathway.49 By comparison, H−T and ET/PT/ET tend to show high selectivity for electron-rich substrates. This feature can be an advantage or disadvantage depending on the application.
Conclusions
The computational and experimental studies outlined herein clarify a series of important mechanistic features of Cu/NFSI-catalyzed benzylic C–H functionalization reactions, emphasizing the generation and functionalization of organic radicals. Full reaction coordinate analysis of benzylic C–H cyanation included an assessment of different HAT species that could react with benzylic C–H bonds. Analysis of these structures implicates a κ-O Cu/NSI adduct as the relevant HAT species and comparison of experimental data with a panel of different substrates across various HAT-mediated C–H functionalization methods highlight the unique benzylic site-selectivity accessed by Cu/NFSI relative to methods proposed to involve ˙OtBu and ˙Cl as the HAT reagent. The energetics of three different CuII-mediated radical functionalization pathways reveal that the preferred pathway can differ depending on the identity of the CuII species in the reaction mixture. For example, cyanide is a good ligand for CuII and lowers the CuII/I redox potential, disfavoring one-electron oxidation of the radical while supporting radical addition to the cyanide ligand of the CuII–CN intermediate. This inner-sphere radical-functionalization mechanism rationalizes the ability to achieve enantioselective cyanation of benzylic C–H bonds. For less coordinating azide and methoxide ligands, the data suggest that the oxidizing intermediate LCuII(Cl)(NSI) will be present in the reaction manifold and that this species can promote outer-sphere oxidation of benzylic radicals to generate benzylic cations. This radical–polar crossover pathway involving stepwise HAT/ET has been compared to two alternative C–H functionalization mechanisms that generate benzylic cation intermediates, H−T and ET/PT/ET. The results rationalize why the HAT/ET sequence accesses a broader C–H substrate scope relative to the other methods. Thus, while the radical–polar crossover mechanism is not compatible with enantioselective bond formation, the HAT/ET sequence presents an advantageous strategy to access reactive benzylic cations. The collective insights gained from this study provide a valuable foundation for future studies, targeting unmet challenges, such as expanding the scope of enantioselective transformation, achieving site-selective functionalization of less-activated C–H bonds, and diversifying reactivity to include heterobenzylic C–H sites.Data availability
The data supporting this article have been included as part of the ESI,† including, experimental selectivity studies, energies of all computed structures, IBO transformations in PDF format, and Cartesian coordinates of DFT-calculated structures in XYZ format. Crystallographic data for compounds have been deposited at the Cambridge Crystallographic Data Centre (CCDC) under access number 2239614.Author contributions
M. M. and J. A. B. contributed equally to this work. The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Amelia Wheaton for assistance with X-ray crystallography, and Austin Bleskacek for help with editing the manuscript. Funding for this work was provided by the NIH (R35 GM134929 to S. S. S), a Ruth L. Kirschstein NRSA fellowship to J. A. B. (F32 GM129909), a doctoral dissertation fellowship from the University of Minnesota (M. M.), and postdoctoral support from the Alexander von Humboldt Foundation (M. M). Spectroscopic instrumentation was partially supported by the NIH (S10 OD020022) and the NSF (CHE-1048642).Notes and references
- K. R. Campos, P. J. Coleman, J. C. Alvarez, S. D. Dreher, R. M. Garbaccio, N. K. Terrett, R. D. Tillyer, M. D. Truppo and E. R. Parmee, Science, 2019, 363, eaat0805 CrossRef CAS PubMed.
- T. Cernak, K. D. Dykstra, S. Tyagarajan, P. Vachal and S. W. Krska, Chem. Soc. Rev., 2016, 45, 546–576 RSC.
- D. C. Blakemore, L. Castro, I. Churcher, D. C. Rees, A. W. Thomas, D. M. Wilson and A. Wood, Nat. Chem., 2018, 10, 383–394 CrossRef CAS PubMed.
- J. Wencel-Delord and F. Glorius, Nat. Chem., 2013, 5, 369–375 CrossRef CAS PubMed.
- D. L. Golden, S.-E. Suh and S. S. Stahl, Nat. Rev. Chem, 2022, 6, 405–427 CrossRef CAS PubMed.
- Z. Zhang, P. Chen and G. Liu, Chem. Soc. Rev., 2022, 51, 1640–1658 RSC.
- M. Kharasch and A. Fono, J. Org. Chem., 1958, 23, 325–326 CrossRef CAS.
- M. S. Kharasch and G. Sosnovsky, J. Am. Chem. Soc., 1958, 80, 756 CrossRef CAS.
- J. K. Kochi, J. Am. Chem. Soc., 1962, 84, 774–784 CrossRef CAS.
- R. T. Gephart, C. L. McMullin, N. G. Sapiezynski, E. S. Jang, M. J. Aguila, T. R. Cundari and T. H. Warren, J. Am. Chem. Soc., 2012, 134, 17350–17353 CrossRef CAS PubMed.
- B. L. Tran, M. Driess and J. F. Hartwig, J. Am. Chem. Soc., 2014, 136, 17292–17301 CrossRef CAS PubMed.
- E. S. Jang, C. L. McMullin, M. Käβ, K. Meyer, T. R. Cundari and T. H. Warren, J. Am. Chem. Soc., 2014, 136, 10930–10940 CrossRef CAS PubMed.
- B. L. Tran, B. Li, M. Driess and J. F. Hartwig, J. Am. Chem. Soc., 2014, 136, 2555–2563 CrossRef CAS PubMed.
- A. Vasilopoulos, S. L. Zultanski and S. S. Stahl, J. Am. Chem. Soc., 2017, 139, 7705–7708 CrossRef CAS PubMed.
- For related studies on C–H fluorination, see: (a) C. R. Pitts, S. Bloom, R. Woltornist, D. J. Auvenshine, L. R. Ryzhkov, M. A. Siegler and T. Lectka, J. Am. Chem. Soc., 2014, 136, 9780–9791 CrossRef CAS PubMed; (b) C. R. Pitts, B. Ling, J. A. Snyder, A. E. Bragg and T. Lectka, J. Am. Chem. Soc., 2016, 138, 6598–6609 CrossRef CAS PubMed; (c) J. B. Roque, R. Sarpong and D. G. Musaev, J. Am. Chem. Soc., 2021, 143, 3889–3900 CrossRef CAS PubMed; (d) Z. Liu, H. Chen, Y. Lv, X. Tan, H. Shen, H.-Z. Yu and C. Li, J. Am. Chem. Soc., 2018, 140, 6169–6175 CrossRef CAS PubMed.
- Z. Ni, Q. Zhang, T. Xiong, Y. Zheng, Y. Li, H. Zhang, J. Zhang and Q. Liu, Angew. Chem., Int. Ed., 2011, 51, 1244–1247 CrossRef PubMed.
- W. Zhang, F. Wang, S. D. McCann, D. Wang, P. Chen, S. S. Stahl and G. Liu, Science, 2016, 353, 1014–1018 CrossRef CAS PubMed.
- W. Zhang, P. Chen and G. Liu, J. Am. Chem. Soc., 2017, 139, 7709–7712 CrossRef CAS PubMed.
- W. Zhang, L. Wu, P. Chen and G. Liu, Angew. Chem., Int. Ed., 2019, 58, 6425–6429 CrossRef CAS PubMed.
- H. Xiao, Z. Liu, H. Shen, B. Zhang, L. Zhu and C. Li, Chem, 2019, 5, 940–949 CAS.
- J. Li, Z. Zhang, L. Wu, W. Zhang, P. Chen, Z. Lin and G. Liu, Nature, 2019, 574, 516–521 CrossRef CAS PubMed.
- H. Hu, S.-J. Chen, M. Mandal, S. M. Pratik, J. A. Buss, S. W. Krska, C. J. Cramer and S. S. Stahl, Nat. Catal., 2020, 3, 358–367 CrossRef CAS PubMed.
- A. Vasilopoulos, D. L. Golden, J. A. Buss and S. S. Stahl, Org. Lett., 2020, 22, 5753–5757 CrossRef CAS PubMed.
- J. A. Buss, A. Vasilopoulos, D. L. Golden and S. S. Stahl, Org. Lett., 2020, 22, 5749–5752 CrossRef CAS PubMed.
- L. Fu, Z. Zhang, P. Chen, Z. Lin and G. Liu, J. Am. Chem. Soc., 2020, 142, 12493–12500 CrossRef CAS PubMed.
- S. Liu, R. Achou, C. Boulanger, G. Pawar, N. Kumar, J. Lusseau, F. Robert and Y. Landais, Chem. Commun., 2020, 56, 13013–13016 RSC.
- S.-E. Suh, L. E. Nkulu, S. Lin, S. W. Krska and S. S. Stahl, Chem. Sci., 2021, 12, 10380–10387 RSC.
- C. Jiang, P. Chen and G. Liu, CCS Chem., 2021, 3, 1884–1893 CrossRef CAS.
- S.-J. Chen, D. L. Golden, S. W. Krska and S. S. Stahl, J. Am. Chem. Soc., 2021, 143, 14438–14444 CrossRef CAS PubMed.
- M. A. Lopez, J. A. Buss and S. S. Stahl, Org. Lett., 2021, 24, 597–601 CrossRef PubMed.
- (a) C. Song, X. Dong, H. Yi, C.-W. Chiang and A. Lei, ACS Catal., 2018, 8, 2195–2199 CrossRef CAS; (b) C. A. Morales-Rivera, P. E. Floreancig and P. Liu, J. Am. Chem. Soc., 2017, 139, 17935–17944 CrossRef CAS PubMed.
- B. J. Lee, K. S. DeGlopper and T. P. Yoon, Angew. Chem., Int. Ed., 2019, 59, 197–202 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (b) B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- (a) H. Zhang, Y. Song, J. Zhao, J. Zhang and Q. Zhang, Angew. Chem., Int. Ed., 2014, 53, 11079 CrossRef CAS PubMed; (b) B. E. Haines, T. Kawakami, K. Kuwata, K. Murakami, K. Itami and D. G. Musaev, Chem. Sci., 2017, 8, 988–1001 RSC.
- Si–F BDE in TMS–F is ∼160.0 kcal mol−1; see, for instance, Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, FL, 1st edn, 2007, DOI:10.1201/9781420007282.
- (a) G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed; (b) J. E. Klein and G. Knizia, Angew. Chem., Int. Ed., 2018, 57, 11913–11917 CrossRef CAS PubMed.
- (a) M. Mandal, C. E. Elwell, C. J. Bouchey, T. J. Zerk, W. B. Tolman and C. J. Cramer, J. Am. Chem. Soc., 2019, 141, 17236–17244 CrossRef CAS PubMed; (b) C. E. Elwell, M. Mandal, C. J. Bouchey, L. Que, C. J. Cramer and W. B. Tolman, Inorg. Chem., 2019, 58, 15872–15879 CrossRef CAS PubMed; (c) M. Mandal, C. J. Cramer, D. G. Truhlar, J. Sauer and L. Gagliardi, ACS Catal., 2020, 10, 10051–10059 CrossRef CAS.
- J. Ozawa and M. Kanai, Org. Lett., 2017, 19, 1430–1433 CrossRef CAS PubMed.
- M. S. Kharasch and H. C. Brown, J. Am. Chem. Soc., 1939, 61, 2142–2150 CrossRef CAS.
- (a) E. N. Bess, R. J. DeLuca, D. J. Tindall, M. S. Oderinde, J. L. Roizen, J. Du Bois and M. S. Sigman, J. Am. Chem. Soc., 2014, 136, 5783–5789 CrossRef CAS PubMed; (b) E. N. Bess, D. M. Guptill, H. M. Davies and M. S. Sigman, Chem. Sci., 2015, 6, 3057–3062 RSC.
- (a) B. Giese and J. Meixner, Angew Chem. Int. Ed. Engl., 1979, 18, 154–155 CrossRef; (b) A. A. Scala, J. Chem. Educ., 2004, 81, 1661–1664 CrossRef CAS.
- We chose not to estimate electron transfer (ET) barriers due to uncertainties in calculating reorganization energies and other factors influencing ET rates, like solvent properties and the driving force for ET. Without precise estimates of these parameters, predicting ET rates with Marcus theory would be speculative. The thermodynamic change in the radical–polar crossover step serves as a lower bound for the ET barrier.
- S.-E. Suh, S.-J. Chen, M. Mandal, I. A. Guzei, C. J. Cramer and S. S. Stahl, J. Am. Chem. Soc., 2020, 142, 11388–11393 CrossRef CAS PubMed.
- D. J. Maloney, S. Chen and S. M. Hecht, Org. Lett., 2006, 8, 1925–1927 CrossRef CAS PubMed.
- L. M. Chapman, J. C. Beck, L. Wu and S. E. Reisman, J. Am. Chem. Soc., 2016, 138, 9803–9806 CrossRef CAS PubMed.
- (a) G. Pandey and R. Laha, Angew. Chem., Int. Ed., 2015, 54, 14875–14879 CrossRef CAS PubMed; (b) G.-X. Li, C. A. Morales-Rivera, F. Gao, Y. Wang, G. He, P. Liu and G. Chen, Chem. Sci., 2017, 8, 7180–7185 RSC; (c) I. N.-M. Leibler, M. A. Tekle-Smith and A. G. Doyle, Nat. Commun., 2021, 12, 6950 CrossRef CAS PubMed; (d) Y. Zhang, N. A. Fitzpatrick, M. Das, I. P. Bedre, H. G. Yayla, M. S. Lall and P. Z. Musacchio, Chem Catal., 2022, 2, 292–308 CrossRef CAS; (e) M. Das, L. Zamani, C. Bratcher and P. Z. Musacchio, J. Am. Chem. Soc., 2023, 145, 3861–3868 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel. G. E. Scuseria, M. A. Robb, et al., Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- (a) B. Dereli, M. A. Ortuño and C. J. Cramer, ChemPhysChem, 2018, 19, 959–966 CrossRef CAS PubMed; (b) T. Malcomson, P. Repiščák, S. Erhardt and M. J. Paterson, ACS Omega, 2022, 7, 45057–45066 CrossRef CAS PubMed.
- (a) K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, ed. V. H. Smith, H. F. Schaefer, and K. Morokuma, Springer Netherlands, Dordrecht, 1986, pp. 155–184 Search PubMed; (b) Y. Kitagawa, K. Saito, and K. Yamaguchi, in Symmetry (Group Theory) and Mathematical Treatment in Chemistry, ed. T. Saito, IntechOpen, Rijeka, 2018, ch. 7, pp. 121–139 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- (a) G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522 CrossRef CAS PubMed; (b) G. Knizia, http://www.iboview.org/, accessed on July 10, 2022.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2239614. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc03597b |
| ‡ These authors contributed equally to this work. |
| § Current address: Department of Chemistry, University of Michigan, Ann Arbor, MI 48109, USA. |
| ¶ Current address: Department of Discovery Chemistry, Merck & Co. Inc., South San Francisco, CA 93080, USA. |
| || Current address: UL Research Institutes, 1603 Orrington St. Suite 2000, Evanston, IL 60201, USA. |
| This journal is © The Royal Society of Chemistry 2024 |