Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ligand field design enables quantum manipulation of spins in Ni2+ complexes†
Michael K.
Wojnar
a,
Krishnendu
Kundu
b,
Arailym
Kairalapova
d,
Xiaoling
Wang
 b,
Andrew
Ozarowski
b,
Andrew
Ozarowski
 b,
Timothy C.
Berkelbach
d,
Stephen
Hill
b,
Timothy C.
Berkelbach
d,
Stephen
Hill
 bc and
Danna E.
Freedman
bc and
Danna E.
Freedman
 *a
*a
aDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: danna@mit.edu
bNational High Magnetic Field Laboratory, Tallahassee, Florida 32310, USA
cDepartment of Physics, Florida State University, Florida 32306, USA
dDepartment of Chemistry, Columbia University, New York, New York 10027, USA
First published on 8th December 2023
Abstract
Creating the next generation of quantum systems requires control and tunability, which are key features of molecules. To design these systems, one must consider the ground-state and excited-state manifolds. One class of systems with promise for quantum sensing applications, which require water solubility, are d8 Ni2+ ions in octahedral symmetry. Yet, most Ni2+ complexes feature large zero-field splitting, precluding manipulation by commercial microwave sources due to the relatively large spin–orbit coupling constant of Ni2+ (630 cm−1). Since low lying excited states also influence axial zero-field splitting, D, a combination of strong field ligands and rigidly held octahedral symmetry can ameliorate these challenges. Towards these ends, we performed a theoretical and computational analysis of the electronic and magnetic structure of a molecular qubit, focusing on the impact of ligand field strength on D. Based on those results, we synthesized 1, [Ni(ttcn)2](BF4)2 (ttcn = 1,4,7-trithiacyclononane), which we computationally predict will have a small D (Dcalc = +1.15 cm−1). High-field high-frequency electron paramagnetic resonance (EPR) data yield spin Hamiltonian parameters: gx = 2.1018(15), gx = 2.1079(15), gx = 2.0964(14), D = +0.555(8) cm−1 and E = +0.072(5) cm−1, which confirm the expected weak zero-field splitting. Dilution of 1 in the diamagnetic Zn analogue, [Ni0.01Zn0.99(ttcn)2](BF4)2 (1′) led to a slight increase in D to ∼0.9 cm−1. The design criteria in minimizing D in 1via combined computational and experimental methods demonstrates a path forward for EPR and optical addressability of a general class of S = 1 spins.
Introduction
The emerging field of quantum information science (QIS) promises to revolutionize myriad areas, including computation, metrology, networking, and sensing.1,2 The fundamental unit of these advancing technologies revolves around the quantum bit, or qubit. Among the well-established qubit candidates are electron spin bearing defects, such as the anionic nitrogen-vacancy pair defect in diamond3,4 and the neutral divacancy in silicon carbide,5–7 where the state of the spin may be prepared and read out with optical light, even to the single-spin level. This spin–optical interface has resulted in rapid progress in the field of nanoscale and quantum sensing, in which these defects detect minute changes in temperature,8,9 pressure,10 magnetic fields,11–13 and electric fields.14–16Translating the electronic structure of these optically-addressable solid-state spin defects (an S = 1 ground state with radiative decay from the excited state) to molecules allows for the combination of the sensitivity of spin with the tunability of molecules. Recent studies of a molecular bottom-up approach to QIS demonstrated molecular control over coherence properties, spectral resolution, interspin distance, as well as optical addressability in molecular spins.17–22 Molecular electronic spin-based qubits may also improve on previously mentioned sensing applications, as the molecular sensor can be placed in direct proximity to the target analyte with Ångstrom-scale precision. A spin–optical interface also primes these tunable “molecular color centers” for potential integration into quantum networks.23 We are interested in implementing an atom-by-atom synthetic approach and engineering the energy levels (ground-state magnetic spin sublevels, excited states tuned by ligand fields) of electronic spin-based transition metal complexes for the manipulation of the molecular spin.
Octahedral (Oh) S = 1 Ni2+ complexes represent an enticing class of molecular quantum sensors due to the potential biocompatibility, as indicated by their chemical stability in the presence of air and water of this general class of molecules and the redox stability of the metal ion. While they feature the required electronic structure for a spin–optical interface, transition metal complexes exhibit large values (>90 GHz) of zero-field splitting (ZFS), due to the large spin–orbit coupling (SOC) constant (630 cm−1 for Ni2+), hindering the measurement of ground-state spin properties of these systems with commercial microwave sources (9 GHz to 90 GHz). Consequently, there is a dearth of information on the dynamic spin properties of Ni2+ spins, without which we lack fundamental understanding of the coherence behavior of the electronic spin.24 Better understanding the characteristics of this class of molecules, in addition to the added potential for optical addressability, may enable the use of these spin-based qubits for biological quantum sensing.
The criteria for a molecular quantum sensor include having discrete, well-defined quantum states that are addressable for manipulation (microwave, radiofrequency excitations). For S = 1 transition-metal-based electronic spin systems, EPR addressability is achieved by minimizing axial ZFS, D. The challenge for late transition metals relates to their large SOC constants, which requires careful tuning of the ligand field in order to minimize the ZFS. In the orbitally non-degenerate case, this can be achieved via incorporation of strong field ligands, as D is inversely proportional to the energetic separation of excited states from the ground state.25 Previously, the only examples of commercial frequency (9–35 GHz) continuous-wave (cw) EPR investigations on Oh Ni2+ spins have focused on [Ni(pyrazole)6]2+, [Ni(H2O)6]2+ and [Ni(NH3)6]2+,26–33 which are exceptionally host- and counterion-dependent, due to the weak field monodentate ligands and the flexible primary coordination sphere. As a result, for a nickel coordination complex with the same coordinating ligands, D can vary by an order of magnitude as a function of counterion.34 Moreover, the weak ligand field also does not exhibit the required electronic structure for a spin–optical interface.
In order to tune the axial ZFS, D, into a desirable microwave energy regime, we can use coordination chemistry to control both the excited state contributions as well as the effective SOC constant, εeff.35,36 A strong interaction between metal and ligands is necessary so that contributions to D are minimized.37 Strong field ligands ensure that the triplet excited states are high in energy, reducing the energetic separation of the ground-state MS = 0 and MS = ±1 spin triplet sublevels. We recently demonstrated this in Cr4+, V3+, and Ni2+ transition metal complexes with aryl, amide, and polypyridine ligands, respectively.21,38–40 We can chemically tune the effective SOC constant through the relativistic nephelauxetic effect or interelectronic repulsion/metal–ligand covalency. The latter effect is typically quantified by the Racah parameter, B,41–43 which decreases with decreasing electronic repulsion. Therefore, in systems where polarizable ligands minimize electron repulsion by electron delocalization (i.e., increased covalency), B decreases.44,45 Ni2+ ions are perfectly geared for ground- and excited-state engineering and characterization of the electronic state manifold due to the abundance of literature on Oh Ni2+ ligand field strength.46–50 Moreover, out of the first-row transition metals that can host a ground-state S = 1 spin, Ni2+ has the largest SOC constant, and thus should exhibit the largest changes in D as a function of ligand environment.43
Results and discussion
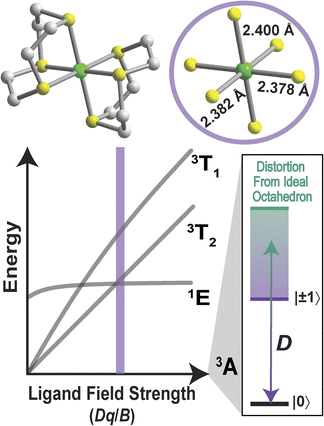
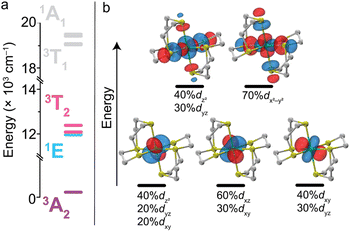
To probe the relativistic nephelauxetic effect in Oh Ni2+ and its effect on the ground-state spin, we elected for a sulfur-rich coordination environment around the ion (Fig. 1). We selected a Ni2+ complex, [Ni(ttcn)2](BF4)2 (compound 1),51,52 with the thioether-based ttcn ligand (ttcn = 1,4,7-trithiacyclononane) for these investigations because it meets our criteria for an EPR-addressable electronic spin-based qubit by combatting the two main contributions to D (SOC and low-lying excited states): (1) the soft sulfur donors give rise to increased covalency, thus reducing metal-based SOC; (2) the ligand field strength of the thioether donors is strong (similar to pyridine donors), pushing the triplet excited states to higher energy, thus minimizing excited state contributions to D; (3) the ethylene spacers in the ttcn ligand allow for minimal distortion of the octahedral coordination environment around Ni2+ (Fig. 1).53 The strong metal–ligand interaction in 1 is evident from the crystal structure data, where the Ni–S bond lengths range from 2.378–2.400 Å, the shortest Ni–S bond lengths in the CCDC database for a NiS6 coordination environment. The primary coordination sphere around the metal ion is close to a perfect octahedron: the average deviations from 90° for the 12 cis angles is Σmean = 1.48° (Σsum = 17.76°).We began by employing computational methods to screen for and predict the ground- and excited-state properties of [Ni(ttcn)2]2+, to see if 1 meets our requirements for a qubit (small ZFS and lowest-lying singlet state for potential spin–flip luminescence). Due to the multiconfigurational nature of the electronic states of 1, we calculate ground- and excited-state energies using the complete active space self-consistent field (CASSCF) method,54 including corrections with second-order n-electron valence state perturbation theory (NEVPT2) method.55 We have performed calculations using both the minimal (8,5) active space for 1, which has eight electrons in the five 3d-orbitals of Ni2+, and a larger (12,12) active space, which adds two doubly-occupied orbitals corresponding to a π bond (with Ni d-orbital character) and five unoccupied 4d-orbitals of Ni2+ (Table S7†). All calculations are performed with the ORCA program,56 and computational details are available in the ESI.† The Ni2+ 3d-orbitals from CASSCF (12,12) are illustrated in Fig. 2. Their energy distribution shows a nearly ideal Oh ligand field splitting: three t2g orbitals (with >95% metal character) lie 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 below two eg orbitals, although the singly-occupied eg orbitals have nonnegligible ligand character (about 15%) due to mixing with sulfur p-orbitals.
000 cm−1 below two eg orbitals, although the singly-occupied eg orbitals have nonnegligible ligand character (about 15%) due to mixing with sulfur p-orbitals.
As expected, our calculations find that 1 is a ground-state S = 1 triplet, 3A2g. The calculated triplet excited states for each T state in Oh symmetry (3T2g, 3T1g) fall within 450 cm−1 of each other, which again reflects the nearly ideal octahedral environment. This symmetry causes the calculated transition dipole moments among the d-orbitals to be minuscule (10−4D), resulting in zero oscillator strength and absorption intensity. The lowest lying triplet manifold, 3T2g, has a mean energy of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158 cm−1 (822.5 nm) above the ground state. The next triplet manifold, 3T1g, has a mean energy of 19
158 cm−1 (822.5 nm) above the ground state. The next triplet manifold, 3T1g, has a mean energy of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208 cm−1 (520.6 nm). These high-energy states illustrate the ligand field strength of ttcn resulting in the ligand field splitting, Dq, of about 1216 cm−1 corresponding to 1/10 energy of the 3A2g → 3T2g transition. These triplet excited-state energies are in good agreement with the experimental absorption spectra discussed below (Table S8†). Additionally, we calculate the energy of the lowest lying singlet state, 1Eg, to be 11
208 cm−1 (520.6 nm). These high-energy states illustrate the ligand field strength of ttcn resulting in the ligand field splitting, Dq, of about 1216 cm−1 corresponding to 1/10 energy of the 3A2g → 3T2g transition. These triplet excited-state energies are in good agreement with the experimental absorption spectra discussed below (Table S8†). Additionally, we calculate the energy of the lowest lying singlet state, 1Eg, to be 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 cm−1 (836.8 nm). The 1Eg and 3T2g states have similar energies, possibly explaining the broadening of 3T2g state and the absence of a separate 1Eg peak in the experimental absorption spectrum (Fig. S32†). Using Tanabe and Sugano's analytical expressions for excited state energies, we estimate the Racah parameters as B = 897 cm−1, C = 2574 cm−1 and C/B is 2.87.57 Despite the triplet energies being very close to the experimental absorption spectra discussed below, the theoretical and experimental Racah parameters are quite different (Table 1). This highlights that Racah parameters are highly sensitive to the absorption energies.58 In the ESI,† we provide results for higher lying states (Table S8†) and CASSCF configurations of each excited triplet and singlet state in terms of the five d-orbitals from Fig. 2 (Tables S9 and S10†).
950 cm−1 (836.8 nm). The 1Eg and 3T2g states have similar energies, possibly explaining the broadening of 3T2g state and the absence of a separate 1Eg peak in the experimental absorption spectrum (Fig. S32†). Using Tanabe and Sugano's analytical expressions for excited state energies, we estimate the Racah parameters as B = 897 cm−1, C = 2574 cm−1 and C/B is 2.87.57 Despite the triplet energies being very close to the experimental absorption spectra discussed below, the theoretical and experimental Racah parameters are quite different (Table 1). This highlights that Racah parameters are highly sensitive to the absorption energies.58 In the ESI,† we provide results for higher lying states (Table S8†) and CASSCF configurations of each excited triplet and singlet state in terms of the five d-orbitals from Fig. 2 (Tables S9 and S10†).
| g iso | D, cm−1 | |E| (cm−1) | Dq (cm−1) | B (cm−1) | C (cm−1) | C/B | |
|---|---|---|---|---|---|---|---|
| 1 | 2.10 | +0.555(8) | 0.072(5) | 1279 | 673 | 2190 | 3.29 |
| 1 calc | 2.16 | +1.15 | 0.3 | 1216 | 897 | 2574 | 2.87 |
We calculate the excited-state contributions to ZFS, which provide a manner in which to rationalize and optimize the magnitudes of ZFS in Oh Ni2+ spins to screen 1 as a molecular spin with low ZFS for commercial microwave addressability. When the symmetry of a complex reduces from a perfect Oh, the ground state triplet splits into three spin sublevels due to the coupling to the excited states. Since the excited state energies for 1 are relatively high for Ni2+ complexes, we expect to observe small D values. Within perturbation theory, the elements of the D tensor are
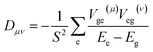 | (1) |
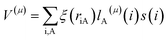 for electron i and nucleus A separated by riA, where ξ(riA) is the radial operator, lA(μ)(i) is the μ component of the orbital angular momentum, and s(i) is the z component of the spin operator.59,60 The ZFS parameters are obtained from the eigenvalues of the D tensor.
for electron i and nucleus A separated by riA, where ξ(riA) is the radial operator, lA(μ)(i) is the μ component of the orbital angular momentum, and s(i) is the z component of the spin operator.59,60 The ZFS parameters are obtained from the eigenvalues of the D tensor.
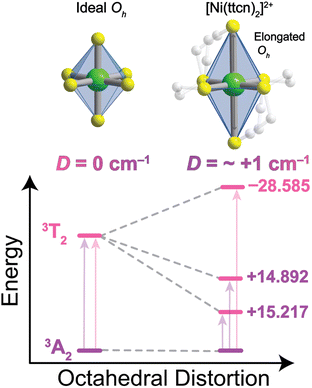
The calculated ZFS parameters are Dcalc = +1.15 cm−1 and E/D = 0.26, which are comparable to our experimentally measured values (described below). As can be seen from (1), the excited states with higher energies have less significant contributions to the ZFS.61 We find that the contributions to Dcalc predominantly come from the six lowest-lying orbital states with the necessary symmetry: three triplet 3T2g and three singlet 1T2g; the positive sign indicates that MS = 0 is lower in energy than MS = ±1 (Table S8†). The electron configurations of these six orbital states are nearly identical (Tables S9 and S10†), but the triplet and singlet states contribute with opposite signs due to the nature of the coupling of the spin operators (see ESI† for further discussion).62,63 The largest contributions to Dcalc come from the three triplet 3T2g states (Fig. 3), with +15.22 cm−1, +14.89 cm−1, −28.59 cm−1 (Dsum = +1.52 cm−1), and the next largest contributions come from the three singlet 1T2g states with −7.34 cm−1, −7.28 cm−1, and +14.23 cm−1 (Dsum = −0.39 cm−1). The transition energy to the 1T2g state is more than twice the transition energy to the 3T2g state, causing the ZFS contributions to be half as large. Taken together, these six roots lead to a computed axial ZFS value of +1.13 cm−1, 98% of the total value. The higher lying 3T1g excited states have minimal contributions to D (<0.01 cm−1, Table S8†) which was previously observed for other Ni2+ complexes.62 The energetically lower 1Eg and 1A1g singlet states contribute less than 0.1 cm−1 because they have the wrong symmetry. The results demonstrate that 1 has a computationally-predicted low ZFS.
To computationally study the impact of the ligand, we performed calculations with the minimal (8,5) active space for both the near-ideal Oh “soft” sulfur-rich [Ni(ttcn)2]2+ and the distorted “hard” nitrogen-rich [Ni(tacn)2]2+ complexes (tacn = 1,4,7-triazacyclononane). We confirm that for 1, our results are qualitatively unchanged with this smaller active space. Specifically, we find that the value of Dcalc (1.07 cm−1) and the six main contributions from triplet 3T2g and singlet 1T2g states are similar for (8,5) and (12,12) active spaces (Tables S11 and S12†). The calculation for the [Ni(tacn)2]2+ system predicts a ZFS of 4.27 cm−1, compared to the experimental value of 2.95 cm−1.62 The same six states contribute to the N-substituted compound, although the triplet contributions are different. Three sublevels comprising the 3T2g state effectively cancel one another in [Ni(ttcn)2]2+, while they do not cancel in [Ni(tacn)2]2+, leading to the larger ZFS value (Table S12†). As [Ni(tacn)2]2+ benefits from a slightly larger ligand field strength compared to [Ni(ttcn)2]2+, this study provided an ab initio demonstration that D decreases (from 4.27 cm−1 to 1.07 cm−1) when we employ a softer ligand in a more rigorously octahedral environment. While stronger ligand fields generally minimize D, we highlight minimizing octahedral distortion will push D towards rigorously zero.
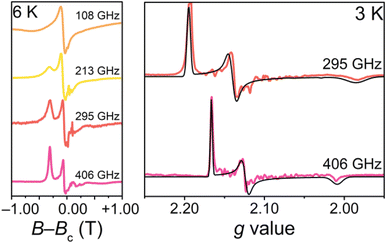
To confirm the ground-state magnetic properties and EPR addressability of 1 that we screened for computationally, we utilized high-field high-frequency cw-EPR spectroscopy (Fig. 4). The observed spectra were modelled with EasySpin and the spin Hamiltonian, 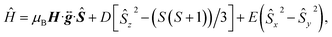 which provides the energies of the MS levels for the spin S as a function of D and E as well as the applied dc magnetic field (H). In this Hamiltonian, Ŝi (i = x, y, and z) are the spin component operators, gi (i = x, y, and z), the components of the diagonal g-tensor, and μB, the Bohr magneton.64 EPR spectroscopy corroborates the S = 1 ground state, and enabled quantification of the axial and rhombic ZFS parameters, D and E. While the resonances broaden with increasing temperature, indicative of competing long-range spin interactions and thermal fluctuations,65 resolved magnetic resonances could be observed and accurately simulated at 3 K. The best simulations for 1 are gx = 2.1018(15), gy = 2.1079(15), gz = 2.0964(14), D = +0.555(8) cm−1, E = +0.072(5) cm−1 (E/D = 0.13) (Fig. 4). We simulate the spectra best with a positive value for D. The giso (2.1018) and ZFS (D = +0.555 cm−1, 18 GHz) parameters in 1 represent some of the lowest values for Oh Ni2+, with the other low ZFS nickel complexes incorporating monodentate weak-field ligands, such as aqua or pyrazole ligands, in rigorously symmetric octahedral coordination environments.26,66–68 The giso value in 1 is closer to ge than in other Ni complexes that exhibit g values from ∼2.11 to 2.30.69 This indicates electron delocalization onto the ligands, resulting in the reduction of the effective spin–orbit coupling constant. A similar effect of reduced g values was observed for the [Co(ttcn)2]2+ (giso = 2.067)53 and [Cu(ttcn)2]2+ (giso = 2.06)70,71 complexes. Moreover, the large contribution of ligand character into the frontier molecular orbitals, i.e., the unpaired electrons are more delocalized, is also apparent in the EPR spectrum and the associated spin Hamiltonian parameters of the isolated [Ni(ttcn)2]3+ complex (giso = 2.065).72 We attribute the g values closer to ge and the low ZFS in 1 to the previously mentioned interconnected variables: reduction of the metal-based SOC constant of nickel via the relativistic nephelauxetic effect59 of the covalent Ni–S interactions. The strong ligand field and near Oh geometry around nickel pushes the excited states to higher energy. We can also compare the low ZFS in 1 with the magnetic parameters in [Ni(tacn)2]2+, in which D = +2.95 cm−1 (88.4 GHz).62 The magnitudes of the ZFS parameters in 1 confirm the EPR addressability of the complex with commercial microwave sources.
which provides the energies of the MS levels for the spin S as a function of D and E as well as the applied dc magnetic field (H). In this Hamiltonian, Ŝi (i = x, y, and z) are the spin component operators, gi (i = x, y, and z), the components of the diagonal g-tensor, and μB, the Bohr magneton.64 EPR spectroscopy corroborates the S = 1 ground state, and enabled quantification of the axial and rhombic ZFS parameters, D and E. While the resonances broaden with increasing temperature, indicative of competing long-range spin interactions and thermal fluctuations,65 resolved magnetic resonances could be observed and accurately simulated at 3 K. The best simulations for 1 are gx = 2.1018(15), gy = 2.1079(15), gz = 2.0964(14), D = +0.555(8) cm−1, E = +0.072(5) cm−1 (E/D = 0.13) (Fig. 4). We simulate the spectra best with a positive value for D. The giso (2.1018) and ZFS (D = +0.555 cm−1, 18 GHz) parameters in 1 represent some of the lowest values for Oh Ni2+, with the other low ZFS nickel complexes incorporating monodentate weak-field ligands, such as aqua or pyrazole ligands, in rigorously symmetric octahedral coordination environments.26,66–68 The giso value in 1 is closer to ge than in other Ni complexes that exhibit g values from ∼2.11 to 2.30.69 This indicates electron delocalization onto the ligands, resulting in the reduction of the effective spin–orbit coupling constant. A similar effect of reduced g values was observed for the [Co(ttcn)2]2+ (giso = 2.067)53 and [Cu(ttcn)2]2+ (giso = 2.06)70,71 complexes. Moreover, the large contribution of ligand character into the frontier molecular orbitals, i.e., the unpaired electrons are more delocalized, is also apparent in the EPR spectrum and the associated spin Hamiltonian parameters of the isolated [Ni(ttcn)2]3+ complex (giso = 2.065).72 We attribute the g values closer to ge and the low ZFS in 1 to the previously mentioned interconnected variables: reduction of the metal-based SOC constant of nickel via the relativistic nephelauxetic effect59 of the covalent Ni–S interactions. The strong ligand field and near Oh geometry around nickel pushes the excited states to higher energy. We can also compare the low ZFS in 1 with the magnetic parameters in [Ni(tacn)2]2+, in which D = +2.95 cm−1 (88.4 GHz).62 The magnitudes of the ZFS parameters in 1 confirm the EPR addressability of the complex with commercial microwave sources.
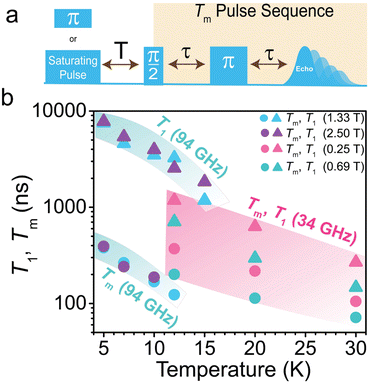
To evaluate the coherence properties of 1 and determine the field and frequency dependence of the spin coherence, we employed multifrequency pulse EPR at both W-band (94 GHz) and Q-band (34 GHz). All pulse EPR experiments were performed on diamagnetic dilutions of [Ni(ttcn)2](BF)2 into the zinc analogue, [Ni0.01Zn0.99(ttcn)2](BF4)2 (1′), to mitigate the detrimental coupling between Ni2+ centers, as was observed by SQUID magnetometry (Fig. S5†). We first measured the echo-detected field-swept (EDFS) spectra for 1′ at both W- and Q-band by applying a two-pulse Hahn-echo detection sequence (π/2–τ–π–τ–echo) at a fixed τ value while sweeping magnetic field. At W-band, the resultant EDFS spectrum of 1 exhibits an intense and broad transition at 2.50 T and a less intense yet sharp transition at 1.33 T (Fig. S18–S21†). At Q-band, the transitions shift to lower fields, with an intense and broad transition at 0.69 T, with a less intense and broad transition at 0.25 T (Fig. S22 and S23†). Variable-temperature (12 K, 20 K, 30 K) EDFS spectra at Q-band also do not exhibit magnetic field shifts in transitions, indicative of the rigid ttcn ligand, as well as the crystalline matrix, minimizing changes in ZFS as a function of temperature. This is in stark contrast to EPR investigations on other Oh Ni2+ complexes, like [Ni(H2O)6]2+, where changes in temperature and pressure caused dramatic increases in ZFS.66,73 The low field feature in both spectra corresponds to the spin-forbidden, ΔMS = 2 transitions, while the broader features originate from spin-allowed, ΔMS = 1.
While the EDFS spectra for 1′ are consistent with predicted spectra based on the magnetic parameters obtained from cw-EPR measurements, there are discrepancies in the ZFS values between 1 and 1′. We attribute these differences in magnetic properties to the crystallization and dilution of 1 in the zinc analogue, as well as cooling to cryogenic temperatures. 1 crystallizes in the monoclinic P21/c space group at 200 K, as two crystallographically independent complexes that lie on an inversion center.74 The zinc complex, [Zn(ttcn)2](BF4)2·2(MeNO2) crystallizes in the orthorhombic Pbca space group at 295 K, with one independent complex that lies on an inversion center.75 Variation in lattice parameters and ZFS upon dilution has previously been demonstrated in Ni2+ quantum magnets as a consequence of anisotropic expansion of M–L bond distances;76,77 enhanced spin coherence in Cr4+ spins has also been shown upon dilution.22 Changes in crystal packing incurred through cooling and dilution in a different symmetry space group for [Zn(ttcn)2]2+ result in an increase in |D| from 0.60 cm−1 (18 GHz)in 1 to two distinct species in 1′ with |D| values of ∼0.9 cm−1 (27 GHz) and ∼1.15 cm−1 (34 GHz), increases of 50% and 110%, respectively, based on simulations of the EDFS spectra (Fig. S20 and S21†).22 The non-zero echo intensity at both 94 GHz and 34 GHz obtained for 1′ demonstrates that we can manipulate multiple transitions in the spin manifold coherently.
We proceeded to determine the phase memory time (Tm), which encompasses all processes that contribute to decoherence or loss of phase memory, including the electron spin T2. We extract these parameters from fitting the decay of the intensity of the two-pulse Hahn-echo sequence (π/2–τ–π–τ–echo) with increasing interpulse delay time τ at both W- and Q-band. We fit the echo decays to mono-exponential functions (I = I0e−2τ/Tm). For 1′, Tm values decay rapidly with increasing temperatures (we provide a full discussion of Tm in the ESI†). We next measured the spin–lattice relaxation time, T1, the time it takes for an ensemble of spins to relax to thermal equilibrium (Fig. 5). To measure T1, we employed two separate pulse sequences for W- and Q-band, due to instrumental limitations. For W-band, we implemented a saturation recovery pulse sequence (long pulse–T–π/2–τ–π–τ–echo), where a long microwave pulse saturates the spin transition. Following the initial pulse saturation, we applied two microwave pulses to detect the realignment of the spin with the dc field as a function of delay time, T, after the long pulse. For Q-band pulse experiments, we employed an inversion recovery pulse sequence (π–T–π/2–τ–π–τ–echo). We acknowledge that spin–lattice relaxation is dependent on the experimental parameters. Spectral diffusion is a convoluting factor in inversion recovery pulse sequences, in which magnetic interactions modify the resonant frequency of excited spins, thereby shortening T1. We fit both saturation and inversion recovery curves with a monoexponential function, I = −I0(e−T/T1 − 1). Spin–lattice relaxation is fast in comparison to other transition-metal-based S = 1 spins21,38 and drops precipitously with increasing temperature and decreasing field (Fig. 5, Table S2†). At 94 GHz and 5 K, T1 is 7.5–7.8 μs and drops to <2 μs at 12 K. At 34 GHz and 12 K, T1 is 0.71–1.2 μs and drops to <0.3 μs at 30 K. This is consistent with the direct and Raman processes limiting T1 at W- and Q-band, respectively which was previously seen in pulse EPR data on S = 1 Ni2+.39 This combination of direct and Raman-driven relaxation is also in agreement with T1 data on OhS = 1 Ni2+ data derived from frequency-dependent alternating current (ac) susceptibility experiments at high fields as observed here.78 While both the direct and Raman processes are inversely dependent on field, we observe an increase in T1 at higher magnetic fields in 1′. We attribute this observation to either spectral diffusion associated with the inversion recovery pulse sequence or to MS spin sublevel mixing, which is more prominent at lower frequency and field. This was previously demonstrated for a high-spin Fe3+ system.79
The electronic absorption spectroscopy data corroborates the computationally-predicted ligand field strength in 1 and provides critical information on the excited state manifold. We observe two peaks in the UV-Vis spectrum of 1 in acetonitrile (Fig. S32†), which correspond to the spin-allowed ligand field transitions: (1) 3A2g → 3T2g at 782 nm (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788 cm−1) (2) 3A2g → 3T1g at 527 nm (18
788 cm−1) (2) 3A2g → 3T1g at 527 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 cm−1), consistent with Oh Ni2+. We did not observe 1E excited state absorption or photoluminescence. With the two observed transitions, we calculate the parameters for Dq and B.57,80 The 3A2g → 3T2g transition energy is equal to 10 Dq as it describes the promotion of an electron from the non-bonding t2g set of orbitals to the anti-bonding eg orbitals; we calculate Dq to be 1279 cm−1. This confirms a strong interaction between the metal d orbitals and the sulfur p orbitals (for comparison, Dq for [Ni(tacn)2]2+ is 1250 cm−1 and for [Ni(bipyridine)3]2+Dq is 1270 cm−1).58,81,82 We calculate the Racah B parameter (covalency parameter) to be 673 cm−1.57,80,83,84 This value is 66% of the free-ion value (1030 cm−1),83 and significantly smaller in comparison to other Ni2+ complexes, including [Ni(tacn)2]2+ (Bsolution = 993 cm−1 and Bsingle crystal = 840 cm−1).81,85–89 The electronic absorption spectroscopy data demonstrates that the thioether ligand provides a strong ligand field around the nickel ion and leads to a reduction in the interelectronic repulsion parameter, B.
975 cm−1), consistent with Oh Ni2+. We did not observe 1E excited state absorption or photoluminescence. With the two observed transitions, we calculate the parameters for Dq and B.57,80 The 3A2g → 3T2g transition energy is equal to 10 Dq as it describes the promotion of an electron from the non-bonding t2g set of orbitals to the anti-bonding eg orbitals; we calculate Dq to be 1279 cm−1. This confirms a strong interaction between the metal d orbitals and the sulfur p orbitals (for comparison, Dq for [Ni(tacn)2]2+ is 1250 cm−1 and for [Ni(bipyridine)3]2+Dq is 1270 cm−1).58,81,82 We calculate the Racah B parameter (covalency parameter) to be 673 cm−1.57,80,83,84 This value is 66% of the free-ion value (1030 cm−1),83 and significantly smaller in comparison to other Ni2+ complexes, including [Ni(tacn)2]2+ (Bsolution = 993 cm−1 and Bsingle crystal = 840 cm−1).81,85–89 The electronic absorption spectroscopy data demonstrates that the thioether ligand provides a strong ligand field around the nickel ion and leads to a reduction in the interelectronic repulsion parameter, B.
Conclusions
The results provide a joint computational and experimental approach toward targeting Oh Ni2+ spins with low axial ZFS to allow for spin manipulation at W/Q-band coupled with the requisite electronic structure for a spin–optical interface. The soft and rigid coordination environment provided by the tridentate thioether ligand leads to a strong field environment around the ion, together with decreased SOC, which contributes to the small ZFS. Nearly ideal octahedral coordination environments have been realized with other Ni2+ complexes with harder nitrogen donors, with much larger values of axial ZFS (∼3 cm−1), highlighting the combination of geometry and SOC in minimizing D.39 Moreover, the rigidity of the ttcn ligand maintains a low ZFS across host matrix, previously not observed for other low ZFS Ni2+ qubits, such as [Ni(H2O)6]2+, [Ni(pyrazole)6]2+, and [Ni(NH3)6]2+. The biocompatibility of these metal ions allows for the potential of sensing under aqueous conditions or even integrating spin qubits into biological architectures, such as DNA, where the orientation and environment of the electronic spin qubit can be controlled.90–921 also possesses the correct electronic structure for optical initialization and readout, but suffers from low extinction coefficients. Incorporating ligands that increase the extinction coefficients (extended planar polypyridine ligands) and ligand field strengths (N-heterocyclic carbenes) of this general class of molecules,93 while maintaining the symmetric primary coordination sphere and lowest-lying excited states, will be the focus of future work.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Conceptualization: M. K. W. and D. E. F.; investigation and formal analysis: M. K. W., K. K., A. K., X. W., and A. O.; resources: X. W., A. O., and S. H.; supervision: D. E. F., S. H., and T. C. B.; all authors contributed to writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr D. W. Laorenza, Dr E. J. Peterson, R. B. Greer, and S. M. Petry for fruitful discussions and for helpful comments on the manuscript. D. E. F., T. C. B., M. K. W., and A. K. acknowledge support from the US Army Research Office under award number W911NF2210120. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-2128556 and the State of Florida. D. E. F. acknowledges support for the integration of molecules into a larger quantum infrastructure from the U.S. Department of Energy Office of Science National Quantum Information Science Research Centers. This work made use of the IMSERC Crystallography facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-2025633), and Northwestern University.References
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141(29), 11339–11352 CrossRef CAS PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Exploiting Chemistry and Molecular Systems for Quantum Information Science, Nat. Rev. Chem, 2020, 4(9), 490–504 CrossRef CAS PubMed.
- A. Gruber, A. Dräbenstedt, C. Tietz, L. Fleury, J. Wrachtrup and C. von. Borczyskowski, Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers, Science, 1997, 276(5321), 2012–2014 CrossRef CAS.
- F. Casola, T. van der Sar and A. Yacoby, Probing Condensed Matter Physics with Magnetometry Based on Nitrogen-Vacancy Centres in Diamond, Nat. Rev. Mater., 2018, 3(1), 1–13 Search PubMed.
- H. Seo, A. L. Falk, P. V. Klimov, K. C. Miao, G. Galli and D. D. Awschalom, Quantum Decoherence Dynamics of Divacancy Spins in Silicon Carbide, Nat. Commun., 2016, 7(1), 12935 CrossRef CAS PubMed.
- D. D. Awschalom, R. Hanson, J. Wrachtrup and B. B. Zhou, Quantum Technologies with Optically Interfaced Solid-State Spins, Nat. Photonics, 2018, 12(9), 516–527 CrossRef CAS.
- A. Bourassa, C. P. Anderson, K. C. Miao, M. Onizhuk, H. Ma, A. L. Crook, H. Abe, J. Ul-Hassan, T. Ohshima, N. T. Son, G. Galli and D. D. Awschalom, Entanglement and Control of Single Nuclear Spins in Isotopically Engineered Silicon Carbide, Nat. Mater., 2020, 19(12), 1319–1325 CrossRef CAS PubMed.
- G. Kucsko, P. C. Maurer, N. Y. Yao, M. Kubo, H. J. Noh, P. K. Lo, H. Park and M. D. Lukin, Nanometre-Scale Thermometry in a Living Cell, Nature, 2013, 500(7460), 54–58 CrossRef CAS PubMed.
- P. Neumann, I. Jakobi, F. Dolde, C. Burk, R. Reuter, G. Waldherr, J. Honert, T. Wolf, A. Brunner, J. H. Shim, D. Suter, H. Sumiya, J. Isoya and J. Wrachtrup, High-Precision Nanoscale Temperature Sensing Using Single Defects in Diamond, Nano Lett., 2013, 13(6), 2738–2742 CrossRef CAS PubMed.
- M. W. Doherty, V. V. Struzhkin, D. A. Simpson, L. P. McGuinness, Y. Meng, A. Stacey, T. J. Karle, R. J. Hemley, N. B. Manson, L. C. L. Hollenberg and S. Prawer, Electronic Properties and Metrology Applications of the Diamond NV− Center under Pressure, Phys. Rev. Lett., 2014, 112(4), 047601 CrossRef PubMed.
- G. Balasubramanian, I. Y. Chan, R. Kolesov, M. Al-Hmoud, J. Tisler, C. Shin, C. Kim, A. Wojcik, P. R. Hemmer, A. Krueger, T. Hanke, A. Leitenstorfer, R. Bratschitsch, F. Jelezko and J. Wrachtrup, Nanoscale Imaging Magnetometry with Diamond Spins under Ambient Conditions, Nature, 2008, 455(7213), 648–651 CrossRef CAS PubMed.
- M. Pelliccione, A. Jenkins, P. Ovartchaiyapong, C. Reetz, E. Emmanouilidou, N. Ni and A. C. Bleszynski Jayich, Scanned Probe Imaging of Nanoscale Magnetism at Cryogenic Temperatures with a Single-Spin Quantum Sensor, Nat. Nanotechnol., 2016, 11(8), 700–705 CrossRef CAS PubMed.
- L. Thiel, Z. Wang, M. A. Tschudin, D. Rohner, I. Gutiérrez-Lezama, N. Ubrig, M. Gibertini, E. Giannini, A. F. Morpurgo and P. Maletinsky, Probing Magnetism in 2D Materials at the Nanoscale with Single-Spin Microscopy, Science, 2019, 364(6444), 973–976 CrossRef CAS PubMed.
- F. Dolde, H. Fedder, M. W. Doherty, T. Nöbauer, F. Rempp, G. Balasubramanian, T. Wolf, F. Reinhard, L. C. L. Hollenberg, F. Jelezko and J. Wrachtrup, Electric-Field Sensing Using Single Diamond Spins, Nat. Phys., 2011, 7(6), 459–463 Search PubMed.
- J. Michl, J. Steiner, A. Denisenko, A. Bülau, A. Zimmermann, K. Nakamura, H. Sumiya, S. Onoda, P. Neumann, J. Isoya and J. Wrachtrup, Robust and Accurate Electric Field Sensing with Solid State Spin Ensembles, Nano Lett., 2019, 19(8), 4904–4910 CrossRef CAS PubMed.
- K. Bian, W. Zheng, X. Zeng, X. Chen, R. Stöhr, A. Denisenko, S. Yang, J. Wrachtrup and Y. Jiang, Nanoscale Electric-Field Imaging Based on a Quantum Sensor and Its Charge-State Control under Ambient Condition, Nat. Commun., 2021, 12(1), 2457 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit, ACS Cent. Sci., 2015, 1(9), 488–492 CrossRef CAS PubMed.
- C. E. Jackson, C.-Y. Lin, S. H. Johnson, J. van Tol and J. M. Zadrozny, Nuclear-Spin-Pattern Control of Electron-Spin Dynamics in a Series of V(IV) Complexes, Chem. Sci., 2019, 10(36), 8447–8454 RSC.
- C.-J. Yu, S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski and D. E. Freedman, Spin and Phonon Design in Modular Arrays of Molecular Qubits, Chem. Mater., 2020, 32(23), 10200–10206 CrossRef CAS.
- S. von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, Spectral Addressability in a Modular Two Qubit System, J. Am. Chem. Soc., 2021, 143(21), 8069–8077 CrossRef CAS PubMed.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Optically Addressable Molecular Spins for Quantum Information Processing, Science, 2020, 370(6522), 1309–1312 CrossRef CAS PubMed.
- S. L. Bayliss, P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. E. Freedman and D. D. Awschalom, Enhancing Spin Coherence in Optically Addressable Molecular Qubits through Host-Matrix Control, Phys. Rev. X, 2022, 12(3), 031028 CAS.
- D. W. Laorenza and D. E. Freedman, Could the Quantum Internet Be Comprised of Molecular Spins with Tunable Optical Interfaces?, J. Am. Chem. Soc., 2022, 144(48), 21810–21825 CrossRef CAS PubMed.
- E. C. Kisgeropoulos, A. C. Manesis and H. S. Shafaat, Ligand Field Inversion as a Mechanism to Gate Bioorganometallic Reactivity: Investigating a Biochemical Model of Acetyl CoA Synthase Using Spectroscopy and Computation, J. Am. Chem. Soc., 2021, 143(2), 849–867 CrossRef CAS PubMed.
- M. S. Fataftah and D. E. Freedman, Progress towards Creating Optically Addressable Molecular Qubits, Chem. Commun., 2018, 54(98), 13773–13781 RSC.
- J. Reedijk and B. Nieuwenhuijse, Interpretation of E.P.R.-Spectra of Powdered Octahedral Nickel(II) Complexes with Nitrogen-Donor Ligands, Recl. Trav. Chim. Pays-Bas, 1972, 91(5), 533–551 CrossRef CAS.
- K. Amrutha and V. Kathirvelu, Interpretation of EPR and Optical Spectra of Ni(II) Ions in Crystalline Lattices at Ambient Temperature, Magn. Reson. Chem., 2022, 60(3), 414–421 CrossRef CAS PubMed.
- K. N. Shrivastava, R. S. Rubins, S. Hutton and J. E. Drumheller, Temperature Dependence of the g Value of Ni2+ in ZnSiF6·6H2O, J. Chem. Phys., 1988, 88(2), 705–706 CrossRef CAS.
- R. S. Rubins and S. K. Jani, Electron Paramagnetic Resonance of Divalent Nickel in Zinc Fluosilicate, J. Chem. Phys., 2008, 66(7), 3297–3299 CrossRef.
- R. S. Rubins, S. L. Hutton and J. E. Drumheller, Temperature Dependence of the Zero-field Splitting of Ni2+ in ZnSiF6· 6H2O and ZnSiF6·6D2O at Low Temperatures, J. Chem. Phys., 1986, 84(8), 4142–4145 CrossRef CAS.
- C. Trapp and C. Shyr, Paramagnetic Resonance in Transition-Metal Hexammine Complexes. I The Ni(II)(NH3)6 Complex Ion, J. Chem. Phys., 1971, 54(1), 196–203 CrossRef CAS.
- J. A. Ochi, W. Sano, S. Isotani and C. E. Hennies, Phase Transition in Metal Hexammine Complexes. II. The EPR Spectra of Ni(NO3)26NH3 and Ni++ Doped Zn(NO3)26NH3 and Cd(NO3)26NH3, J. Chem. Phys., 1975, 62(6), 2115–2118 CrossRef CAS.
- J. A. Ochi, S. Isotani and W. Sano, Crystal Field Distortion Parameter of Nickel Hexammine Complexes, J. Phys. Chem. Solids, 1982, 43(4), 411–412 CrossRef CAS.
- J. Titiš, R. Boča and D. Magnetostructural, Correlation in Nickel(II) Complexes: Reinvestigation of the Zero-Field Splitting, Inorg. Chem., 2010, 49(9), 3971–3973 CrossRef PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 Search PubMed.
- S. C. Coste, T. J. Pearson and D. E. Freedman, Magnetic Anisotropy in Heterobimetallic Complexes, Inorg. Chem., 2019, 58(18), 11893–11902 CrossRef CAS PubMed.
- J. Krzystek, J.-H. Park, M. W. Meisel, M. A. Hitchman, H. Stratemeier, L.-C. Brunel and J. Telser, EPR Spectra from “EPR-Silent” Species: High-Frequency and High-Field EPR Spectroscopy of Pseudotetrahedral Complexes of Nickel(II), Inorg. Chem., 2002, 41(17), 4478–4487 CrossRef CAS PubMed.
- D. W. Laorenza, A. Kairalapova, S. L. Bayliss, T. Goldzak, S. M. Greene, L. R. Weiss, P. Deb, P. J. Mintun, K. A. Collins, D. D. Awschalom, T. C. Berkelbach and D. E. Freedman, Tunable Cr4+ Molecular Color Centers, J. Am. Chem. Soc., 2021, 143(50), 21350–21363 CrossRef CAS PubMed.
- M. K. Wojnar, D. W. Laorenza, R. D. Schaller and D. E. Freedman, Nickel(II) Metal Complexes as Optically Addressable Qubit Candidates, J. Am. Chem. Soc., 2020, 142(35), 14826–14830 CrossRef CAS PubMed.
- M. S. Fataftah, S. L. Bayliss, D. W. Laorenza, X. Wang, B. T. Phelan, C. B. Wilson, P. J. Mintun, B. D. Kovos, M. R. Wasielewski, S. Han, M. S. Sherwin, D. D. Awschalom and D. E. Freedman, Trigonal Bipyramidal V3+ Complex as an Optically Addressable Molecular Qubit Candidate, J. Am. Chem. Soc., 2020, 142(48), 20400–20408 CrossRef CAS PubMed.
- C. K. Jørgensen, The Interelectronic Repulsion and Partly Covalent Bonding in Transition-Group Complexes, Discuss. Faraday Soc., 1958, 26, 110–115 RSC.
- C. E. Schäffer and C. Klixbüll Jørgensen, The Nephelauxetic Series of Ligands Corresponding to Increasing Tendency of Partly Covalent Bonding, J. Inorg. Nucl. Chem., 1958, 8, 143–148 CrossRef.
- B. N. Figgis and I. Goodman, Introduction to Ligand Fields, Interscience Publishers, New York, 1966 Search PubMed.
- C. B. Larsen, J. D. Braun, I. B. Lozada, K. Kunnus, E. Biasin, C. Kolodziej, C. Burda, A. A. Cordones, K. J. Gaffney and D. E. Herbert, Reduction of Electron Repulsion in Highly Covalent Fe-Amido Complexes Counteracts the Impact of a Weak Ligand Field on Excited-State Ordering, J. Am. Chem. Soc., 2021, 143(49), 20645–20656 CrossRef CAS PubMed.
- L. Stein, P. Boden, R. Naumann, C. Förster, G. Niedner-Schatteburg and K. Heinze, The Overlooked NIR Luminescence of Cr(ppy)3, Chem. Commun., 2022, 58(22), 3701–3704 RSC.
- L. Y. Martin, C. R. Sperati and D. H. Busch, The Spectrochemical Properties of Tetragonal Complexes of High Spin Nickel(II) Containing Macrocyclic Ligands, J. Am. Chem. Soc., 1977, 99(9), 2968–2981 CrossRef CAS.
- M. G. Brik, Crystal Field Analysis of the Absorption Spectra and Electron–Phonon Interaction in Ca3Sc2Ge3O12:Ni2+, J. Phys. Chem. Solids, 2006, 67(4), 738–744 CrossRef CAS.
- M. G. Brik, N. M. Avram, C. N. Avram, C. Rudowicz, Y. Y. Yeung and P. Gnutek, Ground and Excited State Absorption of Ni2+ Ions in MgAl2O4: Crystal Field Analysis, J. Alloys Compd., 2007, 432(1), 61–68 CrossRef CAS.
- M. G. Brik, C. N. Avram and N. M. Avram, Comparative Study of Crystal Field Effects for Ni2+ Ion in LiGa5O8, MgF2 and AgCl Crystals, J. Phys. Chem. Solids, 2008, 69(7), 1796–1801 CrossRef CAS.
- N. Mironova-Ulmane, M. G. Brik and I. Sildos, Crystal Field Calculations of Energy Levels of the Ni2+ Ions in MgO, J. Lumin., 2013, 135, 74–78 CrossRef CAS.
- W. N. Setzer, C. A. Ogle, G. S. Wilson and R. S. Glass, 1,4,7-Trithiacyclononane, a Novel Tridentate Thioether Ligand, and the Structure of Its Nickel(II), Cobalt(II), and Copper(II) Complexes, Inorg. Chem., 1983, 22(2), 266–271 CrossRef CAS.
- K. Wieghardt, H.-J. Küppers and J. Weiss', Preparation and Crystal Structure of Bis(l,4,7-Trithiacyclononane)Iron(II) Bis(Hexafluorophosphate) Containing an Octahedral, Low-Spin FeIIS6 Core. Electrochemistry of [M([9]aneS3)2]2+ Complexes (M = Fe, Co, Ni), Inorg. Chem., 1985, 24(19), 3067–3071 CrossRef.
- G. S. Wilson, D. D. Swanson and R. S. Glass, Cobalt(II) Bis(1,4,7-Trithiacyclononane): A Low-Spin Octahedral Complex, Inorg. Chem., 1986, 25(21), 3827–3829 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach, Chem. Phys., 1980, 48(2), 157–173 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, Introduction of n-Electron Valence States for Multireference Perturbation Theory, J. Chem. Phys., 2001, 114(23), 10252–10264 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA Quantum Chemistry Program Package, J. Chem. Phys., 2020, 152(22), 224108 CrossRef CAS PubMed.
- Y. Tanabe and S. Sugano, On the Absorption Spectra of Complex Ions. I, J. Phys. Soc. Jpn., 1954, 9(5), 753–766 CrossRef CAS.
- M. Dorn, K. Mack, L. M. Carrella, E. Rentschler, C. Förster and K. Heinze, Structure and Electronic Properties of an Expanded Terpyridine Complex of Nickel(II) [Ni(ddpd)2](BF4)2, Z. Anorg. Allg. Chem., 2018, 644(14), 706–712 CrossRef CAS.
- F. Neese and E. I. Solomon, Calculation of Zero-Field Splittings, g-Values, and the Relativistic Nephelauxetic Effect in Transition Metal Complexes. Application to High-Spin Ferric Complexes, Inorg. Chem., 1998, 37(26), 6568–6582 CrossRef CAS PubMed.
- S. M. Greer, K. M. Gramigna, C. M. Thomas, S. A. Stoian and S. Hill, Insights into Molecular Magnetism in Metal–Metal Bonded Systems as Revealed by a Spectroscopic and Computational Analysis of Diiron Complexes, Inorg. Chem., 2020, 59(24), 18141–18155 CrossRef CAS PubMed.
- F. El-Khatib, B. Cahier, M. López-Jordà, R. Guillot, E. Rivière, H. Hafez, Z. Saad, J.-J. Girerd, N. Guihéry and T. Mallah, Design of a Binuclear Ni(II) Complex with Large Ising-Type Anisotropy and Weak Anti-Ferromagnetic Coupling, Inorg. Chem., 2017, 56(17), 10655–10663 CrossRef CAS PubMed.
- N. Suaud, G. Rogez, J.-N. Rebilly, M.-A. Bouammali, N. Guihéry, A.-L. Barra and T. Mallah, Playing with Magnetic Anisotropy in Hexacoordinated Mononuclear Ni(II) Complexes, An Interplay Between Symmetry and Geometry, Appl. Magn. Reson., 2020, 51(11), 1215–1231 CrossRef CAS.
- D. Maganas, J. Krzystek, E. Ferentinos, A. M. Whyte, N. Robertson, V. Psycharis, A. Terzis, F. Neese and P. Kyritsis, Investigating Magnetostructural Correlations in the Pseudooctahedral Trans-[NiII{(OPPh2)(EPPh2)N}2(Sol)2] Complexes (E = S, Se; Sol = DMF, THF) by Magnetometry, HFEPR, and Ab Initio Quantum Chemistry, Inorg. Chem., 2012, 51(13), 7218–7231 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR, J. Magn. Reson., 2006, 178(1), 42–55 CrossRef CAS PubMed.
- J. L. Manson, S. H. Lapidus, P. W. Stephens, P. K. Peterson, K. E. Carreiro, H. I. Southerland, T. Lancaster, S. J. Blundell, A. J. Steele, P. A. Goddard, F. L. Pratt, J. Singleton, Y. Kohama, R. D. McDonald, R. E. D. Sesto, N. A. Smith, J. Bendix, S. A. Zvyagin, J. Kang, C. Lee, M.-H. Whangbo, V. S. Zapf and A. Plonczak, Structural, Electronic, and Magnetic Properties of Quasi-1D Quantum Magnets [Ni(HF2)(Pyz)2]X (Pyz = Pyrazine; X = PF6−, SbF6−) Exhibiting Ni-FHF-Ni and Ni-Pyz-Ni Spin Interactions, Inorg. Chem., 2011, 50(13), 5990–6009 CrossRef CAS PubMed.
- K. N. Shrivastava, Zero-Field Splittings in NiSiF6·6H2O as Electron Paramagnetic Resonance Thermometer, Chem. Phys. Lett., 1973, 20(1), 106–107 CrossRef CAS.
- P. B. Sczaniecki and J. Lesiak, EPR Fine Structure of Divalent Nickel Ions in Powders and Single Crystals of Hexakis-Imidazole-Nickel(II) Nitrate, J. Magn. Reson., 1982, 46(2), 185–192 CAS.
- A. Mašlejová, R. Ivaniková, I. Svoboda, B. Papánková, L. Dlháň, D. Mikloš, H. Fuess and R. Boča, Structural Characterization and Magnetic Properties of Hexakis(Imidazole)Nickel(II) Bis(Formate), Bis(Chloroacetate), Bis(2-Chloropropionate) and Hexakis(1-Methyl-Imidazole)Nickel(II) Chloride Dihydrate, Polyhedron, 2006, 25(8), 1823–1830 CrossRef.
- J. Krzystek, A. Ozarowski and J. Telser, Multi-Frequency, High-Field EPR as a Powerful Tool to Accurately Determine Zero-Field Splitting in High-Spin Transition Metal Coordination Complexes, Coord. Chem. Rev., 2006, 250(17), 2308–2324 CrossRef CAS.
- J. A. R. Hartman and S. R. Cooper, Crown Thioether Chemistry. Synthetic, Structural, and Physical Studies of the Copper(II) and Copper(I) Complexes of Hexathia-18-Crown-6, J. Am. Chem. Soc., 1986, 108(6), 1202–1208 CrossRef CAS.
- D. Reinen, A. Ozarowski, B. Jakob, J. Pebler, H. Stratemeier, K. Wieghardt and I. Tolksdorf, Spectroscopic and Magnetic Properties of Pseudooctahedral Cu2+ and Co2+ Complexes with 1,4,7-Triazacyclononane and Its Monooxa and Trithia Analogs as Ligands, Inorg. Chem., 1987, 26(24), 4010–4017 CrossRef CAS.
- A. J. Blake, M. A. Halcrow, A. J. Holder and M. Schroder, Nickel Thioether Chemistry: A Re-Examination of the Electrochemistry of [Ni([9]aneS3)2I2+]. The Single-Crystal X-Rav Structure of a Nickel(III) Thioether Complex, [NiIII([9]aneS3)2][H5O2]3[CIO4]6 ([9]aneS3 = 1,4,7-Trithiacyclononane), J. Chem. Soc., Dalton Trans., 1992, 5, 3427–3431 RSC.
- R. S. Rubins, Dynamic and Static Contributions to the Zero-Field Splitting Term of Divalent Nickel in Fluosilicate Crystals, J. Phys. Chem. Solids, 2005, 66(10), 1675–1682 CrossRef CAS.
- J. P. Lee, G. J. Grant and B. C. Noll, Bis(1,4,7-Trithiacyclononane)Nickel(II) Bis-(Tetrafluoridoborate) Nitromethane Disolvate, Acta Crystallogr. E, 2011, 67(10), m1417–m1418 CrossRef CAS PubMed.
- W. N. Setzer, Q. Guo, G. J. Grant, J. L. Hubbard, R. S. Glass and D. G. VanDerveer, 1,4,7-Trithiacyclononane as a Tridentate Ligand for Complexation of Heavy-Metal Ions: Synthesis and Complexation Studies of Mesocyclic and Macrocyclic Polythioethers IV, Heteroat. Chem., 1990, 1(4), 317–325 CrossRef CAS.
- J. L. Manson, Z. E. Manson, A. Sargent, D. Y. Villa, N. L. Etten, W. J. A. Blackmore, S. P. M. Curley, R. C. Williams, J. Brambleby, P. A. Goddard, A. Ozarowski, M. N. Wilson, B. M. Huddart, T. Lancaster, R. D. Johnson, S. J. Blundell, J. Bendix, K. A. Wheeler, S. H. Lapidus, F. Xiao, S. Birnbaum and J. Singleton, Enhancing Easy-Plane Anisotropy in Bespoke Ni(II) Quantum Magnets, Polyhedron, 2020, 180, 114379 CrossRef CAS.
- J. L. Manson, S. P. M. Curley, R. C. Williams, D. Walker, P. A. Goddard, A. Ozarowski, R. D. Johnson, A. M. Vibhakar, D. Y. Villa, M. L. Rhodehouse, S. M. Birnbaum and J. Singleton, Controlling Magnetic Anisotropy in a Zero-Dimensional S = 1 Magnet Using Isotropic Cation Substitution, J. Am. Chem. Soc., 2021, 143(12), 4633–4638 CrossRef CAS PubMed.
- M. Rubín-Osanz, F. Lambert, F. Shao, E. Rivière, R. Guillot, N. Suaud, N. Guihéry, D. Zueco, A.-L. Barra, T. Mallah and F. Luis, Chemical Tuning of Spin Clock Transitions in Molecular Monomers Based on Nuclear Spin-Free Ni(ii), Chem. Sci., 2021, 12, 5123–5133 RSC.
- J. M. Zadrozny, M. J. Graham, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Unexpected Suppression of Spin–Lattice Relaxation via High Magnetic Field in a High-Spin Iron(iii) Complex, Chem. Commun., 2016, 52(66), 10175–10178 RSC.
- K. Knox, R. G. Shulman and S. Sugano, Covalency Effects in KNiF3. II. Optical Studies, Phys. Rev., 1963, 130(2), 512–516 CrossRef CAS.
- R. Yang and L. J. Zompa, Metal Complexes of Cyclic Triamines. 1. Complexes of 1,4,7-Triazacyclononane ([9]aneN3) with Nickel(II), Copper(II), and Zinc(II), Inorg. Chem., 1976, 15(7), 1499–1502 CrossRef CAS.
- D. A. Vander Griend, D. K. Bediako, M. J. DeVries, N. A. DeJong and L. P. Heeringa, Detailed Spectroscopic, Thermodynamic, and Kinetic Characterization of Nickel(II) Complexes with 2,2′-Bipyridine and 1,10-Phenanthroline Attained via Equilibrium-Restricted Factor Analysis, Inorg. Chem., 2008, 47(2), 656–662 CrossRef CAS PubMed.
- Y. Tanabe and S. Sugano, On the Absorption Spectra of Complex Ions II, J. Phys. Soc. Jpn., 1954, 9(5), 766–779 CrossRef CAS.
- G. Racah, Theory of Complex Spectra. II, Phys. Rev., 1942, 62(9–10), 438–462 CrossRef CAS.
- R. Stranger, S. C. Wallis, L. R. Gahan, C. H. L. Kennard and K. A. Byriel, Spectroscopic and Ligand-Field Analysis of the Spin–Orbit Interaction between the 1Eg and 3T2g States in Bis(1,4,7-Triazacyclononane)Nickel(II), J. Chem. Soc., Dalton Trans., 1992, 20, 2971–2976 RSC.
- M. G. Brik, S. J. Camardello, A. M. Srivastava, N. M. Avram and A. Suchocki, Spin-Forbidden Transitions in the Spectra of Transition Metal Ions and Nephelauxetic Effect, ECS J. Solid State Sci. Technol., 2016, 5(1), R3067–R3077 CrossRef CAS.
- O. S. Wenger, S. Bénard and H. U. Güdel, Crystal Field Effects on the Optical Absorption and Luminescence Properties of Ni2+-Doped Chlorides and Bromides: Crossover in the Emitting Higher Excited State, Inorg. Chem., 2002, 41(23), 5968–5977 CrossRef CAS PubMed.
- M. G. Brik, A. M. Srivastava, N. M. Avram and A. Suchocki, Empirical Relation between Covalence and the Energy Position of the Ni2+ 1E State in Octahedral Complexes, J. Lumin., 2014, 148, 338–341 CrossRef CAS.
- E. T. Basore, X. Liu and J. Qiu, Broadband Near-IR Photoluminescence in Ni2+ Doped Gallium Silicate Glass–Ceramics, J. Mater. Sci.: Mater. Electron., 2019, 30(19), 17715–17724 CrossRef CAS.
- P. W. K. Rothemund, Folding DNA to Create Nanoscale Shapes and Patterns, Nature, 2006, 440(7082), 297–302 CrossRef CAS PubMed.
- R. Veneziano, S. Ratanalert, K. Zhang, F. Zhang, H. Yan, W. Chiu and M. Bathe, Designer Nanoscale DNA Assemblies Programmed from the Top Down, Science, 2016, 352(6293), 1534 CrossRef CAS PubMed.
- E.-C. Wamhoff, J. L. Banal, W. P. Bricker, T. R. Shepherd, M. F. Parsons, R. Veneziano, M. B. Stone, H. Jun, X. Wang and M. Bathe, Programming Structured DNA Assemblies to Probe Biophysical Processes, Annu. Rev. Biophys., 2019, 48(1), 395–419 CrossRef CAS PubMed.
- N. R. East, C. Dab, C. Förster, K. Heinze and C. Reber, Coupled Potential Energy Surfaces Strongly Impact the Lowest-Energy Spin-Flip Transition in Six-Coordinate Nickel(II) Complexes, Inorg. Chem., 2023, 62(23), 9025–9034 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental details, synthetic procedures, UV-Vis spectroscopy, EPR spectroscopic details, powder X-ray crystallographic details, full computational details, and additional computational analysis. See DOI: https://doi.org/10.1039/d3sc04919a |
| This journal is © The Royal Society of Chemistry 2024 |