Snap-shots of cluster growth: structure and properties of a Zintl ion with an Fe₃ core, [Fe₃Sn₁₈]⁴⁻

Abstract

The endohedral Zintl-ion cluster [Fe₃Sn₁₈]⁴⁻ contains a linear Fe₃ core with short Fe–Fe bond lengths of 2.4300(9) Å. The ground state is a septet, with significant σ and π contributions to the Fe–Fe bonds. The Sn₁₈ cage is made up of two partially fused Sn₉ fragments, and is structurally intermediate between [Ni₂CdSn₁₈]⁶⁻, where the fragments are clearly separated and [Pd₂Sn₁₈]⁴⁻, where they are completely fused. It therefore represents an intermediate stage in cluster growth. Analysis of the electronic structure suggests that the presence of the linear Fe–Fe–Fe unit is an important factor in directing reactions towards fusion of the two Sn₉ units rather than the alternative of oligomerization via exo bond formation.

---

Introduction

The chemistry of Zintl ions, and in particular those containing endohedral metals, has been the subject of several recent reviews,^1–9 and applications in catalysis and materials chemistry are beginning to emerge.^10,11 The vast majority of these clusters are relatively small (14 main-group atoms or fewer) and contain a single transition metal ion, often with a closed-shell d¹⁰ configuration: classic examples include the icosahedral triad [Ni/Pd/PtPb₁₂]²⁻,¹² but the range of encapsulated metals now includes much of the d block. Larger clusters containing multiple transition metals are much less common but they offer the possibility of unusual magnetic phenomena and/or metal–metal bonding. Amongst the few known examples,¹³ the Ge₁₈ series [Ni₂InGe₁₈]⁵⁻,¹⁴ [Ni₃Ge₁₈]⁴⁻,¹⁵ and [Pd₂Ge₁₈]⁴⁻ (ref. 16) (Fig. 1) maps out a progressive fusion of the two Ge₉ polyhedra which are well separated in [Ni₂InGe₁₈]⁵⁻ but fully coalesced in the Pd cluster. [Ni₃Ge₁₈]⁴⁻ appears to be an intriguing intermediate case, where the fusion is only partially complete. It is far from clear how these clusters are actually formed in situ, but it is certainly plausible that the stepwise fusion of pre-formed polyhedral E₉ or ME₉ fragments is involved. Indeed, Sevov and Goicoechea proposed the fusion of NiGe₉ and Ni₂Ge₉ units as a possible route to formation of [Ni₃Ge₁₈]⁴⁻,¹⁷ and Dehnen's analysis of fragmentation patterns for [TaGe₄As₈]³⁻ and [TaGe₆As₆]³⁻ identified cluster fragments such as [Ge₂As₂]²⁻ and [Ge₃As]³⁻ that may play a role in growth.¹⁸ The challenge from a synthetic perspective is that these component polyhedra typically carry high negative charges, and so their close approach incurs a high coulombic penalty. Transition metal ions that can bridge two polyhedral units may, therefore, play an important role in fusion by buffering these repulsions and also, potentially, by removing excess electron density through the extrusion of metal in the elemental form. A further complication is that the oxidative fusion of clusters is, at least in principle, in competition with oxidative oligomerisation via the formation of exo E–E bonds (Fig. 1(b)). This phenomenon is well established in Ge chemistry where linked chains of Ge₉ are known.^17,19 A deeper understanding of the factors that control cluster growth and the balance between fusion and oligomerisation may provide access to a wider range of element combinations and compositions, and to tailored structural, magnetic and catalytic properties.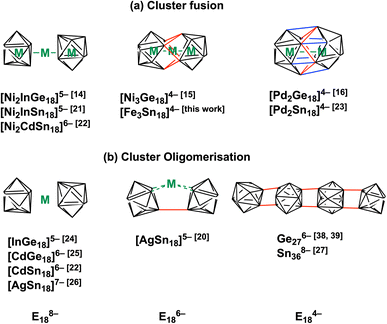

Fig. 1 Cluster fusion vs. cluster oligomerisation of E₉ polyhedra, E = Ge, Sn.^{14–16,19–29}

In this paper, we extend our recent work on the Zintl-ion chemistry of tin by reporting the synthesis of a new cluster, [Fe₃Sn₁₈]⁴⁻, which has a linear Fe₃ chain and Fe–Fe bond lengths of 2.4300(9) Å. The Fe₃ chain is of significant interest in its own right – there are few examples of metal–metal bonded units encapsulated inside Zintl clusters, and the short Fe–Fe distances are a clear a priori indication of strong bonding. Of equal interest is the structure of the Sn₁₈ cage because the degree of fusion of the two Sn₉ polyhedra appears to be mid-way between the completely separated limited, as observed in [Ni₂CdSn₁₈]⁶⁻, and the completely fused limit in [Pd₂Sn₁₈]⁴. [Fe₃Sn₁₈]⁴⁻ is, therefore, the Sn analogue of the Ge₁₈ unit in [Ni₃Ge₁₈]⁴⁻. Our analysis of the electronic structure indicates that the E₁₈ cages in [Ni₃Ge₁₈]⁴⁻ and [Fe₃Sn₁₈]⁴⁻ share a common −6 charge state, as does the Sn₁₈ unit in [AgSn₁₈]⁵⁻,²⁰ where the two Sn₉ units are not fused but rather oligomerised via an exo bond (Fig. 1(b)). A comparison of the different structural chemistry of these isoelectronic species offers a fascinating insight into the factors that control the balance between fusion in [Fe₃Sn₁₈]⁴⁻ and [Ni₃Ge₁₈]⁴⁻ and oligomerisation in [AgSn₁₈]⁵⁻.

Results and discussion

Structure and properties of [Fe₃Sn₁₈]⁴⁻

The reaction of ethylenediamine (en) solutions of K₄Sn₉ with [K(thf)Fe(O^tBu)₃]₂ (thf = tetrahydrofuran) results in the formation of the tri-iron cluster [Fe₃Sn₁₈]⁴⁻ in the form of its [K(2.2.2-crypt)]⁺ salt [K(2.2.2-crypt)]₄[Fe₃Sn₁₈] (1). Electrospray ionisation mass spectrometry (ESI-MS) of freshly-prepared DMF (DMF = dimethylformamide) solutions of 1 reveals a peak attributable to the dianion [Fe₃Sn₁₈]²⁻ (m/z 1152.0323 – note the peak-to-peak separations of 0.5 between isotopologues that confirm the −2 charge, Fig. 2(c)) and also a very weak signal assigned to the cation–dianion pair [K(2.2.2-crypt)Fe₃Sn₁₈]⁻ (m/z 2719.2300). It is common to observe only singly charged anions in the ESI-MS of Zintl clusters, but the large size of the Fe₃Sn₁₈ unit reduces the coulomb repulsion in the dianion to the extent that it is not ionized under the prevailing conditions. 1 crystallises in the monoclinic space group P2₁/c and the unit cell contains a single anionic [Fe₃Sn₁₈]⁴⁻ cluster with four [K(2.2.2-crypt)]⁺ cations (Fig. 2(a) and (b), CCDC 2170116). The Sn₁₈ unit adopts a D_3d-symmetric structure based on two Sn₉ polyhedra in a staggered, face-to-face arrangement, with a chain of three Fe centers aligned along the principal axis. In this section and the following discussion of the electronic structure, we focus first on the Fe₃ chain, where Fe–Fe bonding is the primary interest, before turning to the Sn₁₈ cage which we try to place in the wider context of Zintl-ion chemistry. The Fe–Fe bond lengths of 2.4300(9) Å in 1 are remarkably short, much shorter than those in the other known Fe₂-containing Zintl cluster, [Fe₂Ge₁₆]⁴⁻ (2.636(3) Å). Even shorter bonds are known in Fe₂ dimers such as the Fe^IFe^I paddlewheel complex³⁰ (2.127 Å) and the (as-yet unknown) Fe₂C₃₀ (2.10 Å).³¹ Direct comparison with other Fe₃ chains is restricted to classical coordination compounds such as Guillet's bis[(trimethylsilyl)amido]pyridine complex (Fig. 3(a), referred to henceforth as Fe₃L₃) where the Fe–Fe bond lengths are 2.4416(5) Å (ref. 32) and to the [Fe₃(DpyF)₄]²⁺ complex (DpyF = dipyridylformamide) first synthesised by Cotton and Murrillo³³ and subsequently studied by Hillard and co-workers,³⁴ where the Fe–Fe bond lengths are longer, at 2.7838(5) Å. These two Fe^IIFe^IIFe^II complexes share a common S = 6 ground state and a common formal σ bond order of 0.25 (per Fe–Fe bond), but differ in the distribution of electrons in the levels of π symmetry, with only Fe₃L₃ having an additional π component to the Fe–Fe bond. Correlations between bond order and bond length are notoriously difficult when bridging ligands are present, but nevertheless the similar bond lengths in [Fe₃Sn₁₈]⁴⁻ and Fe₃L₃ offers an initial indication that Fe–Fe π bonding may also be significant in the former. We return to this question in the following discussion of the electronic structure of the cluster. Turning our focus now to the structure of the Sn₁₈ cage, we note first that the cluster can be viewed as two FeSn₉ units, bridged by a third Fe center. We can make useful comparison to the pair of closely-related clusters identified in Fig. 3(b), [Ni₂CdSn₁₈]⁶⁻,²² and [Pd₂Sn₁₈]⁴⁻,²³ where we judge the degree of fusion of the two Sn₉ units in terms of two distinct Sn–Sn distances identified in Fig. 2, Sn8−Sn9′ and Sn4−Sn9′. The average values of these are 3.46 Å and 4.10 Å, respectively in [Fe₃Sn₁₈]⁴⁻ compared to 5.24 Å and 6.71 Å for [Ni₂CdSn₁₈]⁶⁻ and 3.31 Å and 3.10 Å for [Pd₂Sn₁₈]⁶⁻. The Sn8−Sn9′ bond lengths in [Fe₃Sn₁₈]⁴⁻ are therefore very similar to those in [Pd₂Sn₁₈]⁴⁻, but the Sn4−Sn9′ bonds are fully 1 Å longer. On this basis, we argue that the Sn₁₈ cage in [Fe₃Sn₁₈]⁴⁻ represents an intermediate stage in the cluster fusion process that occupies the same central position in Sn cluster chemistry as [Ni₃Ge₁₈]⁴⁻ cluster¹⁵ does in the [Ni₂InGe₁₈]⁵⁻, [Ni₃Ge₁₈]⁴⁻, [Pd₂Ge₁₈]⁴⁻ series identified in Fig. 1.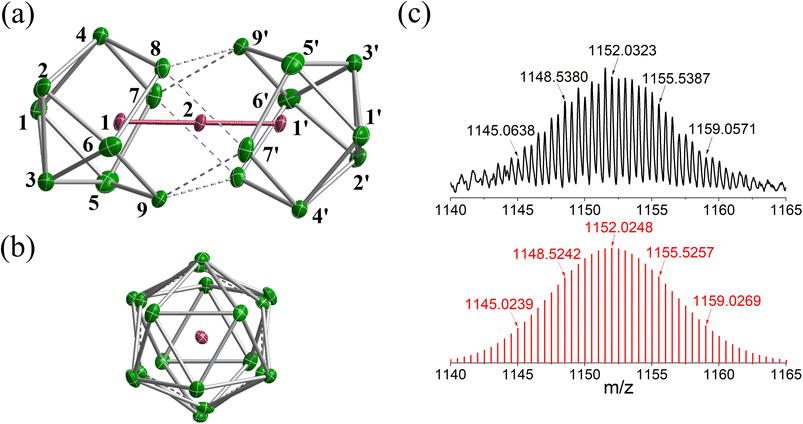

Fig. 2 (a) and (b) Structure of anionic component, [Fe₃Sn₁₈]⁴⁻, of 1 and (c) the ESI-MS of a freshly-prepared solution of 1 in DMF.

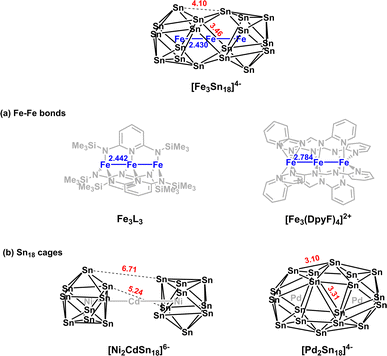Fig. 3 Structural comparisons with [Fe₃Sn₁₈]³⁻: (a) other linear Fe₃ coordination compounds and (b) other E₁₈ Zintl clusters.

Electronic structure

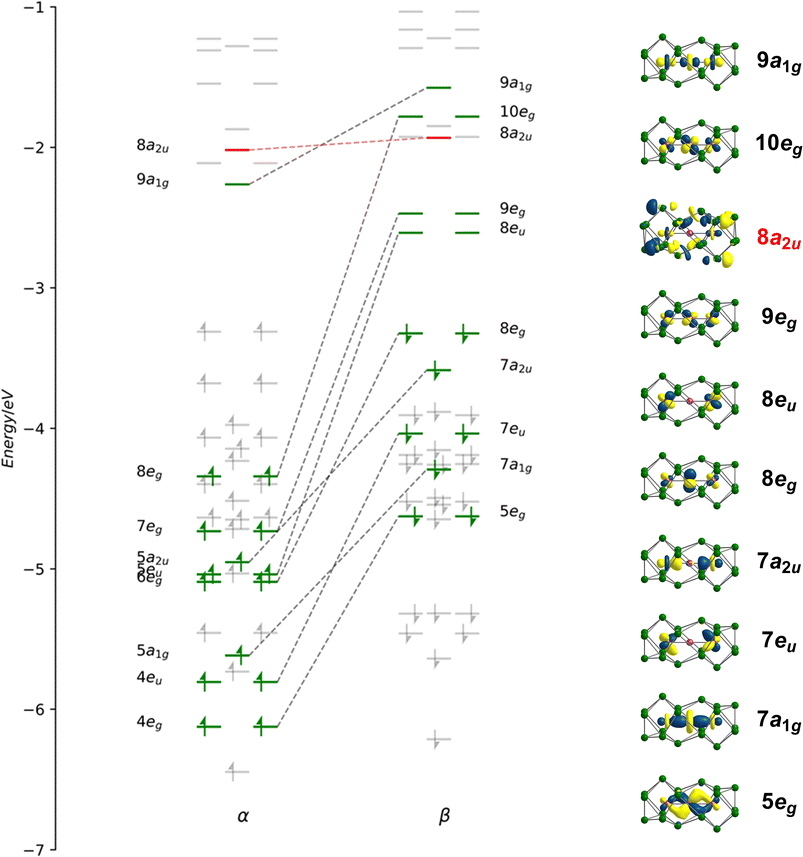
Geometry optimisations using the PBE functional indicate that the lowest energy state for [Fe₃Sn₁₈]⁴⁻ is a spin septet (S = 3), ⁷A_2g, with optimised Fe–Fe bond lengths of 2.45 Å, in excellent agreement with the available X-ray data (Table 1). The Fe–Sn and Sn–Sn bond lengths are also fully consistent with experiment. Despite multiple attempts, we have been unable to measure reproducible magnetic susceptibilities to confirm the paramagnetism of [Fe₃Sn₁₈]⁴⁻: this likely reflects the challenges in producing a homogeneous sample, and in avoiding oxidative degradation during the course of the experiment. The spin-polarised Kohn–Sham eigenvalues and eigenfunctions of the ⁷A_2g ground state are collected in Fig. 4: levels that are localised primarily on the Fe₃ chain are shown in green while those localised primarily on Sn are in grey. The same data, in the form of projected density of states (PDOS) and overlap projected density of states (OPDOS), is presented and discussed in the ESI, Fig. S8.† Of the 100 valence electrons of the cluster, we can identify 22, colored green, that are distributed over the 15 linear combinations of Fe 3d orbitals in Fig. 4 (4e_g, 5a_1g, 4e_u, 7a_2u, 6e_g, 5e_u, 7e_g, 8e_g and 9a_1g in the α set). It is notoriously difficult to assign oxidation formal states in endohedral Zintl clusters, where transition- and main-group metal orbitals are typically well mixed, but the presence of 22 valence electrons indicates a Fe²₃⁺ chain, and hence a Sn₁₈ cluster in a −6 oxidation state.

Fig. 4 (a) Kohn–Sham orbitals for [Fe₃Sn₁₈]⁴⁻ in its ⁷A_2g ground state. Levels shown in green are the primarily Fe-based orbitals while the remainder, in grey, have dominant Sn character. Orbitals with similar spatial characteristics are joined by a dashed line.

Table 1 Selected bond lengths from crystallographic and DFT-optimised structures for the [M₃E₁₈]⁴⁻ family (all distances in Å). See Fig. 2(a) for atom numbering

		M1–M2	M1–E1	M2–E8	E2–E8	E2–E4	E6–E9	E8−E9′	E4−E9′	Ref.
[Fe3Sn18]^4−	X-ray (100 K)	2.4300(9)	2.882	2.689	3.690	3.001	3.004	3.460	4.10	This work
	DFT (^7A2g)	2.45	2.98	2.70	3.64	3.07	3.04	3.50	4.22
[Ni3Ge18]^3−	X-ray (100 K)	2.395(1)	2.487	2.529	3.016	2.749	2.612	3.47	4.05	15
	DFT (^1A1g)	2.43	2.50	2.52	3.09	2.76	2.66	3.29	4.01
[Ni2CdSn18]^6−	X-ray (100 K)	4.201	2.595	3.206	3.549	3.011	2.981	5.24	6.71	22
	DFT (^1A1g)	4.26	2.64	3.13	3.71	3.07	3.02	5.32	6.81

---

Of the 15 metal-based orbitals, only one, the strongly Fe–Fe–Fe σ anti-bonding 9a_1g orbital, is vacant in both spin-α and spin-β manifolds, while the complementary σ bonding and non-bonding orbitals, 5a_1gα, 7a_1gβ and 5a_2uα, 7a_2uβ, are doubly occupied: the σ²σ^nb2σ*⁰ configuration gives a net σ bond order of 0.5 per Fe–Fe bond. Fe–Fe π and δ interactions are mixed in the orbitals of e_g and e_u symmetry, but the π interactions are primarily contained in 4e_g, 4e_u and 8e_g in the α manifold, 5e_g, 7e_u and 10e_g in β. The prominent positive and negative peaks in the OPDOS shown in ESI, Fig. S8,† corresponding to 5e_gβ (π bonding) and 10e_gβ (π antibonding), respectively, confirm the very significant π overlap. The π⁴π^nb4π*² configuration then defines a formal Fe–Fe π bond order of 0.5 per bond. There are no large peaks in the OPDOS for the orbitals with dominant Fe–Fe δ symmetry (5e_uα, 7e_gα, 9e_gα, 8e_uβ, 8e_gβ, 9e_gβ), so δ bonding can be assumed to be negligible, as might be expected at a distance of 2.4300(9) Å. The overall formal Fe–Fe bond order is therefore 1.0 per Fe–Fe bond made up of 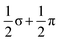. Returning to the comparison with the coordination complexes [Fe(DpyF)₄]²⁺ (ref. 34) and Fe₃L₃,³² identified in Fig. 3, the overall oxidation state of the Fe₃ unit is lower in [Fe₃Sn₁₈]⁴⁻ (Fe²₃⁺vs. Fe⁶₃⁺) and the Fe–Fe σ* orbital is unoccupied, both of which contribute to the lower multiplicity (S = 3 vs. S = 6) and stronger Fe–Fe bonding in the cluster compared to the coordination complexes.

To place the Fe–Fe bonding into the wider context of Zintl cluster chemistry, we can make a connection to Sevov and Goicoechea's [Ni₃Ge₁₈]⁴⁻, which is a spin singlet with a total valence electron count of 106. The additional six electrons occupy the three doubly degenerate, metal-based, spin-β orbitals, 8e_uβ, 9e_gβ and 10e_gβ, eliminating the π component of the metal–metal bond but leaving the σ²σ^nb2σ*⁰ framework intact. The M–M Mayer bond order³⁵ is reduced from 0.95 in [Fe₃Sn₁₈]⁴⁻ to 0.45 in [Ni₃Ge₁₈]⁴⁻, and the delocalisation index (DI)³⁶ from 0.69 to 0.44, both metrics pointing to a significant π component to the Fe–Fe bond in [Fe₃Sn₁₈]⁴⁻. The addition of 6 electrons to the metal chain generates a Ni²₃⁺ unit and, hence, a Ge₁₈ cluster in the −6 oxidation level. Switching our focus now to the Sn₁₈ cage, we can identify a single vacant orbital, 8a_2u, picked out in red in Fig. 4, that has Sn–Sn σ* character between the Sn₃ faces bound to the central Fe atom (Sn8−Sn9′ in Fig. 2). This orbital, along with its doubly-occupied Sn–Sn bonding counterpart, generates a 6-center-2-electron bond that links the two Sn₉ units.

Cluster fusion vs. cluster oligomerisation

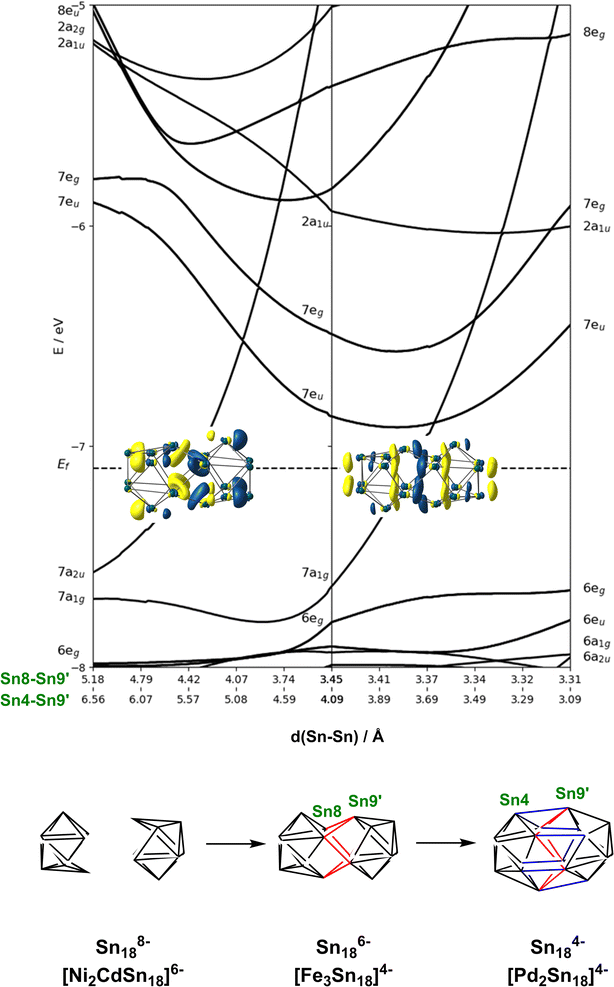
In the previous section we have established a link between the new cluster [Fe₃Sn₁₈]⁴⁻ and [Ni₃Ge₁₈]⁴⁻ through their common oxidation level of −6 for the E₁₈ cluster unit. In this section, we try to identify broader relationships between the family of clusters with 18 tetrel vertices (E₁₈) but rather different structures. Amongst these, we can pick out the two pairs, [Ni₂CdSn₁₈]⁶⁻ and [Ni₂InGe₁₈]⁵⁻and [Pd₂Sn₁₈]⁴⁻ and [Pd₂Ge₁₈]⁴⁻ shown in Fig. 1 all of which share a common point symmetry, D_3d, with [Fe₃Sn₁₈]⁴⁻ and [Ni₃Ge₁₈]⁴⁻. The oxidation states of the E₁₈ unit in these four clusters are rather easier to establish: in [Pd₂Ge₁₈]⁴⁻ and [Pd₂Sn₁₈]⁴⁻, the Pd atoms are diamagnetic and can be assigned straightforwardly a formal oxidation state of 0 (d¹⁰), leaving the Sn₁₈ unit in a −4 charge state. In [Ni₂InGe₁₈]⁵⁻ and [Ni₂CdSn₁₈]⁶⁻, in contrast, the diamagnetism implies Ni⁰, Cd²⁺ and In³⁺ (all d¹⁰), defining a charge of −8 on the Sn₁₈ unit. Structurally, the two E₉ units are separated by more than 4.0 Å in [Ni₂InGe₁₈]⁵⁻ and [Ni₂CdSn₁₈]⁶⁻ but are very tightly compressed in [Pd₂Ge₁₈]⁴⁻ and [Pd₂Sn₁₈]⁴⁻, where the E₁₈ unit forms a continuous ellipsoidal cage. From a structural perspective, [Fe₃Sn₁₈]⁴⁻ and [Ni₃Ge₁₈]⁴⁻ appear to be precisely intermediate between the two limits, with two partially but not fully coalesced E₉ units, consistent with the formal charge assignment of Sn₁₈⁶⁻.

If we wish to analyse the electronic origins of these structural trends we are faced with the immediate problem that in some cases the clusters contain 3 transition metal ions but in others only 2. In order to circumvent this difficulty, we choose to focus on the electronic structure of the empty cage, Sn₁₈, and explore its dependence on charge state: −8 → −6 → −4. The relationship between structure and charge state can be made explicit by the Walsh diagram for the isolated E₁₈ cluster shown in Fig. 5 (calculated using extended Hückel theory). This figure is constructed by extracting the structures of the Sn₁₈ units from DFT optimisations of [Ni₂CdSn₁₈]⁶⁻, [Fe₃Sn₁₈]⁴⁻ and [Pd₂Sn₁₈]⁴⁻ and interpolating between these three geometries. A comment on the choice of reaction coordinate is necessary here. The fusion of the two Sn₉ units proves to be highly asynchronous: the structural impact of the first 2-electron oxidation is very different from the second 2-electron oxidation. In such circumstances, no single structural parameter can adequately capture the changes occurring across the entire spectrum, from 2 × Sn₉⁴⁻ on the left to Sn₁₈⁴⁻ on the right. We therefore choose to identify two distinct Sn–Sn distances that serve as independent measures of structural change. The Sn8−Sn9′ distance is closely related to the distance between the centroids of the two Sn₉ units, and it varies rapidly as we go from 2 × Sn₁₈⁴⁻ to Sn₁₈⁶⁻, and then more slowly from Sn₁₈⁶⁻ to Sn₁₈⁴⁻. The Sn8−Sn9′ distance, in contrast, varies strongly in the left half of the diagram, but is relatively constant as we move from Sn₁₈⁶⁻ to Sn₁₈⁴⁻. We can, therefore associate the first 2-electron oxidation with a relative motion of the two Sn₉ units towards each other, such that both Sn4−Sn9′ and Sn8−Sn9′ contract. The second 2-electron step is then associated almost exclusively with the formation of the Sn4−Sn9′ bonds, with little further change in Sn8−Sn9′.

Fig. 5 Walsh diagram showing the coalescence of the two Sn₉ polyhedra to a single ellipsoidal Sn₁₈ unit. The figure is generated by interpolating between the optimised structures of the Sn₁₈ unit as it is found in the optimised geometries of [Ni₂CdSn₁₈]⁶⁻, [Fe₃Sn₁₈]⁴⁻ and [Pd₂Sn₁₈]⁴⁻.

At the separated limit (left hand side of Fig. 5) there is a total of 40 low-lying valence orbitals (up to 7a_2u) that can accommodate 80 valence electrons, the count for Sn₁₈⁸⁻. The transition from this separated limit to the intermediate structure typical of [Fe₃Sn₁₈]⁴⁻ (or [Ni₃Ge₁₈]⁴⁻) involves a reduction in the separation between the centroids of the two Sn₉ units, resulting in contraction of both the Sn8−Sn9′ and Sn4−Sn9′ distances. The result is the rapid destabilisation of a single orbital, 7a_2u, that is antibonding across Sn8−Sn9′ – this is the Sn–Sn antibonding orbital discussed previously in the context of Fig. 4 (where it was labelled 8a_2u due to the presence of a lower-lying Fe/Ni-based level of the same symmetry that is obviously absent in the empty cluster). In the second step, from the intermediate structure found in [Fe₃Sn₁₈]⁴⁻ to the fully coalesced one in [Pd₂Sn₁₈]⁴⁻, the Sn4−Sn9′ distance contracts from 4.22 Å to 3.10 Å, causing a rapid destabilisation of a second cluster-based orbital, 7a_1g, which is bonding with respect to the Sn8−Sn9′ contact but strongly anti-bonding with respect to Sn8−Sn9′. We note here that Lin and co-workers have also analysed the fusion of two PdSn₉ units from the perspective of the ‘principal interacting orbital’ model,^37–39 where they identified a σ-symmetry interaction between ‘principal interacting orbitals' localised on the Sn4 and Sn9′ atoms. To the extent that the structurally characterised clusters illustrated in Fig. 1 can be viewed as snapshots of the oxidative coalescence of two separated Sn₉ clusters, it seems that the 4-electron oxidation of Sn₁₈⁸⁻ to Sn₁₈⁴⁻ is a rather asynchronous one, with the two units coming together first via the formation of Sn8−Sn9′ bonds (shown in red in Fig. 5), followed by a distinct second 2-electron oxidation step that leads to formation of the Sn4−Sn9′ bonds (shown in blue in Fig. 5), completing the fusion of the two units.§

In the introduction we noted that there is, in principle, a competing pathway for oxidative coupling of Zintl clusters that leads to oligomerisation via exo bond formation rather than fusion to form a single ellipsoidal cage. This is precisely what is observed in the oxidation of [AgSn₁₈]⁷⁻ (ref. 26) to [AgSn₁₈]⁵⁻ (Fig. 1) where the charge on the Sn₁₈ unit (assuming a redox non-innocent Ag⁺ ion) is reduced from −8 to −6, precisely the same as in the [Ni₂CdSn₁₈]⁶⁻ to [Fe₃Sn₁₈]⁴⁻ comparison. What, then, are the factors that determine the preference for fusion of the two Sn₉ units in [Fe₃Sn₁₈]⁴⁻ with retention of three-fold rotational symmetry but oligomerisation in [AgSn₁₈]⁵⁻? From an electronic perspective, the Sn₁₈ units in the two clusters both have a 2-electron bond linking the two Sn₉ units – the only difference is that in [Fe₃Sn₁₈]⁴⁻ this bond is delocalised over 6 Sn–Sn contacts, each with a formal bond order of , while in [AgSn₁₈]⁵⁻ it is localised on one. It is possible that the preference for a fused architecture with a 6-center-2-electron bond in [Fe₃Sn₁₈]⁴⁻ (and also in [Ni₃Ge₁₈]⁴⁻) is connected to the presence of the underlying Fe–Fe–Fe or Ni–Ni–Ni bonded framework, which provides a rigid ‘strut’ that resists the bending at the central metal necessary to form a localised exo Sn–Sn bond. Where metal–metal bonding is absent, as it necessarily is in [AgSn₁₈]⁵⁻, bending to form a localised 2-center-2-electron bond is the preferred outcome: a series of DFT calculations on different isomers of [AgSn₁₈]⁵⁻ confirms a 0.2 eV preference for the bent structure shown in Fig. 1 over the alternative D_3d-symmetric [Fe₃Sn₁₈]⁴⁻-like alternative. Taking the argument a step further, a second 2-electron oxidation step could, in principle, generate clusters with two exo bonds linking the Sn₉ units as an alternative to forming the coalesced cage typical of [Pd₂Sn₁₈]⁴⁻ – doubly bonded E₉ units of this kind have been identified in the Ge₂₇^38,39 and Sn₃₆ nanorod²⁷ where again there is no underlying metal–metal bonded framework to oppose the bending.

Summary and conclusions

In this paper, we have reported the synthesis and structure of a new Zintl-ion cluster, [Fe₃Sn₁₈]⁴⁻, containing a linear Fe₃ chain with short Fe–Fe bond lengths of 2.4300(9) Å. Electronic structure analysis indicates the presence of both Fe–Fe σ and π bonding, with a formal net bond order of 1.0 (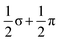) per Fe–Fe bond. The cluster is structurally similar to the [Ni₃Ge₁₈]⁴⁻ anion reported previously by Sevov and co-workers, although the Ni–Ni bonding in that case lacks the π component. The structure of the Sn₁₈ unit in [Fe₃Sn₁₈]⁴⁻ is intermediate between that in [Ni₂CdSn₁₈]⁶⁻, where the two Sn₁₈ units are almost completely separated, and [Pd₂Sn₁₈]⁴⁻, where they are completely fused to form a continuous ellipsoidal Sn₁₈ unit. These structural differences correlate with the redox level of the cage, with successive 2-electron oxidations starting from Sn₁₈⁸⁻ leading first to partial fusion of the two cages and then to their complete coalescence. One of the obvious challenges in forming ever larger Zintl ions from smaller fragments is that the latter carry high negative charges, so their close approach necessarily involves a substantial coulomb barrier. The identification of [Fe₃Sn₁₈]⁴⁻ as an intermediate stage of cluster fusion presents the intriguing possibility that the central metal cation may act as a buffer, templating the close approach of the anionic components. Transfer of electron density from the main-group cage to the transition metal may then drive the fusion of the two polyhedral fragments, with concomitant reduction of the cations and their expulsion as metal atoms, as is observed, for example, in NaSi, where elevated pressures lead to the formation of Na metal with concomitant amorphisation of the Si₄ cluster units through Si–Si bond formation.⁴⁰ The presence of Fe–Fe bonding appears to play an important role in this process by preventing bending at the central metal atom, directing the reaction towards cluster fusion rather than the competing oxidative oligomerisation observed in the [AgSn₁₈]^7−/5− pair.

Experimental section

Materials and reagents

All manipulations and reactions were performed under a nitrogen atmosphere using standard Schlenk or glovebox techniques. Ethylenediamine (en) (Aldrich, 99%) and DMF (Aldrich, 99.8%) were freshly distilled by CaH₂ prior to use, and stored in N₂ prior to use. Tol (Aldrich, 99.8%) was distilled from sodium/benzophenone under nitrogen and stored under nitrogen. 2.2.2-crypt (4,7,13,16,21,24-hexaoxa-1,10-diazabicyclo (8.8.8) hexacosane, purchased from Sigma-Aldrich, 98%) was dried in vacuum for one day prior to use. K₄Sn₉ was synthesised by heating a stoichiometric mixture of the elements (K: +99% and Sn: 99.99% all from Aladdin) at 850 °C for 36 h in a niobium tube. [K(thf)Fe(O^tBu)₃]₂ was prepared according to literature methodology.⁴¹

Synthesis

[K(2.2.2-crypt)]₄[Fe₃Sn₁₈] (1). In a 10 mL vial, K₄Sn₉ (122 mg, 0.100 mmol) and 2.2.2-crypt (113 mg, 0.3 mmol) were dissolved in en (ca. 3 mL) and stirred for 30 min, resulting a dark brown solution. Then [K(thf)Fe(O^tBu)₃]₂ (33 mg, 0.043 mmol) was dispersed in toluene (0.5 mL), producing a light pink suspension, and then added dropwise to the above mixture. After stirring for 3 hours at room temperature, the resulting brown solution was filtered through glass wool and transferred to a test tube, then carefully layered by toluene (ca. 3 mL) to allow for crystallisation. Small brown block-like crystals of 1 (10% yield based on the K₄Sn₉ precursor) were isolated after two weeks.

X-ray crystallography

Crystallographic data for 1 were collected on Rigaku XtalAB Pro MM007 DW diffractometer with graphite monochromated Cu Kα radiation (λ = 1.54184 Å). The crystal structure was solved using direct methods and then refined using SHELXL-2014 (ref. 42) and Olex2,⁴³ with all non-hydrogen atoms refined anisotropically during the final cycles. All hydrogen atoms of the organic molecule were placed by geometrical considerations and were added to the structure factor calculation. The SQUEEZE procedure⁴⁴ to remove the solvent molecules which could not be modeled properly. A summary of the crystallographic data for the title compounds is presented in the ESI, Tables S1 and S2.† These data can be obtained free of charge from The Cambridge Crystallographic Data Centre.

Computational details

All calculations are performed using density functional theory as implemented in the ADF 2021.104 package.⁴⁵ The Perdew–Burke–Ernzerhof (PBE) functional⁴⁶ was used and triple-zeta basis sets included with two polarization functions are used for all atoms.⁴⁷ All electrons are treated as valence in the calculations. Relativistic effects were incorporated using the Zeroth-Order Regular Approximation (ZORA).⁴⁸ A Conductor-like Screening Model (COSMO) with dielectric constant of 78.39 was used to simulate the confining environment of the ionic lattice.⁴⁹ A fine numerical grid was used for the integrations (grid setting ‘verygood’),⁵⁰ and the calculations were considered converged when the commutator of the Fock and density matrices was below 10⁻⁶. Optimized structures were confirmed to be minima through the absence of imaginary frequencies.⁵¹ The sensitivity of the results to choice of functional was also explored by repeating the calculations using the M06-L and PBE0 functionals.^52,53 The Walsh diagram in Fig. 5 was calculated using Extended Hückel theory with the following parameters for the 5s and 5p valence orbitals of Sn: 5s H_ii = −16.16 eV, ζ = 2.30, 5p H_ii = −7.32 eV, ζ = 2.00. The reaction coordinate was defined by interpolating between the structures of the Sn₁₈ unit as it is found in the optimised structures of [Ni₂CdSn₁₈]⁶⁻, [Fe₃Sn₁₈]⁴⁻ and [Pd₂Sn₁₈]⁴⁻. A python script to perform these calculations is available on request.

Data availability

Crystallographic data are available from the CCDC. Full details of optimised geometries are summarised in the ESI.† Input files are available from the authors on request.

Author contributions

W.-X. C. and C.-C. S. performed the synthesis and characterisation, Z. L. and H. W. T. M. performed the computational analysis. Z.-M. S. and J. E. M. conceived the project and supervised the experimental and computational aspects of the research, respectively. All authors contributed to the preparation of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (no. 92161102 and 22371140), the Natural Science Foundation of Tianjin City (no. 21JCZXJC00140) and the PhD Candidate Research Innovation Fund of NKU School of Materials Science and Engineering, and 111 project (B18030) from China (MOE).

References

1. J. Zhao, Q. Du, S. Zhou and V. Kumar, Chem. Rev., 2020, 120, 9021–9163.
2. B. Weinert and S. Dehnen, in Binary and Ternary Intermetalloid Clusters, ed. S. Dehnen, Springer International Publishing, Cham, 2017, pp. 99–134.
3. B. Oelkers, M. V. Butovskii and R. Kempe, Chem.–Eur. J., 2012, 18, 13566–13579.
4. N. Lichtenberger, R. J. Wilson, A. R. Eulenstein, W. Massa, R. Clérac, F. Weigend and S. Dehnen, J. Am. Chem. Soc., 2016, 138, 9033–9036.
5. X. Min, I. A. Popov, F.-X. Pan, L.-J. Li, E. Matito, Z.-M. Sun, L.-S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2016, 55, 5531–5535.
6. D. M. P. Mingos, in Electron Counting Rules for Gold Clusters Which Are Stereochemically Non-rigid and Exhibit Skeletal Isomerism, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 1–67.
7. F. Gam, J. Wei, S. Kahlal, J.-Y. Saillard and J.-F. Halet, in Electron Counting in Ligated High Nuclearity Late Transition Metal Clusters, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 69–102.
8. W. Klein, A. Schier and T. F. Fässler, in Molecules Meet Solids: From Wade–Mingos Clusters to Intermetalloid Clusters, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 149–195.
9. F. Pan, B. Weinert and S. Dehnen, in Binary Zintl Anions Involving Group 13–15 (Semi-)Metal Atoms, and the Relationship of Their Structures to Electron Count, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 103–148.
10. L. A. O. P. Braunstein and P. R. Raithby, in Metal Clusters in Chemistry, Wiley-VCH, 1999.
11. C. Dong, Y. Li, D. Cheng, M. Zhang, J. Liu, Y.-G. Wang, D. Xiao and D. Ma, ACS Catal., 2020, 10, 11011–11045.
12. E. N. Esenturk, J. Fettinger and B. Eichhorn, J. Am. Chem. Soc., 2006, 128, 9178–9186.
13. A. Spiekermann, S. Hoffmann, T. Fässler, I. Krossing and U. Preiss, Angew. Chem., Int. Ed., 2007, 46, 5310–5313.
14. H.-L. Xu, L. Qiao and Z.-M. Sun, Chin. J. Chem., 2023, 41, 2432–2438.
15. J. M. Goicoechea and S. C. Sevov, Angew. Chem., Int. Ed. Engl., 2005, 44, 4026–4028.
16. J. M. Goicoechea and S. C. Sevov, J. Am. Chem. Soc., 2005, 127, 7676–7677.
17. S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25, 5678–5692.
18. S. Mitzinger, L. Broeckaert, W. Massa, F. Weigend and S. Dehnen, Nat. Commun., 2016, 7, 10480.
19. A. Ugrinov and S. C. Sevov, C. R. Chim., 2005, 8, 1878–1882.
20. J.-Q. Wang, B. Wahl and T. Fässler, Angew. Chem., Int. Ed., 2010, 49, 6592–6595.
21. C. Zhang, H. W. T. Morgan, Z.-C. Wang, C. Liu, Z.-M. Sun and J. E. McGrady, Dalton Trans., 2019, 48, 15888–15895.
22. Y.-N. Yang, L. Qiao and Z.-M. Sun, Chin. Chem. Lett., 2023, 34, 107207.
23. Z.-M. Sun, H. Xiao, J. Li and L.-S. Wang, J. Am. Chem. Soc., 2007, 129, 9560–9561.
24. D. F. Hansen, B. Zhou and J. M. Goicoechea, J. Organomet. Chem., 2012, 721–722, 53–61.
25. L. Lin, Y. Wang and L. Xu, Organometallics, 2022, 41, 450–455.
26. F. S. Geitner, W. Klein and T. F. Fässler, Dalton Trans., 2017, 46, 5796–5800.
27. N. V. Tkachenko, W.-X. Chen, H. W. T. Morgan, A. Muñoz-Castro, A. I. Boldyrev and Z.-M. Sun, Chem. Commun., 2022, 58, 6223–6226.
28. A. Ugrinov and S. C. Sevov, J. Am. Chem. Soc., 2002, 124, 10990–10991.
29. L. Yong, S. D. Hoffmann and T. F. Fässler, Z. Anorg. Allg. Chem., 2005, 631, 1149–1153.
30. T. Nguyen, W. Merrill, C. Ni, H. Lei, J. Fettinger, B. Ellis, G. Long, M. Brynda and P. Power, Angew. Chem., Int. Ed. Engl., 2008, 47, 9115–9117.
31. N. Fujima and T. Oda, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115412.
32. G. L. Guillet, K. Y. Arpin, A. M. Boltin, J. B. Gordon, J. A. Rave and P. C. Hillesheim, Inorg. Chem., 2020, 59, 11238–11243.
33. F. Cotton, C. A. Murillo and X. Wang, Inorg. Chem. Commun., 1998, 1, 281–283.
34. A. Srinivasan, R. A. Musgrave, M. Rouzières, R. Clérac, J. E. McGrady and E. A. Hillard, Chem. Commun., 2021, 57, 13357–13360.
35. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
36. J. Poater, M. Solà, M. Duran and X. Fradera, Theor. Chem. Acc., 2002, 107, 362–371.
37. F. K. Sheong, W.-J. Chen, J.-X. Zhang, Y. Li and Z. Lin, Dalton Trans., 2017, 46, 2214–2219.
38. J.-X. Zhang, F. K. Sheong and Z. Lin, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2020, 10, e1469.
39. J.-X. Zhang, F. K. Sheong and Z. Lin, Chem.–Eur. J., 2018, 24, 9639–9650.
40. R. Q. Cabrera, A. Salamat, O. I. Barkalov, O. Leynaud, P. Hutchins, D. Daisenberger, D. Machon, A. Sella, D. W. Lewis and P. F. McMillan, J. Solid State Chem., 2009, 182, 2535–2542.
41. Y. Xia, PhD thesis, Soochow University, Suzhou, China, 2012.
42. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
43. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
44. A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18.
45. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. E. Van Lenthe and E.-J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
48. E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953.
49. C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408.
50. M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819–1827.
51. L. Versluis and T. Ziegler, J. Chem. Phys., 1988, 88, 322–328.
52. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
53. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of the X-ray crystallography, further details of the computational experiments including a list of optimised coordinates of all clusters discussed. CCDC 2170116. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc04709a

‡ These authors contributed equally

§ [Fe₃Sn₁₈]²⁻ was identified as a prominent peak in the ESI-MS in Fig. 2. This cluster is formed by 2-electron oxidation of the [Fe₃Sn₁₈]⁴⁻ and so, if the oxidation is Sn-based, the cage is valence isoelectronic with that in [Pd₂Sn₁₈]⁴⁻. However, the optimised structure does not show a completely coalesced cage, but rather one that is similar to [Fe₃Sn₁₈]⁴− despite the 2-electron oxidation. The presence of the Fe₃ unit clearly prevents the close approach of the two Sn₉ units that is possible for [Pd₂Sn₁₈]⁴−.

---