Covalency versus magnetic axiality in Nd molecular magnets: Nd-photoluminescence, strong ligand-field, and unprecedented nephelauxetic effect in fullerenes NdM₂N@C₈₀ (M = Sc, Lu, Y)

Abstract

Nd-based nitride clusterfullerenes NdM₂N@C₈₀ with rare-earth metals of different sizes (M = Sc, Y, Lu) were synthesized to elucidate the influence of the cluster composition, shape and internal strain on the structural and magnetic properties. Single crystal X-ray diffraction revealed a very short Nd–N bond length in NdSc₂N@C₈₀. For Lu and Y analogs, the further shortening of the Nd–N bond and pyramidalization of the NdM₂N cluster are predicted by DFT calculations as a result of the increased cluster size and a strain caused by the limited size of the fullerene cage. The short distance between Nd and nitride ions leads to a very large ligand-field splitting of Nd³⁺ of 1100–1200 cm⁻¹, while the variation of the NdM₂N cluster composition and concomitant internal strain results in the noticeable modulation of the splitting, which could be directly assessed from the well-resolved fine structure in the Nd-based photoluminescence spectra of NdM₂N@C₈₀ clusterfullerenes. Photoluminescence measurements also revealed an unprecedentedly strong nephelauxetic effect, pointing to a high degree of covalency. The latter appears detrimental to the magnetic axiality despite the strong ligand field. As a result, the ground magnetic state has considerable transversal components of the pseudospin g-tensor, and the slow magnetic relaxation of NdSc₂N@C₈₀ could be observed by AC magnetometry only in the presence of a magnetic field. A combination of the well-resolved magneto-optical states and slow relaxation of magnetization suggests that Nd clusterfullerenes can be useful building blocks for magneto-photonic quantum technologies.

---

Introduction

The partially filled 4f-shell in lanthanide compounds is an inexhaustible source of magnetic and optical phenomena with a plethora of already practical and equally numerous prospective applications. The splitting and wavefunction composition of the ligand-field (LF) levels of the lanthanide ground-state multiplet determine the magnetic anisotropy and magnetization relaxation pathways and therefore are of paramount importance for lanthanide-based molecular magnets, such as single-molecule magnets (SMMs). Optical spectroscopy can contribute to the understanding of the SMM properties by the analysis of the fine structure of f–f transitions, in particular in low-temperature photoluminescence (PL) spectra, and by the correlation of the determined level splitting with magnetic behaviour.^1–5 Since the first report on the Dy(DOTA) complex by Sessoli et al. in 2012,⁶ the vast majority of such studies were devoted to Dy^6–17 and Yb^8,18–25 complexes, with rare instances of Tb,^8,26–28 Ho,²⁹ Nd,^30–33 and Er SMMs.^34,35 Recent trends also include a development of luminescence thermometry based on the temperature-dependent PL of Ln-SMMs,^{2,21,29,36,37} and the use of lanthanide complexes with a narrow optical linewidth for photonic quantum technologies.^38,39

Lanthanide-based endohedral metallofullerenes (Ln-EMFs) represent an important class of SMMs due to their air and thermal stability, ability to encapsulate Ln ions in rather unusual yet simple chemical environments with strong ligand fields, and stabilization of unconventional bonding interactions between lanthanide ions.^40–44Ab initio computational methods are very instrumental in predicting single-ion magnetic anisotropy in Ln-EMFs,^42,45–52 but verification of such predictions by direct experimental access to the LF splitting in fullerene-based Ln-SMMs is still missing. A natural prerequisite for the realization of the Ln-based PL in Ln-EMFs is that the lowest-energy fullerene excited state should have higher energy than the lanthanide emitting state. However, the optical gaps of EMFs rarely exceed 1.5 eV. For instance, recent PL studies of the Y_xSc_3−xN@I_h-C₈₀ (x = 0–3) family revealed that the energy of the triplet emitting state (T₁) in this series depends on the Sc content in the endohedral cluster and varies from 1.51 eV in YSc₂N@C₈₀ to 1.68 eV in Y₃N@C₈₀.^53,54 As M₃N@I_h-C₈₀ clusterfullerenes have the highest optical gaps among EMFs, these energies set the upper limit for Ln-emitting states in Ln-EMFs. The possibility of Ln-based PL in Ln-EMFs is thus essentially restricted to the near-infrared (NIR) range. To date, only different types of Er-EMFs exhibited well-established Er-based NIR luminescence,^55–63 including the fine structure at low temperatures in some of them, and one study reported on Tm-based NIR-PL in Tm-EMFs.⁶⁴ Unfortunately, Er and Tm tend to have easy-plane type magnetic anisotropy in EMFs^42,65 and are thus not well suited for the design of EMF-SMMs. The vast majority of EMF-SMMs are based on Tb,^{41,42,66–70} Dy,^{43,49,51,71–73} and Ho,^42,74 but none of them fulfills the criterion of low Ln-emitting state energy, and thus their Ln-based luminescence is not to be expected unless the fullerene excited states are driven to much higher energies.

Among different lanthanides, Nd seems to be a suitable candidate for Ln-based luminescence in EMF-SMMs. The free-ion energy of the Nd³⁺ NIR-emitting state, ⁴F_3/2 at 1.45 eV,⁷⁵ is just below the fullerene excited triplet state in M₃N@I_h-C₈₀. Nd₃N@I_h-C₈₀ cannot be produced in a reasonable yield because Nd³⁺ ions are too large,⁷⁶ but this limitation can be circumvented by using mixed-metal analogs with smaller rare-earth ions, such as NdSc₂N@I_h-C₈₀.⁷⁷ The high magnetic anisotropy in nitride clusterfullerenes is caused by the close proximity of the nitride N³⁻ to lanthanide ions, and paramagnetic NMR studies of the LnSc₂N@C₈₀ series accompanied by point-charge ligand field calculations demonstrated that Nd³⁺ in NdSc₂N@C₈₀ has the easy-axis type anisotropy favorable for SMMs.⁶⁵ Nd-EMFs are among the least studied Ln-EMFs, and the first example of the SMM behavior of EMFs with light lanthanides, Nd₂@C₈₀(CF₃), has only recently been reported.⁷⁸ This lack of studies echoes the situation with light-lanthanide SMMs in general, which are substantially less explored than their heavy-lanthanide congeners.^79,80 Thus, despite the ubiquitous NIR luminescence known for Nd^III complexes and solids, the reports on the combination of slow relaxation of magnetization and Nd-based luminescence remain scarce.^{30–33,36,81–85}

In this work, we synthesized a series of NdM₂N@C₈₀ (M = Sc, Lu, Y) molecules to study if the ligand-field experienced by the Nd³⁺ ion and SMM performance can be increased by deliberately shortening the Nd–N bond length and increasing the internal strain induced by complementary M³⁺ metal ions of a different size. By detecting the finely structured Nd-based near-infrared photoluminescence of the NdM₂N@C₈₀ series, we demonstrate the largest ligand-field splitting ever reported for Nd³⁺ in molecular compounds. Furthermore, we show that the ligand field splitting in NdM₂N@C₈₀ is indeed modulated by the increase of the size of M³⁺ ions. However, we also found that shortening of the Nd–N bond not only increases the LF splitting, but also enhances the covalency, which manifests itself in the strongest nephelauxetic effect ever observed in the PL spectra of Nd compounds. The influence of the enhanced LF and covalency on the magnetic and SMM properties of NdSc₂N@C₈₀ is evaluated by SQUID magnetometry and X-ray magnetic circular dichroism.

Synthesis and molecular structure

Synthesis and isolation

Metallofullerenes NdM₂N@C₈₀ (M = Sc, Y, Lu) were synthesized by the arc-discharge method using guanidinium thiocyanate as a solid source of nitrogen (see the ESI for further details of synthesis and HPLC separation, Fig. S1–S3†).⁸⁶ The increase of the metal size decreases the propensity of the nitride clusterfullerene formation and thus strongly affects the yield of the arc-discharge synthesis. Thus, in accordance with the ionic radii of M³⁺, the yield of NdM₂N@C₈₀ species follows Sc ≫ Lu > Y. The main efforts were therefore focused on NdSc₂N@C₈₀, which could be accumulated in sufficient amounts for its structural, spectroscopic, and AC/DC magnetic studies. For NdLu₂N@C₈₀ and NdY₂N@C₈₀, as their yield is considerably lower, we only accumulated amounts required for spectroscopic studies. All isolated compounds were characterized by LDI-TOF mass-spectrometry to ensure their compositional purity (Fig. S1–S3†). The UV-Vis-NIR absorption spectra of NdM₂N@C₈₀ showed a typical absorption pattern of M₃N@C₈₀ nitride clusterfullerenes with the I_h fullerene cage isomer (Fig. S4†); no absorption features caused by f–f transitions of Nd³⁺ could be identified. The vibrational spectra of NdSc₂N@C₈₀ (Fig. S5†) are also in line with the data on other M₃N@C₈₀ compounds.

Single-crystal X-ray diffraction

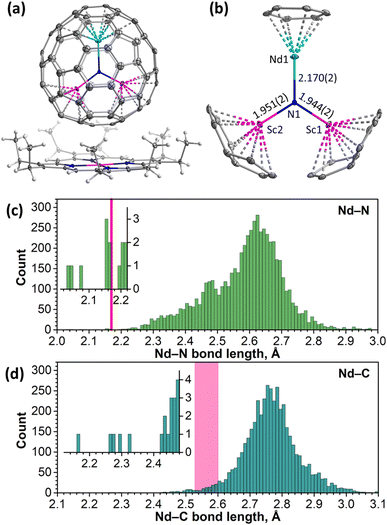
The molecular structure of NdSc₂N@I_h-C₈₀ was established by single-crystal X-ray diffraction (SC-XRD) using a co-crystal with nickel(II) octaethylporphyrin (NiOEP) grown by layering benzene solutions of the fullerene and NiOEP and allowing a slow diffusion thereof for one month. Measurements were performed at 100 K with synchrotron irradiation at the BESSY storage ring (BL14.2, Berlin-Adlershof, Germany).⁸⁷ The XDSAPP2.0 suite was employed for data processing.^88,89 The structure was solved by direct methods and refined with SHELXL-2018.⁹⁰

The NdSc₂N@C₈₀·NiOEP·2C₆H₆ co-crystal gives a rare example of a fully ordered EMF molecule in the crystal, allowing detailed analysis of the molecular structure (Fig. 1a, S6 and Table S1†). The NdSc₂N cluster is planar and oriented perpendicular to the porphyrin backbone. Two Sc atoms are located above NiOEP nitrogens, while Nd is facing the opposite side of the fullerene. This orientation of the cluster is typical for MSc₂N@C₈₀ molecules in co-crystals with NiOEP.^91–94 Nd is coordinated to the fullerene hexagon in an η⁶-fashion with Nd–C distances of 2.527(2)–2.604(2) Å, while the shortest Sc–C bonds of 2.228(3)–2.245(3) Å are to carbons on pentagon/hexagon edges (Fig. 1b).

Fig. 1 (a) NdSc₂N@C₈₀·NiOEP fragment from the NdSc₂N@C₈₀·NiOEP·2C₆H₆ single crystal. (b) NdSc₂N cluster and fullerene carbons nearest to endohedral metals; Nd–C distances in the Nd-(η⁶-C₆) fragment are 2.527(2)–2.604(2) Å. Color code: Nd – cyan, Sc – magenta, N – blue, C – gray, and Ni – red. (c) and (d) Histograms of Nd–N (c) and Nd–C (d) bond lengths in molecular compounds deposited in the CCDC database. Insets show expansion of the ranges with the shortest bonds, and the pink line in (c) and the rectangle in (d) denote Nd–N and Nd–C bond lengths in NdSc₂N@C₈₀.

The large difference of ionic radii⁹⁵ of Nd³⁺ (0.983 Å) and Sc³⁺ (0.745 Å) results in a considerable distortion of the NdSc₂N cluster, with a 0.320(2) Å displacement of nitrogen from the centroid of the C₈₀ cage towards Sc ions. Sc–N bond lengths are 1.944(2) and 1.951(2) Å, while the Nd–N bond length is 2.170(2) Å. Similar structural parameters were found in LnSc₂N@C₈₀ molecules with other light lanthanides, La⁹¹ (La–N 2.196(4) Å, Sc–N 1.943(6)/1.921(7) Å) and Ce⁹³ (Ce–N 2.184(2) Å, and Sc–N 1.942(2)/1.933(2) Å). For heavier lanthanides, the decrease of the Ln³⁺ ionic radius results in a systematic shortening of the Ln–N bond and increase of Sc–N bond lengths. For instance, the Dy–N bond length in DySc₂N@C₈₀ is 2.096(6) Å, while Sc–N bonds are 1.965(6) and 1.978(6) Å.⁹⁴

To consider the structural parameters of NdSc₂N@C₈₀ in a broader context, we analyzed Nd–N and Nd–C bonds for all compounds deposited in the Cambridge Crystallographic Data Centre (CCDC) database. The Nd–N bond length distribution with more than 5800 entries peaks near 2.62 Å (Fig. 1c). The Nd–N bond in NdSc₂N@C₈₀ appears to have one of the shortest lengths in the whole dataset. Shorter Nd–N distances are found only in terminal imides with Nd=N double bonds (2.04–2.08 Å)⁹⁶ and some μ₂-imide^97,98 and amide⁹⁹ complexes (2.15–2.17 Å), all reported by Anwander et al.

Nd–C bond lengths fall closer to a normal range although being still rather short for their type. For comparison, the peak in the Nd–C bond length distribution (4300 entries) is near 2.75 Å (Fig. 1d). Nd–C distances in complexes with ηⁿ-coordinated arenes span the range of 2.65–2.85 Å for variously substituted η⁵-cyclopentadienyls,^100–102 2.60–2.72 Å for η⁸-C₈H₈,^103–105 and 2.845(6)–2.915(7) for η⁹-C₉H₉.¹⁰⁴ In another Nd-EMF characterized by SC-XRD, Nd@C_2v(9)-C₈₂, Nd is coordinated to two carbons in the η²-fashion, and the corresponding Nd–C bonds are rather short, 2.25–2.30 Å.¹⁰⁶

DFT calculations

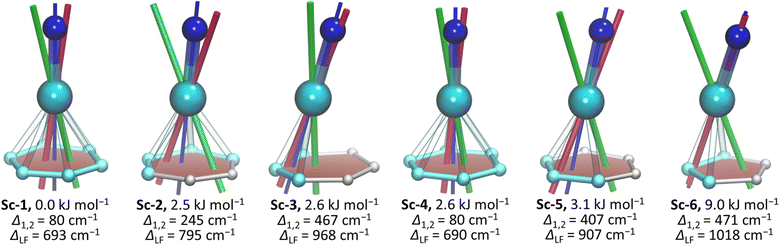
An increase of the metal size in M₃N@C₈₀ molecules leads to the accumulation of the internal strain, which at first manifests itself in the unusually short M–N bonds, and then changes the M₃N cluster shape from planar to pyramidal when the M–N bonds reach their limits of shortening.^107,108 The influence of the metal size on the molecular structures in the NdM₂N@C₈₀ series was analyzed with the help of DFT calculations. As the M₃N cluster can have somewhat different orientations (conformers) inside the fullerene cage, we first performed a full search of conformers for isolated NdSc₂N@C₈₀ molecules. 120 uniformly distributed NdSc₂N cluster orientations inside the C₈₀ cage were generated using Fibonacci sampling¹⁰⁹ and used as starting geometries in DFT optimization. The procedure resulted in 6 unique conformers, of which the most stable one (conformer Sc-1) is identical to the SC-XRD structure (see Fig. S7 in the ESI†). Four others are only 2–3 kJ mol⁻¹ less stable, while the least stable one (Sc-6) has a relative energy of 9 kJ mol⁻¹. For all conformers, DFT calculations predict a planar NdSc₂N cluster, showing that a comparably small Sc³⁺ ion compensates for the large radius of Nd³⁺. DFT-optimized Nd–N bond lengths in all conformers are in the range of 2.22–2.23 Å and overestimated compared to the experimental value by 0.05 Å.

When Sc³⁺ is substituted by larger Lu³⁺ (0.861 Å) and Y³⁺ (0.900 Å), the Nd–N bond lengths in the most stable DFT conformers of NdLu₂N@C₈₀ (Lu-1) and NdY₂N@C₈₀ (Y-1) are shortened to 2.165 Å and 2.170 Å, respectively (Fig. S8 and S9†). These similar values for metals of different sizes indicate that the Nd–N bond has reached its shortening limit. As a result, the NdM₂N cluster cannot sustain a planar shape in NdM₂N@C₈₀ and becomes pyramidal. In different conformers of NdLu₂N@C₈₀ and NdY₂N@C₈₀, the nitrogen is elevated above the NdM₂ plane by 0.37–0.51 Å and 0.52–0.62 Å, respectively (Fig. S8 and S9†).

Photoluminescence and ligand-field splitting

Short Ln–N bonds along with the large negative charge of the nitride ion lead to a strong axial ligand field imposed on lanthanide ions in nitride clusterfullerenes. To address the size of LF splitting in Nd-EMFs experimentally, we turned to photoluminescence spectroscopy. The photophysical behavior of MSc₂N@C₈₀ molecules without a partially filled 4f-shell in the metal can be illustrated by YSc₂N@C₈₀.⁵³ After photoexcitation and internal conversion to S₁, it undergoes a fast intersystem crossing to the T₁ state located at 1.5–1.6 eV above the ground state. However, the energy difference between S₁ and T₁ is only 0.03 eV, facilitating inversed intersystem crossing. As a result, YSc₂N@C₈₀ exhibits thermally activated delayed fluorescence at room temperature and down to 30 K. At lower temperature, the thermal repopulation of the S₁ state from T₁ is frozen, leaving weak phosphorescence as the only radiational decay process.⁵³ However, when the endohedral cluster contains Nd instead of Y, the energy can be further transferred from the fullerene-based T₁ state to the 4f-shell of the lanthanide and produce Nd-based NIR luminescence with the origin at the ⁴F_3/2 state (Fig. 2a). Indeed, our PL measurements of NdSc₂N@C₈₀ showed very characteristic Nd-centered NIR luminescence with three bands caused by ⁴F_3/2 → ⁴I_9/2, ⁴F_3/2 → ⁴I_11/2, and ⁴F_3/2 → ⁴I_13/2 transitions (Fig. 2b). Similar luminescence spectra were also observed for NdLu₂N@C₈₀ and NdY₂N@C₈₀ (Fig. 2b). As far as we know, this is the first observation of Nd-based luminescence in endohedral metallofullerenes.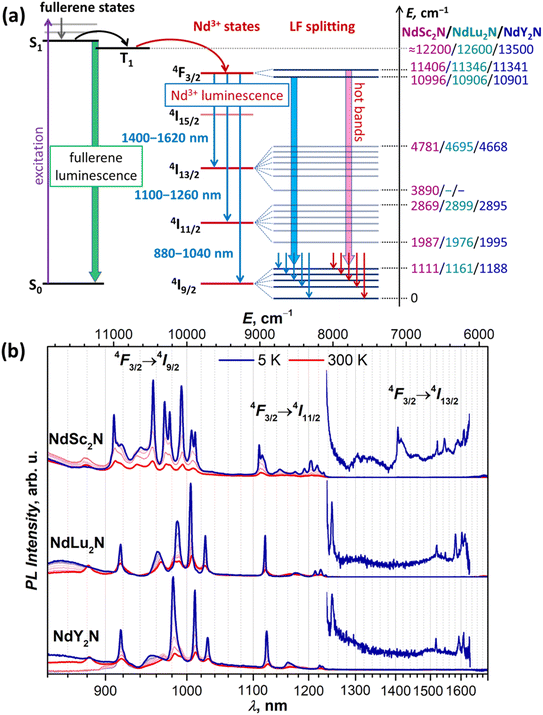

Fig. 2 (a) Schematic description of the Nd-based luminescence in NdM₂N@C₈₀. In non-4f M₃N@C₈₀, a fullerene-based excitation is followed by an internal conversion to the singlet state S₁, which then undergoes intersystem crossing to the triplet state T₁, and both S₁ and T₁ participate in the radiational decay in the form of thermally activated delayed fluorescence and phosphorescence.⁵³ When one M in the endohedral cluster is replaced with Nd, the energy is further transferred from the T₁ state to the 4f-shell of Nd, which then emits from the ⁴F_3/2 state giving three near-infrared ⁴F_3/2 → ⁴I_J PL bands (J = 9/2, 11/2, 13/2). Their fine structure is caused by the ligand-field splitting in each ⁴I_J multiplet, while hot bands appear when the LF-excited state in the ⁴F_3/2 doublet has significant thermal population. (b) Luminescence spectra of solid NdM₂N@C₈₀ (M = Sc, Lu, Y) measured at 5–300 K with 50 K steps using laser excitation at 488 nm. The energy values listed on the right scale in (a) are obtained from PL measurements at 5 K, and the LF splitting of ⁴F_3/2 is estimated from hot bands at 300 K (see Fig. 3a and S12–S17†), while conservative estimations of fullerene T₁ energies are based on the VT-PL data on YSc₂N@C₈₀ and Y₃N@C₈₀ from ref. 53 and preliminary VT-PL measurements of Lu₃N@C₈₀.

The PL spectra of NdM₂N@C₈₀ are remarkable in several aspects. First, the ⁴F_3/2 → ⁴I_J PL bands are shifted from 900 nm, 1060 nm, and 1350 nm, at which they are usually centered in Nd³⁺ complexes,¹¹⁰ to longer wavelengths. Particularly, the characteristic Nd³⁺ emission at 1060 nm used in solid-state lasers is “missing” as the ⁴F_3/2 → ⁴I_11/2 PL band of NdM₂N@C₈₀ occurs at 1100–1250 nm (Fig. 2b). As we discuss below, this shift of PL bands is the manifestation of a strong nephelauxetic effect. Second, the bands have atypical intensity distribution. Normally, the ⁴F_3/2 → ⁴I_11/2 band is the strongest one, followed by ⁴F_3/2 → ⁴I_9/2 with 2–4 times lower intensity, while the ⁴F_3/2 → ⁴I_13/2 band is the weakest. In NdM₂N@C₈₀, the latter is also very weak, but the ⁴F_3/2 → ⁴I_9/2 band is considerably stronger than ⁴F_3/2 → ⁴I_11/2. Third, the luminescence lifetimes of NdM₂N@C₈₀ are very short. PL lifetimes in Nd complexes are usually found in the 0.2–2 μs range. For the polycrystalline film of NdSc₂N@C₈₀, the PL decay is biexponential with the lifetimes of 4.5 ns/13 ns at room temperature, and 4 ns/19 ns between 200 and 5 K, with the longer component having the main contribution with a weight of 80% (Fig. S10†). To check if this fast decay can be caused by intermolecular Nd⋯Nd quenching, the fullerene was diluted in a polystyrene matrix. In the latter, the decay was mono-exponential with the lifetime near 20 ns. Polycrystalline NdLu₂N@C₈₀ and NdY₂N@C₈₀ showed monoexponential PL decay with very weak temperature dependence and lifetimes of 10.5–11.0 ns and 9.0–9.5 ns, respectively (Fig. S11†). These short lifetimes suggest a low quantum yield and explain the weak PL intensity of NdM₂N@C₈₀. Fourth, each PL band of NdM₂N@C₈₀ exhibits unusually broad and well-resolved fine structure already at room temperature. Upon cooling, the narrowing of the lines and increase of their intensity took place down to 50–100 K, while further cooling did not bring considerable changes in the spectra (Fig. 2b and S12–S17†).

LF splitting in PL spectra. The fine structure of PL bands is of primary interest for this work since it represents the LF splitting of ⁴I_J multiplets. In the ⁴F_3/2 → ⁴I_J band, one can expect (2J + 1)/2 lines corresponding to the number of Kramers doublets (KDs) in the ⁴I_J multiplet. However, when not only KD1, but also KD2 of the emitting ⁴F_3/2 state has a significant population, transitions originating from ⁴F_3/2 (KD2) and known as hot bands can increase the number of detectable PL features (Fig. 2a). Further complication may be caused by vibronic transitions, involving vibrational excitations in emitting or final states. Finally, different sites, by which we understand molecules with different surroundings or with different orientations of the endohedral cluster (conformers), may also have unequal energy levels and thus multiply the number of lines in PL spectra. To aid the interpretation of PL spectra, we performed variable-temperature measurements (Fig. 2 and 3 and S12–S17†) since hot bands decrease their intensity and eventually disappear upon cooling. Likewise, zero-phonon electronic transitions tend to exhibit pronounced narrowing at low temperatures, while the accompanying phonon sidebands usually remain broader.

At low temperatures, the ⁴F_3/2 → ⁴I_9/2 band of NdSc₂N@C₈₀ is reduced to seven narrow peaks, of which three are stand-alone and four form two doublets with the splitting of 70 and 50 cm⁻¹ (Fig. 3a). We assign these peaks to five pure electronic ⁴F_3/2(KD1) → ⁴I_9/2(KDn) transitions. The splitting of KD3 and KD5 features into doublets is likely caused by a coexistence of two emitting sites,^53,111 but the lack of analogous splitting for other KDs is not clear. Two broad peaks located between KD1 and KD2, at ΔE = 115 and 370 cm⁻¹, can be tentatively assigned to vibronic transitions, but may also correspond to different conformers (vide infra). The low-T PL spectrum thus allows determination of experimental Δ_1,2 and Δ_LF values in NdSc₂N@C₈₀ as 536 cm⁻¹ and 1061/1110 cm⁻¹. The room-temperature PL spectrum also features a peak at ΔE = −410 cm⁻¹, which disappears upon cooling (Fig. 3a). This hot band is likely caused by the ⁴F_3/2(KD2) → ⁴I_9/2(KD1) transition and thus allows estimation of the LF splitting in the ⁴F_3/2 multiplet.

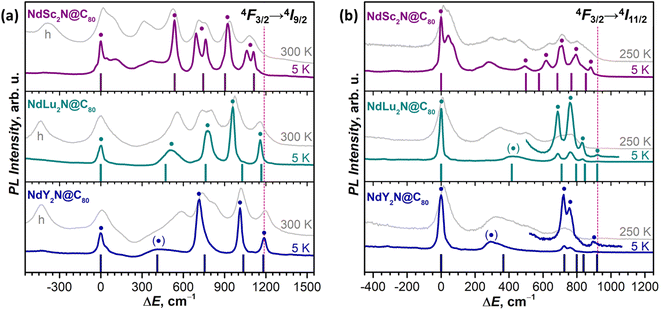Fig. 3 The fine structure of (a) ⁴F_3/2 → ⁴I_9/2 and (b) ⁴F_3/2 → ⁴I_11/2 photoluminescence bands of NdM₂N@C₈₀ (M = Sc, Lu, Y) measured at 5 K and 300 K (250 K). Vertical bars are the CASSCF-computed energies of LF states in ⁴I_9/2 (a) and ⁴I_11/2 (b) multiplets in Sc-3, Lu-3, and Y-3 conformers scaled by 1.15 to account for the systematic underestimation. The peaks assigned to pure electronic ⁴F_3/2(KD1) → ⁴I_J(KDn) transitions are labeled with ● and broad peaks with uncertain assignment to KD2 are labelled with (●). The ΔE scale for each NdM₂N@C₈₀ is given versus the peak of the lowest-energy Kramers doublet in the ⁴I_9/2 or ⁴I_11/2 multiplet. In (a), the peaks at negative ΔE in 300 K spectra labelled with “h” are hot bands caused by the ⁴F_3/2(KD2) → ⁴I_9/2(KD1) transition of each NdM₂N@C₈₀, which allow estimation of Δ_1,2 in the ⁴F_3/2 multiplet. The intensity of 5 K and higher-temperature spectra is given off-scale (see Fig. 2b and S12–S17† for the real relative intensity at different temperatures). To guide the eye, the vertical dashed line marks the highest energy KD in the ⁴F_3/2 → ⁴I_9/2 band (NdY₂N@C₈₀) and in the ⁴F_3/2 → ⁴I_11/2 band (NdLu₂N@C₈₀).

The interpretation of the ⁴F_3/2 → ⁴I_9/2 PL bands of NdLu₂N@C₈₀ and NdY₂N@C₈₀ is more straightforward as they show neither pronounced vibronic features nor additional splitting (Fig. 3 and Table S2†). The five peaks in low-T spectra are thus readily assigned to five KDs of the ⁴I_9/2 multiplet. The only peculiarity is the strongly enhanced linewidth of the KD2 peak, which is still well-defined for NdLu₂N@C₈₀, but is barely discernible for NdY₂N@C₈₀. Such a strong broadening indicates that this state experiences very fast relaxation even at 5 K. The LF splitting of ⁴I_9/2 in the NdM₂N@C₈₀ series increases systematically with the size of the M ion from NdSc₂N@C₈₀ (Δ_LF = 1111 cm⁻¹) to NdLu₂N@C₈₀ (1161 cm⁻¹) and further to NdY₂N@C₈₀ (1188 cm⁻¹). The LF splitting of the ⁴F_3/2 multiplet is also larger for Lu and Y and amounts to 440 cm⁻¹versus 410 cm⁻¹ for Sc. At the same time, Δ_1,2 decreases from 536 cm⁻¹ (Sc) to 510 cm⁻¹ (Lu) and 420 cm⁻¹ (Y). The energies of other KDs also vary considerably in the NdM₂N@C₈₀ series. Besides, not only the energies, but also the intensities of transitions are quite different from Sc to Lu to Y, which indicates that the state composition is also considerably affected by the internal strain.

Thus, analysis of the ⁴F_3/2 → ⁴I_9/2 PL band demonstrates that enclosing Nd³⁺ in a molecular environment with a very short Nd–N bond and further increasing the internal strain by changing the size of the NdM₂N cluster indeed result in a record-high LF splitting in NdM₂N@C₈₀ compounds exceeding 1100 cm⁻¹. For comparison, a resolved structure of LF levels allowing estimation of Δ_LF for the Nd-⁴I_9/2 multiplet was observed in the optical spectra of five Nd-SMMs, including NdTp₃,^112,113 acetato-diphenoxo bridged {ZnNd} complex,³⁰ dinuclear {Nd₂} complexes with 9-anthracenecarboxyl and 2,2′-bipyridine³¹ or phenanthroline³² ligands, and in the Nd complex with N-(diphenylphosphoryl)pyrazine-2-carboxamide.³³ None of them had the Δ_LF exceeding 460 cm⁻¹. Among the Nd-SMMs studied ab initio, Δ_LF values exceeding 500 cm⁻¹ were reported only for three Nd-SMMs: metallocenium complex [Nd(Cp^ttt)₂]B(C₆F₅)₄ (Δ_LF = 672 cm⁻¹ and Δ_1,2 = 130 cm⁻¹),¹⁰⁰ Nd complex with equatorial metallacrowns and axial n-Bu₃PO ligands in hexagonal bipyramidal coordination (Δ_LF = 586 cm⁻¹ and Δ_1,2 = 104 cm⁻¹),¹¹⁴ and (COT)Nd(Cp^ttt) sandwich complex (Δ_LF = 545 cm⁻¹ and Δ_1,2 = 78 cm⁻¹).¹¹⁵ Among non-SMMs, a very large LF splitting almost rivaling the results of this work was determined by Amberger et al. based on absorption and PL spectra and phenomenological crystal-field modelling in some tris(η⁵-cyclopentadienyl)Nd(III) complexes, such as Nd(η⁵-C₅Me₅)₃ (Δ_LF = 861 cm⁻¹),¹¹⁶ Nd(η⁵-C₅Me₄H)₃ (Δ_LF = 1000 cm⁻¹),¹¹⁷ Nd(η⁵-C₅H₄^tBu)₃ and Nd(η⁵-C₅H₄SiMe₃)₃ (in both, Δ_LF = 1030 cm⁻¹).¹¹⁸ The SMM properties of these complexes were not studied, but the ground state with the dominating |±5/2〉 term (see the ESI for results of ab initio calculations†) suggests that the slow relaxation of magnetization can hardly be expected.

In addition to the ground-state LF structure, well-resolved PL spectra also enable analysis of the ⁴I_11/2 multiplet. For NdSc₂N@C₈₀, the experimental KD2 is found at 491 cm⁻¹, whereas the overall Δ_LF(⁴I_11/2) splitting is 880 cm⁻¹, considerably smaller than Δ_LF(⁴I_9/2) of 1111 cm⁻¹. Broad features in the gap between KD1 and KD2 at 50 cm⁻¹ and 280 cm⁻¹ can be preliminary assigned to vibronic transitions. In NdLu₂N@C₈₀ and NdY₂N@C₈₀, the ⁴F_3/2 → ⁴I_11/2 band is dominated by the ⁴F_3/2(KD1) → ⁴I_11/2(KD1) transition, whereas other features have much lower intensity (Fig. 2b and 3b). Similar to the ⁴F_3/2 → ⁴I_9/2 band, the ⁴I_11/2(KD2) peaks appear strongly broadened, which makes their assignment less certain. The Δ_LF(⁴I_11/2) splitting of 920 cm⁻¹ in NdLu₂N@C₈₀ and 900 cm⁻¹ in NdY₂N@C₈₀ exceed that in NdSc₂N@C₈₀.

A complete set of ⁴F_3/2 → ⁴I_13/2 transitions can be identified only for NdSc₂N@C₈₀ (Fig. 2b and Table S2†). Seven KDs of the ⁴I_13/2 multiplet span the energy range of 890 cm⁻¹ and show similar motifs to the ⁴F_3/2 → ⁴I_11/2 band with a large gap between KD1 and KD2 of 530 cm⁻¹ and a dense group of other KDs at higher energy. For NdLu₂N@C₈₀ and NdY₂N@C₈₀, the position of the KD1 peak cannot be determined because of its very low intensity (Fig. 2b), which prevents further analysis of the LF splitting in ⁴I_13/2.

Ab initio calculations of LF splitting. To analyze the composition of LF-split states, we performed ab initio calculations at the CASSCF(3,7)/RASSI level. While the lowest-energy conformer of NdSc₂N@C₈₀ corresponds to the SC-XRD structure in the NdSc₂N@C₈₀·Ni(OEP) co-crystal (Fig. S7†), the energy span of only 9 kJ mol⁻¹ predicted by DFT for other conformers is quite small, and other conformers can also be present in powder samples studied by PL (and later by magnetometry). Therefore, calculations were performed for all six DFT-computed conformers of NdSc₂N@C₈₀. Our earlier ab initio studies of LF in conformers of various Dy-SMMs showed that the influence of the lanthanide coordination to the fullerene cage is noticeable but not decisive.^51,119,120 Unexpectedly, the situation found here for NdSc₂N@C₈₀ is quite dissimilar. The Δ_LF splitting of the ⁴I_9/2 multiplet in different conformers varies from 690 to 1018 cm⁻¹, and even larger relative variation is found for Δ_1,2, which spans from 80 to 470 cm⁻¹ (Fig. 4 and Table S3†).

The variation of the LF splitting can be correlated with the Nd-fullerene coordination motif (Fig. 4). The smallest Δ_1,2 of 80 cm⁻¹ is found for conformers Sc-1 and Sc-4, in which Nd is coordinated to the center of a fullerene hexagon in an η⁶-manner. Even a small shift of Nd from the hexagon center toward a C–C bond yields a 3-fold increase of Δ_1,2 in Sc-2 (hapticity η⁴), while the more pronounced shift toward one of the carbon atoms increases Δ_1,2 to 407 cm⁻¹ in Sc-5 (η³) and further to 467 cm⁻¹ in Sc-3 (η³). The largest Δ_1,2 and Δ_LF values are achieved when Nd faces one carbon atom in Sc-6 (hapticity between η¹ and η³). The deviation of the quantization axis of the ground-state Kramers doublet (KD1) from the Nd–N bond axis (Fig. 4) is another manifestation of the strong influence of the Nd-fullerene coordination. The two axes coincide only in Sc-6, while the angle between them in other conformers reaches 13°.

Fig. 4 Coordination of Nd atoms to the closest carbon atoms in six conformers of NdSc₂N@C₈₀, their geometrical Nd–N axes (thin blue lines) and g_z axes of the two lowest-energy Kramers doublets from CASSCF calculations (KD1 – red lines and KD2 – green lines). Color code: Nd – cyan, N – blue, and C – light cyan (d_Nd–C ≤ 2.6 Å) or light gray (d_Nd–C > 2.6 Å). Nd–C distances shorter than 2.6 Å are shown as bonds. Also listed for each conformer are its relative energy from DFT calculations and Δ_1,2 and Δ_LF splitting from CASSCF calculations.

The comparison of theoretical LF splitting to the fine structure of PL spectra shows that only conformers Sc-3 and Sc-6 agree reasonably well with experimental data (Fig. 5 and S18†), while predictions for other conformers, including the lowest-energy Sc-1, are far off. Thus, it appears that only the conformers, in which Nd is coordinated close to one C atom in the η¹–η³ manner, contribute to the fine structure of PL spectra. The only features which might be attributed to other conformers of NdSc₂N@C₈₀ are broad peaks in the gap between 0 and 500 cm⁻¹ (KD1 and KD2, Fig. 5), for which our preferred assignment is vibronic transitions. It is hard to determine at this moment whether other conformers have more efficient non-radiative decay channels and do not show up in the spectra, or the CASSCF predictions for these conformers are incorrect, or they are destabilized in powder samples. The technical aspects of CASSCF computations also indicate some untrivial behavior. For some conformers, the CASSCF wavefunction was found seamlessly, while for others, they were sensitive to initial guesses, and it took an effort to converge the wavefunction to a decent 4f-pure state.

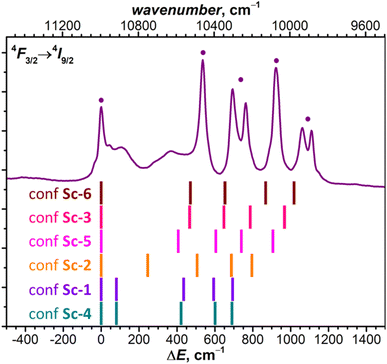Fig. 5 The fine structure of ⁴F_3/2 → ⁴I_9/2 photoluminescence bands of NdSc₂N@C₈₀ measured at 5 K compared to LF splitting of the ⁴I_9/2 multiplet in six conformers of NdSc₂N@C₈₀ from CASSCF calculations (see Tables S3b–S3f† for numerical values).

Following the calculation results on NdSc₂N@C₈₀, for NdLu₂N@C₈₀ and NdY₂N@C₈₀ we performed CASSCF calculations for two representative conformers, conformer Lu(Y)-1 with η⁶-type coordination of Nd, and conformer Lu(Y)-3 with η³-pentagon-coordinated Nd (see Fig. S19†). The difference between LF splitting of conformers is also considerable but less pronounced than in NdSc₂@C₈₀ (Tables S7 and S8†), and the conformer Lu(Y)-3 provides better match to the fine structure in experimental PL spectra (Fig. 3). Remarkably, while the total LF splitting in NdM₂N@C₈₀ increases with the size of M, the Δ_1,2 value exhibits the opposite trend and shows a gradual decrease, which is correctly captured by CASSCF calculations for Lu(Y)-3 (Fig. 3).

LF splitting, magnetic axiality, and covalency. The aims we followed in creating the strongly strained environment around the Nd–N bond was to achieve a large LF splitting and enhanced magnetic axiality. While the LF splitting in NdM₂N@C₈₀ is indeed unprecedentedly large, the problem of axiality appears to be more complicated. For the subsequent analysis, we use conformer Sc-3. Table 1 summarizes the energies of its Kramers doublets (KDs) in the ground-state Nd^3+-4I_9/2 multiplet, along with their composition in the |m_J〉 basis and principal components of pseudospin g-tensors. Analogous data for other conformers can be found in Tables S3, S7, and S8 in the ESI.† Aside from the systematic underestimation of the LF splitting by 10–15%, the calculated spectrum agrees well with the experimental data for all spectrally characterized multiplets (Fig. 3 and S18†). Besides, the ab initio Δ_1,2 value computed for Sc-3 in the ⁴F_3/2 multiplet is 401 cm⁻¹, also in good agreement with the experiment.

Table 1 Ligand-field splitting of the Nd^3+-4I_9/2 multiplet and pseudospin g-tensors of Kramers doublets (KDs) in NdSc₂N@C₈₀ (conformer Sc-3) computed at the CASSCF/RASSI level and with the point-charge model

KD	Exp. E^a cm^−1	Calc. E cm^−1	% Composition in the |mJ〉 basis (J = 9/2) ^b	g x	g y	g z	φ° ^c
a Experimental values are from photoluminescence measurements at 5 K (see Fig. 3a). b For each KD, 4 main terms exceeding 5% are shown in the descending order of their contribution. c φ is the angle between the gz direction of the given KD and that of the ground state KD1.
			CASSCF/RASSI
KD1	0	0	85|±9/2〉 + 7|±5/2〉 + 6|±3/2〉	0.0371	0.0445	5.6890	—
KD2	536	467	48|±5/2〉 + 25|±7/2〉 + 19|±3/2〉 + 8|±1/2〉	0.5312	1.3555	3.1828	21
KD3	693/763	648	31|±3/2〉 + 29|±5/2〉 + 19|±7/2〉 + 14|±9/2〉	0.0369	1.0730	3.6643	25
KD4	923	786	48|±7/2〉 + 30|±3/2〉 + 14|±1/2〉 + 8|±5/2〉	2.0524	0.3009	3.7618	55
KD5	1061/1110	968	70|±1/2〉 + 14|±3/2〉 + 8|±5/2〉 + 8|±7/2〉	4.3734	2.4200	0.4013	7
			Point-charge model
KD1	0	0	99.9|±9/2〉	0.0000	0.0000	6.5437	—
KD2	536	466	99.6|±7/2〉	0.0013	0.0014	5.0823	3
KD3	693/763	643	99.0|±5/2〉	0.0937	0.1002	3.6158	1
KD4	923	770	95.0|±3/2〉 + 4.4|±1/2〉	1.4408	1.4927	2.0604	7
KD5	1061/1110	867	94.8|±1/2〉 + 4.5|±3/2〉	5.0352	2.0948	0.6166	0

---

The strongly axial LF for 4f-prolate Kramers ions (Ce³⁺, Nd³⁺, and Dy³⁺) normally leads to the high purity of KDs in the |m_J〉 representation, with the ground state featuring the largest J_z projection. It also implies that pseudospin g-tensors of KDs have small transversal g_x,y components, colinear principal g_z axes, and g_z values close to 2|m_J|g_J, where g_J is the Landé g-factor. The description we infer from ab initio calculations of Sc-3 is quite different (Table 1; see Table S3† for other conformers). KD1 indeed resembles the |±9/2〉 state with 85% contribution and the quantization axis aligned along the Nd–N bond with a deviation of 4.1°. The g_z and g_x,y values of KD1 are 5.689 and near 0.04, respectively, which can be compared to g_z = 6.545 and g_x,y = 0 expected for the pure |±9/2〉 doublet. However, higher-energy KDs have strongly mixed |m_J〉 composition and enhanced g_x,y components, while their g_z axes are rotated away from that of KD1. In contrast, the ab initio description of the isostructural DySc₂N@C₈₀ is entirely consistent with expectations for a strongly axial ligand field.^45,120 The ground state KD1 has 99.7% weight of the |±15/2〉 state and g_x,y is less than 10⁻⁴, while g_z = 19.84 (versus 20.00 expected for the pure m_J = ±15/2 state).¹²⁰ The next three KDs of DySc₂N@C₈₀ also have high contribution of one of the |±m_J〉 states (>80%), and the principal z axes of their pseudospin g-tensors are nearly collinear. The overall LF splitting in DySc₂N@C₈₀ is 1284 cm⁻¹.

Thus, the molecular environment, in which the strong axiality is expected and indeed realized for Dy, produces quite different properties for Nd. We can recall that Nd³⁺ has considerably larger Steven's factor γ_j (−38 × 10⁶) than Dy³⁺ (1.03 × 10⁶), which increases the weight of B_q^k terms with k = 6 in the ligand field. While for DyM₂N@C₈₀ molecules, B_q², B_q⁴, and B_q⁶ contribute 65–80%, 5–10%, and 10–25% to ab initio computed LF splitting, respectively, in NdM₂N@C₈₀ the balance changes to similar contributions of B_q² and B_q⁶ near 40–45%, while B_q⁴ terms cover 10–15%. The enhanced B_q⁶ weight implies the higher sensitivity of the Nd³⁺ ligand field to the environment, yet the deviation from axiality in NdM₂N@C₈₀ is too strong and cannot be explained by the γ_j factor alone. To understand if low symmetry or unobvious peculiarities of the electrostatic distribution may play a role, we obtained the LF parameters of NdSc₂N@C₈₀ using a point-charge model with LoProp¹²¹ charges from CASSCF calculations scaled by a factor of 1.08 to reproduce the ab initio Δ_1,2 value. The KD energies calculated with such a LF Hamiltonian are not far from ab initio LF energies (Table 1), but the states are described by almost pure |m_J〉 functions, and KD1–KD3 have g_z values close to 2|m_J|g_J. Similar results with a slightly higher degree of m_J-mixing were obtained when the model was adjusted by treating the Nd³⁺ ion quantum chemically at the CASSCF/RASSI level, while keeping point charges instead of all other atoms (Table S5†). From these models, we infer that the electrostatic environment around Nd³⁺ indeed favors LF axiality, while deviations from axiality in NdSc₂N@C₈₀ should be caused by non-electrostatic contributions, such as the covalency.^122–124 Indeed, when CASSCF/RASSI computations were performed for the (NdSc₂N)⁶⁺ cluster augmented with point charges mimicking the carbon atoms of the fullerene cage, a considerable state mixing was observed (Table S5c†). We thus conclude that the expansion of the valence space from Nd³⁺ through NdSc₂N⁶⁺ to NdSc₂N@C₈₀ results in the systematic increase of the m_J mixing in Nd KDs and decrease of the axiality. Significant changes of the LF splitting induced by subtle variation of the local Nd environment in NdSc₂N@C₈₀ conformers also cannot be expected based on simple electrostatic considerations. Point-charge calculations for the conformer Sc-1 do not follow CASSCF results and predict similarly large KD2 energy as in Sc-3 (compare values in Table S5†). These facts highlight the importance of valence interactions and show that pure electrostatic models would be inappropriate for the description of Nd-EMF SMMs.

Comparison to other coordination environments, in which heavy lanthanide analogs exhibit very high magnetic axiality, reveals that the situation found here for NdSc₂N@C₈₀ is not unique for fullerenes but rather describes a common behaviour of Nd in molecular magnets. For instance, [Nd(H₂O)₅L₂]³⁺ complexes with pentagonal bipyramidal coordination and axial phosphine oxide ligands,^125,126 or Nd metallocenium complexes,¹⁰⁰ all have the ground state KD with enhanced |±9/2〉 contribution (86–99%), but their higher-energy KDs are mixed considerably in the |m_J〉 representation. Likewise, the g_x,y values of 0.01–0.02 found in KD1 of these complexes are small in comparison to g_z values near 6.3, but appear quite large when compared to transversal g-tensor components of 10⁻⁴ in KD1 of similar Dy complexes. In other Nd-SMMs, for which ab initio calculations were performed, the degree of axiality is considerably smaller.

Nd–N distance and LF splitting. The discussion above showed that by creating unusually short Nd–N bonds and a highly strained endohedral environment, we achieved large LF splitting but simultaneously increased the degree of covalency and decreased the magnetic axiality. As coordination of Nd to the fullerene π-system also played a considerable role, it is hard to disentangle it from the influence of Nd–N bonding. To study the isolated effect of the extreme shortening of the Nd–N bond, we used the NdN molecule as a toy system and computed LF splitting at different Nd–N distances with a point charge model and ab initio at the CASSCF(3,7)/RASSI level.

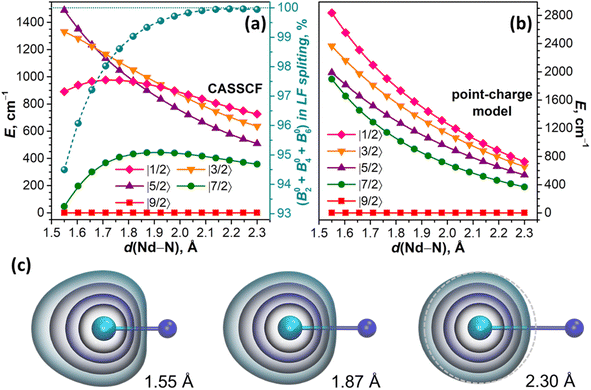
For the linear NdN molecule with the axial ligand field of C_∞v symmetry, the LF Hamiltonian should include only B₀², B₀⁴, and B₀⁶ terms, while LF states are described by pure |m_J〉 functions. At a Nd–N distance of 2.3 Å, the ab initio computed LF splitting is 726 cm⁻¹, and the state energies increase in the descending order of |m_J| (Fig. 6a). The structure of states and their energies are reproduced closely by a point charge model using a LoProp charge of nitrogen (−1.513 e) scaled by a factor of 1.08 (Fig. 6b). The same factor was used then to scale the LoProp charges of nitrogen for point-charge computations at shorter Nd–N distances. According to the electrostatic model, a stepwise decrease of the Nd–N distance from 2.3 Å to 1.55 Å does not change the order of states and only gradually increases the LF splitting to 2836 cm⁻¹, while the energies of all LF states increase monotonously (Fig. 6b). A very different Nd–N distance dependence emerges from CASSCF calculations. The energies of |±7/2〉 and |±1/2〉 doublets relative to |±9/2〉 pass through a maximum and then decrease, and |±3/2〉 also changes a curvature at short Nd–N, and only |±5/2〉 grows continuously in the whole range. The order of |m_J〉 states thus changes several times, and the overall LF splitting at 1.55 Å is almost twice smaller than predicted by the point-charge model (Fig. 6a).

Fig. 6 (a) LF splitting in the NdN molecule computed at the CASSCF/RASSI level as a function of the Nd–N distance and the sum of B₀², B₀⁴, and B₀⁶ contributions to the total LF splitting (cyan spheres with the dashed curve and the scale on the right side); (b) LF splitting in the NdN molecule computed with the point charge model and scaled LoProp atomic charge of N at the same Nd–N distances as in (a); (c) 4f-electron density in Nd–N built upon orbitals from CASSCF(3, 7) calculations, and concentric isosurfaces are plotted at the values of (from inner to outer) 0.25, 0.05, 0.01, and 0.002 a.u.; to guide the eye, the rightmost figure shows a circle centered on the Nd atom and plotted with the gray dashed line.

From the contributions of ab initio computed B_q^k terms to LF splitting provided by the Single_aniso code,^122,127 we infer that the weight of the B₀² term, which amounts to 87% at 2.3 Å, decreases to 49% at 1.55 Å, and the weight of B₀⁶ increases from 7% at 2.3 Å to 38% at 1.55 Å, while the sign of B₀⁶ changes from negative to positive below 2.1 Å (in the point-charge model, B₀⁶ is negative through the whole range). Furthermore, the LF Hamiltonian, comprising only B₀², B₀⁴, and B₀⁶, cannot reproduce the LF splitting at short Nd–N distances, and requires addition of B₀⁸. The weight of the latter increases from negligible 0.05% at 2.3 Å to significant 5.5% at 1.55 Å (Fig. 6a). As B_q^k terms with k > 6 should vanish for pure f orbitals, their non-zero contribution serves as a diagnostic criterion for the breakdown of the assumption of the isolated spherically shaped 4f shell.¹²² Indeed, the shape of 4f-electron density distribution changes from nearly spherical at 2.3 Å to a considerably elongated one at short Nd–N distances (Fig. 6c). This naturally leads to the notion of 4f AOs mixing with other orbitals and the overall increase of the covalency as the Nd–N distance shrinks. Of course, the distance of 1.55 Å is unrealistically short, but it serves here only for a clear-cut demonstration, whereas the effect is already present at more realistic distances (Fig. 6c). Importantly, ab initio calculations of NdM₂N@C₈₀ similarly showed that the LF Hamiltonian including B_q^k terms with k ≤ 6 recovers only ∼95% of the ab initio LF splitting, while covering the remaining 5% requires B_q⁸ terms.

Nephelauxetic effect. The enhanced covalency of the Nd bonding with surrounding atoms in NdM₂N@C₈₀ has an experimental manifestation in the aforementioned red shift of ⁴F_3/2 → ⁴I_J PL bands when compared to other Nd compounds. From the KD1 line of the ⁴F_3/2 → ⁴I_9/2 band in the low-temperature PL spectrum, the energy of the emitting state, KD1 of ⁴F_3/2, is determined to be 10 900–11 000 cm⁻¹, which is lower than the usual energy of the ⁴F_3/2 multiplet by around 1100 cm⁻¹. Such a covalency-induced reduction of the excitation energies in coordination compounds of transition metals and lanthanides is known as the nephelauxetic effect.¹²⁸

Numerical representation of the nephelauxetic effect is often given by nephelauxetic parameters β_F = F²(compound)/F²(free ion), where F² is the second-order Slater integral describing interelectron repulsion, or β′ = ζ_4f/ζ_4f(free ion), where ζ_4f is the Lande spin–orbit coupling constant. The degree of covalency, defined as an admixture of ligand orbitals to f-like orbitals, is sometimes estimated as b^0.5 = [(1 − β)/2]^0.5, although it appears somewhat ambiguous because β_F and β′ can be quite different, F² being more sensitive to the bonding nature.^129,130 For instance, the energy differences between ⁴I_J levels are mainly determined by ζ_4f, and since the gaps between ⁴I_J levels in the NdM₂N@C₈₀ series are similar to other Nd compounds, we can conclude that ζ_4f is not strongly affected. The energy differences between multiplets with different L, on the other hand, are more sensitive to inter-electron repulsion parameters, and the reduced ⁴F_3/2 energy in NdM₂N@C₈₀ indicates that F² is significantly modified.

Experimentally, ζ_4f, F² and other F^k integrals can be determined by fitting the Hamiltonian, comprising free-ion and crystal-field terms, to spectroscopic data. As such a Hamiltonian includes a large number of parameters, extended data on many multiplets in a broad energy range are required for a reliable fitting. In the absence of such data, which is the case for NdM₂N@C₈₀ and the majority of Nd-SMMs, a simplified spectroscopic nephelauxetic parameter β_spec based on the transition energy between selected multiplets can be used: β_spec = ΔE(compound)/ΔE(standard). For the following discussion, we define β_spec as the energy difference between barycenters of ⁴I_9/2 and ⁴F_3/2 multiplets divided by the free ion value⁷⁵ ΔE(⁴F_3/2–⁴I_9/2) = 11 699 cm⁻¹. When the ⁴F_3/2 → ⁴I_9/2 PL band is not resolved into LF components, as is the case for many Nd-SMMs, PL band energy is simply used instead of barycenters, which can introduce an uncertainty to β_spec of ∼0.01.

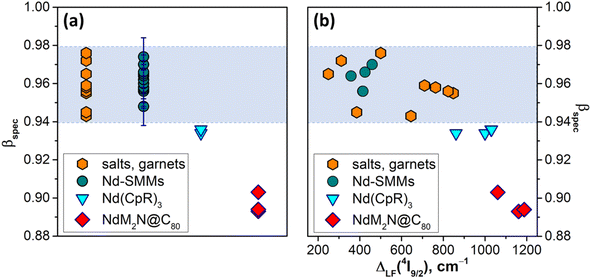
Fig. 7a plots β_spec values in NdM₂N@C₈₀, all 17 PL-characterized Nd-SMMs reported before this work,^{30–33,36,81–85,112,131,132} selected tris(η⁵-cyclopentadienyl)Nd complexes with large ligand field splitting,^116–118 and several inorganic salts and garnets thoroughly characterized by optical spectroscopy^133–139 (see Table S9† for the compound titles, numerical values, and literature references for each entry). The latter group is the most studied experimentally, and for this analysis we selected the set of compounds encompassing the broadest range of β_spec parameters, from the most ionic ones like Nd:LaF₃ (ref. 139) with β_spec = 0.976 to the most covalent Nd:Y₂O₃ (ref. 133) and Nd₂S₃ (ref. 134) with β_spec of 0.943–0.945. A similar span of β_spec from 0.948 to 0.982 is found for Nd-SMMs. It appears safe to state that the β_spec range of 0.94–0.98 is where the vast majority of Nd compounds will be found. Amberger et al. demonstrated that Nd(CpR)₃ complexes (CpR = C₅Me₅, C₅Me₄H, C₅H₄^tBu, C₅H₄SiMe₃, etc.) with enhanced metal–ligand interactions have large LF splitting and reduced nephelauxetic parameters β_F (see ref. 116 for comparison of LF strength and β_F in a series of Nd complexes).^116–118 Likewise, their β_spec values of 0.934–0.936 fall below the normal β_spec range and were presumably the lowest values among Nd-compounds before our study. Analyzed in this broad context, the β_spec parameters found in this work for the NdM₂N@C₈₀ series, 0.893 for NdLu₂N@C₈₀, 0.894 for NdY₂N@C₈₀, and 0.903 for NdSc₂N@C₈₀, are unprecedently small. This very strong nephelauxetic effect evidences one more time that by increasing the internal strain in metallofullerenes we achieved a much higher degree of covalency than is usually observed in Nd compounds. It is also instructive to find that there is seemingly no correlation between the nephelauxetic effect and ligand field splitting for the compounds in the normal β_spec range (Fig. 7b). However, as we leave this range, the decrease of β_spec starts to correlate with the increase of Δ_LF. This is not surprising given that the strengthening of the ligand field is achieved by enhancing the interactions between the lanthanide ion and the ligands, but it will require more compounds with such unusual properties to establish firm correlations.

Fig. 7 (a) Distribution of the spectroscopic nephelauxetic parameter β_spec in four groups of Nd compounds, including NdM₂N@C₈₀ molecules from this work, spectroscopically characterized Nd-SMMs, selected Nd-tris(η⁵-cyclopentadienyl) complexes Nd(CpR)₃, and Nd³⁺ salts and garnets; (b) correlation between β_spec and Δ_LF(⁴I_9/2) for the same compounds. The range of typical β_spec values in Nd compounds is shaded. For many Nd-SMMs, β_spec is estimated from the unresolved ⁴F_3/2 → ⁴I_9/2 PL band instead of multiplet barycenters, which introduces an uncertainty of ∼0.01 plotted in (a). As Δ_LF(⁴I_9/2) is determined spectroscopically only for a small fraction of Nd-SMMs, the number of Nd-SMM datapoints in panel (b) is much smaller than in panel (a).

The strong nephelauxetic effect and ligand field splitting may also be among the reasons for the short luminescence lifetimes of NdM₂N@C₈₀. The low energy of the NIR-emitting state in lanthanide compounds is responsible for the efficient nonradiative vibrational relaxation. For Nd³⁺, the non-radiative relaxation rate is determined by the gap between ⁴F_3/2 and ⁴I_15/2, which typically is around 5400 cm⁻¹. The ⁴I_15/2 multiplet of NdM₂N@C₈₀ is not directly accessible in our experiments, but based on the experimental and computational data on other ⁴I_J multiplets (Table S4†), we can assume that the energy of ⁴I_15/2 is also close to standard values for Nd³⁺ and that the LF splitting of the ⁴I_15/2 multiplet amounts to Δ_LF ≈ 1300 cm⁻¹ (Table S4†). The lower than usual energy of the ⁴F_3/2 state and the strong LF splitting of the ⁴I_15/2 multiplet reduce the gap between the KD1 of ⁴F_3/2 and KD8 of ⁴I_15/2 to ≈3600 cm⁻¹. This low gap opens the possibility for two-phonon relaxation and thus, in accordance with the energy gap law, is a plausible reason for the anomalously short Nd³⁺ luminescence lifetimes in NdM₂N@C₈₀ molecules.

Magnetic properties of NdSc₂N@C₈₀

While the energies of LF states are accessible via PL spectroscopy, experimental verification of the state compositions is not straightforwardly available from this technique. Complimentary information on the ground state may be given by magnetometry. The large Δ_1,2 value in the ⁴I_9/2 multiplet suggests that the low-temperature magnetic properties of NdM₂N@C₈₀ will be dominated by the ground state doublet.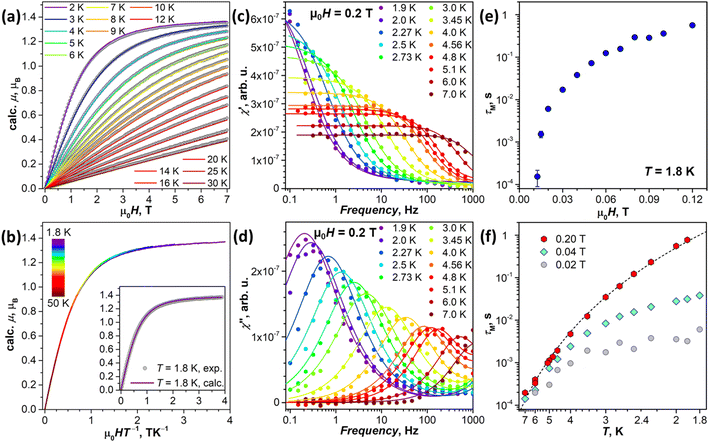

SQUID magnetometry. The experimental magnetic properties of NdSc₂N@C₈₀ powder were first studied by SQUID magnetometry (Fig. 8a and b). The magnetization curves of the sample measured below 30 K are compared to simulations for the pseudospin with the ab initio computed g-tensor for KD1 in Sc-3 in Fig. 8a. A very good match between the shapes of the experimental and calculated curves points to the reliability of the theoretical predictions for the ground state KD. Furthermore, the M versus HT⁻¹ plots superimpose at least up to 50 K (Fig. 8b). It shows that only the ground state KD contributes to the magnetization at these temperatures, in line with the large predicted energy gap between the first and second KDs (Table 1).

Fig. 8 (a) Experimental magnetization curves of NdSc₂N@C₈₀ (gray dots) compared to calculations (colored lines) for pseudospin s˜ = 1/2 with the ab initio computed g-tensor corresponding to the ground-state Kramers doublet (KD1, Table 1). (b) Magnetization curves of NdSc₂N@C₈₀ measured between 1.8 K and 50 K and presented as a function of the HT⁻¹ product; the inset shows the comparison of experimental and calculated data for T = 1.8 K. (c) and (d) AC magnetometry measurements of in-phase χ′ (c) and out-of-phase χ′′ (d) magnetic susceptibility of NdSc₂N@C₈₀ in the constant field of 0.2 T at T = 1.9–7 K; dots are experimental data, and lines are fits with the generalized Debye model, from which relaxation times are extracted. (e) Magnetic field dependence of magnetization relaxation time at T = 1.8 K. (f) Temperature dependencies of magnetization relaxation times measured in the field of 0.02 T, 0.04 T, and 0.2 T; dashed line is a fit of 0.2 T data with the function τ_M⁻¹ = CTⁿ (C = 0.0205 and n = 6.59).

XMCD. The determination of the absolute value of the magnetic moment of NdSc₂N@C₈₀ by SQUID measurements is not sufficiently reliable because of the limited sample amount. Complimentary information on the ground state magnetic properties of NdSc₂N@C₈₀ was thus obtained from X-ray magnetic circular dichroism (XMCD) measurements performed on the sample, which was drop-casted onto a HOPG substrate. In the absence of a magnetic field, the X-ray absorption spectrum of NdSc₂N@C₈₀ has no dichroism and shows the typical absorption features of Nd(III) at the Nd-M_4,5 edges (3d → 4f excitations) (Fig. 9 and S20†). When a magnetic field is applied, circular polarized XAS develops a dichroism proportional to the sample magnetization in the direction of the beam (which was kept parallel to the field in our measurements) (Fig. 9). The maximum of the XMCD signal at the Nd-M₅ edge at a photon energy of 1001.5 eV was used to follow the magnetization of NdSc₂N@C₈₀ during magnetic field ramps between −6 T and +6 T. The magnetization curves measured this way reproduced the results of the SQUID measurements at 5.5 K closely (see Fig. S21 in the ESI†). By applying sum rules^141,142 and tabulated correction factors,¹⁴³ the XAS and XMCD spectra recorded in the field of 6 T were used to calculate the expectation values of angular and spin momentum operators, 〈L̂_z〉 = 2.02 μ_B and 〈Ŝ_z〉 = −0.45 μ_B, and the magnetic moment along the beam direction, μ_z = 1.11 μ_B (see the ESI for the calculation details†). The uncertainty in the determined value of μ_z is mainly caused by ambiguities in integration limits for the Nd-M₄ edge and is estimated to be less than ±0.1 μ_B. The ratio 〈Ŝ_z〉/〈L̂_z〉 = −0.22 is close to the ab initio prediction of −0.24 for the ground state doublet (note that a theoretical expectation for the f³ system is −0.25). For comparison, in the assumption of a disordered powder, the ab initio predicted ground-state g-tensor of NdSc₂N@C₈₀ gives a saturated magnetic moment of 1.38 μ_B. At T = 5.5 K and under an applied magnetic field of 6 T, the theoretical moment is reduced to 1.14 μ_B, which is very close to the value we determined from XMCD measurements. At the same time, the ground state with the pure m_J = ±9/2 composition would have a saturated magnetic moment of 1.65 μ_B, while the value at 5.5 K and 6 T would be 1.43 μ_B. Thus, XMCD measurements confirm the ab initio prediction of the considerable deviation of the NdSc₂N@C₈₀ ground state KD from the pure m_J = ±9/2 state.

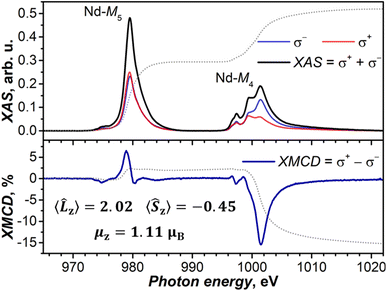Fig. 9 XAS (upper panel) and XMCD (lower panel) spectra of NdSc₂N@C₈₀ at the Nd-M_4,5 edges (3d → 4f), T ≈ 5.5 K, and μ₀H = 6 T. Left-hand and right-hand polarized XAS spectra are denoted as σ⁺ and σ⁻, and non-polarized XAS spectrum is their sum, while XMCD (in %) is their difference normalized to the maximum of XAS. Dotted lines are integrals of XAS and XMCD used in the sum rule analysis, which provided 〈L̂_z〉, 〈Ŝ_z〉, and μ_z values (see the ESI for details†). Measurements were performed at the BOREAS beamline (synchrotron ALBA).¹⁴⁰

ESR spectroscopy. Precise information on the ground-state g-tensor can in principle be obtained by ESR spectroscopy. We therefore performed X-band ESR measurements of frozen NdSc₂N@C₈₀ solution in glassy d₈-toluene. However, the sample did not show any discernible ESR signal at 10 K or higher temperature. Note that with m_J = ±9/2 being the main components of KD1, the ground-state wavefunction requires an admixture of m_J = ±7/2 terms to fulfill the ESR selection rule, Δm_J = ±1. As can be seen in Table 1, the contribution of m_J = ±7/2 terms to KD1 is very small (less than 1%), suggesting that the absence of the ESR signal can be caused by negligible transition matrix elements.

Dynamic magnetic properties. NdSc₂N@C₈₀ did not show hysteresis in DC magnetic measurements, and the sample was further studied by AC magnetometry (Fig. 8c–f and S22†). The relaxation of magnetization was too fast in zero magnetic field, and no peaks of the out-of-phase χ′′ signal were recorded. The slow relaxation at 1.8 K could be detected only in the external fields exceeding 0.015 T (Fig. S22†). The relaxation time τ_M gradually increased with the field and approached tenths of a second near 0.1 T, with a sign of levelling-off at higher fields (Fig. 8e and Table S10†). The fast relaxation in zero field is caused by the quantum tunneling of magnetization (QTM) as the ground state g-tensor has rather large transversal components g_x,y (Table 1). When the constant magnetic field is applied, the QTM is gradually suppressed, resulting in the increase of the relaxation time.

The temperature dependence of τ_M was measured in the fields of 0.02, 0.04, and 0.2 T (Table S11†). The QTM is fully suppressed at 0.2 T, and the temperature dependence of τ_M can be well described by the Raman relaxation mechanism, τ_M⁻¹ = CTⁿ, with the fitted parameters C = 0.0205 ± 0.0026 s⁻¹ K⁻ⁿ and n = 6.59 ± 0.09 (Fig. 8f). The contribution of the QTM, inducing faster relaxation with flatter temperature dependence at lower temperatures, is clearly visible in smaller fields (Fig. 8f). Higher-energy LF states are thus not involved in the reorientation of NdSc₂N@C₈₀ magnetic moment as the system finds an underbarrier shortcut with the help of phonon excitations.

The relaxation behavior observed in this work for NdSc₂N@C₈₀ can be compared to that of non-fullerene Nd-SMMs. As discussed above, Nd-SMMs usually have considerable g_x,y components in the ground state, which lead to fast zero-field QTM. Only three Nd complexes, two of [Nd(H₂O)₅L₂]³⁺ type with pentagonal bipyramidal coordination geometry (L = ^tBuPO(NHⁱPr)₂ in ref. 125 and CyPh₂PO in ref. 126), and the (COT)Nd(Cp^ttt) sandwich diluted with the Y analog,¹¹⁵ exhibited slow relaxation of magnetization in zero magnetic field. In all other Nd-SMMs, the slow relaxation required the DC magnetic field to suppress the fast QTM. [Nd(H₂O)₅(CyPh₂PO)₂]³⁺ and (COT)Nd(Cp^ttt) complexes are also the only Nd-SMMs, for which a narrow magnetic hysteresis could be recorded at 2 K.^115,126 For other Nd-SMMs, the slow relaxation was attested only by AC measurements, implying relaxation times shorter than 1 s. The temperature dependence of relaxation times for some Nd-SMMs was described by the Raman mechanism with an exponent of n = 6–7,^{100,114,126,144–146} similar to the value of n = 6.59 determined in this work for NdSc₂N@C₈₀. When instead the Orbach mechanism was assumed to describe the relaxation of Nd-SMMs, the barriers obtained from the fits of the temperature dependence were usually several times smaller than the energies of excited LF states predicted ab initio.^{113,114,125,126,144–146} This inconsistency is a strong indication that the Orbach mechanism is rarely operative for Nd-SMMs, while relaxation of magnetization is more often governed by the Raman mechanism, which may also involve coupling to optical phonons.

Conclusions

The synthesis of a NdM₂N@C₈₀ series with diamagnetic rare-earth metals of different sizes (M = Sc, Y, Lu) allowed us to analyze the influence of internal strain on the magnetic states and optical properties of Nd³⁺ in these metallofullerenes. We found that Nd³⁺ ions in nitride clusterfullerenes experience the strongest ligand field ever observed in molecular complexes of Nd, causing the LF splitting of the ground-state ⁴I_9/2 multiplet reaching 1100–1200 cm⁻¹. This strong ligand field is the result of the unusually short Nd–N bond lengths and the large negative charge of the nitride ion. At the same time, a confinement of the NdM₂N cluster of a variable size inside the fullerene cage results in the increase of the strain from Sc to Lu to Y, which leads to the change of the geometrical shape of the cluster and substantial variation of the LF splitting pattern of the Nd³⁺ ion. The latter could be directly addressed by photoluminescence spectroscopy, which showed finely structured narrow emission lines caused by f–f transitions in Nd³⁺. When compared to their energies in Nd³⁺ compounds, the PL bands of NdM₂N@C₈₀ are considerably red-shifted, which points to the very strong nephelauxetic effect and enhanced contribution of covalency in Nd bonding.

The enhanced covalency is the price for the large LF splitting and, as shown by ab initio modelling, is the reason for the reduced magnetic axiality in NdM₂N@C₈₀. Point-charge modelling demonstrates that pure electrostatic interactions in these molecules would produce highly axial LF states with sheer m_J wavefunction compositions. Experimental studies of magnetic properties revealed that NdSc₂N@C₈₀ exhibits slow relaxation of magnetization only in the presence of an external magnetic field, whereas its zero-field relaxation is dominated by the fast tunneling process. The large LF splitting also does not help to slow down the in-field relaxation of magnetization, which appears to be governed by the under-barrier Raman mechanism.

The results of this work demonstrate that pushing the LF strength to its extreme by enhancing interactions of Nd ions with surrounding atoms does not improve the magnetic axiality even in the molecular geometry, which favors such axiality for heavy lanthanides. The reason is that the larger ionic radius makes Nd more susceptible to enhanced covalency. Theoretically, the single-ion magnetic anisotropy of Nd³⁺ could be made highly axial by placing point charges at short distances, but in reality, the strong LF would require an interaction with strong ligands placed at close distances, which inevitably leads to the enhanced covalency and all its negative effects on the magnetic axiality discussed in this work. This dichotomy between the strong ligand field and reduced magnetic axiality appears to be a fundamental limitation for creating high-performance SMMs based on light lanthanides. Nevertheless, the large LF splitting appears very instrumental in separating f–f transitions and enabling direct optical access to individual spin states of Nd³⁺, which can be useful for application in magneto-photonic quantum technologies. Another possible consequence of enhanced covalency worth mentioning is that the 4f-shell can become more susceptible to manipulations by other methods like scanning tunneling microscopy, which is usually considered not amenable to probe 4f electrons in molecules due to their core-like behavior. Thus, while Nd-EMFs may not perform great as single molecular magnets, they show good prospects for optically and electronically addressable quantum bits. Importantly, their LF splitting and spin-state wavefunction can be further tuned by varying the composition of the endohedral cluster or exohedral chemical modification of metallofullerenes.

Data availability

The data supporting the findings of this study are available from the corresponding authors upon reasonable request.

Author contributions

WY synthesized fullerenes with help and supervision from FL; MR and FZ performed PL measurements; VD performed DFT calculations under the supervision of SMA; GV and MB performed SQUID measurements; SS performed vibrational spectroscopic studies; MR, GV, MB, LS, CG, MV and AAP performed the XMCD study; SMA performed ab initio calculations; FL grew single-crystals and performed the SC-XRD study; AAP conceived and supervised the study; FL, SMA, and AAP wrote the manuscript with contributions from all co-authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support by the Deutsche Forschungsgemeinschaft (grants PO 1602/7-1, PO 1602/11-1, LI 3055/3-1, and AV 169/3-1) and the China Scholarship Council (Fellowship to W. Y.). Diffraction data have been collected on BL14.2 at the BESSY II electron storage ring operated by the Helmholtz-Zentrum Berlin; we would like to acknowledge the help and support of Manfred Weiss and his group members during the experiments at BESSY II. XMCD measurements at the synchrotron ALBA were performed in the framework of the beamtime proposal ID 20201035073. Computational resources were provided by the Center for High Performance Computing at the TU Dresden. We appreciate the technical support with computational resources in IFW Dresden by Ulrike Nitzsche. Dr Anja Wolter-Giraud and Sebastian Gaβ are acknowledged for the help with SQUID magnetic measurements.

References

1. J. Long, Y. Guari, R. A. S. Ferreira, L. D. Carlos and J. Larionova, Coord. Chem. Rev., 2018, 363, 57–70.
2. R. Marin, G. Brunet and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 1728–1746.
3. J.-H. Jia, Q.-W. Li, Y.-C. Chen, J.-L. Liu and M.-L. Tong, Coord. Chem. Rev., 2019, 378, 365–381.
4. F. Pointillart, B. le Guennic, O. Cador, O. Maury and L. Ouahab, Acc. Chem. Res., 2015, 48, 2834–2842.
5. R. Jankowski, M. Wyczesany and S. Chorazy, Chem. Commun., 2023, 59, 5961–5986.
6. G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606.
7. J. Long, R. Vallat, R. A. S. Ferreira, L. D. Carlos, F. A. Almeida Paz, Y. Guari and J. Larionova, Chem. Commun., 2012, 48, 9974–9976.
8. S. Shintoyo, K. Murakami, T. Fujinami, N. Matsumoto, N. Mochida, T. Ishida, Y. Sunatsuki, M. Watanabe, M. Tsuchimoto, J. Mrozinski, C. Coletti and N. Re, Inorg. Chem., 2014, 53, 10359–10369.
9. Y. Bi, C. Chen, Y.-F. Zhao, Y.-Q. Zhang, S.-D. Jiang, B.-W. Wang, J.-B. Han, J.-L. Sun, Z.-Q. Bian, Z.-M. Wang and S. Gao, Chem. Sci., 2016, 7, 5020–5031.
10. E. Mamontova, J. Long, R. A. S. Ferreira, A. M. P. Botas, D. Luneau, Y. Guari, L. D. Carlos and J. Larionova, Magnetochemistry, 2016, 2, 41.
11. J. Long, E. Mamontova, V. Freitas, D. Luneau, V. Vieru, L. F. Chibotaru, R. A. S. Ferreira, G. Felix, Y. Guari, L. D. Carlos and J. Larionova, RSC Adv., 2016, 6, 108810–108818.
12. Y.-C. Chen, J.-L. Liu, Y. Lan, Z.-Q. Zhong, A. Mansikkamäki, L. Ungur, Q.-W. Li, J.-H. Jia, L. F. Chibotaru, J.-B. Han, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Chem.–Euro. J., 2017, 23, 5708–5715.
13. F. Guégan, F. Riobé, O. Maury, J. Jung, B. Le Guennic, C. Morell and D. Luneau, Inorg. Chem. Front., 2018, 5, 1346–1353.
14. M. Perfetti, M. Gysler, Y. Rechkemmer-Patalen, P. Zhang, H. Taştan, F. Fischer, J. Netz, W. Frey, L. W. Zimmermann, T. Schleid, M. Hakl, M. Orlita, L. Ungur, L. Chibotaru, T. Brock-Nannestad, S. Piligkos and J. van Slageren, Chem. Sci., 2019, 10, 2101–2110.
15. D. Guettas, F. Gendron, G. Fernandez Garcia, F. Riobé, T. Roisnel, O. Maury, G. Pilet, O. Cador and B. Le Guennic, Chem.–Eur. J., 2020, 26, 4389–4395.
16. R. A. S. Ferreira, E. Mamontova, A. M. P. Botas, M. Shestakov, J. Vanacken, V. Moshchalkov, Y. Guari, L. F. Chibotaru, D. Luneau, P. S. André, J. Larionova, J. Long and L. D. Carlos, Adv. Opt. Mater., 2021, 9, 2101495.
17. Y. Liu, B.-H. Lyu, S.-N. Du, G.-Z. Huang, Z.-Y. Ruan, S.-G. Wu, J.-L. Liu and M.-L. Tong, Dalton Trans., 2021, 50, 6778–6783.
18. F. Pointillart, B. L. Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617.
19. K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606.
20. K. Soussi, J. Jung, F. Pointillart, B. Le Guennic, B. Lefeuvre, S. Golhen, O. Cador, Y. Guyot, O. Maury and L. Ouahab, Inorg. Chem. Front., 2015, 2, 1105–1117.
21. G. Brunet, R. Marin, M.-J. Monk, U. Resch-Genger, D. A. Gálico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Chem. Sci., 2019, 10, 6799–6808.
22. F. Guégan, J. Jung, B. Le Guennic, F. Riobé, O. Maury, B. Gillon, J.-F. Jacquot, Y. Guyot, C. Morell and D. Luneau, Inorg. Chem. Front., 2019, 6, 3152–3157.
23. W.-B. Chen, L. Zhong, Y.-J. Zhong, Y.-Q. Zhang, S. Gao and W. Dong, Inorg. Chem. Front., 2020, 7, 3136–3145.
24. F. Gendron, S. Di Pietro, L. Abad Galán, F. Riobé, V. Placide, L. Guy, F. Zinna, L. Di Bari, A. Bensalah-Ledoux, Y. Guyot, G. Pilet, F. Pointillart, B. Baguenard, S. Guy, O. Cador, O. Maury and B. Le Guennic, Inorg. Chem. Front., 2021, 8, 914–926.
25. K. Karachousos-Spiliotakopoulos, V. Tangoulis, N. Panagiotou, A. Tasiopoulos, E. Moreno-Pineda, W. Wernsdorfer, M. Schulze, A. M. P. Botas and L. D. Carlos, Dalton Trans., 2022, 51, 8208–8216.
26. K. Yamashita, R. Miyazaki, Y. Kataoka, T. Nakanishi, Y. Hasegawa, M. Nakano, T. Yamamura and T. Kajiwara, Dalton Trans., 2013, 42, 1987–1990.
27. K. Ehama, Y. Ohmichi, S. Sakamoto, T. Fujinami, N. Matsumoto, N. Mochida, T. Ishida, Y. Sunatsuki, M. Tsuchimoto and N. Re, Inorg. Chem., 2013, 52, 12828–12841.
28. E. A. Mikhalyova, M. Zeller, J. P. Jasinski, R. J. Butcher, L. M. Carrella, A. E. Sedykh, K. S. Gavrilenko, S. S. Smola, M. Frasso, S. C. Cazorla, K. Perera, A. Shi, H. G. Ranjbar, C. Smith, A. Deac, Y. Liu, S. M. McGee, V. P. Dotsenko, M. U. Kumke, K. Müller-Buschbaum, E. Rentschler, A. W. Addison and V. V. Pavlishchuk, Dalton Trans., 2020, 49, 7774–7789.
29. J. Wang, J. J. Zakrzewski, M. Zychowicz, V. Vieru, L. F. Chibotaru, K. Nakabayashi, S. Chorazy and S.-i. Ohkoshi, Chem. Sci., 2021, 12, 730–741.
30. I. Oyarzabal, B. Artetxe, A. Rodríguez-Diéguez, J. Á. García, J. M. Seco and E. Colacio, Dalton Trans., 2016, 45, 9712–9726.
31. B. Casanovas, S. Speed, O. Maury, M. S. El Fallah, M. Font-Bardía and R. Vicente, Eur. J. Inorg. Chem., 2018, 2018, 3859–3867.
32. B. Casanovas, S. Speed, O. Maury, M. Font-Bardía and R. Vicente, Polyhedron, 2019, 169, 187–194.
33. Y. H. Pham, V. A. Trush, M. Korabik, V. M. Amirkhanov and P. Gawryszewska, Dyes Pigm., 2021, 186, 108986.
34. F. Pointillart, B. Le Guennic, T. Cauchy, S. Golhen, O. Cador, O. Maury and L. Ouahab, Inorg. Chem., 2013, 52, 5978.
35. M. Karbowiak, C. Rudowicz, T. Nakamura, R. Murakami and T. Ishida, Chem. Phys. Lett., 2016, 662, 163–168.
36. K. Kumar, D. Abe, K. Komori-Orisaku, O. Stefańczyk, K. Nakabayashi, J. R. Shakirova, S. P. Tunik and S.-i. Ohkoshi, RSC Adv., 2019, 9, 23444–23449.
37. D. Errulat, R. Marin, D. A. Gálico, K. L. M. Harriman, A. Pialat, B. Gabidullin, F. Iikawa, O. D. D. Couto, J. O. Moilanen, E. Hemmer, F. A. Sigoli and M. Murugesu, ACS Cent. Sci., 2019, 5, 1187–1198.
38. D. Serrano, S. K. Kuppusamy, B. Heinrich, O. Fuhr, D. Hunger, M. Ruben and P. Goldner, Nature, 2022, 603, 241–246.
39. D. W. Laorenza and D. E. Freedman, J. Am. Chem. Soc., 2022, 144, 21810–21825.
40. R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, H. Brune, S. Rusponi, F. Nolting, A. Popov, S. Yang, L. Dunsch and T. Greber, J. Am. Chem. Soc., 2012, 134, 9840–9843.
41. L. Spree, F. Liu, V. Neu, M. Rosenkranz, G. Velkos, Y. Wang, S. Schiemenz, J. Dreiser, P. Gargiani, M. Valvidares, C.-H. Chen, B. Büchner, S. M. Avdoshenko and A. A. Popov, Adv. Funct. Mater., 2021, 31, 2105516.
42. F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz, S. Schiemenz, F. Ziegs, K. Nenkov, A. Kostanyan, T. Greber, A. U. B. Wolter, M. Richter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Nat. Commun., 2019, 10, 571.
43. L. Spree and A. A. Popov, Dalton Trans., 2019, 48, 2861–2871.
44. W. Li, C.-R. Wang and T. Wang, Chem. Commun., 2021, 57, 10317–10326.
45. V. Vieru, L. Ungur and L. F. Chibotaru, J. Phys. Chem. Lett., 2013, 4, 3565–3569.
46. F. Cimpoesu, N. Dragoe, H. Ramanantoanina, W. Urland and C. Daul, Phys. Chem. Chem. Phys., 2014, 16, 11337–11348.
47. M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047–14050.
48. G. Rajaraman, M. K. Singh and N. Yadav, Chem. Commun., 2015, 51, 17732–17735.
49. C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov, A. Kostanyan, T. Greber, A. U. B. Wolter and A. A. Popov, Chem. Sci., 2017, 8, 6451–6465.
50. D. S. Krylov, F. Liu, S. M. Avdoshenko, L. Spree, B. Weise, A. Waske, A. U. B. Wolter, B. Büchner and A. A. Popov, Chem. Commun., 2017, 53, 7901–7904.
51. W. Yang, G. Velkos, F. Liu, S. M. Sudarkova, Y. Wang, J. Zhuang, H. Zhang, X. Li, X. Zhang, B. Büchner, S. M. Avdoshenko, A. A. Popov and N. Chen, Adv. Sci., 2019, 6, 1901352.
52. L. Spree, C. Schlesier, A. Kostanyan, R. Westerström, T. Greber, B. Büchner, S. Avdoshenko and A. A. Popov, Chem.–Eur. J., 2020, 26, 2436–2449.
53. M. Zalibera, F. Ziegs, S. Schiemenz, V. Dubrovin, W. Lubitz, A. Savitsky, S. Deng, X.-B. Wang, S. Avdoshenko and A. A. Popov, Chem. Sci., 2021, 12, 7818–7838.
54. M. Zalibera, D. S. Krylov, D. Karagiannis, P.-A. Will, F. Ziegs, S. Schiemenz, W. Lubitz, S. Reineke, A. Savitsky and A. A. Popov, Angew. Chem., Int. Ed., 2018, 57, 277–281.
55. G. Dantelle, A. Tiwari, R. Rahman, S. R. Plant, K. Porfyrakis, M. Mortier, R. A. Taylor and A. D. Briggs, Opt. Mater., 2009, 32, 251–256.
56. A. Tiwari, G. Dantelle, K. Porfyrakis, R. A. Taylor, A. A. R. Watt, A. Ardavan and G. A. D. Briggs, J. Chem. Phys., 2007, 127, 194504.
57. R. M. Macfarlane, D. S. Bethune, S. Stevenson and H. C. Dorn, Chem. Phys. Lett., 2001, 343, 229–234.
58. M. Nie, J. Xiong, C. Zhao, H. Meng, K. Zhang, Y. Han, J. Li, B. Wang, L. Feng, C. Wang and T. Wang, Nano Res., 2019, 12, 1727–1731.
59. M. Nie, L. Yang, C. Zhao, H. Meng, L. Feng, P. Jin, C.-R. Wang and T. Wang, Nanoscale, 2019, 11, 18612–18618.
60. Y. Ito, T. Okazaki, S. Okubo, M. Akachi, Y. Ohno, T. Mizutani, T. Nakamura, R. Kitaura, T. Sugai and H. Shinohara, ACS Nano, 2007, 1, 456–462.
61. S. R. Plant, G. Dantelle, Y. Ito, T. C. Ng, A. Ardavan, H. Shinohara, R. A. Taylor, A. D. Briggs and K. Porfyrakis, Chem. Phys. Lett., 2009, 476, 41–45.
62. D. Xu, Y. Jiang, Y. Wang, T. Zhou, Z. Shi, H. Omachi, H. Shinohara, B. Sun and Z. Wang, Inorg. Chem., 2019, 58, 14325–14330.
63. H. Jin, J. Xin, W. Xiang, Z. Jiang, X. Han, M. Chen, P. Du, Y.-R. Yao and S. Yang, Adv. Mater., 2023, 35, 2304121.
64. Z. Wang, N. Izumi, Y. Nakanishi, T. Koyama, T. Sugai, M. Tange, T. Okazaki and H. Shinohara, ACS Nano, 2016, 10, 4282–4287.
65. Y. Zhang, D. Krylov, M. Rosenkranz, S. Schiemenz and A. A. Popov, Chem. Sci., 2015, 6, 2328–2341.
66. A. Kostanyan, R. Westerström, D. Kunhardt, B. Büchner, A. A. Popov and T. Greber, Phys. Rev. B, 2020, 101, 134429.
67. F. Liu, S. Wang, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, F. Jin, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, Angew. Chem., Int. Ed., 2017, 56, 1830–1834.
68. F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, J. Am. Chem. Soc., 2016, 138, 14764–14771.
69. G. Velkos, D. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp, H. Dorn and A. A. Popov, Angew. Chem., Int. Ed., 2019, 58, 5891–5896.
70. Y. Wang, G. Velkos, N. J. Israel, M. Rosenkranz, B. Büchner, F. Liu and A. A. Popov, J. Am. Chem. Soc., 2021, 143, 18139–18149.
71. F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098.
72. R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, K. Krämer, S.-X. Liu, S. Decurtins, A. Popov, S. Yang, L. Dunsch and T. Greber, Phys. Rev. B, 2014, 89, 060406.
73. Y. Wang, J. Xiong, J. Su, Z.-Q. Hu, F. Ma, R. Sun, X.-Y. Tan, H.-L. Sun, B. Wang, Z. Shi and S. Gao, Nanoscale, 2020, 12, 11130–11135.
74. J. Dreiser, R. Westerström, Y. Zhang, A. A. Popov, L. Dunsch, K. Krämer, S.-X. Liu, S. Decurtins and T. Greber, Chem.–Eur. J., 2014, 20, 13536–13540.
75. J.-F. Wyart, A. Meftah, A. Bachelier, J. Sinzelle, W.-Ü. L. Tchang-Brillet, N. Champion, N. Spector and J. Sugar, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, L77–L82.
76. F. Melin, M. N. Chaur, S. Engmann, B. Elliott, A. Kumbhar, A. J. Athans and L. Echegoyen, Angew. Chem., Int. Ed., 2007, 46, 9032–9035.
77. S. Yang, A. A. Popov, C. Chen and L. Dunsch, J. Phys. Chem. C, 2009, 113, 7616–7623.
78. W. Yang, G. Velkos, M. Rosenkranz, S. Schiemenz, F. Liu and A. A. Popov, Adv. Sci., 2024, 1, 202305190.
79. F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175.
80. A. Borah and R. Murugavel, Coord. Chem. Rev., 2022, 453, 214288.
81. G. Huang, G. Calvez, Y. Suffren, C. Daiguebonne, S. Freslon, O. Guillou and K. Bernot, Magnetochemistry, 2018, 4, 44.
82. B. Casanovas, M. Font-Bardía, S. Speed, M. S. El Fallah and R. Vicente, Eur. J. Inorg. Chem., 2018, 2018, 1928–1937.
83. B. Casanovas, S. Speed, R. Vicente and M. Font-Bardía, Polyhedron, 2019, 173, 114113.
84. R. Vicente, À. Tubau, S. Speed, F. A. Mautner, F. Bierbaumer, R. C. Fischer and S. S. Massoud, New J. Chem., 2021, 45, 14713–14723.
85. H. Chen, L. Sun, K. Zheng, J. Zhang, P. Ma, J. Wang and J. Niu, Dalton Trans., 2022, 51, 10257–10265.
86. S. Yang, L. Zhang, W. Zhang and L. Dunsch, Chem.–Eur. J., 2010, 16, 12398–12405.
87. U. Mueller, R. Förster, M. Hellmig, F. U. Huschmann, A. Kastner, P. Malecki, S. Pühringer, M. Röwer, K. Sparta, M. Steffien, M. Ühlein, P. Wilk and M. S. Weiss, Eur. Phys. J. Plus, 2015, 130, 141.
88. W. Kabsch, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 125–132.
89. K. M. Sparta, M. Krug, U. Heinemann, U. Mueller and M. S. Weiss, J. Appl. Crystallogr., 2016, 49, 1085–1092.
90. G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
91. S. Stevenson, C. B. Rose, J. S. Maslenikova, J. R. Villarreal, M. A. Mackey, B. Q. Mercado, K. Chen, M. M. Olmstead and A. L. Balch, Inorg. Chem., 2012, 51, 13096–13102.
92. S. Stevenson, C. Chancellor, H. M. Lee, M. M. Olmstead and A. L. Balch, Inorg. Chem., 2008, 47, 1420–1427.
93. X. L. Wang, T. M. Zuo, M. M. Olmstead, J. C. Duchamp, T. E. Glass, F. Cromer, A. L. Balch and H. C. Dorn, J. Am. Chem. Soc., 2006, 128, 8884–8889.
94. D. Krylov, F. Liu, A. Brandenburg, L. Spree, V. Bon, S. Kaskel, A. Wolter, B. Buchner, S. Avdoshenko and A. A. Popov, Phys. Chem. Chem. Phys., 2018, 20, 11656–11672.
95. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
96. T. E. Rieser, R. Thim-Spöring, D. Schädle, P. Sirsch, R. Litlabø, K. W. Törnroos, C. Maichle-Mössmer and R. Anwander, J. Am. Chem. Soc., 2022, 144, 4102–4113.
97. D. Schädle, C. Schädle, D. Schneider, C. Maichle-Mössmer and R. Anwander, Organometallics, 2015, 34, 4994–5008.
98. D. Schädle, C. Schädle, K. W. Törnroos and R. Anwander, Organometallics, 2012, 31, 5101–5107.
99. W. J. Evans, R. Anwander, J. W. Ziller and S. I. Khan, Inorg. Chem., 1995, 34, 5927–5930.
100. J. Liu, D. Reta, J. A. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem.–Euro. J., 2019, 25, 7749–7758.
101. R. Taube, S. Maiwald and J. Sieler, J. Organomet. Chem., 2001, 621, 327–336.
102. D. Barbier-Baudry, O. Blacque, A. Hafid, A. Nyassi, H. Sitzmann and M. Visseaux, Eur. J. Inorg. Chem., 2000, 2000, 2333–2336.
103. S. M. Cendrowski-Guillaume, M. Nierlich, M. Lance and M. Ephritikhine, Organometallics, 1998, 17, 786–788.
104. L. Münzfeld, C. Schoo, S. Bestgen, E. Moreno-Pineda, R. Köppe, M. Ruben and P. W. Roesky, Nat. Commun., 2019, 10, 3135.
105. F. M. Sroor, C. G. Hrib, P. Liebing, L. Hilfert, S. Busse and F. T. Edelmann, Dalton Trans., 2016, 45, 13332–13346.
106. Y. Zhang, R. Guan, M. Chen, Y. Shen, Q. Pan, Y. Lian and S. Yang, Inorg. Chem., 2021, 6, 1462–1471.
107. M. M. Olmstead, T. Zuo, H. C. Dorn, T. Li and A. L. Balch, Inorg. Chim. Acta, 2017, 468, 321–326.
108. C. Schlesier, F. Liu, V. Dubrovin, L. Spree, B. Büchner, S. Avdoshenko and A. A. Popov, Nanoscale, 2019, 11, 13139–13153.
109. V. Dubrovin, L.-H. Gan, B. Büchner, A. A. Popov and S. M. Avdoshenko, Phys. Chem. Chem. Phys., 2019, 21, 8197–8200.
110. S. V. Eliseeva and J.-C. G. Bünzli, Chem. Soc. Rev., 2010, 39, 189–227.
111. J. G. M. Morton, A. Tiwari, G. Dantelle, K. Porfyrakis, A. Ardavan and G. A. D. Briggs, Phys. Rev. Lett., 2008, 101, 013002.
112. H. Reddmann, C. Apostolidis, O. Walter and H.-D. Amberger, Z. Anorg. Allg. Chem., 2006, 632, 1405–1408.
113. J. D. Rinehart and J. R. Long, Dalton Trans., 2012, 41, 13572–13574.
114. Q.-W. Li, R.-C. Wan, Y.-C. Chen, J.-L. Liu, L.-F. Wang, J.-H. Jia, N. F. Chilton and M.-L. Tong, Chem. Commun., 2016, 52, 13365–13368.
115. M. D. Korzyński, M. Bernhardt, V. Romankov, J. Dreiser, G. Matmon, F. Pointillart, B. Le Guennic, O. Cador and C. Copéret, Chem. Sci., 2022, 13, 10574–10580.
116. H.-D. Amberger, H. Reddmann, T. J. Mueller and W. J. Evans, J. Organomet. Chem., 2011, 696, 2829–2836.
117. H.-D. Amberger and H. Reddmann, Z. Anorg. Allg. Chem., 2007, 633, 443–452.
118. S. Jank, H. Reddmann, H.-D. Amberger and C. Apostolidis, J. Organomet. Chem., 2004, 689, 3143–3157.
119. R. Westerström, V. Dubrovin, K. Junghans, C. Schlesier, B. Büchner, S. M. Avdoshenko, A. A. Popov, A. Kostanyan, J. Dreiser and T. Greber, Phys. Rev. B, 2021, 104, 224401.
120. Y. Hao, G. Velkos, S. Schiemenz, M. Rosenkranz, Y. Wang, B. Büchner, S. M. Avdoshenko, A. A. Popov and F. Liu, Inorg. Chem. Front., 2023, 10, 468–484.
121. L. Gagliardi, R. Lindh and G. Karlström, J. Chem. Phys., 2004, 121, 4494–4500.
122. L. Ungur and L. F. Chibotaru, Chem.–Euro. J., 2017, 23, 3708–3718.
123. M. Briganti, G. F. Garcia, J. Jung, R. Sessoli, B. Le Guennic and F. Totti, Chem. Sci., 2019, 10, 7233–7245.
124. R. Alessandri, H. Zulfikri, J. Autschbach and H. Bolvin, Chem.–Eur. J., 2018, 24, 5538–5550.
125. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Commun., 2016, 52, 7168–7171.
126. Y.-C. Chen, X.-S. Huang, J.-L. Liu and M.-L. Tong, Inorg. Chem., 2018, 57, 11782–11787.
127. L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112.
128. C. K. Jørgensen, Prog. Inorg. Chem., 1962, 73–124.
129. S. P. Sinha and H. H. Schmidtke, Mol. Phys., 1965, 10, 7–11.
130. D. E. Henrie, Mol. Phys., 1974, 28, 415–421.
131. S. Chorazy, T. Charytanowicz, J. Wang, S.-i. Ohkoshi and B. Sieklucka, Dalton Trans., 2018, 47, 7870–7874.
132. R. Jankowski, J. J. Zakrzewski, M. Zychowicz, J. Wang, Y. Oki, S.-i. Ohkoshi, S. Chorazy and B. Sieklucka, J. Mater. Chem. C, 2021, 9, 10705–10717.
133. N. C. Chang, J. Chem. Phys., 1966, 44, 4044–4050.
134. J. B. Gruber, R. P. Leavitt and C. A. Morrison, J. Chem. Phys., 1983, 79, 1664–1668.
135. J. A. Koningstein and J. E. Geusic, Phys. Rev., 1964, 136, A711–A716.
136. J. B. Gruber, M. E. Hills, T. H. Allik, C. K. Jayasankar, J. R. Quagliano and F. S. Richardson, Phys. Rev. B, 1990, 41, 7999–8012.
137. H. M. Crosswhite, H. Crosswhite, F. W. Kaseta and R. Sarup, J. Chem. Phys., 1976, 64, 1981–1985.
138. R. M. Hammond, M. F. Reid and F. S. Richardson, J. Less-Common Met., 1989, 148, 311–319.
139. W. T. Carnall, H. Crosswhite and H. M. Crosswhite, Energy level structure and transition probabilities in the spectra of the trivalent lanthanides in LaF₃, United States, 1978, DOI:  DOI:10.2172/6417825.
140. A. Barla, J. Nicolás, D. Cocco, S. M. Valvidares, J. Herrero-Martín, P. Gargiani, J. Moldes, C. Ruget, E. Pellegrin and S. Ferrer, J. Synchrotron Radiat., 2016, 23, 1507–1517.
141. B. T. Thole, P. Carra, F. Sette and G. van der Laan, Phys. Rev. Lett., 1992, 68, 1943–1946.
142. P. Carra, B. T. Thole, M. Altarelli and X. Wang, Phys. Rev. Lett., 1993, 70, 694–697.
143. Y. Teramura, A. Tanaka, B. T. Thole and T. Jo, J. Phys. Soc. Jpn., 1996, 65, 3056–3059.
144. M.-X. Xu, Y.-S. Meng, J. Xiong, B.-W. Wang, S.-D. Jiang and S. Gao, Dalton Trans., 2018, 47, 1966–1971.
145. E. Regincós Martí, A. B. Canaj, T. Sharma, A. Celmina, C. Wilson, G. Rajaraman and M. Murrie, Inorg. Chem., 2022, 61, 9906–9917.
146. J. Li, L. Yin, S.-J. Xiong, X.-L. Wu, F. Yu, Z.-W. Ouyang, Z.-C. Xia, Y.-Q. Zhang, J. van Tol, Y. Song and Z. Wang, iScience, 2020, 23, 100926.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental details, SC-XRD data, results of DFT and CASSCF calculations, and magnetic and spectroscopic data. CCDC 2194854. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc05146c

---