Open Access Article
Open Access ArticleTailoring the facet distribution on copper with chloride†
Pedro Mazaira
Couce
 a,
Thor Kongstad
Madsen
a,
Thor Kongstad
Madsen
 a,
Elena
Plaza-Mayoral
a,
Elena
Plaza-Mayoral
 a,
Henrik H.
Kristoffersen
a,
Henrik H.
Kristoffersen
 *a,
Ib
Chorkendorff
*a,
Ib
Chorkendorff
 b,
Kim Nicole
Dalby
b,
Kim Nicole
Dalby
 c,
Ward
van der Stam
c,
Ward
van der Stam
 d,
Jan
Rossmeisl
d,
Jan
Rossmeisl
 a,
María
Escudero-Escribano
a,
María
Escudero-Escribano
 *aef and
Paula
Sebastián-Pascual
*aef and
Paula
Sebastián-Pascual
 *a
*a
aDepartment of Chemistry, Center for High Entropy Catalysis (CHEAC), University of Copenhagen, Universitetsparken 5, 2100 Copenhagen, Denmark. E-mail: paula.pascual@chem.ku.dk; hhk@chem.ku.dk
bDepartment of Physics, Surface Physics and Catalysis, Technical University of Denmark, Fysikvej, DK-2800 Lyngby, Denmark
cTopsoe A/S, Haldor Topsøes Allé 1, DK-2800 Kgs. Lyngby, Denmark
dUtrecht University, Inorganic Chemistry and Catalysis, Debye Institute for Nanomaterials Science, Netherlands
eCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC, Barcelona Institute of Science and Technology, UAB Campus, 08193 Bellaterra, Barcelona, Spain. E-mail: maria.escudero@icn2.cat
fICREA, Pg. Lluís Companys 23, 08010 Barcelona, Spain
First published on 21st December 2023
Abstract
Electrocatalytic reactions are sensitive to the catalyst surface structure. Therefore, finding methods to determine active surface sites with different geometry is essential to address the structure–electrocatalytic performance relationships. In this work, we propose a simple methodology to tune and quantify the surface structure on copper catalysts. We tailor the distribution and ratio of facets on copper by electrochemically oxidizing and reducing the surface in chloride-rich aqueous solutions. We then address the formation of new facets with voltammetric lead (Pb) underpotential deposition (UPD). We first record the voltammetric lead UPD on different single facets, which have intense peaks at different potential values. We use this data to decouple each facet peak-contribution in the lead (Pb) UPD curves of the tailored and multifaceted copper surfaces and determine the geometry of the active sites. We combine experiments with density functional theory (DFT) calculations to assess the ligand effect of chloride anions on the copper facet distribution during the surface oxidation/electrodeposition treatment. Our experiments and Wulff constructions suggest that chloride preferentially adsorbs on the (310) facet, reducing the number of (111) sites and inducing the growth of (310) or n(100) × (110) domains. Our work provides a tool to correlate active sites with copper geometries, which is needed to assess the structure–performance relationships in electrocatalysis. We also demonstrate an easy method for selectively tailoring the facet distribution of copper, which is essential to design a well-defined nanostructured catalyst.
Introduction
Catalysis plays a key role in the transition toward a decarbonized industry.1 Catalytic reactions occur at the active surface sites via the formation of adsorbed intermediates. The binding energies of these active sites vary with their geometric and electronic structure. To rationally address catalytic performance and tailor more active and selective surface structures it is crucial to determine and quantify the active sites of the synthesized nanocatalysts.2,3Copper-based materials are promising catalysts for several electrocatalytic reactions such as the conversion of carbon dioxide (CO2) into valuable chemicals and fuels.4–6 In particular, copper can efficiently convert CO2 into C2+ multicarbon products at room temperature and pressure.4,7–10 The work by Hori and co-workers on well-defined extended single crystalline facets showed that both product selectivity and activity of the CO2 reduction depends on the geometry of the active surface sites. The (111) sites enhance the production of methane whereas (100) sites enhance the carbon–carbon (C–C) coupling reactions, producing C2+ products.11–13 Remarkably n(100) × (110) stepped surfaces, i.e., surfaces formed by (100) terraces with n atomic rows separated by (110) atomic step sites, preferentially produce ethanol, a highly valuable liquid fuel.12–14 Recent studies, using in situ and operando techniques, have focused on addressing which active sites at the catalyst surface promote the conversion of CO2, under reaction conditions.15–17 Based on these studies, researchers have applied different strategies in order to tune and enhance the electrocatalytic performance of copper, including surface nanostructuring and roughening,18–22 adding organic surface modifiers7,23 and tuning the electrolyte–surface interactions.24–26 Nevertheless, a recent study of the state of the art of copper-based catalysts carried out by Christensen et al.7 highlights that these strategies slightly change the “intrinsic” activity of copper toward desirable products when compared to some of the single facets from Hori and co-workers.12 These studies show that, among other parameters, the surface geometry could potentially control the catalytic properties of copper.
The intrinsic performance of electrocatalysts is the current density normalized by the number of active surface sites per area of electrode, i.e., normalized by the electroactive surface area (ECSA).27–29 Nanostructured catalysts, nanoparticles and roughened surfaces typically display enhanced current densities due to their high ECSA as well as a high presence of grain boundaries and undercoordinated sites. Reporting the intrinsic activity of synthetized nanostructures is key because it decouples the effects of having large ECSA in the measured current densities, and gives direct information on how the active sites structure influence the electrocatalysis.30,31 Thus, we find it essential to develop quantitative methods to electrochemically determine both the catalyst ECSA and the geometry of the different active sites on copper, to address how the catalyst surface structure affects performance. Traditionally, the determination of the surface structure and single facets on well-defined nanocatalysts has been performed combining cyclic voltammetry32,33 with scanning probe microscopy and electron microscopy to assess the surface at the atomic or nanoscale level.34,35 Blank cyclic voltammograms give valuable structural information of the entire electrode surface, by measuring the changes in interfacial charge originated from electrolyte adsorption/desorption, surface reconstruction or electric double layer charge/and discharge. These interfacial processes give voltammetric features which both shape and potential value depend on the facet orientation, thereby allowing to decouple the different facet-contributions on polycrystalline surfaces and providing the voltammetric fingerprint of the catalyst.33,36–39
In our previous publication, we showed that lead (Pb) underpotential deposition (UPD) on copper is a valuable method to address the surface structure of multifaceted copper surfaces.40 With the Pb UPD method, we measure with cyclic voltammetry (CV) the reversible deposition/oxidation of a submonolayer of lead on copper, at potentials prior to the thermodynamic bulk deposition of lead on Cu, which is ca. −0.5 V vs. SCE for Pb2+ concentrations of 1 mM.41 Previously, Brisard et al. characterized the lead UPD on Cu(111) and Cu(100) single facets, which displayed sharp peaks with different potential values.41,42 More recently, Hochfilzer et al. have reported the lead UPD CVs on the Cu basal planes in alkaline media, which also displayed intense and structure sensitive features.43 The overall reaction (Pb2+ + 2e− → Pb*) involves the transfer of two electrons, with a lead coverage around 0.5 according to works from Brisard et al.41,42 In our previous work we also showed that the shape, intensity and peak distribution in the lead UPD curves are highly sensitive to any change produced on the copper surface and induced by different electrochemical treatments.40,43 In other words, lead UPD allows us to estimate the contribution of different facets or crystallographic domains by decoupling peaks in the cyclic voltammogram.40
In this study, we propose a simple methodology to estimate the number and geometric structure of active surface sites on copper catalysts. We combine Pb UPD voltammetric experiments on copper single facets, density functional theory (DFT) modelling and ex situ surface-sensitive X-ray photoelectron spectroscopy (XPS) and scanning electron microscopy (SEM) characterization, to address the formation of facets on copper in chloride media. Previous works have reported that chloride adsorption induces the growth of (100) facets on copper.44–46 To address the formation of (100) domains we have compared our reconstructed copper surfaces in chloride media with the basal planes Cu(111), Cu(100), and Cu(110) following a similar strategy to the one we used in our previous work40 and in the work described by Hochfilzer et al.43 In addition, we have also investigated the Cu(310) stepped surface for two reasons: (i) (310) is a special facet highly selective to the production of ethanol and ethylene. Thus, determining the presence of active sites with this geometry is key to address the catalytic performance on copper catalysts;12,47 (ii) The electrochemical behaviour of shaped nanostructures approaches more to stepped surfaces than to the basal planes, as stepped surfaces have lowly coordinated step sites. Cu(310) is a 2(100) × (110) surface, meaning that it contains (100) terraces formed by two rows of atoms separated by atomic steps with (110) geometry.22,48
To change the facet distribution on a polycrystalline extended copper surface, we continuously oxidized and reduced the surface in 0.1 M NaCl solution. In this treatment, we linearly scan the applied potential from a cathodic value in which copper remains reduced, to an anodic value in which copper is oxidized, and to the lower potential limit (−1.0 V vs. SCE) for the re-deposition of copper. The number of formed facets is controlled by adjusting the anodic or oxidation potential (1.0, 1.3, 1.6 and 2.0 V vs. SCE). Then, we use the lead UPD technique to quantitatively address the formation or elimination of facets on copper. We use the experiments on single facets as a reference to decouple the peak contributions in the lead UPD of the tailored polycrystalline copper surface. Finally, using DFT calculations, we rationally explain the ligand effect of chloride anions on the copper facet redistribution process, based on the energetics of chloride adsorption onto the different facets and surface stabilization energies.44,49 Our work presents a new and simple methodology to characterize copper surface structures and evaluate the effect of ligand and capping agents in electrochemical synthesis, relevant to further establish new routes for the preparation of well-defined nanocatalysts.
Experimental
Electrochemical measurements and surface pre-treatment
All electrochemical experiments were performed in a classical three-electrode cell configuration using a glass cell with four entries and a lugging capillary for the reference electrode. The reference electrode was, in all cases, a saturated calomel electrode (SCE). The counter electrode was a Cu wire. The Cu wire was cleaned by submerging it in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volumetric solution of Milli-Q water and nitric acid, followed by rinsing with Milli-Q water. The working electrode was either a Cu single crystal, Cu(hkl) or a Cu polycrystalline, Cu(poly), purchased from MaTecK Company. All experiments have been performed keeping the working electrode in the hanging meniscus configuration and under argon atmosphere.
1 volumetric solution of Milli-Q water and nitric acid, followed by rinsing with Milli-Q water. The working electrode was either a Cu single crystal, Cu(hkl) or a Cu polycrystalline, Cu(poly), purchased from MaTecK Company. All experiments have been performed keeping the working electrode in the hanging meniscus configuration and under argon atmosphere.
Before carrying out the electrochemical experiments, the Cu(poly) surface was mechanically polished three times, using a suspension of alpha alumina particles with a diameter of 1 μm, 0.3 μm, and 0.05 μm, respectively. Once the Cu(poly) was polished to a mirror-like surface, it was sonicated in Milli-Q water five times for 60 seconds. Afterwards, the working electrode was electropolished in a two-electrode cell containing a 10 phosphoric acid: 3 sulphuric acid: 1 Milli-Q water volume ratio solution. Then, we applied a constant potential difference (ΔE) of 1.8 V between the Cu(poly) (anode) and a copper wire (cathode). Finally, the electropolished Cu(poly) was rinsed with Milli-Q water to remove the excess of acid, and we transferred it to the electrochemical cell. The single crystalline electrodes, Cu(hkl), were only electropolished for 30 seconds by applying a ΔE of 1.6 V. All electrochemical experiments have been recorded using a VSP-300 biologic multipotentiostat.
Before all the experiments, the glassware and glass cell were kept overnight in a 1 L saturated solution of KMnO4 plus a few mL of H2SO4 to oxidize all organic pollutants. Then, the glassware was rinsed with a diluted solution of H2O2 + H2SO4, to dissolve the MnO2 waste, and was boiled two to three times in Milli-Q water.
Modification of the facet distribution on Cu using 0.1 M NaCl solution
The electrochemical copper re-faceting was performed in an electrolyte of 0.1 M NaCl. We cycled the electrode at 500 mV s−1 between −1.0 V vs. SCE, where copper remains reduced, to different anodic or oxidation potentials (Eox = 1 V, 1.3 V, 1.6 V or 2 V vs. SCE) where copper is oxidized. The potential cycling was stopped at the reduction potential of −1.0 V vs. SCE. After cycling the electrode in 0.1 M NaCl, the electrode was consecutively cycled in the potential region prior to the oxidation of copper and with a scan rate of 500 mV s−1 to remove traces of copper chloride or copper oxide passivating the surface (Fig. S1†). This step was performed, both in the NaCl solution (between −0.4 V and −0.2 V vs. SCE) and in the solution containing lead (between −0.4 V and −0.2 V vs. SCE). Reproducible lead UPD CVs were obtained on each copper surface (Fig. S2†).Determination of the electroactive surface area and distribution of facets by lead UPD
The CVs of the lead UPD on copper were performed at a pH of ca. 3 using an electrolyte solution of 0.1 M of KClO4 (99.95%, Sigma-Aldrich Merck) + 2 mM of NaCl (99.9% Sigma-Aldrich Merck) + 2 mM of Pb(ClO4)2·(H2O) (99.995%, Sigma-Aldrich Merck) + 1 mM HClO4 (70%, Sigma Aldrich Merck, Suprapur®). The cyclic voltammograms were performed between −0.4 V and −0.2 V vs. SCE with a scan rate of 5 mV s−1.The estimation of the electrochemically active surface area (ECSA) and the determination of different facets on the investigated surfaces relied on the integration of charge involved in the cathodic curve of the lead UPD CVs. The curves and peaks in the lead UPDs CVs were fitted to a Gaussian mathematical function using Origin software, to determine the distribution of facets on the different surfaces. We used the peak-potential values in the lead UPD CVs recorded on Cu single facets, to assess the facet distribution modification on the NaCl-treated copper surfaces. We integrated the charge under the cathodic curves of the lead UPD CVs on Cu single facets and on the Cu(poly) flat extended surfaces, with roughness factor 1, and used the obtained value on Cu(poly) to calculate the increase in ECSA of the NaCl-treated copper surfaces by using the following relation: RFNaCl-Cu = Qlead UPD, NaCl-Cu/Qlead UPD, Cu(poly), where RFNaCl-Cu is the roughness factor of the NaCl-treated Cu sufaces, and Qlead UPD, NaCl-Cu and Qlead UPD, Cu(poly) corresponds to the integrated cathodic charge in the lead UPD CVs on the NaCl-treated samples and on the Cu(poly) (μC cm−2).
Morphology analysis
Before the ex situ morphological characterization using scanning electron microscopy, the NaCl-treated copper samples were cycled in 0.1 M NaCl solution several times at 500 mV s−1 in the potential region prior to the oxidation of copper (between −0.3 V and 0.2 V vs. SCE), until a constant CV was obtained. Then, the samples were cleaned with abundant Milli-Q water. The morphology of the NaCl-treated samples was analysed using a scanning electron microscope at the University of Copenhagen JEOL 7800 F prime at a low voltage of 2 keV. The Cu(poly) flat surface was analysed using the high-resolution Zeiss Gemini 500 field emission scanning electron microscope at Topse A/S. An Inlens and SE2 detector were used at low voltage (2 keV) to take high resolution images with the FE-SEM.X-ray photoelectron spectroscopy (XPS) analysis
All XPS measurements were conducted by a Theta Probe instrument (Thermo Scientific) using an Al anode X-ray source (Kα line = 1486.6 eV). The XPS chamber's base pressure was <5.0 × 10−8 mbar. The X-ray beam size was 400 μm and the pass energy 100 eV. A depth analysis was conducted by sputtering the samples (4 kV and 1.0 μA) with N6 Ar (1.1 × 10−7 mbar) for a total of 30 seconds, 10 seconds per level. The spectra were recorded on each level, being level 0 without sputtering. After the survey scans, C 1s, O 1s, Cu 2p and Cl 2p peaks were measured in steps of 0.1 eV. Thermo Avantage Software was used to carry out the data analysis. Shirley type background was used for all instances. All peaks were fitted with a Gaussian–Lorentzian mix GL(100) shape with full width half maximum (FWHM) fit parameter below 3.5 eV. The survey spectra are represented in the ESI, Fig. S4.† Additionally, broad overview spectra surveys at 1 eV steps were obtained to identify potential sources of contamination.Computational modelling and Wulff constructions
Density functional theory (DFT) with the BEEF-vdW exchange correlation functional50 was used to first model chloride ion adsorption on the (111), (100), (110) and (310) copper facets and then, to calculate surface tensions of the chlorine covered copper facets. The surface cells used to model the four copper facets are depicted with varying coverages of adsorbed Cl* in the ESI, Fig. S9–S12.† The simulations were done in the GPAW DFT environment51 using a plane-wave basis with a cut-off of 600 eV, k-point sampling of 4 × 4 × 1, and copper slabs with at least six atomic layers. The simulated structures were relaxed to a maximum force of under 0.03 eV Å−1.In order to include chloride ion adsorption in the copper surface tensions (γ), we add the bare copper surface energies (γCu) and the total Gibbs free energy stabilization from adsorbing n Cl− ions on the surfaces (ΔGnCl = Gslab+nCl* − Gslab − nGCl−) divided by the surface area (A) (eqn (1)).
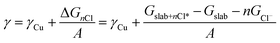 | (1) |
The free energies of copper slabs (Gslab) and copper slabs with n adsorbed Cl* atoms (Gslab+nCl*) are given by the DFT energies adjusted by the configurational entropy, zero-point energy, heating, and vibrational entropy of *Cl species. Ions present unnecessary computational difficulties, so GCl− is obtained by calculating ½Cl2(g) instead of Cl−(aq) and adjusting the Cl2(g) Gibbs free energy (GCl2) by how far the potential is from the ½Cl2(g) + e− ⇌ Cl− equilibrium potential (eqn (2)). This follows the computational hydrogen electrode approach.52
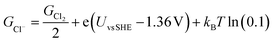 | (2) |
The equilibrium potential of ½Cl2(g) + e− ⇌ Cl− is the standard electrode potential of the reaction (1.36 V vs. SHE)53 adjusted by kBT ln(0.1) to account for the 0.1 M Cl− ion concentration used in the experiments. GCl2 is given by the calculated DFT energy and zero point energy of Cl2(g) and the tabulated entropy and heating of Cl2(g).54 In the modelling, we set Uvs. SCE = Uvs. SHE − 0.248 V, to convert between reference potentials. Solvation effects from the electrolyte are not included in our study. Additional computational details are included in the ESI.†
The obtained surface tensions are used in Wulff constructions with “WulffPack – a package for Wulff constructions”.55
Results and discussion
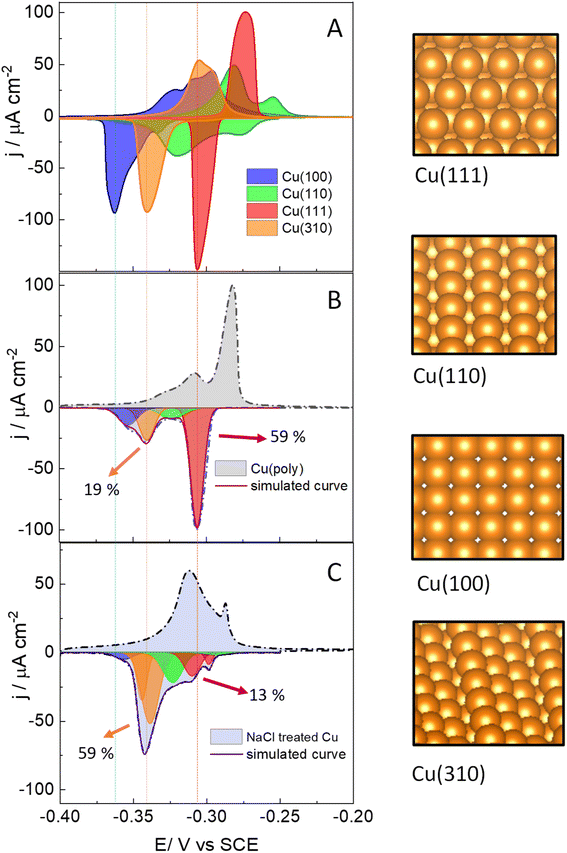
We start assessing the lead UPD on different copper single-crystalline electrodes to identify the potential range at which lead adsorbs and desorbs in each single facet. Fig. 1 shows the lead UPD on Cu(111), Cu(100), Cu(110) and Cu(310) planes. All the lead UPD analysis in this work has been performed at 5 mV s−1 and in 0.1 M KClO4 + 1 mM NaCl + 2 mM Pb(ClO4)2 solution, at pH 3, following our previous work.40 We added chloride to the solution containing lead because chloride enhances the lead UPD kinetics, which results in sharp, intense and decoupled peak in the CV of each single facet, a phenomenon previously reported by Brisard et al.41,42 Each single-facet in Fig. 1 has well-defined features located at different potential values. The peaks recorded in the cathodic or negative scan are sharper than the counter peaks in the anodic scan which are broader and non-symmetric. In Table S1† we have added the potential values of the cathodic peaks in each single facet.The cathodic scan in Fig. 1A shows that Cu(111) (red area) has one single peak at −0.305 V vs. SCE. In contrast, Cu(110) (green area) displays two main peaks (−0.278 V and −0.318 V vs. SCE). The lead UPD CV on Cu(310) (orange area) only displays a single intense feature at −0.340 V. Cu(100) (blue area) displays one main feature at −0.362 V, and a tiny peak at −0.330 V. We ascribe the latter peak to the presence of (310) sites, or short (100) domains disrupted by defect sites, as it appears in the potential region of the Cu(310). Although the electropolishing induces defect sites,56–58 Brisard et al. showed that electropolished copper provide lead UPD curves that are essentially like those recorded on Cu surfaces treated in ultrahigh vacuum (UHV) conditions, and only causes a slight broadening of the peaks, due to the smaller length of the terraces.37,41,42,56 This result shows that the cyclic voltammetry is a useful method to assess the preferential orientation of the surface. It is important to remark that Hochfilzer et al.43 have also reported the lead UPD CVs on Cu(111), Cu(100) and Cu(110) in 0.1 M KOH media, observing that the (100) cathodic peak is shifted to lower potential values than the (110) and the (111) peaks. This peak shift was ascribed to the adsorption of OH groups on Cu which controls the potential window at which Pb UPD occurs on each facet. Our experiments in Fig. 1A are consistent with the results obtained by Hochfilzer et al.43 However, the shape of the CVs in our investigation varies a little bit due to the difference in electrolyte pH and the effect of chloride adsorption on the Pb UPD. Our results, as well as previous works40–43 show that lead UPD on Cu is both structure and electrolyte sensitive and provides a distinguishable voltammetric fingerprint of each single facet. We have integrated the charge under the lead UPD cathodic curves, obtaining values between 316.0 ± 0.4 μC cm−2 for the Cu(310) and 375 ± 19 μC cm−2 for Cu(100) (Table S2†), which are consistent with the charges reported in literature for the lead UPD onto flat and well-defined copper surfaces.41,42
Fig. 1B shows the lead UPD of a Cu polycrystalline electrode, Cu(poly). The lead UPD on Cu(poly) contains several single-facet peaks, that we decouple using mathematical Gaussian functions, following a similar procedure to the one reported in ref. 32. To do the peak decoupling, we use the peak potential of the single facets as a reference. Table S3 and Fig. S3† contain all the details regarding the peak deconvolution of the lead UPD on Cu surfaces, such as peak potential, fraction area and half-width. The integrated cathodic charge on Cu(poly) (Table S2†) was 367 ± 25 μC cm−2, similar to the one on Cu single facets, confirming that the Cu(poly) is flat and has a roughness factor near to 1. The most prominent peak in the lead UPD on Cu(poly) (red peak, Fig. 1B) perfectly aligns with the Cu(111) peak in Fig. 1A (indicated by the dashed lines), showing that large (111) domains exist on Cu(poly). The integrated charge or fraction area of this facet-peak is 59%. Interestingly, Fig. 1B shows a tiny peak at −0.330 V with a fraction area of 19%, suggesting the presence of n(100) × (110) or (310) domains in the Cu(poly). Additionally, there is a second (green) and fourth (blue) peak in Fig. 1B, which are close but do not align with the Cu(100) and Cu(110) features in Fig. 1A, a fact that we ascribe to these peaks being related to short terrace-domains or stepped and defect sites.
After assessing the voltammetric fingerprint of the Cu(poly) surface, we brought the electrode to a cell containing 0.1 M NaCl solution. Then, we applied two consecutive oxidation and reduction cycles at 500 mV s−1 from −1.0 V (Cu remains metallic), to 2.0 V (copper is oxidized), and to −1.0 V (copper is re-deposited). The aim of this experiment is to assess the ligand effect of the chloride anion in the copper nucleation and growth when it is re-deposited at −1.0 V. After that, we performed lead UPD on the re-faceted Cu(poly); the CV results are shown in Fig. 1C. The lead UPD in the chloride re-faceted Cu surface shows a different distribution and peak intensity compared to Cu(poly). The most noticeable changes are that the fraction area of the (111) peak (red peak) has been reduced from 59% to 13%. In contrast, the fraction area of the orange peak in the Cu(poly), which aligns with the Cu(310) single facet in potential, has increased from 19% to a 59% (Fig. 1C). This result strongly suggests that chloride induces the formation of (310) domains on Cu, which is the dominant facet in the NaCl-treated Cu surfaces. Fig. 1C also displays other minor peak contributions, particularly near to the (111) region, which we ascribe to an effect of decreasing the amount of (111) terraces by the oxidation/reduction treatment with chloride anions. The integrated charge under the cathodic curve is 435 ± 70 μC cm−2 (Table S1†), corresponding to only a slight increase of the surface roughness factor of 1.2 compared with the Cu(poly). This result suggests that the electrochemical treatment in 0.1 M NaCl solution primarily induces surface reconstruction and slightly increase the roughness of the surface.
The UPD CVs that we obtain are stable and reproducible. Previous works have shown that lead can induce changes in the atomic structure or form an alloy with the single facets.42,59,60 These phenomena could also explain the low symmetry of the cathodic and anodic scans in the lead UPD CVs. We have carried out consecutive cycles of the lead UPD on the different single and multi-faceted surfaces (Fig. S2†) and we do not observe significant changes of the voltammetric shape during consecutive scans. The lead UPD CVs display an electrochemical behaviour which is unique and characteristic for each orientation, suggesting that the interaction and adsorption of lead on copper is structure sensitive or depending on the orientation. This unique behaviour for each surface allows us to use lead to characterize the structure of the different copper surfaces by recording its lead UPD voltammetric fingerprint (Fig. 1 and S2†).
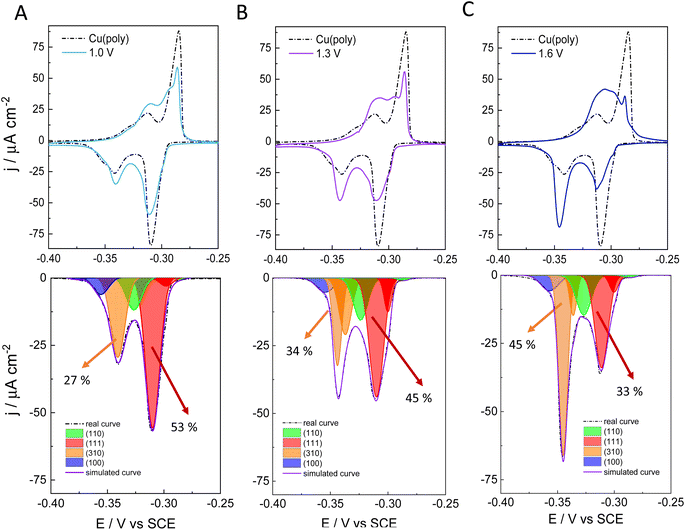
To better assess the capping or ligand role of chloride anions, we have evaluated the effect of applying different oxidation potentials in the formation of new facets on Cu in 0.1 M NaCl. We apply three different oxidation potentials: 1.0 V in Fig. 2A, 1.3 V in Fig. 2B, and 1.6 V in Fig. 2C. In all the experiments, the applied reductive potential is the same (−1.0 V vs. SCE). The aim of this experiment is to monitor and control the growth and number of new facets on Cu. The top panels in Fig. 2A–C show the lead UPD curves on the NaCl-treated Cu surfaces at the three different oxidative potentials (1.0, 1.3 and 1.6 V vs. SCE), overlapped with the lead UPD of the original Cu(poly) (dashed line). Fig. 2 clearly shows that the higher the applied oxidation potential is, the higher the transformation induced by chloride anions is on the Cu(poly). In particular, we observe a progressive decrease of the (111) peak at ca. −0.305 V vs. SCE, whereas the (310) feature at ca. −0.340 V vs. SCE progressively increases upon increasing the oxidation potential. The bottom panels of Fig. 2A–C show the peak deconvolution of the Cu(poly) reconstructed in NaCl at the three different oxidation potentials (Eox). The fraction area of the (111) peak (red area) decreases from 59% in Cu(poly) (Fig. 1B) to 53% at Eox = 1.0 V, to 45% at Eox = 1.3 V and to 33% at Eox = 1.6 V. In contrast, the fraction area of the (310) peak (orange area) increases from 19% in Cu(poly) to 27% at Eox = 1.0 V, to 34% at Eox = 1.3 V, to 45% at Eox = 1.6 V. This result suggests that chloride mainly reduces the large (111) terrace-domains in the Cu(poly) and promotes the formation of (310) or n(100) × (110) domains. We note that there are little variations in the wideness and potential of the peaks (Table S3†), a fact that we relate to a modification in the terrace length induced by the aggressive treatment in 0.1 M NaCl.32 To better estimate the (310)/(111) domain ratio in each surface modification one could multiply the fraction area (310)/fraction area (111) ratio by a factor of 1.1. The value of 1.1 is obtained by dividing the cathodic charge value of the (111) facet (350 μC cm−2, Table S2†) by the cathodic charge value of the (310) facet (316 μC cm−2, Table S2†). In other words, the factor of 1.1 takes into account that the (310) facet is a more open structure than the (111) structure. Thus, we observe a change in the (310)/(111) ratio of approximately 0.6 in Fig. 3A, 0.8 in Fig. 2B, and 1.5 in Fig. 2C.
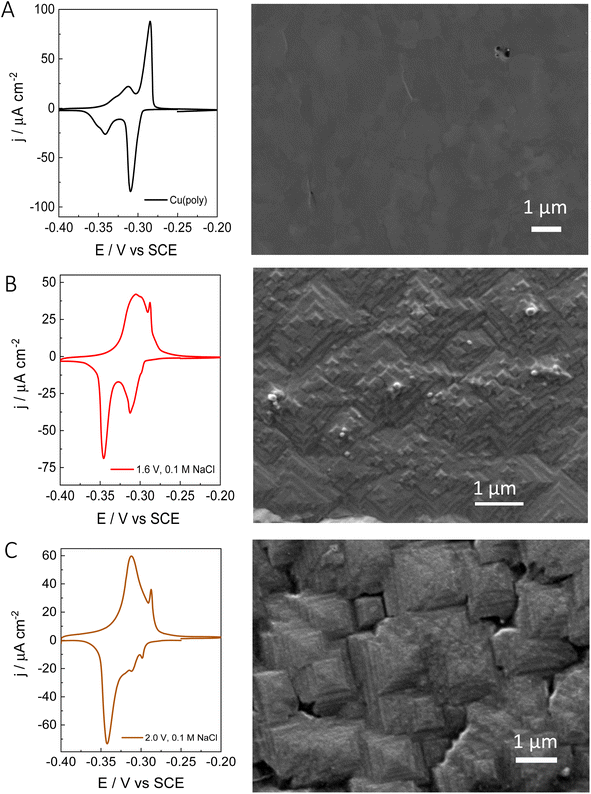
After evaluating the effect of chloride in the formation of new (310) facets by combining voltammetric lead UPD, we have performed ex situ surface characterization of our re-constructed copper samples. Fig. 3 shows the lead UPD CVs as well as the corresponding SEM image of the Cu(poly) pretreated under different conditions. Fig. 3A shows the results on the electropolished Cu(poly). The SEM image does not show any features and appears relatively flat compared to the other samples (e.g.Fig. 2B and C). Fig. S4† shows the SEM image of the same Cu(poly) at a higher magnification (a scale bar of 300 nm), and although no SEM surface roughness measurements were obtained it does appear that that the Cu(poly) has a flat surface. Fig. 3B shows the results on the Cu(poly) that has been reconstructed in 0.1 M NaCl by applying an oxidation potential of 1.6 V. Although at this potential the lead UPD CV shows a prominent (310) peak, the voltammetric features in the (111) voltammetric region have not been completely suppressed. The SEM image in Fig. 3B and S4† shows the presence of motifs, some of them with square shape, which suggest the presence of (100) sites.14Fig. 3C shows the surface reconstruction treatment at 2.0 V in NaCl, in which the features in the voltammetric (111) region has been almost suppressed. Interestingly, the SEM shows that the surface morphology has evolved from the motifs in Fig. 3B, to highly stepped features, larger than 1 μm, and with the shape of truncated tetragonal pyramids. This morphology is observed in large areas of the electrode, as displayed in Fig. S4C,† and remains unchanged after carrying out the lead UPD. In other words, the lead UPD does not modify the chloride-induced surface morphology on copper at the nanoscale. The SEM analysis shows that our proposed treatment with chloride forms a well-defined morphology with shaped features. This result is in line with the voltammetric lead UPD analysis which suggests the formation of Cu surfaces with high exposure of (310) or n(100) × (110) domains. The large size of the features, sometimes larger than 1 μm, could explain the low increase in roughness that we have measured with lead UPD.
The XPS spectrum of a Cu surface treated in 0.1 M NaCl solution at 2.0 V vs. SCE was taken to assess the surface chemical composition. Details on the XPS measurements are in the experimental section and in the ESI of this work in Fig. S5 and S6.† Fig. S5† displays the XPS survey of the sample. No chloride was detected before applying the sputtering treatment and only oxygen and copper were detectable on the surface. The presence of copper oxide was ascribed to exposure of the sample to air and cleaning with Milli-Q water. However, the atomic percentage of oxygen rapidly decreases after a few sputtering cycles, while the atomic percentage of copper increases, which suggests a core of metallic copper (see details in Fig. S7 and S8†).
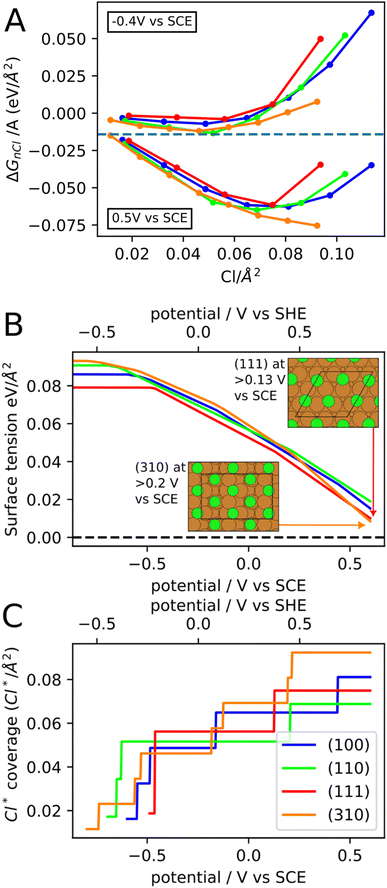
To further understand the effect of chloride anions on the copper re-faceting, we have studied chloride ion adsorption on the (111), (100), (110) and (310) copper facets with DFT assuming 0.1 M concentration of Cl− in the electrolyte. Fig. 4A shows ΔGnCl/A (eqn (1)) for the four facets as a function of Cl* coverage and at two different potentials. At a given potential, the minimum of the ΔGnCl/A curve both specifies the preferred Cl* coverage and the stabilization of the surface tension from Cl* adsorption. The chloride ion adsorption energies contain an explicit dependence on the potential (Uvs. SHE in eqn (2)), which means that both the Cl* coverage and the surface tension stabilization increase with potential. For instance, at −0.4 V vs. SCE the (310) facet contain 0.05 Cl* species per Å2, which stabilizes the surface tension by −0.012 eV Å−2 whereas at 0.5 V the (310) facet contains 0.09 Cl* species per Å2, which stabilizes the surface tension by −0.073 eV Å−2. It has been experimentally observed that the chloride adsorption reactivity increases for less close-packed facets in the following order; Cu(111) < Cu(100) < Cu(110).61 We find the same reactivity relationship in Fig. 4A, where the (110) line is mostly below the (100) and (111) lines. Furthermore, we find that the Cu(310) facet is the most reactive towards chloride adsorption at most Cl* coverages, which fits with Cu(310) being the least close-packed of the four facets.
The facet- and potential-dependent copper surface tensions (including stabilization from chloride anion adsorption, i.e. γ in eqn (1)) are shown in Fig. 4B. At low potentials (below −0.6 V vs. SCE), where the facets contain none or very little Cl* coverage, the surface tensions have the following order (111) < (100) < (110) < (310). The same order has been found in previous studies,62,63 however, the exact bare copper surface energies seem to depend on DFT functional. At high potentials, the (310) facet is significantly more stabilized than the other facets resulting in (310) becoming the most stable facet above 0.5 V vs. SCE.
The Cl* coverages that correspond to the most stable ΔGnCl/A at different potentials are shown in Fig. 4C. Importantly, at high potential, the (310) facet contain the highest Cl* coverage of the investigated facets and will therefore experience the most surface tension stabilization from chloride anion adsorption. The high concentration of Cl* on (310) facets is due to (310) having shelfs of (100) surface at an angle to the surface plane. The simulated Cl* coverages can unfortunately only be changed in stepwise fashion (rather than continuously), since the computational surface cells have to contain an integer number of Cl atoms. This is likely the reason for the pronounced stepwise nature of the Cl* coverage increase, which should therefore be considered an artefact of the simulations.
We are aware that copper dissolution is significant above ∼0 V vs. SCE;64 however, as long as metallic copper remains, it seems reasonable that the facet distribution of the copper metal will be influenced by the stability of the Cl* covered facets. We have therefore used the surface tensions in Fig. 4C, to make Wulff constructions, which we believe are representative for polycrystalline copper surfaces with bead geometry in 0.1 M NaCl electrolyte at different applied potentials. The Wulff constructions for −0.8, −0.33, 0.13, and 0.6 V vs. SCE are shown in Fig. 5. At −0.8 V vs. SCE none of the facets contain any adsorbed Cl* species and crystals are dominated by (111) and to a lesser extend (100) facets. This facet distribution only changes a little with potential, until 0.6 V vs. SCE, where the (310) facet is most stable and now dominates the facet distribution. At high applied potentials, the generated Wulff construction develop tetrahexahedron nanostructures, where four (310) surfaces meet to form a square pyramid on each side of the crystal. Interestingly, these tetrahexaedron shapes resemble the morphology displayed in the SEM image of Fig. 3C and S4C,† which show that the NaCl-treated Cu surface contain multiple stepped and truncated square pyramids.
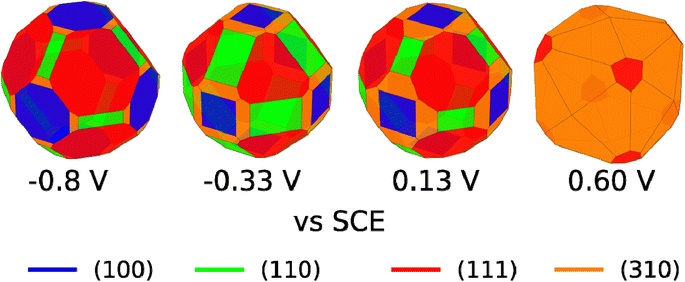 | ||
| Fig. 5 Wulff constructions for copper particles in 0.1 M NaCl electrolyte at −0.8, −0.33, 0.13, and 0.6 V vs. SCE. | ||
We remark that, experimentally, we apply potentials more positive than 0.60 V vs. SCE to change the facet distribution on Cu due to several reasons: (i) simulations are made on a Cu(poly) bead in which the equilibrium condition at a certain potential is reached. (ii) In our experiments, we apply oxidation/reduction potential cycles at a very fast scan rate of 500 mV s−1 and therefore this equilibrium condition is not necessarily reached. Facet distribution is dependent on experimental parameters such as scan rate or number of cycles. The experimental conditions of this work, i.e., scan rate of 500 mV s−1 and two potential cycles, were selected aiming to carry out controlled tuning of the facet distribution (Fig. 2).
Previous works have confirmed that chloride induces the formation of cubic nano features with exposed (100) facets on the surface.44–46,65–67 In our work we go a step forward and suggest that chloride specifically induces the formation of n(100) × (110) or (310) sites. We suggest that the formation of n(100) × (110) sites induced by chloride during the electrochemical treatment may play a key role in the conversion of the CO2 to alcohols and not only to ethylene.13 We stress that future works should aim to address the changes in product selectivity with the degree of surface reconstruction induced by chloride on copper. Moreover, experiments performed with operando scanning probe microscopy20 and operando grazing incidence X-ray diffraction (GIXRD)68 will shed lights on the changes in structure and defects induced by chloride and the stability of these surfaces during the electrocatalysis. We also highlight that future research should be performed to evaluate the effect of other anions and halides on the facet distribution of copper. As copper oxidizes easily, the chemical synthesis of well-defined nanocatalysts is usually performed in organic or anhydrous solvents.69,70 The strategies presented in this work open the possibility of selectively tailoring copper surfaces with well-defined distribution of facets by using electrochemical methods and halide-rich aqueous solutions.
Although we show that lead UPD is a valuable technique to determine preferential orientations on copper, the method still requires further improvements, specially to capture and characterize the presence of small domains and defects. Due to the impact of defect sites in electrocatalysis,44 we encourage to perform experiments on a wide range of stepped surfaces. Experiments on stepped surfaces will give information on how the lead adsorption/desorption changes when the terrace length decreases and the density of steps increases. This study will be crucial to elucidate the amount of defects as well as their geometry in nanostructured surfaces. We also believe that these additional experiments will provide better simulations or e.g. an electrochemical isotherm71 that describes the lead adsorption desorption on different copper surfaces with variable complexity.
Conclusions
In this work, we have shown that voltammetric lead UPD is a valuable tool to characterize and determine the distribution of single facet-domains in multifaceted copper surfaces. We show that lead UPD provides sharp, intense, and distinguishable voltammetric features on copper single crystalline electrodes. The characteristic lead UPD profile of the single facets can be used to decouple the formation of new facets in copper surfaces that have been electrochemically re-constructed in NaCl solution. We experimentally show the capping effect of the chloride anion, which induces the formation of shape stepped square pyramids with exposed (310) facets on copper. These results are supported by DFT calculations on modelling the chloride adsorption and Wulff constructions. Finally, we show that we can easily tune the (310)/(111) ratio using chloride anions, by simply adjusting experimental parameters during the electrochemical deposition, such as applied oxidation potential, number of cycles and scan rate, as shown in the recorded lead UPD CVs. Our work also opens new opportunities to selectively tailor the facet distribution on copper via electroplating techniques in halide-rich aqueous solutions. We believe that the methods reported in this work, which are accessible to most electrochemistry laboratories, will be key to electrochemically synthesize well-defined catalysts, and addressing the intrinsic electrocatalytic properties of a broad range of copper-based materials.Data availability
The DFT calculations, atomic structures, and python scripts for the Wulff constructions can be accessed online at: https://nano.ku.dk/english/research/theoretical-electrocatalysis/katladb/copper-with-chloride.Author contributions
P. M. C.: investigation, formal analysis, data curation, writing –review and editing, visualization. T. K. M.: investigation, formal analysis, data curation, writing – original draft, visualization. E. P. M.: investigation, formal analysis, data curation, writing – original draft, visualization. H. H. K.: supervision, methodology, conceptualization, writing – review and editing, visualization, project administration. I. C.: methodology, formal analysis, writing – review & editing. K. N. D.: investigation, formal analysis, data curation, writing – review and editing. W. v. d. S.: supervision, conceptualization, writing – review and editing. J. R. supervision, conceptualization, writing – review and editing, funding acquisition. M. E. E. supervision, conceptualization, writing – review and editing, project administration, funding acquisition. P. S. P. supervision, methodology, conceptualization, writing – original draft, visualization, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Villum Foundation for financially supporting this project through a Villum Young Investigator Grant (project number: 19142). This work was also supported by the Danish foundation through the DFF-Research Project1 (Thematic Research, green transition) grant with number: 0217-00213A. We acknowledge support from the Danish National Research Foundation Center for High Entropy Alloy Catalysis (CHEAC, DNRF-149). P. S. P. also acknowledges the Villum Foundation for its financial support (Villum Young Investigator grant, project number: 53090).References
- P. De Luna, C. Hahn, D. Higgins, S. A. Jaffer, T. F. Jaramillo and E. H. Sargent, Science, 2019, 364, eaav3506 CrossRef CAS
.
- C. Vogt and B. M. Weckhuysen, Nat. Rev. Chem, 2022, 6, 89–111 CrossRef PubMed
.
- A. S. Bandarenka and M. T. M. Koper, J. Catal., 2013, 308, 11–24 CrossRef CAS
.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS
.
- I. E. L. Stephens, K. Chan, A. Bagger, S. W. Boettcher, J. Bonin, E. Boutin, A. Buckley, R. Buonsanti, E. Cave, X. Chang, S. W. Chee, A. H. M. da Silva, P. De Luna, O. Einsle, B. Endrődi, M. E. Escribano, J. V de Araujo, M. C. Figueiredo, C. Hahn, K. U. Hansen, S. Haussener, S. Hunegnaw, Z. Huo, Y. J. Hwang, C. Janáky, B. S. Jayathilake, F. Jiao, Z. P. Jovanov, P. Karimi, M. T. M. Koper, K. Kuhl, W. H. Lee, Z. Liang, X. Liu, S. Ma, M. Ma, H.-S. Oh, M. Robert, B. R. Cuenya, J. Rossmeisl, C. Roy, M. P. Ryan, E. H. Sargent, P. Sebastián-Pascual, B. Seger, L. Steier, P. Strasser, A. S. Varela, R. E. Vos, X. Wang, B. Xu, H. Yadegari and Y. Zhou, J. Phys. Energy, 2022, 4, 042003 CrossRef
.
-
Y. Hori, in Modern Aspects of Electrochemistry no. 42, Springer, 2017, vol. 91, pp. 399–404 Search PubMed
.
- O. Christensen, S. Zhao, Z. Sun, A. Bagger, J. V. Lauritsen, S. U. Pedersen, K. Daasbjerg and J. Rossmeisl, ACS Catal., 2022, 12, 15737–15749 CrossRef CAS
.
- Y. Zhou, A. J. Martín, F. Dattila, S. Xi, N. López, J. Pérez-Ramírez and B. S. Yeo, Nat. Catal., 2022, 5, 545–554 CrossRef CAS
.
- S. J. Raaijman, M. P. Schellekens, P. J. Corbett and M. T. M. Koper, Angew. Chem., Int. Ed., 2021, 60, 21732–21736 CrossRef CAS
.
- J. Gao, A. Bahmanpour, O. Kröcher, S. M. Zakeeruddin, D. Ren and M. Grätzel, Nat. Chem., 2023, 15, 705–713 CrossRef CAS
.
- Y. Hori, R. Takahashi, Y. Yoshinami and A. Murata, J. Phys. Chem. B, 1997, 101, 7075–7081 CrossRef CAS
.
- Y. Hori, I. Takahashi, O. Koga and N. Hoshi, J. Mol. Catal. A: Chem., 2003, 199, 39–47 CrossRef CAS
.
- A. Bagger, W. Ju, A. S. Varela, P. Strasser and J. Rossmeisl, ACS Catal., 2019, 9, 7894–7899 CrossRef CAS
.
- R. M. Arán-Ais, F. Scholten, S. Kunze, R. Rizo and B. Roldan Cuenya, Nat. Energy, 2020, 5, 317–325 CrossRef
.
- Y. Zhu, J. Wang, H. Chu, Y.-C. Chu and H. M. Chen, ACS Energy Lett., 2020, 5, 1281–1291 CrossRef CAS
.
- A. Bergmann and B. Roldan Cuenya, ACS Catal., 2019, 9, 10020–10043 CrossRef CAS
.
- Y. Yang, S. Louisia, S. Yu, J. Jin, I. Roh, C. Chen, M. V. F. Guzman, J. Feijóo, P.-C. Chen, H. Wang, C. J. Pollock, X. Huang, Y.-T. Shao, C. Wang, D. A. Muller, H. D. Abruña and P. Yang, Nature, 2023, 614, 262–269 CrossRef CAS PubMed
.
- K. Jiang, Y. Huang, G. Zeng, F. M. Toma, W. A. Goddard and A. T. Bell, ACS Energy Lett., 2020, 5, 1206–1214 CrossRef CAS
.
- L. Zaza, K. Rossi and R. Buonsanti, ACS Energy Lett., 2022, 7, 1284–1291 CrossRef CAS
.
- F. Scholten, K.-L. C. Nguyen, J. P. Bruce, M. Heyde and B. Roldán Cuenya, Angew. Chem., Int. Ed., 2021, 133, 19318–19324 CrossRef
.
- C. Choi, S. Kwon, T. Cheng, M. Xu, P. Tieu, C. Lee, J. Cai, H. M. Lee, X. Pan, X. Duan, W. A. Goddard and Y. Huang, Nat. Catal., 2020, 3, 804–812 CrossRef CAS
.
- J. A. Gauthier, J. H. Stenlid, F. Abild-Pedersen, M. Head-Gordon and A. T. Bell, ACS Energy Lett., 2021, 6, 3252–3260 CrossRef CAS
.
- S. Zhao, O. Christensen, Z. Sun, H. Liang, A. Bagger, K. Torbensen, P. Nazari, J. V. Lauritsen, S. U. Pedersen, J. Rossmeisl and K. Daasbjerg, Nat. Commun., 2023, 14, 844 CrossRef CAS
.
- J. Li, X. Li, C. M. Gunathunge and M. M. Waegele, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9220–9229 CrossRef CAS
.
- M. C. O. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. T. M. Koper, Nat. Catal., 2021, 4, 654–662 CrossRef CAS
.
- S. Garg, Q. Xu, A. B. Moss, M. Mirolo, W. Deng, I. Chorkendorff, J. Drnec and B. Seger, Energy Environ. Sci., 2023, 16, 1631–1643 RSC
.
- S. Anantharaj, P. E. Karthik and S. Noda, Angew. Chem., Int. Ed., 2021, 60, 23051–23067 CrossRef CAS PubMed
.
- A. R. Akbashev, ACS Catal., 2022, 12, 4296–4301 CrossRef CAS
.
- N. C. Röttcher, Y.-P. Ku, M. Minichova, K. Ehelebe and S. Cherevko, J. Phys.: Energy, 2023, 5, 24007 Search PubMed
.
- E. Plaza-Mayoral, I. J. Pereira, K. N. Dalby, K. D. Jensen, I. Chorkendorff, H. Falsig, P. Sebastián-Pascual and M. Escudero-Escribano, ACS Appl. Energy Mater., 2022, 5, 10632–10644 CrossRef CAS
.
- E. Plaza-Mayoral, P. Sebastián-Pascual, K. N. Dalby, K. D. Jensen, I. Chorkendorff, H. Falsig and M. Escudero-Escribano, Electrochim. Acta, 2021, 398, 139309 CrossRef CAS
.
- E. Garnier, F. J. Vidal-Iglesias, J. M. Feliu and J. Solla-Gullón, Front. Chem., 2019, 7, 527 CrossRef CAS PubMed
.
- J. Solla-Gullón and J. M. Feliu, Curr. Opin. Electrochem., 2020, 22, 65–71 CrossRef
.
- H. Mistry, A. S. Varela, S. Kühl, P. Strasser and B. R. Cuenya, Nat. Rev. Mater., 2016, 1, 16009 CrossRef CAS
.
- C. Hahn, T. Hatsukade, Y.-G. Kim, A. Vailionis, J. H. Baricuatro, D. C. Higgins, S. A. Nitopi, M. P. Soriaga and T. F. Jaramillo, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5918–5923 CrossRef CAS PubMed
.
- V. Climent and J. M. Feliu, J. Solid State Electrochem., 2011, 15, 1297–1315 CrossRef CAS
.
- A. Tiwari, T. Maagaard, I. Chorkendorff and S. Horch, ACS Energy Lett., 2019, 4, 1645–1649 CrossRef CAS
.
- A. Tiwari, H. H. Heenen, A. S. Bjørnlund, T. Maagaard, E. Cho, I. Chorkendorff, H. H. Kristoffersen, K. Chan and S. Horch, J. Phys. Chem. Lett., 2020, 1450–1455 CrossRef CAS PubMed
.
- P. Sebastián-Pascual and M. Escudero-Escribano, ACS Energy Lett., 2020, 5, 130–135 CrossRef
.
- P. Sebastián-Pascual and M. Escudero-Escribano, J. Electroanal. Chem., 2021, 896, 115446 CrossRef
.
- G. M. Brisard, E. Zenati, H. A. Gasteiger, N. M. Markovic and P. N. Ross, Langmuir, 1995, 11, 2221–2230 CrossRef CAS
.
- G. M. Brisard, E. Zenati, H. A. Gasteiger, N. M. Marković and P. N. Ross, Langmuir, 1997, 13, 2390–2397 CrossRef CAS
.
- D. Hochfilzer, A. Tiwari, E. L. Clark, A. S. Bjørnlund, T. Maagaard, S. Horch, B. Seger, I. Chorkendorff and J. Kibsgaard, Langmuir, 2022, 38, 1514–1521 CrossRef CAS PubMed
.
- D. Gao, I. Sinev, F. Scholten, R. M. Arán-Ais, N. J. Divins, K. Kvashnina, J. Timoshenko and B. Roldan Cuenya, Angew. Chem., Int. Ed., 2019, 58, 2–9 CrossRef
.
- A. S. Varela, W. Ju, T. Reier and P. Strasser, ACS Catal., 2016, 6, 2136–2144 CrossRef CAS
.
- T. Kim and G. T. R. Palmore, Nat. Commun., 2020, 11, 3622 CrossRef CAS
.
- Y. H. Ichiro Takahashi, O. Koga and N. Hoshi, J. Electroanal. Chem., 2002, 533, 135–143 CrossRef
.
- Q.-S. Chen, F. J. Vidal-Iglesias, J. Solla-Gullón, S.-G. Sun and J. M. Feliu, Chem. Sci., 2012, 3, 136–147 RSC
.
- Z. Zhao, J. Zhang, M. Lei and Y. Lum, Nano res. energy, 2023, 2, e9120044 CrossRef
.
- J. Wellendorff, A. Lundgaard, K. T. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B, 2012, 85, 235149 CrossRef
.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens.Matter, 2010, 22, 253202 CrossRef CAS PubMed
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
.
- S. G. Bratsch, J. Phys. Chem. Ref. Data, 1989, 18, 1–21 CrossRef CAS
.
- https://janaf.nist.gov/ .
- https://wulffpack.materialsmodeling.org/ .
- S. J. Raaijman, N. Arulmozhi, A. H. M. da Silva and M. T. M. Koper, J. Electrochem. Soc., 2021, 168, 96510 CrossRef CAS
.
- G. H. Simon, C. S. Kley and B. Roldan Cuenya, Angew. Chem., Int. Ed., 2021, 60, 2561–2568 CrossRef CAS
.
- I. Chorkendorff, S. Horch, A. K. Engstfeld, I. E. L. Stephens and T. Maagaard, Chem.–A Euro. J., 2018, 24, 17743 CrossRef
.
- T. P. Moffat, J. Phys. Chem. B, 1998, 102, 10020–10026 CrossRef CAS
.
- A. Taranovskyy, S. Guézo, H. Matsushima, Y. Gründer and O. M. Magnussen, Phys. Chem. Chem. Phys., 2012, 14, 10579–10588 RSC
.
-
K. Wandelt, in Encyclopedia of Interfacial Chemistry, ed. K. Wandelt, Elsevier, Oxford, 2018, pp. 166–181 Search PubMed
.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS
.
- J. Wang and S.-Q. Wang, Surf. Sci., 2014, 630, 216–224 CrossRef CAS
.
- M. Kabasakaloğlu, T. Kıyak, O. Şendil and A. Asan, Appl. Surf. Sci., 2002, 193, 167–174 CrossRef
.
- F. S. Roberts, K. P. Kuhl and A. Nilsson, Angew. Chem., Int. Ed., 2015, 127, 5268–5271 CrossRef
.
- Y. Kwon, Y. Lum, E. L. Clark, J. W. Ager and A. T. Bell, ChemElectroChem, 2016, 3, 1012–1019 CrossRef CAS
.
- D. Gao, F. Scholten and B. Roldan Cuenya, ACS Catal., 2017, 7, 5112–5120 CrossRef CAS
.
- Y. Jia, K. Jiang, H. Wang and X. Yao, Chem, 2019, 5, 1371–1397 CAS
.
- J. R. Pankhurst, L. Castilla-Amorós, D. C. Stoian, J. Vavra, V. Mantella, P. P. Albertini and R. Buonsanti, J. Am. Chem. Soc., 2022, 144, 12261–12271 CrossRef CAS PubMed
.
- A. Loiudice, P. Lobaccaro, E. A. Kamali, T. Thao, B. H. Huang, J. W. Ager and R. Buonsanti, Angew. Chem., Int. Ed., 2016, 55, 5789–5792 CrossRef CAS PubMed
.
- R. Gómez, J. M. Orts, B. Álvarez-Ruiz and J. M. Feliu, J. Phys. Chem. B, 2004, 108, 228–238 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Complementary CVs of lead UPD on a Cu(311) surface. FE-SEM and SEM analysis of a Cu(poly) and NaCl-treated Cu samples; the survey of the XPS analysis on the prepared NaCl-treated Cu electrode at 2.0 V vs. SCE, and the position of the C 1s and O 1s and Cu 2p peaks; the atomic profile percentage of O and Cu at different etching times; the calculated charges and roughness factors from the lead UPD CVs on Cu single facets and Cu(poly), and on NaCl-treated Cu electrodes; the peak deconvolution analysis of the lead UPD CVs with the values of the deconvoluted peak potential, peak fraction area and half width. See DOI: https://doi.org/10.1039/d3sc05988j |
| This journal is © The Royal Society of Chemistry 2024 |