Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal–carbon bonding in early lanthanide substituted cyclopentadienyl complexes probed by pulsed EPR spectroscopy†
Lydia E.
Nodaraki‡
ab,
Jingjing
Liu‡
a,
Ana-Maria
Ariciu
ab,
Fabrizio
Ortu
 a,
Meagan S.
Oakley
a,
Meagan S.
Oakley
 a,
Letitia
Birnoschi
a,
Gemma K.
Gransbury
a,
Letitia
Birnoschi
a,
Gemma K.
Gransbury
 a,
Philip J.
Cobb
a,
Jack
Emerson-King
a,
Philip J.
Cobb
a,
Jack
Emerson-King
 a,
Nicholas F.
Chilton
a,
Nicholas F.
Chilton
 *a,
David P.
Mills
*a,
David P.
Mills
 *a,
Eric J. L.
McInnes
*ab and
Floriana
Tuna
*a,
Eric J. L.
McInnes
*ab and
Floriana
Tuna
 *ab
*ab
aDepartment of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: floriana.tuna@manchester.ac.uk; nicholas.chilton@manchester.ac.uk; david.mills@manchester.ac.uk; eric.mcinnes@manchester.ac.uk
bPhoton Science Institute, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
First published on 16th January 2024
Abstract
We examine lanthanide (Ln)–ligand bonding in a family of early Ln3+ complexes [Ln(Cptt)3] (1-Ln, Ln = La, Ce, Nd, Sm; Cptt = C5H3tBu2-1,3) by pulsed electron paramagnetic resonance (EPR) methods, and provide the first characterization of 1-La and 1-Nd by single crystal XRD, multinuclear NMR, IR and UV/Vis/NIR spectroscopy. We measure electron spin T1 and Tm relaxation times of 12 and 0.2 μs (1-Nd), 89 and 1 μs (1-Ce) and 150 and 1.7 μs (1-Sm), respectively, at 5 K: the T1 relaxation of 1-Nd is more than 102 times faster than its valence isoelectronic uranium analogue. 13C and 1H hyperfine sublevel correlation (HYSCORE) spectroscopy reveals that the extent of covalency is negligible in these Ln compounds, with much smaller hyperfine interactions than observed for equivalent actinide (Th and U) complexes. This is corroborated by ab initio calculations, confirming the predominant electrostatic nature of the metal–ligand bonding in these complexes.
Introduction
Lanthanides (Ln) have numerous applications due to their unique physicochemical properties.1 The text-book description of the electronic structure of Ln ions in the dominant 3+ oxidation state is that due to poor shielding the valence 4f orbitals are “core-like,” and as a result chemical bonding involving Ln ions is predominantly ionic. In contrast to Ln, the early actinides (An) exhibit variable oxidation states and participation in metal–ligand multiple bonding, which indicates greater involvement of the 5f (and 6d) valence orbitals in bonding regimes.2 This is important because the differences in chemical bonding has direct impacts on the chemical behavior of Ln and An ions,3 and such differences are exploited in, for example, separations chemistry.4,5 Moreover, subtle variations in f-element-ligand bonding is important in determining electronic properties and hence applications in, for example, luminescence,6 paramagnetic NMR,7 and molecular magnetism.8 Use of relatively soft donor ligands, such as substituted cyclopentadienyls (CpR), can introduce interesting bonding regimes, and their Ln/An complexes have been studied for many years.9–11 Such materials have found interest not just in chemical synthesis, but also due to their electronic structure leading to, for example, the stabilization of unprecedented metal oxidation states12 and properties of single-molecule magnets.13 The archetypal examples are the [Ln/An(Cp)3] type complexes, and indeed these have long been used as a computational test-bed to investigate trends in the nature of f-element bonding.14–18Since the majority of Ln3+ and An3+ ions are paramagnetic, electron paramagnetic resonance (EPR) spectroscopy should carry important information on metal–ligand bonding, particularly if resolution of ligand nuclear hyperfine interactions can be resolved. However, this is rarely the case in continuous wave (CW) EPR because of the intrinsically broad linewidths. This can in principle be addressed by pulsed EPR hyperfine methods.19 However, there are surprisingly few pulsed EPR studies on molecular Ln complexes,20 with the notable exception of those of the 8S7/2 Gd3+ ion, and even fewer for An complexes.21–23 Most Ln3+ pulsed EPR studies have been performed on doped minerals or glasses, and have tended to focus on relaxation behaviour.24 In 2011 Denning and co-workers reported pulsed EPR measurements on [Yb(Cp)3], enabling quantification of the significant spin density at the 13C atoms of the Cp rings,25 which was discussed in terms of mixing of the 2F7/2 ground term with low-lying charge-transfer states. More recently, some of us reported pulsed EPR studies of two An complexes, [An(Cptt)3] (1-An; An = Th, U; Cptt = C5H3tBu2-1,3), again showing significant spin density on the Cptt ligands for both the U3+ and Th3+ analogues.21
Here we report studies, including pulsed EPR, on a family of early Ln3+ complexes [Ln(Cptt)3] (1-Ln, Ln = La, Ce, Nd, Sm). This allows: (i) investigation of trends in metal–arene interactions across the series, from the “parent” diamagnetic, f0 complex through the paramagnetic f1,3,5 analogues. The latter are chosen because they are all Kramers ions and hence are expected to be EPR-active; (ii) comparison of ligand spin density with the late Ln3+ complex [Yb(Cp)3] studied by Denning et al.;25 (iii) comparision of 1-Ln with the early An3+ homologues 1-An.21 The latter includes direct comparison of the valence isoelectronic Nd3+ (4f3) and U3+ (5f3) pair, which is the only comparison available between 4f and 5f M3+ ions that does not require designated radiochemical laboratories (although Ce3+ and Th3+ have the same number of valence electrons, the Th3+ ion often favours a 6d1 rather than 5f1 configuration).26
Complexes 1-Ln are readily prepared by reacting LnCl3 with three equivalents of KCptt; 1-Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 and 1-Sm
27 and 1-Sm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 have been prepared previously by alternative synthetic routes, whilst 1-La and 1-Nd are structurally characterised here for the first time. We report the CW and pulsed EPR data for 1-Ce, 1-Nd and 1-Sm, along with the NMR data of diamagnetic 1-La. We quantify the hyperfine interaction in paramagnetic 1-Ln with ligand nuclei, originating from interaction with the Ln3+ centres, and show that we can model these data using a simple point-dipole model. This is in agreement with fully-ab initio complete active space self-consistent field spin–orbit (CASSCF-SO) calculations that directly report hyperfine coupling parameters,29 as well as spin densities. We find, using either the simple or ab initio methods, that there is negligible spin density on the Cptt ligands in 1-Ln, in contrast to unequivocal spin delocalisation in U3+ and Th3+ analogues [An(Cptt)3],21 clearly highlighting the differences between early 4f and early 5f bonding in tris-Cp complexes.14–18 Since the ability to perform such studies are limited by electron spin relaxation times, we also report relaxation data for 1-Ln by pulsed EPR methods. We find that 4f 1-Ln relax orders of magnitude faster than their 5f An analogues,21 despite preconceptions that relaxation rates increase for heavier elements due to increased spin–orbit coupling.
28 have been prepared previously by alternative synthetic routes, whilst 1-La and 1-Nd are structurally characterised here for the first time. We report the CW and pulsed EPR data for 1-Ce, 1-Nd and 1-Sm, along with the NMR data of diamagnetic 1-La. We quantify the hyperfine interaction in paramagnetic 1-Ln with ligand nuclei, originating from interaction with the Ln3+ centres, and show that we can model these data using a simple point-dipole model. This is in agreement with fully-ab initio complete active space self-consistent field spin–orbit (CASSCF-SO) calculations that directly report hyperfine coupling parameters,29 as well as spin densities. We find, using either the simple or ab initio methods, that there is negligible spin density on the Cptt ligands in 1-Ln, in contrast to unequivocal spin delocalisation in U3+ and Th3+ analogues [An(Cptt)3],21 clearly highlighting the differences between early 4f and early 5f bonding in tris-Cp complexes.14–18 Since the ability to perform such studies are limited by electron spin relaxation times, we also report relaxation data for 1-Ln by pulsed EPR methods. We find that 4f 1-Ln relax orders of magnitude faster than their 5f An analogues,21 despite preconceptions that relaxation rates increase for heavier elements due to increased spin–orbit coupling.
Results and discussion
Synthesis
Complexes 1-Ln (Ln = La, Ce, Nd, Sm) were prepared from the parent LnCl3 and three equivalents of KCptt (Scheme 1) by modification of the reported syntheses of 1-Sm using SmI3 and KCptt,28 and 1-Ce from Ce(OTf)3 and LiCptt.27 The crystalline yields for 1-La, 1-Ce, 1-Nd and 1-Sm were 41%, 54%, 34% and 52%, respectively. We attempted to extend the 1-Ln series to smaller Ln, but in our hands we found that applying the same synthetic methodology to GdCl3 gave no isolable products, likely due to the higher Lewis acidity of the smaller Ln3+ ions.1 NMR spectroscopy was used to analyse C6D6 solutions of 1-Ln (ESI, Fig. S1–S5†). 1H NMR spectra were fully assigned for all 1-Ln; in each case three signals were observed in a ratio of 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 that correspond to the tBu groups and the two unique environments of the Cptt ring protons, respectively. The paramagnetism of 1-Ce, 1-Nd and 1-Sm precluded assignment of their 13C{1H} NMR spectra, however, for diamagnetic 1-La this could be interpreted, with the two tBu group resonances seen at 32.77 and 33.75 ppm and the three Cptt ring carbon environments found at 110.57 (CH-Cp), 110.69 (CH-Cp) and 143.45 (C-Cp) ppm. Although NMR spectroscopy showed few protic impurities, elemental analysis results for 1-Ln consistently gave low carbon values; this was previously seen for [An(Cptt)3],21 and is ascribed to carbide formation leading to partial combustion, a common issue with these experiments.30 In the case of 1-Sm elemental analysis results were not in accord with expected values. However, microcrystalline samples of 1-Ln gave essentially superimposable ATR-IR spectra (ESI, Fig. S6–S10†), and when these samples were suspended in a minimum amount of fomblin they gave poorly resolved powder XRD patterns (Fig. S13–S16†) that are similar to each other and show peaks in common with predicted patterns from single crystal XRD data (see below). Together, the characterisation data obtained show the bulk purities of samples of 1-Ln.
3 that correspond to the tBu groups and the two unique environments of the Cptt ring protons, respectively. The paramagnetism of 1-Ce, 1-Nd and 1-Sm precluded assignment of their 13C{1H} NMR spectra, however, for diamagnetic 1-La this could be interpreted, with the two tBu group resonances seen at 32.77 and 33.75 ppm and the three Cptt ring carbon environments found at 110.57 (CH-Cp), 110.69 (CH-Cp) and 143.45 (C-Cp) ppm. Although NMR spectroscopy showed few protic impurities, elemental analysis results for 1-Ln consistently gave low carbon values; this was previously seen for [An(Cptt)3],21 and is ascribed to carbide formation leading to partial combustion, a common issue with these experiments.30 In the case of 1-Sm elemental analysis results were not in accord with expected values. However, microcrystalline samples of 1-Ln gave essentially superimposable ATR-IR spectra (ESI, Fig. S6–S10†), and when these samples were suspended in a minimum amount of fomblin they gave poorly resolved powder XRD patterns (Fig. S13–S16†) that are similar to each other and show peaks in common with predicted patterns from single crystal XRD data (see below). Together, the characterisation data obtained show the bulk purities of samples of 1-Ln.
Crystallography
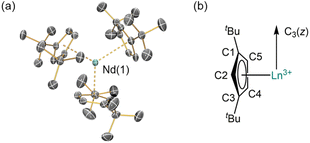
The solid-state structures of 1-Ln were determined by single crystal XRD (1-Nd is depicted in Fig. 1, see ESI, Fig. S11 and S12† for selected distances and angles of 1-La and 1-Nd). The structural data of 1-La and 1-Nd are reported here for the first time, whilst 1-Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 and 1-Sm
27 and 1-Sm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 have been reported previously; although 1-Ln are isostructural they are not all isomorphic. As expected, the structures of 1-Ln are trigonal planar with respect to the η5-Cptt centroids, with the three C2 atoms (Fig. 1) in the plane defined by the Ln3+ ion and the three Cptt centroids. The three Cptt ligands adopt the same orientation to form a “picket-fence” motif with three tBu groups above and three below the trigonal plane. Complexes 1-Ln do not show high symmetry in the solid state, consistent with the solid-state structures of [M(Cptt)3] (M = Th,21 U,21 Yb31). The mean Ln⋯Cpcentroid distances decrease regularly across the lanthanide series [mean La⋯Cpcentroid = 2.635 Å; Ce⋯Cpcentroid = 2.596 Å;27 Nd⋯Cpcentroid = 2.56 Å; Sm⋯Cpcentroid = 2.531 Å;28 Yb⋯Cpcentroid = 2.47 Å31]. Additionally, the mean M⋯Cpcentroid distances in 1-Nd are shorter than those seen in [U(Cptt)3] [2.570 Å],21 which has an analogous electronic configuration (Nd3+: [Xe]4f3; U3+: [Rn]5f3). Conversely, in 1-Ce, the mean M⋯Cpcentroid distances are longer than those seen in [Th(Cptt)3] [2.566 Å],21 which has a different valence electronic configuration (Ce3+: [Xe]4f1; Th3+: [Rn]6d1) due to the near-degeneracy of the 5f and 6d orbitals for Th2 and the stabilization of the 6dz2 orbital in trigonal ligand environments.26,32
28 have been reported previously; although 1-Ln are isostructural they are not all isomorphic. As expected, the structures of 1-Ln are trigonal planar with respect to the η5-Cptt centroids, with the three C2 atoms (Fig. 1) in the plane defined by the Ln3+ ion and the three Cptt centroids. The three Cptt ligands adopt the same orientation to form a “picket-fence” motif with three tBu groups above and three below the trigonal plane. Complexes 1-Ln do not show high symmetry in the solid state, consistent with the solid-state structures of [M(Cptt)3] (M = Th,21 U,21 Yb31). The mean Ln⋯Cpcentroid distances decrease regularly across the lanthanide series [mean La⋯Cpcentroid = 2.635 Å; Ce⋯Cpcentroid = 2.596 Å;27 Nd⋯Cpcentroid = 2.56 Å; Sm⋯Cpcentroid = 2.531 Å;28 Yb⋯Cpcentroid = 2.47 Å31]. Additionally, the mean M⋯Cpcentroid distances in 1-Nd are shorter than those seen in [U(Cptt)3] [2.570 Å],21 which has an analogous electronic configuration (Nd3+: [Xe]4f3; U3+: [Rn]5f3). Conversely, in 1-Ce, the mean M⋯Cpcentroid distances are longer than those seen in [Th(Cptt)3] [2.566 Å],21 which has a different valence electronic configuration (Ce3+: [Xe]4f1; Th3+: [Rn]6d1) due to the near-degeneracy of the 5f and 6d orbitals for Th2 and the stabilization of the 6dz2 orbital in trigonal ligand environments.26,32
Solution phase optical properties
The electronic spectra of 0.5 mM toluene solutions of 1-Ln (Fig. 2 and ESI, Fig. S17–S21†) are as expected;11-La with a closed shell La3+ ion is essentially colourless, with charge-transfer (CT) bands restricted to the UV region, whilst 1-Ce, 1-Nd and 1-Sm are pale purple, pale green, and pale orange, respectively. Due to their Laporte-forbidden nature, even spin-allowed f–f transitions are relatively weak (ε < 400 mol−1 dm3 cm−1),1 so CT bands tailing in from the UV region dominate the spectra. The f–f transitions in 1-Nd were clearly observed, with the most intense absorption at![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/char_e131.gif) max = 16
max = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1 (ε = 390 mol−1 dm3 cm−1) likely arising from the 4I9/2 → 4G5/2/4G7/2 transition.33 In contrast, 1-Ce shows a strong broad absorption at
750 cm−1 (ε = 390 mol−1 dm3 cm−1) likely arising from the 4I9/2 → 4G5/2/4G7/2 transition.33 In contrast, 1-Ce shows a strong broad absorption at ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/char_e131.gif) max = 17
max = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 (ε = 230 mol−1 dm3 cm−1) due to [Xe]4f1 → [Xe]4f05d1 transitions, which are formally allowed by electric dipole selection rules. The electronic spectrum of 1-Sm shows a weak set of f–f transitions in the near-IR region around 7000 cm−1 (ε < 50 mol−1 dm3 cm−1), likely arising from the 6H5/2 → 6FJ transitions.33
400 cm−1 (ε = 230 mol−1 dm3 cm−1) due to [Xe]4f1 → [Xe]4f05d1 transitions, which are formally allowed by electric dipole selection rules. The electronic spectrum of 1-Sm shows a weak set of f–f transitions in the near-IR region around 7000 cm−1 (ε < 50 mol−1 dm3 cm−1), likely arising from the 6H5/2 → 6FJ transitions.33
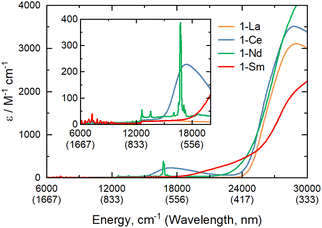 | ||
Fig. 2 UV/vis/NIR spectra of 1-La, 1-Ce, 1-Nd, 1-Sm, from 6000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (inset 6000–20 000 cm−1 (inset 6000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) recorded as 0.5 mM solutions in toluene at room temperature. 000 cm−1) recorded as 0.5 mM solutions in toluene at room temperature. | ||
Magnetism
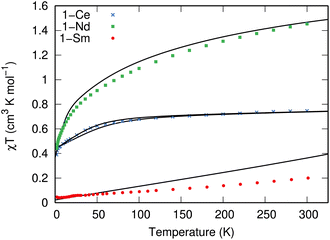
The measured χT values of 1.45 and 0.75 cm3 mol−1 K at 300 K for 1-Nd and 1-Ce, respectively (Fig. 3), are close to the expected values of 1.63 and 0.80 cm3 mol−1 K for Nd3+ (4I9/2) and Ce3+ (2F5/2).1 The χT product decreases gradually upon cooling until below 50 or 60 K, where it drops to reach 0.44 and 0.30 cm3 mol−1 K at 1.8 K, respectively. For 1-Sm, χT is 0.20 cm3 mol−1 K at 300 K, which is larger than expected for an isolated free-ion 6H5/2 term of 0.09 cm3 mol−1 K, owing to a combination of thermal population of the low-lying 6H7/2 term and temperature independent paramagnetism. The decrease of χT in all cases is due to the depopulation of the crystal field states. Isothermal magnetisation measurements of all compounds deviate from values expected for pure Ising-like mJ states (ESI, Fig. S22–S24†),34 indicating significant mixing of mJ states. To corroborate these results, we performed CASSCF-SO calculations using a minimal n-electrons in 7 orbital active space (where n = 1 for Ce3+, n = 3 for Nd3+ and n = 5 for Sm3+; see ESI† for details) and the solid-state XRD geometries (Tables S10–S13†). These give excellent reproductions of the magnetic data (Fig. 3 and S22–S24†) and confirm substantially mixed mJ states (Tables S10–S13†); the ground Kramers doublet for 1-Ce is dominated by |mJ| = 1/2, with the first excited state at 105–135 cm−1, while for 1-Nd the ground Kramers doublet is dominated by mJ = ±5/2 mixed with ∓7/2, with a first excited state at 26 cm−1. For 1-Sm the ground Kramers doublet is dominated by mJ = ±3/2, with a first excited state at 400 cm−1.EPR spectroscopy
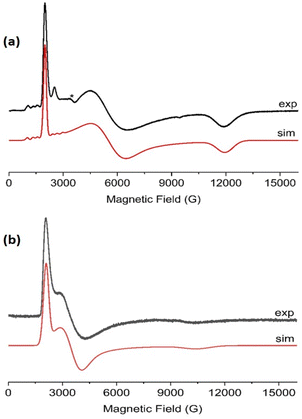
CW EPR spectra of 1-Nd, 1-Ce and 1-Sm are observed at temperatures below ∼30 K (Fig. 4 and ESI, Fig. S25–S27†). Much sharper spectra are observed from powders (such that it is difficult to remove polycrystalline effects) than from frozen solutions (toluene/hexane 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v), indicating some relaxation and strain of the structures in the latter medium. The spectra are dominated in each case by the rhombic or axial effective g-values arising from transitions within a thermally isolated ground Kramers doublet of the ground Russell-Saunders state, which can be treated as an effective spin-1/2. In this approximation, the frozen solution EPR spectrum for 1-Nd (Fig. 4a) can be modeled with the spin Hamiltonian eqn (1).
1 v/v), indicating some relaxation and strain of the structures in the latter medium. The spectra are dominated in each case by the rhombic or axial effective g-values arising from transitions within a thermally isolated ground Kramers doublet of the ground Russell-Saunders state, which can be treated as an effective spin-1/2. In this approximation, the frozen solution EPR spectrum for 1-Nd (Fig. 4a) can be modeled with the spin Hamiltonian eqn (1).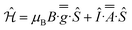 | (1) |
This gives gx,y,z = 3.33, 1.22, 0.56, and hyperfine coupling constants of Ax = 1280 MHz (Ay and Az unresolved; we have assumed ![[g with combining double overline]](https://www.rsc.org/images/entities/i_char_0067_033f.gif) and
and ![[A with combining double overline]](https://www.rsc.org/images/entities/i_char_0041_033f.gif) are collinear) to the I = 7/2 nuclear spin of Nd (natural abundance: 12.2% 143Nd and 8.3% 145Nd). Similarly, frozen solution spectra of 1-Ce and 1-Sm can be simulated with gx,y,z = 3.15, 1.88, 0.64 for 1-Ce (Fig. 4b; note there are no isotopes of Ce with I ≠ 0), and gx = gy = 0.92 for 1-Sm (Fig. S27†). The gz component of 1-Sm is not well resolved in CW spectra but is more clearly defined in pulsed spectra giving gz = 0.45 (Fig. S28;† see below). CW spectra of the related [Nd(Cp′′)3] (Cp′′ = C5H3-(SiMe3)2-1,3) have been reported,35 and although the precise g-values differ the pattern is similar.
are collinear) to the I = 7/2 nuclear spin of Nd (natural abundance: 12.2% 143Nd and 8.3% 145Nd). Similarly, frozen solution spectra of 1-Ce and 1-Sm can be simulated with gx,y,z = 3.15, 1.88, 0.64 for 1-Ce (Fig. 4b; note there are no isotopes of Ce with I ≠ 0), and gx = gy = 0.92 for 1-Sm (Fig. S27†). The gz component of 1-Sm is not well resolved in CW spectra but is more clearly defined in pulsed spectra giving gz = 0.45 (Fig. S28;† see below). CW spectra of the related [Nd(Cp′′)3] (Cp′′ = C5H3-(SiMe3)2-1,3) have been reported,35 and although the precise g-values differ the pattern is similar.
For 1-Ce and 1-Nd, CASSCF-SO calculations (Tables S10–S13; † note there are two non-equivalent molecules in the XRD structure of 1-Ce) give effective g-values for the lowest Kramers doublets as gx,y,z = 2.1, 3.0, 0.7 and 2.2, 2.4, 1.1, respectively, with the numerically smallest value (gz) corresponding to the orientation of the pseudo-C3 axis (Fig. 1); the anisotropy patterns agree with the experiments. For 1-Sm, CASSCF-SO calculations give gx,y,z = 0.4, 0.4, 0.6 for the lowest Kramers doublet. This has the opposite sense of anisotropy (gx,y < gz) to the experimental data (gx,y > gz), but given the numerically similar and very low (all < 1) effective g-values, such a switch in anisotropy will be very sensitive to subtle state mixing effects. Nevertheless, given the axially symmetric form of the EPR spectrum, gz must be associated with the pseudo-C3 axis.
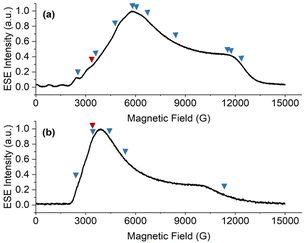
Pulsed EPR spectroscopy
Echo-detected field-swept spectra (EDFS) of 1-Nd, 1-Ce and 1-Sm (in toluene-hexane) are observed up to 10 K (see ESI† for all pulsed EPR spectra). These were recorded by integration of the Hahn echo generated with the standard pulse sequence π/2–τ–π–echo, where π/2 and π are microwave pulses and τ is the inter-pulse delay.19 The EDFS spectra at 5 K for 1-Nd, 1-Ce and 1-Sm (Fig. 5, S28 and S29†) are consistent with the CW spectra, Q-band EDFS are consistent with the rhombic g-values of 1-Nd and 1-Ce (Fig. S30†).Measurements of the spin-lattice (T1) and phase-memory (Tm) relaxation times were performed at X-band on 10 mM frozen solution samples of 1-Nd, 1-Ce and 1-Sm at 5 K. T1 data were recorded with an inversion recovery pulse sequence, and the data fitted with a bi-exponential function (see ESI eqn (3);† Fig. S34 and S35†), where the fastest process is assigned to the spectral diffusion and the slow process is attributed to the spin-lattice relaxation.36 The T1 value for 1-Nd is field-dependent and reaches a maximum value of 12 μs at the highest field g-value (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 G, Table S3†). Measured at the maximum of the EDFS (6040 G), T1 is 5 μs. Much longer maximum T1 times of 89 and 150 μs were obtained for 1-Ce (at the high-field g-value, 11
360 G, Table S3†). Measured at the maximum of the EDFS (6040 G), T1 is 5 μs. Much longer maximum T1 times of 89 and 150 μs were obtained for 1-Ce (at the high-field g-value, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 G) and 1-Sm (at the low-field g-value, 6936 G), respectively (Tables S4 and S5†). For comparison, T1 measured at the EDFS maxima are 78 and 118 μs for 1-Ce and 1-Sm, respectively. We note that the measured T1 data are anisotropic (Fig. S34 and S35, Tables S3–S5†), and the anisotropy (evaluated as the ratio of T1,‖/T1,⊥)37 is most significant for 1-Nd which also has the greatest g-anisotropy.
228 G) and 1-Sm (at the low-field g-value, 6936 G), respectively (Tables S4 and S5†). For comparison, T1 measured at the EDFS maxima are 78 and 118 μs for 1-Ce and 1-Sm, respectively. We note that the measured T1 data are anisotropic (Fig. S34 and S35, Tables S3–S5†), and the anisotropy (evaluated as the ratio of T1,‖/T1,⊥)37 is most significant for 1-Nd which also has the greatest g-anisotropy.
T m was determined by fitting Hahn echo decays to a stretched exponential function (see ESI eqn (1); Fig. S31–S33†).38 The maximum Tm relaxation times observed are 0.7, 1.0 and 1.7 μs for 1-Nd, 1-Ce and 1-Sm, respectively (Tables S3–S5†), in each case measured at the highest field g-value. Tm measured at the EDFS maxima are 0.5, 0.6 and 1.6 μs, respectively.
An interesting comparison can be made between 1-Nd and its valence isoelectronic An3+ analog 1-U. Complex 1-U has T1 and Tm times of 860 and 0.8 μs, measured at the EDFS maximum under similar conditions,21 compared to 5 and 0.5 μs for 1-Nd. Hence, T1 for the Ln3+ 4f3 complex is more than two orders of magnitude shorter than for its An3+ 5f3 analogue. In general, electron spin-lattice relaxation times are expected to decrease going down the Periodic table, as modulation of the electronic structure by vibrational modes (which is a dominant factor for T1 relaxation in immobilised samples24) impacts the orbital angular momentum. This is connected to the spin via spin–orbit coupling (SOC), and SOC increases with atomic number;39 the values for for Nd3+ and U3+ are 900 and ca. 1700 cm−1, respectively.40 It seems reasonable to assume that the slower T1 relaxation of 1-U is due to the partial quenching of the orbital angular momentum by the larger crystal field interaction for U3+cf. Nd3+. This is promising for future pulsed EPR studies of An-containing materials. The 4f1 complex 1-Ce also has a much shorter T1 than its An3+ analogue 1-Th (T1ca. 21 ms under similar conditions):21 this is due to the orbital singlet 6d1 configuration of 1-Th,26 compared to 4f1 for 1-Ce.
Comparing the relaxation data for the 1-Ln series, it could be inferred that 1-Nd has the shortest T1 because it has the largest ground state orbital angular momentum (L = 6) and indeed the largest total angular momentum (J = 9/2). However, comparison with T1 data for these Ln3+ ions at similar concentrations and temperatures in water/ethanol glasses gives a different trend, with Nd3+ having the longest T1.41 This emphasises the importance of the crystal field on the relaxation behaviour of Ln3+ ions. In our case, of the three complexes studied, 1-Nd has, by some margin, the lowest energy excited state and indeed the smallest energy spread of mJ states desite having the largest multiplicity (Tables S10–S13†). More densely packed electronic states renders the states more sensitive to perturbations (following textbook perturbation theory arguments), and so we can speculate that this exposes 1-Nd to more influences from spin-vibration coupling, and thus causes a shorter T1.
The Tm values for 1-Ln complexes studied are all similar, around the 1 μs mark. These are ample to allow further investigation of the complexes by multi-pulse microwave sequences. In order to quantify the weak hyperfine interactions between the electron spin(s) and surrounding 1H and 13C nuclei, we employed two-dimensional hyperfine sub-level correlation (HYSCORE) spectroscopy, which uses a four-pulse spin echo envelope modulation sequence; π/2–τ–π/2–t1–π–t2–π/2–echo, with t1 and t2 independently varied.42 In the HYSCORE experiment the first two π/2 pulses generate nuclear coherences, which are then transferred between electron spin states by the π pulse. In the 2D frequency domain spectrum, cross-peaks appear for weakly-coupled nuclei (2|νn| > |A|) in the (+, +) quadrant straddling the nuclear Larmor frequencies (νn). Ridges in the spectra are due to the anisotropic hyperfine couplings.43
X-band HYSCORE spectra measured at static magnetic fields corresponding to orientations in the molecular xy plane for 1-Nd and 1-Ce (B0 = 353.0 and 348.2 mT, respectively) reveal signals from 13C and 1H nuclei (Fig. 6). HYSCORE signals for 1-Sm were too weak to detect when measured under similar conditions; this does not appear to be relaxation limited given the similar Tm (see above), and may be a function of the very low effective g-values.24 The 13C features for 1-Nd and 1-Ce are similar, consisting of a ridge extending beyond the 13C Larmor frequency by ca. ± 1 MHz. The 1H features are also similar, with a ridge extending νn ± 2.5 MHz.
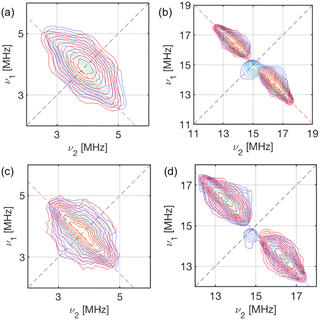 | ||
| Fig. 6 X-Band HYSCORE spectra for 1-Nd (a and b; static field B0 = 353.0 mT) and 1-Ce (c and d; B0 = 348.2 mT) at 5 K. (a and c) 13C region (blue) for 1-Nd and 1-Ce, respectively, and calculated spectra (red) based on a dipolar model including C1–C5 (Tables S8 and S9†); (b and d) 1H region (blue) for 1-Nd and 1-Ce, respectively, and calculated spectra (red) based on a dipolar model including H2, H4 and H5 (Tables S8 and S9†). The red dashed anti-diagonal lines indicate the nuclear Larmor frequency for 13C (a and c) or 1H (b and d). | ||
In a first attempt to model the HYSCORE data of 1-Ce and 1-Nd, we used a simple point dipolar approach assuming the electron spin density to be located at the Ln3+ ion, calculated (ESI, eqn (4)†) using the experimental g-values and the atomic coordinates from XRD (thus neglecting structural relaxation in solution). The calculated point dipolar hyperfine values for the Cp-ring hydrogen and carbon atoms (Tables S8 and S9†) were then used with EasySpin44,45 to calculate HYSCORE spectra. The calculated spectra show excellent agreement with the experimental data (Fig. 6).
Comparing the HYSCORE data of 4f 1-Ce and 1-Nd to their 5f analogues 1-An, 13C HYSCORE spectra measured for 1-Th under equivalent conditions have ridges that spread νn ± 2.4 MHz,21 substantially larger than for 1-Ce. We did not have sufficient signal to measure the full 13C hyperfine pattern for 1-U, but we did measure well-resolved 1H ridges in the gx,y region:21 these spanned νn ± 2.5 MHz, which is much larger than for 1-Nd. The spectra for 1-Th and 1-U could not be modelled on a simple point dipole basis, requiring significant additional contributions to the hyperfine interactions.
We futher confirmed these results using CASSCF-SO calculations (see ESI†). To compare with the HYSCORE experiment, we approximate solution phase structures by optimising the molecular geometry of each complex in the gas-phase using density-functional theory (DFT) methods (see ESI† for details), and then use the optimised geometries to perform another set of minimal CASSCF-SO calculations; note that these calculations explicitly include CF, SO and interelectronic repulsion effects of the f-shell ground configuration. We then use the Hyperion package to calculate the relativistic hyperfine coupling tensors directly for the nuclei of interest (Tables S14 and S15†);29 note that the Hyperion method implicitly includes all through space dipolar and Fermi contact terms, as well as relativistic paramagnetic spin–orbit terms. Inspection of the computed hyperfine values show the C(Cp) and H(Cp) atoms couple more strongly than any other Cptt ligand atoms. Hence, we simulate 13C and 1H HYSCORE spectra using five C and three H nuclei from one Cptt ligand, again using EasySpin; these calculations provide excellent reproductions of the experimental data (Fig. S36†). The calculated Mulliken spin populations (Table S16†), show that only ∼0.1% of the total spin density is transferred to the C1–C5 atoms of the three Cptt ligands. However, we note that the density does increase slightly with increasing Ln3+ atomic number (1-Ce < 1-Nd < 1-Sm).
Conclusions
We have synthesised a family of Ln3+ complexes [Ln(Cptt)3] (1-Ln; Ln = La, Ce, Nd, Sm) using a salt metathesis route. The solid-state structures of 1-Ln reveal that the distances between the Ln3+ centres and the Cptt centroids decrease regularly from La3+ to Sm3+ due to the ionic radii of Ln3+ ions decreasing across the series. Complexes 1-La and 1-Nd exhibit pseudo-trigonal planar geometries, which is consistent with the previously reported structures of 1-Ce,271-Sm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 and 1-Yb.31 Continuous wave and pulsed EPR studies were performed on 1-Nd, 1-Ce, and 1-Sm. The CW spectra show rhombic systems with anisotropic g-values for both frozen solution and powder samples for 1-Nd and 1-Ce. HYSCORE spectroscopy shows resonances for 13C and 1H regions for both 1-Nd and 1-Ce, and point-dipole simulations provide excellent agreement with experimental data. CASSCF-SO calculations effectively reproduce magnetic data, and fully-ab initio simulations of the HYSCORE spectra are also in excellent agreement with experiment, confirming minimal spin density at ligand nuclei. The larger ligand hyperfine interactions observed for 1-Th (ref. 21) cf. 1-Ce are consistent with the 6d1vs. 4f1 configurations of Th3+ and Ce3+, respectively, and the significant radial extent of the 6d orbital(s). Comparing the results for 1-Nd with 1-U shows larger ligand hyperfines observed for the latter, highlighting the difference between 4f and 5f valence orbitals.
28 and 1-Yb.31 Continuous wave and pulsed EPR studies were performed on 1-Nd, 1-Ce, and 1-Sm. The CW spectra show rhombic systems with anisotropic g-values for both frozen solution and powder samples for 1-Nd and 1-Ce. HYSCORE spectroscopy shows resonances for 13C and 1H regions for both 1-Nd and 1-Ce, and point-dipole simulations provide excellent agreement with experimental data. CASSCF-SO calculations effectively reproduce magnetic data, and fully-ab initio simulations of the HYSCORE spectra are also in excellent agreement with experiment, confirming minimal spin density at ligand nuclei. The larger ligand hyperfine interactions observed for 1-Th (ref. 21) cf. 1-Ce are consistent with the 6d1vs. 4f1 configurations of Th3+ and Ce3+, respectively, and the significant radial extent of the 6d orbital(s). Comparing the results for 1-Nd with 1-U shows larger ligand hyperfines observed for the latter, highlighting the difference between 4f and 5f valence orbitals.
The results show that the interactions between Ln3+ ions and these cyclopentadienyl ligands in these early Ln organometallic complexes 1-Ln can be considered as being largely ionic in the sense of minimal transfer of spin density from the 4f to ligand orbitals. The results are consistent with early CW EPR studies of U3+ and Nd3+ doped fluorite46 (and later studies on other inorganic lattices),47 where superhyperfine coupling to 19F was observed for the former but not the latter. These are mineral lattices with hard ligands, and we have now shown related effects in molecular species with soft arene ligand sets. The results on 1-Ln also contrast with HYSCORE studies of the closely related [Yb(Cp)3] complex,25 a late Ln complex (4f13), which showed far more significant transfer of spin density from 4f to arene and can hence be described as being “more covalent” in this sense, despite the smaller ionic radius of the Yb3+ ion. This is consistent with Denning's conclusion25 that this “increased covalency” is due to the low reduction potential of Yb3+ combined with an electron-rich ligand leading to greater metal-to-ligand charge transfer character in the ground state. This highlights the importance of ligand substituents and Ln ion charge density in controlling the magnitude of 4f metal–ligand interactions, and shows that pulsed EPR spectroscopy is a sensitive probe to study these effects.
Experimental
Materials and methods
General synthesis of 1-Ln. THF (30 mL) was added to a pre-cooled (−78 °C) ampoule containing LnCl3 (2 mmol) and KCptt (6 mmol). The reaction mixture was allowed to reflux for 16 hours. The solvent was removed in vacuo and toluene (30 mL) was added. The reaction mixture was allowed to reflux for 40 hours. The resultant suspension was allowed to settle for 3 hours and filtered. The solution was concentrated to ca. 2 mL and stored at 8 °C to afford crystals of 1-Ln.
1-La: colourless crystals (0.550 g, 41%). Anal calcd (%) for C39H63La: C, 69.81; H, 9.47. Found (%): C, 67.03; H, 9.50. 1H NMR (C6D6, 400 MHz, 298 K): δ = 1.35 (s, 54H, C(CH3)3), 6.21 (s, 3H, Cp-H), 6.28 (s, 6H, Cp-H) ppm. 13C{1H} NMR (C6D6, 100 MHz, 298 K): δ = 32.77 (C(CH3)3), 33.75 (C(CH3)3), 110.57 (CH-Cp ring), 110.69 (CH-Cp ring), 143.45 (C-Cp ring) ppm. FTIR (ATR, microcrystalline): ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/char_e131.gif) = 2960 (s), 2899 (w), 2862 (w), 1459 (m), 1388 (w), 1356 (m), 1252 (s), 1198 (w), 1163 (w), 1088 (br, s), 1018 (s), 927 (w), 803 (s), 736 (s), 660 (w), 605 (w) cm−1.
= 2960 (s), 2899 (w), 2862 (w), 1459 (m), 1388 (w), 1356 (m), 1252 (s), 1198 (w), 1163 (w), 1088 (br, s), 1018 (s), 927 (w), 803 (s), 736 (s), 660 (w), 605 (w) cm−1.
1-Ce: blue crystals (0.726 g, 54%). Anal calcd (%) for C39H63Ce: C, 69.68; H, 9.45. Found (%): C, 67.49; H, 9.43. 1H NMR (C6D6, 500 MHz, 298 K): δ = −5.01 (s, 54H, C(CH3)3), 17.14 (s, 6H, Cp-H), 26.30 (s, 3H, Cp-H) ppm. The paramagnetism of 1-Ce precluded assignment of its 13C{1H} NMR spectrum. FTIR (ATR, microcrystalline): ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/char_e131.gif) = 2951 (br, s), 2899 (w), 2863 (w), 1459 (s), 1388 (m), 1356 (s), 1298 (w), 1251 (s), 1198 (m), 1164 (s), 1051 (m), 1021 (m), 927 (s), 806 (s), 738 (s), 674 (s), 659 (s), 604 (w), 556 (br, w), 480 (w), 422 (m) cm−1.
= 2951 (br, s), 2899 (w), 2863 (w), 1459 (s), 1388 (m), 1356 (s), 1298 (w), 1251 (s), 1198 (m), 1164 (s), 1051 (m), 1021 (m), 927 (s), 806 (s), 738 (s), 674 (s), 659 (s), 604 (w), 556 (br, w), 480 (w), 422 (m) cm−1.
1-Nd: green crystals (0.460 g, 34%). Anal calcd (%) for C39H63Nd: C, 69.26; H, 9.40. Found (%): C, 65.81; H, 9.30. 1H NMR (C6D6, 400 MHz, 298 K): δ = −9.06 (s, 54H, C(CH3)3), 12.68 (s, 6H, Cp-H), 34.47 (s, 3H, Cp-H). The paramagnetism of 1-Nd precluded assignment of its 13C{1H} NMR spectrum. FTIR (ATR, microcrystalline): ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/char_e131.gif) = 2950 (s), 2899 (w), 2863 (w), 1459 (s), 1388 (w), 1356 (s), 1251 (s), 1164 (m), 1060 (br, w), 1021 (w), 927 (s), 806 (s), 737 (s), 659 (s), 605 (w), 423 (w) cm−1.
= 2950 (s), 2899 (w), 2863 (w), 1459 (s), 1388 (w), 1356 (s), 1251 (s), 1164 (m), 1060 (br, w), 1021 (w), 927 (s), 806 (s), 737 (s), 659 (s), 605 (w), 423 (w) cm−1.
1-Sm: orange crystals (0.716 g, 52%). 1H NMR (C6D6, 400 MHz, 298 K): δ = −1.58 (s, 54H, C(CH3)3), 18.66 (s, 6H, Cp-H), 21.19 (s, 3H, Cp-H). The paramagnetism of 1-Sm precluded assignment of its 13C{1H} NMR spectrum. FTIR (ATR, microcrystalline): ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/char_e131.gif) = 2952 (s), 2901 (m), 2864 (w), 1460 (s), 1390 (s), 1366 (s), 1298 (s), 1250 (s), 1199 (s), 1164 (s), 1085 (w), 1060 (w), 1022 (m), 927 (s), 807 (s), 741 (s), 700 (s), 661 (s), 606 (m), 560 (m), 519 (w), 483 (w), 426 (s) cm−1.
= 2952 (s), 2901 (m), 2864 (w), 1460 (s), 1390 (s), 1366 (s), 1298 (s), 1250 (s), 1199 (s), 1164 (s), 1085 (w), 1060 (w), 1022 (m), 927 (s), 807 (s), 741 (s), 700 (s), 661 (s), 606 (m), 560 (m), 519 (w), 483 (w), 426 (s) cm−1.
Data availability
Additional experimental details for physical and computational data associated with this manuscript (PDF). Additional research data supporting this publication are available from Figshare at https://figshare.com/10.6084/m9.figshare.23302253.Author contributions
F. T., E. J. L. M. and D. P. M. provided the original concept. L. N. and A.-M. A. collected and modelled EPR data. J. L., F. O., P. J. C. and J. E-K. synthesized and characterized the complexes and collected, solved and refined the single crystal and powder XRD data. F. O. further refined the single crystal XRD data and finalized cifs. L. N. and G. K. G. collected and analyzed magnetic data. M. S. O. and L. B. performed calculations. N. F. C. supervised the calculations, D. P. M. supervised the synthesis and characterization of compounds, and F. T. and E. J. L. M. supervised EPR spectroscopy. L. N., J. L., N. F. C., D. P. M., E. J. L. M. and F. T. wrote the manuscript, with contributions from all other authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Engineering and Physical Sciences Research Council (studentship to L. N. and EP/P002560/1), the China Scholarship Council (studentship to J. L.), The European Commission Marie Curie Initial Training Network ‘Magic’ (studentship to A. M. A), the Ministry of Defence (studentship to L. B.), the Royal Society (fellowship URF191320 to N. F. C.), Natural Sciences and Engineering Research Council of Canada (fellowship 557458 to M. S. O.), the European Research Council (StG-851504 to N. F. C., CoG-816268 to D. P. M.) The University of Manchester Single Crystal X-ray Diffraction Service (EP/P001386/1), The University of Manchester Computational Shared Facility for computational resources, and the EPSRC UK EPR National Research Facility (EP/W014521/1, EP/V035231/1) for supporting this work.References
- The Rare Earth Elements: Fundamentals and Applications, ed. D. A. Atwood, John Wiley and Sons Ltd., Chichester, 2012 Search PubMed.
- The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstei and J. Fuger, Springer, Dordrecht, 3rd edn, 2006 Search PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef CAS.
- H. H. Dam, D. N. Reinhoudt and W. Verboom, Chem. Soc. Rev., 2007, 36, 367–377 RSC.
- K. L. Nash, Solvent Extr. Ion Exch., 1993, 11, 729–768 CrossRef CAS.
- L. Ungur, B. Szabo, Z. A. ALOthman, A. A. S. Al-Khatani and L. F. Chibotaru, Inorg. Chem., 2022, 61, 5972–5976 CrossRef CAS PubMed.
- D. Parker, E. A. Suturina, I. Kuprov and N. F. Chilton, Acc. Chem. Res., 2020, 53, 1520–1534 CrossRef CAS PubMed.
- M. Brigante, G. F. Garcia, J. Jung, R. Sessoli, B. Le Guennic and F. Totti, Chem. Sci., 2019, 10, 7233–7245 RSC.
- H. Schumann, J. A. Meese-Marktscheffel and L. Esser, Chem. Rev., 1995, 95, 865–986 CrossRef CAS.
- O. Walter, Chem.–Eur. J., 2019, 25, 2927–2934 CrossRef CAS PubMed.
- M. Ephritikhine, Organometallics, 2013, 32, 2464–2488 CrossRef CAS.
- W. J. Evans, Organometallics, 2016, 35, 3088–3100 CrossRef CAS.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- B. E. Bursten, L. F. Rhodes and R. J. Strittmatter, J. Am. Chem. Soc., 1989, 111, 2756–2758 CrossRef CAS.
- R. J. Strittmatter and B. E. Bursten, J. Am. Chem. Soc., 1991, 113, 552–559 CrossRef CAS.
- N. Kaltsoyannis and B. E. Bursten, J. Organomet. Chem., 1997, 528, 19–33 CrossRef CAS.
- I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131 RSC.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, Oxford, 2001 Search PubMed.
- For recent examples, see: (a) M. Shiddiq, D. Komijnai, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed; (b) K. Kundu, J. R. K. White, S. A. Moehring, J. M. Yu, J. W. Ziller, F. Furche, W. J. Evans and S. Hill, Nat. Chem., 2022, 14, 392–397 CrossRef CAS PubMed; (c) A.-M. Ariciu, D. H. Woen, D. N. Huh, L. E. Nodaraki, A. K. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans and F. Tuna, Nat. Commun., 2019, 10, 3330 CrossRef PubMed; (d) K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- A. Formanuik, A.-M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. Mclnnes and D. P. Mills, Nat. Chem., 2017, 9, 578–583 CrossRef CAS PubMed.
- G. Rao, A. B. Altman, A. C. Brown, L. Z. Tao, T. A. Stich, J. Arnold and R. D. Britt, Inorg. Chem., 2019, 58, 7978–7988 CrossRef CAS PubMed.
- L. Barluzzi, N. Jori, T. He, T. Rajeshkumar, R. Scopelliti, L. Maron, P. Oyala, T. Agapie and M. Mazzanti, Chem. Commun., 2022, 58, 4655–4658 RSC.
- For a recent review, see: J. E. McPeak, S. S. Eaton and G. R. Eaton, Methods Enzymol., 2021, 651, 63–101 CAS.
- R. G. Denning, J. Harmer, J. C. Green and M. Irwin, J. Am. Chem. Soc., 2011, 133, 20644–20660 CrossRef CAS PubMed.
- W. K. Kot, G. V. Shalimov, N. M. Edelstein, M. A. Edelman and M. F. Lappert, J. Am. Chem. Soc., 1988, 110, 986–987 CrossRef CAS.
- C. D. Sofield and R. A. Andersen, J. Organomet. Chem., 1995, 501, 271–276 CrossRef CAS.
- N. A. Pushkarevsky, I. Y. Ilyin, P. A. Petrov, D. G. Samsonenko, M. R. Ryzhikov, P. W. Roesky and S. N. Konchenko, Organometallics, 2017, 36, 1287–1295 CrossRef CAS.
- L. Birnoschi and N. F. Chilton, J. Chem. Theory Comput., 2022, 18, 4719–4732 CrossRef CAS PubMed.
- R. E. H. Kuveke, L. Barwise, Y. van Ingen, K. Vashisth, N. Roberts, S. S. Chitnis, J. L. Dutton, C. D. Martin and R. L. Melen, ACS Cent. Sci., 2022, 8, 855–863 CrossRef CAS PubMed.
- A. V. Khvostov, B. M. Bulychev, V. K. Belsky and A. I. Sizov, J. Organomet. Chem., 1998, 568, 113–119 CrossRef CAS.
- F. Ortu, A. Formanuik, J. R. Innes and D. P. Mills, Dalton Trans., 2016, 45, 7537–7549 RSC.
- V. A. Volkovich, A. B. Ivanov, S. M. Yakimov, D. V. Tsarevskii, O. A. Golovanova, V. V. Sukhikh and T. R. Griffiths, AIP Conf. Proc., 2016, 1767, 020023 CrossRef.
- J.-L. Liu, Y.-C. Chen and M. L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- W. W. Lukens, M. Speldrich, P. Yang, T. J. Duignan, J. Autschbach and P. Kögerler, Dalton Trans., 2016, 45, 11508–11521 RSC.
- S. S. Eaton and G. R. Eaton, in Biological Magnetic Resonance Volume 19: Distance Measurements in Biological Systems by EPR, ed. L. J. Berliner, G. R. Eaton and S. S. Eaton, Kluwer Academic/Plenum Publishers, New York, 2002, pp. 29–154 Search PubMed.
- N. P. Kazmierczak and R. G. Hadt, J. Am. Chem. Soc., 2022, 144, 20804–20814 CrossRef CAS PubMed.
- K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626 RSC.
- R. Husted, J.-L. Du, G. R. Eaton and S. S. Eaton, Magn. Reson. Chem., 1995, 33, S66–S69 CrossRef CAS.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, 1970 Search PubMed.
- S. S. Eaton and G. R. Eaton, J. Magn. Reson., 2023, 348, 107392 CrossRef CAS PubMed.
- S. Van Doorslear, eMagRes, 2017, 6, 51–69 Search PubMed.
- J. Harmer, G. Mitrikas and A. Schweiger, Advanced Pulse EPR Methods for the Characterization of Metalloproteins, In High Resolution EPR, ed. G. Hanson and L. Berliner, Springer Science, New York, 2009, vol. 28, pp. 13–61 Search PubMed.
- S. Stoll and A. Schwieger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- S. Stoll and R. D. Britt, Phys. Chem. Chem. Phys., 2009, 11, 6614–6625 RSC.
- B. Bleaney, P. M. Llewellyn and D. A. Jones, Proc. R. Soc. B, 1956, 69, 858–860 Search PubMed.
- L. K. Aminov, I. N. Kurkin and B. Z. Malkin, Phys. Solid State, 2013, 55, 1343–1363 CrossRef CAS.
- F. Jaroschik, F. Nief, X. F. Le Goff and L. Ricard, Organometallics, 2007, 26, 3552–3558 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2271676 and 2271677. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc06175b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |