Controlling glass forming kinetics in 2D perovskites using organic cation isomers

Abstract

The recent discovery of glass-forming metal halide perovskites (MHPs) provides opportunities to broaden the application domain beyond traditionally celebrated optoelectronic research fueled by associated crystalline counterparts. In this regard, it is crucial to diversify the compositional space of glass-forming MHPs and introduce varied crystallization kinetics via synthetic structural engineering. Here, we compare two MHPs with slightly varying structural attributes, utilizing isomer organic cations with the same elemental composition, and demonstrate how this change in functional group position impacts the kinetics of glass formation and subsequent crystallization by multiple orders of magnitude. (S)-(−)-1-(1-Naphthyl)ethylammonium lead bromide (S(1-1)NPB) exhibits a lower melting point (T_m) of 175 °C and the melt readily vitrifies under a critical cooling rate (CCR) of 0.3 °C s⁻¹. In contrast, (S)-(−)-1-(2-naphthyl)ethylammonium lead bromide (S(1-2)NPB) displays a T_m ∼193 °C and requires a CCR of 2500 °C s⁻¹, necessitating the use of ultrafast calorimetry for glass formation and study of the underlying kinetics. The distinct T_m and glass-formation kinetics of the isomer MHPs are further understood through a combination of calorimetric and single-crystal X-ray diffraction studies on their crystalline counterparts, highlighting the influence of altered organic–inorganic hydrogen bonding interactions and entropic changes around melting, providing insights into the factors driving their divergent behaviors.

---

Introduction

2D metal halide perovskites (MHPs), renowned for their diverse crystalline structures^1,2 that allow for integrated organic and inorganic character/functionality,³ have captivated the scientific community with their immense potential in the fields of photovoltaics,^4–6 emitters,^7,8 and sensors.^9–11 Extensive research efforts dedicated to unraveling their intricate properties have led to improved device performance, propelling the boundaries of technological advancement. Embarking on a departure from the traditional belief that hybrid perovskites exclusively exist in the crystalline state, a transformative observation emerged with the discovery of glass formation in an exemplary 2D MHP [(S)-(−)-1-(1-naphthyl)ethylammonium]₂PbBr₄ (commonly referred as SNPB but henceforth referred as S(1-1)NPB to clarify the isomer choice)^12,13 and a series of 3D organometallic perovskites¹⁴ through low temperature melt-quenching under laboratory timescales (minute-scale).^12,13,15 The glassy state of MHPs has the potential to expand their range of properties, notably due to changes in short and long range ordering relative to the crystalline state, similar to what has been observed in other glassy semiconductors.¹⁶ Moreover, the ability to switch reversibly between the glassy and crystalline states¹² opens up new avenues for MHP applications, including memory,^17,18 computing,¹⁹ metamaterials,²⁰ and photonic devices,²¹ ushering in a new era of possibilities in the realm of MHP research.

Glasses can broadly be categorized as good or poor glass formers, depending on their ease of vitrification and the required critical cooling rate (CCR).²² This classification has a direct impact on their glass-crystal transformation rates. Good glass formers can be vitrified with lower critical cooling rates (10⁻⁵ to 10⁰ °C s⁻¹) and tend to exhibit slow or negligible glass-crystal transformations within practical timescales. Examples of good glass formers include inorganic oxides,²³ certain molecular organics,²⁴ polymeric,²⁵ and hybrid metal–organic framework glasses.²⁶ These glasses find applications in fields such as optical fibers,²⁷ gas storage,²⁸ and phase-change energy storage systems.^29,30 On the other hand, poor glass formers require very high cooling rates (10³ to 10¹⁰ °C s⁻¹) and exhibit faster glass-crystallization kinetics.³¹ They are suitable for applications that require fast switching times, such as memory¹⁷ and computing devices.¹⁹ Metals³² and some chalcogenides,³¹ particularly Ge–Sb–Te (GST), are known to possess such characteristics. Given the wide range of available organic cations and inorganic frameworks capable of forming 2D or 1D MHPs³³ and the ability to tune their thermal properties, including the melting temperature (T_m) with a range of over 150 °C,^34–41 it is conceivable that within the MHP family, a wide range of glass-forming ability and varying crystallization kinetics can be achieved. The previously reported S(1-1)NPB perovskite, known for its exemplary glass-forming ability, exhibits a low T_m of 175 °C and a CCR of as low as 0.3 °C s⁻¹ with slow glass-crystal transformation kinetics.^12,42 However, in order to broaden the application potential of MHPs in fields that demand rapid switching, it is crucial to develop the capability to control and modulate the glass-forming and glass-crystallization kinetics.

In this study, we examine and modulate the glass-forming and glass-crystallization kinetics in a 2D MHP by replacing the (S)-(−)-1-(1-naphthyl)ethylammonium (S(1-1)NEA) cation in S(1-1)NPB with isomeric (S)-(−)-1-(2-naphthyl)ethylammonium (S(1-2)NEA), which ultimately leads to differing arrangement of the organic cations, intermolecular interactions, and structural distortions for the crystalline versions of the MHPs, despite the same overall atomic composition.⁴³ Interestingly, the resulting 2D MHPs, namely S(1-1)NPB and [(S)-(−)-1-(2-naphthyl)ethylammonium]₂PbBr₄ (henceforth referred to as S(1-2)NPB), exhibit vastly different glass-forming properties. S(1-1)NPB demonstrates facile glass formation under laboratory timescales, while S(1-2)NPB does not readily vitrify under conditions achievable using conventional calorimetry. Additionally, melt-quenching in thin-film configuration doesn't permit complete vitrification of S(1-2)NPB under typical laboratory experimental timescales, thus, necessitating the use of ultrafast calorimetry⁴⁴ to study in situ glass formation and glass-crystallization kinetics.

By employing a range of cooling and heating rates spanning two orders of magnitude, we determine the CCR required for glass formation and the characteristic glass transition temperature (T_g) in S(1-2)NPB. Additionally, a Kissinger kinetic modeling is performed to calculate the activation energy required for glass-crystal transformation over a wide temperature range (∼70 °C) facilitated by various heating rates (50–5000 °C s⁻¹). Finally, the distinct thermal and glass-forming properties are elucidated through a comprehensive analysis of the crystal structures of the two MHPs, by scrutinizing the intricate interplay of hydrogen (H) bonding interactions between the organic and inorganic sub lattices, and by understanding the entropic changes around melting. The findings provided in this work establish a fundamental framework for analyzing the impact of structural factors on the kinetics of glass formation and crystallization and serve as a new material design strategy to diversify the family of glass forming MHPs, aiding in broadening their application space.

Results and discussion

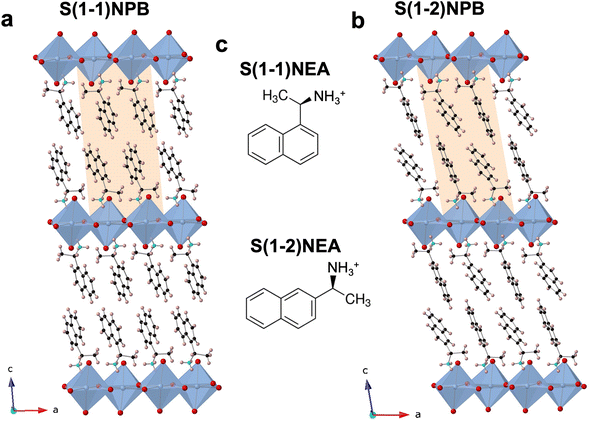
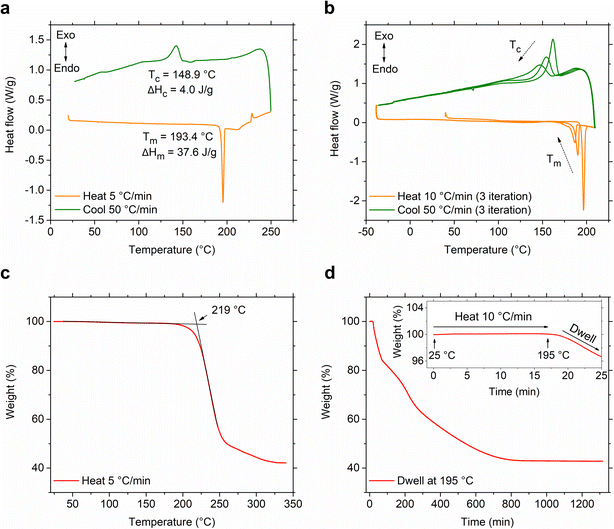
The relative positional shift of the ethylammonium group with respect to the naphthyl group, specifically S(1-1)NEA versus S(1-2)NEA, prospectively should provide distinct structure-directing characteristics and form two 2D MHP systems, namely S(1-1)NPB and S(1-2)NPB, which can be expected to exhibit varying orientations and relative arrangements of the organic cations, along with associated diverse structural properties. Recently, Moon et al. reported the crystal structure of S(1-2)NPB,⁴³ showing that, similar to the S(1-1)NPB,⁴⁵ it adopts a Ruddlesden–Popper type perovskite arrangement with a non-centrosymmetric P2₁ space group (Fig. 1, Table S1†), resulting from the incorporation of well-ordered chiral cation bilayers intercalated between 2D inorganic layers comprising corner-sharing PbBr₆ octahedra. Both systems possess rigid and bulky naphthyl-containing cations; however, their distinct structural characteristics offer an important opportunity to explore the underlying structural factors influencing their thermal and glass-forming properties. Motivated by the previously observed intriguing reversible crystal–glass transition in S(1-1)NPB,¹² the group of S(1-1)NPB and S(1-2)NPB represents a promising opportunity to investigate and compare their glass formation kinetics and gain a deeper understanding of the structural origin of the thermal properties.

Fig. 1 Schematic single-crystal structures of (a) S(1-1)NPB and (b) S(1-2)NPB. Unit cells in (a) and (b) are indicated by shaded parallelograms. (c) The molecular structures of S(1-1)NEA and S(1-2)NEA cations. The different molecular structures induce the characteristic orientations of organic cations within the 2D HOIPs. Blue, red, black, turquoise, and beige spheres denote Pb, Br, C, N, and H atoms, respectively.

A conventional differential scanning calorimetry (DSC) measurement of S(1-2)NPB reveals a higher melting point, T_m = 193.4 °C (Fig. 2a), compared to the S(1-1)NPB counterpart, which has a melting point of 175.0 °C,^12,13 as also recently reported by Moon et al.⁴³ Furthermore, unlike S(1-1)NPB, which vitrifies into a glassy state at a moderate cooling rate of 20 °C min⁻¹,¹²S(1-2)NPB does not undergo glass formation even at a cooling rate of 50 °C min⁻¹ (maximum achievable in conventional DSC in the temperature range of interest, Fig. 2a). Instead, an exothermic peak appears during the melt cooling step. However, melt cooling does not lead to complete recovery to a crystalline phase, as indicated by the smaller enthalpy of melt crystallization (ΔH_c = 4.0 J g⁻¹) compared to the enthalpy of melting (ΔH_m = 37.6 J g⁻¹). Incomplete melt crystallization may be attributed to one of two prospective phenomena—i.e., either partial glass formation or significant decomposition of the MHP. To investigate this observation further, we conducted an iterative DSC measurement and extended it to even lower temperatures, down to −25 °C, with the expectation of possibly observing a glass transition or the cold crystallization of the partial formed glass during the subsequent heating run. However, in the subsequent runs, no signatures of glass transition or cold crystallization were observed; a decrease in T_m and ΔH_m, as well as melt crystallization temperature (T_c) and ΔH_c over three iterations (Fig. 2b) point to the partial decomposition (organic and hydrogen halide components) of the S(1-2)NPB sample during repeated heat-cool cycles.^35,37,46 We expect that S(1-2)NPB will be more susceptible to decomposition upon melting relative to S(1-1)NPB due to the higher T_m. Thermogravimetric analysis (TGA) performed on S(1-2)NPB crystals reveals a degradation onset temperature (T_d) of ∼219 °C, exceeding the T_m of ∼193 °C (Fig. 2c). However, partial decomposition cannot be precluded even at temperatures below T_d, due to the kinetic nature of the decomposition.^37,46Fig. 2d shows a TGA profile for S(1-2)NPB crystals maintained at 195 °C (slightly above T_m), confirming substantial degradation of the sample when subjected to prolonged exposure at elevated temperatures. Furthermore, ¹H nuclear magnetic resonance (NMR) measurements conducted on S(1-2)NPB samples that underwent single and multiple extended cycles of melt-quenching in ambient conditions reveal a partial loss of organic molecules (indicated by a reduction in the area under the NMR peaks associated with the H atoms, Fig. S1 and Table S2†) accompanied by a certain degree of molecular degradation (as evidenced by broadening and shifting of peak positions, Fig. S1†), when compared to the pristine S(1-2)NPB sample. The above results highlight the importance of considering sample degradation when exploring hybrid perovskite properties at temperatures near or exceeding 200 °C, as also highlighted during our recent evaluation of the glass-formation characteristics of 1-MeHa₂PbI₄.⁴⁶ The use of ultrafast calorimetry, nevertheless, largely circumvents decomposition due to the rapid measurement timescales, as discussed later in the text.

Fig. 2 Conventional differential scanning calorimetry (DSC) analysis of the S(1-2)NPB sample. (a) The heating and cooling DSC scans depict complete melting of the sample, accompanied by partial melt crystallization with distinct temperatures (T_m, T_c) and corresponding enthalpies (ΔH_m, ΔH_c). (b) Iterative heating and cooling DSC cycles reveal a decrease in temperature and enthalpies of melting and crystallization as a function of iteration. No glass formation or cold crystallization behavior is observed over an extended temperature range (lower end). (c) Thermogravimetric analysis (TGA) of the S(1-2)NPB crystals on continuous heating and (d) isothermal hold (dwell) at 195 °C (>T_m) over multiple hours. The weight change to ∼43% at elevated temperature indicates the decomposition (complete organic loss) of the sample to inorganic PbBr₂. The inset in (d) shows a magnified portion of the curve during the initial heating from 25 °C to 195 °C, just before dwelling at 195 °C for ∼22 hours.

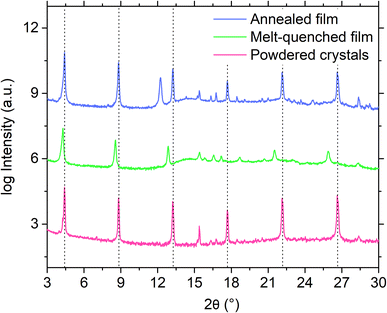
Furthermore, attempts to prepare a melt-quenched film of S(1-2)NPB using a melt pressing technique, which had previously led to complete glass formation for S(1-1)NPB¹² and offers higher cooling rates (see ESI†), did not result in complete vitrification. Instead, crystalline peaks corresponding to the (00l) family of planes were observed in the melt-quenched film (Fig. 3). Interestingly, we observe a significant shift in the 00l plane peak positions coupled with broader full width at half maximum (FWHM) values compared to those of the pristine powdered crystals, likely reflecting some disordering introduced by the quenching process. Upon annealing the film at 140 °C for 5 minutes, the diffraction peaks sharpened (Table S3†), indicating enhanced crystallinity, and the 00l plane peaks shifted back to the positions observed for the original crystals.⁴⁷ Additionally, multiple peaks corresponding to different crystallographic orientations of the film emerged in the annealed film, which match with the simulated powder pattern obtained from the single crystal X-ray diffraction (SC-XRD) data (Fig. S2†). The details of the (002) XRD peak position and the corresponding FWHM for all the curves in Fig. 3 and S2 are listed in Table S3.†

Fig. 3 Logarithmic scale XRD profiles of S(1-2)NPB powdered crystals, melt-quenched film, and annealed film. The spectra of the films are taken under an overlayer of Kapton as a part of the melt processing to avoid loss of material upon heating. The (00l) family of crystalline peaks for the powdered crystals are shown by vertical dotted black lines as a guide to the eyes. The vertical axis is only for representation of scale of magnitude, i.e., the curves are vertically offset for clarity.

Based on the above analysis, we conclude that S(1-2)NPB has a higher tendency to crystallize during the melt-quenching process relative to S(1-1)NPB, indicating that conventional laboratory-scale cooling rates are not sufficient to access a glassy state. Additionally, the higher T_m of S(1-2)NPB increases the likelihood of partial decomposition when maintained in the melt state over a prolonged duration. Earlier studies have suggested that partial decomposition, which includes the loss of organic components, aids in frustrating the reordering process during melt-quenching and facilitates glass formation compared to a pure stoichiometric melt.^14,46,48 However, glass formation upon partial decomposition during multiple heat-cool cycles (Fig. 2b) is not observed under the employed melt-quench rate of 50 °C min⁻¹, suggesting the requirement of faster cooling rate for vitrification of the S(1-2)NPB melt. As a result, an ultrafast (“flash”) calorimetry technique,^44,46 which provides ultrafast cooling (up to 4000 °C s⁻¹) and heating (up to 40 000 °C s⁻¹) rates, is employed to achieve and study vitrification in the S(1-2)NPB system. The faster heating/cooling timescales provided by the ultrafast calorimetry may also circumvent the decomposition of the MHPs at elevated temperatures, which typically occurs during conventional DSC measurements. To achieve the combined effects, ultrafast colorimetry is thus performed on a small single crystal of S(1-2)NPB (∼166 ng, as described in the ESI†).⁴⁹ Additionally, a small amount of silicone oil has been applied to cover the sample, providing protection against significant decomposition during heating and maintaining the sample at elevated temperatures.⁴⁶ Measurements conducted solely on silicone oil did not reveal any discernible features, indicating that silicone oil itself does not undergo any transitions within the temperature range of interest (Fig. S3†).

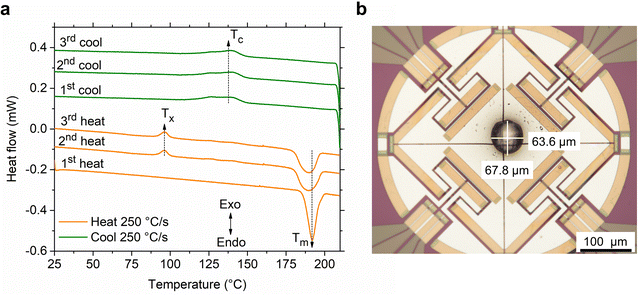
As a preliminary test, three heat-cool cycles were performed on S(1-2)NPB perovskite using the ultrafast calorimetry technique (Fig. 4a), similar to the conventional DSC measurements (Fig. 2b). In the first heating cycle, the single crystal of the material exhibits a sharp melting peak (T_m ≈ 192 °C). Upon cooling the melt at the same rate (250 °C s⁻¹), we observe a broad exothermic peak, indicating melt crystallization (T_c). The broadness of the peak derives from the kinetic nature of crystallization, as induced by employing a higher melt-cooling rate (250 °C s⁻¹) compared to the conventional DSC method (0.8 °C s⁻¹ or 50 °C min⁻¹). In the second heating cycle, the material exhibits cold crystallization (T_x), suggesting partial glass formation during the preceding cooling cycle. After complete crystallization during continued heating, the sample melts (T_m) again, but with a broader endotherm. The broadening of the melting peak could be attributed to the change in the form factor of the sample i.e., formation of a blob (Fig. 4b) leading to a change in overall thermal conductivity profile (i.e., thermal gradient) across the sample in the second heating run as opposed to a lamellar flat crystal (used in the 1^st heating cycle) with a more uniform thermal profile.⁵⁰ Nevertheless, slight decomposition of the crystal at elevated temperature cannot be precluded, which could aid in broadening of the melting peak alongside a slight reduction of T_m (Fig. 4a).⁴⁶ Upon cooling the melt, we observe a similar exothermic peak associated with partial melt crystallization, similar to the first cooling cycle with comparable enthalpy values (Table S4†). The glass formation ratio, detailed in Table S4,† reveals vitrification of ∼30% of the melt into a glassy state after melt-quenching, which crystallizes on subsequent heating. To demonstrate the consistency of the thermal features, we performed a third iteration of heating and cooling, which showed the preservation of thermal characteristics without significant changes, confirming that the sample is not undergoing significant decomposition during the subsequent cycling (Fig. 4a).

Fig. 4 (a) Three iterations of ultrafast calorimetric (flash-DSC) measurement performed on a single crystal of S(1-2)NPB. The first heating cycle (250 °C s⁻¹) shows a sharp initial melting (T_m) step. Cooling the formed melt (at the same ramp rate) results in partial glass formation and partial melt crystallization (T_c). During the second heating cycle, cold crystallization (T_x) of the partially formed glass is observed with subsequent melting (T_m) of the fully crystallized volume. A third iteration is provided to show consistency of the thermal features. The vertical axis is only for representation of scale of magnitude, i.e., the curves are vertically offset for clarity. (b) Optical microscopy image of the crystallized S(1-2)NPB sample (diameter of ∼65 µm) mounted on UFS-1 chip under silicone oil. The image was captured at the conclusion of all the measurements conducted on the sample.

After recognizing the usefulness of the flash-DSC instrument in effectively demonstrating the melting, partial glass formation, and cold crystallization of the S(1-2)NPB sample, we proceeded to conduct an iterative heating-cooling test. In this test, we varied the cooling rates (250–5000 °C s⁻¹) while maintaining the same heating rate (250 °C s⁻¹), aiming to determine the CCR required for complete glass formation. As shown in Fig. 5a, the S(1-2)NPB sample exhibits partial melt crystallization (T_c) up to cooling rates of 1000 °C s⁻¹ (as indicated in the inset for clarity). However, when cooled at rates higher than this, specifically at 2500 °C s⁻¹, the curve does not exhibit any exothermic crystallization feature. Instead, a glass transition regime is observed, characterized by a change in the baseline (due to a change in specific heat capacity) of the measured curve.^{12,42,46,51,52} Cooling at even higher rates, such as 5000 °C s⁻¹, also resulted in glass formation; however, it is accompanied by the loss of signal at temperatures below ∼50 °C due to instrument cooling rate limitations in this temperature range.⁴⁴ Upon analyzing the subsequent heating curves (Fig. 5b), we observe a clear trend toward increasing cold crystallization exothermic peak intensity and area with increased preceding cooling rate.

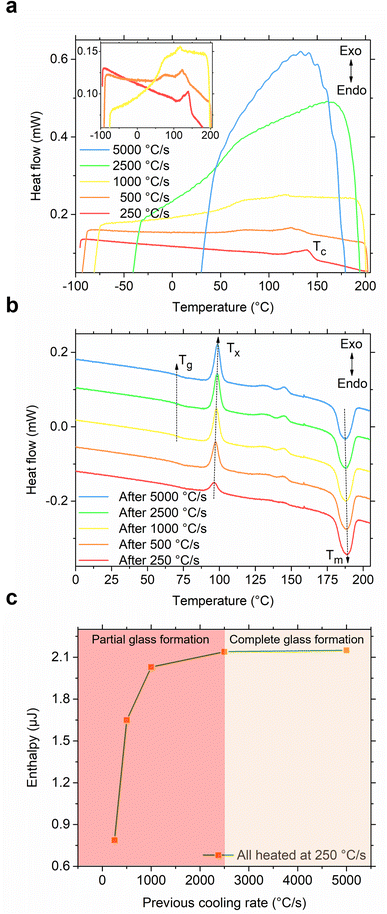Fig. 5 Determination of critical cooling rate (CCR). (a) Cooling curves of S(1-2)NPB melt obtained at various cooling rates. A partial melt crystallization peak (T_c) is observed for a cooling rate up to 1000 °C s⁻¹ (see inset). However, cooling at higher rates (such as 2500 °C s⁻¹) results only in a change of baseline (with no observed peaks in the green curve) suggesting complete glass formation. The vertical axis is only for representation of scale of magnitude, i.e., the curves are vertically offset for clarity. (b) Subsequent heating cycles, all performed at 250 °C s⁻¹, reveal a glass transition regime (T_g; refer to Fig. S4† for a close-up view). Cold crystallization (T_x) exotherms after various cooling rates (250–5000 °C s⁻¹) show an increase in cold crystallization enthalpy (ΔH_x) as the preceding cooling rate increases, which saturates after melt-quenching at 2500 °C s⁻¹ due to the complete recovery of the crystallized phase during subsequent heating. Broad features in the temperature range ∼125–150 °C could potentially result from secondary crystallization effects arising from multiple ordering processes and associated kinetics, possibly attributable to the hybrid nature of the organic–inorganic MHP when subjected to ultrafast heating.^53,54 The vertical axis is only for representation of scale of magnitude, i.e., the curves are vertically offset for clarity. (c) Enthalpy of the primary cold crystallization (area under the heat flow vs. temperature curve) during heating at 250 °C s⁻¹ after the melt quenching of S(1-2)NPB sample at various cooling rates. The glass formation ratios after melt-quenching at various cooling rates are provided in Table S5† for reference.

When comparing the cooling rates of 250 °C s⁻¹ and 2500 °C s⁻¹, it becomes evident that the larger cold crystallization peak observed during the subsequent heating cycle results from essentially complete vitrification in the latter case. On the other hand, when cooled at 250 °C s⁻¹, the sample undergoes partial melt crystallization during cooling and additional cold crystallization during subsequent heating. Fig. 5c plots the enthalpy of the primary cold crystallization as a function of the preceding melt cooling rate and points to a saturation of the crystallization enthalpy beyond 2500 °C s⁻¹, suggesting that this cooling rate serves as the approximate CCR for S(1-2)NPB. The glass formation ratio after melt-quenching at various cooling rates (250–5000 °C s⁻¹) is provided in Table S5† for reference. Furthermore, a glass transition (T_g) regime during heating (Fig. 5b) has also been observed at temperatures prior to cold crystallization (T_x). Notably, the S(1-1)NPB counterpart demonstrates a considerably lower CCR value of only 0.33 °C s⁻¹,¹² which is approximately 7500 times lower than for the S(1-2)NPB perovskite being investigated. This observation emphasizes how the diverse positions of functional groups in the organic cation can significantly influence the glass-forming kinetics across multiple orders of magnitude.

After determining the CCR, we conducted a study on the kinetics of glass-crystallization of S(1-2)NPB. The sample was repeatedly subjected to glass formation by cooling it at 2500 °C s⁻¹ and then heating at various ramp rates spanning two orders of magnitude, ranging from 50 to 5000 °C s⁻¹. All the cooling curves obtained consistently exhibit a distinct glass transition regime, with a reproducible T_g of 52.6 °C (obtained by mid-point height method,⁵⁵ Fig. S5†). The heating curves display noticeable shifts in the T_x (indicated by arrows in Fig. 6a), ranging from 87.3 °C to 154.2 °C when the heating rate is varied from 50–5000 °C s⁻¹, respectively. The T_g values are also seen to shift towards higher temperatures (Fig. S6†) on increasing the heating rate akin to what was observed in the S(1-1)NPB system.⁴² The gradual shift in T_x and T_g on increasing the heating rate is attributed to the competition between the internal molecular reorganization timescale vs. the external experimental timescale provided to the sample during the respective transition through control of heating rates. The shifts in the transition temperatures (T_x and T_g) reveal that they are predominantly governed by the underlying kinetics of molecular/atomic motions, in contrast to T_m, which is a single valued thermodynamic quantity (i.e., not significantly affected by the heating ramp rates).⁴⁶ Moreover, when comparing the initial heating cycle (50 °C s⁻¹) with the final heating cycle studied (also at 50 °C s⁻¹, obtained immediately after the kinetic analysis), the positions of the T_x and T_m remain unchanged (Fig. S7†). This observation further highlights the robustness of the measurement and indicates minimal organic and hydrogen bromide loss during heating cycles, as facilitated by the presence of silicone oil and the very short heating times.⁴⁶ For instance, in the conventional DSC experiment conducted in Fig. 2b, the sample remains above T_m (during heating, dwelling, and cooling) for about 2.1 minutes in one cycle. In contrast, during the flash-DSC measurement (Fig. 5), the sample only stays above T_m for approximately 0.1 second, leading to insignificant degradation.

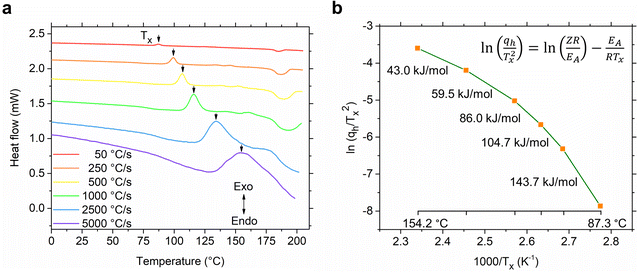Fig. 6 Kinetics of glass crystallization. (a) Heating curves of S(1-2)NPB obtained at different ramp rates after the glass formation step (melt quenching at CCR, see Fig. S5†). The shift in the cold crystallization peak (T_x, shown by arrow) with increasing heating rate suggests the kinetic nature of glass-crystallization behavior. The vertical axis is only for representation of scale of magnitude, i.e., the curves are vertically offset for clarity. (b) The shifts in T_x values are used in constructing a Kissinger plot to determine the activation energy of glass crystallization (E_A, slope of the curve). The slope of the plot shows a large deviation from a linear trend over the course of change in heating ramp rates (50–5000 °C s⁻¹), revealing breakdown of Arrhenius behavior.

The observed notable shifts in the T_x values across various heating rates can be utilized to determine the activation energy of the glass-crystallization process for S(1-2)NPB by employing the well-established model proposed by Kissinger.^56,57 The Kissinger model extends the principles of Arrhenius and first-order reaction rate equations to non-isothermal conditions and allows for the determination of the activation energy (E_A) associated with the glass-crystallization process by considering the change in the peak position of the cold crystallization exotherm (T_x) as a function of the heating rate (q_h).^56,57 This model offers a straightforward approach to extract the activation energy (E_A) using eqn (i):

where R is the gas constant and Z is a pre-exponential factor from the Arrhenius equation.

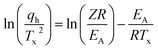In conventional DSC measurements, the range of q_h is limited, resulting in a Kissinger plot that typically appears as a straight line and thereby providing a single E_A value.^31,42 Our previous work on crystallization kinetics of S(1-1)NPB shows this behavior—i.e., the Kissinger plot displayed a linear relationship with a single activation energy of approximately 365 kJ mol⁻¹ centered at around 110 °C.⁴² However, in cases where a wider range of heating rates is employed (as in flash-DSC measurements), the plot may exhibit nonlinearity, indicating a departure from Arrhenius behavior.³¹ The Kissinger plot for S(1-2)NPB exhibits such behavior (Fig. 6b), where the obtained slope shows a curvature, resulting in a decrease in E_A with increasing temperature (143.7 to 43.0 kJ mol⁻¹ with increasing temperature from 87.3 to 154.2 °C). This behavior is not uncommon and has previously been observed in many glass-forming chalcogenide materials.^31,58–62 Comparing activation energy of glass crystallization across different glass-forming families, including organic, inorganic, hybrid, and metallic glasses, might not be meaningful due to their distinct characteristic temperatures (T_g and T_x). However, meaningful comparisons can be made within a specific glass-forming family, such as MHPs under similar energy landscapes. For instance, comparing S(1-1)NPB and S(1-2)NPB at ∼110 °C (similar energy landscape) reveals a significant difference. S(1-1)NPB has an activation energy of 365 kJ mol⁻¹ for glass-crystal transformation, while S(1-2)NPB exhibits a much lower activation energy of approximately 86 kJ mol⁻¹. The lower activation energy in S(1-2)NPB indicates a faster reorganization timescale of the glass, i.e., a higher propensity for crystallization compared to the S(1-1)NPB counterpart. However, it is crucial to note that the lower E_A value of glass-crystallization in S(1-2)NPB serves only as a necessary condition for explaining higher CCR (Table 1), and the authors are not aware of any direct mathematical relationship that exists between them.

Table 1 Comparison of thermal and glass forming/crystallization characteristics of S(1-1)NPB and S(1-2)NPB. The thermal and glass forming characteristics of S(1-1)NPB are taken from our previous works^12,42

	S(1-1)NPB	S(1-2)NPB
T m	175.0 °C	193.4 °C
ΔHm	43.2 J g^−1	37.6 J g^−1
ΔSm	96.5 mJ g^−1 K^−1	80.6 mJ g^−1 K^−1
CCR	0.3 °C s^−1	2500 °C s^−1
E A (at 110 °C)	∼365 kJ mol^−1	∼86 kJ mol^−1

---

In the case of S(1-2)NPB, the process of glass formation does not necessitate significant removal of organic and hydrogen halide components, contrasting with the recently described case for 1-methylhexylammonium lead iodide (1-MeHa₂PbI₄) perovskite comprising flexible aliphatic organic cations, which requires ∼15% mass loss to achieve vitrification under the cooling rates supported by flash-DSC.⁴⁶ Given that flash-DSC employs an ∼100 ng-scale single crystal for the measurement, the effect of particle size on the crystallization kinetics of the S(1-2)NPB glass could not readily be examined in the current study. However, there is no evidence from the current flash-DSC data pointing toward distinction between nucleation and growth processes, rather yielding a convoluted feature (Fig. 6a) similar to what was previously observed in S(1-1)NPB using conventional DSC.⁴²

Table 1 lists the thermal and kinetic parameters for both glass-forming MHP systems considered in the current study. The high T_m of S(1-2)NPB ∼193 °C relative to S(1-1)NPB ∼175 °C has been recently reported by Moon et al. and attributed to the distinct organic–inorganic H-bonding interactions in the two MHPs.⁴³ Specifically, the different configurations of S(1-1)NEA and S(1-2)NEA cations impact the relative positioning of the ammonium groups in relation to the halogen atoms in the inorganic sub-lattice and the associated organic–inorganic H-bonding interactions, resulting in deeper penetration of the ammonium groups and enhanced strength and asymmetry of H-bonding in S(1-2)NPB.⁴³ Based on our independent SC-XRD structural investigation, average penetrations of the ammonium groups (measured as the distances of the N atoms from the plane of axial Br atoms) of 0.26 Å for S(1-2)NPB and 0.17 Å for S(1-1)NPB (Table S6†) are determined, which supports and validates the results reported by Moon et al.⁴³ Acknowledging that the precise measurement of H atom positions is limited when using SC-XRD, where approximations rely on the positions of heavier N and C atoms,⁶³ we have devised a supplementary methodology that quantitatively compiles and contrasts the positioning of N atoms in relation to the inorganic lattice, which serves as a means to assess the strength of organic–inorganic H-bonding. Both S(1-1)NEA and S(1-2)NEA cations predominantly adopt two types of orientations (cation A and B) in the unit cells (Fig. 7). We find overall shorter N–Pb/Br distances for cation B in S(1-2)NPB relative to S(1-1)NPB (Fig. S8†), suggesting that S(1-2)NEA cation B is positioned in closer proximity to the inorganic lattice and therefore potentially exhibits stronger H-bonding. The analysis details are reported in ESI Section S1 in the ESI.† If H atom positions and associated H-bonding interactions are considered for independent cations A and B (Table S9 and Fig. S9†), as quantified by the H-bond lengths and angles, the values for S(1-2)NPB cation A do not show a clear distinction in relative strength compared to S(1-1)NEA cation A. In contrast, S(1-2)NEA cation B exhibits stronger H-bonding, as indicated by shorter bond lengths and larger bond angles compared to S(1-1)NEA cation B, suggesting an enhanced H-bonding strength in S(1-2)NPB (Table S9†) and perhaps contributing to a higher T_m. The combined N–Pb/Br distances and H-bonding analysis and resultant consistent evaluation results from SC-XRD provide a convincing methodology to evaluate relative H-bonding strength between the two systems (see ESI Section S1 in the ESI† for more details).

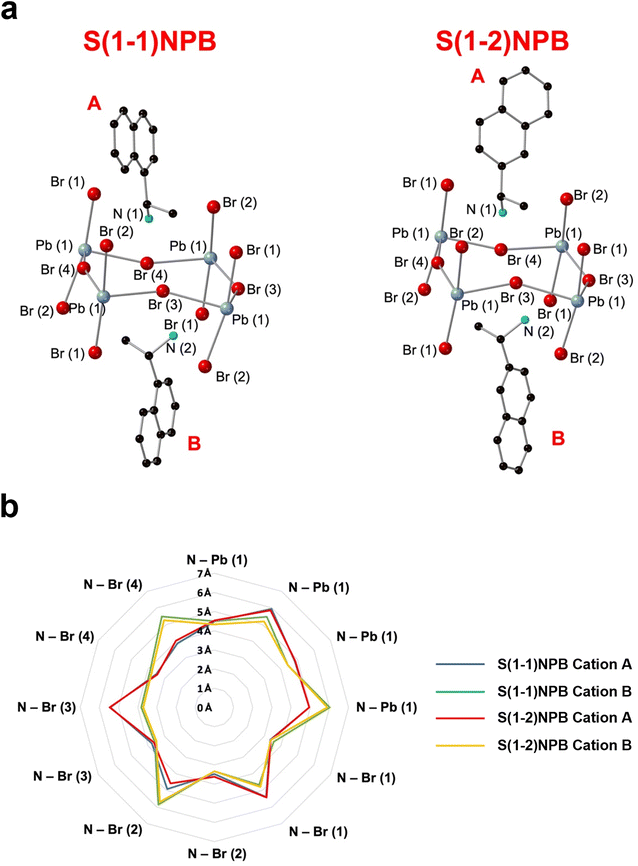Fig. 7 (a) Schematic of cation A and B in S(1-1)NPB and S(1-2)NPB for calculation of N–Pb/Br distances (Tables S7 and S8†). Blue, red, black, and turquoise spheres denote Pb, Br, C, and N atoms, respectively. The obtained data for S(1-1)NPB is derived from our previously published work.⁴⁵ (b) Radar chart of the N–Pb/Br distances of type A and B cations in S(1-1)NPB and S(1-2)NPB. Blue and green lines denote the cation A and B of S(1-1)NPB, respectively. Red and yellow lines indicate the cation A and B of S(1-2)NPB, respectively.

While strong cohesive forces (organic–inorganic H-bonding in the case of MHPs) in the crystalline state are conventionally considered an indicator of higher T_m, this characteristic temperature is influenced by both the enthalpy and entropy contributions surrounding the melting phenomenon. At equilibrium, T_m is defined by the ratio of enthalpy of melting/fusion to the corresponding change in entropy i.e., ΔH_m/ΔS_m.⁶⁴ When comparing S(1-1)NPB (T_m = 175 °C, ΔH_m = 43.2 J g⁻¹) with its racemic counterpart i.e., rac(1-1)NPB (T_m = 221 °C, ΔH_m = 71.0 J g⁻¹),¹² for example, ΔH_m qualitatively scales with T_m, suggesting a predominantly enthalpy driven melting transition, a perhaps trivial occurrence related to enthalpy–entropy compensation as typically observed in many homologous organic systems.^65,66 However, S(1-2)NPB exhibits a higher T_m compared to S(1-1)NPB, although the measured ΔH_m for S(1-2)NPB is smaller, at 37.6 J g⁻¹, than the value of 43.2 J g⁻¹ for S(1-1)NPB (Table 1; possibly attributable to different coordination in the melt states of the two systems)⁶⁷ indicating that the driving force behind the higher T_m in S(1-2)NPB likely extends beyond the strength of cohesive forces in the crystalline state to the entropic contribution during the melting transition.^67,68 The higher computed ΔS_m = 96.5 mJ g⁻¹ K⁻¹ of S(1-1)NPB relative to ΔS_m = 80.6 for S(1-2)NPB (Table 1) therefore presumably (at least in part) underlies the lower T_m.^69–71 A more quantitative analysis of the various modes of entropy in the molten states and the local ordering in the melt state is therefore needed to better clarify this point, which is a subject of future interest. Nevertheless, examination of the free organic amines in the MHP structure reinforces the above observation; molecular S(1-1)NEA is a liquid at room temperature and exhibits a relatively high boiling point of 152 °C,⁷² whereas the amine S(1-2)NEA only melts above 53 °C but shows a lower boiling point of 143 °C.⁷³ The disparate trend in characteristic temperatures indicates a stronger cohesive force in molecular S(1-1)NEA, resulting in a higher boiling point, but a lower T_m due to higher ΔS_m. A similar trend in T_m is recorded in molecular organics containing naphthalene with methyl substitution at the first (−30 °C) and second (34 °C) carbon positions.⁷⁰

Hence, while many physical properties such as boiling point, heat of vaporization, density, and refractive indexes can be defined through change in cohesive forces, the melting behavior is dictated by the combined contributions of both the cohesive forces and the corresponding entropy change,⁷⁰ thus providing an added flexibility when selecting organic cations before synthesizing a hybrid perovskite with predictable trend in melting behavior. Moreover, a higher T_m of S(1-2)NPB may induce faster crystallization kinetics during cooling due to elevated internal thermal energy of the system, which increases the probability of overcoming the nucleation energy barrier during melt-quenching,^67,74 and contributes to an increased CCR required to obtain a glassy state. On the other hand, S(1-1)NPB resists crystallization, partially because of the lower T_m, and also perhaps due to the higher ΔS_m (presumably indicative of a greater number of orientations in the melt state), which reduces the overall probability for molecules to attain the precise (and singular) orientation necessary to facilitate crystallization.^24,75

Conclusion

In summary, we demonstrate that the two isomeric cations of S(1-1)NPB and S(1-2)NPB lead to distinct melting, glass formation and glass-crystallization kinetics. While glass formation can be achieved under conventional calorimetry timescales in S(1-1)NPB, with a CCR of ∼0.3 °C s⁻¹, vitrification in S(1-2)NPB mandates the application of ultrafast calorimetry, resulting in a CCR of as high as 2500 °C s⁻¹. Kissinger kinetic modeling points to a significantly higher crystallization activation energy (E_A) of ∼365 kJ mol⁻¹ for S(1-1)NPB compared to ∼86 kJ mol⁻¹ for S(1-2)NPB under similar energy landscape, consistent with the faster reorganization timescales in the latter. Such distinct thermal properties illustrate the notable impact of structure-directing characteristics of organic cations on the glass-forming kinetics of the resulting MHPs. The influence of structural and thermodynamic attributes on disparate glass-forming and crystallization kinetics is also examined using a combined analysis of the organic–inorganic H-bonding interactions in the crystalline state and enthalpy/entropy balance around the melting transition, both highlighting the enhanced organic–inorganic H-bonding strength and likely reduced melt entropy in S(1-2)NPB as the underlying reasons for increased T_m and faster crystallization kinetics compared to S(1-1)NPB. The approach of cation isomer-induced structural modification serves as an important material design strategy, showing the potential for modulating the glass-forming kinetics in 2D perovskites across multiple orders of magnitude and further benefiting the prospects for emerging applications. The current study also highlights the importance of considering loss/degradation of the organic and hydrogen halide components of the hybrid at elevated temperatures, especially for hybrids like S(1-2)NPB that melt at temperatures approaching and/or exceeding 200 °C, and point to the need to minimize time in this elevated temperature range during such studies (e.g., as for flash-DSC) or for prospective applications. Variations in optoelectronic properties are anticipated between the newly reported glassy and crystalline states of S(1-2)NPB, similar to experimental observations in S(1-1)NPB, such as a 50 nm blue shift in optical absorbance¹² and a two-order reduction in electrical conductivity⁷⁶ in the glassy state compared to the crystalline state for S(1-1)NPB. However, given the exceedingly high CCR necessary for vitrifying S(1-2)NPB, optoelectronic investigations were not conducted as part of the current study, thus remaining a subject of future interest.

Data availability

The X-ray crystallographic data for this paper, namely for the compound S-1-2-NPB, has been deposited in The Cambridge Crystallographic Data Center (CCDC) database under deposition number 2342431. These data can be obtained free of charge viahttps://www.ccdc.cam.ac.uk/structures/ and also from the Hybrid³ perovskite database viahttps://materials.hybrid3.duke.edu/materials/search using the search terms: “S-1-2-NPB”.

Author contributions

A. S. and D. B. M. conceptualized the study. C. A. and Y. X. carried out the crystal synthesis. Y. X. conducted single crystal diffraction experiments and corresponding structural analysis. A. S. conducted thin-film melt deposition, NMR sample preparation, X-ray diffraction, conventional DSC, flash-DSC, enthalpy/entropy balance, and analysis of the respective data along with the numerical modelling of the crystallization kinetics. B. G. B. and Y. X. conducted NMR measurements and analysis. All the authors contributed to the discussion and helped edit the manuscript into its final form.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Science Foundation under Grant No. DMR-2114117.

References

1. B. Saparov and D. B. Mitzi, Organic–inorganic perovskites: structural versatility for functional materials design, Chem. Rev., 2016, 116, 4558–4596.
2. D. B. Mitzi, Synthesis, structure, and properties of organic‐inorganic perovskites and related materials, Prog. Inorg. Chem., 1999, 48, 1–121.
3. D. B. Mitzi, K. Chondroudis and C. R. Kagan, Organic-inorganic electronics, IBM J. Res. Dev., 2001, 45, 29–45.
4. H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim and M. G. Kim, Perovskite solar cells with atomically coherent interlayers on SnO₂ electrodes, Nature, 2021, 598, 444–450.
5. Best Research-Cell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html, accessed November 2023.
6. A. K. Jena, A. Kulkarni and T. Miyasaka, Halide perovskite photovoltaics: background, status, and future prospects, Chem. Rev., 2019, 119, 3036–3103.
7. J. Jiang, Z. Chu, Z. Yin, J. Li, Y. Yang, J. Chen, J. Wu, J. You and X. Zhang, Red Perovskite Light‐Emitting Diodes with Efficiency Exceeding 25% Realized by Co‐Spacer Cations, Adv. Mater., 2022, 34, 2204460.
8. D. Yang, B. Zhao, T. Yang, R. Lai, D. Lan, R. H. Friend and D. Di, Toward Stable and Efficient Perovskite Light‐Emitting Diodes, Adv. Funct. Mater., 2022, 32, 2109495.
9. G. Li, Y. Wang, L. Huang and W. Sun, Research progress of high-sensitivity perovskite photodetectors: a review of photodetectors: noise, structure, and materials, ACS Appl. Electron. Mater., 2022, 4, 1485–1505.
10. K. Sakhatskyi, B. Turedi, G. J. Matt, E. Wu, A. Sakhatska, V. Bartosh, M. N. Lintangpradipto, R. Naphade, I. Shorubalko, O. F. Mohammed, S. Yakunin, O. M. Bakr and M. V. Kovalenko, Stable perovskite single-crystal X-ray imaging detectors with single-photon sensitivity, Nat. Photonics, 2023, 17, 510–517.
11. F. Liu, R. Wu, J. Wei, W. Nie, A. D. Mohite, S. Brovelli, L. Manna and H. Li, Recent progress in halide perovskite radiation detectors for gamma-ray spectroscopy, ACS Energy Lett., 2022, 7, 1066–1085.
12. A. Singh, M. K. Jana and D. B. Mitzi, Reversible crystal–glass transition in a metal halide perovskite, Adv. Mater., 2021, 33, 2005868.
13. A. Singh, M. Jana and D. B. Mitzi, US Pat., 11825728, 2023.
14. B. K. Shaw, A. R. Hughes, M. Ducamp, S. Moss, A. Debnath, A. F. Sapnik, M. F. Thorne, L. N. McHugh, A. Pugliese, D. S. Keeble, P. Chater, J. M. B. Garcia, X. Moya, S. K. Saha, D. A. Keen, F.-X. Coudert, F. Blanc and T. D. Bennett, Melting of hybrid organic–inorganic perovskites, Nat. Chem., 2021, 13, 778–785.
15. C. Ye, L. N. McHugh, C. Chen, S. E. Dutton and T. D. Bennett, Glass Formation in Hybrid Organic‐Inorganic Perovskites, Angew. Chem., Int. Ed., 2023, 135, e202302406.
16. K. Tanaka, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer, S. Mahajan and P. Veyssière, Elsevier, Oxford, 2001, pp. 1123–1131,  DOI:10.1016/B0-08-043152-6/00210-2.
17. M. Wuttig and N. Yamada, Phase-change materials for rewriteable data storage, Nat. Mater., 2007, 6, 824–832.
18. W. Zhang, R. Mazzarello, M. Wuttig and E. Ma, Designing crystallization in phase-change materials for universal memory and neuro-inspired computing, Nat. Rev. Mater., 2019, 4, 150–168.
19. D. Ielmini and H.-S. P. Wong, In-memory computing with resistive switching devices, Nat. Electron., 2018, 1, 333–343.
20. Q. Wang, E. T. Rogers, B. Gholipour, C.-M. Wang, G. Yuan, J. Teng and N. I. Zheludev, Optically reconfigurable metasurfaces and photonic devices based on phase change materials, Nat. Photonics, 2016, 10, 60–65.
21. M. Wuttig, H. Bhaskaran and T. Taubner, Phase-change materials for non-volatile photonic applications, Nat. Photonics, 2017, 11, 465–476.
22. C. A. Angell, Formation of glasses from liquids and biopolymers, Science, 1995, 267, 1924–1935.
23. E. D. Zanotto and D. R. Cassar, The microscopic origin of the extreme glass-forming ability of Albite and B₂O₃, Sci. Rep., 2017, 7, 43022.
24. J. T. Dull, Y. Wang, H. Johnson, K. Shayegan, E. Shapiro, R. D. Priestley, Y. H. Geerts and B. P. Rand, Thermal Properties, Molecular Structure, and Thin-Film Organic Semiconductor Crystallization, J. Phys. Chem. C, 2020, 124, 27213–27221.
25. U. Ali, K. J. B. A. Karim and N. A. Buang, A review of the properties and applications of poly(methyl methacrylate) (PMMA), Polym. Rev., 2015, 55, 678–705.
26. A. Qiao, T. D. Bennett, H. Tao, A. Krajnc, G. Mali, C. M. Doherty, A. W. Thornton, J. C. Mauro, G. N. Greaves and Y. Yue, A metal–organic framework with ultrahigh glass-forming ability, Sci. Adv., 2018, 4, eaao6827.
27. J. Ballato, H. Ebendorff-Heidepriem, J. Zhao, L. Petit and J. Troles, Glass and process development for the next generation of optical fibers: a review, Fibers, 2017, 5, 11.
28. L. Frentzel-Beyme, P. Kolodzeiski, J.-B. Weiß, A. Schneemann and S. Henke, Quantification of gas-accessible microporosity in metal-organic framework glasses, Nat. Commun., 2022, 13, 7750.
29. D. Lilley, A. K. Menon, S. Kaur, S. Lubner and R. S. Prasher, Phase change materials for thermal energy storage: a perspective on linking phonon physics to performance, J. Appl. Phys., 2021, 130, 220903.
30. R. D. McGillicuddy, S. Thapa, M. B. Wenny, M. I. Gonzalez and J. A. Mason, Metal–organic phase-change materials for thermal energy storage, J. Am. Chem. Soc., 2020, 142, 19170–19180.
31. J. Orava, A. á. Greer, B. Gholipour, D. Hewak and C. Smith, Characterization of supercooled liquid Ge₂Sb₂Te₅ and its crystallization by ultrafast-heating calorimetry, Nat. Mater., 2012, 11, 279–283.
32. M. Salinga, B. Kersting, I. Ronneberger, V. P. Jonnalagadda, X. T. Vu, M. Le Gallo, I. Giannopoulos, O. Cojocaru-Mirédin, R. Mazzarello and A. Sebastian, Monatomic phase change memory, Nat. Mater., 2018, 17, 681–685.
33. L. Mao, C. C. Stoumpos and M. G. Kanatzidis, Two-dimensional hybrid halide perovskites: principles and promises, J. Am. Chem. Soc., 2018, 141, 1171–1190.
34. T. Li, W. A. Dunlap-Shohl, E. W. Reinheimer, P. Le Magueres and D. B. Mitzi, Melting temperature suppression of layered hybrid lead halide perovskites via organic ammonium cation branching, Chem. Sci., 2019, 10, 1168–1175.
35. D. B. Mitzi, Synthesis, crystal structure, and optical and thermal properties of (C₄H₉NH₃)₂MI₄ (M = Ge, Sn, Pb), Chem. Mater., 1996, 8, 791–800.
36. M. B. H. Salah, N. Mercier, S. Dabos‐Seignon and C. Botta, Solvent‐Free Preparation and Moderate Congruent Melting Temperature of Layered Lead Iodide Perovskites for Thin‐Film Formation, Angew. Chem., Int. Ed., 2022, 134, e202206665.
37. A. Singh, E. Crace, Y. Xie and D. B. Mitzi, Two-dimensional lead-free hybrid perovskite semiconductor with reduced melting temperature, Chem. Commun., 2023, 59, 8302–8305.
38. F. Hleli, N. Mercier, M. Ben Haj Salah, M. Allain, N. Zouari, F. Massuyeau and R. Gautier, Chemistry in the Molten State: Opportunities for Designing and Tuning the Emission Properties of Halide Perovskites, Inorg. Chem., 2023, 62, 14252–14260.
39. D. B. Mitzi, C. D. Dimitrakopoulos, J. Rosner, D. R. Medeiros, Z. Xu and C. Noyan, Hybrid field‐effect transistor based on a low‐temperature melt‐processed channel layer, Adv. Mater., 2002, 14, 1772–1776.
40. D. B. Mitzi, D. R. Medeiros and P. W. DeHaven, Low-Temperature Melt Processing of Organic–Inorganic Hybrid Films, Chem. Mater., 2002, 14, 2839–2841.
41. E. J. Crace, A. Singh, S. Haley, B. Claes and D. B. Mitzi, Meltable Hybrid Antimony and Bismuth Iodide One-Dimensional Perovskites, Inorg. Chem., 2023, 62, 16161–16169.
42. A. Singh and D. B. Mitzi, Crystallization Kinetics in a Glass-Forming Hybrid Metal Halide Perovskite, ACS Mater. Lett., 2022, 4, 1840–1847.
43. J. Son, S. Ma, Y.-K. Jung, J. Tan, G. Jang, H. Lee, C. U. Lee, J. Lee, S. Moon, W. Jeong, A. Walsh and J. Moon, Unraveling chirality transfer mechanism by structural isomer-derived hydrogen bonding interaction in 2D chiral perovskite, Nat. Commun., 2023, 14, 3124.
44. V. Mathot, M. Pyda, T. Pijpers, G. V. Poel, E. Van de Kerkhof, S. Van Herwaarden, F. Van Herwaarden and A. Leenaers, The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): first findings on polymers, Thermochim. Acta, 2011, 522, 36–45.
45. M. K. Jana, R. Song, H. Liu, D. R. Khanal, S. M. Janke, R. Zhao, C. Liu, Z. V. Vardeny, V. Blum and D. B. Mitzi, Organic-to-inorganic structural chirality transfer in a 2D hybrid perovskite and impact on Rashba-Dresselhaus spin-orbit coupling, Nat. Commun., 2020, 11, 4699.
46. A. Singh, Y. Kim, R. Henry, H. Ade and D. B. Mitzi, Study of Glass Formation and Crystallization Kinetics in a 2D Metal Halide Perovskite Using Ultrafast Calorimetry, J. Am. Chem. Soc., 2023, 145, 18623–18633.
47. Introduction to X-Ray Powder Diffraction Data Analysis, http://prism.mit.edu/xray/documents/2%20Introduction%20to%20XRPD%20Data%20Analysis.pdf, accessed November 2023.
48. B. K. Shaw, C. Castillo-Blas, M. F. Thorne, M. L. R. Gómez, T. Forrest, M. D. Lopez, P. A. Chater, L. N. McHugh, D. A. Keen and T. D. Bennett, Principles of melting in hybrid organic–inorganic perovskite and polymorphic ABX 3 structures, Chem. Sci., 2022, 13, 2033–2042.
49. J. Schawe, Practical aspects of the flash DSC 1: sample preparation for measurements of polymers, https://www.mt.com/us/en/home/supportive_content/matchar_apps/MatChar_UC364.html, accessed November 2023.
50. J. Seo, R. D. McGillicuddy, A. H. Slavney, S. Zhang, R. Ukani, A. A. Yakovenko, S.-L. Zheng and J. A. Mason, Colossal barocaloric effects with ultralow hysteresis in two-dimensional metal–halide perovskites, Nat. Commun., 2022, 13, 2536.
51. B. Wunderlich, Study of the change in specific heat of monomeric and polymeric glasses during the glass transition, J. Phys. Chem., 1960, 64, 1052–1056.
52. E. Parodi, L. E. Govaert and G. W. M. Peters, Glass transition temperature versus structure of polyamide 6: a flash-DSC study, Thermochim. Acta, 2017, 657, 110–122.
53. Y. Xie, R. Song, A. Singh, M. K. Jana, V. Blum and D. B. Mitzi, Kinetically Controlled Structural Transitions in Layered Halide-Based Perovskites: An Approach to Modulate Spin Splitting, J. Am. Chem. Soc., 2022, 144, 15223–15235.
54. J. E. Schawe and J. E. Schawe, AIP Conference Proceedings, AIP Publishing LLC, 2016, vol. 1713, p. 070001,  DOI:10.1063/1.4942287, accessed November 2023.
55. Evaluation Possibilities for the Glass Transition, https://www.mt.com/us/en/home/supportive_content/matchar_apps/MatChar_HB401.html, accessed November 2023.
56. R. L. Blaine and H. E. Kissinger, Homer Kissinger and the Kissinger equation, Thermochim. Acta, 2012, 540, 1–6.
57. H. E. Kissinger, Variation of peak temperature with heating rate in differential thermal analysis, J. Res. Natl. Bur. Stand. (U. S.), 1956, 57, 217–221.
58. B. Chen, G. H. Ten Brink, G. Palasantzas and B. J. Kooi, Crystallization kinetics of GeSbTe phase-change nanoparticles resolved by ultrafast calorimetry, J. Phys. Chem. C, 2017, 121, 8569–8578.
59. B. Chen, J. Momand, P. A. Vermeulen and B. J. Kooi, Crystallization kinetics of supercooled liquid Ge–Sb based on ultrafast calorimetry, Cryst. Growth Des., 2016, 16, 242–248.
60. B. Chen, D. de Wal, G. H. Ten Brink, G. Palasantzas and B. J. Kooi, Resolving crystallization kinetics of GeTe phase-change nanoparticles by ultrafast calorimetry, Cryst. Growth Des., 2018, 18, 1041–1046.
61. Y. Chen, G. Wang, L. Song, X. Shen, J. Wang, J. Huo, R. Wang, T. Xu, S. Dai and Q. Nie, Unraveling the crystallization kinetics of supercooled liquid GeTe by ultrafast calorimetry, Cryst. Growth Des., 2017, 17, 3687–3693.
62. Y. Chen, R. Wang, X. Shen, J. Wang and T. Xu, New methods versus old questions: crystallization kinetics of S, Se, and Te, Cryst. Growth Des., 2019, 19, 1103–1110.
63. P. Muller, R. Herbst-Irmer, A. Spek, T. Schneider and M. Sawaya, Crystal Structure Refinement: A Crystallographer's Guide to SHELXL, OUP Oxford, 2006.
64. R. Conradt, Thermodynamics and Kinetics of Glass, in Springer Handbook of Glass, ed. Musgraves J. D., Hu J. and Calvez L., Springer Handbooks. Springer, Cham, 2019, pp. 51–77.
65. D. H. Williams, D. P. O'Brien and B. Bardsley, Enthalpy/entropy compensation as a competition between dynamics and bonding: the relevance to melting of crystals and biological aggregates, J. Am. Chem. Soc., 2001, 123, 737–738.
66. L. Ventola, T. Calvet, M. Cuevas-Diarte, M. Ramirez, H. Oonk, D. Mondieig and P. Negrier, Melting behaviour in the n-alkanol family. Enthalpy–entropy compensation, Phys. Chem. Chem. Phys., 2004, 6, 1786–1791.
67. M. Liu, R. D. McGillicuddy, H. Vuong, S. Tao, A. H. Slavney, M. I. Gonzalez, S. J. Billinge and J. A. Mason, Network-Forming Liquids from Metal–Bis (acetamide) Frameworks with Low Melting Temperatures, J. Am. Chem. Soc., 2021, 143, 2801–2811.
68. M. Liu, A. H. Slavney, S. Tao, R. D. McGillicuddy, C. C. Lee, M. B. Wenny, S. J. Billinge and J. A. Mason, Designing Glass and Crystalline Phases of Metal–Bis (acetamide) Networks to Promote High Optical Contrast, J. Am. Chem. Soc., 2022, 144, 22262–22271.
69. R.-M. Dannenfelser and S. H. Yalkowsky, Estimation of entropy of melting from molecular structure: a non-group contribution method, Ind. Eng. Chem. Res., 1996, 35, 1483–1486.
70. J. Wei, Molecular symmetry, rotational entropy, and elevated melting points, Ind. Eng. Chem. Res., 1999, 38, 5019–5027.
71. R. Brown and R. Brown, Melting point and molecular symmetry, J. Chem. Educ., 2000, 77, 724.
72. Chemical detail, https://www.fishersci.com/shop/products/s-1-1-naphthyl-ethylamine-99-thermo-scientific/AAA1717603, accessed November 2023.
73. Chemical detail, https://www.fishersci.com/shop/products/s-1-2-naphthyl-ethylamine-tci-america-2/N07261G, accessed November 2023.
74. N. Ma and S. Horike, Metal–organic network-forming glasses, Chem. Rev., 2022, 122, 4163–4203.
75. L. Yu, S. M. Reutzel-Edens and C. A. Mitchell, Crystallization and polymorphism of conformationally flexible molecules: problems, patterns, and strategies, Org. Proc. Res. Dev., 2000, 4, 396–402.
76. Y. Zhao, J. Zhao, Y. Guo, J. Zhao, J. Feng, Y. Geng, J. Yang, H. Gao, M. Yuan and L. Jiang, Reversible phase transition for switchable second harmonic generation in 2D perovskite microwires, SmartMat, 2022, 3, 657–667.

---

Footnotes

† Electronic supplementary information (ESI) available: Methods; structural refinement data for S(1-2)NPB; summary of integration of NMR peaks for pristine and melt-processed S(1-2)NPB crystals; FWHM values calculated from XRD pattern of crystalline powder, melt-quenched and annealed films; glass formation ratio during preliminary testing of vitrification for S(1-2)NPB melt at a cooling rate of 250 °C s⁻¹; glass formation ratio for S(1-2)NPB vitrification at various cooling rates (250–5000 °C s⁻¹); ¹H NMR spectra of the pristine and melt-quenched S(1-2)NPB crystals; simulated vs. experimental XRD pattern for S(1-2)NPB; flash-DSC heating and cooling curves of silicone oil; glass transition regime on heating for S(1-2)NPB; glass transition regime on cooling for S(1-2)NPB; glass transition regime on heating at various ramp rates for S(1-2)NPB; reproducibility test of the kinetic study for S(1-2)NPB; supplementary Section S1: organic–inorganic H-bonding analysis; ammonium group penetration into the inorganic sub-lattice; calculated difference in N–Pb/Br distances of cation A and B for S(1-1)NPB and S(1-2)NPB; organic to inorganic distances for S(1-1)NPB; organic to inorganic distances for S(1-2)NPB; hydrogen bonding interactions for S(1-1)NPB vs. S(1-2)NPB with distinct cation orientations; hydrogen bonding distances and angles for S(1-1)NPB vs. S(1-2)NPB. See DOI: https://doi.org/10.1039/d3sc06461a

‡ These authors contributed equally to this work.

---