Open Access Article
Open Access ArticleLessons learnt in photocatalysis – the influence of solvent polarity and the photostability of the photocatalyst†
Megan Amy
Bryden
a,
Francis
Millward
a,
Oliver S.
Lee
 a,
Lauren
Cork
a,
Malte C.
Gather
a,
Lauren
Cork
a,
Malte C.
Gather
 b,
Andreas
Steffen
b,
Andreas
Steffen
 c and
Eli
Zysman-Colman
c and
Eli
Zysman-Colman
 *a
*a
aOrganic Semiconductor Centre, EaStCHEM School of Chemistry, University of St Andrews, Fife, St Andrews, KY16 9ST, UK. E-mail: eli.zysman-colman@st-andrews.ac.uk; Web: https://www.zysman-colman.com Fax: +44 (0)1334 463808; Tel: +44 (0)1334 463826
bDepartment of Chemistry, Humboldt Centre for Nano- and Biophotonics, University of Cologne, Greinstr. 4-6, 50939, Cologne, Germany
cFakultät für Chemie und Chemische Biologie, Anorganische Chemie, Technische Universität Dortumund, Otto-Hahn-Str., 644227, Dortmund, Germany
First published on 8th February 2024
Abstract
Herein, we show that there is significant variation in both the triplet energies and redox properties of photocatalysts as a function of solvent based on a study of eight PCs in four solvents of varying polarity. A range of photocatalytic electron and energy transfer reactions were investigated using a subset of the PCs. For the photoredox reactions, the yields are not correlated with solvent polarity. Instead, when the PC could promote the formation of the target product, we observed photodegradation for all PCs across all solvents, something that is rarely investigated in the literature. This, therefore, makes it difficult to ascertain whether the parent PC and/or the photodegraded product is responsible for the photochemistry, or indeed, whether photodegradation is actually detrimental to the reaction yield. Conversely, the PCs were found to be photostable for energy transfer reactions; however, yields were not correlated to the triplet energies of the PCs, highlighting that triplet energies alone are not a suitable descriptor to discriminate the performance between PCs in photoinduced energy transfer processes.
Introduction
Homogeneous photocatalysis has cemented itself over the last 15 years as a fruitful strategy for the synthesis of organic compounds, including those of relevance to the pharmaceutical and agrochemical industries, allowing access to a wide range of reactivities that would otherwise be thermally inaccessible.1–4 During this renaissance of photocatalysis, enormous progress has been made in both reaction and photocatalyst (PC) development. However, a broad overview of the use of organic PCs5 has revealed that the photophysical and electrochemical parameters are frequently taken from the prior art, which are obtained in conditions distinct from those used in the reaction. Thus, the effect of the medium is not considered when assessing the thermodynamic driving force for the required photochemistry. An accurate account of the optoelectronic properties of the PC in the same media used in the photocatalysis is needed to obtain an informed insight into to mechanism of the photocatalysis.Photocatalysis reactions generally proceed through one of two distinct pathways: photoinduced electron transfer (PET), commonly termed photoredox catalysis, and photoinduced energy transfer (PEnT) (Fig. 1). Both scenarios are initiated by photoexcitation of the PC to generate PC*. Providing that the lifetime of its excited state is sufficiently long-lived (on the order of nanoseconds), diffusion of the substrate and PC* to form an encounter complex occurs competitively to other radiative or non-radiative decay pathways. The rate of the photocatalytic reaction is generally assumed to be dependent upon the concentration of PC*, which is itself correlated with the molar absorptivity ε of the PC at the wavelength(s) of irradiation as well as its excited-state lifetime.
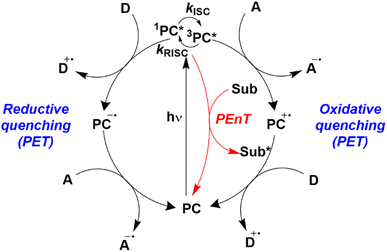 | ||
| Fig. 1 Energy transfer, oxidative quenching, and reductive quenching photocatalytic cycles where D is an electron donor, A is an electron acceptor and Sub is a substrate. A and D can be reagents (substrates), reaction intermediates, other catalytic species, or sacrificial agents. Figure taken from ref. 5. | ||
Assuming a productive encounter complex forms, the photocatalysis can then occur. In photoredox catalysis, single electron transfer (SET) between the PC* and the substrate ensues and depending on whether PC* gains or loses an electron this is termed reductive or oxidative quenching, respectively. A second SET event is subsequently required to close the photocatalytic cycle and regenerate the PC; in the oxidative quenching cycle, this SET is from a substrate to the PC+˙, while in the reductive quenching cycle, this SET is from PC−˙ to a substrate.
Marcus theory governs the propensity for SET where the redox potentials of the PC must be sufficiently oxidizing or reducing relative to the substrate to allow for the electron transfer to occur.6,7 The change in Gibbs energy for PET, ΔG0, must be exergonic and is related to both the ground-state redox potentials of the PC and the substrate (with one being classified as the electron donor and one as the electron acceptor, depending on the mechanism in question) as well as the optical gap, E0,0, of the PC. For example, in oxidative quenching, where the PC acts as a photoreductant (and is thus an electron donor), ΔG0 can be defined as in eqn (1), where e is the electronic charge and A is the electron acceptor as in Fig. 1.8,9
| ΔG0 = e[E0(PC+˙/PC) − E0(A/A−˙)] − E0,0 | (1) |
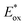 is defined in eqn (3).
is defined in eqn (3).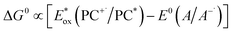 | (2) |
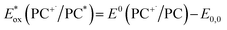 | (3) |
Should a reductive quenching cycle be operational, the PC acts as photooxidant (and is thereby an electron acceptor), and ΔG0 can be written as eqn (4), where D is the electron donor as in Fig. 1.
| ΔG0 = e[E0(D+˙/D) − E0(PC/PC−˙)] − E0,0 | (4) |
Eqn (4) can be expressed in terms of the excited-state reduction potential of the PC, as shown in eqn (5), where 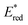 is defined in eqn (6).
is defined in eqn (6).
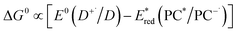 | (5) |
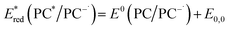 | (6) |
The kinetics of electron transfer, kPET, are related to ΔG0. For example, in the normal Marcus regime, increasing the absolute value of ΔG0 results in an increased kPET, according to eqn (7).10
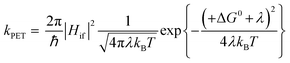 | (7) |
Aside from PET, photocatalysis can also proceed via an energy transfer event from the excited PC to a substrate. PEnT typically occurs through either a Förster or a Dexter energy transfer mechanism, where the latter is far more prevalent in the photocatalysis literature. Dexter energy transfer (DET) occurs through a simultaneous double electron exchange mechanism between the PC* and the substrate in its ground state.11 For this to be operational, the excited-state energies between the donor (the PC) and the acceptor (the substrate) must be close as there must be spectral overlap between the emission of the PC and the absorption of the substrate; the difference in triplet energies (ET) of the PC and substrate are commonly used as a surrogate for spectral overlap to predict whether a transformation is likely to occur via DET (eqn (8)).12
| ΔET = ET(PC) − ET(A) | (8) |
The matching of excited-state energies is encompassed in the spectral overlap requirement of DET, that is the overlap of the phosphorescence of the PC and the spin-forbidden absorption of the substrate. Practically, spectral overlap in these cases is challenging to quantify on account of the spin-forbidden nature of the transitions, especially the low absorptivity of the triplet absorption of organic substrates. Additionally, DET also requires orbital overlap between the two species involved in the encounter complex. The quantitative correlation of these prerequisites with the rate constant of DET, kDET, is described by eqn (9).
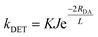 | (9) |
A smaller ΔET (eqn (8)) will correlate with a greater degree of spectral overlap, and as a consequence, a faster kDET (eqn (9)). In addition, for the energy transfer to be exergonic, ΔET should be greater than zero. For the cases where ΔET < 0, the transition is endergonic. As spectral overlap remains a requirement of DET, the implication of ΔET < 0 is that the PC* must have vibrational or rotational states that are greater in energy than some of those of the acceptor in its electronic excited state in order for the DET to be thermodynamically feasible.12
To fully assess and understand the yields achieved by a particular PC in a photocatalytic reaction, the aforementioned optoelectronic parameters that govern PET or PEnT must be determined. For example, for PET an accurate measurement of both the ground and excited state redox potentials, the latter dependent on the excited-state (singlet or triplet, depending on the type of PC) optical gaps, are required. For PEnT, the ET of the PC should be evaluated. These parameters in many cases are solvent dependent13–16 and the values that are cited in the photocatalysis literature are frequently recorded in different media to that used in the photocatalysis reaction, thus obscuring the real thermodynamic driving force. To best identify a suitable PC for a specific reaction and to rationalize its performance, assuming that kPET/kPEnT governs reaction yield, optoelectronic data obtained in the same solvent need to be available. In terms of photophysical measurements, as long as the PC is sufficiently soluble in the solvent, a useful measurement can be taken; however, for electrochemical measurements that require a conductive solution, non-polar solvents are generally unsuitable. Gratifyingly, a survey of the photocatalysis literature indicates that polar aprotic solvents are most often used, particularly MeCN, DMSO and DMF.5 A library of these parameters would serve as a useful resource to aid in the decision making as to which PC should be used for a particular reaction class and substrate. Indeed, an accurate knowledge of the optoelectronic properties of the PC in concert with those of the substrate(s) are essential for an analysis of the thermodynamic driving force for a particular reaction. However, an assessment of the competing kinetics of both photophysical and photochemical processes are often neglected, as are the solubility and the stability of reaction intermediates. To address this identified issue and given the complex influences the solvent can have on a photocatalytic reaction, we selected a series of eight versatile and commonly used PCs for optoelectronic characterization in four solvents of varying polarity, to understand how variation of the photophysical properties of the PC with solvent polarity can be correlated to photocatalytic performance. Although we recognise that solvent polarity will also influence the optoelectronic properties of the substrates in the photocatalysis reaction, as a first step we have focused exclusively on the PC in this study. We then evaluated the efficiency of some of these PCs in representative photocatalysis reactions, encompassing reactions across a range of these solvents proceeding via either PET or PEnT mechanisms, and attempted to correlate yields to the thermodynamic parameters of the PCs.
Results and discussion
The popular PCs [Ru(bpy)3](PF6)2 (bpy = 2,2′-bipyridine), [Ir(ppy)2(dtbbpy)]PF6 (ppy = 2-phenylpyridinato and dtbbpy = 4,4′-di-tert-butyl-2,2′-bipyridine), [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 [(dF(CF3)ppy) = 2-(2,4-difluorophenyl)-5-trifluoromethylpyridinato], [Cu(dmp)(xantphos)]PF6 (dmp = 4,7-dimethyl-1,10-phenanthroline and xantphos = 4,5-bis(diphenylphosphino)-9,9-dimethylxanthene), Eosin Y, 4CzIPN [2,4,5,6-tetrakis(9H-carbazol-9-yl)isophthalonitrile], 2CzPN [4,5-di(9H-carbazol-9-yl)phthalonitrile] and pDTCz-DPmS [9,9′-(sulfonylbis(pyrimidine-5,2-diyl))bis(3,6-di-tert-butyl-9H-carbazole] were selected as representative PCs (Fig. 2). Each of these compounds has been extensively employed in the literature as a PC across a myriad of different photocatalytic reactions; pDTCz-DPmS was recently shown by us to be an effective PC in both PEnT and PET reactions.17The photophysical properties of these eight PCs should first be established and validated prior to the investigation of how these properties may be influenced by solvent choice. [Ru(bpy)3](PF6)2, [Ir(ppy)2(dtbbpy)]PF6 and [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 are all widely studied phosphorescent emitters that have long-lived excited states with emission lifetimes that are on the order of sub-microsecond to microsecond.18 The presence of the transition metal induces significant spin–orbit coupling (SOC), as this is proportional to the atomic mass of the atoms involved in the emissive transition. The enhanced SOC facilitates spin mixing between singlet and triplet excited states, thus enabling rapid intersystem crossing (ISC) and phosphorescence. In these complexes the ISC quantum yield, ϕISC, is near unity,19 therefore subsequent photochemistry using these PCs originates exclusively from the triplet manifold.
[Cu(dmp)(xantphos)]PF6, Eosin Y, 4CzIPN, 2CzPN and pDTCz-DPmS instead emit via thermally activated delayed fluorescence (TADF).20–23 After photoexcitation, the compound rapidly relaxes to its first singlet excited state (S1), after which fluorescence can occur, which in the case of TADF compounds is referred to as prompt fluorescence, with emission lifetimes on the order of nanoseconds. SOC is much less efficient in these compounds than in Ru and Ir complexes, however, the degree of state mixing is inversely proportional to the energy difference between the excited singlet and triplet states. These five compounds instead display a small energy gap, ΔEST, (i.e., <0.2 eV) between the first singlet and triplet excited states (S1 and T1, respectively), thus enabling both ISC and reverse ISC (RISC) to occur.24 One of the manifestations of ISC/RISC in these compounds is the presence of delayed fluorescence, with emission lifetimes on the order of microseconds. A corollary is that both S1 and T1 states are populated. When ISC and RISC (kISC and kRISC, respectively) are fast relative to electron or energy transfer (kPET and kPEnT, respectively), a steady-state approximation may be assumed, and a Boltzmann distribution will govern the relative populations of the singlet and triplet excited states. This implies that the majority of excitons will exist in the triplet state owing to its lower energy.25 If kISC and kRISC are competitive or slower relative to kPET and kPEnT, then the relative populations of the excited states are determined by the relative magnitude of the rate constants. Regardless, as the energy gap between the S1 and T1 states is much smaller than the energy gap between these and the ground state of the substrates, then there should be a similar thermodynamic driving force for PET originating from either of these excited states. Most of the organic TADF PCs used for photocatalysis in the literature thus far5 possess very small ΔEST and thus show fast kISC/kRISC, and therefore PET is more likely to occur from the T1. Here, we assume that the thermodynamic driving force for PET is related to the energy difference of the oxidised PC and the reduced substrate, or the reduced PC and the oxidised substate, as shown in eqn (1) and (4), and that coulombic interactions play only a minor role.
The solvents MeCN, DMF, DCM, and THF that were chosen for this study frequently feature in photocatalysis reactions and span a broad polarity range, reflected in their Reichardt solvent polarity values, ENT, of THF (0.207), DCM (0.309), DMF (0.386) and MeCN (0.460).26 However, they have varying electrochemical windows, meaning that in some circumstances, direct electrochemical measurement of either the oxidation or reduction potential becomes impossible, thus accurate theoretical predictions of the associated ionisation potential (IP) and electron affinity (EA) would be useful.
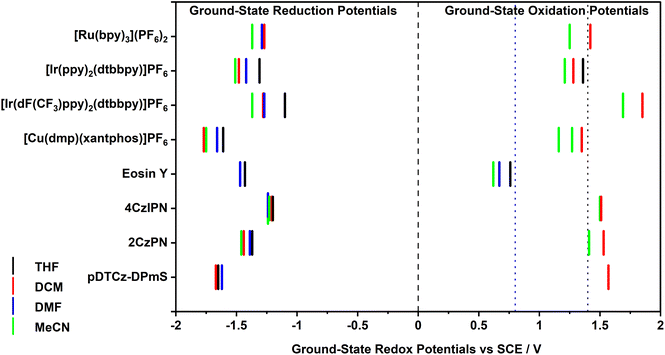
Electrochemical characterization
The ground-state redox potentials of the PCs in the four solvents were determined using a combination of cyclic voltammetry (CV) and differential pulse voltammetry (DPV). While both MeCN and DCM are useful solvents for electrochemistry on account of their wide redox window, THF and DMF both have narrow electrochemical windows and so oxidation processes cannot necessarily be captured in these solvents (Fig. 3). As a result, the ground-state oxidation potential, Eox, could not be obtained for the majority of the PCs in these two solvents. Fortunately, the ground-state reduction potential, Ered, could be acquired in all four solvents when solubility allowed; indeed, all electrochemistry solutions were homogeneous, except for Eosin Y in THF, which was a suspension. The redox potentials versus SCE are collated in Table S10,† with the relevant cyclic and differential pulse voltammograms documented in the ESI (Fig. S9–S16†). In all cases but one, the redox potentials are similar to those reported in the literature, varying at most by 0.04 V in the case of [Cu(dmp)(xantphos)]PF6. The literature redox potentials for Eosin Y differ quite strongly to those obtained here; we attribute this difference due to the different solvent system used in the literature (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeCN
1 MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O) compared to the measurements undertaken in this study, which were in THF, DMF or MeCN (poor solubility in DCM prevented data from being acquired in this solvent for this PC).
H2O) compared to the measurements undertaken in this study, which were in THF, DMF or MeCN (poor solubility in DCM prevented data from being acquired in this solvent for this PC).
In all instances, the values of Eox are cathodically shifted with increasing solvent polarity (Table S10†), typically varying between 100–200 mV; however, in the case of 4CzIPN, Eox remains essentially constant (e.g., Eox = 1.51 V and 1.50 V, in DCM and MeCN, respectively). This indicates that in more polar media, such as MeCN, most of the PC+˙ will be poorer ground-state oxidants. For example, a simple switch from MeCN to DCM allows [Ru(bpy)3]3+, which equates to PC+˙, to increase its ground-state oxidising ability from Eox = 1.25 V to 1.42 V, respectively, which represents a potentially significant 170 mV change in thermodynamic driving force for a redox-neutral photocatalytic reaction. However, since Eox could generally only be obtained in two solvents (DCM and MeCN), it is not possible to extrapolate trends in the values with respect to solvent polarity. The CV of the complex [Cu(dmp)(xantphos)]PF6 exhibited two oxidation waves in MeCN at a scan rate of 0.1 V s−1, one of which is likely due to PC degradation following the oxidation of Cu(I) to Cu(II).27
The Ered values were generally found to also shift cathodically with increasing solvent polarity (Table S10†), suggesting that polar media serve to render the PC−˙ a stronger ground-state reductant. For example, the Ered of [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 shifts from −1.10 V in THF to −1.37 V in MeCN. Unexpectedly, DMF tends not to fit this trend, often providing intermediate Ered values between those measured in THF and DCM, despite being more polar than DCM.26 The Ered value of Eosin Y in MeCN also fails to fit the trend, being much less negative than in the less polar solvents (e.g., Ered = −1.23 V and −1.43 V in MeCN and THF, respectively). It is not clear at this stage why these values differ so significantly, especially given that the UV-Vis absorption spectrum is insensitive to solvent polarity (vide infra), which implies that all solvents contain the same structural form of Eosin Y. As solvent polarity increases, the energy gap between the ground state oxidation and reduction potentials, ΔE, was generally found to decrease (Table S10†). However, as stipulated previously, we can only cautiously assign this trend given that Eox could typically only be determined in two out of four of the solvents.
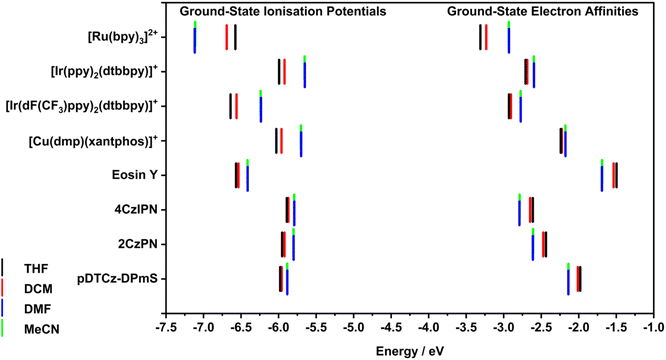
In order to understand the origins of the effect of solvent on the electrochemical properties of the PC we conducted DFT studies to predict the redox properties of the PCs. As a first step, the IP and EA of each PC was calculated using DFT via the delta-SCF approach in each of the four solvents of interest (Fig. 4 and Table S9†). Each solvent was modelled implicitly, using the integral equation formalism polarizable continuum model (IEF-PCM)28 and the default dielectric constant for each solvent as implemented in Gaussian 16.29 For all the DFT results, the organometallic complexes were modelled as single species (i.e., without their outer-sphere counter anion), due to the difficulty of optimising the interaction with a loosely bound ligand. Such a methodology has been effectively used to accurately predict IP and EA in previous reports.30,31 Both the IP and EA are reported as electron binding energies (i.e., as negative values) to function as more accurate predictions of the PC's oxidation and reduction potentials than those that are estimated from HOMO and LUMO energies.
The calculated IPs showed a strong dependence on the solvent (Table S9†), with an average range of 265 meV across the four solvents, and a greatest absolute difference of 541 meV for [Ru(bpy)3]2+ in THF (−6.58 eV) versus in DMF (−7.12 eV). The calculated IPs for all the PCs were less negative in higher polarity solvents (equivalent to a cathodic shift of the Eox), except for [Ru(bpy)3]2+, which has a more negative IP in the more polar solvents. This may be due to the more shielded electron density on the metal in this complex than the other compounds.
A larger absolute value of IP signifies that a greater amount of energy is required to remove an electron and as such, can be correlated to a more positive ground-state oxidation potential, Eox. In relation to photocatalysis, this would make the PC+˙ a stronger ground-state oxidant (Fig. 1). Thus, in more polar solvents, only [Ru(bpy)3]3+ is predicted to be a stronger ground-state oxidant, while the other seven PC+˙ are predicted to be weaker oxidants, with their oxidizing capacity increasing with decreasing solvent polarity. This computed trend for the PCs [excluding [Ru(bpy)3](PF6)2] matched the experimental data. However, as stated previously, as only a limited number of experimental Eox values could be obtained due to the narrow electrochemical window of THF and DMF, we thus can only cautiously conclude from this reduced data set that the calculated IPs are an accurate indicator of the trends in Eox as a function of solvent.
Moreover, the charged organometallic complexes showed a more pronounced sensitivity to solvent polarity than the organic PCs, with the IPs of the former varying by an average of 401 meV compared to only 124 meV for the latter. In both classes, however, the predicted IPs showed almost no change (3 meV on average) between DMF and MeCN, despite the large apparent difference in polarity between the two solvents. It should be noted that caution must be taken in cross-comparing the two types of PCs (organometallic and organic), given that different levels of theory were used in determining the IP and EA values, with B3LYP/6-31+G**/SBKJC-VDZ-ECP/GD3BJ and PBE0/6-31G**/GD3BJ being used for the two classes, respectively, and that the complexes themselves are charged while the organic dyes are neutral in their ground state. Despite the different levels of theory being used in the calculations for metal-containing and organic PCs, the prediction that IP would vary more considerably for organometallic compared to organic PCs was matched experimentally. The Eox varied on average by 170 mV between the least and most polar solvent for the former, and only by 90 mV for the latter.
By contrast, the calculated EAs showed less variation with solvent than the IPs (Table S9†), varying by only 177 meV on average, with the greatest variance being 381 meV for [Ru(bpy)3]2+ in THF (−3.33 eV) versus in MeCN (−2.93 eV). Clearly distinct behaviours are observed between the organometallic and organic PCs, with the former all possessing a less negative EA in more polar solvents (equivalent to a cathodically shifted Ered), and the latter experiencing a more negative EA in more polar solvents (equivalent to an anodically shifted Ered). Experimentally, Ered was cathodically shifted for all PCs, suggesting the DFT predicted EA is only appropriate for modelling organometallic PCs. The magnitude of this change is similar for both classes, with an average of 178 meV for the organometallic PCs and 176 meV for the organic PCs. Experimentally, these changes are 180 mV and 120 mV for the two classes, respectively. As was observed for the IPs, the calculated EAs show almost no variation (2 meV on average) between the two most polar solvents (DMF and MeCN).
These trends result in three pairs of PCs having nearly equivalent EAs in DMF and MeCN, despite having relatively distinct EAs in the less polar THF and quite different chemical structures. These pairings are pDTCz-DPmS and [Cu(dmp)(xantphos)]+ (ca. −2.16 ± 0.02 eV), 2CzPN and [Ir(ppy)2(dtbbpy)]+ (ca. −2.60 ± 0.01 eV), and 4CzIPN and [Ir(dF(CF3)ppy)2(dtbbpy)]+ (ca. −2.78 ± 0.01 eV). Thus, as solvent polarity increases, the electron affinity of many of the PCs studied converge, and the implication is that the two PC−˙ in each of these pairs would be expected to be equivalent ground-state reducing agents. In practice, while the Ered of the PCs does differ between DMF and MeCN, similar reduction potentials for these pairings are observed. For example, in DMF, the Ered values differ by only 0.03–0.04 V between the pairings, e.g., pDTCz-DPmS and [Cu(dmp)(xantphos)]PF6 have Ered = −1.62 and −1.66 V, respectively, in DMF, while in THF, the difference is far more pronounced (Ered = −1.61 and −1.77 V, respectively).
Photophysical studies
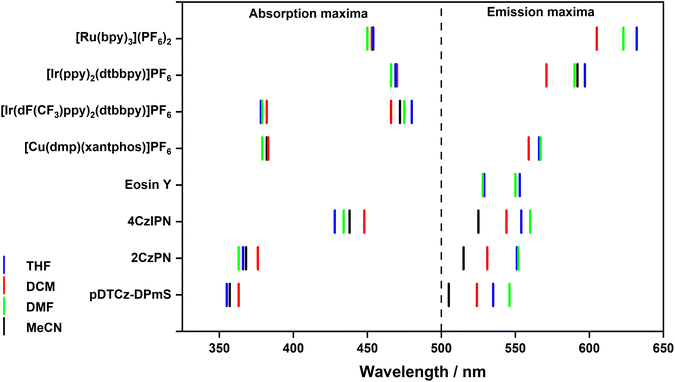
The UV-Vis absorption spectra of the PCs across the four solvents are shown in Fig. S17–S25,† with the absorption maxima and molar absorptivity collated in Table S15† and reflected graphically in Fig. 5. If there is a large change in the permanent dipole moments between ground and excited states, solvatochromism can be observed. For the majority of the PCs investigated, and particularly for the transition metal complexes, minimal changes in the absorption profile were detected. Molecules with a small permanent dipole moment in the ground state (close to zero) often display negligible absorption solvatochromism.32 Notably though, the lowest energy absorption bands of 4CzIPN, 2CzPN, and pDTCz-DPmS, which are of charge-transfer (CT) character, display a minor red-shift in DCM, in agreement with the findings of Ishimatsu et al.33Perhaps more importantly though are the subtle changes in the molar absorptivity with changes in solvent. For PCs with lowest energy absorption bands that are combinations of many closely lying states, changes in solvents can cause different relative changes to the energies of LE and CT states, and consequently, small variations in ε can be observed, as may be the case for the changes in spectra for 4CzIPN and 2CzPN (Fig. S24 and S25†). In photocatalysis, the reaction rate is dependent on the number of photons absorbed by the PC, which is governed by ε. Modern excitation sources, such as Kessil LEDs, emit light over a narrow range, with a spectrum that is Gaussian in nature.34 By contrast, compact fluorescence light (CFL) sources emit irregularly yet broadly over the visible light spectrum.35 Thus, one surrogate for an assessment of reaction rates of photocatalysis reactions using LED excitation sources would be to evaluate the relative magnitude of ε of the different photocatalysts at the wavelength of maximum intensity of the excitation source, noting that this provides only a crude estimate given that light is absorbed by the PC across the entire emission spectrum of the excitation source.
Any subtle changes in the UV-Vis absorption spectra will ultimately have an impact on the ε value, meaning that aside from the thermodynamic driving force that may change with solvent (such as redox potentials), the kinetics of the reaction will also be impacted by the polarity of the solvent. To allow for a fair cross-comparison of the PCs, the same optical density of the excited PC should be present in the reaction mixture. This in practice is not done (and would not be something that most synthetic photochemists would take into account) and we can only comment on the variation of the ε values at the excitation wavelengths chosen for the photocatalysis reactions (456 nm and 390 nm) and assess how this may correlate with the yield of the reaction.
If the excited-state dipole moment (μe) is greater in magnitude than the permanent dipole moment associated with the ground state (μg), positive emission solvatochromism is more pronounced than the absorption solvatochromism.36 For PCs whose lowest energy excited state is CT in nature, μe is expected to be large, thus leading to a strong positive solvatochromism (Fig. S26–S33†).37 Positive solvatochromism is observed in each of the organic PCs 4CzIPN, 2CzPN and pDTCz-DPmS (Fig. 5 and Table S15†), confirming the CT character of the emissive S1 state. The emission of the PC [Ru(bpy)3](PF6)2 also exhibits positive solvatochromism on account of its lowest-lying metal-to-ligand charge-transfer (3MLCT) excited state. The emission profile of [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 is, however, structured, reflecting an excited state of ligand-centred (3LC) character. The more locally excited (LE) nature of this excited state renders its energy effectively insensitive to solvent polarity.38 Similarly, there is no significant change in the emission energy of Eosin Y, implying an excited state that is of predominant LE character.
Across the solvents, [Ir(ppy)2(dtbbpy)]PF6 displays an unstructured emission profile indicative of an excited state of CT character, which aligns with the literature characterization of the emissive T1 state in MeCN as one of mixed 3MLCT/3LLCT.39 A modestly red-shifted emission with increasing solvent polarity is observed. The implication of the small degree of solvatochromism is that the emissive excited state has a small permanent dipole moment40 and that the CT state must be weaker relative to the CT states of the other PCs where a larger degree of positive solvatochromism is observed. [Cu(dmp)(xantphos)]PF6 exhibits a low energy emission band at 556–567 nm, that is insensitive to the solvent environment, except for a minor 5 nm hypsochromic shift in DCM. The broad spectral appearance justifies the assignment of this emitting state being MLCT in nature.41
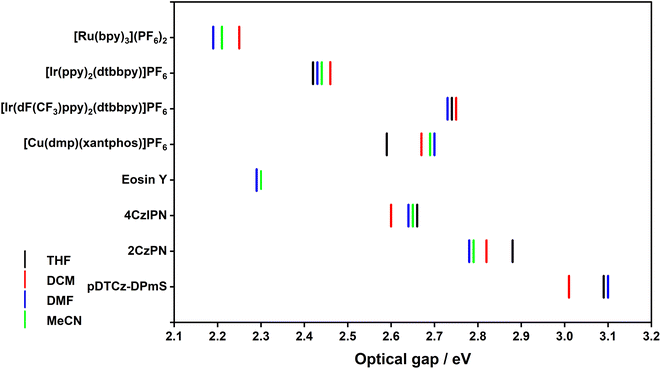
As illustrated in Fig. S26–S33,† solvent can influence the energy and profile of the emission spectra of the PC and, as a result, in the optical gap, E0,0 (Table S16† and Fig. 6). For the 4d and 5d transition metal PCs, the optical gap between the ground state and first triplet excited state, E0,0(T1), is most significant because, as previously discussed, PET occurs exclusively from the triplet excited state. E0,0(T1) can therefore be inferred from the onset of the phosphorescence spectrum. For the organic PCs and [Cu(dmp)(xantphos)]PF6 it is less clearly defined whether the SET will originate from the S1 or T1 states owing to their intrinsic TADF nature. However, as previously discussed, it is more likely that the SET will occur from the T1 state. Despite this, from the room temperature, steady-state emission measurements, only E0,0(S1) can be determined (from the intersection point between the normalized absorption and emission spectra). Therefore, this value was used for subsequent determination of excited-state redox potentials.
Generally, E0,0 decreases with increasing solvent polarity (Fig. 6), reflecting the positive solvatochromism exhibited by many of the PCs in this study. For example, the E0,0(S1) of 2CzPN decreases from 2.88 eV in THF to 2.79 eV in MeCN. For PCs where the emission energy is fairly solvent insensitive, there is of course minimal variation in E0,0, as exemplified by [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, wherein the E0,0(T1) ranges narrowly between 2.73–2.75 eV across all four solvents (Table S16†).
Since triplet energies are used as a diagnostic tool to predict whether DET is thermodynamically feasible, the ET of a subset of the PCs were additionally estimated. In the case of [Ru(bpy)3](PF6)2 and [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, the ET is given in Table 1. For [Cu(dmp)(xantphos)]PF6 and 4CzIPN, however, the steady-state emission spectrum cannot be analogously used to infer the ET of these compounds.
The ET measurements for TADF compounds are typically obtained from the gated emission spectra at 77 K; however, at this low temperature the solvent forms a glass. In the glass, there is no opportunity for solvent reorganization and thus, the measurements at 77 K do not capture any reorganization of the solvent dipoles that would be responsible for the stabilization of the CT states. We nonetheless measured the gated emission spectra of [Cu(dmp)(xantphos)]PF6 and 4CzIPN (Fig. S44–S47†), with the T1 values provided in Table S17.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42
42
The ET of both [Cu(dmp)(xantphos)]PF6 and 4CzIPN was shown to only change by 0.01 eV between 2-MeTHF and BuCN; providing an average ET of 2.62 eV and 2.72 eV for the two PCs, respectively. However, we were acutely aware that this estimate of ET would not be the true value, given that at low temperature, we may not be in the relaxed T1 state. Therefore, these values are an overestimation of the true ET value at RT in these solvents. In an effort to directly measure the ET value, we attempted time resolved emission slicing (TRES); however, the lack of significant triplet character in the emission properties of both [Cu(dmp)(xantphos)]PF6 and 4CzIPN at RT in these solvents rendered this measurement unproductive for the determination of ET. We thus estimated the ET from the difference between the experimentally determined S1 energy at RT and the ΔEST obtained at 77 K. The ΔEST of these PCs can be inferred from the difference in energy of the onsets of the steady-state and millisecond-gated emission spectra at 77 K (Table S17†).43 Since the S1 state of TADF compounds typically has greater CT character than the T1 state, the S1 state will be stabilized to a greater degree than the T1 state in polar solvents, meaning that ΔEST values will decrease in polar solvents compared to the value obtained at 77 K. Thus, the true value of ET will be lower in energy than the one estimated by us. Using our method, the ΔEST was determined at 77 K to be 0.03 eV for 4CzIPN, resulting in an estimated ET value of 2.62 eV in MeCN.44
The experimentally determined/estimated ET values of the PCs are collated in Table 1, alongside literature values when available. For [Ru(bpy)3](PF6)2, the ET varies by 0.06 eV between the two solvents while for [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, there is a mere 0.02 eV variation. This reflects the nature of the excited state; for the former, the excited state is 3MLCT in character and for the latter, the excited state is of 3LC character. As such, a greater variation in ET is observed for [Ru(bpy)3](PF6)2. For [Cu(dmp)(xantphos)]PF6 and 4CzIPN, there is a 0.11 eV and 0.06 eV variation, respectively, between the two solvents, again reflecting the CT nature of the excited state. The changes in ET with solvent polarity are rather small, between 60–110 meV for the PCs with excited states of CT character. This implies that the polarity of the solvent will have little impact on the efficiency of DET reactions, presuming of course, that ET values are indeed a useful indicator of DET efficiency.
| E T/eV | |||||
|---|---|---|---|---|---|
| THF | DCM | DMF | MeCN | Literature | |
| a For [Ru(bpy)3](PF6)2 and [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, ET determined from the tangential onset from the steady-state emission in THF, DCM, DMF and MeCN. For [Cu(dmp)(xantphos)]PF6 and 4CzIPN, ET was estimated from ET = ES − ΔEST, where ES = E0,0 (the energy of S1) was determined from the intersection point between the normalized absorption and emission spectra and ΔEST was determined from the tangential onset of the 77 K steady-state emission and 77 K gated emission (using a 1–9 ms time window). The λexc for [Ru(bpy)3](PF6)2, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6 and 4CzIPN were 450, 380, 380, and 420 nm, respectively. Values in parentheses indicate the ET values obtained from DFT calculations (for more details consult the ESI). b Value taken from ref. 48, which is the emission maximum in EtOH glass at 77 K. c Value taken from ref. 38, which is the emission maximum in MeCN. d Value taken from ref. 49, which was determined from the highest energy peak from the structured phosphorescence spectrum in toluene at 77 K. | |||||
| [Ru(bpy)3](PF6)2 | (1.95) | 2.25 (1.95) | 2.19 (1.92) | 2.21 (1.92) | 2.07b |
| [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 | 2.74 (2.42) | 2.75 (2.43) | 2.73 (2.42) | 2.74 (2.58) | 2.60c |
| [Cu(dmp)(xantphos)]PF6 | 2.43 (1.70) | 2.51 (1.80) | 2.54 (1.79) | 2.53 (1.79) | |
| 4CzIPN | 2.63 (2.15) | 2.57 (2.11) | 2.61 (2.09) | 2.62 (2.11) | 2.53d |
The ET values obtained from the DFT calculations are also provided in Table 1 (please see ESI† for further details). For [Ru(bpy)3](PF6)2, little change is predicted between solvents (up to 0.03 eV), while for 4CzIPN there is a slightly larger degree spread of ET values across the four solvents (0.06 eV) and for [Cu(dmp)(xantphos)]PF6 this is even larger still at 0.10 eV. Unexpectedly, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 has a significantly larger difference in ET, up to 0.15 eV. Regardless, all ET values predicted by DFT calculations are remarkably lower than that obtained experimentally; on average, 0.29 eV, 0.28 eV, 0.73 eV and 0.49 eV for [Ru(bpy)3](PF6)2, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6 and 4CzIPN, respectively. This suggests that in silico calculations are not an effective method in this case for estimating ET.
There is considerable variability when comparing the experimentally obtained ET values in our study to those reported in the literature. This divergence in the ET likely reflects the different methodologies used to determine ET. For example, in MeCN the experimentally determined ET value for [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 is 2.74 eV, while in the literature the ET is consistently reported at around 2.60 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45–47 with the reference for the original source of this value typically belonging to the first report from Bernhard and co-workers.38 This values presumably stems from the emission maximum, λPL, quoted as 2.58 eV in MeCN. Thus, the different ET values reflect the use of spectral onsets by us versus peak maxima by Bernhard and co-workers.
45–47 with the reference for the original source of this value typically belonging to the first report from Bernhard and co-workers.38 This values presumably stems from the emission maximum, λPL, quoted as 2.58 eV in MeCN. Thus, the different ET values reflect the use of spectral onsets by us versus peak maxima by Bernhard and co-workers.
Excited-state redox properties
The excited-state redox potentials,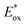 and
and 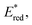 which are themselves dependent on the E0,0 values and the ground-state redox potentials, are provided in Table S11† and visualised in Fig. 7. In all cases,
which are themselves dependent on the E0,0 values and the ground-state redox potentials, are provided in Table S11† and visualised in Fig. 7. In all cases, 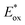 becomes more negative with increasing solvent polarity. This indicates that each of the PCs in this study is a better photoreductant in more polar solvents like MeCN. [Ir(ppy)2(dtbbpy)]PF6 adheres to this trend particularly clearly, with
becomes more negative with increasing solvent polarity. This indicates that each of the PCs in this study is a better photoreductant in more polar solvents like MeCN. [Ir(ppy)2(dtbbpy)]PF6 adheres to this trend particularly clearly, with 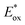 changing from −1.06 V in THF to −1.18 V and −1.23 V in DCM and MeCN, respectively.
changing from −1.06 V in THF to −1.18 V and −1.23 V in DCM and MeCN, respectively.
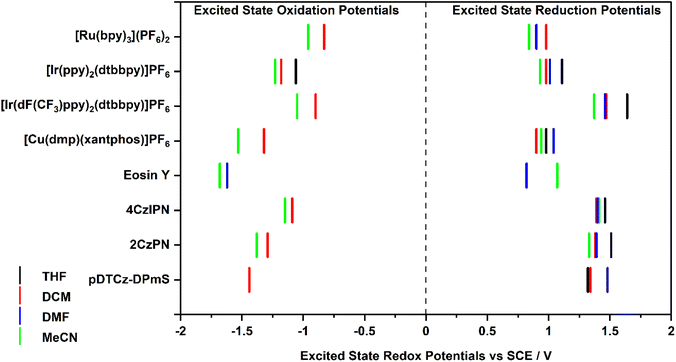 | ||
Fig. 7 Summary of the excited-state redox potentials of the eight PCs in the four solvents. Only the  based on the first Eox for [Cu(dmp)(xantphos)]PF6 in MeCN is provided. based on the first Eox for [Cu(dmp)(xantphos)]PF6 in MeCN is provided. | ||
Conversely,  tends to become less positive with increasing solvent polarity, signifying that the PC is a stronger photooxidant in less polar solvents such as THF. For example, the
tends to become less positive with increasing solvent polarity, signifying that the PC is a stronger photooxidant in less polar solvents such as THF. For example, the  of [Ru(bpy)3](PF6)2 increases from 0.84 V in MeCN to 0.90 V and 0.98 V in DMF and DCM, respectively. However, for the other PCs, DMF surprisingly tends to provide stronger photooxidizing
of [Ru(bpy)3](PF6)2 increases from 0.84 V in MeCN to 0.90 V and 0.98 V in DMF and DCM, respectively. However, for the other PCs, DMF surprisingly tends to provide stronger photooxidizing 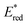 values than the less polar DCM. This is a consequence of the behaviour noted for the Ered, whereby the values obtained for DMF are more anodically shifted than expected. This therefore translates to more anodic values for
values than the less polar DCM. This is a consequence of the behaviour noted for the Ered, whereby the values obtained for DMF are more anodically shifted than expected. This therefore translates to more anodic values for 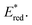
Taken together, it becomes clear that a change in solvent can cause changes of up to 270 mV in the excited-state redox potentials (e.g.[Ir(dF(CF3)ppy)2(dtbbpy)]PF6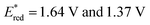 in THF and MeCN, respectively). Variations this significant in redox potentials can potentially be the difference between no reaction and product formation in a photoredox catalysis reaction. Also, depending on the nature of the lowest energy excited state, solvent dependent shifts can occur with changes in λmax of up to 35 nm in THF to MeCN for 4CzIPN, which can influence the spectral overlap between the PC and the substrate in PEnT catalysis.
in THF and MeCN, respectively). Variations this significant in redox potentials can potentially be the difference between no reaction and product formation in a photoredox catalysis reaction. Also, depending on the nature of the lowest energy excited state, solvent dependent shifts can occur with changes in λmax of up to 35 nm in THF to MeCN for 4CzIPN, which can influence the spectral overlap between the PC and the substrate in PEnT catalysis.
Photocatalysis testing – photoinduced electron transfer (PET)
After demonstrating that the optoelectronic properties of the eight PCs do vary significantly with solvent, we sought to establish whether there were any correlations between these values and reaction yields in a photocatalysis reaction. Since data collection was most comprehensive for Ered and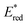 as opposed to Eox and
as opposed to Eox and  we initially focused on evaluating a photoredox reaction proceeding via a reductive quenching cycle.
we initially focused on evaluating a photoredox reaction proceeding via a reductive quenching cycle.
As such, the photocatalytic pinacol coupling reaction was chosen as a model reaction, using benzaldehyde as the substrate (Fig. 8).50,51 This reaction has previously been described to proceed through a reductive quenching cycle, whereby the excited PC is reduced by the sacrificial reductant N,N-diisopropylethylamine (DIPEA) [(E(DIPEA˙+/DIPEA) = 0.65 V vs. SCE in MeCN], which then is employed to reduce the aldehyde to its radical anion. Although reduction of benzaldehyde is challenging (Ered = −1.80 V vs. SCE in DMF),52 the weak attraction of the protonated DIPEA with the aldehyde has been proposed to render this process less thermodynamically demanding.50
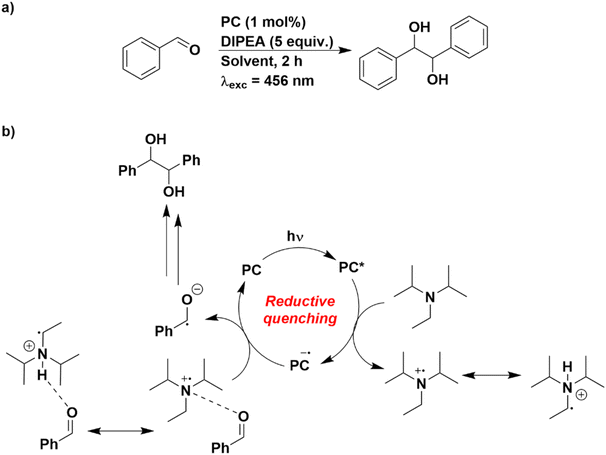 | ||
| Fig. 8 (a) Reaction scheme for the pinacol coupling. (b) Putative mechanistic cycle proposed in ref. 50. | ||
The oxidation potential of DIPEA was first measured in each of the solvents used (Fig. S17 and Table S12†). There is a progressive cathodic shift of the Eox of DIPEA with increasingly solvent polarity (Eox = 0.93 V in THF and 0.65 V in MeCN). Therefore, despite the PCs generally being weaker photoreductants in more polar solvents, this is somewhat offset by DIPEA being more easily oxidised in polar media.
In the first instance, the conditions of Schmid et al.,51 were followed. As documented in the literature, and confirmed in our set-up, [Ru(bpy)3](PF6)2 cannot perform this reaction in any of the four solvents investigated (Table 2).50,51 This is likely due to [Ru(bpy)3]−˙ being a poorer ground-state reductant than the other PCs. Eosin Y also performed poorly (2–4% yield), with this likely owing to its low photooxidizing potential. 4CzIPN provided low yields in most of the solvents (7–10% yield) but this increased in THF to 28%. For the other 3 PCs, [Ir(ppy)2(dtbbpy)]PF6, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 and [Cu(dmp)(xantphos)]PF6, the yields tended to increase with increasing solvent polarity from DCM to DMF to MeCN; however, the yields in THF do not fit this trend, and instead are much higher than expected based on its low polarity.
| 1H NMR yield/% | ||||
|---|---|---|---|---|
| THF | DCM | DMF | MeCN | |
| a Yields determined by 1H NMR analysis of the crude reaction mixture using 1,3,5-trimethoxybenzene as the internal standard. Yields provided are the sum of the meso:dl isomers and are the average yields of at least two independent runs with the standard deviation provided. b Reactions conducted for 2 h. c Reactions conducted for 24 h. | ||||
| [Ru(bpy)3](PF6)2 | 0b | 0b | 0b | 0b |
| [Ir(ppy)2(dtbbpy)]PF6 | 52 ± 3b | 17 ± 1b | 50 ± 3b | 57 ± 1b |
| 72 ± 1c | 37 ± 1c | 63 ± 1c | 68 ± 2c | |
| [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 | 53 ± 1b | 27 ± 2b | 29 ± 3b | 60 ± 3b |
| 63 ± 0c | 44 ± 1c | 50 ± 3c | 56 ± 1c | |
| [Cu(dmp)(xantphos)]PF6 | 64 ± 1b | 11 ± 1b | 14 ± 0b | 59 ± 1b |
| 74 ± 1c | 48 ± 1c | 69 ± 2c | 68 ± 0c | |
| Eosin Y | 2 ± 0b | 2 ± 1b | 4 ± 0b | 4 ± 1b |
| 9 ± 1c | 21 ± 2c | 12 ± 2c | 33 ± 6c | |
| 4CzIPN | 28 ± 1b | 8 ± 1b | 10 ± 2b | 7 ± 2b |
| 61 ± 2c | 45 ± 1c | 61 ± 3c | 67 ± 1c | |
| 2CzPN | 31 ± 1c | 11 ± 0c | 3 ± 1c | 2 ± 0c |
In light of our recent work, where we showed that increasing the reaction time of the pinacol reaction from 2 h to 24 h can lead to substantial increases in reaction yield,17 we conducted the reactions using each of [Ir(ppy)2(dtbbpy)]PF6, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6, Eosin Y, 4CzIPN and 2CzPN over 24 h (Table 2). At this longer reaction time it was observed that, in general, with increasing solvent polarity the yield of the target product increases. This correlates with the trend observed in the electrochemistry (Fig. 3); as the solvent becomes more polar, the PC−˙ becomes a more potent ground-state reducing agent and therefore has a greater thermodynamic driving force to undergo the challenging reduction of benzaldehyde. This trend is particularly evident for [Ir(ppy)2(dtbbpy)]PF6, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6, 4CzIPN and Eosin Y. However, THF tends to not fit this correlation, and instead usually provided the highest yields across all the solvents. For Eosin Y, abnormally low yields in DMF were observed, although it is not clear at this stage what is its origin. Unexpectedly, 2CzPN displays the opposite trend to the other PCs, namely, the yield of product decreases with increasing solvent polarity.
Aside from the redox potentials changing as a function of solvent, the molar absorptivity of the PCs is also affected, thereby affecting the concentration of the PC* and the probability for a formation of a productive encounter complex. The ε values of the PCs at 456 nm, the excitation wavelength, are provided in Table S13.† There is, however, no correlation between these ε values and yields. The implication of a lack of correlation where one should exist, suggests that under the reaction conditions, the rate of PET between PC* and DIPEA does not govern the product yield. Rather, the second SET, involving the challenging reduction of benzaldehyde, is more likely to the rate-limiting step in the reaction. Under our reaction conditions, the mixture is a homogeneous solution, except for Eosin Y in THF and DCM, and Ru(bpy)3(PF6)2 in THF. Changes in solubility of the PC and reagents may also have an impact upon final product yields, however, this cannot be evidenced in our dataset; Ru(bpy)3(PF6)2 was unsuccessful in all solvents, irrespective of polarity, and no trends could be ascertained for Eosin Y.
Alongside redox potentials and molar absorptivity, it is important to acknowledge that other off-cycle processes within the reaction may be solvent dependent such as PC degradation and unproductive side reactions. These will affect the global yield achieved and the rates of these processes may also be solvent dependent. This therefore makes establishing correlations between solvent polarity and yield difficult to ascertain.
To better understand the variations in yield with solvent, Stern–Volmer (SV) quenching studies were performed with some of the PCs in the four solvents, using DIPEA as the quencher. We could observe no correlation between the SV quenching results and the solvent polarity (Fig. S54–S59 and Table S19†). Since the Stern–Volmer quenching studies surprisingly provided no additional insight into the yields obtained, we next assessed the photostability of the PCs in each solvent under the pinacol coupling reaction conditions. UV-Vis absorption spectra were acquired before and after each 24 h reaction (see Fig. S60–S65† for all UV-Vis absorption spectra). It was observed that the absorption spectra of all the PCs changes significantly after the reaction compared to before.
For both iridium PCs, [Ir(ppy)2(dtbbpy)]PF6 and [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, the MLCT/LLCT absorption band remains relatively unchanged after irradiation in THF, DMF and MeCN, but at wavelengths below 300 nm, the spectra are typically blue-shifted compared to those before irradiation. This implies that structural changes are likely occurring on the ancillary ligand during the pinacol coupling reaction, a conclusion that is consistent with the work of Bawden et al.53 who showed that 2,2′-bipyridine type ancillary ligands, when used in combination with hydrogen atom transfer (HAT) electron donors, are susceptible to reaction; for example, [Ir(ppy)2(dtbbpy)]+ was shown to form [Ir(ppy)2(dtb-H3-bpy)] when irradiated with blue LEDs in the presence of DIPEA or triethylamine. In DCM, the absorption spectra of both iridium PCs show considerable changes also in the visible region, particularly the formation of a new band at 412 nm, as well as a band at 314 nm for [Ir(dF(CF3)ppy)2(dtbbpy)]PF6. This suggests that there is significantly more photodegradation in DCM relative to the other solvents, implying that the solvent itself may not be benign under the reaction conditions, which may be why the observed yields are lowest in this solvent. Homolysis of the C–Cl bond in DCM can occur photochemically, subsequently decomposing this solvent, although very high energy excitation is typically required to induce this (typically less than 225 nm).54 It has however been documented that DCM can decompose in the presence of heterogeneous photocatalysts, such as TiO2, with UV irradiation above 300 nm.
Similar to the iridium complexes, the UV region of the absorption spectrum of [Cu(dmp)(xantphos)]PF6 is blue-shifted after irradiation in all four solvents, implying a structural modification of the ligands. In DCM and DMF, new bands appear at 412 nm and 326 nm, respectively, pointing to a greater degree of photodegradation of the complex in these solvents. Spectroelectrochemistry studies of [Cu(dmp)(xantphos)]PF6 have previously documented that upon oxidation the ligands in this complex dissociate to form the diimine homoleptic counterpart [Cu(dmp)2]PF6, which has a λabs at 456 nm in MeCN.41 It is possible that a similar dissociation of the xantphos ligand may occur under the reaction conditions, particularly in DCM, associated with the emergence of a new band at 412 nm in the absorption spectrum.
The UV and near visible regions of the absorption spectrum of Eosin Y remain relatively constant before and after irradiation, regardless of solvent. However, the band between 450–550 nm disappears almost completely after irradiation. Such a loss of absorptivity for Eosin Y upon irradiation is not unprecedented. Indeed, Alvarez-Martin et al.55 showed that irradiation of aqueous solutions of Eosin Y (in its dianionic form) using various wavelength LEDs (broad-band UV light, 405 nm, and 532 nm) resulted in a loss of the distinctive 450–550 nm band, which the authors claimed was a result of a reaction between the photoexcited Eosin Y and reactive oxygen species causing a decomposition of the PC. Moreover, the UV-vis absorption spectrum of Eosin Y has previously been shown to be sensitive to pH. In a photoborylation reaction of diazonium salts using Eosin Y as the PC, no band between 450–550 nm was present in the UV-vis absorption spectrum, while after the addition of base, this band appeared.56 This is presumably due to the formation of the dianonic form of Eosin Y that is associated with this band. Therefore, under the present reaction conditions, the loss of this band after irradiation suggests that the dianionic form of Eosin Y is no longer present, either because it resides back in the neutral form (although this seems unlikely due to the large excess of basic amine present), or the PC has degraded.
The low energy CT band in the absorption spectra of both 2CzPN and 4CzIPN is significantly blue-shifted after irradiation, consistent with photosubstitution studies previously reported by us and others.17,57,58 In particular, the work of Kwon et al. revealed that one of the cyano groups can be substituted by an alkyl group when the cyanoarene-based PCs are irradiated in the presence of DIPEA; in the case of 4CzIPN, the nitrile was photosubstituted by an ethyl group as the major product, and a methyl group as the minor product.59 Although 4CzIPN is observed to photodegrade similarly in all four solvents, the absorption spectra of 2CzPN are considerably less changed in THF relative to DCM, DMF, and MeCN. This observation is consistent with 2CzPN achieving a higher yield in THF of 31% compared to the 2–11% yield in the other solvents, implying that the photodegradation occurring in the other solvents inhibits the photocatalysis, likely due to the poorer spectral overlap with the 456 nm excitation source. Based on these photostability results and literature precedent, we preliminarily concluded that amine sacrificial donors can react with all of the PCs, thereby altering their photophysics. This therefore renders this class of reaction as more of a photosensitization than one that is widely described as photocatalysis.
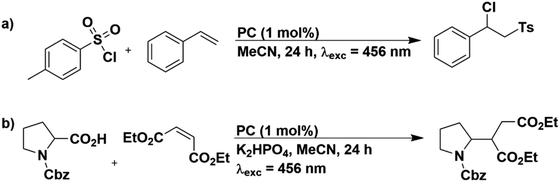
In order to assess the photostability of the PCs when applied to reactions not involving sacrificial amine donors, we selected two other photoredox reactions: an atom transfer radical addition (ATRA) reaction of tosyl chloride with styrene (Fig. 9a)60 and the Giese type addition of N-Cbz-Pro to diethyl maleate (Fig. 9b).61,62
The 1H NMR yields obtained in these reactions for the PCs in MeCN are provided in Tables S21 and S22.† For both reactions, literature yields could be replicated in our set-up; in the ATRA reaction [Ru(bpy)3](PF6)2 achieved 75% yield of the target product, which is comparable to the literature yield of 80%.60 Similarly, in the Giese type addition reaction, 4CzIPN yielded 77% of the functionalized product using our set-up, comparable to the 80% literature yield.61 The UV-Vis absorption profiles before and after irradiation for all PCs employed in both reactions are given in Fig. S67–S69.† In general, PCs that did not promote the formation of the target product or did so only in very low yields largely retained their UV-Vis absorption profile. For example, 4CzIPN yielded only 3% of the target product in the ATRA reaction and the UV-Vis absorption spectrum is essentially unchanged after the reaction compared to that prior to irradiation (Fig. S68b†). In contrast, when PCs can photocatalyze the reaction, the UV-Vis absorption profile is significantly altered. This is exemplified for [Ru(bpy)3](PF6)2, which produces 75% of the product in the ATRA reaction and after irradiation, the characteristic MLCT absorption band at 450 nm is blue-shifted to 400 nm (Fig. S67a†).
To check whether the PCs were degrading into the same species, irrespective of reaction conditions, the post-irradiation absorption spectra were overlayed for [Ir(ppy)2(dtbbpy)]PF6, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6 and 4CzIPN (Fig. S71†), since these PCs were shown to produce the desired product in at least two of the three photoredox reactions considered. For the metal complexes, no trend could be discerned; however, for 4CzIPN, the post-irradiation absorption spectra obtained in both the pinacol coupling reaction and the Giese type addition reaction are almost identical (Fig. S71d†), implying that for this PC, the photodegradation product is similar. This is very likely linked to the photosubstitution of the nitrile group of 4CzIPN for an alkyl group from DIPEA in the pinacol coupling, as shown by Kwon et al.,59 and for an alkyl group from the decarboxylated N-Cbz-Pro, as shown by the work of König and co-workers.57
The photostability experiments from the ATRA and the Giese type addition reactions indicated that photodegradation of the PCs is not limited to reactions containing sacrificial amine donors, but instead is observed more widely in these other representative photoredox reactions. As such, it is clear that the photostability of the PC should be assessed as a required experiment by the photocatalysis community. Recently, a few reports have explored the complex issue of photostability, for example Wenger et al. noted that functionalised isoacridone dyes tended to decompose upon irradiation in solution;63 the predominant photodecomposition pathway was proposed to involve the T1 state, which is sensitized in the presence of anthracene. The photodegradation of the PC may be a reason why some PCs perform poorer than expected in certain reactions, despite having suitable thermodynamic properties, which may explain why trends in PC yields cannot always be rationalized by factors such as redox potentials. The photodegradation of the PC means that it becomes difficult to ascertain whether the parent compound and/or its photodegraded version is/are the active PC(s) in the reaction. Alternatively, it is possible that photodegradation is an unproductive side reaction and is detrimental to the photocatalysis.
Photocatalysis testing – photoinduced energy transfer (PEnT)
To understand the influence of solvent in a PEnT mechanism, the popular E/Z isomerisation of alkenes was chosen as a representative reaction. Four of the aforementioned PCs, [Ru(bpy)3](PF6)2, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6 and 4CzIPN were investigated in the E/Z isomerisation of stilbene across all four solvents (Fig. 10). The E and Z isomers of stilbene have ET of 2.2 and 2.5 eV, respectively, determined from the absorption spectra in ethyl iodide.64 Therefore, to maximise the yield of the Z-isomer, simplistically the PC should have an ET within the range of 2.2–2.5 eV. This allows the PC to chemoselectively transfer energy to the E alkene, converting it to the Z isomer without also sensitizing the Z isomer back to the E isomer.The experimentally derived ET values of the PCs (Table 1) can then be applied to the target E/Z isomerization of E-stilbene (Fig. 10). Given that the ET of the E and Z isomers of stilbene are determined from the onset of the absorption spectra in ethyl iodide and the ET of the PCs are determined from the onset of emission spectra (steady-state or gated emission at 77 K), the triplet energies are not strictly directly comparable since different methods and solvents have been used for their estimation. However, since triplet energies only serve to predict whether an energy transfer reaction is thermodynamically feasible, these PC ET values are still a useful tool to gauge the success or lack thereof for each PC.
It was predicted that [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, [Cu(dmp)(xantphos)]PF6 and 4CzIPN (ET = 2.74 eV, 2.53 eV and 2.62 eV in MeCN, respectively) should all be capable of inducing the E/Z isomerisation, although are unlikely to do so chemoselectively owing to their too high ET values. [Cu(dmp)(xantphos)]PF6, however, has a lower ET value of 2.43 eV in THF, indicating that in this solvent, an improved Z/E ratio should theoretically be obtained relative to the other solvents. [Ru(bpy)3](PF6)2 has a much lower ET (2.19–2.25 eV), close to the value of E-stilbene (2.2 eV), hence may also be able to selectively sensitize E-stilbene.
The 1H NMR yields are summarised in Table 3. Both [Ru(bpy)3](PF6)2 and 4CzIPN performed excellently in the reaction, yielding an average of 90 and 88%, respectively, of the Z isomer. These results are consistent with those obtained in the literature (87% for [Ru(bpy)3](PF6)2 using a 26 W CFL as the irradiation source in DMF for 18 h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 and 87% for 4CzIPN using λexc = 390 nm in DMF for 18 h).17 The use of [Cu(dmp)(xantphos)]PF6 yielded 84% of the target Z-alkene, while [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 yielded only an average 60% of the target product. In the reverse reaction, the Z/E isomerisation of Z-stilbene, a yield of 7% of E-stilbene was obtained using [Ru(bpy)3](PF6)2 in MeCN (Table S24†), with 89% of Z-stilbene remaining. This mirrors the results of the forward E/Z isomerisation reaction; 91% of Z-isomer is formed when irradiating E-stilbene, indicating that the same Z/E ratio is obtained whether irradiating E-stilbene or Z-stilbene for 24 h.
65 and 87% for 4CzIPN using λexc = 390 nm in DMF for 18 h).17 The use of [Cu(dmp)(xantphos)]PF6 yielded 84% of the target Z-alkene, while [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 yielded only an average 60% of the target product. In the reverse reaction, the Z/E isomerisation of Z-stilbene, a yield of 7% of E-stilbene was obtained using [Ru(bpy)3](PF6)2 in MeCN (Table S24†), with 89% of Z-stilbene remaining. This mirrors the results of the forward E/Z isomerisation reaction; 91% of Z-isomer is formed when irradiating E-stilbene, indicating that the same Z/E ratio is obtained whether irradiating E-stilbene or Z-stilbene for 24 h.
| 1H NMR yield/% | |||||
|---|---|---|---|---|---|
| THF | DCM | DMF | MeCN | Average | |
| a Yields determined by 1H NMR analysis of the crude reaction mixture using 1,3,5-trimethoxybenzene as the internal standard. Yields and errors provided are the average of at least two independent runs. The average yield across all solvents is provided in the average column. b Yield from ref. 65 using a 26 W CFL as the excitation source in DMF for 18 h. c Yield from ref. 17 using λexc = 390 nm in DMF for 18 h. | |||||
| [Ru(bpy)3](PF6)2 | 88 ± 1 | 91 ± 1 | 91 ± 2 (87)b | 91 ± 3 | 90 ± 1 |
| [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 | 63 ± 1 | 57 ± 1 | 58 ± 1 | 60 ± 1 | 60 ± 2 |
| [Cu(dmp)(xantphos)]PF6 | 84 ± 1 | 82 ± 1 | 83 ± 1 | 85 ± 1 | 84 ± 1 |
| 4CzIPN | 86 ± 1 | 89 ± 1 | 89 ± 1 (87)c | 89 ± 2 | 88 ± 1 |
For all four PCs investigated, the outcome of the reaction was shown to be insensitive to solvent choice as yields varied by no more than 6% across the four solvents. Notably, despite remarkably different ET values for [Ru(bpy)3](PF6)2 and 4CzIPN (2.21 and 2.62 eV in MeCN, respectively), the yield of Z-stilbene is nearly identical (91% and 89% in MeCN, respectively). These results highlight the inadequacy of using the PC triplet energies as a predictive tool for the efficiency of the DET PEnT. Indeed, the failure of the ET of the PC as an accurate predictor of identifying the best PC for the E/Z isomerization of alkenes has previously been discussed by Singh et al.66 In their study, no correlation could be found between the phosphorescence peak maxima of seven iridium PCs and the log(Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E) ratio of the alkene.67 It was found that as the steric volume of the PC increases, the Z
E) ratio of the alkene.67 It was found that as the steric volume of the PC increases, the Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E ratio decreases, which was rationalized by the authors as poorer orbital overlap between the substrate and the PC as the PC size increases, an essential requirement for efficient DET. Our work and this example illustrate the pitfalls of only using ET as a tool for predicting the efficiencies of DET reactions when both orbital and spectral overlap intrinsically effect the DET rates.
E ratio decreases, which was rationalized by the authors as poorer orbital overlap between the substrate and the PC as the PC size increases, an essential requirement for efficient DET. Our work and this example illustrate the pitfalls of only using ET as a tool for predicting the efficiencies of DET reactions when both orbital and spectral overlap intrinsically effect the DET rates.
To verify the photostability of the PC under the PEnT reaction conditions, we obtained the UV-vis absorption spectra of the E/Z isomerization reactions before and after irradiation for all four PCs across all four solvents (Fig. S72–S75†). In this case, the PCs appear to be photostable since minimal changes in the absorption spectra were observed.
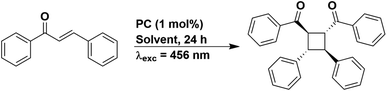
Since solvent choice appeared to not be relevant to the E/Z isomerisation of stilbene, we also chose to evaluate the [2 + 2] cycloaddition of trans-chalcone (Fig. 11), a reaction that also proceeds via a DET mechanism.68 The PC is proposed to transfer energy to trans-chalcone (ET = 2.13 eV in 1,4-dioxane),68 which subsequently dimerizes. A PC used in the literature, [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, yielded 50% of the target product using 1,4-dioxane as the solvent. Using our set-up, the yield obtained for [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 varied from 40%, 37%, 22% and 31% in THF, DCM, DMF and MeCN, respectively (Table S25†), despite this PC having comparable triplet energies across all these four solvents (2.73–2.75 eV). We then attempted to correlate these yields to the emission lifetime of [Ir(dF(CF3)ppy)2(dtbbpy)]PF6, since the PC needs to be suitably long-lived to undergo a collisional interaction with trans-chalcone and the DET. The emission lifetimes in THF, DCM, DMF and MeCN are 2014, 2007, 1597, and 2311 ns, respectively (Table S18†). The same yields (within error) were achieved in THF and DCM, which correlates with their similar emission lifetimes in these two solvents, while DMF provides the lowest yield and has the shortest emission lifetime. Despite [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 having the longest emission lifetime in MeCN, the yield in this solvent was intermediate of those obtained for the other solvents.
Similar to the PET studies, we assessed PC stability by acquiring the UV-vis absorption spectra before and after irradiation; however, the UV-vis absorption profile of trans-chalcone (Fig. S78†) dominated the spectra, making it difficult to identify any changes to the absorption behaviour of the PC. We thus turned to 19F NMR spectroscopy as a tool to probe whether the PC [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 had degraded. In all solvents, the peaks observed in the 19F NMR spectra post-irradiation aligned with those for the as-synthesized PC (Fig. S81 and S82†). This firstly indicates that at least with respect to the dF(CF3)ppy ligand, the PC remains unchanged. Given that the chemical shifts of the 19F resonances of the dF(CF3)ppy ligand are very subtly sensitive to changes in the ancillary ligand [see Fig. S79 and S80† for a comparison of the 19F NMR spectra of [Ir(dF(CF3)ppy)2(dtbbpy)]PF6 with [Ir(dF(CF3)ppy)2(bpy)]PF6], the unaltered 19F NMR spectra post irradiation implies that this PC is photostable under these reaction conditions.
Conclusions
We have shown that the optoelectronic properties of a representative selection of popular photocatalysts are sensitive to solvent polarity. This sensitivity was observed to be more pronounced for the metal complexes in comparison to the organic PCs, as predicted by DFT. Given that variation of up to 270 mV was observed in the redox potentials as a function of solvent, greater attention should be paid to this factor when assessing the thermodynamic feasibility of a PC to react with a particular substrate. To better predict the capacity of a PC to undergo specific SET with a substrate, optoelectronic properties should be measured in the same solvent used for the subsequent photochemistry, this will also facilitate the rationalisation of proposed reaction mechanisms.We investigated the impact of solvent in model electron transfer and energy transfer photocatalysis reactions. In the case of photoredox catalysis, the PCs that could successfully form the target product were found to photodegrade, and as shown in the pinacol coupling reaction, this occurred regardless of solvent choice. The implication of this observation is that photochemical reactions involving radical chemistry appear to alter the properties of the PC and in these cases, it would be more appropriate to call these reactions photosensitized rather than photocatalyzed. Significantly greater attention should be paid to the photostability of PC in photoredox catalysis as this may explain why some PCs may perform better than others.
In relation to energy transfer reactions, the solvent choice had a more pronounced effect on the ET for PCs that have low-lying CT excited states. For both PEnT reactions, no photodegradation of the PC was observed; however, ET was found to be an unreliable indicator of PEnT efficiency. This study reveals that the long-held dogma used to identify the optimal PCs for both PET and PEnT reactions should be questioned.
Although we attempted to provide a framework for making an informed decision on the best solvent for a photocatalysis reaction, no model could be established. An empirical screening approach for solvent choice unfortunately remains the best way to determine the most appropriate solvent for a particular reaction.
Data availability
The research data supporting this publication can be accessed at: https://doi.org/10.17630/790b47ab-b5f6-4184-9a92-e5ada861627c.Author contributions
OSL conducted DFT calculations. FM conducted UV-vis absorption spectroscopy and electrochemical measurements. MAB conducted steady-state emission measurements. LC conducted time-resolved emission measurements and Stern–Volmer quenching studies. MAB and FM completed the photocatalysis reactions. MAB conducted the photostability studies. The manuscript was written by MAB, OSL, AS and EZ-C. All authors read and approved the completed manuscript. E. Z.-C. conceived the project. M. A. B., F. M., L. C. performed all of the experiments and acquired all of the optoelectronic characterization. F. M. and O. S. L. performed the DFT studies. All authors contributed to the authorship of the text.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the University of St Andrews, Syngenta, and the EPSRC Centre for Doctoral Training in Critical Resource Catalysis (CRITICAT and EaSI-CAT) for financial support [PhD studentship to “M. B.”; grant code: EP/L016419/1]. We thank the European Union H2020 research and innovation program under the Marie S. Curie Grant Agreement (PhotoReAct, No. 956324) for support to E. Z.-C. We thank Umicore AG for the gift of materials. We thank Prof. Denis Jacquemin for helpful discussions.References
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 10075–10166 CrossRef CAS PubMed.
- C. R. J. Stephenson, T. P. Yoon and D. W. C. MacMillan, Visible Light Photocatalysis in Organic Chemistry, Wiley-VCH, Germany, 2018 Search PubMed.
- J. Twilton, C. C. Le, P. Zhang, M. H. Shaw, R. W. Evans and D. W. C. Macmillan, Nat. Rev. Chem., 2017, 1, 0052 CrossRef CAS.
- G. E. M. Crisenza and P. Melchiorre, Nat. Commun., 2020, 11, 803–806 CrossRef PubMed.
- M. A. Bryden and E. Zysman-Colman, Chem. Soc. Rev., 2021, 50, 7587–7680 RSC.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 29, 21–31 RSC.
- D. Rehm and A. Weller, Berichte der Bunsengesellschaft, 1969, 73, 834–839 CrossRef CAS.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259–271 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850 CrossRef CAS.
- F. Strieth-kalthoff, M. J. James, M. Teders, L. Pitzer and F. Glorius, Chem. Soc. Rev., 2018, 47, 7190–7202 RSC.
- K. M. Kadish, L.-L. Wang, A. Thuriere, L. Giribabu, R. Garcia, E. Van Caemelbecka and J. L. Bear, Inorg. Chem., 2003, 42, 8309–8319 CrossRef CAS PubMed.
- K. Sasaki, T. Kashimura, M. Ohura, Y. Ohsaki and N. Ohta, J. Electrochem. Soc., 1990, 137, 2437–2443 CrossRef CAS.
- A. Defusco, N. Minezawa, L. V. Slipchenko, F. Zahariev and M. S. Gordon, J. Phys. Chem. Lett., 2011, 2, 2184–2192 CrossRef CAS.
- N. Mataga, Y. Kaifu and M. Koizumi, Bull. Chem. Soc. Jpn., 1956, 29, 465–470 CrossRef CAS.
- M. A. Bryden, F. Millward, T. Matulaitis, D. Chen, M. Villa, A. Fermi, S. Cetin, P. Ceroni and E. Zysman-Colman, J. Org. Chem., 2023, 88, 6364–6373 CrossRef CAS PubMed.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- A. Juris and V. Balzani, Coord. Chem. Rev., 1998, 84, 85–277 CrossRef.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- P. L. Dos Santos, D. Chen, P. Rajamalli, T. Matulaitis, D. B. Cordes, A. M. Z. Slawin, D. Jacquemin, E. Zysman-Colman and I. D. W. Samuel, ACS Appl. Mater. Interfaces, 2019, 11, 45171–45179 CrossRef CAS PubMed.
- C. A. Parker and C. G. Hatchard, Trans. Faraday Soc., 1961, 57, 1894–1904 RSC.
- C. Li, C. F. R. MacKenzie, S. A. Said, A. K. Pal, M. A. Haghighatbin, A. Babaei, M. Sessolo, D. B. Cordes, A. M. Z. Slawin, P. C. J. Kamer, H. J. Bolink, C. F. Hogan and E. Zysman-Colman, Inorg. Chem., 2021, 60, 10323–10339 CrossRef CAS PubMed.
- M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed.
- L. Bergmann, New Emitters for OLEDs: The Coordination- and Photo-Chemistry of Mononuclear Neutral Copper(I) Complexes, Logos Verlag, Berlin, 2016 Search PubMed.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- M. Heberle, S. Tschierlei, N. Rockstroh, M. Ringenberg, W. Frey, H. Junge, M. Beller, S. Lochbrunner and M. Karnahl, Chem.–Eur. J., 2017, 23, 312–319 CrossRef CAS PubMed.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Peterssom, H. Nakatsuji, X. Li, M. Caricato, A. V Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian Inc, Wallingford CT, 2019 Search PubMed.
- C. G. Zhan, J. A. Nichols and D. A. Dixon, J. Phys. Chem. A, 2003, 107, 4184–4195 CrossRef CAS.
- P. K. Nayak and N. Periasamy, Org. Electron., 2009, 10, 1396–1400 CrossRef CAS.
- D. K. A. Phan Huu, S. Saseendran and A. Painelli, J. Mater. Chem. C, 2022, 10, 4620–4628 RSC.
- R. Ishimatsu, S. Matsunami, K. Shizu, C. Adachi, K. Nakano and T. Imato, J. Phys. Chem. A, 2013, 117, 5607–5612 CrossRef CAS PubMed.
- The full width half maximum (FWHM) of the Kessil LEDs used in this report (390 nm and 456 nm) are approximately 20 and 25 nm, respectively, as estimated from the emission spectra of the LEDs provided by Kessil.
- F. Abdel-Rahman, B. Okeremgbo, F. Alhamadah, S. Jamadar, K. Anthony and M. A. Saleh, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2017, 52, 433–439 CrossRef CAS PubMed.
- B. Bardi, D. Giavazzi, E. Ferrari, A. Iagatti, M. Di Donato, D. K. A. Phan Huu, F. Di Maiolo, C. Sissa, M. Masino, A. Lapini and A. Painelli, Mater. Horiz., 2023, 10, 4172–4182 RSC.
- S. Nigam and S. Rutan, Appl. Spectrosc., 2001, 55, 362A–370A CrossRef CAS.
- M. S. Lowry, J. I. Goldsmith, J. D. Slinker, R. Rohl, R. A. Pascal, G. G. Malliaras and S. Bernhard, Chem. Mater., 2005, 17, 5712–5719 CrossRef CAS.
- S. Ladouceur, D. Fortin and E. Zysman-Colman, Inorg. Chem., 2011, 50, 11514–11526 CrossRef CAS PubMed.
- E. Crovini, R. Dhali, D. Sun, T. Matulaitis, T. Comerford, A. M. Z. Slawin, C. Sissa, F. Azzolin, F. Di Maiolo, A. Painelli and E. Zysman-Colman, J. Mater. Chem. C, 2023, 11, 8284–8292 RSC.
- Y. Zhang, M. Heberle, M. Wächtler, M. Karnahl and B. Dietzek, RSC Adv., 2016, 6, 105801–105805 RSC.
- The low temperature nature of this experiment restricts the solvent choice; 2-MeTHF was used in replacement of THF and BuCN was used instead of MeCN. Unfortunately, no alternative for DCM or DMF could be found.
- This assumes that the time-gated emission spectrum at 77 K results from the phosphorescence from the T1 state.
- R. Ishimatsu, et al., Extrapolate activation energies for 4CzIPN in a range of solvent polarities, J. Phys. Chem. A, 2013, 117(27), 5607–5612 CrossRef PubMed , for example, in MeCN this value was found to be 0.10 eV at 300 K..
- K. Teegardin, J. I. Day, J. Chan and J. Weaver, Org. Process Res. Dev., 2016, 20, 1156–1163 CrossRef CAS PubMed.
- M. S. Oderinde, J. Kempson, D. Smith, N. A. Meanwell, E. Mao, J. Pawluczyk, M. Vetrichelvan, M. Pitchai, A. Karmakar, R. Rampulla, J. Li, T. G. Murali Dhar and A. Mathur, Eur. J. Org. Chem., 2020, 41–46 CrossRef CAS.
- A. E. Hurtley, Z. Lu and T. P. Yoon, Angew. Chem., Int. Ed., 2014, 53, 8991–8994 CrossRef CAS PubMed.
- V. Grosshenny, A. Harriman, F. M. Romero and R. Ziessel, J. Phys. Chem., 1996, 100, 17472–17484 CrossRef CAS.
- S. Huang, Q. Zhang, Y. Shiota, T. Nakagawa, K. Kuwabara, K. Yoshizawa and C. Adachi, J. Chem. Theory Comput., 2013, 9, 3872–3877 CrossRef CAS PubMed.
- M. Nakajima, E. Fava, S. Loescher, Z. Jiang and M. Rueping, Angew. Chem., Int. Ed., 2015, 54, 8828–8832 CrossRef CAS PubMed.
- L. Schmid, C. Kerzig, A. Prescimone and O. S. Wenger, JACS Au, 2021, 1, 819–832 CrossRef CAS PubMed.
- K. Izutsu, Electrochemistry in Nonaqueous Solutions, Wiley-VCH, Weinheim, 2009 Search PubMed.
- J. C. Bawden, P. S. Francis, S. DiLuzio, D. J. Hayne, E. H. Doeven, J. Truong, R. Alexander, L. C. Henderson, D. E. Gómez, M. Massi, B. I. Armstrong, F. A. Draper, S. Bernhard and T. U. Connell, J. Am. Chem. Soc., 2022, 144, 11189–11202 CrossRef CAS PubMed.
- K. J. Doyle, H. Tran, M. Baldoni-Olivencia, M. Karabulut and P. E. Hoggard, Inorg. Chem., 2008, 47, 7029–7034 CrossRef CAS PubMed.
- A. Alvarez-Martin, S. Trashin, M. Cuykx, A. Covaci, K. De Wael and K. Janssens, Dyes Pigm., 2017, 145, 376–384 CrossRef CAS.
- M. Majek, F. Filace and A. J. Von Wangelin, Beilstein J. Org. Chem., 2014, 10, 981–989 CrossRef PubMed.
- S. Grotjahn and B. König, Org. Lett., 2021, 23, 3146–3150 CrossRef CAS PubMed.
- C. Prentice, J. Morrison, A. D. Smith and E. Zysman-Colman, Chem.–Eur. J., 2022, 29, e202202998 CrossRef PubMed.
- Y. Kwon, J. Lee, Y. Noh, D. Kim, Y. Lee, C. Yu, J. C. Roldao, S. Feng, J. Gierschner, R. Wannemacher and M. S. Kwon, Nat. Commun., 2023, 14, 92 CrossRef CAS PubMed.
- A. Hossain, S. Engl, E. Lutsker and O. Reiser, ACS Catal., 2019, 9, 1103–1109 CrossRef CAS.
- E. Speckmeier, T. G. Fischer and K. Zeitler, J. Am. Chem. Soc., 2018, 140, 15353–15365 CrossRef CAS PubMed.
- L. Chu, C. Ohta, Z. Zuo and D. W. C. MacMillan, J. Am. Chem. Soc., 2014, 136, 10886–10889 CrossRef CAS PubMed.
- B. Pfund, V. Hutskalova, C. Sparr and O. S. Wenger, Chem. Sci., 2023, 11180–11191 RSC.
- W. G. Herkstroeter and D. S. McClure, J. Am. Chem. Soc., 1968, 90, 4522–4527 CrossRef CAS PubMed.
- J. Lu, B. Pattengale, Q. Liu, S. Yang, W. Shi, S. Li, J. Huang and J. Zhang, J. Am. Chem. Soc., 2018, 140, 13719–13725 CrossRef CAS PubMed.
- A. Singh, C. J. Fennell and J. D. Weaver, Chem. Sci., 2016, 7, 6796–6802 RSC.
- The photocatalysis was conducted in DMF, at 65 degrees celcius using blue LEDs as the irradiation source.
- T. Lei, C. Zhou, M. Huang, L. Zhao, B. Yang, C. Ye, H. Xiao, Q. Meng, V. Ramamurthy, C. Tung and L. Wu, Angew. Chem., Int. Ed., 2017, 129, 15609–15612 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures, electrochemistry, UV-vis absorption, and photoluminescence spectra (room temperature steady state, 77 K steady state, 77 K gated emission and room temperature time resolved photoluminescence spectra), details of DFT calculations (including coordinates of optimised structures), photocatalysis procedure, photostability studies and Stern–Volmer quenching studies. See DOI: https://doi.org/10.1039/d3sc06499a |
| This journal is © The Royal Society of Chemistry 2024 |