Open Access Article
Open Access ArticleThe glass phase in the grain boundary of Na3Zr2Si2PO12, created by gallium modulation†
Chenjie
Lou
a,
Wenda
Zhang
ab,
Jie
Liu
a,
Yanan
Gao
a,
Xuan
Sun
ac,
Jipeng
Fu
 cd,
Yongchao
Shi
a,
Ligang
Xu
a,
Huajie
Luo
e,
Yongjin
Chen
a,
Xiang
Gao
a,
Xiaojun
Kuang
cd,
Yongchao
Shi
a,
Ligang
Xu
a,
Huajie
Luo
e,
Yongjin
Chen
a,
Xiang
Gao
a,
Xiaojun
Kuang
 b,
Lei
Su
a and
Mingxue
Tang
b,
Lei
Su
a and
Mingxue
Tang
 *ae
*ae
aCenter for High Pressure Science and Technology Advanced Research, Beijing 100193, China. E-mail: mingxue.tang@hpstar.ac.cn
bCollege of Materials Science and Engineering, Guilin University of Technology, Guilin 541004, China
cChina Key Laboratory of Rare Earth Optoelectronic Materials and Devices of Zhejiang Province, Institute of Optoelectronic Materials and Devices, China Jiliang University, Hangzhou 310018, China
dNarada Power Source Co., Ltd., Hangzhou 311305, China
eUniversity of Science and Technology Beijing, Beijing 100083, China
First published on 31st January 2024
Abstract
Na3Zr2Si2PO12 has been proven to be a promising electrolyte for solid-state sodium batteries. However, its poor conductivity prevents application, caused by the large ionic resistance created by the grain boundary. Herein, we propose an additional glass phase (Na–Ga–Si–P–O phase) to connect the grain boundary via Ga ion introduction, resulting in enhanced sodium-ion conduction and electrochemical performance. The optimized Na3Zr2Si2PO12-0.15Ga electrolyte exhibits Na+ conductivity of 1.65 mS cm−1 at room temperature and a low activation energy of 0.16 eV, with 20% newly formed glass phase enclosing the grain boundary. Temperature-dependent NMR line shapes and spin-lattice relaxation were used to estimate the Na self-diffusion and Na ion hopping. The dense glass-ceramic electrolyte design strategy and the structure–dynamics–property correlation from NMR, can be extended to the optimization of other materials.
Introduction
Spurred by the fast growing demand for large-scale storage such as power grids and electric vehicles, sodium-ion batteries have received considerable attention due to being sodium rich, low cost and environmentally-friendly.1 Simultaneously, solid-state batteries assembled with solid electrolytes have become a hot topic because they can effectively inhibit the occurrence of fire and explosions.2–5 Therefore, designing proper solid-state sodium electrolytes (SSSEs) and understanding their working mechanism are key to improving the performance of solid-state sodium batteries (SSSBs). Among the reported SSSEs, NASICON (Na Super Ionic CONductor) family, which were first reported by Hong and Goodenough in 1976,6,7 show high ionic conductivity, good chemical and thermal stability. NASICON can generally be written as Na1+xZr2SixP3−xO12 (0 ≤ x ≤ 3), occupying a rhombohedral structure with space group R/3c. However, for compositions in the range 1.8 ≤ x ≤ 2.2, NASICON present with a monoclinic structure (space group C2/c).6–9 It is claimed that Na1+xZr2SixP3−xO12 achieves the highest total conductivity when x = 2.7,8,10–13 The NASICON structure consists of octahedral ZrO6 and tetrahedral PO43−/SiO44−, sharing a corner oxygen and demonstrating a 3D ion transport channel, which provides efficient conduction pathways for Na ions. The substitution of the Zr4+ site can effectively adjust the lattice parameters and hence the ion conductivity of Na3Zr2Si2PO12, such as Ca2+,14 Sc3+,15 Ge4+ (ref. 16) and Nb5+.17 However, lattice fine-tuning can play a limited role in the improvement of ion conductivity when considering grain boundaries within Na3Zr2Si2PO12. The introduction of a second phase is a smart strategy to pack the grain boundary (GB) and improve conductivity as a whole, such as NaF,18 Na2B4O7 (ref. 19) and Na2SiO3.20 Saito and coworkers investigated the influence of trivalent ions on NASICON-type Na1.5M0.5Zr1.5(PO4)3 (M = Al3+, Ga3+, Cr3+, Sc3+, Fe3+, In3+, Yb3+, Y3+); the lattice parameters showed negligible changes when increasing Al3+ and Ga3+ content because of the formation of grain boundary phases rather than the substitution for Zr4+ ions.21 However, the distribution, content and presence of a new phase, together with the structure–activity correlation are still not clearly understood.Herein, we propose a NASICON-type glass-ceramic electrolyte Na3Zr2Si2PO12-xGa (x = 0–0.2) (NZSP-xGa). By introducing the Ga ion, a binder-like glass phase (Na–Ga–Si–P–O phase) is formed surrounding the grains, resulting in an enhanced density electrolyte pellet, corresponding to improved total conductivity. Solid state nuclear magnetic resonance (ssNMR) with multiple isotopes is employed to characterize and quantify the structure evolution upon Ga modulation at an atomic scale. Additionally, 23Na NMR spectra and relaxation at various temperatures are performed and analyzed to evaluate the Na self-diffusion and Na ion hopping, in order to correlate the glass phase and the dynamics of the Na ion.
Results and discussion
Crystal structure and ionic transportation
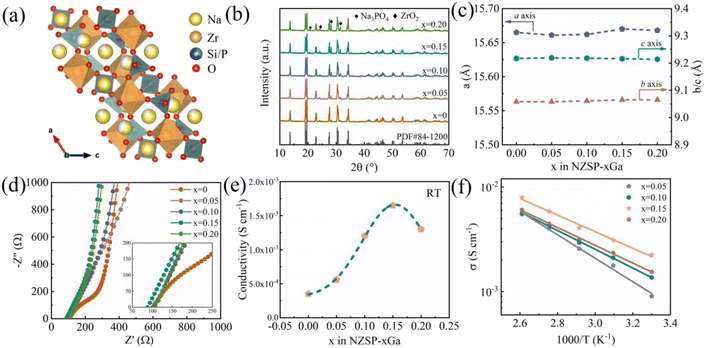
The structure of NZSP is shown in Fig. 1a and a 3D frame work is presented for delivering ions. As shown in Fig. 1b, all diffraction peaks in the X-ray diffraction (XRD) pattern can be indexed to a monoclinic structure (PDF# 84-1200) with a space group of C2/c except for the minor Na3PO4 and ZrO2. The NASICON does not transit from the monoclinic phase to rhomboidal phase with the introduction of Ga ions because no substitution is observed between the Ga and Zr atoms,15 which is also supported by the large reaction energy of 0.6144 eV from the DFT calculations with the structure shown in Fig. S1† and results shown in Table S1.† Fig. S2† displays the partial enlargement of the XRD patterns, showing the monoclinic structure. ZrO2 is a common residual phase for all types of NASICON samples and is difficult to avoid.15,18,22Fig. S3† shows the typical refined curves of NZSP-xGa, the Rietveld refined parameters are listed in Tables S2–S6.† The refined parameters of NZSP-0.15Ga are a = 15.6703 Å, b = 9.0654 Å and c = 9.2162 Å (Table 1). All Refined lattice parameters of NZSP-xGa are summarized in Fig. 1c, showing no significant change with the increase of Ga content.21 Scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy mappings (EDS) are shown in Fig. S4 and S5–S8,† showing all elements are uniformly distributed and the density grows with increasing Ga ion. The conductivities of NZSP-xGa were analyzed by AC impedance. As displayed in Fig. 1d for the Nyquist plots at room temperature, the NZSP-0Ga sample shows a linear tail at low frequency and a semicircle at higher frequency. While NZSP-0.15Ga presents a linear tail and a distorted semi-circle, which is possibly caused by the significantly decreased grain boundary from the filled glass phase. The inset displays the enlarged high frequency region of the corresponding impedance spectra. The total conductivities of NZSP-xGa at room temperature (RT) are shown in Fig. 1e, with the maximum conductivity σtotal = 1.65 mS cm−1 when x = 0.15. With the increase of Ga, the content of the non-conductive phase (ZrO2 and Na3PO4) gradually increases. Therefore, it is vital to optimize the content that the glass phase can fill the grain boundary with maximum conductivity; the NZSP-0.2Ga shows lower conductivity than that of NZSP-0.15Ga due to the overweight non-conductive phase caused by the Ga. Activation energy (Ea) was further evaluated via AC impedance spectra obtained at different temperatures. Fig. S9† exhibits the impedance spectra of NZSP-0.15Ga in the temperature range 30 °C to 110 °C. Arrhenius plots of NZSP-xGa are shown in Fig. 1f and the Ea of NZSP-0.15Ga is calculated to be the smallest value at 0.16 eV, among these NZSP-xGa samples (Table S7†). The growth of lithium dendrites in solid-state batteries is claimed to result in the high electronic conductivity of solid electrolytes.23 The electronic conductivity of NZSP-0.15Ga was measured using DC polarization (Fig. S10†), with a value of 3 × 10−8 S cm−1 at RT, which can suppress the formation of dendrites.23 The cyclic voltammetry (CV) curve of the stainless steel (SS)| NZSP-0.15Ga| Na cell shown in Fig. S11† indicates that the NZSP-0.15Ga occupies a wide electrochemical stability window, larger than 6 V.
| Sample | Space group | a (Å) | b (Å) | c (Å) |
|---|---|---|---|---|
| 0Ga | C2/c | 15.665 | 9.058 | 9.217 |
| 0.05Ga | C2/c | 15.661 | 9.058 | 9.219 |
| 0.10Ga | C2/c | 15.662 | 9.061 | 9.218 |
| 0.15Ga | C2/c | 15.670 | 9.065 | 9.216 |
| 0.20Ga | C2/c | 15.668 | 9.065 | 9.214 |
The formation of glass phase
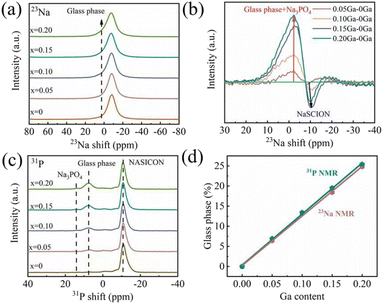
To further evaluate the reason for the increase of ionic transportation properties, scanning electron microscope (SEM), high resolution transmission electron microscope (HRTEM) and selected area electron diffraction (SAED) measurements were applied to observe the cross-section of the NZSP-0Ga and NZSP-0.15Ga. Fig. 2a is the SEM image of NZSP-0.15Ga, a molten glass phase filled the grains in NZSP-0.15Ga, resulting in improved connection inside the electrolyte. The HRTEM shown in Fig. 2b clearly reveals the existence of the glass phase. Fig. S12† shows the lattice fringes of 0.45 nm for the (0 2 0) plane of NZSP-0.15Ga. The dark-field STEM image and EDS mappings of NZSP-0.15Ga contain both a crystalline and glass phase (Fig. 2c and d). The Ga element mainly distributes in the glass phase, which is also supported by the EDS point scanning (Fig. S13†). EDS linear scanning across this particle is shown in Fig. S14† as well. The content of Na and P are relatively homogenous in both the NASICON and glass phases. The Si element has a slightly larger concentration in the glass phase. The sudden increase in Zr content in NASICON is possibly due to the presence of ZrO2. Additionally, the HRTEM, SAED and EDS mapping of NZSP-0Ga are shown in Fig. S15.† The corresponding SAED patterns of the NASICON and glass phases in Fig. 2c are shown in Fig. 2e and f, respectively. There are no obvious lattice fringes and diffraction spots in Fig. 2f, indicative of the existence of the glass phase.Nuclear magnetic resonance (NMR) has proven to be a suitable technology to gain the local structure and surrounding structure on the atomic scale, together with atomic dynamics.24–28 Here, solid state magic angle spinning (MAS) 23Na NMR spectra (Fig. 3a) show a broad signal at −8 ppm for all NASICON samples due to fast exchange occurring on three Na sites.15 With the increase of Ga content, a 23Na signal at around 0–10 ppm is observed because of the formation of the glass phase. The comparison is plotted in Fig. S16† for better clarification. The glass phase grows with the increase of Ga content. Fig. 3b shows the spectra of NZSP-xGa subtracted from the spectrum of NZSP-0Ga, displaying the glass phase at around 0–10 ppm. Fig. 3c shows the well-resolved 31P NMR spectra, the main peak at around −11 ppm is assigned to the NASICON phase, the signals at 7 ppm and 13.5 ppm are attributed to the glass phase and Na3PO4, respectively.18 The contents of the glass phase and Na3PO4 impurity increase with the increase of Ga. From the 31P NMR spectra, the glass phase is also highlighted as a zirconium-deficient impurity.29,30 This is caused by the modulation of Ga, as Zr elements precipitate out as ZrO2. Since ZrO2 has been proved to be nonconductive,31,32 it is necessary to adjust the content of the glass phase for filling the GB and obtaining an optimized total conductivity. It is difficult to obtain quantitative information on the glass phase via some conventional methods, such as Rietveld refinement. However, solid state NMR is an effective tool to obtain quantitative information on the glass phase. The deconvolution of 23Na spectra and 31P spectra are shown in Fig. S17 and S18,† the simulation results are listed in Table S8 and S9.† And the corresponding quantitative results are plotted in Fig. 3d, from which both 23Na and 31P NMR analysis show good linearity with the change of Ga content, indicating that the glass phase can be regulated by adjusting the content of Ga elements. As such, the best ionic conductivity is determined when x = 0.15 Ga content with glass phase occupancy of 20%, as shown in Fig. 3d.
NMR spin-lattice relaxometry (SLR) is a key parameter to determine the lattice environment and ionic motion in solid-state electrolytes.33–38 Since 23Na is a quadrupolar nuclear method, a saturation recovery technique is employed to obtained a reliable relaxation time (T1) (Fig. S19†),39 the glass phase shows relatively slow relaxation (long T1 in 10−2 s) compared to the NASICON phase (10−4 s). Spin-lattice relaxation (T1) of 23Na for all NZSP-xGa were measured and biexponentially fitted, except for the one without Ga addition (Fig. 4a), the inset shows a zoom-in for clear evidence of the extra glass phase. The fitted relaxation times are shown in Fig. 4b, with the typical values (T1) of the NASICON and glass phase in the range 4 × 10−4 s and 2 × 10−2 s, respectively. As a short T1 means fast ion motion in NASICON,15 therefore, the movement of Na ions in NASICON is faster than that in the glass phase.
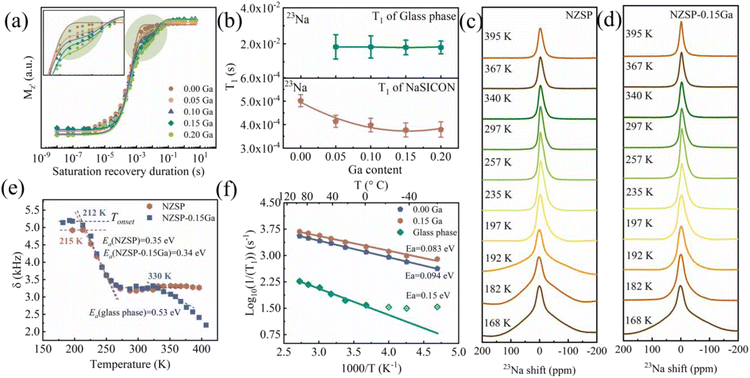 | ||
| Fig. 4 Spin-lattice relaxation time T1 and Na+ ion dynamics of NASICON and the glass phase. (a) 23Na saturation recovery fitting curve for the data obtained at room temperature of NZSP-0.15Ga. (b) The fitting results of 23Na T1 relaxation time of NZSP-0.15Ga. (c) and (d) Static 23Na spectra of NZSP and NZSP-0.15Ga at different temperatures. (e) 23Na NMR line widths δ of the central line versus temperature. (f) Arrhenius plot of the 23Na NMR SLR rates of NZSP-0Ga and NZSP-0.15Ga. The solid line is the fit according to eqn (2). The derivation of the data at the lower temperature range is not used for the fit.33 | ||
The minimum T1 is observed for NZSP-0.15Ga, indicating the fastest Na ion movement as expected from AC impedance. Fig. S20† shows the saturation recovery of the 31P signals. T1 (NASICON) ≈ 70 s and T1 (glass phase) ≈ 4 s are analyzed. The T1 value of the glass phase is much smaller than that of NASICON, being similar than the results of the crystalline and amorphous T1 in other studies.40
To investigate Na+ ion dynamics in NZSP-0Ga and NZSP-0.15Ga electrolytes, 23Na NMR line shapes and 23Na spin–lattice relaxation (SLR) rates at different temperatures were recorded and analyzed. The analysis of static 23Na NMR central lines at different temperatures provides information on ion dynamics that average the dipole–dipole interactions of the Na nuclei.41,42 Variable-temperature 23Na NMR lines under static conditions of NZSP-0Ga and NZSP-0.15Ga are shown in Fig. 4c and d. It is interesting that at low temperatures (<192 for NZSP-0Ga and <168 K for NZSP-0.15Ga), there is a broad component with a linewidth larger than 25 kHz, which could be the quadrupole intensities arising from the interaction of the spin −3/2 nucleus with electric field gradients produced by the electric charge distribution in the neighbourhood of the Na nuclei.43
Below 210 K, the 23Na spectra usually show a two-component line shape: narrowed Lorentzian-like and broad Gaussian-like lines superimposed. The Gaussian-like line shows the distribution of resonance frequencies due to non-averaged dipolar Na–Na coupling.43 The full width at half-maximum (FWHM) (Fig. 4e) of the wide line is more than 4.92 kHz and 5.20 kHz for NZSP-0Ga and NZSP-0.15Ga, respectively. This is from the so-called rigid lattice line width, corresponding to Na+ jump rates (τ−1) smaller than ω/2π. With the increase of temperature, 23Na–23Na dipole–dipole interactions are continuously averaged due to the enhanced motion of the Na spins. The onset temperature Tonset of motion narrowing (MN) is about 210 K, at which the central transition linewidths of both phases decreases significantly. The NMR central line width of NZSP-0Ga and NZSP-0.15Ga follow the typical MN, accompanied by a change in line shape from Gaussian to Lorentzian.
When the temperature is higher than 272 K, dipole–dipole interactions are completely averaged due to sufficiently fast Na diffusion, the peak becomes extremely narrow. The residual line width is mainly governed by the inhomogeneities of the external magnetic field. A narrowing of the width δ which is already decreased to 3.2 kHz for both NZSP-0Ga and NZSP-0.15Ga when the temperature reaches 287 K. Upon further increasing the temperature to 400 K, the FWHM of NZSP-0Ga remains almost constant. However, the linewidths of NZSP-0.15Ga show an obvious drop at 330 K. The first drop at 212 K and the second drop at 330 K in the FWHM are attributed to the averaged 23Na–23Na dipole–dipole interactions in NASICON and the glass phase, respectively. The linewidth finally decreased to 2.19 kHz when the temperature reaches 404 K. The further reduction of FWHM extracted from MN indicates that the formed glass phase improved the connection among the grain boundaries and thus resulted in accelerated Na motion and promoted the Na+ jump rates. The 23Na NMR spectra under MAS at different temperatures were also examined (Fig. S21†), and the quadrupole coupling constant (CQ) changes with the temperature increases.44
To evaluate the Na+ dynamics, the Waugh–Fedin expression was used to calculate the activation energy Ea, based on the evolution of static spectra, for the estimation of the hopping capability,45
| EMNa = 1.617 × 10−3 × Tonset. | (1) |
According to the Waugh–Fedin expression, the activation energy Ea of NZSP-0Ga, NZSP-0.15Ga and the glass phase are 0.35 eV, 0.3s4 eV and 0.53 eV, respectively. The activation energies of NZSP-0Ga and NZSP-0.15Ga are almost the same, indicating the reduced overall activation energy is due to the filled glass phase, which is in good agreement with the phenomenon probed by spin–lattice relaxometry rates NMR, as shown below.
According to the equation put forward by Bloembergen, Purcell, and Pound (BPP), at the temperature of Tonset, the mean Na+ jump rate (τ−1) can be roughly estimated via the relation τ−1 ≈ ΔωRL, where τ−1 is the jump rate, and ΔωRL/2π = ΔνRL, which is the rigid lattice line-width.
From Fig. 4e, ΔνRL (NZSP-0Ga) = 4.92 kHz is determined for the pure NZSP at 215 K, and ΔνRL (NZSP-0.15Ga) = 5.2 kHz is acquired at 212 K for the Ga modulated NZSP. The corresponding jump rates are, τ−1(NZSP-0Ga) = 3.1 × 104 s−1 at 215 K and τ−1(NZSP-0.15Ga) = 3.3 × 104 s−1 at 212 K, respectively, indicating that the jump rate of NZSP-0.15Ga is higher than that of NZSP-0Ga at low temperature.
In general, the temperature dependence of jump rate τ−1 follows an Arrhenius relation,
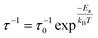 | (2) |
Spin–lattice relaxometry (SLR) rates (1/T1) are directly related to the Na+ dynamics and jumping process.46,4723Na NMR SLR rates of NZSP-0Ga and NZSP-0.15Ga at different temperatures were measured and analyzed for activation energy Ea as shown in Fig. 4f.36,38 The activation energy Ea of NZSP-0Ga and NZSP-0.15Ga at the low-temperature flank were fitted using eqn (3). the Ea of the entire NZSP-0.15Ga system is obtained as 0.083 eV, being lower than that of NZSP-0Ga (0.094 eV), and the Ea of the pure glass phase in NZSP-0.15Ga is calculated as about 0.15 eV, much higher than that of NASICON. The Ea values obtained from SLR NMR rates is lower than the results from the AC impedance and MN curve, because the Ea at the low-temperature flank corresponds to the short-range Na+ diffusion, which is lower than the value of long-range Na+ diffusion.33,38 And the laboratory SLR rate is sensitive to the fast (localized) jump process, which displays a lower activation energy.41 Nevertheless, the trend of activation energies from relaxation and linewidth are similar, and the Ea of the glass phase is slightly higher. However, the overall activation energy of the whole pellet is reduced due to the filled glass phase.
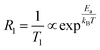 | (3) |
Application in solid-state sodium batteries
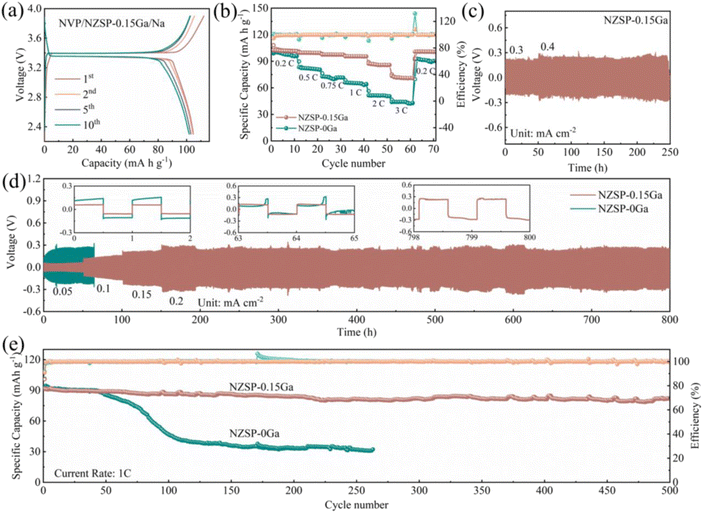
Solid-state batteries were constructed using Na3V2(PO4)3 (NVP) and metallic Na for electrochemical tests. As displayed in Fig. 5a, the charge/discharge curve of the Na| NZSP-0.15Ga| NVP battery shows that the initial charge and discharge capacities at 0.2C are 112 and 105 mA h g−1, respectively. An initial coulombic efficiency of 93.8% and good rate performance are achieved (Fig. 5b). The discharge capacities are 108, 102, 98, 96, 89 and 75 mA h g−1 at cycling rates of 0.2C, 0.5C, 0.75C, 1C, 2C and 3C, respectively. Under a cycling rate of 0.5C (Fig. S22†), the specific discharge capacities are maintained at 92.3 mA h g−1 after 100 cycles with the average coulombic efficiency of 99%, together with a capacity retention of 92%. To check the long-term cycling performance of NZSP-0.15Ga, the solid-state battery was measured at 1C (Fig. 5e), after 500 cycles, the capacity remains at 82.1 mA h g−1 with the average coulombic efficiency remaining at almost 100% with a capacity retention of 90%. These good performances reveal that NZSP-0.15Ga is a good electrolyte candidate for solid-state batteries. In addition, to investigate the electrochemical stability of NZSP-0.15Ga, the Na| NZSP-0.15Ga| Na symmetric cell was cycled at a current density of 0.3–0.4 mA cm−2 at room temperature. The Na| NZSP-0.15Ga| Na cell retains its capacity over 250 h at RT as shown in Fig. 5c; the long term galvanostatic cycling was performed under current densities of 0.05–0.2 mA cm−2 (Fig. 5d), demonstrate long term Na plating and stripping for more than 800 h, also at RT. In comparison, the Na| NZSP-0Ga| Na symmetrical cell exhibits a short circuit after cycling for 65 h. The electrochemical performances of NZSP-0.15Ga proposed in this work are also competitive when compared to the reported work listed in Table S10.†The stability of the electrolyte is also investigated using the comparison of NMR spectra at pristine and cycled states. As shown in Fig. S23,† there is no obvious change detected for the 23Na, 31P and 29Si NMR spectra before and after cycling, indicating that NZSP-0.15Ga maintained a good structure during the electrochemical reaction process. The 23Na T1 relaxation time of NASICON (3.6 × 10−4 s) and the glass phase (1.4 × 10−2 s) after cycling is shown in Fig. S24,† being similar to the values of the pristine electrolyte. The TEM and SEM of NZSP-0.15Ga after cycling are shown in Fig. S25 and S26,† which also show that the structure is maintained after 100 cycles.
Conclusions
In summary, we obtained a NASICON-type glass-ceramics electrolyte NZSP, with the introduction of Ga ions. An optimum total conductivity of 1.65 mS cm−1 at room temperature and activation energy of 0.16 eV, were achieved when x = 0.15 (NZSP-0.15Ga). The formed glass phase can be quantified by both 23Na and 31P NMR analysis and is assigned to the zirconium-deficient Na–Ga–Si–P–O phase. The Na+ ion dynamics of NZSP and the glass phase were studied by temperature-dependent NMR spectral shape and spin–lattice relaxation in the laboratory frame. The laboratory spin–lattice relaxation rate shows low activation energies (0.08–0.15 eV) because it is sensitive to a fast (localized) jump process. The motional narrowing (MN) curve provides a rough estimate of the activation energy, but information on Na ion motion and diffusion processes can be obtained effectively from the change of FWHM. The results show that the glass phase in NASICON-type glass-ceramics electrolyte can help to improve the Na motion and Na+-ion jump rates, with decreased activation energy. Excellent rate and cycle performances further demonstrate the superiority of the Ga modulated NASICON-type glass-ceramics electrolyte. This work provides a new idea for the preparation of glass-ceramic electrolytes, and proves that local structure and dynamic information from NMR plays an important role in the design and understanding of novel phases for advancing energy materials.Data availability
All experimental procedures and ESI tables and figures are available in the ESI.†Author contributions
Chenjie Lou performed the synthesis, characterisation, data curation, formal analysis, investigation, methodology and writing. Wenda Zhang, Jie Liu, Yanan Gao, Xuan Sun, Yongchao Shi, Jipeng Fu, Huajie Luo, Yongjin Chen and Xiang Gao performed the XRD, TEM characterisation and analysis. Ligang Xu helped to perform the NMR experiment and analyze the data. Xiaojun Kuang and Lei Su helped to write the manuscript. Mingxue Tang was responsible for the conceptualization, funding acquisition, methodology, project administration, supervision and writing. The manuscript was written by Chenjie Lou and Mingxue Tang with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 22090043 and 21974007). The Natural Science Foundation (Grant No. LQ21E020006) and the Key Research and Development Program of Zhejiang Province (Grant No. 2021C01175) are also appreciated.Notes and references
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, Angew. Chem., Int. Ed., 2015, 54, 3431–3448 CrossRef CAS PubMed.
- C. Zhao, L. Liu, X. Qi, Y. Lu, F. Wu, J. Zhao, Y. Yu, Y.-S. Hu and L. Chen, Adv. Energy Mater., 2018, 8, 1703012 CrossRef.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- R. Li, D. Jiang, P. Du, C. Yuan, X. Cui, Q. Tang, J. Zheng, Y. Li, K. Lu, X. Ren, S. Gao and X. Zhan, Chem. Sci., 2022, 13, 14132–14140 RSC.
- Y. Lu, L. Li, Q. Zhang, Y. Cai, Y. Ni and J. Chen, Chem. Sci., 2022, 13, 3416–3423 RSC.
- H.-P. Hong, Mater. Res. Bull., 1976, 11, 173–182 CrossRef CAS.
- J. Goodenough, H.-P. Hong and J. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS.
- J. Boilot, J. Salanié, G. Desplanches and D. Le Potier, Mater. Res. Bull., 1979, 14, 1469–1477 CrossRef CAS.
- H. Kohler, H. Schulz and O. Melnikov, Mater. Res. Bull., 1983, 18, 1143–1152 CrossRef CAS.
- S. Ydeandersen, J. Lundsgaard, L. Moller and J. Engell, Solid State Ionics, 1984, 14, 73–79 CrossRef CAS.
- R. Gordon, G. Miller, B. Mcentire, E. Beck and J. Rasmussen, Solid State Ionics, 1981, 3–4, 243–248 CrossRef CAS.
- Y. Huang, Interdisciplinary Materials, 2022, 1, 323–329 CrossRef.
- L. Zhang, Y. Liu, Y. You, A. Vinu and L. Mai, Interdisciplinary Materials, 2023, 2, 91–110 CrossRef.
- Y. Lu, J. A. Alonso, Q. Yi, L. Lu, Z. L. Wang and C. Sun, Adv. Energy Mater., 2019, 9, 1901205 CrossRef.
- F. Sun, Y. Xiang, Q. Sun, G. Zhong, M. N. Banis, Y. Liu, R. Li, R. Fu, M. Zheng, T. Sham, Y. Yang, X. Sun and X. Sun, Adv. Funct. Mater., 2021, 31, 2102129 CrossRef CAS.
- Z. Zhang, Z. Zou, K. Kaup, R. Xiao, S. Shi, M. Avdeev, Y. Hu, D. Wang, B. He, H. Li, X. Huang, L. F. Nazar and L. Chen, Adv. Energy Mater., 2019, 9, 1902373 CrossRef CAS.
- Y. Liu, L. Liu, J. Peng, X. Zhou, D. Liang, L. Zhao, J. Su, B. Zhang, S. Li, N. Zhang, Q. Ma and F. Tietz, J. Power Sources, 2022, 518, 230765 CrossRef CAS.
- Y. Shao, G. Zhong, Y. Lu, L. Liu, C. Zhao, Q. Zhang, Y.-S. Hu, Y. Yang and L. Chen, Energy Storage Mater., 2019, 23, 514–521 CrossRef.
- Y. Zhao, C. Wang, Y. Dai and H. Jin, Nano Energy, 2021, 88, 106293 CrossRef CAS.
- H. Wang, G. Zhao, S. Wang, D. Liu, Z. Mei, Q. An, J. Jiang and H. Guo, Nanoscale, 2022, 14, 823–832 RSC.
- Y. Saito, K. Ado, T. Asai, H. Kageyama and O. Nakamura, Solid State Ionics, 1992, 58, 327–331 CrossRef CAS.
- P. Jiang, G. Du, Y. Shi, F. She, P. Guo, G. Qian, X. Lu, F. Xie and X. Lu, Chem. Eng. J., 2023, 451, 138771 CrossRef CAS.
- F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187–196 CrossRef CAS.
- J. Zheng, M. Tang and Y. Hu, Angew. Chem., Int. Ed., 2016, 55, 12538–12542 CrossRef CAS PubMed.
- K. Hui, J. Fu, J. Liu, Y. Chen, X. Gao, T. Gao, Q. Wei, C. Li, H. Zhang and M. Tang, Carbon Energy, 2021, 3, 709–720 CrossRef CAS.
- P. Ding, L. Wu, Z. Lin, C. Lou, M. Tang, X. Guo, H. Guo, Y. Wang and H. Yu, J. Am. Chem. Soc., 2023, 145, 1548–1556 CrossRef CAS PubMed.
- B. Karasulu, S. P. Emge, M. F. Groh, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2020, 142, 3132–3148 CrossRef CAS PubMed.
- G. Sun, C. Lou, B. Yi, W. Jia, Z. Wei, S. Yao, Z. Lu, G. Chen, Z. Shen, M. Tang and F. Du, Nat. Commun., 2023, 14, 6501 CrossRef CAS PubMed.
- C. Jäger, G. Scheler, U. Sternberg, S. Barth and A. Feltz, Chem. Phys. Lett., 1988, 147, 49–52 CrossRef.
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J.-N. Chotard, C. P. Grey, M. S. Islam and C. Masquelier, Chem. Mater., 2018, 30, 2618–2630 CrossRef CAS.
- F. Krok, Solid State Ionics, 1989, 36, 251–254 CrossRef CAS.
- S. Naqash, F. Tietz, E. Yazhenskikh, M. Müller and O. Guillon, Solid State Ionics, 2019, 336, 57–66 CrossRef CAS.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302 CrossRef.
- C. Yu, S. Ganapathy, J. Hageman, L. van Eijck, E. R. H. van Eck, L. Zhang, T. Schwietert, S. Basak, E. M. Kelder and M. Wagemaker, ACS Appl. Mater. Interfaces, 2018, 10, 33296–33306 CrossRef CAS PubMed.
- V. Epp, Ö. Gün, H.-J. Deiseroth and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 7123 RSC.
- S. Ganapathy, C. Yu, E. R. H. van Eck and M. Wagemaker, ACS Energy Lett., 2019, 4, 1092–1097 CrossRef CAS.
- C. Yu, Y. Li, M. Willans, Y. Zhao, K. R. Adair, F. Zhao, W. Li, S. Deng, J. Liang, M. N. Banis, R. Li, H. Huang, L. Zhang, R. Yang, S. Lu, Y. Huang and X. Sun, Nano Energy, 2020, 69, 104396 CrossRef CAS.
- J. Fu, S. Wang, J. Liang, S. H. Alahakoon, D. Wu, J. Luo, H. Duan, S. Zhang, F. Zhao, W. Li, M. Li, X. Hao, X. Li, J. Chen, N. Chen, G. King, L.-Y. Chang, R. Li, Y. Huang, M. Gu, T.-K. Sham, Y. Mo and X. Sun, J. Am. Chem. Soc., 2022, jacs.2c09446 Search PubMed.
- Q. Zhou, B. Xu, P. Chien, Y. Li, B. Huang, N. Wu, H. Xu, N. S. Grundish, Y. Hu and J. B. Goodenough, Small Methods, 2020, 4, 2000764 CrossRef CAS.
- K. Okada, D. Hirai, S. Kumada, A. Kosugi, Y. Hayashi and Y. Onuki, J. Pharm. Sci., 2019, 108, 451–456 CrossRef CAS PubMed.
- K. Hogrefe, N. Minafra, W. G. Zeier and H. M. R. Wilkening, J. Phys. Chem. C, 2021, 125, 2306–2317 CrossRef CAS PubMed.
- M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291–9300 CrossRef CAS.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378 RSC.
- H. J. Jakobsen, A. R. Hove, H. Bildsøe and J. Skibsted, J. Magn. Reson., 2006, 180, 170–177 CrossRef CAS PubMed.
- J. S. Waugh and I. Fedin, Soviet Physics-Solid State, 1963, 4, 1633–1636 Search PubMed.
- H. Mehrer, Diffusion in solids: fundamentals, methods, 2007, https://xs2.studiodahu.com/scholar?q=Mehrer%2C+H.+Diffusion+in+solids%3A+fundamentals%2C+methods%2C+materials%2C+diffusion-controlled+processes%3B+Springer+Science+%26+Business+Media%2C+2007%3B+vol.+155 Search PubMed.
- T. Springer and R. E. Lechner, in Diffusion in Condensed Matter, ed. P. Heitjans and J. Kärger, Springer-Verlag, Berlin/Heidelberg, 2005, pp. 93–164 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section; Rietveld refinement; SEM and EDS as well as elemental mappings; SAED analysis; Nyquist plots, DC polarization and CV curve; NMR analysis; etc. See DOI: https://doi.org/10.1039/d3sc06578b |
| This journal is © The Royal Society of Chemistry 2024 |