Open Access Article
Open Access ArticleWhat defines electrophilicity in carbonyl compounds†
F. Matthias
Bickelhaupt
 *abc and
Israel
Fernández
*abc and
Israel
Fernández
 *d
*d
aDepartment of Chemistry and Pharmaceutical Sciences, AIMMS, Vrije Universiteit Amsterdam, The Netherlands. E-mail: f.m.bickelhaupt@vu.nl
bInstitute for Molecules and Materials (IMM), Radboud University, Nijmegen, The Netherlands
cDepartment of Chemical Sciences, University of Johannesburg, South Africa
dDepartamento de Química Orgánica, Centro de Innovación en Química Avanzada (ORFEO-CINQA), Facultad de Ciencias Químicas, Universidad Complutense de Madrid Ciudad Universitaria, 28040-Madrid, Spain. E-mail: israel@quim.ucm.es
First published on 6th February 2024
Abstract
The origin of the electrophilicity of a series of cyclohexanones and benzaldehydes is investigated using the activation strain model and quantitative Kohn–Sham molecular orbital (MO) theory. We find that this electrophilicity is mainly determined by the electrostatic attractions between the carbonyl compound and the nucleophile (cyanide) along the entire reaction coordinate. Donor–acceptor frontier molecular orbital interactions, on which the current rationale behind electrophilicity trends is based, appear to have little or no significant influence on the reactivity of these carbonyl compounds.
Introduction
The terms electrophile and nucleophile, coined by Ingold1 based on the earlier definitions by Lewis and Weehler,2 constitute a pivotal concept in chemistry. An electrophile typically refers to a species able to form a chemical bond by accepting an electron pair from a nucleophile. In this sense, the concept of electrophilicity, i.e. the relative reactivity of an electrophilic reagent, is, according to the IUPAC Goldbook,3 directly related to Lewis acidity. Despite that, whereas Lewis acidity is a thermodynamic quantity (measured by relative equilibrium constants), electrophilicity is assumed to be a kinetic quantity (estimated from relative rate constants).From an experimental point of view, the estimation and/or quantification of the relative electrophilicity of a system was challenging until the pioneering work by Mayr and co-workers,4 who introduced nucleophilicity/electrophilicity scales based on the experimental rate constants for a large series of polar reactions. Thus, their famous equation log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sN(N + E), characterizes electrophiles by the parameter E (electrophilicity) and nucleophiles by two solvent-dependent quantities, N (nucleophilicity) and sN (susceptibility).
k = sN(N + E), characterizes electrophiles by the parameter E (electrophilicity) and nucleophiles by two solvent-dependent quantities, N (nucleophilicity) and sN (susceptibility).
From a theoretical point of view, electrophilicity is mostly quantified by means of the so-called Conceptual Density Functional Theory (CDFT) developed by Parr and Yang.5 Within the CDFT approach, the electrophilicity index (ω)6 is defined in terms of the chemical hardness (η)5,7 and the chemical potential (μ)5,7 as:
| ω = μ2/2η |
This finding therefore suggests that the widely accepted orbital control (especially, the energy of the π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) molecular orbital)11 is not the main factor governing the relative electrophilicity of carbonyl compounds. A similar finding was found by us recently in a completely different context but also involving carbonyl groups.12,13 It was found that the catalysis of various reactions, such as Diels–Alder or Michael addition, is not, as widely accepted, caused by enhancing FMO interactions, but by a significant reduction in the Pauli repulsion between the key occupied molecular orbitals of the reactants, as revealed by the Activation Strain Model (ASM)14 of reactivity and energy decomposition analysis (EDA) methods.15 The lack of fundamental knowledge on the ultimate factors controlling the electrophilicity of carbonyl compounds, especially ketones and aldehydes,10 prompted us to apply our combined ASM-EDA approach to reveal the origin of the relative electrophilicity of carbonyl compounds.
O) molecular orbital)11 is not the main factor governing the relative electrophilicity of carbonyl compounds. A similar finding was found by us recently in a completely different context but also involving carbonyl groups.12,13 It was found that the catalysis of various reactions, such as Diels–Alder or Michael addition, is not, as widely accepted, caused by enhancing FMO interactions, but by a significant reduction in the Pauli repulsion between the key occupied molecular orbitals of the reactants, as revealed by the Activation Strain Model (ASM)14 of reactivity and energy decomposition analysis (EDA) methods.15 The lack of fundamental knowledge on the ultimate factors controlling the electrophilicity of carbonyl compounds, especially ketones and aldehydes,10 prompted us to apply our combined ASM-EDA approach to reveal the origin of the relative electrophilicity of carbonyl compounds.
Results and discussion
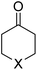
We first focused on the relative electrophilicity of cyclohexanones, species experimentally investigated by Mayr and co-workers.10 By studying the so-called Darzens condensation,16 a process related to the useful Corey–Chaykovsky epoxidation,17 the authors found that electrophilicity of the parent cyclohexanone (E = −19.9) increases with the presence of substituents in 4-relative position to the carbonyl group (Table 1). In particular, the cyclohexanones where the CH2 group in position 4 was replaced by an oxygen or sulphur atom were found to exhibit an enhanced electrophilicity (E = −17.9 and −16.9, respectively).| 1-X | E | ω | ΔG‡ | ΔEintc | ΔEPaulic | ΔVelstatc | ΔEorbc | ΔEorb(ρ1)c | |
|---|---|---|---|---|---|---|---|---|---|
| a Values measured by Mayr and co-workers (see ref. 10). b Computed at the M06-2X/TZ2P//M06-2X/6-311+G* level. Values within parentheses refer to the local electrophilicity index (ωc) taken from ref. 10. c Computed at the same consistent C⋯C bond-forming distance of 2.06 Å. d Not determined. | |||||||||
|
1-CH2 | −19.9 | 0.93 (0.15) | 6.5 | −20.7 | 94.5 | −60.0 | −55.2 | −47.1 |
| 1-NMe | −18.4 | 0.88 (0.15) | 5.1 | −22.5 | 95.2 | −62.1 | −55.5 | −47.2 | |
| 1-C(O2C2H4) | −18.2 | 0.92 (0.15) | 5.4 | −22.8 | 94.8 | −61.8 | −55.8 | −46.9 | |
| 1-O | −17.9 | 1.01 (0.18) | 2.7 | −24.5 | 95.5 | −64.9 | −55.0 | −47.3 | |
| 1-S | −16.9 | 0.92 (0.19) | 1.0 | −25.9 | 95.6 | −65.7 | −55.9 | −47.4 | |
| 1-PMe | n.d.d | 0.89 (n.d.)d | 2.8 | −24.3 | 95.0 | −62.8 | −56.4 | −47.4 | |
| 1-C(Me2) | n.d.d | 0.93 (n.d.)d | 5.8 | −21.4 | 95.0 | −60.4 | −56.0 | −47.2 | |
The reasons behind the electrophilicity trend shown in Table 1 are however essentially unknown so far. Therefore, we decided to explore the simple addition of cyanide (CN−) to the cyclohexanones 1 depicted in Table 1. This particular nucleophile was selected because is a potent nucleophile (N = 16.27 in the Mayr's scale)4d and its contribution to the total strain is practically negligible. In all cases, the process leads to the formation of the corresponding cyanohydrin adducts through transition states where the CN− nucleophile follows the expected Bürgi–Dunitz angle (ca. 110°).18 Interestingly, the computed activation barriers follow the same trend as the electrophilic E values, confirming that the substitution at the 4-position enhances the electrophilicity of the parent cyclohexanone (particularly for 1-O and 1-S, which exhibit rather low activation barriers). At variance, and in agreement with the findings by Mayr and co-workers,10 no correlation was found between the computed barriers and the Parr's global electrophilicity indices, ω. No correlation was found either when using the local electrophilicity indices at the carbonyl carbon atom (see Table 1).10
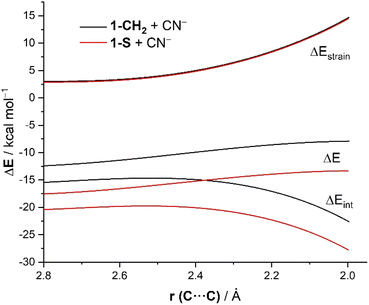
To understand the origins of the enhanced reactivity of substituted cyclohexanones with respect to the parent system, we applied next the Activation Strain Model (ASM)14 of reactivity. To this end, we compared the cyanide addition reactions involving the extreme situations represented by cyclohexanone 1-CH2 and its sulphur-substituted counterpart 1-S. Fig. 1 shows the corresponding Activation Strain Diagrams (ASDs) for both transformations from the early stages of the processes up to the corresponding transition states projected onto the (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )C⋯C(N) bond-forming distance. From the data in Fig. 1, it becomes evident that the higher reactivity of 1-S is not at all due to the strain term, which is nearly identical for both reactions but derives exclusively from a stronger interaction between the reagents along the entire reaction coordinate. The crucial role of the interaction between the reagents is further confirmed by the good linear relationship (correlation coefficient of 0.96) observed when plotting the computed barriers versus the ΔEint values (computed at the same consistent C⋯C bond-forming distance of 2.06 Å).
)C⋯C(N) bond-forming distance. From the data in Fig. 1, it becomes evident that the higher reactivity of 1-S is not at all due to the strain term, which is nearly identical for both reactions but derives exclusively from a stronger interaction between the reagents along the entire reaction coordinate. The crucial role of the interaction between the reagents is further confirmed by the good linear relationship (correlation coefficient of 0.96) observed when plotting the computed barriers versus the ΔEint values (computed at the same consistent C⋯C bond-forming distance of 2.06 Å).
The stronger interaction computed for the processes involving the substituted cyclohexanones in comparison with the parent system may be initially traced to the stabilization of the key π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) molecular orbital. For instance, whereas the energy of this π*–LUMO in 1-CH2 is 0.37 eV, a lower value was computed for the more reactive systems 1-O (0.24 eV) or 1-S (0.19 eV). This should be translated into stronger orbital interactions in these substituted systems. However, from the Energy Decomposition Analysis (EDA) data in Table 1, computed at the same consistent C⋯C bond-forming distance, it becomes clear that the total orbital interaction term, ΔEorb, remains nearly constant (ca. −55.5 kcal mol−1, average). This indicates that the HOMO(CN−) → π*–LUMO(C
O) molecular orbital. For instance, whereas the energy of this π*–LUMO in 1-CH2 is 0.37 eV, a lower value was computed for the more reactive systems 1-O (0.24 eV) or 1-S (0.19 eV). This should be translated into stronger orbital interactions in these substituted systems. However, from the Energy Decomposition Analysis (EDA) data in Table 1, computed at the same consistent C⋯C bond-forming distance, it becomes clear that the total orbital interaction term, ΔEorb, remains nearly constant (ca. −55.5 kcal mol−1, average). This indicates that the HOMO(CN−) → π*–LUMO(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) interaction, is not, as traditionally assumed, the main factor controlling the interaction between the reactants and explains why the Parr's ω values fail to measure the electrophilicity of these cyclic ketones.
O) interaction, is not, as traditionally assumed, the main factor controlling the interaction between the reactants and explains why the Parr's ω values fail to measure the electrophilicity of these cyclic ketones.
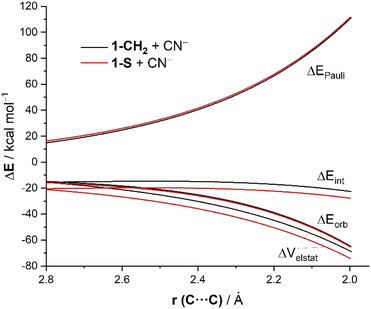
The same conclusion can be drawn by analyzing the evolution of the EDA terms along the entire reaction coordinate (i.e. from the beginning of the process up to the corresponding transition states). As shown in Fig. 2, the stronger interaction computed for the addition of cyanide to 1-S in comparison to the analogous process involving the parent cyclohexanone 1-CH2 is due neither to the Pauli repulsion nor the orbital interactions, which are nearly identical for both processes, but exclusively to stronger electrostatic attractions between the reactants along the entire reaction coordinate. The ΔVelstat term is not only the dominant attractive term but also its evolution parallels that of the total interaction energy. Indeed, a very good linear correlation (correlation coefficient of 0.93) was found when plotting the ΔEint term vs. the ΔVelstat (at the same consistent C⋯C bond-forming distance of 2.06 Å). Therefore, the relative electrophilicity of the studied cyclohexanones seems to be exclusively defined, not by orbital interactions as traditionally considered, but by the electrostatic interactions between the electrophile and the nucleophile.
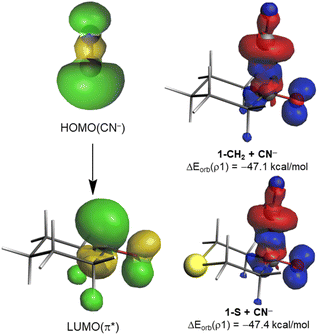
The origin of the counterintuitive computed nearly identical orbital interactions for all the considered cyclohexanones deserves further analysis. We first applied the Natural Orbital from Chemical Valence (NOCV)19 extension of the EDA method to not only visualize but also quantify the main orbital interactions involved in the considered nucleophilic addition. As expected, the EDA-NOCV method indicates that the main contribution to the total ΔEorb term (>90%) comes from the HOMO(nucleophile) → π*–LUMO(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) molecular orbital interaction (Fig. 3). Interestingly, the corresponding associated stabilization energies, ΔEorb(ρ1), are nearly identical for all processes (see Table 1 and Fig. 3 for the values of the representative reactions involving 1-CH2 and 1-S at the same consistent C⋯C bond-forming distance). This is mainly due to the rather similar π*–LUMO(C
O) molecular orbital interaction (Fig. 3). Interestingly, the corresponding associated stabilization energies, ΔEorb(ρ1), are nearly identical for all processes (see Table 1 and Fig. 3 for the values of the representative reactions involving 1-CH2 and 1-S at the same consistent C⋯C bond-forming distance). This is mainly due to the rather similar π*–LUMO(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) orbital energy (see above) and the nearly identical 〈HOMO(CN−)|π*–LUMO(C
O) orbital energy (see above) and the nearly identical 〈HOMO(CN−)|π*–LUMO(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)〉 overlap (S = 0.33 and 0.34 for 1-CH2 and 1-S; values computed at the same point r(C⋯C) along the reaction coordinate). As a result, the total electronic charge transferred from the HOMO(CN−) to the π*–LUMO(C
O)〉 overlap (S = 0.33 and 0.34 for 1-CH2 and 1-S; values computed at the same point r(C⋯C) along the reaction coordinate). As a result, the total electronic charge transferred from the HOMO(CN−) to the π*–LUMO(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) hardly varies in all systems (0.646e vs. 0.647e for 1-CH2 and 1-S, respectively, at the same C⋯C bond-forming distance). This circumstance renders the molecular orbital interaction and, consequently, ω irrelevant in defining the actually measured or computed relative electrophilicity of the considered cyclohexanones.
O) hardly varies in all systems (0.646e vs. 0.647e for 1-CH2 and 1-S, respectively, at the same C⋯C bond-forming distance). This circumstance renders the molecular orbital interaction and, consequently, ω irrelevant in defining the actually measured or computed relative electrophilicity of the considered cyclohexanones.
It is reasonable to assume that the above results might be biased due to the charged nature of the cyanide nucleophile. To check whether the electrostatic attractions also play a crucial role in analogous reactions involving neutral nucleophiles, we compared the processes involving 1-CH2 and 1-S with the ylide nucleophiles Me2S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CN (N = 16.23), Me2S
CH–CN (N = 16.23), Me2S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CO2Me (N = 15.85) and Me2S
CH–CO2Me (N = 15.85) and Me2S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–p(NO2)C6H4 (N = 18.42), which present similar N values as cyanide.4d In addition, we also considered the negatively charged [Cl–CH–SO2Ph]− nucleophile, used in the experiments involving these cyclohexanones,10 because the negative charge is much more delocalized than in cyanide. From the data in Table 2, 1-S is confirmed to be a better electrophile than 1-CH2 according to the lower barriers computed for all the nucleophilic additions. Interestingly, regardless of the nucleophile the interaction energy between the electrophile and the nucleophile (computed at a consistent C⋯C bond-forming distance close to that of the corresponding transition states) is systematically stronger (i.e. more negative) for the processes involving 1-S. Once again, it is found that even when neutral nucleophiles are involved, the crucial electrostatic term, ΔVelstat, is not only the major contribution to the total ΔEint but is also comparatively more stabilizing for the reactions involving 1-S. Therefore, these results further confirm the crucial role of electrostatic attractions in controlling the electrophilicity of these cyclohexanones.
CH–p(NO2)C6H4 (N = 18.42), which present similar N values as cyanide.4d In addition, we also considered the negatively charged [Cl–CH–SO2Ph]− nucleophile, used in the experiments involving these cyclohexanones,10 because the negative charge is much more delocalized than in cyanide. From the data in Table 2, 1-S is confirmed to be a better electrophile than 1-CH2 according to the lower barriers computed for all the nucleophilic additions. Interestingly, regardless of the nucleophile the interaction energy between the electrophile and the nucleophile (computed at a consistent C⋯C bond-forming distance close to that of the corresponding transition states) is systematically stronger (i.e. more negative) for the processes involving 1-S. Once again, it is found that even when neutral nucleophiles are involved, the crucial electrostatic term, ΔVelstat, is not only the major contribution to the total ΔEint but is also comparatively more stabilizing for the reactions involving 1-S. Therefore, these results further confirm the crucial role of electrostatic attractions in controlling the electrophilicity of these cyclohexanones.
| System | Nucleophile | ΔG‡ | ΔEint | ΔEPauli | ΔVelstat | ΔEorb |
|---|---|---|---|---|---|---|
| 1-X | ||||||
| a Computed at the same consistent C⋯C bond-forming distance (i.e. the distance in the transition state of the 1-S process). | ||||||
| 1-CH2 | Me2S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CN CH–CN |
20.7 | −21.4 | 180.5 | −109.2 | −92.7 |
| 1-S | 19.6 | −22.7 | 180.5 | −109.7 | −93.5 | |
| 1-CH2 | Me2S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CO2Me CH–CO2Me |
24.8 | −23.0 | 180.9 | −109.8 | −94.1 |
| 1-S | 23.7 | −24.6 | 181.7 | −111.0 | −95.2 | |
| 1-CH2 | Me2S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–p(NO2)C6H4 CH–p(NO2)C6H4 |
19.6 | −19.6 | 138.6 | −87.7 | −70.4 |
| 1-S | 18.0 | −21.6 | 139.9 | −89.2 | −72.2 | |
| 1-CH2 | [Cl–CH–SO2Ph]− | 10.3 | −22.4 | 141.8 | −87.7 | −77.4 |
| 1-S | 5.1 | −27.6 | 143.5 | −91.9 | −49.6 | |
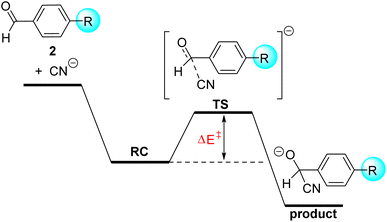
The somehow unexpected close relationship between electrophilicity and electrostatic interactions prompted us to explore the generality of this finding. So, we decided to investigate the similar cyanide nucleophilic addition to a series of benzaldehydes differently substituted at the 4-position of the aryl ring. Similar to the analogous process involving cyclohexanones, in all cases the reaction affords the corresponding adduct through the respective transition states which again follow the expected Bürgi–Dunitz trajectory. In this transformation, we also located an initial reactant complex (RC) which lies below the separate reactants and has been therefore used as the reference level to compute the corresponding activation barriers (Fig. 4).
From the computed barriers gathered in Table 3, it appears that the presence of an electron-withdrawing group in the para position enhances the electrophilicity of the benzaldehyde whereas electron-donor groups provoke the opposite effect, which confirms expectations based on the corresponding σ-Hammett constants.20 In addition, we find that the C⋯C bond-forming distance in the corresponding transition states becomes systematically longer from 2-NMe2 (r = 2.073 Å) to 2-NO2 (r = 2.232 Å), which indicates that the transition state is reached earlier as the acceptor ability of the substituent increases. In line with this, we establish an excellent linear correlation between the computed barriers and the C⋯C bond-forming distance in the TS (correlation coefficient of 0.99). These reactions, therefore, follow the Hammond–Leffer postulate.21
| System | ΔE‡ | ω | ΔEstrain | ΔEint | ΔEPauli | ΔVelstat | ΔEorb (ΔEorb(ρ1)) |
|---|---|---|---|---|---|---|---|
| 2-R | |||||||
| a Computed at the same consistent C⋯C bond-forming distance of 2.232 Å | |||||||
| 2-NMe2 | 9.0 | 1.1 | 9.1 | −13.5 | 58.9 | −34.0 | −38.3 (−33.7) |
| 2-tBu | 8.6 | 1.4 | 6.3 | −15.1 | 58.8 | −35.3 | −38.6 (−34.3) |
| 2-Me | 8.4 | 1.5 | 5.9 | −14.8 | 58.8 | −35.5 | −38.1 (−34.2) |
| 2-H | 8.2 | 1.6 | 6.1 | −15.8 | 58.7 | −36.6 | −37.8 (−34.4) |
| 2-Br | 7.1 | 1.8 | 6.2 | −20.0 | 59.1 | −40.0 | −39.2 (−35.1) |
| 2-CF3 | 5.9 | 1.9 | 6.3 | −22.5 | 59.2 | −42.7 | −39.1 (−35.8) |
| 2-CN | 5.3 | 2.2 | 5.7 | −24.9 | 59.6 | −44.4 | −40.0 (−36.4) |
| 2-NO2 | 4.9 | 2.5 | 5.9 | −26.3 | 59.8 | −45.7 | −40.4 (−37.0) |
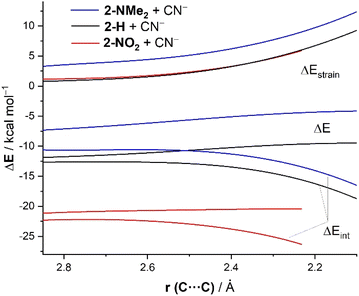
To quantitatively understand the reactivity trend observed in the cyanide addition to benzaldehydes, we have applied once again the ASM of reactivity. To this end, we focus on three representative processes involving unsubstituted (2-H), electron-donor substituted (2-NMe2), and electron-acceptor substituted (2-NO2) benzaldehydes. Fig. 5 shows the corresponding ASDs for these reactions once again from the beginning of the process up to the corresponding transition states and projected onto the forming (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )C⋯C(N) bond-forming distance. As shown in Fig. 5, the enhanced reactivity of p-NO2–benzaldehyde 2-NO2 in comparison with the parent benzaldehyde 2-H is again solely due to the stronger interaction energy between the reactants along the entire reaction coordinate. The deformation strain energy, ΔEstrain, is nearly identical for both transformations. The reaction involving p-NMe2–benzaldehyde 2-NMe2 exhibits the weakest, i.e., the least stabilizing ΔEint along the entire series which, together with a more destabilizing strain energy, results in a higher barrier and thus a reduced reactivity (i.e., electrophilicity) for this system. The crucial role of the interaction between the reagents is further confirmed by the excellent linear correlation (correlation coefficient of 0.99, see Fig. 6) between the computed barriers and the ΔEint values, computed at the same consistent C⋯C bond-forming distance of 2.232 Å (i.e., the value for the transition state involving 2-NO2).
)C⋯C(N) bond-forming distance. As shown in Fig. 5, the enhanced reactivity of p-NO2–benzaldehyde 2-NO2 in comparison with the parent benzaldehyde 2-H is again solely due to the stronger interaction energy between the reactants along the entire reaction coordinate. The deformation strain energy, ΔEstrain, is nearly identical for both transformations. The reaction involving p-NMe2–benzaldehyde 2-NMe2 exhibits the weakest, i.e., the least stabilizing ΔEint along the entire series which, together with a more destabilizing strain energy, results in a higher barrier and thus a reduced reactivity (i.e., electrophilicity) for this system. The crucial role of the interaction between the reagents is further confirmed by the excellent linear correlation (correlation coefficient of 0.99, see Fig. 6) between the computed barriers and the ΔEint values, computed at the same consistent C⋯C bond-forming distance of 2.232 Å (i.e., the value for the transition state involving 2-NO2).
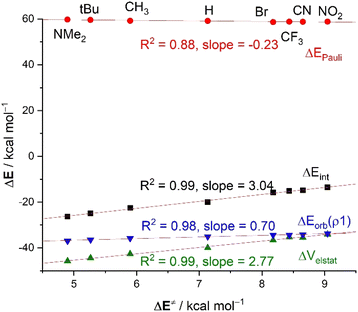
For this particular transformation, we found that the computed electrophilicity indices, ω, do follow the same trend as the activation barriers (correlation coefficient of 0.92), which would suggest that the electrophilicity of the considered benzaldehydes could be defined by the energy of their FMOs. This is in line with the computed key HOMO(CN−) → π*–LUMO(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) molecular orbital interactions, reflected by the ΔEorb(ρ1) term, which also follows the same trend, i.e., this HOMO–LUMO interaction becomes stronger as the electron-withdrawing ability of the substituent increases (see Table 3). As a result, we find in this case a good correlation between the barriers and ΔEorb(ρ1) term (R2 = 0.98, Fig. 6). This can be initially ascribed to the stabilization of the π*(C
O) molecular orbital interactions, reflected by the ΔEorb(ρ1) term, which also follows the same trend, i.e., this HOMO–LUMO interaction becomes stronger as the electron-withdrawing ability of the substituent increases (see Table 3). As a result, we find in this case a good correlation between the barriers and ΔEorb(ρ1) term (R2 = 0.98, Fig. 6). This can be initially ascribed to the stabilization of the π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–LUMO (e.g., εLUMO = −0.87, −1.14 and −2.44 eV, for 2-NMe2, 2-H and 2-NO2, respectively, at the same consistent point r(C⋯C) along the reaction coordinate) and is once again related to the total electronic charge transferred from the nucleophile to the π*(C
O)–LUMO (e.g., εLUMO = −0.87, −1.14 and −2.44 eV, for 2-NMe2, 2-H and 2-NO2, respectively, at the same consistent point r(C⋯C) along the reaction coordinate) and is once again related to the total electronic charge transferred from the nucleophile to the π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) orbital of the substrate, which clearly increases from 2-NMe2 (0.600e) to 2-NO2 (0.632e). Despite that, the variation in the ΔEorb(ρ1) term along the series is not remarkable (ca. 3 kcal mol−1) which is reflected in the low slope (0.70) of the corresponding correlation line. This indicates a low sensitivity of the reactivity (i.e. electrophilicity) with the FMO interactions. The same holds for the ΔEPauli term, which hardly varies along the entire series either (Fig. 6). This is due to the overlap between the key occupied molecular orbitals of both reactants, in particular, the 〈π(C
O) orbital of the substrate, which clearly increases from 2-NMe2 (0.600e) to 2-NO2 (0.632e). Despite that, the variation in the ΔEorb(ρ1) term along the series is not remarkable (ca. 3 kcal mol−1) which is reflected in the low slope (0.70) of the corresponding correlation line. This indicates a low sensitivity of the reactivity (i.e. electrophilicity) with the FMO interactions. The same holds for the ΔEPauli term, which hardly varies along the entire series either (Fig. 6). This is due to the overlap between the key occupied molecular orbitals of both reactants, in particular, the 〈π(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)(2)|HOMO(CN−)〉, which changes not that much when comparing the extreme situations involving 2-NMe2 (S = 0.06) with 2-NO2 (S = 0.08).
O)(2)|HOMO(CN−)〉, which changes not that much when comparing the extreme situations involving 2-NMe2 (S = 0.06) with 2-NO2 (S = 0.08).
At variance, the electrostatic attraction is again the main factor controlling both, the magnitude of, and the trend in, the interaction ΔEint between the deformed reactants. Indeed, as clearly shown in Fig. 6, the ΔVelstat values parallel the ΔEint values, which is translated into a very good correlation between the computed barriers and the ΔVelstat term (correlation coefficient of 0.99). In this case, the computed high slope of 2.77 indicates a much higher sensitivity of the actual electrophilicity for the electrostatic interactions.
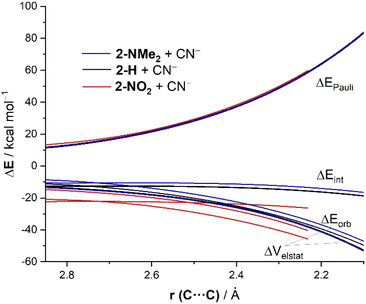
The same conclusion can be drawn when plotting the evolution of the EDA terms along the entire reaction coordinate for the processes involving 2-NMe2, 2-H and 2-NO2. As graphically shown in Fig. 7, the Pauli repulsion term is nearly identical in all the reactions. At variance, the orbital interactions are only slightly stronger for the process involving 2-NO2 as compared to the analogous reaction involving 2-NMe2 or 2-H. However, the electrostatic attraction (ΔVelstat) becomes the decisive factor leading to the observed trend in ΔEint (2-NO2 > 2-H > 2-NMe2). Thus, ΔVelstat steadily strengthens from 2-NO2 to 2-H and to 2-NMe2 and, in this way, causes the same trend in ΔEint and, ultimately, in the actual relative electrophilicity of these benzaldehydes as reflected by ΔE‡.22
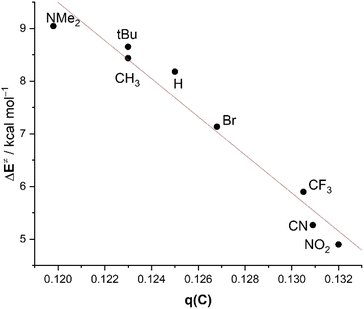
The trend in the key term, ΔVelstat, which as commented above controls the reactivity of the system, can be directly related to the variation of the charge at the carbonyl carbon atom. The latter becomes more positive with the higher electron-withdrawing capacity of the substituent. For instance, the computed Hirshfeld charge at this carbonyl carbon atom steadily increases from +0.119 in 2-NMe2 to +0.132 in 2-NO2. For this reason, an excellent linear correlation (R2 = 0.96) arises between the activation barrier and the charge of the carbonyl carbon atom of the considered benzaldehydes (Fig. 8).
Conclusions
According to our activation strain and quantitative MO analyses, the electrophilicity of our model organic carbonyls (i.e. cyclohexanones or benzaldehydes) is mainly determined by the electrostatic attractions between the electrophile and nucleophile reactants along the reaction coordinate. For the particular case of p-substituted benzaldehydes, it is found that the relative electrophilicity is related to the charge on the carbonylic carbon atom, which directly depends on the electron-withdrawing or donating power of the para-substituent. The more positive the carbonylic carbon atom, the more stabilizing the electrostatic interaction with the CN− nucleophile and, thus, the lower the activation energy. At variance, the relative electrophilicity of these benzaldehydes exhibits a low sensitivity with the FMO interactions, although the key π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) MO becomes more and more stabilized with the electron-withdrawing ability of the substituent.
O) MO becomes more and more stabilized with the electron-withdrawing ability of the substituent.
This finding becomes even more evident in the cyclohexanones series considered herein, as for these systems, the key π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) remains almost constant, which is translated into nearly identical FMO interactions. As a consequence, the trend in the relative electrophilicity of these systems greatly deviates from the trend predicted by the widely used ω index, as confirmed experimentally.9
O) remains almost constant, which is translated into nearly identical FMO interactions. As a consequence, the trend in the relative electrophilicity of these systems greatly deviates from the trend predicted by the widely used ω index, as confirmed experimentally.9
Our finding, i.e. the electrostatic interactions as the main factor governing the electrophilicity of carbonyl compounds, therefore contrasts with, and replaces the traditional rationalization of the electrophilicity trends based exclusively on the FMO interactions, at least for the series of nucleophiles considered in this study.
Computational details
Geometry optimizations of the molecules were performed without symmetry constraints using the Gaussian16 (RevB.01) suite of program23 at the M06-2X24/6-311+G* level. Reactants and adducts were characterized by frequency calculations and have positive definite Hessian matrices. Transition states show only one negative eigenvalue in their diagonalized force constant matrices, and their associated eigenvectors were confirmed to correspond to the motion along the reaction coordinate under consideration using the Intrinsic Reaction Coordinate (IRC) method.25Activation strain model (ASM) of reactivity and energy decomposition analysis (EDA) methods
Within the ASM method,14 the potential energy surface ΔE(ζ) is decomposed along the reaction coordinate, ζ, into two contributions, namely the strain ΔEstrain(ζ) associated with the deformation (or distortion) required by the individual reactants during the process and the interaction ΔEint(ζ) between these increasingly deformed reactants:| ΔE(ζ) = ΔEstrain(ζ) + ΔEint(ζ) |
Within the EDA method,14 the interaction energy can be further decomposed into the following chemically meaningful terms:
| ΔEint(ζ) = ΔVelstat(ζ) + ΔEPauli(ζ) + ΔEorb(ζ) |
The term ΔVelstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the deformed reactants and is usually attractive. The Pauli repulsion ΔEPauli comprises the destabilizing interactions between occupied orbitals and is responsible for any steric repulsion. The orbital interaction ΔEorb accounts for bond pair formation, charge transfer (interaction between occupied orbitals on one moiety with unoccupied orbitals on the other, including HOMO–LUMO interactions), and polarization (empty-occupied orbital mixing on one fragment due to the presence of another fragment). Moreover, the NOCV (Natural Orbital for Chemical Valence)19 extension of the EDA method has been also used to further partition the ΔEorb term. The EDA-NOCV approach provides pairwise energy contributions for each pair of interacting orbitals to the total bond energy.
The program package ADF26 was used for EDA calculations using the optimized M06-2X/6-311+G* geometries at the same DFT level in conjunction with a triple-ζ-quality basis set using uncontracted slater-type orbitals (STOs) augmented by two sets of polarization functions with a frozen-core approximation for the core electrons.27 Auxiliary sets of s, p, d, f, and g STOs were used to fit the molecular densities and to represent the Coulomb and exchange potentials accurately in each SCF cycle.28 Scalar relativistic effects were incorporated by applying the zeroth-order regular approximation (ZORA).29 This level of theory is denoted ZORA-M06-2X/TZ2P//M06-2X/6-311+G*.
Data availability
Cartesian coordinates and energies of all species discussed in the text are available in the ESI.†Author contributions
I. F. initial conceptualization, calculations and manuscript writing. F. M. B. discussion, conceptualization, and manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish MCIN/AEI/10.13039/501100011033 (Grants PID2019-106184GB-I00, PID2022-139318NB-I00 and RED2022-134287-T) and the Dutch Research Council (NWO).Notes and references
- C. K. Ingold, J. Chem. Soc. D, 1933, 1120 RSC.
- (a) G. N. Lewis and P. Wheeler, Zeitschrift für Physikalische Chemie, 1906, 56U, 179 CrossRef; (b) G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762 CrossRef CAS.
- IUPAC, Compendium of Chemical Terminology, the “Gold Book”, compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 2nd edn, 1997, online version (2019–) created by S. J. Chalk, DOI:10.1351/goldbook.
- (a) H. Mayr, T. Bug, M. F. Gotta, N. Hering, B. Irrgang, B. Janker, B. Kempf, R. Loos, A. R. Ofial, G. Remennikov and H. Schimmel, J. Am. Chem. Soc., 2001, 123, 9500 CrossRef CAS PubMed; (b) R. Lucius, R. Loos and H. Mayr, Angew. Chem., Int. Ed., 2002, 41, 91 CrossRef CAS; (c) H. Mayr, B. Kempf and A. R. Ofial, Acc. Chem. Res., 2003, 36, 66 CrossRef CAS PubMed; (d) For a database of nucleophilicity parameters N/sN, and electrophilicity parameters E, check the link: https://www.cup.lmu.de/oc/mayr/reaktionsdatenbank2/.
- (a) R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Clarendon Press, New York, 1989 Search PubMed; (b) P. Geerlings, F. de Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793 CrossRef CAS PubMed.
- R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065 CrossRef CAS PubMed.
- There are in addition other alternative definitions in CDFT using the finite difference approximation, (a) E. Chamorro, P. K. Chattara and P. Fuentealba, J. Phys. Chem. A, 2003, 107, 7068 CrossRef CAS PubMed; second-order Taylor expansions of the energy, (b) J. L. Gázquez, A. Cedillo and A. Vela, J. Phys. Chem. A, 2007, 111, 1966 CrossRef PubMed; and advances including the two-parabola model, (c) A. U. Orozco-Valencia, J. L. Gázquez and A. Vela, J. Phys. Chem. A, 2018, 122, 1796 CrossRef PubMed. See also, (d) E. Chamorro, M. Duque-Noreña and P. Pérez, J. Mol. Struct.: THEOCHEM, 2009, 896, 73 CrossRef CAS.
- Z. Li, H. Jangra, Q. Chen, P. Mayer, A. R. Ofial, H. Zipse and H. Mayr, J. Am. Chem. Soc., 2018, 140, 5500 CrossRef CAS PubMed.
- See, for instance: (a) J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford University Press, London, England, 2nd edn, 2014 Search PubMed; (b) E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006 Search PubMed.
- (a) T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2019, 58, 8922 CrossRef CAS PubMed; (b) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2020, 59, 6201 CrossRef CAS PubMed; (c) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Chem. Sci., 2020, 11, 8105 RSC.
- T. A. Hamlin, F. M. Bickelhaupt and I. Fernández, Acc. Chem. Res., 2021, 54, 1972 CrossRef CAS PubMed.
- (a) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC; (b) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649 CrossRef CAS PubMed; (c) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 CrossRef CAS PubMed. See also; (d) I. Fernández, in Discovering the Future of Molecular Sciences, ed. B. Pignataro, Wiley-VCH, Weinheim, 2014, pp. 165–187 Search PubMed; (e) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- For reviews on the EDA method, see: (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed; (b) I. Fernández, in Applied Theoretical Organic Chemistry, ed. D. J. Tantillo, World Scientific, New Jersey, 2018, pp. 191–226 Search PubMed.
- (a) G. Darzens, Comptes Rendus, 1904, 139, 1214 CAS; (b) G. Darzens, Comptes Rendus, 1905, 141, 766 CAS; (c) G. Darzens, Comptes Rendus, 1906, 142, 214 CAS; (d) G. Darzens and P. Lefébure, Comptes Rendus, 1906, 142, 714 CAS.
- (a) E. J. Corey and M. Chaykovsky, J. Am. Chem. Soc., 1965, 87, 1353 CrossRef CAS; (b) A. W. Johnson and R. B. LaCount, J. Am. Chem. Soc., 1961, 83, 417 CrossRef CAS.
- For recent studies by us on the origin of the Bürgi-Dunitz angle in nucleophilic additions to carbonyl groups, see: (a) H. A. Rodríguez, F. M. Bickelhaupt and I. Fernández, ChemPhysChem, 2023, 24, e202300379 CrossRef PubMed; (b) I. Fernández, F. M. Bickelhaupt and D. Svatunek, J. Chem. Theory Comput., 2023, 19, 7300 CrossRef PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS PubMed.
- (a) L. P. Hammett, Chem. Rev., 1935, 17, 125 CrossRef CAS; (b) L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 2nd edn, 1970 Search PubMed. For studies using the EDA method to understand substituent effects, see also: (c) I. Fernández and G. Frenking, J. Org. Chem., 2006, 71, 2251 CrossRef PubMed; (d) O. A. Stasyuk, H. Szatylowicz, T. M. Krygowski and C. Fonseca Guerra, Phys. Chem. Chem. Phys., 2016, 18, 11624 RSC.
- (a) G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334 CrossRef CAS; (b) A. Pross, Theoretical and Physical Principles in Organic Reactivity, Wiley, Hoboken, 1995 Search PubMed.
- The same trend is found when considering solvent effects in the calculations. At the COSMO-ZORA-M06-2X/TZ2P//PCM(CH2Cl2)M06-2X/6-311+G* level, the ΔVelstat term increases in the order −46.5 kcal mol−1 (2-NMe2), −53.5 kcal mol−1 (2-H) and −64.7 kcal mol−1 (2-NO2).
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision, B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS; (b) ADF2020, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- J. G. Snijders, P. Vernooijs and E. J. Baerends, At. Data Nucl. Data Tables, 1981, 26, 483 CrossRef CAS.
- J. Krijn and E. J. Baerends, Fit Functions in the HFS-Method, Internal Report (in Dutch), Vrije Universiteit Amsterdam, The Netherlands, 1984 Search PubMed.
- (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS; (c) E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates and energies of all the species discussed in the text. See DOI: https://doi.org/10.1039/d3sc05595g |
| This journal is © The Royal Society of Chemistry 2024 |