Open Access Article
Open Access ArticleTuning hydrogen bond network connectivity in the electric double layer with cations†
Bo
Tang
a,
Yeguang
Fang
b,
Shuang
Zhu
a,
Qi
Bai
a,
Xiaojiao
Li
a,
Laiyang
Wei
a,
Zhenyu
Li
 *c and
Chongqin
Zhu
*c and
Chongqin
Zhu
 *a
*a
aKey Laboratory of Theoretical and Computational Photochemistry, Ministry of Education, College of Chemistry, Beijing Normal University, Beijing 100875, China. E-mail: cqzhu@bnu.edu.cn
bLaboratory of Theoretical and Computational Nanoscience, CAS Key Laboratory of Nanosystem and Hierarchical Fabrication, CAS Center for Excellence in Nanoscience, National Center for Nanoscience and Technology, Beijing 100190, China
cHefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China. E-mail: zyli@ustc.edu.cn
First published on 9th April 2024
Abstract
Hydrogen bond (H-bond) network connectivity in electric double layers (EDLs) is of paramount importance for interfacial HER/HOR electrocatalytic processes. However, it remains unclear whether the cation-specific effect on H-bond network connectivity in EDLs exists. Herein, we report simulation evidence from ab initio molecular dynamics that cations at Pt(111)/water interfaces can tune the structure and the connectivity of H-bond networks in EDLs. As the surface charge density σ becomes more negative, we show that the connectivity of the H-bond networks in EDLs of the Na+ and Ca2+ systems decreases markedly; in stark contrast, the connectivity of the H-bond networks in EDLs of the Mg2+ system increases slightly. Further analysis revealed that the interplay between the hydration of cations and the interfacial water structure plays a key role in the connectivity of H-bond networks in EDLs. These findings highlight the key roles of cations in EDLs and electrocatalysis.
Introduction
The structure and composition of the electrical double layer (EDL) at the interface of the electrolyte solution and catalyst surface during electrochemical processes play a paramount role in the activity and selectivity of a wide range of electrocatalytic reactions. Examples of such reactions include the hydrogen evolution reaction (HER),1–5 hydrogen oxidation reaction (HOR), oxygen reduction reaction (ORR),6–9 CO oxidation, CO reduction reaction (CORR), and CO2 reduction reaction (CO2RR).10–13 Although the cations at EDLs are electrochemically inactive, they have shown to highly affect the strengths of interfacial electric fields, the structures of interface water, and the local pH values, etc. Consequently, various mechanisms have been proposed to account for the cation effects on different catalytic reactions. For example, Singh et al. proposed that hydrolysis of the cation's solvation layer buffers the interfacial pH, thereby regulating the local CO2 concentration and affecting CO2RR activity.14 However, Ayemoba and Cuesta reported that the buffering of local pH by cations was overestimated.15 Qin et al. illustrated that K+ can promote the CO2 activation through an inner-sphere mechanism.16,17 Strmcnik and co-workers found that the trend of the interaction energies between cations and surface adsorbed OH follows the order Li+ ≫ Na+ > K+ > Cs+, which is contrary to the activities of the ORR, the HOR and the oxidation of methanol on Pt, suggesting that the cations block the Pt active sites for electrocatalytic reactions.2 Very recently, Goyal et al. showed that interfacial cations on the Au electrode can alter the kinetics of the HER by stabilizing the transition state of the rate-determining Volmer step.18In addition, several researchers have recently proposed that interfacial hydrogen-bond (H-bond) networks may play a key role in the kinetics of interfacial proton-coupled electron transfer processes, thereby affecting the kinetics and selectivity of electrocatalytic interface reactions. For example, Wang et al. used a library of protic ionic liquids in an interfacial layer of Pt and Au to strengthen H-bonds between ORR products and the ionic liquid, thereby enhancing the ORR activity up to fivefold.19 Berg et al. found that the acidic part of thiophenol could generate an extended H-bond network between phosphate-H+-phosphate dimers and amides, leading to efficient regeneration of the photocatalysis.20 What's more, Wang et al. revealed that the integration of diaminotriazine with Cu-porphyrin could construct numerous H-bond networks, which were beneficial for proton migration and intermediate stabilization, thus improving the performance of electrochemical CO2RR.21 Very recently, Chen et al. discovered that the connectivity of the H-bond network in the double layer dominates the pH kinetic effects of HER/HOR electrocatalytic processes at Pt–water interfaces. In comparison to alkaline environments, the H-bond network at the interface exhibits higher continuity under acidic conditions, resulting in enhanced HER/HOR reaction activity.22
Despite much effort in studying the effects of cations on the dynamics and structure of interface water, cation-specific effect on the H-bond network connectivity in EDLs and underlying mechanisms have not yet been explored. In this study, we employed ab initio molecular dynamics (AIMD) simulations to investigate the structure and the connectivity of H-bond networks in EDLs with Na+, Ca2+ and Mg2+as counter charges at Pt(111)/water interfaces. Here we selected Na+, Ca2+ and Mg2+ because Mg2+ and Ca2+ carry similar charges, and Na+ and Ca2+ have a similar ionic size. We find that there is a water gap zone at the electrode surface, which leads to a significant reduction in the connectivity of H-bond networks. When the surface charge density σ continuously changes from −13.38 to −53.52 μC cm−2, the connectivity of H-bond networks in EDLs of the Na+ and Ca2+ systems decreases monotonically. In contrast, the connectivity of H-bond networks in EDLs of the Mg2+ system increases slightly. This interesting behavior is attributed to the fact that the electrostatic attraction between the cation and the electrode surface, as well as the size of the cation notably affect the distance between the cation and the electrode surface, which in turn dictates the structure of H-bond networks in EDLs via the interplay between the hydration of cations and the interfacial water structure.
Methods
Models of electrified interfaces
The Pt(111) surface was modelled using an orthogonal p(6 × 6) periodic slab with 4 atomic layers and separated from its periodic images with a vacuum region. The vacuum is fully filled with water molecules, and the density of the bulk water was close to 1 g cm−3. The overall size of the surface model was 16.615 × 14.389 × 30 Å3. EDLs were modelled by introducing metal atoms (i.e., Na, Mg, or Ca) near the Pt(111) surface. The metal atoms cannot diffuse to the bulk water on the time scale of AIMD due to electrostatic forces. Bader charge analysis of Mg, Ca and Na atoms shows that Mg, Ca and Na atoms carry positive charges of ∼+1.65e, ∼+1.60e and ∼+0.89e respectively, indicating that Mg, Ca and Na atoms are indeed ionized. Varying the number of cations in the system is equivalent to controlling the surface charge density (σ). Using this approach, electrified Pt(111)/water interfaces with σ = −13.38, −26.76, −40.14, or −53.52 μC cm−2 were constructed (Fig. S1†). Note that similar EDL models have been used successfully in previous studies.23,24Computational details
The second generation Car–Parrinello molecular dynamics (SGCPMD)25–27 was used to sample configurations for interface systems, and this method has been widely applied for metal/water systems.23,24,28 The simulations were run in a canonical ensemble at 330 K and the propagation of the equations of motion is based on the Langevin dynamics. The Langevin friction coefficient (γL) was set to 0.001 fs−1, and the intrinsic friction coefficients (γD) were 5 × 105 fs−1 for Pt, 2.2 × 104 fs−1 for H2O, Mg and Na, respectively. The correction step was obtained by 6 iterations of the orbital transformation (OT) optimization algorithm.29 The temperature of the Ca2+ system is controlled using the Nose–Hoover chain thermostat.30 The time step of the AIMD simulations was 0.5 fs. All AIMD simulations were sampled for up to 15–30 ps to ensure that the interface systems were well equilibrated, and the last 10–15 ps data were collected for analysis.All calculations were performed using the CP2K package with the QUICKSTEP module.31,32 The exchange–correlation interactions of electrons were treated using the Perdew–Burke–Ernzerhof (PBE) functional33 with Grimme's van der Waal correction34,35 (PBE-D3). Goedecker–Teter–Hutter (GTH) norm-conserved pseudopotentials36 were used to represent the core electrons. Double-ζ with one set of polarization functions (DZVP) Gaussian basis sets were used, and the energy cutoff was set to 400 Ry.
Results and discussion
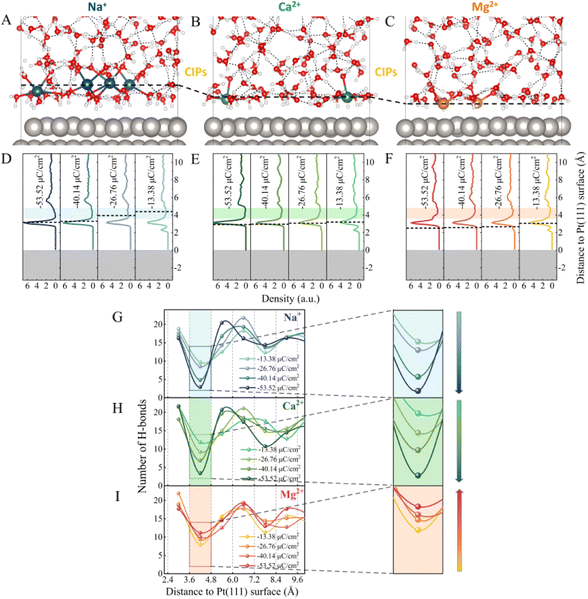
As illustrated in Fig. S1,† a series of ion-water/Pt(111) interfaces with different σ were modelled. Typical AIMD snapshots of the Mg2+–water/Pt, Ca2+–water/Pt and Na+–water/Pt interfaces with σ = −26.76 μC cm−2 are shown in Fig. 1A–C, and additional snapshots are illustrated in Fig. S2.† The planes consisting of the cations closest to the electrode surface are defined as the counter ion planes (CIPs) and are represented by black dashed lines (Fig. 1A–F). Remarkably, CIPs are located at different distances away from the electrode surface for Mg2+, Ca2+ and Na+ systems. Fig. 1D–F show profiles of water density along the surface normal direction at different surface charge densities. Independently of σ, all three systems show a sharp main peak at the height of ∼3.1 Å, i.e., a water layer is located at ∼3.1 Å height. In contrast, the height of the CIP increases with σ for all three systems. In addition, the distribution of the different cations in EDLs relative to water molecules exhibits a very different behavior. Specifically, in the Na+ system, the CIP is separated from the electrode surface by the water layer, whereas in the Mg2+ system, the CIP is located between the electrode surface and the water layer. By contrast, in the Ca2+ system, the CIP is close to the water layer. These differences can be attributed to the interaction between cations and the electrode surface as well as the size of cations. Mg2+ and Ca2+ carry more positive charges, almost twice as much as Na+, indicating that the electrostatic interaction between Mg2+/Ca2+ and the electrode surface is much stronger than that between Na+ and the electrode surface. Therefore, Mg2+ and Ca2+ are closer to the electrode surface than Na+. On the other hand, Mg2+ is much closer to the electrode surface than Ca2+ because the size of Mg2+ is smaller than Ca2+.As shown in Fig. 1D–F, at σ = −13.38 μC cm−2, there are two major peaks for the three systems. One peak is located at h = ∼2.3 Å, which corresponds to water molecules directly chemisorbed on the electrode surface. The other peak is located at h = ∼3.3 Å, which is much more intense and represents non-chemisorbed water molecules. In addition to the sharp peaks, all three systems have a gap zone located between heights of 3.6 Å and 4.8 Å, where the water density is lowest (the shaded areas in Fig. 1D–F). The distribution of the number of H-bonds (Fig. 1G–I) reveals that the depletion of water molecules in this gap zone reduces the connectivity of H-bond networks. Furthermore, as the surface charge density becomes more negative, i.e., from −13.38 to −53.52 μC cm−2, we note that the number of H-bonds in the gap zone monotonically decreases from 9.7 and 11.9 to 2.9 and 3.4 in the Na+ and Ca2+ systems, respectively (Fig. 1G and H). In contrast, in the Mg2+ system, although the water density profiles in the gap zone are similar to those of the Na+ and Ca2+ systems (Fig. 1F), the dependence of the connectivity of H-bond networks on the σ is quite different. Surprisingly, the number of H-bonds in this gap zone gradually increases from 8.0 to 11.2 as σ changes from −13.38 to −53.52 μC cm−2 (Fig. 1I). Similar results were observed for the systems with the *H intermediates present on the Pt electrode (Fig. S3†). Specifically, the number of H-bonds in the gap zone of the Na+–Pt(*H) system decreases as the surface charge density becomes more negative, while the number of H-bonds in the gap zone of the Mg2+–Pt(*H) system increases. It is noteworthy that the height of the gap zone decreases of the Na+–Pt(*H) system decreases as the surface charge density becomes more negative, while the height of the gap zone of the Mg2+–Pt(*H) system remains almost constant. The different trends in the σ-dependent gap zone heights should be attributed to the different hCIP of the Na+–Pt(*H) and Mg2+–Pt(*H) systems (black dashed lines in Fig. S3A and S3B†).
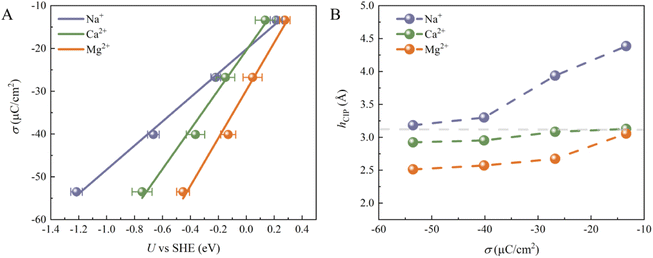
Although the cations at EDLs are electrochemically inactive, they are more than just counter charges to electrode surface charges. We then calculated the electrode potential (U) at each surface charge density using the recently developed computational standard hydrogen electrode method.37 The convergence of the computed U can be found in Fig. S4.† As shown in Fig. 2A, U decreases for all systems as σ becomes more negative. Indeed, the change in U (Δψ) can be decomposed into two parts:23 (1) the usual potential change (Δψsol) induced by the interface dipole of hCIP; (2) the potential due to water chemisorption (ΔψA). At potentials slightly more negative than PZC, both ΔψA and Δψsol contribute to the overall electrode potential. In contrast, at much more negative potentials than PZC, all chemisorbed water is desorbed from the surface (Fig. 1D–F), indicating that ΔψA = 0 and only Δψsol contributes to the overall electrode potential. In addition, σ shows almost linearly dependence on the U, and similar results have been illustrated in previous work.24 The slope corresponds to the Helmholtz capacitance (CH = dσ/dU). The CH of the three systems follows the sequence Mg2+ (∼55.83 μF cm−2) > Ca2+ (∼46.24 μF cm−2) > Na+ (∼28.15 μF cm−2), which is largely due to the different Helmholtz layer widths in these three systems (Fig. 2B). We note that previous experiments on the CH of Mg2+, Ca2+ and Li+ systems show a similar trend: Mg2+ > Ca2+ > Li+.38,39 Since the size of Mg2+ (rMg2+ = 0.72 Å) is the smallest of the three cations, the height of CIP (hCIP) for the Mg2+ system is lowest. Interestingly, the hCIP of the Ca2+ system is much lower than that of the Na+ system, despite their similar sizes (rNa+ = 1.02 Å and rCa2+ = 1.00 Å), which should be due to the stronger electrostatic attraction between Ca2+ and the electrode surface. Furthermore, the hCIP becomes lower as the σ becomes more negative in all systems, which means that the width of the Helmholtz layer decreases as the electrode potential becomes more negative. At σ = −53.52 μC cm−2, Mg2+ can be viewed as a specific adsorbed ion due to its low hCIP (∼2.5 Å) and weak diffusivity (Fig. S5†).40–42
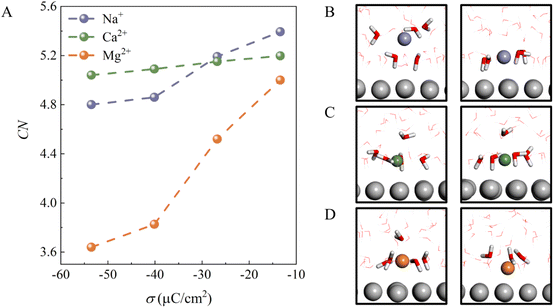
To understand why the H-bond network connectivity in EDLs behaves so differently with decreasing σ in the presence of different cations, we first analyzed the interaction between the cations and water molecules in EDLs. Fig. 3A plots the average numbers of water molecules in different ionic hydration shells, i.e., coordination number (CN), as a function of σ. For all cations, CN decreases as σ becomes more negative due to the competition between electrostatic attraction and solvation of the ion. This can be understood by the fact that the interaction of cations with water molecules plays a dominant role when the electrode surface charge is less negative, and thus CN is high. Specifically, for Na+ and Ca2+ ions, CN decreases from 5.4 and 5.2 to 4.8 and 5.0 as σ changes from −13.38 to −53.52 μC cm−2, respectively. It is clear that the decrease in the CN of Na+ is larger than that of Ca2+ because the CIP height of the Na+ system varies more as σ becomes more negative. Furthermore, we note that at less negative surface charge density (σ = −13.38 μC cm−2), Na+ has a fully solvated structure at the EDL, as in bulk water (Fig. 3B), whereas Ca2+ and Mg2+ are partially solvated at the EDL (Fig. 3C and D), which should be attributed to stronger electrostatic interactions and low CIP heights. Interestingly, although the CIP heights of the Mg2+ system only decrease from 3.1 to 2.5 with a change in σ from −13.38 to −53.52 μC cm−2, the CN of Mg2+ decreases the most of the three systems. This is due to the fact that the CIP of the Mg2+ system is located between the electrode surface and the water layer (Fig. 1F), and thus the number of water molecules in the vicinity of Mg2+ varies sharply with the height of CIP. In other words, the interaction between the cations and water molecules in EDLs is highly dependent on the CIP height.
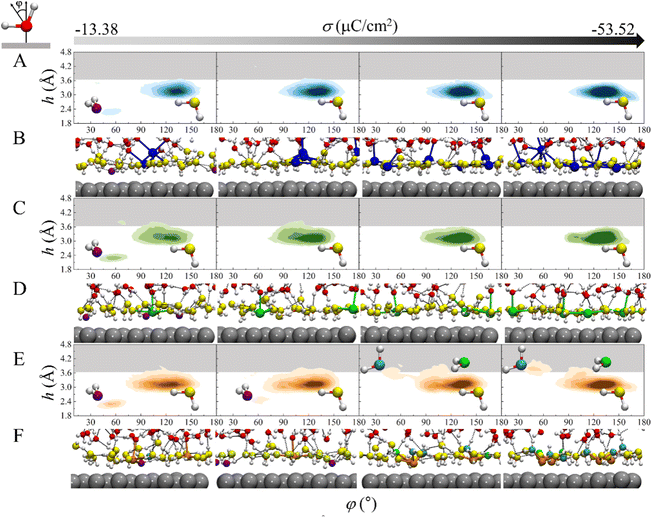
To gain more insight into the mechanism underlying the cation-specific effect on the H-bond network connectivity in EDLs, structures of interfacial water for these three systems at different charge densities were analyzed. The 2D probability distributions of the angle φ between the bisector of water and the surface normal as a function of height h above the electrode surface for the three systems at different σ were plotted (Fig. 4A, C and 4E). At σ = −13.38 μC cm−2, there are two major peaks for the three systems: one peak is located at h = ∼2.3 Å and φ = ∼53°, which corresponds to the “two-H-up” water molecule that is directly chemisorbed on the electrode surface (in purple in Fig. 4B, D, 4F and S6†); the other peak is located at h = ∼3.3 Å and φ = ∼128°, which is much more intense and represents the “one-H-down” non-chemisorbed water molecules (in yellow in Fig. 4B, D, 4F and S6†). Similar results were found for the Pt(111)/water interface system.23,24 The presence of chemisorbed and nonchemisorbed water at the interface is mainly due to water–metal interactions. At the very negative potential, there is no chemisorption of water on the surface due to coulombic repulsion, and hence the peak at h = ∼2.3 Å disappears. Note that due to water–water interactions, both chemisorbed and nonchemisorbed water form H-bonds with neighboring water molecules. At much more negative charge densities, the peaks corresponding to chemisorbed water disappear in the three systems due to coulombic repulsion. For Na+ and Ca2+ systems, at σ ≤ −26.76 μC cm−2, there is only one peak corresponding to the “one-H-down” water structure (Fig. 4A and C), where the other hydrogen of the water forms H-bonds with the neighboring water. As σ becomes more negative, the peak for the “one-H-down” water becomes more intense, indicating that a more ordered interfacial water structure is formed. In sharp contrast, for the Mg2+ system, a new peak appears gradually at h = 3.5–3.8 Å and φ = ∼46°, which corresponds to the “one-H-up” water molecule (in cyan in Fig. 4E), when σ becomes more negative. In addition, a small peak is observed at h = ∼3.6 Å and φ = ∼105° corresponding to the “two-H-parallel” water molecule (in green in Fig. 4F). Interestingly, at a more negative surface charge density (σ = −53.52 μC cm−2), the peak for the “one-H-up” water moves to a height of ∼3.9 Å from the surface, located in the H-bond gap zone (gray region in Fig. 4), suggesting that more water molecules enter this H-bond gap zone.
An arising question is why the interfacial water structure is so different in the Mg2+ system? Our AIMD simulations show that the CIP height of Mg2+ is lower than that of Ca2+ and Na+ due to the small size of the cation and the strong electrostatic attraction between the cation and the electrode surface. On the other hand, the radial distribution functions of O atoms surrounding the cations show that the solvation shell radius of the Mg2+ (∼2.1 Å) is much smaller than that of the Na+ (∼2.4 Å) and Ca2+ (∼2.4 Å) (Fig. S7†). Due to the high valence state of Mg2+ and the small CIP height, the shaping effect of electric field on water orientation is weak, and thus “two-H-parallel” and “one-H-up” water molecules are observed (in green, cyan in Fig. 4F).
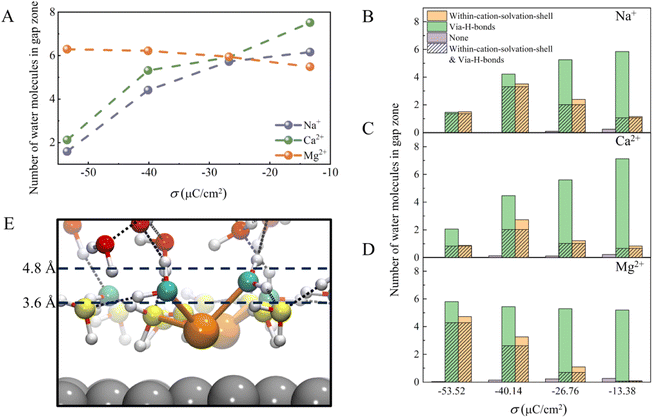
There are two ways to reduce the H-bond network connectivity in the H-bond gap zone: one is to reduce the number of water molecules, and the other is to reduce the number of H-bonds per water molecule. To determine which one is more important, we calculated the number of water molecules and the number of H-bonds per water molecule in the H-bond gap zone of the whole systems for various σ. As shown in Fig. 5A, when σ changes from −13.37 to −53.52 μC cm−2, the number of water molecules in the H-bond gap zone in the Na+ and Ca2+ systems decreases sharply from 6.0 and 7.5 to 1.5 and 2.1, respectively, while the number of water molecules in the H-bond gap zone in the Mg2+ system increases slightly from 5.5 to 6.3. However, in all three systems, the difference in the number of H-bonds per water in the H-bond gap zone of the three systems seems not significant at the same σ (Fig. S8†). In other words, the number of water molecules in the H-bond gap zone can be seriously affected by cations.
Further, we analyzed interactions between the water molecules in the H-bond gap zone and the interfacial water molecules or cations by counting the number of water molecules within the solvation shell of cations (namely, within-cation-solvation-shell water molecules) and the number of water molecules interacting with interfacial water molecules via H-bonds (namely, via-H-bonds water molecules) at different σ. As shown in Fig. 5B–D, almost no water molecules (namely, none) neither form H-bonds with the interfacial water nor are within the solvation shell of the cations, indicating that there are strong interactions between the water molecules in the H-bond gap zone and the interfacial water molecules or cations. When the surface charge density is less negative (σ = −13.38 μC cm−2), the number of via-H-bonds water molecules is high, much higher than the number of within-cation-solvation-shell water molecules, in these three systems, which suggests that the water molecules in the H-bond gap zone interact with EDLs mainly via H-bonding with interfacial water molecules. As σ becomes more negative, the number of via-H-bonds water molecules in the Na+ and Ca2+ systems decreases sharply from 5.8 and 7.1 to 1.5 and 2.1, respectively, while the number of within-cation-solvation-shell water molecules does not change much. In contrast, the number of via-H-bonds water molecules in the Mg2+ system increases slightly from 5.2 to 5.8 with decreasing σ, which is attributed to a sharp increase in the number of within-cation-solvation-shell water molecules from 0.1 to 4.7. Specifically, as σ becomes more negative, interfacial water molecules tend to adopt a more ordered network structure, and it becomes more difficult for the water molecules in the H-bond gap zone to form H-bonds with interfacial water molecules. As a result, the number of water molecules in the H-bond gap zone of the Na+ and Ca2+ systems decreases with negative changing of σ. However, in the Mg2+ system, O(H2O)⋯Mg2+ electrostatic attraction between water molecules in the H-bond gap zone and Mg2+ increases with negative changing of σ, compensating for the weakening of the interaction between the interfacial water and water molecule in the H-bond gap zone (Fig. 5E). Thus, there is a slight increase in the number of water molecules in the H-bond gap zone of the Mg2+ system.
Conclusions and discussions
Recently, the importance of H-bond networks in EDLs for reaction kinetics has received increasing attention, which has contributed significantly to the fundamental understanding of modern electrocatalysis.19,22,41,43–51 Although there have been recent reports on the cation effect on interfacial H-bond networks.11,48–52 The atomic-scale mechanisms and cation-specific effects on H-bond networks remain unclear. In fact, the effect of cations on the electrocatalytic kinetics is usually attributed to the strength of noncovalent interactions between cations in EDLs and reaction species.16,17,48,53–59 In our work, we have investigated the cation-specific effect on H-bond network connectivity in EDLs.Strikingly different H-bond network connectivity scenarios emerge when different cations are present. The interplay between the hydration of cations and the interfacial water structure plays a key role in the H-bond network connectivity in EDLs. As σ becomes more negative, more interfacial water molecules adapt to the “one-H-down” structure, resulting in a decrease in the number of water molecules in the H-bond gap zone. On the other hand, cations can help to stabilize the water molecules in the H-bond gap zone if the hydration of the cations and the distance between the cations and the electrode surface are appropriate. Overall, the interplay between the hydration of cations and the interfacial water structure can tune the number of water molecules in the H-bond gap zone and thus the connectivity of H-bond networks in EDLs. Our work demonstrates the cation-specific effect on H-bond network connectivity in EDLs.
Our findings may help to improve the electrocatalytic performance. In addition to hydrogen transfer (HT) from the closest interfacial water molecules to the electrode surface, HT between bulk water and the interfacial water via the H-bond networks in the EDL is also essential to the whole electrochemical process. Chen et al. revealed that the origin of the large kinetic pH effect in the HER is caused by the significantly different connectivity of H-bond networks in EDLs, and not by differences in the free energy barrier of the Volmer reaction.22 Note the protonation of *CO2 (*CO2-to-*COOH) is the second key step in the CO2RR, and the water molecules adjacent to the electrode surface are the source of hydrogen transfer. Therefore, this step may also be affected by the H-bond network connectivity. Our AIMD simulations demonstrate that the ability of cations to tune the connectivity of H-bond networks exhibits an ion-specific effect. This implies that the connectivity of H-bond networks can be increased by selecting appropriate cations, thereby facilitating the HT from bulk water to interfacial water, and thus increasing the activity of *CO2-to-*COOH.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
C.-Q. Z. and B. T. conceived and designed the project and wrote the manuscript. Z.-Y. L. provided some theoretical guidance. B. T. performed the calculation, and B. T., Y.-G. F., S. Z., X.-J. L., Q. B. and W.-L. Y. analyzed the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C.-Q. Z. is grateful for funding supported by the National Key Research and Development Program of China (2021YFA1500700) and the National Natural Science Foundation of China (22173011). B. T. is thankful for the support of the supercomputer center of USTC.Notes and references
- X. Li, B. Lv, X. P. Zhang, X. Jin, K. Guo, D. Zhou, H. Bian, W. Zhang, U. P. Apfel and R. Cao, Introducing Water-Network-Assisted Proton Transfer for Boosted Electrocatalytic Hydrogen Evolution with Cobalt Corrole, Angew. Chem., Int. Ed., 2022, 61(9), e202114310 CrossRef CAS PubMed.
- D. Strmcnik, M. Uchimura, R. Subbaraman, N. Danilovic, D. Van Der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Improving the hydrogen oxidation reaction rate by promotion of hydroxyl adsorption, Nat. Chem., 2013, 5(4), 300–306 CrossRef CAS PubMed.
- J. Y. Yang, R. M. Bullock, W. J. Shaw, B. Twamley, K. Fraze, M. R. DuBois and D. L. DuBois, Mechanistic insights into catalytic H2 oxidation by Ni complexes containing a diphosphine ligand with a positioned amine base, J. Am. Chem. Soc., 2009, 131(16), 5935–5945 CrossRef CAS PubMed.
- M. L. Helm, M. P. Stewart, R. M. Bullock, M. R. DuBois and D. L. DuBois, A synthetic nickel electrocatalyst with a turnover frequency above 100,000 s−1 for H2 production, Science, 2011, 333(6044), 863–866 CrossRef CAS PubMed.
- M. O'Hagan, W. J. Shaw, S. Raugei, S. Chen, J. Y. Yang, U. J. Kilgore, D. L. DuBois and R. M. Bullock, Moving protons with pendant amines: Proton mobility in a nickel catalyst for oxidation of hydrogen, J. Am. Chem. Soc., 2011, 133(36), 14301–14312 CrossRef PubMed.
- C. J. Barile, E. C. Tse, Y. Li, T. B. Sobyra, S. C. Zimmerman, A. Hosseini and A. A. Gewirth, Proton switch for modulating oxygen reduction by a copper electrocatalyst embedded in a hybrid bilayer membrane, Nat. Mater., 2014, 13(6), 619–623 CrossRef CAS PubMed.
- E. C. Tse, C. J. Barile, N. A. Kirchschlager, Y. Li, J. P. Gewargis, S. C. Zimmerman, A. Hosseini and A. A. Gewirth, Proton transfer dynamics control the mechanism of O2 reduction by a non-precious metal electrocatalyst, Nat. Mater., 2016, 15(7), 754–759 CrossRef CAS PubMed.
- X. Zhang, X. Zhao, P. Zhu, Z. Adler, Z.-Y. Wu, Y. Liu and H. Wang, Electrochemical oxygen reduction to hydrogen peroxide at practical rates in strong acidic media, Nat. Commun., 2022, 13(1), 2880 CrossRef CAS PubMed.
- Y. Wang, Y. Yang, S. Jia, X. Wang, K. Lyu, Y. Peng, H. Zheng, X. Wei, H. Ren and L. Xiao, Synergistic Mn-Co catalyst outperforms Pt on high-rate oxygen reduction for alkaline polymer electrolyte fuel cells, Nat. Commun., 2019, 10(1), 1506 CrossRef PubMed.
- J. E. Huang, F. Li, A. Ozden, A. Sedighian Rasouli, F. P. García de Arquer, S. Liu, S. Zhang, M. Luo, X. Wang and Y. Lum, CO2 electrolysis to multicarbon products in strong acid, Science, 2021, 372(6546), 1074–1078 CrossRef CAS PubMed.
- J. Gu, S. Liu, W. Ni, W. Ren, S. Haussener and X. Hu, Modulating electric field distribution by alkali cations for CO2 electroreduction in strongly acidic medium, Nat. Catal., 2022, 5(4), 268–276 CrossRef CAS.
- S. Zhu, E. P. Delmo, T. Li, X. Qin, J. Tian, L. Zhang and M. Shao, Recent advances in catalyst structure and composition engineering strategies for regulating CO2 electrochemical reduction, Adv. Mater., 2021, 33(50), 2005484 CrossRef CAS PubMed.
- C. J. Bondue, M. Graf, A. Goyal and M. T. Koper, Suppression of hydrogen evolution in acidic electrolytes by electrochemical CO2 reduction, J. Am. Chem. Soc., 2020, 143(1), 279–285 CrossRef PubMed.
- M. R. Singh, Y. Kwon, Y. Lum, J. W. Ager III and A. T. Bell, Hydrolysis of Electrolyte Cations Enhances the Electrochemical Reduction of CO2 over Ag and Cu, J. Am. Chem. Soc., 2016, 138(39), 13006–13012 CrossRef CAS PubMed.
- O. Ayemoba and A. Cuesta, Spectroscopic Evidence of Size-Dependent Buffering of Interfacial pH by Cation Hydrolysis during CO2 Electroreduction, ACS Appl. Mater. Interfaces, 2017, 9(33), 27377–27382 CrossRef CAS PubMed.
- X. Qin, T. Vegge and H. A. Hansen, Cation-coordinated inner-sphere CO2 electroreduction at Au–water interfaces, J. Am. Chem. Soc., 2023, 145(3), 1897–1905 CrossRef CAS PubMed.
- X. Qin, H. A. Hansen, K. Honkala and M. M. Melander, Cation-induced changes in the inner-and outer-sphere mechanisms of electrocatalytic CO2 reduction, Nat. Commun., 2023, 14(1), 7607 CrossRef CAS PubMed.
- A. Goyal and M. T. Koper, The interrelated effect of cations and electrolyte pH on the hydrogen evolution reaction on gold electrodes in alkaline media, Angew. Chem., Int. Ed., 2021, 60(24), 13452–13462 CrossRef CAS PubMed.
- T. Wang, Y. Zhang, B. Huang, B. Cai, R. R. Rao, L. Giordano, S.-G. Sun and Y. Shao-Horn, Enhancing oxygen reduction electrocatalysis by tuning interfacial hydrogen bonds, Nat. Catal., 2021, 4(9), 753–762 CrossRef CAS.
- N. Berg, S. Bergwinkl, P. Nuernberger, D. Horinek and R. M. Gschwind, Extended Hydrogen Bond Networks for Effective Proton-Coupled Electron Transfer (PCET) Reactions: The Unexpected Role of Thiophenol and Its Acidic Channel in Photocatalytic Hydroamidations, J. Am. Chem. Soc., 2021, 143(2), 724–735 CrossRef CAS PubMed.
- Y. R. Wang, M. Liu, G. K. Gao, Y. L. Yang, R. X. Yang, H. M. Ding, Y. Chen, S. L. Li and Y. Q. Lan, Implanting numerous hydrogen-bonding networks in a Cu-porphyrin-based nanosheet to boost CH4 selectivity in neutral-media CO2 electroreduction, Angew. Chem., Int. Ed., 2021, 60(40), 21952–21958 CrossRef CAS PubMed.
- P. Li, Y. Jiang, Y. Hu, Y. Men, Y. Liu, W. Cai and S. Chen, Hydrogen bond network connectivity in the electric double layer dominates the kinetic pH effect in hydrogen electrocatalysis on Pt, Nat. Catal., 2022, 5(10), 900–911 CrossRef CAS.
- J.-B. Le, Q.-Y. Fan, J.-Q. Li and J. Cheng, Molecular origin of negative component of Helmholtz capacitance at electrified Pt (111)/water interface, Sci. Adv., 2020, 6(41), eabb1219 CrossRef CAS PubMed.
- J.-B. Le, A. Chen, L. Li, J.-F. Xiong, J. Lan, Y.-P. Liu, M. Iannuzzi and J. Cheng, Modeling electrified Pt (111)-Had/water interfaces from ab Initio molecular dynamics, JACS Au, 2021, 1(5), 569–577 CrossRef CAS PubMed.
- T. D. Kühne, M. Krack, F. R. Mohamed and M. Parrinello, Efficient and accurate Car-Parrinello-like approach to Born-Oppenheimer molecular dynamics, Phys. Rev. Lett., 2007, 98(6), 066401 CrossRef PubMed.
- T. D. Kühne, Second generation Car–Parrinello molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(4), 391–406 Search PubMed.
- J. Hutter, Car–Parrinello molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(4), 604–612 CAS.
- J. Lan, J. r. Hutter and M. Iannuzzi, First-principles simulations of an aqueous CO/Pt (111) interface, J. Phys. Chem. C, 2018, 122(42), 24068–24076 CrossRef CAS.
- J. VandeVondele and J. Hutter, An efficient orbital transformation method for electronic structure calculations, J. Chem. Phys., 2003, 118(10), 4365–4369 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover chains: The canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97(4), 2635–2643 CrossRef.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167(2), 103–128 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, cp2k: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(1), 15–25 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25(12), 1463–1473 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(3), 1703 CrossRef CAS PubMed.
- J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Determining potentials of zero charge of metal electrodes versus the standard hydrogen electrode from density-functional-theory-based molecular dynamics, Phys. Rev. Lett., 2017, 119(1), 016801 CrossRef PubMed.
- J. C. Icaza and R. K. Guduru, Effect of ion charges on the electric double layer capacitance of activated carbon in aqueous electrolyte systems, J. Power Sources, 2016, 336, 360–366 CrossRef CAS.
- L. Guan, L. Yu and G. Z. Chen, Capacitive and non-capacitive faradaic charge storage, Electrochim. Acta, 2016, 206, 464–478 CrossRef CAS.
- P. Li, Y. Liu and S. Chen, Microscopic EDL structures and charge–potential relation on stepped platinum surface: Insights from the ab initio molecular dynamics simulations, J. Chem. Phys., 2022, 156(10), 14701 CrossRef PubMed.
- P. Li, Y. Jiao, J. Huang and S. Chen, Electric Double Layer Effects in Electrocatalysis: Insights from Ab Initio Simulation and Hierarchical Continuum Modeling, JACS Au, 2023, 3(10), 2640–2659 CrossRef CAS PubMed.
- J. Huang, M. Li, M. J. Eslamibidgoli, M. Eikerling and A. Groß, Cation overcrowding effect on the oxygen evolution reaction, JACS Au, 2021, 1(10), 1752–1765 CrossRef CAS PubMed.
- Q. Sun, N. J. Oliveira, S. Kwon, S. Tyukhtenko, J. J. Guo, N. Myrthil, S. A. Lopez, I. Kendrick, S. Mukerjee and L. Ma, Understanding hydrogen electrocatalysis by probing the hydrogen-bond network of water at the electrified Pt–solution interface, Nat. Energy, 2023, 8, 859–869 CrossRef CAS.
- J. Li, X. Li, C. M. Gunathunge and M. M. Waegele, Hydrogen bonding steers the product selectivity of electrocatalytic CO reduction, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(19), 9220–9229 CrossRef CAS PubMed.
- W. D. Guerra, E. Odella, M. Secor, J. J. Goings, M. N. Urrutia, B. L. Wadsworth, M. Gervaldo, L. E. Sereno, T. A. Moore, G. F. Moore, S. Hammes-Schiffer and A. L. Moore, Role of Intact Hydrogen-Bond Networks in Multiproton-Coupled Electron Transfer, J. Am. Chem. Soc., 2020, 142(52), 21842–21851 CrossRef CAS PubMed.
- L. Su, J. Chen, F. Yang, P. Li, Y. Jin, W. Luo and S. Chen, Electric-Double-Layer Origin of the Kinetic pH Effect of Hydrogen Electrocatalysis Revealed by a Universal Hydroxide Adsorption-Dependent Inflection-Point Behavior, J. Am. Chem. Soc., 2023, 145(22), 12051–12058 CrossRef CAS PubMed.
- A. Serva, M. Salanne, M. Havenith and S. Pezzotti, Size dependence of hydrophobic hydration at electrified gold/water interfaces, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(15), e2023867118 CrossRef CAS PubMed.
- H. Khani, A. R. Puente Santiago and T. He, An Interfacial View of Cation Effects on Electrocatalysis Systems, Angew. Chem., 2023, e202306103 CAS.
- M. C. O. Monteiro, A. Goyal, P. Moerland and M. T. M. Koper, Understanding Cation Trends for Hydrogen Evolution on Platinum and Gold Electrodes in Alkaline Media, ACS Catal., 2021, 11(23), 14328–14335 CrossRef CAS PubMed.
- A. H. Shah, Z. Zhang, Z. Huang, S. Wang, G. Zhong, C. Wan, A. N. Alexandrova, Y. Huang and X. Duan, The role of alkali metal cations and platinum-surface hydroxyl in the alkaline hydrogen evolution reaction, Nat. Catal., 2022, 5(10), 923–933 CrossRef CAS.
- B. Huang, R. R. Rao, S. You, K. Hpone Myint, Y. Song, Y. Wang, W. Ding, L. Giordano, Y. Zhang, T. Wang, S. Muy, Y. Katayama, J. C. Grossman, A. P. Willard, K. Xu, Y. Jiang and Y. Shao-Horn, Cation- and pH-Dependent Hydrogen Evolution and Oxidation Reaction Kinetics, JACS Au, 2021, 1(10), 1674–1687 CrossRef CAS PubMed.
- X. Y. Li, T. Wang, Y. C. Cai, Z. D. Meng, J. W. Nan, J. Y. Ye, J. Yi, D. P. Zhan, N. Tian and Z. Y. Zhou, Mechanism of Cations Suppressing Proton Diffusion Kinetics for Electrocatalysis, Angew. Chem., Int. Ed., 2023, 62(14), e202218669 CrossRef CAS PubMed.
- J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, Promoter Effects of Alkali Metal Cations on the Electrochemical Reduction of Carbon Dioxide, J. Am. Chem. Soc., 2017, 139(32), 11277–11287 CrossRef CAS PubMed.
- M. C. O. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. T. M. Koper, Absence of CO2 electroreduction on copper, gold and silver electrodes without metal cations in solution, Nat. Catal., 2021, 4(8), 654–662 CrossRef CAS.
- J.-B. Le, A. Chen, Y. Kuang and J. Cheng, Molecular understanding of cation effects on double layers and their significance to CO-CO dimerization, Natl. Sci. Rev., 2023, 10(9), nwad105 CrossRef PubMed.
- B. Pan, Y. Wang and Y. Li, Understanding and leveraging the effect of cations in the electrical double layer for electrochemical CO2 reduction, Chem Catal., 2022, 2(6), 1267–1276 CrossRef CAS.
- S. Y. Lee, J. Kim, G. Bak, E. Lee, D. Kim, S. Yoo, J. Kim, H. Yun and Y. J. Hwang, Probing Cation Effects on *CO Intermediates from Electroreduction of CO2 through Operando Raman Spectroscopy, J. Am. Chem. Soc., 2023, 145(42), 23068–23075 CrossRef CAS PubMed.
- H. Liu, J. Liu and B. Yang, Promotional role of a cation intermediate complex in C2 formation from electrochemical reduction of CO2 over Cu, ACS Catal., 2021, 11(19), 12336–12343 CrossRef CAS.
- M. C. Monteiro, F. Dattila, N. r. López and M. T. Koper, The role of cation acidity on the competition between hydrogen evolution and CO2 reduction on gold electrodes, J. Am. Chem. Soc., 2021, 144(4), 1589–1602 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc06904d |
| This journal is © The Royal Society of Chemistry 2024 |