Open Access Article
Open Access ArticleParticipation of electrochemically inserted protons in the hydrogen evolution reaction on tungsten oxides†
Michael A.
Spencer
 a,
Noah P.
Holzapfel
a,
Noah P.
Holzapfel
 a,
Kyung-Eun
You
b,
Giannis
Mpourmpakis
a,
Kyung-Eun
You
b,
Giannis
Mpourmpakis
 b and
Veronica
Augustyn
b and
Veronica
Augustyn
 *a
*a
aDepartment of Materials Science and Engineering, North Carolina State University, 911 Partners Way, Raleigh, NC 27606, USA. E-mail: vaugust@ncsu.edu
bDepartment of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, PA 15260, USA
First published on 14th March 2024
Abstract
Understanding the mechanisms by which electrodes undergo the hydrogen evolution reaction (HER) is necessary to design better materials for aqueous energy storage and conversion. Here, we investigate the HER mechanism on tungsten oxide electrodes, which are stable in acidic electrolytes and can undergo proton-insertion coupled electron transfer concomitant with the HER. Electrochemical characterization showed that anhydrous and hydrated tungsten oxides undergo changes in HER activity coincident with changes in proton composition, with activity in the order HxWO3·H2O > HxWO3 > HxWO3·2H2O. We used operando X-ray diffraction and density functional theory to understand the structural and electronic changes in the materials at high states of proton insertion, when the oxides are most active towards the HER. H0.69WO3·H2O and H0.65WO3 have similar proton composition, structural symmetry, and electronic properties at the onset of the HER, yet exhibit different activity. We hypothesize that the electrochemically inserted protons can diffuse in hydrogen bronzes and participate in the HER. This would render the oxide volume, and not just the surface, as a proton and electron reservoir at high overpotentials. HER activity is highest in HxWO3·H2O, which optimizes both the degree of proton insertion and solid-state proton transport kinetics. Our results highlight the interplay between the HER and proton insertion-coupled electron transfer on transition metal oxides, many of which are non-blocking electrodes towards protons.
1. Introduction
The hydrogen evolution reaction (HER) is the cathodic reaction in electrochemical water splitting that leads to the formation of H2 gas, which can be used as an energy dense fuel or precursor for chemical synthesis.1,2 On the other hand, it can also be a parasitic reaction that limits the potential window of aqueous energy storage devices and competes with other electrochemical reduction reactions, like those involved in the conversion of CO2.3–5 Understanding electrode properties that influence the HER is therefore necessary to advance aqueous energy storage and conversion devices. The HER is part of a broad class of proton-coupled electron transfer (PCET) reactions which are ubiquitous in aqueous electrochemical environments. Based on the possibility of PCET, HER electrocatalysts can be divided into three types (Fig. 1): (a) proton-blocking electrocatalysts, (b) non proton-blocking electrocatalysts, and (c) reconstruction electrocatalysts (materials undergoing conversion or dissolution and deposition reactions). Gold and platinum represent proton-blocking electrocatalysts, where the bulk composition of the electrocatalyst remains constant and the proton reduction and HER take place at the surface.6–8 In acidic pH, the elementary steps of the HER on a proton-blocking electrocatalyst surface, where * indicates a surface adsorption site, proceed as follows:| Volmer step: * + H+aq + e− ↔ H* | (1) |
| Heyrovsky step: H* + H+aq + e− ↔ H2(g) | (2) |
| Tafel step: H* + H* ↔ H2(g) | (3) |
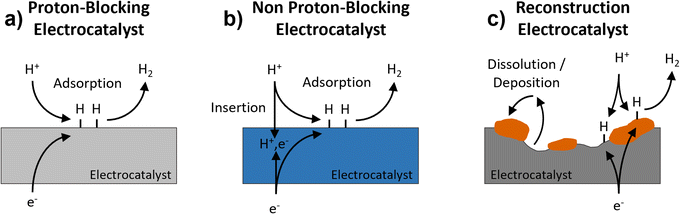 | ||
| Fig. 1 Schematic representation of three types of electrocatalysts for the HER: (a) proton-blocking electrocatalyst, (b) non proton-blocking electrocatalyst, and (c) reconstruction electrocatalyst. | ||
Importantly, adsorbed hydrogen (H*) produced in (1) is a reactant for H2 in (2) and (3). The binding energy of adsorbed hydrogen species on different electrode surfaces has long been used as a catalytic activity descriptor to design, for example, different metal alloys for HER electrocatalysts.9,10
Palladium represents the most well studied non proton-blocking electrocatalyst (Fig. 1b). In Pd, H* can be either a reactant for steps (2) and (3) or diffuse into the electrocatalyst, forming PdHx.11 In this kind of electrocatalyst, the bulk hydrogen composition changes as a function of applied potential which leads to changes in the structure and properties of the electrocatalyst, PdHx. A Devanathan–Stachurski electrochemical double cell utilizes a Pd membrane to separate two compartments. Upon cathodic polarization on one side of the membrane, the absorbed hydrogen transports through the Pd membrane and subsequently undergoes reactivity on the other side of the membrane.12–15 Blom et al. proposed that the mobility of hydrogen in palladium allows hydrogen to interact with different active sites, which is critical to understanding its electrochemical reactivity during CO2 reduction to formate.16
A broader class of non proton-blocking electrodes are the transition metal oxides. The search for non-precious metal catalysts involves compounds such as transition metal oxides.17 The presence of a transition metal means that these materials have tunable redox activity which is necessary for high capacity energy storage electrodes as well as for highly active electrocatalysts. Many transition metal oxides exhibit structures that enable proton-insertion coupled electron transfer.18–21 Proton-insertion coupled electron transfer reactions with transition metal oxides (MO) lead to changes in the composition, structure, and properties of the oxide host prior to or congruent with the HER:20,22–24
| MO + H+aq + e− ↔ HinsMO | (4) |
This leads to the possible participation of electrochemically inserted protons (Hins) in the HER, in parallel to H* on proton-blocking electrocatalysts. For example, following the Heyrovsky and Tafel steps in eqn (2) and (3):
| Hins + H+aq + e− ↔ H2(g) | (5) |
| Hins + H* ↔ H2(g) | (6) |
| Hins + Hins ↔ H2(g) | (7) |
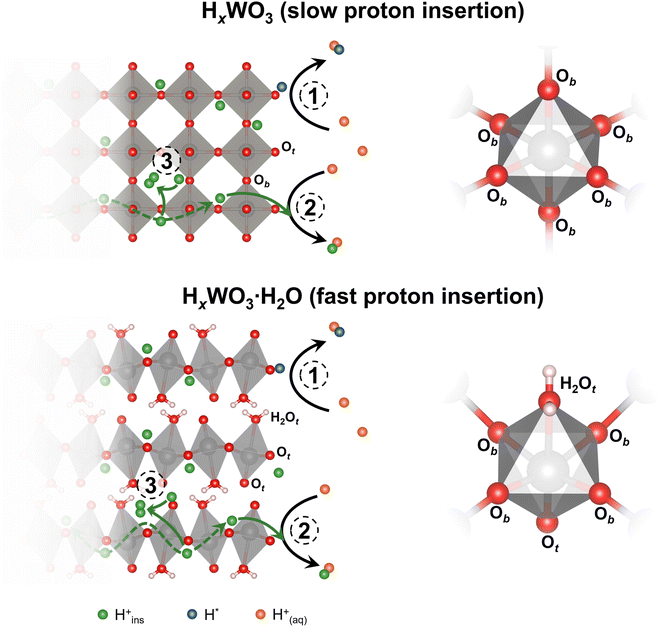
Tungsten oxides undergo reversible proton insertion-coupled electron transfer in acidic electrolytes. This reaction leads to a semiconductor-to-metal transition and is accompanied by changes in the crystal structure, octahedral tilting, and surface proton binding energies of the oxide.25–28 Our group showed that the layered structures of the tungsten oxide hydrates confine structural deformation during proton insertion to two dimensions, as opposed to three dimensions in the anhydrous WO3, leading to faster proton insertion kinetics.26,29 Recently, we showed that proton insertion was necessary to activate tungsten oxides for the HER by comparing the HER activity of WO3·H2O and octylammonium-pillared WO3, which suppressed proton insertion.30 Furthermore, Miu et al. used experimental and computational methods to show that the hydrogen binding energy at different active sites and the corresponding HER activity of WO3 were dependent on the degree of protonation, x in HxWO3.31 These outcomes emphasize the importance of the changes in composition, structure, and properties associated with proton insertion that precede the onset of the HER.
Herein, we study the influence of proton composition and degree of hydration on the HER activity of tungsten oxides and propose that electrochemically inserted protons participate in the HER. Transient and steady-state electrochemical characterization techniques showed that anhydrous and hydrated tungsten oxides have differences in their HER activity that were associated with changes in proton composition. HxWO3·H2O had the highest activity, followed by HxWO3 and finally HxWO3·2H2O. Operando X-ray diffraction (XRD) measurements showed that proton insertion into WO3·H2O and WO3·2H2O resulted in minor deviations in octahedral tilting, while WO3 went through two phase transitions: monoclinic → tetragonal → cubic, which involve significant changes in octahedral tilting and off-center displacements of the W6+-ion. At high states of proton insertion, HxWO3 and HxWO3·H2O trend toward higher symmetry, while HxWO3·2H2O remains in a low symmetry monoclinic phase. This result suggests that higher symmetry crystal structures, which promote electronic conductivity, lead to higher electrocatalytic activity. Given that H0.69WO3·H2O and H0.65WO3 have similar surface area and morphology, proton composition, structural symmetry, and electronic properties at the onset of HER activity, an additional factor must explain the difference in their HER overpotential and kinetics. To explain this difference, we propose that the protonated materials can serve as proton reservoirs for the HER, whereby electrochemically inserted protons participate in the HER. Participation of inserted protons would lead to a rate dependence on bulk proton transport, which would favor HER activity in H0.69WO3·H2O vs. H0.65WO3. Our results emphasize the importance and possible involvement of the inserted protons undergoing PCET reactions on the surface of electrocatalysts.
2. Experimental methods
2.1 Synthesis of tungsten oxides
Monoclinic tungsten oxide dihydrate (WO3·2H2O) was synthesized using the Freedman method.32 Briefly, 50 mL of 1 M Na2WO4·2H2O (99+% Acros Organics) was added dropwise to 450 mL of 3 M HCl (Certified ACS Plus, Fisher Chemical) that was stirred at 300 rpm at room temperature. This mixture was stirred overnight, and the precipitate was collected via vacuum filtration and washed with DI water until the pH of the rinse solution reached ∼6. Orthorhombic tungsten oxide monohydrate (WO3·H2O) was prepared by heating WO3·2H2O at 120 °C overnight in air. Monoclinic tungsten trioxide (WO3) was prepared by heating at 350 °C for 5 hours in air with a heating rate of 5 °C min−1.2.2 Physical characterization
Scanning electron microscopy (SEM) was performed using a field emission Hitachi SU8700 microscope. Ex situ SEM was performed on a field emission FEI Verios 460L microscope. X-ray diffraction was performed on a PANalytical Empyrean diffractometer in the Bragg–Brentano geometry with Cu Kα radiation (Kα1/Kα2λ = 1.5406 Å/1.5444 Å).2.3 Electrocatalysis measurements
Electrocatalysis measurements were performed using the rotating disk electrode (RDE) setup in a Teflon cell (both from Pine Research Instrumentation). The Teflon cell was cleaned with detergent, 1 M KOH, and aqua regia (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HCl to HNO3), with thorough deionized water rinses between each step. The electrolyte was 0.5 M H2SO4 (ACS TraceMetal Grade). A porous glass frit bubbler was used to purge the electrolyte with hydrogen gas (ARC3), and hydrogen was bubbled in the cell throughout each measurement. The counter electrode was a graphite rod in a glass compartment (pine), and the reference electrode was Hg/Hg2SO4 in sat'd K2SO4 (Pine Research Instrumentation). The reference electrode was calibrated using a reversible hydrogen electrode (RHE). To prepare the RHE, we first electrodeposited platinum on a platinum rod (99.997%, Alfa Aesar). This electrodeposition took place in a 41 mM solution of H2PtCl4 (>99.9% trace metals basis, Sigma-Aldrich) in 1 M HCl with a platinum counter electrode. A constant current of 10 mA cm−2 was passed through the working electrode for 30 s. The platinum electrode was rinsed thoroughly with deionized water and transferred to an electrochemical cell with 0.5 M H2SO4 saturated with hydrogen gas. Hydrogen gas continuously flowed over the platinized platinum electrode, which maintained a constant concentration of dissolved H2 and a hydrogen pressure slightly higher than 1 atm since excess hydrogen escaped through an open port. The H/H+ redox couple that forms as a result of H2 dissociation on the platinized platinum was therefore suitable for use as a RHE. The OCV was measured versus the RHE until the potential reached a plateau (typically 20 minutes), and the average potential during the plateau was used as the calibrated potential of the Hg/Hg2SO4 reference electrode on the RHE scale. The potential measured vs. Hg/Hg2SO4 was converted to the RHE using the calibration potential according to eqn (8):
1 HCl to HNO3), with thorough deionized water rinses between each step. The electrolyte was 0.5 M H2SO4 (ACS TraceMetal Grade). A porous glass frit bubbler was used to purge the electrolyte with hydrogen gas (ARC3), and hydrogen was bubbled in the cell throughout each measurement. The counter electrode was a graphite rod in a glass compartment (pine), and the reference electrode was Hg/Hg2SO4 in sat'd K2SO4 (Pine Research Instrumentation). The reference electrode was calibrated using a reversible hydrogen electrode (RHE). To prepare the RHE, we first electrodeposited platinum on a platinum rod (99.997%, Alfa Aesar). This electrodeposition took place in a 41 mM solution of H2PtCl4 (>99.9% trace metals basis, Sigma-Aldrich) in 1 M HCl with a platinum counter electrode. A constant current of 10 mA cm−2 was passed through the working electrode for 30 s. The platinum electrode was rinsed thoroughly with deionized water and transferred to an electrochemical cell with 0.5 M H2SO4 saturated with hydrogen gas. Hydrogen gas continuously flowed over the platinized platinum electrode, which maintained a constant concentration of dissolved H2 and a hydrogen pressure slightly higher than 1 atm since excess hydrogen escaped through an open port. The H/H+ redox couple that forms as a result of H2 dissociation on the platinized platinum was therefore suitable for use as a RHE. The OCV was measured versus the RHE until the potential reached a plateau (typically 20 minutes), and the average potential during the plateau was used as the calibrated potential of the Hg/Hg2SO4 reference electrode on the RHE scale. The potential measured vs. Hg/Hg2SO4 was converted to the RHE using the calibration potential according to eqn (8):| ERHE = Em,REF + EREF | (8) |
The working electrode was a drop cast film deposited on a glassy carbon change-disk RDE (Pine Research Instrumentation). The glassy carbon disk was polished using a 0.05 μm alumina slurry. After polishing, it was rinsed with deionized water and sonicated for 10 minutes in detergent and 10 minutes in ethanol. The clean glassy carbon was dried at 60 °C in air for at least 1 hour. The electrocatalyst dispersion was prepared by mixing 20 mg of the active material with 29.45 μg of Nafion (Ion Power) dispersed in 5 mL of ethanol. The dispersion was sonicated for 30 minutes in an ice bath. Immediately following sonication and vortexing, 5 μL of the dispersion was deposited on the glassy carbon change-disk electrode. The resulting film contained 100 μg cm−2 active material and 0.15 μg cm2 Nafion.
Electrochemical impedance spectroscopy (EIS) was performed on the pristine electrode at open circuit voltage using a frequency range of 500 kHz to 100 mHz and an amplitude of 10 mV. The potential was corrected for iR losses according to eqn (9):
| E = Em − iR | (9) |
All subsequent measurements were performed using a rotation rate of 1600 rpm. Each electrode underwent 3 cyclic voltammetry (CV) cycles at 10 mV s−1. The potential range for the conditioning cycles was limited to a lower cutoff potential that did not reach the onset of the HER (this potential cutoff was dependent on the electrocatalyst). The HER activity was studied using CV and chronoamperometry. The CV measurements were carried out with a scan rate of 10 mV s−1 with an upper cutoff potential of −0.1 V vs. Hg/Hg2SO4, and the lower cutoff potential was defined as the potential at which the current reached 10 mA cm−2 (based on the geometric surface area). Chronoamperometry measurements were performed by stepping the potential in 20 mV increments from 0 V vs. RHE to potentials where the current exceeded 10 mA cm−2. Each step was held for 3 minutes unless otherwise stated. All measurements were performed with a Bio-Logic SP-50e potentiostat.
2.4 Operando XRD measurements
Synchrotron XRD was performed at the stanford synchrotron radiation lightsource (SSRL) on beam line 2-1 in Bragg–Brentano geometry using an incident X-ray energy of 17 keV (λ = 0.72932 Å). The instrument was equipped with a Pilatus 100 K area detector, and the 2D diffraction data was compiled and integrated using a python script specifically developed for angle-resolved measurements at SSRL beam line 2-1.Slurry electrodes were used for the operando XRD measurements. Slurries consisted of 80 wt% active material, 10 wt% nafion, and 10 wt% acetylene black dispersed in ethanol using 3 rounds of mixing at 2000 rpm for 2.5 min in a Thinky mixer (Thinky USA, model AR-100). Slurries were cast on stainless steel mesh (Fisher Scientific) and carbon paper (Fuel Cell Earth) substrates with a final active material loading of 2–6 mg cm−2 and dried at 50 °C. The mass loading and substrate are reported for each experiment. Electrodes were cycled using cyclic voltammetry and linear sweep voltammetry using a Bio-Logic SP150 potentiostat in an operando electrochemical cell (Fig. S1;† based on a cell design reported in a previous study).33 The reference electrode was a leakless Ag/AgCl reference electrode (eDAQ), and the counter electrode was carbon paper. The potential recorded from the leakless Ag/AgCl reference electrode was adjusted to the RHE scale by comparing the half wave potential of the WO3·H2O redox peak in a 3-electrode cell containing a calibrated Hg/Hg2SO4 in saturated K2SO4 reference electrode and graphite counter electrode. Each electrode was cycled in fresh 0.5 M H2SO4 (ACS TraceMetal Grade, Fisher Scientific).
Operando diffraction patterns were collected at a fixed 2θ position every 1 second when the scan rate was 10 mV s−1 and every 10 seconds when the scan rate was 1 mV s−1. Each 2θ position provided the diffraction pattern for 2θ values ± ∼3.4°, and diffraction results for different 2θ ranges were collected during sequential cyclic voltammetry cycles using the same electrode. Results from multiple 2θ ranges were stitched together to obtain the full diffraction patterns used for structural refinement and analysis. Table 1 summarizes the 2θ range collected for each sample, along with the electrode substrate, slurry mass loading, scan rate, and potential range. Pawley refinements of the diffraction data were carried out using the TOPAS-Academic (Version 6) software package to determine the lattice parameters.34,35
| Material | Mass loading (mg cm−2) | Substrate | Technique | Scan rate (mV s−1) | Potential range (V vs. RHE) | 2θ range (°) |
|---|---|---|---|---|---|---|
| WO3 | 2 | SS | CV | 1 | −0.308 to 0.642 | 9.63–30.10 |
| WO3·H2O | 6 | CP | CV | 10 | −0.493 to 0.644 | 4.13–29.76 |
| WO3·H2O | 6 | CP | Stepwise LSV | 10 | −0.493 to 0.670 | 3.23–41.89 |
| WO3·2H2O | 2 | SS | CV | 10 | −0.358 to 0.640 | 2.83–26.61 |
2.5 Density functional theory (DFT) calculations
The geometry and electronic structure of anhydrous and hydrated tungsten oxides were studied by DFT calculations, using the periodic plane wave code Vienna ab initio simulation package (VASP 6.1).36,37 Meta-generalized gradient approximation (meta-GGA) functionals, such as the strongly constrained and appropriately normed (SCAN) functional,38 are more computationally demanding than GGA functionals but provide higher accuracy in properties including band gaps, lattice parameters, formation energies, and energy barriers of non-metals.39–41 Therefore, we used the second version of the regularized SCAN (r2SCAN)42 to treat electron exchange-correlation with the rVV10 non-local correlation functional (b = 11.95) and to semi-empirically describe the van der Waals interactions.43,44 We employed the “PAW 54” pseudopotentials within the projector augmented wave (PAW) framework to describe the ion–electron interaction.45 The number of valence electrons treated were 14, 6, and 1, respectively for W, O, and H. For the geometry optimization of tungsten oxides, we sampled the Brillouin zone using Gamma-centered grids with constant spacing density of 0.3 Å−1 applying Gaussian smearing (σ = 0.03 eV) of partial occupancies, with a plane-wave cut-off energy of 680 eV and energy and force convergence criteria of 10−6 eV and 0.02 eV Å−1, respectively. Spin polarization and Harris–Foulke-type corrections for the calculation of forces were also considered.46 All the geometries were relaxed using the conjugate gradient algorithm to minimize the total energy. The most stable optimized structures were selected after thorough examination of different hydrogen binding sites (i.e. binding configurations) and are presented in Fig. S2† with the lattice parameters in Table S1.† The theoretical bandgap and band structure of the tungsten oxides were evaluated through DFT calculations of fully relaxed structures, employing a denser spacing density of 0.1 Å−1 for Gamma-centered grids. Transition states were determined by relaxation of solid state nudged elastic band (ssNEB) with the climbing image (CI) method.47–503. Results & discussion
3.1 Activation of the HER on tungsten oxides
Anhydrous WO3 and hydrated tungsten oxides (WO3, WO3·H2O, and WO3·2H2O) were selected for this study since all three materials undergo proton insertion-coupled electron transfer reactions and are therefore non proton-blocking electrodes in acidic electrolytes. Furthermore, they exhibit unique structural characteristics. WO3·2H2O contains layers of corner-sharing WO5(H2O) octahedra separated by interlayer water molecules (Fig. 2c). Subsequent dehydration leads to the removal of the interlayer water and redistribution of bound water to form WO3·H2O (Fig. 2b) and eventually the bound water is removed and the interlayer collapses to form WO3 (Fig. 2a). This dehydration mechanism is supported by thermogravimetric analysis, which shows two sequential mass loss regions that correspond to the total removal of 2H2O from WO3·2H2O.25,30 Powder XRD patterns for each hydration state (Fig. S3†) confirm the formation of monoclinic (P21/n) WO3·2H2O, orthorhombic (Pmnb) WO3·H2O, and monoclinic (P21/n) WO3. SEM shows that the same morphology was maintained for each hydration state (Fig. S4†). The acid–precipitation reaction resulted in nanoplatelets with lateral dimensions on the order of 100–300 nm and thicknesses on the order of 10 s of nm (equivalent to ∼20–100 inorganic layers in the hydrated materials). The lack of morphology and particle size changes in SEM suggests the surface areas are comparable between different hydration states. Therefore, differences in electrochemical reactivity can be attributed to the degree of hydration and the local coordination environment of tungsten (layered vs. interconnected structure, and presence or absence of a coordinated water in the octahedra).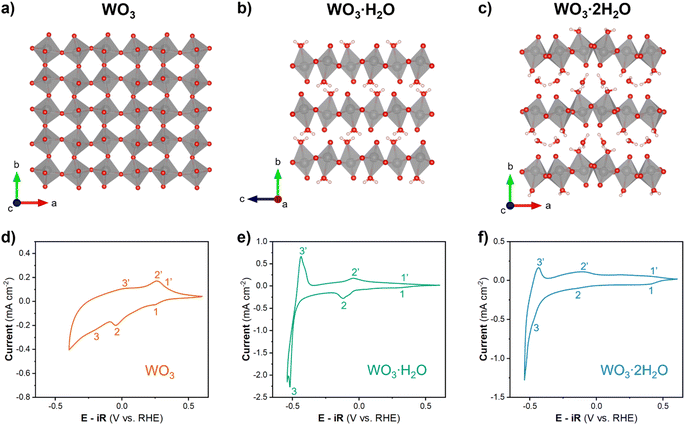 | ||
| Fig. 2 Crystal structures of (a) monoclinic WO3, (b) orthorhombic WO3·H2O, and (c) monoclinic WO3·2H2O.51 Cyclic voltammograms of (d) WO3, (e) WO3·H2O, and (f) WO3·2H2O with a rotation rate of 1600 rpm and scan rate of 10 mV s−1 in 0.5 M H2SO4. | ||
The electrochemical behavior of WO3·nH2O (n = 0, 1, 2) was investigated using cyclic voltammetry of thin films. Fig. 2d–f show cyclic voltammograms of each material in a limited potential range where the current response is predominantly attributed to proton insertion coupled electron transfer, before the onset of the HER:
| WO3·nH2O + xH+ + xe− ↔ HxWO3·nH2O (n = 0, 1, 2) | (10) |
The shape of a CV can provide insights into the type of electrochemical reaction and its kinetics.52 WO3 (Fig. 2d) shows an asymmetric CV response with three observable redox events (marked by 1/1′, 2,2′, and 3/3′). The peak potential separation is indicative of the reversibility of the electrochemical reaction. Based on this assessment, the 1/1′ redox event with ΔEp ≈ 100 mV at 10 mV s−1 is more reversible as compared to the 2/2′ redox event that has a ΔEp ≈ 300 mV at 10 mV s−1. It is difficult to assign peak potentials to the broad peaks of the 3/3′ redox event, however, this response is typical for a solid-solution insertion reaction (as discussed in the following sections). The CV of WO3·H2O (Fig. 2e) shows distinct redox events centered at 0.3 V (1/1′), −0.08 V (2/2′), and −0.48 V (3/3′) all with a ΔEp ≈ 80 mV at 10 mV s−1. Between the sharp redox peaks, there is also a non-negligible current response that can be attributed to solid-solution insertion of protons. The small peak potential separation suggests facile kinetics for proton insertion and de-insertion in WO3·H2O. WO3·2H2O (Fig. 2f) shows two redox events (1/1′ and 2/2′) with broad current responses in the potential range of −0.4 to 0.5 V vs. RHE and another redox event (3/3′) centered at approximately −0.47 V vs. RHE. The broad redox peaks make it difficult to quantify ΔEp for WO3·2H2O, but the approximate values for each redox event are less than 100 mV. Similar to WO3·H2O, this suggests favorable kinetics for proton insertion and de-insertion into WO3·2H2O. In our prior work, we hypothesized that the favorable kinetics of WO3·2H2O were due to its more limited structural deformation upon proton insertion.26,29 The results from cyclic voltammetry reveal that each hydration state of WO3·nH2O has multiple redox events that take place prior to reaching potentials necessary to catalyze the HER, and the ΔEp trends show that proton insertion is more reversible in WO3·H2O and WO3·2H2O as compared to WO3. In other words, removal of H+/e− is kinetically more facile in hydrated tungsten oxides compared to anhydrous tungsten oxide, a factor that may influence HER activity.
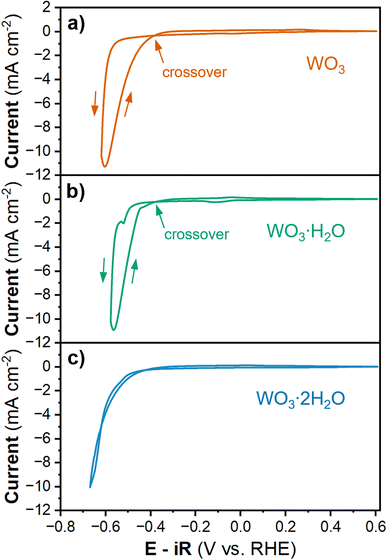
To study the HER activity of tungsten oxides, we decreased the cathodic potential limit during cyclic voltammetry, which led to a significant increase in cathodic current density (Fig. 3). In proton-blocking electrodes, the HER current measured during the cathodic and anodic voltammetry scans is equal.53 However, for WO3 and WO3·H2O, the anodic scan exhibits higher magnitude HER currents at lower overpotentials than the cathodic scan. This crossover between the cathodic and anodic scans indicates an activation process taking place simultaneously with the onset of the HER. In other words, the material that forms at higher overpotentials has a higher activity compared to that which is present prior to the initial onset of HER. Conversely, the anodic and cathodic HER current of WO3·2H2O are nearly the same, suggesting there is no further activation process at high overpotentials. The overpotential for HER during the anodic and cathodic scans for each hydration state of tungsten oxide were determined by the potential required to reach ∼10 mA cm−2 based on the geometric area, as summarized in Table 2. WO3·2H2O exhibited the highest overpotential of 661 mV during both scans. WO3·H2O exhibits the lowest overpotential with a cathodic overpotential of 578 mV and anodic overpotential of 547.9 mV (a 30 mV improvement after further activation). The cathodic overpotential of WO3 was 626.6 mV and the anodic overpotential was 589.3 mV (a 37 mV improvement after further activation). The proton insertion reactions that precede the onset of the HER reveal that the tungsten oxides are dynamic electrocatalysts. Furthermore, the activation processes that lead to the crossover feature during cyclic voltammetry of WO3 and WO3·H2O are rate and potential dependent.
| Material | CV ηcathodic (mV) | Current (mA cm−2) | CV ηanodic (mV) | Current (mA cm−2) | Δη (mV) | CA η (mV) | Tafel slope (mV dec−1) |
|---|---|---|---|---|---|---|---|
| WO3 | 626.6 | −10.007 | 589.3 | −10.009 | −37.3 | 531.7 | 49.4 |
| WO3·H2O | 578.0 | −10.098 | 547.9 | −10.002 | −30.1 | 501.0 | 36.6 |
| WO3·2H2O | 661.0 | −10.002 | 661.3 | −10.005 | 0.3 | 621.5 | 95.8 |
To ensure that material transformation was not the rate limiting step when determining the HER activity of the oxides, we obtained quasi-equilibrium HER currents using stepwise chronoamperometry. The potential was stepped in 20 mV intervals from 0 V to the onset of HER activity, and each step was held for 3 minutes. Holding the potential for 3 minutes allowed sufficient time for proton insertion reactions to complete, and the remaining plateau current was attributed to the HER. The average current from the last 30 s of each step was plotted as the absolute value of current density |j| on a log scale vs. overpotential in Fig. 4a. Although this method does not allow for a direct measurement of overpotential at 10 mA cm−2, this value can be interpolated from the linear portion of the log(|j|) vs. η plot. The overpotentials from quasi-equilibrium CA results were 531.7 mV for WO3, 501.0 mV for WO3·H2O, and 621.5 mV for WO3·2H2O. The overpotentials from CA were all lower than the cathodic or anodic overpotentials measured using cyclic voltammetry. Comparing ηcathodic from CV to η from CA, WO3 exhibited the most significant improvement of 94.9 mV, followed by WO3·H2O at 77 mV and WO3·2H2O at 39.5 mV. We attribute this difference to the quasi-equilibrium conditions of the CA measurement.
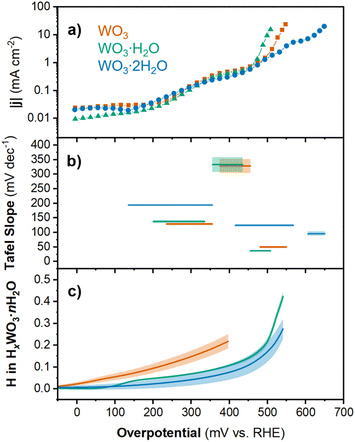 | ||
| Fig. 4 Chronoamperometry results for WO3, WO3·H2O, and WO3·2H2O showing the (a) current density and (b) Tafel slope as a function of overpotential (shading respresents the standard error of fit for each linear region). (c) Proton composition in HxWO3·nH2O (n = 0, 1, 2) as a function of overpotential (calculated using method 2; see Discussion 1 in ESI†). Shading represents the standard deviation from the average of three separate electrodes. | ||
The log(|j|) vs. overpotential results for each material provide additional information about the electrochemical reactivity and kinetics of the HER. First, we observed that between 0 and 450 mV, the current response was similar for all three materials. The current was negligible up to η ≈ 150 mV. This was followed by an increase in current in the range of 150 < η < 350 mV and another plateau between 350 < η < 450 mV. Finally, the onset of HER occurred for each material at η > 450 mV. The current response at intermediate overpotentials suggests that each material exhibits low HER activity until the onset of an activation process. In the high overpotential region (η > 450 mV), we observe the onset of HER. The slope of the linear region (Tafel slope) provides mechanistic information about the reaction kinetics.54 Generally, the lower the Tafel slope the faster the reaction. The materials showed the following Tafel slopes in the linear region where |j| > 1 mA cm−2: 49.4 mV dec−1 for HxWO3, 36.6 mV dec−1 for HxWO3·H2O, and 95.8 mV dec−1 for HxWO3·2H2O (see ESI Fig. S5† for more details). These Tafel slopes suggest that the HER kinetics decrease in the order of HxWO3·H2O > HxWO3 > HxWO3·2H2O.
The Tafel slope can describe the rate determining step in the HER. The first step in the HER for proton-blocking electrodes is the Volmer reaction with a characteristic Tafel slope of 120 mV dec−1. After the Volmer step, the HER can proceed by (1) the Tafel step with a Tafel slope of 30 mV dec−1, or (2) the Heyrovsky step with a Tafel slope of 40 mV dec−1.6,55,56 It is also possible to observe Tafel slopes characteristic of a reaction that does not involve electron transfer, which in the HER would occur between the first and second electron transfer reactions and correspond to a Tafel slope of 60 mV.57 Intermediate values between these “cardinal” values can exist, which are attributed to chemical rate determining steps during the HER. WO3·H2O has a Tafel slope close to 40 mV dec−1, which indicates that the second electron transfer during the HER is the rate determining step (Heyrovsky step following the convention on proton-blocking electrodes). The anhydrous WO3 has a slightly higher Tafel slope close to 60 mV dec−1, suggesting that the rate determining step follows the first electron transfer but does not involve electron transfer. Finally, WO3·2H2O has a Tafel slope close to 120 mV dec−1, where the rate determining step can be attributed to the first electron transfer reaction (Volmer). It is important to note that factors such as the H coverage and symmetry factor of the reaction can influence the Tafel slope, therefore, these Tafel slope assignments should only be considered as the suggested rate determining steps. However, these results demonstrate that the HER kinetics and rate determining steps are dependent not only on the extent of proton insertion, but also the hydration state of tungsten oxide. The overpotentials and Tafel slopes for each hydration state of tungsten oxide were compared to the performance of commercial Pt/C and other non-precious metal catalysts in Table S2 and Fig. S6.† Whereas most catalysts with a high overpotential show high Tafel slopes, the tungsten oxides exhibit high overpotentials with low Tafel slopes, suggesting fast reaction kinetics once sufficient overpotential is reached. To determine the origin of the different onset potentials and Tafel slopes for each hydration state of tungsten oxide, we considered the proton composition, bulk structural transformations, and changes in the electronic structure of each material.
3.2 Proton composition as a function of potential
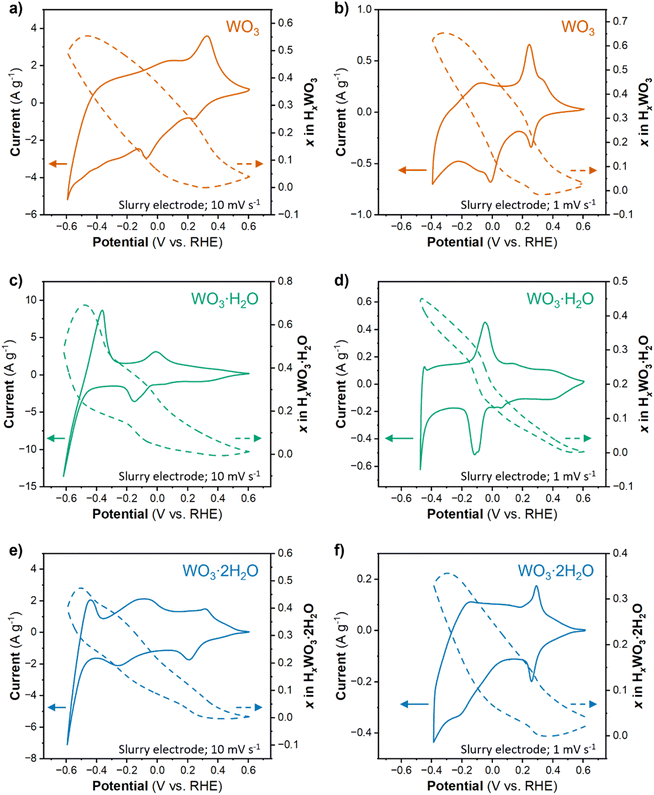
The proton composition of the oxide (x in HxWO3·nH2O; n = 0, 1, 2) determines its structure and thus, properties during the HER. The protonated tungsten oxides, also called hydrogen bronzes, are effectively new electrocatalysts compared to the precatalyst states present in the uncycled electrode (the unprotonated oxides). We performed cyclic voltammetry on high mass loading (6 mg cm−2) electrodes where Qinsert ≫ QHER in a wide potential range. The amount of proton insertion as a function of potential was determined using the corrected Q − Q0 approach (see Discussion 1 in ESI† for a detailed explanation of techniques used to calculate the proton composition). Fig. 5a, c and e show the CV results and proton compositions for HxWO3, HxWO3·H2O, and HxWO3·2H2O slurry electrodes in 0.5 M H2SO4 at 10 mV s−1. The maximum proton composition for each material was H0.55WO3, H0.69WO3·H2O, and H0.47WO3·2H2O.The electrocatalytic measurements revealed a significant enhancement in HER activity upon switching from a non-equilibrium technique (cyclic voltammetry) to a quasi-equilibrium technique (chronoamperometry). Under quasi-equilibrium conditions, there is more time for proton insertion reactions to reach completion, which particularly impacted WO3. Fig. 5b shows the CV and proton composition of HxWO3 cycled at 1 mV s−1. The maximum capacity reached 75.3 mA h g−1 (corresponding to H0.65WO3) – a difference of 0.1H+ per W compared to results from a shorter timescale using a scan rate of 10 mV s−1. We also cycled the hydrated tungsten oxides at 1 mV s−1 (Fig. 5d and f), however, at slow scan rates the final reduction event (3/3′ in Fig. 2e and f) coincides with the onset of HER activity and complicates the quantification of proton insertion at high overpotentials. Although slower scan rates limit the accessible potential window, the slope of the proton composition as a function of potential for WO3·H2O and WO3·2H2O was greater when scan rate = 1 mV s−1 (Fig. 5d and f) compared to the results when scan rate = 10 mV s−1 (Fig. 5c and e). Two observations from this analysis of proton composition are (1) the highest HER activity correlates with the materials containing the highest proton content at potentials close to the onset of the HER, and (2) longer reaction times during quasi-equilibrium conditions lead to higher HER activity (smaller overpotentials) in all three materials. Quantitatively, the results show that HxWO3·H2O and HxWO3 reach similar proton compositions between 0.69 and 0.65H+ per W, whereas HxWO3·2H2O only reaches ∼0.5H+ per W. Further assessment of the structural and electronic properties is necessary to explain the HER activity trends, especially in the case of H0.69WO3·H2O and H0.65WO3 which have similar proton compositions.
3.3 Structural transformations as a function of potential/composition
Electrochemical proton insertion into tungsten oxides leads to changes in octahedral tilting and phase transformations. To understand the structures present in HxWO3·nH2O (n = 0, 1, 2) at the onset of HER activity, we performed operando synchrotron XRD during cyclic voltammetry. WO3·H2O and WO3·2H2O were cycled at 10 mV s−1 and WO3 was cycled at 1 mV s−1 to ensure that all possible phase transformations could be observed since the proton insertion kinetics in the anhydrous material are slower than the layered hydrates. Fig. S8† shows the CVs for each electrode in the operando electrochemical cell, in agreement with the features observed using the RDE (Fig. 2d–f) and slurry electrodes in a 3-electrode cell (Fig. 5).
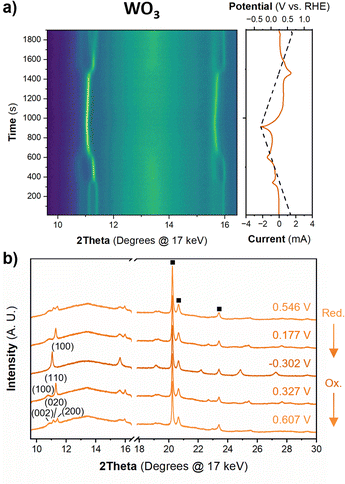
Fig. 6 shows the diffraction patterns and corresponding potential and current as a function of time for WO3 during cyclic voltammetry in 0.5 M H2SO4 at 1 mV s−1. After the first proton insertion event with a peak potential (Ep) of 0.26 V vs. RHE, the peaks originally associated with the (002), (020), and (200) indices of the monoclinic cell at 10.84, 11.14, and 11.40° 2θ, respectively, merge into two peaks indicating a structural transition to higher symmetry. The 1D XRD pattern collected at 0.177 V (vs. RHE) can be well fit to the tetragonal P4/nm space group symmetry with no observable tilting of the octahedra while the antiparallel displacements of W6+-ions remain.58 After the second proton insertion event at Ep = 0.0 V vs. RHE, the (100) and (110) reflections positioned at 10.76 and 11.29° 2θ, respectively, merge into a single peak suggesting another transition to higher symmetry. The 1D pattern collected under an applied potential of −0.30 V (vs. RHE) was fit to a cubic unit cell with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry.59 The perovskite-like structure does not demonstrate any observable tilts, nor does it allow for the displacement of the W6+-ion. The broad current response between −0.1 and −0.28 V vs. RHE is attributed to proton insertion into cubic HxWO3 without further structural transitions (solid solution proton insertion). Fig. 7 shows potential dependent proton composition and pseudo-cubic a-lattice parameter (ap) calculated from the lattice parameters of each phase using eqn (S2)–(S4).† After the pure cubic structure forms, ap continues to increase from 3.770 Å at −0.083 V to 3.787 Å at −0.282 V vs. RHE. The same series of transitions occurred in reverse order as protons de-inserted during the anodic cyclic voltammetry scan from −0.31 V to 0.64 V vs. RHE.
m space group symmetry.59 The perovskite-like structure does not demonstrate any observable tilts, nor does it allow for the displacement of the W6+-ion. The broad current response between −0.1 and −0.28 V vs. RHE is attributed to proton insertion into cubic HxWO3 without further structural transitions (solid solution proton insertion). Fig. 7 shows potential dependent proton composition and pseudo-cubic a-lattice parameter (ap) calculated from the lattice parameters of each phase using eqn (S2)–(S4).† After the pure cubic structure forms, ap continues to increase from 3.770 Å at −0.083 V to 3.787 Å at −0.282 V vs. RHE. The same series of transitions occurred in reverse order as protons de-inserted during the anodic cyclic voltammetry scan from −0.31 V to 0.64 V vs. RHE.
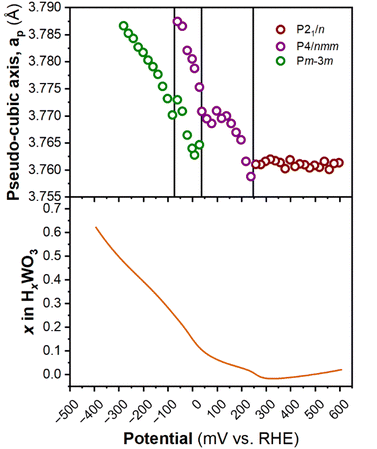 | ||
| Fig. 7 Pseudo-cubic parameter a (from operando XRD), and proton composition of WO3 (from Fig. 5b) as a function of potential during a cathodic cyclic voltammetry scan in 0.5 M H2SO4 at 1 mV s−1. | ||
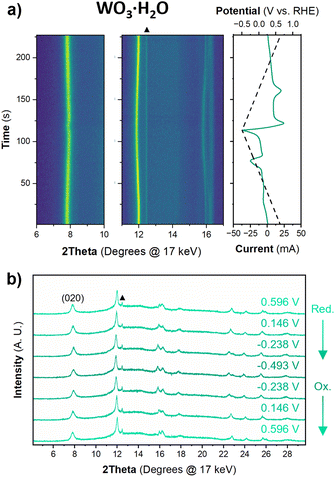
The structure of WO3·H2O was reported previously by Szymanski and Roberts as a primitive orthorhombic cell with Pmnb space group symmetry (see Discussion 2 in ESI† for more details on the structural refinements).60Fig. 8 shows the operando XRD data for WO3·H2O at 10 mV s−1. Multiple reduction and oxidation events were observed (right panel in Fig. 8a), however, the diffraction results do not indicate any solid-state phase transitions associated with these events. Moreover, no morphology changes were observed via ex situ SEM (Fig. S9†) between the pristine and cycled slurry electrode, when cycled to a cathodic cutoff potential of −0.8 V vs. RHE, suggesting that no dissolution and redeposition process is taking place. Instead, Pawley refinements of 1D diffraction patterns at various potentials (Fig. 8b) could be modeled by a contraction of the interlayer distance and in-plane expansion of the inorganic layers with increasing proton content (Fig. 9). To verify this observation, we turned to DFT calculations. We found the contraction and expansion trends to align with the DFT-computed lattice parameters shown in Table S1.† This behavior is also in agreement with prior literature that reported similar trends up to a proton composition of H0.12WO3·H2O.61 The lack of phase transformations is consistent with the faster proton (de)insertion kinetics compared to WO3 observed during cyclic voltammetry.
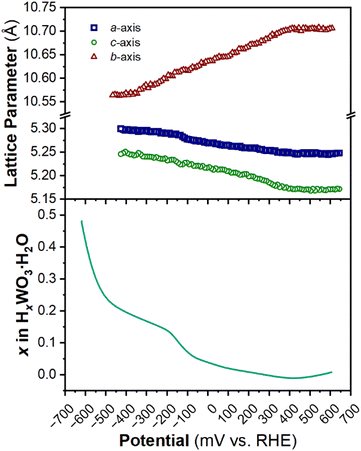 | ||
| Fig. 9 Trend of lattice parameters (from Pawley refinements of the operando XRD) and proton composition in HxWO3·H2O (from Fig. 5c) as a function of potential during the cathodic cyclic voltammetry scan in 0.5 M H2SO4 at 10 mV s−1. | ||
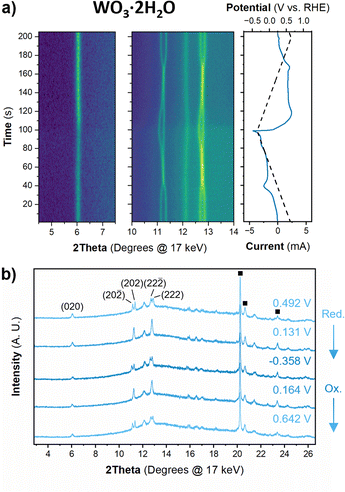
The structure of WO3·2H2O was reported by Li et al., in 2000 from powder XRD. It has a monoclinic cell with P21/n symmetry with a complex pattern of octahedral tilting.62 During electrochemical proton insertion, operando XRD results (Fig. 10) show that the (20![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) and (202) reflections at 11.16 and 11.34° 2θ, respectively, merge as the potential is scanned from 0.642 V to −0.05 V vs. RHE, and they proceed to split at higher proton compositions between −0.05 V and −0.358 V vs. RHE. This trend is also observed with the (22
) and (202) reflections at 11.16 and 11.34° 2θ, respectively, merge as the potential is scanned from 0.642 V to −0.05 V vs. RHE, and they proceed to split at higher proton compositions between −0.05 V and −0.358 V vs. RHE. This trend is also observed with the (22![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) and (222) reflections at 12.70 and 12.88° 2θ, respectively. Furthermore, the (020) peak position remains constant, indicating that the interlayer spacing does not change during proton (de)insertion. The opposite transitions occur during deprotonation in the anodic scan of the CV. Pawley refinements were performed on 1D diffraction patterns of the full 2θ range recorded during the operando measurements of WO3·2H2O. All the collected diffraction patterns could be modeled with the monoclinic P21/n structure with changes in the a- and c-lattice parameters, with the most significant change in the a-axis (Fig. 11). Overall, upon proton insertion and de-insertion in HxWO3·2H2O, the structural transitions are limited to the ac-plane and may be associated with changes in the degree of tilting and changes in bond lengths within the inorganic layers.
) and (222) reflections at 12.70 and 12.88° 2θ, respectively. Furthermore, the (020) peak position remains constant, indicating that the interlayer spacing does not change during proton (de)insertion. The opposite transitions occur during deprotonation in the anodic scan of the CV. Pawley refinements were performed on 1D diffraction patterns of the full 2θ range recorded during the operando measurements of WO3·2H2O. All the collected diffraction patterns could be modeled with the monoclinic P21/n structure with changes in the a- and c-lattice parameters, with the most significant change in the a-axis (Fig. 11). Overall, upon proton insertion and de-insertion in HxWO3·2H2O, the structural transitions are limited to the ac-plane and may be associated with changes in the degree of tilting and changes in bond lengths within the inorganic layers.
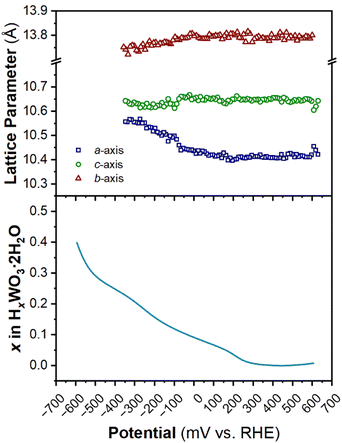 | ||
| Fig. 11 Trend of lattice parameters (from Pawley refinements of the operando XRD) and proton composition in HxWO3·2H2O (from Fig. 5e) as a function of potential during the cathodic cyclic voltammetry scan in 0.5 M H2SO4 at 10 mV s−1. | ||
Overall, these results show that WO3 undergoes phase transformations from monoclinic to tetragonal and tetragonal to cubic accompanied by the loss of octahedral tilting and second order Jahn–Teller distortions upon proton insertion. Conversely, proton insertion into tungsten oxide hydrates causes changes in the degree of tilting without any observed phase transformations. WO3·H2O trends toward higher symmetry, based on the observation of some diffraction peaks beginning to merge, while WO3·2H2O trends toward higher symmetry at low proton compositions but reverts back to lower symmetry and a higher degree of tilting at high proton compositions.
3.4 Origin of hydration state dependence of HER activity on protonated tungsten oxides
Taking together the electrocatalytic activity, proton composition, and structure of each electrocatalyst in this study, it is possible to consider the origin of the apparent hydration state dependence of the HER activity of tungsten oxides. The highest HER activity was observed in HxWO3·H2O, followed by HxWO3, and finally HxWO3·2H2O with a significantly higher overpotential and Tafel slope. Here we discuss several factors that may influence electrocatalytic activity: (1) surface area, (2) electronic conductivity, (3) hydrogen adsorption energy, and (4) participation of inserted protons. Finally, we propose a mechanism for the HER activity differences between each tungsten oxide material characterized here.We first consider the influence of surface area: the larger the electrochemical interface, the higher the areal current on a geometric basis. SEM images in Fig. S4† show that the particle size and morphology is independent of the hydration state of WO3·nH2O (n = 0, 1, 2), therefore, we do not expect there to be differences in the electrocatalytically active surface area. Second, we consider the influence of the electronic conductivity: electron transport is necessary for the interfacial electrochemical reaction to take place. Electronic conductivity is dependent on the crystal structure and proton composition. Proton insertion is accompanied by electrons that partially fill the W 5d orbitals of the conduction band, leading to a semiconductor-to-metal transition at low proton compositions in tungsten oxides.25,63–65 By conducting DFT calculations, we observed that the band gap diminishes to zero for all three tungsten oxides when they are protonated, as depicted in Fig. 12. The band structure analysis clearly reveals that proton-insertion coupled electron transfer partially populates energy bands within the conduction band of the tungsten oxides, as indicated by the presence of multiple conduction bands at the Fermi level. For WO3 and WO3·H2O, the theoretical band gaps of their pristine (non-protonated) structures exceeded 1.9 eV, which represents a moderate underestimation compared to the experimentally observed band gap (WO3; 2.6 eV, WO3·H2O; 2.17).66–68 Note that this discrepancy is a typical observation associated with the use of meta-GGA functionals, as is the prediction of a direct bandgap of WO3.69 The energy difference between the direct and indirect band gaps is very small (∼0.01 eV) with hybrid functionals. However, the band gap width most closely aligns with experimental results and is similarly reflected in our calculations. Notably, the protonation of WO3 and WO3·H2O to H0.5WO3 and H0.5WO3·H2O leads to a semiconductor-to-metal transition. On the other hand, protonated H0.5WO3·2H2O exhibits two thermodynamically competitive configurations (<0.001 eV of energy difference), both involving hydrogen binding to bridging oxygen sites. One configuration exhibits a vanishing band gap, while the other remains a semiconductor with a band gap of 0.43 eV (Fig. S10†). This observation provides a plausible explanation for the relatively lower electrocatalytic activity observed in HxWO3·2H2O compared to HxWO3 and HxWO3·H2O. Orthorhombic H0.69WO3·H2O and cubic H0.65WO3 exhibit similar maximum observable proton compositions, have relatively high symmetry crystal structures, and DFT calculations confirm that both undergo the semiconductor-to-metal transition. Further inspection of the calculated band structures of Fig. 12 reveals that the H0.5WO3·H2O exhibits a wider dispersion of bands than the H0.5WO3, which could facilitate higher electronic conductivity.70 Although DFT does not provide a quantitative measure of electronic conductivity, the band structure analysis is consistent with the experimentally observed HER trends and could possibly provide a link between the oxide's conductivity and catalytic activity.
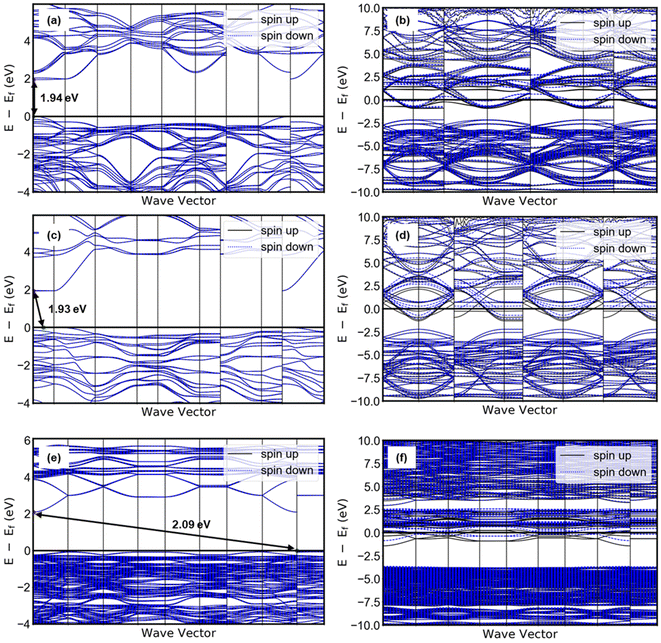 | ||
| Fig. 12 Band structure of pristine (left) and protonated (right) tungsten oxides: (a) WO3, (b) H0.5WO3, (c) WO3·H2O, (d) H0.5WO3·H2O, (e) WO3·2H2O, (f) H0.5WO3·2H2O. | ||
Third, we consider the hydrogen adsorption energy. The hydrogen adsorption energy on tungsten oxides is dependent on the proton composition. Miu et al. demonstrated computationally that H0.5WO3 and H0.625WO3 were responsible for HER activity and that the most energetically favorable hydrogen adsorption site becomes the W metal center as opposed to a bridging or terminal oxygen (shown schematically in Fig. 13).31 Our results show that HxWO3 and HxWO3·H2O reach proton compositions greater than 0.5, therefore, these electrocatalysts are expected to have reactive surface sites.
Finally, we consider the role of the inserted protons. A possible explanation for the origin of the hydration state dependence of HER activity on tungsten oxides is that they are non proton-blocking electrocatalysts. Prior literature demonstrates that bulk protons can participate in surface reactions. For example, during coulometry to study proton conduction in solids, bulk protons are reduced and released as hydrogen gas.71 Coulometric measurements performed on potassium dihydrogen phosphate and lithium hydrazinium sulfate revealed that the volume of hydrogen gas was linearly proportional to the charge passed through the crystals.71 This mechanism is similar to the concept of exsolution of metal nanoparticles on perovskite transition metal oxides in reducing conditions, with the difference being that the exsolved substance here, hydrogen, is a gas.72 In non-aqueous electrolytes, proton-containing transition metal oxides such as H2Ti6O13 and H2WO4 can convert to lithium or sodium-containing TMOs, with protons proposed to leave the structure in the form of hydrogen.73–75 Sub-surface protons are also shown to be more reactive than surface adsorbed protons, leading to the participation of sub-surface protons in surface catalytic reactions.76,77 Similarly, a reverse hydrogen spillover mechanism was proposed for a Ru@HxWO3 electrocatalyst, whereby protons transferred from HxWO3 to Ru, thus increasing the hydrogen coverage and the overall HER activity.78
We hypothesize that bulk, electrochemically inserted protons participate in the HER on HxWO3·nH2O electrocatalysts. In this scenario, we propose three possible reaction mechanisms for the formation of hydrogen (shown schematically in Fig. 13): (1) combination of two aqueous protons at a surface active site following the Volmer–Heyrovsky or Volmer–Tafel steps (eqn (1)–(3)); (2) combination of one inserted proton with one aqueous proton that each transport to a surface active site (eqn (5) or (6)); and (3) combination of two inserted protons at a confined active site to form H2 confined in the oxide lattice (eqn (7)). The participation of bulk protons in the HER means that electrochemically protonated tungsten oxides serve as a proton reservoir for the HER, whereby the kinetics of proton transport from the bulk insertion site to the electrocatalytically active site will influence the HER kinetics/activity. Our DFT calculations suggest that the surface mediated mechanisms are likely to be dominating the HER of protonated tungsten oxides, albeit, with the involvement of lattice protons. As depicted in Fig. S11,† proton conduction in the bulk is highly favored due to barrierless activation for H0.5WO3 and very low activation (0.14 eV) for H0.5WO3·H2O. These low barriers for bulk proton conduction are accessible at room temperature. We note that in the case of H0.5WO3, the barrierless activation is a result of symmetric oxygen sites (due to the specific 0.5 stoichiometry in hydrogen) that exchange protons (Fig. S11a†) and we should not generalize that the anhydrous oxide would show a barrierless proton conduction (e.g. at different degrees of protonation). However, low activation energies for hydrogen spillover in bulk have been reported in WO3,79 in agreement with our observations of facile proton conduction. In contrast, Fig. S12† demonstrates that hydrogen formation within the oxide lattice presents activation barriers of 2.25 and 1.98 eV, for H0.5WO3 and H0.5WO3·H2O respectively (additional higher energy barriers for H0.5WO3·H2O are presented in Fig. S13†). These barriers are significantly higher than previously reported energy barriers of 0.50 eV for water-mediated hydrogen formation on the surface of H0.5WO3.31 For H0.69WO3·H2O and H0.65WO3, we further attribute the difference in activity to the difference in bulk proton transport kinetics. Dickens et al. experimentally determined the proton diffusion coefficients of HxWO3 and HxWO3·H2O (where 0 < x < 0.2) using a current-pulse relaxation method.80 Proton transport in HxWO3·H2O is fast (D ∼10−6 cm2 s−1) due to the low energy transport pathways that exist in the layered structure. However, proton transport in HxWO3 is slower (D ∼10−11 cm2 s−1). Although both structures exhibit low activation energies for proton transport as shown in the DFT calculations, the monohydrated structure exhibits faster proton transport kinetics possibly due to the multiple diffusion pathways facilitated by the hydrogen bonds of lattice water (Fig. S11†). Based on this hypothesized mechanism, we propose that the difference in proton transport kinetics of electrochemically inserted protons can further justify the difference in the HER activity of H0.65WO3 and H0.69WO3·H2O, where faster proton transport in H0.69WO3·H2O leads to a larger HER current contribution from the inserted protons and a higher overall HER activity.
4. Conclusions
We systematically studied the HER activity of three hydration states of tungsten oxide (WO3·nH2O; n = 0, 1, 2), and discussed the possible origin of the hydration state dependent electrocatalytic activity of these proton insertion type electrocatalysts. Cyclic voltammetry revealed the critical role of proton insertion in the activation of tungsten oxides for the HER. Stepwise chronoamperometry measurements were used to measure the electrocatalytic activity of the equilibrium composition of each electrocatalyst. H0.69WO3·H2O was the most active electrocatalyst with an overpotential of 501.0 mV, followed by H0.65WO3 (η = 531.7 mV) and H0.47WO3·2H2O (η = 621.5 mV). Using slurry electrodes, we calculated the equilibrium proton composition in the maximum accessible potential window, and we found that proton composition scaled positively with HER activity. Operando XRD measurements revealed the structural changes that occur during proton (de)insertion using cyclic voltammetry. Upon proton insertion into HxWO3, the monoclinic structure transitions to tetragonal and then to cubic. Conversely, HxWO3·H2O (orthorhombic) and HxWO3·2H2O (monoclinic) do not undergo phase transitions. These results show that higher symmetry corresponds with higher HER activity. The trends in activity, proton composition, and structural symmetry suggest that the bulk properties of these electrocatalysts can directly influence the electrocatalytic activity. Furthermore, we propose that bulk, electrochemically inserted protons can participate in the HER, whereby the inserted protons serve as a proton reservoir and thus the proton transport properties of each hydration state can explain the differences in electrocatalytic activity. The band structure calculated by DFT suggests a semiconductor-to-metal transition in the electronic structure of all tungsten oxides by proton intercalation and a competition from a state with a gap in the dihydrate case, rationalizing the experimental HER catalytic activity trends. In addition, DFT calculations demonstrate that proton transport in bulk of the oxides is facile with very small activation barriers. The outcomes of this study emphasize the importance of systematically studying dynamic processes that take place on non proton-blocking electrocatalysts. Furthermore, when an inserting species also serves as a reactant in the electrocatalytic reaction of interest, it is possible that the reactant directly participates in the reaction thus contributing to the observed activity.Data availability
Data from this work is openly available at https://doi.org/10.5281/zenodo.10802721.Author contributions
M. A. S.: conceptualization, investigation, formal analysis, methodology, writing, review & editing; N. P. H.: conceptualization, formal analysis, writing, review & editing; K.-E. Y.: investigation, formal analysis, writing; G. M.: funding acquisition, supervision, resources, writing, review & editing; V. A.: funding acquisition, resources, conceptualization, supervision, writing, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Paul Kempler and Dr Michaela Burke for helpful discussions on electrochemical measurements. We thank Charles L. Troxel, Dr Nicholas Strange, and Dr Johanna Nelson Weker for assistance during operando XRD measurements at SSRL. We also thank Ishita Kamboj for acquiring SEM images of the pristine materials studied in this work. Materials synthesis, physical characterization, operando XRD, and electrochemical characterization were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Early Career Research Program, under Award No. DE-SC0020234. DFT calculations were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Award No. DESC0023465. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. This work was performed in part at the Analytical Instrumentation Facility (AIF), North Carolina State University, which is supported by the State of North Carolina and the National Science Foundation (Award No. ECCS-2025064). The AIF is a member of the North Carolina Research Triangle Nanotechnology Network (RTNN), a site in the National Nanotechnology Coordinated Infrastructure (NNCI). G.M. and K.Y. acknowledge computational support from the Center for Research Computing at the University of Pittsburgh, RRID:SCR_022735, through the resources provided. Specifically, this work used the H2P cluster, which is supported by NSF award number OAC-2117681.References
- International Energy Agency, Global Hydrogen Review 2022, Paris, 2022, https://www.iea.org/reports/global-hydrogen-review-2022 Search PubMed.
- E. Taibi, R. Miranda, W. Vanhoudt, T. Winkel, J.-C. Lanoix and F. Barth, Hydrogen from Renewable Power: Technology Outlook for the Energy Transition, 2018 Search PubMed.
- Y. Liang and Y. Yao, Designing modern aqueous batteries, Nat. Rev. Mater., 2022, 8(2), 109–122, DOI:10.1038/s41578-022-00511-3.
- J. Liu, C. Xu, Z. Chen, S. Ni and Z. X. Shen, Progress in aqueous rechargeable batteries, Green Energy Environ., 2018, 3(1), 20–41, DOI:10.1016/j.gee.2017.10.001.
- J. Gu, S. Liu, W. Ni, W. Ren, S. Haussener and X. Hu, Modulating electric field distribution by alkali cations for CO2 electroreduction in strongly acidic medium, Nat. Catal., 2022, 5(4), 268–276, DOI:10.1038/s41929-022-00761-y.
- B. E. Conway and B. V. Tilak, Interfacial processes involving electrocatalytic evolution and oxidation of H2, and the role of chemisorbed H, Electrochim. Acta, 2002, 47, 3571–3594 CrossRef CAS.
- F. P. Bowden and E. K. Rideal, The electrolytic behaviour of thin films. Part I.—Hydrogen, Proc. R. Soc. Lon. Ser. A, 1928, 120(784), 59–79, DOI:10.1098/rspa.1928.0135.
- S. Trasatti, Work function, electronegativity, and electrochemical behaviour of metals III. Electrolytic hydrogen evolution in acid solutions, J. Electroanal. Chem., 1972, 39, 163–184 CrossRef CAS.
- F. C. Østergaard, A. Bagger and J. Rossmeisl, Predicting catalytic activity in hydrogen evolution reaction, Curr. Opin. Electrochem., 2022, 35, 101037, DOI:10.1016/j.coelec.2022.101037.
- R. Parsons, The rate of electrolytic hydrogen evolution and the heat of adsorption of hydrogen, Trans. Faraday Soc., 1958, 54, 1053–1063 RSC.
- R. C. Wvarezza, M. C. Montemayor, E. Fatas and A. J. Arvia, Electrochemical study of hydrogen absorption in polycrystalline palladium, J. Electroanal. Chem. Interfacial Electrochem., 1991, 313, 301 Search PubMed.
- M. A. V. Devanathan and Z. Stachurski, The adsorption and diffusion of electrolytic hydrogen in palladium, Proc. R. Soc. Lond. A Math Phys. Sci., 1962, 270(1340), 90–102, DOI:10.1098/rspa.1962.0205.
- B. Y. Tang, R. P. Bisbey, K. M. Lodaya, W. L. Toh and Y. Surendranath, Reaction environment impacts charge transfer but not chemical reaction steps in hydrogen evolution catalysis, Nat. Catal., 2023, 6(4), 339–350, DOI:10.1038/s41929-023-00943-2.
- R. S. Sherbo, A. Kurimoto, C. M. Brown and C. P. Berlinguette, Efficient electrocatalytic hydrogenation with a palladium membrane reactor, J. Am. Chem. Soc., 2019, 141(19), 7815–7821, DOI:10.1021/jacs.9b01442.
- R. S. Sherbo, R. S. Delima, V. A. Chiykowski, B. P. MacLeod and C. P. Berlinguette, Complete electron economy by pairing electrolysis with hydrogenation, Nat. Catal., 2018, 1(7), 501–507, DOI:10.1038/s41929-018-0083-8.
- M. J. W. Blom, W. P. M. van Swaaij, G. Mul and S. R. A. Kersten, Mechanism and micro kinetic model for electroreduction of CO2 on Pd/C: the role of different palladium hydride phases, ACS Catal., 2021, 11(12), 6883–6891, DOI:10.1021/acscatal.1c01325.
- Y. Zhu, Q. Lin, Y. Zhong, H. A. Tahini, Z. Shao and H. Wang, Metal oxide-based materials as an emerging family of hydrogen evolution electrocatalysts, Energy Environ. Sci., 2020, 13(10), 3361–3392, 10.1039/D0EE02485F.
- Y. Xu, X. Wu and X. Ji, The renaissance of proton batteries, Small Struct., 2021, 2(5), 202000113, DOI:10.1002/sstr.202000113.
- N. Makivić, J.-Y. Cho, K. D. Harris, J.-M. Tarascon, B. Limoges and V. Balland, Evidence of bulk proton insertion in nanostructured anatase and amorphous TiO2 electrodes, Chem. Mater., 2021, 33(9), 3436–3448, DOI:10.1021/acs.chemmater.1c00840.
- S. Fleischmann, Y. Sun, N. C. Osti, R. Wang, E. Mamontov, D. E. Jiang and V. Augustyn, Interlayer separation in hydrogen titanates enables electrochemical proton intercalation, J. Mater. Chem. A, 2020, 8(1), 412–421, 10.1039/c9ta11098d.
- D. Sheng, X. Liu, Q. Zhang, H. Yi, X. Wang, S. Fu, S. Zhou, J. Shen and A. Gao, Intercalation reaction of molybdenum trioxide cathode for rechargeable ion batteries, Batteries Supercaps, 2023, 6, e202200569, DOI:10.1002/batt.202200569.
- Y. Lu, W. J. Yin, K. L. Peng, K. Wang, Q. Hu, A. Selloni, F. R. Chen, L. M. Liu and M. L. Sui, Self-hydrogenated shell promoting photocatalytic H2 evolution on anatase TiO2, Nat. Commun., 2018, 9(1), 2752, DOI:10.1038/s41467-018-05144-1.
- J. Przyluski and K. Kolbrecka, Voltametric behaviour of TinO2n−1 ceramic electrodes close to the hydrogen evolution reaction, J. Appl. Electrochem., 1993, 23, 1063–1068 CrossRef CAS.
- M. W. Khalil and M. A. Abdel Rahim, Hydrogen evolution reaction on titanium and oxide-covered titanium electrodes, Materwiss Werksttech, 1991, 22(10), 390–395, DOI:10.1002/mawe.19910221007.
- J. B. Mitchell, W. C. Lo, A. Genc, J. LeBeau and V. Augustyn, Transition from battery to pseudocapacitor behavior via structural water in tungsten oxide, Chem. Mater., 2017, 29(9), 3928–3937, DOI:10.1021/acs.chemmater.6b05485.
- J. B. Mitchell, N. R. Geise, A. R. Paterson, N. C. Osti, Y. Sun, S. Fleischmann, R. Zhang, L. A. Madsen, M. F. Toney, D. E. Jiang, A. I. Kolesnikov, E. Mamontov and V. Augustyn, Confined Interlayer water promotes structural stability for high-rate electrochemical proton intercalation in tungsten oxide hydrates, ACS Energy Lett., 2019, 4(12), 2805–2812, DOI:10.1021/acsenergylett.9b02040.
- H. Jiang, J. J. Hong, X. Wu, T. W. Surta, Y. Qi, S. Dong, Z. Li, D. P. Leonard, J. J. Holoubek, J. C. Wong, J. J. Razink, X. Zhang and X. Ji, Insights on the proton insertion mechanism in the electrode of hexagonal tungsten oxide hydrate, J. Am. Chem. Soc., 2018, 140(37), 11556–11559, DOI:10.1021/jacs.8b03959.
- H. Farsi, F. Gobal and Z. Barzgari, A study of hydrated nanostructured tungsten trioxide as an electroactive material for pseudocapacitors, Ionics (Kiel), 2013, 19(2), 287–294, DOI:10.1007/s11581-012-0726-8.
- R. Wang, J. B. Mitchell, Q. Gao, W. Tsai, S. Boyd, M. Pharr, N. Balke and V. Augustyn, Operando atomic force microscopy reveals mechanics of structural water driven battery-to-pseudocapacitor transition, ACS Nano, 2018, 12, 6032–6039, DOI:10.1021/acsnano.8b02273.
- M. A. Spencer, J. Fortunato and V. Augustyn, Electrochemical proton insertion modulates the hydrogen evolution reaction on tungsten oxides, J. Chem. Phys., 2022, 156(6), 064704, DOI:10.1063/5.0082459.
- E. V. Miu, J. R. McKone and G. Mpourmpakis, The sensitivity of metal oxide electrocatalysis to bulk hydrogen intercalation: hydrogen evolution on tungsten oxide, J. Am. Chem. Soc., 2022, 144(14), 6420–6433, DOI:10.1021/jacs.2c00825.
- M. L. Freedman, The tungstic acids, J. Am. Chem. Soc., 1959, 81(15), 3834–3839, DOI:10.1021/ja01524a009.
- C. Cao, H. G. Steinrück, B. Shyam, K. H. Stone and M. F. Toney, In situ study of silicon electrode lithiation with X-ray reflectivity, Nano Lett., 2016, 16(12), 7394–7401, DOI:10.1021/acs.nanolett.6b02926.
- J. Perl, J. Shin, J. Schümann, B. Faddegon and H. Paganetti, TOPAS: an innovative proton monte carlo platform for research and clinical applications, Med. Phys., 2012, 39(11), 6818–6837, DOI:10.1118/1.4758060.
- B. Faddegon, J. Ramos-Méndez, J. Schuemann, A. McNamara, J. Shin, J. Perl and H. Paganetti, The TOPAS tool for particle simulation, a monte carlo simulation tool for physics, biology and clinical research, Phys. Med., 2020, 72, 114–121, DOI:10.1016/j.ejmp.2020.03.019.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269, DOI:10.1103/PhysRevB.49.14251.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly constrained and appropriately normed semilocal density functional, Phys. Rev. Lett., 2015, 115(3), 036402, DOI:10.1103/PhysRevLett.115.036402.
- J. P. Perdew, W. Yang, K. Burke, Z. Yang, E. K. U. Gross, M. Scheffler, G. E. Scuseria, T. M. Henderson, I. Y. Zhang, A. Ruzsinszky, H. Peng, J. Sun, E. Trushin and A. Görling, Understanding band gaps of solids in generalized kohn–sham theory, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(11), 2801–2806, DOI:10.1073/pnas.1621352114.
- M. Kothakonda, A. D. Kaplan, E. B. Isaacs, C. J. Bartel, J. W. Furness, J. Ning, C. Wolverton, J. P. Perdew and J. Sun, Testing the r2SCAN density functional for the thermodynamic stability of solids with and without a van der waals correction, ACS Mater. Au, 2023, 3(2), 102–111, DOI:10.1021/acsmaterialsau.2c00059.
- A. D. Kaplan, C. Shahi, P. Bhetwal, R. K. Sah and J. P. Perdew, Understanding density-driven errors for reaction barrier heights, J. Chem. Theory Comput., 2023, 19(2), 532–543, DOI:10.1021/acs.jctc.2c00953.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215, DOI:10.1021/acs.jpclett.0c02405.
- R. Sabatini, T. Gorni and S. de Gironcoli, Nonlocal van der waals density functional made simple and efficient, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(4), 041108, DOI:10.1103/PhysRevB.87.041108.
- J. Ning, M. Kothakonda, J. W. Furness, A. D. Kaplan, S. Ehlert, J. G. Brandenburg, J. P. Perdew and J. Sun, Workhorse minimally empirical dispersion-corrected density functional with tests for weakly bound systems: R2SCAN+rVV 10, Phys. Rev. B, 2022, 106(7), 075422, DOI:10.1103/PhysRevB.106.075422.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- J. Harris, Simplified method for calculating the energy of weakly interacting fragments, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31(4), 1770–1779, DOI:10.1103/PhysRevB.31.1770.
- D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, A generalized solid-state nudged elastic band method, J. Chem. Phys., 2012, 136(7), 074103, DOI:10.1063/1.3684549.
- P. Xiao and G. Henkelman, Communication: from graphite to diamond: reaction pathways of the phase transition, J. Chem. Phys., 2012, 137(10), 101101, DOI:10.1063/1.4752249.
- P. Xiao, J.-G. Cheng, J.-S. Zhou, J. B. Goodenough and G. Henkelman, Mechanism of the CaIrO3 post-perovskite phase transition under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(14), 144102, DOI:10.1103/PhysRevB.88.144102.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904, DOI:10.1063/1.1329672.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276, DOI:10.1107/S0021889811038970.
- Y. Gogotsi and R. M. Penner, Energy storage in nanomaterials – capacitive, pseudocapacitive, or battery-like?, ACS Nano, 2018, 12(3), 2081–2083, DOI:10.1021/acsnano.8b01914.
- J. T. Bender, A. S. Petersen, F. C. Østergaard, M. A. Wood, S. M. J. Heffernan, D. J. Milliron, J. Rossmeisl and J. Resasco, Understanding cation effects on the hydrogen evolution reaction, ACS Energy Lett., 2023, 8(1), 657–665, DOI:10.1021/acsenergylett.2c02500.
- Y. H. Fang and Z. P. Liu, Tafel Kinetics of electrocatalytic reactions: from experiment to first-principles, ACS Catal., 2014, 5, 4364–4376, DOI:10.1021/cs501312v.
- B. E. Conway and B. V. Tilak, Advance in Catalysis, ed. D. D. Eley, H. Pines and P. B. Weisz, Academic Press Inc., New York, 1992, vol. 38 Search PubMed.
- B. E. Conway and J. O’M Bockris, Electrolytic hydrogen evolution kinetics and its relation to the electronic and adsorptive properties of the metal, J. Chem. Phys., 1957, 26(3), 532–541, DOI:10.1063/1.1743339.
- A. M. Limaye, J. S. Zeng, A. P. Willard and K. Manthiram, Bayesian data analysis reveals no preference for cardinal tafel slopes in CO2 reduction electrocatalysis, Nat. Commun., 2021, 12(1), 703, DOI:10.1038/s41467-021-20924-y.
- P. G. Dickens and R. J. Hurditch, X-ray and neutron diffraction studies of a tetragonal hydrogen bronze HxWO3, Nature, 1967, 215, 1266–1267 CrossRef CAS.
- V. O. Glemser and C. K. Naumann, Wolframblauverbindungen; Wasserstoffanaloga der wolframbronzen HxWO3, Z. Anorg. Allg. Chem., 1951, 265, 288–302, DOI:10.1002/zaac.19512650413.
- J. T. Szymanski and A. C. Roberts, The crystal structure of tungstite, WO3·H2O, Can. Mineral., 1984, 22, 681–688 CAS.
- C. Guéry, C. Choquet, F. Dujeancourt, J. M. Tarascon and J. C. Lassègues, Infrared and X-ray studies of hydrogen intercalation in different tungsten trioxides and tungsten trioxide hydrates, J. Solid State Electrochem., 1997, 1(3), 199–207, DOI:10.1007/s100080050049.
- Y. M. Li, M. Hibino, M. Miyayania and T. Kudo, Proton conductivity of tungsten trioxide hydrates at intermediate temperature, Solid State Ionics, 2000, 134, 271–279 CrossRef CAS.
- H. R. Shanks, P. H. Sidles and G. C. Danielson, Electrical properties of the tungsten bronzes, Adv. Chem., 1963, 39, 237–245 CAS.
- C. G. Granqvist, Handbook of Inorganic Electrochromic Materials, Elsevier, 1995 Search PubMed.
- U. O. Krašovec, A. urca Vuk and B. Orel, IR Spectroscopic Studies of Charged-Discharged Crystalline WO3 Films, 2001, vol. 46, https://www.elsevier.nl/locate/electacta Search PubMed.
- E. A. Salje, New type of electro-optic effect in semiconducting WO3, J. Appl. Crystallogr., 1974, 7(6), 615–617, DOI:10.1107/S0021889874010545.
- F. P. Koffyberg, K. Dwight and A. Wold, Interband transitions of semiconducting oxides determined from photoelectrolysis spectra, Solid State Commun., 1979, 30(7), 433–437, DOI:10.1016/0038-1098(79)91182-7.
- P. Wang, B. Huang, X. Qin, X. Zhang, Y. Dai and M.-H. Whangbo, Ag/AgBr/WO3·H2O: visible-light photocatalyst for bacteria destruction, Inorg. Chem., 2009, 48(22), 10697–10702, DOI:10.1021/ic9014652.
- F. Wang, C. Di Valentin and G. Pacchioni, Electronic and structural properties of WO3: a systematic hybrid DFT study, J. Phys. Chem. C, 2011, 115(16), 8345–8353, DOI:10.1021/jp201057m.
- H. W. Eng, P. W. Barnes, B. M. Auer and P. M. Woodward, Investigations of the electronic structure of d0 transition metal oxides belonging to the perovskite family, J. Solid State Chem., 2003, 175(1), 94–109, DOI:10.1016/S0022-4596(03)00289-5.
- V. H. Schmidt, Simple coulometer for studying protonic conduction in crystals, J. Sci. Instrum., 1965, 42, 889 CrossRef CAS PubMed.
- Z. Sun, C. Hao, S. Toan, R. Zhang, H. Li, Y. Wu, H. Liu and Z. Sun, Recent advances in exsolved perovskite oxide construction: exsolution theory, modulation, challenges, and prospects, J. Mater. Chem. A, 2023, 17961–17976, 10.1039/d3ta03292b.
- J. C. Pérez-Flores, C. Baehtz, M. Hoelzel, A. Kuhn and F. García-Alvarado, H2Ti6O13, a new protonated titanate prepared by Li+/H+ ion exchange: synthesis, crystal structure and electrochemical Li insertion properties, RSC Adv., 2012, 2(8), 3530–3540, 10.1039/c2ra01134d.
- N. Kumagai, N. Kumagai and K. Tanno, Electrochemical characteristics and structural changes of molybdenum trioxide hydrates as cathode materials for lithium batteries, J. Appl. Electrochem., 1988, 18, 857–862 CrossRef CAS.
- N. Kumagai, N. Kumagai and K. Tanno, Electrochemical and structural characteristics of tungstic acids as cathode materials for lithium batteries, Appl. Phys. A, 1989, 49, 83–89 CrossRef.
- A. D. Johnson, S. P. Daley, A. L. Utz and S. T. Ceyer, The chemistry of bulk hydrogen: reaction of hydrogen embedded in nickel with adsorbed CH3, Science, 1992, 257(5067), 223–225, DOI:10.1126/science.257.5067.223.
- A. Michaelides, P. Hu and A. Alavi, Physical origin of the high reactivity of subsurface hydrogen in catalytic hydrogenation, J. Chem. Phys., 1999, 111(4), 1343–1345, DOI:10.1063/1.479392.
- J. Chen, C. Chen, M. Qin, B. Li, B. Lin, Q. Mao, H. Yang, B. Liu and Y. Wang, Reversible hydrogen spillover in Ru-WO3-x enhances hydrogen evolution activity in neutral PH water splitting, Nat. Commun., 2022, 13(1), 5382, DOI:10.1038/s41467-022-33007-3.
- K. Shun, K. Mori, S. Masuda, N. Hashimoto, Y. Hinuma, H. Kobayashi and H. Yamashita, Revealing hydrogen spillover pathways in reducible metal oxides, Chem. Sci., 2022, 13(27), 8137–8147, 10.1039/D2SC00871H.
- P. G. Dickens, S. J. Hibble and R. H. Jarman, Hydrogen insertion compounds of transition metal oxides, J. Electron. Mater., 1981, 10(6), 999–1009, DOI:10.1007/BF02661189.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00102h |
| This journal is © The Royal Society of Chemistry 2024 |