Open Access Article
Open Access ArticleCan local heating and molecular crowders disintegrate amyloid aggregates?†
Naresh
Kumar
 a,
Prabir
Khatua
b and
Sudipta Kumar
Sinha
a,
Prabir
Khatua
b and
Sudipta Kumar
Sinha
 a
a
aDepartment of Chemistry, Theoretical and Computational Biophysical Chemistry Group, Indian Institute of Technology Ropar, Rupnagar, Punjab 140001, India. E-mail: sudipta@iitrpr.ac.in; Tel: +91-01881-232066
bDepartment of Chemistry, GITAM School of Science, GITAM (Deemed to be University), Bengaluru 562163, India
First published on 19th March 2024
Abstract
The present study employs a blend of molecular dynamics simulations and a theoretical model to explore the potential disintegration mechanism of a matured Aβ octamer, aiming to offer a strategy to combat Alzheimer's disease. We investigate local heating and crowding effects on Aβ disintegration by selectively heating key Aβ segments and varying the concentration of sodium dodecyl sulphate (SDS), respectively. Despite initiation of disruption, Aβ aggregates resist complete disintegration during local heating due to rapid thermal energy distribution to the surrounding water. Conversely, although SDS molecules effectively inhibit Aβ aggregation at higher concentration through micelle formation, they fail to completely disintegrate the aggregate due to the exceedingly high energy barrier. To address the sampling challenge posed by the formidable energy barrier, we have performed well-tempered metadynamics simulations. Simulations reveal a multi-step disintegration mechanism for the Aβ octamer, suggesting a probable sequence: octamer → pentamer/hexamer ⇌ tetramer → monomer, with a rate-determining step constituting 45 kJ mol−1 barrier during the octamer to pentamer/hexamer transition. Additionally, we have proposed a novel two-state mean-field model based on Ising spins that offers an insight into the kinetics of the Aβ growth process and external perturbation effects on disintegration. Thus, the current simulation study, coupled with the newly introduced mean-field model, offers an insight into the detailed mechanisms underlying the Aβ aggregation process, guiding potential strategies for effective disintegration of Aβ aggregates.
1 Introduction
The formation of amyloids due to the aggregation of proteins is associated with various neurodegenerative diseases such as Alzheimer's and Parkinson's. Alzheimer's disease (AD) is the most common form of dementia that affects memory, thinking power, and behavioural patterns, eventually leading to death. The primary cause behind the pathogenesis of AD is the aggregation of the Aβ peptide, a widely accepted hypothesis in the researchers' community.1,2 Therefore, understanding the molecular factors controlling the Aβ aggregation and discovering drug molecules capable of preventing or at least slowing down the Aβ aggregation is a central goal of AD research.The Aβ peptide forms small soluble oligomers at the early stages of aggregation, which further aggregate into insoluble fibrils and accumulate in the brain.3–6 Hydrophobic amino acids play a central role in the aggregation.7 These residues localize at three distinct regions, namely, (i) the central hydrophobic core, Aβ16–20(KLVFF), (ii) second central region, Aβ29–35(GAIIGLM), and (iii) C-terminal, Aβ36–42(VGGVVIA).8–10 The aggregation process is initiated by forming an aggregation-prone structure that involves the coil-to-β-hairpin structural transition of individual monomers.11–15 This aggregation-prone structure changes the functional properties of the Aβ peptide by forming soluble oligomers that induce intracellular toxicity by crossing the plasma membrane.2 While this information has added significant insight into AD research, a comprehensive picture of the aggregation mechanism is still elusive, and thus further research is needed.
The current understanding of AD research implies that the potential therapeutic strategy for treating Alzheimer's patients is to inhibit the growth of soluble oligomers/fibrils and simultaneously disintegrate the matured oligomers/fibrils. Thus, a more realistic therapeutic approach should be to develop methods to ensure that the Aβ peptide will exist in its non-toxic monomeric form, disintegrating the oligomers/fibrils. Numerous approaches are proposed in this regard, but their practical implementation is a real challenge. For example, various small molecules, including peptides, peptidomimetics, nanoparticles, nano chaperones, macrocycles, etc., have been shown to inhibit Aβ oligomerization.16–21 Recently, Nguyen et al. reviewed a series of experimental and computational findings regarding the monomers, oligomeric intermediates, and fibrils of the amyloid proteins in aqueous and membrane medium and discussed their implications for Alzheimer's disease.2 Many other similar studies using experiments and molecular dynamics simulation studies have been performed to get more insight into the structural aspects of Aβ peptide and AD.22–28 A very recent study reports that external electric or magnetic fields can disintegrate the Aβ oligomers and maybe a potential strategy to treat Alzheimer's patients.21 Similarly, different strategies to disintegrate the amyloid aggregates have been reported, e.g., by ultrasonic waves,29,30 infrared laser,31 laser induced disruption,32 free electron laser irradiation,33etc.34 Despite the discovery of such small inhibitory molecules or the use of external fields for treating Alzheimer's patients, the lack of biocompatibility of the inhibitory molecules primarily renders challenges toward the success of obtaining clinically viable therapeutics. Hence, current AD research focuses on designing biocompatible drug molecules that can inhibit oligomerization and maintain the Aβ peptide in its monomeric form.
Lipopeptide-based nanomaterials derived from naturally occurring biological building blocks have received significant attention in AD research owing to their safety, biodegradability, and biocompatibility.35,36 For instance, Bera et al.,37 in their recent microscopic investigation, illustrated that a myristoyl-KPGPK lipopeptide-based nanovesicle dramatically hinders the random coil to β-sheet transformation of the transmembrane GxxxGxxxGxxxG motif of Aβ-protein and human myelin protein zero, a prerequisite for the oligomerization of the peptide. Förster resonance energy transfer (FRET) assay performed with the synthesized Cy-3 (FRET donor) and Cy-5 (FRET acceptor)-conjugated peptide further confirms that the nanovesicle strongly inhibits the fibril formation of the peptide. Furthermore, this study highlights a suitable balance between the hydrophilic and hydrophobic interaction caused by the nanovesicle, a necessary step for the inhibition. While this could serve as an essential insight for clinically viable drug design, the study failed to address some critical questions necessary for further testing the clinical efficiency of this nanovesicle. For example, they confirmed the nanovesicle's inhibition effect by performing experiments starting from the monomeric form of the peptide. However, this cannot guarantee whether this nanovesicle can disintegrate the already formed oligomer, which is an important criterion to be a clinically viable AD drug. Therefore, it is worthwhile to probe (i) whether such a nanovesicle can disintegrate an already-formed oligomer and (ii) the molecular origin behind the inhibition by the nanovesicle.
In this work, we aim to address the two points mentioned above by molecular dynamics simulations (details are presented in the ESI†). However, unlike the experimental study mentioned above, we consider sodium dodecyl sulfate (SDS). There are two rationales behind choosing this surfactant molecule over myristoyl-KPGPK lipopeptide. First, SDS is a much simpler molecule than the myristoyl-KPGPK lipopeptide, thus reducing the computational cost. Second, SDS molecules can self-assemble to form micelles due to amphiphilic moieties and hence can mimic a similar environment to myristoyl-KPGPK nanovesicles. Moreover, SDS molecules self-assemble to form tiny clusters at low concentrations and vesicles at high concentrations and modify the solution properties. This property of the SDS molecule has an added advantage as this allows us to modify the strength of intermolecular interactions between the SDS molecules and the Aβ peptide by varying the number of SDS molecules. Since the intermolecular interactions between the monomers primarily guide the aggregation process, the variation of the number of molecules gives us scope to shed light into the aggregation process and, hence, predict what type of interactions must be present in a drug molecule to exhibit the inhibition of aggregation.
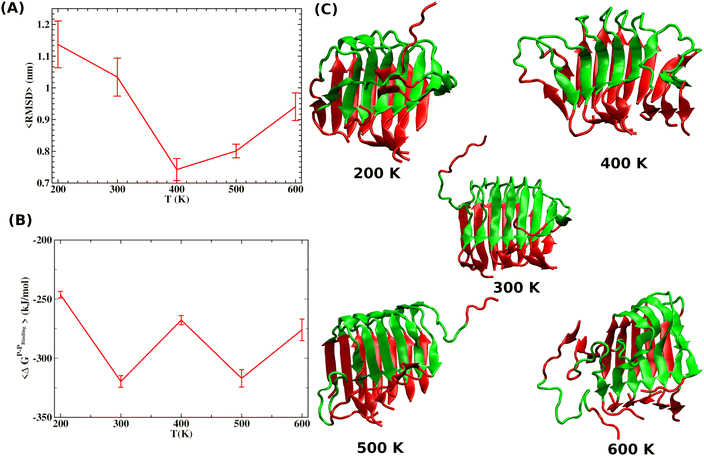
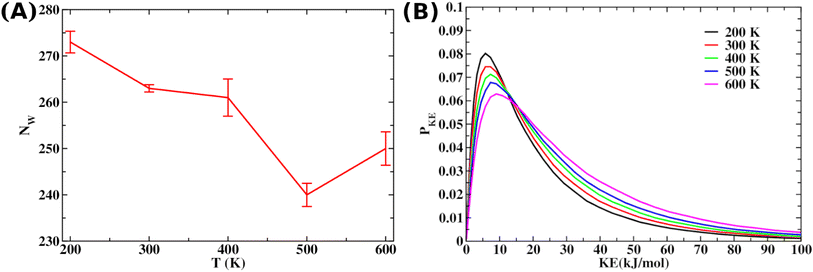
We have also investigated whether thermal heating can disrupt the already formed Aβ oligomer. Here we address whether heating can disrupt the β-sheets of the monomers present in the oligomer. If this strategy works for disintegrating the Aβ oligomers, this will be a clinically viable option if the temperature ranges within tolerable physiological conditions. Hence, we apply a moderate temperature only on regions of Aβ peptides primarily known to be responsible for aggregation. Such an application of temperature is simply done by increasing the kinetic energy of the specific atoms of Aβ peptide; hence, we call this “local heating”.
Herein in this study, we tackle the intricacies of the Aβ aggregation process through a unique combination of molecular dynamics simulations and a novel mean-field model. We assess the influence of external perturbations such as a molecular crowder (sodium dodecyl sulphate) and/or “local heating” (selective heating of Aβ segments through increase of the kinetic energy of the respective segments) on disrupting the Aβ octamer using conventional molecular dynamics simulations. While partly disrupted, complete disruption of the Aβ octamer does not happen due to the exceedingly high energy barrier on applying these external perturbations. Well-tempered metadynamics simulations overcome sampling challenges, providing detailed insights into the Aβ disintegration process. Additionally, a two-state mean-field model based on Ising spins introduced for the first time in this study explains the kinetics and external perturbation effects of Aβ disintegration. This integrated approach hence sheds light on the Aβ aggregation mechanism, guiding potential strategies for effective disintegration.
2 Results and discussion
2.1 Equilibrium properties under perturbation
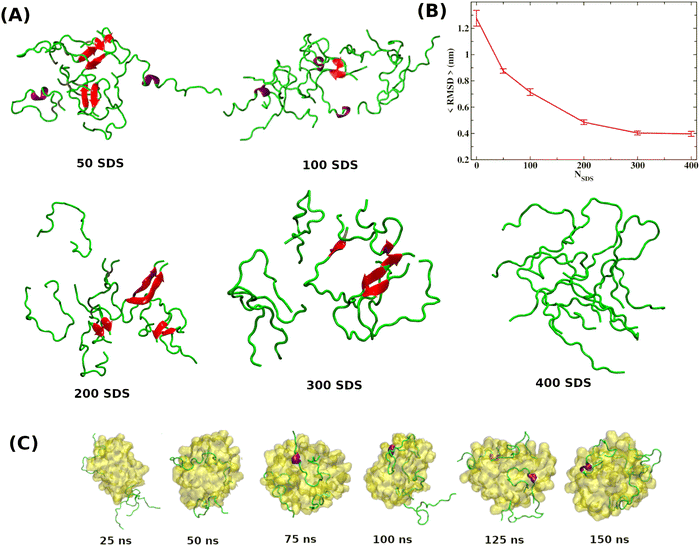
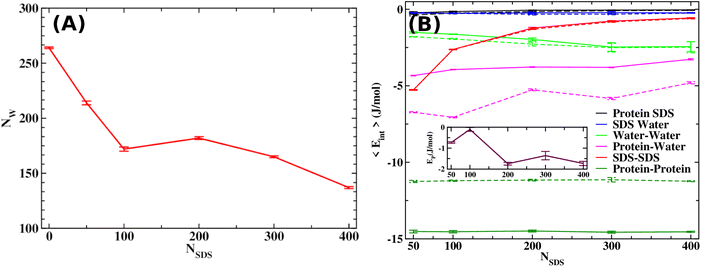
As discussed in the introduction, the most effective approach to treat Alzheimer's disease is to maintain the Aβ peptides in the monomeric non-toxic form by inhibiting the aggregation as well as by disintegrating the preformed Aβ peptide oligomers/fibrils. One recent experiment demonstrated the inhibitory effect of myristoyl-KPGPK lipopeptide-based nanovesicles on Aβ aggregation but did not explore their ability to disintegrate the preformed Aβ oligomer. In this simulation study, we investigate the disintegrating potential of a simpler molecule, sodium dodecyl sulfate (SDS), which possesses similar characteristics to the lipopeptide. We specifically address two points discussed in the following section. (i) Can the SDS molecule disintegrate the Aβ oligomer? (ii) Is there any effect of SDS concentration on Aβ aggregation?2.2 Free energy landscape
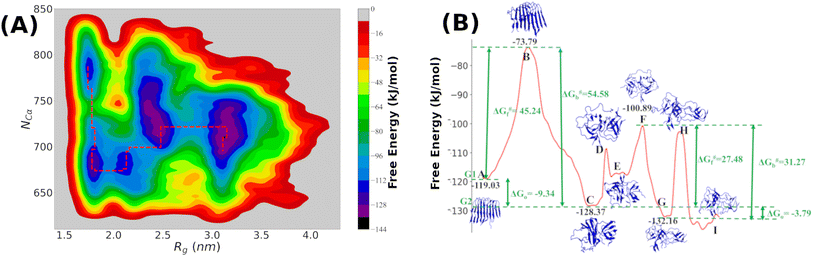
It is clear from the above discussion that the local heating and the molecular crowders cannot disintegrate the already formed Aβ aggregate due to the exceedingly high energy barrier, restricting the conventional simulation techniques to study a process in detail. To overcome such a problem of conventional MD simulations, we, therefore, investigate the disintegration pathway by performing metadynamics simulations, one of the most commonly used free energy simulation techniques.17 Here we conduct the metadynamics simulations using two collective variables, namely Rg and NCα. The details of the metadynamics simulation are presented in the ESI.†2.3 Mean field model
The complex Aβ aggregation/disintegration process, marked by a sequential structural transition in the free energy landscape obtained from metadynamics simulations has led us to the question: can a simple theoretical model capture the driver for transitioning between free and aggregate states? To address this, we introduce a two-state mean-field model, enabling the determination of critical aggregate size, transition rate, and growth kinetics mechanism. In this minimal model, we consider the peptides as a collection of identical spins whose states are defined by two numbers, −1 and +1, for free and aggregate conditions. We use the average value of the spins as an order parameter to describe this system's degree of aggregation or nucleation kinetics. The evolution of nucleation and growth kinetics can be expressed by representing the order parameter in terms of mole fraction of the aggregate, x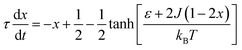 | (1) |
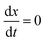
 | (2) |
Fig. 7A shows that the system exhibits bistability where the free and aggregated states correspond with x = 0 and x = 1. We observed a hysteresis loop in our model, as shown in the inset of Fig. 7A. This is a clear signature of phase transitions triggered by the cooperative effect, reflecting the origin of kinetic lag time as often observed in aggregation kinetics. As discussed in the model, the origin of such a cooperative effect can be correlated with the random coupled interaction between peptides and surrounding molecules, which inhibits ordering in the aggregate by loosening lateral hydrogen bond interaction among the β sheet region of the peptides. We find that peptides remain in free states until the value of J reaches a value of 4.8 kJ mol−1, and then sharp transitions occur. The graphical solution of eqn (2) gives us three equilibrium points at xeq = 0.028, 0.152, 0.996 at J = 4.8 kJ mol−1 and ε = −4.67 kJ mol−1. Two of them, 0.028 and 0.996, are stable, corresponding to aggregate and free states, respectively. The unstable solution corresponds to the critical nucleus size and the number is xeq = 0.152, corresponding to the pentamer as a nucleation point for the growth kinetics of Aβ peptides. We obtain a similar number by counting the numbers of the Aβ peptides at the first barrier of the minimum energy path. Therefore, we find a close resemblance between the results obtained from our metadynamics simulation and the proposed mean field model. Therefore, our extracted parameter from the MD simulation analysis provides a quantitative picture behind the Aβ peptide aggregation mechanism.
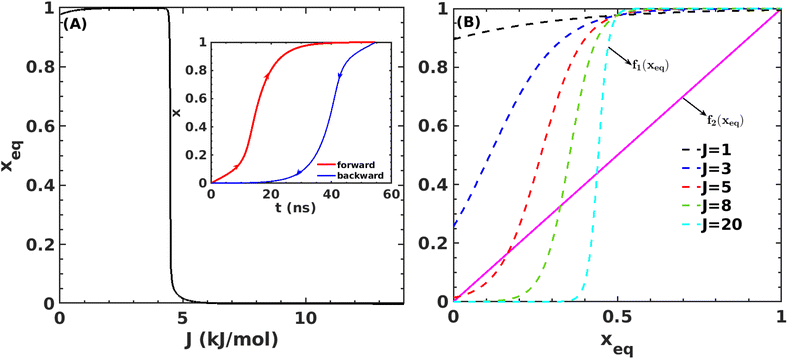 | ||
Fig. 7 (A) Variation in xeq with coupling parameter, J. Inset figure represents the formation of a hysteresis loop during the forward process, i.e., aggregate to the free state, and backward process, i.e., free state to aggregated state. (B) Graphical solution of eqn (2) for the first barrier where 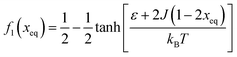 and f2(xeq) = xeq. The dashed line represents the function f1 at different J values while the solid line represents the f2. and f2(xeq) = xeq. The dashed line represents the function f1 at different J values while the solid line represents the f2. | ||
| ε = ε0 + ΔεT(T − T0) (temperature effect) |
| ε = ε0 + ΔεCCc (Crowder effect) |
We use gradient Δε = −0.01 kJ mol−1 K−1 and 0.002 kJ mol−1 into our mean-field model to observe the effect of temperature and crowder effects. We set ε = −4.67 kJ mol−1 and J = 4.8 kJ mol−1 throughout our calculation to explore their effects. We chose them because the peptides stay in the free form below those parameter values. Fig. 8A shows the effect of temperature on the kinetics of the aggregated states. It shows that at lower temperatures, T = 200 K, peptides remain in the aggregated form for extended periods. However, the aggregated peptides undergo a transition to form free monomeric states with the increase in temperature, a signature we observe in our MD simulation study. Fig. 8B represents the plot of mole fraction peptide in a free state with increased concentration of SDS surfactant molecules. It suggests that as the concentration of crowders increases, aggregates are stabilized. Therefore, our proposed model captures the nucleation and growth kinetics of Aβ peptide in the presence of heat and crowder from our theoretical analysis.
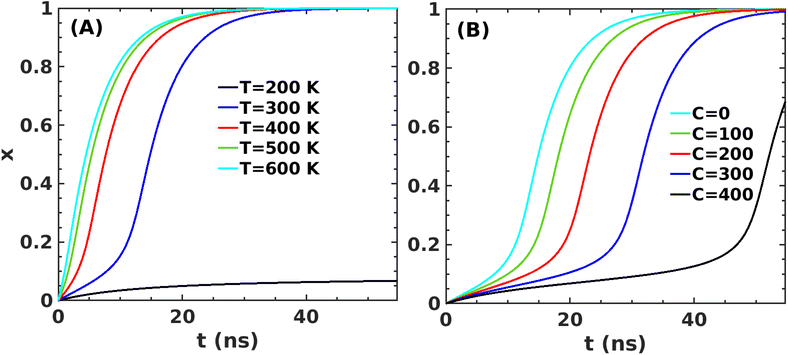 | ||
| Fig. 8 Variation in x for the first barrier from state A to state C (in Fig. 5B) as a function of time for J = 4.8 kJ mol−1 and ε0 = −4.67 kJ mol−1 (A) at several temperatures and (B) at several concentrations of the crowder. | ||
3 Conclusions
Amyloid β (Aβ) peptide self-assembles into larger aggregates, playing a pivotal role in Alzheimer's disease (AD). These aggregates, found in an AD patient's brain, are potentially toxic and can cause serious damage to the brain. Hence, identifying a strategy to prevent the aggregation of Aβ peptide and concurrently promoting the clearance of existing Aβ aggregates are two essential goals in AD research. Successfully achieving these goals involves addressing two key questions: (i) elucidating the underlying molecular details of the growth process of Aβ aggregates and (ii) devising ways to disassemble existing Aβ aggregates or, at the very least, impede their growth process.In this study, we used a combination of state-of-the-art molecular simulations and a theoretical model to answer the two above-mentioned questions. Our investigation especially delved into the efficacy of disintegrating the Aβ octamer, a crucial nucleus that could subsequently aggregate to form even larger aggregates.49,50 We employed detailed conventional molecular dynamics simulations to assess the impact of both local heating and the molecular crowder sodium dodecyl sulfate (SDS) on this process. Employing well-tempered metadynamics simulations, we further explored the disintegration pathway of Aβ octamer and the associated barrier. Finally, we introduced a novel two-state mean-field model based on Ising spins, offering an explanation on the growth kinetics and the prediction of the critical nucleus size on considering the cooperative effect of Aβ monomer association.
We elevated the temperature of crucial Aβ segments (25 to 37 residues) by appropriately scaling the kinetic energy to explore the influence of local heating, while the concentration of the SDS was varied to examine the crowding effect. Results revealed that Aβ aggregates resist complete disintegration during local heating despite initiation of disruption. We found that rapid distribution of thermal energy from the peptide segments to the surrounding water impedes complete breakdown of the aggregates. Conversely, although SDS molecules effectively inhibit Aβ aggregation by inducing destabilization, they fail to completely disintegrate the aggregate due to an exceedingly high energy barrier.
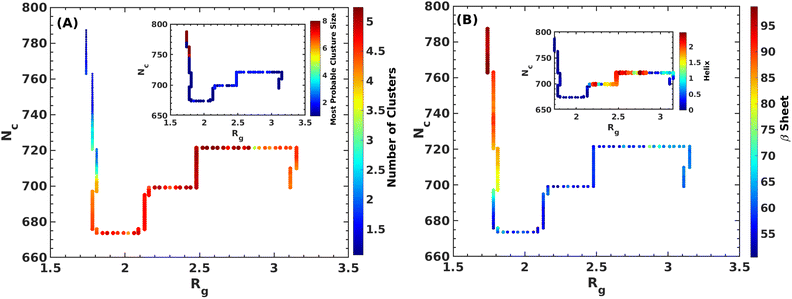
We addressed the exceedingly high energy barrier for the defibrillation process observed in the conventional simulations by employing metadynamics simulations. Exploration of the free energy landscape constructed from such metadynamics simulations enabled us to deduce the disintegration pathway of the Aβ octamer. Results indicated a primary energy barrier of 45 kJ mol−1, followed by several barriers of approximately half the primary barrier. Cluster analysis and structural characterization of the clusters showed that the octamer to pentamer/hexamer transition constitutes the rate-determining step with a barrier of 45 kJ mol−1, followed by several shallow barriers of 20 kJ mol−1, resulting in the equilibrium between the tetramer and hexamer. Such a tetramer–hexamer equilibrium sets the ultimate fate of the aggregate into the dispersed monomeric state with a negligible population of the Aβ octamer. We thus conjecture that octamer → pentamer/hexamer ⇌ tetramer → monomer is the most probable disintegration pathway of the Aβ octamer.
Finally, we incorporated the free energy data (free energy barrier and the free energy values) into our proposed two-state mean-field model based on Ising spins. This simple yet potent model not only allowed us to capture the kinetics of the growth process but also offered an explanation for the influence of local heating and crowder on the disintegration process of the Aβ aggregates. Importantly, incorporation of the free energy data corresponding to the primary barrier into the model revealed a pentamer to be the critical size. The observed consistency of the pentamer as the critical size, as deduced from metadynamics simulations, underscores the effectiveness of our proposed mean-field model. Thus, the current simulation study, coupled with the newly introduced mean-field model, offers an insight into the detailed mechanisms underlying the Aβ aggregation process.
Data availability
Yes, we have provided all the required data related to this paper in the ESI.†Author contributions
S. K. S., N. K., and P. K. designed the research, performed the research, and wrote the paper. N. K. analyzed the data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. K. S. is supported by SERB, the Department of Science and Technology, and the Government of India (CRG/2022/000345).Notes and references
- J. Hardy, Has the amyloid cascade hypothesis for Alzheimer’s disease been proved?, Curr. Alzheimer Res., 2006, 3, 71–73 CrossRef CAS PubMed.
- P. H. Nguyen, A. Ramamoorthy, B. R. Sahoo, J. Zheng, P. Faller, J. E. Straub, L. Dominguez, J.-E. Shea, N. V. Dokholyan and A. De Simone, et al. , Chem. Rev., 2021, 121, 2545–2647 CrossRef CAS PubMed.
- D. J. Selkoe, Physiol. Rev., 2001, 81, 740–766 CrossRef PubMed.
- M. A. Findeis, Pharmacol. Ther., 2007, 116, 266–286 CrossRef CAS PubMed.
- J. T. Jerrett and P. T. Lansbury, Cell, 1993, 73, 1055–1058 CrossRef PubMed.
- D. Chakraborty, J. E. Straub and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 19926–19937 CrossRef CAS PubMed.
- X. Han and H. Gefei, ACS Chem. Neurosci., 2018, 9, 198–210 CrossRef CAS PubMed.
- L. Triguero, R. Singh and R. Prabhakar, J. Phys. Chem. B, 2008, 112, 2159–2167 CrossRef CAS PubMed.
- A. D. Williams, E. Portelius, I. Kheterpal, J.-t. Guo, K. D. Cook, Y. Xu and R. Wetzel, J. Mol. Biol., 2004, 335, 833–842 CrossRef CAS PubMed.
- W. M. Berhanu and U. H. Hansmann, PLoS One, 2012, 7, e41479 CrossRef CAS PubMed.
- A. Abelein, J. P. Abrahams, J. Danielsson, A. Gräslund, J. Jarvet, J. Luo, A. Tiiman and S. K. Wärmländer, JBIC, J. Biol. Inorg. Chem., 2014, 19, 623–634 CrossRef CAS PubMed.
- S. G. Itoh and H. Okumura, J. Phys. Chem. B, 2014, 118, 11428–11436 CrossRef CAS PubMed.
- S. Maity, M. Hashemi and Y. L. Lyubchenko, Sci. Rep., 2017, 7, 2344 CrossRef PubMed.
- S. G. Itoh, M. Yagi-Utsumi, K. Kato and H. Okumura, ACS Chem. Neurosci., 2022, 13, 3139–3151 CrossRef CAS PubMed.
- M. Khaled, I. Ronnback, L. L. Ilag, A. Graslund, B. Strodel and N. Osterlund, J. Am. Chem. Soc., 2023, 145, 18340–18354 CrossRef CAS PubMed.
- S. Giorgetti, C. Greco, P. Tortora and F. A. Aprile, Int. J. Mol. Sci., 2018, 19, 2677 CrossRef PubMed.
- J. A. Lemkul and D. R. Bevan, Biochemistry, 2010, 49, 3935–3946 CrossRef CAS PubMed.
- Y. Qiao, M. Zhang, J. Zheng and G. Liang, et al. , Phys. Chem. Chem. Phys., 2017, 19, 155–166 RSC.
- J. Lu, Q. Cao, C. Wang, J. Zheng, F. Luo, J. Xie, Y. Li, X. Ma, L. He and D. Eisenberg, et al. , Front. Mol. Neurosci., 2019, 12, 54 CrossRef CAS PubMed.
- P. Velander, L. Wu, F. Henderson, S. Zhang, D. R. Bevan and B. Xu, Biochem. Pharmacol., 2017, 139, 40–55 CrossRef CAS PubMed.
- S. Kalita, H. Bergman, K. D. Dubey and S. Shaik, J. Am. Chem. Soc., 2023, 145(6), 3543–3553 CrossRef CAS PubMed.
- F. S. Ruggeri, J. Adamcik, J. S. Jeong, H. A. Lashuel, R. Mezzenga and G. Dietler, Angew. Chem., 2015, 127, 2492–2496 CrossRef.
- B. Caughey and P. T. Lansbury Jr, Annu. Rev. Neurosci., 2003, 26, 267–298 CrossRef CAS PubMed.
- J. T. Jarrett and P. T. Lansbury Jr, Cell, 1993, 73, 1055–1058 CrossRef CAS PubMed.
- J. Meinhardt, G. G. Tartaglia, A. Pawar, T. Christopeit, P. Hortschansky, V. Schroeckh, C. M. Dobson, M. Vendruscolo and M. Fändrich, Protein Sci., 2007, 16, 1214–1222 CrossRef CAS PubMed.
- A. K. Paravastu, I. Qahwash, R. D. Leapman, S. C. Meredith and R. Tycko, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 7443–7448 CrossRef CAS PubMed.
- B. Strodel, Curr. Opin. Struct. Biol., 2021, 67, 145–152 CrossRef CAS PubMed.
- H. Okumura, J. Phys. Chem. B, 2023, 127, 10931–10940 CrossRef CAS PubMed.
- H. Okumura and S. G. Itoh, J. Am. Chem. Soc., 2014, 136, 10549–10552 CrossRef CAS PubMed.
- M. Hoang Viet, P. Derreumaux and P. H. Nguyen, J. Chem. Phys., 2016, 145, 174113 CrossRef PubMed.
- M. Hoang Viet, P. Derreumaux, M. S. Li, C. Roland, C. Sagui and P. H. Nguyen, J. Chem. Phys., 2015, 143, 155101 CrossRef PubMed.
- H. Okumura, S. G. Itoh, K. Nakamura and T. Kawasaki, J. Phys. Chem. B, 2021, 125, 4964–4976 CrossRef CAS PubMed.
- H. Okumura, S. G. Itoh, H. Zen and K. Nakamura, PLoS One, 2023, 18, e0291093 CrossRef CAS PubMed.
- A. B. Poma, T. T. M. Thu, L. T. M. Tri, H. L. Nguyen and M. S. Li, J. Phys. Chem. B, 2021, 125, 7628–7637 CrossRef CAS PubMed.
- A. Levin, T. A. Hakala, L. Schnaider, G. J. Bernardes, E. Gazit and T. P. Knowles, Nat. Rev. Chem, 2020, 4, 615–634 CrossRef CAS.
- G. Wei, Z. Su, N. P. Reynolds, P. Arosio, I. W. Hamley, E. Gazit and R. Mezzenga, Chem. Soc. Rev., 2017, 46, 4661–4708 RSC.
- T. Bera, P. C. Saha, T. Chatterjee, S. Kar and S. Guha, Bioconjugate Chem., 2022, 33, 1201–1209 CrossRef CAS PubMed.
- S. Menon and N. Sengupta, Biochim. Biophys. Acta, Proteins Proteomics, 2019, 1867, 941–953 CrossRef CAS PubMed.
- D. C. Latshaw, M. Cheon and C. K. Hall, J. Phys. Chem. B, 2014, 18, 13513–13526 CrossRef PubMed.
- J. D. Camino, P. Gracia and N. Cremades, Biophys. Chem., 2021, 269, 106520 CrossRef CAS PubMed.
- P. Khatua, J. C. Jose, N. Sengupta and S. Bandyopadhyay, Phys. Chem. Chem. Phys., 2016, 18, 30144–30159 RSC.
- J. D. Camino, P. Gracia and N. Cremades, Biophys. Chem., 2021, 269, 106520 CrossRef CAS PubMed.
- D. Thirumalai, G. Reddy and J. E. Straub, Acc. Chem. Res., 2012, 45, 83–92 CrossRef CAS PubMed.
- S.-H. Chong and S. Ham, Acc. Chem. Res., 2015, 48, 956–965 CrossRef CAS PubMed.
- I. Marcos-Alcalde, J. Setoain, J. I. Mendieta-Moreno, J. Mendieta and P. Gomez-Puertas, Bioinformatics, 2015, 31, 3853–3855 CrossRef CAS PubMed.
- A. Mukherjee and B. Bagchi, J. Chem. Phys., 2004, 120, 1602–1612 CrossRef CAS PubMed.
- T. Pal, S. Sahoo, K. P. Ghanta and S. Bandyopadhyay, J. Mol. Liq., 2022, 368, 120779 CrossRef CAS.
- R. Nelson, M. R. Sawaya, M. Balbirnie, A. Ø. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778 CrossRef CAS PubMed.
- G. Bitan, M. D. Kirkitadze, A. Lomakin, S. S. Vollers, G. B. Benedek and D. B. Teplow, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 330–335 CrossRef CAS PubMed.
- C.-T. Lee and E. M. Terentjev, J. Chem. Phys., 2017, 147, 105103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00103f |
| This journal is © The Royal Society of Chemistry 2024 |