Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrafast photophysics of an orange–red thermally activated delayed fluorescence emitter: the role of external structural restraint†
Yixuan
Gao
a,
Yaxin
Wang
a,
Zilong
Guo
 *a,
Yan
Wan
*a,
Yan
Wan
 c,
Zheng
Xue
b,
Yandong
Han
c,
Zheng
Xue
b,
Yandong
Han
 b,
Wensheng
Yang
b,
Wensheng
Yang
 ab and
Xiaonan
Ma
ab and
Xiaonan
Ma
 *a
*a
aInstitute of Molecular Plus, Tianjin University, Tianjin 300072, P. R. China. E-mail: xiaonanma@tju.edu.cn; zilong.guo@tju.edu.cn
bEngineering Research Center for Nanomaterials, Henan University, Kaifeng 475004, P. R. China
cCollege of Chemistry, Beijing Normal University, Beijing 100875, P. R. China
First published on 3rd April 2024
Abstract
The application of thermally activated delay fluorescence (TADF) emitters in the orange–red regime usually suffers from the fast non-radiative decay of emissive singlet states (kSNR), leading to low emitting efficiency in corresponding organic light-emitting diode (OLED) devices. Although kSNR has been quantitatively described by energy gap law, how ultrafast molecular motions are associated with the kSNR of TADF emitters remains largely unknown, which limits the development of new strategies for improving the emitting efficiency of corresponding OLED devices. In this work, we employed two commercial TADF emitters (TDBA-Ac and PzTDBA) as a model system and attempted to clarify the relationship between ultrafast excited-state structural relaxation (ES-SR) and kSNR. Spectroscopic and theoretical investigations indicated that S1/S0 ES-SR is directly associated with promoting vibrational modes, which are considerably involved in electronic–vibrational coupling through the Huang–Rhys factor, while kSNR is largely affected by the reorganization energy of the promoting modes. By restraining S1/S0 ES-SR in doping films, the kSNR of TADF emitters can be greatly reduced, resulting in high emitting efficiency. Therefore, by establishing the connection among S1/S0 ES-SR, promoting modes and kSNR of TADF emitters, our work clarified the key role of external structural restraint for achieving high emitting efficiency in TADF-based OLED devices.
Introduction
Organic light-emitting diode (OLED) technology is becoming increasingly attractive due to its great potential for ultra-high definition (UHD) displays.1–5 As a key factor in the performance of OLED devices, external quantum efficiency (ηEQE) is described as the ratio between the number of emitted photons and number of injected carriers. In most cases, the ηEQE of OLED devices can be expressed as the product of several contributing terms:6,7| ηEQE = γ × ηEUE × ΦF × ηout | (1) |
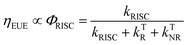 | (2) |
Enormous efforts have been made towards designing thermally activated delayed fluorescence (TADF) emitters with minimized singlet–triplet energy gap (ΔEST) and enhanced spin–orbit coupling (SOC) to enable thermal conversion of T1 → S1, which can potentially push ηEUE to ∼100%.12–15 Since the kRISC of TADF emitters is usually on a time scale of 103–105 s−1, ηEUE is generally associated with slow dynamics of TADF emitters, which has been intensively investigated.14,16–18
In addition to the efficient utilization of current-generated triplet states, the ΦF of TADF emitters greatly affects the ηEQE of the corresponding OLED devices, which describes the ratio of singlet (S1) states that can be radiatively relaxed to the S0 state, i.e., competing plausible relaxation channels for the S1 state (Fig. S1†):19–21
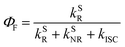 | (3) |
| ΦF = ΦPF + ΦDF | (4) |
For organic TADF emitters, kISC is usually slow (107–108 s−1),16,22 for which the presence of rapid non-radiative decay is a key factor that can significantly reduce the ΦF of TADF emitters. In a weak coupling regime, the rate constant of the S1 state non-radiative decay (kSNR) with energy gap (ΔES1–S0) and electronic coupling (C) can be described as23–25
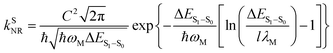 | (5) |
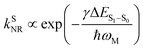 | (6) |
Recently, enormous efforts have been made towards developing long-wavelength TADF-based OLED devices with a high ηEQE,28,35 in which the low ΦF of TADF emitters is usually regarded as the main obstacle.28,38–40 Therefore, one can expect opportunities to further improve the ηEQE of TADF-based long-wavelength OLED devices by somehow effectively slowing down the kSNR rate.41–44 Recently, Kwon and co-workers reported an acceptor–donor–acceptor (ADA) type TADF emitter (PzTDBA, Scheme 1) and realized >30% of the ηEQE of orange–red OLED devices.45 Although the excited-state mechanism that is responsible for the high ηEQE is still ambiguous, the reported ∼100% ΦF of PzTDBA in doping films indicates that non-radiative decay of the S1 state is nearly terminated, which seems to violate the well-known energy gap law (eqn (6)). Therefore, understanding the underlying ultrafast photophysics that is associated with the slow kSNR of PzTDBA might provide inspiration for designing high-performance TADF emitters in the long-wavelength regime.
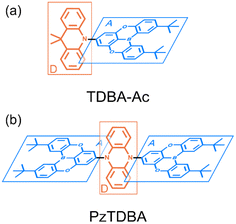 | ||
| Scheme 1 Illustrated chemical structure of investigated TADF emitters: (a) TDBA-Ac, D–A type; (b) PzTDBA, A–D–A type. The charge donors and acceptors are displayed in blue and red, respectively. | ||
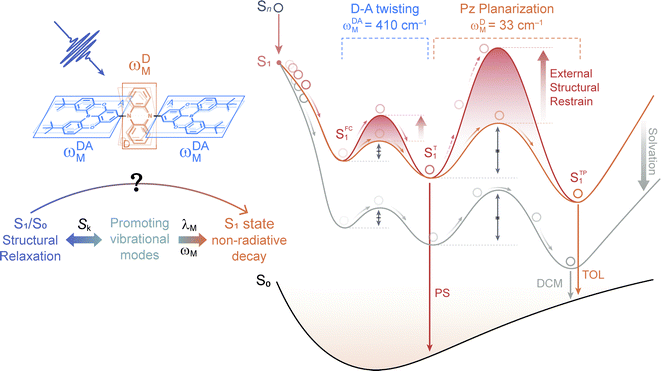
In this work, the ultrafast photophysics of an orange–red TADF emitter (PzTDBA, ADA-type) and its DA-type analogue (TDBA-Ac, deep-blue) was investigated using femtosecond transient absorption (fs-TA), time-resolved fluorescence (tr-FL) and theoretical vibrational analysis.46 Compared with the one-step D–A twisting of the TDBA-Ac emitter, PzTDBA exhibits two-step S0/S1 excited-state structural relaxation (ES-SR), i.e. fast D–A twisting and slow planarization of the Pz group. The promoting vibrational modes associated with the S0/S1 ES-SR motions of the TDBA-Ac and PzTDBA emitters were theoretically identified, which dominate the electronic-vibrational coupling (EVC) of the S1 state. Meanwhile, promoting modes contribute to fast kSNR through the corresponding reorganization energy contribution (λM). In doping films, the S0/S1 ES-SR motions of PzTDBA are suppressed by external structural restraint, which greatly slows down kSNR and leads to ∼100% ΦF. Our work established the connection among the S0/S1 ES-SR, promoting modes and S1 state non-radiative decay and indicated the key role of medium rigidity in improving the emitting efficiency of TADF emitters, which should provide inspiration for the future development of TADF emitters.
Results and discussion
Low-lying excited states and steady state spectra
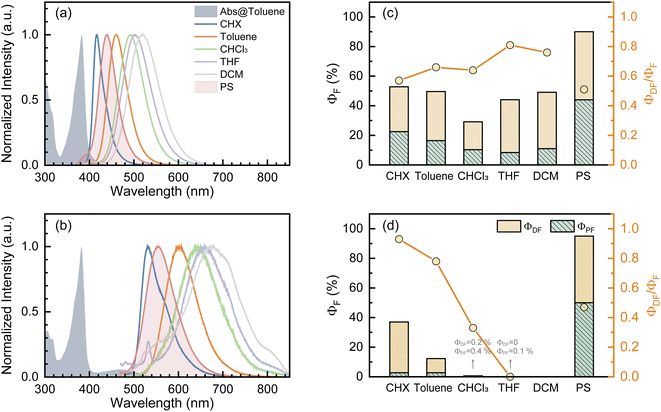
Fundamental photophysics of TDBA-Ac and PzTDBA emitters were first investigated in solvents with different polarities (Table S1†). In OLED devices, TADF emitters are usually doped in a wide-bandgap organic semiconductor as the host. To avoid multi-photon excitation of the host in fs-TA experiments, we prepared doping films (2 wt%) of TADF emitters by employing polystyrene (PS) as the host, and the polarity of the PS medium (ε = 2.6–2.7, Δf = 0.03) was determined to be comparable with toluene (Fig. S2†).47,48 The UV/Vis absorption and fluorescence spectra of the TDBA-Ac and PzTDBA emitters in various solutions and films (2 wt%) can be seen in Fig. 1 and S3.† The TD-DFT (M06-2X/6-311G**, PCM = toluene) calculated vertical low-lying singlet and triplet states (S1–S3, T1–T3) are listed in Table S2† with the visualized distribution of frontier orbitals (HOMO−2 to LUMO+2) shown in Table S3.† The lowest-lying S1 states of TDBA-Ac and PzTDBA are dominated by the H → L transition, corresponding to the charge transfer state (noted as 1CTDA) with low oscillator strength, which can be seen as weak absorption of TDBA-Ac (400–450 nm) and PzTDBA (420–540 nm). Upon UV excitation, solvatochromism was observed for TDBA-Ac and PzTDBA, indicating that the fluorescence emission originated from the lowest-lying 1CTDA state.49,50 Intriguingly, ∼1000 cm−1 (TDBA-Ac) and ∼1400 cm−1 (PzTDBA) blue-shifted emissions were observed in PS doping films compared to in toluene (comparable polarity), indicating the presence of multifaceted interactions, which are discussed below.The T1 state of TDBA-Ac was identified as a local excited state on the acceptor (noted as 3LEA) while the T1 excitation of PzTDBA was localized on the donor (3LED), which allows direct T1 → S1 RISC (3LED/A → 1CTDA).51,52 Meanwhile, the T2 states of TDBA-Ac and PzTDBA were recognized as charge transfer states (3CTDA). With identical orbital wavefunction to the 1CTDA state, the corresponding T2 → S1 RISC (3CTDA → 1CTDA) is forbidden.51,52 By further confirming the CT/LE nature of low-lying singlet/triplet states through natural transition orbital (NTO) analysis (Fig. S4 and S5†) and hole–electron analysis (Table S4†),53,54 the T1 → S1 (3LED/A → 1CTDA) transition was assigned as the accessible RISC channel that is responsible for the delayed fluorescence of TDBA-Ac and PzTDBA.
The thermally accessible ΔEST is critical for RISC, while estimating ΔEST through the vertical excitation energy of S1 and T1 states was reported to be unreliable.55 Thus, we further optimized the S1 and T1 geometry of the TDBA-Ac and PzTDBA emitters to estimate adiabatic 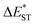 . As listed in Table 1, TDBA-Ac and PzTDBA exhibit
. As listed in Table 1, TDBA-Ac and PzTDBA exhibit 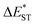 of ∼0.3 eV and ∼0.26 eV in low-polarity media (CHX and TOL, Δf < 0.02), respectively, facilitating RISC for harvesting T1 states with moderate 〈S1|ĤSO|T1〉. However, increasing to medium polarity (in DCM, Δf = 0.22) leads to enlarged
of ∼0.3 eV and ∼0.26 eV in low-polarity media (CHX and TOL, Δf < 0.02), respectively, facilitating RISC for harvesting T1 states with moderate 〈S1|ĤSO|T1〉. However, increasing to medium polarity (in DCM, Δf = 0.22) leads to enlarged 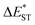 (>0.33 eV) for TDBA-Ac and PzTDBA with nearly unchanged 〈T1|ĤSO|S1〉, which might explain the reduced RISC rate (kRISC). Note that the vertical (ΔEST) and adiabatic
(>0.33 eV) for TDBA-Ac and PzTDBA with nearly unchanged 〈T1|ĤSO|S1〉, which might explain the reduced RISC rate (kRISC). Note that the vertical (ΔEST) and adiabatic 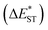 singlet-triplet energy gap does not have a certain magnitude relationship as it depends on multiple factors, such as the different ES-SR in the S1/T1 states and steepness of the corresponding potential energy surface (PES), which are simplified as schematic diagrams (Fig. S6†). The total ΦF and corresponding prompt/delayed (ΦPF/ΦDF) contribution of TDBA-Ac and PzTDBA were further measured in different solutions and PS doping films. As illustrated in Fig. 1c, TDBA-Ac exhibits nearly solvent-independent ΦF (30–50%). With increasing solvent polarity, the solvation of the 1CTDA (S1) state and unchanged energy level of the 3LEA (T1) state resulted in reduced ΔEST,50,56 which is consistent with the observed increasing of the ΦDF contribution (ΦDF/ΦF, Fig. 1c). Upon optical excitation, S1 → T1 → S1 is the only feasible channel for delayed fluorescence,17,38,57 and increased ΦDF/ΦF might correspond to higher ΦISC and ΦRISC. In contrast, the ΦF of PzTDBA rapidly decreased from 37% in non-polar CHX to undetectably low in polar mediums, which implies different relaxation of the photo-generated S1 state. Intriguingly, TDBA-Ac and PzTDBA exhibit nearly 100% ΦF and an evenly divided contribution of ΦPF and ΦDF (ΦDF/ΦF ≈ 50%) in PS doping films, indicating that the S1 state decay is dominantly radiative, while all ISC-generated T1 states can be harvested through subsequent RISC. Considering the importance of ΦF, resolving the photophysics behind the fully radiative relaxation of orange–red PzTDBA in doping film would be of high interest.
singlet-triplet energy gap does not have a certain magnitude relationship as it depends on multiple factors, such as the different ES-SR in the S1/T1 states and steepness of the corresponding potential energy surface (PES), which are simplified as schematic diagrams (Fig. S6†). The total ΦF and corresponding prompt/delayed (ΦPF/ΦDF) contribution of TDBA-Ac and PzTDBA were further measured in different solutions and PS doping films. As illustrated in Fig. 1c, TDBA-Ac exhibits nearly solvent-independent ΦF (30–50%). With increasing solvent polarity, the solvation of the 1CTDA (S1) state and unchanged energy level of the 3LEA (T1) state resulted in reduced ΔEST,50,56 which is consistent with the observed increasing of the ΦDF contribution (ΦDF/ΦF, Fig. 1c). Upon optical excitation, S1 → T1 → S1 is the only feasible channel for delayed fluorescence,17,38,57 and increased ΦDF/ΦF might correspond to higher ΦISC and ΦRISC. In contrast, the ΦF of PzTDBA rapidly decreased from 37% in non-polar CHX to undetectably low in polar mediums, which implies different relaxation of the photo-generated S1 state. Intriguingly, TDBA-Ac and PzTDBA exhibit nearly 100% ΦF and an evenly divided contribution of ΦPF and ΦDF (ΦDF/ΦF ≈ 50%) in PS doping films, indicating that the S1 state decay is dominantly radiative, while all ISC-generated T1 states can be harvested through subsequent RISC. Considering the importance of ΦF, resolving the photophysics behind the fully radiative relaxation of orange–red PzTDBA in doping film would be of high interest.
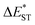 ) of TDBA-Ac and PzTDBA in different mediums using PCM as the model; SOC matrix elements for ISC (〈S1|ĤSO|T1〉) and RISC (〈T1|ĤSO|S1〉) were calculated by using the linear response approach
) of TDBA-Ac and PzTDBA in different mediums using PCM as the model; SOC matrix elements for ISC (〈S1|ĤSO|T1〉) and RISC (〈T1|ĤSO|S1〉) were calculated by using the linear response approach
tr-FL and excited-state relaxation
The time-resolved fluorescence (tr-FL) measurements of TDBA-Ac and PzTDBA were further performed by time-correlated single-photon counting (TCSPC) upon excitation at λex = 400 nm.The resulting traces were fitted as the sum of prompt (τPF) and delayed (τDF) components (Fig. S7, S8† and Table 2). Combining with measured ΦPF and ΦDF, the rate constants for ISC (S1 → T1, kISC) and RISC (T1 → S1, kRISC) as well as corresponding ΦISC and ΦRISC were estimated (Table 2). With calculated SOC matrix elements (〈S1|ĤSO|T1〉 and 〈T1|ĤSO|S1〉), we attempted to reproduce the experimentally extracted values of kISC and kRISC using the thermal vibration correlation function (TVCF)16,54,58 and semi-classical Marcus59,60 approaches. However, as shown in Table S5,† TVCF and Marcus approaches failed to describe kISC and kRISC, which might be attributed to the ignorance of non-Condon effects, such as Herzberg–Teller coupling and spin–vibronic coupling.61–63 Meanwhile, we noticed that calculation errors for the kISC of PzTDBA are much more significant than for TDBA-Ac, which might imply higher structural flexibility of PzTDBA and will be discussed in detail below. By further estimating the experimental values of kSR, kSNR and kTNR (Table 2), the quantitative contribution of the plausible relaxation channels was calculated for the S1 and T1 states.
| TDBA-Ac | PzTDBA | |||||||
|---|---|---|---|---|---|---|---|---|
| CHX | TOL | DCM | PS | CHX | TOL | DCM | PS | |
| a Concentration of 10−5 M. b Doping concentration of 2 wt%. c Calculated by kPF = 1/τPF and kDF = 1/τDF. d Rate constants kSR, kISC, kRISC and kTNR were calculated using the method described by Adachi et al.10,19 e Calculated using kSNR = kPF − kSR − kISC. f Calculated using ΦISC = kISC/(kISC + kSR + kSNR). g Calculated using ΦRISC = ΦDF/(1 − ΦPF). | ||||||||
| τ PF/ns | 6.72 | 21.35 | 36.15 | 14.12 | 8.70 | 23.95 | 13.62 | 38.25 |
| τ DF/μs | 0.15 | 0.14 | 0.48 | 1.21 | 0.10 | 0.29 | 0.23 | 1.10 |
| Φ F | 0.53 | 0.49 | 0.47 | 0.90 | 0.37 | 0.13 | <0.01 | 0.95 |
| Φ PF | 0.23 | 0.16 | 0.11 | 0.44 | 0.03 | 0.03 | <0.01 | 0.50 |
| Φ DF | 0.30 | 0.33 | 0.36 | 0.46 | 0.34 | 0.10 | 0 | 0.45 |
| Φ ISC | 0.57 | 0.67 | 0.78 | 0.51 | 0.93 | 0.78 | 0 | 0.47 |
| Φ RISC | 0.39 | 0.39 | 0.43 | 0.82 | 0.35 | 0.10 | 0 | 0.90 |
| k PF/107 s−1 | 14.88 | 4.69 | 2.77 | 7.14 | 11.49 | 4.17 | 7.35 | 2.63 |
| k SR/106 s−1 | 33.48 | 7.70 | 3.05 | 31.43 | 3.10 | 1.13 | — | 13.16 |
| k SNR/106 s−1 | 30.29 | 7.82 | 3.16 | 3.49 | 5.28 | 8.02 | 73.46 | 0.69 |
| k ISC/107 s−1 | 8.50 | 3.14 | 2.15 | 3.65 | 10.66 | 3.25 | — | 1.25 |
| k DF/106 s−1 | 3.57 | 3.54 | 1.01 | 0.74 | 3.63 | 0.43 | — | 0.86 |
| k RISC/105 s−1 | 18.75 | 17.57 | 4.98 | 6.69 | 13.42 | 0.52 | — | 8.20 |
| k TNR/105 s−1 | 31.50 | 32.55 | 9.60 | 4.49 | 35.91 | 4.24 | — | 4.53 |
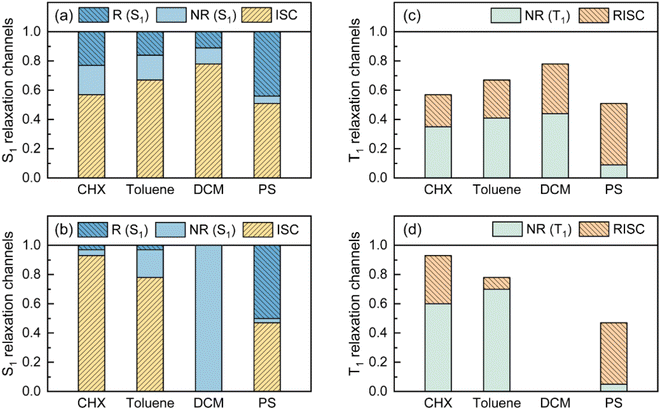
As visualized in Fig. 2, the S1 relaxation of TDBA-Ac is dominated by the slightly increased ISC with increased solvent polarity, while the ISC-generated T1 states can be converted to S1 with nearly identical ΦRISC, which leads to the nearly unchanged ΦF of TDBA-Ac in CHX (0.53), TOL (0.49) and DCM (0.47). In contrast, although ISC still dominates the S1 decay of PzTDBA in CHX and TOL, the generated T1 states largely decay non-radiatively to S0 rather than thermally converting to S1via RISC, for which a low ΦF was observed in CHX (0.37) and TOL (0.13). In high-polarity DCM, the S1 decay of PzTDBA is predominately occupied by the non-radiative path to S0, leading to an undetectable ΦF (<0.01), which might be attributed to the exponentially increased kSNR described by band-gap law with the reducing of the S1 → S0 energy gap (ΔES1–S0).
Intriguingly, TDBA-Ac and PzTDBA exhibit nearly identical pattern of S1 and T1 decay in PS doping films, which is largely differed with observation in solutions. The S1 decay of TDBA-Ac and PzTDBA in PS doping films are dominated by equally divided radiative decay (S1 → S0) and ISC (S1 → T1), while ISC-generated T1 states can be further converted to S1 through efficient RISC (ΦRISC > 0.9). Due to negligible role of non-radiative path in both S1 (<5%) and T1 (<10%) state decay, TDBA-Ac and PzTDBA exhibit unexpectedly high ΦF in PS doping films, which agrees with the reported high ηEQE of corresponding OLED devices.45,46 However, such high ΦF (0.95) of PzTDBA observed in PS doping film seems to be inconsistent with the energy gap law, implying unique photophysics by which non-radiative decay of S1 state can be greatly suppressed.
fs-TA and structural relaxation
The fs-TA signal upon UV excitation (λex = 320 nm) of TDBA-Ac and PzTDBA in CHX solution and PS doping film were recorded by broadband probe (λprobe = 350–750 nm) with delay times up to 7.0 ns, and the temporal resolution of fs-TA was measured to be ∼90 fs. As shown in Fig. S9 and S10,† the measured fs-TA signals of TDBA-Ac and PzTDBA are contributed by negative ground-state bleaching (GSB) in the λprobe = 350–400 nm regime, and the positive excited-state absorption (ESA) band extended in the longer wavelength region up to λprobe = 750 nm.Upon UV excitation, high-lying Sn states can be populated, followed by rapid internal conversion (IC, Sn → S1) to the long-lived S1 state, which explains the dramatically reshaped ESA in the 1 ps delay time.64,65 For the subsequent delay times of 1 ps to 1 ns, fs-TA evolution visualizes wavepacket motion that highly depends on the topology of S1 PES.41,66–68 For instance, the role of the excited-state structural relaxation (ES-SR) in the S1 state decay of DA- and DAD/ADA-type TADF emitters has been intensively reported.69–73 Suffering from the poor structural sensitivity of UV/Vis fs-TA, S1/S0 ES-SR usually leads to minimized alternation of the ESA shape, which is consistent with the observed fs-TA of TDBA-Ac and PzTDBA for 1 ps to 1 ns delay times.41,74
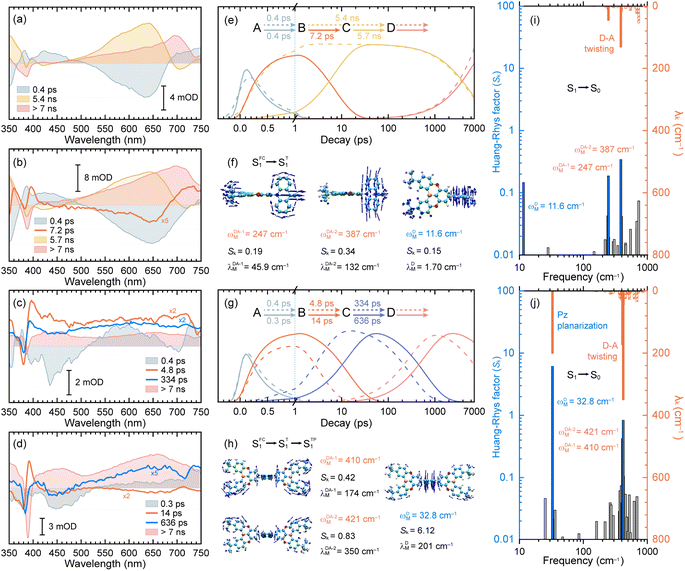
For characterizing S1/S0 ES-SR, the geometries of TDBA-Ac and PzTDBA in the S0, S1 and T1 states were optimized using DFT and TD-DFT approaches. The resulting structures are illustrated in Table S6,† while total reorganization energies (λS0→S1 and λS1→S0) were calculated for evaluating the ES-SR of the TDBA-Ac and PzTDBA emitters together with the root of the mean squared displacement (RMSDS1/S0) between the S0 and S1 states (Fig. S11†). As listed in Table 3, the calculated values of λS0→S1, λS1→S0 and RMSDS1/S0 indicate a more pronounced ES-ER of PzTDBA in the S1 state than TDBA-Ac, which obviously cannot be attributed to structural extension (DA to ADA structure) as the total reorganization energy and RMSD are not additive. To evaluate the contribution of each of the molecular fragments of the TDBA-Ac and PzTDBA emitters to the ES-SR, several critical structural parameters were defined, as illustrated in Fig. S12† and measured (Table 3) for the S0 and S1 states. Upon vertical excitation, TDBA-Ac and PzTDBA initially remain in S0 geometry in the Franck–Condon (FC) region, following by ES-SR until reaching the global minimum of S1 PES, i.e. optimized S1 geometry. For TDBA-Ac, S1/S0 ES-SR featured a slight increase in the D–A twisting angle β from 89.82° (SFC1) to 92.00° (ST1), while the dihedral angles of the Ac (α) and TDBA (γ) framework bending remained nearly unchanged in the S1 state decay. In contrast, ADA-type PzTDBA exhibits higher flexibility than that of TDBA-Ac. In addition to the fast motion of the D–A twisting angle (β) from 79.72°/79.06° (SFC1) to 89.02°/91.43° (ST1), framework planarization of the center donor (Pz) was observed as the dihedral angle (α) increased from 164.57° (ST1) to 180.00° (STP1). The simultaneous S0–S1 state changing of α and β angles may correspond to a two-step S1/S0 ES-SR (SFC1 → ST1 → STP1), which has been widely reported,75,76i.e. fast D–A twisting (SFC1 → ST1) followed by slow framework planarization (ST1 → STP1). Target analysis was further performed to acquire quantitative information on S1/S0 ES-SR that may play a key role in the S1 state relaxation. By including three or four sequential decay processes, measured fs-TA data can be well-reproduced by the displayed decay-associated spectra (DAS) of each decay components and concentration evolution of each transient species (Fig. 3), while species-associated spectra (SAS) can be seen in Fig. S13 and S14.†
| TDBA-Ac | PzTDBA | |||||
|---|---|---|---|---|---|---|
| *α (°) | **β (°) | ***γ (°) | *α (°) | **β1/β2 (°) | ***γ1/γ2 (°) | |
| a *Bending dihedral angle of donor (Ac/Pz); **donor–acceptor twisting angle; ***bending dihedral angle of acceptor (TDBA). | ||||||
| S0 geometry | 176.50 | 89.82 | 11.36 | 164.57 | 79.72/79.06 | 11.56/10.99 |
| S1 geometry | 175.45 | 92.00 | 12.12 | 180.00 | 89.02/91.43 | 11.65/11.37 |
| T1 geometry | 176.57 | 90.82 | 4.77 | 180.00 | 88.60/91.33 | 11.40/11.40 |
| λ S0→S1 (cm−1) | 1161 | 2790 | ||||
| λ S1→S0 (cm−1) | 1273 | 2552 | ||||
| RMSDS1/S0 (Å) | 0.053 | 0.241 | ||||
The initial decay (A → B) with 300–400 fs time constant was accompanied by considerable ESA reshaping, corresponding to rapid IC (Sn → S1). The fs-TA was subsequently dominated by S1/S0 ES-SR until the wavepacket reached the global minimum of S1 PES. For PzTDBA, highlighted two-step S1/S0 ES-SR (B → C → D, i.e. SFC1 → ST1 → STP1) predicted by calculated S0 and S1 geometries was observed, featuring a slight ESA reshaping. The observed fast (4.8 ps in CHX, SFC1 → ST1) and slow (334 ps in CHX, ST1 → STP1) steps correspond to D–A twisting (β1/β2 angles) and Pz planarization (α angle), respectively.
For TDBA-Ac, one-step S1/S0 ES-SR was observed (7.2 ps, SFC1 → ST1) in the PS doping film, corresponding to the D–A twisting (β angle), which is comparable with the fast S1/S0 ES-SR step of PzTDBA. However, S1/S0 ES-SR of TDBA-Ac was unobservable in CHX, which might be attributed to a less pronounced S0 → S1 structural change than for PzTDBA, i.e. nearly unchanged β angle in the S0 (89.82°) and S1 (92.00°) states.
Intriguingly, the extracted time constants of D–A twisting (SFC1 → ST1, 14.0 ps) and Pz planarization (ST1 → STP1, 636 ps) of PzTDBA in the PS doping film are 2–3 times slower than corresponding S1/S0 ES-SR steps in CHX (Fig. 3g and S15†), implying a higher potential barrier for S1 PES, which is consistent with our fs-TA observations for multiple-resonance emitters.77 Moreover, slow S1 isomerization of azo-benzene embedded in polymer films was reported previously, attributing to external structural restraint from polymer micro-networks.78
As discussed above, the fluorescence emission of PzTDBA was strongly quenched (ΦF = 0.37 in CHX) in solutions due to the presence of fast non-radiative decay, while a high ΦF (>0.95) in the PS doping film may be feasible if non-radiative S1 → S0 decay can be greatly suppressed. Our fs-TA data revealed higher S1/S0 ES-SR barriers of PzTDBA in PS doping films than in CHX, which might imply the presence of an underlying association between S1/S0 ES-SR and the non-radiative decay of the S1 state, i.e. restrained S1/S0 ES-SR leads to suppressed non-radiative decay. Conversely, kSNR was described to be highly correlated with promoting vibrational modes by the energy gap law (eqn (5)).21,23 Thus, we attempted to unveil the underlying relationship among the S1/S0 ES-SR, promoting modes and non-radiative decay of the S1 state.
Vibrational analysis and non-radiative decay
The energy gap law (eqn (5)) clearly describes how promoting vibrational modes affect kSNR through their vibrational frequency (ωM) and reorganization energy (λM), while promoting modes are vibrational modes that are considerably involved in the EVC of the S1 state through a pronounced Huang-Rhys (HR) factor (Sk).24,79,80 We further calculated the Sk and λk contribution of each of the vibrational modes involved in the S1 → S0 transition (Fig. 3i and j), in which the promoting modes associated with the kSNR of TDBA-Ac and PzTDBA are illustrated in Fig. 3f and h, respectively.As shown in Fig. 3j and h, three promoting modes were identified for the S1 → S0 transition of PzTDBA due to considerable Sk. The modes at 410 cm−1 (ωDA-1M) and 421 cm−1 (ωDA-2M) correspond to symmetric and asymmetric D–A twisting and exhibit considerable reorganization energy contributions (λDA-1M = 174 cm−1 and λDA-2M = 350 cm−1), which are associated with the fast S1/S0 ES-SR step observed on fs-TA of PzTDBA, i.e. SFC1 → ST1 with the D–A twisting motion. For TDBA-Ac (Fig. 3i and f), the corresponding S1/S0 ES-SR of D–A twisting is associated with promoting modes at ωDA-1M = 247 cm−1 and ωDA-2M = 387 cm−1 with substantially lower λDA-1M (45.9 cm−1) and λDA-2M (132 cm−1), which is consistent with its rigid structure predicted theoretically, i.e. less pronounced S1/S0 ES-SR than PzTDBA.
Meanwhile, S1 → S0 decay of PzTDBA features a promoting mode at ωDM = 32.8 cm−1 with a surprisingly high HR factor (Sk = 6.12) and considerable reorganization energy (λDM = 201.1 cm−1), corresponding to the bending motion of the Pz framework, which is clearly associated with the observed slow S1/S0 ES-SR step of PzTDBA, i.e. ST1 → STP1. Intriguingly, this particular mode was also observed for TDBA-Ac at ωDM = 11.6 cm−1 with a much lower HR factor (Sk = 0.15) and a two orders of magnitude lower reorganization energy contribution (λDM = 1.70 cm−1) than that of PzTDBA, indicating that it was excluded from the S1 → S0 decay of TDBA-Ac. As a result, the second S1/S0 ES-SR step (ST1 → STP1) was absent from the fs-TA signal of TDBA-Ac.
Furthermore, we investigated the influence of medium polarity on the promoting modes of the TDBA-Ac and PzTDBA emitters. As shown in Fig. S16,† for PzTDBA in DCM solution, an extra promoting mode at 15.4 cm−1 was observed with considerable Sk but ignorable λk, which might be less associated with the non-radiative decay of S1 state PzTDBA. In contrast, a promoting mode at 12.4 cm−1 was observed for TDBA-Ac with considerable Sk (8.71) and λk (108.23 cm−1) in DCM solution, which is very different from the case of TDBA-Ac in low-polarity solvents, indicating that the S1/S0 ES-SR of TDBA-Ac (DA-type) is more evidentially coupled with charge transfer than PzTDBA (ADA-type).
As discussed above, the one- (TDBA-Ac, SFC1 → ST1) and two-step (PzTDBA, ST1 → STP1) S1/S0 ES-SR are directly associated with promoting vibrational modes that are considerably involved in the EVC of the S1 state through their HR factor. Meanwhile, promoting modes contribute to the kSNR of the S1 state through corresponding λM, which implies that S1/S0 ES-SR can significantly affect kSNR (and subsequently ΦF) through the promoting vibrational modes (Fig. 4). For instance, the one-step S1/S0 ES-SR of TDBA-Ac is associated with vibrational modes with low Sk and λM, while the promoting modes associated with the two-step S1/S0 ES-SR of PzTDBA have much higher Sk and λM. As a result, the non-radiative channel plays a minor role in the S1 decay of structurally rigid TDBA-Ac, while the emission of structurally flexible PzTDBA is severely hampered by the fast non-radiative decay of the S1 state. Furthermore, the two-step S1/S0 ES-SR motions of PzTDBA are greatly suppressed in the PS doping films due to the external structural restraint, for which the S1 non-radiative decay associated with the promoting modes might be correspondingly weakened, leading to the greatly improved ΦF of PzTDBA in the doping films. In this sense, the external structural restraint for S1/S0 ES-SR motions might be critical for achieving a high ηEQE for TADF-based OLED devices.
To directly verify the influence of the external structural restraint on the S1 non-radiative decay of PzTDBA, we measured temperature-dependent emission spectra of PzTDBA in polyethylene oxide (PEO) doping films (Fig. S18†). With a glass transition temperature (Tg) of 220 K, PEO provides a “softer” microenvironment than PS (Tg = 373 K) and can be further “softened” by increasing the temperature.81,82 As a TADF emitter, PzTDBA was expected to be more fluorescent at higher temperatures due to faster RISC. However, we observed clear fluorescence quenching with increasing temperature in the 297–347 K range, indicating that non-radiative decay was enhanced in the medium with reduced external structural restraint, which is consistent with our analysis described above.
Note that we cannot perform vibrational analysis for TADF emitters with the presence of the external structural restraint, but we speculate that the λM of the promoting modes of PzTDBA might be greatly reduced due to the external structural restraint, in agreement with slowed S1/S0 ES-SR motions in the doping films, especially the Pz bending mode (ωDM) associated with the slow S1/S0 ES-SR step (ST1 → STP1) might be terminated. As a result, ST1 instead of STP1 might dominate the emission of PzTDBA in the PS doping films (see Fig. 4), which explains the observed blue-shifted emission in the PS doping film compared with the case in toluene solution, which has comparable polarity to the PS medium. Meanwhile, the emission of PzTDBA in solutions mainly originates from STP1 due to the accessible barrier of ST1 → STP1, which thus suffers from the plague of non-radiative decay (Fig. 4).
Last but not least, in addition to the S1 state, we noticed that TDBA-Ac and PzTDBA exhibit a suppressed non-radiative decay channel of the T1 state in the PS doping films compared to in solutions (Fig. 2c and d), which inspired us to consider the role of T1/S0 ES-SR in the non-radiative decay of the T1 state. As shown in Fig. S17,†TDBA-Ac exhibits several vibrational modes with considerable Sk in the region <100 cm−1, but the low λM implies that ES-SR may not be strongly associated with non-radiative T1 → S0 decay. In contrast, the promoting modes of PzTDBA at 32.9 cm−1 and 421/410 cm−1 contribute considerable λM, while pronounced T1/S0 ES-SR was indicated (Table 3), including Pz bending and D–A twisting. Therefore, it might be plausible that the non-radiative T1 → S0 decay is similarly associated with two T1/S0 ES-SR motions, because the non-radiative T1 → S0 decay of PzTDBA was strongly suppressed in the PS doping film due to the external structural restraint. However, unlike S1 relaxation, without direct spectroscopic evidence of T1/S0 ES-SR in different media, verifying this hypothesis requires further investigation.
Conclusions
To summarize, we performed a comprehensive investigation of the photophysics of two TADF emitters, TDBA-Ac (DA-type, blue light) and PzTDBA (ADA-type, orange–red light), using fs-TA, tr-FL and theoretical approaches. Compared with the one-step S1/S0 ES-SR (SFC1 → ST1) of TDBA-Ac, the S1 state decay of PzTDBA is dominated by two steps, S1/S0 ES-SR (SFC1 → ST1 → STP1), while greatly slowed S1/S0 ES-SR motions of PzTDBA were observed in the PS doping films due to the external structural restraints. Vibrational analysis indicated that the S1/S0 ES-SR motions are directly associated with the promoting modes that are considerably involved in the EVC of the S1 state through their own Sk, while the promoting modes contribute to fast kSNRvia λM. In doping films, the external structural restraint leads to suppressed S1/S0 ES-SR and reorganization energy contribution of the promoting modes, resulting in slowed kSNR and a highly fluorescent S1 state that is favorable for OLED application. With TDBA-Ac and PzTDBA as model systems, we established the connection among the S0/S1 ES-SR, promoting modes and kSNR of TADF emitters, which indicated the key role of the external structural restraint in obtaining high ΦF TADF emitters. Our work also provides a new direction for OLED design, and it might be necessary to take the rigidity of host materials used for the emitting layer into consideration to avoid emission quenching through fast non-radiative decay associated with the S1/S0 ES-SR of TADF emitters, especially for TADF emitters with a relatively small band gap, which might be a useful reference for future OLED application.Data availability
All experimental and calculational data are available from the corresponding author upon reasonable request.Author contributions
Yixuan Gao: conceptualization, methodology, investigation, data curation, formal analysis, visualization, and writing – original draft; Yaxin Wang: methodology, data curation, formal analysis, and validation; Zilong Guo: investigation, visualization, project administration, and supervision; Yan Wan: methodology and resources; Zheng Xue and Yandong Han: resources and project administration; Wensheng Yang: supervision, resources, and funding acquisition; Xiaonan Ma: conceptualization, formal analysis, funding acquisition, supervision, and writing – review and editing.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the financial support from the National Key Research & Development Program of China (Grant No. 2020YFA0714603 and 2020YFA0714604). We thank Dr Yingli Niu (Beijing Jiaotong University) for his useful tutoring on MOMAP calculation and Dr Lei Zhou (HORIBA Scientific, Beijing) for valuable discussion on tr-FL measurements.Notes and references
- Y.-Z. Shi, H. Wu, K. Wang, J. Yu, X.-M. Ou and X.-H. Zhang, Chem. Sci., 2022, 13, 3625–3651 RSC
.
- Y. Huang, E.-L. Hsiang, M.-Y. Deng and S.-T. Wu, Light: Sci. Appl., 2020, 9, 105 CrossRef CAS PubMed
.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC
.
- G. Hong, X. Gan, C. Leonhardt, Z. Zhang, J. Seibert, J. M. Busch and S. Bräse, Adv. Mater., 2021, 33, 2005630 CrossRef CAS PubMed
.
- H.-W. Chen, J.-H. Lee, B.-Y. Lin, S. Chen and S.-T. Wu, Light: Sci. Appl., 2017, 7, 17168 CrossRef PubMed
.
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS
.
- K. Goushi, K. Yoshida, K. Sato and C. Adachi, Nat. Photonics, 2012, 6, 253–258 CrossRef CAS
.
- L. J. Rothberg and A. J. Lovinger, J. Mater. Res., 1996, 11, 3174–3187 CrossRef CAS
.
- M. Pope, H. P. Kallmann and P. Magnante, J. Chem. Phys., 1963, 38, 2042–2043 CrossRef CAS
.
- Q. Zhang, B. Li, S. Huang, H. Nomura, H. Tanaka and C. Adachi, Nat. Photonics, 2014, 8, 326–332 CrossRef CAS
.
- H. Noda, H. Nakanotani and C. Adachi, Sci. Adv., 2018, 4, eaao6910 CrossRef PubMed
.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed
.
- J. M. Kaminski, A. Rodríguez-Serrano, F. Dinkelbach, H. Miranda-Salinas, A. P. Monkman and C. M. Marian, Chem. Sci., 2022, 13, 7057–7066 RSC
.
- H. Noda, X.-K. Chen, H. Nakanotani, T. Hosokai, M. Miyajima, N. Notsuka, Y. Kashima, J.-L. Brédas and C. Adachi, Nat. Mater., 2019, 18, 1084–1090 CrossRef CAS PubMed
.
- M. Cai, M. Auffray, D. Zhang, Y. Zhang, R. Nagata, Z. Lin, X. Tang, C.-Y. Chan, Y.-T. Lee, T. Huang, X. Song, Y. Tsuchiya, C. Adachi and L. Duan, Chem. Eng. J., 2021, 420, 127591 CrossRef CAS
.
- Q. Peng, D. Fan, R. Duan, Y. Yi, Y. Niu, D. Wang and Z. Shuai, J. Phys. Chem. C, 2017, 121, 13448–13456 CrossRef CAS
.
- T. Hosokai, H. Matsuzaki, H. Nakanotani, K. Tokumaru, T. Tsutsui, A. Furube, K. Nasu, H. Nomura, M. Yahiro and C. Adachi, Sci. Adv., 2017, 3, e1603282 CrossRef
.
- K. R. Naveen, P. Palanisamy, M. Y. Chae and J. H. Kwon, Chem. Commun., 2023, 59, 3685–3702 RSC
.
- Q. Zhang, H. Kuwabara, W. J. Potscavage, S. Huang, Y. Hatae, T. Shibata and C. Adachi, J. Am. Chem. Soc., 2014, 136, 18070–18081 CrossRef CAS PubMed
.
- Z. Kuang, G. He, H. Song, X. Wang, Z. Hu, H. Sun, Y. Wan, Q. Guo and A. Xia, J. Phys. Chem. C, 2018, 122, 3727–3737 CrossRef CAS
.
- J. A. Treadway, B. Loeb, R. Lopez, P. A. Anderson, F. R. Keene and T. J. Meyer, Inorg. Chem., 1996, 35, 2242–2246 CrossRef CAS PubMed
.
- T. Ogiwara, Y. Wakikawa and T. Ikoma, J. Phys. Chem. A, 2015, 119, 3415–3418 CrossRef CAS PubMed
.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS
.
- Y.-C. Wei, S. F. Wang, Y. Hu, L.-S. Liao, D.-G. Chen, K.-H. Chang, C.-W. Wang, S.-H. Liu, W.-H. Chan, J.-L. Liao, W.-Y. Hung, T.-H. Wang, P.-T. Chen, H.-F. Hsu, Y. Chi and P.-T. Chou, Nat. Photonics, 2020, 14, 570–577 CrossRef CAS
.
- C. E. Whittle, J. A. Weinstein, M. W. George and K. S. Schanze, Inorg. Chem., 2001, 40, 4053–4062 CrossRef CAS PubMed
.
- J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Köhler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417 CrossRef CAS PubMed
.
- J. V. Caspar and T. J. Meyer, J. Phys. Chem., 1983, 87, 952–957 CrossRef CAS
.
- Y. Xiao, H. Wang, Z. Xie, M. Shen, R. Huang, Y. Miao, G. Liu, T. Yu and W. Huang, Chem. Sci., 2022, 13, 8906–8923 RSC
.
- Y. Liu, X. Xiao, Y. Ran, Z. Bin and J. You, Chem. Sci., 2021, 12, 9408–9412 RSC
.
- C. Wang, X. Li, Y. Gao, L. Wang, S. Zhang, L. Zhao, P. Lu, B. Yang, S. Su and Y. Ma, Adv. Opt. Mater., 2017, 5, 1700441 CrossRef
.
- A. Abdurahman, Y. Chen, X. Ai, O. Ablikim, Y. Gao, S. Dong, B. Li, B. Yang, M. Zhang and F. Li, J. Mater. Chem. C, 2018, 6, 11248–11254 RSC
.
- T.-L. Wu, M.-J. Huang, C.-C. Lin, P.-Y. Huang, T.-Y. Chou, R.-W. Chen-Cheng, H.-W. Lin, R.-S. Liu and C.-H. Cheng, Nat. Photonics, 2018, 12, 235–240 CrossRef CAS
.
- H. J. Kim, H. Kang, J. Jeong, S. H. Park, C. W. Koh, C. W. Kim, H. Y. Woo, M. J. Cho, S. Park and D. H. Choi, Adv. Funct. Mater., 2021, 31, 2102588 CrossRef CAS
.
- X. Tang, Q. Bai, T. Shan, J. Li, Y. Gao, F. Liu, H. Liu, Q. Peng, B. Yang, F. Li and P. Lu, Adv. Funct. Mater., 2018, 28, 1705813 CrossRef
.
- S. Sharma and A. K. Pal, J. Mater. Chem. C, 2022, 10, 15681–15707 RSC
.
- G. Chen, J. R. Swartzfager and J. B. Asbury, J. Am. Chem. Soc., 2023, 145, 25495–25504 CrossRef CAS PubMed
.
- Y. Liu, J. Yang, Z. Mao, Y. Wang, J. Zhao, S.-J. Su and Z. Chi, Chem. Sci., 2023, 14, 1551–1556 RSC
.
- Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020 CrossRef CAS
.
- J. Xu, Y. Dai, J. Zhang, Z. Jia, Q. Meng and J. Qiao, Adv. Opt. Mater., 2023, 2300989 Search PubMed
.
- Z. Li, J.-R. Zhang, X.-K. Tian, S. Yang, S. Chen, H. Zhou and X.-G. Yang, Chem. Sci., 2022, 13, 9381–9386 RSC
.
- W. Zhang, H. Song, J. Kong, Z. Kuang, M. Li, Q. Guo, C. Chen and A. Xia, J. Phys. Chem. C, 2019, 123, 19322–19332 CrossRef CAS
.
- H. Miranda-Salinas, A. Rodriguez-Serrano, J. M. Kaminski, F. Dinkelbach, N. Hiromichi, Y. Kusakabe, H. Kaji, C. M. Marian and A. P. Monkman, J. Phys. Chem. C, 2023, 127, 8607–8617 CrossRef CAS PubMed
.
- T. Yang, B. Liang, Z. Cheng, C. Li, G. Lu and Y. Wang, J. Phys. Chem. C, 2019, 123, 18585–18592 CrossRef CAS
.
- J.-L. He, Y. Tang, K. Zhang, Y. Zhao, Y.-C. Lin, C.-K. Hsu, C.-H. Chen, T.-L. Chiu, J.-H. Lee, C.-K. Wang, C.-C. Wu and J. Fan, Mater. Horiz., 2022, 9, 772–779 RSC
.
- D. Karthik, Y. H. Jung, H. Lee, S. Hwang, B. Seo, J. Kim, C. W. Han and J. H. Kwon, Adv. Mater., 2021, 33, 2007724 CrossRef CAS PubMed
.
- D. H. Ahn, S. W. Kim, H. Lee, I. J. Ko, D. Karthik, J. Y. Lee and J. H. Kwon, Nat. Photonics, 2019, 13, 540–546 CrossRef CAS
.
- P. J. B. Clarricoats, Proc. IEE-Part C Monogr., 1962, 109, 401 CrossRef
.
- Z. Tang, C. Chang, F. Bao, L. Tian, H. Liu, M. Wang, C. Zhu and J. Xu, Polymers, 2021, 13, 284 CrossRef CAS PubMed
.
- X. Niu, P. Gautam, Z. Kuang, C. P. Yu, Y. Guo, H. Song, Q. Guo, J. M. W. Chan and A. Xia, Phys. Chem. Chem. Phys., 2019, 21, 17323–17331 RSC
.
- W. Zhang, J. Kong, D. Hu, M. Tao, X. Niu, S. Vdović, D. Aumiler, Y. Ma and A. Xia, J. Phys. Chem. C, 2020, 124, 5574–5582 CrossRef CAS
.
- M. K. Etherington, J. Gibson, H. F. Higginbotham, T. J. Penfold and A. P. Monkman, Nat. Commun., 2016, 7, 13680 CrossRef CAS PubMed
.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS PubMed
.
- Y. Wang, Z. Guo, Y. Gao, Y. Tian, Y. Deng, X. Ma and W. Yang, J. Phys. Chem. Lett., 2022, 13, 6664–6673 CrossRef CAS PubMed
.
- Y. Wang, Y. Tian, Y. Gao, Z. Guo, Z. Xue, Y. Han, W. Yang and X. Ma, J. Phys. Chem. Lett., 2023, 14, 9665–9676 CrossRef CAS PubMed
.
- H. Sun, C. Zhong and J.-L. Brédas, J. Chem. Theory Comput., 2015, 11, 3851–3858 CrossRef CAS PubMed
.
- X. Zhao and J. Zhao, Chem. Commun., 2022, 58, 7666–7669 RSC
.
- H. Noda, H. Nakanotani and C. Adachi, Chem. Lett., 2019, 48, 126–129 CrossRef CAS
.
- Q. Ou, Y. Shao and Z. Shuai, J. Am. Chem. Soc., 2021, 143, 17786–17792 CrossRef CAS
.
- N. Aizawa, Y. Harabuchi, S. Maeda and Y.-J. Pu, Nat. Commun., 2020, 11, 3909 CrossRef CAS PubMed
.
- Y. Olivier, B. Yurash, L. Muccioli, G. D'Avino, O. Mikhnenko, J. C. Sancho-García, C. Adachi, T.-Q. Nguyen and D. Beljonne, Phys. Rev. Mater., 2017, 1, 075602 CrossRef
.
- S. Lin, Z. Pei, B. Zhang, H. Ma and W. Liang, J. Phys. Chem. A, 2022, 126, 239–248 CrossRef CAS PubMed
.
- J. Tatchen, N. Gilka and C. M. Marian, Phys. Chem. Chem. Phys., 2007, 9, 5209 RSC
.
- B. R. Henry and W. Siebrand, J. Chem. Phys., 1971, 54, 1072–1085 CrossRef CAS
.
- K. A. Zachariasse, M. Grobys, I. Riickert and W. Kiihnle, J. Photochem. Photobiol., A, 1997, 105, 373–383 CrossRef CAS
.
- M. C. Drummer, R. B. Weerasooriya, N. Gupta, B. T. Phelan, A. J. S. Valentine, A. A. Cordones, X. Li, L. X. Chen and K. D. Glusac, J. Phys. Chem. C, 2022, 126, 1946–1957 CrossRef CAS
.
- T. Bolze, J. Wree, F. Kanal, D. Schleier and P. Nuernberger, ChemPhysChem, 2018, 19, 138–147 CrossRef CAS PubMed
.
- H. Song, H. Zhao, Y. Guo, A. M. Philip, Q. Guo, M. Hariharan and A. Xia, J. Phys. Chem. C, 2020, 124, 237–245 CrossRef CAS
.
- J. Köhler, T. Quast, J. Buback, I. Fischer, T. Brixner, P. Nuernberger, B. Geiß, J. Mager and C. Lambert, Phys. Chem. Chem. Phys., 2012, 14, 11081 RSC
.
- Y. Rout, C. Montanari, E. Pasciucco, R. Misra and B. Carlotti, J. Am. Chem. Soc., 2021, 143, 9933–9943 CrossRef CAS PubMed
.
- Z. Zhang, Y.-S. Wu, K.-C. Tang, C.-L. Chen, J.-W. Ho, J. Su, H. Tian and P.-T. Chou, J. Am. Chem. Soc., 2015, 137, 8509–8520 CrossRef CAS PubMed
.
- Y. Chen, K.-H. Chang, F.-Y. Meng, S.-M. Tseng and P.-T. Chou, Angew. Chem., Int. Ed., 2021, 60, 7205–7212 CrossRef CAS PubMed
.
- Z. Ma, Z. Yang, L. Mu, L. Deng, L. Chen, B. Wang, X. Qiao, D. Hu, B. Yang, D. Ma, J. Peng and Y. Ma, Chem. Sci., 2021, 12, 14808–14814 RSC
.
- Y. Wen, S. Xiao, H. Liu, X. Tian, J. De, T. Lu, Z. Yang, D. Zou, Y. Lv, S.-T. Zhang, Q. Su and B. Yang, J. Mater. Chem. C, 2021, 9, 17511–17517 RSC
.
- V. Karunakaran and S. Das, J. Phys. Chem. B, 2016, 120, 7016–7023 CrossRef CAS
.
- Y. Gao, Y. Wang, Z. Guo, Y. Wan, C. Li, B. Yang, W. Yang and X. Ma, J. Phys. Chem. B, 2022, 126, 2729–2739 CrossRef CAS
.
- C.-W. Ju, B. Li, L. Li, W. Yan, C. Cui, X. Ma and D. Zhao, J. Am. Chem. Soc., 2021, 143, 5903–5916 CrossRef CAS PubMed
.
- H. Gao, S. Shen, Y. Qin, G. Liu, T. Gao, X. Dong, Z. Pang, X. Xie, P. Wang and Y. Wang, J. Phys. Chem. Lett., 2022, 7561–7567 CrossRef CAS PubMed
.
- J. Bahrenburg, F. Renth, F. Temps, F. Plamper and W. Richtering, Phys. Chem. Chem. Phys., 2014, 16, 11549 RSC
.
- H.-M. Pan, C.-C. Wu, C.-Y. Lin, C.-S. Hsu, Y.-C. Tsai, P. Chowdhury, C.-H. Wang, K.-H. Chang, C.-H. Yang, M.-H. Liu, Y.-C. Chen, S.-P. Su, Y.-J. Lee, H. K. Chiang, Y.-H. Chan and P.-T. Chou, J. Am. Chem. Soc., 2023, 145, 516–526 CrossRef CAS PubMed
.
- Y.-C. Wei, B.-H. Chen, R.-S. Ye, H.-W. Huang, J.-X. Su, C.-Y. Lin, J. Hodgkiss, L.-Y. Hsu, Y. Chi, K. Chen, C.-H. Lu, S.-D. Yang and P.-T. Chou, Angew. Chem., Int. Ed., 2023, 62, e202300815 CrossRef CAS PubMed
.
- C. Fanggao, G. A. Saunders, E. F. Lambson, R. N. Hampton, G. Carini, G. Di Marco and M. Lanza, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 425–433 CrossRef CAS
.
- M. Hénot, A. Chennevière, E. Drockenmuller, K. Shull, L. Léger and F. Restagno, Eur. Phys. J. E, 2017, 40, 11 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00460d |
| This journal is © The Royal Society of Chemistry 2024 |