Open Access Article
Open Access ArticleUnravelling the role of spin–vibrational coupling in designing high-performance pentagonal bipyramidal Dy(III) single ion magnets†‡
Sourav
Dey§
 ,
Tanu
Sharma§
,
Tanu
Sharma§
 and
Gopalan
Rajaraman
and
Gopalan
Rajaraman
 *
*
Department of Chemistry, Indian Institute of Technology Bombay, Powai 400076, Mumbai, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 22nd March 2024
Abstract
At the cutting edge of high-performance single-molecule magnets (SMMs) lie lanthanide-based complexes, renowned for their potent magnetic anisotropy. SMMs containing one metal centre are defined as single-ion magnets (SIMs). The performance of SMMs is measured generally via the barrier height for magnetisation reversal (Ueff) and blocking temperature (TB), below which the magnetisation is fully frozen. To enhance the Ueff and TB values in lanthanide-based SMMs, the static crystal field splitting of mJ levels has been effectively adjusted through ligand design, leveraging the oblate/prolate ground state 4f electron density shape. However, the maximum fine-tuning achievable through ligand design, known as the axial limit, has already been reached in this class of compounds. This necessitates new design principles to enhance SMM characteristics to better suit end-user applications. Among other avenues that can be explored to improve SMM characteristics, a deeper understanding of spin–phonon coupling is critical to advancing TB values. However, there are only a handful of examples where this has been deciphered. In this work, using a combination of DFT and ab initio CASSCF calculations, we have performed spin–phonon calculations on five classes of pentagonal bipyramidal Dy(III) SIMs exhibiting TB values in the range of 4.5 K to 36 K ([Dy(bbpen)Br] (1, H2bbpen = N,N′-bis(2-hydroxybenzyl)-N,N′-bis(2-methylpyridyl)ethylenediamine), [Dy(OCMe3)Br(THF)5][BPh4] (2) [Dy(OSiMe3)Br(THF)5] [BPh4] (3), [Dy(LN5)(Ph3SiO)2](BPh4)·CH2Cl2 (4) and [L2Dy(H2O)5][I]3·L2·H2O (5, L = tBuPO(NHiPr)2)). Unlike the method employed elsewhere for the calculation of spin–phonon coupling, in this work, we have employed a set of criteria and intuitively selected vibrational modes to perform the spin–phonon coupling analysis. The approach provided here not only reduces the computational cost significantly but also suggests chemical intuition to improve the performance of this class of compounds. Our calculations reveal that low-energy vibrational modes govern the magnetisation relaxation in these SIMs. A flexible first coordination sphere found on some of the complexes was found to be responsible for low-energy vibrations that flip the magnetisation, reducing the TB values drastically (complexes 2 and 3). On the other hand, a rigid first coordination sphere and a stiff ligand framework move the spin–vibrational coupling that causes the relaxation to lie beyond the secondary coordination sphere, resulting in an increase in TB values. Our calculations also reveal that not only the atoms in the first coordination sphere but also those in the secondary coordination sphere affect the performance of the SMMs. Learning from this exercise, we have undertaken several in silico models based on these vibrations to improve the TB values. Some of these predictions were correlated with literature precedents, offering confidence in the methodology employed. To this end, our comprehensive investigation, involving twenty-three molecules/models and five sets of geometries for pentagonal bipyramidal Dy(III) single-ion magnets (SIMs), unveils a treasure trove of chemically sound design clues, poised to enhance the TB values in this fascinating molecular realm.
1. Introduction
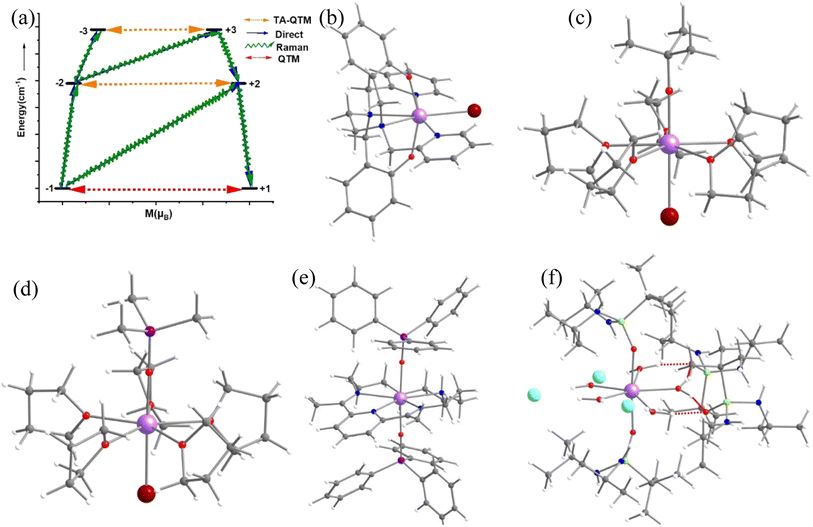
Single-molecule magnets (SMMs) are nanoscale molecule-based magnets exhibiting permanent magnetisation similar to bulk magnets, opening up the bottom-up approach to molecule-based devices such as the new generation of information storage devices, solid-state Q-bits for quantum computing and spintronics devices. However, to employ these molecules in end-user applications, magnetic relaxation time (τ), the timescale in which an SMM preserves its magnetisation, and blocking temperature (TB) below which the magnetisation is fully frozen need to be improved.1–9 Furthermore, the molecule should be stable under ambient conditions for the fabrication process to realise the potential applications proposed. While early SMMs based on transition metal clusters yielded TB values in the range of liquid helium temperatures, the advent of lanthanide-based SMMs significantly improved TB values.10–12 The first mononuclear lanthanide-based SMM, [TbPc2]− (Pc = phthalocyanine), was discovered in 2003 and is reported to have a TB value of 1.7 K and Ueff of 230 cm−1.13 Thereafter, many lanthanide-based SMMs have been reported until 2015, but the TB value did not reach beyond 5–8 K despite having a very large Ueff value.13–34 The breakthrough in lanthanide-based SIMs was achieved in 2016 when a pentagonal bipyramidal [L2Dy(H2O)5][I]3·L2·H2O (L = tBuPO(NHiPr)2) molecule was reported with a TB value of 12 K (based on zero-field cooled/field cooled (ZFC/FC)) by some of us,35 and at the same time several pentagonal bipyramidal family molecules were also reported by others with slightly larger TB values.35–38 We have further demonstrated the role of weak equatorial and strong axial ligand fields in designing high-performance SIMs with very large Ueff and TB values. This is followed by several pseudo pentagonal bipyramidal complexes in the literature where Ueff and TB values reached as high as 1800 K and 36 K, respectively.36,37,39–45 Later years witnessed a tremendous increase in TB values by a class of SIMs commonly called dysprosocenium class of molecules having TB values as high as 80 K – although this class of molecules lacks ambient stability posing further challenges in taking these molecules to end-user applications.46,47The magnetisation relaxation of a SIM occurs via quantum tunnelling of magnetisation (QTM) at very low temperatures due to the low-symmetry component of the crystal field (CF).12 At higher temperatures, it occurs through various spin–vibrational couplings such as direct, Raman and Orbach pathways.12 The direct process is a barrier-less process which involves a direct transition from the “up” to the “down” spin state, where the crystal lattice absorbs the energy released by the spin system.12 The Orbach process is a multiple one-phonon phenomenon where magnetisation relaxation occurs by a sequential absorption of phonons involving excited mJ states and then sequential emission of phonons to reach the ground state by reversing its magnetisation.1–5,48–50 This Orbach relaxation becomes very slow at low temperatures due to the lack of thermally available phonons to initiate this process.1,2,4,5,51 The Raman process is similar to the Orbach process, but it involves a virtual intermediate state of lattice and spin system which destroys the blocking barrier of magnetisation reversal (see Fig. 1a for the general description described here).
The three key features that are commonly employed to block the magnetisation relaxation of an SMM are (i) a large mJ ground state (mJ = ±J), (ii) designing a ligand environment around the metal centre to maintain a large separation between successive mJ levels of the bistable ground state and (iii) minimal admixing between the mJ states.1–4,52 It is worthwhile to mention that the search for potential SIMs fulfilling the criteria (i), (ii), and (iii) is considered within the framework of the Orbach process. In this regard, the recent discovery of dysprosocenium SIMs has divulged the importance of spin–vibration coupling in controlling magnetisation relaxation.5,46,47,53–58 Although synthetic chemists have extensively tried to control spin–vibration coupling through molecular design, design principles to control such effects are still elusive.47 Therefore, to design high-performance SIMs, one needs to deepen the understanding of spin–vibrational coupling by theoretical methods.
A recent theoretical study also demonstrated that further enhancement of TB and Ueff is challenging in dysprosium complexes as magnetic anisotropy reaches its axial limit.5 In this regard, the pentagonal bipyramidal family of SIMs has an edge due to a large variation in the Ueff (37–1200 cm−1) and TB (2–30 K) values observed, offering significant room for further improvement in TB values.10,11,35,36,38–40,42,59–71 It is noteworthy to mention that raising the TB value from 60 K to 80 K in dysprosocenium complexes is related to the judicial design of ligands to efficiently decouple the vibrationally active normal mode coupled to the spin states.46 To fine-tune the magnetic anisotropy in pentagonal bipyramidal Dy(III) SIMs, one needs a thorough understanding of the related spin–phonon coupling. Spin–vibration coupling occurs when a molecular vibration (due to the temperature) modulates the crystal field Hamiltonian of a metal centre. This coupling is directly related to spin–lattice relaxation, and over the past few years, an in-depth investigation of spin–vibration coupling by ab initio CASSCF methods has been reported. However, such studies are limited only to a handful of molecules as these calculations are computationally demanding, and alternative methods that are still accurate in understanding the spin–phonon/vibrational problem are of supreme interest to the community.1–5,38,46,71,72 Although efforts have been made to employ semiempirical methods, they lack the predictive potential for such systems.8,9,72
In this work, employing a combination of DFT and the ab initio SA-CASSCF/RASSI-SO/SINGLE_ANISO approach, we have studied in detail the pentagonal bipyramidal family of molecules to thoroughly understand their electronic structure and spin–vibrational correlations to the blocking temperatures. The approach established in this work leverages the Boltzmann distribution and oscillator strength of vibrational modes, eliminating the necessity for conducting numerous CASSCF calculations to extract pertinent chemical insights. For our study, we have chosen five pseudo pentagonal bipyramidal Dy(III) SIMs, namely [Dy(bbpen)Br] (1, H2bbpen = N,N′-bis(2-hydroxybenzyl)-N,N′-bis(2-methylpyridyl)ethylenediamine),38 [Dy(OCMe3)Br(THF)5][BPh4] (2)43 and [Dy(OSiMe3)Br(THF)5][BPh4] (3),43, [Dy(LN5)(Ph3SiO)2](BPh4)·CH2Cl2 (4)73 and [L2Dy(H2O)5][I]3·L2·H2O (5, L = tBuPO(NHiPr)2)35 where the Ueff and TB (from FC/ZFC) range from 400–1200 cm−1 and 9–16 K, respectively (see Fig. 1b–f and Table S1‡). For the dysprosocenium class of molecules, TB values are approximately similar, but a pentagonal bipyramidal family of complexes has more diverse Ueff and TB values (see Table S1‡), suggesting room for further enhancement. Here, by performing the spin–vibration calculations, we aim to address the following: (i) Why do the pentagonal bipyramidal Dy(III) SIMs, despite possessing similar structures and Ueff values, have a diverse set of TB values (4.5 K – 36 K, see Table S1‡)? (ii) What is the nature of vibrationally active normal mode causing the transition from the ground KD (Kramers Doublet) to the first excited KD in this class of compounds? (iii) How are these spin–phonon vibrations correlated with the TB values? (iv) Is it possible to quench vibrations that cause relaxation via judicial choice of ligand design? (v) What are the design clues that need to be factored in to enhance the TB values in this class of molecule?
1.1 Computational procedures for spin–phonon relaxation
The vibrational modes of a complex were determined from the geometry optimisation in the gas phase within the DFT framework (see computational details). Frequency calculations were utilised to confirm that the optimised geometries are true minima on the potential energy surface.46,53In the absence of a magnetic field, the effective Hamiltonian can be written as;74
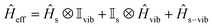 | (1) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) s,
s, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) vib and
vib and ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) s−vib represent the crystal field (spin-system), vibration and spin–vibrational Hamiltonian.
s−vib represent the crystal field (spin-system), vibration and spin–vibrational Hamiltonian.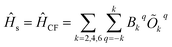 | (2) |
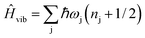 | (3) |
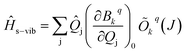 | (4) |
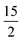 and MJ runs over
and MJ runs over 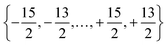 ). The ωj and nj correspond to the frequency of the vibrational level of mode j. The
). The ωj and nj correspond to the frequency of the vibrational level of mode j. The ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) j and
j and 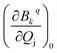 represent the vibrational coordinate and vibronic coupling of mode j.
represent the vibrational coordinate and vibronic coupling of mode j.
The ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) s and
s and ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) vib in eqn (1) are defined on the basis of |MJ, nj〉 using the Kronecker product. Therefore, to define
vib in eqn (1) are defined on the basis of |MJ, nj〉 using the Kronecker product. Therefore, to define ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) s−vib on the same basis, we considered a weak coupling regime where vibrations remain unaffected by electronic levels. As a result, the
s−vib on the same basis, we considered a weak coupling regime where vibrations remain unaffected by electronic levels. As a result, the ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) s−vib can be written as,
s−vib can be written as,
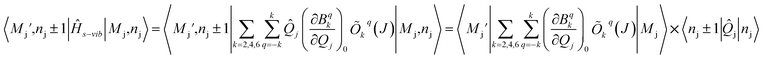 | (5) |
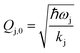 where ωj and kj denote the frequency and force constant of vibrational mode j). The equilibrium geometry was then distorted within the range of −Qj,0 → +Qj,0 along the displacement vectors
where ωj and kj denote the frequency and force constant of vibrational mode j). The equilibrium geometry was then distorted within the range of −Qj,0 → +Qj,0 along the displacement vectors 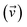 for each mode using:
for each mode using: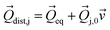 | (6) |
Then we performed CASSCF/RASSI-SO/SINGLE_ANISO calculations for each distorted geometry 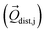 and extracted the crystal field parameters (CFPs) in Stevens notation. The extracted CFPs were then fitted using second-order polynomials to obtain the first-order vibrionic couplings
and extracted the crystal field parameters (CFPs) in Stevens notation. The extracted CFPs were then fitted using second-order polynomials to obtain the first-order vibrionic couplings 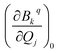 . The overall vibronic coupling strength (Sj) of a given mode is extracted by adding the effect of 27 CFPs as follows:
. The overall vibronic coupling strength (Sj) of a given mode is extracted by adding the effect of 27 CFPs as follows:
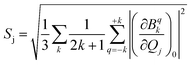 | (7) |
All the energies of the vibrational modes are calculated using the ((1 + 1/2)ℏω) formula, after scaling the frequencies considering the employed computational setup.75 The methodology developed in this study relies on the Boltzmann distribution and oscillator strength of vibrational modes. It involves the inclusion of all vibrational modes until the sum of Boltzmann populations reaches 1 at 100 K. Among these modes, only those with significant oscillator strength were considered. This approach eliminates the need to perform hundreds of CASSCF calculations, streamlining the process of extracting the relevant chemical insights. For complexes 2–5, we have only calculated the coupling strength Sj for the vibrational modes having large oscillator strength that has reduced the computational cost significantly.
2. Results and discussion
2.1 Controlling Ueff and TB in complex 1 by intuitive chemical substitution using spin–phonon lens
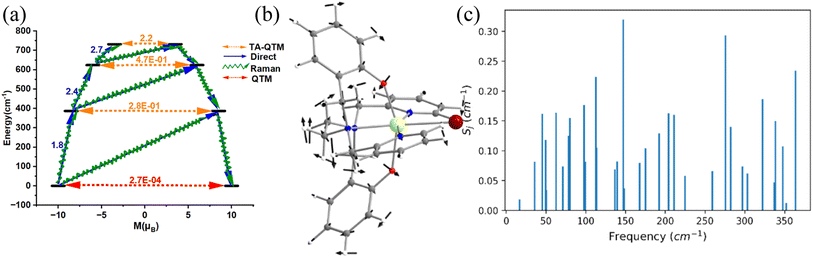
Complex 1 (see Fig. 1a) is reported to exhibit zero-field slow relaxation of magnetisation with a Ueff and TB value of 712 cm−1 and 14 K (sweep rate 20 Oe s−1), respectively.38 Earlier ab initio CASSCF calculations on this complex revealed magnetisation relaxation via the third excited KD, yielding a Ucal value of 721 cm−1 (Fig. 2a), which agrees well with the Ueff value. To assess and analyse the role of dynamic correlation, we have also performed CASPT2 calculations (see computational details) for this complex. This yields a Ucal value of 701.2 cm−1, which is similar to the CASSCF results. Also, all other metrics related to the magnetic properties are similar for both sets, offering confidence in this methodology (see Table S3‡). The geometry optimisation of 1 yields a geometry closely resembling the X-ray structure (Table S2, Fig. S1 and Appendix S1‡). This is also reflected in the ab initio CASSCF calculations, where both X-ray and optimised geometries yield a similar energy spectrum, g-tensors and CF parameters (Tables S3 and S4‡), supporting the methodology used in obtaining good geometries for estimating magnetic properties.For the spin–phonon coupling calculations, we have selected 35 vibrational modes that possess a total population of 1.00 below 100 K (most of the SMMs show opening of hysteresis below 100 K) assuming Boltzmann distribution (see Fig. 2b, S2–S13 and Table S5‡). The coupling strengths Sj of the 35 vibrational modes of 1 are depicted in Fig. 2c (Table S5 and Fig. S14‡), which implies that the ω16 and ω26 (Fig. 2c) vibrational modes are associated with a large coupling strength and, therefore, should cause the magnetisation relaxation. Further analysis suggests that these modes are associated with a large oscillator strength, as this leads to a larger degree of deformation of the first and second coordination spheres as witnessed in earlier cases.46,53,57,74,76 Therefore, we have only considered the vibrational modes with large oscillator strength for complexes 2–5 to reduce the computational cost of spin–phonon coupling. The first excited state of ω26 vibrational mode (ΔE = 387 cm−1 (KD1–KD2) vs. υ = 397 cm−1 ((1 + 1/2)ℏω); the ΔE and υ refer to the Kramers doublet gap and the scaled vibrational frequencies, respectively) is also closer to the KD1–KD2 energy gap which further reinforces that this mode should cause the magnetisation relaxation. The ω26 vibrational mode of 1, which is suggestive of being responsible for magnetisation relaxation, has several functional group movements (Fig. 2). The significant vibrational movement was noted for (i) the hydrogen atom at the meta position of the pyridine rings, (ii) the para position of the phenolate rings, and (iii) the –CH2 linker groups attached to pyridine and phenolate donor atoms (Fig. 2). As these were the key vibrations correlated with magnetisation relaxation, any attempt to quench these vibrations is expected to enhance the effective energy barrier/TB values. The substitution of these hydrogens will make the vibrational mode off-resonant and is, therefore, expected to improve the performance.
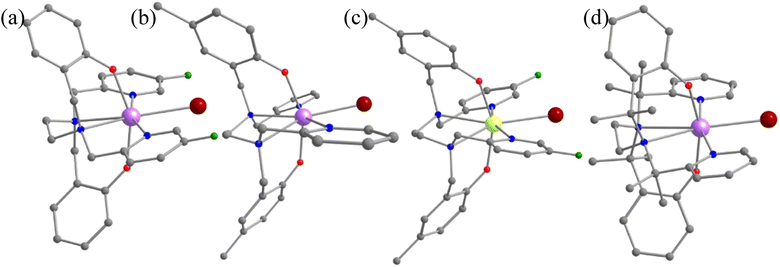
A quick Cambridge structural database search for such substituted geometries reveals substitution of the meta position hydrogen atom by fluorides reported by Li and co-workers [(Dy(bbpen-F)Br], see Fig. 3).39 We then performed ab initio calculations on the optimised geometry (called 1-F, Appendix S2‡) that yields a Ucal value of 763.2 cm−1, which is ca. 50 cm−1 higher, suggesting enhancement in the effective energy barrier via this substitution as expected (Table S6‡). This value matches the experimentally reported Ueff value of 798.4 cm−1. More importantly, as expected, the pyridinic contribution to the ω26 vibrational mode diminished (Table S7‡), and these are accompanied by a substantial enhancement in the TB values (14 K@20 Oe s−1 to 30 K@20 Oe s−1). This is also corroborated by the decrease in the equatorial ligand field due to the negative inductive (−I) effect of the fluoride atom in the equatorial pyridine ring. A similar CCDC search also yielded another structure where the para position of the phenolate hydrogen was substituted by CH3 groups ([Dy(bbpen-CH3)Br], 1-pCH3, see Fig. 3). The ab initio calculations on the optimised geometry of 1-pCH3 (Appendix S3‡) yield a Ucal value of 764.1 cm−1 (Table S8‡), reaffirming a larger value compared to 1 due to an increase in the axial ligand field. Not only does this value match the experimentally reported value of 806.9 cm−1, but the TB values are also marginally larger (15 K@20 Oe s−1). Furthermore, as expected, the phenolate contribution to the ω26 frequencies diminished, leading to a red shift (Table S7‡) of these frequencies in 1-pCH3. Furthermore, an enhancement of the computed B02 axial CF parameter is observed in 1-F and 1-pCH3 compared to 1 (Table S3‡).
A further search yielded another structure where the para position of the phenolate hydrogen was substituted by CH3 groups and para position hydrogen atoms by fluorides ([Dy(bmbpen-F)Br], 1-pCH3F, see Fig. 3).77 The ab initio calculations on the optimised geometry of 1-pCH3F (Appendix S4‡) yielded a Ucal value of 842.5 cm−1, reaffirming a larger value compared to 1, 1-F and 1-pCH3 (Table S9‡). Although the Ucal value is slightly overestimated compared to the Ueff value of 782.3 cm−1, more importantly, the TB value (36 K@20 Oe s−1) is significantly higher than that of all 1, 1-F and 1-pCH3. As expected, the phenolate and pyridine contributions to the ω26 frequencies diminished, leading to a red shift (Table S7‡) of these frequencies in 1-pCH3F. This reiterates that the approach developed here not only hints at ligand design that targets enhancement in Ueff values but also the vibrations that are strongly correlated with the TB values.
Furthermore, the –CH2 linker groups attached to pyridine and phenolate donors were found to have a significant vibrational movement. We attempted to alter those C–H bonds and modelled the corresponding –CH2 groups using –C(Me)2 groups (see Fig. 3 model 1-CH3). For this model, the O–Dy–O angle increases to 162.9° and the Dy–N bond length elongates to 2.948 Å (Table S2, Fig. 3 and Appendix S4‡). The ab initio CASSCF calculations on 1-CH3 reveal an increase in the KD1–KD2 energy gap, energy splitting of the eight KDs and axial B02 CF parameter compared to 1 by 0.14, 0.50 and 0.06%, respectively (Tables S4 and S10‡). The magnetisation relaxation in 1-CH3 was found to occur via the third excited KD, resulting in a Ucal value of 1039.5 cm−1, which is ca. 300 cm−1 larger than that of 1. Quite interestingly, a red shift of vibrational mode is observed from 1 to 1-CH3 (192.8 cm−1 (Table S7‡)). The blocking barrier and normal models of 1, 1-F, 1-pCH3, 1-pCH3F and 1-CH3 imply that there is a strong correlation between the ω26 normal mode and the TB values.
2.2 Role of the equatorial ligand field in dictating Ueff and TB in complexes 2 and 3
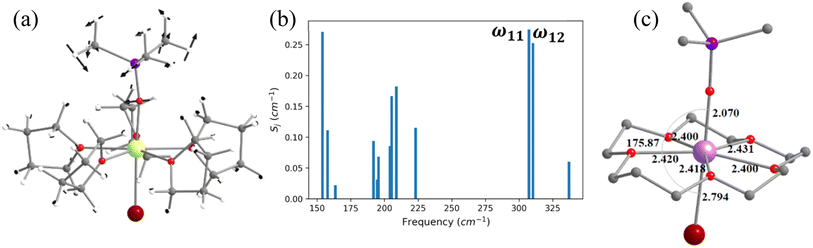
The magnetic properties of complexes 2 and 3 (Fig. 4 and 5) were studied by Zheng and co-workers, along with a family of other pentagonal bipyramidal SMMs. Both of them show zero-field slow relaxation of magnetisation with Ueff values of 569 ± 126 (2) and 509 ± 49 cm−1 (3), respectively, with a TH (blocking temperature derived from the hysteresis loop, see for example ref. 43) value of 9 K (sweep rate 15 Oe s−1).43 These two complexes are structurally similar, except that the –OCMe3 group present in 2 is replaced by the –OSiMe3 group in 3 (Fig. 4 and 5).43 This replacement leads to a 0.07 Å enhancement in the Dy–OSiMe3 bond length in 3 compared to Dy–OCMe3 bond length in 2, resulting in a lower Ueff in 3 compared to 2 (Tables S11–S14‡). The geometry optimisation of 2 and 3 also yields geometries and magnetic properties similar to those of X-ray structures (Table S11, Fig. S16, and Appendix S5 and S6‡), and particularly the estimated CF parameters are strikingly similar (see Table S15‡). The ab initio CASSCF (CASPT2) calculations performed on these complexes yield a Ucal value of 492.9 cm−1 (488.8 cm−1) and 570.2 cm−1 (553.8 cm−1) for 2 and 3, respectively. These values are in agreement with experiments and further iterate that dynamic correlations incorporated via the CASPT2 method have not substantially modified the metric of magnetic properties estimated, and therefore, it is safe to proceed further with the CASSCF calculations (see Tables S13 and S14‡).To find out the most important vibrational modes for spin–phonon coupling, we have selected 21 vibrational modes (Fig. 4, S17–S23 and Table S16‡) for 2 and 13 vibrational modes with the energy for 3 (Fig. 5, S25–S29, Tables S16 and S17‡). By analysing the coupling strength, we found that ω7 and ω8 vibrational modes for 2 and ω1, ω11 and ω12 vibrational modes for 3 are responsible for the spin–phonon coupling from the KD1 to the KD2 transition (Fig. 4, 5, S23, S30 and Tables S16 and S17‡). The second excited state of ω7 vibrational mode of 2 and ω1 vibrational mode of 3 (ΔE = 361 cm−1vs. υ = 390 cm−1) for 2 and 360 cm−1 (ΔE) vs. 370 cm−1 (υ) for 3 is also closer to the KD1–KD2 energy gap, which further reinforces that these modes should cause magnetisation relaxation. These vibrational modes have a significant impact on many functional groups. Among these vibrations, the displacement of the Dy ion was found to be prominent (Fig. 4 and 5). As these vibrations are responsible for magnetisation relaxation, any attempt to quench these vibrations will increase the Ueff/TB values. Therefore, to quench the in-plane movement of the Dy atom, there are two approaches: (i) substituting the Dy with a heavier isotopic analogue78–80 and (ii) enhancing the Dy–ligand equatorial bond strength. To achieve this, we have replaced the five THF molecules in the equatorial plane in complexes 2 and 3 with a 16-crown-5 macrocyclic ring (models 2-crown and 3-crown, see Fig. 3(d) and 4(d)). Although these are models at present, some of us have recently reported [{(18-crown-6)Ln(dippH)3}{(18-crown-6)Ln(dippH)2(dippH2)}]·[I3] (with Ln = Ce, Pr and Nd and dippH2 = 2,6-diisopropylphenylphosphates) complexes of a similar kind with various lanthanide ions exhibiting attractive SIM characteristics.81–83 The 2-crown and 3-crown have shorter Dy–O bond lengths (reduced by ∼0.02–0.04 Å, except Dy–Br bond length) and a marginal 1–2° increase in the O–Dy–Br angle compared to 2 and 3 (Fig. 4c, 5(c), Tables S11 and S12, and Appendix S7 and S8‡).
The ab initio calculations reveal enhancement of the KD1–KD2 energy gap, the energy splitting of the eight KDs, as well as axial B02 CF parameters in 2-crown (3-crown) compared to 2 (3) (Tables S15, S18 and S19‡). The magnetisation relaxation of 2-crown (3-crown) is expected to take place via the 3rd excited KD due to the large thermally assisted quantum tunnelling of magnetisation (TA-QTM)value, yielding a Ucal value of 832.8 cm−1 (869.1) cm−1, ca. 300 (350) cm−1 larger than that of 2 (3). It is worthwhile to mention that the contribution of the in-plane movement of the Dy atom to the ω7 (ω1 for 3-crown) frequencies diminished, leading to a red shift (Table S20‡) of these frequencies, and this is expected to enhance the TB values.
2.3 Role of N–H vibrations in fine-tuning the Ueff and TB values in complex 4
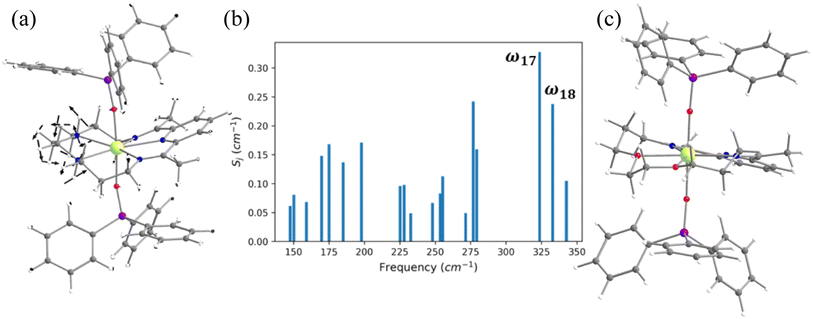
In the earlier section, we have shown how a crown-ether ligand in the equatorial position quenches the low-energy vibrational modes that are correlated with the magnetisation relaxation. These two models are predictions, but an analogous complex containing a macrocyclic Schiff-based ligand at the equatorial position has been reported earlier by Murrie and our group [Dy(LN5)(Ph3SiO)2](BPh4)·CH2Cl2 (4, Fig. 6).73 However, due to the complexity of the functional groups involved in the equatorial position, similar vibrations in 4 were absent. We have carefully analysed various vibrational modes at the equatorial plane, which could help improve the performance of 4. Complex 4 exhibits zero-field slow relaxation of magnetisation with a very large Ueff of 791.4 cm−1 and TB of 14 K (sweep rate 100 Oe s−1). The ab initio calculations on this complex yield a Ucal value that is in excellent agreement with the Ueff value reported (791.4 vs. 722.8 cm−1). On the other hand, the O–Dy–O angle reduces to 2.5° in the optimised structure compared to the X-ray geometry (Tables S21, S22 and Fig. S31‡), and the optimised geometry yields magnetic characteristics and CF parameters, which are similar to those of the X-ray structure (see Tables S22 and S23‡).For the spin–phonon coupling calculations of 4, we selected nineteen vibrational modes (Fig. S32–S38 and Table S24‡) with a large oscillator strength in the range of KD1–KD2 energy gap. By analysing the coupling strength (Fig. 6, S39 and Table S24‡), we found that the ω17 and ω18 vibrational modes are likely to be responsible for the spin–phonon coupling of the KD1 → KD2 transition. These vibrations are found to be correlated with the N–H vibrations present in the equatorial plane (Fig. 6). To quench these vibrations, we have replaced the –NH group with its isoelectronic analogue oxygens resulting in 4-N3O2 (Fig. 6 and Appendix S10‡). As expected, a red shift of the ω17 vibrational mode (327.1 (4) cm−1 → 377.2 cm−1 (4-N3O2) cm−1, Table S26‡) is observed in 4-N3O2. The ab initio calculations on 4-N3O2 revealed an enhancement in the energy splitting of the eight KDs compared to 4 (Table S25‡). The magnetisation relaxation of 4-N3O2 occurs via the third excited KD due to significant transverse anisotropy yielding a Ucal value of 998.7 cm−1 (Table S25‡), which is ca. 200 cm−1 larger than that of 4.
2.4 Role of out-of-plane bending of water in controlling the Ueff and TB values in complex 5
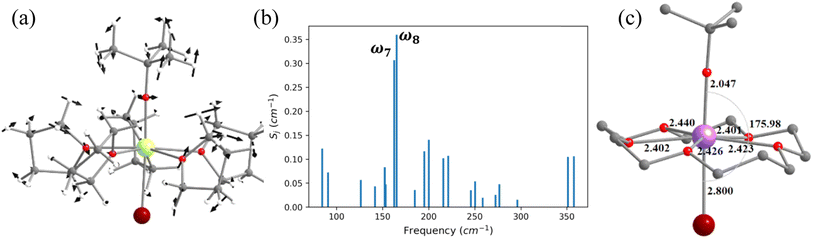
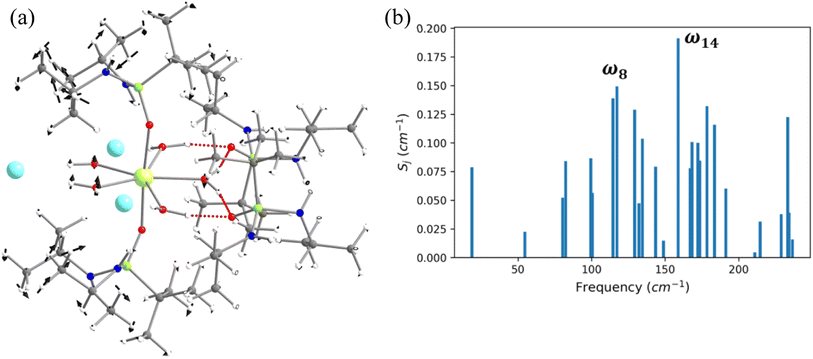
In this last section, we will unveil the nature of vibration correlated with the magnetisation relaxation in the [L2Dy(H2O)5]3+ family of SMMs where a large Ueff and TB were observed (Fig. 7).35,36,60,61,67,84 The complex 5 is reported to possess a large Ueff value and TB value of 453 cm−1 and 16 K (sweep rate 20 Oe s−1), respectively.35 The ab initio CASSCF calculations on the X-ray structure of 5 indicated that the stabilisation of mJ = |±15/2〉 and |±13/2〉 in the ground and first excited state, respectively. The magnetisation relaxation occurs via the second excited KD, yielding a Ucal value of 471.3 cm−1, slightly overestimated compared to the Ueff value (Table S27‡). The ab initio calculations on this optimised structure reveal a moderate change in energy values and g tensors compared to the X-ray geometry as the equatorial oxygens become out-of-plane in the optimised structure (Table S28, Fig. S40 and Appendix S11‡). However, the computed CF parameters in the optimised structure are similar (Table S29‡) to those in the X-ray structure, and more importantly, the ground and first excited KDs possess dominant contributions from mJ = |±15/2〉 and |±13/2〉 states, respectively.For the spin–phonon coupling calculations on 5, we selected twenty-seven vibrational modes (shown in Fig. 7, S41–S49 and Table S30‡). The CF parameter values at the several displacements of these normal modes are shown in Fig. S50.‡ By analysing the coupling strength, we find that the ω8 and ω14 vibrational modes are likely responsible for the spin–phonon coupling of the KD1 → KD2 transition. The second excited state of ω8 vibrational mode of 2 (ΔE = 268 cm−1vs. υ = 282 cm−1) is also closer to the KD1–KD2 energy gap, which further reinforces that these modes should cause the magnetisation relaxation. These ω8 and ω14 and ω13, vibrational modes have a significant movement for the equatorial oxygens (out-of-plane) and axial –CH3 groups. Therefore, quenching the movement of the equatorial oxygens should increase the Ueff and TB values of 5.
3. Discussion
The advancement in molecular nanomagnets has led to the growth of plenty of SMMs with very large Ueff values, but the TB values remain a small fraction of them due to the under-barrier relaxation processes. In this regard, the study of spin–phonon coupling in dysprosocenium complex [Dy(Cpttt)2][B(C6F5)4] (Cpttt = {C5H2tBu3-1,2,4}) has made an important breakthrough, not only because this holds a record high TB value, but also because they have shown which vibrations are linked with the magnetisation relaxation.46 Based on their study, two years later, another novel dysprosocenium SIM, [(CpiPr5)Dy(Cp*)]+ (CpiPr5, penta-iso-propylcyclopentadienyl; Cp*, pentamethylcyclopentadienyl) was discovered quenching the vibrations governing the magnetisation relaxation.53 On the other hand, Lunghi and co-workers recently demonstrated the role of anharmonic phonons in dictating the under-barrier magnetisation relaxation.1–4,49,52,85–87 Therefore, spin–phonon coupling calculations are of utmost importance to unveil the underlying physical process of magnetisation relaxation and provide a clear indication of how the relaxation process is linked with molecular motions. As a result, it can provide the design criteria for potential SMMs with chemical tuning to quench the vibrations associated with Orbach and Raman relaxation processes.The calculations of spin–phonon coupling require thousands of ab initio calculations, which are computationally demanding and often do not directly yield chemical insights to improve the TB values. Furthermore, we have confined ourselves to the vibrations having significant oscillator strength that also lies within the KD1–KD2 energy gap so that magnetisation relaxation from mJ = |±15/2〉 to |±13/2〉 of the ground 6H15/2 state can be gauged.46,57,74,76,88,89 Our calculations reveal that not only the atoms in the first coordination sphere but also those in the secondary coordination sphere affect the magnetisation relaxation. In the case of complex 5, the out-of-plane bending vibrations of the equatorial oxygens govern the magnetisation relaxation, and therefore, disrupting this movement might increase the Ueff and TB values. It is worth mentioning that in the Cl and Br analogues of complex 5 ([L2Dy(H2O)5][Cl]3·L2 (6) and [L2Dy(H2O)5][Br]3·L2·H2O (7), L = tBuPO(NHiPr)2), the Ueff and TB values decrease from I to Br and Cl analogues (TB (sweep rate 20 Oe s−1) = 16.0 K for I, 14.0 K for Br and 9.0 K for Cl).90 This may be ascribed to the equatorial planarity of water molecules, which decreases from I to Br to Cl analogues of 5. The vibrational modes should be near-resonant with the KD1–KD2 energy gap for the magnetisation relaxation in the Orbach regime. In our case, the energy of the vibrational modes is far lower than the KD1–KD2 energy gap, diminishing the TB values. From the literature, we have also found an increase in the TB value from [Dy(OPCy3)(H2O)5]Cl3·OPCy3·H2O·EtOH (8, TB(sweep rate = 200 Oe s−1) = 11 K) to [Dy(OPCy3)(H2O)5]Br3·2OPCy3·2H2O·2EtOH (9, TB(sweep rate = 200 Oe s−1) = 20 K).36 On the other hand, a significant improvement in the blocking barrier is observed going from [Dy(HMPA)2(H2O)5]Cl3·HMPA (10, HMPA = Ueff = 460 K) to [Dy(HMPA)2(H2O)5]I3·2HMPA (11, Ueff = 600 K).61 The Ueff and TB values of complexes 8, 9, 10 and 11 further support that movement of the oxygen atoms is linked with the magnetisation relaxation in the [L2Dy(H2O)5]3+ family of SMMs.
In this manuscript, by analysing the spin–phonon coupling, we have shown that the modulation of geometry via simple ligand substitution can shift the vibrations and decouple with the KD1–KD2 gap that is linked with the magnetisation relaxation in 1-F, 1-pCH3, 1-pCH3F and 1-CH3 in comparison with the parent geometry 1. As a result of this, an enhancement of Ueff and TB values is observed compared to the parent complex. On the other hand, the electrostatic polarisation of the donor atom strongly affects the spin–phonon coupling, as suggested by Lunghi and co-workers.4 They demonstrated that employing a ligand system where the donor atom charges are not significantly affected by vibrations should lead to a potential SMM. In the case of complexes 2 and 3, introducing a crown ether ligand in the equatorial position in place of the five THF molecules minimizes the electronic delocalisation, leading to an increase in the Ueff values. In the case of complex 4, the replacement of –NH groups by oxygen also reduces the electronic delocalisation; hence, a significant improvement in the Ueff value is observed in 4-N3O2 compared to 4. It should be noted that the organometallic complex with a haptic ligand and complexes with a carbene ligand show very high TB values due to the minimal polarisation in the first coordination sphere.
By leveraging the outcomes of spin–phonon calculations conducted on complexes 1–5, a comprehensive analysis of the TB values across all studied complexes has become possible, shedding particular light on the intriguingly low values observed in complexes 2 and 3. It is worthwhile to mention that among complexes 1–5, the largest TB value is observed for complex 5 (16 K), followed by 1 ≈ 4 (14 K) and 2 ≈ 3 (9 K). From these values, we can suggest that the TB value is the lowest for complexes where the significant movement of metals and atoms in the first coordination controls the magnetisation relaxation. This is the case with complexes 2 and 3, where the vibration involving in-plane movement of the Dy ion is associated with the magnetisation relaxation, and this is primarily due to the flexible first coordination sphere atoms. In the case of complex 4, the atoms in the second coordination sphere, such as hydrogen atoms of –NH groups, control the magnetisation relaxation. Therefore its TB is slightly higher than that of complexes 2 and 3. In the case of complex 1, the hydrogen atoms associated with the phenyl and pyridine rings in the third coordination sphere govern the magnetisation relaxation. Finally, in the case of complex 5, the H-bonding interactions with the counter anions are linked with the magnetisation relaxation. As the counter anions involved in this case are beyond the coordination sphere, this complex TB value is the largest among all. Hence, the establishment of a rigid first coordination sphere surrounding Dy(III) is an imperative requirement when designing prospective SMMs. This should also be accompanied by a minimum electrostatic polarisation of the corresponding donor atoms. Given the diverse nature of associated vibrations within this molecular class, a more extensive dataset encompassing all pentagonal bipyramidal Dy(III) complexes, coupled with the power of AI/ML tools, holds tremendous potential to forge a path forward. Excitingly, this endeavour is currently underway in our laboratory.
4. Conclusions
In summary, by studying twenty-three molecules/models in the family of pseudo-D5h Dy(III) single-ion magnets using DFT and ab initio CASSCF calculations, we have deciphered the large variation in the blocking temperature (TB) observed in this class of molecules. The variation observed was attributed to the interplay between the spin–vibrational coupling and crystal field splitting of the ground state. The J = 15/2 term of the 6H15/2 ground state is split into 2J mJ crystal field sub-states. We begin with complex 1, where ω26 normal mode vibrations have multiple atom movements that include C–H bond vibrations of (i) the meta position of pyridine rings, (ii) the para position of the phenolate rings, and (iii) the –CH2 linker connecting the amine nitrogen atom with pyridine/phenolate donor atoms. We then discovered molecules from the literature where this vibrational mode was restricted in several analogous molecules 1-F, 1-pCH3, 1-pCH3F and 1-CH3 that systematically attempt to shift the ω26 normal mode to create an off-resonance scenario with the relaxation mechanism. The next set contains molecules 2 and 3, whose flexible first coordination sphere yields inferior SIM performance. To circumvent this problem, 2-crown and 3-crown were modelled with a rigid first coordination sphere, yielding better performance. Complex 4 has a macrocyclic Schiff-based ligand at the equatorial position, where N–H vibrations were the weak point and model 4-N3O2 aims to address this issue. Complex 5, on the other hand, has five water molecules in the equatorial plane, and out-of-plane bending of the water molecules is a major factor in the relaxation mechanism. Although this cannot be eliminated, complexes 6 and 7 with –Cl and –Br analogues are added to affirm this point in this class of molecules. Complexes 8, 9, 10 and 11 have a similar ligand framework but with a variation in the secondary coordination sphere and were studied to probe this effect. The main conclusions drawn from our work are mentioned below.4.1 Predicting and enhancing the TB by recognising the vibration responsible for relaxation
In the [Dy(bbpen)Br] (1) complex and analogue structures with substitution on the ligand periphery (such as 1-F, 1-pCH3, 1-pCH3F), the ω26 vibration corresponds to the vibrations of donor atoms at the first coordination sphere. This is due to the flexible coordination sphere provided by the ligand framework. Any chemical substitution that shifts this vibration is expected to enhance the TB values. Quite interestingly, this coincides with a literature report where such substitution performed by a trial-and-error method was found to improvise the TB values, affirming faith in the model proposed. Armed with such outcomes, we further targeted the –CH2 linkers that connect the amine nitrogen atom to the pyridinic ring at the equatorial positions and in silico models have been proposed to boost the TB values further.4.2 Importance of the equatorial ligand field in dictating TB
The two complexes [Dy(OCMe3)Br(THF)5][BPh4] (2) and [Dy(OSiMe3)Br(THF)5][BPh4] (3) studied exhibit very low TB values and these are attributed to the vibration involving the asymmetric stretching of the O–Dy–Br bond along the axial direction coupled with in plane bending of the equatorial THF molecule. This is essentially due to the very weak equatorial coordination that provides enhanced axiality as desired but also offers low in-plane bendings, which causes magnetisation relaxation, reducing the TB values. To arrest such movements, we have in silico-modelled geometries where a crown ether ligand replaced five THF molecules. This model is expected to boost the TB value further. Studies on [Dy(LN5)(Ph3SiO)2](BPh4)·CH2Cl2 (4) reveal a similar scenario, and a suitable ligand substitution (N–H by O) was offered to boost the performance.4.3 Controlling H-bonding interactions to improve TB values
Our calculations on [L2Dy(H2O)5][I]3·L2·H2O (5) suggest that out-of-plane bending of the water molecules is one of the major factors in the relaxation mechanism. As these water molecules are in H-bonding interaction with the counteranions, efforts to modulate these vibrations will be proven to be beneficial. There are already literature reports where the TB values were found to be enhanced if the equatorial planarity of the water molecules was improved via ligand design/cluster aggregation.Through the meticulous execution of DFT and ab initio CASSCF calculations on a comprehensive set of pentagonal bipyramidal complexes/models, we have successfully elucidated the underlying factors contributing to the significant variation in TB values within this family. Moreover, we present a chemically viable methodology to fine-tune the performance of this intriguing molecular class for the first time.
5. Methodology
All the gas phase geometry optimisations and calculations of normal modes of complexes 1–5 were performed within the unrestricted DFT framework utilizing the Gaussian09 programme package.91 The X-ray structure (without counter anions and solvent molecules except in complex 5) was employed as a starting point for geometry optimisation. The hybrid B3LYP exchange-correlation functional (including dispersion corrections for 5) was employed for the geometry optimisation.92–94 The Dy(III) ion was replaced by Y(III) to aid smooth SCF convergence. We have used Stuttgart's effective core potential (SDD ECP, 28 core electrons) basis set for yttrium and iodine atoms.95,96 For other elements, a 6-31G* basis set was employed.97 For the geometry optimisation of model complexes, we have used SDD for yttrium and iodine, the Ahlrichs triple-ζ plus polarisation basis set for oxygen, nitrogen, fluorine and bromine and the 6-31G* basis set for carbon and hydrogen atoms.95–98 We have also optimised structures 1 and 2, taking Dy as the central ion by employing the triple zeta basis set utilizing Cundari–Stevens (CS) relativistic effective core potential (Fig. S51‡). We have observed that it makes minimal changes with respect to the former structures. Therefore, for the remainder of the manuscript, we have exclusively used Y. The harmonic vibrational modes and vibrational spectra were estimated with an isotope mass of 162.5 (the mass of the most abundant isotope of dysprosium) for the yttrium atom to obtain the correct reduced masses.72,76All the ab initio CASSCF/RASSI-SO/SINGLE_ANISO calculations on the X-ray, optimised, and model complexes were performed using the MOLCAS 8.2 programme package.99 We have used Douglas–Kroll–Hess (DKH) Hamiltonian to take into account the relativistic effect of the metal centre.100 The Cholesky decomposition technique was used to reduce the size of the disk space.101 The basis sets of our calculations have been taken from the ANO-RCC (atomic natural orbital-relativistically core correlated) library available in MOLCAS. Here, we have used the VTZP quality basis set for Dy, the VDZP quality basis set for the atoms in the first coordination sphere, and the VDZ quality basis set for the atoms from the secondary coordination sphere onwards. The active space for the complete active space self-consistent field (CASSCF) calculations consists of nine 4f electrons in seven 4f orbitals of Dy(III). We have performed state average CASSCF calculations for the twenty-one sextets of Dy(III) ions. The quartet and doublet spin states of Dy(III) were not considered in our calculations to reduce the computational cost since they do not contribute significantly to the spin–orbit energies, as seen from earlier studies. However, the twenty-one spin-free states were mixed by spin–orbit coupling in the RASSI-SO module. Thereafter, the SINGLE_ANISO module was used to compute the g-tensors, crystal field parameters, and magnetic properties such as susceptibility, QTM, TA-QTM etc. To incorporate dynamic correlations we have also performed complete active space second order perturbation theory (CASPT2) calculations for complexes 1, 2 and 3, where the Ucal values found were similar to those of CASSCF (complexes 1-caspt2, 2-caspt2 and 3-caspt2 given in Tables S3, S13 and S14‡).
Data availability
The datasets supporting this article have been uploaded as part of the ESI.‡Author contributions
GR has designed and executed the project. SD and TS performed all calculations and also contributed to the manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Bombay for its supercomputing facility. S. D thanks IIT Bombay for an IPDF fellowship. G. R. would like to acknowledge DST and SERB (CRG/2018/00430; SB/SJF/2019-20/12; and SPR/2019/001145) for funding. TS is thankful to CSIR for the fellowship. We thank Dr Aman Ullah (ICMol, University of Valencia) for providing effective insights during the calculations and analysis.References
- A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059 RSC.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 1–7 RSC.
- A. Lunghi and S. Sanvito, J. Chem. Phys., 2020, 153, 174113 CrossRef CAS PubMed.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS.
- D. Reta, J. G. C. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt and N. F. Chilton, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- J. G. Kragskow, J. Marbey, C. D. Buch, J. Nehrkorn, M. Ozerov, S. Piligkos, S. Hill and N. F. Chilton, Nat. Commun., 2022, 13, 1–10 Search PubMed.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275 RSC.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Arino and E. Coronado, Chem. Sci., 2020, 11, 1593–1598 RSC.
- A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Coord. Chem. Rev., 2018, 367, 163–216 CrossRef CAS.
- S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216–239 CrossRef CAS.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. McInnes, L. F. Chibotaru and R. E. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- R. J. Blagg, C. A. Muryn, E. J. McInnes, F. Tuna and R. E. Winpenny, Angew. Chem., 2011, 123, 6660–6663 CrossRef.
- R. J. Blagg, F. Tuna, E. J. McInnes and R. E. Winpenny, Chem. Commun., 2011, 47, 10587–10589 RSC.
- L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., 2014, 126, 4502–4506 CrossRef.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS.
- J. J. Le Roy, I. Korobkov and M. Murugesu, Chem. Commun., 2014, 50, 1602–1604 RSC.
- J. J. Le Roy, M. Jeletic, S. I. Gorelsky, I. Korobkov, L. Ungur, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 3502–3510 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem.–Eur. J., 2014, 20, 9524–9529 CrossRef CAS.
- A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., 2015, 127, 5962–5966 CrossRef.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- D. Tanaka, T. Inose, H. Tanaka, S. Lee, N. Ishikawa and T. Ogawa, Chem. Commun., 2012, 48, 7796–7798 RSC.
- L. J. Batchelor, I. Cimatti, R. Guillot, F. Tuna, W. Wernsdorfer, L. Ungur, L. F. Chibotaru, V. E. Campbell and T. Mallah, Dalton Trans., 2014, 43, 12146–12149 RSC.
- A. K. Mondal, S. Goswami and S. Konar, Dalton Trans., 2015, 44, 5086–5094 RSC.
- W. Cao, C. Gao, Y.-Q. Zhang, D. Qi, T. Liu, K. Wang, C. Duan, S. Gao and J. Jiang, Chem. Sci., 2015, 6, 5947–5954 RSC.
- S.-S. Liu, K. Lang, Y.-Q. Zhang, Q. Yang, B.-W. Wang and S. Gao, Dalton Trans., 2016, 45, 8149–8153 RSC.
- K.-X. Yu, Y.-S. Ding, T. Han, J.-D. Leng and Y.-Z. Zheng, Inorg. Chem. Front., 2016, 3, 1028–1034 RSC.
- Y.-L. Wang, Y. Ma, X. Yang, J. Tang, P. Cheng, Q.-L. Wang, L.-C. Li and D.-Z. Liao, Inorg. Chem., 2013, 52, 7380–7386 CrossRef CAS PubMed.
- V. E. Campbell, H. Bolvin, E. Rivière, R. Guillot, W. Wernsdorfer and T. Mallah, Inorg. Chem., 2014, 53, 2598–2605 CrossRef CAS PubMed.
- S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., 2010, 122, 7610–7613 CrossRef.
- G.-J. Chen, C.-Y. Gao, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, D.-Z. Liao and P. Cheng, Dalton Trans., 2011, 40, 5579–5583 RSC.
- G. J. Chen, Y. N. Guo, J. L. Tian, J. Tang, W. Gu, X. Liu, S. P. Yan, P. Cheng and D. Z. Liao, Chem.–Eur. J., 2012, 18, 2484–2487 CrossRef CAS PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191 RSC.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS.
- Y. S. Ding, N. F. Chilton, R. E. Winpenny and Y. Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer and S. Gao, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- L. Zhu, B. Yin, P. Ma and D. Li, Inorg. Chem., 2020, 59, 16117–16121 CrossRef CAS PubMed.
- M. Li, H. Wu, Q. Yang, H. Ke, B. Yin, Q. Shi, W. Wang, Q. Wei, G. Xie and S. Chen, Chem.–Eur. J., 2017, 23, 17775–17787 CrossRef CAS PubMed.
- S. Zhang, H. Wu, L. Sun, H. Ke, S. Chen, B. Yin, Q. Wei, D. Yang and S. Gao, J. Mater. Chem. C, 2017, 5, 1369–1382 RSC.
- Z. Jiang, L. Sun, Q. Yang, B. Yin, H. Ke, J. Han, Q. Wei, G. Xie and S. Chen, J. Mater. Chem. C, 2018, 6, 4273–4280 RSC.
- Y. S. Ding, T. Han, Y. Q. Zhai, D. Reta, N. F. Chilton, R. E. Winpenny and Y. Z. Zheng, Chem.–Eur. J., 2020, 26, 5893–5902 CrossRef CAS PubMed.
- L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Dalton Trans., 2016, 45, 16635–16643 RSC.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC.
- A. Lunghi and S. Sanvito, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS.
- A. Lunghi, Appl. Magn. Reson., 2020, 51, 1343–1356 CrossRef CAS.
- R. Nabi, J. Kragskow, J. Staab, D. Reta, J. Skelton and N. Chilton, J. Am. Chem. Soc., 2023, 145, 24558–24567 CAS.
- S. Mondal and A. Lunghi, J. Am. Chem. Soc., 2022, 144, 22965–22975 CrossRef CAS.
- A. Albino, S. Benci, L. Tesi, M. Atzori, R. Torre, S. Sanvito, R. Sessoli and A. Lunghi, Inorg. Chem., 2019, 58, 10260–10268 CrossRef CAS.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- C. A. Goodwin, D. Reta, F. Ortu, J. Liu, N. F. Chilton and D. P. Mills, Chem. Commun., 2018, 54, 9182–9185 RSC.
- C. A. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714–18724 CrossRef CAS PubMed.
- P. Evans, D. Reta, G. F. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940 CrossRef CAS PubMed.
- A. Ullah, J. Cerdá, J. J. Baldovi, S. A. Varganov, J. Aragó and A. Gaita-Arino, J. Phys. Chem. Lett., 2019, 10, 7678–7683 CrossRef CAS.
- M. Amoza, L. Maxwell, N. Aliaga-Alcalde, S. Gómez-Coca and E. Ruiz, Chem.–Eur. J., 2021, 27, 16440–16447 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316 RSC.
- Y. C. Chen, J. L. Liu, Y. Lan, Z. Q. Zhong, A. Mansikkamaki, L. Ungur, Q. W. Li, J. H. Jia, L. F. Chibotaru, J. B. Han, W. Wernsdorfer, X. M. Chen and M. L. Tong, Chem.–Eur. J., 2017, 23, 5708–5715 CrossRef CAS PubMed.
- A. B. Canaj, M. K. Singh, C. Wilson, G. Rajaraman and M. Murrie, Chem. Commun., 2018, 54, 8273–8276 RSC.
- A. B. Canaj, S. Dey, C. Wilson, O. Cespedes, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 56, 12037–12040 RSC.
- A. Sarkar and G. Rajaraman, Chem. Sci., 2020, 11, 10324–10330 RSC.
- Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. Winpenny, Y.-Z. Zheng and N. F. Chilton, Nat. Commun., 2018, 9, 3134 CrossRef.
- Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Q.-C. Luo, T. Han and Y.-Z. Zheng, Inorg. Chem. Front., 2020, 7, 4367–4376 RSC.
- P. Kalita, N. Ahmed, A. K. Bar, S. Dey, A. Jana, G. Rajaraman, J.-P. Sutter and V. Chandrasekhar, Inorg. Chem., 2020, 59, 6603–6612 CrossRef CAS PubMed.
- I. F. Díaz-Ortega, J. M. Herrera, S. Dey, H. Nojiri, G. Rajaraman and E. Colacio, Inorg. Chem. Front., 2020, 7, 689–699 RSC.
- M. S. Norre, C. Gao, S. Dey, S. K. Gupta, A. Borah, R. Murugavel, G. Rajaraman and J. Overgaard, Inorg. Chem., 2020, 59, 717–729 CrossRef CAS PubMed.
- A. K. Bar, P. Kalita, J.-P. Sutter and V. Chandrasekhar, Inorg. Chem., 2018, 57, 2398–2401 CrossRef CAS PubMed.
- S. K. Gupta, S. Dey, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem.–Eur. J., 2022, 28, e202103585 CrossRef CAS PubMed.
- K.-X. Yu, J. G. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. F. Chilton and Y.-Z. Zheng, Chem, 2020, 6, 1777–1793 CAS.
- F. Ortu, D. Reta, Y.-S. Ding, C. A. Goodwin, M. P. Gregson, E. J. McInnes, R. E. Winpenny, Y.-Z. Zheng, S. T. Liddle and D. P. Mills, Dalton Trans., 2019, 48, 8541–8545 RSC.
- A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 56, 12037–12040 RSC.
- A. L. Blockmon, A. Ullah, K. D. Hughey, Y. Duan, K. R. O'Neal, M. Ozerov, J. J. Baldoví, J. Aragó, A. Gaita-Ariño and E. Coronado, Inorg. Chem., 2021, 60, 14096–14104 CrossRef CAS PubMed.
- https://cccbdb.nist.gov/vsfx.asp .
- J. G. Kragskow, J. Marbey, C. D. Buch, J. Nehrkorn, M. Ozerov, S. Piligkos, S. Hill and N. F. Chilton, Nat. Commun., 2022, 13, 825 CrossRef CAS PubMed.
- L. Zhu, Y. Dong, B. Yin, P. Ma and D. Li, Dalton Trans., 2021, 50, 12607–12618 RSC.
- L. Tesi, Z. Salman, I. Cimatti, F. Pointillart, K. Bernot, M. Mannini and R. Sessoli, Chem. Commun., 2018, 54, 7826–7829 RSC.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- G. Huang, X. Yi, J. Jung, O. Guillou, O. Cador, F. Pointillart, B. Le Guennic and K. Bernot, Eur. J. Inorg. Chem., 2018, 2018, 326–332 CrossRef CAS.
- H. Wada, S. Ooka, T. Yamamura and T. Kajiwara, Inorg. Chem., 2017, 56, 147–155 CrossRef CAS PubMed.
- L. Maxwell, M. Amoza and E. Ruiz, Inorg. Chem., 2018, 57, 13225–13234 CrossRef CAS PubMed.
- A. Borah, S. Dey, S. K. Gupta, G. Rajaraman and R. Murugavel, Dalton Trans., 2023, 52, 8943–8955 RSC.
- S. K. Gupta, S. Dey, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem.–Eur. J., 2022, 28, e202103585 CrossRef CAS PubMed.
- A. Lunghi and S. Sanvito, Nat. Rev. Chem, 2022, 6, 761–781 CrossRef CAS PubMed.
- S. Mondal and A. Lunghi, arXiv, 2022, preprint, arXiv:2212.11705, DOI:10.48550/arXiv.2212.11705.
- A. Lunghi, arXiv, 2022, preprint, arXiv:2202.03776, DOI:10.48550/arXiv.2202.03776.
- L. Escalera-Moreno, N. Suaud, A. Gaita-Arino and E. Coronado, J. Phys. Chem. Lett., 2017, 8, 1695–1700 CrossRef CAS PubMed.
- D. López-Alcalá, A. M. Ruiz and J. J. Baldoví, Nanomater., 2023, 13, 1172 CrossRef PubMed.
- R. Murugavel, S. K. Gupta, S. Dey, T. Rajeshkumar and G. Rajaraman, Chem.–Eur. J., 2021, 27, 1–12 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147 CrossRef CAS.
- X. Cao, J. Chem. Phys., 2001, 115, 7348 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos and L. Gagliardi, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- M. Reiher, Theor. Chem. Acc., 2006, 116, 241–252 Search PubMed.
- F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS PubMed.
Footnotes |
| † Dedicated to the 60th birthday of Prof. R. Murugavel. |
| ‡ Electronic supplementary information (ESI) available: This contains structural parameters in optimised versus crystal structures, tables containing ab initio calculated parameters, additional figures, optimised geometries, frequencies of the various normal modes of vibrations, computed crystal field parameters, and optimised coordinates of the complexes. See DOI: https://doi.org/10.1039/d4sc00823e |
| § Both authors contributed equally to this manuscript. |
| This journal is © The Royal Society of Chemistry 2024 |