Open Access Article
Open Access ArticleIlluminating the multiple Lewis acidity of triaryl-boranes via atropisomeric dative adducts†
Benjámin
Kovács
 a,
Tamás
Földes
a,
Tamás
Földes
 b,
Márk
Szabó
a,
Éva
Dorkó
b,
Bianka
Kótai
b,
Gergely
Laczkó
b,
Márk
Szabó
a,
Éva
Dorkó
b,
Bianka
Kótai
b,
Gergely
Laczkó
 bc,
Tamás
Holczbauer
b,
Attila
Domján
*a,
Imre
Pápai
bc,
Tamás
Holczbauer
b,
Attila
Domján
*a,
Imre
Pápai
 *b and
Tibor
Soós
*b and
Tibor
Soós
 *b
*b
aCentre for Structural Science, HUN-REN Research Centre for Natural Sciences, Magyar tudósok körútja 2, H-1117 Budapest, Hungary. E-mail: domjan.attila@ttk.hu
bInstitute of Organic Chemistry, HUN-REN Research Centre for Natural Sciences, Magyar tudósok körútja 2, H-1117 Budapest, Hungary. E-mail: papai.imre@ttk.hu; soos.tibor@ttk.hu
cHevesy György PhD School of Chemistry, Eötvös Loránd University, P. O. Box 32, Budapest, H-1518, Hungary
First published on 26th August 2024
Abstract
Using the principle that constrained conformational spaces can generate novel and hidden molecular properties, we challenged the commonly held perception that a single-centered Lewis acid reacting with a single-centered Lewis base always forms a single Lewis adduct. Accordingly, the emergence of single-centered but multiple Lewis acidity among sterically hindered and non-symmetric triaryl-boranes is reported. These Lewis acids feature several diastereotopic faces providing multiple binding sites at the same Lewis acid center in the interaction with Lewis bases giving rise to adducts with diastereomeric structures. We demonstrate that with a proper choice of the base, atropisomeric adduct species can be formed that interconvert via the dissociative mechanism rather than conformational isomerism. The existence of this exotic and peculiar molecular phenomenon was experimentally confirmed by the formation of atropisomeric piperidine-borane adducts using state-of-the-art NMR techniques in combination with computational methods.
Introduction
The ensemble of conformations a given molecule can access is of utmost importance, since each conformation defines a 3D shape, which in turn determines the molecule's physical, chemical and biological properties.1,2 Thus, the exploration of conformational space, including the less abundant conformations, is a prerequisite to gain a deeper understanding of these properties.As molecular geometry and function are interrelated, there has been growing interest in remodeling the conformational space and designing molecules that can adopt the desired shape with minimal or no energetic penalty. The common strategy that guided these efforts was to impose structural constraints via steric repulsion or ring strains. As a result of these challenging undertakings, peculiar reactivities,3 well-designed emissive systems,4 rarely observed metastable conformational and redox states5 and enhanced ligand bindings6 have been engineered.
Along the above lines, we took up the challenge of demonstrating the existence of a peculiar molecular phenomenon that enables multiple Lewis acidity (MLA) to be assigned to a single-centered Lewis acid (LA). IUPAC defines Lewis acidity as ‘the thermodynamic tendency of a substrate to act as a Lewis acid’7 which is routinely described by a single equilibrium constant associated with a single dative adduct. In contrast, we envisioned that sterically crowded and non-symmetric triaryl-boranes, i.e. those involving an LA center with diastereotopic faces and confinement,8 are able to form distinct dative LA–LB adducts9 with the same single-centered achiral Lewis base (LB). Accordingly, these Lewis adducts represent different stereoisomeric states formed in competitive association pathways. Due to hindered rotations around single bonds, these LA–LB stereoisomers are diastereomeric atropisomers, which can be distinguished at ambient temperature, and thus, the Lewis acidity of these boranes can be described by not a single, but multiple equilibrium constants. Atropisomerism is a unique case of stereoisomerism caused by restricted rotation around a single covalent bond that is not constrained in a ring. While this phenomenon commonly refers to C(sp2)–C(sp2) single bonds, there are some less common examples for atropisomerism as a result of restricted rotation around C(sp3)–C(sp2) or even C(sp3)–C(sp3) single bonds (see Fig. 1 for selected examples).10 In this study we demonstrate that atropisomeric LA–LB adducts with dual restricted rotation around B(sp3)–N(sp3) and B(sp3)–Ar(sp2) bonds are formed between fluoro-chloro triaryl-boranes and amines within the same reaction.
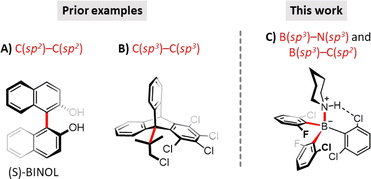 | ||
| Fig. 1 Selected examples of molecules featuring (A) C(sp2)–C(sp2) and (B) C(sp3)–C(sp3) atropisomeric states10 and a (C) dual B(sp3)–N(sp3) and B(sp3)–Ar(sp2) type atropisomeric adducts reported in our present work. Bonds corresponding to restricted rotations are highlighted in red. | ||
The challenge outlined inevitably poses an additional fundamental question: when do we consider configurational, conformational, and stereochemical isomers as distinct, isomeric molecules with different properties, including reactivity and symmetry? This question cannot be answered without specifying important experimental conditions such as the time scale of observation, temperature, pressure, etc. That is, these molecular properties are definable only within limits. As an example, owing to the sterical congestion, R- and S-binaphthol (Fig. 1A) are atropisomers at ambient temperature and fundamental chiral building blocks for chiral catalysis. So, these conformational isomers are distinct molecules at room temperature with different reactivities in asymmetric reactions. Nevertheless, over 200 °C reaction temperature or million years of observation period, R- and S-binaphthols should be treated as non-distinct, equivalent molecules.
In virtue of above, we had to specify the external parameters under which the existence of MLA was investigated. Considering practical aspects and the potential of future use, we have confined ourselves to the most relevant parameters of routine organic chemistry (e.g. ambient temperature, 1 atm pressure, and ms-days timescale). Thus, to be distinguished as distinct molecules, the formed isomeric dative LA–LB adducts must be detectable by NMR at ambient temperature. Additionally, the structure of the LA should be such that its conformational isomers can be handled as non-distinct, equivalent molecules at ambient temperature. So, the sterical congestion around the Lewis acidic center must be large enough to form atropisomeric dative adducts, but not too large to halt the conformational isomerism of the LA itself at ambient temperature.
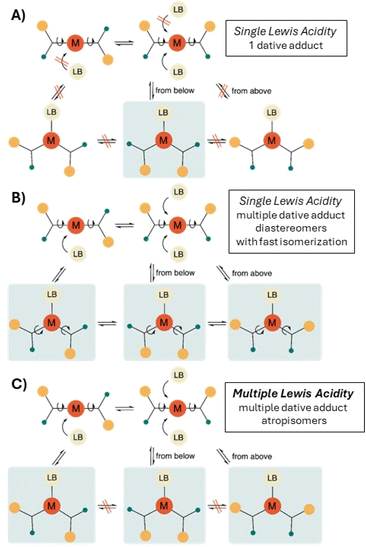
It is then worthwhile to further specify the phenomenon of single-centered, but multiple Lewis acidity and to discuss the challenges associated with its observation. First and foremost, the presence of non-equivalent, diastereotopic faces as distinct ‘binding sites’ of the Lewis acid is a necessary but not sufficient condition for MLA. It is possible that, for steric and/or electronic reasons, only one dative adduct is produced, i.e. a diastereoselective adduct formation occurs and single Lewis acidity can be determined (Fig. 2A).9a,e If the formation of multiple adducts is kinetically and thermodynamically possible, we might expect that all observable atropisomeric dative adducts are formed in different, mutually competitive chemical reactions between the same LA and LB. However, if the thermodynamic equilibrium between the detected LA–LB adducts is also established by rapid conformational isomerisation (via rotation around single bonds) as well as slow dissociation–association, then the situation should be considered a case of single Lewis acidity, which, again, can be described by a single equilibrium constant (Fig. 2B). Thus, multiple Lewis acidity can only emerge, if either stable, non-dissociable atropisomeric dative adducts are formed between the diastereotopic LA and the same LB (in a kinetically controlled manner) or the interconversion of the atropisomeric dative adducts requires the breaking and reforming of the dative bond (Fig. 2C). Indeed, in the latter case each LA–LB atropisomer represents a reversible association pathway, and thus, the Lewis acidity can be described by as many equilibrium constants as the number of LA–LB atropisomer detected. Finally, it should be noted that not only the strength of Lewis acidity (hydricity, Gutmann–Beckett, etc.), but also its multiplicity is a situation-dependent phenomenon, so it can happen that the very same LA can exhibit single or multiple Lewis acidity with different LBs.
In this paper, we report chemical evidence that the hypothesized phenomenon that enables multiple Lewis acidity to be assigned exists, even at ambient temperature. Indeed, combined computational and NMR studies revealed that the crowded LA–LB atropisomeric adducts (Fig. 1C) display such high rotational barriers that their isomerization pathway is dissociative.
Results and discussion
Diastereotopicity of non-symmetrically halogenated triaryl-boranes
To encounter single-centered MLA and characterize the corresponding atropisomers, we turned our focus towards frustrated Lewis pair11 (FLP) chemistry. This field employs specific LA and LB combinations that are incapable of stable dative adduct formation due to steric hindrance. Thus, a ‘quasi-metastable’ state arises that can be utilized for bond activation in multiple reactions including hydrogenation.12 Recently, we developed a set of halogenated triaryl-borane catalysts for FLP promoted reductive aminations.13 To optimize catalyst performance, we deliberately replaced the F atoms in ortho positions with Cl atoms that provided a set of fluoro-chloro boranes, I, II and III (Fig. 3A) with gradual differences both in their steric and electronic properties. Since the metrics of Lewis acidity are base-dependent, various complementary methods have been used to assess their LA strength, corresponding to global, effective and intrinsic Lewis acidity.14 As expected for such sterically crowded systems, there has been an offset between these complementary methods. Surprisingly, however, these methods and catalytic test reactions indicated a non-linear relationship between the level of F-to-Cl substitution and the relative Lewis acidity (especially the Gutmann–Beckett method15) or the catalytic activity.13 Indeed, while the introduction of the bulkier Cl atoms into boranes II and III gradually increased the electron deficiency of the boron centers, it profoundly reshaped the energy landscape of their dative adducts with Et3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or the hydride anion (H−) through the counteracting change in steric effects (front- and back-strains).
O or the hydride anion (H−) through the counteracting change in steric effects (front- and back-strains).
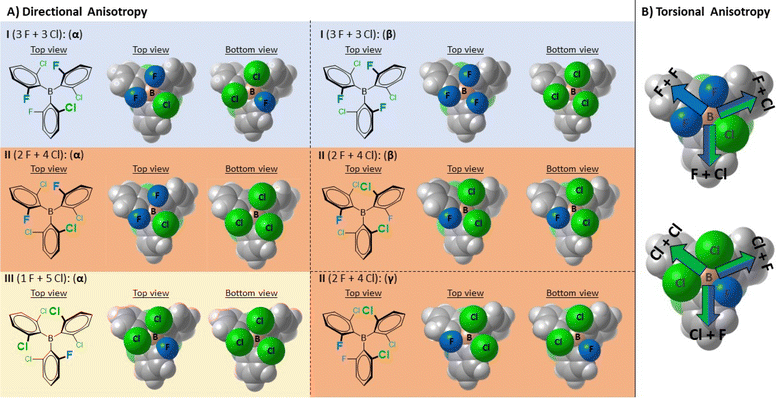 | ||
| Fig. 3 (A) Illustration of the diastereotopicity of non-symmetrically halogenated triaryl-borane catalysts I, II and III (highlighted with blue, orange and cream backgrounds). Due to the presence of only one non-symmetrically substituted aryl ring, borane III has only one rotamer. The rotameric states of each borane are shown in van der Waals representations from top and bottom views. The corresponding rotameric states are denoted with Greek letters which refer to the order of their calculated stability, with the α-state being the respective lowest energy state (Table S2†). (B) Illustration of the torsional anisotropy upon dative bond formation with appropriate Lewis bases (having no C3 symmetry) using the top and bottom views of the I(α) structure. The colored arrows indicate distinct molecular confinements for the incoming Lewis base. The F atoms are colored blue, and the Cl atoms are colored green. | ||
This interesting and somewhat unusual behavior upon dative adduct formation prompted us to conduct further and more detailed structural studies with boranes I–III. After a thorough analysis of their structures, we postulated that each of these special boranes individually features diastereotopic faces (Fig. 3), possibly resulting in diastereomeric adducts upon interaction with an achiral LB and thus might possess MLA. In these BAr3 structures, the aryl rings adopt propeller shaped conformations (see the computed I–III rotameric states in ESI Section 2 in the ESI†); however, the particular o-F and o-Cl substitution patterns decrease the molecular symmetry and these boranes can display both directional and torsional structural anisotropy upon dative adduct formation. In contrast to III, a more complex situation is expected to emerge for boranes I and II, as the rotation of the non-symmetrically substituted aryl rings around the B(sp2)–Ar(sp2) single bonds results in multiple rotamers (2 and 3 for I and II, respectively), which, in principle, would further diversify the global and intrinsic Lewis acidities and their diastereotopicity. Additionally, we also hypothesized that the distinct conformations of the dative borane adducts might be detected as the enhanced rotational barriers imposed upon the dative adduct formation would hinder the rotational isomerism of the thermally accessible conformational states. Accordingly, these isomeric LA–LB adducts would be atropisomers, stemming from directional and/or torsional anisotropy of the LA upon dative bond formation and the hindered internal rotations around the B(sp3)–Ar(sp2) and B(sp3)–N(sp3) single bonds (using N-based LB).
Computed hydride-borane adduct atropisomers
Having dissected the stereochemical features of boranes I–III, we addressed the question whether their atropisomeric dative adducts are sufficiently populated at ambient temperature, thereby not imposing constraints on detecting the MLA phenomenon, i.e. the Fig. 2A case. The selected hydride anion LB was expected to scan the diastereotopicity of the borane rotamers without the complicating effects of torsional anisotropy and front strain (Fig. 4). Thus, we carried out quantum chemical calculations to determine the thermodynamic driving force (ΔGh) to generate the [H–I]−, [H–II]− and [H–III]− hydride dative adducts of distinct conformational states. The geometry optimizations and the estimation of finite temperature and solvent effects were carried out at the B3LYP-D3/6-311G(d,p) level of DFT. For relative stability predictions, the electronic energies were computed for the optimized geometries using the LNO-CCSD(T) method extrapolated to the complete basis set (CBS) limit (for additional computational details, see the ESI†). Most importantly, as displayed in Fig. 4, for each of I,16II and III the MLA phenomenon can in principle be a possibility as even the less stable conformers of their respective hydride adducts are predicted to be sufficiently populated (ΔΔGh ≤ 3.5 kcal mol−1). Namely, there is no thermodynamic driving force for diastereoselective hydride adduct formation. Nevertheless, potential energy scan analysis (ESI Section 8†) indicated that the B(sp3)–Ar(sp2) bonds can freely rotate in these hydride adducts, suggesting that these are still single Lewis acidity cases, i.e. the Fig. 2B case, and their Lewis acidity, paired with the hydride anion LB (hydricity), should be calculated as a population weighted average of all the different conformers/atropisomers. Notably, for any borane studied, the rotameric state with the most fluorine atoms on the side opposite to the attacking hydride yields the most stable hydride adduct as it imposes the weakest back-strain effects (see strain-analysis in ESI Section 11†).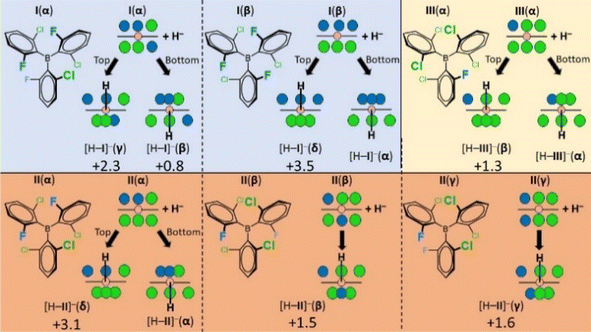 | ||
| Fig. 4 The schematic representation of the triaryl-borane structures and their hydride adducts (F: blue, Cl: green, and B: pink spheres). The ‘top’ and ‘bottom’ approaches refer to the diastereotopic views presented in Fig. 3. In the sp3 states the spatial density of halogen ligands differs on the two sides of the adducts leading to increased back-strain (congested ligands) and decreased front-strain (sparser ligands). The combination of rotameric states and diastereotopic faces engenders multiple, atropisomeric hydride adduct conformers for each borane. The respective ΔGh values are shown in Table S3.† Here, the ΔΔGh values with respect to the most stable conformational state (α) are indicated for the higher energy hydride adduct conformers in kcal mol−1 at 298.15 K. | ||
Detection of the piperidine-borane adducts' atropisomeric states
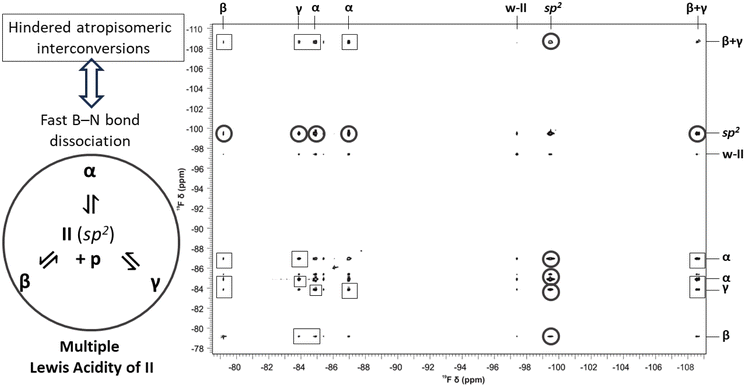
Next, we sought to identify a suitable LB which can evoke the case of multiple Lewis acidity in the dative adduct formation with boranes I, II and III. Importantly, the 19F NMR spectra of the respective boranes (Fig. S9–S11†) showed an averaged 19F signal indicating that there were no distinct rotamers in the sp2 state at ambient temperatures due to the free rotation around the boron center. To investigate not only the structural but also the dynamic properties of the emerging dative adducts of these boranes, various NMR methods and complementary computational studies were utilized. Although detection of conformational isomers of small molecules is inherently challenging using ensemble methods such as NMR spectroscopy, screening of a variety of commercially available amines proved successful. Indeed, in most cases, either the lack of dative adduct formation or rapid isomerization in the sp3 state could be detected (for details on the full library of LB amines see ESI Fig. S2†) providing no clear-cut proof for the MLA phenomenon (Fig. 2B). Gratifyingly, piperidine (p) was found to be able to form atropisomeric, long-lived dative adducts with each of I, II, and III, demonstrated by 19F NMR (for all 19F NMR spectra see ESI Section 3†). Exemplified by the 19F NMR spectra of the p + II mixture, in the slow exchange regime (Fig. 5) the 19F signals of the distinct p-adduct atropisomers are well-resolved and appear typically high upfield- (<−107 ppm) or downfield-shifted (>−90 ppm) with respect to the non-interacting sp2-hybridized borane II signal (∼−100 ppm, see Fig. S12–S14†). Importantly, p is a structurally more complex and sterically more demanding LB than the H− and is suitable to probe the torsional anisotropy (Fig. 3B) of boranes I–III as well. Thus, upon the approach of p to a particular diastereotopic face of I, II or III, even more dative-adduct atropisomers might emerge due to the rotational constraints around the B(sp3)–N(sp3) dative bond. Indeed, for all three boranes, the number of the corresponding p-adduct 19F signals is always a multiple of the number of F atom(s) in the given borane, which implies that the adducts p–I, p–II and p–III present several stable atropisomeric states simultaneously. Also notable is that after adding 3 equivalents of p, the 19F signal of the sp2-hybridized boranes was not observable in the spectra of I and II and they remained absent even at higher temperatures. In contrast, the free borane III was still observable in the slow exchange regime owing to its highly crowded structure; thus, its ‘free’ sp2 state with p is preferred. The dative bond formation between p and the boranes and the concomitant changes in electron density around the boron atom were further corroborated by 11B NMR (for the 11B spectra, see Fig. S3–S8†).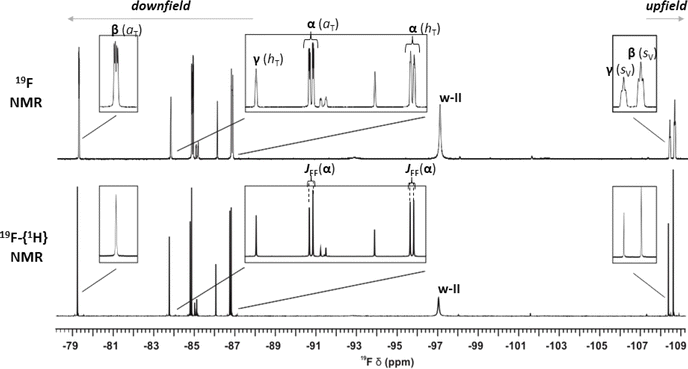 | ||
Fig. 5 The 1D 19F NMR spectrum (564 MHz, 298.2 K) of a mixture of p and II in toluene-d8 using a p to II ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 without (top) and with (bottom) 1H-decoupling during acquisition. The two F atoms in p–II combined with the three distinct atropisomeric states (α, β, or γ) generate six resolved p–II19F signals. The represented conformation and specific F atom position (aV, aT, hV, hT, sV or sT, see Fig. 6A) are indicated for each p–II signal. For the p–II(α) signals the effect of 19F–19F through a space J-coupling (JFF) of 39.5 Hz between the aT and hT positioned 19F spins is apparent as in the 1H-decoupled spectrum they remain doublets as opposed to the p–II(β) and p–II(γ) signals which simplify to a singlet. The broad signal marked as ‘w–II’ that remains close to the sp2-hybridized borane peak position represents slowly diffusing species that comprise interacting II, p, and residual water molecules encompassed in a single solvent cage (the characterization of these aqueous species is detailed in ESI Section 9†). 1 without (top) and with (bottom) 1H-decoupling during acquisition. The two F atoms in p–II combined with the three distinct atropisomeric states (α, β, or γ) generate six resolved p–II19F signals. The represented conformation and specific F atom position (aV, aT, hV, hT, sV or sT, see Fig. 6A) are indicated for each p–II signal. For the p–II(α) signals the effect of 19F–19F through a space J-coupling (JFF) of 39.5 Hz between the aT and hT positioned 19F spins is apparent as in the 1H-decoupled spectrum they remain doublets as opposed to the p–II(β) and p–II(γ) signals which simplify to a singlet. The broad signal marked as ‘w–II’ that remains close to the sp2-hybridized borane peak position represents slowly diffusing species that comprise interacting II, p, and residual water molecules encompassed in a single solvent cage (the characterization of these aqueous species is detailed in ESI Section 9†). | ||
To aid the structural assignment of the expected atropisomeric states of p–I, p–II and p–III, computational studies were conducted (ESI Section 4†) following the structure calculation protocol used for the hydride adduct calculations (all computed p-borane structures along with the corresponding ΔGa values are reported in Tables S4–S6†). Importantly, the calculated dative p-adduct structures display clear differences from the hydride adducts as a result of enhanced steric effects and the lower symmetry of the p LB. Nevertheless, they share a common molecular topology regarding the relative orientation of p and the borane's aryl rings. This is illustrated in Fig. 6A with the energetically lowest lying (α) conformer of p–II. The structurally common features are (i) the N atom of p donates the equatorial lone electron pair to the boron to establish the dative bond, (ii) one borane’ aryl ring is oriented vertically thereby pointing one of its halogen atoms towards the amine proton of p (HN) to form a hydrogen bond, and (iii) the second borane’ aryl ring, which also interacts with HN, is tilted about 45° from the B–N axis (iv) while the third aromatic ring is in horizontal orientation, that is, nearly perpendicular to the B–N axis. We designated the emerging halogen atom positions on the vertical and tilted aryl rings as being in the ‘syn’ or ‘anti’ position with respect to the incoming p. Thus, given the observed ring topology preference, any p-adduct atropisomer can be defined in a straightforward way through the specific F/Cl spatial distribution pattern between the horizontal (h), syn (s) and anti (a) position pairs. Notably, due to the emerging hydrogen bond with the syn positioned aryl halides and back-strain interactions, in all three p-borane systems, the vertical and tilted fluorinated ring(s) prefer the F atom in the syn and anti positions, respectively. Also, the horizontal fluorinated ring adopts a more stable orientation with the F atom pointing towards the tilted ring. Based on the computed Gibbs free energies of adduct formation (ΔGa) the expected affinity of the boranes for dative bonding with p follows the general order of III < II < I which indicates the impact of the growing back-strain to destabilize the dative adducts (Tables S4–S6†). The importance of back-strain effects in adduct formation is supported by activation-strain analysis presented in ESI Section 11.† We also note that the presence of hydrogen bonds in these piperidine-borane adducts may contribute considerably to the thermodynamic stability of the various atropisomeric adducts (although the most stable isomers feature the weaker Cl⋯H–N bond), but it is unlikely that the hydrogen bonding interactions (acting as a ‘structural pin’17) are the prerequisite of the formation of distinguishable atropisomeric states. This is confirmed by the fact that borane-LB adducts formed with bases having no N–H protons (for instance LB = quinuclidine, see Section 12 of the ESI†) also show multiple resonances in the 19F NMR spectra, pointing to multiple atropisomeric adduct states.
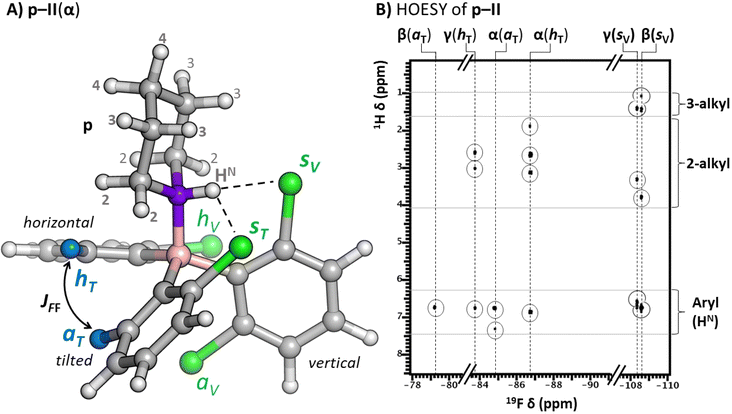 | ||
| Fig. 6 (A) The common ring topology of the computed p-adduct structures illustrated with the lowest lying (α) conformation of p–II. The emerging halogen atom positions are denoted as horizontal (h), syn (s) or anti (a) whereas the subscripts specify whether the halogen atom is located on (s, a) or points towards (h) the tilted (T) or vertical (V) ring. The hydrogen bonding interaction between the HN and the syn-positioned ligands is indicated with black dashed lines. The p–II(α) features the two F atoms (blue) in the aT and hT positions through which a through-space JFF coupling of 39.5 Hz emerges (see α(aT) and α(hT) signals in Fig. 5). (B) The 19F–1H HOESY correlations of the p–II atropisomers (α, β and γ) are highlighted with circles. The s-fluorines (of the β and γ atropisomers) are found sufficiently close in space to most of the p ring to be correlated with the HN and most of the alkyl p hydrogens; the h-fluorines (α, γ) are correlated with a limited number of alkyl p hydrogens; in contrast, the a-fluorines (α and β) do not display HOESY contacts with p. | ||
To validate the assignment of the experimentally observed p-borane atropisomeric states to the computed structures, 19F chemical shift calculations (ESI Section 5†) at the B3LYP-D3/6-311+G(2d,p) level of DFT and 19F–1H HOESY18 measurements (Fig. 6B, S28 and S29†) were performed. These revealed correlations in the frequency, linewidth, and fine structure of the 19F signals with the fluorine atom allocated to the proposed horizontal, syn or anti position (for the full 19F NMR signal assignment process see ESI Section 6†). That is, the hydrogen bonding interaction of syn positioned fluorines with the p N–H group is reflected by the upfield shift of their 19F signals and the unusually high 1H–19F J-coupling of 20–25 Hz that exists through the H⋯F hydrogen bond.19 By distinguishing the downfield-shifted horizontal and anti-positioned 19F signals as well, we concluded that the respective 4, 3 and 3 computed atropisomeric states of p–I, p–II and p–III indeed form under experimental conditions (Table 1). Our assignment was further supported by the good agreement between the experimental and computed 19F chemical shifts (Fig. S30†) and conformational probability distributions (Table S10†). The spatial vicinity of fluorine atoms in the p–I(α), p–I(β), p–I(δ) and p–II(α) structures could be confirmed by 19F–19F through space J-couplings20 (JFF) ranging between 15 Hz and 80 Hz (all the extracted JFF values are specified in Table S9†).
| p-Borane adduct | Detected atropisomer | |||
|---|---|---|---|---|
| α | β | γ | δ | |
| p–I | a T s V h T (85%) | a T a V h T (10%) | a T s V h V (3%) | s V s T h T (2%) |
| p–II | a T h T (51%) | a T s V (30%) | h T s V (19%) | |
| p–III | a T (61%) | h T (30%) | s V (9%) | |
Kinetic stability of the piperidine-borane adducts
At room temperature, due to the kinetic lability of the dative p–III adduct, the sp2III and the p–III atropisomeric states are not detectable as they are in fast exchange at the NMR timescale (Fig. S15†). In contrast, for the p + II and p + I systems the respective sp2 state and dative adduct atropisomer signals are resolved (p + II: e.g.Fig. 5 or S16;†p + I: e.g. Fig. S17†). Notably, for the p + II and p + I systems applying the piperidine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) borane = 1
borane = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio or excess of piperidine, the sp2 borane signal remains unobservable due to the high conversion rate of piperidine and the boranes into the corresponding dative adducts. Thus, to detect the sp2 signal, excess of the borane is required.
1 ratio or excess of piperidine, the sp2 borane signal remains unobservable due to the high conversion rate of piperidine and the boranes into the corresponding dative adducts. Thus, to detect the sp2 signal, excess of the borane is required.
Further insights into the kinetic stability of the observed p-adducts were also gained through the temperature dependence of the linewidths in the corresponding 19F-NMR spectra. The NMR peaks of p–III resolve at low temperatures (<253 K) only; however, they display severe line broadenings throughout (Fig. S15†). At ∼273 K, the signals start to coalesce, and at higher temperatures a weighted average signal is visible that represents the fast-exchanging ensemble of the p–III atropisomers and the borane III (which notedly incorporates the ‘frustrated’ state). The signals of p–II display moderate line broadenings starting at 293 K and they remain in the slow exchange regime even at 333 K (Fig. S16†); while the signals of p–I do not display any broadenings unless the temperature is raised to 323 K (Fig. S17†). These results imply that the kinetic stability of the p-adducts follows the order of III < II < I which is in agreement with the thermodynamic trend predicted by computation.
Dynamic behavior of the piperidine-borane atropisomeric adducts
After observing the existence of multiple distinct atropisomeric LA–LB adducts at ambient temperature, we started to investigate their dynamic behavior in order to verify if the MLA can be assigned to these systems. To characterize the emerging dynamic behavior of the dative piperidine–borane adducts, two-dimensional 19F Exchange Spectroscopy (EXSY) measurements21 were performed in the slow exchange regime (for all the EXSY spectra, the extracted exchange rate constants and thermodynamic parameters see ESI Section 7.†) To retain the sp2-hybridized borane state observable throughout, the p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) borane ratio was inverted to 1
borane ratio was inverted to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
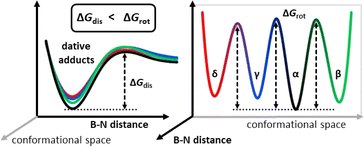
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in the mixtures of p with I or II. Under optimal experimental conditions (temperature, mixing time) the corresponding 2D 19F EXSY spectra show qualitatively the same behavior for all the p-adducts, see that of the p + II system as illustrated in Fig. 7 (p + III: ESI Fig. S31, p + I: Fig. S33†). That is, each fluorine resonance of any chosen p-adduct atropisomer shows correlation peaks with those of its other atropisomers and with the corresponding sp2 form as well. These respectively indicate that on the timescale of the experiments the simultaneously existing p-adduct atropisomeric states are in slow exchange with each other; meanwhile, they undergo rapid dissociation and reassociation of the B–N dative bond through the dissociated states of the atropisomeric adduct. The exchange processes and the related barriers are illustrated in Fig. 8 in terms of schematic free energy surface projections. Based on the corresponding conformational exchange rates and dissociation rates (p–I: Table S16, p–II: Table S13, and p–III: Table S11†) extracted from the EXSY peak integrals (ESI Section 1.1†), for any given atropisomeric state of p–I or p–III its exchange with another atropisomer is generally 1–2 orders of magnitude slower than its dissociation. Unfortunately, signal overlaps prevented us from unequivocally quantifying the exchange rates for p–II with the free borane II (Fig. S10†). Nevertheless, a 2D 19F EXSY spectrum was recorded on the p–II system with minimal mixing time (2 ms) that displays the exchanges of p–II with the free borane II while the atropisomeric exchanges remain unobservable (Fig. S32†). Furthermore, for p–I and p–II the atropisomeric exchanges appear to be parallel in terms of fluorine NMR exchanges, that is, any F atom of a detected atropisomer undergoes chemical exchanges with all the F atoms of each detected atropisomer. The exchange rates of the different F-pairs that can be associated with the same atropisomeric exchange fall within an order of magnitude (Table S12†). Consequentially, upon an atropisomeric exchange process there is no correlation between the initial and final position of the F atoms, that is, the orientation of the aryl rings. All these imply that, for the atropisomeric exchanges of these p-borane adducts, neither free nor correlated rotation22 around B(sp3)–Ar(sp2) or B(sp3)–N(sp3) single bonds of the dative adduct is operative. Thus, the atropisomeric exchanges for the investigated p-adducts, i.e. their conformational isomerism rather take place through the sp2 borane state where the rotations of the aryl rings are free and essentially, they occur as the side-processes of the dissociation–reassociation equilibrium between p and the borane (Fig. 8). Accordingly, all p-borane atropisomers are formed in different chemical reactions between the same Lewis acid (I, II or III) and base (p) which directly proves the concept of MLA for these triaryl-boranes. To further corroborate this finding, a series of DFT potential energy surface scans were performed using the p–II(α) and II structures (ESI Section 8†). These showed that in contrast with the sp2 borane state (12–14 kcal mol−1), rotations around the central B(sp3) atom (i.e. B–C and B–N bonds) are hampered in the dative bonded p-adduct state with the associated barrier heights ranging between 25 and 53 kcal mol−1. These values are also significantly higher than the experimentally measured barrier heights (17–20 kcal mol−1) for the atropisomeric exchanges of the p–II adduct (Table S14†) which demote the interconversion of the p-adduct atropisomeric states via internal rotations in comparison to the breaking of the dative B–N bond. Hence, in the case of these dative adducts, the non-stable dative bonding underlies the conformational dynamic equilibrium between their respective atropisomers via breaking and reforming the dative bond and it seems that these atropisomers have a rather rigid structure, ultimately adhering to the nomenclature ‘atropos’, i.e. ‘without turn’.
2 in the mixtures of p with I or II. Under optimal experimental conditions (temperature, mixing time) the corresponding 2D 19F EXSY spectra show qualitatively the same behavior for all the p-adducts, see that of the p + II system as illustrated in Fig. 7 (p + III: ESI Fig. S31, p + I: Fig. S33†). That is, each fluorine resonance of any chosen p-adduct atropisomer shows correlation peaks with those of its other atropisomers and with the corresponding sp2 form as well. These respectively indicate that on the timescale of the experiments the simultaneously existing p-adduct atropisomeric states are in slow exchange with each other; meanwhile, they undergo rapid dissociation and reassociation of the B–N dative bond through the dissociated states of the atropisomeric adduct. The exchange processes and the related barriers are illustrated in Fig. 8 in terms of schematic free energy surface projections. Based on the corresponding conformational exchange rates and dissociation rates (p–I: Table S16, p–II: Table S13, and p–III: Table S11†) extracted from the EXSY peak integrals (ESI Section 1.1†), for any given atropisomeric state of p–I or p–III its exchange with another atropisomer is generally 1–2 orders of magnitude slower than its dissociation. Unfortunately, signal overlaps prevented us from unequivocally quantifying the exchange rates for p–II with the free borane II (Fig. S10†). Nevertheless, a 2D 19F EXSY spectrum was recorded on the p–II system with minimal mixing time (2 ms) that displays the exchanges of p–II with the free borane II while the atropisomeric exchanges remain unobservable (Fig. S32†). Furthermore, for p–I and p–II the atropisomeric exchanges appear to be parallel in terms of fluorine NMR exchanges, that is, any F atom of a detected atropisomer undergoes chemical exchanges with all the F atoms of each detected atropisomer. The exchange rates of the different F-pairs that can be associated with the same atropisomeric exchange fall within an order of magnitude (Table S12†). Consequentially, upon an atropisomeric exchange process there is no correlation between the initial and final position of the F atoms, that is, the orientation of the aryl rings. All these imply that, for the atropisomeric exchanges of these p-borane adducts, neither free nor correlated rotation22 around B(sp3)–Ar(sp2) or B(sp3)–N(sp3) single bonds of the dative adduct is operative. Thus, the atropisomeric exchanges for the investigated p-adducts, i.e. their conformational isomerism rather take place through the sp2 borane state where the rotations of the aryl rings are free and essentially, they occur as the side-processes of the dissociation–reassociation equilibrium between p and the borane (Fig. 8). Accordingly, all p-borane atropisomers are formed in different chemical reactions between the same Lewis acid (I, II or III) and base (p) which directly proves the concept of MLA for these triaryl-boranes. To further corroborate this finding, a series of DFT potential energy surface scans were performed using the p–II(α) and II structures (ESI Section 8†). These showed that in contrast with the sp2 borane state (12–14 kcal mol−1), rotations around the central B(sp3) atom (i.e. B–C and B–N bonds) are hampered in the dative bonded p-adduct state with the associated barrier heights ranging between 25 and 53 kcal mol−1. These values are also significantly higher than the experimentally measured barrier heights (17–20 kcal mol−1) for the atropisomeric exchanges of the p–II adduct (Table S14†) which demote the interconversion of the p-adduct atropisomeric states via internal rotations in comparison to the breaking of the dative B–N bond. Hence, in the case of these dative adducts, the non-stable dative bonding underlies the conformational dynamic equilibrium between their respective atropisomers via breaking and reforming the dative bond and it seems that these atropisomers have a rather rigid structure, ultimately adhering to the nomenclature ‘atropos’, i.e. ‘without turn’.
Conclusions
In summary, we demonstrated the emergence of a noteworthy molecular phenomenon, the single-centered, but multiple Lewis acidity for specific Lewis acidic boranes. The observation of this particular property was possible for ortho-halogenated triaryl-boranes, I, II and III, with appropriate steric crowding and symmetry design around the Lewis acidic center. These boranes proved to be able to form atropisomeric and kinetically labile dative adducts with piperidine owing to their inherent structural anisotropy and hindered internal rotation in the LA–LB adducts around the B(sp3)–Ar(sp2) and B(sp3)–N(sp3) bonds. The static and dynamic properties of the atropisomeric, dative piperidine-borane adduct ensembles were investigated by NMR spectroscopy and computational structural analysis. Notably, the evolving back strain upon dative adduct formation influenced not only the thermodynamics but also the kinetics of the dissociative equilibria in which the atropisomeric interconversions are fundamentally dissociative in nature as they take place via the ‘frustrated’ or the entirely dissociated state of the sp2 borane. In addition to revealing a non-conventional molecular phenomenon via elusive dative adduct atropisomers, these findings are expected to broaden the current conceptual framework of Lewis acidity and draw attention to the possible emergence of a more complex scenario upon Lewis acidity strength assessment. Additionally, our work provides a tool that is ready to be placed at the disposal of chemists to evoke this property and may open new vistas for the deliberate design of diastereomeric assemblies in materials and biological science23 and development of homogeneous confined catalysts with built-in functionality or higher-order stereogenicity.24Data availability
The data that supports the findings of this study are available in the ESI of this article.†Author contributions
B. Kovács assigned the p-borane adduct atropisomers and created the original drafts of the manuscript together with T. S. and T. F. The NMR measurements were performed by M. S., and B. Kovács and A. D. M. S. obtained the kinetic and thermodynamic data of the p-borane adducts. The computations were designed and analyzed by T. F. with the contribution of B. Kótai and G. L. under the supervision of I. P. The X-ray structures were determined by T. H. É. D. synthesized the boranes and prepared the NMR samples. The concept of multiple Lewis acidity was conceived by T. S. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the National Research, Development, and Innovation Office (NKFIH) is gratefully acknowledged (grants K-142486, K-147280 and ÚNKP-23-3-I-ELTE-206). We greatly appreciate the referees' insightful and helpful comments on our manuscript, which improved its quality and clarity.Notes and references
- Selected reviews: (a) R. W. Hoffmann, Angew. Chem., Int. Ed., 1992, 31(9), 1124–1134 CrossRef; (b) S. D. Appavoo, S. Huh, D. B. Diaz and A. K. Yudin, Chem. Rev., 2019, 119(17), 9724–9752 CrossRef CAS PubMed; (c) H. K. Ganguly and G. Basu, Biophys. Rev., 2020, 12(1), 25–39 CrossRef CAS PubMed.
- Recent studies focusing on conformers: (a) G. C. A. da Hora, M. Oh, M. C. Mifflin, L. Digal, A. G. Roberts and J. M. J. Swanson, J. Am. Chem. Soc., 2024, 146(7), 4444–4454 CrossRef CAS PubMed; (b) S. H. Rüdisser, E. Matabaro, L. Sonderegger, P. Güntert, M. Künzler and A. D. Gossert, J. Am. Chem. Soc., 2023, 145(50), 27601–27615 CrossRef PubMed; (c) R. K. R. Sannapureddi, M. K. Mohanty, L. Salmon and B. Sathyamoorthy, J. Am. Chem. Soc., 2023, 145(28), 15370–15380 CrossRef CAS PubMed; (d) X. Fu, B. Zhu and X. Hu, J. Am. Chem. Soc., 2023, 145(29), 15668–15673 CrossRef CAS PubMed; (e) E. B. Crull, A. N. Jain, P. C. D. Hawkins, A. E. Cleves, E. I. Graziani and R. T. Williamson, J. Nat. Prod., 2023, 86(7), 1862–1869 CrossRef CAS PubMed; (f) C. M. Nunes, J. P. L. Roque, S. Doddipatla, S. A. Wood, R. J. McMahon and R. Fausto, J. Am. Chem. Soc., 2022, 144(45), 20866–20874 CrossRef CAS PubMed; (g) F. Bohle and S. Grimme, Angew. Chem., Int. Ed., 2022, 61(14), e202113905 CrossRef CAS PubMed; (h) B. Linclau, Z. Wang, B. Jeffries, J. Graton, R. J. Carbajo, D. Sinnaeve, J.-Y. Le Questel, J. S. Scott and E. Chiarparin, Angew. Chem., Int. Ed., 2022, 134(7), e202114862 CrossRef; (i) R. Costil, A. J. Sterling, F. Duarte and J. Clayden, Angew. Chem., Int. Ed., 2020, 59(42), 18768–18773 CrossRef PubMed; (j) P. J. Canfield, I. M. Blake, Z.-L. Cai, I. J. Luck, E. Krausz, R. Kobayashi, J. R. Reimers and M. J. A Crossley, Nat. Chem., 2018, 10(6), 615–624 CrossRef CAS PubMed.
- Selected examples: (a) K. Iizuka, H. Takezawa and M. Fujita, J. Am. Chem. Soc., 2023, 145(48), 25971–25975 CrossRef CAS PubMed; (b) R. E. Looper, D. Pizzirani and S. L. Schreiber, Org. Lett., 2006, 8(10), 2063–2066 CrossRef CAS PubMed; (c) M. Kindermann, I. Stahl, M. Reimold, W. M. Pankau and G. von Kiedrowski, Angew. Chem., Int. Ed., 2005, 117(41), 6908–6913 CrossRef; (d) H. Yamataka, O. Aleksiuk, S. E. Biali and Z. Rappoport, J. Am. Chem. Soc., 1996, 118(50), 12580–12587 CrossRef CAS; (e) R. S. Brown, H. Slebocka-Tilk, A. J. Bennet, G. Bellucci, R. Bianchini and R. Ambrosetti, J. Am. Chem. Soc., 1990, 112(17), 6310–6316 CrossRef CAS; (f) Z. Rappoport and S. E. Biali, Acc. Chem. Res., 1988, 21(12), 442–449 CrossRef CAS; (g) T. T. Tidwell, Tetrahedron, 1978, 34(13), 1855–1868 CrossRef CAS; (h) S. Milstien and L. A. Cohen, Proc. Natl. Acad. Sci. U.S.A., 1970, 67(3), 1143–1147 CrossRef CAS PubMed; (i) T. Hannah and S. S. Chitnish, Chem. Soc. Rev., 2024, 53(2), 764–792 RSC; (j) A. Maiti, R. Yadav and L. Greb, Adv. Inorg. Chem., 2023, 82, 261–299 CrossRef.
- Selected examples: (a) Z. Zong, Q. Zhang, S.-H. Qiu, Q. Wang, C. Zhao, C.-X. Zhao, H. Tian and D.-H. Qu, Angew. Chem., Int. Ed., 2022, 61(13), e202116414 CrossRef CAS PubMed; (b) S. Neubacher and S. Hennig, Angew. Chem., Int. Ed., 2019, 58(5), 1266–1279 CrossRef CAS PubMed; (c) E. Y. Zhou, H. J. Knox, C. Liu, W. Zhao and J. Chan, J. Am. Chem. Soc., 2019, 141(44), 17601–17609 CrossRef CAS PubMed; (d) A. S. Walker, P. R. Rablen and A. Schepartz, J. Am. Chem. Soc., 2016, 138(22), 7143–7150 CrossRef CAS PubMed; (e) W. Zhao and E. M. Carreira, Angew. Chem., 2005, 117(11), 1705–1707 CrossRef.
- (a) B. Prajapati, M. D. Ambhore, D.-K. Dang, P. J. Chmielewski, T. Lis, C. J. Gómez-García, P. M. Zimmerman and M. Stępień, Nat. Chem., 2023, 15, 1541–1548 CrossRef CAS PubMed; (b) P. Yang, M. J. Širvinskas, B. Li, N. W. Heller, H. Rong, G. He, A. K. Yudin and G. Chen, J. Am. Chem. Soc., 2023, 145(25), 13968–13978 CrossRef CAS PubMed; (c) D. B. Diaz, S. D. Appavoo, A. F. Bogdanchikova, Y. Lebedev, T. J. McTiernan, G. dos Passos Gomes and A. K. Yudin, Nat. Chem., 2021, 13(3), 218–225 CrossRef CAS PubMed; (d) I. Columbus, R. E. Hoffman and S. E. Biali, J. Am. Chem. Soc., 1996, 118(29), 6890–6896 CrossRef CAS; (e) O. Golan, Z. Goren and S. E. Biali, J. Am. Chem. Soc., 1990, 112(25), 9300–9307 CrossRef CAS.
- Selected examples: (a) L.-P. Yang, L. Zhang, M. Quan, J. S. Ward, Y.-L. Ma, H. Zhou, K. Rissanen and W. Jiang, Nat. Commun., 2020, 11(1), 2740 CrossRef CAS PubMed; (b) T. Suzuki, S. Yanaka, T. Watanabe, G. Yan, T. Satoh, H. Yagi, T. Yamaguchi and K. Kato, Biochemistry, 2019, 59(34), 3180–3185 CrossRef PubMed; (c) D. W. Carney, K. R. Schmitz, J. V. Truong, R. T. Sauer and J. K. Sello, J. Am. Chem. Soc., 2014, 136(5), 1922–1929 CrossRef CAS PubMed; (d) M. A. Campbella and J. Wengel, Chem. Soc. Rev., 2011, 40(12), 5680–5689 RSC; (e) S. J. Miller and R. B. Grubbs, J. Am. Chem. Soc., 1995, 117(21), 5855–5856 CrossRef CAS.
- IUPAC, Compendium of Chemical Terminology, 2nd edn (the “Gold Book”), 1997, Online corrected version: (2006–) “Lewis acid”, DOI:10.1351/goldbook.L03508.
- The definition and role of confinement in homogeneous catalysis: B. Mitschke, M. Turberg and B. List, Chem, 2020, 6, 2515–2532 CAS.
- Examples can be found scattered in the literature where the possibility of multiple adduct formation is raised as a result of directional anisotropy: (a) A. Poater, X. Solans-Monfort, E. Clot, C. Copéret and O. Eisenstein, J. Am. Chem. Soc., 2007, 129(26), 8207–8216 CrossRef CAS PubMed; (b) A. Hamza, K. Sorochkina, B. Kótai, K. Chernichenko, D. Berta, M. Bolte, M. Nieger, T. Repo and I. Pápai, ACS Catal., 2020, 10(23), 14290–14301 CrossRef CAS; (c) L. Zapf, M. Riethmann, S. A. Föhrenbacher, M. Finze and U. Radius, Chem. Sci., 2023, 14(9), 2275–2288 RSC , Experimental structural studies: ; (d) I. D. Gridnev and T. Imamoto, Acc. Chem. Res., 2004, 37(9), 633–644 CrossRef CAS PubMed; (e) P. Chaudhary, J. T. Goettel, H. P. A. Mercier, S. Sowlati-Hashjin, P. Hazendonk and M. Gerken, Chem. - Eur. J., 2015, 21(16), 6247–6256 CrossRef CAS PubMed; (f) A. M. R. Hall, D. B. G. Berry, J. N. Crossley, A. Codina, I. Clegg, J. P. Lowe, A. Buchard and U. Hintermair, ACS Catal., 2021, 11(21), 13649–13659 CrossRef CAS PubMed; (g) J. Bykowski, D. Turnbull, N. Hahn, R. T. Boeré, S. D. Wetmore and M. Gerken, Inorg. Chem., 2021, 60(20), 15695–15711 CrossRef CAS PubMed , Structurally analogous boranes have been synthesized; however, neither the theoretical possibility of the multiple Lewis acidity phenomenon had previously been conceptualized nor had the multiple Lewis acidity phenomenon been perceived: ; (h) S. Toyota, M. Asakura, M. Ōki and F. Toda, Bull. Chem. Soc. Jpn., 2000, 73(10), 2357–2362 CrossRef CAS; (i) M. Kemper, E. Engelage and C. Merten, Angew. Chem., Int. Ed., 2021, 60(6), 2958–2962 CrossRef CAS PubMed , Finally, multiple adduct formation can be the result of multiple Lewis basicity. In this respect many prominent ligands can be found in the literature which may raise the issue of multiple Lewis basicity. Selected examples: ; (j) M. Kosugi, M. Kameyama and T. Migita, Chem. Lett., 1983, 12(6), 927–928 CrossRef; (k) A. Zapf, R. Jackstell, F. Rataboul, T. Riermeier, A. Monsees, C. Fuhrmann, N. Shaikh, U. Dingerdissen and M. Beller, Chem. Commun., 2004, 38–39 RSC; (l) D. S. Surry and S. L. Buchwald, Chem. Sci., 2010, 2, 27–50 RSC; (m) Z. L. Niemeyer, A. Milo, D. P. Hickey and M. S. Sigman, Nat. Chem., 2016, 8, 610–617 CrossRef CAS PubMed; (n) S. Zhao, T. Gensch, B. Murray, Z. L. Niemeyer, M. S. Sigman and M. R. Biscoe, Science, 2018, 362, 670–674 CrossRef CAS PubMed; (o) J. W. Lehmann, I. T. Crouch, D. J. Blair, M. Trobe, P. Wang, J. Li and M. D. Burke, Nat. Commun., 2019, 10, 1263 CrossRef PubMed , Additionally, there are some studies that have indicated the ability of certain Lewis basic ligands to have multiple bonding modes, but their NMR studies revealed that these scenarios are analogous to case B in Fig. 2 and can therefore be considered a single Lewis basicity. See for example: ; (p) M. T. Ashby, J. Am. Chem. Soc., 1995, 117(7), 2000–2007 CrossRef CAS; (q) R. A. Widenhoefer, H. A. Zhong and S. L. Buchwald, Organometallics, 1996, 15(12), 2745–2754 CrossRef CAS; (r) J. A. S. Howell, M. G. Palin, P. McArdle, D. Cunningham, Z. Goldschmidt, H. E. Gottlieb and D. Hezroni-Langerman, Inorg. Chem., 1991, 30(25), 4685–4687 CrossRef; (s) S. H. Newman-Stonebraker, J. Y. Wang, P. D. Jeffrey and A. G. Doyle, J. Am. Chem. Soc., 2022, 144(42), 19635–19648 CrossRef CAS PubMed.
- M. Ōki, The Chemistry of Rotational Isomers, Springer, Berlin, Heidelberg, 1993, pp. 20–50 Search PubMed.
- (a) D. W. Stephan and G. E. Erker, Angew. Chem., Int. Ed., 2010, 49(1), 46–76 CrossRef CAS PubMed; (b) T. Soós, Pure Appl. Chem., 2011, 83(3), 667–675 Search PubMed; (c) D. W. Stephan, Science, 2016, 354, aaf7229 CrossRef PubMed 6317.
- (a) T. A. Rokob, A. Hamza, A. Stirling, T. Soós and I. Pápai, Angew. Chem., 2008, 120(13), 2469–2472 CrossRef; (b) A. Hamza, A. Stirling, T. A. Rokob and I. Pápai, Int. J. Quantum Chem., 2009, 109(11), 2416–2425 CrossRef CAS.
- É. Dorkó, M. Szabó, B. Kótai, I. Pápai, A. Domján and T. Soós, Angew. Chem., 2017, 129(32), 9640–9644 CrossRef . In this work for I, II and III, the reduction potentials determined in dichloromethane by CV: −2.1V, −2.0V, and −1.9V; the Gutmann–Beckett relative strength: 77%, 5%, and 4%; the relative hydricity (kcal mol−1, the lower energy value refers to weaker Lewis acidity): −15.3, −16.0, and −17.2..
- (a) To understand the offset between some Lewis acidity scales and effort towards the unification of various Lewis acidity scales, see: P. Erdmann and L. Greb, Angew. Chem., 2022, 134(4), e202114550 CrossRef; (b) Further effort to develop a quantitative and Lewis-base-independent metric of Lewis acidity: A. R. Jupp, T. C. Johnstone and D. W. Stephan, Dalton Trans., 2018, 47(20), 7029–7035 RSC.
- (a) U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257 CrossRef CAS; (b) M. A. Beckett, G. C. Strickland, J. R. Holland and K. S. A Varma, Polymer, 1996, 37(20), 4629–4631 CrossRef CAS.
- We also calculated the fluoride ion affinities of the rotamers of Lewis acid I as fluoride is the hard-type Lewis base analog of the hydride. This study showed that the hard-type ligand neither changed the trend nor affected the energy differences between the atropisomeric dative adducts (ESI Section 10†). For a related analysis demonstrating that fluoride, hydride, and hydroxide affinities follow the same trends and relative energy differences towards Ar2CH+ cations, see: C. Schindele, K. N. Houk and H. Mayr, J. Am. Chem. Soc., 2002, 124, 11208–11214 CrossRef CAS PubMed.
- Recent evidence suggests that the conformational stabilization in certain macrocycles is primarily due to intramolecular hydrogen bonding, which acts as a “structural pin”: S. D. Appavoo, N. W. Heller, C. T. van Campenhout, G. J. Saunders and A. K. Yudin, Angew. Chem., Int. Ed., 2024, 63(28), e202402372 CrossRef CAS PubMed.
- 19F–1H HOESY studies towards establishing hydrogen–fluorine internuclear distances in fluorinated organic compounds and adducts: (a) G. Ciancaleoni, R. Bertani, L. Rocchigiani, P. Sgarbossa, C. Zuccaccia and A. Macchioni, Chem. - Eur. J., 2015, 21(1), 440–447 CrossRef CAS PubMed; (b) Y. Lingscheid, M. Paul, A. Bröhl, J.-M. Neudörfl and R. Giernoth, Magn. Reson. Chem., 2018, 56(2), 80–85 CrossRef CAS PubMed; (c) L. Dewis, R. Crouch, D. Russell and C. Butts, Magn. Reson. Chem., 2019, 57(12), 1143–1149 CrossRef CAS PubMed; (d) Q. M. Dang, J. H. Simpson, C. A. Parish and M. C. Leopold, J. Phys. Chem. A, 2021, 125(42), 9377–9393 CrossRef CAS PubMed.
- For hydrogen bond JHF values: (a) G. N. M. Reddy, M. V. V. Kumar, T. N. G. Row and N. Suryaprakash, Phys. Chem. Chem. Phys., 2010, 12, 13232–13237 RSC; (b) D. Kumari, S. Hebbar and N. Suryaprakash, Chem. Phys. Lett., 2012, 525, 129–133 CrossRef; (c) S. R. Chaudhari, S. Mogurampelly and N. Suryaprakash, J. Phys. Chem. B, 2013, 117(4), 1123–1129 CrossRef CAS PubMed.
- On through-space 19F–19F couplings in multifluorinated organic compounds and adducts: (a) L. Ernst and K. A. Ibrom, Angew. Chem., Int. Ed., 1995, 34(17), 1881–1882 CrossRef CAS; (b) F. B. Mallory, C. W. Mallory, K. E. Butler, M. B. Lewis, A. Q. Xia, E. D. Luzik, L. E. Fredenburgh, M. M. Ramanjulu, Q. N. Van, M. M. Francl, D. A. Freed, C. C. Wray, C. Hann, M. Nerz-Stormes, P. J. Carroll and L. E. Chirlian, J. Am. Chem. Soc., 2000, 122(17), 4108–4116 CrossRef CAS; (c) J.-C. Hierso, Chem. Rev., 2014, 114(9), 4838–4867 CrossRef CAS; (d) H. W. Orton, H. Qianzhu, E. H. Abdelkader, E. I. Habel, Y. J. Tan, R. L. Frkic, C. J. Jackson, T. Huber and G. Otting, J. Am. Chem. Soc., 2021, 143(46), 19587–19598 CrossRef CAS PubMed.
- Selected EXSY applications in coordination chemistry: (a) A. Pastor and E. Martínez-Viviente, Coord. Chem. Rev., 2008, 252(21–22), 2314–2345 CrossRef CAS; (b) M. B. Schmid, K. Zeitler and R. M. Gschwind, Angew. Chem., Int. Ed., 2010, 29(49), 4997–5003 CrossRef PubMed; (c) K. A. D'Angelo and M. S. Taylor, J. Am. Chem. Soc., 2016, 138(34), 11058–11066 CrossRef PubMed.
- H. Iwamura and K. Mislow, Acc. Chem. Res., 1988, 21(4), 175–182 CrossRef CAS.
- Z. Liu, Z. Zhang and R. O. Ritchie, Adv. Funct. Mater., 2020, 30(10), 1908121 CrossRef CAS.
- (a) X. Wu, R. M. Witzig, R. Beaud, C. Fischer, D. Häussinger and C. Sparr, Nat. Catal., 2021, 4(6), 457–462 CrossRef CAS; (b) T. A. Schmidt and C. Sparr, Acc. Chem. Res., 2021, 54(12), 2764–2774 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2004799 and 2004800. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc00925h |
| This journal is © The Royal Society of Chemistry 2024 |