Multipodal Au–C grafting of calix[4]arene molecules on gold nanorods

Abstract

The interface robustness and spatial arrangement of functional molecules on metallic nanomaterials play a key part in the potential applications of functional nano-objects. The design of mechanically stable and electronically coupled attachments with the underlying metal is essential to bring specific desirable properties to the resulting hybrid materials. In this context, rigid multipodal platforms constitute a unique opportunity for the controllable grafting of functionality. Herein, we provide for the first time an in-depth description of the interface between gold nanorods and a chemically-grafted multipodal platform based on diazonium salts. Thanks to Raman and X-ray photoelectron spectroscopies and theoretical modeling, we deliver insights on the structural and electronic properties of the hybrid material. More importantly, it allows for the accurate assignment of Raman bands. The combination of experimental and theoretical results establishes the formation of four carbon–gold anchors for the calix[4]arene macrocycle leading to the exceptional stability of the functionalized nano-objects. Our results lay the foundations for the future design of robust and versatile platforms.

---

Introduction

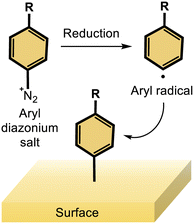
Ligands are crucial for the colloidal synthesis of nanomaterials, enabling the regulation of their sizes and morphologies, but their role goes well beyond this aspect. The binding of organic ligands to the metallic surface is an efficient method for increasing the robustness of metal nanoparticles, which is a critical point for many applications, but eventually also for boosting their specific properties. For instance, adequate surface modification improves the colloidal stability, biocompatibility and the antifouling ability for biological applications,^1–3 could confer or guide optoelectronics properties of the nano-object when significant level of coupling occurs between the ligand and the metal,⁴ or could increase the efficiency, the selectivity or the durability of nanocatalysts in several key electrocatalytic processes.^5–7 Hence, a wealth of surface chemistry approaches have been developed to tailor the ligand/metal interface, notably with gold nanoobjects, ranging from physisorption (electrostatic adsorption) to the more robust chemisorption of molecules or polymers. While thiolated derivatives are well-known capping ligands for gold nanoparticles thanks to strong Au–S bonds,^8,9 the reductive grafting of aryldiazonium salts forming Au–C bonds is nowadays recognized as a promising strategy for the design of strong interfaces.¹⁰

The reduction of an aryldiazonium function into the corresponding aryl radical enables a robust grafting of the aryl moiety onto a wide variety of materials (insulating, semi-conductor or metal), either as flat massive materials or nanomaterials (Scheme 1).^11,12 This strategy however often leads to the formation a multilayered coating. Interestingly, the controlled formation of monolayers has been demonstrated through a unique strategy developed by some of us, based on the reductive grafting of calix[4]arene tetra-diazonium salts.^13,14 Calix[4]arenes are macrocyclic molecules made up of four methylene-bridged aromatic subunits. In our approach, the calix[4]arene diazonium salts are constrained in a cone conformation, orienting the four diazonium moieties on the large rim of the calixarene. This rigid structure is exploited to design interesting molecular platforms for diazonium surface grafting, yielding well-packed and dense monolayers coating the surfaces. Thus, the reductive grafting of calix[4]arene tetra-diazonium salts onto gold, silver and platinum nanoparticles^15–17 has led to the preparation of electrocatalysts with excellent performances in oxygen reduction reaction (ORR) and methanol oxidation reaction (MOR) processes, notably because of their very good stability.^17,18 Similarly, this strategy enabled the development of various ultrastable calix[4]arene-coated silver and gold nanomaterials that were used for sensing applications in the biomedical field.^19,20

Scheme 1 Reductive grafting of an aryldiazonium salt on a surface.

Yet, little is known about the nature of the interface between the grafted calix[4]arene and the nano-objects. In particular, the multiple nature of the anchoring mode of the calix[4]arene to the metallic surfaces remains unclear. This aspect is of importance because multipodal ligands are particularly interesting building blocks since they allow for a better control of molecular interactions.^21–24 Notably, the perpendicular orientation of terminal functional groups with respect to the surface is more likely to be guided by the binding mode of a rigid scaffold. In addition, a multisite anchor should lead to significantly stronger adsorption, hence larger stability, and maximize electronic coupling between the ligands and the metal.^23,25,26 Rigid multipods are beneficial for controlling their lateral arrangement on the surface along with the spatial arrangement of the terminal exposed functional groups because of the sterically hindered footprint of such ligands. Especially for the calix[4]arene molecules herein, the spatial arrangement of terminal groups is dictated by the small rim geometry. Nevertheless, such architectures are generally built with thiols as anchoring moieties whereas multipodal rigid platforms are scarcely based on the diazonium anchoring function despite its strong interest. A key point is whether a four anchoring mode of the calix[4]arene is possible, especially when considering that the diazonium chemistry is a “one-shot” grafting procedure, rendering reorganization of the interface impossible, unlike the case with thiol-gold self-assembled monolayers.²⁷

To unravel the nature of the interface between the gold surface and the diazonium-derived aryl layer, Raman spectroscopy has been used for gold nano-objects, greatly benefiting from the coupling with quantum chemistry calculations for the assignment of bands.^28,29 Unfortunately, these theoretical treatments often require models that represent the metal surface as small size molecular clusters to reduce the computational effort, which can be detrimental to the modeling of spectroscopic signatures.^30–33 However, the use of the computationally efficient density functional tight-binding (DFTB) approach can circumvent this limitation.^34–36 In particular, DFTB has been shown to accurately describe both ground and excited states of gold–organics hybrid materials^37–40 with an adapted set of parameters.⁴¹ Interestingly, this framework extends beyond the typical size limitations of standard DFT models for Raman spectra simulation,⁴² facilitating the comparison with experimental data.

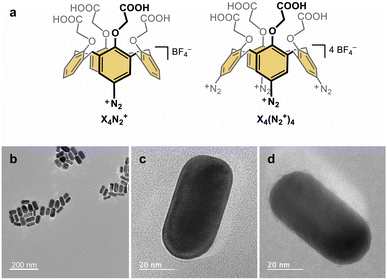
In this work, we present the original synthesis of gold nanorods functionalized with the monopodal calix[4]arene mono-diazonium X₄N₂⁺ and the multipodal calix[4]arene tetra-diazonium X₄(N₂⁺)₄ bearing four carboxyl groups at their small rim (Fig. 1a). Despite, their strong capping to the nanorods, we successfully exchange the CTAB surfactants by the calix[4]arene molecules. Using a combination of UV-visible absorption spectroscopy, high-resolution transmission electron microscopy (HRTEM), X-ray photoelectron spectroscopy (XPS), Raman spectroscopy, and a theoretical description within the DFTB framework, we shed light on the gold–carbon hybrid interface. After characterizing the nature of the bonds, we thoroughly detail the Raman spectra of the mono- and tetrapodal calix[4]arenes grafted on the gold nanorods surface. The combination of experimental and computed spectra allows us to rationalize the shifts of the Au–C bond peaks as a function of the anchoring configuration. Our findings demonstrate the utility of Raman spectroscopy in identifying the number of Au–C bonds per molecule and establish that multipodal grafting is achieved through diazonium chemistry owing to the rigid macrocyclic structure of calix[4]arene. The four-anchoring mode is found to be the most favorable binding mode for the tetrapodal calix[4]arene, demonstrating that such a calixarene coating yields a very stable and well-structured hybrid scaffold, useful as a building block for electrocatalysis or sensing.

Fig. 1 (a) Structures of calix[4]arene mono-diazonium, X₄N₂⁺, and calix[4]arene tetra-diazonium, X₄(N₂⁺)₄, salts. TEM images of capped gold nanorods functionalized with (b) CTAB, (c) X₄N₂⁺, and (d) X₄(N₂⁺)₄.

Results and discussion

Synthesis of gold nanorods coated with calix[4]arene molecules

Functionalization of the gold nanorods is achieved through a ligand exchange route. Firstly, gold nanorods capped with CTAB surfactants are synthesized through the seed-mediated growth method.⁴³ CTAB-capped gold seeds are added to an aqueous solution containing HAuCl₄, CTAB, and AgNO₃ in the presence of a mild reducing agent (ascorbic acid), allowing the anisotropic growth process. Gold nanorods are obtained with an aspect ratio of ca. 2.2, having an average length of 62.1 ± 6.0 nm and a small axis D of 27.7 ± 3.8 nm (Fig. 1b–d). For the functionalization of the gold nanorods with X₄N₂⁺ and X₄(N₂⁺)₄, NaBH₄ is added to the nanorod suspensions before the addition of the calix[4]arene diazonium salts.^44,45 NaBH₄ allows the reduction of the calix[4]arene diazonium salts and helps in the removal of CTAB surfactants thanks to the high affinity of hydride ions for gold.

UV-visible absorption spectroscopy and transmission electron microscopy

The electronic absorption spectra are recorded before the addition of NaBH₄, after the addition of NaBH₄ (under stirring) and after addition of calix[4]arene diazonium salts and incubation overnight (Fig. S5, ESI†). As expected for anisotropic nanorods, the spectra exhibit two maximum absorption bands associated with the excitation of localized surface plasmons (LSP): the weaker band at ca. 520 nm corresponds to the LSP mode along the small axis (transverse mode), while a stronger and well-defined band at ca. 625 nm is attributed to the LSP along the main axis (longitudinal mode). A blue shift of the LSPR bands is observed following the addition of NaBH₄, notably for the longitudinal mode by 8–10 nm. Upon addition of calix[4]arene salts and overnight stirring, the bands are redshifted again as previously reported.^44,45 Such behaviour suggests that the CTAB are removed through borohydride addition and replaced by the calix[4]arene ligands. HRTEM analysis of the calix[4]arene-coated nanorods indicates the absence of significant etching of the materials due to the borohydride treatment (Fig. 1b–d, S6–S8 and Table S1, ESI†).

X-ray photoelectron spectroscopy

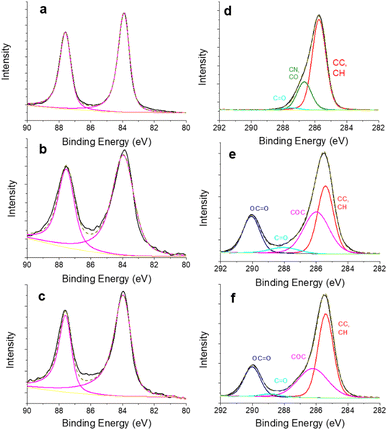
The surface composition of the gold nanorods is further analysed through XPS measurements. The colloids are simply deposited onto a silicon substrate. The survey spectra of the nanorods coated with CTAB and with the calix[4]arene ligands exhibit striking differences. The former spectrum shows photoelectron peaks attributed to bromine (Br 3p at 181.6 eV, 3.2% at.), nitrogen (N 1s at 403 eV, 2.6% at.) and gold (Au 4f at 83.9 eV, 1.4% at.), along with a dominant contribution of C 1s (285.5 eV, 81.5% at.) (Fig. S9, ESI†). The presence of N 1s and Br 3p accounts for the CTAB surfactant. In contrast, the latter spectra corresponding to calix[4]arene-coated nanorods mainly display photoelectron peaks due to C 1s and O 1s, without any contribution of Br 3p and with little or no contribution of N 1s signal. These observations suggest the efficient removal of CTAB. To get further insights into the surface chemistry of the gold nanorods, high resolution core level spectra of C 1s and Au 4f regions are recorded and peak-fitted (Fig. 2). For the three samples, the Au 4f regions show the characteristic doublet structure of Au 4f_7/2 and Au f_5/2 with an energy separation of 3.65 eV (Fig. 2a–c). The peaks are adequately fitted with an asymmetric lineshape, as expected for a metallic species. More interestingly, the C 1s signal is strongly different when comparing the nanorods capped with CTAB on the one hand and with calix[4]arene molecules on the other hand (Fig. 2d–f).

Fig. 2 High resolution core level peak-fitted spectra for (a–c) the Au 4f, and (d–f) C 1s regions of gold nanorods deposited onto silicon substrates. (a and d) CTAB capped gold nanorods, (b and e) gold nanorods coated from X₄N₂⁺, and (c and f) from X₄(N₂⁺)₄.

The C 1s signal of CTAB coated nanorods can be decomposed into two components that agree with the CTAB structure along with contributions (C–O, C=O) due to carbon contamination, which is usually observed. As expected, the C 1s signals for the calix[4]arene capped nanorods are similar and can be decomposed into three main components, at 285.4 ± 0.1 eV for carbon atoms involved in C–C, C–H bonds, at 286.1 ± 0.1 eV for carbon atoms in C–O–C bonds and at 289.9 ± 0.2 eV for carbons atoms involved in the carboxylate termini. A small contribution (2–6%) at 288.9 eV can be assigned to C=O functions, probably due to carbonaceous contamination. The atomic ratio for C–O–C and O–C=O components are equal to 1.75 and 1.8 for the monopodal and multipodal calix[4]arenes, respectively. These values are close to the expected theoretical value equal to 2 for a calix[4]arene structure. All the XPS observations suggest that the CTAB have been successfully removed from the surface, and efficiently replaced by the calix[4]arenes. However, no further information concerning the exact nature of the gold/ligand interface with the calix[4]arene moieties could be drawn from our XPS measurements, notably because the electronegativity of C and Au are very close (2.55 and 2.54, respectively according to the Pauling scale). Thus we engage in a computational investigation coupled with Raman spectroscopic analysis to reach a fine description of the two types of calix[4]arenes grafting.

Adsorption energies

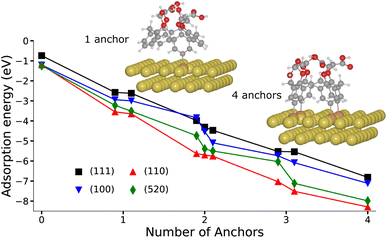
We perform calculations based on the self-consistent charge density functional tight-binding (SCC-DFTB) method (see ESI for Computational details†) to characterize the electronic and structural properties of the grafted layers from X₄N₂⁺ and X₄(N₂⁺)₄ onto gold nanorods. The expected morphology for gold nanorods synthesized in the described synthetic conditions (vide supra) consists in (110) and (100), and possibly (520), facets on the side, while tips present a mixture of (111) and (110) facets.^46,47 Because of the respective dimensions of the molecule and of the planes of gold atoms found in a gold nanorod with a diameter greater than 20 nm, we approximate the nanorod by a series of surfaces (see ESI†).

Various cases must be considered for the interaction between calix[4]arene and Au surfaces (Fig. S10–S13 ESI†). For X₄N₂⁺, after reduction of the diazonium group, the molecule presents one phenyl radical that can form an Au–C bond. However, for X₄(N₂⁺)₄, four phenyl radical anchors are in principle available. In that case, we consider the creation of 1 to 4 bonds with the gold surface, with hydrogen atoms saturating the unbound radicals in the 1, 2 and 3 bonds configurations. Finally, to cover the entire range of molecule/surface interactions, we also consider the case of a fully hydrogen-saturated calix[4]arene that cannot be involved in any Au–C bond.

Fig. 3 presents the variation of the adsorption energy with respect to the number of anchors for all possible conformers and regioisomers on the four considered facets. In the fully hydrogen-saturated calix[4]arene configuration, the molecule is only simply physisorbed on the gold surface with an adsorption energy varying between −0.74 and −1.24 eV, and a shortest Au–C distance comprised between 3.16 and 3.57 Å, depending on the facet (Tables S2 and S3, ESI†). When one phenyl radical is formed, hence yielding 1 possible anchor, the Au–C bonding distance is shortened to ca. 2.2 Å, and the adsorption energy vary among −2.58 to −3.65 eV. As the number of anchors is increased, the adsorption energy becomes more and more exothermic, reaching values for the 4-anchored molecule between −8.29 eV (Au(110)) and −6.81 eV (Au(111)). It is interesting to note that the adsorption energy per anchor is not constant but increases from an average of −3.13 eV for 1 anchor, to −1.89 eV for 4 anchors (Fig. S15 and Table S3, ESI†). This variation is due to the geometry distortions undergone by the gold surfaces and the molecule in order to create 4 Au–C bonds. However, the formation of 4 bonds from the calix[4]arene tetra-diazonium cations remains energetically very favourable.

Fig. 3 DFTB adsorption energies of calix[4]arene on Au(100), Au(110), Au(111), and Au(520) surfaces as a function of the number of anchors. Insets show the side view of the lowest energy geometries of the one and four anchored calix[4]arene on Au(111). H, C, O and Au atoms are depicted in white, grey, red, and yellow, respectively.

We explore further the nature of the Au–C bond by considering the density of states (DOS) projected on the orbitals of the C and Au atoms forming a bond in the case of the monopodal calix[4]arene (Fig. S16, ESI†). We observe overlapping peaks of C(2s,p), Au(6s,p) and Au(5d) orbitals near below and above the Fermi level. The partial charge densities computed at those peaks reveal the σ and σ* orbitals resulting from their hybridization establishing the existence of covalent Au–C bonds.

Raman spectroscopy

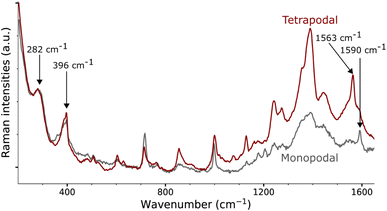
Gold nanorods functionalized from X₄N₂⁺ and X₄(N₂⁺)₄ are characterized by Raman spectroscopy using a 785 nm laser (Fig. 4, see ESI† for details). Both spectra show a strong signal below 250 cm⁻¹, due to peaks at 168 and 120 cm⁻¹. The first band at 168 cm⁻¹ could be assigned to Au–Br stretching originating from residual CTAB adsorption on gold surface.³¹ The second band at 120 cm⁻¹, which is of the highest intensity, is due to Au lattice vibration.⁴⁸ The assignment of other bands for these large molecules grafted on nanorods is conducted with the assistance of DFTB calculations.

Fig. 4 Experimental Raman spectra of mono- (grey line) and tetrapodal (red line) calix[4]arene on gold nanorods. The highlighted peaks correspond to modes involving large Au–C distance variations (see text).

In the case of gold nano-objects, the appearance of a shallow peak in the 400–550 cm⁻¹ region has also been used as a marker of successful covalent grafting.^{27,30–32,49–52} The Raman spectra of nanorods functionalized with the mono- and tetrapodal calix[4]arenes both show a peak at 396 cm⁻¹ (Fig. 4). This band is usually assigned to the stretching mode of the Au–C bond (ν_Au–C). However, this assignment comes from measurements performed on gold complexes with non-aromatic ligands (CO, CN, Me),^{30,31,48,49,53,54} and not on coated surfaces or nano-objects, which could greatly affect the position of the mode. In the following, we will once more depict the gold nanorod as a series of surfaces. Our approach will be illustrated on the Au(111) surface, a facet primarily found on the tips of the nanorods, where the plasmon-induced electric-field enhancement is the greatest considering the morphology of the nanorod and the excitation wavelength used.⁵⁵

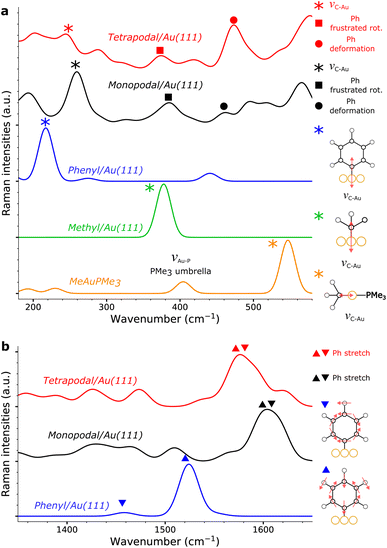
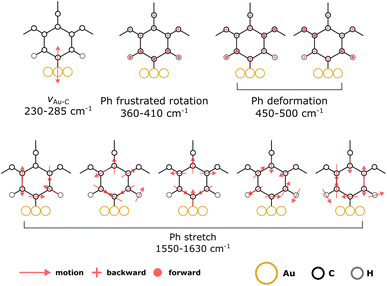
Within the SCC-DFTB model, we simulate the Raman spectra of three typical complexes used to identify ν_Au–C: Au(CN)₂⁻, MeAuPMe₃, and Me₃AuPMe₃ (Fig. 5a, S19 and S20, ESI†).^53,54 For each molecule, we describe the Au–C stretching mode with excellent accuracy (2% error) between 400 and 550 cm⁻¹ (Fig. 5a, Tables 1 and S4, ESI†), confirming the experimental assignment. However, when we no longer consider a gold complex, but a molecule anchored on a gold surface (e.g. methyl), the Au–C stretching mode is shifted towards lower frequencies, ν_Au–C = 378 cm⁻¹ (Fig. 5a and Table 1), in good agreement with the experimental assignment for an alkyl chain grafted on gold (ν_Au–C = 387 cm⁻¹).³² If we consider a system closer to the calix[4]arene molecule, as a phenyl anchored on Au(111), the shift becomes even greater with ν_Au–C = 218 cm⁻¹ (Fig. 5a and Table 1). Finally, considering the mono- and tetra-anchored calix[4]arene molecules on gold, we find groups of stretching modes at 230–285 cm⁻¹ (Fig. 5a and 6). These contributions fit well with the peak identified at 282 cm⁻¹ in both experimental spectra, that we can assign to the Au–C stretching mode ν_Au–C. The peak appearing at 396 cm⁻¹, initially assigned to the Au–C stretching mode, corresponds, in our simulations, to the frustrated rotations of the phenyl rings found at 360–410 cm⁻¹. Hence, the bands in the 200–600 cm⁻¹ area of the Raman spectra confirm the covalent grafting of both calix[4]arenes after reduction of their corresponding mono- and tetra-diazonium cations. However, there is no significant difference between the two systems, preventing us from determining the number of anchors that we can obtain from the tetra-diazonium molecule.

Fig. 5 (a) Simulated Raman spectra between 200 and 550 cm⁻¹ for the free-standing gold complex MeAuPMe₃ (Me = methyl, gold line), Me (green line) and phenyl (Ph, blue line) adsorbed on Au(111) and the mono- (black line) and tetrapodal (red line) calix[4]arene molecules chemisorbed on Au(111) after reduction of the X₄N₂⁺ and X₄(N₂⁺)₄ diazonium cations. A schematic representation of selected vibrational modes is provided. (b) Simulated Raman spectra between 1400 and 1600 cm⁻¹ for adsorbed Ph, mono- and tetrapodal calix[4]arene on Au(111) with schematic representation of selected modes.

Table 1 Computed Raman-active modes for the gold complex MeAuPMe₃, as well as methyl (Me) and phenyl (Ph) groups adsorbed on Au(111) with qualitative assignment of the vibrations. When available, the experimental reference is provided in parenthesis

Vibration	MeAuPMe3	Me/Au(111)	Ph/Au(111)
Au–C stretch (νAu–C)	546 (535 (ref. 53))	378	218
Ph stretch (νPh)			1458, 1524

---

Fig. 6 Schematic representation of selected vibrational modes of calix[4]arene adsorbed on Au(111).

A closer look at the simulated Raman spectrum of the phenyl chemisorbed on Au(111) reveals another interesting region around 1500 cm⁻¹ in which intense Raman peaks can be observed, corresponding to stretching modes of the phenyl ring, ν_Ph, indirectly affected by the Au–C bond (Fig. 5b and Table 1). The same modes are obtained in the simulated spectra of the grafted calix[4]arene (Fig. 5b and 6). Indeed, the mono-anchored molecule presents a peak at 1604 cm⁻¹, while the same mode appears at 1576 cm⁻¹ for the tetra-anchored calix[4]arene because of the stiffening of the structure imposed by the multiple anchors. Corresponding bands are observed on the experimental Raman spectra of the grafted mono- and tetrapodal calix[4]arenes (Fig. 4) after reduction of the X₄N₂⁺ and X₄(N₂⁺)₄ diazonium cations at 1590 and 1563 cm⁻¹, respectively. The 27 cm⁻¹ downward shift when going from mono- to tetrapodal macrocycles matches the computed trend and is a signature of the multiple anchoring of the tetrapodal calix[4]arene on Au(111).

Interestingly, when performing the Raman spectroscopy using a lower excitation wavelength, i.e. 638 nm, there is no clear shift of the large peak found at 1580 cm⁻¹ (Fig. S18, ESI†). This can be interpreted based on the simulation of the spectra coming from the different facets. Indeed, under the given conditions, it is expected that the electric-field enhancement is no longer localized at the tips of the nanorod, but is distributed over its body which is composed of larger fractions of (100), (110), and (520) facets.^46,47,55 When considering the simulated spectra of those facets (Fig. S24, ESI†), one can see that the phenyl stretching mode appears for both mono- and tetrapodal functionalized surfaces at the same frequency. Hence, a 638 nm excitation leads to overlapping signals, while a 785 nm laser excitation leads to specific features for the gold nanorods coated from the grafting of X₄N₂⁺ and X₄(N₂⁺)₄, respectively.

Let us note that more peaks can be found in the 550–1400 cm⁻¹ region. Unfortunately, these modes cannot be clearly assigned and consist in an undistinguishable blend of CH₂ wagging, O–C bond deformation, and phenyl H out-of-plane distortions. As a consequence, we cannot rationalize the evolution of the signals in that frequency window going from the mono- to the tetrapodal system.

The combination of the adsorption energies and Raman spectra establish the formation of 4 Au–C bonds per calix[4]arene when the gold nanorod is coated from the grafting of X₄(N₂⁺)₄. Indeed, adsorption energies show the significant thermodynamical incentive for a calix[4]arene to form as many Au–C bonds as possible, while the experimentally observed Raman spectrum on the (111) facet correspond to the multipodal grafting of X₄(N₂⁺)₄. Although, we do not obtain a specific Raman signal for multiple anchoring modes on the other facets, the even stronger adsorption energies found on the (100), (110), and (520) facets, strongly suggests that a multiple anchoring is also found on these planes.

Conclusion

In summary, we describe the efficient and robust functionalization of gold nanorods using the reductive diazonium grafting of rigid calix[4]arene macrocycles bearing one or four anchoring functions. The treatment of the as-synthesized gold nanorods with NaBH₄ enables an efficient exchange of ligands from CTAB to the calix[4]arene molecules, without loss of the nanorods size/shape as demonstrated by HRTEM/UV-visible absorption spectroscopy. The grafting of the molecules is further demonstrated through Raman spectroscopy and XPS. While computational approaches depict a highly energetically favourable scenario for the multiple anchoring of the tetra-diazonium calix[4]arene, it is firmly established through DFTB-aided assignment of Raman peaks. In particular, we show that the band at 280 cm⁻¹ is indicative of the creation of Au–C bonds, while the band at 1500–1600 cm⁻¹ allows discrimination between mono and multiple anchoring points. Leveraging the easily functionalized nature of calix[4]arene macrocycles, their well-controlled orientation, and now decrypted spectroscopic signature, this work provides a blueprint for the future design of functional hybrid nanomaterials.

Data availability

The data supporting this article have been included as part of the ESI.† The starting and relaxed geometries for all systems are provided separately, together with the input files for the DFTB+ code for (i) the geometry relaxation, and (ii) the computation of Raman intensities.

Author contributions

I. J. and V. M. synthesized the calix[4]arene diazonium molecules. A. O, C. L., G. B. and V. L. synthesized the gold nanorods. A. O. performed the TEM and UV-vis absorption spectroscopic analyses. C. L. performed and analysed the XPS measurements. Y. L. and C. L. performed experimental Raman analyses. A. T. performed the computational investigation with the help of A. F. and M. K. A. T., M. K., C. L. and A. F. designed the paper, then edited by all co-authors. C. L. and M. K. have conceptualized and supervised the work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work in France was supported by Agence Nationale pour la Recherche (MARCEL project, grant number ANR-21-CE50-0034-MARCEL) and was granted access to the HPC resources of [TGCC/CINES/IDRIS] under the allocation 2022-A0130907682 made by GENCI. Raman spectra were acquired at H2P2 platform (Biosit – UAR 3480 CNRS-INSERM-University of Rennes). The authors are very grateful to A. Fautrel for his help in recording the Raman spectra. L. Rault is thanked for her assistance in TEM experiments performed on THEMIS platform (CPER-FEDER 2007–2014, UAR ScanMAT 2025, University of Rennes). The authors are grateful to J. Hamon (Institut des Matériaux de Nantes (IMN), Nantes, France) for his help in recording the XPS spectra. The authors also thank M. Escadeillas for recording Raman spectra at the platform SIR, UAR ScanMAT 2025, University of Rennes. Y. R Leroux and Q. Lenne are also acknowledged for their contribution in the synthesis/characterization of the gold nanorods.

Notes and references

1. N. Erathodiyil and J. Y. Ying, Acc. Chem. Res., 2011, 44, 925–935.
2. A. Gupta, W. Ndugire, C.-M. Hirschbiegel, L. Grigely and V. M. Rotello, Acc. Chem. Res., 2023, 56, 2151–2169.
3. S. Zhang, R. Geryak, J. Geldmeier, S. Kim and V. V. Tsukruk, Chem. Rev., 2017, 117, 12942–13038.
4. A. M. Steiner, F. Lissel, A. Fery, J. Lauth and M. Scheele, Angew. Chem., Int. Ed., 2021, 60, 1152–1175.
5. J. Wang, F. Zhang, X. Kang and S. Chen, Curr. Opin. Electrochem., 2019, 13, 40–46.
6. Q. Lenne, Y. R. Leroux and C. Lagrost, ChemElectroChem, 2020, 7, 2345–2363.
7. L. Lu, S. Zou and B. Fang, ACS Catal., 2021, 11, 6020–6058.
8. M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802.
9. M. Brust, J. Fink, D. Bethell, D. J. Schiffrin and C. Kiely, J. Chem. Soc., Chem. Commun., 1995, 1655–1656.
10. F. Mirkhalaf, J. Paprotny and D. J. Schiffrin, J. Am. Chem. Soc., 2006, 128, 7400–7401.
11. D. Bélanger and J. Pinson, Chem. Soc. Rev., 2011, 40, 3995.
12. A. A. Mohamed, Z. Salmi, S. A. Dahoumane, A. Mekki, B. Carbonnier and M. M. Chehimi, Adv. Colloid Interface Sci., 2015, 225, 16–36.
13. A. Mattiuzzi, I. Jabin, C. Mangeney, C. Roux, O. Reinaud, L. Santos, J.-F. Bergamini, P. Hapiot and C. Lagrost, Nat. Commun., 2012, 3, 1130.
14. L. Troian-Gautier, A. Mattiuzzi, O. Reinaud, C. Lagrost and I. Jabin, Org. Biomol. Chem., 2020, 18, 3624–3637.
15. L. Troian-Gautier, H. Valkenier, A. Mattiuzzi, I. Jabin, N. V. den Brande, B. V. Mele, J. Hubert, F. Reniers, G. Bruylants, C. Lagrost and Y. Leroux, Chem. Commun., 2016, 52, 10493–10496.
16. M. Retout, I. Jabin and G. Bruylants, ACS Omega, 2021, 6, 19675–19684.
17. Q. Lenne, A. Mattiuzzi, I. Jabin, L. Troian-Gautier, J. Hamon, Y. R. Leroux and C. Lagrost, ChemSusChem, 2023, 16, e202201990.
18. Q. Lenne, M. Retout, B. Gosselin, G. Bruylants, I. Jabin, J. Hamon, C. Lagrost and Y. R. Leroux, Chem. Commun., 2022, 58, 3334–3337.
19. B. Gosselin, G. Bruylants and I. Jabin, ACS Appl. Nano Mater., 2024, 7, 6169–6177.
20. M. Retout, B. Gosselin, A. Adrović, P. Blond, I. Jabin and G. Bruylants, Nanoscale, 2023, 15, 11981–11989.
21. B. Baisch, D. Raffa, U. Jung, O. M. Magnussen, C. Nicolas, J. Lacour, J. Kubitschke and R. Herges, J. Am. Chem. Soc., 2009, 131, 442–443.
22. M. Valášek, M. Lindner and M. Mayor, Beilstein J. Nanotechnol., 2016, 7, 374–405.
23. Z.-Q. Li, J.-H. Tang and Y.-W. Zhong, Chem.–Asian J., 2019, 14, 3119–3126.
24. F. S. Benneckendorf, V. Rohnacher, E. Sauter, S. Hillebrandt, M. Münch, C. Wang, S. Casalini, K. Ihrig, S. Beck, D. Jänsch, J. Freudenberg, W. Jaegermann, P. Samorì, A. Pucci, U. H. F. Bunz, M. Zharnikov and K. Müllen, ACS Appl. Mater. Interfaces, 2020, 12, 6565–6572.
25. S. J. Nemat, D. V. den Eynden, L. Deblock, M. Heilmann, J. M. Köster, M. Parvizian, K. Tiefenbacher and J. D. Roo, Chem. Commun., 2021, 57, 4694–4697.
26. M. Valášek and M. Mayor, Chem.–Eur. J., 2017, 23, 13538–13548.
27. D. M. Shewchuk and M. T. McDermott, Langmuir, 2009, 25, 4556–4563.
28. E. D. L. Llave, A. Ricci, E. J. Calvo and D. A. Scherlis, J. Phys. Chem. C, 2008, 112, 17611–17617.
29. Q. Tang and D. E. Jiang, Chem. Mater., 2017, 29, 6908–6915.
30. L. Laurentius, S. R. Stoyanov, S. Gusarov, A. Kovalenko, R. Du, G. P. Lopinski and M. T. McDermott, ACS Nano, 2011, 5, 4219–4227.
31. R. Ahmad, L. Boubekeur-Lecaque, M. Nguyen, S. Lau-Truong, A. Lamouri, P. Decorse, A. Galtayries, J. Pinson, N. Felidj and C. Mangeney, J. Phys. Chem. C, 2014, 118, 19098–19105.
32. A. Berisha, C. Combellas, F. Kanoufi, J. Médard, P. Decorse, C. Mangeney, I. Kherbouche, M. Seydou, F. Maurel and J. Pinson, Langmuir, 2018, 34, 11264–11271.
33. R. L. Thimes, A. V. Santos, R. Chen, G. Kaur, L. Jensen, D. M. Jenkins and J. P. Camden, J. Phys. Chem. Lett., 2023, 14, 4219–4224.
34. M. Elstner, J. Phys. Chem. A, 2007, 111, 5614–5621.
35. S. Pal, D. J. Trivedi, A. V. Akimov, B. Aradi, T. Frauenheim and O. V. Prezhdo, J. Chem. Theory Comput., 2016, 12, 1436–1448.
36. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101.
37. L. F. Oliveira, N. Tarrat, J. Cuny, J. Morillo, D. Lemoine, F. Spiegelman and M. Rapacioli, J. Phys. Chem. A, 2016, 120, 8469–8483.
38. K. Maghrebi, I. Chantrenne, S. Messaoudi, T. Frauenheim, A. Fihey and C. R. Lien-Medrano, J. Phys. Chem. C, 2023, 127, 19675–19686.
39. K. H. Au-Yeung, T. Kühne, O. Aiboudi, S. Sarkar, O. Guskova, D. A. Ryndyk, T. Heine, F. Lissel and F. Moresco, Nanoscale Adv., 2022, 4, 4351–4357.
40. X. Wu, T. van der Heide, S. Wen, T. Frauenheim, S. Tretiak, C. Yam and Y. Zhang, Chem. Sci., 2023, 14, 4714–4723.
41. A. Fihey, C. Hettich, J. Touzeau, F. Maurel, A. Perrier, C. Köhler, B. Aradi and T. Frauenheim, J. Comput. Chem., 2015, 36, 2075–2087.
42. H. A. Witek, K. Morokuma and A. Stradomska, J. Chem. Phys., 2004, 121, 5171–5178.
43. B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962.
44. J. He, S. Unser, I. Bruzas, R. Cary, Z. Shi, R. Mehra, K. Aron and L. Sagle, Colloids Surf., B, 2018, 163, 140–145.
45. S. M. Ansar, F. S. Ameer, W. Hu, S. Zou, C. U. Pittman and D. Zhang, Nano Lett., 2013, 13, 1226–1229.
46. E. Carbó-Argibay, B. Rodríguez-González, S. Gómez-Graña, A. Guerrero-Martínez, I. Pastoriza-Santos, J. Pérez-Juste and L. M. Liz-Marzán, Angew. Chem., Int. Ed., 2010, 49, 9397–9400.
47. K. Park, L. F. Drummy, R. C. Wadams, H. Koerner, D. Nepal, L. Fabris and R. A. Vaia, Chem. Mater., 2013, 25, 555–563.
48. G. Socrates, Infrared and Raman Characteristic Group Frequencies: Tables and Charts, Wiley, Hoboken, NJ, USA, 3rd edn, 2004.
49. Y. Luo, Y. Xiao, D. Onidas, L. Iannazzo, M. Ethève-Quelquejeu, A. Lamouri, N. Félidj, S. Mahouche-Chergui, T. Brulé, N. Gagey-Eilstein, F. Gazeau and C. Mangeney, Chem. Commun., 2020, 56, 6822–6825.
50. S. Betelu, I. Tijunelyte, L. Boubekeur-Lecaque, I. Ignatiadis, J. Ibrahim, S. Gaboreau, C. Berho, T. Toury, E. Guenin, N. Lidgi-Guigui, N. Félidj, E. Rinnert and M. L. D. L. Chapelle, J. Phys. Chem. C, 2016, 120, 18158–18166.
51. W. Hong, H. Li, S.-X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431.
52. L. Guo, L. Ma, Y. Zhang, X. Cheng, Y. Xu, J. Wang, E. Wang and Z. Peng, Langmuir, 2016, 32, 11514–11519.
53. C. F. Shaw and R. S. Tobias, Inorg. Chem., 1973, 12, 965–978.
54. S. Bruni, A. L. Bandini, F. Cariati and F. Speroni, Inorg. Chim. Acta, 1993, 203, 127–128.
55. M. Kobylko, P.-E. Coulon, A. Slablab, A. Fafin, J. Cardin, C. Dufour, A. Losquin, M. Kociak, I. Monnet, D. Mailly, X. Lafosse, C. Ulysse, E. Garcia-Caurel and G. Rizza, Phys. Rev. Appl., 2018, 9, 064038.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis details; Experimental setups; Computational details; Additional UV-visible spectroscopy, XPS, Raman spectroscopy, and Computational results. See DOI: https://doi.org/10.1039/d4sc02355b

---